Abstract
Objective:
In radiotherapy treatments, it is crucial to monitor the performance of linear accelerator (linac) components, including gantry, collimation system and electronic portal imaging device (EPID) during arc deliveries. In this study, a simple EPID-based measurement method is suggested in conjunction with an algorithm to investigate the stability of these systems at various gantry angles with the aim of evaluating machine-related errors in treatments.
Methods:
The EPID sag, gantry sag, changes in source-to-detector distance (SDD), EPID and collimator skewness, EPID tilt and the sag in leaf bank assembly owing to linac rotation were separately investigated by acquisition of 37 EPID images of a simple phantom with 5 ball bearings at various gantry angles. A fast and robust software package was developed for automated analysis of the image data. Nine Elekta AB (Stockholm, Sweden) linacs of different models and number of years in service were investigated.
Results:
The average EPID sag was within 2 mm for all tested linacs. Some machines showed >1-mm gantry sag. Changes in the SDD values were within 1.3 cm. EPID skewness and tilt values were <1° in all machines. The maximum sag in multileaf collimator leaf bank assemblies was around 1 mm. A meaningful correlation was found between the age of the linacs and their mechanical performance.
Conclusions and Advances in knowledge:
The method and software developed in this study provide a simple tool for effective investigation of the behaviour of Elekta linac components with gantry rotation. Such a comprehensive study has been performed for the first time on Elekta machines.
Rotation of the treatment beam around the patient is one of the common features in radiotherapy. However, it is known that the gravity effect on several tons of radiation shielding, beam generation and shaping systems, and other components in the gantry head introduces deviations to the gantry rotation pattern from an ideal circle.1–5 Gravity can also induce sagging of the beam collimation system.3,6,7 Rotation of the gantry during treatment delivery can lead to additional multileaf collimator (MLC) errors (systematic shifts) owing to the displacement of the leaf bank assembly.7–9 Moreover, linear accelerator (linac) rotation can affect gantry-mounted accessories such as the electronic portal imaging device (EPID), since the EPID-supporting arm is not mechanically perfect and rigidly attached. With the growing application of EPIDs in pre- and post-treatment dosimetry verification,10–15 real-time dosimetry verification16,17 and real-time tumour tracking for intrafraction motion management in modern radiotherapy,18–20 it is essential to characterize and account for the mechanical system imperfections of linacs.
There have been several studies in the literature on investigation of the EPID/gantry/collimator excursions during arc deliveries, which have been discussed in previous articles.4,7,21 Our former studies were focused on using EPID-based methods for evaluation of the performance of Varian linacs (Varian® Medical Systems, Palo Alto, CA). In this work, investigation is extended to the behaviour of components of Elekta linacs (Elekta AB, Stockholm, Sweden) at various gantry angles with some additional details. The aim of this study is to use a simple phantom design and collect the required data for investigation of: (a) gantry sag; (b) EPID sag, skewness and tilt; and (c) MLC bank assembly sag in Elekta machines at different gantry angles. Fast, accurate methods and algorithms are developed for automated data analysis and quantification of the system characteristics. Finally, based on the results acquired for several linacs, a generalized pattern (map) is derived for each of the above components with a sufficiently low level of uncertainty. Parameterizations of this map enable generic corrections to be applied during data acquisition and processing, which could be applicable to all Elekta EPIDs used for dosimetry or patient positioning.
METHODS AND MATERIALS
In this section, measurement conditions are described followed by the techniques and analysis methods used in each step of the work.
Measurements
Measurements were carried out on eight Elekta linacs (Elekta AB) including four Synergy®, two Versa HDTM and two SL 20 models, all equipped with iViewGTTM Perkin Elmer a-Si EPIDs (model: XRD 1640 ×N19 ES, scintillator type: DRZ PI200 and copper filter). The active area of detector arrays was 41 × 41 cm2 with 1024 × 1024 pixel resolution. Elekta linacs (Figure A in the Supplementary material) have a drum-shaped base structure, and the gantry rotates on a single or double drive assembly. Double drive systems are an upgraded version of the single drive assemblies and use four wheels to drive the gantry instead of two, which provides better stability of the system. The EPID panel is mounted on a movable supporting arm that extends out of the drum structure. Specifications of the linacs used in this study are given in Table A in the Supplementary material. Linac 7 is the same as Linac 1 following the upgrade of its MLC to a new model. The modifications took place during this project, and as a result, the number of leaves was increased from 80 to 160, which caused an additional 70-kg weight imposed to the gantry head.
In this study, five tungsten carbide ball bearings with 4.8-mm diameter were used as phantom. Four of the ball bearings were embedded in a 2-mm thick solid water slab and were fixed to the gantry head using the screw holes. The fifth was positioned at nominal linac isocentre based on room lasers. It was fixed to the treatment couch top with a plastic rod while the treatment couch and collimator were both set at zero angle22 (Figure A in the Supplementary material).
Both 6- and 18-MV beams were used for irradiations with 24.0 × 24.0-cm2 MLC-defined fields at zero collimator angle. EPID images were exported in digital imaging and communications in medicine (DICOM) format with 10-MU irradiations per image at 10° intervals, providing 37 images for an entire gantry rotation. Each set of measurements were performed three times to yield the reproducibility of results. The test was performed in both clockwise (CW) and counter-CW (CCW) directions, and at 90° collimator angle to check any possible effects. The nominal source-to-detector distance (SDD) was 160 cm. The data acquired at zero gantry angle were taken as reference to determine relative deviations at other angles, since reference machine data acquisition and calibrations are performed at zero gantry angle. All results were scaled back to the isocentre plane, except for the changes in SDD during arc. Data analysis and algorithm development were performed using MATLAB® programming language and software (MathWorks®, Natick, MA).
Analysis methods
A sample snapshot is shown in Figure B in the Supplementary material. In this section, details of the analysis method for characterization of each component are explained separately. A single set of 37 images acquired with a whole gantry rotation provides data for all of the components under investigation, and the software needs to be run only once to load all images and output the entire set of results. The algorithm for determination of the centre of each ball bearing and the field edges has been explained elsewhere.7,21,23
The elapsed time for the procedure is about 27 min, including approximately 6 min for the set-up, approximately 20 min for acquiring images and exporting them, and approximately 1 min for the processing of data using a computer with 4.00 GB random access memory and 2.60 GHz central processing unit.
Electronic portal imaging device sag
To find the EPID sag, the centre of the ball bearing (e) positioned at the nominal isocentre is determined in each image and is compared with its position in the image acquired at zero gantry angle. Calculations are based on Equations (1) and (2).
| (1) |
| (2) |
where and are the EPID sag in the x (cross-plane) and y (in-plane) directions at θ gantry angle; and are the positions of the ball bearing (e) in the x and y directions at θ gantry angle. (A cos θ) and (B sin θ) are applied to correct for displacements of the ball bearing (e) owing to laser misalignments. More details on these corrections can be found in another publication.21 The EPID sag values at zero gantry angle are denoted as and .
Gantry sag
To measure the gantry sag values, positions of the four ball bearings fixed to the gantry head (a, b, c and d) are averaged in both directions (x and y) at each gantry angle. These values represent a combination of the EPID sag and the gantry wobble. To determine the net gantry sag, the values for EPID sag are subtracted from the EPID + gantry sag [Equations (3) and (4)].
| (3) |
| (4) |
where and are the averages of the x and y positions of the four ball bearings.
Changes in source-to-detector distance
The change in the SDD as a result of gantry rotation (Figure A in the Supplementary material) is calculated using Equation (5). This effect is a result of both EPID sag and gantry wobble along the radiation beam direction.
| (5) |
where is the SDD at zero gantry angle as read out from the DICOM header; and are the averaged positions of ball bearings (a) and (c), and (b) and (d), respectively, at the gantry angle θ.
Electronic portal imaging device and collimator skewness
A combination of EPID and collimator (gantry head) skewness is determined at every gantry angle from Equation (6). The method is based on a geometrical calculation that uses the position of one ball bearing pair from the four attached to the gantry head [(a) and (b), or (c) and (d)] at zero and θ gantry angles.
| (6) |
where is the combined skewness of the EPID and collimator in degrees. It is worthwhile to mention that skewness (yaw) is defined as the rotation in the EPID/collimator plane. The combined skewness of the EPID and collimator has been investigated, since the software cannot differentiate between the causes of rotations. The positive direction is the CW rotation.
Electronic portal imaging device tilt
The EPID tilt in the in-plane (pitch) and in the cross-plane (roll) is determined using Equations (7) and (8), respectively. To find these values, only the four ball bearings fixed to the gantry head are considered:
| (7) |
| (8) |
These equations are based on simple geometric relations using the distances between the ball bearing pairs (a and b), and (c and d) at various gantry angles.
The indices G, T, L and R denote gun, target, left and right directions. The above values are compared with the tilt at zero gantry angle that was selected as the reference.
Sag in the leaf bank assembly
The sag in the MLC bank assembly corresponding to each gantry angle in the G, T, L and R directions in the in-plane and cross-plane directions is quantified using Equations (9)–(12).
| (9) |
| (10) |
| (11) |
| (12) |
where etc. represent the positions of the four field edges at each gantry angle. and are based on the averaged leaf positions in each bank.
RESULTS
Electronic portal imaging device sag
Results of EPID sag measurements in all linacs are given in Figure 1 and Table B in the Supplementary material. The range of variations is considered as the difference between maximum and minimum values in the data for each linac. The largest range of variations amongst all linacs is given in Table B in the Supplementary material for each direction.
Figure 1.
Comparison of electronic portal imaging device (EPID) sag measurement results for the tested Elekta linear accelerators (linacs) (Elekta AB, Stockholm, Sweden) in (a) cross-plane and (b) in-plane directions. The solid lines show the fitted curves through the average of data points at each angle.
The largest root mean square deviation (RMSD) across the compared sets of data in all linacs are also listed in Table B in the Supplementary material (for instance, the RMSD between the CW and CCW gantry rotations is calculated for each machine and the largest RMSD amongst all linacs is reported).
The values of EPID sag were <0.5 mm in the cross-plane direction in all linacs, while larger deviations were observed in the in-plane direction. However, they were all within 2 mm, which is the accepted criterion for non-stereotactic linacs, based on the American Association of Physicists in Medicine Task Group 142 report.24
Gantry sag
Measurement results of gantry sag at various gantry angles for all linacs are given in Figure 2 and Table C in the Supplementary material.
Figure 2.
Comparison of gantry sag measurement results for the tested Elekta linear accelerators (linacs) (Elekta AB, Stockholm, Sweden) in: (a) cross-plane and (b) in-plane directions. The solid lines show the fitted curves through the average of data points at each angle. EPID, electronic portal imaging device.
As shown in Figure 2, some linacs moved further than the 1-mm acceptance criterion for gantry sag.24 The measured gantry sag in Linacs 1 and 7 were compared to investigate the effect of recent system upgrades. Only minor differences were observed in the sag patterns, since the new MLC system was only 70 kg heavier, and weight balance adjustments were performed on the gantry as part of the procedure. It must be noted that the linac control system and gantry look-up tables were upgraded too.
Changes in source-to-detector distance
Results of the measured changes in the SDD in the beam direction are shown in Figure 3 and listed in Table D in the Supplementary material.
Figure 3.
Comparison of the results of changes in the source-to-detector distance (SDD) for the tested Elekta linear accelerators (linacs) (Elekta AB, Stockholm, Sweden). The solid line shows the fitted curve through the average of data points at each gantry angle.
Figure 3 shows that the change in SDD of all tested linacs was greater than the 5-mm accepted criterion.24 The largest change in the SDD was 12.9 mm, which results in 0.81% image magnification and corresponds to 0.65% change in dose when the EPID is used for absolute dosimetry.
Electronic portal imaging device and collimator skewness
Results of measurements of the EPID and collimator skewness for all linacs are compared in Figure 4 and Table E in the Supplementary material.
Figure 4.
Comparison of the measured skewness in electronic portal imaging device (EPID) and collimator for the tested Elekta linear accelerators (linacs) (Elekta AB, Stockholm, Sweden). The solid line shows the fitted curve through the average of data points at each gantry angle.
The patterns of EPID and collimator skewness were quite similar, and their values were <0.3° for all tested linacs.
Electronic portal imaging device tilt
Results of the EPID tilt measurements for all linacs are given in Figure 5 and Table F in the Supplementary material.
Figure 5.
Comparison of electronic portal imaging device (EPID) tilt measurement results for the tested Elekta linear accelerators (linacs) (Elekta AB, Stockholm, Sweden) in: (a) cross-plane and (b) in-plane directions. The solid lines show the fitted curves through the average of data points at each angle.
The detected EPID tilt values were negligible for all tested linacs. The scale of graphs in Figure 5 indicates the precision of the algorithm.
Sag in the leaf bank assembly
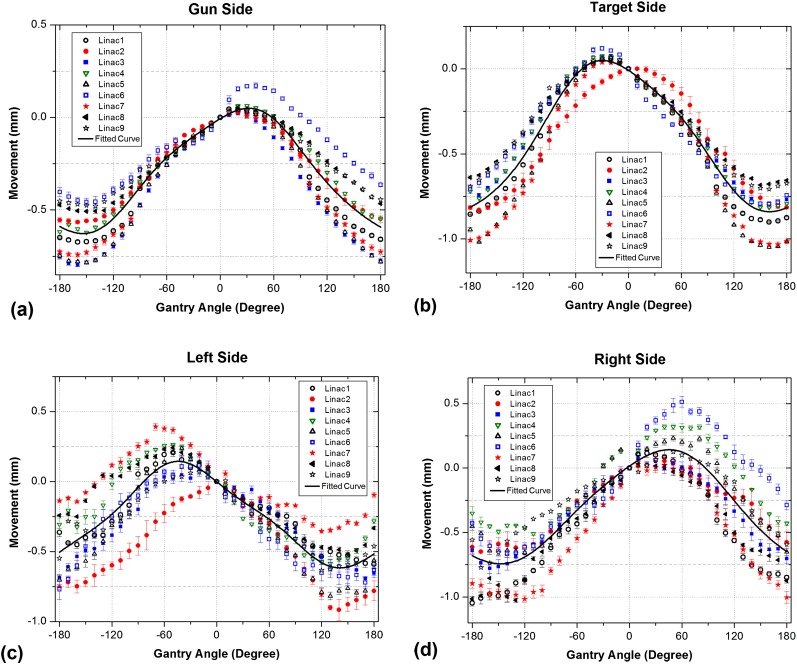
Figure 6 and Table G in the Supplementary material show the measured sag patterns in the leaf bank assembly of the tested linacs in four directions.
Figure 6.
Comparison of the measured sag values in leaf bank assemblies of the tested Elekta linear accelerators (linacs) (Elekta AB, Stockholm, Sweden) for: (a) gun side, (b) target side, (c) left side and (d) right side. The solid lines show the fitted curves through the average of data points at each angle.
The range of sag in the leaf bank assemblies, which produces systematic error, was around 1 mm in all directions over all tested linacs. Although the acceptance limit for deviations in MLC positioning is within 1 mm,24 it has been shown that some complex clinical techniques may be sensitive to smaller variations in MLC leaf positioning.9
Age dependence
The possibility of a relationship between the age of a linac and its performance was also investigated using Pearson's correlation coefficient between two variables, which is defined in Equation (13):
| (13) |
where x is the age of the linac, and y is the number of largest deviations found in the results for each linac. Values of close to one indicate a strong positive correlation, which is equivalent to a high degree of linear dependence between the two variables. The calculated for the tests performed in this study was 0.9318, which means that the weakest performance in most tests correspond to older machines (Figure 7), as expected.
Figure 7.
Illustration of the number of times a linear accelerator (linac) had a maximum deviation across the sets of results and the age of the linac.
DISCUSSION
A comprehensive study was performed on several Elekta linacs to investigate the mechanical stability of their gantries, MLC leaf bank assemblies and MV imagers (EPIDs) at different gantry angles. This could provide a measure of the stability of these systems during delivery of modern radiotherapy treatments in arcs. All aforementioned linac components are affected by gravitational force during gantry rotation owing to their structural imperfections. Information on the impact of rotation on these systems will assist in delivery of more accurate treatments by improving pre-treatment verification of complex plans, real-time tumour tracking, real-time dosimetry and linac quality assurance processes.
In this study, a simple measurement method was proposed to simultaneously quantify the gantry, leaf bank and EPID movements at a number of gantry angles. A simple phantom was designed with just 5 metallic markers in the beam, and a large amount of information on the system characteristics were extracted from 37 EPID images. The analyses were performed using in-house developed software that proved to be accurate, robust and fast. The set of EPID images taken at different gantry angles were analysed in one execution of the software, and the required geometric parameters were automatically produced.
The EPID sag measurement results over a range of machines showed that, on average, the EPIDs moved by 0.4 mm in the cross-plane and by 1.6 mm in the in-plane directions. The difference between deviations in the two directions was attributed to the structure of the EPID support system with the middle arm providing more freedom of movement along the in-plane direction. These values were comparable with the previous reports on Elekta linacs.12,25 The EPID sag pattern in the cross-plane showed a leap at around zero gantry angle similar to the one previously observed in Varian linacs.21,26 This was attributed to the complexity of the mechanical structure of the system that has many junctions and several sliding or bolted mechanical parts. If an Elekta EPID shows large values of sag, it would be advisable to check the detector arm fixings, lubricate its locking mechanism and lateral drive assembly, inspect the longitudinal drive belts and check the detector panel movements.
The average range of gantry sag values was 1.2 mm in the in-plane and 0.6 mm in the cross-plane directions (Table C in the Supplementary material). These values were similar to Varian machines,4,21 but the sag pattern in the cross-plane direction was different. In Varian linacs, a sudden jump was observed around the zero gantry angle, whereas the pattern was quite smooth for Elekta machines. This was attributed to substantial differences in the gantry drive assemblies.
If large gantry sag values are detected in Elekta linacs, it may indicate that the fixing clamps of the gantry base or the drive gearbox have become loose. It may be necessary to check the drive belt for breakage and examine all subassemblies in the gantry.
The change in SDD as a result of gantry rotation was 11.2 mm on average. The SDD change in Elekta EPIDs has previously been reported to be around 9.2 mm27 by two independent methods. These values are comparable with the report on Varian machines equipped with R-type arms, which have shown changes up to 13 mm.10,28
The values found for EPID and collimator skewness, and EPID tilt were reported for the first time and were found to be <1°. It should be mentioned that the reported tilt is attributed to EPID only, since no tilt is expected from the gantry and the ball bearings are fixed firmly to the head and any displacement is assumed negligible.
In Elekta linacs, the leaf bank assembly and the optical leaf tracking system are mounted on a drive leaf guide frame. This frame can move under the influence of gravity; therefore, although displacements of each individual leaf can be accurately detected, the optical tracking system is unable to recognize the sag in the MLC leaf bank assembly.
The average sag in the leaf bank assemblies of the tested Elekta linacs were around 1 mm in all directions. Much smaller sag values were found for Varian linacs, which were reported as: 0.15 mm on the gun side, 0.05 mm on the target side, 0.52 mm on the left side and 0.55 mm on the right side.7 This could be partly owing to the magnification of leaf bank movements, which is larger for Elekta linacs as a result of their shorter distance from the source.29
According to Tables B–G in the Supplementary material, changing the direction of gantry rotation (CW or CCW) did not affect the results, and the largest detected differences (0.4 mm) were the size of a pixel in the imager in all experiments over all machines. All experiments were highly reproducible, and the largest standard deviation between three sets of similar set-ups (i.e. worst reproducibility) was 0.5 mm, which came from an 18-year-old linac. The tests with 6- and 18-MV were performed with the aim of checking for the effect of source change on the position of ball bearing shadows in the images. The difference was negligible as expected.
The effect of collimator rotation by 90° on the weight balance in linac head was investigated at different gantry angles. It was found that the impact was quite small and was most pronounced in the sag of MLC bank assembly (approximately 0.3 mm) owing to the change in the components of gravitational force on the leaf banks.
The behaviour of the Elekta linac components investigated in this study generally followed a similar pattern (Figure C in the Supplementary meterial). The only exception was gantry sag in the cross-plane direction that is most likely to be caused by differences in the level of tension on the drive belts of different machines. The general transformation functions generated for each component provides information on these patterns by averaging the data over all linacs (Table H in the Supplementary material).
Based on the results of this study and using Pearson's correlation coefficient, it was found that the mechanical performance of older linacs was weaker than that of new machines. This confirmed a general assumption using a scientific approach.
CONCLUSION
With the emergence of complex technology in modern radiotherapy, reliable methods are required to ensure accurate delivery of treatments. In this work, a large amount of information on the characteristics of Elekta linac components at different gantry angles was provided using EPID images acquired with five metallic markers in the beam. A fast and accurate software package was developed for the analysis of images, and several linacs at different number of years in service were investigated and compared with the reports in the literature for Elekta and Varian linacs.
Contributor Information
P Rowshanfarzad, Email: pejman.rowshanfarzad@uwa.edu.au.
H L Riis, Email: Hans.Lynggaard.Riis@rsyd.dk.
S J Zimmermann, Email: sune.j.zimmermann@rsyd.dk.
M A Ebert, Email: Martin.Ebert@health.wa.gov.au.
REFERENCES
- 1.Winkler P, Bergmann H, Stuecklschweiger G, Guss H. Introducing a system for automated control of rotation axes, collimator and laser adjustment for a medical linear accelerator. Phys Med Biol 2003; 48: 1123–32. doi: 10.1088/0031-9155/48/9/303 [DOI] [PubMed] [Google Scholar]
- 2.Rosca F, Lorenz F, Hacker FL, Chin LM, Ramakrishna N, Zygmanski P. An MLC-based linac QA procedure for the characterization of radiation isocenter and room lasers' position. Med Phys 2006; 33: 1780–7. doi: 10.1118/1.2198171 [DOI] [PubMed] [Google Scholar]
- 3.Du W, Gao S. Measuring the wobble of radiation field centers during gantry rotation and collimator movement on a linear accelerator. Med Phys 2011; 38: 4575–78. doi: 10.1118/1.3609098 [DOI] [PubMed] [Google Scholar]
- 4.Du W, Gao S, Wang X, Kudchadker RJ. Quantifying the gantry sag on linear accelerators and introducing an MLC-based compensation strategy. Med Phys 2012; 39: 2156–62. doi: 10.1118/1.3697528 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Riis HL, Zimmermann SJ, Hjelm-Hansen M. Gantry and isocenter displacements of a linear accelerator caused by an add-on micromultileaf collimator. Med Phys 2013; 40: 031707. doi: 10.1118/1.4789921 [DOI] [PubMed] [Google Scholar]
- 6.Mubata CD, Childs P, Bidmead AM. A quality assurance procedure for the Varian multi-leaf collimator. Phys Med Biol 1997; 42: 423–31. doi: 10.1088/0031-9155/42/2/014 [DOI] [PubMed] [Google Scholar]
- 7.Rowshanfarzad P, Sabet M, O’Connor DJ, Greer PB. Investigation of the sag in linac secondary collimator and MLC carriage during arc deliveries. Phys Med Biol 2012; 57: N209–24. doi: 10.1088/0031-9155/57/12/N209 [DOI] [PubMed] [Google Scholar]
- 8.Agnew A, Agnew CE, Grattan MW, Hounsell AR, McGarry CK. Monitoring daily MLC positional errors using trajectory log files and EPID measurements for IMRT and VMAT deliveries. Phys Med Biol 2014; 59: N49–63. doi: 10.1088/0031-9155/59/9/N49 [DOI] [PubMed] [Google Scholar]
- 9.Rangel A, Dunscombe P. Tolerances on MLC leaf position accuracy for IMRT delivery with a dynamic MLC. Med Phys 2009; 36: 3304–9. doi: 10.1118/1.3134244 [DOI] [PubMed] [Google Scholar]
- 10.Ansbacher W. Three-dimensional portal image-based dose reconstruction in a virtual phantom for rapid evaluation of IMRT plans. Med Phys 2006; 33: 3369–82. doi: 10.1118/1.2241997 [DOI] [PubMed] [Google Scholar]
- 11.McCurdy BM, Greer PB. Dosimetric properties of an amorphous-silicon EPID used in continuous acquisition mode for application to dynamic and arc IMRT. Med Phys 2009; 36: 3028–39. doi: 10.1118/1.3148822 [DOI] [PubMed] [Google Scholar]
- 12.Mans A, Remeijer P, Olaciregui-Ruiz I, Wendling M, Sonke JJ, Mijnheer B, et al. 3D dosimetric verification of volumetric-modulated arc therapy by portal dosimetry. Radiother Oncol 2010; 94: 181–7. doi: 10.1016/j.radonc.2009.12.020 [DOI] [PubMed] [Google Scholar]
- 13.Grattan MW, McGarry CK. Mechanical characterization of the varian Exact-arm and R-arm support systems for eight aS500 electronic portal imaging devices. Med Phys 2010; 37: 1707–13. doi: 10.1118/1.3368604 [DOI] [PubMed] [Google Scholar]
- 14.Bailey DW, Kumaraswamy L, Bakhtiari M, Malhotra HK, Podgorsak MB. EPID dosimetry for pretreatment quality assurance with two commercial systems. J Appl Clin Med Phys 2012; 13: 3736. doi: 10.1120/jacmp.v13i4.3736 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Siji C, Musthafa M, Ganapathi Raman R, Haneefa A, Hridya VT. Pretreatment patient specific quality assurance and gamma index variation study in gantry dependent EPID positions for IMRT prostate treatments. J Radiother 2014; 2014. doi: 10.1155/2014/325057 [DOI] [Google Scholar]
- 16.Fuangrod T, Woodruff H, van Uytven E, McCurdy B, Kuncic Z, O'Connor DJ, et al. A system for EPID-based real-time treatment delivery verification during dynamic IMRT treatment. Med Phys 2013; 40: 091907. doi: 10.1118/1.4817484 [DOI] [PubMed] [Google Scholar]
- 17.Woodruff HC, Fuangrod T, Rowshanfarzad P, McCurdy BM, Greer PB. Gantry-angle resolved VMAT pretreatment verification using EPID image prediction. Med Phys 2013; 40: 081715. doi: 10.1118/1.4816384 [DOI] [PubMed] [Google Scholar]
- 18.Liu W, Wiersma RD, Mao W, Luxton G, Xing L. Real-time 3D internal marker tracking during arc radiotherapy by the use of combined MV–kV imaging. Phys Med Biol 2008; 53: 7197–213. doi: 10.1088/0031-9155/53/24/013 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Han-Oh S, Yi BY, Lerma F, Berman BL, Gui M, Yu C. Verification of MLC based real-time tumor tracking using an electronic portal imaging device. Med Phys 2010; 37: 2435–40. doi: 10.1118/1.3425789 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Ng JA, Booth JT, Poulsen PR, Fledelius W, Worm ES, Eade T, et al. Kilovoltage intrafraction monitoring for prostate intensity modulated arc therapy: first clinical results. Int J Radiat Oncol Biol Phys 2012; 84: e655–61. doi: 10.1016/j.ijrobp.2012.07.2367 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Rowshanfarzad P, Sabet M, O’Connor DJ, McCowan PM, McCurdy BM, Greer PB. Detection and correction for EPID and gantry sag during arc delivery using cine EPID imaging. Med Phys 2012; 39: 623–35. doi: 10.1118/1.3673958 [DOI] [PubMed] [Google Scholar]
- 22.Rowshanfarzad P, McGarry CK, Barnes MP, Sabet M, Ebert MA. An EPID-based method for comprehensive verification of gantry, EPID and the MLC carriage positional accuracy in Varian linacs during arc treatments, Radiat Oncol 2014; 9: 249. doi: 10.1186/s13014-014-0249-8 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Rowshanfarzad P, Sabet M, O’Connor DJ, Greer PB. Verification of the linac isocentre for stereotactic radiosurgery using cine-EPID imaging and arc delivery. Med Phys 2011; 38: 3963–70. doi: 10.1118/1.3597836 [DOI] [PubMed] [Google Scholar]
- 24.Klein EE, Hanley J, Bayouth J, Yin FF, Simon W, Dresser S, et al. ; Task Group 142, American Association of Physicists in Medicine. Task Group 142 report: quality assurance of medical accelerators. Med Phys 2009; 36: 4197–212. doi: 10.1118/1.3190392 [DOI] [PubMed] [Google Scholar]
- 25.Jin GH, Zhu JH, Chen LX, Deng XW, Huang BT, Yuan K, Liu XW. Gantry angle-dependent correction of dose detection error due to panel position displacement in IMRT dose verification using EPIDs. Phys Med 2014; 30: 209–14. doi: 10.1016/j.ejmp.2013.05.042 [DOI] [PubMed] [Google Scholar]
- 26.Bakhtiari M, Kumaraswamy L, Bailey DW, de Boer S, Malhotra HK, Podgorsak MB. Using an EPID for patient-specific VMAT quality assurance. Med Phys 2011; 38: 1366–73. doi: 10.1118/1.3552925 [DOI] [PubMed] [Google Scholar]
- 27.Clarke MF, Budgell GJ. Use of an amorphous silicon EPID for measuring MLC calibration at varying gantry angle. Phys Med Biol 2008; 53: 473–85. doi: 10.1088/0031-9155/53/2/013 [DOI] [PubMed] [Google Scholar]
- 28.Chin PW, Lewis DG, Spezi E. Correction for dose-response variations in a scanning liquid ion chamber EPID as a function of linac gantry angle. Phys Med Biol 2004; 49: N93–103. doi: 10.1088/0031-9155/49/8/n01 [DOI] [PubMed] [Google Scholar]
- 29.Huq MS, Das IJ, Steinberg T, Galvin JM. A dosimetric comparison of various multileaf collimators. Phys Med Biol 2002; 47: N159–70. doi: 10.1088/0031-9155/47/12/401 [DOI] [PubMed] [Google Scholar]