Intensity modulated proton therapy

Abstract

Intensity modulated proton therapy (IMPT) implies the electromagnetic spatial control of well-circumscribed “pencil beams” of protons of variable energy and intensity. Proton pencil beams take advantage of the charged-particle Bragg peak—the characteristic peak of dose at the end of range—combined with the modulation of pencil beam variables to create target-local modulations in dose that achieves the dose objectives. IMPT improves on X-ray intensity modulated beams (intensity modulated radiotherapy or volumetric modulated arc therapy) with dose modulation along the beam axis as well as lateral, in-field, dose modulation. The clinical practice of IMPT further improves the healthy tissue vs target dose differential in comparison with X-rays and thus allows increased target dose with dose reduction elsewhere. In addition, heavy-charged-particle beams allow for the modulation of biological effects, which is of active interest in combination with dose “painting” within a target. The clinical utilization of IMPT is actively pursued but technical, physical and clinical questions remain. Technical questions pertain to control processes for manipulating pencil beams from the creation of the proton beam to delivery within the patient within the accuracy requirement. Physical questions pertain to the interplay between the proton penetration and variations between planned and actual patient anatomical representation and the intrinsic uncertainty in tissue stopping powers (the measure of energy loss per unit distance). Clinical questions remain concerning the impact and management of the technical and physical questions within the context of the daily treatment delivery, the clinical benefit of IMPT and the biological response differential compared with X-rays against which clinical benefit will be judged. It is expected that IMPT will replace other modes of proton field delivery. Proton radiotherapy, since its first practice 50 years ago, always required the highest level of accuracy and pioneered volumetric treatment planning and imaging at a level of quality now standard in X-ray therapy. IMPT requires not only the highest precision tools but also the highest level of system integration of the services required to deliver high-precision radiotherapy.

The practice of proton radiotherapy covers 50 years since the first proton patient at the Berkeley Lawrence Livermore Laboratory (Berkeley, CA). In that period, a few post-research proton accelerators have been transformed into semi-clinical facilities and commenced treatments. One such facility at the Harvard Cyclotron Laboratory (Cambridge, MA) had a 160 MeV accelerator well suited for the treatment of cranial neoplasms¹ in parallel with similar practice in Sweden,² eyes³ and large field treatments.⁴ These sites were managed in three semi-independent clinical programmes that persist today at the F H Burr Proton Therapy Center at the Massachusetts General Hospital in Boston.

The large field programme required the development of proton field scattering and energy modulation techniques to achieve uniform fields and spread-out Bragg peak modulated (SOBP) fields of constant penetration range and modulation. The large field programme was only possible after the introduction of CT to model these fields, with apertures and range compensators to control the lateral extent and penetration around the three dimensional (3D) target volume extent as identified on CT.^5,6 The fields were created by mechanical means, which allowed their early clinical use in the absence of electronic controls.

The practice of SOBP proton radiotherapy required all the quality management features of modern radiotherapy: volumetric treatment planning, accurate immobilization and verification and on-treatment imaging. The practice of SOBP proton radiotherapy established the axiom of radiotherapy: accuracy improves healthy tissue dose avoidance and target coverage and higher target dose achieves cure. The promise and realization of cure was demonstrated in patients with otherwise incurable chordoma.^7,8 The practice of SOBP proton radiotherapy persists today, and most patients are still treated with SOBP fields.

The primary proton beam out of an accelerator is, in the absence of scattering materials, a collimated well-circumscribed “pencil” beam and easily manipulated by electromagnetic means. The proton pencil beam allows dose modulation in the patient with four degrees of freedom: number of protons (NP) to control the local dose deposition, energy to control the local penetration and magnetic deflection to control the off-axis position. The size of the pencil beam is a fifth degree of freedom although not readily available. Spot size control would positively impact delivery efficiency, as “larger” spots can deliver more protons in vivo given safety constraints (see section on back-of-the-envelope calculations), albeit possibly with an increase of integral dose. The spot size is typically characterized by the gaussian width σ of the pencil beam lateral intensity distribution and quantified in air at the isocentre.

Proton pencil beams thus have one (or two) more degrees of freedom, penetration dose modulation, compared with intensity modulated radiotherapy [IMRT or volumetric arc therapy (VMAT)] fields. Proton fields (at dose equilibrium) exhibit the charged-particle Bragg peak depth dose characterized by a sharp dose increase, the “spot” at the energy characteristic penetration range and absence of dose beyond this distal range. The full electromagnetic control of the heavy-charged-particle pencil beam combined with the Bragg peak and absence of distal dose makes pencil beam scanning (PBS) an easier and more powerful delivery system for modulated therapy compared with the mechanical multileaf collimators (MLCs) required in X-ray IMRT (or VMATs), as well as the creation of SOBP fields.

We use the label “pencil beam (spot) scanning” (where “spot” refers to the location of the Bragg peak in the patient) for the technical mode of delivery and the label “intensity modulated proton therapy (IMPT)” for the clinical mode of PBS where each individual field is allowed to assume an arbitrary dose distribution, and only the full set of fields in the treatment fraction, as in IMRT, assumes the desired dose fraction distribution. Other clinical modes exist, but IMPT is simply the desired, although presumably the most challenging, goal of PBS and our focus here.

Clinical PBS was systematically developed and applied at the Paul Scherrer Institute in Villigen Switzerland.^9,10 Their original clinical system consisted of a very compact isocentric gantry combined with a couch and a scanning system that scanned a single line of pencil beams (i.e. irradiating planes in the patient) and thus required patient movement to accommodate multiple planes. The gantry transported protons at a fixed set of constant energies, whose energy at the patient was modulated by a set of mechanical degraders. The system implemented full modulation of all pencil beam parameters, albeit by considerable mechanical means. This unique design demonstrates, amongst other things, the possible variability of delivery systems, although all modern systems employ near-complete electromagnetic modes to implement scanning. Nevertheless, modern system designs and choice of components will influence the technical and clinical quality of scanning.

As stated, technical, physical and clinical challenges remain for the effective clinical deployment of IMPT. A pre-IMPT point–counterpoint argued that while IMPT may in-silico outperform IMRT, its expense and complexity exceeds that of IMRT and that of SOBP treatments.¹¹ A rebuttal¹² argued that IMPT will become generally available and its use necessary to fully exploit the dosimetric advantages of proton radiotherapy. Indeed, IMPT (or more precisely PBS) delivery technology is now standard and is, in fact, more cost-effective and simpler in terms of commissioning¹³ and operation compared with other delivery modes of proton radiotherapy. Overall costs, depending on accounting, are generally assumed to be twice that of IMRT and remain an issue.

The sections below elaborate on these individual issues. We argue that clinical IMPT requires a system approach whereby the current (i.e. in X-ray radiotherapy) individuality of treatment management components must be integrated to achieve optimal performance. Optimal performance combined with exploitation of dosimetric advantages, in turn, can lead to an improved cost profile. The hypothesis is if IMRT is cost-effective in some end point (see, for example, Kohler et al¹⁴), then IMPT can exceed this cost-effectiveness criterion through additional dose advantages or through increased performance such as may be achieved through hypofractionation.

THE CLINICAL PROMISE

Proton dose distributions have two primary dosimetric advantages: improved control of the dose fall-off at the target volume edges [and thus improved control of penumbral separation between the target and organs at risk (OARs)] and significant (30–50%) reduction in the integral dose bath in the patient. Improved edge definition of the proton dose distribution also improves dose painting. The first is of significance in treatment sites with nearby OARs such as those in the head and neck region. The second is of significance for all treatment volumes and whose benefit increases with increasing target volumes.

The numerical dosimetric advantage of IMPT is self-evident. Nevertheless, and for the first time in radiotherapy, the axiomatic benefits of improved dosimetry are questioned primarily in light of the presumed higher capital and maintenance cost of proton radiotherapy equipment where it is fair to assume that the operational costs are on par with those for advanced radiotherapy. The quantification of the outcome benefit is therefore critical, but a reduction in the cost of deploying proton radiotherapy facilities is necessary. The latter is dependent on many factors. For example, it is one aim of advanced radiotherapy to reduce the number of treatment fractions by increasing the fraction size. In this aim, proton radiotherapy certainly excels because if higher X-ray doses can be delivered with the same therapeutic effect and with equal morbidity, certainly proton therapy can deliver even higher doses. Thus, proton radiotherapy may use hypofractionation with increased clinical and financial opportunity. In short, proton radiotherapy will succeed if it is a modality that is used to go beyond the constraints of X-ray therapy.

We present three cases to illustrate the dosimetric adequacy of IMPT in the oropharynx [kindly provided to us by Olga Hamming-Vrieze, MD, from the Dutch Cancer Institute (NKI, the Netherlands) based on work performed during an extended visit at the Massachusetts General Hospital, Boston, USA] and a sarcoma in the leg and breast.

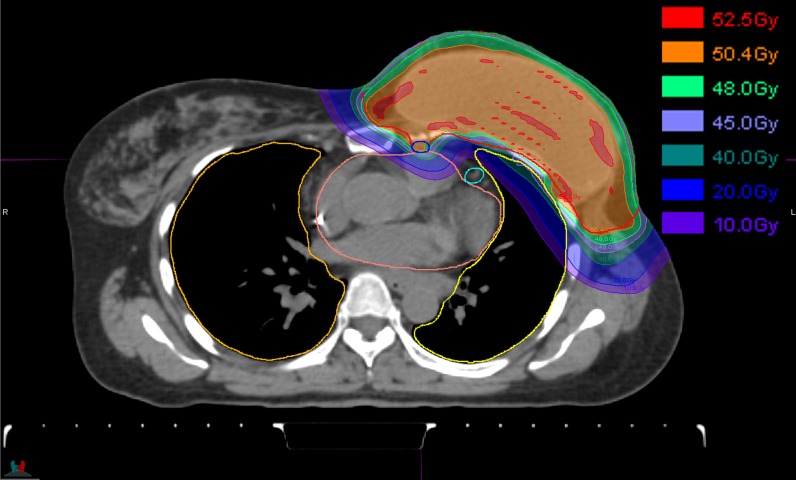
The first case is a single-field IMPT breast irradiation technique used at the Massachusetts General Hospital as described by Depauw et al.¹⁵ This technique replaces the multifield photon/electron fields necessary to achieve dose coverage in this irregular and spread-out anatomy. Figure 1 shows an example treatment field, albeit planned with smaller spots (<σ> approximately 4 mm but not including the scatter effects of the range shifter and inpatient) compared with our current delivery system.

Figure 1.

A breast treatment of post-surgical breast (including the implant reconstruction) and axial and supraclavicular lymph nodes.¹⁵ The treatment uses a single oblique field that covers all target (sub)volumes. The treatment field uses an 80-mm lucite absorber to lower the available energies from our cyclotron and deliver dose up to the skin. Clinically, the reduction in the dose to the left lung and the left anterior descending artery is of interest.

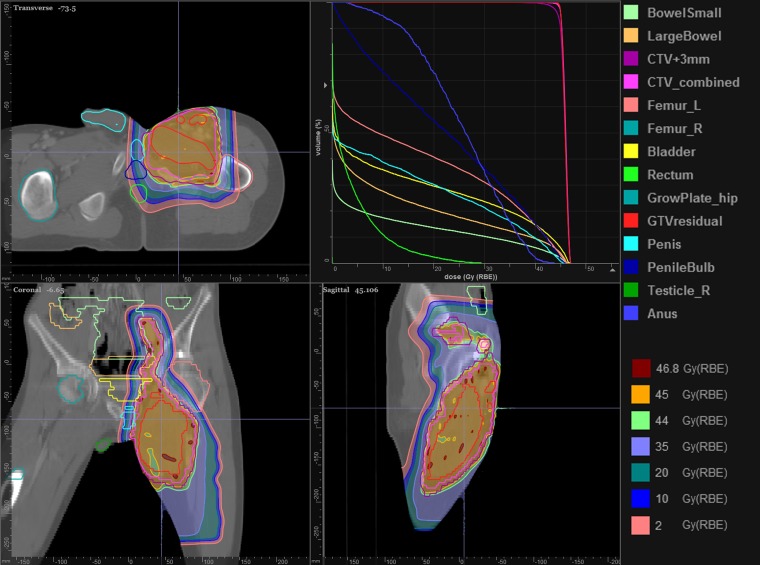
The second case is a large sarcoma of the right upper leg in a young adolescent male. Of particular concern, aggravated by our current “large” spot size (<σ> approximately 11 mm), is avoiding dose to the testes. Figure 2 shows the achieved treatment plan that uses two anterior fields each with an aperture (Figure 3) necessitated by the length of the target volume and the need to shield the testes. The two fields have a 5-cm overlap (Figure 4) in which both fields place pencil beam spots. The optimizer, intrinsically, creates a smooth gradient across the overlap, which ensures, at least, a robust dose match in the presence of couch movement between the two field isocenters.

Figure 2.

Treatment of a young male for a sarcoma to the right leg. The treatment uses two fields to accommodate the length of the target volume. The testes dose is of concern, and apertures are used to ensure the sharpest penumbral dose fall-off. The organs in the dose–volume histogram are listed on the right, where R/L refer to right/left. CTV, clinical target volume; GTV, gross tumour volume.

Figure 3.

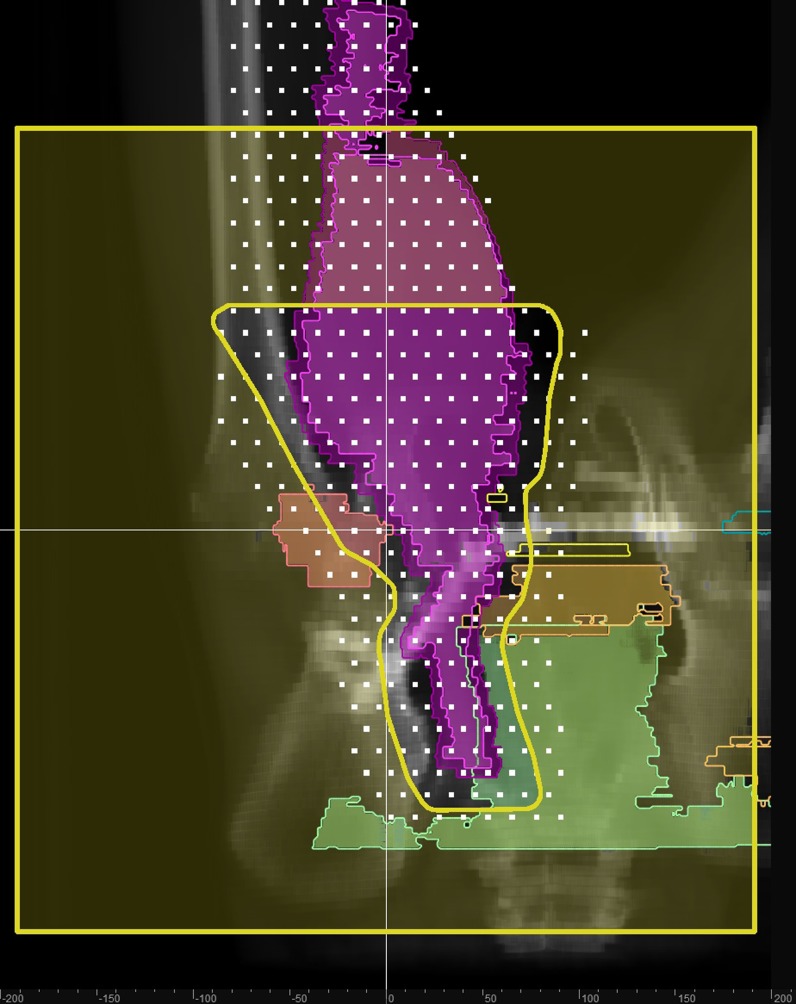
The aperture for the superior field, its edge shown in yellow. The white squares indicate the placement of the spots at a single energy from both fields. The spot energy corresponds to variable penetration (owing to patient heterogeneity and skin curvature) in the patient, and the organ projections are outlined at the corresponding penetration.

Figure 4.

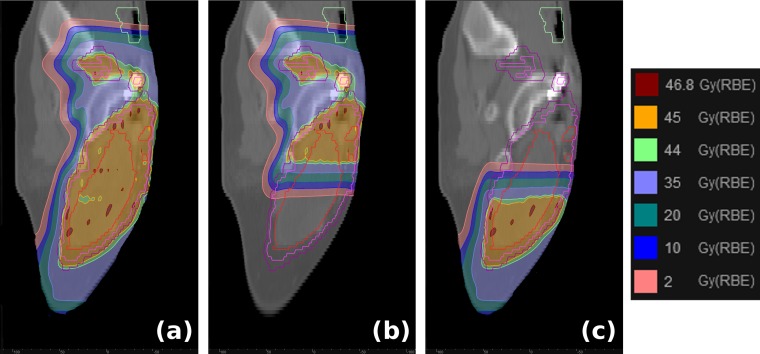
Demonstration of field matching by overlapping the placement of pencil-beam spots from each field across a 5-cm region in the target volume and unconstrained by the aperture edge (i.e. the aperture is used only to shield the testes and lateral healthy tissue). The resulting dose distribution shows a very smooth penumbral gradient across the 5-cm overlap and ensures that any couch movement uncertainty between the two fields has negligible effect.

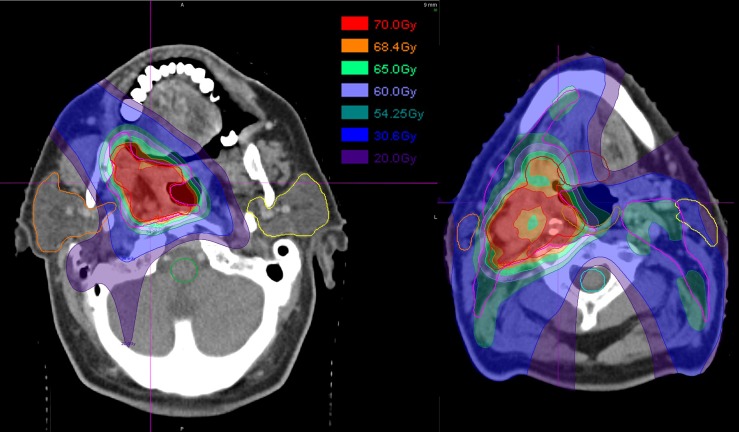
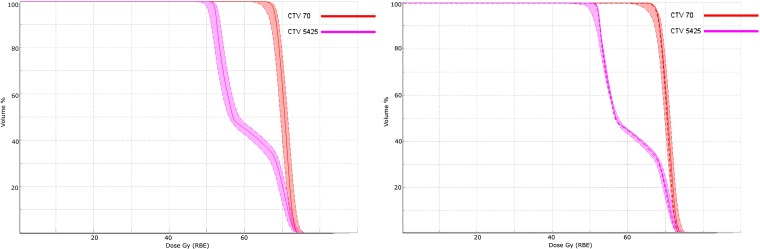
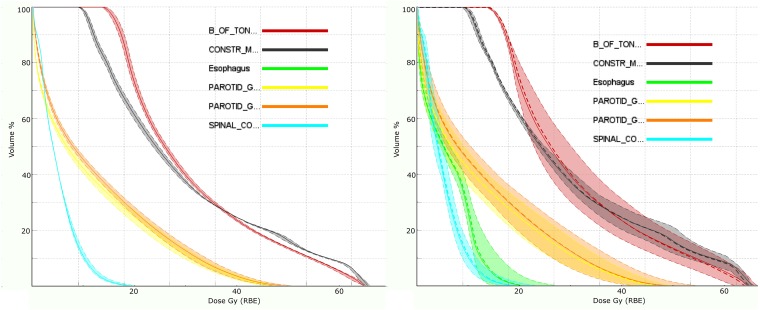
The third case is a complex oropharyngeal carcinoma that includes two CTV volumes [to 54.25 and 70.00 Gy (radiobiological effect, RBE, see section on radiobiological considerations)] and lymph node targets. The treatment approach uses three fields—posterior and ±45° anterior obliques—where each field positions spots (<σ> approximately 7 mm) throughout the target volumes. The treatment prescription has multiple constraints within which the physician wishes to further consider many objectives (Table 1). Figure 5 shows the multilevel dose on two axial sections. Figures 6 and 7 show the degradation of the doses to the targets and OARs in the presence of the (intrinsic) uncertainty in range (3%) and in geometric positioning of the patient. The dose–volume histograms (DVHs) in the figures consider the maximum/minimum DVH envelope given the extent of the uncertainties. Note that the effect on the target volumes is relatively minor (up to about 10% underdose) and similar for both the range and set-up uncertainties if the set-up uncertainty would be systematic (Figures 6 and 7 legends). The effect on the OARs is more dramatic, especially for the set-up uncertainty if, again, it would be a systematic error.

Table 1.

Partial list of prescription constraints and objectives for the oropharyngeal carcinoma. These constraints and objectives are input to the multicriteria optimization algorithm to achieve the set of Pareto optimal treatment plans that present the optimal trade-off scenarios of the competing objectives. Constraints cannot be violated, and the optimizer will ensure (for example) that the maximum brain stem dose is <55 Gy (radiobiological effect). Each objective evaluation results in a set of values for that objective that can be achieved with respect to other objectives and within the constraints. For example, giving the spinal cord maximum dose of 50 Gy does allow the spinal cord minimization of the mean to achieve a maximum dose of 20 Gy (see dose–volume histogram for spinal cord in Figure 8)

Structure	Type of prescription	Value [Gy (RBE)]
Constraints
Spinal cord	Maximum	50
Brain stem	Maximum	55
Parotid (right/left)	Maximum mean	26
Submandibular gland	Maximum mean	39
Constrictor muscle	Maximum mean	50
CTV [70 Gy (RBE)]	Minimum	66
CTV [54.25 Gy (RBE)]	Minimum	51
CTV (54.25)–CTV (70)	Maximum mean	55
Objectives
CTV (70) and CTV (54.25)	Minimize maximum (dose)
CTV (70) and CTV (54.25)	Maximize minimum (dose)
CTV (70)	Minimize underdose	70
CTV (54.25)	Minimize underdose	54.25
CTV (54.25)	Minimize overdose	54.25
All organs at risk (including those for which a constraint is specified)	Minimize mean
Mandible	Minimize maximum

CTV, clinical target volume.

Figure 5.

Multitarget treatment of oropharyngeal tumour with three intensity modulated proton fields (a single posterior field and anterior right and left oblique approaches). Each field was allowed to cover the target volumes, clinical target volume (CTV) 70 Gy (radiobiological effect) and CTV 54.25 Gy (radiobiological effect) (see also Table 1 and Figure 6 where the dose-volume histogram (DVH) line colours correspond to the contour colours) from its respective direction. Target coverage, indicated by the colour gradient and the DVHs in Figure 6, was considered adequate given the trade-off dose analysis. Finally, the possible level of dose inhomogeneity in an intensity modulated proton composite dose distribution can be appreciated by the cold spot (about 5%) in the target volume. The large number of intensity modulated proton parameters, i.e. the individual spot intensities, creates a very large set of possible dose configuration in the multicriteria optimization process. The fields had a 47-mm range shifter to lower the cyclotron minimum energy. The list of constraints and objectives is shown in Table 1.

Figure 6.

Dose–volume histograms (DVHs) for the target volumes (and their prescription dose as indicated in the labels). The DVH on the left (right) shows the nominal DVH value (solid lines) as calculated by the treatment planning system and the level of uncertainty (the band around the nominal value) from the nominal DVH when the range (set-up) deviations are considered. The uncertainty band is the bounding envelope that contains all the possible DVH curves given the interval of uncertainties. The deviations are considered as maximal deviations and the results are upper and lower values and not standard deviations. Note that the effects of either uncertainty (range or set-up) are on par and both show a possible 10% underdose if such an uncertainty were to occur. Note, however, that the range uncertainty is a systematic error, while the set-up uncertainty is a random error. The systematic uncertainty is more severe and can only be mitigated by a robust treatment plan that ensures coverage always. The set-up uncertainty converges to the mean (dotted line) over the course of treatment unless the treatment is hypofractionated for which the statistical averaging effect is reduced. The obvious cold spot in Figure 5 appears to only involve a small volume fraction as no noticeable dip is visible in the DVH (left).

Figure 7.

Dose–volume histograms for the organs at risk as in Figure 6. Note that the range uncertainty now has a negligible effect on the organs at risk (left panel). The reason is simply that the fields don't “range-out” into a structure. The shift uncertainty, however, does have a large effect (right panel). Mitigation requires (in the absence of a robust treatment plan) decreasing the maximum organ at risk dose such that the dose during delivery will not exceed tolerance. Again, however, the dose will converge to the mean (dotted line) over many treatments. Thus, a true dose assessment will require the incorporation of the statistical nature of the delivery process in the treatment planning system to uncover the true deviation.

The examples demonstrate that IMPT is effective in treating irregular volumes, large volumes and complex multidose level volumes. The first two cases are intrinsically more robust owing to their single-field nature. The single-field aspect, at least, reduces the cumulative effect of adding the multiple fields. They remain as sensitive to anatomical and set-up uncertainties. All cases show the flexibility of IMPT where a small number of fields^1–3 are able to achieve highly conformal dose distributions. The first two cases also illustrate that IMPT achieves considerable healthy tissue sparing.

TECHNOLOGY

IMPT technology comprises the beam production system (BPS), the beam delivery system (BDS) and the patient monitoring system (PMS). The BPS is the accelerator and beam transport system that produces the proton beam of the requested properties (energy, intensity and spot size) at the entrance of the BDS. The BDS spatially manipulates the proton beam to produce the desired dose distribution in the patient. The BDS, typically, is the master controller of the delivery process. It receives the treatment instructions (the “plan”), executes the commands to produce, transport and manipulate the beam and is the central coordinator of the control and safety strategy. The PMS monitors the geometric state of the patient and produces the feedback information to the BPS to synchronize the delivery process with the patient geometric state. An often-used PMS device is a breathing monitoring device that interrupts the delivery when the breathing signal correlates with a particular out-of-field target condition. The PMS includes imaging devices that may be used to establish the correct correspondence of the patient with respect to the beam.¹⁶

The BPS is an accelerator whose choice is dictated by a particular vendor. Accelerator types include cyclotron, synchrotron or linear accelerator. There is no a priori “best” technology, as the choice has to be made on the desired clinical performance of the integrated system including all the software support systems. The BDS includes a set of scanning magnets and monitoring chambers that allow for precise and instantaneous monitoring of the proton beam. The PMS is often specific to a particular treatment site and typically accommodated as an auxiliary system to the BDS.

Clinical performance is dictated by the overall system, i.e. the choices for and integration of BPS, BDS and PMS. It is this combination, the treatment delivery system (TDS), as implemented by a particular vendor, that establishes the clinical performance possibilities of the clinical device and that may reduce or augment differences between component choices.

The TDS, at the basic level, is a proton pencil beam sequencer where each pencil beam is specified by its parameters, which are¹ energy (E) specified typically in BPS settings and related to the range in patient,² intensity specified in either number of protons (NP) or monitor units (MU) (we believe the specification in terms of NP is much preferred as it is a readily transferable quantity between institutions while MU is specific to an institution),³ lateral deflection (XY) specified in a reference plane and⁴ pencil beam spot size (σ) specified at a reference plane in-air, i.e. excluding inpatient scattering contributions or otherwise. The creation of the set of pencil beams and their individual value quadruplets is the task of the TPE (see below).

Here, we note that some limitations are based on the systems themselves. Current systems deliver pencil beam spots in layers of constant energies. This limitation is primarily a consequence of the long energy switching times of cyclotrons and synchrotrons. The first requires a mechanical beam intervention; the second (typically) requires the acceleration of a new proton bunch. Both are in the order of 1 s, which is much slower compared with the interspot scanning speed in the order of 0.001 s. Energy switching time is a limitation,¹⁷ and effort is expanded to improve on energy switching speed or to achieve continuous energy switching.^18,19 The spot size is typically fixed for a particular installation and thus not available as a modifiable parameter for treatment planning. In addition, the spot size tends to increase as a function of decreasing energy as a consequence of beam-line vacuum windows and ionization chambers in the nozzle and of beam extraction characteristics from the accelerator. This is highly undesirable, as the smallest spot size is needed for especially those lesions that are close to the surface (i.e. orbital tumours). Finally, no system effectively produces a beam whose energy has less than 4 cm penetration (in water). This implies that full automation promised or implied by IMPT is not fully realized to date, and IMPT delivery will rely on range shifters and apertures to produce the lowest energies and the sharpest penumbrae.

The heart of the TDS is the BDS. It requests, delivers and monitors the sequence of spots. Mitigation strategies for changes in patient state, of which the PMS here is a simple example, will require in-depth engineering of the BDS spot delivery logic to accommodate more complex patient changes such as motion control.²⁰ Current technologies place the burden of the mitigation strategy on the TPS, which is expected to produce a static treatment plan that accommodates the effects of motion (for example) such that the delivered treatment dose remains within a certain tolerance envelope. This certainly limits the optimality of the achievable treatment dose. If the BDS (for example) could adapt and change the spot sequence as a function of the motion trajectory, then the resultant dose could achieve a higher degree of conformality. Such capability will require a tight integration between the BDS and the TPS to accommodate, in essence, real-time update of dose information in the presence of the time and dose evolution of the spot delivery sequence in synchrony with the time evolution of the patient state.

PHYSICS

Proton pencil beam physics constraints the ability to control dose at a “point” in the patient. First, the proton interactions in the patient are governed by the stopping power that quantifies the energy loss to the medium (primarily in ionization processes and secondarily in proton–nucleus interactions). The interactions result in a decrease in proton energy, i.e. it “slows” down, and a deflection (primarily through Coulomb scatter) of the proton. Inpatient scatter, characterized by its gaussian spread σ_M, increases the penumbra by about 2% of the radiological depth penetration.

The intrinsic uncertainty in the stopping power value is a large concern. In practice, the CT Hounsfield unit (a measure of the electron density) serves as a surrogate and is converted into relative (to water) stopping power based on an empirical conversion.²¹ In practice, the overall uncertainty is assumed to be in the order of 3%,²² which for a 10-cm proton range translates to 3 mm! The stopping power uncertainty thus has a large impact on our ability to place a Bragg peak spot in the patient, and the uncertainty must be mitigated. Physical mitigations include measuring the stopping power in patient directly through proton transmission imaging (analogous to X-ray or CT imaging),^23,24 measuring the proton penetration in vivo through measurement of gamma emissions produced in the proton interactions,²⁵ multispectral CT²⁶ or combined CT and proton radiography,²⁷ improved dose transport calculations with Monte Carlo (MC) (also limited by stopping power values)²⁸ and, most immediately practical and perhaps most effective, uncertainty mitigation in treatment planning and consistent on-treatment imaging (below).

The proton inpatient scatter is convolved with the incoming proton pencil beam size, assumed gaussian, quantified by the spread σ_p. It is a primary TDS requirement to make the spread as small as possible. The spread magnitude is dictated by the beam production, transport optics and materials present in the beam. The desired spread is in the order of 3–5 mm, although even “large” spot sizes have clinical utility.²⁹ It might be desirable to vary the spot size and use it as an optimization variable in treatment planning to achieve more rapid filling of the target.

If we consider the scatter in the patient (see above), we obtain a minimum spread in patient of ${\sigma }_{\text{T}}=\sqrt{9{\text{mm}}^2+0.000625R^2}$, which indicates that the “real” pencil beam size is quickly dominated by the scatter in patient. Thus, for a 100-/150-/200-/250-mm range and spot σ_p = 3 mm, the total spread is 3.9/4.8/5.8/6.9 mm at the Bragg peak. Clinically, the smallest spot size is needed in “shallow” lesions such as in the orbital or cervical anatomy. There are two technical problems that limit the spot size at those shallow depths. First, it is difficult to produce and transport a sufficiently low-energy beam (i.e. R ∼ 1–4 cm) to the patient. These lower ranges are needed and can only be achieved by inserting a range shifter somewhere in the beam path. Second, depending on the accelerator, beam extraction increases the spot size as the energy decreases in contradiction to the clinical need. A smaller effective spot can then only be achieved by edge collimation with an aperture. Thus, even though IMPT is intrinsically “electronic,” clinical cases remain that require hardware mitigation of delivery limitations. Finally, the distal target penumbra is degraded compared with SOBP fields that use a range compensator. The use of a range compensator ensures that “every” proton stops at the surface, and, thus, the distal penumbra is close to the distal fall-off of the pristine peak. In the absence of a range compensator and in the absence of continuous energy control, the distal surface penumbra degrades to that of the lateral penumbra, i.e. about ×2 the pristine peak penumbra. Safai et al³⁰ discuss the clinical spot size features in patient.

The spot size at depth limits the resolution of our ability to shape the dose distribution at the target penumbral edge and in the target if dose painting is desired. For prostate, for example, our pencil beam brush (in gaussian σ) for lateral beams is in the order of 10 mm (approximately 10 CT pixels in prostate CT); for head and neck in the order of 5 mm (approximately 10 CT pixels in head and neck CT). Ions heavier than protons have much less scatter and hence are able to produce sharper penumbrae.

The number of protons in a spot is the critical treatment delivery control in IMPT. It is the basic product of the treatment planning process where the set of spots selected for the patient fields are assigned the intensities to achieve the prescription. A back-of-the-envelope calculation sets the number of protons to 1,000,000 (1 Mp) to deliver 1 cGy to 1 cm³. Thus, 1 Gy to 1 L requires 100 Gp (one hundred giga proton or 10¹¹ protons). We place a 1-L cube of 100 mm on side with its centre at 15 cm depth and deliver these protons in about 20 layers. The deepest layer contributes about 40% of these protons i.e. 4 × 10¹⁰ over 10,000 mm² or 4 Mp mm⁻². Our ideal spot size of 3 mm combined with the in-medium scatter results in a spot of about 6 mm, i.e. an effective area of about 100 mm². The number of protons per spot would be about 400 Mp if the spots were placed at about 6 mm spot-to-spot. If they are spaced at 3 mm, the spot intensity reduces by a factor of four to about 100 Mp/spot. Proximal layers have considerably fewer protons per spot. Thus, a BPS has to be able to deliver a range of protons between 0.1 Mp/spot and 1 Gp/spot. The upper limit on proton spot charge is limited by the safe instantaneous dose in the case of an unanticipated error in delivery. An instantaneous dose limit of, for example, 10 Gy limits the spot charge to 1 Gp. Practice confirms the range of spot charge between 0.1 and 500.0 Mp/spot (for spot size approximately 3 mm) as practical in terms of achieving treatment plans for 2 Gy (RBE) fractions. In practice, at least in our system, the lower limit of the proton spot charge can be raised to 1 Mp without degradation of plan quality. The accurate control over the clinical dynamic range of spot charge is a critical design and safety element of the TDS.

The above back-of-the-envelope calculation shows the strong relation between spot size, presumed precision given by the beam optics spot size in air vs actual precision given the real spot size in patient, number of protons per spot and the impact on the delivery system. The spot terminal positions typically form a three dimensional grid that encloses the target volume and where the lateral grid spacing corresponds to the spot size and the depth spacing corresponds to the Bragg peak width. The depth coordinate starts at the deepest radiological depth that reaches the target distal surface (plus margin) and subsequently places proximal layers separated by the width of the pristine peak. These layers, however, regularly spaced in energy are not regularly spaced in depth and are subject to considerable displacement relative to each other dependent on patient heterogeneities. Smart spot placement^17,31 can reduce the number of spots and layers considerably, which improves computational performance in the TPS, improves delivery time and improves the charge per spot profile. In addition, the use of a range compensator can reduce the number of layers significantly, as the range compensator acts like an energy “sorter.”

Protons interact in medium primarily through Coulomb scattering interactions with orbital electrons. A small fraction of protons interact with the nucleus, which produces neutrons and protons at large scattered angles. Given a depth dose distribution, the dose from these nuclear interactions varies as a function of depth and as a function of the (initial) proton energy. The characterization of this halo, so dubbed because of its large lateral extent, complicates the empirical characterization^13,32 of dose in patient but must be considered because of its non-negligible (i.e. approximately 2–5%) effect on the absolute dose prediction. MC calculations intrinsically consider the effect.

TREATMENT PLANNING

Treatment planning is the function that translates the physician's prescription and intent into a treatment plan that contains the set of equipment parameters that control the dose deposition in patient expected to be equivalent to the treatment plan predicted dose. This definition implies many requirements for proton treatment planning, often above and beyond those implied for photon treatment planning.

Optimization

The physician's prescription is a set of quantified statements (i.e. maximum dose to target), suitable for numeric manipulation in an optimization algorithm, and generalized intent or objectives (i.e. minimize dose to the brain stem). The quality of a particular objective is limited by the prescription that fixes the boundaries of what remains possible in a trade-off consideration of competing objectives. IMPT has a large number of variables: the value for each of the 1000–10,000 pencil beam spots. Thus, the physician will have considerable choice to consider one or more trade-offs to meet the overall intent or to further “improve” the treatment plan given a prescription. The prescription typically is the pragmatic copy of an X-ray prescription and hence reflects the constraints of X-ray radiotherapy, which presumably can be improved by the improved IMPT dose distribution.

Multicriteria decision analysis [or multicriteria optimization (MCO)] is a subfield of operations research that formalizes the inherent conflict in multiple criteria in the decision-making process. Pareto optimality (named for its inventor, V. Pareto) is one formal technique that computes the set of optimal solutions in terms of values for each criterion such that improving one such criterion necessarily worsens all other criteria. Thus, any Pareto optimal treatment plan is the best achievable given set of trade-off values (i.e. reducing brain stem dose necessarily results in worsening target coverage). MCO treatment planning is emerging as a necessary improvement on current “single” plan optimization methods. For these “single” plan methods, the user has no choice but to achieve a “better” plan through trial and error while not, in fact, knowing the optimality of any achieved plan.

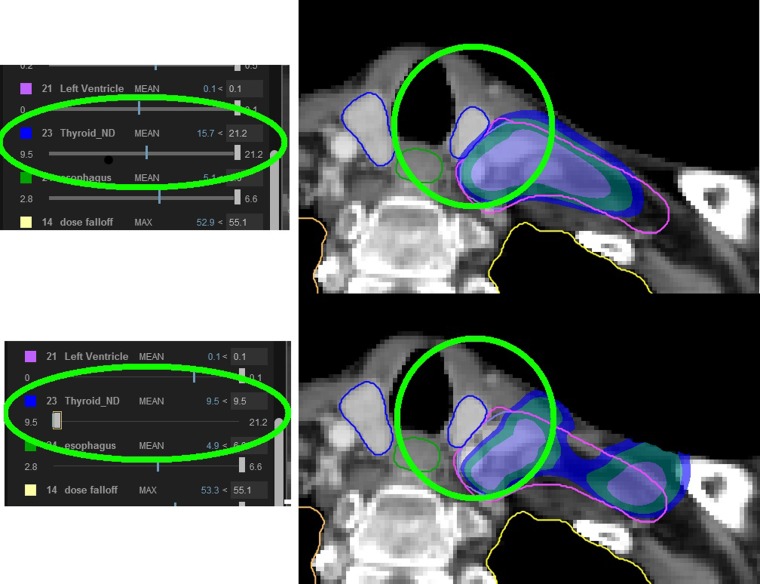
Common MCO techniques use multilevel optimization³³ or Pareto optimization.³⁴ For multilevel optimization, the optimization proceeds stage-wise whereby each stage takes the optimized plan from the previous stage and attempts to optimize the current stage given additional criteria (i.e. now minimize the brain stem dose for the plan that has maximized the minimum target dose). Each stage produces a single plan and requires re-execution of the pipeline beyond a current stage if their optimization criterion is changed. Pareto optimization computes the multispace of all Pareto optimal plans. Of course, this space is very large and in practice approximated by a sufficient set of plans that represent the whole space and where other plans are obtained through interpolation. The user can traverse this space by selecting the value for a particular constraint (i.e. minimized brain stem dose is 45 vs 50 Gy) and inspect the consequence of this choice in the presence of the value change on all other intent values (i.e. the target minimum dose drops to 65 vs 70 Gy as a consequence). Our clinical practice uses Pareto optimization to quantitatively assess clinical trade-off.³⁵ Figure 8 shows the use of MCO in the breast treatment case (Figure 1) to allow the physician to consider the effect of lowering the thyroid dose, albeit with an unavoidable lowering of target coverage.

Figure 8.

Demonstration of the use of multicriteria optimization to achieve improved thyroid minimum dose, albeit with worsened target coverage for the breast chestwall irradiation shown in Figure 1. The use of multicriteria optimization allows the physician to navigate the space of trade-offs while maintaining the absolute constraints of a treatment prescription. The sliders on the left show the value range for minimizing the mean thyroid dose. The slider shows the minimum and maximum achievable values of 9.5 Gy and 21.2 Gy (radiobiological effect) and the current values of 15.7 (top) and 9.5 (bottom). The white rectangle is the user control to change the trade-off value. The dose display shows how the dose “pulls” away from the oesophagus in the bottom, which results in reduced target coverage (dose inside the purple contour).

Dose accuracy

Accurate modelling of dose in the patient is limited by the presence of physical uncertainties such as stopping power accuracy, dose to tissue³⁶ calculation, dose calibration¹³ and by the presence of geometric and anatomical uncertainties. Standard practice for clinical dose computations uses pencil beam algorithms (PBAs)³⁷ whose spatial precision is limited (theoretically and at best) to the multiple Coulomb scatter (σ > 0.02 × R) resolution and whose dosimetric accuracy is limited by the approximation of water equivalence of any structure.²² An empirical pencil beam calculation can therefore not model deep heterogeneities better than the Coulomb scatter resolution. This may lead to underprediction or overprediction of dose around deep (relative to the penetration of the proton beam) heterogeneities. Only MC can resolve details of such effects, if any.

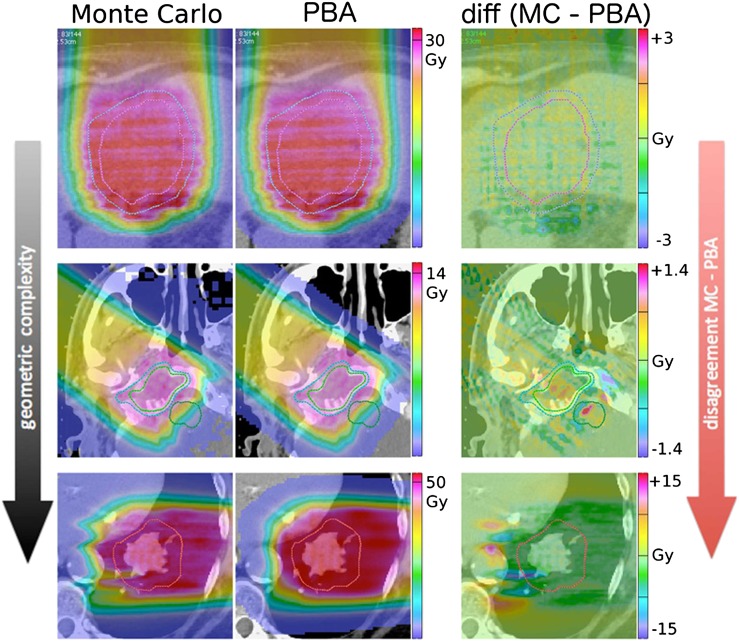
Figure 9 (see also Grassberger et al³⁸) shows fields in three example patients (liver, base of skull and lung) and demonstrates how the discrepancy between MC simulation and PBA increases with increasing geometrical complexity.

Figure 9.

Dose distributions calculated using Monte Carlo (MC, left column), pencil beam algorithm (PBA, middle column) and their difference (right column) in three example patients with varying complexity (liver top row, base of skull middle row, lung bottom row). The PBA modelling of the increasingly complex topology of heterogeneities causes an increase differential with the more able MC. Adapted from Grassberger et al.³⁸

Schuemann et al²⁸ discuss the need for site-specific range margins (albeit applied to SOBP fields) based on a comparison of the distal dose surfaces achieved by a PBA (in-house implementation based on Hong et al³⁷) and MC (TOPAS³⁹) where each calculation produced the identical SOBP in water. They observe deviations (MC-PBA), for head and neck fields, for example, in the order of −2 mm (or −1.5% relative to the nominal range) for the points along the same ray where the 90% distal dose is achieved. Other treatment sites showed similar but significantly different systematic deviation. This result indicates that the PBA overestimates the proton penetration. Conversely, it implies, depending on prescription practices, that the distal target is underdosed by individual fields. The overall impact of the single-field deviation is mitigated, in our practice, through the use of multiple fields. It should also be emphasized that the transition to MC-based clinical computations is inevitable, if only because computing hardware technologies place such calculations within reasonable times,⁴⁰ but even an MC calculation needs to be benchmarked and calibrated against measurements and the community must establish standard and traceable benchmarks for its clinical deployment.⁴¹

Any dose calculation is a systematic deviation from the “true” dose distribution yet compatible with clinical practice that empirically and formally equates dose computed within practice-guided accuracy to expected and observed outcome in the patient. For proton radiotherapy, this means that prescription and calculation practices must be consistent. It is precisely within the domain of IMPT with its various uncertainties that much effort is expended to ensure this consistency. Improvements such as those achievable through MC dose calculations²⁸ must be translated into clinical practice while being cognizant of the empirical expectation.

Motion management

Dose prediction in the patient must consider the effect of temporal changes—set-up uncertainties, anatomical changes and organ motion—in the patient to which proton dose distributions are particularly sensitive. In X-ray therapy, such changes are well respected by (artificially) folding the uncertainties into a planning margin around a structure such that if the dose to the margined structure is achieved, dose to the structure itself certainly is achieved. The margin expansion technique is possible for X-ray therapy because the X-ray dose envelope is spatially invariant within the clinical uncertainties. Changes in radiological density change the X-ray attenuation by the order of 4% cm^–1. Thus, geometrically placing the target within (or structure without) this envelope ensures compliance with the dose intent. In proton therapy, the concept of a planning (target) expansion volume is invalid as the dose envelope is sensitive to the uncertainties. Changes in radiological density change the position of the Bragg peak 100% cm^–1. Changes must be considered explicitly. For SOBP treatments, these changes are considered by increasing the penetration range and modulation of the SOBP field, by increasing the aperture and by “smearing” the range compensator.⁴² None of these options apply to IMPT.

Current TPSs, typically, allow the user to specify the expected variances in position of the isocentre and of the range. The nominal computed plan is tested against its representation at combinations of variant values, and the user must consider whether the variant plans remain acceptable.

We wish, however, to compute a treatment plan in which the dose constraints and objectives are met for every possible set of uncertainty values. That is, the treatment plan must be “robust” (or insensitive) in the presence of presumed uncertainties. This computation requires the computation of many (in the order of 10 or more) combinations where the treatment plan is optimized simultaneously over all combinations.^43,44

Similarly, in the consideration of motion, the treatment plan is optimized simultaneously over all volumetric representations of the moving anatomy such as are available through a four dimensional CT. This, of course, increases the computational combinations by a factor of 10 again!

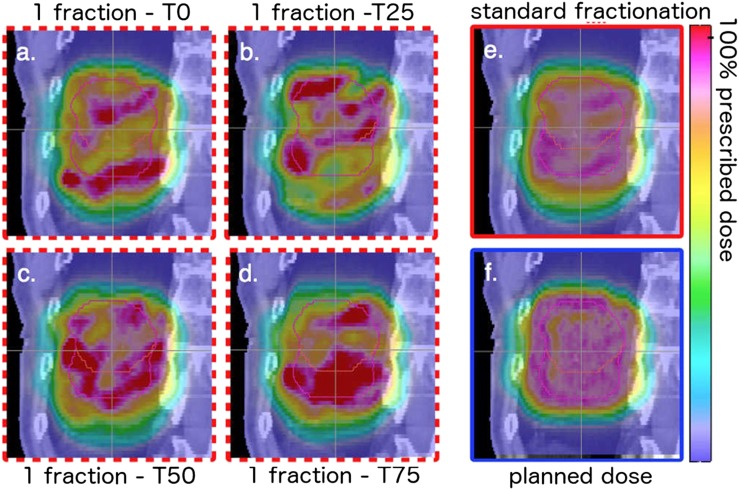
Finally, both IMRT and IMPT have a time structure: the movement of the MLC in IMRT and the temporal sequence of the pencil beam spots in IMPT. The MLC temporal structure is largely decoupled from the motion problem, and, again, uncertainties can be folded into an appropriate margin.⁴⁵ The spot sequence is fast (200–1000 cm s^–1) but is constrained by the energy switching time, currently in the order of 1 s. Thus, the temporal evolution of the spot sequence must be synchronized with the temporal evolution of the motion⁴⁶ to assess the correlation between the operational envelope of the TDS—magnet speed, energy switching time, spot size, etc.—and the patient dynamics. If these factors are not considered, the interference between the dynamic pencil beam delivery and the tumour motion, typically referred to as interplay effect, can lead to dose degradation within the target, as demonstrated in Figure 10.⁴⁷ Panels Figure 10a–d show the dose distributions after a single fraction for delivery starting at varying points in the breathing cycle (T0, peak inhale; T50, end exhale), and Figure 10e shows how delivery over many fractions can mitigate the interplay effect.

Figure 10.

Sagittal view of the dose distributions for a patient with lung cancer with clinical target volume in end-exhale phase (red, small contour) and internal clinical target volume (pink, large contour). The tumour motion amplitude is 30 mm. Panels (a) through (d) denote the one-fraction cases for delivery starting in four breathing phases, panel (e) the dose distribution after a standard course of fractionation, and panel (f) the planned dose distribution on the static CT. Adapted from Grassberger et al.⁴⁷

In short, treatment planning must move to a complete simulation system of the treatment and patient dynamics. Such simulations, however, must correlate with the actual state of the patient at any given point in the treatment course. Unlike the “population average” method by van Herk et al,⁴⁵ IMPT must incorporate sufficient daily imaging and treatment plan dosimetry verification, and adaptation if needed, to ensure that the treatment plan remains within specification. This, in turn, will relax the computational burden of the pre-treatment treatment plan but increase this burden at the time of treatment, as uncertainties can be assessed directly and accounted for with increased precision.

Robust treatment planning

Robust treatment planning aims to achieve treatment plans whose delivery parameters create a dose distribution that satisfies the clinical prescription if the patient's treatment representation remains within an uncertainty envelope considered in the treatment plan. The robust plan is obtained by simultaneously optimizing the treatment plan parameters over all (or adequately represented) uncertainty scenarios such that the treatment plan satisfies the prescription. Robust treatment planning, in essence, perpetuates the concept that a single pre-treatment treatment plan can or must be achieved. In clinical practice, however, the uncertainty envelope can be managed through daily volumetric imaging to reduce the uncertainty to its minimum and to allow for per-treatment reoptimization of the treatment plan. Thus, site-specific analysis should identify the inherent robustness of the nominal treatment approach as quantified by dosimetric quality indicators and as quantified by the biological response variation. In general, any treatment plan should be computed with its uncertainty intervals, a necessity identified long ago⁴⁸ yet still not available in clinical practice. Finally, robust treatment planning or its (proposed above) site-specific substitute is the correct method for managing the “PTV” concept in proton planning.⁴⁹

Robust optimization considers primary physical and mathematical statements of the problem. The latter considerations include, amongst others, worst-case⁵⁰ and likelihood analysis,⁵¹ which consider the details of the time evolution of the treatment course treatment delivery. Of specific significance in the latter is the actual simulation or estimation of the treatment delivery sequence in the presence of organ motion.^46,52,53 In any case, the only definitive marker will be equivalence of biological response over the course of treatment that current treatment planning does not quantify well.

The level of robustness also depends on the quality of the optimization process itself. Indeed, a simplistic optimization algorithm⁵⁴ might overemphasize the use of the distal, and sharpest, edge of the proton beam. Such an overemphasis might result in a plan that uses that distal edge to achieve the sharpest penumbral fall-off between the target and an OAR. This, however, ignores the currently largest uncertainty, i.e. the actual position of that edge. Thus, robustness invariably depends on how the dose contributions from multiple beams interdigitate, which favours smooth individual beam dose distributions (see, for example, Figure 4).

Radiobiological considerations

The clinical radiobiological response in tissue from proton interactions events is assumed equivalent to those from photon (X-ray) interactions except for a uniform scaling RBE factor of 1.10. The unit of proton dose is therefore given as Gy (RBE) and implies that the stated value [say 50 Gy (RBE)] is equal to that of ⁶⁰C (as a traceable dosimetry standard) delivered dose.

The interaction profile of proton events is more differentiated as this single factor implies. Even in clinical practice, the biological dose penetration of a Bragg peak (say to 100 mm at 90% peak dose) is projected deeper in the order of 1–2 mm (i.e. 101–102 mm)⁵⁵ and is one reason for not placing the distal penumbra between a target volume and a critical structure (the other reason, again, is range uncertainty). Beyond this obvious effect, the “real” RBE for proton is not known and is confounded with clinical experience based largely on SOBP treatments that tend to use a large number of fields (approximately 10 in our practice) for complex cases (such as may be exemplified in the treatment of chordoma) and where any local RBE enhancement is minimized because of the field arrangement. Paganetti et al⁵⁵ do consider the clinical consequence of a 5–10% underestimation in the RBE value, which equates to an overdose in the patient (i.e. >1.1 ⁶⁰C dose). An overdose effect on a complication response depends on the shape of the dose–response curve. The authors conclude that a 10% underestimation would result in an unacceptable rise in complication. Given the absence of such an increase in clinical practice, the clinical use of RBE = 1.1 appears justified.

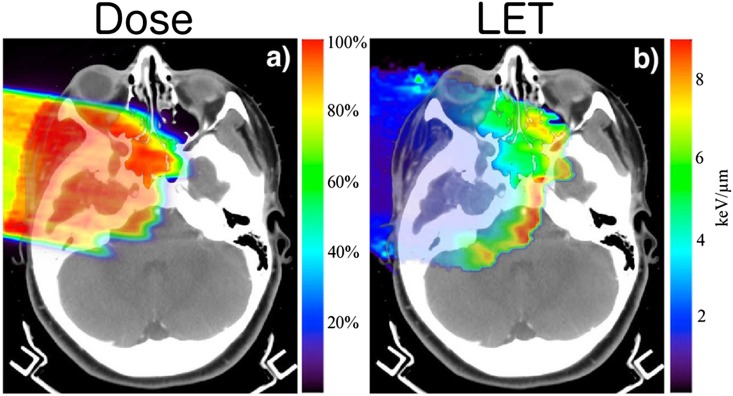
The physical effect responsible for RBE variation is the variation in linear energy transfer (LET), which quantifies how much energy the proton particle transfers per unit traversed distance. The dose-averaged LET distribution⁵⁶ from primary protons is in the order of 0.5 keV μm⁻¹ and rises steeply across the Bragg peak to 10 keV μm^–1, while secondary protons have an LET of about 12 keV μm^–1. Thus, secondary protons whose contribution to the dose is at most 10% (see also Clasie et al¹³) have a much larger effect on LET, and thus RBE, heterogeneity. The LET for SOBP fields increases at the distal edge of the SOBP field, as the most distal peak in the SOBP field carries a very significant weight (approximately 75%) compared with the other pristine peaks in the SOBP field. Figure 11 exemplifies this for a SOBP field in a patient, showing the marked increase in LET towards the end of range.

Figure 11.

Dose (left) and linear energy transfer (LET, in units of keV/Mm) (right) distributions for a scattered proton field in a base of skull patient. As expected for a scattered proton field, the LET increases toward where the most distal peak deposits most of the dose and hence its LET increase dominates the overall LET differential over the field. An intensity modulated (IMPT) field, in combination with other fields in the IMPT set, will smooth the LET differential over the target. The IMPT field set optimization, however, could include specific increase of LET differentials within the target such as may be of advantage in dose-painting scenarios. Adapted from Grassberger and Paganetti.⁵⁶

For IMPT fields, the individual peaks have a very different contribution profile to the dose in patient. The individual peak weights are selected to achieve the dose objectives but without, in general, a consideration of the underlying LET heterogeneity. The large number of IMPT spots and the use of MC allow for optimization of the dose distribution, the desired LET profile and biological response.^57–59

IMAGING

Proton interactions in patient allow for unique in-treatment imaging opportunities. First, a pencil beam is a “probe” when directed at a particular position in the patient and where one has prior knowledge about where the signal is generated. The proton pencil beam energy is precisely known, and its energy change can be accurately measured in proton transmission measurements, which result in a proton radiograph that measures integrated stopping power²³ in exact analogy to an X-ray radiograph that measures photon attenuation. The high-dose gradient in proton dose distribution will create a more explicit differential tissue response that can be quantified in, for example, MRI imaging.

Proton transmission radiography has been proposed as a method to acquire full tomographic reconstruction of the patient volume where the volume values are the patient-specific stopping power values. This method, however, is limited in its resolution owing to the relatively high scatter of the proton, which degrades the precision of the stopping power value. The proton scatter effect cannot be mitigated, unlike that of CT X-rays where collimation reduces the scatter contribution to the signal. Similarly, the inability of such collimation mitigation in CBCT overwhelms the scatter contribution such that a CBCT image, in itself, does not produce sufficiently accurate Hounsfield units.⁶⁰ Instead, the use of CBCT in proton (adaptive) radiotherapy requires the reference to an accurate CT image to re-establish the relation between current anatomy and Hounsfield number.⁶¹ An alternative method is to combine proton transmission radiographs with the patient CT. The patient CT, itself, already allows for a stopping power precision of the order of 2%. This prior knowledge combined with the information from the proton radiographs allows for accurate patient stopping power reconstruction.²⁷

MRI has high spatial accuracy and high sensitivity to radiation-induced tissue dynamics. MRI as a dose monitor has been applied, post-treatment, to assess dose response in craniospinal treatment, where vertebral bone marrow is transformed into fat,⁶² and in liver, where radiation damage inhibits enzymatic uptake and allows for distinct imaging of irradiated tissues vs non-irradiated tissues possibly within the treatment course.⁶³

The nuclear interactions of protons create radioactive isotopes whose activity can be measured with PET⁶⁴ or characteristic γ-spectroscopy.²⁵ In vivo PET measurements for proton radiotherapy suffer from washout and rapid decay of the most prominent oxygen signal. PET images can be acquired in the treatment room and thus benefit from the oxygen signal or, at least, acquired within an acceptable time window to preserve overall activity, albeit at the expense of more washout.⁶⁵ γ-spectroscopy must be performed during treatment, as the signal only exists at the time of interaction. This could enable instant range verification of proton beams within the patient or even be used to determine the elemental composition of the tissue being irradiated.⁶⁶

OPERATIONS

The treatment planning process must become, in general and certainly for proton therapy, independent of the first and often only treatment plan developed before the start of treatment. The current dependence on the pre-treatment treatment plan necessitates an overreliance on robust estimation and simulation of uncertainties and certainly cannot predict or accommodate changes over the course of treatment. Instead, the treatment planning process has to be integrated with the treatment delivery process. The latter must accommodate, in the recurring treatment session, up-to-date acquisition of volumetric image data to assess the current state of the external and internal anatomy and to predict the dose from the proposed treatment fraction plan parameters. If the predicted dose deviates beyond tolerance from the expected dose, the fraction plan parameters will be adjusted within the treatment session itself to allow uninterrupted and optimal treatment.

The above requirements are those of adaptive radiotherapy. Their realization, however, requires more integration than is afforded by the current troika of therapy systems: the TPS, the treatment management system (TMS) and the TDS. Their current deployment models are semi-autonomous, with the TPS as the most singular activity and a modest integration between the TMS and the TDS to coordinate treatment delivery, verification and recording.

Functional integration is driven by two efforts in standardization: the digital imaging and communications in medicine (DICOM) second-generation definition of data objects to encapsulate data and their workflow context⁶⁷ and the IHE-RO (“Integrating the Healthcare Enterprise-Radiation Oncology”⁶⁸) effort to improve the functionality of the radiotherapy clinic by standardization of actions and data within and between actor systems in the radiotherapy clinic. IHE-RO facilitates the DICOM second-generation definitions as the elements of these actions and data. IHE-RO and DICOM second-generation (emerging) standards carry the promise of true interoperability.

A few significant manufacturers dominate the general radiotherapy market who can turn this promise into reality. The proton radiotherapy market, however, exhibits considerable multivendor activity and may emerge as a proofing ground for these standards for two reasons. First, proton radiotherapy requirements are assumed to be a functional copy of photon radiotherapy requirements with little specificity to proton radiotherapy. Thus, the application of a system in photon radiotherapy may not be optimal in proton radiotherapy. This carries the risk that proton systems will underperform, which will hamper the effective deployment of proton systems. Second, proton radiotherapy must adapt the treatment delivery parameters to the patient and has the intrinsic technology to allow for daily and even intra-fraction adaptation depending on the changing patient conditions. Thus, proton radiotherapy treatment execution will singularly benefit from the efforts in standardization and implementation.

CONCLUSION

The clinical, physical and mathematical scope necessary to deploy IMPT are now well identified through the considerable effort in computational and physical studies that analyse the fundamental constraints of proton (and, in general, ion therapy). IMPT will require the most consequent implementation of adaptive radiotherapy to ensure that its use will be optimal in terms of clinical gain and operation.