Biomechanical Assessment in Models of Glaucomatous Optic Neuropathy

Abstract

The biomechanical environment within the eye is of interest in both the regulation of intraocular pressure and the loss of retinal ganglion cell axons in glaucomatous optic neuropathy. Unfortunately, this environment is complex and difficult to determine. Here we provide a brief introduction to basic concepts of mechanics (stress, strain, constitutive relationships) as applied to the eye, and then describe a variety of experimental and computational approaches used to study ocular biomechanics. These include finite element modeling, direct experimental measurements of tissue displacements using optical and other techniques, direct experimental measurement of tissue microstructure, and combinations thereof. Thanks to notable technical and conceptual advances in all of these areas, we are slowly gaining a better understanding of how tissue biomechanical properties in both the anterior and posterior segments may influence the development of, and risk for, glaucomatous optic neuropathy. Although many challenging research questions remain unanswered, the potential of this body of work is exciting; projects underway include the coupling of clinical imaging with biomechanical modeling to create new diagnostic tools, development of IOP control strategies based on improved understanding the mechanobiology of the outflow tract, and attempts to develop novel biomechanically-based therapeutic strategies for preservation of vision in glaucoma.

1 Introduction

Although glaucoma can occur at any level of intraocular pressure [IOP], significant, sustained IOP reduction benefits patients (Anderson et al., 2001; Gaasterland et al., 2000; Heijl et al., 2002; Leske et al., 2003), and thus all current therapeutic approaches modulate aqueous humor dynamics to attempt to reduce IOP. These clinical observations have led many to suggest that biomechanical factors acting on the cells and matrix of the optic nerve head [ONH] contribute to the loss of retinal ganglion cell [RGC] axonal function in glaucoma (Burgoyne et al., 2005; Clark et al., 1995; Dandona et al., 1991; Hernandez et al., 1994; Martin et al., 2006; Minckler, 1986; Quigley and Anderson, 1977; Quigley et al., 2000a, 2000b; Sigal and Ethier, 2009), a concept that is consistent with clinical and experimental data. For example, RGC axonal damage occurs within the lamina cribrosa [LC] (Anderson and Hendrickson, 1974) where significant physical tissue deformation occurs (Sigal et al., 2007), patterns of vision loss in glaucoma are consistent with the heterogeneous physical structure of the LC (Quigley and Addicks, 1981), and ONH astrocytes are mechanosensitive (Kirwan et al., 2005, 2004; Rogers et al., 2012a, 2012b).

Broadly, Ocular Biomechanics strives to apply engineering concepts from the field of mechanics to understand the physiology and pathophysiology of the eye; here we focus on concepts specifically relevant to glaucomatous optic neuropathy. In the anterior segment, the primary interest is in the interactions between IOP and outflow pathway tissues, and specifically how tissue mechanics may influence IOP. In the posterior segment, biomechanical studies seek to understand how the structure and mechanical properties of the posterior sclera and lamina cribrosa determine the biomechanical environment and physiological function of ONH tissues. The findings may help explain why certain individuals and groups are more predisposed to develop glaucoma; why glaucoma risk increases with age; and the biological and clinical implications of glaucoma-induced alterations in tissue properties and structure. Moreover, findings in the posterior segment may help motivate the development of collagen cross-linking and other therapeutic approaches.

As readers will appreciate, the direct measurement of relevant biomechanics is challenging, and thus research typically takes a two-pronged approach, in which experimental and computational studies complement one other. For example, early investigations of posterior segment biomechanics used computational approaches that incorporated idealized geometries and simplified properties of the ONH and surrounding tissues based on ex vivo measurements (Sigal et al., 2005). The models examined the effects of the anatomy and stiffness of the posterior sclera and LC, finding that ONH deformation is particularly sensitive to the stiffness of the sclera relative to the lamina cribrosa. The importance of the sclera can be understood from a mechanical point of view by considering the lamina cribrosa as a more compliant disk in a stiff shell. The IOP generates tensile stresses in the scleral shell acting to expand the disk, as well as a translaminar pressure difference that causes posterior bowing of the LC. The amount of posterior bowing relative to disk expansion is determined by the relative stiffness of the sclera relative to the LC, with the counter-intuitive result that an increase in IOP can cause either anterior or posterior LC motion, depending on tissue stiffness, physiological cup shape and other factors (Sigal et al., 2011).

Such modeling predictions helped motivate experimental investigations of the biomechanics of the posterior sclera and ONH to evaluate the effects of factors such as age, race, presence of glaucoma damage, and pharmacological treatments. A number of studies have applied full-field deformation measurement methods, such as electronic speckle pattern interferometry and digital image correlation with optical and ultrasound imaging, to map the displacement field on the posterior globe surface or in a longitudinal section of the posterior sclera, then applied computational inverse analysis to determine the regionally varying material properties. More recent advances in imaging technologies, such as nonlinear optical microscopy, optical coherence tomography, and micro-computed tomography, are beginning to allow for similar detailed evaluation of the biomechanics of the LC (Campbell et al., 2015; Girard et al., 2013; Sigal et al., 2014a).

In this review, we first describe fundamental concepts of mechanics as applied to the structures of the eye. The description emphasizes the physical significance of mechanics concepts rather than mathematical rigor. Next, we survey recent experimental and modeling investigations of the structure and mechanical behavior of the tissues of the posterior segment. We conclude with a brief discussion of anterior segment biomechanics in glaucoma and a list of key questions in the field.

2 Fundamental concepts of solid mechanics

2.1 Displacements and strains

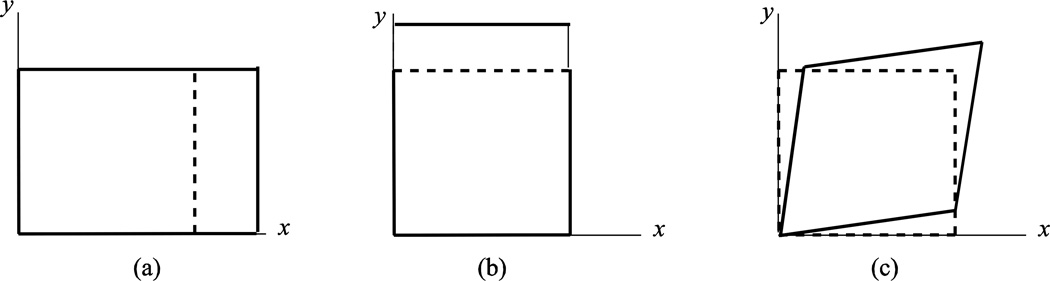
Here we consider how a deformable object, such as an ocular tissue, changes size and shape as it moves. For most objects, the undeformed shape is used as the reference configuration for defining motion and strains¹. An object can respond to applied loading in general by changing in size and shape. To understand the possible shape changes, consider a square of material as shown in Figure 1. The square can experience a length change along the x and y directions to arrive at a new rectangular shape. The stretch is defined as the ratio of the deformed length to undeformed length. In addition, the square can also shear, distorting the initially right angles to create a rhombus. The concepts of stretch and shear are universal in that they are independent of the size of the object. Thus the same measures can be applied to describe equivalent states of deformation in a human sclera, Schlemm’s canal cells, or a scleral strip excised for laboratory testing.

Figure 1.

Deformation modes of a square: (a) stretch along the × direction, (b) stretch along the y direction, and (c) shear in the xy plane.

Strain is a mathematical description of all the possible shape changes at a given point in the object. There are many descriptions for strains, but the two most commonly used in biomechanics are the Green-Lagrange strain (also referred to Green strain) and the small strain approximation. Both describe the change in shape relative to the reference configuration. For an object in three dimensions, there are 6 independent strain components: 3 normal strains and 3 shear strains. Figure 1 illustrates the concept of normal and shear strains in two dimensions for a square. For the small strain approximation, the normal strains is defined as the change in length normalized by the reference length, and the shear strain is the angle change. The components of the Green-Lagrange strain have a similar physical significance, and provide a more accurate description when there are large strains and rotations, e.g. there is a 1% error in the strain tensor when strains exceed 0.1 and/or rotations exceed 16°.

The strain components are defined for a given orientation (e.g. x,y,z) and can be calculated for a different orientation using the mathematical formulas of coordinate transformation. For the sclera and cornea, which are approximately spherical, it is more convenient to consider strains in a spherical coordinate system. The normal strains in a spherical coordinate system denote the length change in the radial and hoop (circumferential and meridional) directions. From the 6 strain components, we can also calculate the principal strains. These are normal strains in a special orientation, namely one in which there are no shear strains. The largest principal strain denotes the maximum normal strain over all orientations. We can also calculate the maximum shear strain over all orientations.

2.2 Stresses

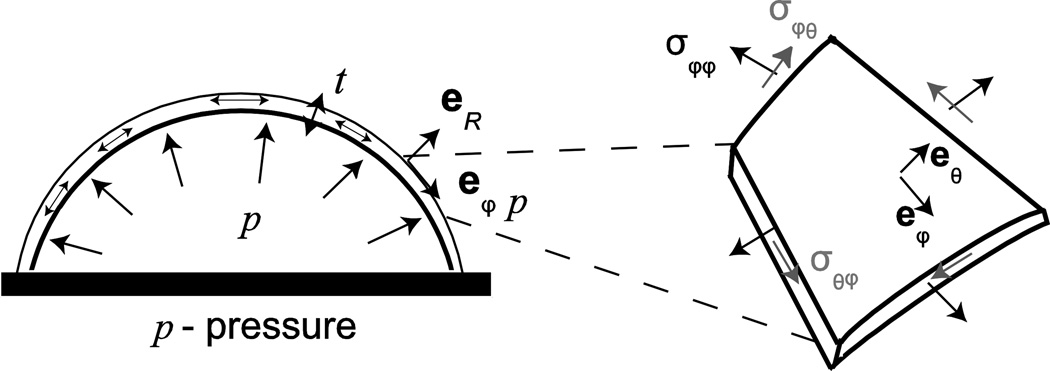
Stress is a mathematical description of how forces are distributed over an area. There are 3 normal components and 3 shear components of stress. A normal stress is generated by a force applied perpendicular (normal) to a surface, while a shear stress describes a force being applied parallel (tangential) to the surface. The stress components can also be calculated for different orientations using coordinate transformation. In a spherical coordinate system, the hoop stresses refer to normal stresses acting on the circumference (“hoop”) of a sphere, while radial stresses act on the thickness of a spherical shell (Fig 2). The principal stresses provide the maximum and minimum normal stresses, from which the maximum shear stress can be deduced.

Figure 2.

A thin spherical shell under inflation showing the biaxial stress state in the spherical (r,θ,ϕ) coordinate system. σ refers to stress and e_R, e_θ, and e_ϕ refer to unit vectors in the (r, θ,ϕ) directions.

For large deformations, there are different mathematical descriptions of stress. The components of the Cauchy stress describe a force normalized by the deformed area, which is referred to as a true stress. The deformed areas can be difficult to measure in experiments, and a corresponding engineering stress, named the first Piola-Kirchhoff stress, is defined as the force normalized by the undeformed area. The second Piola-Kirchhoff stress does not have a physical interpretation as a force distributed over an area. However, it is a useful mechanics concept because the product of the second Piola-Kirchhoff stress and the Green strain describes the strain energy stored in a material. The different descriptions for stress are related by strains and rotations.

2.3 Equilibrium and Laplace’s law

The components of the Cauchy stress are normalized forces and must satisfy the principle of equilibrium, i.e. Newton’s second law for non-accelerating bodies. The stress components can be determined directly from equilibrium when loading is provided by pressure or forces, and when bending can be neglected. Bending occurs when the applied forces and moments cause a change in the curvature of the structure, and leads to stresses that vary in magnitude along the thickness of the structure. An important problem in Ocular Biomechanics is a spherical shell subjected to an inner pressure p (Figure 2), where the shell represents the eye-wall and p is the IOP. For thin shells, also referred to as membranes, where the thickness is less than a tenth of the radius, t < r/10, the radial stress and variations of the stresses in the radial direction can be neglected. Then given the spherical symmetry of the structure and applied pressure, the only stresses present in the body are the hoop stresses. The force of the hoop stress acting on the wall must balance that from the pressure acting on the internal surface. The result is Laplace’s law for a thin spherical membrane,

$${\sigma }_{\phi }={\sigma }_{\theta }=\frac{pr}{2t}$$ (1)

Laplace’s law can also be generalized for non-spherical axisymmetric shells (Humphrey, 2002). The key assumptions of Laplace’s law are that the shell is thin, such that stresses do not vary through the thickness; and that bending is negligible. For the eye wall, these assumptions mean that Laplace’s law cannot be applied to calculate stresses in the peripapillary sclera, ONH, or the limbus, where there are large changes in the thickness, curvature, and/or material properties.

2.4 Stress-strain relations

A constitutive relationship (stress-strain relationship) is a mathematical descriptions of the relationship between the stress state and the strain state of a material. A constitutive relationship is an intrinsic property of the material, and is independent of the geometry and applied loading. For a tissue, such as the sclera, which is both a structure and a material, it is necessary to distinguish between the material behavior, which describes the stress-strain relationship, and the structural behavior, which describes the pressure-strain or the pressure-displacement relationship and depends on the thickness and radius of curvature of the sclera.

For small strains, the material behavior can be described by a linear elastic constitutive relationship, such as Hooke’s Law. An elastic relationship describes the situation in which there is no energy dissipation (e.g. no viscous effects); linearity further implies a proportional relationship between stress and strain. An isotropic material is one which contains a random, featureless microstructure. For such a material, the material properties are the same in all orientations, and the isotropic Hooke’s law is described by two independent material properties, the Young’s modulus and Poisson’s ratio. Consider a uniaxial stress state, where there is only one normal stress component. The tensile stress causes the material to stretch in the loading direction and compress in the transverse directions. The Young’s modulus is the stiffness (slope) of the stress-strain curve, and the Poisson’s ratio is the negative of the ratio of the transverse strain and axial strain. For isotropic materials, a Poisson’s ratio of 0.5 describes an incompressible material that can deform without changing volume, which is often a good approximation for (water-filled) tissues. The slope of the stress-strain curve depends on the stress state. For a state of equibiaxial tension, where there are 2 equal normal stress components, the slope of the biaxial stress-strain curve is 2 times the Young’s modulus for an incompressible material. The slope of the shear stress-strain curve is shear modulus, and is one third of the Young’s modulus for an incompressible material.

Isotropic materials are simple. However, connective tissues, including biomechanically important ocular tissues, are anisotropic because they are reinforced by collagen and elastin fibers. The presence of a single dominant fiber orientation causes the material to be stiffer along the fiber direction, but does not affect the stiffness in the material plane transverse to the fiber direction Constitutive relations for anisotropic materials contain more parameters to describe the Young’s modulus, shear modulus, and Poisson’s ratio along different orientation. For example, an orthotropic material is a material with differing properties in each of 3 perpendicular directions, and the orthotropic Hooke’s Law has 9 material properties: 3 Young’s moduli, 3 shear moduli, and 3 Poisson’s ratios for the three orthogonal directions. More general anisotropic materials also couple shear and normal stress and strain, where a shear strain can generate normal stresses and vice versa.

A hyperelastic constitutive model describes a nonlinear, non-dissipative, relationship between stress and strain for large deformation. The formulation of hyperelastic models is different than for linear elastic models, in that they begin with the definition of the strain energy density, defined as the energy stored in a deformed body normalized by reference volume. The strain energy allows the body to return to its undeformed shape upon release of the applied force. The stress is defined as the derivative of the strain energy density with respect to the strain. The mathematical formulation of the strain energy density is restricted by a number of physical considerations, including anisotropy. From the above discussion, the reader will appreciate that it can be challenging to accurately and completely describe the elastic behavior of tissues, which can often be a hindrance in numerical modeling studies.

To this point we have only considered elastic behavior. However, tissues also exhibit viscoelastic behavior, in which the tissue has characteristics of both an elastic solid and a viscous fluid. More specifically, in such materials, the stress at a given location depends not only on the local strain, but also on how quickly the strain is changing (the strain rate) and, in general, on the history of strains experienced by the tissue. The inflation response of the sclera shows noticeable rate-dependence and creep under constant pressure (Myers et al. 2010a, 2010b, Coudrillier et al. 2012). A stiffer pressure-strain response and smaller hysteresis was obtained at the faster loading rate, 1.0 mmHg/s, compared to 0.05 mmHg/s. However, dynamic mechanical analysis testing of the sclera, which subjects the tissues to sinusoidal cyclic loading, found that the tissue exhibited little viscoelastic behavior at 1 Hz (Palko et al., 2011). These effects can be challenging to account for in interpreting experimental measurements, and can significantly complicate numerical modeling of tissue biomechanics.

3 Imaging and Computational Modeling

As can be appreciated from the introductory material above, assessment of ocular tissue biomechanics is challenging. Ideally, we would like to know both stresses and strains at every location within the tissue of interest. Broadly speaking, there are two approaches to obtaining this information. In the first, imaging is used to determine tissue microstructure (e.g. collagen density and orientation) and anatomy, which is then fed into a computational model that predicts tissue stresses and strains for a given loading condition. Such approaches are critically dependent on an accurate description of the microstructure and anatomy and a method of deducing a constitutive relationship from microstructural information. The second approach uses direct measurement of tissue displacements, from which tissue strains are determined. These strains are then used, in combination with a constitutive relationship, to deduce tissue stresses. In practice, a combination of these two approaches is often taken, since some experimental measurements are impossible or infeasible. Here we consider each of these approaches in turn.

3.1 Quantification of Tissue Microstructure

The biomechanical behavior of most connective tissues is dominated by collagen and elastin, with a smaller contribution from proteoglycans; hence, most studies focus on quantifying these components. Outcomes of interest include the amount of a given constituent and, for fibrous proteins such as collagen, the constituent’s orientation distribution. We speak of a distribution of orientations in tissues since, except in tendons, collagen and elastin fibers are not mono-aligned; this dispersion of alignments has important biomechanical consequences. In the case of collagen, which can exist in various states of extension, the so-called crimp state, describing the extent of collagen undulation, is also an important outcome.

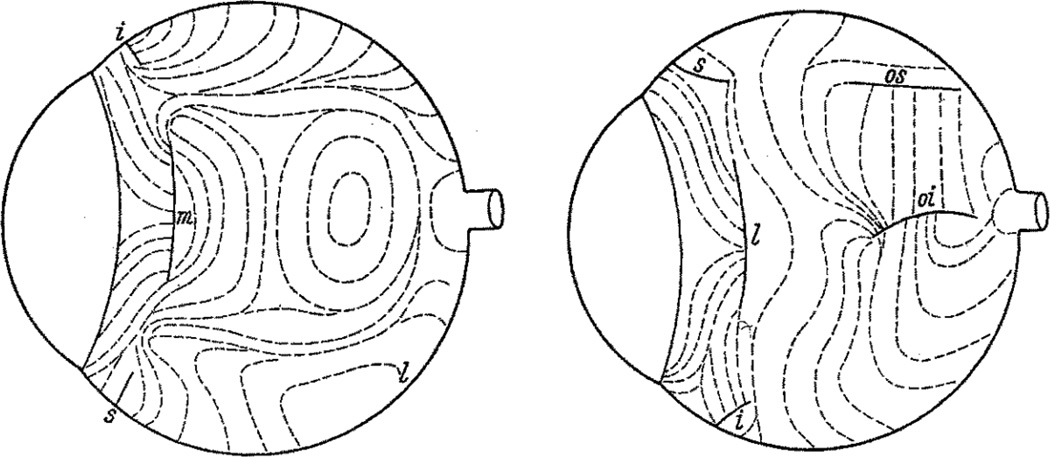
The earliest attempt to relate tissue microstructure to biomechanics in the eye was carried out by Kokott (1934) in a remarkable study of scleral collagen orientation using the slit lamp (Figure 3). Investigation of tissue microstructure below the ocular surface has classically employed histology based on semi-thin or ultrathin sections. For example, the microarchitectures of both the sclera and lamina cribrosa have been studied by light and electron microscopy in various species, e.g. (Cone-Kimball et al., 2013; Quigley and Cone, 2013; Quigley et al., 1991a, 1991b). These approaches provide significant detail about e.g. fibril size distribution and orientation, but are relatively labor-intensive, especially if local quantitative information is desired.

Figure 3.

Scleral collagen fiber orientation in the human eye mapped by direct slit lamp observations of the ocular surface, as observed from the nasal (left) and temporal (right) sides. The complex arrangement of fibers is evident. Letters refer to the locations of muscle insertions: m, l, i and s are medialis, lateralis, inferior and superior recti, respectively; os and oi are the superior and inferior oblique, respectively. From (Kokott, 1934).

Other techniques are available that are suitable for more quantitative outcomes. One such class relies on the scattering of electromagnetic radiation as it interacts with fibrillar structures in the tissue (collagen, elastin). For example, small-angle light scattering [SALS], introduced to the study of tissue microarchitecture by Sacks and co-workers (1997), has been used to map fiber orientation in the normal rat sclera (Girard et al., 2011a) and in the human sclera (Danford et al., 2013; Yan et al., 2011), with the latter studies showing changes with age, race and glaucoma status. A related approach, known as wide-angle X-ray scattering [WAXS], uses X-rays instead of light to specifically map the collagen fiber orientation. First used in an ocular context to study the microstructure of cornea (Meek and Boote, 2009), more recently WAXS has been used to quantify collagen fiber orientation in mouse (Pijanka et al., 2014) and human (Pijanka et al., 2012) scleras. These data in turn have been used to quantify the biomechanical effects of scleral fiber anisotropy on ONH biomechanics (Coudrillier et al., 2013). Mathematical formulations have also been developed to describe the distribution of fiber population orientations within tissue, whether measured by WAXS or SALS (Gouget et al., 2012). A benefit of SALS and WAXS measurements is that they provide a detailed distribution of fiber orientation at each measurement point. Drawbacks include the fact that this distribution is essentially integrated through the thickness of the tissue (more correctly, along the beam path), precluding obtaining depth-resolved information without subdividing the tissue sample (Pijanka et al., 2012).

There are also approaches that provide full-field information about fiber orientation. For example, nonlinear optical microscopy has been used to image collagen and elastin in connective tissues, e.g. (Timmins et al., 2010). These images can be processed using Fourier transform or other techniques (Sander and Barocas, 2009) to extract fiber orientation distribution functions over the field of view (Pijanka et al., 2012). It is also possible to exploit information from polarization microscopy to determine collagen fiber orientation and crimp, and how these quantities vary with location and IOP in ONH tissues (Gomez et al., 2014; Jan et al., 2013; Sigal et al., 2013, 2014b). There have also been recent efforts to use the so-called magic angle MRI approach to characterize fiber orientation in cornea and sclera without use of contrast agent (Ho et al., 2014); improvements in spatial resolution will likely be needed for this technique to be competitive.

There are special considerations when studying the microstructure of the lamina cribrosa. In human eyes, where the lamina cribrosa is formed of collagenous beams, it has been assumed that collagen fibers are essentially aligned with the beams; thus, imaging modalities that reveal beam anatomy also provide some microstructural information. The most important of these is optical coherence tomography [OCT]; regrettably, clinical OCT systems in the past have lacked the spatial resolution and depth-of-penetration to reveal individual LC beams. However, with the advent of enhanced-depth and long wavelength OCT imaging hardware, as well as image post-processing algorithms (Girard et al., 2011b), this limitation is being overcome somewhat (Sigal et al., 2014c). Ambitious and exciting efforts are now under way to characterize the in vivo biomechanics of the lamina (Girard et al., 2014). Alternatively, multimodal nonlinear optical microscopy techniques provides depth-resolved imaging and molecular-specific ex vivo measurements of the microstructure of the ONH. Collagen and elastin fiber structures can be simultaneously measured using second harmonic generation [SHG] and two-photon excitation fluorescence imaging (Kamma-Lorger et al., 2010; Winkler et al., 2010). SHG measurements have also been used to measure the deformation of the lamina cribrosa (Albon et al., 2000; Sigal et al., 2014a). This method also has the potential to measure the local strain environment of the resident cells and axons of the ONH.

In addition to OCT and conventional histology, there are a number of specialized techniques to extract quantitative information about beam lamina cribrosa structure. A 3D histomorphometric system has been developed and applied to study ONH (including LC) structure. This system provides high-resolution images of multiple ONH tissues, including LC beams, and has been used to study connective tissue changes in experimental glaucoma (Burgoyne et al., 2004; Downs et al., 2007; Yang et al., 2011, 2007a, 2007b). Beam architecture (orientation, connective tissue volume fraction) gathered in this way has also been used to drive finite element models of ONH biomechanics (Roberts et al., 2010a, 2009, 2006). Drawbacks to this approach include the need to use fixed tissue and the time-consuming nature of the 3D reconstructions. More recent efforts have involved micro-CT imaging of the laminar beams, which rapidly provides a fully registered 3D data set but requires use of contrast agent (Campbell et al., 2015); ongoing work attempts to overcome the latter limitation.

4 Experimental Measurements of Tissue Deformation

An alternate approach to characterizing tissue biomechanics is to directly measure deformations while controlling loads, or alternatively, to measure the loads required to achieve a certain deformation. Within this broad approach there are a number of specific techniques that we consider below. One of these techniques is particularly well-suited to the eye, namely inflation testing; because it has been so widely used in the context of scleral and posterior segment ocular biomechanics, we consider it in a separate section.

The simplest testing method for characterizing tissue biomechanics is uniaxial extension, in which a thin strip of the tissue of interest is held at each end and stretched. Such experiments can be carried out in load-controlled mode, in which a defined stress is applied to the tissue and the resulting deformation is monitored, e.g. through optical tracking of markers on the tissue surface. An extension of this approach is biaxial testing, in which a square or rectangular tissue sample is held on all four sides and stretched in two orthogonal directions. Such tests are relatively easy to carry out, using either commercial or custom-built devices. Moreover, they directly measure the stress-strain response and material properties of the tissues.

However, there are a number of drawbacks to this testing approach. One of the most important is that excision of the tissue sample inevitably results in severing of collagen fibers, which can alter how the tissue sample bears load and can also release residual deformations (Wang et al., 2015). Further, the attachment of the tissue sample to the testing device is not straightforward, especially in the case of biaxial testing where firm edge attachment is required while still allowing tissue stretching in two orthogonal directions (Eilaghi et al., 2009; Sun et al., 2005). In practice, there is a minimum tissue sample size, e.g. for biaxial testing, it is challenging to work with samples less than about 5 mm square. Also, it is difficult to account for local variations in properties and/or sample thickness, and such testing may not replicate the in situ loading conditions, especially for non-planar tissues and/or tissues that undergo significant bending in situ. Finally, as with many other testing methods, it is important to apply an appropriate preconditioning regimen to the tissue, see e.g. (Downs et al., 2005). Preconditioning subjects the specimen to repeated load-unload cycles to achieve repeatable stress-strain measurements. In fact, strip tests are more affected by preconditioning than inflation tests (Coudrillier et al., 2012; Myers et al., 2010b; Tonge et al., 2013a). Lari et al. (2012) showed that the stress-strain response measured by uniaxial tests is significantly different than by inflation tests, a discrepancy possibly due to the significant preconditioning effects of uniaxial strip tests.

Despite these drawbacks, useful data has been obtained for uniaxial and biaxial testing. Eilaghi et al. (2010), applied biaxial mechanical testing to the sclera and found a nearly transversely anisotropic stress response and large inter-individual variations. Spoerl and colleagues carried out uniaxial strip testing on scleral samples, some including the lamina cribrosa, to evaluate the stiffening effects of various agents (Spoerl et al., 2005; Wollensak and Spoerl, 2004). Palko and coworkers have studied uniaxial extension of scleral strips from control dogs (2011) and from animals with an ADAMTS10 mutation (2013). However, generally speaking, uniaxial and biaxial testing is being replaced by other testing approaches in ocular biomechanics.

Atomic force microscopy [AFM] force mapping is an indentation-based method for determining compressive tissue stiffness. In this technique, a cantilever with a sharpened tip or an attached microsphere is brought towards an immobilized tissue sample. As the cantilever tip (or sphere) contacts the sample, the cantilever bends and the tissue sample deforms. By measuring cantilever deformation and knowing the displacement of the base of the cantilever, it is possible to deduce the force applied to the tissue sample and tissue deformation. A model, such as the Hertz model, is then used to fit this data to obtain tissue stiffness (Charras and Horton, 2002; Radmacher, 1997). Due to its sensitivity and the small size of the cantilever tip/sphere, AFM is very well-suited to interrogation of tissue samples that are both small (<2 mm) and soft (effective modulus as low as tens of Pascals). However, it must be remarked that AFM primarily measures the compressive modulus of tissue. It is a characteristic of most connective tissues that the stress-strain behavior differs in tension and compression, due to the nature of collagen and elastic fibers. This can sometimes limit the utility of AFM results, although relative comparisons are often valid. For example, Braunsmann and colleagues (2012) have compared LC and peripapillary scleral stiffness in control and pseudoexfoliation [PEX] glaucoma eyes, observing a significant decrease in effective Young’s modulus in both tissues in PEX eyes. Other limitations of AFM are that the effective tissue stiffness that results from the data fitting depends on assumptions about tissue properties and structure, e.g. many analyses assume an isotropic and incompressible tissue. Finally, the stiffness so obtained depends in a sensitive way on cantilever tip/sphere size, with interrogation essentially occurring over length scales comparable to this size. For heterogeneous tissues, the resulting data can thus be hard to interpret.

4.1 Inflation Experiments

Inflation tests measure the deformation of the corneoscleral shell during controlled pressurization, which applies a biaxial stress state to the tissues of the eye wall. The stress magnitude scales with the applied pressure, but the biaxial stress ratio is fixed by the deformed shape of the tissue. In this sense, inflation tests are less versatile than biaxial strip tests, which offer independent control of the biaxial stress ratio. Another drawback is that inflation tests measure a structural response rather than a material response. The stress applied to tissues must be inferred from a theoretical model, such as Laplace’s law (Eq. 1) or from a computational model. However, inflation testing best approximates the normal biomechanical state of the eye, specifically including the effects of eye wall curvature and minimizing artefacts due to tissue excision.

4.1.1 Experimental Setup

The essential equipment for inflation testing includes a fluid injection system, which can be provided simply by a water column or more precisely by a programmable syringe pump with a pressure transducer and feedback controller; a specimen holder; a hydration or humidity chamber; a displacement measurement system; and a thickness measurement system, such as an ultrasonic transducer (Fazio et al., 2012b; Girard et al., 2009a; Murienne et al., 2014). Inflation methods have been developed for both the excised posterior scleral shell and whole globes. Whole globe tests require less specimen preparation and a simpler experimental setup, which makes inflation testing of the mouse sclera feasible (Myers et al., 2010b). The inflation response of whole globes is a systemic response that includes contributions from internal ocular components, which is physiologically realistic but which complicates isolation of the corneoscleral shell response. Inflation experiments of the excised posterior scleral shell require an infusion chamber with inlets for syringe injection and pressure measurement. The specimen can be either glued or clamped in a holder and secured to the infusion chamber. The displacement response to pressurization is highly dependent on where the specimen is glued to the holder and the associated boundary conditions at this location.

Most inflation experiments use a nonzero baseline (reference) pressure to prevent the globe or scleral cup from wrinkling and buckling. The minimum baseline pressure differs between humans and animal models, varies with eye size, and with thickness and length of the excised scleral cup. Myers and colleagues (2010b; Nguyen et al., 2013) found that different mouse eyes unwrinkled at different pressures, ranging from 6–10 mmHg. Girard et al. (2009a) used 5 mmHg for a baseline pressure for the posterior cup of monkey eyes, while Coudrillier et al. (2012) used a lower 1.5 mmHg baseline pressure for the thicker human posterior sclera. A number of other works have also used 5 mmHg as the reference pressure for the human sclera (Fazio et al., 2012b; Pyne et al., 2014; Tang and Liu, 2012).

A wide variety of deformation measurement and analysis techniques have been developed for inflation testing of the sclera. Early inflation experiments used optical systems to measure the displacement of discrete points or markers on the tissue. Woo et al. (1972) designed a laser-based system to measure the relative displacement of two markers placed on either side of the specimen apex. A number of studies also imaged optically the movement of markers and analytically calculated local strains from their relative displacements (Bisplinghoff et al., 2009; Girard et al., 2008; Lari et al., 2012; Thornton et al., 2009). Advances in non-contact measurement techniques have allowed recent investigations to measure the full two-dimensional and three-dimensional deformation field of the specimen surface. Full-field deformation measurement methods allow the spatial variation in the material properties to be determined from inflation testing. This is particularly important for the sclera, because it exhibits large spatial variations in the collagen structure, thickness, and curvature, all of which produce large spatial variations in the inflation strain response (Coudrillier et al., 2013, 2012; Fazio et al., 2012b; Girard et al., 2009b; Grytz et al., 2014b). The following subsections briefly describe three of the more widely used full-field deformation measurement methods in Ocular Biomechanics: digital image correlation, ultrasound speckle tracking, and electronic speckle pattern interferometry.

4.1.2 Digital Image Correlation

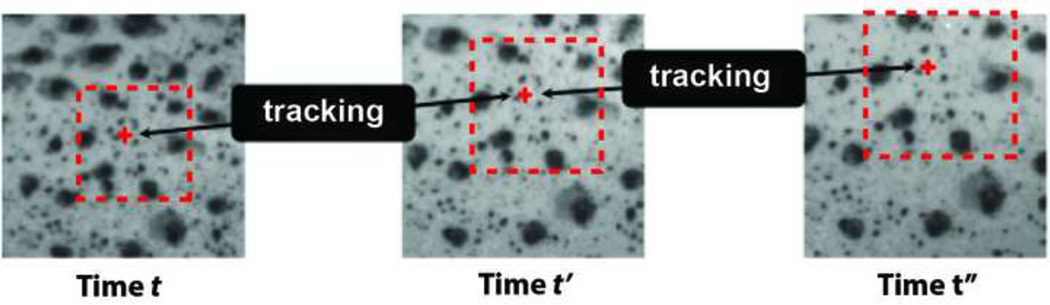
Digital image correlation [DIC] is a full-field non-contact method used to measure the displacements of structures subjected to mechanical loading (Schreier et al., 2009) (Figure 4). It is based on post-processing analysis of digital images and thus can be used with a wide variety of imaging systems, including conventional CCD camera systems and OCT systems for cross-sectional imaging. The imaging method determines the spatial and time resolution of the DIC measurment; thus DIC can be paired with a CCD camera system to study viscoelastic behavior (Coudrillier et al., 2012), and with second harmonic generation imaging (Sigal et al., 2014a) or atomic force microscopy to achieve microscale and even nanoscale deformation measurements. For optical imaging, specimen preparation involves dusting or spraying the surface with a non-damaging contrast agent, such as India ink, graphite, or toner powder. The key is to uniformly cover the surface with a disordered pattern (Figure 4) to provide a random distribution of gray image intensity. This can be difficult to achieve if the tissue has large surface variations. Some tissues and imaging modalities have a natural texture that can be used as speckles for DIC. The illumination over the specimen should be uniform, which can be achieved with indirect, diffused, or reflected light. Glare spots and shadows reduce contrast and result in poor correlation.

Figure 4.

Motion tracking of a material point by DIC from initial time t to a later time t”. The black dots are speckles generated by spray painting India ink over the surface of the sclera. The material point is illustrated by a red dot and the dashed line is the pixel subset.

After DIC is used to measure the displacement field, the strain field can be computed then used to determine the local mechanical behavior of the tissue. DIC has been applied to characterize a wide range of soft biological tissues (Boyce et al., 2008; Cheng and Gan, 2008; Sutton et al., 2007; Tonge et al., 2013b; Wang et al., 2003; Zhang et al., 2002), in part because it requires minimal specimen preparation. The primary disadvantage of DIC is that the accuracy and uncertainty is strongly dependent on the quality and noise of the speckle pattern, lighting, and imaging system (Ke et al., 2011; Ning et al., 2011; Wang et al., 2011). The displacement error and uncertainty of DIC methods are higher than for interferometric methods, and are not well characterized for non-homogenous deformations (Cirello and Pasta, 2010; Soons et al., 2012; Zhang et al., 2002).

Two-dimensional DIC

In the most common implementation of two-dimensional 2D–DIC, a single-view imaging system is used to capture a sequence of images of the deforming specimen. The first image is usually selected as a reference image and used to track the motion of points in subsequent images (Figure 4). For each point in the reference image, the distribution of image intensity surrounding the point is used to track the displacement in subsequent images by optimizing a correlation criterion. The accuracy and uncertainty in 2D–DIC displacement and strain measurements are well characterized in the literature for rigid body motion and uniform strain conditions. 2D–DIC is sensitive to out-of-plane motions, which can generate significant errors in in-plane strain measurements (Sutton et al., 2008).

Myers et al. (2010b) used a commercial 2D–DIC system, Vic2D (Correlated Solutions, Columbia, SC, USA), to track the displacement of the sclera of mouse eyes imaged in-profile under the microscope. The experiment tracked the motion of the scleral edge, the boundary between the profile image of the eye and the background, to minimize 2D–DIC error from out-of-plane motion. The experimental setup has been applied to evaluate differences in scleral properties between mouse strains (Nguyen et al., 2013; Steinhart et al., 2012) and with age (Myers et al., 2010c), as well as for the effect of experimental intraocular pressure elevation on scleral behavior (Nguyen et al., 2013; Steinhart et al., 2012) and of scleral stiffening on glaucoma progression (Kimball et al., 2014). Results showed that chronic experimental intraocular pressure elevation increased the stiffness but decreased the anisotropy of the pressure-strain inflation response (Nguyen et al., 2013). A collagen 8 mutant mouse strain with a stiffer baseline inflation response was more resistant to retinal ganglion cell axon loss (Steinhart et al., 2012); however stiffening the mouse sclera with glyceraldehyde increased axon loss (Kimball et al., 2014). The seemingly conflicting results indicate a complex relationship between scleral stiffness and optic nerve deformation that requires more detailed investigations.

The correlation algorithms used in the above studies are point-wise methods that independently track the displacements of each point in the reference image. Alternatively, global correlation algorithms apply interpolation functions to represent the displacement of the entire image and optimize a correlation criterion over the whole image. This method can provide smoother displacement and strain fields. Sigal et al. (2014a) applied a finite-element based DIC algorithm to analyze 2D projections of SHG images of the human lamina cribrosa for the displacement and strain fields arising from whole globe inflation.

Three-dimensional DIC

Three-dimensional DIC [3D–DIC] operates on a series of images of a deforming surface, acquired by a multi-view camera system (usually a stereovision system) from different viewpoints. The camera system is calibrated to determine the coordinate system of the cameras, their relative positions, and distortion coefficients. DIC is used to perform cross-camera matching of the reference images from each camera to reconstruct the 3D geometry. The displacement field of the 3D surface is obtained by correlating between the deformed and reference images. Compared to 2D–DIC, 3D–DIC has an additional source of error from the 3D reconstruction of the specimen surface (Becker et al., 2006; Siebert et al., 2007). The baseline accuracy and uncertainty have been measured for 3D–DIC under static conditions (Becker et al., 2006; Fazzini et al., 2010; Hu et al., 2011; Ke et al., 2011; Myers et al., 2010b; Wang et al., 2003) and rigid body translation (Coudrillier et al., 2012; Ke et al., 2011) for both curved and planar objects (Hu et al., 2011; Ke et al., 2011). For stereo-vision systems, the out-of-plane displacement error and uncertainty are sensitive to the camera stereo-angle.

Myers et al. (2010a) used a commercial 3D–DIC system, Vic3D (Correlated Solutions, Columbia, SC, USA), to measure the inflation response of bovine sclera. Murienne et al., (2014) measured significant changes in the inflation response of porcine sclera with removal of sulfated glycosaminoglycans by chondroitinase. Coudrillier et al., (2015, 2014, 2013, 2012) measured the inflation response of the human sclera and compared for the effects of age and glaucoma damage, and diabetes. The inflation response in all regions of the sclera stiffened significantly with age in the range of 40–90 years old (Coudrillier et al., 2012). The meridional strain inflation response in the peripapillary sclera was stiffer for specimens from glaucoma donors. The circumferential strain in the peripapillary sclera showed slower creep (increase in strain over time under constant pressure) for specimens from donors diagnosed with glaucoma than donors without glaucoma.

A 2-camera stereovision setup is unable to image complex surface topography with sharp transitions, such as at the scleral-ONH interface. To overcome this limitation, Pyne et al. (2014) developed the sequential digital image correlation method that used a single stationary camera to image a specimen mounted on a stage that can rotate 90° about 2 orthogonal axes. In the method, the specimen is subjected to a sequence of rotations about the 2 axes. The specimen is imaged after each rotation to emulate a conventional multi-camera stereovision system. The method provided greatly improved reconstruction of the ONH region compared to conventional 3D–DIC. However, the method requires a significant amount of time to image the specimen at each pressure step, which prevents it from being used to measure the time-dependent viscoelastic response.

Digital Volume Correlation

Digital volume correlation [DVC] extends the DIC method to measure the 3D displacement field in 3D volumes (Bay, 2008; Franck et al., 2007). DVC requires an imaging system that can penetrate through the thickness of tissues, such as laser scanning optical microscopy, OCT, or micro-computed tomography. The principals of DVC are similar to DIC. A sequence of images of the specimen in the undeformed and deformed configurations is acquired. The images are divided into subvolumes surrounding material points of the reference image, which are compared to subvolumes in subsequent images for displacement tracking. Similar types of correlation criterion, shape functions for deformation, sub pixel interpolation schemes, and optimization schemes applies for DVC as for DIC. Franck et al. (2011, 2007) developed a DVC method that analyzed images acquired by a laser scanning confocal microscope for traction force microcopy of cells in a 3D matrix. Girard et al. (2013) applied DVC to two sets of in vivo OCT volume images of the human optic nerve head. Their algorithm used first order shape functions to determine the 3D displacement vector and the full deformation gradient. Girard et al. (2011b) also developed a contrast enhancement algorithm for OCT images of the optic nerve head.

4.1.3 Electronic Speckle Pattern Interferometry

Electronic Speckle Pattern Interferometry [ESPI] is a non-contact optical method that uses the interference between an object beam and a reference beam to measure the displacement of a surface (Jones and Wykes, 1989; Sharp, 1989; Wykes, 1982). In a typical setup, a laser beam is passed through a beam splitter to produce a reference beam and an object beam. The latter is reflected off of the specimen surface to form a speckle pattern. The reflected object beam and reference beam are combined to produce an interference fringe pattern, which is recorded by a CCD camera (Figure 5). Deformation of the specimen surface changes the phase difference between the reflected and object beams, which is related to the displacement components in the image plane through the wavelength of the laser and the illumination angle relative to the specimen surface. The full 3D displacement field can be measured by analyzing the speckle fringes from at least 3 illumination directions.

Figure 5.

Raw speckle fringes generated from one illumination direction from inflation of a rubber sheet from 10 to 10.2 mmHg, used to track surface displacement using ESPI. Reproduced from Girard et al. (2009a).

The advantage of ESPI and other laser-based methods is that they can achieve submicron displacement accuracy. Fazio et al. (2012a) measured the displacement caused by inflation of a rubber specimen by 0.5 mmHg and reported a displacement uncertainty of 16 nm for a single pressure increment. However, the measurement range of ESPI is small, typically less than 100 µm (Cirello and Pasta, 2010; Soons et al., 2012; Zhang and Arola), and larger displacements must be approached incrementally. The inflation experiments of Girard et al. (2009a) and Fazio et al. (2012a, 2012b) applied pressure increments of 0.01 to 0.2 mmHg to span a range of 5 to 45 mmHg (Fazio et al., 2012b). The high sensitivity of ESPI also requires the specimen to be static during the measurement (Soons et al., 2012); for example, scleral specimens were allowed to equilibrate after each pressure step to remove the effects of creep before being recorded. Another disadvantage of ESPI is that it does not provide the surface geometry of the specimen, and an independent system is needed to reconstruct the surface geometry for strain calculation. Fazio et al. (2012b) used a 3D digitizer (MicroScribe G2X, Immersion, San Jose, CA) with a resolution of 0.2 mm to reconstruct the geometry of the human scleral specimens at 10 mmHg, then fit the results to a generalized sphere.

Girard and coworkers (2011c, 2009a, 2009c) applied a commercial ESPI system, Q-100 (Dantec Dynamics A/S, Denmark), for inflation testing of the posterior sclera of monkey eyes. The studies investigated the effect of age and chronic exposure to intraocular pressure elevation. Fazio and coworkers (2014a, 2014b, 2012b) applied the same ESPI system to investigate the human posterior sclera. The authors reported large sectorial differences in the maximum principal strain response, with the largest tensile strains in the temporal and inferior quadrants of the peripapillary sclera (Fazio et al., 2012b). The pressure-strain inflation response was generally stiffer with age and the sectorial variation in strain also differed with age (Fazio et al., 2014a). The age-related stiffening was larger for specimens from donors of African descent (Fazio et al., 2014b).

4.1.4 Ultrasonic Speckle Tracking

Tang et al. (2012) developed an ultrasonic speckle tracking (UTS) method to measure the strain response of the sclera to inflation. The method used a high-frequency ultrasound system to perform cross-sectional imaging of the posterior scleral cup of porcine eyes under controlled pressurization. A digitizer was used to sample radiofrequency ultrasound at a high sampling rate, and the authors developed a method to process the radiofrequency data for displacement correlation with improved the displacement sensitivity. The UTS method has high temporal resolution, and can be used to measure the time-dependent response of the tissue. The method provided the distribution of radial and hoop strains through the cross section, and the results showed significant compressive radial strain and non-uniform distributions of radial and hoop strains through the thickness. A later study reported that fluid infusion caused larger spikes in IOP in eyes with stiffer scleras (Morris et al., 2013).

5 Computational Techniques

The equilibrium equations that govern the deformation of elastic and viscoelastic objects are well-known (Timoshenko and Goodier, 1970), and thus, solution of these equations can in principle provide complete information about stresses and strains within tissues. There are a number of excellent commercial and open-source software packages that are available for this purpose, including ones that are specific to connective tissues (Maas et al., 2012). Most of these packages are based on a technique known as the finite element method (Zienkiewicz et al., 2005). In brief, in this method, the complex tissue geometry is decomposed into a large number of small non-overlapping sub-regions (termed elements), after which the governing equations are approximately solved over each element to construct a complete solution within the entire tissue region of interest.

The steps to developing a finite element analysis are as follows. A geometrical model of the tissue structure is created, either from anatomic measurements or from digital reconstruction of imaging data. The geometrical model is discretized into elements in a step called meshing, and boundary conditions are applied to the external surfaces of the tissue; these involve specification of loads, e.g. the IOP, or of displacements. Constitutive relations are specified for the tissues and the equilibrium equations are solved to find the displacement field. Finite element analysis has been used to investigate the effect of material properties, collagen microstructure, and anatomical dimensions of the sclera and lamina cribrosa on the deformation of the optic nerve head (Norman et al., 2011; Roberts et al., 2010b; Sigal, 2009; Sigal et al., 2011, 2010, 2009, 2008, 2005).

There are many technical issues associated with the finite element method. It can be challenging to create a representative geometrical model that incorporates all relevant anatomic features, and to then subdivide this geometry into well-formed elements. Fortunately, there are both commercial and open-source software packages for this latter meshing step. The accuracy of the numerical solution produced by the finite element method improves as the elements decrease in size. Unfortunately, the accuracy is not known a priori, and a well-designed computational study should include a mesh refinement analysis which assesses how the solution changes as elements become smaller. Another large source of error is the boundary conditions, which for tissues are typically complex or in many cases unknown. Grytz et al. (2014b) used spring elements to approximate the unknown boundary conditions at the holder for the inflation testing of the posterior sclera. The stiffness of the spring elements were determined using inverse finite element analysis along with the material parameters and anisotropy. Coudrillier et al. (2013) investigated the effects of different boundary conditions for the ONH-scleral interface on the results of the inverse finite element analysis.

The inverse finite element method uses finite element analysis and an optimization algorithm to determine the parameters of a constitutive relation from a known (measured) displacement field. The finite element method is used to compute a displacement field for an initial (guessed or estimated) set of parameters for the constitutive relationship. The computed displacements are compared to experimental data, and the parameters are iteratively improved to provide a best match between computed and measured displacements. Girard et al. (2009b) applied the inverse finite element method to determine the material properties and anisotropic collagen structure of the sclera of monkey eyes from ESPI data of inflation tests. The results showed that the tangent modulus and structural stiffness increased significantly with age, and also increased on average in eyes exposed to chronic IOP elevation. Grytz et al. (2014a, 2014b) applied the inverse finite element method to analyze ESPI data from inflation tests to infer material properties, including collagen anisotropy and crimping, for the human sclera. Results showed that the shear modulus increased with age and the collagen fibril crimp angle, describing the extent of collagen crimping, decreased significantly with age. Both effects increase the stiffness of the scleral material response. Further, the shear modulus was significantly higher and crimp fiber angle was smaller for donors of African descent compared to donors of European descent. Coudrillier et al. (Coudrillier et al., 2015, 2014, 2013) performed an inverse finite element analysis of 3D–DIC inflation data of the human sclera. The authors created specimen specific finite element models from the 3D–DIC reconstruction of the surface geometry, and applied specimen-specific WAXS measurements to assign parameters for the collagen structure in each element (Coudrillier et al., 2013) (Figure 6). The inverse finite element analysis was used to determine the material properties of the collagen fibers and non-fibrillar matrix, showing that the shear modulus of the non-fibrillar matrix increased with age and diabetes diagnosis (Coudrillier et al., 2014). The sclera of diabetic donors also showed a larger increase in the matrix and collagen stiffness with age (Coudrillier et al., 2014).

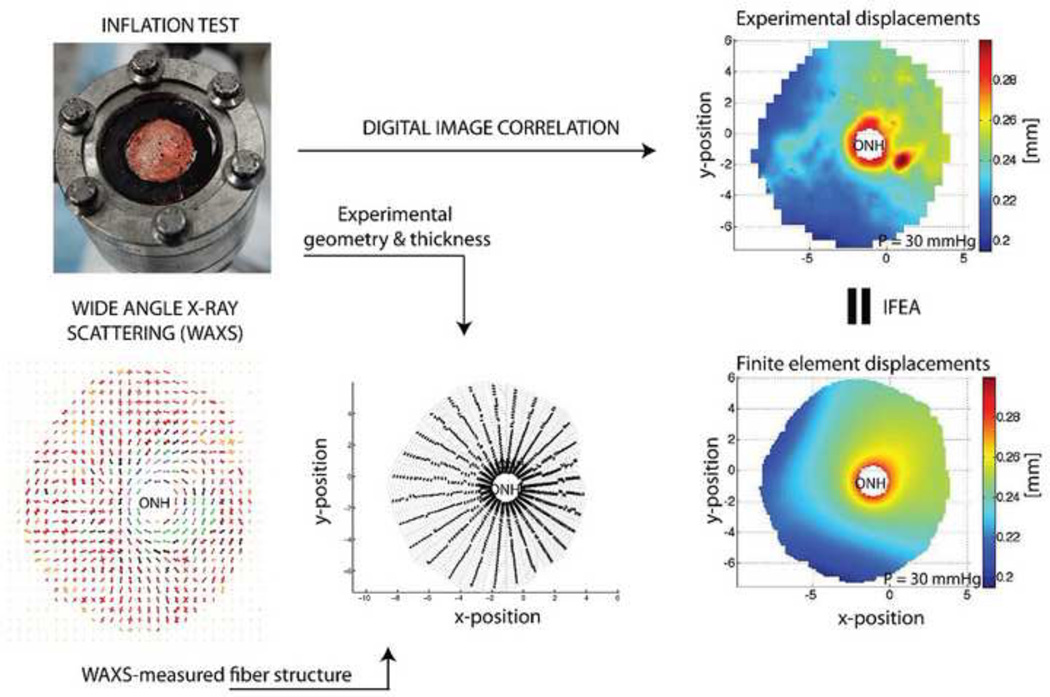
Figure 6.

Overview of ocular inflation testing and inverse finite element analysis (IFEA). An eye or posterior segment is clamped in a chamber (top left) and pressurized while measuring scleral deformation (top right). The scleral shell geometry and thickness are measured (bottom middle) and combined with information about collagen fiber orientation (bottom left) in a finite element model that predicts scleral displacements (bottom right). Iterative adjustment of tissue mechanical properties in the finite element model until approximate matching of measured and computed displacements allows deduction of local tissue mechanical properties. Top left panel reproduced from (Coudrillier et al., 2012).

6 Anterior Segment Biomechanics in Glaucoma

Although there has been less study of anterior segment biomechanics in glaucoma as compared to work on the posterior segment, it has been appreciated for many years that the aqueous outflow biomechanics is important that that this system contains mechanically responsive cells and tissues. For example, Johnstone and Grant (1973) showed that the trabecular meshwork deforms substantially as IOP varies. Acott, Bradley and others in the field have demonstrated that the outflow system includes a biomechanically-influenced homeostatic feedback mechanism, and have identified some of the key molecular players (Acott et al., 2014; Bradley et al., 2001; Bradley and Acott, 1998; Gonzalez et al., 2000; Stamer and Acott, 2012; Vittitow and Borras, 2004). Unfortunately, it has been extremely challenging to measure and model the biomechanical state of the outflow system, and only a modest number of studies have attempted to do so. Johnson and Kamm (1983) created an early model of IOP-induced Schlemm’s canal collapse which relied on indirect estimates of trabecular meshwork stiffness. This model was later extended to estimate fluid shear stresses in Schlemm’s canal in both humans (Ethier et al., 2004) and mice (Stamer et al., 2011), concluding that they could be of sufficient magnitude to play a mechanobiologic role in aqueous outflow. Other models have considered the hydrodynamic effects of proteoglycan gels in the trabecular meshwork, e.g. (Ethier et al., 1986; Seiler and Wollensak, 1985).

Direct measurements of trabecular meshwork and Schlemm’s canal endothelial mechanical properties have appeared recently. In an important study, Last et al. (2011) used atomic force microscopy to measure the compressive stiffness (Young’s modulus) of normal and glaucomatous trabecular meshwork, observing that the latter tissue could be 1–2 orders of magnitude stiffer than normal (control) trabecular meshworks. This result may have been influenced by tissue mounting procedures (Morgan et al., 2014) and is somewhat at odds with recent measurements of trabecular meshwork stiffness made using a uniaxial stretching approach (Camras et al., 2012). Given the responsiveness of trabecular meshwork cells (Thomasy et al., 2012; Wood et al., 2011) and Schlemm’s canal endothelial cells (Overby et al., 2014) to substrate mechanical properties, future measurements of how trabecular meshwork stiffness changes in glaucoma will be very important. Indeed, this and other work in this area is aimed at developing novel IOP-control strategies based on improved biomechanical and mechanobiological understanding of outflow pathway tissues (Stamer and Acott, 2012).

Atomic force microscopy and uniaxial stretching measurements both require excision of tissue from its native environment and subsequent handling, which can potentially induce artifacts. It is thus extremely appealing to consider measurement approaches which allow visualization of in situ tissue deformation under different loads, an option which has recently become viable with the development of high-resolution OCT systems. For example, Kagemann and colleagues (2012, 2011) have described OCT systems and image processing techniques to allow identification of trabecular meshwork deformations as IOP is changed and that have the potential to provide important in vivo estimates of tissue mechanical properties. Similarly, using an enucleated eye preparation, Wang, Johnstone and colleagues have used OCT imaging to map trabecular meshwork motion and some measures of deformation in eyes as IOP is varied in a controlled fashion (Hariri et al., 2014; Li et al., 2013, 2012). Although these studies have not directly yielded mechanical properties of the outflow system, they certainly have the potential to do so.

7 Conclusions

The study of Ocular Biomechanics in glaucoma is at an exciting stage. New computational approaches and, particularly, new experimental techniques, are being used to characterize both anterior and posterior segment ocular biomechanics in novel ways and with higher-than-ever accuracy and spatial resolution. This information is helping us understand and potentially treat the riddle that is glaucoma.

We conclude with a (necessarily incomplete) list of “grand challenges” whose solution will help realize the potential for both clinical and basic science impact in the field of Ocular Biomechanics.

1. Can novel experimental techniques and approaches be developed and validated to better characterize the full 3D biomechanical environment of relevant ocular tissues in glaucoma?

2. Can imaging-based techniques for assessing trabecular meshwork and optic nerve head tissue biomechanical properties in vivo be validated and shown to have diagnostic benefit for patients?

3. How can image-based computational models for the biomechanics of the optic nerve head be validated and applied to assess outcome of therapeutic strategies?

4. Can the mechanobiology and/or biomechanical environment of outflow pathway and/or ONH cells be altered for therapeutic benefit? In particular, will treatments designed to modify the stiffness of posterior segment connective tissues have therapeutic benefit in glaucoma?

5. What are the critical biomechanical factors (strain, strain rate, strain history, etc.) that contribute to the cascade of events that culminates in RGC axonal dysfunction in glaucoma?

6. How applicable is biomechanical understanding gained from animal models of glaucoma to the human disease?

It is worth further commenting on Challenge 5. Implicit in the fact that we have listed this as a challenge is the reality that the mechanism(s) whereby deformation of the cells and tissues of the ONH lead to loss of RGC axons remain uncertain. Over the years, a number of hypotheses have been proposed to explain this pathway, including direct mechanical compression of RGC axonal bundles by shearing of LC pores leading to transport blockade (Ernest and Potts, 1968; Minckler, 1986; Quigley and Anderson, 1977, 1976); mechano-sensitive conversion of ONH astrocytes to a reactive phenotype (Beckel et al., 2014; Howell et al., 2007; Johnson et al., 1996; Morgan, 2000; Sun et al., 2013; Tehrani et al., 2014); and impairment of ONH blood flow due to deformation of capillaries within the LC, consistent with clinical findings of altered ONH blood flow in some types of glaucoma (Flammer et al., 2002). It is very possible that all of these factors contribute to the pathogenesis of RGC axonal dysfunction and damage (Burgoyne, 2011; Downs et al., 2008; Sigal and Ethier, 2009), and one could imagine that the relative contribution of each factor would be patient-specific.

A better understanding of these complex processes will clearly rely on animal models of glaucoma, the subject of this special issue. In this context, it is important to understand that although animal models are valuable and demonstrate important features of human glaucoma, e.g. IOP-related loss of retinal ganglion cell axons, there are also species-dependent biomechanical differences in the ONH; hence our listing of Challenge 6 above. For example, the widely-use mouse and rat lack a true collagenous lamina cribrosa, instead having a so-called “glial lamina” characterized by a relative abundance of astrocytes (Howell et al., 2007; Lye-barthel et al., 2013; Morrison et al., 1995; Sun et al., 2009). Further, rats and mice have an elaborate perineural vascular plexus that differs markedly from the vascular anatomy of the human ONH (Morrison et al., 1999; Sugiyama et al., 1999). The biomechanical implications of these anatomic differences are unknown, but likely significant, and thus merit further study. The non-human primate has a true collagenous lamina (Burgoyne et al., 2004) and is therefore presumably biomechanically more similar to the human than are rodent models, but of course is expensive and complex to work with. It is noteworthy that there are species that may occupy a “sweet spot” between rodents and monkeys, specifically having a true collagenous lamina cribrosa (and thus presumably being biomechanically “close” to humans) yet being cheaper and easier to work with than monkeys. One example is the tree shrew (Albon et al., 2007), widely used in myopia research. Development and validation of models of glaucomatous optic neuropathy in such species would be a valuable addition to the field.

Abbreviations

AFM

Atomic force microscopy

DIC

Digital image correlation

DVC

Digital volume correlation

ESPI

Electronic Speckle Pattern Interferometry

IOP

intraocular pressure

LC

lamina cribrosa [LC]

ONH

optic nerve head

OCT

optical coherence tomography

PEX

pseudoexfoliation

RGC

retinal ganglion cell

SHG

second harmonic generation

SALS

small-angle light scattering3D–

DIC

Three-dimensional DIC

WAXS

wide-angle X-ray scattering

Mechanics-related definitions

Crimp

Here, the extent of collagen undulation, related to whether collagen fibers are loaded or unloaded.

Isotropic

Refers to a material whose properties are the same in all three orthogonal directions Preconditioning

Strain

Quantification of the normalized deformation of an object

Stress

Force per unit area acting within or on an object

Tensor

A mathematical entity that describes a quantity that incorporates information about two (or more) directions. A tensor is a generalization of a vector, which incorporates information about only one direction.

Viscoelasticity

A characteristic of certain materials (including many tissues) that behave both as an elastic solid and a viscous fluid.