Genetic Algorithm Optimized Triply Compensated Pulses in NMR Spectroscopy

Abstract

Sensitivity and resolution in NMR experiments are affected by magnetic field inhomogeneities (of both external and RF), errors in pulse calibration, and offset effects due to finite length of RF pulses. To remedy these problems, built-in compensation mechanisms for these experimental imperfections are often necessary. Here, we propose a new family of phase-modulated constant-amplitude broadband pulses with high compensation for RF inhomogeneity and heteronuclear coupling evolution. These pulses were optimized using a genetic algorithm (GA), which consists in a global optimization method inspired by Nature’s evolutionary processes. The newly designed π and π/2 pulses belong to the ‘Type A’ (or general rotors) symmetric composite pulses. These GA-optimized pulses are relatively short compared to other general rotors and can be used for excitation and inversion, as well as refocusing pulses in spin-echo experiments. The performance of the GA-optimized pulses was assessed in Magic Angle Spinning (MAS) solid-state NMR experiments using a crystalline U – ¹³C, ¹⁵N NAVL peptide as well as U – ¹³C, ¹⁵N microcrystalline ubiquitin. GA optimization of NMR pulse sequences opens a window for improving current experiments and designing new robust pulse sequences.

INTRODUCTION

At the base of all NMR experiments, there is the evolution of spin systems under various average Hamiltonians to generate a desired spin state and observe its time evolution. For the preparation of these specific spin states, average Hamiltonians are obtained using a time-ordered sequence of RF pulses and delays (i.e., pulse sequences). An ideal RF pulse flips the nuclear spins coherently throughout the spatial and spectral dimension of the NMR sample. However, inhomogeneities in the spatial (RF inhomogeneity --- spatial dependence of RF field strength along the sample volume) and spectral dimensions (offset effect --- due to finite pulse width in time domain), as well as errors in pulse calibration deviate the nuclear spin magnetization from its ideal trajectory. These factors affect both sensitivity and resolution in NMR experiments. To overcome this problem, one may use systematic compensation methods such as composite [3, 4] or adiabatic [5] pulses. Composite pulses consist of a sequence of RF pulses that are designed to emulate the effect of a single excitation or inversion pulse. Based on the type of compensation, composite pulses are categorized as: a) broadband pulses, which compensate for offset effects [6-10]; b) composite pulses for RF inhomogeneity compensation [9, 11-13]; c) dual-compensated pulses, which operate simultaneously on both offset effects and RF inhomogeneity [14, 15]; and d) compensated pulses for zz interactions [7, 16], which include heteronuclear dipolar and scalar coupling ($I_z^1{S}_z^2$) as well as weak scalar couplings in homonuclear spin pairs ($I_z^1{I}_z^2$). However, none of these pulses are designed to compensate for RF inhomogeneity, offset effects, and zz interactions, simultaneously. Additionally, composite pulses that are designed to achieve specific initial states (such as excitation and inversion pulses) and are not applicable without detailed analysis of the whole pulse sequence.

To address these issues we have designed new triply compensated pulses using the Genetic Algorithm (GA). GA is a global optimization method that was first proposed by John Holland in 1975 [17]. GA optimization is based on natural biological evolution [18] that operates on a population of solutions encoded into a chromosome-like data structure. The evolution of the solutions is obtained by applying recombination operators [18, 19]. As with the natural selection of living organisms, the solutions originating from each generation displaying the greatest fitness have a higher probability to be selected for the next generation. The process continues until the best solution to a specific problem is reached. This approach has been previously applied for designing new NMR experiments [20], improving RF excitation and inversion accuracy [21], and optimizing simple pulse sequences [22-24]. Unlike other pulse engineering methods in NMR, such as gradient ascent [25, 26], Nelder–Mead simplex algorithm [27], etc., GA is a stochastic global optimization method.

In this paper, we used GA to design smooth, phase-modulated, constant-amplitude, broadband pulses with RF inhomogeneity compensation. These short phase-modulated pulses have optimal compensation towards fidelity loss due to the evolution of the zz interactions during pulsing, which makes the pulses robust even at low RF powers. The GA-optimized pulses described here belong to the ‘type A’ composite pulses (also known as general rotors)[4], which do not apply any phase distortion to the magnetization. Phase distortionless π pulses were originally developed by Tycko et al. in 1985 [28], and these are applied in both NMR Quantum Information Processing [29] [30] and SQUID [31]. Also, multiple compensated pulses were previously designed by Nimbalkar in ‘Fantastic Four’ pulses [32] and ‘J compensated concurrent shapes’ by Ehni et al. [33][32]. However, they were designed for liquid state NMR, where heteronuclear coupling constants are of the order of 100 Hz. Our fully compensated (‘type A’ or general rotors) composite pulses described here are of general application and operate on a wide variety of initial conditions [4], which represents a significant advantage over traditional composite pulses. We also introduce a practical way of characterizing dual compensation pulses, then used this method to analyze the robustness of our GA optimized dual compensation composite pulses along with other dual compensated ‘type A’ pulses reported in the literature that show the best performance according to our figure of merit.

THEORY

An ideal pulse operation (U_θ) flips the spins uniformly throughout the spatial and spectral dimension of the sample. Experimental pulse imperfections such as RF inhomogeneity, pulse calibration errors and offset effect due to finite width of RF pulse, deviate the spin magnetization from its ideal path which conversely affects sensitivity and resolution of the NMR experiments. Hence, an experimental pulse operation is a function of the offset that can be quantified by relative resonance offset, ΔB/B₀, and RF amplitude, B₁/${\mathrm{B}}_1^0$, where B₁ is the RF strength experienced by the sample which is deviated from the applied field (${\mathrm{B}}_1^0$). Also, for coupled spin systems, the evolution of the coupling interactions during the pulse will result in a further loss of fidelity, which can be severe when the magnitudes of both coupling strength and RF fields are comparable. Under non-spinning conditions, a pulse operation with a single hard RF pulse of field strength ~30 kHz for nitrogen or carbon spin systems under the effect of either Cα-Hα (−46 kHz) or NH (21 kHz) dipolar couplings will result in a fidelity loss of ~10%. Of course, as many pulses are combined in a unique pulse sequence the fidelity loss accumulates. In order to appreciate this phenomenon, let’s first consider a IS spin system with zz interactions of strength D and under the effect of a RF field B₁ with phase φ applied on spin I. The corresponding Hamiltonian, H, for the spin I can be written as:

$$H=2\pi \left[B_1\right(\mathit{cos}\phi I_x+\mathit{sin}\phi I_y)+\Delta B{I}_z+D{I}_z{S}_z]$$ 1

Since the individual Hamiltonian terms do not commute, the analytical formalism to generate an ideal single spin rotation using the Hamiltonian in Eqn. 1 is complex, although an approximated solution can be obtained using the Magnus expansion [28]. To obtain a solution to this problem, we simulated the Hamiltonian (H) using GA optimization and found the best phase modulation that emulates the effects of a single spin rotation over a range of offsets, RF inhomogeneities, and coupling interactions. A general experimental pulse unitary operation on an isolated spin pair defined by H can be written as:

$$U_{\theta }^e=\mathit{exp}(-iH\tau )$$ 2

where H is a function of relative resonance offset (ΔB/$B_1^0$), relative RF strength ( B₁/$B_1^0$), and relative coupling strength ( D/$B_1^0$). Therefore, the operator $U_{\theta }^e$ can be written as $U_{\theta }^e(\Delta B∕B_1^0,B_1∕B_1^0,D∕B_1^0)$. The functional dependence of $U_{\theta }^e$ can be evaluated from Eqn.1 and Eqn.2. For quantifying the robustness of π/2 and π rotations in $U_{\theta }^e(\Delta B∕B_1^0,B_1∕B_1^0,D∕B_1^0)$, we have used the fidelity ($\mathcal{F}$) formula [34] (Eqn. 3):

$$\mathcal{F}(\Delta B∕B_1^0,B_1∕B_1^0,D∕B_1^0)=\text{Trace}\left(U_{\theta }^e\right(\Delta B∕B_1^0,B_1∕B_1^0,D∕B_1^0)\times U_{\pi ∕2\text{or}\pi }^{†})$$ 3

where U_{π/2 or π} is the unitary operator for ideal π/2 or π RF pulses with phase x, and is given by

$$U_{\pi ∕2\text{or}\pi }=\mathit{exp}(-i(\pi ∕2\text{or}\pi \left)I_x\right)$$ 4

The formula in Eqn. 3 calculates the fidelity of the pulse for specified values of $\Delta B∕B_1^0,B_1∕B_1^0$, and D/$B_1^0$. The flipping action of $U_{\theta }^e$ throughout the experimental range of offsets and RF amplitudes can be quantified using the volume under the fidelity surface generated by (ΔB/$B_1^0$) and (B₁/$B_1^0$). By maximizing this fidelity volume via optimization methods, it is possible to obtain robust dual compensated pulses. For the GA optimization, we selected the fitness function as the volume under the fidelity surface with (ΔB/$B_1^0$) varying from −1 to +1 and (B₁/$B_1^0$) from 0.5 to 1.5. These ranges can be manipulated to get dual compensation or single compensation for either offset or RF inhomogeneity. In the optimization procedure, the coupling strength, D, is set as a constraint to achieve zz compensation over a range of experimental zz interactions along with dual compensation, enabling only those solutions with fidelity loss changes less than a critical value (~1%) to evolve.

MATERIAL AND METHODS

The MAS solid-state NMR experiments were performed using a crystalline N-acetyl-L-¹⁵N-valyl-L-¹⁵N-leucine (NAVL) dipeptide [35] and Uniformly labelled (¹³C, ¹⁵N) microcrystalline ubiquitin[36]. The experiments with NAVL were carried out on a VNMRS 700 MHz solid-state NMR spectrometer (Agilent) using 10 kHz spinning speed at a temperature of 298K. The experiments with microcrystalline ubiquitin were performed on a Bruker AVANCEIII 700 MHz spectrometer with a spinning speed of 12 kHz and at 298K. For each 1D spectrum, we acquired 128 scans with a relaxation delay of 2 s.

To optimize the triply compensated pulses, we used the global optimization toolbox included in MATLAB®. The calculations were carried out using a simultaneous optimization of 200 phase points that took approximately 2 days on a personal computer equipped with an Intel Corei7 (2.7 GHz) processor. For most cases, we obtained well-performing pulses with 20-50 phase point optimization. To obtain smooth phase shape, however, a minimum of 150 parameters is required. For most calculations, we started with a random phase set and used a population size of 50 individuals evolved for 10⁴ generations. For the population type, we used the ‘doubleVector’ routine and the parental selection was performed with the ‘Roulette’ selection method with an ‘elite count’ of 2. For all optimizations, the ‘Uniform’ mutation with a ‘rate’ of 0.05 was used and the ‘Arithmetic’ crossover function was used. All of the routines utilized are available at http://www.mathworks.com/help/gads/genetic-algorithm-options.html.

RESULTS

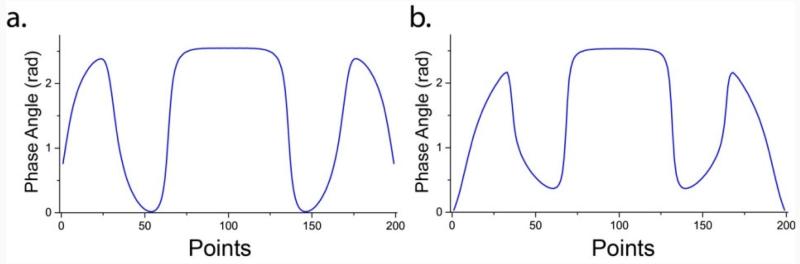
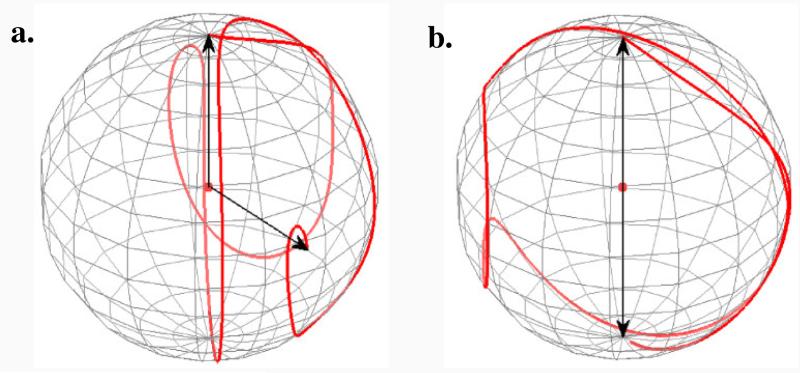
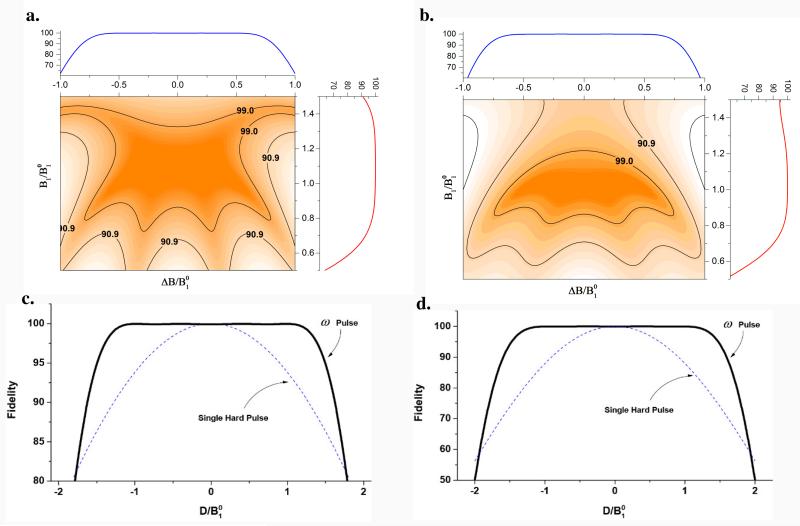
For the GA optimization of the compensated pulses, we used 200 independent parameters that constitute the phases of a 200 point shaped pulse at constant amplitude. Specifically, we used a population of 50 individuals and evolved for 10⁴ generations to find the best solution, i.e., the best phase modulation set for robust π/2 and π rotations (U_π/2 and U_π, Eqn. 4). To search for the best phase modulation, we performed more than three optimizations, every time with different initial populations for each operator. However, all of the attempts resulted in the same shape of the fitness function, suggesting that we had reached a possible global minimum for the given constraints. The length of the optimized pulse was restricted by a fixed total nutation angle, Θ, and equal to the product of the applied RF field strength $B_1^0$ and pulse length τ. In general, for an arbitrary shaped pulse, Θ represents the area under the amplitude shape of the RF. The total nutation angle Θ can be considered as a resource for the optimization, and can be controlled using either $B_1^0$ or τ. Experimental conditions limit both variables, therefore, all optimizations were designed to reach maximum achievable robustness for a given Θ. In our case, we used Θ = 5π and generated a phase modulation with a maximum dual compensation area for that specific value. Subsequently, we improved the robustness of the pulse by using Θ = 9π, 9.2 π and 11π. The GA-optimized phase modulations for robust π/2 and π rotation pulses of length Θ = 5π are shown in Figure 1a and Figure 1b, respectively. The optimal trajectories of spin magnetization on the Bloch sphere representation (obtained by starting from I_z) are shown in Figure 2. The length of these trajectories is proportional to the total nutation angle Θ. We numerically evaluated the fidelity profiles of these pulses for π/2 (Figure 3a) and π pulses (Figure 3b). For standard experimental range of chemical shift and RF inhomogeneity, the fidelity of these GA optimized pulses are more than 99%, which can be considered as an ideal pulse operation in experimental NMR. The response of these pulses to the zz interaction with relative interaction strength is shown in Figure 3c and Figure 3d. A robust fidelity response is observed for those coupling strengths that are comparable to the applied RF field strength.

Figure 1. GA optimized phase modulated shapes for robust π/2 (a) and π (b) rotation pulses of length 5π.

Total evolution times for these pulses are 5 times of the length of hard π pulse with same rf strength (for B₁ = 40KHz, pulse length for GA optimized pulse is 62.5μS). To convert points into time consider that 1 point = 5π/(2π$B_1^0$ × 200).

Figure 2.

Bloch sphere trajectories of I_z magnetization under the action of GA optimized π/2 (a) and π (b) pulses (Figure 1), for the case, ΔB = 0 and B₁/$B_1^0$ = 1.

Figure 3.

Fidelity surface contours of the phase modulated π/2 (a) and π (b) pulses shown in Figure 1 with ‘relative resonance offset’ (ΔB/${\mathrm{B}}_1^0$) and relative rf strength (B₁/${\mathrm{B}}_1^0$). Inner contour represents a fidelity of 99%. c and d shows change in fidelity (%) with relative zz interaction strength (D / ${\mathrm{B}}_1^0$) π/2 and π pulses. Inner dotted line shows the response of single hard pulse of the same rf strength.

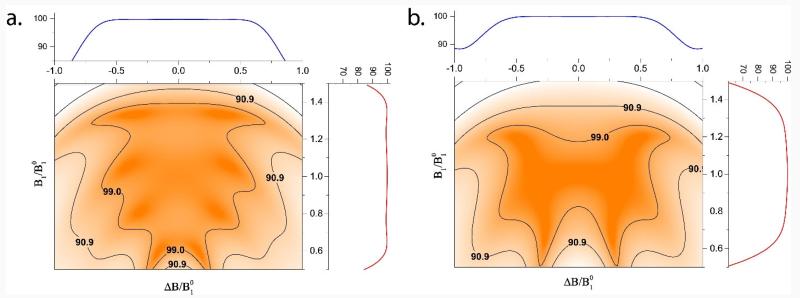
We also optimized pulses with larger dual compensation area by increasing the total nutation angle Θ. The obtained phase modulations for Θ = 9π are shown in Figure 4. These phase modulations comprise nine π pulses, with a robust π rotation. The nine pulse phase modulation, {114.4°, 162.2°, 200.5°, 174.3°, 48.1°, 174.3°, 200.5°, 162.2°, 114.4°}, was designed with more weightage with respect to the RF strength, and hence, it had better RF compensation than offset (Figure 4a). Conversely, the nine pulse phase modulation shown in Figure 4b was designed with more weightage on the offset effects. The phase values obtained in this case were {104.5°, 152°, 206.1°, 182.8°, 47.8°, 182.8°, 206.1°, 152°, 104.5°}. By calibrating the relative weight of the total nutation angles as well as offset and RF compensations, it is possible to design composite pulses with specific characteristics. However, it should be kept in mind that improving the compensation by extending overall tip angle (Θ) has limitations due to long-range couplings as well as relaxation phenomena, which will come into picture when pulsing time increases.

Figure 4.

Fidelity surface contour plots of GA optimized nine π pulses with an effective action of robust π rotation, designed with more weightage on rf inhomogeneity (a) and offset (b). Inner contour represents a fidelity of 99%.

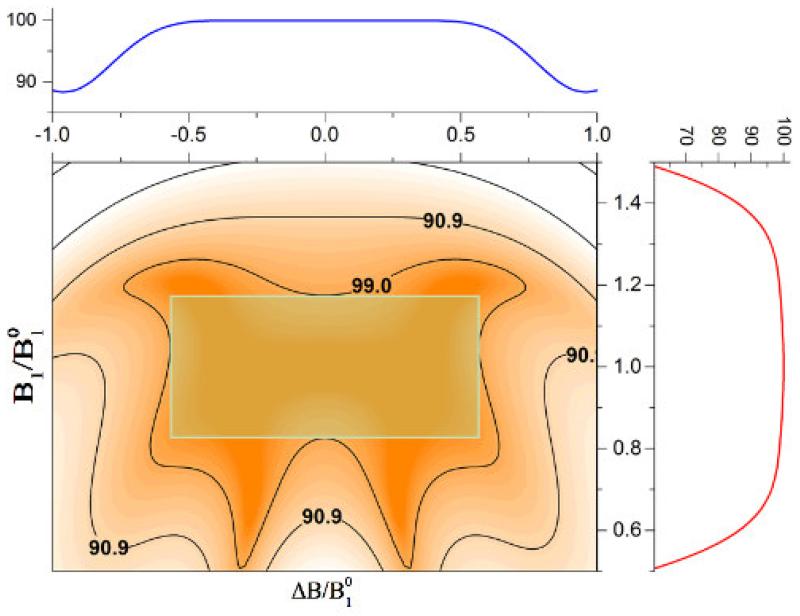
For the characterization of dual compensated pulses, Odedra et al. [2] used independent compensation ranges of each variable by fixing the other parameters at an ideal value. Simultaneous error (in RF strength and offset) handling of dual compensated pulses cannot be fully characterized by these independent compensation ranges. In another approach, Poon et al. [37] used the values of major and minor axes of the largest ellipse fitting within the 95^th percentile of the fidelity contour surface plot. A major drawback of these representations is that at maximum possible range of one parameter (e.g., relative RF strength), the second (relative offset) cannot have its full compensation range. In this work, we define a new figure of merit for dual compensation pulses which is termed ‘99fidelity rectangle’. The 99fidelity rectangle is the maximum area of a rectangle fitted in the fidelity profile, which is centered at ΔB/$B_1^0$ = 0 and B₁/$B_1^0$ = 1, with all fidelity points greater than or equal to 99%. A 2D fidelity map (ΔB/$B_1^0$) versus (B₁/$B_1^0$) is shown in Figure 5, with the yellow rectangle (99fidelity rectangle) centered at ΔB/$B_1^0$ = 0 and B₁/$B_1^0$ = 1 showing the area corresponding to a fidelity greater than 99%.

Figure 5.

Maximum area rectangle fitted at the center (ΔB / $B_1^0$ = 0 and B₁ / $B_1^0$ = 1) of a fidelity profile (Figure 4b). All points inside the rectangle have a fidelity greater than 99% (called the 99fidelity rectangle). The dimension of this 99fidelity rectangle is (±0.57) × (±0.18), meaning the given composite pulse has 99% fidelity for the range of relative resonance offsets from −0.57 to +0.57 and relative RF amplitudes from −0.18 to +0.18.

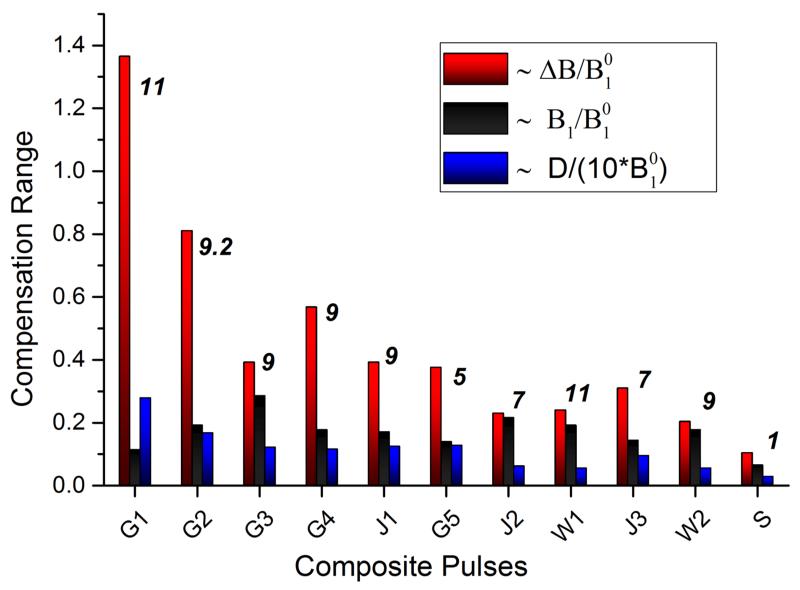
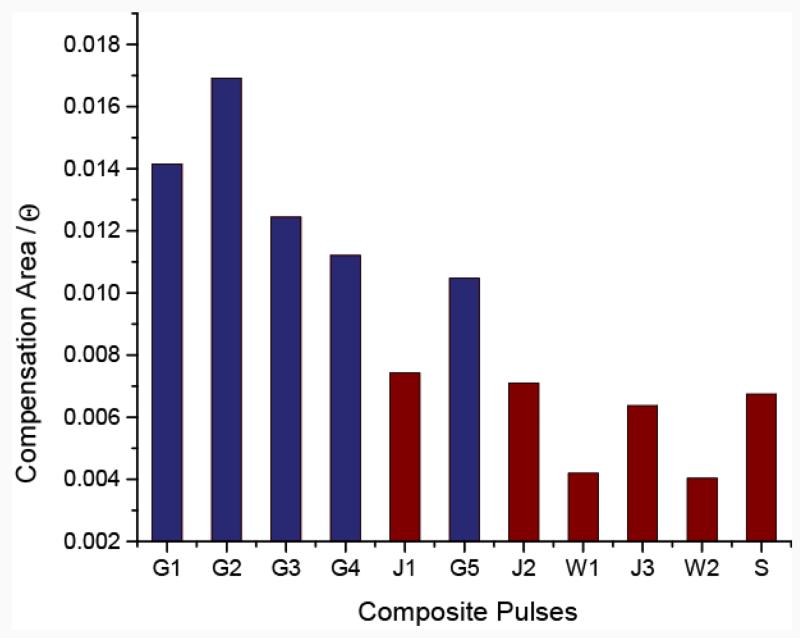
We performed a comparative study of GA optimized pulses with other ‘general rotors’ in literature [1, 2], using the 99fidelity rectangle. To this extent, we selected the best performing dual compensated ‘type A’ composite pulses: ASBO-9(B1), ASBO-11(B1) by Odedra et al. [2], and composite pulses by Jones et al. [1]. For ease of comparison, we renamed these composite pulses W1 for ASBO-11(B1), W2 for ASBO-9(B1) and J1,J2 for those reported in reference [1]. All of these composite π pulses are listed in Table 1 and the comparison, along with the theoretical (simulated) 99fidelity rectangles for each pulse, are reported in Figure 6. As shown in Figure 6, GA optimized pulses (G1 to G5) have better compensation towards simultaneous experimental inhomogeneities and hence can perform efficient pulse operation in a variety of experimental conditions. G1 and G2 can be used for applications involving broadband rotation, with moderate RF inhomogeneity compensation; the G3 pulse is suitable for cases that require dual compensation above typical experimental inhomogeneities. In order to find composite pulses that utilize the minimum amount of resources (RF power and pulse duration), we have carried out computer simulations and analyzed the area of compensation using the 99fidelity rectangle achieved per unit Θ (Figure 7). Based on these data, GA general rotors are the most economical solutions as demonstrated by the level of compensation achieved per unit source Θ. The robustness of the GA-optimized composite π/2 pulses (Figure 1) was also analyzed using the 99fidelity rectangle method (Table 2) and compared with the performance of CORPSE [29] and SCROFULOUS [30] sequences. Based on the dimensions of the 99fidelity rectangle, it is possible to conclude that our approach is more robust than both CORPSE and SCROFULOUS pulses (Figure S2).

Table 1.

‘type A’ composite pulses used for performance study. Flip angle of all the individual pulses are π except for G1, G2 and G5, which are constant amplitude pulses of length 11π, 9.2π and 5π respectively.

Label	Phases	Reference
W1	{260°, 103.5°, 187°, 119.5°, 292°, 0°, 68°, 240.5°, 173°, 256.5°, 100°}	[2]
W2	{268.5°, 62°, 6.5°, 131°, 0°, 229°, 353.5°, 298°, 91.5°}	[2]
J1	{282.1°, 339.5°, 339.4°, 159.4°, 114.6°, 159.4°, 339.4°, 339.5°, 282.1°}	[1]
J2	{252.5°,265.0°, 97.5°, 170.0°, 97.5°, 265.0°, 252.5°}	[1]
G1	300 point shape file (Varian shape file available with supplementary files)	This article
G2	144 point shape file (Varian shape file available with supplementary files)	This article
G3	{ 114.4°, 162.2°, 200.5°, 174.3°, 48.1°, 174.3°, 200.5°, 162.2°, 114.4°}	This article (Figure 4a)
G4	{ 104.5°, 152°, 206.1°, 182.8°, 47.8°, 182.8°, 206.1°, 152°, 104.5°}	This article (Figure 4b)
G5	199 point shape file (Figure 1b) (Varian shape file available with sup- plementary documents)	This article (Figure 3b)

Figure 6.

Robustness of ‘general rotors’ characterized using 99fidelity dimensions. All composite pulses are shown Table 1. Composite pulse G1-G5 are GA optimized, J1 and J2 are from [1], W1 and W2 are from [2] and S is single π pulse. Red and black bars represent the dimensions of 99fidelity rectangle; whereas blue bars represent the 1/10^th of the compensation for scalar coupling. The number above compensation bars shows the total nutation angle (Θ) of the pulse in π units.

Figure 7.

99fidelity rectangle area achieved per unit Θ for different dual compensated π pulses (Table 1). GA optimized pulses are shown in blue.

Table 2.

99fidelity rectangle dimensions of GA optimized composite π/2 pulse (Figure 1) and single hard π/2 pulse.

	(ΔB/${\mathrm{B}}_1^0$)	(B1/${\mathrm{B}}_1^0$)	(J/${\mathrm{B}}_1^0$)
GA optimized π/2 (Figure 1a)	±0.48	±0.204	±1.3116
Single Pulse π/2	±0.16	±0.132	±0.407

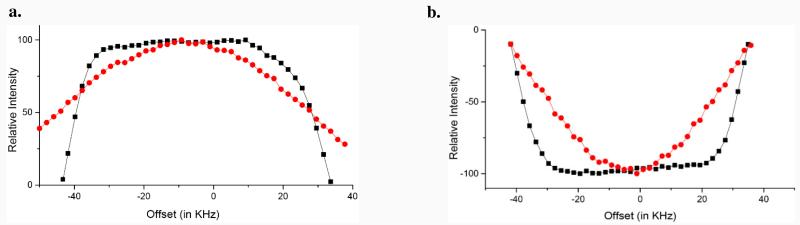
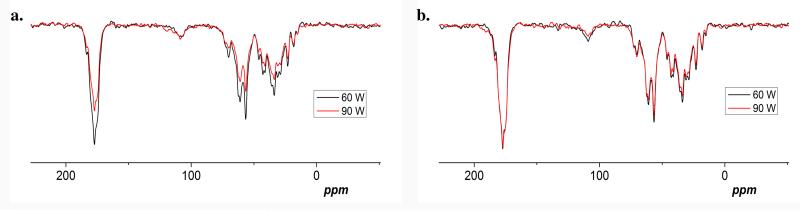
To assess the performance of these new pulses, we tested the GA optimized triply compensated π and π/2 pulses with total nutation angle Θ = 5π experiments on a crystalline N-acetyl-L-¹⁵N-valyl-L-¹⁵N-leucine (NAVL) dipeptide sample and U – ¹³C, ¹⁵N microcrystalline ubiquitin using MAS NMR experiments. Since the generation of an entire two-dimensional experimental profile requires a prohibitive number of experiments, as proof-of-concept we performed a representative experiment determining the offset response of these pulses for an RF amplitude of 40 kHz and a duration of 62.5μs. Figure 8 shows the offset response of π and π/2 pulses (both GA optimized and single hard pulses with same RF amplitude) in NAVL spinning at 10 kHz. The response curves clearly demonstrate the advantages of GA-optimized ‘type A’ general rotors with respect to the single hard pulse. We also performed experiments using microcrystalline ubiquitin spinning at 12 kHz. Figure 9 demonstrates the performance of single hard π pulse and GA optimized π pulse of length 5π in the presence of offset and RF inhomogeneity/pulse calibration error. These experiments were performed at power levels 60 (black) and 90 Watts (red), respectively. Note that 60 Watts is the calibrated power level for a π pulse of length 12.5 μs. Using an hard pulse on the Bruker 700 MHz spectrometer, the irradiation on the ¹³C channel at 116 ppm generated an offset of CO and Cα chemical shifts of approximately ±10 kHz away from the resonance frequency. In contrast, GA optimized pulses shows near uniform performance for both power levels (Figure 9).

Figure 8.

¹³C peak intensity of NAVL peptide (see Supplementary Figure 1) using GA optimized (a) π/2 (Figure 1a) and (b) π (Figure 1b) pulses along with single hard pulse responses (shown in red).

Figure 9.

Experimental ¹³C spectra of microcrystalline ubiquitin spinning at 12 kHz to demonstrate the action of (a) single hard pi pulses and (b) GA optimized pi pulses of length 5π. The experiments were performed at two different power levels to show the advantage of GA optimized π pulses. The black spectra are with power level 60 W, which is the calibrated power for π pulse of length 12.5 μs. The red spectra are with power level 90 W. In 700 MHz spectrometer, irradiating at the 116 ppm (of ¹³C), the chemical shift offset CO and Ca were ~±10 kHz away from the resonance. GA pulses shows near uniform performance for both power levels. This demonstrates robust performance of GA pulses in presence of RF inhomogeneity/pulse calibration errors along with an offset of ~±10 kHz.

DISCUSSION

Spatial and spectral inhomogeneities of RF pulses as well as errors in pulse calibration deviate the nuclear spin magnetization from its ideal trajectory. Robust pulse operation in NMR must compensate all these experimental imperfections. Traditional composite pulses are singly compensated, i.e., tailored for only one type of experimental imperfection. For instance, broadband pulses are singly compensated pulse for offset effects. A simultaneous compensation of both offset and RF inhomogeneity makes the pulse more robust for experimental implementation, and performs well even without fine calibration of RF pulses.

Here, we show the design of robust ‘type A’ RF pulses with inbuilt compensation towards common experimental errors. We treated the robust RF pulse design in NMR as an optimization problem. The basic strategy was to maximize the robustness of a pulse (quantified using a fitness function) by searching over its space parameters (amplitude, phase, and frequency). Formulating a good and expressive fitness function is the most important step in pulse design. Target operations of the pulse optimization as well as its compensation type are then controlled by the fitness function. Excitation and inversion composite pulses are designed to prepare specific states from I_z magnetization. This limits the application of these composite pulses to selected cases. For example, an inversion (I_z → −I_z) composite pulse acquire an extra phase to the spin magnetization in refocusing (I _{x or y} → −I_{x or y}) action. On the contrary, ‘type A’ composite pulses (or general rotors) grant a significant advantage as, in principle, these pulses can act on any initial spin state[4].

To improve the performance of ‘type A’ general rotors, we utilized GA, which explores exhaustively large search spaces [38, 39]. In fact, recent work by Manu and Kumar shows that GA can be successfully applied to pulse sequence optimization [22-24]. Using GA optimization, we designed robust RF pulses with triple compensation. To illustrate the features of these new pulses, we utilized a new figure of merit, the ‘99fidelity’ rectangle, which reports more faithfully on the performance of the dual compensated pulses. 99fidelity rectangle is more intuitive and practical way of characterizing dual compensation pulses. We were motivated by the basic idea that a dual compensated pulse with an RF compensation value of 0.5 and offset compensation value of 0.5 should compensate for a system with simultaneous imperfections of 0.5 in both RF and offset, whose compensation values are indicated as relative resonance offset and relative amplitude. Using this figure of merit, we have studied the best performing ‘type A’ composite pulses reported in the literature and compared them with our newly optimized GA pulses. Out of all the composite pulses with same total nutation angle, the GA-optimized pulses show a wider compensation range, showing a superior compensation for π and π/2 pulses in the presence of RF and offset imperfections.

Importantly, we found that GA optimized pulses are very robust with respect to phase errors. In fact, we tested their performance with both systematic and random phase errors up to a maximum value of ±5° for 200 point shaped π and π/2 pulses. The response curve is shown in Figure S3. Since these pulses can find use in solid-state MAS spectroscopy, we investigated the effects of the interference between sample spinning and pulse sequence for axially symmetric chemical shift anisotropy (CSA). Even in this case, we found that our pulses are rather robust with respect to single hard π pulse. These results are summarized in Figures S4 and S5, where the fidelity responses for both GA-optimized pulses and hard pulses are reported. Indeed, the curves for the hard pulses (Figure S5) show a poor fidelity response, while the GA-optimized pulses show almost 100% fidelity when the number of rotations (n_ωr) approaches eight cycles, i.e., high spinning rates. Finally, we compared the fidelity response of hard π pulses and GA optimized pulses with respect to the homonuclear dipolar coupling (Figure S6). In this case, the performance of the two pulses was very similar with fidelity greater than 99% for D_H/B₁ = [−0.2, +0.2]. For a RF strength of 40 kHz, this range will be from −8 kHz to +8 kHz and a typical homonuclear ¹³C coupling for peptides and proteins under MAS is around 4.2 kHz.

Moreover, total nutation angle (Θ) of a composite pulses can be considered as a resource for obtaining error compensation. Experimentally Θ is controlled by RF field strength and pulsing time. In order to compare composite pulses with different total nutation angle, we evaluated the compensation per unit resource (Θ) for each composite pulses. Here compensation is quantified by the area of 99fidelity rectangle ($\mathcal{A}$). Figure 7 shows the comparison of various composite pulses based on the $\mathcal{A}$/Θ ratio. For composite pulses designed using different pulse engineering techniques with the same Θ, the ratio ($\mathcal{A}$/Θ) indicates the conversion (Θ → $\mathcal{A}$) efficiency of the pulse engineering technique used. As shown in Figure 7, GA optimized composite pulses have better $\mathcal{A}$/Θ, which projects the efficiency of GA optimization in NMR pulse design.

CONCLUSIONS

In conclusion, we present a new family of triply compensated pulses optimized via the Genetic Algorithm. We demonstrate that the global optimization offered by GA optimized pulses are the best alternate π and π/2 pulses for systems with simultaneous imperfections in RF and offset. Importantly, these GA optimized pulses are short compared to other general rotors, making it easier to implement them in both solution and solid-state NMR spectroscopy as excitation/inversion pulses, refocusing pulses in spin echo experiments as well as quantum gates in quantum Information Processing [1, 40-42]. We anticipate that the applications of GA optimization in NMR pulse sequences will open another window of opportunity for improving NMR pulse sequences and designing new experiments.