Explained variance in the thermoregulatory responses to exercise: the independent roles of biophysical and fitness/fatness-related factors

Abstract

Individual variation in the thermoregulatory responses to exercise is notoriously large. Although aerobic fitness (V̇o_{2 max}) and body fatness are traditionally considered important predictors of individual core temperature and sweating responses, recent evidence indicates potentially important and independent roles for biophysical factors. Using stepwise regression, we examined the proportion of individual variability in rectal temperature changes (ΔT_re), whole body sweat loss (WBSL), and steady-state local sweat rate (LSR_ss) independently described by 1) biophysical factors associated with metabolic heat production (H_prod) and evaporative heat balance requirements (E_req) relative to body size and 2) factors independently related to V̇o_{2 max} and body fatness. In a total of 69 trials, 28 males of wide-ranging morphological traits and V̇o_{2 max} values cycled at workloads corresponding to a range of absolute H_prod (410–898 W) and relative intensities (32.2–82.0% V̇o_{2 max}) for 60 min in 24.8 ± 0.7°C and 33.4 ± 12.2% relative humidity. H_prod (in W/kg total body mass) alone described ∼50% of the variability in ΔT_re (adjusted to r² = 0.496; P < 0.001), whereas surface area-to-mass ratio and body fat percentage (BF%) explained an additional 4.3 and 2.3% of variability, respectively. For WBSL, E_req (in W) alone explained ∼71% of variance (adjusted to r² = 0.713, P < 0.001), and the inclusion of BF% explained an additional 1.3%. Similarly, E_req (in W/m²) correlated significantly with LSR_ss (adjusted to r² = 0.603, P < 0.001), whereas %V̇o_{2 max} described an additional ∼4% of total variance. In conclusion, biophysical parameters related to H_prod, E_req, and body size explain 54–71% of the individual variability in ΔT_re, WBSL, and LSR_ss, and only 1–4% of additional variance is explained by factors related to fitness or fatness.

individual human thermoregulatory responses to exercise are highly variable. For example, changes in core temperature from rest can vary between individuals by as much as 1.1°C at a fixed absolute rate of metabolic heat production (H_prod) of ∼350 W (28) and by up to 1.9°C at a fixed relative exercise intensity corresponding to 75% of the maximum rate of oxygen uptake (V̇o_{2 max}) (35). As such, predicting individual heat stress risk in both occupational and sport-related settings remains a challenge. This high interindividual variability may be explained by a host of physiological and biophysical characteristics. Among young healthy individuals of the same sex, previous studies have identified aerobic fitness (i.e., V̇o_{2 max}) and body fatness [body fat percentage (BF%)] as important predictors of individual core temperature and sweating responses to exercise (14–18, 31).

More recently, studies from our laboratory suggest that fixing biophysical factors related to H_prod per unit of total body mass (in W/kg TBM) and evaporative heat balance requirements (E_req) per unit of body surface area (in W/m²) can eliminate systematic differences in core temperature and local sweating between groups of different body size (7) and V̇o_{2 max} (22). However, the proportion of the interindividual variability of thermoregulatory responses independently described by these biophysical factors, and whether fitness- and/or fatness-related variables describe any of the residual variability, is currently unknown.

In many previous studies (5, 14–16, 18), exercise has been performed at a fixed %V̇o_{2 max} or absolute workload by a subject cohort heterogeneous for V̇o_{2 max} and body morphology. Significant correlates of a specific thermoregulatory variable have then been identified using multiple regression analysis. However, this approach may be limited if the prescription of a single absolute or relative intensity resulted in high collinearity between independent biophysical and physiological variables. For example, at a fixed %V̇o_{2 max}, individuals with a higher V̇o_{2 max} in ml·kg⁻¹·min⁻¹ (who tend to be smaller in body size and lower in body fatness) will generate more heat per unit of body mass and have greater evaporative heat balance requirements per unit of BSA. As a result, greater changes in core temperature, whole body sweat rates, and local sweat rates would be expected in individuals with a higher V̇o_{2 max} and lower body fatness, but not necessarily because of those characteristics per se. Similarly, exercise at a fixed absolute workload (i.e., similar absolute heat production and evaporative heat balance requirements) will typically result in greater H_prod (in W/kg TBM) and E_req (in W/m²) in high-V̇o_{2 max}, low-fatness individuals, since they often have a smaller body size. It thus stands to reason that associations between thermoregulatory responses, aerobic fitness, and body fatness reported previously may not necessarily reflect an independent effect of these factors on core temperature and sweating but perhaps arise from circumstantial collinearity between these independent variables and factors such as H_prod (in W/kg TBM) and E_req (in W and/or W/m²).

To resolve this issue, an experimental approach is required that includes exercise intensities spanning a wide range of absolute and relative workloads in a subject group of heterogeneous morphological and fitness-related characteristics. By using such an approach, the amount of individual variability in the change in core temperature, whole body sweat rate, and local sweat rate independently explained by H_prod (W/kg TBM), E_req (W), and E_req (W/m²), respectively, can be identified, and whether factors independently related to aerobic fitness and body fatness explain any residual variance in these thermoregulatory responses may be determined. Fitness-related parameters such as V̇o_{2 max} expressed in terms of lean body mass (LBM) or lean mass of the exercising legs (leg LM) may also influence core temperature (27), whereas higher levels of adiposity may lead to greater changes in core temperature due to its greater insulative properties and/or lower average specific heat capacity (2, 25). Additionally, tissue composition within body regions involved in thermogenesis, such as the legs during cycling or running, could alter heat exchange between neighboring tissues.

The purpose of this study was to test the hypotheses that during exercise in compensable conditions 1) the best descriptors of the individual variation in the change in rectal temperature (ΔT_re), whole body sweat loss (WBSL), and steady-state local sweat rate (LSR_ss) are H_prod (W/kg TBM), E_req (W), and E_req (W/m²), respectively, and 2) factors related to aerobic fitness and body fatness contribute minimally, if at all, to the residual variance in these responses.

METHODS

The experimental protocol was approved by the University of Ottawa Health Sciences and Science Research Ethics Board and conformed to the ethical principles outlined in the Declaration of Helsinki. The procedures and potential risks were explained to all subjects prior to experimentation, after which informed consent was obtained in writing. Subjects also completed a Physical Activity Readiness Questionnaire and an American Heart Association/American College of Sports Medicine Health/Fitness Facility Preparticipation Screening Questionnaire. Subject characteristics are summarized in Table 1. A total of 28 healthy male volunteers were tested, and each subject performed multiple trials (69 total trials). All subjects were nonsmokers, reported no history of cardiovascular, metabolic, neurological, or respiratory diseases, and were not taking any medications at the time of participation. Some of the data presented herein have been reported previously in separate studies (7, 22).

Table 1.

Mean subject characteristics

	Mean	SD	Minimum	Maximum
Age, yr	23.6	3.5	20.0	32.6
TBM, kg	78.2	11.3	59.8	100.4
BSA, m2	1.96	0.15	1.68	2.26
Absolute V̇o2max, l/min	3.86	0.68	2.73	5.27
Fat mass, kg	12.9	6.6	4.9	26.4
LBM, kg	63.3	8.3	48.1	85.8
Leg LM, kg	23.5	3.4	17.3	31.5

Data are presented for 28 subjects. TBM, total body mass; BSA, body surface area; V̇o_2max, maximum rate of oxygen uptake; LBM, lean body mass; leg LM, lean mass of the exercising legs.

Preliminary trial.

Subjects arrived at the laboratory ≥2 h postprandial, having avoided alcohol, caffeine, and exercise in the 12 h prior to testing. Upon arrival, subjects voided their bladders before standing height and body mass were measured with a wall-mounted stadiometer and digital scale (HR-200 and BWB-800; Tanita, Arlington Heights, IL). The formula of DuBois and DuBois (9) was later applied to calculate BSA. While wearing only a hospital gown and underwear, body composition was measured using dual-energy X-ray absorptiometry (GE Medical Systems, Madison, WI). Scans were analyzed for BF%, fat mass, and nonosseous LBM on the left and right sides of the arm, leg, and trunk. Leg LM was taken as the total lean mass of left and right legs.

Following anthropometry, an incremental test to exhaustion was performed during semirecumbent cycling at a self-selected cadence to determine V̇o_{2 max}. The test began at an external workload of 80 W and increased by 20 W/min until volitional exhaustion according to Canadian Society for Exercise Physiology guidelines (8). In all trials, the rate of oxygen uptake (V̇o₂) was measured breath by breath, and the highest 1-min average value was taken as V̇o_{2 max}. At least 48 h separated the preliminary trial from the first experimental trial.

Experimental trials.

Experimental trials were performed at the same time of day to avoid potential effects of circadian rhythm and were separated by ≥48 h. In the 12 h prior to experimental trials, subjects were instructed to avoid alcohol, caffeine, and strenuous exercise. A light meal with ∼500 ml of water was consumed 2 h before arrival. Upon arrival, urine-specific gravity (USG) was measured first to determine hydration status. Euhydration was accepted as a USG of <1.025 (24). Subjects then changed into standard athletic clothing (running shorts, socks, and shoes) and inserted a rectal thermocouple. A body mass measurement was then taken, followed by instrumentation and 30 min of baseline data collection. The exercise protocol consisted of semirecumbent cycling at 80 rpm for 60 min. External workload (119 ± 29 W) was set to elicit either 60% of V̇o_{2 max} (502–898 W) or a H_prod of ∼500 W (32.2–67.6% of V̇o_{2 max}), 6.5 W/kg (40.3–59.6% of V̇o_{2 max}), or 9.0 W/kg (52.7–77.1% of V̇o_{2 max}). Ambient conditions were 24.8 ± 0.7°C and 33.4 ± 12.2% relative humidity, and an air velocity of 1.2 ± 0.1 m/s was provided by a mechanical fan placed 1.25 m in front of the ergometer (2 m in front of the subject). Core temperature, skin temperatures, and LSR measurements were taken continuously. Body mass was measured immediately prior to exercise (i.e., at baseline) and upon completion of exercise while fully instrumented, with all instrument cables secured to the same spot on an adjacent equipment cart. Neither food nor fluid was ingested between instrumentation and the end of exercise.

Instrumentation.

A general-purpose pediatric thermocouple probe (Mallinckrodt Medical, St. Louis, MO) was inserted ∼12 cm beyond the anal sphincter to determine T_re; ΔT_re is expressed as the difference between end-exercise and baseline values, which were taken as 5-min averages during the final minutes of exercise and rest, respectively. Skin temperatures were measured using thermistors (Concept Engineering, Old Saybrook, CT) at eight skin sites. A weighted average of forehead (0.07), shoulder (0.07), triceps (0.07), chest (0.175), scapula (0.175), hand (0.05), thigh (0.19), and calf (0.20) skin temperatures was used to calculate mean skin temperature (T_sk) (21), which was then employed to estimate E_req (see below). Temperatures were measured every 5 s with a data acquisition unit (NI cDAQ-9172; National Instruments, Austin, TX) and LabView software (Version 7.0; National Instruments).

Body mass was measured in triplicate during experimental trials using a precision scale with an accuracy of ±2 g (Combics 2; Sartorius, Mississauga, ON, Canada). Values for WBSL were determined as the 60-min change in body mass minus respiratory vapor exchange and metabolic mass losses (29).

Measurements of LSR were taken on the forearm using a ventilated capsule ∼5 cm distal to the antecubital space or an absorbent patch (no. 2164 laminated Airlaid; Technical Absorbents, Grimsby, UK). Dry air flowed through the capsule at 1.80 l/min (FMA-A2307; Omega Engineering, Stamford, CT), and the humidity of effluent air was measured every 5 s by a capacitance hygrometer (HMT333; Vaisala, Vantaa, Finland). Precut absorbent patches were sealed in a plastic bag and then weighed on a digital scale (Denver Instrument, Bohemia, NY). Every 15 min, a patch was placed on the ventral side of the forearm and secured with a compression garment (Under Armor, Baltimore, MD). After the sampling period, the patches were removed, sealed in the original plastic bag, and reweighed. LSR_ss values are expressed in milligrams of sweat per square centimeter of surface area covered by a capsule or absorbent patch per minute (mg·cm⁻²·min⁻¹) over the final 20 min of exercise. Since steady-state local sweating measurements with absorbent patches strongly agree with those from ventilated capsules (32), forearm LSR measurements using both methods were included in the LSR_ss analyses.

Heat balance calculations.

Using 1-min average values for V̇o₂ and the respiratory exchange ratio collected with a metabolic cart (Vmax Encore; CareFusion, Yorba Linda, CA), metabolic rate (M) was estimated as

$$\text{M}=\dot{\text{V}}{\stackrel{}{o}}_2\frac{\left(\right(\frac{\text{RER}-0.7}{0.3}){{\mathrm{e}}_{\mathrm{c}}}_{})+\left(\right(\frac{1.0-\text{RER}}{0.3}){\text{e}}_{\text{f}})}{\left(\text{60}\right)\left(\text{BSA}\right)}\left(1,000\right)\left[\text{W}/{\text{m}}^2\right]$$

where e_c and e_f are the energetic equivalents for carbohydrate (21.13 kJ/l O₂) and fat (19.62 kJ/l O₂), respectively. H_prod was calculated as the difference between metabolic rate and the external work rate, which was regulated by a semirecumbent cycle ergometer (Lode Corival, Groningen, The Netherlands). The rate of dry heat exchange (H_dry) was calculated as:

$${\text{H}}_{\text{dry}}=\text{C}+\text{R}\left[\text{W}/{\text{m}}^2\right]$$

$$\text{C}={\text{h}}_{\text{c}}\left({\text{T}}_{\text{sk}}-{\text{T}}_{\text{a}}\right)\left[\text{W}/{\text{m}}^2\right]$$

$$\text{R}={\text{h}}_{\text{r}}\left({\text{T}}_{\text{sk}}-{\text{T}}_{\mathrm{r}}\right)\left[\text{W}/{\text{m}}^2\right]$$

where C and R represent convective and radiant heat exchange, respectively, T_a and T_sk denote ambient and mean skin temperatures (°C), respectively, T_r is the mean radiant temperature (°C), which was assumed to the equivalent to ambient temperature in the laboratory setting, h_c is the convective heat transfer coefficient, and h_r is the radiant heat transfer coefficient:

$${\text{h}}_{\text{c}}=8.3{\text{v}}^{0.6}\left[\text{W}\cdot {\text{m}}^{-2}\cdot {\text{K}}^{-1}\right]$$

$${\text{h}}_{\text{r}}=4\epsilon \sigma \left({\text{BSA}}_{\text{r}}/\text{BSA}\right){\left(\left({\text{T}}_{\text{sk}}+{\text{T}}_{\text{r}}\right)/2+273.15\right)}^3\left[\text{W}\cdot {\text{m}}^{-2}\cdot {\text{K}}^{-1}\right]$$

where v is air velocity (m/s), ε is skin emissivity (0.95), σ is the Stefan-Boltzmann constant (5.67·10⁻⁸ W·m⁻²·K⁻⁴), and BSA_r/BSA is the nondimensional effective radiant surface area for a seated individual valued at 0.70 (26).

Respiratory heat exchange (H_resp) was calculated as

$${\text{E}}_{\text{res}}+{\text{C}}_{\text{res}}=0.0173\left({\text{H}}_{\text{prod}}\right)\left(5.87-{\text{P}}_{\text{a}}\right)+0.0014\left({\text{H}}_{\text{prod}}\right)\left(34-{\text{T}}_{\text{a}}\right)\left[{\text{W/m}}^2\right]$$

where E_res and C_res are evaporative and convective heat loss from the respiratory tract, respectively, and P_a is the ambient vapor pressure (kPa). The rate of evaporation required for heat balance (E_req) was expressed as

$${\text{E}}_{\text{req}}={\text{H}}_{\text{prod}}-{\text{H}}_{\text{dry}}-{\text{H}}_{\text{resp}}\left[{\text{W/m}}^2\right]$$

The calculation of E_req was based on the 60-min average values of each heat balance parameter included in the equation. The maximum rate of evaporation to the environment (E_max) was determined by

$${\text{E}}_{\text{max}}={\text{h}}_{\text{e}}\left({\text{P}}_{\text{sk,s}}-{\text{P}}_{\text{a}}\right)\left[{\text{W/m}}^2\right]$$

where h_e is the evaporative heat transfer coefficient, calculated as the product of h_c and the Lewis relation coefficient (16.5 K/kPa), and P_sk,s − P_a is the skin-air vapor pressure gradient. Absolute humidity was measured using a dew point mirror (RH Systems, Albuquerque, NM).

The value of P_s,sk was calculated based on T_sk using Antoine's equation:

$${\text{P}}_{\text{sa}}=10\cdot \exp \left[18.956-4030.18/\left({\text{T}}_{\text{sk}}+235\right)\right]\left[\text{kPa}\right]$$

As per convention, heat balance parameters were calculated in W/m²; however, these values are expressed in W or W/kg where appropriate.

Statistics.

Individual data are presented as means ± SD. Statistical analyses were performed using SPSS version 22 (IBM, Armonk, NY). Data were initially screened for normality by calculating skewness and kurtosis; values within ±2.00 were deemed acceptable (38). Correlation coefficients (r) were established between thermoregulatory (ΔT_re, WBSL, and LSR_ss) and relevant morphological (BSA/mass), fitness-related (relative V̇o_{2 max} in ml·kg⁻¹·min⁻¹, ml·kg LBM⁻¹·min⁻¹, and ml·kg leg LM⁻¹·min⁻¹; %V̇o_{2 max}), body fatness-related (BF%), and other biophysical variables related to H_prod and E_req (H_prod in W, W/m², W/kg TBM, W/kg LBM, and W/kg leg LM; E_req in W and W/m²; E_req/E_max). Correlations were considered significant at the P < 0.05 level.

Stepwise multiple regression analyses were conducted using a forward selection entry method. A total of 69 cases were included. Parameters were included in each model based on significant (P < 0.05) correlation with the residual variance. To avoid unacceptable collinearity between predictors within the final model, independent variables were included only if the resultant tolerance value was >0.5 (1). Data were screened for influential cases using Cook's distances and standardized residuals, and the normality of the residuals was confirmed by calculating their skewness and kurtosis. Since some subjects performed multiple trials, residuals from each final regression model were tested for autocorrelation using the Durbin-Watson test (d). Based on the number of independent variables and cases included in each model, positive autocorrelation would have been indicated by d < 1.525 (ΔT_re) and d < 1.554 (WBSL, LSR_ss), whereas negative autocorrelation would have been indicated by d > 2.465 (ΔT_re) and d > 2.446 (WBSL, LSR_ss), at the 0.05 level (36).

RESULTS

Individual characteristics and mean trial values.

Subjects were similar in age but demonstrated high variability in their absolute V̇o_{2 max} and morphological traits (Table 1). This variability, coupled with different target work rates, resulted in a wide range of H_prod, E_req, and %V̇o_{2 max} values (Table 2). Calculated skewness and kurtosis were <2.00 for all parameters, indicative of normally distributed values (Table 2).

Table 2.

Descriptive statistics for all dependent and independent variables

	Mean	SD	Minimum	Maximum	Median	Skewness	Kurtosis
Dependent variables
ΔTre, °C	0.92	0.28	0.35	1.89	0.92	0.424	1.080
WBSL, g	474	165	250	978	435	1.178	1.182
LSRss, mg·cm−2·min−1	0.44	0.21	0.13	1.01	0.40	0.859	0.024
Independent variables
BSA/mass, cm2/kg	251	19	216	288	252	0.144	−0.846
BF%	17.2	6.9	6.8	32.5	16.0	0.544	−0.579
Relative V̇o2max
ml·kg−1·min−1	49.3	8.0	36.0	65.0	50.9	0.007	−0.943
ml·kg LBM−1·min−1	60.9	8.9	45.8	84.2	60.4	0.714	0.169
ml·kg leg LM−1·min−1	163.0	19.6	132.0	200.1	160.9	0.290	−0.919
%V̇o2max	54.0	10.7	32.2	82.0	54.8	0.327	−0.376
Hprod
W	590	127	410	898	550	1.120	0.295
W/m2	301	56	232	468	281	1.088	0.389
W/kg TBM	7.54	1.43	5.22	12.12	7.10	0.904	0.815
W/kg LBM	9.22	1.65	6.44	13.42	8.74	0.629	−0.442
W/kg leg LM	41.42	12.32	20.14	65.34	42.78	−0.019	−0.951
Ereq
W	392	107	256	672	357	1.199	0.556
W/m2	200	49	137	350	190	1.170	0.782
Ereq/Emax (ND)	0.41	0.11	0.26	0.74	0.39	1.173	1.498

Data are presented for 69 total trials. ΔT_re, change in rectal temperature; WBSL, whole body sweat loss; LSR_ss, mean steady-state forearm local sweat rate; BSA/mass, body surface area-to-mass ratio; BF%, body fat percentage; H_prod, rate of metabolic heat production; E_req, rate of evaporation required for heat balance; E_max, maximum potential for evaporative heat loss; ND, no denomination. Skewness and kurtosis values in the range of ±2.00 were considered acceptable (38).

Correlation analysis.

Bivariate correlation analyses for the thermoregulatory responses are presented in Fig. 1. The BF% correlated negatively (P = 0.045) with ΔT_re, whereas BSA/mass, relative V̇o_{2 max} (ml·kg⁻¹·min⁻¹ and ml·kg leg LM⁻¹·min⁻¹), %V̇o_{2 max}, and H_prod (W, W/m², W/kg TBM, and W/kg LBM) correlated positively with ΔT_re (P < 0.05). Neither relative V̇o_{2 max} (ml·kg LBM⁻¹·min⁻¹) nor H_prod (W/kg leg LM) demonstrated any significant association with ΔT_re. Both WBSL and LSR_ss were positively correlated with %V̇o_{2 max}, E_req (W and W/m²), and E_req/E_max (P < 0.001), but WBSL also showed a negative correlation with BSA/mass (P = 0.011). BF% and relative V̇o_{2 max} (in ml·kg⁻¹·min⁻¹, ml·kg LBM⁻¹·min⁻¹, and ml·kg leg LM⁻¹·min⁻¹) were not associated with WBSL or LSR_ss. The relationships between each dependent thermoregulatory variable and the most strongly associated independent variable are illustrated in Fig. 2.

Fig. 1.

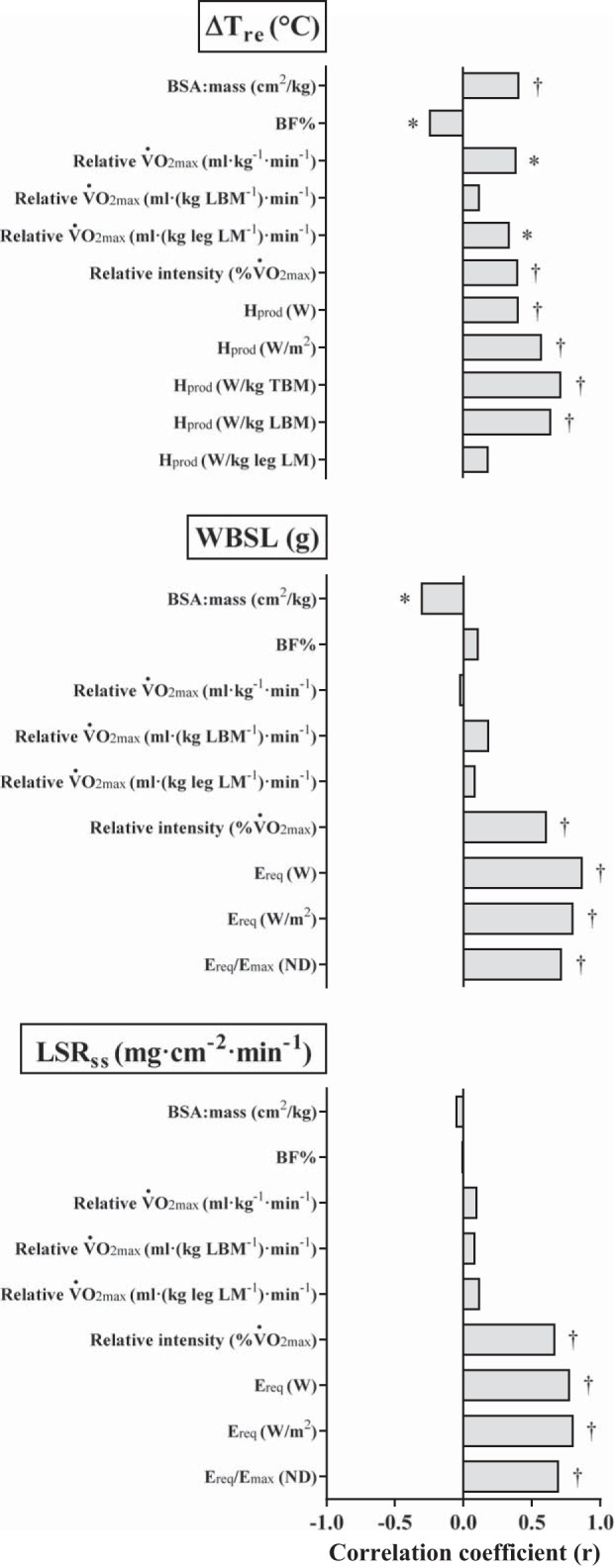
Correlation coefficients (r) for associations between thermoregulatory responses and the relevant independent variables. *P < 0.05; †P ≤ 0.001. BF%, body fat percentage; LBM, lean body mass; TBM, total body mass; leg LM, lean mass of the exercising legs; V̇o_{2 max}, maximum rate of oxygen uptake; H_prod, rate of metabolic heat production; WBSL, whole body sweat loss; E_req, evaporative heat balance requirements; E_max, maximum rate of evaporation to the environment; LSR_ss, steady-state local sweat rate. ND, no denomination.

Fig. 2.

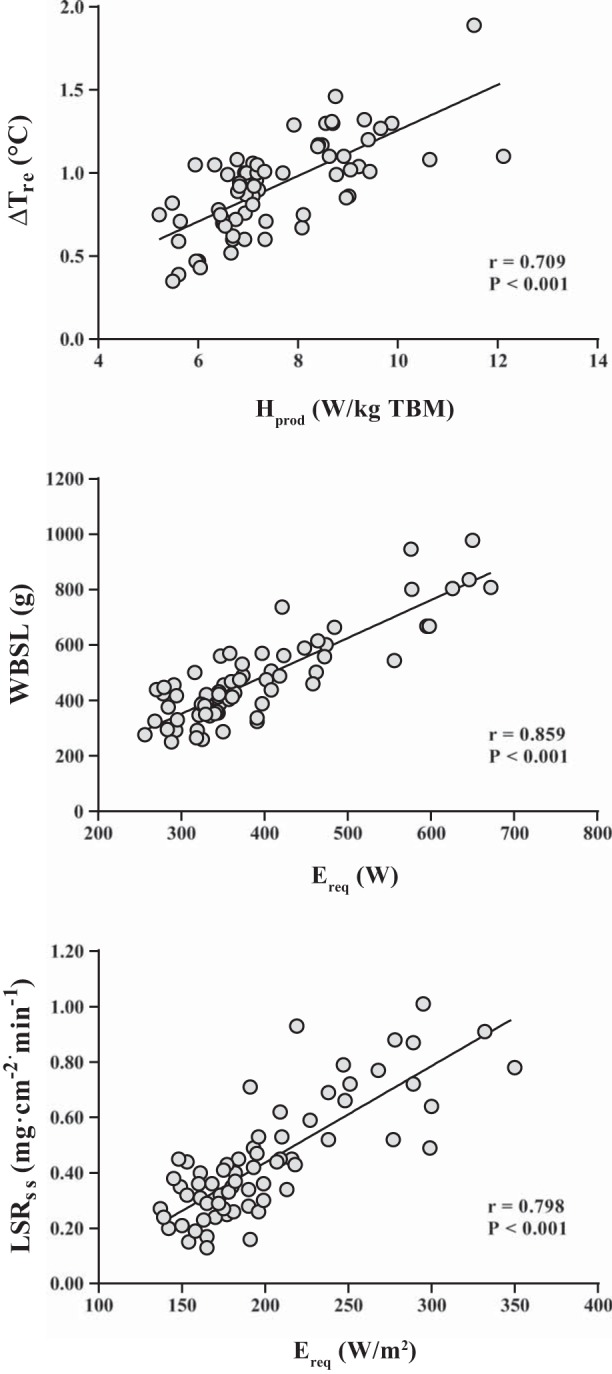
Scatter plots illustrating the relationship between each thermoregulatory response and the independent variable demonstrating the strongest association. ΔT_re, change in rectal temperature.

Multiple regression models.

Tests for autocorrelation revealed d statistical values of 2.363 for ΔT_re, 1.877 for WBSL, and 1.950 for LSR_ss, indicating no evidence of positive or negative autocorrelation in the models.

The output of the stepwise multiple-regression models with all relevant statistics is shown in Table 3. The final models included H_prod (W/kg), BSA/mass, and BF% for ΔT_re, E_req (W) and BF% for WBSL, and E_req (W/m²) and %V̇o_{2 max} for LSR_ss. Together, H_prod (W/kg TBM), BSA/mass, and BF% correlated significantly with the individual variation in ΔT_re, explaining ∼56% of the total variance. However, H_prod (W/kg TBM) alone described ∼50% of the variance in ΔT_re (adjusted to r² = 0.496, P < 0.001), whereas BSA/mass and BF% described only an additional 4.3 and 2.3%, respectively, of the total variability. Whereas E_req (W) and BF% correlated significantly with WBSL, explaining 72.6% of the total variance, the contribution of BF% was only 1.3% above E_req (W) alone (adjusted to r² = 0.713, P < 0.001). Similarly, both E_req (W/m²) and %V̇o_{2 max} correlated significantly with LSR_ss, explaining ∼64% of the total variance, but E_req (W/m²) itself explained ∼60% of the variance in LSR_ss (adjusted r² = 0.603, P < 0.001), with %V̇o_{2 max} explaining only an additional ∼4% of the total variance.

Table 3.

Final multiple regression models for changes in rectal temperature, whole-body sweat loss, and steady-state local sweat rate

	b	SE	P Value	Tolerance	r2 Value
ΔTre , °C
Constant	−1.502	0.423	0.001
Hprod, W/kg TBM	0.135	0.015	< 0.001	0.856	49.6%
BSA/mass (cm2/kg)	0.005	0.001	0.001	0.660	4.3%
BF%	0.009	0.003	0.038	0.612	2.3%
Adjusted r2	0.562
SEE	0.197
WBSL, g
Constant	−107.683	48.374	0.030
Ereq, W	1.362	0.105	< 0.001	1.000	71.3%
BF%	2.987	1.632	0.048	1.000	1.3%
Adjusted r2	0.726
SEE	0.187
LSRss, mg·cm−2·min−1
Constant	−0.387	0.080	< 0.001
Ereq,W/m2	0.003	<0.001	< 0.001	0.583	60.3%
%V̇o2max	0.005	0.001	0.006	0.583	3.8%
Adjusted r2	0.641
SEE	0.184

Tolerance values indicate acceptable collinearity and thus model stability. b, Unstandardized regression coefficients; SE, standard error of the slope coefficient or intercept; SE_E, standard error of the estimate for the regression equation; r², partial contribution to total variance.

DISCUSSION

The primary findings of the present study were that biophysical parameters related to H_prod (and thus E_req), TBM, and BSA alone explain 54–71% of the individual variability in ΔT_re, WBSL, and LSR_ss. Residual variance in ΔT_re and WBSL correlated with BF%, whereas residual variance in LSR_ss correlated significantly with %V̇o_{2 max}; however, these factors explained only ∼1–4% of the remaining variability in each thermoregulatory response. As such, biophysical factors predominantly described the individual variability in core temperature and sweating responses to exercise, whereas aerobic fitness and body fatness described minimal variability.

Changes in core temperature.

After 60 min of exercise, H_prod (W/kg TBM) was found to be the best predictor of the individual ΔT_re response (Fig. 2). Previous studies have demonstrated that core temperature rises with absolute metabolic rate (i.e., heat production) (18, 22, 33, 34) and negatively correlates with TBM (5, 15–18, 34). However, we recently reported similar ΔT_re at fixed rates of heat production in W/kg between independent participant groups with an ∼24-kg difference in TBM and consequently large differences in absolute heat production in W (7). This approach was shown to permit unbiased independent-group comparisons of core temperature between groups unmatched for TBM, and the current data extend these findings, showing that ∼50% of the individual variability in ΔT_re can be explained by H_prod (W/kg TBM) alone.

In addition, BSA/mass and BF% correlated positively with the residual variance in ΔT_re (Table 3). BSA/mass independently explained an additional ∼4% of variability, with a higher BSA/mass apparently leading to a greater ΔT_re. This finding, although minor, was unexpected. Although a positive relationship between BSA/mass and core temperature has been reported previously (5, 15, 18), albeit not independently of H_prod (W/kg TBM), a greater BSA/mass should in theory lead to a greater heat loss potential per unit mass and thus a negative association between BSA/mass and ΔT_re (37). The reason for this relationship is presently unclear but could be indicative of an influence of body shape for a given TBM on internal heat distribution.

Theoretically, the lower specific heat capacity of adipose tissue should lead to greater changes in core temperature for a given level of heat storage and TBM (2, 23). Nevertheless, the relationship between core temperature and body fatness appears equivocal, as studies have (16, 18) or have not (5, 15, 17, 34) demonstrated an association between core temperature and BF%. Independent-group comparisons have been equally puzzling. For example, similar ΔT_re were reported in lean vs. obese adult and prepubertal females (4, 19) but were greater in prepubertal vs. adult males (20) during treadmill walking at a fixed metabolic rate per unit TBM in warm/hot and dry conditions. Similarly, we have found previously that differences in BF% of ∼10% did not affect ΔT_re at fixed levels of H_prod (W/kg TBM) (6, 7, 22). In the present study, once H_prod (W/kg TBM) and BSA/mass were included in the regression model, BF% correlated with the residual variance in ΔT_re but explained only ∼2% of the total variability. If an independent effect of BF% on core temperature truly exists, it appears to be relatively minor over the range of BF% tested (6.8–32.5%; Table 2). Future studies should assess the influence of BF% on core temperature and WBSL at more extreme levels of adiposity.

Although bivariate analysis showed that H_prod (W/kg LBM) was correlated with ΔT_re, neither H_prod (W/kg LBM) nor H_prod (W/kg leg LM) explained any individual variation in ΔT_re independently of H_prod (W/kg TBM). As noted above, changes in internal temperature should partially reflect total mass for a given change in heat content. Since H_prod (W/kg LBM) and H_prod (W/kg leg LM) ignore components of TBM that could otherwise store heat during exercise, it is not surprising that these factors were excluded from the final ΔT_re model.

Strong associations between absolute (l/min) or relative (ml·kg⁻¹·min⁻¹) V̇o_{2 max} and core temperature (15–17), and similar end-exercise core temperatures between fit and unfit individuals at a given %V̇o_{2 max} (12, 13, 31) appear to support the contention that aerobic fitness influences core temperature regulation (30). However, we found that no fitness-related parameters independently described the individual variation in ΔT_re (Table 3). The discrepancy between findings likely reflects the experimental protocols used and the independent variables included in previous regression models. Since V̇o_{2 max} is often inversely related to TBM (15, 16), greater changes in core temperature would be expected in high-V̇o_{2 max} individuals at a fixed %V̇o_{2 max} due to higher H_prod (W) and a lower TBM and at a fixed absolute workload due to smaller TBM despite similar H_prod (W), both of which result in greater H_prod (W/kg TBM) (7). As a result, previously reported associations between V̇o_{2 max} and changes in core temperature may not be due to an influence of fitness per se but perhaps reflect collinearity between V̇o_{2 max} and H_prod (W/kg TBM), which has not been dissociated in previous studies.

Whole body sweat loss.

Gagnon et al. (10) demonstrated recently that E_req (W) alone explains 93% of the variance in steady-state whole body sweat rate. The present data reaffirm those results, as E_req (W) was the principal determinant of WBSL (Fig. 2), explaining ∼71% of the individual variability in WBSL. The stronger association between E_req (W) and whole body sweat rate reported by Gagnon et al. (10) may reflect some differences in sweating efficiency (i.e., the proportion of secreted sweat that evaporates). The combination of environmental conditions and fan-forced air flow likely resulted in near-complete sweat evaporation in most trials in the present study; however, this may not have been the case at higher exercise intensities. A small amount of dripping sweat could have thus introduced some variation to our WBSL measurements unexplained by E_req (W).

Gagnon et al. (10) did not assess the potential role of BF% in describing the variation in individual WBSL responses. The inclusion of BF% in the present study added 1.3% to the explained variance in WBSL, a very minor contribution compared with E_req (W) alone (∼71%). It is unclear why BF% would be included in the WBSL model, but given that BF% alone was not associated with WBSL (Fig. 1), it is unlikely that higher body fatness directly causes greater whole body sweat production for a given E_req (W). Additionally, no fitness-related parameters (including %V̇o_{2 max}) correlated with the residual variance in WBSL (Table 3), a finding in contrast to previous studies (14, 18). As in the case of ΔT_re, the absence of any effect of fitness on WBSL was likely the result of circumstantial collinearity in previous studies between V̇o_{2 max} and E_req (W) at the same %V̇o_{2 max}.

Steady-state local sweat rate.

In a recent study, we showed that average local sweat rate is similar between groups unmatched for BSA at fixed E_req (W/m²) but different for a given E_req (W) (7). In the present study, ∼60% of the individual variability in LSR_ss was explained by E_req (W/m²) alone, with no additional contribution of E_req (W). For a given E_req (W) in conditions permitting full evaporation, whole body sweat production will be similar regardless of body size (7, 10); however, in individuals with lower BSA, an equivalent amount of sweat will be secreted over smaller skin surface area. Since local sweat rate is expressed relative to the measurement area, LSR_ss should be higher in smaller people for a given E_req (W). Alternatively, a fixed E_req (W/m²) should lead to similar LSR_ss irrespective of body size but very different WBSL responses, as a higher E_req (W) would be attained in individuals with a larger BSA. This latter point emphasizes the need for investigators to examine sweating responses using different variants of E_req/E_max ratio for whole body sweating responses and E_req (W/m²) for local sweating responses.

In addition to E_req (W/m²), %V̇o_{2 max} correlated positively with the residual variance in forearm LSR_ss, suggesting that exercise at a given E_req (W/m²) will lead to a higher LSR_ss if the exercise intensity corresponds to a greater %V̇o_{2 max}. During exercise at a set E_req (W/m²), and despite similar core and skin temperature responses, an independent effect %V̇o_{2 max} on local sweat rate has been shown previously (6, 23), but this effect was observed only on the forehead, not the forearm, and without any influence on whole body sweat rate (6). This finding suggested possible differential control of regional sweating in glabrous (forehead) vs. nonglabrous (forearm) in response to greater relative strain; however, this would not explain the present findings since individual variance in forearm LSR_ss was explained partially by %V̇o_{2 max} (Fig. 3). Nevertheless, it is important to highlight that the contribution of %V̇o_{2 max} (∼4%) to the explanation of residual variability in LSR_ss, although statistically significant, was very minor.

Perspectives.

The present findings have important implications for modeling thermoregulatory strain and contribute to a better understanding of the factors that may predispose particular individuals to a greater risk of heat injury during exercise. For example, individuals who are small will demonstrate similar changes in core temperature irrespective of aerobic fitness if they are working at a similar metabolic rate, which would be the case if work rate was externally governed. Likewise, our findings indicate that high sweat rates commonly seen in individuals with high body fat during weight-bearing activities are not necessarily due to fatness per se but are likely due to the greater evaporative heat balance requirements associated with the greater heat production required to carry that mass. Indeed, a lean person of the same mass will demonstrate similar rates of sweating and will therefore need to ingest the same volume of fluid to maintain hydration status. Limitations of the present study include the fact that only male subjects were tested. Females demonstrate a lower whole body sweating sensitivity, resulting in greater ΔT_re despite a similar heat production (7.5 W/kg) during exercise in hot, dry conditions (11). Therefore, in addition to biophysical factors, sex must also be considered when examining individual factors contributing to the core temperature response. Additionally, the present findings may be applied only to physiologically compensable conditions. In conditions of reduced sweating efficiency, E_req/E_max is likely a better predictor of individual whole body and local sweating responses (3), and during uncompensable heat stress the degree of uncompensability expressed relative to total body mass (i.e., E_req − E_max in W/kg) may be a better predictor of core temperature changes during exercise. Future studies should assess this notion.

Finally, Havenith et al. (16), along with Havenith and van Middendorp (18), previously used standardized regression coefficients to compare the contribution of different predictors to the explained variance in absolute core temperature during exercise in the heat. Adopting such an analysis method in the present study yields similar results to those reported in Table 2, with a total of ∼9–18% of the contribution of the main predictor transferred to the other predictor(s) in each model. It is important to recognize, however, that each analytical approach answers a different question about a model. Presenting the relative contribution of each parameter to the explained variance without standardization (Table 2) demonstrates the predictive capability of a model. Since our study was designed primarily to determine the best predictors of each thermoregulatory variable in question, and whether additional parameters contribute to the description of any of the residual variance, we argue that this was the most suitable approach. Nonetheless, both analysis methods underline that biophysical factors are of primary importance when explaining individual variability of core temperature and sweating responses.

Conclusion.

Biophysical factors related to heat production and body size explained ∼54–71% of the individual variability in the core temperature and thermoregulatory sweating responses to exercise in a compensable environment. Specifically, our results show that individual changes in core temperature, WBSL, and LSR_ss are described primarily by the individual variation in the rate of heat production relative to total body mass, the absolute rate of evaporation required for heat balance, and the rate of evaporation required for heat balance relative to body surface area, respectively. In contrast, the role of aerobic fitness and body fatness on these individual responses was minimal, explaining only ∼1–4% of residual variability.

GRANTS

This research was supported by a Natural Sciences and Engineering Research Council of Canada (NSERC) Discovery Grant (no. 386143-2010, O. Jay). M. N. Cramer was supported by an NSERC Postgraduate Doctoral Scholarship (PGS-D) and a University of Ottawa Excellence Scholarship.

DISCLOSURES

No conflicts of interest, financial or otherwise, are declared by the authors.

AUTHOR CONTRIBUTIONS

M.N.C. and O.J. conception and design of research; M.N.C. performed experiments; M.N.C. and O.J. analyzed data; M.N.C. and O.J. interpreted results of experiments; M.N.C. prepared figures; M.N.C. and O.J. drafted manuscript; M.N.C. and O.J. edited and revised manuscript; M.N.C. and O.J. approved final version of manuscript.