A novel locus of resistance to severe malaria in a region of ancient balancing selection

The high prevalence of sickle haemoglobin in Africa shows that malaria has been a major force for human evolutionary selection, but surprisingly few other polymorphisms have been proven to confer resistance to malaria in large epidemiological studies^1–3. To address this problem we conducted a multi-centre genome-wide association study (GWAS) of life-threatening Plasmodium falciparum infection (severe malaria) in over 11,000 African children with replication data in a further 14,000 individuals. Here we report a novel malaria resistance locus close to a cluster of genes encoding glycophorins that are receptors for erythrocyte invasion by P. falciparum. We identify a haplotype at this locus which provides 33% protection against severe malaria (OR=0.67, 95%CI=0.60–0.76, P=9.5×10⁻¹¹) and is linked to polymorphisms previously shown to have features of ancient balancing selection, based on haplotype sharing between humans and chimpanzees⁴. Taken together with previous observations on the malaria-protective role of blood group O^1–3,5, these data reveal that two of the strongest GWAS signals for severe malaria lie in or close to genes encoding the glycosylated surface coat of the erythrocyte cell membrane, both within regions of the genome where it appears that evolution has maintained diversity for millions of years. These findings provide new insights into the host-parasite interactions that are critical in determining the outcome of malaria infection.

In the discovery phase of this study we analysed GWAS data on 5,633 children with severe malaria and 5,919 population controls from The Gambia, Kenya and Malawi, and in the replication phase we analysed candidate SNPs in a further 13,946 case control samples from Burkina Faso, Cameroon, The Gambia, Ghana, Malawi, Mali and Tanzania (Extended Data Figure 1). The majority of samples used in the discovery phase have been analysed previously by lower resolution GWAS methods³. For this analysis we improved resolution by directly typing all samples at approximately 2.5 million SNPs using the Illumina Omni2.5M platform, followed by quality control (Extended Data Figures 1 and 2) and imputation of genotypes at over 10 million SNPs using haplotype data from the 1000 Genomes Project⁶. Imputation performance varied across populations, with accuracy decreasing as a function of the similarity between study and reference individuals (Extended Data Figure 3). When testing for genetic association, principal components analysis was used to correct for population structure (Extended Data Figure 4a–e) which reflected both geography and self-reported ethnicity. Similar results were obtained using a mixed-model approach (Extended Data Figure 4f).

To assess the evidence for association in the discovery phase we used an approach which allows for heterogeneity in the protective effect of an allele across different study sites. This could be particularly important in our data as high levels of genetic and ethnic diversity in Africa can result in variable patterns of linkage disequilibrium between study sites that can complicate GWAS analysis⁷. Other potential sources of heterogeneity include allelic heterogeneity and multiple independent origins of malaria resistance loci, as has been well documented at the HBB locus^1,3, as well as the high levels of genetic diversity in the parasite⁸. Specifically, we used a Bayesian approach that combines evidence across multiple models of association by specifying a prior probability on the size and similarity of genetic effect across populations, as well as the mode of inheritance¹. A single statistical summary of the signal of association was obtained by averaging the evidence across models, weighting each by its prior probability, and comparing the evidence to the null model of no association (model averaged Bayes factor; BF_avg). Having observed the data, a posterior probability was assigned to each model (Pr_model) conditional on it being a true association and the model assumptions, which are described in the Methods and Extended Data Figure 5. We replicated previously reported GWAS signals^2,3,9 at the HBB (BF_avg=5.8×10²⁴), ABO (BF_avg=6.7×10⁹) and ATP2B4 (BF_avg=4.4×10⁵) loci, and a detailed analysis of key variants at these and other previously reported loci is presented elsewhere¹. A previously reported association near the gene MARVELD3² did not replicate in this dataset (Supplementary Note 1). Genome-wide patterns of association with severe malaria at the 34 regions of the genome containing a variant with either a Bayes factor for the most probable model (BF_max) > 2.5×10⁴ or with a model averaged Bayes factor (BF_avg) > 2.5×10³ are summarised in Extended Data Figure 6 and Supplementary Table 1. Details of the evidence for association in these regions can be viewed online at www.malariagen.net/resource/14.

These data provide a rich resource of new candidate loci for further investigation. Here we focus on a region of chromosome 4 shown in Figure 1, where the strongest signal of association (at SNP rs184895969) is located between the gene FREM3 and a cluster of three glycophorin genes (GYPE, GYPB and GYPA). Glycophorins are sialoglycoproteins that are abundantly expressed in the erythrocyte membrane, providing a hydrophilic surface coat that is necessary for erythrocytes to flow freely in the circulation. A complex system of single-nucleotide and structural variants in this region determine the MNS blood group system¹⁰. These genes play a functional role in invasion of erythrocytes by P. falciparum. Glycophorin A is the receptor for the P. falciparum erythrocyte-binding ligand EBA-175¹¹, and glycophorin B is a receptor for the parasite ligand EBL-1¹². To follow up this observation, selected SNPs at this locus were genotyped by Sequenom iPLEX MassArray in the discovery and replication sample sets outlined above (Figure 1 and Extended Data Figure 7a). The combined dataset of 25,498 samples provided convincing evidence of association at rs186873296 by standard fixed-effect meta-analysis (P = 9.5×10⁻¹¹) as well as by the above Bayesian approach (BF_overall = 1.3×10⁸; Figure 2 and Methods). The minor allele frequency of rs186873296 was higher in East Africa than West Africa, and the greatest evidence of association was seen in Kenya where it was most common, with an allele frequency of approximately 10%. Using only replication data to avoid winner’s curse, and assuming an additive model, we estimate that carrying one copy of the derived (non-ancestral) allele reduces the risk of severe malaria by about 40% in Kenya (OR = 0.60, 95% CI=0.46–0.79), with a slightly smaller effect across all populations (OR = 0.67, 95%CI 0.56–0.80 in frequentist fixed-effect meta-analysis). Further details are given in Supplementary Note 2.

Figure 1.

Signal of association with severe malaria across the FREM3/GYPE region. a) evidence for association (log₁₀BF_avg) in the discovery data. Black plusses denote SNPs that were directly typed, and black triangles denote SNPs selected for typing on the Sequenom platform. Dotted red vertical lines indicate a region of 0.25cM±25kb centred at the lead SNP (rs184895969). Coloured circles denote the correlation (outer circles) and |D’| (inner circles) with rs184895969 in controls, computed from imputed haplotypes. b) Polymorphisms shared between humans and chimpanzees, eQTLs, and previously reported associations with other phenotypes. c,d) Genes in the region and the HapMap combined recombination rate.

Figure 2.

Evidence for association at SNPs in the FREM3/GYPE region assuming an additive model of association. a) Forest plot showing sample size, estimated odds ratio and 95% confidence interval for the lead imputed SNP in each population and under fixed-effect meta-analysis. The frequency of the protective allele in controls in each population is shown to the right. b) The posterior weight on different models of heterogeneity at rs184895969 under the prior used in the GWAS. Model names are described in Methods. c) Forest plot for the Sequenom-typed SNP rs186873296 in discovery and replication samples, with fixed-effect meta-analysis across all populations and across East African populations (here taken as Kenya, Malawi, Tanzania and Cameroon.)

The glycophorin gene cluster has a complex pattern of gene conversion and structural variation that has been previously noted; indeed it has been proposed that selective pressure due to pathogens, including malaria, has contributed to shaping diversity in this region^10,13–16. Using the human reference sequence and mapped sequence read data from the 1000 Genomes Project, we identified the boundaries of a 350kb region of sequence homology surrounding these genes as well as a set of segregating gene deletions (Extended Data Figure 8). The lead imputed marker (rs184895969) is located within 10kb of this complex region. Imputation accuracy within the region is low using current reference data, so it is possible that the causal variant lies within the glycophorin genes themselves but that this is obscured in the current imputed dataset. With this caveat, we computed a credible set of putatively causal variants in the region; this set includes both the lead imputed marker and a linked missense mutation (rs181620317) in FREM3 (Extended Data Figure 7b). We note that the protective allele at rs184895969 was associated with increased GYPA transcription in published gene expression data for HapMap lymphoblastoid cell lines¹⁷ (P = 0.016; Extended Data Figure 9); other regional analyses are described in Supplementary Notes 1–2. Improved African genome variation reference panels^7,18 are needed to understand the complex patterns of variation in this region so that the causal variant of malaria resistance can be fine-mapped with greater confidence.

A striking feature of these data is that all of the loci which reach conventional criteria for genome-wide significance (P < 5×10⁻⁸ using a fixed effects model) are in or near genes that play a key role in erythrocytes (HBB, ABO, ATP2B4, FREM3/GYPE), the primary host cell of P. falciparum. Other erythrocyte-related genes are identified in the discovery phase analysis but do not reach genome-wide significance, including EPB41, which encodes erythrocyte membrane protein band 4.1 and has been implicated as a possible receptor for P. falciparum invasion¹⁹ (rs2985337: BF_avg=3443; fixed-effect meta-analysis OR=1.16, 95%CI=1.09–1.23, P=1.2×10⁻⁶; see Extended Data Figure 6).

An intriguing feature of the ABO locus is that it contains a number of polymorphisms that are shared between humans and other primates, and recent analyses of sequence variation across species indicated that some of these are ancient polymorphisms that have been maintained by balancing selection over millions of years²⁰. The current findings are of particular interest since the FREM3/GYPE is one of the most prominent examples of putative ancient balancing selection in a genome-wide analysis of haplotype sharing between humans and chimpanzees⁴. The peak GWAS signal at this locus is less than 45kb away from the shared human-chimp haplotype, which falls within the region covered by the credible set (Extended Data Figure 7b), although it does not exhibit a strong association with severe malaria (Supplementary Note 3). To explore the genealogical relationship between the putative ancient balanced polymorphisms (ABPs) and SNPs associated with severe malaria in the FREM3/GYPE region, we inferred an ancestral tree²¹ from the African (YRI + LWK) part of the 1000 Genomes data and used it to order haplotypes in the region, labelled with the positions of ABPs, malaria-associated SNPs, and other variants of interest (Figure 3). All three haplotypes carrying the protective allele at the directly-typed marker with most evidence of association (rs186873296) carry the minor allele at the ABP markers (D’=1, P=0.017). By inferring the positions of putative causal mutations on the estimated genealogical tree²¹ at the lead imputed marker (rs184895969) we found evidence for a single protective mutation in Kenya (log10 BF=3.09; OR=0.6) estimated to lie on the branch ancestral to the protective allele at the lead marker. Although the most likely position for an additional mutation was on the branch ancestral to the ABPs, a single haplotype explains most of the signal of association in this region.

Figure 3.

Haplotype analysis across the FREM3/GYPE region. Left hand panel shows haplotypes at 7321 polymorphic SNPs between 144.5Mb and 145.2Mb on chromosome 4 in the LWK and YRI samples of the 1000 Genomes reference panel. Key variants (Methods and Supplementary Note 2) are enlarged for clarity and labelled, with reference and non-reference alleles coloured blue and yellow respectively. On the right is the estimated topology of the genealogical tree at rs184895969. Dots indicate the position of the inferred protective mutation in Kenya and the branch ancestral to the ABPs, and are labelled with the estimated odds ratios (OR).

These observations raise the question of whether malaria resistance loci are more likely to be found in regions of the genome that show evidence of ancient balancing selection. We therefore analysed the relationship between the regions of association in our GWAS and 125 regions of the genome found by Leffler et al⁴ to contain haplotypes shared between humans and chimpanzees. The SNPs defining these haplotypes (ABPs) were not themselves enriched for association with severe malaria (P > 0.1, Methods). We used a simulation approach to assess the physical proximity of ABPs to the peak of association within the 34 strongest regions of association (tier 1) and 73 weaker signals (tier 2), and observed a significant relationship with tier 1 over a range of length scales (Extended Data Figure 10a,d). We also identified the nearest gene to the lead marker within each association region as well as the gene nearest to each ABP haplotype, and performed a gene-based test for genome-wide enrichment. Strong evidence for enrichment was seen at tier 1 loci (OR 41.0; P=4×10⁻⁷ by Fisher’s exact test, P_sim=5×10⁻⁴ using a simulation approach described in Methods, and P=1×10⁻⁴ using the INRICH algorithm²²; Extended Data Figures 10b–d) and a weaker trend at tier 2 loci (OR 7.7, P_sim=0.15). Apart from ABO and FREM3/GYPE, there were six other GWAS loci (4 in tier 1, 2 in tier 2) where the nearest gene to the lead marker was also the nearest gene to an ABP haplotype (DSCAM, NRG1, CNTNAP5, TMEM132C, CACNA2D1, RYR2). Although the current association evidence at these loci do not satisfy conventional criteria for genome-wide significance and they should be regarded as putative until convincingly replicated, it is noteworthy that they are all involved in key aspects of membrane biology (Supplementary Note 3).

In the largest genetic association study of malaria to date, we have identified a new locus of resistance to severe malaria that lies next to a cluster of glycophorin genes involved in erythrocyte invasion by P. falciparum, and that also overlaps a locus of putative ancient balancing selection identified by analysis of haplotype sharing between humans and chimpanzees. It is possible that malaria is not the cause of the ancient balancing selection, or that it is just one of a number of opposing evolutionary driving forces, as at ABO, where blood group O reduces the risk of severe malaria but increases the risk of severe cholera²³. Nonetheless, these new findings raise the intriguing question of whether natural selection on malaria susceptibility has been shaping genetic diversity in humans and their ancestors for millions of years. P. falciparum is closely related to the chimpanzee parasite P. reichenowi and other parasites of African Great Apes^24–26. It has been proposed that P. falciparum was introduced into human populations from chimpanzees or gorillas in the recent past, but this remains a matter of intense debate^25–27. Population genetic data are consistent with an ancient origin followed by a marked expansion of the parasite population approximately ten thousand years ago, coincident with the introduction of agriculture²⁸. The P. falciparum genome possesses a huge repertoire of polymorphism⁸ and it is possible that the host and parasite genomes are engaged in a longstanding evolutionary arms race, each maintaining diversity to try to outflank the other²⁹. Intriguingly, the parasite surface receptor EBA-175, which directly binds glycophorin A during red cell invasion, also contains structural polymorphisms with features of ancient dimorphism³⁰. The present findings provide new leads both to investigate these evolutionary mechanisms and to discover further genetic determinants of resistance to severe malaria in African children.

Methods

Samples, ethics and clinical information

Samples were collected from nine partner projects from across sub-Saharan Africa (Extended Data Figure 1a) as described previously^1,3. The studies and sample sets described in this manuscript form part of a larger ongoing project within the Malaria Genomic Epidemiology Network (www.malariagen.net). We used the World Health Organisation definition of severe malaria which comprises a broad spectrum of life-threatening clinical complications of Plasmodium falciparum infection^29,31. Investigators from study sites worked together to agree on principles for sharing data and standardising clinical definitions, and to define best ethical practices across different local settings including the development of guidelines for informed consent. Relevant ethics committees are listed in Extended Data Figure 1a. Further information on policies, research and the consent process may be found on the MalariaGEN website (http://www.malariagen.net/community/ethics-governance).

DNA extraction and Sequenom typing

As described previously^1,3, all samples submitted to the MalariaGEN Resource Centre underwent a standard set of procedures that included quantification using picogreen, genotyping of 65 polymorphisms (including HbS - rs334, and 3 gender-typing SNPs) on the Sequenom iPLEX MassArray platform and matching to baseline clinical data (e.g. gender, ethnic group and case-control status).

High-density genotyping

Three cohorts (Gambia, Malawi and Kenya) were genotyped on the Illumina HumanOmni2.5–4 (Kenya) and Illumina HumanOmni2.5–8 (Gambia, Malawi) platforms. As described previously³ we used three different calling algorithms (Illuminus³², Illumina’s Gencall algorithm as provided in BeadStudio, and GenoSNP³³), each of which uses slightly different information in the data. We formed final genotype calls by taking consensus between the three algorithms. Genotypes where any two of the three calling algorithms were discordant, and genotypes where fewer than two algorithms were confident enough to make a call were treated as missing. This process showed improved calling, evaluated using Mendelian error counts in a subset of Kenyan samples, relative to each of the three algorithms separately (data not shown).

Following genotype calling, we aligned genotypes to the forward strand of the human reference sequence (GRCh37), using both the Illumina-supplied manifest and publically available strand files (www.well.ox.ac.uk/~wrayner/strand) obtained by mapping allele probes to the reference by BLAT³⁴. We removed SNPs whose position or strand mismatched between the Illumina manifest and the strand file. To simplify analyses, we restricted attention to the set of SNPs having the same name, chromosome, position, strand, and probe sequences across the two genotyping platforms. Because the Omni2.5M contains multiple probes for some variants, we further removed SNPs to ensure positions were unique. In total we were left with 2322985 SNPs in each cohort across the autosomes and the X and Y chromosomes. We note that SNPs annotated as lying on the pseudo-autosomal region (PAR) of the X chromosome were not included, as these had position equal to 0 in the manifest for the HumanOmni2.5–4 array. Finally, we flipped alleles where necessary so that in downstream analyses the first allele always corresponds to the reference allele of the human genome sequence.

Sample Quality Control

We performed sample QC separately on each cohort by computing autosome-wide averages of normalised X channel intensity, normalised Y channel intensity, and heterozygosity and missingness based on the consensus call. To identify outlying samples we applied ABERRANT³⁵, adjusting the lambda parameter per cohort to account for differences in genotyping quality (Extended Data Figure 1d–f). In Gambia, a tail of samples showing low heterozygosity but otherwise appearing to be well typed was apparent. We explicitly included these samples in downstream analyses.

To estimate genome-wide relatedness between samples, we selected a list of 178775 high quality SNPs satisfying the criteria missingness < 1%, MAF > 1% and thinned to be at least 0.005cM apart and to have pairwise r² < 0.3. Treating each cohort separately, we used SHELLFISH (www.stats.ox.ac.uk/~davison/software/shellfish/shellfish.php) to compute a matrix of pairwise relatedness values R = (r_ij) between samples, where r_ij denotes the genome-wide average covariance of frequency-normalised genotypes in individuals i and j. In samples with few close relationships, the value of r_ij can be thought of as an estimate of kinship³⁶ with, for example, values close to 1 representing identity between samples, and values close to zero reflecting a lack of close relatedness (relative to the rest of the sample). To remove samples with duplicate typing and close relationships, we excluded one of each pair of samples with r_ij > 0.2, taking all remaining samples through to phasing and imputation. Extended Data Figure 1c lists the number of samples before and after QC, and the number removed by each QC step; (*) denotes the number of samples removed after explicitly including samples with low heterozygosity in Gambia.

We used SHELLFISH to compute principal components (PCs) on the post-QC sample set. Consistent with our removal of poor quality, duplicate and closely related samples, principal components plots show no substantially outlying samples (see Extended Data Figure 4a–c). The top few principal components in each cohort reflect substantial population structure, as evidenced by colouring by reported ethnicity. As found previously^3,9, the top principal components are also significantly correlated with case-control status (Extended Data Figure 4d), indicating that population structure may act as a confounding factor in association analyses if not controlled.

Genotyping Quality Control

Treating each cohort separately, we used SNPTEST (mathgen.stats.ox.ac.uk/genetics_software/snptest/snptest.html) to test for association at each autosomal SNP using a genotypic model of association which allows for different effects at heterozygote and homozygote genotypes, including the leading 5 principal components as covariates. Genotypic model association tests are particularly sensitive to confounding by genotyping error³⁷, and we used the resulting P-values as a guide to finding appropriate QC criteria. To detect potential spurious genotypes due to batch effects, we modelled genotypes as predicted by the leading 5 principal components and case/control status in a linear regression framework in R³⁸, and tested whether including an indicator of the plate on which each sample was genotyped contributed significantly to model fit. We refer to this as the “Plate test”. For downstream analyses we excluded SNPs with minor allele frequency < 1%, missing data proportion > 5% (in Gambia and Malawi) or > 2.5% (in Kenya, which had fewer missing genotypes overall), Hardy-Weinberg P < 1×10⁻²⁰ in controls, or Plate-test P < 0.01. We inspected cluster plots of all remaining SNPs showing association test P < 1×10⁻⁵ (Gambia) or P < 1×10⁻⁴ (Kenya, Malawi) and excluded those with clear genotyping problems. Extended Data Figure 2a shows the number of SNPs excluded by each criterion. The post-exclusion genome-wide association analysis is shown in Extended Data Figure 2c.

SNP QC on the X chromosome was performed as on the autosomes, with a few differences as follows. We treated males and females separately, using a genotypic model of association in females and an allelic model in males (who have only one copy of the X chromosome). Because genotype calling was performed blind to the gender of samples, some males appear to be heterozygous at some X chromosome SNPs. We treated all such heterozygous calls as missing. We computed missing data proportion and plate test P-values in males and females separately, and tested for departure from Hardy-Weinberg in female controls and for differences in frequency between males and females. We excluded SNPs with MAF < 1%, missingness > 5% (Gambia, Malawi) or 2.5% (Kenya) in males or females, or plate test P < 0.01 in males or females. We further excluded SNPs with Hardy-Weinberg P < 1×10⁻²⁰ in female controls or showing significant difference in allele frequencies between males and females (P < 1×10⁻²⁰). Extended Data Figure 2b shows the number of SNPs excluded by each criterion.

Some regions of the X chromosome showed an elevated number of male heterozygote calls, contributing to the high number of SNPs excluded due to missingness in males. These included SNPs in the pseudo-autosomal regions at either end of the chromosome³⁹ (indicating that XY designation in the chip manifests does not adequately cover these regions) as well as SNPs within the X transposed region near the centromere.

Phasing and imputation

We phased genotype data in each cohort separately using SHAPEIT v2.r644⁴⁰, specifying 200 hidden states and an effective population size of 17469, as recommended for African populations by the SHAPEIT documentation, and phasing each chromosome separately. We used IMPUTE v2.3.0^41,42 to impute phased genotypes into the 1000 Genomes⁶ Phase I integrated variant set (version of 24th August 2012, as downloaded from the IMPUTE website, which we refer to here as the 1000 Genomes reference panel) in 5Mb chunks with a buffer region of 500kb. For phasing and imputation we used the combined HapMap recombination map in build 37 coordinates included with the 1000 Genomes reference panel. Unless otherwise stated, downstream analyses included only SNPs with minor allele frequency > 0.5% and impute info metric > 0.75.

Assessment of imputation

At each genotyped SNP, IMPUTE computes squared correlation (referred to here as accuracy) and concordance between typed genotypes and genotypes obtained by masking the SNP and re-imputing. To assess imputation performance, we plotted the cumulative distribution of concordance (Extended Data Figure 3a) and accuracy (Extended Data Figure 3b), accuracy by frequency (Extended Data Figure 3d) as well as average per-sample accuracy (Extended Data Figure 3c). We also assessed accuracy relative to direct typing on the Sequenom platform at variants typed in the FREM3/GYPE, ARL14 and INPP4B regions of association as described below.

Association testing and meta-analysis

Association testing

We used SNPTEST to test for association at approximately 38 million variants obtained through imputation, including 5 PCs as covariates to control for population structure separately in each cohort. SNPTEST uses a missing data likelihood to account for the uncertainty in genotypes at imputed SNPs. We fit additive, dominant, recessive, and heterozygote models of association and ran SNPTEST separately in each imputation chunk. Below, we refer to the estimated effect size for population i and mode of inheritance m as β_i,m and its estimated standard error as SE_i,m.

Frequentist meta-analysis

For each SNP and each mode of inheritance (additive, dominant, recessive, heterozygote) we computed the fixed-effect inverse variance-weighted meta-analysis effect size, standard error, and P-value. In this context, fixed-effect meta-analysis assumes a single true effect size which is identical between the three cohorts, and can be thought of as finding the maximum likelihood estimate of the effect size under the assumption that the likelihood in cohort i is proportional to the density of the normal distribution with mean β_i,m and standard error SE_i,m.

Bayesian meta-analysis

We have previously^1,3 used Bayesian meta-analysis techniques to allow for between-population heterogeneity of effect sizes in these three cohorts. Here, we applied this method to compute Bayes factors for association under four modes of inheritance and six different models of correlation between cohorts. In this framework, true effect sizes are modelled by a multivariate normal distribution centred on zero and with a given prior covariance matrix which can be written as σ²P, where σ² is a prior variance controlling the magnitude of plausible effects and P is a prior correlation matrix.

The correlation models we used were:

Fixed effects (all elements of P equal to 1): as with frequentist fixed-effect meta-analysis, this assumes effect sizes are equal across the three cohorts.

Correlated effects (all off-diagonal elements of P equal to 0.96): this assumes effect sizes are similar but allows for some variability.

Independent effects (all off-diagonal elements of P equal to 0.1): this assumes there is little similarity between effect sizes in different cohorts.

Structured effects We also considered models where effects in the two East African populations (Kenya and Malawi) were more similar to each other than to that in Gambia. We assumed either effects were fixed between Kenya and Malawi and correlated (ρ=0.96) between East Africa and Gambia (we refer to this as the fixed-structured-effect model), or that effects were correlated (ρ=0.96) between Kenya and Malawi and largely independent with Gambia (ρ=0.1) (referred to as the correlated-structured-effect model).

We used prior variance parameters of σ²=0.2², reflecting a belief in relatively small effects (odds ratio < 1.5 with 95% probability)³⁷, and σ²=0.75², reflecting a belief in larger effects (odds ratio < 4.5 with 95% probability).

To form a single summary measure of evidence for association we formed a model-averaged Bayes factor (BF), referred to as the mean BF and denoted BF_avg, as a weighted average of model-specific Bayes factors using the following weighting scheme. We assigned weights of 0.4 for additive mode of inheritance and 0.2 for dominant, recessive, or heterozygote modes of inheritance, reflecting a belief that variants which tag causal variants by LD are more likely to display additive effects. We assigned a weight of 0.4, 0.2, and 0.1 to fixed-, correlated-, and independent-effect models, and 0.2 and 0.1 to fixed-structured and correlated-structured effects models. Finally we assigned weight of 0.5 to small-effect models (σ²=0.2²) and large-effect models (σ²=0.75²). Overall prior weights were assigned by multiplying across these categories; for example, the model representing small effect size distribution, fixed-effect across cohorts with additive mode of inheritance (denoted small-fix-add) was assigned prior weight equal to 0.5×0.4×0.4=0.08, while the model representing small, correlated-structured, dominant effects (denoted small-cor-str-dom) was assigned a prior weight of 0.5×0.1×0.2=0.01. For each SNP we also recorded the model having the highest posterior weight, and refer to its Bayes factor as the max BF (denoted BF_max). Extended Data Figure 5a depicts slices through the combined prior on effect sizes across three cohorts for additive effect models. The mean BF behaves similarly to a minimum over all four fixed-effect meta-analysis P-values, but additionally captures effects that vary between cohorts (Extended Data Figure 5b).

As described previously^1,3, to computed model-specific Bayes factors efficiently we used an approximation of the likelihood by the density of a normal distribution with the estimated mean (β_i,m) and standard error (SE_i,m) in each cohort. Thus, overall, observed effect sizes are modelled as normally distributed around zero with covariance that depends on the prior covariance in true effect sizes and on model standard errors,

$$({\beta }_{i,m})\sim N(0,{\sigma }^{2}P+V)$$

where V is a diagonal matrix with ith diagonal entry equal to the squared standard error, SE²_i,m. The approximate or asymptotic Bayes factor can then be computed by evaluating a ratio of two normal densities. In the univariate case this method is the same as described previously by Wakefield⁴³. To facilitate working with genome-wide meta-analysis results, we wrote custom software to compute frequentist and Bayesian meta-analyses, and stored details of genotype counts, association model fit, and meta-analysis results directly in a SQLite database file.

Further discussion of the Bayesian approach can be found in Supplementary Note 4.

X chromosome association testing and meta-analysis

Association testing on the X chromosome was performed as for the autosomes with a few differences as follows. We ran SNPTEST separately in males and females, estimating effect sizes under additive, dominant, recessive and heterozygote modes of inheritance in females. In this usage, SNPTEST assumes a model of complete inactivation so encodes male genotypes as 0/1 and females as 0/0.5/1 for an additive mode of inheritance. We than meta-analysed the six gender-specific association analyses to produce frequentist fixed-effect and model-averaged bayesian meta-analyses.

For Bayesian analysis, in addition to summing over models of between-population heterogeneity, we adopted the view that differences in sex might lead to heterogeneity in effect. We therefore included models of heterogeneity between males and females as follows. Let ρ_sex denote the correlation between effects in male and female samples within a single population. We included models where males and females have the same effect (ρ_sex=1, termed fixed-sex model and given prior weight 0.45), correlated effects (ρ_sex=0.96, termed correlated-sex model and given prior weight 0.225) or essentially independent effects (ρ_sex=0.1, termed independent-sex model and given prior weight 0.225). Because some parts of the X chromosome escape inactivation^39,44, we also included a model where the effect in females is twice that in males (given prior weight 0.1).

To fully specify prior correlation for each model, for each pair of populations A,B we also need to specify the correlation (denoted ρ_cross) between males in A and females in B. We set ρ_cross = ρ_pop × ρ_sex where ρ_pop is the chosen prior correlation between same-sex samples in A and B (i.e. ρ_pop =1, 0.96 or 0.1 as defined above).

As above, we formed overall weights by multiplying across categories, so that for example the model of small, additive effects that are fixed across populations and across sexes (denoted small-fixsex-fix-add) had prior weight 0.5×0.4×0.4×0.45=0.036.

Linear mixed model analysis

To compare association test results for logistic regression as implemented in SNPTEST with the use of a linear mixed model, we reran association test scans in each discovery cohort using the program MMM⁴⁵. We used the same genome-wide relatedness matrix as used to compute principal components (see above) and assumed an additive model of association. We plotted the –log10( P-value ) for MMM against the corresponding –log10( P-value ) based on the SNPTEST scan (which used 5 PCs as described above), for each discovery population and for fixed-effect meta-analysis (Extended Data Figure 4f). P-values under both methods at tier 1 loci are listed in Supplementary Table 1.

Lead SNPs, region and tier definitions

We formed a list of lead SNPs within approximately independent regions of interest as follows. We restricted to variants with IMPUTE info measure at least 0.75 across all three populations and ranked variants by the model-averaged Bayes factor (highest to lowest). We iteratively picked lead SNPs from the top of the list and excluded other variants within a recombination interval of 0.25cM±25kb centred at the lead SNP (referred to below as the association region), continuing until no more SNPs remained with BF_avg>250 or BF_max>2500.

We grouped lead SNPs into two tiers as follows:

• tier 1: all lead SNPs with BF_avg>2500 or BF_max>25000

• tier 2: all lead SNPs not in tier 1 with BF_avg>1000 or BF_max>10000

In total, across the autosomes and the X chromosome there were 34 regions in tier 1 and 73 in tier 2, with association regions covering approximately 13Mb and 26Mb of the genome respectively.

Regional association analysis

For each tier 1 and 2 region, we examined the pattern of association in the region, generating a regional association plot for the region annotated with details of the meta-analysis for the lead SNP as follows.

LD computation

In each region we computed pairwise LD statistics between the lead SNP and surrounding SNPs using best-guess imputed haplotypes for control samples across three populations. To facilitate this computation, we stored imputed haplotypes in a SQLite-format database allowing us effective random access to haplotype data. We used R to compute both Pearson correlation coefficient (r²) and Lewontin’s |D’| between the lead SNP and all other SNPs in the region.

Regional association plot

For each SNP in tier 1 and 2 we plotted log10(BF_avg) in the association region around the lead SNP plus 1Mb on either side, colouring points according to LD, with outer circles representing r² and inner circles representing |D’|. We further annotated SNPs that were typed in at least one cohort (using black plusses) and SNPs that had Sequenom genotype data available (with black triangles).

Regional annotations

We plotted all ABP variants (Supplementary Tables 4 and 5 of Leffler et al⁴), eQTLs from the Genotype-Tissue Expression project⁴⁶ (GTEx), and previously reported⁴⁷ GWAS loci. Where SNPs matched an imputed or typed variant, we computed LD statistics and coloured these points as above. We plotted all RefSeq genes (as downloaded from the UCSC Genome Browser MySQL database⁴⁸ on 2013-03-18) in the region, annotating the direction of transcription. We further plotted local recombination rate estimates from the HapMap combined recombination map included with the IMPUTE haplotypes described above.

Meta-analysis

We annotated plots with effect sizes and confidence intervals for the lead SNP for each mode of inheritance (additive, dominant, recessive and heterozygote) that informed the model averaging. We also produced barplots showing the posterior distribution on models of association using the prior weights described above.

Cluster plots

Finally, for each region, we produced and inspected cluster plots for all typed SNPs with BF_avg >= 10 that were not excluded by QC. As phasing fills in missing genotypes and potentially improves genotype calling based on LD with surrounding SNPs, we coloured plots based on genotype calls taken from the output of phasing.

Website

Regional association plots and cluster plots can be viewed online at http://www.malariagen.net/resource/14.

Validation and replication typing

Based on a preliminary version of the data presented here we selected SNPs for typing on the Sequenom platform across the whole MalariaGEN Consortial Project 1 sample set, which includes the discovery samples, further cases and controls in the same populations that were not included in the GWAS, and further large sample sets from five other populations from sub-Saharan Africa (see Extended Data Figure 1a). Data were available for SNPs tagging the lead markers in the FREM3/GYPE, INPP4B and ARL14 regions (r²>0.5 in controls, as estimated using the EM algorithm) as well as other regions not represented in tier 1.

Replication analysis

Replication analysis using Sequenom data was restricted to the set of samples with less than 10% missingness as measured across the set of 70 SNPs chosen for replication typing. In each population we conducted logistic regression in R, including five principal components (discovery samples) or reported ethnicity (replication samples) as covariates to control for population structure. For each GWAS lead SNP, we examined each Sequenom SNP in the region and computed r² and |D’| with the lead SNP. To allow for the effects of incomplete LD on the Bayesian model fitting, we recomputed the Bayesian analysis in the discovery samples based on Sequenom genotypes at each SNP, to obtain a Sequenom-based mean Bayes factor and a ‘best model’ Bayes factor at the model with highest posterior weight. Where LD is incomplete or where imputation is imperfect, this model may differ from the best model for imputed data.

For each SNP we computed fixed-effect meta-analysis across discovery samples, across replication samples, and across all samples. We also computed the Bayes factor for replication samples (BF_replication) for the model with highest posterior weight in the discovery samples. To compute an overall Bayes factor for association, we combined the discovery BF_avg computed at the imputed lead marker with the replication bayes factor at the Sequenom SNP, as BF_overall = BF_avg x BF_replication. We use the imputed lead marker here because the number of discovery samples directly typed was smaller than the number of imputed samples. Conditional on the lead imputed and replication markers reflecting the same signal of association, this BF_overall represents an overall measure of the evidence for association at the locus that reflects all the samples in our study.

A discussion of the replication evidence in the FREM3/GYPE, INPP4B and ARL14 regions can be found in Supplementary Note 1.

MalariaGEN encourages individual study sites to perform more detailed analyses of local patterns of disease association, and a Tanzanian-focused analysis of FREM3 and other candidate SNPs that were genotyped as part of this study is reported elsewhere⁴⁹.

Credible interval analysis

In a given region of the genome, under the assumption that exactly one variant (that is accessible to our typing or imputation) is causal, the posterior probability that each variant is the causal variant can be computed by a simple reweighting of Bayes factors⁵⁰. Using this approach we computed 95% and 99% credible intervals (i.e. the smallest set of SNPs accounting for 95% or 99% of the posterior mass) for variants in the association region around rs184895969, plus a margin of 50kb at either end (Extended Data Figure 7b). We noted that rs181620317, which is annotated as a missense mutation for the gene FREM3, is within the 95% confidence interval in our data. We note that while this analysis is simple and appealing, its interpretation depends on assumptions about the true disease model, and on the behaviour of imputation in the region⁵⁰; in particular the difficulty of imputing variants around the three glycophorin genes (Extended Data Figure 8) might make this analysis fail to capture putatively important variation within or around GYPA, GYPB, or GYPE.

Sequence homology and alignability in the glycophorin region

To investigate the location of our GWAS signal with respect to the pattern of sequence homology around the three glycophorin genes, we generated a dot plot (Extended Data Figure 8a) showing co-occurrence of k-mers in the human reference sequence⁵¹ in the region. Considerable sequence homology was observed over a region of about 350kb covering the three genes. Our lead GWAS marker and the ABPs lie just outside this region.

The high level of homology should affect our ability to align probes or sequences to this part of the genome. To confirm this, we also plotted the UCSC alignability track (‘CRG alignability 100’, Extended Data Figure 8c), which shows the degree to which the 100-mer starting at each position in the reference sequence is alignable (with a value of 1/n indicating that the 100-mer aligns to n positions across the genome, allowing up to two mismatches). As expected, even short regions of shared kmers affect alignability considerably, with alignability dropping to an average of about 0.7 within the large region of homology. Similarly, we plotted imputation performance (as measured by the IMPUTE info score) and observed a marked drop within the region of sequence homology.

Structural variation in the glycophorin region

We attempted to identify structural variation in the glycophorin region by examining sequence read data generated by the 1000 Genomes’ project, using the set of BAM files available from the 1000G project in October 2014, downloaded from ftp://ftp.1000genomes.ebi.ac.uk/vol1/ftp/data. These data contain a mixture of read lengths, with most reads of at least 90bp and some reads of 76bp. We considered only reads with mappinq quality at least 20. For each sample we computed coverage across the glycophorin region, normalised by average coverage computed across chromosome 1, and refer to these values here as ‘coverage’.

Coverage values across the region were correlated with genome alignability (as defined above), with coverage dropping substantially in regions of low alignability. We therefore restricted attention to the set of perfectly alignable positions, here defined as positions such that every 100-mer overlapping the position in the reference sequence aligns uniquely, allowing up to two mismatches (and computed using the CRG alignability 100 track described above). As expected, coverage at perfectly alignable positions showed little or none of the variation present in genome alignability (Extended Data Figure 8e–g).

Two large structural variants, present at frequencies of at least 1% in LWK+YRI, were evident in coverage data. Genotypes for both these variants were called by the 1000 Genomes phase I and are referred to as esv2668125 (also called MERGED_DEL_2_26708) and esv2662558 (also called MERGED_DEL_2_26722). Both deletions putatively represent deletions of all or part of GYPB. We noted some uncertainty as to the location of the breakpoints of both deletions - with 1000 Genomes’ breakpoints differing from the breakpoints as they appeared in coverage data by at least 10kb. We further noted that three samples (NA18519, NA19185, NA19222) that were called as heterozygote for one or both deletions by the 1000 Genomes project, appeared to have homozygous genotypes (red, blue and green lines, Extended Data Figure 8e–g).

Expression QTL analysis

To investigate the effect of associated SNPs in the FREM3 region on expression of nearby genes, we downloaded publically available data on RNA expression levels¹⁷ in HapMap samples, and plotted expression levels of genes in the region (Figure 1) against genotypes at the lead SNP and other SNPs of interest in African samples (YRI+LWK, Extended Data Figure 9). Data was available for genes INPP4B, USP38, GAB1, SMARCA5, GYPE, GYPB, GYPA, HHIP, ANAPC10 and ABCE1, with three probes available for GYPE, two for GAB1 and one probe for each of the other genes. Five samples in this dataset (NA19318, NA19324, NA19377, NA19429, NA19190) carry the protective allele at the lead marker rs184895969, while only two carry the protective allele at the directly-typed rs186873296. For each gene and SNP we tested for a trend of genotype on expression using linear regression. Extended Data 9 shows all probes for the glycophorins as well as other regional genes for which a P-value less than 0.05 was observed.

GENECLUSTER analysis

We used the program TREESIM²¹ to estimate an ancestral recombination graph for the LWK and YRI individuals in the 1000 Genomes Project haplotype data in a region from 144.6Mb to 144.8Mb on chromosome 4 centred on the lead SNP in the FREM3 / GYPE region. We then ran GENECLUSTER²¹ in the region, allowing it to assign either one or two causal mutations in each marginal genealogy. GENECLUSTER works by probabilistically assigning study individuals to the tips of the tree estimated by TREESIM, and attempts to explain case/control status by assigning causal mutations to the branches of the tree in a Bayesian framework. This analysis is somewhat similar in spirit to our marginal SNP analysis, but has important differences. In particular, GENECLUSTER may detect associated mutations anywhere on the tree (which may not correspond directly to any typed or imputed variant), and can assess models of association involving more than a single causal variant. However, GENECLUSTER does not take into account principal components or otherwise control for population structure, and for computational reasons we only included the Luhyan (LWK) and Yoruban (YRI) populations from the 1000 Genomes reference panel in the analysis.

To investigate the relationship between ancestry and variants of interest, we plotted IMPUTE reference panel haplotypes in the region ordered by the marginal tree at the position of the imputed lead marker (rs184895969), annotating the lead imputed and Sequenom-typed markers, ABPs, previously reported GYPE eQTLs⁵², common deletions, and variants determining the M/N and S/s blood groups as described in Supplementary Note 2 (Figure 3).

Analysis of enrichment of malaria-associated loci in functional categories

Full details of enrichment analyses are provided in Supplementary Note 3.

Code availability

The SNPTEST software for genome-wide association testing is available at https://mathgen.stats.ox.ac.uk/genetics_software/snptest/snptest.html.

Executables and source code for inthinnerator are available at http://www.well.ox.ac.uk/~gav/inthinnerator.

Further software for generating key results for this paper will be made available at http://www.malariagen.net/resource/14.

Extended Data

Extended Data Figure 1.

Sample collections included in the study. a) Study sites and ethics approving institutions. b) Phenotypic makeup of discovery and replication samples from each site. ‘UNCOMPLICATED’ refers to case individuals who were not identified as cerebral malaria (CM) or severe malarial anaemia (SMA) cases. ‘BOTH” refers to individuals who have both CM and SMA phenotypes. c) Overall sample counts and number of samples excluded by each QC criterion. (*) denotes the number of samples removed after explicitly including samples with low heterozygosity in Gambia. (†) The Kenyan cohort included parents of a subset of case samples; these were not used in subsequent analyses. d) Plots of average genome-wide heterozygosity and missingness with outliers coloured, as output by the ABERRANT algorithm.

Extended Data Figure 2.

Genotyped SNP quality control (QC) for the 3 discovery cohorts. a,b) Total numbers of pre- and post-QC SNPs on a) the autosomes and b) the X chromosome, and numbers of SNPs excluded by each QC criteria. MAF refers to minor allele frequency, HWE to Hardy-Weinberg equilibrium, Plate to the plate test of association and Diff. to the test of difference in frequency between males and females. Details of QC are given in Methods. c) Plot showing the –log10(P values) for the genotypic association test in the discovery data including the first 5 principal components as covariates. Grey dots show SNPs that are removed due to the QC as defined in Methods. The total fraction of SNPs removed from each cohort is given at the top of the plot.

Extended Data Figure 3.

Imputation performance. a,b) Empirical distribution of concordance and accuracy (r²) between typed and re-imputed SNPs in the three discovery cohorts. Solid lines represent SNPs with frequency below 5% and dashed lines represent SNPs with frequency of at least 5%. c) Per-sample concordance and accuracy (type 0 r²) across the whole genome, as estimated by reimputing genotyped SNPs. Values are averaged over imputation chunks. d) Average accuracy between genotype and re-imputed SNPs in each cohort, plotted against frequency, in 1% frequency bins.

Extended Data Figure 4.

Top ten principal components (PCs) in a) Gambia, b) Malawi and c) Kenya. Where ethnicity was reported, points are coloured by ethnicity for ethnicities with at least 50 samples. d) Logistic regression P-values and direction of effect for the top ten principal components on Severe Malaria status in each cohort. e) qq-plots for additive model association test P-values in Gambia, Malawi, Kenya, and for fixed-effect meta-analysis. Dashed lines represent the 99% confidence interval computed marginally at each variant. Circles and points represent points lying respectively outside and inside the 99% confidence interval. f) Comparison of association test P-values for logistic regression (SNPTEST, x-axis) and linear mixed model (MMM, y-axis) for Gambia, Malawi, Kenya, and for fixed-effect meta-analysis. Variants in tier 1 are coloured blue, with the lead marker at the FREM3/GYPE region coloured red.

Extended Data Figure 5.

Detail of Bayesian analysis of discovery cohorts. a) Visualisation of slices through the combined prior on effect sizes in three cohorts for mode-of-inheritance-specific models. Top row: slices through the prior effect size on Kenya (x-axis) and Malawi (y-axis) for constant effect size in Gambia (panels). Bottom row: slices through the prior effect size on Kenya (x-axis) and Gambia (y-axis) for constant effect size in Malawi (panels). Red lines represent a factor of 10 in the prior density. b) Comparison of BF_avg (x-axis) with the minimum fixed-effect meta-analysis P-value minimized across additive, dominant, recessive or heterozygote modes of inheritance (y-axis). Values are plotted on log10 and –log10 scales. Colour indicates the heterogeneity model of the model with the highest posterior weight. c) Sensitivity of BF_avg to changes in prior. Plots show BF_avg ratio (y-axis) plotted against one-dimensional parameterisations of the prior (x-axis), for the 32 autosomal SNPs in tier 1. Solid lines represent variants with minor allele frequency < 5% averaged across populations, and dashed lines variants with minor allele frequency >= 5%. Black dots indicate the lead marker at the FREM3/GYPE locus. Colour indicates the effect size, mode of inheritance, or heterogeneity model for the model with highest posterior weight under the GWAS prior. Dashed grey vertical lines indicate the x-axis value corresponding to the prior used in the GWAS, and one-half and twice that value. Plots are parameterised by i) the prior standard deviation of the small-effect model keeping the prior standard deviation of the large and small-effect models in the ratio 0.75:0.2; ii-v) the prior weight on additive, dominant, recessive or heterozygote modes of inheritance; vi-x) the prior weight on fixed, correlated, independent, fixed-structured and correlated-structured models. For each parameterisation prior weights on other models are kept in the same relative proportion. For further details see Supplementary Note 4.

Extended Data Figure 6.

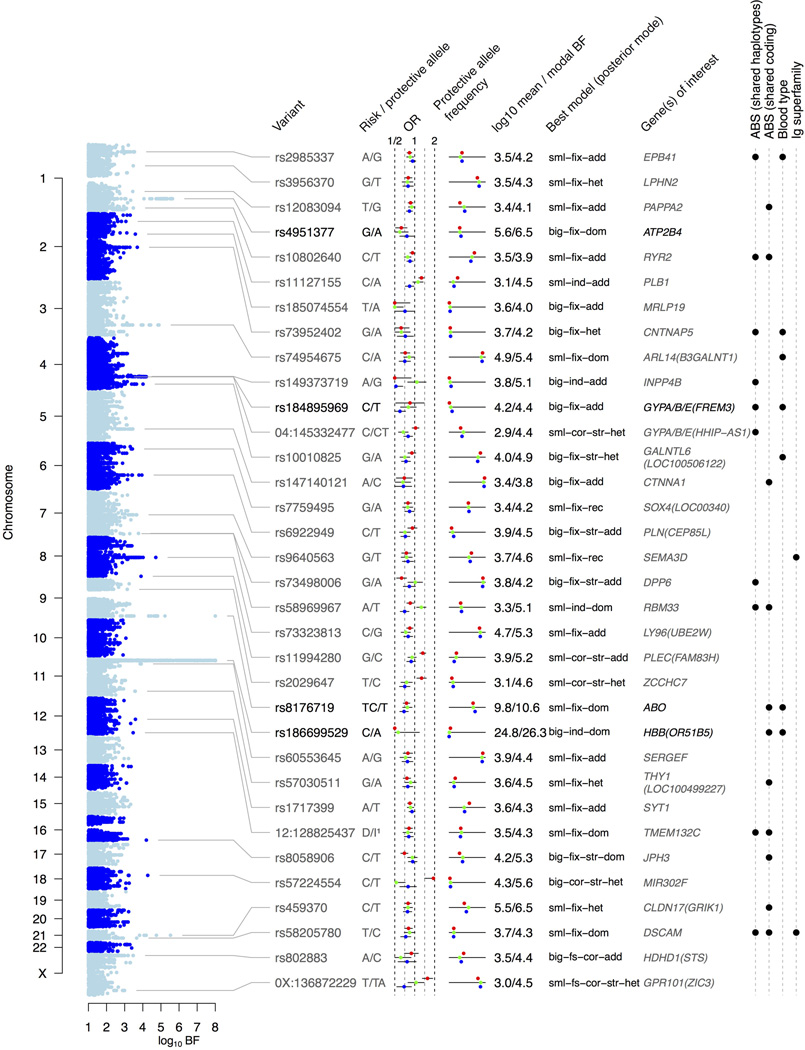
Strongest regions of association in the Bayesian analysis of the three discovery cohorts. Plot on left shows the log10 model- averaged Bayes Factor (BF_avg). Table shows the SNP with the highest BF_avg in each region (lead SNP), gene(s) of interest in the region, the model with the highest posterior weight at the lead SNP and its BF. Coloured points indicate the odds ratio (OR) and the protective allele frequency in Gambia (red), Malawi (green) and Kenya (Blue). The right hand columns indicate regions containing shared chimp-human haplotypes or coding SNPs⁴ (ABPs), blood group genes, or Immunoglobulin superfamily genes.

Extended Data Figure 7.

a) Evidence for association at directly-typed SNPs in the FREM3/GYPE, INPP4B and ARL14 regions. b) Posterior probability that variants in the FREM3/GYPE region are causal assuming a single variant in the region is causal⁵⁰, based on the BF_avg for typed and imputed variants. Dashed lines indicate the 95% and 99% credible sets. See Figure 1 legend for further details. c) Details of SNPs encoding the common MNS blood groups. Coordinates and alleles are with respect to the NCBI b37 human reference sequence. d) Evidence for possible independence of effects at the FREM3 and INPP4B loci in Kenya by conditional analysis. Y-axis represents -log10(association P-value) conditional on the imputed dosage at rs184895969. Points are coloured by LD with the top SNP rs13103597. e) Forest plot showing sample size, estimated odds ratio and 95% confidence interval for the lead imputed SNP (rs149373719) in INPP4B under an additive model of association. f) Bar plot showing the posterior weight on different models of heterogeneity at rs149373719 under the prior used in the GWAS, assuming an additive model of association. g) Forest plot showing evidence in both discovery and replication samples in the Sequenom data at rs77389579 in INPP4B. See Figure 2 legend for further details.

Extended Data Figure 8.

Sequence homology, alignability and structural variation in the glycophorin region. a) co-occurrence of 100-mers (upper triangle) and 25-mers (lower triangle) in the human reference sequence. Each point represents a kmer that maps to the locations indicated by the x and y axis positions, either on the same strand (black points) or opposite strands (red points). Green vertical lines in this and subsequent panels delineate the region of high homology surrounding the three glycophorins. b) the location of the lead GWAS marker, ABPs, and protein-coding genes in the region. c) alignability of the 100-mer at each position of the reference, up to two mismatches. Values are taken from the UCSC genome browser mappability track and averaged over 5kb bins. d) IMPUTE info in Kenya for variants with frequency at least 5%, averaged over 5kb bins. e–f) coverage for samples from YRI and LWK in 1000G Phase 1 carrying esv2662558, carrying esv2668125, or not carrying either deletion, respectively. Coverage for each individual is normalised by the mean coverage for that individual across chromosome 1, and only computed at positions with alignability = 1 for all 100-mers overlapping the position, and for reads with mapping quality at least 20. Values are averaged over 5kb (grey) and 10kb (blue) bins. Three samples with apparently erroneous calls in the 1000G Phase1 genotype release are coloured (NA18519, red; NA19185, yellow; NA19222, green) and assigned to the status indicated by their coverage profile. The bottom row represents a sample of 30 individuals not carrying the deletion selected at random in addition to the two with erroneous genotype calls. Coverage computation was performed using the BAM files available from the 1000G project in October 2014, downloaded from ftp://ftp.1000genomes.ebi.ac.uk/vol1/ftp/data. Four African samples in the Phase 1 release were not assessed because they are not included in this directory.

Extended Data Figure 9.

Correlation between the genotypes at SNPs of interest within the GYPE/A/B locus and reported gene transcription levels in samples from the YRI and LWK HapMap cohorts¹⁷. P values are for a trend test of association where more than one genotype class is present. Only assays targeting the glycophorins, and those with a P-value below 0.05 are shown.

Extended Data Figure 10.

Detail of enrichment analysis. a) Red histogram: the empirical distribution of the log₁₀ distance of observed tier 1 loci to the nearest ABP haplotype. Grey histogram: distribution of distances for 10,000 simulated tier 1 sets. b) The log₁₀ distance of tier 1 (filled red circles) and tier 2 (empty circles) loci to the nearest ABP, plotted against their rank in BF_avg order (stronger signals have lower rank). Loci are annotated with the nearest gene where a gene exists within the association region. Asterisks denote nearest genes that are also the nearest gene to an ABP shared haplotype. c) Empirical null distribution of the odds ratio for the enrichment of tier 1 loci in the set of genes closest to an ABP shared haplotype, based on 10,000 simulated SNP sets. The red asterisk and text indicate the odds ratio for the observed tier 1 loci. d) Distribution of the proportion of the genome which identifies a given gene as nearest, for genes in or not in the set annotated as nearest an ABP haplotype. Left: distribution of the length of the genome for which the given gene is unambiguously the closest gene. Middle: distribution of the number of SNPs in our study for which the given gene is the closest gene. Right: distribution of the number of SNPs in our study for which the given gene is the nearest gene within a recombination interval of 2.5cM±25kb around the SNP, as used to determine nearest genes to GWAS lead SNPs. e) Empirical P-values for enrichment of ABP haplotypes and coding SNPs in tier 1 and tier 2 GWAS regions. Second column: P-values for enrichment by gene overlap. Third to tenth column: P-values for enrichment by proximity at different length scales. †Results for simulations using SNPs frequency-matched to GWAS tier 1 loci in 1% frequency bins. ††Results for simulations excluding the regions of ABO, HBB, ATP2B4, FREM3, INPP4B, and HHIP-AS1.

Author contributions

Writing group: Gavin Band1, Dominic P. Kwiatkowski1,2, Kirk A. Rockett1,2, Chris C.A. Spencer1

Data analysis: Gavin Band1, Geraldine M. Clarke1, Katja Kivinen2, Quang Si Le1, Ellen M. Leffler1, Dominic P. Kwiatkowski1,2, Kirk A. Rockett1,2, Chris C.A. Spencer1

Project management: Kirk A. Rockett1,2, Chris C.A. Spencer1, Victoria Cornelius1, David J. Conway3,24, Thomas N. Williams15,16, Terrie Taylor23, Dominic P. Kwiatkowski1,2

Study site lead investigators: David J. Conway3,24, Kalifa A. Bojang3, Ogobara Doumbo5, Mahamadou A. Thera5, David Modiano6, Sodiomon B. Sirima7, Michael D. Wilson9, Kwadwo A. Koram9, Tsiri Agbenyega10,22, Eric Achidi14,20, Thomas N. Williams15,16, Kevin Marsh15, Hugh Reyburn17,18, Chris Drakeley17,18, Eleanor Riley18, Terrie Taylor23, Malcolm Molyneux19

Clinical data and sample collection: Muminatou Jallow3,4, Kalifa A. Bojang3, David J. Conway3,24, Margaret Pinder3, Ogobara Doumbo5, Mahamadou A. Thera5, Ousmane B. Toure5, Salimata Konate5, Sibiri Sissoko5, Edith C. Bougouma7, Valentina D. Mangano6, David Modiano6, Sodiomon B. Sirima7, Lucas N. Amenga-Etego8, Anita K. Ghansah9, Abraham V. O. Hodgson8, Kwadwo A. Koram9, Michael D. Wilson9, Tsiri Agbenyega10,22, Daniel Ansong10,22, Anthony Enimil10, Jennifer Evans11,12, Eric Achidi14,20, Tobias O. Apinjoh13, Alexander Macharia15, Kevin Marsh15, Carolyne M. Ndila15, Charles Newton15, Norbert Peshu15, Sophie Uyoga15, Thomas N. Williams15,16, Chris Drakeley17,18, Alphaxard Manjurano17,18, Hugh Reyburn17,18, Eleanor Riley18, David Kachala19, Malcolm Molyneux19, Vysaul Nyirongo19, Terrie Taylor23

Sample processing, genotyping, data management and project coordination: Kirk A. Rockett1,2, Katja Kivinen2, Daniel Mead2, Eleanor Drury2, Sarah Auburn1, Susana G. Campino2, Bronwyn MacInnis2, Jim Stalker2, Emma Gray2, Christina Hubbart1, Anna E. Jeffreys1, Kate Rowlands1, Alieu Mendy1, Rachel Craik1, Kathryn Fitzpatrick1, Sile Molloy1, Lee Hart1, Robert Hutton1, Angeliki Kerasidou1,21, Kimberly J. Johnson1, Victoria Cornelius1

Author affiliations

¹ Wellcome Trust Centre for Human Genetics, University of Oxford, Roosevelt Drive, Oxford OX3 7BN, UK.

² The Wellcome Trust Sanger Institute, Hinxton, Cambridge CB10 1SA, UK.

³ Medical Research Council Unit, Atlantic Boulevard, Serrekunda, The Gambia.

⁴ Royal Victoria Teaching Hospital, Independence Drive, Banjul, The Gambia.

⁵ Malaria Research and Training Centre, Faculty of Medicine University of Bamako Bamako Mali.

⁶ University of Rome La Sapienza, Italy.

⁷ Centre National de Recherche et de Formation sur le Paludisme (CNRFP), Ouagadougou, Burkina Faso.

⁸ Navrongo Health Research Centre, Navrongo, Ghana.

⁹ Noguchi Memorial Institute for Medical Research, Accra, Ghana.

¹⁰ Komfo Anokye Teaching Hospital, Kumasi, Ghana

¹¹ Department of Molecular Medicine, Bernhard Nocht Institute for Tropical Medicine, Postfach 30 41 2, D-20324 Hamburg, Germany.

¹² Kumasi Centre for Collaborative Research, Kumasi, Ghana.

¹³ Department of Biochemistry & Molecular Biology, University of Buea, Buea, South West Region, Cameroon.

¹⁴ Department of Medical Laboratory Sciences, University of Buea, Buea, South West Region, Cameroon.

¹⁵ KEMRI-Wellcome Trust Research Programme, PO Box 230, Kilifi, Kenya.

¹⁶ Faculty of Medicine, Department of Medicine, Imperial College, Exhibition Road, London SW7 2AZ, UK.

¹⁷ Joint Malaria Programme, Kilimanjaro Christian Medical Centre, PO box 2228, Moshi, Tanzania.

¹⁸ Faculty of Infectious and Tropical Diseases, London School of Hygiene and Tropical Medicine, Keppel Street, London, UK.

¹⁹ Malawi-Liverpool-Wellcome Trust Clinical Research Programme, College of Medicine, University of Malawi, PO Box 30096, Blantyre, Malawi.

²⁰ Weatherall Institute of Molecular Medicine, Oxford University, Oxford, UK.

²¹ The Ethox Centre, Nuffield Department of Population Health, University of Oxford, Old Road Campus, Oxford, OX3 7LF.

²² Kwame Nkrumah University of Science and Technology, Kumasi, Ghana.

²³ Blantyre Malaria Project, College of Medicine, University of Malawi.

²⁴ Department of Pathogen Molecular Biology, London School of Hygiene and Tropical Medicine, Keppel Street, London, WC1E 7HT, UK.