Complex constraints on allometry revealed by artificial selection on the wing of Drosophila melanogaster

Significance

Many traits scale precisely with size, but it is unknown whether this is due to selection for optimal function or due to evolutionary constraint. We use artificial selection to demonstrate that wing-shape scaling in fruit flies can respond to selection. This evolved response in scaling was lost during a few generations after selection ended, but other selected changes in wing shape persisted. Shape–size scaling in fly wings is therefore evolvable, but adaptation is apparently constrained by selection that may not be on wings. This may explain why scaling relationships are often evolutionarily conserved.

Abstract

Precise exponential scaling with size is a fundamental aspect of phenotypic variation. These allometric power laws are often invariant across taxa and have long been hypothesized to reflect developmental constraints. Here we test this hypothesis by investigating the evolutionary potential of an allometric scaling relationship in drosophilid wing shape that is nearly invariant across 111 species separated by at least 50 million years of evolution. In only 26 generations of artificial selection in a population of Drosophila melanogaster, we were able to drive the allometric slope to the outer range of those found among the 111 sampled species. This response was rapidly lost when selection was suspended. Only a small proportion of this reversal could be explained by breakup of linkage disequilibrium, and direct selection on wing shape is also unlikely to explain the reversal, because the more divergent wing shapes produced by selection on the allometric intercept did not revert. We hypothesize that the reversal was instead caused by internal selection arising from pleiotropic links to unknown traits. Our results also suggest that the observed selection response in the allometric slope was due to a component expressed late in larval development and that variation in earlier development did not respond to selection. Together, these results are consistent with a role for pleiotropic constraints in explaining the remarkable evolutionary stability of allometric scaling.

Allometric scaling is a ubiquitous aspect of biological variation that is often strongly conserved across evolutionary time and typically explains a large fraction of observed variation in morphology, physiology, or life history (1–7). This evolutionary conservatism can be explained either by stabilizing selection or by developmental or physiological constraints (8–17). Allometric power laws have been thought to reflect developmental constraints for nearly a century (6). Arguments of allometric constraints were used to explain patterns of macroevolution by architects of the modern synthesis such as Huxley (5), Simpson (18), and Rensch (19), and played a major role in Gould and Lewontin’s (20) criticism of the “adaptationist programme.” The idea of allometric constraints may, at least partially, have originated from the multiplicative growth model underlying Huxley’s derivation of the allometric power law for morphological traits.

Julian Huxley (5, 21) showed that when a trait is under common growth regulation with size, the relationship between the trait Y and a size measure X is a power function of the form Y = aX^b, where a and b are constants. On a log–log scale, power functions become linear, with log(a) representing the intercept and b representing the slope of the allometric relationship log(Y) = log(a) + b log(X). Allometric power laws summarize variation among developmental stages (ontogenetic allometry), individuals in a population (static allometry), and populations or species (evolutionary allometry) (22). The three levels of allometry are related, and a higher level of allometry can be expressed as a function of allometry at lower levels (23). Limited potential for evolution at a lower level in this allometric hierarchy would then cause constraints at all higher levels (6, 23).

Because of their fundamental importance and their relation to developmental constraints, there has been interest in testing the evolvability of scaling relationships in general and, in particular, the evolvability and evolutionary invariance of the static allometric slope. In a recent review, Voje et al. (6) argued that, although there is abundant evidence for evolvability of intercepts of static allometric relations (i.e., mean shape), there are few clear demonstrations of additive genetic variance or microevolutionary changes in allometric slopes. Although there are many claims of evolvable allometric slopes in the literature, most are problematic due to various conceptual and methodological issues (see refs. 6 and 24–26).

One exception is Pavlicev et al.’s (27) finding of small but significant heritabilities for several allometric exponents in an intercross between mouse strains selected for large and small body size. Another case comes from Tobler and Nijhout (28), where 10 generations of selection on wing mass in the moth Manduca sexta produced a small change in wing–body scaling (see ref. 6 for a reanalysis). This was, however, an indirect response, so it is unclear how free the slope was to evolve on its own. The result is also based on observing the relationship in a single generation, calling its replicability into question (see ref. 26 for further discussion). In the only study that performed artificial selection separately and directly on the allometric slope and intercept, Egset et al. (29) found a clear response in the intercept but not in the slope of a tail–body allometry in guppies (Poecilia reticulata). The power of this study was also limited, however, because it extended only over three generations. From comparative analyses, there is clear evidence of evolution of static slopes on long time scales, but no clear cases of substantial change over less than a million years (6).

Here we test the evolutionary potential of both the static allometric intercept and slope of an aspect of wing shape allometry in D. melanogaster. To do this, we use a series of large-scale artificial selection experiments (58,046 measured flies in total) and compare the selection response to the natural variation in wing shape allometry obtained from a comparative study of 111 drosophilid species (20,345 measured flies).

Results and Discussion

In the Dipteran family Drosophilidae, the length of wing vein L2 shows tight and positive evolutionary and static allometries with wing size (Fig. 1). The L2 vein intersects the leading edge of the wing (vein L1) in a relatively proximal position in small wings and more distally in larger wings (Fig. 1). Our comparative analysis shows that both the intercept and the slope of the static allometry have evolved, but at very low rates (Table S1). For the intercept, the estimated standard deviation of change from a Brownian motion model of evolution ranges from 0.026 to 0.042 log_e millimeters per million years depending on how deep the phylogeny is considered to be. This corresponds to average changes in relative L2 length of less than 4% per million years. Similarly, the slope changed with an estimated standard deviation of less than 0.037 slope units per million years. Hence, wing shape allometry is strongly conserved in drosophilids.

Fig. 1.

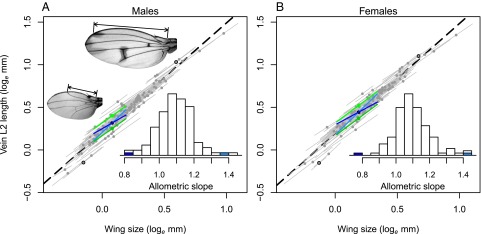
Allometric relationships of males (A) and females (B) within and among 111 drosophilid species. Among-species (evolutionary) allometry (dashed line; slope males = 1.282 ± 0.029, R² = 0.95; slope females = 1.291 ± 0.029, R² = 0.95), within-species (static) allometries (gray lines; average slope males = 1.091 ± 0.095, average R² = 0.89; average slope females = 1.095 ± 0.096, average R² = 0.92), and the selection responses (green and blue lines; see Fig. 2 for explanation of color coding). The pictures illustrate our measure of L2 vein length (double-headed arrows) in a small (Dettopsomyia nigrovittata) and a large (Idomyia mimica) species (encircled dots). Wing size is the square root of wing area. (Inset) The histograms show the among-species distribution of slopes with the final slopes of the up- and down-selected populations in blue.

Table S1.

Estimated evolutionary rates for allometric intercepts and slope using a Brownian-motion model of evolution

Parameter	Rate	95% confidence interval	Unit
Depth of phylogeny 50 My
Allometric intercept	0.00180	0.00130–0.00241	(loge mm)2/My
Allometric slope	0.00138	0.00095–0.00196	slope2/My
Depth of phylogeny 133 My
Allometric intercept	0.00068	0.00049–0.00091	(loge mm)2/My
Allometric slope	0.00052	0.00036–0.00074	slope2/My

The depth of the phylogeny is highly uncertain; we therefore give the rates for phylogenies of two depths (50 My or 133 My). The unit denoted slope is the proportional change in vein L2 length for a proportional change in wing size, (log_e mm)/(log_e mm), or the elasticity of vein L2 length to wing size. Note that the rates are given as increase in variance of traits over time. In Results and Discussion, we give the square root of the rates (standard deviations), to increase interpretability. Because the intercept is on the natural log scale, the standard deviation is approximately the coefficient of variation, and multiplying these values by 100 scales them as percent of the trait mean.

It proved easy to change the allometric intercept (i.e., mean shape) by selecting on the residuals of the log–log regression (Fig. 2A). After seven generations of selection on the intercept, the average length of vein L2 had increased by ∼8.5% (from 1.34 mm to 1.46 mm in males and from 1.58 mm to 1.70 mm in females) in the “up-selected” populations and decreased by ∼6.5% (from 1.34 mm to 1.26 mm in males and from 1.58 mm to 1.47 mm in females) in the “down-selected” populations. Hence, the average length of vein L2 had become as large in the up-selected males as in the down-selected females (Fig. 2A) whereas the sexual size dimorphism remained unchanged. This selection response of about 1% per generation is rapid evolution on a macroevolutionary scale. Only four generations of artificial selection were sufficient to produce a change comparable to the one observed over a million years of evolution, as judged from the average change in the comparative data. This change was also stable. During 16 generations without artificial selection, the intercept returned less than 0.15% per generation toward the original value (Fig. 2A). Hence, natural selection on wing shape was weak in the laboratory environment. These results show that mean shape is highly evolvable in this population, as it is in many insects (30–35). The stasis of wing shape among drosophilids must therefore be due to other factors than the lack of genetic variation.

Fig. 2.

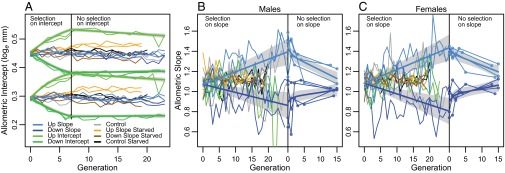
Change in allometric intercept (A), and allometric slope for males (B) and females (C) for the two replicates of each selection regime. The model fit for the different selection regimes are given by the thick lines with ±SE in gray; see Tables S2, S3, and S4 for parameter estimates. In A, males have the lower intercept (trait mean). In B, the outlier up-intercept generation 22 had a slope of −0.17. The selection stopped at generations 25 and 26 in the slope-selected populations. In addition, we budded off a population from each replicate at generation 23 and maintained these new populations under relaxed selection. Therefore, the generation axis has two scales in B and C, with the right-hand scale denoting generations under relaxed selection. The populations were measured at each generation except during relaxed selection on slope, where measurements are indicated by circles.

Table S2.

Allometric parameters and the change in intercept during the intercept-selection experiment

Parameter	Estimate	SE	Unit
Males
Common intercept at t = 0	0.29520	0.00276	loge mm
Linear change per generation Control at t = 0–23	−0.00025	0.00018	(loge mm)/t
Linear change per generation Up Selection at t = 0–7	0.01998	0.00310	(loge mm)/t
Linear change per generation Down Selection at t = 0–7	−0.01353	0.00310	(loge mm)/t
Quadratic change per generation Up Selection at t = 0–7	−0.00114	0.00046	(loge mm)/t2
Quadratic change per generation Down Selection at t = 0–7	0.00059	0.00046	(loge mm)/t2
Linear change per generation Up Selection at t = 7–23	−0.00136	0.00059	(loge mm)/t
Linear change per generation Down Selection at t = 7–23	0.00014	0.00059	(loge mm)/t
Common static allometric slope	1.07830	0.00739	slope
Females
Common intercept at t = 0	0.45481	0.00276	loge mm
Linear change per generation Control at t = 0–23	−0.00053	0.00018	(loge mm)/t
Linear change per generation Up Selection at t = 0–7	0.01603	0.00310	(loge mm)/t
Linear change per generation Down Selection at t = 0–7	−0.01617	0.00310	(loge mm)/t
Quadratic change per generation Up Selection at t = 0–7	−0.00069	0.00046	(loge mm)/t2
Quadratic change per generation Down Selection at t = 0–7	0.00084	0.00046	(loge mm)/t2
Linear change per generation Up Selection at t = 7–23	−0.00136	0.00059	(loge mm)/t
Linear change per generation Down Selection at t = 7–23	0.00030	0.00059	(loge mm)/t
Common static allometric slope	1.09650	0.00736	slope

Generation is denoted t, and the unit denoted slope is the proportional change in vein L2 length for a proportional change in wing size.

Table S3.

Allometric slopes and their change during the slope-selection experiment

Parameter	Estimate	SE	Unit
Males
Common slope at t = 0	1.08186	0.02145	slope
Linear change per generation Up Selection	0.01185	0.00561	slope/t
Linear change per generation Down Selection	−0.00939	0.00561	slope/t
Linear change per generation Control	0.00062	0.00570	slope/t
Females
Common slope at t = 0	1.09302	0.02139	slope
Linear change per generation Up Selection	0.01265	0.00561	slope/t
Linear change per generation Down Selection	−0.01185	0.00561	slope/t
Linear change per generation Control	0.00126	0.00570	slope/t

See Table S2 for explanation of units.

Table S4.

Allometric slopes and their change during relaxed selection in the slope-selection experiment

Parameter	Estimate	SE	Unit
Males
Initial slope Up Selection	1.43663	0.05860	slope
Initial slope Down Selection	0.89016	0.05897	slope
Total change due to LD Up Selection	−0.06487	0.09414	slope/(1 – rt)
Total change due to LD Down Selection	0.05153	0.09318	slope/(1 – rt)
Linear change per generation Up Selection	−0.01614	0.00655	slope/t
Linear change per generation Down Selection	0.00499	0.00633	slope/t
Females
Initial slope Up Selection	1.40965	0.05661	slope
Initial slope Down Selection	0.89304	0.05902	slope
Total change due to LD Up Selection	−0.02268	0.09194	slope/(1 – rt)
Total change due to LD Down Selection	0.06968	0.09429	slope/(1 – rt)
Linear change per generation Up Selection	−0.01272	0.00633	slope/t
Linear change per generation Down Selection	0.00670	0.00646	slope/t

The constant r is the average recombination fraction in Drosophila melanogaster (0.365); LD, linkage disequilibrium. See Table S2 for explanation of units.

Selecting on the static allometric slope is challenging because it is a property of a population that is not expressed at the individual level. To construct an individual-based selection index, we used Huxley’s (5, 21) allometric model, which is based on individual growth parameters (see SI Materials and Methods). These individual growth parameters can be expressed as individual allometries that relate to the static allometry in the same way as ontogenetic allometries (see ref. 23). Under this model, individuals that are near the bivariate phenotypic mean (i.e., average wing size and vein length) could have any breeding value for slope, and selection of those individuals would contribute nothing to the selection differential for slope. Therefore, although natural selection on slope may operate through favoring a particular trait–size relationship and generate high fitness for individuals at the bivariate phenotypic mean, a ridge-like selection index would be inefficient for generating selection on slope. Instead, we derived a saddle-shaped “fitness” function that simultaneously maximizes selection on slope while minimizing selection on size, variance in size, and the allometric intercept (Fig. 3 and SI Materials and Methods). The result was that clusters of larger and smaller than average flies were selected within each sex in each generation.

Fig. 3.

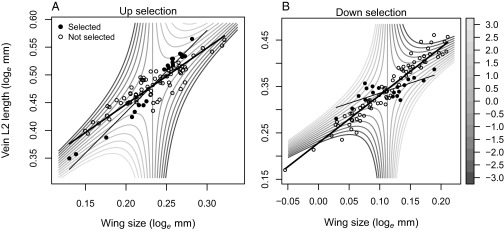
Saddle function used as selection index (grayscale legend). Examples of selection to increase (A) and decrease (B) the allometric slope (thick regression lines). The 20 individuals (filled circles), out of 100, with the highest selection indices were selected. The thin regression lines give the allometric slope among the selected individuals. Females from generation zero (A) and one (B) in replicate A are shown.

The responses of the allometric slopes were erratic, but, after 26 generations, the male and female slopes had changed from 1.08 and 1.09 in the original populations to 1.39 and 1.42 in the up-selected populations and to 0.84 and 0.78 in the down-selected populations (Fig. 2 B and C). These are large changes, resulting in allometric slopes in the outer range of those found in the sampled species (Fig. 1). The allometry in the original population implies that a 10% increase in wing size increased L2 length by 10.9% (for females). After 26 generations of selection, this had changed so that a 10% increase in wing size would now increase L2 length by 14.2% in the up-selected females and 7.8% in the down-selected females. Figs. S1 and S2 give a visual representation of the response to selection on the wing outline.

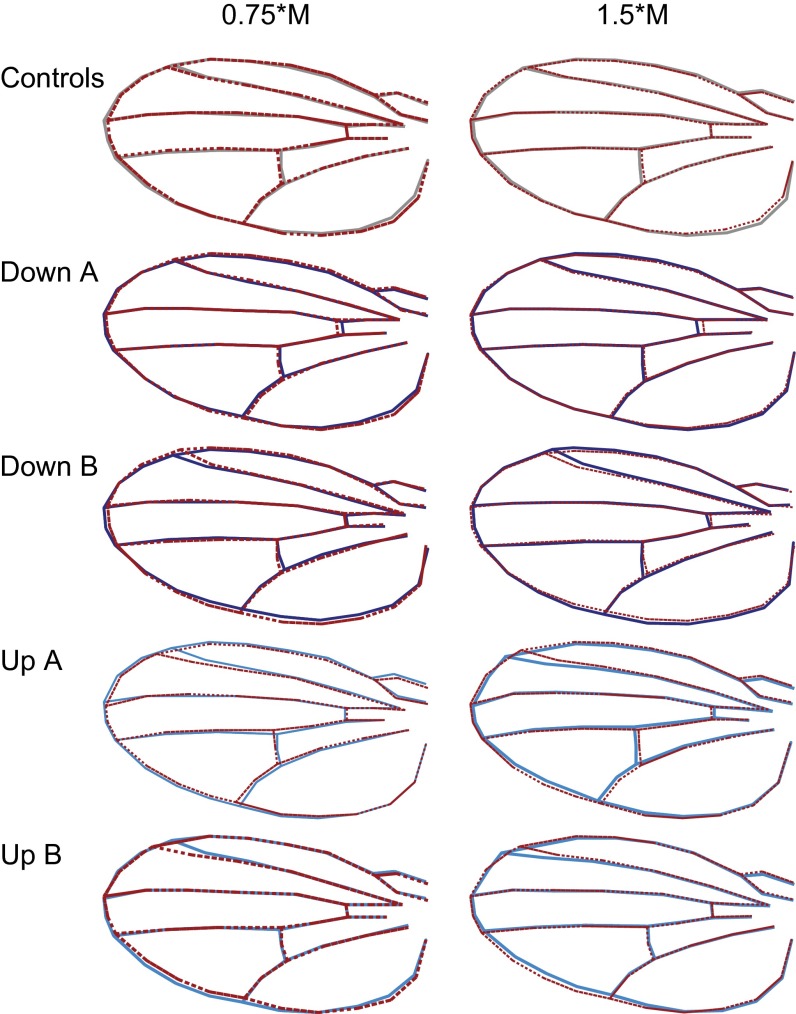
Fig. S1.

Change in wing shape with size (allometry) of the controls and the slope-selected populations relative to the isometric expectation (dotted red lines). The two replicated down-selected populations are denoted “Down A” and “Down B,” and the two replicated up-selected populations are denoted “Up A” and “Up B.” Shapes were constructed as point estimates of multivariate regressions of shape (i.e., 58 shape variables) on wing area evaluated at standard values given by 0.75× median size of each population (Left) and 1.5× median size of each population (Right), then averaged over sexes and generations 21–24. Isometric expectation is based on the shape at median size of each population, scaled by 0.75× and 1.5× at the lower and upper end, respectively. In the control, the allometric relationship was slightly above 1, making the position of the landmark 4 (see Fig. S3) more proximal in small wings than in large wings (position on each side of the isometric expectation). The decrease in the allometric slope in the down-selected populations reverses this effect; landmark 4 becomes more distal in small wings and more proximal in large wings. In the up-selected populations where the allometric slope is increased, the normal trend is amplified, with landmark 4 becoming even more proximal in small wings and even more distal in large wings.

Fig. S2.

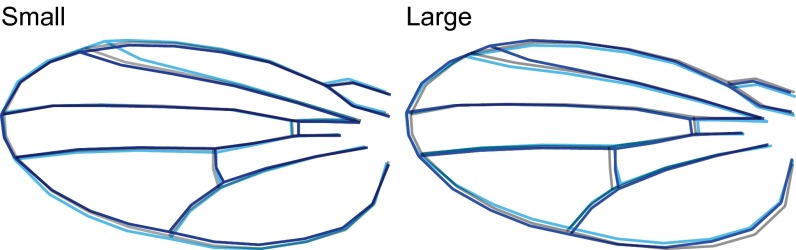
Response of wing-shape allometry to selection on the allometric slope. The image on the Left represents the mean shape of wings that are 0.75× the median wing area, and the image on the Right represents the mean shapes of wings that are 1.5× the median wing area. Control is in gray and average response of up-selected populations are in light blue and of down-selected populations are in dark blue. Shapes were constructed as in Fig. S1, but using the median of the control as reference and averaged over replicated populations in addition to sexes and generations. All contours were scaled to the same size to facilitate visualization of shape differences. The direct response to selection is best seen for the change in position of landmark 4 (see Fig. S3) relative to the control. In up-selected populations with increased allometric slope, the position of landmark 4 is more distal in small wings and more proximal in large wings relative to the control, whereas the opposite pattern is apparent in the down-selected populations with decreased allometric slope.

The statistical support for selection responses in the static allometric slope is strong, as judged from the Akaike Information Criterion (AIC; Table 1). The average responses of the up- and the down-selected lines were significantly different from each other, although not from the average of the two controls (Table 1). The relationship between the change in slope and a measure of cumulative selection strength was also statistically significant for all comparisons except for the males in one of the down-selected populations (Fig. 4), and several generations after selection ended, the average allometric slopes of the up- and down-selected lines still differed significantly from each other and from the starting value (Fig. 2 B and C). We noticed an erratic and diverging behavior of the allometric slopes in the control lines (Fig. 2 B and C). This strange behavior may, at least partly, be due to smaller sample size in these lines, resulting in less precise estimates of the slopes.

Table 1.

Response to selection on slope in the unstarved populations (see Table S3), given in contrasts between treatments (with SE)

Treatment contrast	Difference
Males
Up – Down	0.0212 ± 0.0078
Up – Control	0.0112 ± 0.0078
Down – Control	−0.0100 ± 0.0078
Females
Up – Down	0.0245 ± 0.0078
Up – Control	0.0114 ± 0.0078
Down – Control	−0.0131 ± 0.0078

The units are change in allometric slope per generation. A model with only a common linear effect for each sex instead of an effect of each treatment (Up, Down, and Control) for each sex increase the AIC-score by 38. The same statistical model is used to produce the results of this table and Table S3, but the relevant fixed effects are here expressed as contrasts.

Fig. 4.

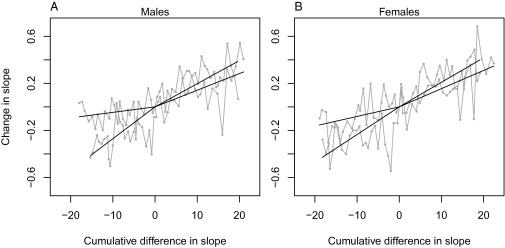
The selection response of the allometric slope as a function of a measure of cumulative selection strength in males (A) and females (B). The cumulative selection strength is measured as the cumulative difference between the allometric slope of all individuals under selection and the allometric slope of the selected individuals (i.e., the difference between the thick and the thin regression line in Fig. 3). Note that this is not a proper measure of the selection differential because it does not reflect the difference in the underlying slope of each individual. Therefore, the regression lines in the figure do not represent true realized heritabilities, but still give some information about the response to selection. The regression lines, slope ± SE, are 0.0196 ± 0.0022 and 0.0142 ± 0.0022 for up-selected males, 0.0047 ± 0.0025 and 0.0271 ± 0.0029 for down-selected males, 0.0209 ± 0.0024 and 0.0155 ± 0.0022 for up-selected females, and 0.0081 ± 0.0025 and 0.0235 ± 0.0026 for down-selected females.

The precision with which the allometric slope can be estimated depends on the range of sizes investigated. We therefore expected that an increased range of sizes would improve our ability to select on the allometric slope by making it easier to detect flies with extreme breeding values for allometric slope. We thus performed the same selection experiment on independent populations in which size variation was increased by starving half of the larvae over the last 2 d of development. These populations produced adult flies with a much wider range of sizes. Contrary to our expectation, the allometric slope did not respond to selection in these “starved” populations (Fig. 2 B and C and Table S5).

Table S5.

Allometric slopes and their change in the slope-selected populations subjected to the starvation treatment

Parameters	Estimate	SE	Unit
Males
Common slope at t = 0	1.13597	0.00991	slope
Linear change per generation Control	−0.00075	0.00146	slope/t
Linear change per generation Up Selection	−0.00063	0.00139	slope/t
Linear change per generation Down Selection	−0.00193	0.00140	slope/t
Females
Common slope at t = 0	1.12814	0.00966	slope
Linear change per generation Control	0.00028	0.00145	slope/t
Linear change per generation Up Selection	−0.00059	0.00137	slope/t
Linear change per generation Down Selection	−0.00169	0.00139	slope/t

See Table S2 for explanation of units.

To understand the lack of selection response in these “starved” populations, we subjected flies from the unstarved slope-selected populations to the same type of starvation one generation after selection ended. Surprisingly, the entire evolved difference in the allometric slope disappeared in these starved flies. The difference in static allometric slope between the up- and the down-selected populations was only 0.022 ± 0.061 when the flies were starved, compared with 0.271 ± 0.061 in their unstarved siblings in the same generation (averaged over replicates and sexes). This genotype-by-environment interaction and the erratic selection response underscore the need for an experimental design with replicated controlled environments when investigating genetic differences in static slopes (as argued in ref. 26). We hypothesize that the developmental processes responsible for the observed selection response in allometric slope are acting during the late third instar, when growth is precluded in the starved flies. The allometric relations may thus be the result of developmental “palimpsests” (36), where subsequent developmental processes are written on top of each other to partially mask variation created at different stages. Our results suggest that some of these processes are evolvable, causing a selection response in the slope, whereas others constrain small flies to remain on the original static allometric line.

A potentially confounding source of response to selection is the creation of linkage disequilibrium between alleles that affect wing size and alleles that affect L2 length. Such linkage disequilibrium could have generated a change in the allometric slope without changes in allele frequency. For example, an association between alleles that increase wing size with alleles that increase L2 length would increase the allometric slope between wing size and L2 length. To minimize linkage disequilibrium, we used disassortative mating when selecting on the static allometric slope. Female flies in the cluster above mean wing size were mated with male flies from below and vice versa (see Materials and Methods), so that recombination would be maximally effective in breaking up linkage disequilibrium. However, this does not completely prevent association between alleles, and we need to consider if the reversal of the response could have been due to breakup of linkage disequilibrium. Assuming an average recombination fraction of r = 0.365 between random loci in D. melanogaster (37), we estimated that the maximum fraction of the response that could be due to linkage disequilibrium averaged only 19.9 ± 22.6% and 14.3 ± 24.0% in males and females, respectively.

Nongenetic inheritance, such as parental (e.g., maternal) effects, may, in principle, affect the response to selection (38) but is not likely to be important in this case, as there are no indications of heritable nongenetic effects on wing shape in drosophilids.

We consider natural selection to be the most likely cause of the reversal toward the ancestral allometric slope. However, natural selection for restoring optimal wing function, for example due to selection for flight or courtship behavior, does not seem to be strong in the laboratory environment. In the presence of such selection, we expect that the intercept-selected populations would also have rapidly returned to their starting value. These populations instead showed little reversal of the selection response over an even longer time period, despite being more different from the initial wing shape than the slope-selected populations. Therefore, the more likely alternative is that the evolutionary change in allometric slope generated deleterious pleiotropic responses in other aspects of the phenotype, resulting in strong natural selection in the laboratory environment.

We have shown that a phylogenetically nearly invariant allometric slope can evolve rapidly under selection, but that this seems to generate countervailing natural selection to return the allometric slope to its initial value. This suggests that conserved allometric scaling may be best explained by pleiotropic constraints (12). Riedl (39, 40) proposed that fundamental developmental processes may become increasingly constrained, or burdened, by other processes that interact with or depend on them. Under this hypothesis, aspects of the developmental system that lead to precise allometric scaling also affect other aspects of organismal form and function, leading to deleterious pleiotropic effects when they are altered. If true, this hypothesis could provide a general explanation for the striking evolutionary conservatism of allometric power laws, while still leaving open the possibility for allometries to be optimized by natural selection over long time scales through compensatory mutations.

SI Materials and Methods

Derivation of Populations for the Selection Experiment.

The 30 inbred lines from the Drosophila Genetic Reference Panel (45) used to form the initial population were RAL 149, 324, 383, 486, 563, 714, 761, 787, 796, 801, 802, 804, 808, 819, 821, 822, 832, 843, 849, 850, 853, 859, 861, 879, 887, 897, 900, 907, 911, and 913. For the initial set of crosses, healthy lines were crossed with lines that were less fecund. Each cross, including reciprocals, was set up in six replicate vials of five or six females and three males. Virgin females and males were collected from the F₁ offspring, and the next round of pairwise crosses was set up once a sufficient number of flies had been obtained. This procedure was continued until a single population resulted.

To found the initial (Generation 0) populations subjected to intercept and slope selection, we sampled 100 flies of each sex from the base population. For each of the starved control starting populations, we sampled 50 flies of each sex, and, for each of the well-fed control starting populations, we sampled 40 flies of each sex.

Rearing of Selected Populations.

Throughout the experiment, all of the selected populations (except those undergoing the starvation treatment; see below) were reared in 22-mm-diameter cylindrical vials containing ∼4 mL of food medium composed of yeast, corn flour, sucrose, propionic acid, and agar, plus an antibiotic (cycled between streptomycin, penicillin, and tetracycline). Vials were stored in an incubator at 25 °C, 55–65% relative humidity, with a 12:12 h light/dark cycle. In all populations, flies were split into several vials for rearing, with roughly equal numbers of males and females. The number of adult flies in each vial was kept sufficiently low (less than 13 flies of each sex) to avoid high larval densities. Adult flies were allowed to lay eggs for 1 d, then transfered to new vials for an additional day, then discarded. To encourage remating, male and female parents were separated at the first transfer, and placed in vials with opposite-sex flies from a different vial. When flies began to eclose, virgins were collected at 8-h intervals and separated by sex. Virgins were kept in vials with no more than 10 females or 15 males until imaging.

In a second set of populations, we attempted to generate more efficient selection on the allometric slope by increasing the variance in size, potentially reducing the sampling variance in the estimation of the allometric slope. This was achieved by subjecting half the larvae in those populations to a starvation treatment, similar to that of Stillwell et al. (48). Larvae prevented from feeding after they reach a critical size for pupariation (approximately the start of the third larval instar) can eclose, but forego the most rapid period of growth, resulting in very small adults; following starvation, adults can have a thorax length as small as half the average size of fully fed flies. Thus, combining starved and normally reared flies greatly increases the variance in size among flies. Each generation, the selected adult flies in the starved populations were split evenly into two groups: One half was allowed to lay eggs in vials as described above, and their larvae were fed throughout the larval phase. The other half was confined overnight in a 90-mm Petri dish with standard food medium, during which time they mated and laid eggs. The following day, adults were removed from these egg layers, and the Petri dishes were placed in an incubator for 4–6 d. The dishes were checked regularly, and when most of the larvae appeared to have reached critical size for survival to adulthood, they were removed from the dish and placed in vials containing agar only, with no more than 20 larvae per vial. These larvae continued to consume the nonnutritive agar medium for several days before pupariation. Because the timing of development varied greatly among the selected populations, we used the average size as determined by visual inspection to determine when the larvae had reached the critical size. Equal numbers of adults from starvation and normal treatments were imaged in the starved populations.

Later in the course of the experiment, the fecundity of the two replicate starved slope-selected populations decreased. To counter this, we induced females to lay more eggs by removing the males from egg layers after the first day and replacing them with mated females from a stock bearing the Tubby (Tb) and white (w) mutations. The increased density of ovipositing females encouraged further egg laying by the selected females. The Tb phenotype enabled us to identify and remove the mutant larvae; mutant adults that remained were identified by the w eye color mutation and removed. Even with this method, however, we were sometimes unable to collect the full 200 virgin flies from each population toward the end of the experiment.

Justification of the Allometric Slope Selection Index.

We developed a selection index based on Huxley’s allometric model. Huxley (5) showed that a trait’s size (Y) relates to body size (X) by an allometric relation if both trait size and body size depend on some common growth variable G, such that dX/dt = uXG and dY/dt = vYG, where u and v are specific constants for body size and trait size, respectively, and t is the time of growth. Solving these differential equations for X and Y at some developmental stage (e.g., t = adult) gives the power functions

$$\begin{array}{c}X=X_0{Q}^u,\\ Y=Y_0{Q}^v,\end{array}$$

where X₀ and Y₀ are initial values for X and Y, and Q is G integrated over [t = 0, t = adult]. Transforming these power functions to the natural log scale gives

$$\begin{array}{l}x=x_0+uq,\\ y=y_0+vq,\end{array}$$

where the lowercase letters x, y, and q are used to indicate log_e-transformed variables. From this, we get the allometric equation

$$y={\text{log}}_e\left[a\right]+bx,$$

where the allometric slope b = v/u, and the allometric intercept log_e[a] = y₀ – bx₀. We are interested in selecting on the ratio v/u. Assuming that u and v as well as relative fitness (w) are multivariate normally distributed with no correlation between u and v, the selection differential of the ratio b = v/u is given by

$$\begin{array}{c}\text{S}\left[b\right]=\text{Cov}\left[\frac{v}{u},w\right]\\ =\text{Cov}\left[\frac{1}{u},w\right]\overline{v}+\text{E}\left[\frac{1}{u}\left(v-\overline{v}\right)\left(w-1\right)\right]\\ \approx \frac{1}{\overline{u}}\left(\text{Cov}\left[v,w\right]-\text{E}\left[\frac{1}{u}\right]\text{Cov}\left[u,w\right]\right)\\ =\frac{1}{\overline{u}}\left(\text{S}\left[v\right]-\overline{b}\text{S}\left[u\right]\right),\end{array}$$

where E[.] or one overbar denotes the expectation, S[v] = Cov[v, w], S[u] = Cov[u, w], and $\overline{b}=E\left[v/u\right]$. The approximation is from the Taylor series $1/u\approx 1/\overline{u}-(u-\overline{u})/{\overline{u}}^2$, and is a good approximation when the coefficient of variation (CV) of u is small. From this, we see that the selection differential on v/u is proportional to the selection differential on v (S[v]) minus the selection differential on u (S[u]) weighted by the average allometric slope. To obtain these selection differentials, we use the standard quadratic relative fitness function w = μ + β_xx + β_yy + ½γ_xx²+ ½γ_yy²+γ_xyxy, where μ is the intercept and β_x, β_y, γ_x, γ_y, and γ_xy can be interpreted as the standard linear and quadratic selection gradients of x and y. We scale so that $\overline{x}=0$ and $\overline{y}=0$; the selection differentials S[v] and S[u] as functions of the selection gradients are then given by

$$\begin{array}{l}\text{S}\left[v\right]=\text{Var}\left[q\right]\text{Var}\left[v\right]\left({\gamma }_y+\overline{u}{\gamma }_{xy}\right),\\ \text{S}\left[u\right]=\text{Var}\left[q\right]\text{Var}\left[u\right]\left({\gamma }_x+\overline{v}{\gamma }_{xy}\right).\end{array}$$

Substituting this into the equation for the selection differential on b, we obtain

$$\text{S}\left[b\right]=\frac{1}{\overline{u}}\text{Var}\left[q\right]\left(\text{Var}\left[v\right]{\gamma }_y-\overline{b}\text{Var}\left[u\right]{\gamma }_x+\overline{u}\left(\text{Var}\left[v\right]-{\overline{b}}^2\text{Var}\left[u\right]\right){\gamma }_{xy}\right).$$ [S1]

This equation shows that disruptive selection on y (positive γ_y) and stabilizing selection on x (negative γ_x) both select for increased allometric slope. A positive correlational selection gradient (γ_xy), on the other hand, contributes to increased allometric slope only when

$$\text{Var}\left[v\right]>{\overline{b}}^2\text{Var}\left[u\right].$$

This is because the correlational selection generates a selection differential both on Cov[x, y] and on Var[x]. Assuming that the average allometric slope ($\overline{b}$) equals the ratio Cov[x, y]/Var[x], we can simplify Eq. S1 by ensuring that there is no selection on Var[x]. To accomplish this, we use the following argument from standard quantitative genetic theory: We know that the selection differential of the phenotypic covariance matrix (S[P]), when there is no linear selection, is given by S[P] = PγP, where γ is the matrix of quadratic selection gradients. Under the assumption of multivariate normality, we can derive the selection differential of the variance of x,

$$\text{S}\left[\text{Var}\left[x\right]\right]=\text{Var}{\left[x\right]}^2{\gamma }_x+2\text{Var}\left[x\right]\text{Cov}\left[x,y\right]{\gamma }_{xy}+\text{Cov}\left[x,y\right]{\gamma }_y.$$

This shows that there is no selection differential on the variance of x (S[Var[x]] = 0) when ${\gamma }_x=-2\overline{b}{\gamma }_{xy}$ and γ_y = 0. Substituting ${\gamma }_x=-2\overline{b}{\gamma }_{xy}$ and γ_y = 0 into Eq. S1 gives

$$\text{S}\left[b\right]=\text{Var}\left[q\right]\left({\overline{b}}^2\text{Var}\left[u\right]\left(\frac{2}{\overline{u}}-1\right)+\text{Var}\left[v\right]\right){\gamma }_{xy}.$$

Biologically realistic values of u are less than 1 and certainly not higher than 2, because the amount of resources allocated to X is most likely a diminishing function of the total amount of resources available (Q). This means that this selection differential of the allometric slope is proportional to γ_xy when there is no selection on the variance of x.

The average individual allometric slope ($\overline{b}$) in the above models relates to the observed static allometric slope, b_static = Cov[x, y]/Var[x], in the same way as the average ontogenetic allometric slope relates to the static allometric slope (see ref. 23). In essence, this means a change in $\overline{b}$ is expected to give the same change in b_static, and that $\overline{b}$ = b_static if both the individual allometric intercept (${\text{log}}_e\left[a\right]$) and slope (b) are uncorrelated with size (x).

Based on the above results, we constructed the selection index for the slope as

$$W_{slope}={\beta }_x\left(x-\overline{x}\right)+{\beta }_y\left(y-\overline{y}\right)+\frac{1}{2}{\gamma }_x{\left(x-\overline{x}\right)}^2+{\gamma }_{xy}\left(x-\overline{x}\right)\left(y-\overline{y}\right),$$

where γ_xy = 1 for the up selection (increase in slope) and −1 for the down selection (decrease in slope). We did not directly use β_x = 0, β_y = 0, and γ_x = –2$\overline{b}$γ_xy, because it is unlikely that the sample distribution is perfectly multivariate normal. Instead, the function (W_slope) was optimized for the parameters β_x, β_y, and γ_x, to generate as little selection as possible on the means of x and y and on the variance of x.

Selection Procedure.

For the intercept selection, we wanted the average size of the selected individuals to be as similar as possible to the average size of all individuals in the population (i.e., no selection on size). To do this, we searched a wide range of values of β₁ to find the value that minimized the value of (S[x])², where β₁ is the directional selection gradient on size and S[x] is the selection differential on size (i.e., the difference between the mean size of the selected individuals and the mean size of all individuals in the population).

For the slope selection, the optimization was done in three rounds to estimate the parameters β_x, β_y, and γ_x. First, we searched through a range of different values for γ_x with β_x = 0 and β_y = 0, to minimize (S[Var[x]])², where S[.] denotes the selection differential. Next, we searched through a wide range of combinations of values of β_x and β_y to minimize ${\left(\text{S}\left[x\right]/\overline{x}\right)}^2+{\left(\text{S}\left[y\right]/\overline{y}\right)}^2$ with γ_x at its current optimized value [i.e., the value that gave the lowest (S[Var[x]])²]. Finally, we did a second round of searching through different values of γ_x to minimize (S[Var[x]])², but this time with β_x and β_y at the optimized values.

Statistical Analyses of the Comparative Data.

To estimate the rate of evolution for the allometric intercept, we fitted a Brownian-motion model of evolution using the phylogenetic mixed model (46)

$$y_{ijk}=u_i+b_i{x}_{ij•}+a_j+{\epsilon }_{ijk},$$

where y is log_e L2 length, x is log_e wing size (square root of wing area), u is the common intercept for each sex, b is the evolutionary allometric slope for each sex, a is the phylogenetic effect, and ε is the residual term. The subscripts i, j, and k, represent sex, species, and individual, respectively, and subscript • means the average taken over the indicated level. The residuals are assumed to be independent identically normally distributed, whereas the phylogenetic effects are assumed to be distributed as a ∼ N(0, ${\sigma }_{\text{rate}}^{\mathit{2}}$ A), where A is a phylogenetic relatedness matrix in which the elements are the shared branch length of species scaled to unit depth. This matrix was computed from a published phylogeny (42) with two species added based on other published evidence: Drosophila arizonae (41) and D. athabasca (49). Note that six species were not included in this analysis because they were not in our phylogeny (Homoneura sp., Leucophenga sp., Monochaetoscinella sp., Neogriphoneura sordida, Samoaia leonensis, and Thaumatomyia sp.). The rate (increase in variance) per million years is given by ${\sigma }_{\text{rate}}^{\mathit{2}}$/t, where t is the depth of the phylogeny in millions of years. Because the depth of this phylogeny is highly uncertain (47), we used both a “best guess” of 133 million years and a conservative estimate of 50 million years to estimate the rate.

To estimate the rate of evolution for the allometric slope, we fitted a similar model as for the intercept,

$$y_{ijk}-y_{ij\mathrm{•}}=b_i\left(x_{ijk}-x_{ij\mathrm{•}}\right)+a_j\left(x_{ijk}-x_{ij\mathrm{•}}\right)+{\epsilon }_{ijk},$$

where b is the common within-species slope for each sex separately. The phylogenetic effects of the slope (a_j) are assumed to be distributed as the phylogenetic effects of the intercept, and the residuals (ε_ijk) are assumed to be independent identically normally distributed. The per-million-year evolutionary rate for the slope was calculated in the same way as for the intercept.

The static allometric relationships within each sex for each species, presented in Fig. 1, were estimated by standard linear regression models with log_e L2 length as the response variable and log_e wing size as the explanatory variable. The evolutionary allometry for each sex was a linear regression on the species means with log_e L2 length as response and log_e wing size as predictor.

Statistical Analyses of the Selection Experiment.

Changes and differences in allometric intercept and slope of log_e vein L2 length on log_e wing size (square-root wing area) were analyzed by a series of linear mixed-effects models because of the hierarchical structure of the data.

For the selection on the intercept, we wanted to estimate the following parameters: the average wing size (intercept) in the starting generation for each sex i ($u_i$), the average allometric slope for each sex ($b_i$), the linear change per generation of the intercept for all treatments j (up selected, down selected, and control) nested within sex ($a_{1ij}$), the quadratic response to selection of the intercept for the up- and down-selection treatment for each sex separately ($a_{2ij}$), and the linear effect of relaxed selection on the intercept for the up and down selection treatment for each sex separately ($a_{3ij}$). To estimate these parameters, we fitted a broken-stick mixed model with log_e vein L2 length ($y_{ijklm}$) as a function of log_e wing size centered within sex ($x_{ijklm}-x_{i\mathrm{•}\mathrm{•}\mathrm{•}}$) and generation (t),

$$y_{ijklm}=u_i+b_i\left(x_{ijklm}-x_{i\mathrm{•}\mathrm{•}\mathrm{•}}\right)+a_{1ij}{t}_1+a_{2ij}{t}_1^{2}K+a_{3ij}{t}_{2}K+c_{ijk}{t}_1+d_{ijkl}+{\epsilon }_{ijklm},$$

where subscripts k, l, and m denote population (nested within treatment), generation (nested within population), and individual, respectively. Subscript • means the average taken over the indicated level. We implemented the broken-stick regression model through the values of t₁ and t₂: t₁ represents generations 0–7 for the selected populations (treatment up and down) and generations 0–23 for the controls. For the selected populations, t₁ takes the values 0–7 for generations 0–7 and value 0 for generations 8–23. For the controls, t₁ takes the values 0–23 for generations 0–23. The other generation variable, t₂, represents generations 8–23; t₂ takes the values 0 for generations 0–7 and 0–15 for generations 8–23. The indicator variable K takes the value 0 for the control treatment and 1 for the up and down selection treatments. We also included two random effects ($c_{ijk}$ and $d_{ijkl}$). The first random effect, $c_{ijk}$, is the deviation of each replicated population nested within treatment from the rest of the model, assumed to be independent identically normally distributed. The second random effect, $d_{ijkl},$ is the deviation of each generation (nested within population) from the rest of the model. This second random effect is assumed to be multivariate normally distributed with a variance term multiplied with a relatedness matrix (A) to account for temporal autocorrelation. The diagonal elements of A are unity, and the off-diagonal elements are given by 0.5^Δt, where Δt is the difference in number of generations for elements of A belonging to the same population, and zero for all other elements. The residuals (${\epsilon }_{ijklm}$), the deviation of each individual fly from the model prediction, are assumed to be independent identically normally distributed.

For the selection on the slope, we wanted to estimate the following parameters: the common allometric slope for all treatments in the starting generation for each sex i separately ($b_i$) and the linear change in allometric slope per generation t for each treatment j (up selected, down selected, and control) nested within sex ($a_{ij}$). To estimate these parameters, we used a random regression model where we used log_e vein L2 length centered on the within-generation sex mean for each population k ($y_{ijklm}-y_{ijkl\mathrm{\cdot }}$) as response variable, and log_e wing size within-generation sex mean for each population k ($x_{ijklm}-x_{ijkl\mathrm{\cdot }}$) and generation (t) as explanatory variables,

$$y_{ijklm}-y_{ijkl\mathrm{•}}=b_i\left(x_{ijklm}-x_{ijkl\mathrm{•}}\right)+a_{ij}\left(x_{ijklm}-x_{ijkl\mathrm{•}}\right)t+c_{ijk}\left(x_{ijklm}-x_{ijkl\mathrm{•}}\right)t+d_{ijkl}\left(x_{ijklm}-x_{ijkl\mathrm{•}}\right)+{\epsilon }_{ijklm},$$

where the subscripts denote the same as in the model for selection on the intercept. The random effects $c_{ijk}$ give the deviation to the treatment mean in the change of the allometric slope for each population (nested within treatment), $d_{ijkl}$ gives the deviation in the allometric slope from the rest of the model for each generation l (nested within population), and ${\epsilon }_{ijklm}$ is the residual deviation of each fly. The random effects are assumed to be independent identically normally distributed, except $d_{ijkl}$, which is distributed as $d_{ijkl}$ in the model for the intercept.

Separate analyses of the unstarved and the starved populations were conducted using this model.

For the change in slope after selection in the unstarved populations, we wanted to estimate the following parameters: the average slope in the first generation for each treatment j (up and down selected) nested within sex i ($b_{ij}$), the linear change in the allometric slope per generation of random mating t for each treatment nested within sex ($a_{1ij}$), and the change in allometric slope per generation of random mating due to breakup of linkage disequilibrium for each treatment nested within sex ($a_{2ij}$). We fitted the following random regression model:

$$\begin{array}{c}{y}_{ijklm}-y_{ijkl\mathrm{•}}=b_{ij}\left(x_{ijklm}-x_{ijkl\mathrm{•}}\right)+a_{1ij}\left(x_{ijklm}-x_{ijkl\mathrm{•}}\right)t+a_{2ij}\left(x_{ijklm}-x_{ijkl\mathrm{•}}\right)\left(1-r^t\right)\\ +c_{ijk}\left(x_{ijklm}-x_{ijkl\mathrm{•}}\right)+d_{ijkl}\left(x_{ijklm}-x_{ijkl\mathrm{•}}\right)+{\epsilon }_{ijklm},\end{array}$$

where the subscripts denote the same as in the model for the selection on the intercept. The effect of linkage disequilibrium is a linear function of 1 – r^t, where r is the average recombination fraction, 0.365 in D. melanogaster (37), and t is number of generations of random mating. Hence, by including breakup of linkage disequilibrium as a linear effect in our model, we obtain an estimate of the asymptote at linkage equilibrium. The random effect $c_{ijk}$ gives the deviation of the treatment mean allometric slope for each population (nested within treatment), $d_{ijkl}$ gives the deviation in the allometric slope from the rest of the model for each generation l (nested within population), and ${\epsilon }_{ijklm}$ is the residual deviation of each fly. The random effects are assumed to be independent identically normally distributed.

To estimate the maximum fraction of the selection response that was due to linkage disequilibrium in each sex ($q_i$), we replaced the term $a_{2ij}\left(x_{ijklm}-x_{ijkl\mathrm{•}}\right)\left(1-r^t\right)$ in the above random regression model with $q_i\left(x_{ijklm}-x_{ijkl\mathrm{•}}\right)\left(1-r^t\right)K$. In this model, the selection response in all treatments is scaled to 1 by using the scaling factor K with values 0.327 and 0.365 for the females and males, respectively, in the up-selection treatment, and −0.190 and −0.182 for the females and males, respectively, in the down-selection treatment. The value of $K$ is the difference between the allometric slope in the starting generation and after selection ended (generation 0 of relaxed selection). Hence, the parameter $q_i$ is an estimate of the maximum average fraction of the total selection response that is consistent with linkage disequilibrium across treatments. The reason that this is the maximum fraction is that natural selection in the laboratory environment could also cause exponential decay.

To investigate the effect of starvation on the evolved slopes, we subjected some of the larvae of the unstarved populations to the starvation treatment one generation after selection ended. We estimated the difference in allometric slope between the up- and down-selected populations both for starved and nonstarved flies using analysis of covariance.

All analyses were done in R (50) using the packages lme4 (51) and pedigreemm (52).

Materials and Methods

Comparative Data.

Species were obtained by collection from the wild, from the Drosophila Species Stock Center, or from other collectors. The full list of 111 taxa, specifications, their collection locations, and sample sizes are reported in Table S6. Flies were reared using combinations of food, temperature, and rearing environments suggested to be optimal for each particular species based on the instructions from the source or from published sources. Wild-collected specimens were measured when we were unable to rear the flies in the laboratory. Most of the 111 taxa are currently classified in the paraphyletic genus Drosophila or to genera in the subfamily Drosophilinae (41, 42). In addition, we included two species of steganine drosophilids and five outgroup species from other families. Four drosophilid species are represented by more than one subspecies. Most species had sample sizes of around 200 measured flies, and the total sample size was 20,345.

Table S6.

Taxa included with total sample size (N)

Family	Genus	Species (subspecies)*	Location of collection	Source†	Flies‡	N
Chloropidae	Monochaetoscinella	Sp.	Tallahassee, FL	Coll.	Wild	48
Chloropidae	Thaumatomyia	Sp.	Tallahassee, FL	Coll.	Wild	22
Drosophilidae	Chymomyza	procnemis	Oahu, HI; Georgia	SS 20000–2631.1	Lab	120
Drosophilidae	Dettopsomyia	nigrovittata	Tallahassee, FL	Coll.	Wild	15
Drosophilidae	Drosophila	acutilabella	Tallahassee, FL	Coll.	Wild, F1	205
Drosophilidae	Drosophila	affinis	Tallahassee, FL	Coll.	Lab	209
Drosophilidae	Drosophila	algonquin	Michigan, OH	Coll.	Lab (wild)	237
Drosophilidae	Drosophila	americana (americana)	Chinook, MT	SS 15010–0951.2	Lab	109
Drosophilidae	Drosophila	americana (texana)	Morrilton, AR	SS 15010–1041.23	Lab	215
Drosophilidae	Drosophila	ananassae	Tallahassee area, FL; south Georgia	Coll.	Lab	235
Drosophilidae	Drosophila	arizonae	Riverside, CA; Baja California, Mexico; Tucson, AZ	Laura Reed	Lab	275
Drosophilidae	Drosophila	athabasca	Toronto, ON, Canada	Coll.	Lab	79
Drosophilidae	Drosophila	azteca	Lassen, CA	Coll.	Lab	49
Drosophilidae	Drosophila	bifasciata	Maggia, Ticino, Switzerland	SS 14012–0181.1	Lab	217
Drosophilidae	Drosophila	busckii	Tallahassee, FL	Coll.	Wild, F1	105
Drosophilidae	Drosophila	cardini	Tallahassee area, FL	Coll.	Lab	210
Drosophilidae	Drosophila	elegans	India	J. David	Lab	215
Drosophilidae	Drosophila	emarginata	Huatusco, Veracruz, Mexico	SS 14042–0841.6	Lab	232
Drosophilidae	Drosophila	equinoxialis	Panama	Coll.	Lab	214
Drosophilidae	Drosophila	erecta	unknown	SS 14021–0224.0	Lab	193
Drosophilidae	Drosophila	eugracilis	Palawan, Philippines	SS 14026–0451.1	Lab	212
Drosophilidae	Drosophila	euronotus	Tallahassee, FL	Coll.	F1, Lab (wild)	296
Drosophilidae	Drosophila	falleni	Tallahassee, FL	Coll.	F1, F2 (wild)	277
Drosophilidae	Drosophila	ficusphila	Khan-ing Tong, Taiwan	SS 14025–0441.1	Lab	226
Drosophilidae	Drosophila	aff. florae	Tallahassee, FL	Coll.	Wild, F1	210
Drosophilidae	Drosophila	funebris	Pentwater, MI	Coll.	Lab (wild)	216
Drosophilidae	Drosophila	gaucha	Montevideo, Uruguay	J. David	Lab	209
Drosophilidae	Drosophila	greeni	Africa	J. David	Lab	206
Drosophilidae	Drosophila	guanche	Tenerife, Canary Islands	SS 14011–0095.0	Lab	209
Drosophilidae	Drosophila	guttifera	Tallahassee, FL	Coll.	Wild, F1	99
Drosophilidae	Drosophila	hydei	Tallahassee, FL	Coll.	Lab	134
Drosophilidae	Drosophila	immigrans	Tallahassee, FL	Coll.	Lab	164
Drosophilidae	Drosophila	kikkawai	India	J. David	Lab	213
Drosophilidae	Drosophila	lucipennis	Chi-tou, Taiwan; Wulai, Taiwan	SS 14023–0331.0; 14023–0331.1	Lab	245
Drosophilidae	Drosophila	macrospina	Tallahassee, FL	Coll.	Wild, F1, F2	72
Drosophilidae	Drosophila	malerkotliana	Tallahassee, FL	Coll.	Lab	220
Drosophilidae	Drosophila	mauritiana	Mauritius	J. David	Lab	203
Drosophilidae	Drosophila	melanica	Patagonia, AZ; northern Florida and southern Georgia	SS 15030–1141.2	Lab	267
Drosophilidae	Drosophila	melanogaster	Wabasso, FL	Coll.	Wild	247
Drosophilidae	Drosophila	mercatorum	Asheville, NC	Coll.	Lab	209
Drosophilidae	Drosophila	micromelanica	Smithville, TX	SS 15030–1151.1	Lab	155
Drosophilidae	Drosophila	mimetica	Southeast Asia	John True	Lab	19
Drosophilidae	Drosophila	mojavensis	Baja California, Mexico; California	Laura Reed	Lab	163
Drosophilidae	Drosophila	mulleri	central-east Florida	Coll.	Lab	195
Drosophilidae	Drosophila	nasuta	Gabon, Africa	J. David	Lab	196
Drosophilidae	Drosophila	nebulosa	south Florida	Coll.	Lab	212
Drosophilidae	Drosophila	neocordata	Minas Gerais, Brazil	SS 14041–0831.0	Lab	217
Drosophilidae	Drosophila	neotestacea	Rochester, NY; northern Georgia	Coll.	Lab; Wild, F1	208
Drosophilidae	Drosophila	nigromelanica	Tallahassee, FL	Coll.	Wild, F1	204
Drosophilidae	Drosophila	nikananu	Ivory Coast	SS 14028–0601.0	Lab	209
Drosophilidae	Drosophila	occidentalis	Madera County, CA	Coll.	Wild, F1, F2	205
Drosophilidae	Drosophila	paramelanica	Pentwater, MI; Smokemont, NC	SS 15030–1161.2	Lab	323
Drosophilidae	Drosophila	paulistorum	Central America	SS 14030–0771.13	Lab	201
Drosophilidae	Drosophila	peninsularis	central Florida	Coll.	Lab	206
Drosophilidae	Drosophila	persimilis	Mount St. Helena, CA	Jody Hey	Lab	55
Drosophilidae	Drosophila	pictiventris	Great Inagua, Bahamas	SS 12000–0072.0	Lab	112
Drosophilidae	Drosophila	pinicola	Lassen, CA	Coll.	Lab	202
Drosophilidae	Drosophila	pseudoobscura (bogotana)	Sutatausa, Susa, Potosi, Colombia	Jody Hey	Lab	73
Drosophilidae	Drosophila	pseudoobscura (pseudoobscura)	Tucson, AZ	SS 14011–0121.0	Lab	198
Drosophilidae	Drosophila	putrida	Tallahassee, FL	Coll.	Wild, F1	210
Drosophilidae	Drosophila	recens	Calamity Pond, NY; Deer Isle, ME; Big Moose, NY	Coll.	Lab	224
Drosophilidae	Drosophila	repleta	Tallahassee, FL	Coll.	Wild, F1, Lab	217
Drosophilidae	Drosophila	robusta	Tallahassee, FL	Coll.	Lab	101
Drosophilidae	Drosophila	saltans	San Jose, Costa Rica	SS 14045–0911.0	Lab	181
Drosophilidae	Drosophila	santomea	Sao Tome y Principe	SS	Lab	205
Drosophilidae	Drosophila	sechellia	Seychelles	J. David	Lab	210
Drosophilidae	Drosophila	seguyi	Africa	J. David	Lab	210
Drosophilidae	Drosophila	simulans	Tallahassee, FL	Coll.	Lab	195
Drosophilidae	Drosophila	stalkeri	Guantanamo Bay, Cuba	SS 15081–1451.10	Lab	203
Drosophilidae	Drosophila	sturtevanti	south Florida	Coll.	Wild, Lab	223
Drosophilidae	Drosophila	subobscura	Gif-sur-Yvette, France	G. Gilchrist	Gilchrist et al. (42)	69
Drosophilidae	Drosophila	sulfurigaster (albostrigata)	Siem Reap, Cambodia	SS 15112–1811.4	Lab	209
Drosophilidae	Drosophila	sulfurigaster (bilimbata)	Tantalus, Oahu, HI	SS 15112–1821.0	Lab	224
Drosophilidae	Drosophila	sulfurigaster (sulfurigaster)	Queensland, Australia	SS 15112–1831.0	Lab	210
Drosophilidae	Drosophila	takahashii	Nepal, Asia	SS 14022–0311.0	Lab	198
Drosophilidae	Drosophila	testacea	Germany	unknown	Lab	40
Drosophilidae	Drosophila	tripunctata	Tallahassee, FL; Pentwater, MI	Coll.	Wild, Lab	218
Drosophilidae	Drosophila	virilis	Pasadena, CA	SS 15010–1051.0	Lab	199
Drosophilidae	Drosophila	willistoni	northern Florida	Coll.	Lab	268
Drosophilidae	Drosophila	yakuba	Ivory Coast, Africa	SS 14021–0261.0;	Lab	209
Drosophilidae	Hirtodrosophila	duncani	Tallahassee, FL; Kalamazoo, MI	Coll.	F1, F2, Lab (wild)	219
Drosophilidae	Hirtodrosophila	Sp.	south Florida	Coll.	Lab	240
Drosophilidae	Hirtodrosophila	thoracis	Tallahassee area, FL	Coll.	Wild, F1	352
Drosophilidae	Idiomyia	biseriata	Mount Kaala, Oahu, HI	SS 15291–2551.1	Lab	210
Drosophilidae	Idiomyia	crucigera	Pupukea, Oahu, HI	SS 15287–2531.0	Lab	211
Drosophilidae	Idiomyia	eurypeza	Kumuwela, Kauai, HI	SS 15290–2581.0	Lab	210
Drosophilidae	Idiomyia	grimshawi	Auwahi, Maui, HI	SS 15287–2541.0	Lab	190
Drosophilidae	Idiomyia	gymnobasis	Auwahi, Maui, HI	SS 15284–2501.0	Lab	209
Drosophilidae	Idiomyia	mimica	Kipuka Ki, HI	SS 15292–2561.0	Lab	216
Drosophilidae	Idiomyia	soonae	Pawaina, HI	SS 15290–2591.0	Lab	212
Drosophilidae	Leucophenga	Sp.	central Florida	Coll.	Wild	10
Drosophilidae	Leucophenga	varia	Tallahassee, FL	Coll.	Wild	29
Drosophilidae	Mycodrosophila	claytonae	Tallahassee area, FL	Coll.	Wild, F1	197
Drosophilidae	Mycodrosophila	dimidiata	Tallahassee area, FL	Coll.	Wild	208
Drosophilidae	Samoaia	leonensis	Samoaia	SS 80000–2761.03	Lab	201
Drosophilidae	Scaptodrosophila	deflexa	France	J. David	Lab	201
Drosophilidae	Scaptodrosophila	dorsocentralis	Japan	J. David	Lab	85
Drosophilidae	Scaptodrosophila	latifasciaeformis	north and central Florida	Coll.	Wild, Lab	204
Drosophilidae	Scaptodrosophila	lebanonensis (casteeli)	Veyo, Utah	SS 11010–0011.0	Lab	207
Drosophilidae	Scaptodrosophila	lebanonensis (lebanonensis)	Beirut, Lebanon	SS 11010–0021.0	Lab	211
Drosophilidae	Scaptodrosophila	stonei	Tehran, Iran	SS 11010–0041.1	Lab	210
Drosophilidae	Scaptomyza	adusta	north Florida; south Georgia	Coll.	Lab (wild)	235
Drosophilidae	Scaptomyza	palmae	Kahala Mountains, HI	SS 33000–2681.1	Lab	212
Drosophilidae	Zaprionus	ghesquierei	Gabon, Africa	J. David	Lab	224
Drosophilidae	Zaprionus	indianus	Brazil	J. David	Lab	208
Drosophilidae	Zaprionus	inermis	Koutaba, Cameroun	SS 50000–2746.0	Lab	148
Drosophilidae	Zaprionus	sepsoides	Kongo	SS 50000–2744.0	Lab	200
Drosophilidae	Zaprionus	Sg. Anaprionus	India	J. David	Lab	200
Ephydridae	Discocerina	obscurella	Leon County, FL	Coll.	Wild	34
Lauxaniidae	Homoneura	Sp.	Tallahassee, FL	Coll.	Wild	70
Lauxaniidae	Neogriphoneura	Sordida	Tallahassee, FL	Coll.	Wild	68

^*Sg., species identified to subgenus; Sp., unknown species.

^†Coll., collected by members of the Houle laboratory; SS, species obtained from the US Drosophila Species Stock Center. Number following is the stock number. Other stocks were obtained through the generosity of Jean David, Jody Hey, Laura Reed, and John True. George Gilchrist furnished images of wings of D. subobscura from Gilchirst et al. (42).

^‡F1 (F2), offspring (grand-offspring) of wild collected flies; Lab, flies measured after multiple generations in laboratory culture. Wild, flies measured captured in the wild.

Wing Measurements.

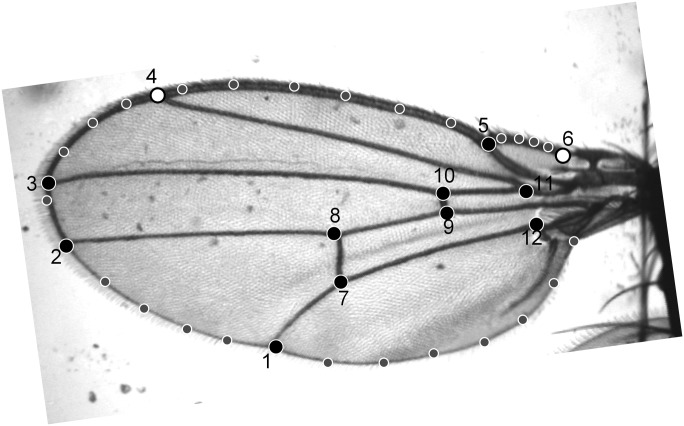
The full procedure for imaging wings and for estimating vein locations and corresponding landmarks has been described by Houle et al. (43). In short, the left wing of a live CO₂-anesthetized fly is immobilized in a suction device, a digital image of the wing is obtained, and the program Wings3.8 (44) is used to fit cubic B-splines to the wing veins, from which the coordinates of landmarks and semilandmarks are extracted. The length of vein L2 was estimated as the straight-line distance between the humeral break in the costa and the distal end of L2. The square root of wing area was used as a measure of wing size. See Fig. S3 for detailed information on the wing measurements.

Fig. S3.

Picture of a D. melanogaster wing with landmarks. The 12 numbered landmarks are vein intersections and the humeral break in the costa (landmark 6). The landmarks in gray are semilandmarks evenly spaced between each pair of landmarks on the outline. We used the distance between landmarks 4 and 6 as a measure of L2 length. Landmark 11 was not used because it is much less precisely estimated than landmark 6. In the selected D. melanogaster populations, area was estimated using the surveyor’s formula as the polygon bounded by landmark 6, the juncture of the costa with the vein L1, and the notch between the wing blade and alula; six evenly spaced semilandmarks along the costa between the first two landmarks; and 24 evenly spaced semilandmarks along the wing margin between the latter two landmarks. For the comparative data, we calculated wing area using the surveyor’s formula on the convex hull of a set of 16 evenly spaced points along the spline curve of the wing outline, plus the landmark defining the humeral break. We used the square root of wing area as measure of wing size.

Derivation of Populations for the Selection Experiment.

The initial population was made by intercrossing 30 inbred lines obtained from the Drosophila Genetic Reference Panel (45). This population was allowed to mate freely for one generation before being divided into the selected populations. We maintained 16 different populations in this experiment: two selected for increase and two for decrease in allometric intercept, two for increase and two for decrease in allometric slope, two for increase and two for decrease in slope with the starvation treatment, and two unstarved and two starved controls. Details are given in SI Materials and Methods.

Rearing of Selected Populations.

Details are given in SI Materials and Methods.

Justification of the Allometric Slope Selection Index.

Details are given in SI Materials and Methods.

Selection Procedure.

In the two replicate control populations, 20–25 virgin females and 20–25 males were chosen haphazardly and imaged before being divided into two vials to produce the next generation.

In the two replicate starved control populations, 50 virgin females and 50 males were imaged, then divided haphazardly into four groups of 25 flies each (12 or 13 of each sex). Two groups were placed in vials and their larvae fed normally; the other two were placed in “egg layers,” and their larvae underwent the starvation treatment (see SI Materials and Methods). Note that these two populations were started later in the experiment (at generation 5 of the other populations).

Two replicate populations were maintained for each direction (up and down) of selection on the allometric intercept. Each generation in each population, 100 virgin females and 100 males were chosen haphazardly and imaged. From these, 20–25 of each sex were selected to produce the next generation, using the selection index

$$W_{int}={\beta }_1\left(x-\overline{x}\right)+{\beta }_2\left(y-{\text{log}}_e\left[a\right]-bx\right),$$

where x is log_e wing size (square-root wing area), $\overline{x}$ is the average of x, y is log_e L2 length, log_e[a] is the allometric intercept, b is the allometric slope, and the term (y - log_e[a] - bx) is the residuals of the allometric regression. For the up selection, β₂ = 1, and for the down selection, β₂ = –1, whereas β₁ was optimized to reduce selection on size (see SI Materials and Methods). The selection index was fitted independently each generation within each selected population, and the flies were stored in individual vials from imaging until the selection index score of each fly was calculated. Selection on the intercept was maintained in both replicates (A and B) for seven generations for both the up and the down directions. After this, the A replicates were discarded, whereas up- and down-selected populations in replicate B were maintained with relaxed selection (i.e., the same mating regime as in the control populations) for an additional 16 generations.

For each direction (up and down) of selection on the allometric slope, we kept two replicate populations (A and B). Each generation in each population, 100 virgin females and 100 males were imaged, of which 24 were selected using the selection index

$$W_{slope}={\beta }_x\left(x-\overline{x}\right)+{\beta }_y\left(y-\overline{y}\right)+\frac{1}{2}{\gamma }_x{\left(x-\overline{x}\right)}^2+{\gamma }_{xy}\left(x-\overline{x}\right)\left(y-\overline{y}\right),$$

where γ_xy = 1 for the up selection (increase in slope) and -1 for the down selection (decrease in slope). This function was optimized by choosing values of the parameters β_x, β_y, and γ_x, to minimize selection on the means of x and y and on the variance of x (see SI Materials and Methods). The selection index was fitted independently each generation within each selected population, and the flies were stored in individual vials after imaging until the selection index score of each fly was calculated. To prevent linkage disequilibrium, we enforced disassortative mating on size by first dividing the selected flies into two groups, one containing the largest 12 females and smallest 12 males, the other with the smallest 12 females and largest 12 males. Each of these groups was then split at random into two groups of six males and six females, and each such group was placed in vials with another group of opposite-sex flies of contrasting size. These flies were allowed to mate and lay eggs overnight. Selection was carried out for 26 generations in replicate A and for 25 generations in replicate B. After this, we maintained the populations for an additional 13 generations in replicate A and 14 generations in replicate B under relaxed selection (i.e., the same mating regime as the control populations). At generation 23, we split off a population from each of the replicates and maintained these new populations under relaxed selection for 15 generations. At several points during the period of relaxed selection, we imaged 100 males and 100 females from each of the populations (see Fig. 2B).

We also maintained two replicate starved slope-selected populations for each direction of slope selection. These were subjected to the same selection regime as the unstarved slope-selected populations but reared using the starvation treatment. Selection was carried out for 19 generations in these populations. Details are given in SI Materials and Methods.

Statistical Analyses.

To estimate the rate of evolution for the allometric intercept and slope, we fitted a Brownian-motion model of evolution using a phylogenetic mixed model (46). Because the depth of the phylogeny is highly uncertain (47), we used both a best guess of 133 million years and a conservative estimate of 50 million years to estimate the rate.

For the selection experiment, changes and differences in allometric intercept and slope of log_e vein L2 length on log_e wing size (square-root wing area) were analyzed by a series of linear mixed-effects models because of the hierarchical structure of the data. Details are given in SI Materials and Methods.