Lateral chirality-sorting optical forces

Significance

In light of the difficulty often associated with sorting and characterizing materials by chirality, new research aimed toward the development of passive optical methods has stirred considerable excitement at the interface of analytical chemistry and physical optics. We describe here a mechanism through which chirality-sorting optical forces emerge through the interaction with the spin-angular momentum of light, a property that the community has recently learned to control with great sophistication using modern nanophotonics. In particular, the forces may be oriented perpendicularly to the propagation direction of evanescent waves, leading to a helicity-dependent lateral deflection of chiral particles in opposite directions. The highly unusual transverse optical force described herein is the strongest of its kind discovered so far to our knowledge.

Abstract

The transverse component of the spin angular momentum of evanescent waves gives rise to lateral optical forces on chiral particles, which have the unusual property of acting in a direction in which there is neither a field gradient nor wave propagation. Because their direction and strength depends on the chiral polarizability of the particle, they act as chirality-sorting and may offer a mechanism for passive chirality spectroscopy. The absolute strength of the forces also substantially exceeds that of other recently predicted sideways optical forces.

Chirality [from Greek $\chi \mathit{ϵ}\iota \rho$ (kheir), “hand”] is a type of asymmetry where an object is geometrically distinct from its mirror image, no matter how it is held or rotated (1). Such objects abound in nature, human hands being the classic example. Even though they share all properties other than their helicity, a chiral object and its mirror image differ in their interaction with chiral environments, such as, for example, biological systems. Analyzing and separating substances by chirality consequently represents an important problem in research and industry, affecting especially pharmaceuticals and agrochemicals (2–5). Whereas the sorting of substances by chirality normally has to be addressed through the introduction of a specific chiral resolving agent (6, 7), the manifestation of chirality in the electromagnetic response of materials has raised the question of passive sorting using optical forces (10–16). In ref. 16 Wang and Chan recently predicted an electromagnetic plane wave to exert a lateral optical force on a chiral particle above a reflective surface, which emerges as the particle interacts with the reflection of its scattered field. This highly unusual force acts in a direction in which there is neither wave propagation nor an intensity gradient, and deflects particles with opposite helicities toward opposite sides. Apart from its fundamental interest, such a force may in theory be useful for all-optical enantiomer sorting with a single, unstructured beam. In ref. 17, Bliokh et al. almost simultaneously predicted another lateral force that is exerted on nonchiral particles in an evanescent wave. This force is a consequence of the linear momentum of the wave that is associated with its extraordinary spin angular momentum (SAM), which was first described by F. J. Belifante in the context of quantum field theory, and which vanishes for a propagating plane wave (18, 19).

In this paper we show that lateral forces can be achieved using a third mechanism, which is also inherently chirality-sorting. The forces emerge through a direct interaction of the optical SAM with chiral particles, and push either in the direction of the SAM vector or opposite to it, depending on the helicity of the particle. In general, the strength and direction of optical SAM may be estimated by considering that SAM manifests itself as a helical polarization of the electromagnetic field. For example, the SAM density of a right-circularly polarized plane wave points in the direction of propagation, and the SAM density of a left-circularly polarized wave in the direction opposite to the direction of propagation. Among plane waves, a circularly polarized wave has the highest optical SAM density, whereas a linearly polarized wave carries none. Elliptically polarized waves represent intermediate cases between these two extremes—the mathematical expression for the optical SAM density of an electromagnetic wave can be found in Supporting Information. The optical forces arising through the interaction of light with chiral matter may be intuited by considering that an electromagnetic wave with helical polarization will induce corresponding helical dipole (and multipole) moments in a scatterer. If the scatterer is chiral (one may picture a subwavelength metal helix), then the strength of the induced moments depends on the matching of the helicity of the electromagnetic wave to the helicity of the scatterer. The forces described in this paper, as well as other chirality-sorting optical forces, emerge because the induced moments in the scatterer result in radiation in a helicity-dependent preferred direction, which causes corresponding recoil.

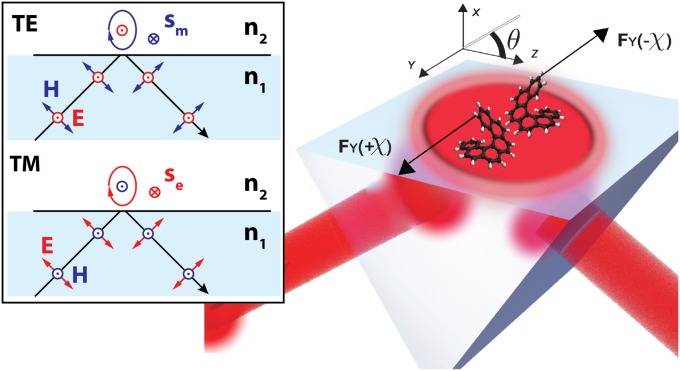
The effect discussed in this paper enables the tailoring of chirality-sorting optical forces by engineering the local SAM density of optical fields, such that fields with transverse SAM can be used to achieve lateral forces. Fields with transverse SAM arise, for example, when light is totally internally reflected at an interface (20–22). Fig. 1, Inset shows how totally internally reflected transverse-electric (TE) or transverse-magnetic (TM) polarized waves give rise to evanescent waves with elliptically polarized magnetic and electric fields, respectively. The polarization ellipses of the latter lie in the plane of incidence, implying optical SAM transverse to the direction of wave propagation.

Fig. 1.

Chirality-dependent lateral forces in an evanescent field. An evanescent field arises as light in a high index medium ($n_1$) is totally internally reflected at the interface with a low index medium ($n_2$) at an angle θ beyond the critical angle. Particles in an evanescent field with transverse spin angular momentum experience lateral forces depending on their chiral polarizability χ, with particles with opposite helicities experiencing lateral forces in oppose directions. (Inset) Totally internally reflected TE and TM waves give rise to evanescent waves that have transverse spin due to their elliptically polarized magnetic (TE) and electric (TM) fields.

We investigate the lateral chirality-sorting forces by calculating the forces on a small chiral particle in an evanescent field and show that the magnitude of the lateral component of the force substantially exceeds those of the previously predicted lateral forces. To this end, we discuss the optical forces exerted by an electromagnetic wave on a small chiral particle in general and then treat the specific case of an evanescent wave. We then use a nanosphere made of a chiral material to model a small chiral particle and compare the emerging lateral force to the strength of the lateral force that may arise due to the other two effects discussed by Wang and Chan (16) and Bliokh et al. (17). The optical forces exerted on an object are rigorously calculated by first finding the distribution of electromagnetic fields, and then integrating the Maxwell stress tensor over a surface enclosing the object (23). The scattering problem associated with finding the field distributions is tremendously simplified in the dipole approximation, which holds in the so-called Rayleigh limit that applies to particles much smaller than the wavelength. The dipole solution is sufficiently accurate for most molecular scattering problems and is furthermore the basis for efficient numerical methods that are used to find solutions for complex larger objects (24). We consider the optical forces on a small particle in a source-free, lossless, nondispersive, and isotropic medium with relative electric permittivity ε and relative magnetic permeability μ. In the dipole approximation, and in the absence of a permanent electric or magnetic dipole moment of the particle, the time-averaged total optical force $\mathbf{F}$ exerted on the particle by a monochromatic electromagnetic wave is given by (25):

$$\begin{array}{r}\mathbf{F}=\underset{{\mathbf{F}}_{\mathbf{0}}}{\underbrace{\frac{1}{2}\text{Re}\left\{\mathbf{d}\left(\nabla \otimes {\mathbf{E}}^{\ast }\right)+\mathbf{m}\left(\nabla \otimes {\mathbf{H}}^{\ast }\right)\right\}}}\\ -\underset{{\mathbf{F}}_{\mathbf{i}\mathbf{n}\mathbf{t}}}{\underbrace{\frac{k^4}{3}\text{Re}\left\{\sqrt{\frac{1}{\mu \mathit{ϵ}}}\left(\mathbf{d}\times {\mathbf{m}}^{\ast }\right)\right\}}},\end{array}$$ [1]

where $\mathbf{E}$ and $\mathbf{H}$ are the electric and magnetic field vectors of the incident electromagnetic wave at the location of the particle, $\mathbf{d}$ and $\mathbf{m}$ are the electric and magnetic dipole moments of the particle that are induced by the incident field, $k=n\omega /c$ is the wavenumber of the electromagnetic wave, ω is the frequency, c is the speed of light in vacuum, and $n=\sqrt{\mathit{ϵ}\mu }$ is the refractive index of the medium surrounding the dipole. The fields are written in complex phasor notation throughout this paper, where the factor $\exp \left(-i\omega t\right)$ giving the time dependence is implied, and the superscript asterisk denotes the complex conjugate. Vector quantities are indicated by bold letters, and all expressions are given in Gaussian units unless stated otherwise. $\widehat{\mathbf{x}},\widehat{\mathbf{y}}$, and $\widehat{\mathbf{z}}$ are unit vectors along the corresponding coordinate axes. The symbol $\otimes$ denotes the dyadic product, so that the terms of the form $\mathbf{W}\left(\nabla \otimes \mathbf{V}\right)$ in Eq. 1 have elements ${\left[\mathbf{W}\left(\nabla \otimes \mathbf{V}\right)\right]}_i={\displaystyle {\sum }_j{W}_j{\partial }_i{V}_j}$ for $i,j\in \left\{x,y,z\right\}$ (25) and can be written as $\mathbf{W}\left(\nabla \otimes \mathbf{V}\right)=\left(\mathbf{W}\cdot \nabla \right)\mathbf{V}+\mathbf{W}\times \left(\nabla \times \mathbf{V}\right)$ in terms of more commonly used vector operators. Eq. 1 shows that the optical force has a component ${\mathbf{F}}_{\mathbf{0}}$ corresponding to the force exerted by the incident field on the particle’s electric and magnetic dipole moments, and a component ${\mathbf{F}}_{\mathbf{i}\mathbf{n}\mathbf{t}}$ that results from a direct interaction of the two dipole moments. In case of the evanescent field, it is the ${\mathbf{F}}_{\mathbf{i}\mathbf{n}\mathbf{t}}$ term that gives rise to the lateral electromagnetic spin force. Chirality manifests itself in the electromagnetic response of a material through a cross-coupling of the induced electric and magnetic polarizations, such that an electric field also gives rise to a magnetic polarization, and vice versa (26, 27). Assuming isotropic polarizabilities and no permanent dipole moment, the electric and magnetic dipole moments induced by fields incident on a chiral particle are $\mathbf{d}={\alpha }_{\text{e}}\mathbf{E}+\text{i}\chi \mathbf{H}$ and $\mathbf{m}={\alpha }_{\text{m}}\mathbf{H}-\text{i}\chi \mathbf{E}$, where ${\alpha }_{\text{e}}$ and ${\alpha }_{\text{m}}$ are the electric and magnetic polarizabilities (16). The chiral polarizability of the particle χ captures the chiral nature of the dipole, such that setting $\chi =0$ recovers the case of an achiral dipole. It is worth mentioning that, although the chiral polarizability is an inherently dynamic quantity, the dynamic dipole polarizabilities ${\alpha }_{\text{e}}$ and ${\alpha }_{\text{m}}$ differ from the more frequently listed corresponding static polarizabilities ${\alpha }_{\text{e}}^{\left(0\right)}$ and ${\alpha }_{\text{m}}^{\left(0\right)}$ by a radiation correction as ${\alpha }_{\text{e}}={\left[1-\left(i2k^3/3\mathit{ϵ}\right){\alpha }_{\text{e}}^{\left(0\right)}\right]}^{-1}{\alpha }_{\text{e}}^{\left(0\right)}$ and ${\alpha }_{\text{m}}={\left[1-\left(i2k^3/3\mu \right){\alpha }_{\text{m}}^{\left(0\right)}\right]}^{-1}{\alpha }_{\text{m}}^{\left(0\right)}$ (28, 29). Although the static polarizability turns out to be sufficiently accurate in the particular case of the small metallic sphere considered in ref. 17, omission of the radiation correction can in general lead to a substantial underestimation of the optical forces (Supporting Information). The full expression for the force exerted on a chiral dipole by an electromagnetic field is obtained by inserting the expressions for the electric and magnetic dipole moments into Eq. 1:

$$\begin{array}{l}{\mathbf{F}}_{\mathbf{0}}=\underset{\text{Gradient}\hspace{0.17em}\text{Force}}{\underbrace{\frac{1}{g}\left({\mathit{ϵ}}^{-1}\mathrm{Re}\left\{{\alpha }_{\text{e}}\right\}\nabla u_{\text{e}}+{\mu }^{-1}\mathrm{Re}\left\{{\alpha }_{\text{m}}\right\}\nabla u_{\text{m}}\right)-\frac{\omega }{g}\mathrm{Re}\left\{\chi \right\}\nabla h}}\hspace{0.17em}\\ +\underset{\text{Radiation}\hspace{0.17em}\text{Pressure}}{\underbrace{\frac{2\omega }{g}\left(\mu \mathrm{Im}\left\{{\alpha }_{\text{e}}\right\}{\mathbf{p}}_{\mathbf{e}}^{\mathbf{o}}+\mathit{ϵ}\mathrm{Im}\left\{{\alpha }_{\text{m}}\right\}{\mathbf{p}}_{\mathbf{m}}^{\mathbf{o}}\right)-\frac{c}{g}\mathrm{Im}\left\{\chi \right\}\left[\nabla \times \mathbf{p}-2k^2\mathbf{s}\right]}}\end{array}$$ [2]

$${\mathbf{F}}_{\mathbf{i}\mathbf{n}\mathbf{t}}=-\frac{2\omega }{g}\frac{k^3}{3}\left(\text{Re}\left\{{\alpha }_{\text{e}}{\alpha }_{\text{m}}^{*}\right\}\mathbf{p}-\mathrm{Im}\left\{{\alpha }_{\text{e}}{\alpha }_{\text{m}}^{*}\right\}{\mathbf{p}}^{″}+{\left|\chi \right|}^2\mathbf{p}\right)-\frac{2\omega }{g}\frac{2k^4}{3n}\left(\mathit{ϵ}\mathrm{Re}\left\{\chi {\alpha }_{\text{m}}^{*}\right\}{\mathbf{s}}_{\mathbf{m}}+\mu \mathrm{Re}\left\{\chi {\alpha }_{\text{e}}^{*}\right\}{\mathbf{s}}_{\mathbf{e}}\right).$$ [3]

Here we marked the terms corresponding to the familiar gradient force and radiation pressure in the first-order term ${\mathbf{F}}_{\mathbf{0}}$ (Eq. 2), both of which are modified when the dipole is chiral (i.e., when $\chi \ne 0$). The lateral forces are contained in the ${\mathbf{F}}_{\mathbf{i}\mathbf{n}\mathbf{t}}$ term, where an additional force term proportional to $k^4$ emerges for chiral dipoles (the final term of Eq. 3). This term shows that the spin momentum density of the field gives rise to a linear momentum transfer on chiral particles, which occurs in opposite directions for opposite signs of χ (i.e., opposite helicities). The prefactor $g={\left(4\pi \right)}^{-1}$ arises from the use of Gaussian units, $u_{\text{e}}=\left(g\mathit{ϵ}/4\right){\left|\mathbf{E}\right|}^2$ and $u_{\text{m}}=\left(g\mu /4\right){\left|\mathbf{H}\right|}^2$ are the energy densities of the electric and the magnetic field, and $h=\left(g/2\omega \right)\mathrm{Im}\left\{\mathbf{E}\cdot {\mathbf{H}}^{\ast }\right\}$ is the time-averaged optical helicity density (17, 18). The time-averaged Poynting momentum density $\mathbf{p}=\left(g/2c\right)\mathrm{Re}\left\{\mathbf{E}\times {\mathbf{H}}^{\ast }\right\}$ can be decomposed as $\mathbf{p}={\mathbf{p}}^{\mathbf{o}}+{\mathbf{p}}^{\mathbf{s}}$ into a component related to the orbital angular momentum, ${\mathbf{p}}^{\mathbf{o}}$, and the Belifante momentum ${\mathbf{p}}^{\mathbf{s}}$ related to the spin momentum density $\mathbf{s}$. These quantities can be individually further separated into their electric and magnetic components, in particular ${\mathbf{p}}^{\mathbf{o}}={\mathbf{p}}_{\mathbf{e}}^{\mathbf{o}}+{\mathbf{p}}_{\mathbf{m}}^{\mathbf{o}}$ and $\mathbf{s}={\mathbf{s}}_{\mathbf{e}}+{\mathbf{s}}_{\mathbf{m}}$ (Supporting Information contains a full list of the definitions of the field quantities, which are discussed in detail in ref. 17). Invoking a fluid mechanics analogy, the term $\nabla \times \mathbf{p}$ may be interpreted as the vorticity of the Poynting momentum density. ${\mathit{p}}^{″}=\left(g/2c\right)\mathrm{Im}\left\{\mathbf{E}\times {\mathbf{H}}^{\ast }\right\}$ is the imaginary Poynting momentum (17, 30). For a monochromatic wave, the momentum and spin densities are (17):

$${\mathbf{p}}^{\mathbf{s}}=-\frac{g}{8\omega }\nabla \times \left[{\left(i\mu \right)}^{-1}\mathbf{E}\times {\mathbf{E}}^{\ast }+{\left(i\mathit{ϵ}\right)}^{-1}\mathbf{H}\times {\mathbf{H}}^{\ast }\right]$$ (4)

$${\mathbf{p}}^{\mathbf{o}}=-\frac{g}{4\omega }\text{Im}\left\{{\mu }^{-1}\mathbf{E}\left(\nabla \otimes {\mathbf{E}}^{\ast }\right)+{\mathit{ϵ}}^{-1}\mathbf{H}\left(\nabla \otimes {\mathbf{H}}^{\ast }\right)\right\}$$ [5]

$$\mathbf{s}=-\frac{g}{4\omega }\left({\left(\mu i\right)}^{-1}\mathbf{E}\times {\mathbf{E}}^{\ast }+{\left(\mathit{ϵ}i\right)}^{-1}\mathbf{H}\times {\mathbf{H}}^{\ast }\right),$$ [6]

where the magnetic and electric contributions correspond to the terms proportional to the electric and magnetic fields. Evaluating Eqs. 2 and 3 for a plane wave $\mathbf{E}=\sqrt{\mu }{\mathbf{E}}_{\mathbf{0}}\exp \left(ikz\right)$ propagating in the $\widehat{\mathbf{z}}$ direction shows that the forces are entirely in the direction of propagation:

$${\mathbf{F}}_{\mathbf{0}}=\left[\left(\text{Im}\left\{\mu {\alpha }_{\text{e}}\right\}+\text{Im}\left\{\mathit{ϵ}{\alpha }_{\text{m}}\right\}\right)/2+\text{Im}\left\{\chi \right\}n\sigma \right]Ik\hspace{0.17em}\widehat{\mathbf{z}}$$ [7]

$${\mathbf{F}}_{\mathbf{i}\mathbf{n}\mathbf{t}}=-\left[\left(\mathit{ϵ}\mathrm{Re}\left\{\chi {\alpha }_{\text{m}}^{*}\right\}+\mu \mathrm{Re}\left\{\chi {\alpha }_{\text{e}}^{*}\right\}\right)\sigma /n+\mathrm{Re}\left\{{\alpha }_{\text{e}}{\alpha }_{\text{m}}^{*}\right\}+{\left|\chi \right|}^2\right]I{k}^4/3\hspace{0.17em}\widehat{\mathbf{z}},$$ [8]

where $I=n^{-1}\left|\mathbf{E}\times {\mathbf{H}}^{\ast }\right|={\left|{\mathbf{E}}_{\mathbf{0}}\right|}^2$. The factor $\sigma =-2\mathrm{Im}\left\{\left(\mathbf{E}\cdot \widehat{\mathbf{x}}\right)\left({\mathbf{E}}^{\ast }\cdot \widehat{\mathbf{y}}\right)\right\}/\left({\left|\mathbf{E}\cdot \widehat{\mathbf{x}}\right|}^2+{\left|\mathbf{E}\cdot \widehat{\mathbf{y}}\right|}^2\right)$ is a measure for the degree of circular polarization (ellipticity) of the wave in the $\left(\text{x},\text{y}\right)$ plane, such that $\sigma =+1$ for right circular polarization and $\sigma =-1$ for left circular polarization. In the calculations that follow, we will furthermore use the parameters $\tau =\left({\left|\mathbf{E}\cdot \widehat{\mathbf{x}}\right|}^2-{\left|\mathbf{E}\cdot \widehat{\mathbf{y}}\right|}^2\right)/\left({\left|\mathbf{E}\cdot \widehat{\mathbf{x}}\right|}^2+{\left|\mathbf{E}\cdot \widehat{\mathbf{y}}\right|}^2\right)$ and $\xi =2\mathrm{Re}\left\{\left(\mathbf{E}\cdot \widehat{\mathbf{x}}\right)\left({\mathbf{E}}^{\ast }\cdot \widehat{\mathbf{y}}\right)\right\}/\left({\left|\mathbf{E}\cdot \widehat{\mathbf{x}}\right|}^2+{\left|\mathbf{E}\cdot \widehat{\mathbf{y}}\right|}^2\right)$ as measures for the linear polarization in the $\left(\text{x},\text{y}\right)$ plane, such that $\tau =\left\{+1,-1\right\}$ correspond to linear polarization along $\left\{x,y\right\}$ and $\xi =\left\{+1,-1\right\}$ correspond to linear polarization at angles of $\left\{+45°,-45°\right\}$ with respect to the x axis. The helicity-dependent change of the radiation pressure due to the chiral polarizability χ that shows up in Eq. 8 has previously been used for sorting highly chiral liquid crystal droplets in optical lattices (11). We now may consider an evanescent wave created by the total internal reflection of light at an interface in the (z,y) plane, which has the form $\mathbf{E}=\sqrt{\mu }{\mathbf{E}}_{\mathbf{0}}\exp \left(-\kappa x\right)\exp \left(i{k}_{\text{z}}z\right)$. If the evanescent field is propagating in a medium with index $n_2=\sqrt{\mathit{ϵ}\mu }$ and was created through the total internal reflection of a beam in a medium with index $n_1$ incident on the interface with angle θ in the (x,z) plane (Fig. 1), then the wave vector components are given by $k_z=\left(n_1/n_2\right)\sin \left(\theta \right)k$, $k_x=\sqrt{k^2-k_z^2}$, and $\kappa =\sqrt{k_z^2-k^2}=i{k}_x$, where $k=n_2\omega /c$. The energy and momentum densities of an evanescent field relevant for the calculation of the forces with Eqs. 2 and 3 are listed in Supporting Information. Notably, evanescent fields have longitudinally polarized field components (Supporting Information), which give rise to transverse spin angular momentum (17, 31). As mentioned, in case of a p-polarized wave ($\tau =1$) it is the electric field that is elliptically polarized in the (x,z) plane, and in case of an s-polarized wave ($\tau =-1$) it is the magnetic field. Correspondingly, the out of plane electric and magnetic spin components are given by $\left(\widehat{\mathbf{y}}\cdot {\mathbf{s}}_{\mathbf{e}}\right)=\left(1+\tau \right)\frac{g}{4\omega }\frac{\kappa }{k_z}{I}_{\text{e}}$ and $\left(\widehat{\mathbf{y}}\cdot {\mathbf{s}}_{\mathbf{m}}\right)=\left(1-\tau \right)\frac{g}{4\omega }\frac{\kappa }{k_z}{I}_{\text{e}}$. Using Eqs. 2–6 the forces exerted on a chiral dipole by an evanescent field are given by

$$\begin{array}{r}{\mathbf{F}}_{\mathbf{0}}=\kappa I_{\text{e}}\left[\mathrm{Re}\left\{\chi \right\}{n}_2\sigma -\frac{1}{2}\left(\mathrm{Re}\left\{\mu {\alpha }_{\text{e}}\right\}\left(1+\tau \frac{{\kappa }^2}{k_{\text{z}}^2}\right)+\mathrm{Re}\left\{\mathit{ϵ}{\alpha }_{\text{m}}\right\}\left(1-\tau \frac{{\kappa }^2}{k_{\text{z}}^2}\right)\right)\right]\widehat{\mathbf{x}}\\ \frac{I_{\text{e}}}{2}{k}_{\text{z}}\left[\mathrm{Im}\left\{\mu {\alpha }_{\text{e}}\right\}\left(1+\tau \frac{{\kappa }^2}{k_{\text{z}}^2}\right)+\mathrm{Im}\left\{\mathit{ϵ}{\alpha }_{\text{m}}\right\}\left(1-\tau \frac{{\kappa }^2}{k_{\text{z}}^2}\right)+2\mathrm{Im}\left\{\chi \right\}\sigma n_2\right]\widehat{\mathbf{z}}\end{array}$$ [9]

$$\begin{array}{r}{\mathbf{F}}_{\mathbf{i}\mathbf{n}\mathbf{t}}=-I_{\text{e}}\frac{k^4}{3}\frac{\kappa }{k_z}\left[\mathrm{Re}\left\{{\alpha }_{\text{e}}{\alpha }_{\text{m}}^{*}\right\}\sigma +\mathrm{Im}\left\{{\alpha }_{\text{e}}^{*}{\alpha }_{\text{m}}\right\}\xi +\sigma {\left|\chi \right|}^2+\underset{\text{Chirality}-\text{sorting}\hspace{0.17em}\text{Lateral}\hspace{0.17em}\text{Force}}{\underbrace{\frac{\mathit{ϵ}}{n_2}\left(1-\tau \right)\mathrm{Re}\left\{\chi {\alpha }_{\text{m}}^{*}\right\}+\frac{\mu }{n_2}\left(1+\tau \right)\mathrm{Re}\left\{\chi {\alpha }_{\text{e}}^{*}\right\}}}\right]\widehat{\mathbf{y}}\\ -I_{\text{e}}\frac{k^4}{3}\frac{k}{k_{\text{z}}}\left[\mathrm{Re}\left\{{\alpha }_{\text{e}}{\alpha }_{\text{m}}^{*}\right\}+{\left|\chi \right|}^2+\frac{\sigma }{n_2}\left(\mathit{ϵ}\mathrm{Re}\left\{\chi {\alpha }_{\text{m}}^{*}\right\}+\mu \mathrm{Re}\left\{\chi {\alpha }_{\text{e}}^{*}\right\}\right)\right]\widehat{\mathbf{z}}\\ -I_{\text{e}}\frac{k^4}{3}\frac{\kappa k}{k_{\text{z}}^2}\left(\frac{\xi }{n_2}\left(\mathrm{Re}\left\{\mu \chi {\alpha }_{\text{e}}^{*}\right\}-\mathrm{Re}\left\{\mathit{ϵ}\chi {\alpha }_{\text{m}}^{*}\right\}\right)+\mathrm{Im}\left\{{\alpha }_{\text{e}}^{*}{\alpha }_{\text{m}}\right\}\tau \right)\widehat{\mathbf{x}}\end{array}$$ [10]

with $I_{\text{e}}=\frac{{\left|{\mathbf{E}}_{\mathbf{0}}\right|}^2}{1+\tau {\left(\kappa /k_{\text{z}}\right)}^2}\exp \left(-2\kappa x\right)$. The lateral forces experienced by the dipole are due to the ${\mathbf{F}}_{\mathbf{i}\mathbf{n}\mathbf{t}}$ term and given by the first line of Eq. 10. Adjusting the polarization to $\tau =\pm 1$ renders the lateral forces directly proportional to χ, and their direction is therefore helicity-dependent. Unfortunately, the chirality-dependent lateral forces caused by $\nabla \times \mathbf{p}$ and $\mathbf{s}$ in the ${\mathbf{F}}_{\mathbf{0}}$ force term exactly cancel each other (32). Small perturbations of the force that may arise due to the reflection of the field scattered by the particle at the interface at which the evanescent field is generated are neglected.

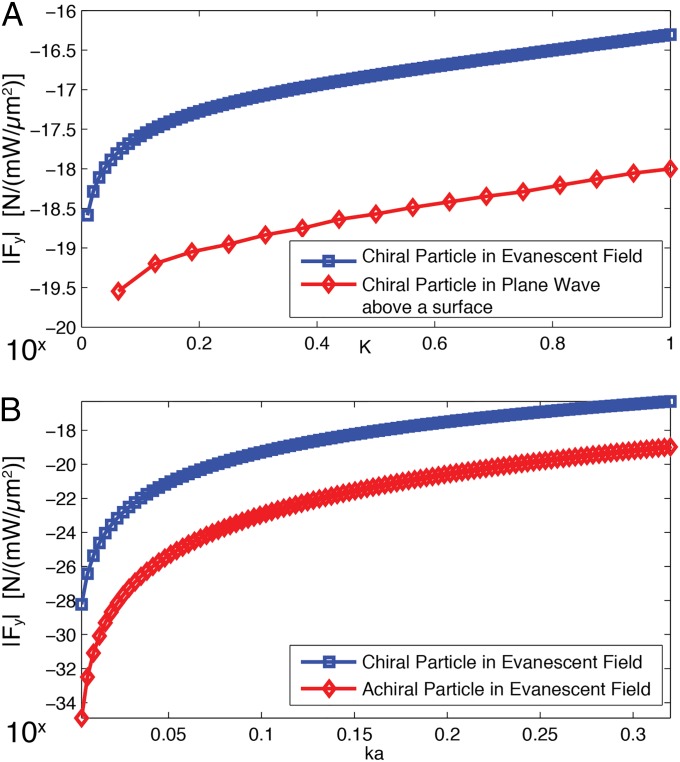
Fig. 2 compares the strength of the force to those of the lateral forces predicted by Wang and Chan (16) and Bliokh et al. (17) as it depends on the chirality and the size of a spherical nanoparticle in an electromagnetic field. In each case, the lateral force emerging through the interaction of the transverse SAM with the chiral particle is stronger by about 1.75 and 4 orders of magnitude over the considered range. Here material chirality is parametrized using the chirality parameter $K=c\chi \in \left[-\mathrm{1,1}\right]$ assuming real values to mirror what was done in ref. 16. The derivation of the expression of the force on such a sphere is listed in Supporting Information, as well as a discussion of the force on helicene molecules and gold nanohelices, which represent other types of chiral particles frequently considered in the literature, and which helps to further illustrate the characteristic magnitude of the force. We furthermore include calculations of the nonlateral force terms acting on these objects.

Fig. 2.

Lateral optical forces. The previously predicted lateral optical forces in comparison with the lateral force on a chiral particle in an evanescent field. The absolute value of the lateral force $F_{\text{y}}$ is shown on a logarithmic scale in base 10. (A) The lateral optical force on a chiral nanosphere in a plane wave above a reflective surface according to Wang and Chan (16) and due to an evanescent field with $\tau =1$ as a function of the chirality parameter K for positive helicity (20, 33) (Supporting Information). The sphere is nonmagnetic, situated 60 nm above the surface, and has a dielectric constant of ${\mathit{ϵ}}_{\text{s}}=2$ and a radius of 30 nm. In case of the force in the evanescent field, the intensity refers to the intensity of a beam that is totally internally reflected at a flint glass/air interface at an angle of $\theta =36.4°$. (B) The lateral force on an achiral sphere ($K=0$) due to the Belifante spin momentum density according to Bliokh et al. (17) and on an equivalent chiral sphere ($K=1$) as a function of $ka$, where a is the radius of the sphere and $k=n_2\omega /c$ is the wavenumber of the evanescent field. In both cases the sphere is nonmagnetic and situated at a height of 30 nm, has dielectric constant ${\mathit{ϵ}}_{\text{s}}=2$, and experiences the evanescent field generated at a flint glass/air interface at an incident angle of $\theta =36.4°$. In the former case the polarization of the evanescent field has $\sigma =1$ and in the latter $\tau =1$.

In summary, we predict lateral forces on materials with chiral optical response in evanescent fields, which push particles with opposite helicities in opposite directions with strength dependent on the chiral polarizability. The forces result from the direct interaction of the evanescent field’s transverse optical SAM density of the wave with the chiral electromagnetic response of the particle, and are particularly strong in comparison with previously predicted lateral optical forces. Transverse SAM may arise whenever light is laterally confined, so that the effect described in this paper represents a natural choice for the optical sorting by material chirality in an integrated system. The effect can be produced by a single beam, which avoids standing wave patterns that limit the separation of enantiomers to the width of interference fringes. However, the use of multiple beams may enable the cancellation of the longitudinal force component or, given the possibility of generating transverse spin, even the generation of spin-optical lateral forces in free space beams (34). The fact that the optical spin force described here represents by far the strongest force acting in the lateral direction renders the effect in a sense background-free, which is useful given the generally weak nature of chiral optical effects. Although we limited the discussion to the simplest case of an evanescent field created by the total internal reflection of light at a single interface, there is significant potential for improving the strength of the force by further engineering the light field. Natural choices for this are the intense and inherently evanescent fields of plasmonic excitations, or optical waveguides designed to have regions with high field enhancement, such as slot waveguides (35). We furthermore limited the discussion to the Rayleigh limit, where compact closed-form expressions exist, although the optical manipulation of objects smaller than a few 100 nm in liquid suspension is in general very challenging due to thermal agitation. Other than by tailoring the light fields, this may in particular be overcome in a low-pressure environment, for example in deflecting molecular beams (36). Larger particles may take advantage of resonances (such as Mie resonances) and are bound to experience much stronger forces. An experimental verification of the optical spin force on chiral media is very likely possible using a remarkable recently demonstrated method for measuring lateral optical forces using a cantilever with extremely low compliance (37). By immersing the cantilever into an evanescent field, Antognozzi et al. (37) were able to measure the substantially weaker lateral spin force on achiral materials with femtonewton resolution. In an experiment measuring the force described in this paper, a chiral particle could either be attached to the cantilever, or the cantilever may be manufactured from a chiral material itself (${\text{TeO}}_2$ being a standard material).

Evanescent Field

Snell–Descartes Law.

When a propagating wave in a medium of index $n_1$ arrives at the interface with a medium n with an incident angle θ the angle ${\theta }_t$ of the transmitted beam is given by Snell–Descartes law as:

$$n_2\sin \left({\theta }_{\text{t}}\right)=n_{1}sin\left(\theta \right).$$ [S1]

The amplitude of the transmitted wave is subject to the incident polarization. If the incident electric field is oriented perpendicularly to the plane of incidence the wave is called s-polarized (or TE polarized). If the incident electric field is oriented parallel to the plane of incidence the wave is called p-polarized (or TM polarized). The transmission coefficients giving the amplitude of the transmitted wave for an incident s-wave and an incident a p-wave are given respectively by

$$ts={\left|\frac{{\mathbf{E}}_{\mathbf{t}}}{{\mathbf{E}}_{\mathbf{i}\mathbf{n}\mathbf{c}}}\right|}_{s-wave}=\frac{2n_1\cos \left(\theta \right)}{n_1\cos \left(\theta \right)+n_2\cos \left({\theta }_{\text{t}}\right)}$$ [S2]

$$tp={\left|\frac{{\mathbf{E}}_{\mathbf{t}}}{{\mathbf{E}}_{\mathbf{i}\mathbf{n}\mathbf{c}}}\right|}_{p-wave}=\frac{2n_1\cos \left(\theta \right)}{n_2\cos \left(\theta \right)+n_{1}cos\left({\theta }_{\text{t}}\right)},$$ [S3]

where ${\mathbf{E}}_{\mathbf{t}}$ stands for the transmitted field and ${\mathbf{E}}_{\mathbf{i}\mathbf{n}\mathbf{c}}$ stands for the incident field in both case.

Considering Eq. S1 in case of $n_2<n_1$ there exists a critical angle of the incidence ${\theta }_c$ such that $\theta >{\theta }_{\text{c}}$ implies $\text{sin}\left({\theta }_{\text{t}}\right)>1$. This corresponds to a complex angle of transmission ${\theta }_{\text{t}}$. In this regime the incident beam is totally internally reflected, giving rise to an evanescent field.

Structure of the EM Field.

We can write the incident wave as

$${\mathbf{E}}_{\mathbf{i}\mathbf{n}\mathbf{c}}=\frac{\sqrt{{\mu }_1}{A}_{\text{inc}}}{\sqrt{1+{\left|{\eta }_{\text{inc}}\right|}^2}}\left({\mathbf{e}}_{\mathbf{p}}+{\eta }_{\text{inc}}{\mathbf{e}}_{\mathbf{s}}\right)\exp \left(i{\mathbf{k}}_{\mathbf{i}\mathbf{n}\mathbf{c}}.\mathbf{r}\right).$$ [S4]

Here ${\mathbf{e}}_{\mathbf{s}}$ and ${\mathbf{e}}_{\mathbf{p}}$ are the unit vectors corresponding, respectively, to s and p polarization. $A_{\text{inc}}$ corresponds to the amplitude of the wave such that ${\mu }_1{\left|A_{\text{inc}}\right|}^2={\Vert {\mathbf{E}}_{\mathbf{i}\mathbf{n}\mathbf{c}}\Vert }^2$. $\Vert k_{\text{inc}}\Vert =\frac{n_1\omega }{\text{c}}$, where $n_1$ is the index of the medium as defined previously, ${\mu }_1$ the magnetic permittivity of this medium, and ${\mathit{ϵ}}_1$ its permeability such that $n_1=\sqrt{{\mathit{ϵ}}_1{\mu }_1}$. A time dependency of $\exp \left(-i\omega t\right)$ is assumed. It is also obvious in Eq. S4 that ${\eta }_{\text{inc}}$ characterizes the polarization, such that if ${\eta }_{\text{inc}}=\pm i$ the wave is circularly polarized. In the same way ${\eta }_{\text{inc}}=0$ is a purely p polarized wave and ${\eta }_{inc}=\pm \mathrm{\infty }$ is a purely s polarized wave.

Then, after transmission through the interface when $\theta >{\theta }_{\text{c}}$ we have the evanescent field

$$\mathbf{E}=\sqrt{\mu }{\mathbf{E}}_{\mathbf{0}}\exp \left(-\kappa x\right)\exp \left(i{k}_{\text{z}}z\right)=\frac{\sqrt{\mu }{A}_2}{\sqrt{1+{\left|{\eta }_2\right|}^2}}\left(\begin{array}{c}1\\ \frac{{\eta }_2}{\alpha }\\ -i\frac{\kappa }{k\alpha }\end{array}\right)\exp \left(-\kappa x\right)\exp \left(i{k}_{z}z\right).$$ [S5]

Here we defined $\alpha =\text{sin}\left({\theta }_{\text{t}}\right)=\frac{k_{\text{z}}}{k}$ and $k=n_2\frac{\omega }{c}$ and $n_2$ is the medium above the prism, where the evanescent wave is located. As previously $A_2$ corresponds to the amplitude of the wave and can be derived with $A_2=\alpha \sqrt{\frac{{\mu }_1}{\mu }}\frac{\sqrt{{\left|tp\right|}^2+{\left|{\eta }_{\text{inc}}ts\right|}^2}}{\sqrt{1+{\left|{\eta }_{\text{inc}}\right|}^2}}{A}_{\text{inc}}$ and we define the intensity as $I_{\text{e}}=\frac{{\left|{\mathbf{E}}_{\mathbf{0}}\right|}^2}{1+\tau {\left(\kappa /k_{\text{z}}\right)}^2}\exp \left(-2\kappa x\right)={\left|A_2\right|}^2{e}^{\left(-2\kappa x\right)}$. Also, μ is the magnetic permittivity of this medium and ε its permeability such that $n_2=\sqrt{\mathit{ϵ}\mu }$. Also $\kappa =k\sqrt{{\alpha }^2-1}=i{k}_{\text{x}}$, as found in the main text. The polarization is described by ${\eta }_2={\eta }_{\text{inc}}\left(ts/tp\right)$. Eqs. S2 and S3 give in this case

$$ts=\frac{2n_1\cos \left(\theta \right)}{n_1\cos \left(\theta \right)+i{n}_2\sqrt{{\alpha }^2-1}}$$ [S6]

$$tp=\frac{2n_1\cos \left(\theta \right)}{n_2\cos \left(\theta \right)+i{n}_1\sqrt{{\alpha }^2-1}}.$$ [S7]

Defining ${\mathbf{E}}_{\mathbf{0}}=\frac{A_2}{\sqrt{1+{\left|{\eta }_2\right|}^2}}\left(\begin{array}{c}1\\ \frac{{\eta }_2}{\alpha }\\ -i\frac{\kappa }{k\alpha }\end{array}\right)$ we obtain the form that appears in the main text.

Using this notation we can define the degree of linear, diagonal, and circular polarization in the {x,y} plane as in the main text with

$$\sigma =\frac{-2\mathrm{Im}\left\{\left(\mathbf{E}\cdot \widehat{\mathbf{x}}\right)\left({\mathbf{E}}^{\ast }\cdot \widehat{\mathbf{y}}\right)\right\}}{\left({\left|\mathbf{E}\cdot \widehat{\mathbf{x}}\right|}^2+{\left|\mathbf{E}\cdot \widehat{\mathbf{y}}\right|}^2\right)}=\frac{2Im\left({\eta }_2\right)}{1+{\left|{\eta }_2\right|}^2}$$ [S8]

$$\xi =\frac{2\mathrm{Re}\left\{\left(\mathbf{E}\cdot \widehat{\mathbf{x}}\right)\left({\mathbf{E}}^{\ast }\cdot \widehat{\mathbf{y}}\right)\right\}}{\left({\left|\mathbf{E}\cdot \widehat{\mathbf{x}}\right|}^2+{\left|\mathbf{E}\cdot \widehat{\mathbf{y}}\right|}^2\right)}=\frac{2Re\left({\eta }_2\right)}{1+{\left|{\eta }_2\right|}^2}$$ [S9]

$$\tau =\frac{\left({\left|\mathbf{E}\cdot \widehat{\mathbf{x}}\right|}^2-{\left|\mathbf{E}\cdot \widehat{\mathbf{y}}\right|}^2\right)}{\left({\left|\mathbf{E}\cdot \widehat{\mathbf{x}}\right|}^2+{\left|\mathbf{E}\cdot \widehat{\mathbf{y}}\right|}^2\right)}=\frac{1-{\left|{\eta }_2\right|}^2}{1+{\left|{\eta }_2\right|}^2}.$$ [S10]

So, in terms of the parameter ${\eta }_{inc}$, which defines the incident polarization,

$$\sigma =\frac{2Im\left({\eta }_{\text{inc}}\frac{ts}{tp}\right)}{1+{\left|{\eta }_{\text{inc}}\frac{ts}{tp}\right|}^2},\xi =\frac{2Re\left({\eta }_{\text{inc}}\frac{ts}{tp}\right)}{1+{\left|{\eta }_{\text{inc}}\frac{ts}{tp}\right|}^2},\tau =\frac{1-{\left|{\eta }_{\text{inc}}\frac{ts}{tp}\right|}^2}{1+{\left|{\eta }_{\text{inc}}\frac{ts}{tp}\right|}^2}.$$ [S11]

These parameters are defined such that $\tau =1$ corresponds to a p-wave, $\tau =-1$ corresponds to an s-wave, $\sigma =1$ to a left circularly polarized plane wave in the x–y plane, $\sigma =-1$ to a right circularly polarized wave in the x–y plane, and $\xi =\pm 1$ corresponds to opposite diagonal polarizations in the x–y plane.

Derivation of the Force Eqs. 2 and 3

Derivation of ${\mathbf{F}}_{\mathbf{i}\mathbf{n}\mathbf{t}}$.

Considering Eq. 1 in the main text:

$$\begin{array}{r}{\mathbf{F}}_{\mathbf{i}\mathbf{n}\mathbf{t}}=-\frac{k^4}{3}\mathrm{Re}\{\sqrt{\frac{1}{\mu \mathit{ϵ}}}[{\alpha }_{\text{e}}{\alpha }_{\text{m}}^{*}\left(\mathbf{E}\times {\mathbf{H}}^{\text{*}}\right)+i{\alpha }_{\text{e}}{\chi }^{\text{*}}\left(\mathbf{E}\times {\mathbf{E}}^{\text{*}}\right)\\ +i{\alpha }_{\text{m}}^{*}\chi \left(\mathbf{H}\times {\mathbf{H}}^{\text{*}}\right)+{\left|\chi \right|}^2\left({\mathbf{E}}^{\ast }\times \mathbf{H}\right)]\}.\end{array}$$ [S12]

Using that $\mathrm{Re}\left\{\mathbf{E}\times {\mathbf{H}}^{\ast }\right\}=\frac{2c}{g}\mathbf{p}=\frac{2\omega }{g}\mathbf{p}\frac{\sqrt{\mu \mathit{ϵ}}}{k}$ and $\text{Im}\left\{\mathbf{E}\times {\mathbf{E}}^{\ast }\right\}=\frac{-4\omega \mu }{g}{\mathbf{s}}_{\mathbf{e}}$ and $\mathrm{Im}\left\{\mathbf{H}\times {\mathbf{H}}^{\ast }\right\}=\frac{-4\omega \mathit{ϵ}}{g}{\mathbf{s}}_{\mathbf{m}}$ and $\mathrm{Re}\left\{\mathbf{E}\times {\mathbf{E}}^{\ast }\right\}=\mathrm{Re}\left\{\mathbf{H}\times {\mathbf{H}}^{\ast }\right\}=0$ and using ${\mathit{p}}^{″}=\frac{g}{2c}\mathrm{Im}\left\{\mathbf{E}\times {\mathbf{H}}^{\text{*}}\right\}$ we obtain

$${\mathbf{F}}_{\mathbf{i}\mathbf{n}\mathbf{t}}=-\frac{2\omega }{g}\frac{k^3}{3}\left(\mathrm{Re}\left\{{\alpha }_{\text{e}}{\alpha }_{\text{m}}^{*}\right\}\mathbf{p}-\mathrm{Im}\left\{{\alpha }_{\text{e}}{\alpha }_{\text{m}}^{*}\right\}{\mathbf{p}}^{″}+{\left|\chi \right|}^2\mathbf{p}\right)-\frac{2\omega }{g}\frac{2k^4}{3n_2}\left(\mathit{ϵ}\mathrm{Re}\left\{\chi {\alpha }_{\text{m}}^{*}\right\}{\mathbf{s}}_{\mathbf{m}}+\mu \text{Re}\left\{\chi {\alpha }_{\text{e}}^{*}\right\}{\mathbf{s}}_{\mathbf{e}}\right)$$ [S13]

as it appears in the main text in Eq. 3.

Derivation of ${\mathbf{F}}_{\mathbf{0}}$.

From Eq. 1 in the main text we have

$$\begin{array}{r}{\mathbf{F}}_{\mathbf{0}}=\frac{1}{2}\mathrm{Re}\{{\alpha }_e\mathbf{E}\left(\nabla \otimes {\mathbf{E}}^{\ast }\right)+{\alpha }_m\mathbf{H}\left(\nabla \otimes {\mathbf{H}}^{\ast }\right)\\ +i\chi \left[\mathbf{H}\left(\nabla \otimes {\mathbf{E}}^{\ast }\right)-\mathbf{E}\left(\nabla \otimes {\mathbf{H}}^{\ast }\right)\right]\}.\end{array}$$ [S14]

Using $\mathbf{W}\left(\nabla \otimes \mathbf{V}\right)=\left(\mathbf{W}\cdot \nabla \right)\mathbf{V}+\mathbf{W}\times \left(\nabla \times \mathbf{V}\right)$ and the definitions in Table S1 we can write the first term as (38)

$$\frac{1}{2}\mathrm{Re}\left\{{\alpha }_{\text{e}}\mathbf{E}\left(\nabla \otimes {\mathbf{E}}^{\ast }\right)\right\}=\frac{2\omega }{g}\mu \mathrm{Im}\left\{{\alpha }_{\text{e}}\right\}{\mathbf{p}}_{\mathbf{e}}^{\mathbf{o}}+\frac{1}{2}\mathrm{Re}\left\{{\alpha }_e\right\}\frac{1}{2}\nabla {\left|\mathbf{E}\right|}^2$$ [S15]

with ${\mathbf{p}}^{\mathbf{o}}$ defined in Table S1 using that $\frac{1}{2}\nabla {\left|\mathbf{E}\right|}^2=\frac{2}{\mathit{ϵ}g}\nabla u_e$. Similarly rewriting the magnetic term, it follows that

$$\frac{1}{2}\mathrm{Re}\left\{{\alpha }_e\mathbf{E}\left(\nabla \otimes {\mathbf{E}}^{\ast }\right)+{\alpha }_m\mathbf{H}\left(\nabla \otimes {\mathbf{H}}^{\ast }\right)\right\}=\frac{1}{g}\left({\mathit{ϵ}}^{-1}\mathrm{Re}\left\{{\alpha }_{\text{e}}\right\}\nabla u_{\text{e}}+{\mu }^{-1}\mathrm{Re}\left\{{\alpha }_{\text{m}}\right\}\nabla u_{\text{m}}\right)+\frac{2\omega }{g}\left(\mu \mathrm{Im}\left\{{\alpha }_{\text{e}}\right\}{\mathbf{p}}_{\mathbf{e}}^{\mathbf{o}}+\mathit{ϵ}\mathrm{Im}\left\{{\alpha }_{\text{m}}\right\}{\mathbf{p}}_{\mathbf{m}}^{\mathbf{o}}\right).$$ [S16]

This is the achiral part of the force. Now considering the third and fourth terms and using again the identity $\mathbf{W}\left(\nabla \otimes \mathbf{V}\right)=\left(\mathbf{W}\cdot \nabla \right)\mathbf{V}+\mathbf{W}\times \left(\nabla \times \mathbf{V}\right)$ we obtain

$$\frac{1}{2}\mathrm{Re}\left\{i\chi \left[\mathbf{H}\left(\nabla \otimes {\mathbf{E}}^{\ast }\right)-\mathbf{E}\left(\nabla \otimes {\mathbf{H}}^{\ast }\right)\right]\right\}=\frac{1}{2}\mathrm{Re}\left\{i\chi \left[\left(\mathbf{H}\cdot \nabla \right){\mathbf{E}}^{\ast }-\left(\mathbf{E}\cdot \nabla \right){\mathbf{H}}^{\ast }+\mathbf{H}\times \left(\nabla \times {\mathbf{E}}^{\ast }\right)-\mathbf{E}\times \left(\nabla \times {\mathbf{H}}^{\ast }\right)\right]\right\}=-\frac{1}{2}\mathrm{Im}\left\{\chi \left[\left(\mathbf{H}\cdot \nabla \right){\mathbf{E}}^{\ast }-\left(\mathbf{E}\cdot \nabla \right){\mathbf{H}}^{\ast }+\mathbf{H}\times \left(\nabla \times {\mathbf{E}}^{\text{*}}\right)-\mathbf{E}\times \left(\nabla \times {\mathbf{H}}^{\ast }\right)\right]\right\}=-\frac{1}{2}\mathrm{Re}\left\{\chi \right\}\mathrm{Im}\left\{\nabla \left({\mathbf{E}}^{\ast }\cdot \mathbf{H}\right)\right\}-\frac{1}{2}\mathrm{Im}\left\{\chi \right\}\mathrm{Re}\left\{\left(\mathbf{H}\cdot \nabla \right){\mathbf{E}}^{\ast }-\left(\mathbf{E}\cdot \nabla \right){\mathbf{H}}^{\ast }\right\}-\frac{1}{2}\text{Im}\left\{\chi \right\}\mathrm{Re}\left\{\mathbf{H}\times \left(\nabla \times {\mathbf{E}}^{\ast }\right)-\mathbf{E}\times \left(\nabla \times {\mathbf{H}}^{\ast }\right)\right\}-\frac{1}{2}\mathrm{Re}\left\{\chi \right\}\mathrm{Im}\left\{\mathbf{H}\times \left(\nabla \times {\mathbf{E}}^{\ast }\right)-\mathbf{E}\times \left(\nabla \times {\mathbf{H}}^{\ast }\right)\right\}.$$ [S17]

Then, using Maxwell’s equations in Gaussian units (17) $\nabla \times {\mathbf{E}}^{\ast }=-i{n}_{2}k{\mathit{ϵ}}^{-1}{\mathbf{H}}^{\ast }$ and $\nabla \times {\mathbf{H}}^{\ast }=ik{n}_2{\mu }^{-1}{\mathbf{E}}^{\ast }$ and the definition of helicity, $h=\frac{g}{2\omega }\text{Im}\left\{{\mathbf{E}}^{\ast }\cdot \mathbf{H}\right\}$, we obtain

$$\frac{1}{2}\text{Re}\left\{i\chi \left[\mathbf{H}\left(\nabla \otimes {\mathbf{E}}^{\ast }\right)-\mathbf{E}\left(\nabla \otimes {\mathbf{H}}^{\ast }\right)\right]\right\}=-\frac{\omega }{g}\text{Re}\left\{\chi \right\}\nabla h-\frac{1}{2}\mathrm{Im}\left\{\chi \right\}\nabla \times \text{Re}\left\{\mathbf{E}\times {\mathbf{H}}^{\ast }\right\}+\frac{1}{2}\mathrm{Im}\left\{\chi \right\}\text{Re}\left\{ik{n}_2\left[{\mathit{ϵ}}^{-1}\mathbf{H}\times \left({\mathbf{H}}^{\ast }\right)+{\mu }^{-1}\mathbf{E}\times \left({\mathbf{E}}^{\ast }\right)\right]\right\}+\frac{1}{2}\text{Re}\left\{\chi \right\}\text{Im}\left\{ik{n}_2\left[{\mathit{ϵ}}^{-1}\mathbf{H}\times \left({\mathbf{H}}^{\ast }\right)+{\mu }^{-1}\mathbf{E}\times \left({\mathbf{E}}^{\ast }\right)\right]\right\}.$$ [S18]

Also, using that $\frac{2c}{g}\mathbf{p}=\mathrm{Re}\left\{\mathbf{E}\times {\mathbf{H}}^{\text{*}}\right\}$ and $\mathrm{Re}\left\{\left[{\mathit{ϵ}}^{-1}\mathbf{H}\times \left({\mathbf{H}}^{\ast }\right)+{\mu }^{-1}\mathbf{E}\times \left({\mathbf{E}}^{\ast }\right)\right]\right\}=0$ we have

$$\frac{1}{2}\text{Re}\left\{i\chi \left[\mathbf{H}\left(\nabla \otimes {\mathbf{E}}^{\ast }\right)-\mathbf{E}\left(\nabla \otimes {\mathbf{H}}^{\ast }\right)\right]\right\}=-\frac{\omega }{g}\text{Re}\left\{\chi \right\}\nabla h-\frac{c}{g}\text{Im}\left\{\chi \right\}\nabla \times \mathbf{p}-\frac{1}{2}\mathrm{Im}\left\{\chi \right\}\mathrm{Im}\left\{k{n}_2\left[{\mathit{ϵ}}^{-1}\mathbf{H}\times {\mathbf{H}}^{\ast }+{\mu }^{-1}\mathbf{E}\times {\mathbf{E}}^{\ast }\right]\right\}.$$ [S19]

Finally, using that $n_2\mathrm{Im}\left\{{\mathit{ϵ}}^{-1}\mathbf{H}\times \left({\mathbf{H}}^{\ast }\right)+{\mu }^{-1}\mathbf{E}\times \left({\mathbf{E}}^{\ast }\right)\right\}=-\frac{4n_2\omega }{g}\mathbf{s}=-\frac{4c}{g}k\mathbf{s}$ we obtain

$$\frac{1}{2}\text{Re}\left\{i\chi \left[\mathbf{H}\left(\nabla \otimes {\mathbf{E}}^{\ast }\right)-\mathbf{E}\left(\nabla \otimes {\mathbf{H}}^{\ast }\right)\right]\right\}=-\frac{\omega }{g}\text{Re}\left\{\chi \right\}\nabla h-\frac{c}{g}\mathrm{Im}\left\{\chi \right\}\left(\nabla \times \mathbf{p}-2k^2\mathbf{s}\right).$$ [S20]

This is the chiral part of the force. So, combining the four terms of ${\mathbf{F}}_{\mathbf{0}}$ we finally have

$${\mathbf{F}}_{\mathbf{0}}=\frac{1}{g}\left({\mathit{ϵ}}^{-1}\mathrm{Re}\left\{{\alpha }_{\text{e}}\right\}\nabla u_{\text{e}}+{\mu }^{-1}\mathrm{Re}\left\{{\alpha }_{\text{m}}\right\}\nabla u_{\text{m}}\right)+\frac{2\omega }{g}\left(\mu \mathrm{Im}\left\{{\alpha }_{\text{e}}\right\}{\mathbf{p}}_{\mathbf{e}}^{\mathbf{o}}+\mathit{ϵ}\mathrm{Im}\left\{{\alpha }_{\text{m}}\right\}{\mathbf{p}}_{\mathbf{m}}^{\mathbf{o}}\right)-\frac{\omega }{g}\mathrm{Re}\left\{\chi \right\}\nabla h-\frac{c}{g}\mathrm{Im}\left\{\chi \right\}\left[\nabla \times \mathbf{p}-2k^2\mathbf{s}\right],$$ [S21]

as it appears in the main text in Eq. 2.

Table S1.

Definition of the field quantities relevant for the emergence of the optical forces on small chiral particles

Definition of the quantity	Description
$\mathbf{p}=\left(g/2c\right)\mathrm{Re}\left\{\mathbf{E}\times {\mathbf{H}}^{\ast }\right\}$	Poynting momentum density
${\mathbf{p}}^{″}=\left(g/2c\right)\mathrm{Im}\left\{\mathbf{E}\times {\mathbf{H}}^{\ast }\right\}$	Value of the imaginary adjoint to the Poynting momentum density
${\mathbf{p}}^{\mathbf{o}}=-\frac{g}{4\omega }\mathrm{Im}\left\{{\mu }^{-1}\mathbf{E}\left(\nabla \otimes {\mathbf{E}}^{\ast }\right)+{\mathit{ϵ}}^{-1}\mathbf{H}\left(\nabla \otimes {\mathbf{H}}^{\ast }\right)\right\}$	Orbital (or canonical) Poynting momentum density
${\mathbf{p}}_{\mathbf{e}}^{\mathbf{o}}=-\frac{g}{4\omega }\text{Im}\left\{{\mu }^{-1}\mathbf{E}\left(\nabla \otimes {\mathbf{E}}^{\ast }\right)\right\}$	Electric contribution to the orbital Poynting momentum density
${\mathbf{p}}_{\mathbf{m}}^{\mathbf{o}}=-\frac{g}{4\omega }\text{Im}\left\{{\mathit{ϵ}}^{-1}\mathbf{H}\left(\nabla \otimes {\mathbf{H}}^{\ast }\right)\right\}$	Magnetic contribution to the orbital Poynting momentum density
${\mathbf{p}}^{\mathbf{s}}=-\frac{g}{8\omega }\nabla \times \left[{\left(i\mu \right)}^{-1}\mathbf{E}\times {\mathbf{E}}^{\ast }+{\left(i\mathit{ϵ}\right)}^{-1}\mathbf{H}\times {\mathbf{H}}^{\ast }\right]$	Spin part of the Poynting momentum density (Belinfante spin momentum)
${\mathbf{p}}_{\mathbf{e}}^{\mathbf{s}}=-\frac{g}{8\omega }\nabla \times \left[{\left(i\mu \right)}^{-1}\mathbf{E}\times {\mathbf{E}}^{\ast }\right]$	Electric contribution to the spin momentum density
${\mathbf{p}}_{\mathbf{m}}^{\mathbf{s}}=-\frac{g}{8\omega }\nabla \times \left[{\left(i\mathit{ϵ}\right)}^{-1}\mathbf{H}\times {\mathbf{H}}^{\ast }\right]$	Magnetic contribution to the spin momentum density
$\mathbf{s}=-\frac{g}{4\omega }\left({\left(\mu i\right)}^{-1}\mathbf{E}\times {\mathbf{E}}^{\ast }+{\left(\mathit{ϵ}i\right)}^{-1}\mathbf{H}\times {\mathbf{H}}^{\ast }\right)$	SAM density
${\mathbf{s}}_{\mathbf{e}}=-\frac{g}{4\omega }\left({\left(\mu i\right)}^{-1}\mathbf{E}\times {\mathbf{E}}^{\ast }\right)$	Electric contribution to the SAM density
${\mathbf{s}}_{\mathbf{m}}=-\frac{g}{4\omega }\left({\left(\mathit{ϵ}i\right)}^{-1}\mathbf{H}\times {\mathbf{H}}^{\ast }\right)$	Magnetic contribution to the SAM
$h=\left(g/2\omega \right)\mathrm{Im}\left\{\mathbf{E}\cdot {\mathbf{H}}^{\ast }\right\}$	Helicity
$\nabla \times \mathbf{p}=\frac{g}{2c}\nabla \times \text{Re}\left\{\mathbf{E}\times {\mathbf{H}}^{\ast }\right\}$	Vorticity of the photon flow
$u_{\text{e}}=\frac{g}{4}\mathit{ϵ}{\left|\mathbf{E}\right|}^2$	Electric contribution to the energy density
$u_{\text{m}}=\frac{g}{4}\mu {\left|\mathbf{H}\right|}^2$	Magnetic contribution to the energy density
$I=n^{-1}\left|\mathbf{E}\times {\mathbf{H}}^{\text{*}}\right|$	Intensity

A derivation and discussion of many quantities can be found in Bliokh et al. (17).

Table S2.

Field quantities of a propagating wave and an evanescent wave

Symbol	For a propagating wave $\mathbf{E}=\sqrt{\mu }{\mathbf{E}}_{\mathbf{0}}\exp \left(ikz\right)I={\left|{\mathbf{E}}_{\mathbf{0}}\right|}^2$	For an evanescent field $\mathbf{E}=\sqrt{\mu }{\mathbf{E}}_{\mathbf{0}}\exp \left(-\kappa x\right)\exp \left(i{k}_{\text{z}}z\right)I_{\text{e}}=\frac{{\left|{\mathbf{E}}_{\mathbf{0}}\right|}^2}{1+\tau {\left(\kappa /k_{\text{z}}\right)}^2}\exp \left(-2\kappa x\right)$	Quantity
$\mathbf{p}$	$\frac{g}{2\omega }I{k}_{\text{z}}\widehat{\mathbf{z}}$	$\frac{g}{2\omega }{I}_{\text{e}}\left(\sigma \frac{\kappa k}{k_{\text{z}}}\widehat{\mathbf{y}}+\frac{k^2}{k_{\text{z}}}\widehat{\mathbf{z}}\right)$	Poynting momentum density
${\mathbf{p}}^{″}$	0	$\frac{g}{2\omega }{I}_{\text{e}}\left(\tau \frac{\kappa k^2}{k_z^2}\widehat{\mathbf{x}}+\xi \frac{\kappa k}{k_z}\widehat{\mathbf{y}}\right)$	Value of the imaginary adjoint to the Poynting momentum density
${\mathbf{p}}^{\mathbf{o}}$	$\frac{g}{2\omega }I{k}_z\widehat{\mathbf{z}}$	$\frac{g}{2\omega }{I}_{\text{e}}{k}_z\widehat{\mathbf{z}}$	Orbital (or canonical) Poynting momentum density
${\mathbf{p}}_{\mathbf{e}}^{\mathbf{o}}$	$\frac{g}{4\omega }I{k}_z\widehat{\mathbf{z}}$	$\frac{g}{4\omega }{I}_{\text{e}}\left(1+\frac{{\kappa }^2}{k_z^2}\right)k_z\widehat{\mathbf{z}}$	Electric contribution to the orbital Poynting momentum density
${\mathbf{p}}_{\mathbf{m}}^{\mathbf{o}}$	$\frac{g}{4\omega }I{k}_z\widehat{\mathbf{z}}$	$\frac{g}{4\omega }{I}_{\text{e}}\left(1-\frac{{\kappa }^2}{k_z^2}\right)k_z\widehat{\mathbf{z}}$	Magnetic contribution to the orbital Poynting momentum density
${\mathbf{p}}^{\mathbf{s}}$	0	$\frac{g}{2\omega }{I}_{\text{e}}\left(-\frac{{\kappa }^2}{k_z^2}\widehat{\mathbf{z}}+\sigma \frac{\kappa k}{k_z}\widehat{\mathbf{y}}\right)$	Spin part of the Poynting momentum density [Belinfante’s momentum (17, 19)]
${\mathbf{p}}_{\mathbf{e}}^{\mathbf{s}}$	0	$\frac{g}{4\omega }{I}_{\text{e}}\left(-\left(1+\tau \right)\frac{{\kappa }^2}{k_z^2}\widehat{\mathbf{z}}+\sigma \frac{\kappa k}{k_z}\widehat{\mathbf{y}}\right)$	Electric contribution to the spin momentum density
${\mathbf{p}}_{\mathbf{m}}^{\mathbf{s}}$	0	$\frac{g}{4\omega }{I}_{\text{e}}\left(-\left(1-\tau \right)\frac{{\kappa }^2}{k_z^2}\widehat{\mathbf{z}}+\sigma \frac{\kappa k}{k_z}\widehat{\mathbf{y}}\right)$	Magnetic contribution to the spin momentum density
$\mathbf{s}$	$\frac{g}{2\omega }I\sigma \widehat{\mathbf{z}}$	$\frac{g}{2\omega }{I}_{\text{e}}\left(\sigma \frac{k}{k_z}\widehat{\mathbf{z}}+\frac{\kappa }{k_z}\widehat{\mathbf{y}}\right)$	SAM density
${\mathbf{s}}_{\mathbf{e}}$	$\frac{g}{4\omega }I\sigma \widehat{\mathbf{z}}$	$\frac{g}{4\omega }{I}_{\text{e}}\left(\sigma \frac{k}{k_z}\widehat{\mathbf{z}}+\left(1+\tau \right)\frac{\kappa }{k_z}\widehat{\mathbf{y}}+\xi \frac{\kappa k}{k_z^2}\widehat{\mathbf{x}}\right)$	Electric contribution to the SAM density
${\mathbf{s}}_{\mathbf{m}}$	$\frac{g}{4\omega }I\sigma \widehat{\mathbf{z}}$	$\frac{g}{4\omega }{I}_{\text{e}}\left(\sigma \frac{k}{k_z}\widehat{\mathbf{z}}+\left(1-\tau \right)\frac{\kappa }{k_z}\widehat{\mathbf{y}}-\xi \frac{\kappa k}{k_z^2}\widehat{\mathbf{x}}\right)$	Magnetic contribution to the SAM
h	$\frac{g}{2\omega }In\sigma$	$\frac{g}{2\omega }{I}_{\text{e}}{n}_2\sigma$	Helicity
$\nabla \times \mathbf{p}$	0	$\frac{g}{2\omega }{I}_{\text{e}}\left(2\frac{\kappa k^2}{k_z}\widehat{\mathbf{y}}-2\sigma \frac{{\kappa }^{2}k}{k_{\text{z}}}\widehat{\mathbf{z}}\right)$	Vorticity of the photon flow
$u_{\text{e}}$	$\frac{g{n}^2}{4}I$	$\frac{g{n}_2^2}{4}{I}_{\text{e}}\left(1+\tau \frac{{\kappa }^2}{k_{\text{z}}^2}\right)$	Electric contribution to energy density
$u_{\text{m}}$	$\frac{g{n}^2}{4}I$	$\frac{g{n}_2^2}{4}{I}_{\text{e}}\left(1-\tau \frac{{\kappa }^2}{k_{\text{z}}^2}\right)$	Magnetic contribution to energy density

Summary of the physical quantities involved in the force for a propagating plane wave and for an evanescent field. The magnetic and electric contributions to the orbital and spin angular momenta are listed explicitly.

Lateral Forces on a Molecule, a Nanosphere, and a Gold Nanohelix

In this section we briefly discuss the lateral forces that arise on three types of small chiral particles that commonly arise in the literature and leave the details of the associated calculations to the next section.

Helicene Molecules.

The optical manipulation of objects smaller than a few hundred nanometers in liquid suspension is in general very challenging due to thermal agitation. However, the optical sorting of individual atoms or molecules by chirality may nevertheless be possible in low-pressure environments or by tailoring the fields in modern metamaterials. A molecule of hexahelicene has a real chiral polarizability of $\chi =-6.2\cdot {10}^{-2}\hspace{0.17em}{\mathrm{\AA }}^3$ at a wavelength of 589.3 nm, which lies well outside of the molecule’s absorption band (39). At the same wavelength, the static electric polarizability of hexahelicene is ${\alpha }_{\text{e}}=10.4\hspace{0.17em}{\mathrm{\AA }}^3$ with the magnetic polarizability $\left|{\alpha }_{\text{m}}\right|<{10}^{-5}\left|{\alpha }_{\text{e}}\right|$. We consider a beam with a given intensity that is totally internally reflected at the interface of heavy flint glass ($n_1=1.74$) and air ($n_2=1$) at an angle of $\theta =36.4°$, which is close to the critical angle and gives the strongest force given the angle-dependent intensity and wave-vector of the evanescent field. Situated 60 nm above the interface, the hexahelicene molecule experiences a lateral force of $F_{\text{y}}\simeq 2.04\cdot {10}^{-19}\text{pN}/\left(\text{mW}/\mathrm{\mu }{\text{m}}^2\right)$ if $\sigma =1$ [circularly polarized in the (x,y) plane] and $F_{\text{y}}\simeq 4.04\cdot {10}^{-19}\text{pN}/\left(\text{mW}/\mathrm{\mu }{\text{m}}^2\right)$ if $\tau =1$ (p-polarized). Stronger optical forces are possible within the absorption band, where the chiral polarizability is complex and highly dependent on the wavelength. Coronene is a close relative of hexahelicene that is achiral but has the same size and electric polarizability as helicene. The lateral force on this achiral molecule due to the Belifante momentum density ${\mathbf{p}}^{\mathbf{s}}$ as predicted by Bliokh et al. (17) is $F_{\text{y}}\simeq {\mathrm{1.7.10}}^{-21}\text{pN}/\left(\text{mW}/\mathrm{\mu }{\text{m}}^2\right)$ for $\sigma =1$ and vanishes for $\sigma =0$ [linearly polarized in (x,y) plane]. The strength of the nonlateral forces are $F_0\cdot \widehat{\mathbf{x}}=-3.13\cdot {10}^{-9}\text{pN}/\left(\text{mW}/\mathrm{\mu }{\text{m}}^2\right)$, $F_0\cdot \widehat{\mathbf{z}}=1.94\cdot {10}^{-16}\text{pN}/\left(\text{mW}/\mathrm{\mu }{\text{m}}^2\right)$, and $F_{\text{int}}\cdot \widehat{\mathbf{z}}=-1.02\cdot {10}^{-20}\text{pN}/\left(\text{mW}/\mathrm{\mu }{\text{m}}^2\right)$.

Spherical Nanoparticles.

The polarizability of a chiral particle may be calculated using bi-isotropic constitutive relations for the material of the particle, where material chirality is parametrized with a chirality parameter $K\in \left[-\mathrm{1,1}\right]$ (16). The derivation and the somewhat bulky expressions for the polarizabilities of a small chiral sphere are given in the following section. Examples of spherical particles with highly chiral electromagnetic response are cholesteric liquid crystal droplets (11). Assuming the refractive index of 5CB (4-cyano-4′-pentylbiphenyl) of $n_{\text{s}}=1.597$ and $K=1$ for a 30-nm sphere in water with index $n_2=1.33$, letting an incident beam with 589-nm wavelength totally internally reflect at $\theta =52°$ in heavy flint glass ($n_1=1.74$) causes a lateral force of $F_{\text{y}}\simeq 2.6\cdot {10}^{-5}\text{pN}/\left(\text{mW}/\mathrm{\mu }{\text{m}}^2\right)$ if the sphere is floating 60 nm above the flint glass surface and $\tau =1$. The strength of the nonlateral forces are $F_0\cdot \widehat{\mathbf{x}}=-4.73\ast {10}^{-3}\text{pN}/\left(\text{mW}/\mathrm{\mu }{\text{m}}^2\right)$, $F_0\cdot \widehat{\mathbf{z}}=2.30\cdot {10}^{-4}\text{pN}/\left(\text{mW}/\mathrm{\mu }{\text{m}}^2\right)$, and $F_{\text{int}}\cdot \widehat{\mathbf{z}}=-1.87\cdot {10}^{-4}\text{pN}/\left(\text{mW}/\mathrm{\mu }{\text{m}}^2\right)$.

The lateral force on a chiral sphere above a reflective surface in a propagating field as predicted by Wang and Chan (16) corresponds to $F_{\text{y}}={10}^{-6}\text{pN}/\left(\text{mW}/\mathrm{\mu }{\text{m}}^2\right)$ for a sphere with 30-nm radius in vacuum with a dielectric constant of $\mathit{ϵ}=2$ and chirality parameter $K=1$ when it is located 60 nm above a metal surface and illuminated with a plane wave that has $\tau =1$ and a wavelength of 600 nm. In comparison, the same sphere would experience chirality-sorting lateral force of $F_{\text{y}}=4.6\cdot {10}^{-5}\text{pN}/\left(\text{mW}/\mathrm{\mu }{\text{m}}^2\right)$ at the same height above the surface in an evanescent field that is created by total internal reflection at $\theta =36.4°$ in heavy flint glass ($n_1=1.74$).

Nanohelices.

Increasing interest in chiral optical materials has recently driven the development of artificial nanostructures with extreme chiral responses (40–43), including artificially chiral effective media (27). Metallic nanohelices in particular enable the analytical estimation of their very strong chiral polarizability and have recently been fabricated at size scales small enough to reach plasmonic resonances in the visible range (41). A perfectly conducting 50-nm helix with 25-nm diameter and one loop has a chiral polarizability of $\chi =2.72\cdot {10}^7\hspace{0.17em}{\mathrm{\AA }}^3$ and a static electric polarizability of ${\alpha }_{\text{e}}=2.56\cdot {10}^8\hspace{0.17em}{\mathrm{\AA }}^3$ (26). Situated 30 nm above the surface in an evanescent field with wavelength of 589 nm and $\tau =1$, a lateral force of $F_{\text{y}}=-4.25\cdot {10}^{-3}\text{pN}/\left(\text{mW}/\mathrm{\mu }{\text{m}}^2\right)$ results if the beam is totally internally reflected at a flint glass/air interface at a $\theta =36.4°$ angle. The strength of the nonlateral forces are $F_0\cdot \widehat{\mathbf{x}}=-\mathrm{1,16}\cdot {10}^{-1}\text{pN}/\left(\text{mW}/\mathrm{\mu }{\text{m}}^2\right)$, $F_0\cdot \widehat{\mathbf{z}}=0\text{pN}/\left(\text{mW}/\mathrm{\mu }{\text{m}}^2\right)$, and $F_{\text{int}}\cdot \widehat{\mathbf{z}}=-1.82\ast {10}^{-3}\text{pN}/\left(\text{mW}/\mathrm{\mu }{\text{m}}^2\right)$.

Optical Forces on a Sphere

As stated in the main text, if the sphere and the surrounding medium are assumed nonmagnetic the static polarizabilities are given at the first nonzero order by

$${\alpha }_{\text{e}}^0=\mathit{ϵ}{a}^3\frac{\left({\mathit{ϵ}}_{\text{p}}-\mathit{ϵ}\right)}{{\mathit{ϵ}}_{\text{p}}+2\mathit{ϵ}}$$ [S22]

$${\alpha }_m^0=\frac{{\mathit{ϵ}}_{\text{p}}-\mathit{ϵ}}{30\mathit{ϵ}}{k}^2{a}^5.$$ [S23]

Here a refers to the radius of the sphere and ${\mathit{ϵ}}_{\text{p}}$ and ε are the relative permittivity of the sphere and the surrounding medium, respectively. Using Draine’s correction we obtain the dynamic polarizabilities as ${\alpha }_{\text{e}}={\left[1-\left(i2k^3/3\mathit{ϵ}\right){\alpha }_{\text{e}}^{\left(0\right)}\right]}^{-1}{\alpha }_{\text{e}}^{\left(0\right)}$ and ${\alpha }_{\text{m}}={\left[1-\left(i2k^3/3\right){\alpha }_{\text{m}}^{\left(0\right)}\right]}^{-1}{\alpha }_{\text{m}}^{\left(0\right)}$. The forces on an achiral sphere are then

$${\mathbf{F}}_{\mathbf{0}}=-\frac{\kappa I_{\text{e}}}{2}{a}^3\mathit{ϵ}\mathrm{Re}\left\{\frac{{\mathit{ϵ}}_{\text{p}}-\mathit{ϵ}}{{\mathit{ϵ}}_{\text{p}}+2\mathit{ϵ}}\right\}\left(1+\tau \frac{{\kappa }^2}{k_{\text{z}}^2}\right)\widehat{\mathbf{x}}$$ [S24]

$$\frac{I_{\text{e}}}{2}{k}_{\text{z}}{a}^3\left(\mathit{ϵ}\mathrm{Im}\left\{\frac{{\mathit{ϵ}}_{\text{p}}-\mathit{ϵ}}{{\mathit{ϵ}}_{\text{p}}+2\mathit{ϵ}}\right\}+\frac{2\mathit{ϵ}}{3}{\left(ka\right)}^3\mathrm{Re}\left\{{\left(\frac{{\mathit{ϵ}}_{\text{p}}-\mathit{ϵ}}{{\mathit{ϵ}}_{\text{p}}+2\mathit{ϵ}}\right)}^2\right\}\right)\left(1+\tau \frac{{\kappa }^2}{k_{\text{z}}^2}\right)\widehat{\mathbf{z}}$$ [S25]

$${\mathbf{F}}_{\mathbf{i}\mathbf{n}\mathbf{t}}=-I_{\text{e}}\frac{k^4}{3}\frac{\kappa }{k_z}{\left|\frac{{\mathit{ϵ}}_{\text{p}}-\mathit{ϵ}}{2\mathit{ϵ}+{\mathit{ϵ}}_{\text{p}}}\right|}^2\left[\frac{1}{30}\mathrm{Re}\left\{{\mathit{ϵ}}_{\text{p}}+2\right\}{k}^2{a}^8\sigma +\left(\frac{1}{30}\mathrm{Im}\left\{{\mathit{ϵ}}_{\text{p}}\right\}{k}^2{a}^8-\frac{2}{90}{k}^5{a}^{11}\mathrm{Re}\left\{\frac{\left({\mathit{ϵ}}_{\text{p}}-\mathit{ϵ}\right){\left({\mathit{ϵ}}_{\text{p}}+2\mathit{ϵ}\right)}^{\text{*}}}{{\mathit{ϵ}}_{\text{p}}+2\mathit{ϵ}}\right\}\right)\xi \right]\widehat{\mathbf{y}}$$ [S26]

$$-I_{\text{e}}\frac{k^4}{3}\frac{k}{k_{\text{z}}}\left[\frac{1}{30}{\left|\frac{{\mathit{ϵ}}_{\text{p}}-\mathit{ϵ}}{2\mathit{ϵ}+{\mathit{ϵ}}_{\text{p}}}\right|}^2\mathrm{Re}\left\{{\mathit{ϵ}}_{\text{p}}+2\right\}{k}^2{a}^8\right]\widehat{\mathbf{z}}$$ [S27]

$$-I_{\text{e}}\frac{k^4}{3}\frac{\kappa k}{k_{\text{z}}^2}{\left|\frac{{\mathit{ϵ}}_{\text{p}}-\mathit{ϵ}}{2\mathit{ϵ}+{\mathit{ϵ}}_{\text{p}}}\right|}^2\left[\left(\frac{1}{30}\mathrm{Im}\left\{{\mathit{ϵ}}_{\text{p}}\right\}{k}^2{a}^8-\frac{2}{90}{k}^5{a}^{11}\mathrm{Re}\left\{\frac{\left({\mathit{ϵ}}_{\text{p}}-\mathit{ϵ}\right){\left({\mathit{ϵ}}_{\text{p}}+2\mathit{ϵ}\right)}^{\text{*}}}{{\mathit{ϵ}}_{\text{p}}+2\mathit{ϵ}}\right\}\right)\tau \right]\widehat{\mathbf{x}}.$$ [S28]

For a chiral sphere the polarizabilities depend on the chirality of the sphere and of the surrounding medium. Assuming a nonchiral, nonmagnetic surrounding medium and ${\mu }_{\text{p}}=1$ Lakthakia et al. (26) showed that we can derive:

$${\alpha }_e^0=a^3\mathit{ϵ}\frac{\left[-2K^2\frac{\mathit{ϵ}}{{\mathit{ϵ}}_{\text{p}}}+3\left(\mathit{ϵ}p-\mathit{ϵ}\right)\right]}{4K^2\frac{\mathit{ϵ}}{{\mathit{ϵ}}_p}-3\left(2\mathit{ϵ}+{\mathit{ϵ}}_p\right)}$$ [S29]

$${\alpha }_m^0=a^3\frac{\left[-2K^2\frac{\mathit{ϵ}}{{\mathit{ϵ}}_p}\right]}{4K^2\frac{\mathit{ϵ}}{{\mathit{ϵ}}_p}-3\left(2\mathit{ϵ}+{\mathit{ϵ}}_p\right)}$$ [S30]

$$\chi =-3a^3\frac{K\mathit{ϵ}}{4K^2\frac{\mathit{ϵ}}{{\mathit{ϵ}}_p}-3\left(2\mathit{ϵ}+{\mathit{ϵ}}_p\right)},$$ [S31]

where a is the radius of the sphere and K the chiral parameter such that the usual dispersion relation for two opposite circularly polarized plane waves in the medium of the sphere is (16) $k_{\pm }=\left(\sqrt{{\mathit{ϵ}}_{\text{p}}}\pm K\right)\frac{\omega }{c}.$

Chiral Polarizability of a Helix

We know that we have the electric and magnetic dipole moments $\mathbf{d}$ and $\mathbf{m}$ induced by fields incident on a chiral particle with isotropic polarizabilities and no permanent dipole moment given by (16)

$$\mathbf{d}={\alpha }_{\text{e}}\mathbf{E}+\mathbf{i}\chi \mathbf{H}\mathbf{m}={\alpha }_{\text{m}}\mathbf{H}-\mathbf{i}\chi \mathbf{E},$$ [S32]

where ${\alpha }_{\text{e}}$ and ${\alpha }_{\text{m}}$ are the dynamic electric and magnetic polarizabilities. The chiral polarizability of the particle χ captures the chiral nature of the dipole, such that setting $\chi =0$ recovers the behavior for an achiral dipole. For a perfectly conducting helix in the Rayleigh regime and a perfect metal we know from ref. 33 that the polarizabilities are in Gaussian units by

$$\chi ={\alpha }_{\text{e}}\left(\frac{\pi a^{2}k}{2l}\right)$$ [S33]

$${\alpha }_{\text{e}}=\frac{{\left(l\right)}^2}{4\pi k^{2}a\left(L/{\mu }_{0}a\right)},$$ [S34]

where a is the radius of the helix, l its length taken, and L its inductance in SI units and here $L/{\mu }_{0}a$ is taken in SI units. For a helix with one loop we have $L\simeq \frac{{\mu }_0{a}^2\pi }{l}\left(1-\frac{16a}{3\pi l}+\frac{2a^2}{l^2}-\frac{4a^4}{l^4}\right)\left(\text{SI}\right)$ and we obtain

$$\chi \simeq \frac{l^2}{4\pi k}{\left(1-\frac{16a}{3\pi l}+\frac{2a^2}{l^2}-\frac{4a^4}{l^4}\right)}^{-1}$$ [S35]

$${\alpha }_{\text{e}}\simeq \frac{l^3}{4{\pi }^2{k}^2{a}^2}{\left(1-\frac{16a}{3\pi l}+\frac{2a^2}{l^2}-\frac{4a^4}{l^4}\right)}^{-1}.$$ [S36]

Using l = 50 nm and a = 12.5 nm so that the diameter is 2a = l/2 = 25 nm we obtain $\frac{1}{1-\frac{16a}{3\pi l}+\frac{2a^2}{l^2}-\frac{4a^4}{l^4}}\simeq \mathrm{1.46.}$

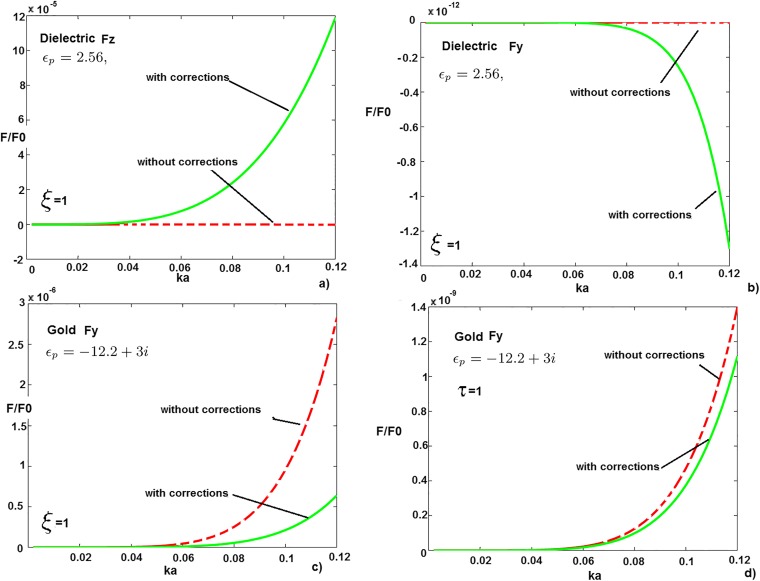
Fig. S1.

Impact of Draine’s correction on the optical force. The optical force on an achiral sphere with radius a and dielectric constant ${\mathit{ϵ}}_{\text{p}}$ in an evanescent field with wavenumber $k=n_2\frac{\omega }{c}$ as a function of $ka$ using the static polarizability (red, dashed line) and the dynamic polarizability after Draine’s correction (green, continuous line). A and B correspond to the force on a dielectric sphere with ${\mathit{ϵ}}_{\text{p}}=2.56$ and an incident polarization corresponding to $\xi =1$ (linear diagonal polarization), respectively, along the z direction (parallel to ${\mathbf{p}}^{\mathrm{o}}$, A) and the y direction (lateral optical force, B). C and D correspond to the lateral optical force using a gold sphere with ${\mathit{ϵ}}_{\text{p}}=-12.2+3i$ with an incident polarization of the beam corresponding, respectively, to $\xi =1$ (linear diagonal polarization, C) and $\tau =1$ (linear horizontal polarization, D). The force is normalized by $F0=\left(a^2/4\pi \right)I_{\text{inc}}$, where $I_{\text{inc}}={\left|{\mathbf{E}}_{\mathbf{i}\mathbf{n}\mathbf{c}}\right|}^2$ is the square modulus of the incident electric field. The sphere is suspended in water (index $n_2=1.33$) and the evanescent field is generated by total internal reflection in a prism of index $n_1=1.74$.Taking an incident intensity of $1.0\text{mW}/\mathrm{\mu }{\text{m}}^2$ we have $F0/a^2=I_{\text{inc}}/4\pi \simeq 3.3\cdot {10}^{-4}\text{N}\cdot {\text{cm}}^{-2}$. Here the incident angle of total internal reflection is $\theta \simeq 51$ ° (so, above the critical angle, which is around $\theta =49.5$ °). Note that in B the force without correction is zero.