Skip to main content
PMC home page
ACS AuthorChoice logoLink to ACS AuthorChoice
. 2015 Sep 27;137(42):13545–13555. doi: 10.1021/jacs.5b07327

Dependence of Vibronic Coupling on Molecular Geometry and Environment: Bridging Hydrogen Atom Transfer and Electron–Proton Transfer

Aparna Karippara Harshan 1, Tao Yu 1, Alexander V Soudackov 1, Sharon Hammes-Schiffer 1,*
PMCID: PMC4629534  PMID: 26412613

Abstract

graphic file with name ja-2015-073274_0011.jpg

The rate constants for typical concerted proton-coupled electron transfer (PCET) reactions depend on the vibronic coupling between the diabatic reactant and product states. The form of the vibronic coupling is different for electronically adiabatic and nonadiabatic reactions, which are associated with hydrogen atom transfer (HAT) and electron–proton transfer (EPT) mechanisms, respectively. Most PCET rate constant expressions rely on the Condon approximation, which assumes that the vibronic coupling is independent of the nuclear coordinates of the solute and the solvent or protein. Herein we test the Condon approximation for PCET vibronic couplings. The dependence of the vibronic coupling on molecular geometry is investigated for an open and a stacked transition state geometry of the phenoxyl-phenol self-exchange reaction. The calculations indicate that the open geometry is electronically nonadiabatic, corresponding to an EPT mechanism that involves significant electronic charge redistribution, while the stacked geometry is predominantly electronically adiabatic, corresponding primarily to an HAT mechanism. Consequently, a single molecular system can exhibit both HAT and EPT character. The dependence of the vibronic coupling on the solvent or protein configuration is examined for the soybean lipoxygenase enzyme. The calculations indicate that this PCET reaction is electronically nonadiabatic with a vibronic coupling that does not depend significantly on the protein environment. Thus, the Condon approximation is shown to be valid for the solvent and protein nuclear coordinates but invalid for the solute nuclear coordinates in certain PCET systems. These results have significant implications for the calculation of rate constants, as well as mechanistic interpretations, of PCET reactions.

1. Introduction

Proton-coupled electron transfer (PCET) reactions encompass a broad spectrum of mechanisms.1−6 For example, such reactions may be sequential or concerted, depending on the existence of a stable intermediate. If a stable intermediate is observed, then the reaction is clearly sequential, but detection of the intermediate may depend on the experimental apparatus. Thus, the absence of an observable intermediate does not definitively imply a concerted reaction. In some cases, the reaction can be determined to be concerted if the products of single electron transfer (ET) and single proton transfer (PT) are much less thermodynamically favorable than the product of the concerted mechanism. This information can often be obtained from the pKa’s and reduction potentials. This paper will focus on PCET reactions that have been determined to be concerted through such an analysis.

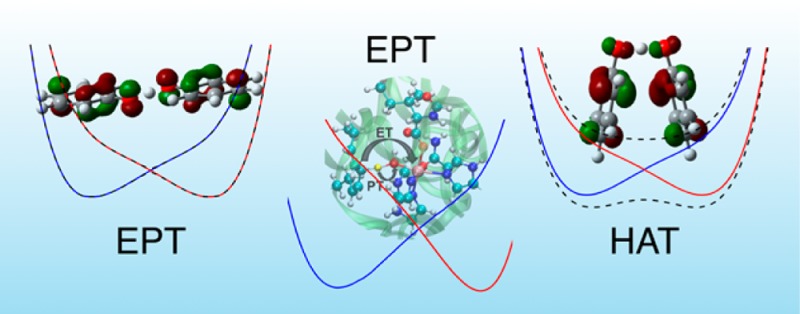
Concerted PCET reactions may be further broken down into hydrogen atom transfer (HAT) and electron–proton transfer (EPT).7 Traditionally, HAT reactions are characterized by the electron and proton transferring between the same donor and acceptor and hence do not involve a significant change in the electronic charge distribution. In contrast, EPT reactions are characterized by the electron and proton transferring between different donors and acceptors and thus result in a significant change in the electronic charge distribution. According to these traditional definitions, the donor and acceptor could be an atom, a molecular orbital (MO), or a chemical bond, although such definitions are not rigorous because the quantum mechanical electron and proton tend to be delocalized, and the MO or chemical bond analysis depends on the representation and level of theory. To provide a more quantitative and well-defined distinction, previously HAT and EPT reactions were shown to be associated with electronically adiabatic and nonadiabatic proton transfer, respectively.8,9 The distinction between HAT and EPT by the degree of electron–proton nonadiabaticity is consistent with the traditional characterizations mentioned above because the nonadiabatic coupling along the proton transfer coordinate reflects the change in electronic charge distribution as the proton transfers. Thus, a significant change in charge distribution is associated with the electronically nonadiabatic EPT reaction but not with the electronically adiabatic HAT reaction.

Several diagnostics have been devised for distinguishing between HAT and EPT reactions in terms of electron–proton nonadiabaticity.8−10 A semiclassical formalism developed by Georgievskii and Stuchebrukhov11 can be used to calculate an effective proton tunneling time τp and an electronic transition time τe as well as an adiabaticity parameter that is defined to be the ratio of these two quantities, p = τp/τe. The reaction is electronically adiabatic if p ≫ 1 because the electrons respond instantaneously to the proton motion, and the system remains on the electronic ground state. The reaction is electronically nonadiabatic if p ≪ 1 because the electrons are unable to respond instantaneously to the proton motion, and excited electronic states are involved. Another diagnostic of electron–proton nonadiabaticity is the magnitude of the first-derivative nonadiabatic coupling between the ground and first excited electronic states along the proton coordinate. A related diagnostic is the magnitude of the change in the electronic charge distribution along the proton coordinate, as reflected by the dipole moment or partial atomic charges.

These diagnostics have been applied to several molecular systems and, more recently, to an enzymatic system. The prototypical examples are the benzyl-toluene and phenoxyl-phenol self-exchange reactions. The former has been shown to be electronically adiabatic (HAT), while the latter has been shown to be electronically nonadiabatic (EPT) according to the diagnostics for electron–proton nonadiabaticity.8,9 These systems, as well as related systems, have also been studied with other theoretical methods.12−15 More recently, the PCET reaction catalyzed by the soybean lipoxygenase (SLO) enzyme was shown to be electronically nonadiabatic (EPT) by applying these diagnostics to a gas-phase model system.16 All of these systems were shown to be vibronically nonadiabatic in that the overall vibronic coupling is small compared to the thermal energy kBT, thereby validating the use of a golden rule rate constant expression. This vibronic nonadiabaticity is related to the response of the solvent or protein environment to the electron–proton subsystem and is determined by different criteria that have been discussed elsewhere.3,17 Theoretical calculations based on the nonadiabatic treatment of the SLO enzyme have reproduced the experimentally observed hydrogen/deuterium kinetic isotope effect of ∼80 in the wild-type enzyme and up to ∼500 in mutant enzymes.18−23

The nonadiabatic PCET rate constant expressions rely on the Condon approximation for the vibronic coupling.3,24,25 In nonadiabatic electron transfer theory, the Condon approximation is based on the assumption that the electronic coupling is independent of the nuclear configuration.26−29 For vibronically nonadiabatic PCET reactions, the Condon approximation is based on the assumption that the vibronic coupling is independent of the nuclear configuration, including both the molecular geometry of the PCET solute complex and the solvent or protein environment. An exception is that the dependence of the vibronic coupling on the proton donor–acceptor distance is included explicitly in the nonadiabatic PCET rate constant expressions.25 For situations in which the Condon approximation breaks down, a given PCET system could span the electronically adiabatic and nonadiabatic regimes. For both electron transfer and PCET systems, these two regimes may be spanned as the donor–acceptor distances are varied, but the dependence of the coupling and the degree of nonadiabaticity on other geometrical coordinates, as well as the environmental configuration, is less obvious.

In this paper, we examine the dependence of the magnitude of the vibronic coupling and the degree of electron–proton nonadiabaticity on the molecular geometry and on the solvent or protein configuration. The dependence on molecular geometry is investigated for the phenoxyl-phenol self-exchange system because two transition states corresponding to either an open or a stacked geometry have been identified for this type of system.13 In particular, for the related benzyl-toluene system, transition states have been optimized with either an open geometry12 or a stacked geometry,13 and the stacked geometry was found to be lower in energy by 4.0 kcal/mol at the level of theory used in ref (13). The present study focuses on the phenoxyl-phenol system, which also exhibits both types of transition state geometries. The open geometry of the phenoxyl-phenol system has already been shown to be electronically nonadiabatic,8,9 but herein we also study the stacked geometry. The dependence on the solvent and protein environment is investigated for the PCET reaction catalyzed by the SLO enzyme. The previous studies focused on a fully quantum mechanical gas-phase model of the substrate–cofactor complex.16 Herein we use mixed quantum mechanical/molecular mechanical (QM/MM) methods to include the protein and solvent environment. These calculations test the validity of the Condon approximation for PCET vibronic couplings in solution and proteins. The results have significant implications for applications to PCET in chemical and biological processes.

2. Theory and Computational Methods

2.1. General Theory

The semiclassical formalism for calculating the effective proton tunneling time and electronic transition time is described in detail elsewhere.8,11 In this section, we only provide the expressions that are used to calculate the quantities necessary to determine the adiabaticity parameter and the semiclassical vibronic coupling. The effective proton tunneling time is

2.1. 1

and the effective electronic transition time is

2.1. 2

Here Vel is the electronic coupling between the two diabatic electronic states, |ΔF| is the difference between the slopes of the diabatic proton potential energy curves at the crossing point, and vt = (2(Vc – E)/mp)1/2, where Vc is the energy at which the potential energy curves cross, mp is the proton mass, and E is the tunneling energy, which is defined as the energy of the degenerate proton vibrational levels in the reactant and product potential wells. As mentioned above, the adiabaticity parameter is defined as p = τp/τe.

The vibronic coupling can be calculated in several different ways, including a full basis set Hamiltonian matrix diagonalization or a semiclassical approach, which have been shown to provide numerically equivalent results for these types of systems.9 For systems that are known to be in the electronically adiabatic or nonadiabatic regime, expressions derived in these limits can be utilized. Specifically, the vibronic coupling in the electronically adiabatic regime, denoted V(ad), is half the tunneling splitting associated with the ground electronic state. The vibronic coupling in the electronically nonadiabatic regime, denoted V(nad), is given by the following expression:

2.1. 3

where S is the overlap integral between the proton vibrational wave functions calculated for the reactant and product diabatic potentials. In principle, this overlap can be calculated for any pair of reactant and product proton vibrational wave functions, but in this paper we calculate it for only the ground proton vibrational states.

The semiclassical coupling spans the electronically adiabatic and nonadiabatic regimes and is expressed as

2.1. 4

where

2.1. 5

Here Γ(x) is the gamma function, and p is the adiabaticity parameter defined above. The derivation of these equations is based on the general semiclassical tunneling model and is given in ref (11). In this paper, we calculated the vibronic coupling with all of these methods for the phenoxyl-phenol system to enable a comparison. For the SLO system, however, the vibronic coupling was calculated only with the electronically nonadiabatic expression given in eq 3.

The diabatic proton potential energy curves can be calculated in two different ways. For relatively small molecular systems, the adiabatic proton potential energy curves associated with the ground and first excited adiabatic electronic states can be calculated along the proton coordinate with the complete active space self-consistent field (CASSCF) method.30,31 Subsequently, a diabatization procedure that is exact for two states along a single coordinate (i.e., the nonadiabatic coupling between the two states is identically zero along this coordinate)9,32 can be used to generate the diabatic proton potential energy curves from these adiabatic electronic states as well as the nonadiabatic coupling between them.9 Alternatively, constrained density functional theory-configuration interaction (CDFT-CI)33−35 can be used to generate the diabatic proton potential energy curves and the corresponding electronic couplings. In CDFT-CI, the coupling between the two constrained states is approximated as the off-diagonal Hamiltonian matrix element between the two Slater determinants comprised of the Kohn–Sham orbitals for the constrained states.33−35 We applied both the CASSCF and CDFT-CI methods to the phenoxyl-phenol molecular system and showed that these two methods lead to qualitatively similar results. Due to computational limitations, we applied only the CDFT-CI method to the SLO enzymatic system and included the protein and solvent environment using a QM/MM approach.

The other two diagnostics for electron–proton nonadiabaticity are the nonadiabatic coupling and the change in electronic charge distribution along the proton coordinate. We calculated the nonadiabatic coupling between the lowest two adiabatic electronic states along the one-dimensional proton coordinate with the CASSCF method for the phenoxyl-phenol system. This scalar coupling is defined as

2.1. 6

where Ψlel(re;rp) and Ψ2(re;rp) are the ground and first excited adiabatic electronic states, respectively, along the proton coordinate rp. In addition, the dipole moment of the ground electronic state as the proton moves along the proton donor–acceptor axis was calculated using CASSCF for the phenoxyl-phenol system and using ground state DFT for the SLO system.

2.2. Computational Details for Phenoxyl-Phenol System

For the phenoxyl-phenol calculations, two different transition state structures, denoted the “open” and “stacked” geometries, were optimized with density functional theory (DFT) at the M06-2X/6-311+G** level of theory36−38 in the gas phase using Gaussian09.39 These structures are depicted in Figure 1. At this level of theory, the stacked transition state structure is 4.1 kcal/mol lower in energy than the open transition state structure. For each structure, the adiabatic proton potential energy curves associated with the ground and first excited adiabatic electronic states were obtained by calculating the state-averaged CASSCF energies in the gas phase as the transferring proton was moved along a grid spanning the proton donor–acceptor axis with all other atoms fixed. On the basis of careful analysis of the active spaces over the range of proton coordinates, CAS(3,6) calculations state-averaged over two states were performed for the open structure, and CAS(7,8) calculations state-averaged over four states were performed for the stacked structure to ensure that the active space was conserved along the proton transfer coordinate. Note that these structures are not transition states at the CASSCF level but are useful symmetric structures for the analysis described below.

Figure 1.

Figure 1

Open in a new tab

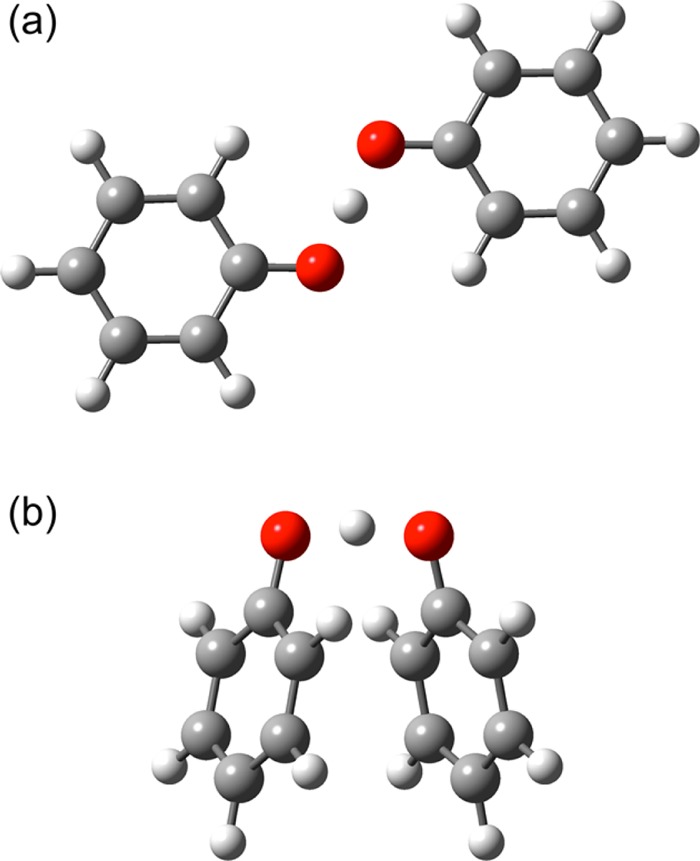
Open (a) and stacked (b) transition state structures for the self-exchange phenoxyl-phenol reaction calculated at the DFT/M06-2X/6-311+G** level of theory. The proton is transferring between the two red oxygen atoms.

Additional types of calculations were performed for comparison to these CASSCF results. The effects of dynamic correlation were investigated by performing second-order perturbation theory CASSCF (CASPT2) calculations and comparing the results with those obtained from the CASSCF calculations. The CASSCF energies and first-derivative nonadiabatic couplings reported in the main paper were performed with Molpro,40 but the comparison of CASSCF and CASPT2 results provided in the Supporting Information was performed with Molcas.41−43 In addition, CDFT-CI calculations with the ωB97X functional44 were performed using Q-Chem45 to obtain the diabatic proton potential energy curves for comparison to the CASSCF results. For the CDFT-CI calculations, the spin density was constrained to be zero on the phenol (left side) and unity on the phenoxyl (right side) fragment for the reactant diabatic state and the reverse for the product diabatic state. The 6-31G** basis set was used for the CASSCF and CDFT-CI calculations. Note that the M06-2X functional was used for the geometry optimizations because it includes dispersion effects, whereas the ωB97X functional was used for calculating the diabatic states and couplings with CDFT-CI because it includes long-range corrections, which are important for describing charge transfer states. A previous benchmarking study16 illustrated that CDFT-CI calculations with the ωB97X functional resulted in similar diabatic states and couplings as those obtained with the CASSCF method for the phenoxyl-phenol system.

The adiabatic electronic states obtained from the CASSCF calculations were diabatized using the method described in previous work.9 The proton vibrational wave functions for each diabatic proton potential energy curve were calculated using the Fourier Grid Hamiltonian method.46 The double adiabatic states defined as products of diabatic electronic states and associated proton vibrational states were used as a basis set to construct a Hamiltonian matrix. Diagonalization of this full basis set Hamiltonian matrix provides the vibronic eigenfunctions and eigenvalues. The vibronic coupling calculated from this full basis set Hamiltonian diagonalization, denoted V(full), is half the energy difference between the two lowest-energy vibronic states. This vibronic coupling was compared to the vibronic coupling calculated with the semiclassical approach, as given in eq 4, and to the vibronic couplings calculated in the adiabatic and nonadiabatic limits.

2.3. Computational Details for Soybean Lipoxygenase System

The SLO calculations included the protein environment based on snapshots from an equilibrated molecular dynamics (MD) trajectory of the protein solvated with explicit TIP3P47 water molecules. The crystal structure of SLO with PDB code 3PZW(48) was used as the initial protein structure, and the linoleic acid (LA) substrate was docked to the active site of this enzyme. A description of the initial preparation of the system and the equilibration procedure, as well as other computational details related to the classical MD simulations, is provided in the Supporting Information. Three snapshots were obtained from the 20 ns production MD trajectory for the subsequent QM/MM calculations. Because of the large size of this system, the CASSCF calculations performed on the phenoxyl-phenol system were not computationally tractable, and standard QM/MM methods that are typically applied to protein systems49,50 were used instead.

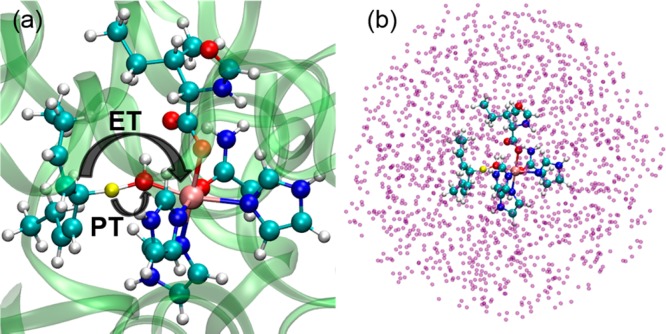
For each of the three snapshots obtained from the MD simulation, a QM/MM geometry optimization was performed for a system comprised of the SLO–LA complex and all solvent molecules and ions within 5 Å of at least one atom in the SLO–LA complex. The QM region contained 87 atoms, including Fe–OH, partial side chains of residues 499, 504, 690, 694, and 839, and a portion of the linoleic acid. The QM atoms are depicted in the ball and stick representation in Figure 2, where the transferring hydrogen atom is highlighted in yellow. The boundary between the QM and MM regions was treated with the hydrogen capping method.51 In the geometry optimization, only the atoms within 20 Å of Fe were allowed to move. The QM region was treated with DFT using with the B3LYP functional,52,53 in conjunction with the 6-31G* basis set for all nonmetal atoms and the LANL2DZ54,55 basis set for the Fe atom. The MM region was described by the OPLS2005 force field.47,49,56 To obtain a reasonable QM/MM configuration corresponding to the crossing point of the diabatic free energy curves in PCET theory,3,24 constrained QM/MM geometry optimizations were performed. In one set of optimizations, the donor-proton and acceptor-proton distances were constrained to be 1.32 and 1.38 Å, respectively. In another set of optimizations, both of these distances were constrained to be 1.35 Å. All QM/MM geometry optimizations were performed using the QSite module in the Schrödinger package.49,50,57

Figure 2.

Figure 2

Open in a new tab

(a) Depiction of the SLO-LA complex used for the QM/MM calculations, where the QM region is indicated by the ball-and-stick representation, the transferring hydrogen is highlighted in yellow, and the MM region is indicated by the ribbon representation. The proton (yellow) is transferring from the carbon (cyan) to the oxygen (red), and the electron is effectively transferring from the π backbone of the LA substrate (cyan) to the iron (mauve). (b) Depiction of the system used for the QM/MM CDFT-CI calculations, where the QM region is indicated by the ball-and-stick representation, and the surrounding MM charges associated with the protein and solvent environment are indicated by purple spheres.

The diabatic proton potential energy curves were obtained by performing QM/MM CDFT-CI calculations for each of the six optimized geometries.33−35 In these calculations, the proton was moved along a grid spanning the linear axis connecting the donor carbon and the acceptor oxygen atoms with all other nuclei fixed. The MM atoms within 10 Å of at least one of the QM atoms were included in the MM region for the QM/MM CDFT-CI calculations. These MM atoms were treated as external charges with magnitudes defined by the OPLS2005 force field. Each MM charge was represented as a Gaussian blurred charge with a width of 3 Å to describe their electrostatic interactions with the QM electrons and nuclei for the CDFT-CI calculations. The ωB97X functional with the 6-31G** basis set was used for the QM region. The diabatic states were obtained by constraining the spin densities on the LA and Fe-cofactor fragments to be 0 and 5, respectively, for the reactant state and 1 and 4, respectively, for the product state.16 The QM/MM CDFT-CI calculations were performed with Q-Chem.45 The ground proton vibrational wave functions were calculated for each diabatic state using the FGH method, and the vibronic coupling was calculated using the electronically nonadiabatic expression given in eq 3.

3. Results

3.1. Phenoxyl-Phenol System

The open and stacked transition state geometries of the phenoxyl-phenol system are depicted in Figure 1. The proton donor–acceptor O–O distance is 2.4 Å in both optimized structures. The O–H–O angle is 180° for the open and 166° for the stacked geometry. These structural properties indicate the presence of a reasonably strong hydrogen bond in both geometries. The vibrational mode associated with the transition state imaginary frequency corresponds to proton transfer between the two oxygen atoms for both geometries. Previous studies indicated that the self-exchange reaction for the open geometry of the phenoxyl-phenol system corresponds to the EPT mechanism and is electronically nonadiabatic, while the self-exchange reaction for the open geometry of the benzyl-toluene system corresponds to the HAT mechanism and is electronically adiabatic.8,12 For the benzyl-toluene system, a stacked transition state geometry has been found to be lower in energy than the open geometry of this system.13

Figure 3 depicts the two highest-energy occupied MOs for both the open and stacked geometries of the phenoxyl-phenol system, where the lower MO is doubly occupied and the higher MO is singly occupied. For the open geometry, the PT interface region of these MOs is dominated by 2p orbitals perpendicular to the proton donor–acceptor axis with a π-bonding interaction in the doubly occupied MO. In contrast, for the stacked geometry, the PT interface region of these MOs is dominated by atomic orbitals oriented along the proton donor–acceptor axis with a σ-bonding interaction in the doubly occupied MO. The character of the MOs in the PT interface region for the stacked geometry is similar to that observed for both the open12 and stacked13 geometries of the benzyl-toluene system, which was determined to be electronically adiabatic.8,9 Another significant difference between the MOs for the open and stacked geometries of the phenoxyl-phenol system is that the stacked geometry exhibits a π-stacking interaction between the two aromatic rings. As depicted in Figure 3, the doubly occupied and singly occupied MOs exhibit bonding and antibonding interactions, respectively, between the aromatic ring orbitals, resulting in a net bonding interaction between the ring moieties for the stacked geometry. This π-stacking bonding interaction increases the electronic coupling, thereby decreasing the electronic transition time relative to the effective proton tunneling time. This analysis suggests that the stacked geometry of the phenoxyl-phenol system may be associated with electronically adiabatic HAT, in contrast to the previously studied open geometry of this system, which was determined to be associated with electronically nonadiabatic EPT.

Figure 3.

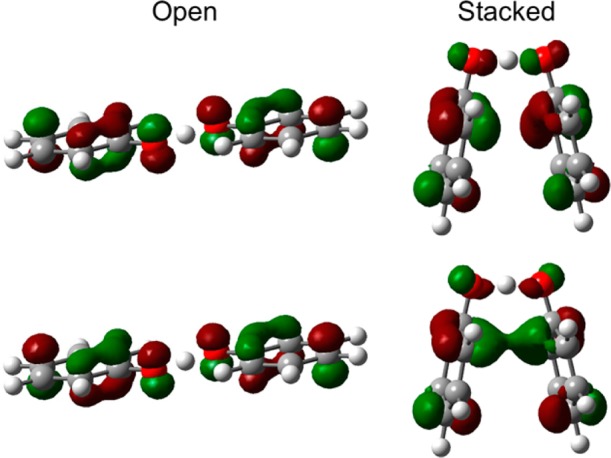
Figure 3

Open in a new tab

Highest occupied MOs for the open (left) and stacked (right) geometries of the phenoxyl-phenol system for the dominant configuration obtained from the CASSCF/6-31G** calculations. The lower MO is doubly occupied, and the higher MO is singly occupied.

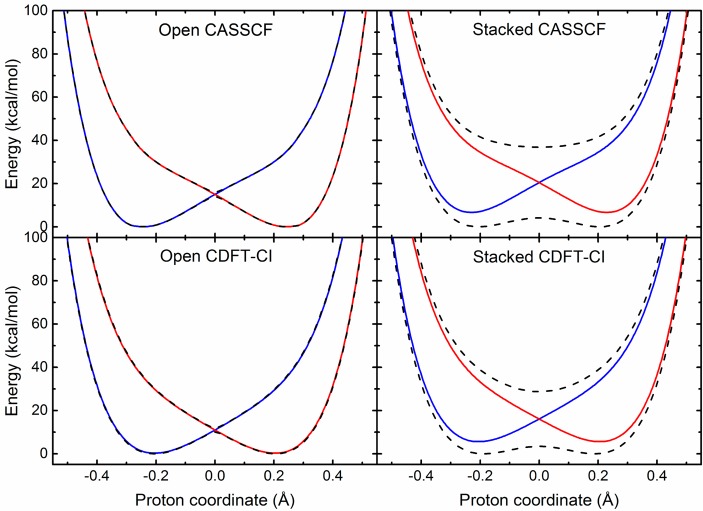
The CASSCF and CDFT-CI proton potential energy curves for both the open and stacked geometries of the phenoxyl-phenol system are depicted Figure 4. For each geometry, the CASSCF and CDFT-CI proton potential energy curves are qualitatively similar, thereby supporting the use of the CDFT-CI method with the ωB97X functional for other PCET systems, including the SLO system discussed below. Additional CASSCF calculations that included four adiabatic electronic states were also performed, but the second and third excited states were found to be much higher in energy than the first excited state (Figure S1), providing validation for the use of a two-state model. Moreover, the adiabatic proton potential energy curves were also calculated with CASPT2 to examine the effects of dynamical correlation, and the CASSCF and CASPT2 curves were found to be similar (Figure S2).

Figure 4.

Figure 4

Open in a new tab

Adiabatic (black dashed lines) and diabatic (blue and red solid lines) proton potential energy curves for the open (left panels) and stacked (right panels) geometries of the phenoxyl-phenol system obtained using the CASSCF/6-31G** (upper panels) and CDFT-CI/ωB97X/6-31G** (lower panels) methods.

Figure 4 depicts both the adiabatic (black dashed lines) and diabatic (blue and red solid lines) proton potential energy curves. These curves are qualitatively different for the open and stacked geometries. In particular, the splitting between the ground and first excited adiabatic states is much greater for the stacked geometry. Moreover, the adiabatic and diabatic proton potential energy curves are virtually indistinguishable except in the crossing region for the open geometry but differ significantly for the entire range of proton coordinates for the stacked geometry. These differences are consistent with electronically nonadiabatic self-exchange for the open geometry but electronically adiabatic self-exchange for the stacked geometry.

The degree of electron–proton nonadiabaticity was quantified within the semiclassical formalism by calculating the effective proton tunneling time τp and the electronic transition time τe, as well as the adiabaticity parameter p, which is the ratio of these two quantities. The values of these parameters are given in Table 1. For the open structure, the effective proton tunneling time is much smaller than the electronic transition time, with p ≪ 1, indicating that the reaction is electronically nonadiabatic. For the stacked structure, the effective proton tunneling time is larger than the electronic transition time, with p > 1, indicating that the reaction is predominantly electronically adiabatic. As discussed below, however, the proton tunneling time and electronic transition time are similar for the stacked structure, with a ratio of p = 1.4, so the self-exchange reaction for this geometry can be viewed as being in the intermediate regime between electronically adiabatic and nonadiabatic.

Table 1. Electronic Couplings, Semiclassical Parameters, and Vibronic Couplings Calculated with Various Methods for Open and Stacked Geometries of Phenoxyl-Phenol System.

geometry Vel (cm–1) τp (fs) τe (fs) p = τp/τe
open 376 0.076 14.12 0.00535
stacked 5735 1.272 0.926 1.374
geometrya V(full) V(sc) V(ad) V(na)b
open 8.57 9.05 50.86 8.55 (8.74)
stacked 263 260 276 203 (205)
Open in a new tab
a

Vibronic couplings given in cm−1.

b

The first value for V(na) is the matrix element of the product of Vel(rp) and the ground reactant and product proton vibrational wave functions, and the value in parentheses is obtained from eq 3 with Vel calculated at rp = 0 (i.e., the product of Vel and the overlap integral between the ground reactant and product proton vibrational wave functions). The similarity between these two values indicates that Vel does not depend strongly on rp.

Table 1 also provides the vibronic couplings calculated with the full basis set diagonalization method, the semiclassical approach, and the methods that are valid in the adiabatic and nonadiabatic regimes. For both geometries, the full basis set diagonalization and semiclassical couplings are similar to each other because both of these approaches are valid in the adiabatic and nonadiabatic limits as well as the intermediate regime. Thus, the coupling calculated with these two approaches will be denoted the “general” coupling. For the open geometry, the nonadiabatic coupling agrees well with the general coupling, whereas for the stacked geometry, the adiabatic coupling agrees better with the general coupling. These calculations provide further evidence that the open and stacked geometries correspond to electronically nonadiabatic and predominantly electronically adiabatic reactions, respectively.

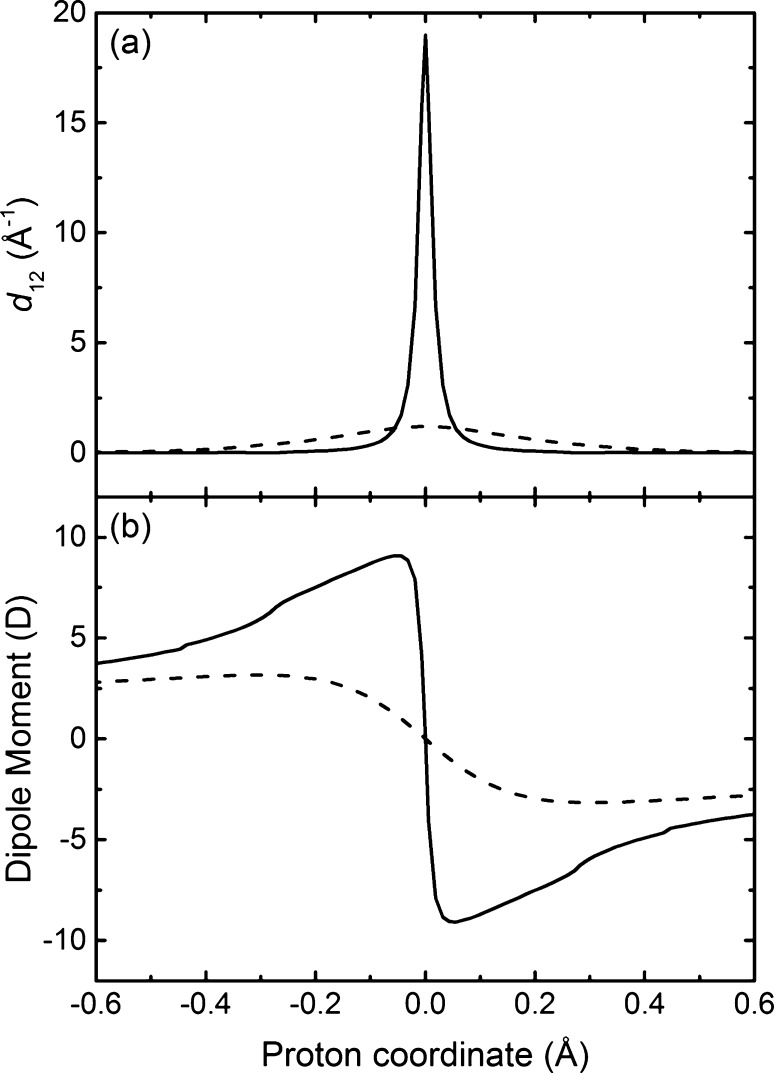
Figure 5 depicts the first-derivative nonadiabatic coupling vector and the dipole moment vector projected along the proton donor–acceptor axis as the proton moves from the donor to the acceptor. The open geometry exhibits a substantial peak in the nonadiabatic coupling and a drastic change in the dipole moment as the proton moves across the midpoint of the proton donor–acceptor axis, whereas the stacked geometry does not exhibit any significant nonadiabatic coupling and only relatively minor and more gradual changes in dipole moment as the proton moves along this axis. Furthermore, the electrostatic potential maps shown in Figure 6 exhibit significant electronic charge transfer between the two aromatic rings as the proton transfers for the open geometry and a much smaller degree of electronic charge transfer between the two rings as the proton transfers for the stacked geometry. In addition, the spin densities depicted in Figure 7 illustrate that the unpaired spin density shifts from one ring to the other as the proton transfers in the open geometry but remains delocalized over both rings during proton transfer for the stacked geometry. These observations are consistent with electronically nonadiabatic behavior for the open geometry, corresponding to an EPT mechanism, and predominantly electronically adiabatic behavior for the stacked geometry, corresponding more closely to an HAT mechanism.

Figure 5.

Figure 5

Open in a new tab

(a) Component of the first-order nonadiabatic coupling vector, as defined in eq 6, between the CASSCF/6-31G** ground and first excited adiabatic electronic states as the proton moves along the proton donor–acceptor axis for the open (solid) and stacked (dashed) geometries of the phenoxyl-phenol system. (b) Component of the dipole moment vector as the proton moves along the proton donor–acceptor axis for the CASSCF/6-31G** ground adiabatic electronic state for the open (solid) and stacked (dashed) geometries of the phenoxyl-phenol system.

Figure 6.

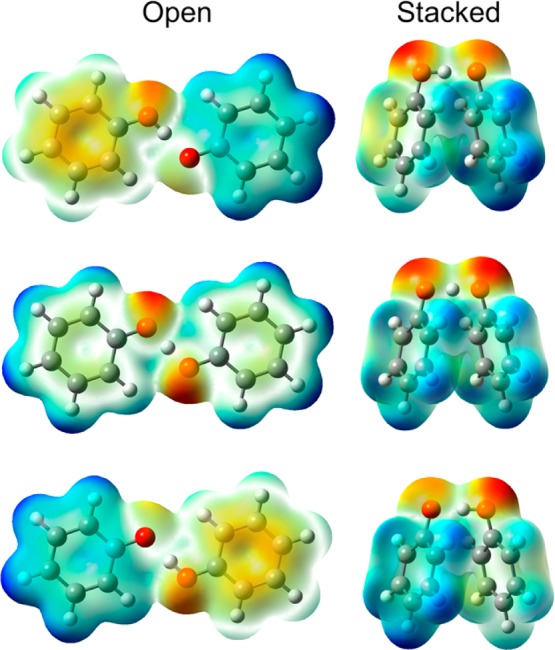
Figure 6

Open in a new tab

Electrostatic potential maps for the ground adiabatic electronic states generated with DFT/ωB97X/6-31G** for the reactant (top), transition state (middle), and product (bottom) positions of the transferring hydrogen for the open (left) and stacked (right) geometries of the phenoxyl-phenol system. The density isosurface value is 0.005, and negatively and positively charged regions are indicated by red and blue coloring, respectively.

Figure 7.

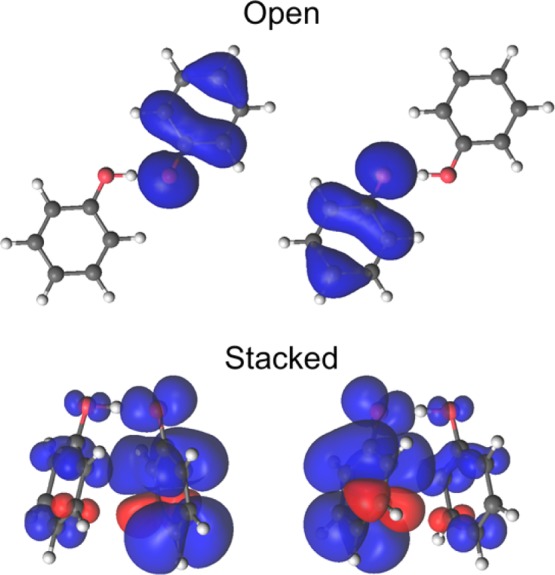
Figure 7

Open in a new tab

Spin densities for the open (top) and stacked (bottom) geometries of the phenoxyl-phenol system obtained from CASSCF/6-31G** ground state calculations for the reactant (left) and product (right) positions of the transferring hydrogen.

We emphasize that the stacked geometry does exhibit a small amount of electronic charge redistribution between the two aromatic rings during proton transfer, as indicated by the changes in dipole moment and electrostatic potential, and therefore is not a pure HAT reaction. In other words, the self-exchange reaction for the stacked geometry is not fully electronically adiabatic, as also indicated by the adiabaticity parameter, which is greater than unity but not as large as was observed for the open geometry of the benzyl-toluene system, which is considered to be a pure HAT reaction. The adiabaticity parameter is 1.4 for the stacked geometry of the phenoxyl-phenol system and 3.5 for the open geometry of the benzyl-toluene system.8 (For further comparison, calculations on the stacked geometry of the benzyl-toluene system13 are provided in Figure S3, indicating an adiabaticity parameter of 10.0.) On the basis of this analysis, we classify the stacked geometry of the phenoxyl-phenol system as a predominantly electronically adiabatic reaction that can be described as an HAT mechanism with a small amount of EPT character. Consequently, the stacked geometry represents an example of a system that is in the intermediate regime between electronically adiabatic and nonadiabatic, or between HAT and EPT, although it is closer toward the electronically adiabatic HAT limit.

Thus, all of these analyses indicate that the open and stacked geometries of the phenoxyl-phenol system are in different regimes. Specifically, the open geometry is electronically nonadiabatic, corresponding to an EPT reaction, while the stacked geometry is in the intermediate regime but predominantly electronically adiabatic, corresponding to an HAT reaction. As given in Table 1, the electronic coupling is significantly greater for the stacked geometry than for the open geometry because of the π-stacking interaction between the rings, as indicated by the MOs in Figure 3. This stacking interaction decreases the electronic transition time to the extent that the electrons are able to respond instantaneously to the proton motion, thereby leading to an electronically adiabatic proton transfer that remains on the electronic ground state. This reaction involves only a small amount of electronic charge redistribution between the rings, supporting the designation of a primarily HAT mechanism for this geometry. In contrast, the open geometry involves a significant shift in electronic charge distribution from one ring to the other, and these rings are further apart with weaker interactions, supporting the designation of EPT for this geometry. These calculations illustrate that a single molecular system can span the electronically adiabatic and nonadiabatic limits as it explores configurational space via thermal fluctuations. Moreover, at certain geometries the reaction may lie in the intermediate regime between the electronically adiabatic and nonadiabatic limits and therefore can no longer be designated as either HAT or EPT.

3.2. Soybean Lipoxygenase System

To investigate the impact of the protein and solvent environment on the vibronic coupling, we performed QM/MM calculations on the SLO-LA system depicted in Figure 2. The classical MD simulations and QM/MM geometry optimizations were performed for the solvated enzyme system depicted in Figure 2a, where the QM region is shown in the ball-and-stick representation. The QM/MM CDFT-CI calculations were performed for the somewhat truncated system depicted in Figure 2b. The atomic charges in the MM region, depicted as purple spheres in Figure 2b, were included in the QM/MM CDFT-CI calculations using an electrostatic embedding method. Two types of constrained QM/MM geometry optimizations were performed for each of three different configurations along the classical MD trajectory, leading to a total of six SLO configurations. For each configuration, the reactant and product diabatic proton potential energy curves, as well as the electronic coupling between these two states, were calculated using the QM/MM CDFT-CI approach.

The reactant and product diabatic proton potential energy curves obtained for one of these configurations are depicted in Figure 8. These curves were shifted to ensure that the ground proton vibrational energy levels are degenerate. The analogous curves for the other five configurations are provided in the Supporting Information. These proton potential energy curves are similar to each other and to those obtained previously for a gas-phase model of the SLO-LA system.16 These results demonstrate that the electrostatic effects from the protein environment in this system do not significantly perturb the shape of the diabatic proton potential energy curves.

Figure 8.

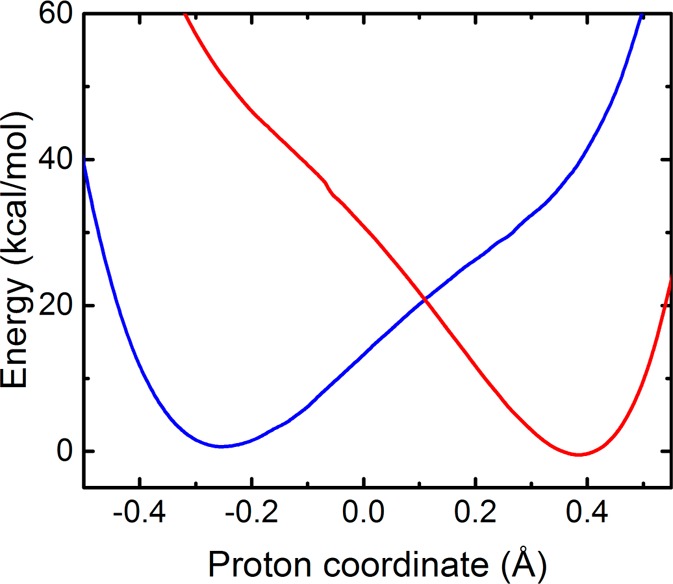
Figure 8

Open in a new tab

Diabatic proton potential energy curves for the SLO system calculated with QM/MM CDFT-CI/ωB97X/6-31G** for a configuration obtained by QM/MM geometry optimization with the donor-proton and acceptor-proton distances constrained to be 1.35 Å. The diabatic states were shifted to ensure that the ground proton vibrational energy levels are degenerate. The analogous diabatic proton potential energy curves for five other configurations are provided in Figure S4.

Table 2 provides the electronic couplings, as well as the effective proton tunneling time τp, the electronic transition time τe, and the adiabaticity parameter p, for three different SLO configurations. For this system, the effective proton tunneling time is much smaller than the electronic transition time, with p ≪ 1, demonstrating that this reaction is electronically nonadiabatic. Further evidence of nonadiabaticity is provided by Figure 9, which depicts the dipole moment of the QM region in the field of MM point charges as the proton moves along the donor–acceptor axis for the ground electronic state obtained with QM/MM DFT/ωB97X/6-31G**. The drastic change in dipole moment as the proton passes through the middle of the proton donor–acceptor axis indicates a substantial amount of electronic charge transfer from the LA substrate to the Fe-cofactor as the proton transfers. In addition, the spin densities depicted in Figure 10 illustrate that the electron effectively transfers from the π backbone of the LA substrate to the iron of the cofactor, resulting in unpaired spin density along the π backbone of the LA substrate after the proton has transferred.

Table 2. Electronic Couplings, Semiclassical Parameters, and Nonadiabatic Vibronic Couplings for the SLO System.

geometry Vel (cm–1) τp (fs) τe (fs) p = τp/τe V(na) (cm–1)
QM/MM Ia 1500 0.23 3.53 0.07 2.6
QM/MM II 1798 0.27 2.95 0.09 3.6
QM/MM III 2273 0.31 2.34 0.13 3.9
gas-phase modelb 1607 0.22 3.3 0.07 1.8
Open in a new tab
a

Geometries I, II, and III were obtained from QM/MM geometry optimizations of three different snapshots from a classical MD trajectory. The QM/MM optimizations were conducted with the donor-proton and acceptor-proton distances constrained to be 1.35 Å. Results for three other geometries are provided in Table S2.

b

This result was obtained by previous studies on a gas-phase SLO-LA model system.16

Figure 9.

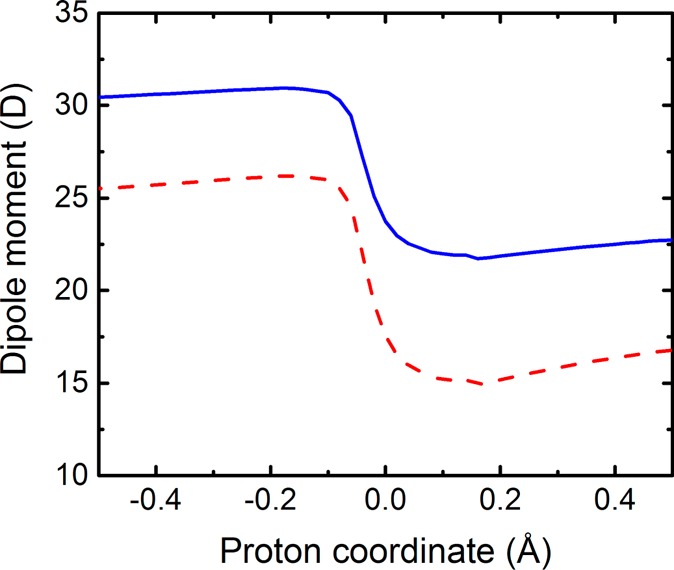
Figure 9

Open in a new tab

Dipole moment as the proton transfers from the donor to the acceptor for an SLO configuration obtained by QM/MM geometry optimization with the donor-proton and acceptor-proton distances constrained to be 1.35 Å. The magnitude of the total dipole moment vector (solid blue line) and the dipole moment vector projected onto the axis connecting the donor carbon and the Fe (dashed red line) were calculated for the QM region in the field of MM point charges for the QM/MM DFT/ωB97X/6-31G** ground adiabatic electronic state as the proton moves along the proton donor–acceptor axis. Analogous figures for five other SLO configurations are provided in Figure S5.

Figure 10.

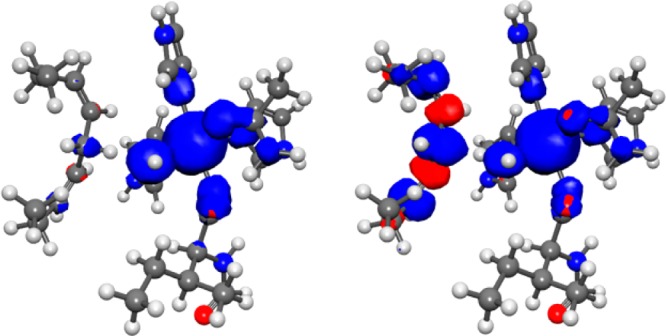
Figure 10

Open in a new tab

Spin densities for the reactant (left) and product (right) positions of the transferring hydrogen corresponding to the minima of the reactant and product diabatic curves, respectively, in Figure 8 for the SLO-LA system. The spin densities were calculated for the QM region in the field of MM point charges for the QM/MM DFT/ωB97X/6-31G** ground adiabatic electronic state.

Because this reaction was determined to be electronically nonadiabatic, the vibronic coupling was calculated using eq 3, which is valid in the electronically nonadiabatic regime. As shown in Table 2, the semiclassical parameters and vibronic couplings are similar for the three different protein configurations as well as for the gas-phase model studied previously. This agreement for the four different environments illustrates that the protein environment does not significantly impact the vibronic coupling, thereby providing validation for the Condon approximation.26−29 As further validation of these findings, calculations using nonadiabatic rate constant expressions relying on the Condon approximation have reproduced the experimentally observed hydrogen/deuterium kinetic isotope effects and their temperature dependencies.18−23

3.3. Comparison of Phenoxyl-Phenol and SLO-LA Systems

A comparison of the analyses of electron–proton nonadiabaticity for the phenoxyl-phenol and SLO-LA systems indicates that the SLO-LA system is more similar to the open structure than to the stacked structure of the phenoxyl-phenol system. Both the open phenoxyl-phenol and the SLO-LA systems exhibit a substantial change in the electronic charge distribution during proton transfer, as illustrated in Figure 5b and Figure 6 for the phenoxyl-phenol system and in Figure 9 for the SLO-LA system. The spin densities for these two systems also indicate a significant shift of the unpaired spin density during proton transfer, as depicted by Figure 7 for the phenoxyl-phenol system and Figure 10 for the SLO-LA system. Moreover, the adiabaticity parameter is less than unity for both systems, namely 0.005 for the open phenoxyl-phenol system and ∼0.1 for the SLO-LA system, compared to the value of 1.4 for the stacked phenoxyl-phenol system. On the basis of these analyses, both the open structure of the phenoxyl-phenol system and the SLO-LA system are in the electronically nonadiabatic regime and therefore represent EPT, although the SLO-LA system could be viewed as less nonadiabatic in terms of the adiabaticity parameter.

4. Conclusions

In this paper, we tested the Condon approximation for PCET vibronic couplings, which strongly impact the rate constants. Calculations of the vibronic coupling for the phenoxyl-phenol self-exchange reaction illustrate that the open geometry is electronically nonadiabatic, while the stacked geometry is in the intermediate regime but is predominantly electronically adiabatic. The electronic coupling is significantly greater for the stacked geometry than for the open geometry because of the π-stacking bonding interaction between the rings in the stacked geometry. Moreover, the self-exchange reaction involves substantially more electronic charge redistribution in the open geometry than in the stacked geometry. On the basis of this analysis, the reaction is identified as EPT in the open geometry but primarily HAT, with a small amount of EPT character, in the stacked geometry. These calculations demonstrate a breakdown in the Condon approximation in that the vibronic coupling depends strongly on the geometry of the PCET complex. This geometric dependence is not simply a dependence on the donor–acceptor distance, which is a well-known phenomenon, but rather is a more interesting dependence on the intramolecular angle between the planes of two aromatic rings. Calculations of the vibronic coupling for the SLO-LA enzyme indicate that this reaction is electronically nonadiabatic, corresponding to EPT, similar to the open geometry of the phenoxyl-phenol system. Furthermore, these calculations illustrate that the vibronic coupling for the SLO-LA enzyme does not depend significantly on the solvent or protein environment.

Thus, these calculations suggest that the Condon approximation is valid for the solvent and protein nuclear coordinates but could be invalid for the solute nuclear coordinates, particularly intramolecular coordinates that influence the π-stacking interactions for systems with aromatic rings. Moreover, a single molecular system can span the electronically adiabatic and nonadiabatic limits through thermal fluctuations that lead to conformational changes. The form of the vibronic coupling is different in these two regimes, as well as in the intermediate regime. The mechanistic interpretation is also different in these two regimes, resulting in the possibility that a single system can exhibit both HAT and EPT character. Thus, simulations of PCET reactions, calculations of PCET rate constants, and mechanistic interpretations should account for the possibility of spanning both regimes, as well as the potential breakdown of the Condon approximation, for certain types of systems.

Acknowledgments

We are grateful to Gino DiLabio for bringing the stacked transition state geometry of the phenoxyl-phenol system to our attention and for providing the initial coordinates for both geometries. This work was funded by the National Institutes of Health Grant GM056207 (soybean lipoxygenase) and the Center for Chemical Innovation of the National Science Foundation Solar Fuels Grant CHE-1305124 (phenoxyl-phenol system).

Supporting Information Available

The Supporting Information is available free of charge on the ACS Publications website at DOI: 10.1021/jacs.5b07327.

  • Adiabatic and diabatic proton potential energy curves obtained with CASSCF and CASPT2 for the phenoxyl-phenol system; structures and energies for the open and stacked geometries of the phenoxyl-phenol system; diabatic curves, semiclassical parameters, and vibronic couplings obtained with CASSCF for the stacked benzyl-toluene system; diabatic curves, dipole moments, electronic couplings, semiclassical parameters, and vibronic couplings obtained with QM/MM CDFT-CI for the SLO system with different protein configurations; structures of QM regions from SLO QM/MM optimizations (PDF)

Author Contributions

† These authors contributed equally.

The authors declare no competing financial interest.

Supplementary Material

ja5b07327_si_001.pdf (1.1MB, pdf)

References

  1. Cukier R.; Nocera D. G. Annu. Rev. Phys. Chem. 1998, 49, 337. 10.1146/annurev.physchem.49.1.337. [DOI] [PubMed] [Google Scholar]
  2. Huynh M. H. V.; Meyer T. J. Chem. Rev. 2007, 107, 5004. 10.1021/cr0500030. [DOI] [PMC free article] [PubMed] [Google Scholar]
  3. Hammes-Schiffer S.; Soudackov A. V. J. Phys. Chem. B 2008, 112, 14108. 10.1021/jp805876e. [DOI] [PMC free article] [PubMed] [Google Scholar]
  4. Hammes-Schiffer S.; Stuchebrukhov A. A. Chem. Rev. 2010, 110, 6939. 10.1021/cr1001436. [DOI] [PMC free article] [PubMed] [Google Scholar]
  5. Warren J. J.; Tronic T. A.; Mayer J. M. Chem. Rev. 2010, 110, 6961. 10.1021/cr100085k. [DOI] [PMC free article] [PubMed] [Google Scholar]
  6. Hammes-Schiffer S. Energy Environ. Sci. 2012, 5, 7696. 10.1039/c2ee03361e. [DOI] [Google Scholar]
  7. Note that the use of EPT to denote a type of concerted PCET is not universal throughout the literature but is used consistently throughout this work.
  8. Skone J. H.; Soudackov A. V.; Hammes-Schiffer S. J. Am. Chem. Soc. 2006, 128, 16655. 10.1021/ja0656548. [DOI] [PubMed] [Google Scholar]
  9. Sirjoosingh A.; Hammes-Schiffer S. J. Phys. Chem. A 2011, 115, 2367. 10.1021/jp111210c. [DOI] [PubMed] [Google Scholar]
  10. Sirjoosingh A.; Hammes-Schiffer S. J. Chem. Theory Comput. 2011, 7, 2831. 10.1021/ct200356b. [DOI] [PubMed] [Google Scholar]
  11. Georgievskii Y.; Stuchebrukhov A. A. J. Chem. Phys. 2000, 113, 10438. 10.1063/1.1323723. [DOI] [Google Scholar]
  12. Mayer J. M.; Hrovat D. A.; Thomas J. L.; Borden W. T. J. Am. Chem. Soc. 2002, 124, 11142. 10.1021/ja012732c. [DOI] [PubMed] [Google Scholar]
  13. DiLabio G. A.; Johnson E. R. J. Am. Chem. Soc. 2007, 129, 6199. 10.1021/ja068090g. [DOI] [PubMed] [Google Scholar]
  14. Tishchenko O.; Truhlar D. G.; Ceulemans A.; Nguyen M. T. J. Am. Chem. Soc. 2008, 130, 7000. 10.1021/ja7102907. [DOI] [PubMed] [Google Scholar]
  15. Cembran A.; Provorse M. R.; Wang C. W.; Wu W.; Gao J. L. J. Chem. Theory Comput. 2012, 8, 4347. 10.1021/ct3004595. [DOI] [PMC free article] [PubMed] [Google Scholar]
  16. Soudackov A. V.; Hammes-Schiffer S. J. Phys. Chem. Lett. 2014, 5, 3274. 10.1021/jz501655v. [DOI] [PMC free article] [PubMed] [Google Scholar]
  17. Barzykin A. V.; Frantsuzov P. A.; Seki K.; Tachiya M. Adv. Chem. Phys. 2002, 123, 511. 10.1002/0471231509.ch9. [DOI] [Google Scholar]
  18. Knapp M. J.; Rickert K.; Klinman J. P. J. Am. Chem. Soc. 2002, 124, 3865. 10.1021/ja012205t. [DOI] [PubMed] [Google Scholar]
  19. Hatcher E.; Soudackov A. V.; Hammes-Schiffer S. J. Am. Chem. Soc. 2004, 126, 5763. 10.1021/ja039606o. [DOI] [PubMed] [Google Scholar]
  20. Hatcher E.; Soudackov A. V.; Hammes-Schiffer S. J. Am. Chem. Soc. 2007, 129, 187. 10.1021/ja0667211. [DOI] [PubMed] [Google Scholar]
  21. Meyer M. P.; Tomchick D. R.; Klinman J. P. Proc. Natl. Acad. Sci. U. S. A. 2008, 105, 1146. 10.1073/pnas.0710643105. [DOI] [PMC free article] [PubMed] [Google Scholar]
  22. Edwards S. J.; Soudackov A. V.; Hammes-Schiffer S. J. Phys. Chem. B 2010, 114, 6653. 10.1021/jp100133p. [DOI] [PMC free article] [PubMed] [Google Scholar]
  23. Hu S.; Sharma S. C.; Scouras A. D.; Soudackov A. V.; Carr C. A. M.; Hammes-Schiffer S.; Alber T.; Klinman J. P. J. Am. Chem. Soc. 2014, 136, 8157. 10.1021/ja502726s. [DOI] [PMC free article] [PubMed] [Google Scholar]
  24. Soudackov A.; Hammes-Schiffer S. J. Chem. Phys. 2000, 113, 2385. 10.1063/1.482053. [DOI] [Google Scholar]
  25. Soudackov A.; Hatcher E.; Hammes-Schiffer S. J. Chem. Phys. 2005, 122, 014505. 10.1063/1.1814635. [DOI] [PubMed] [Google Scholar]
  26. Beratan D. N.; Hopfield J. J. J. Chem. Phys. 1984, 81, 5753. 10.1063/1.447627. [DOI] [Google Scholar]
  27. Cave R. J.; Newton M. D. J. Chem. Phys. 1997, 106, 9213. 10.1063/1.474023. [DOI] [Google Scholar]
  28. Toutounji M. M.; Ratner M. A. J. Phys. Chem. A 2000, 104, 8566. 10.1021/jp001271z. [DOI] [Google Scholar]
  29. Newton M. D. Theor. Chem. Acc. 2003, 110, 307. 10.1007/s00214-003-0504-9. [DOI] [Google Scholar]
  30. Werner H. J.; Knowles P. J. J. Chem. Phys. 1985, 82, 5053. 10.1063/1.448627. [DOI] [Google Scholar]
  31. Knowles P. J.; Werner H. J. Chem. Phys. Lett. 1985, 115, 259. 10.1016/0009-2614(85)80025-7. [DOI] [Google Scholar]
  32. Baer M. Chem. Phys. Lett. 1975, 35, 112. 10.1016/0009-2614(75)85599-0. [DOI] [Google Scholar]
  33. Wu Q.; Van Voorhis T. J. Chem. Theory Comput. 2006, 2, 765. 10.1021/ct0503163. [DOI] [PubMed] [Google Scholar]
  34. Wu Q.; Van Voorhis T. J. Phys. Chem. A 2006, 110, 9212. 10.1021/jp061848y. [DOI] [PubMed] [Google Scholar]
  35. Wu Q.; Cheng C. L.; Van Voorhis T. J. Chem. Phys. 2007, 127, 164119. 10.1063/1.2800022. [DOI] [PubMed] [Google Scholar]
  36. Zhao Y.; Schultz N. E.; Truhlar D. G. J. Chem. Theory Comput. 2006, 2, 364. 10.1021/ct0502763. [DOI] [PubMed] [Google Scholar]
  37. Krishnan R.; Binkley J. S.; Seeger R.; Pople J. A. J. Chem. Phys. 1980, 72, 650. 10.1063/1.438955. [DOI] [Google Scholar]
  38. Clark T.; Chandrasekhar J.; Spitznagel G. W.; Schleyer P. V. J. Comput. Chem. 1983, 4, 294. 10.1002/jcc.540040303. [DOI] [Google Scholar]
  39. Frisch M. J. T., G W.; Schlegel H. B.; Scuseria G. E.; Robb M. A.; Cheeseman J. R.; Scalmani G.; Barone V.; Mennucci B.; Petersson G. A.; Nakatsuji H.; Caricato M.; Li X.; Hratchian H. P.; Izmaylov A. F.; Bloino J.; Zheng G.; Sonnenberg J. L.; Hada M.; Ehara M.; Toyota K.; Fukuda R.; Hasegawa J.; Ishida M.; Nakajima T.; Honda Y.; Kitao O.; Nakai H.; Vreven T.; Montgomery J. A. Jr.; Peralta J. E.; Ogliaro F.; Bearpark M.; Heyd J. J.; Brothers E.; Kudin K. N.; Staroverov V. N.; Kobayashi R.; Normand J.; Raghavachari K.; Rendell A.; Burant J. C.; Iyengar S. S.; Tomasi J.; Cossi M.; Rega N.; Millam J. M.; Klene M.; Knox J. E.; Cross J. B.; Bakken V.; Adamo C.; Jaramillo J.; Gomperts R.; Stratmann R. E.; Yazyev O.; Austin A. J.; Cammi R.; Pomelli C.; Ochterski J. W.; Martin R. L.; Morokuma K.; Zakrzewski V. G.; Voth G. A.; Salvador P.; Dannenberg J. J.; Dapprich S.; Daniels A. D.; Farkas Ö.; Foresman J. B.; Ortiz J. V.; Cioslowski J.; Fox D. J.. Gaussian 09; Gaussian Inc., Wallingford, CT, 2009.
  40. Werner H.-J. K., P J.; Knizia G.; Manby F. R.; Schütz M.; Celani P.; Korona T.; Lindh R.; Mitrushenkov A.; Rauhut G.; Shamasundar K. R.; Adler T. B.; Amos R. D.; Bernhardsson A.; Berning A.; Cooper D. L.; Deegan M. J. O.; Dobbyn A.; Eckert J. F.; Goll E.; Hampel C.; Hesselmann A.; Hetzer G.; Hrenar T.; Jansen G.; Köppl C.; Liu Y.; A. Lloyd W. R.; Mata A.; May A.; McNicholas J. S. J.; Meyer W.; Mura M. E.; Nicklass A.; O’Neill D. P.; Palmieri P.; Peng D.; Pflüger K.; Pitzer R.; Reiher M.; Shiozaki T.; Stoll H.; Stone A. J.; Tarroni R.; Thorsteinsson T.; Wang M.. MOLPRO; version 2010.1; University College Cardiff Consultants Limited: Wales, U.K., see http://www.molpro.net.
  41. Aquilante F.; De Vico L.; Ferre N.; Ghigo G.; Malmqvist P. A.; Neogrady P.; Pedersen T. B.; Pitonak M.; Reiher M.; Roos B. O.; Serrano-Andres L.; Urban M.; Veryazov V.; Lindh R. J. Comput. Chem. 2010, 31, 224. 10.1002/jcc.21318. [DOI] [PubMed] [Google Scholar]
  42. Karlstrom G.; Lindh R.; Malmqvist P. A.; Roos B. O.; Ryde U.; Veryazov V.; Widmark P. O.; Cossi M.; Schimmelpfennig B.; Neogrady P.; Seijo L. Comput. Mater. Sci. 2003, 28, 222. 10.1016/S0927-0256(03)00109-5. [DOI] [Google Scholar]
  43. Veryazov V.; Widmark P. O.; Serrano-Andres L.; Lindh R.; Roos B. O. Int. J. Quantum Chem. 2004, 100, 626. 10.1002/qua.20166. [DOI] [Google Scholar]
  44. Chai J. D.; Head-Gordon M. J. Chem. Phys. 2008, 128, 084106. 10.1063/1.2834918. [DOI] [PubMed] [Google Scholar]
  45. Shao Y.; Molnar L. F.; Jung Y.; Kussmann J.; Ochsenfeld C.; Brown S. T.; Gilbert A. T. B.; Slipchenko L. V.; Levchenko S. V.; O’Neill D. P.; DiStasio R. A.; Lochan R. C.; Wang T.; Beran G. J. O.; Besley N. A.; Herbert J. M.; Lin C. Y.; Van Voorhis T.; Chien S. H.; Sodt A.; Steele R. P.; Rassolov V. A.; Maslen P. E.; Korambath P. P.; Adamson R. D.; Austin B.; Baker J.; Byrd E. F. C.; Dachsel H.; Doerksen R. J.; Dreuw A.; Dunietz B. D.; Dutoi A. D.; Furlani T. R.; Gwaltney S. R.; Heyden A.; Hirata S.; Hsu C. P.; Kedziora G.; Khalliulin R. Z.; Klunzinger P.; Lee A. M.; Lee M. S.; Liang W.; Lotan I.; Nair N.; Peters B.; Proynov E. I.; Pieniazek P. A.; Rhee Y. M.; Ritchie J.; Rosta E.; Sherrill C. D.; Simmonett A. C.; Subotnik J. E.; Woodcock H. L.; Zhang W.; Bell A. T.; Chakraborty A. K.; Chipman D. M.; Keil F. J.; Warshel A.; Hehre W. J.; Schaefer H. F.; Kong J.; Krylov A. I.; Gill P. M. W.; Head-Gordon M. Phys. Chem. Chem. Phys. 2006, 8, 3172. 10.1039/b517914a. [DOI] [PubMed] [Google Scholar]
  46. Marston C. C.; Balint-kurti G. G. J. Chem. Phys. 1989, 91, 3571. 10.1063/1.456888. [DOI] [Google Scholar]
  47. Jorgensen W. L.; Chandrasekhar J.; Madura J. D.; Impey R. W.; Klein M. L. J. Chem. Phys. 1983, 79, 926. 10.1063/1.445869. [DOI] [Google Scholar]
  48. Chruszcz M.; Wlodawer A.; Minor W. Biophys. J. 2008, 95, 1. 10.1529/biophysj.108.131789. [DOI] [PMC free article] [PubMed] [Google Scholar]
  49. Philipp D. M.; Friesner R. A. J. Comput. Chem. 1999, 20, 1468.. [DOI] [Google Scholar]
  50. Murphy R. B.; Philipp D. M.; Friesner R. A. J. Comput. Chem. 2000, 21, 1442.. [DOI] [Google Scholar]
  51. Vasilyev V. V. J. Mol. Struct.: THEOCHEM 1994, 304, 129. 10.1016/S0166-1280(96)80005-4. [DOI] [Google Scholar]
  52. Becke A. D. J. Chem. Phys. 1993, 98, 5648. 10.1063/1.464913. [DOI] [Google Scholar]
  53. Lee C. T.; Yang W. T.; Parr R. G. Phys. Rev. B: Condens. Matter Mater. Phys. 1988, 37, 785. 10.1103/PhysRevB.37.785. [DOI] [PubMed] [Google Scholar]
  54. Hay P. J.; Wadt W. R. J. Chem. Phys. 1985, 82, 270. 10.1063/1.448799. [DOI] [Google Scholar]
  55. Hay P. J.; Wadt W. R. J. Chem. Phys. 1985, 82, 299. 10.1063/1.448975. [DOI] [Google Scholar]
  56. Kaminski G. A.; Friesner R. A.; Tirado-Rives J.; Jorgensen W. L. J. Phys. Chem. B 2001, 105, 6474. 10.1021/jp003919d. [DOI] [Google Scholar]
  57. QSite; version 6.2; Schrödinger, LLC: New York, 2014.

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

ja5b07327_si_001.pdf (1.1MB, pdf)

Articles from Journal of the American Chemical Society are provided here courtesy of American Chemical Society

RESOURCES