Bioinspired Polarization Imaging Sensors: From Circuits and Optics to Signal Processing Algorithms and Biomedical Applications

Abstract

In this paper, we present recent work on bioinspired polarization imaging sensors and their applications in biomedicine. In particular, we focus on three different aspects of these sensors. First, we describe the electro–optical challenges in realizing a bioinspired polarization imager, and in particular, we provide a detailed description of a recent low-power complementary metal–oxide–semiconductor (CMOS) polarization imager. Second, we focus on signal processing algorithms tailored for this new class of bioinspired polarization imaging sensors, such as calibration and interpolation. Third, the emergence of these sensors has enabled rapid progress in characterizing polarization signals and environmental parameters in nature, as well as several biomedical areas, such as label-free optical neural recording, dynamic tissue strength analysis, and early diagnosis of flat cancerous lesions in a murine colorectal tumor model. We highlight results obtained from these three areas and discuss future applications for these sensors.

I. INTRODUCTION

Nature provides many ingenious ways of sensing the surrounding environment. Sensing the presence of a predator might mean the difference between life and death. Detecting the presence of food means the difference between starvation and survival. Catching a signal from afar could result in finding a mate. For these and numerous other scenarios, organisms have evolved many different structures and techniques suitable for their own survival. Mimicking nature's techniques with modern technology has the potential for engineering unique sensors that can enhance our understanding of the world.

Of the senses evolved by nature, vision provides some of the most varied examples to emulate. From the compound eyes of invertebrates to the human visual system, with many other subtle variations found in nature, vision is a very powerful way for organisms to interact with the environment. Vision is such an important sense that image-forming eyes have evolved independently over 50 times [1].

The purpose of all eyes is to convert light into some sort of neural signaling interpreted by the brain. Photosensitive cells within the eye act as photoreceptors, triggering a chain of action potentials when they sense light. In some animals, these photosensitive cells detect different wavelengths of light through pigmented cells, resulting in color vision. In other animals, integration of microvilli above the photosensitive cells has allowed polarization-sensitive vision.

A variety of electronic sensors have been developed to mimic biological vision. These sensors have found wide use across many different fields. From astrophysics to biology and medicine, electronic image sensors have revolutionized the scientific understanding of the world. Similar to animal vision, these electronic sensors also contain a photosensitive element, called a pixel, that produces a change in voltage or current when light converts into electron–hole pairs. Sampling this output at given integration times results in a signal proportional to the intensity of light during this integration period. Color selectivity can also be implemented by matching spectral filters directly to the pixels, similar to pigmentation in animals [2]. Most color image sensors are constructed by monolithically integrated pixel-pitch-matched color filters (e.g., red, green, and blue color filters) with an array of complementary metal–oxide–semiconductor (CMOS) or charge-coupled device (CCD) detectors, producing color images in the visible (400–700 nm) spectrum [3], [4].

Some modern image sensors can detect polarization information present in light [5]–[13]. Advances in nano-fabrication technology have allowed for the integration of polarization filters directly onto photosensitive pixels, in a similar fashion to color sensors [14]–[18]. These polarization sensors contain no moving parts, operate at real-time or faster frame rates, and can use standard lenses. This new type of polarization sensor has opened up new avenues of exploration of polarization phenomena [19]–[21].

In this paper, we present recent work on bioinspired polarization imaging sensors and its applications to biomedicine. We begin with a brief theoretical discussion of the polarization properties of light that provides the framework for realizing bioinspired polarization sensors in CMOS technology. Next, we give a discussion of some of the devices which are used for polarization detection, including many bioinspired polarization sensors. We include the design of a current mode, CMOS polarization sensor we have developed. We discuss the many signal processing challenges this new class of polarization sensors require, from calibration and interpolation, to human interpretable display. Next, we include a systematic optical and electronic method of testing these new types of sensors. We finally conclude with three biomedical applications of these sensors. We use the bioinspired current mode sensor to make in vivo measurements of neural activity in an insect brain. We further demonstrate that a bioinspired sensor can measure the real-time dynamics of soft tissue. We finally show how a bioinspired polarization sensor can be used as a tool to enhance endoscopy.

II. THEORY OF POLARIZATION

Polarization is a fundamental property of electromagnetic waves. It describes the phase difference between the x and y components of the electromagnetic field when it is viewed as a propagating plane wave

$$\mathbf{E}=E_{0,x}\cos (\omega t-kz+{\delta }_x)\widehat{x}+E_{0,y}\cos (\omega t-kz+{\delta }_y)\widehat{y}$$ (1)

where E_0,x and E_0,y are the respective amplitudes of the x and y fields, ω is the frequency, t is the time, k is the wave number, z is the direction of propagation, and δ_x and δ_y are the respective phases.

From (1), the type of polarization is characterized from δ_x – δ_y, because the difference in the phases is what shapes the wavefront of the propagating waves. If the phase difference is random, the light is unpolarized; if the phases are the same, the light is linearly polarized; if the phases are unequal but constant, the light is elliptically polarized. A special case of elliptical polarization is observed when the phase difference is exactly π/2, which transforms the wavefront into a circle, and so the propagating light is termed circularly polarized. Most of the light waves encountered in nature are partially polarized, a linear combination of unpolarized light waves and completely polarized light waves.

A. Mathematical Treatment of Light Properties via Stokes–Mueller Formalism

The classic treatment of incoherent polarized light uses the Stokes–Mueller formalism [22]. The mathematical framework for polarized light is derived mostly from the seminal work by Sir Gabriel Stokes. From his work, the intensity of light measured through a linear polarizer at angle θ and a phase retarder ϕ can be mathematically represented as

$$I(\theta ,\varphi )=\frac{1}{2}(S_0+S_1\cos 2\theta +S_2\sin 2\theta \cos \varphi +S_3\sin 2\theta \sin \varphi ).$$ (2)

The terms S₀ through S₃ are called the Stokes parameters, and each describes a polarization property of the light wave. The S₀ parameter describes the total intensity; S₁ describes how much of the light is polarized in the vertical or horizontal direction; S₂ describes how much of the light is polarized at ±45° to the x/y-axis along the direction of propagation; and S₃ describes the circular polarization properties of the light wave. The Stokes parameters are commonly expressed as a vector, which relates these parameters to the electromagnetic wave equation (1)

$$\left[\begin{array}{c}\hfill S_0\hfill \\ \hfill S_1\hfill \\ \hfill S_2\hfill \\ \hfill S_3\hfill \end{array}\right]=\left[\begin{array}{c}\hfill E_{0,x}^2+E_{0,y}^2\hfill \\ \hfill E_{0,x}^2-E_{0,y}^2\hfill \\ \hfill 2E_{0,x}{E}_{0,y}\cos \delta \hfill \\ \hfill 2E_{0,x}{E}_{0,y}\sin \delta \hfill \end{array}\right].$$ (3)

In (3), δ is the phase difference between the two orthogonal components of the light wave δ_x – δ_y.

Treating the Stokes parameters as a vector allows for the easy superposition of many incident incoherent beams of light, which allows for an elegant mathematical treatment of light properties, ranging from unpolarized to partially polarized and completely polarized light. This is achieved by expressing the light as the weighted summation of a fully polarized signal and a completely unpolarized signal. Furthermore, Mueller matrices can be used to model the change in polarization from interaction with optical elements (reflection, refraction, or scattering) during light propagation in a medium, such as lenses, filters, or biological tissue [23]. A Mueller matrix is a 4 × 4 real-valued matrix that mathematically represents how an optical element changes the polarization of light. The change in polarization is computed from the matrix–vector product of an incident Stokes vector S, with the matrix for a component M.

Two additional parameters are typically computed from the four-element Stokes vector. The first parameter is the degree of polarization (DoP), which estimates how much of the light is polarized. The DoP is computed from (4a) and is measured on a scale from 0 to 1, with 0 being completely unpolarized and 1 being completely polarized. The DoP can be further expressed in two components, the degree of linear polarization (DoLP) and the degree of circular polarization (DoCP). The DoLP (4b) measures how linearly polarized the light is, with 0 being no linear polarization and 1 being completely linearly polarized.

Similarly, the DoCP (4c) measures how circularly polarized the light is, with 0 being no circular polarization and 1 being completely circularly polarized

$$\mathrm{DoP}=\frac{\sqrt{S_1^2+S_2^2+S_3^2}}{S_0}$$ (4a)

$$\mathrm{DoLP}=\frac{\sqrt{S_1^2+S_2^2}}{S_0}$$ (4b)

$$\mathrm{DoCP}=\frac{S_3}{S_0}.$$ (4c)

The second metric is the angle of polarization (AoP), which gives the orientation of the polarization wavefront. This is the angle of the plane that the light wave describes as it propagates in space and time and is computed as

$$\mathrm{AoP}=\frac{1}{2}{\tan }^{-1}\left(\frac{S_2}{S_1}\right).$$ (5)

B. Polarization of Light Through Reflection and Refraction

Because polarization is a fundamental property of light, many organisms have evolved the capability to detect it in the natural world. To understand how this capability is useful, it helps to understand how light becomes polarized. In nature, light becomes polarized usually through reflectance or refractance of light off of an object, or through scattering as it encounters particles as it propagates through space. The DoP of the emerging light wave, after interacting with a surface, is based on the relative index of refraction between the reflecting material and medium of propagation, as well as the angle of reflection. The Mueller matrix for light reflection from a surface is

$${\mathbf{M}}_{\mathbf{reflect}}=\frac{1}{2}\left(\frac{\tan {\theta }_{-}}{\sin {\theta }_{+}}\right)\left(\begin{array}{cc}\hfill {\cos }^2{\theta }_{-}+{\cos }^2{\theta }_{+}\hfill & \hfill {\cos }^2{\theta }_{-}-{\cos }^2{\theta }_{+}\hfill \\ \hfill {\cos }^2{\theta }_{-}-{\cos }^2{\theta }_{+}\hfill & \hfill {\cos }^2{\theta }_{-}+{\cos }^2{\theta }_{+}\hfill \\ \hfill 0\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 0\hfill \\ \hfill -2\cos {\theta }_{+}\cos {\theta }_{-}\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill -2\cos {\theta }_{+}\cos {\theta }_{-}\hfill \end{array}\right)$$ (6)

where θ₋ is the incident angle θ_i subtracted from the refracted angle θ_r, and θ₊ is the addition of θ_i and θ_r. The following equation presents the Mueller matrix of the light refracted through the surface:

$${\mathbf{M}}_{\mathbf{refract}}=\left(\frac{\sin 2{\theta }_i\sin 2{\theta }_r}{2{\left(\sin {\theta }_{+}\cos {\theta }_{-}\right)}^2}\right)\times \left(\begin{array}{cccc}\hfill {\cos }^2{\theta }_{-}+1\hfill & \hfill {\cos }^2{\theta }_{-}-1\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill {\cos }^2{\theta }_{-}-1\hfill & \hfill {\cos }^2{\theta }_{-}+1\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill 2\cos {\theta }_{-}\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 2\cos {\theta }_{-}\hfill \end{array}\right).$$ (7)

The incident and refracted angles are related by Snell's law, which relates the index of medium 1 (n₁) and the incident angle (θ_i) to the index of medium 2 (n₂) and the refracted angle (θ_r)

$$n_1\sin {\theta }_i=n_2\sin {\theta }_r.$$ (8)

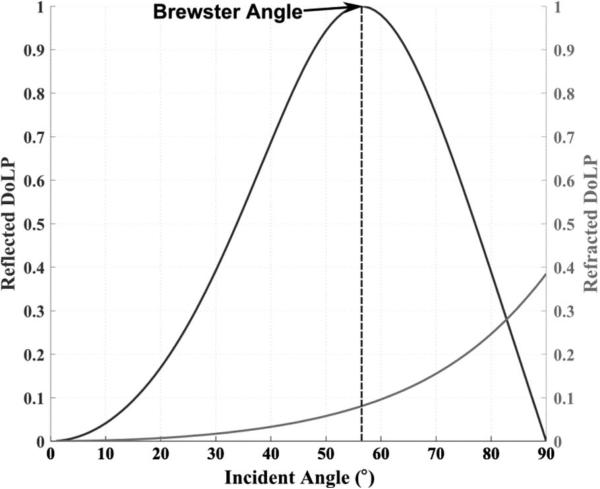
The Stokes vector for light reflected from a surface can be computed by multiplying the incident Stokes vector with the Mueller matrix of reflection from the surface (6). Assuming an incident unpolarized light (i.e., S_in = [1 0 0 0]^T), computing the reflected light S_out = S. M_reflect, for all possible incident angles (0° to 90°), results in a graph like Fig. 1, which is an example using air (n₁ = 1) and glass (n₂ = 1:5) as the two indices of refraction. In Fig. 1, the black line represents reflection and the gray line represents refraction of light. As can be seen in Fig. 1, the DoLP for glass has a maximum value of 1 for an incident angle of 56.7° . This angle is known as the Brewster angle, and it is often used to determine the index of refraction of a material in instruments such as ellipsometers.

Fig. 1.

Degree of linearly polarized light for both reflected and refracted light as a function of incident angle. In this example, air (n₁ = 1) and glass (n₂ = 1:5) are the two indices of refraction. The maximum degree of linear polarization occurs at the Brewster angle, information that can be used to identify the index of refraction of a material.

This same concept has been utilized in nature. For example, water beetles, which are attracted to the horizontally polarized light that reflects off of the surface of water, typically land on the water surface at 53° , which is the Brewster angle of water [24]. By measuring the maximum polarization signatures of the reflected light as a function of incident/reflected angle, water beetles estimate the Brewster angle of the water surface and possibly uniquely determine the location of water surfaces.

C. Polarization of Light Through Scattering

Light scatters when it encounters a charge or particle in free space. The charge or particle impacts the electric field as the field propagates through space, and this influence can affect the polarization state of the light. An example is the Rayleigh model of the sky. In the Rayleigh model, light scattered from a particle in a direction orthogonal to the axis of propagation becomes linearly polarized. This ballistic scattering from the many particles in the atmosphere creates a polarization pattern in both DoLP and AoP across the sky based on the position of the sun. In nature, the desert ant Cataglyphis fortis uses this polarization pattern of the sky to aid its navigation to and from home [25]. Honeybees also use sky polarization as part of their “waggle dance” to indicate the direction of food [26]. There is even increasing evidence that birds combine magnetic fields and celestial polarization for navigation purposes [27], [28].

Optical scattering is present in biological tissue as well. The scattering agents for light as it propagates through tissue include cells, organelles, and particles, among others. Because many of these components can be on the order of the wavelength of the propagating light, the Mie approximate solution to the Maxwell equations, which is typically referred to as the Mie scattering model, can be used to describe the effects of scattering on polarization. Absorption by tissue attenuates the intensity of light, while scattering causes a depolarization of light in the general direction of propagation. The density of the scattering agents in a tissue influences the depolarization signature of the imaged tissue. For example, high-scattering agents are typically found in cancerous tissue, which leads to depolarization of the reflected or refracted light from a tissue. Hence, there is a high correlation of light depolarization with cancerous and precancerous tissue, and detecting polarization of light can aid in early detection of these tissues [20].

III. CMOS SENSORS WITH POLARIZATION SELECTIVITY

Natural biological designs have served as the motivation for many unique sensor topologies. Real-time (i.e., 30 frames/s), full-frame image sensors [4] are a simple approach to a visual system, capturing all visual information at a given time. However, this typically creates bottlenecks in data transmission, as well as non-real-time information processing due to the large volume of image data presented to a digital processor such as computer, digital signal processors (DSPs), or field-programmable gate arrays (FPGAs). Signal processing at the focal plane, as it is typically performed in nature, can lead to significant reduction of data that are both transmitted and processed off-chip. Hence, sparse signal processing, as is found in the early visual processing in many species, such as the mantis shrimp, can serve as inspiration for efficient, low-power artificial imaging systems [29].

In the mid-1980s, a new sensor design philosophy emerged, where engineers looked at biology to gain understanding in developing lower power visual, auditory, and olfactory sensors. Some early designs [30] attempted a complete silicon model of the retina, using logarithmic photoreceptors with resistive interconnects to produce an array whose voltage at a location is a weighted spatial average of neighboring photoreceptors. Other designs sought to replicate neural firing patterns by asynchronously outputting only when detecting significant changes from each photosensitive pixel [31]–[33] or significant color changes from color-sensitive pixels [34], [35]. Some designs have even sought to directly mimic the compound eye of insects [36].

One of the main benefits of these systems has been a low-power and real-time realization of information extraction at the sensor level. These sensors have found a niche in various remote-sensing applications where power is a major constraint for sensor development [37]. Furthermore, in these applications, extracting information at the sensor level and transmitting preprocessed data can greatly reduce bandwidth and overall power consumption.

A. Overview of Classical Polarization Imaging Sensors

The polarization selectivity depends on the ability to measure the Stokes parameters. From (2), the intensity of light measured with a linear polarizer with a retarder depends on the angle of the linear polarizer (θ), the phase retardance (ϕ), and the four Stokes parameters. A unique solution for the Stokes parameters in (2) thus requires a number of measurements equal to the number of desired Stokes parameters.

To determine all four Stokes parameters, four distinct measurements are made with linear polarization filters and quarter-wave retarders. Hence, the four Stokes parameters can be determined as follows:

$$\left[\begin{array}{c}\hfill S_0=I(0°,0°)+I(90°,0°)\hfill \\ \hfill S_1=I(0°,0°)-I(90°,0°)\hfill \\ \hfill S_2=I(45°,0°)-I(135°,0°)\hfill \\ \hfill S_3=S_0-2I(45°,90°)\hfill \end{array}\right].$$ (9)

In these equations, I(0° , 0°) is the intensity of the e-vector filtered with a 0° linear polarization filter and no phase retardation, I(45°, 0°) is the intensity of the e-vector filtered with a 45° linear polarization filter and no phase retardation, and so on. The fourth Stokes parameter is computed with a 45° linear polarization filter and a quarter-wave retarder.

The most predominant method of Stokes measurement solves these equations by rotating a linear polarization filter and retarder in front of the sensor, capturing a static image at each rotation. This type of sensor is called a division-of-time polarimeter [38], since it requires capturing the same scene at multiple steps in time. This simple design suffers from a reduced frame rate, as each complete set of measurements requires multiple frames. It also requires a static scene for the duration of the measurement, since any change in the scene between rotations would induce a motion blur. As this is the simplest method for measuring static scenes, division-of-time polarimeters have realized a number of applications, from 3-D shape reconstruction [39], haze reduction [40], mapping the connectome [41], and many others.

An alternate method with static optics projects the same scene to multiple sensors. Each sensor uses a different polarizer and/or retarder in front of the optical sensor to solve for the different Stokes parameters. This type of modality is called division of amplitude [38] since the same optical scene is projected full frame multiple times at reduced amplitude per projection. The drawback to this system can be the bulk and expense of having a large array of optics and multiple sensors. Maintaining a fixed alignment of the optics so all sensors see the same coregistered image also poses a challenge to this polarization architecture, which typically requires image registration in software. These types of instruments have found some use in unmanned aerial vehicle (UAV) applications [42], [43], target detection in cluttered environments [44], and measuring the ocean radiance distribution [45]. A similar optically static method uses optics to project the same scene to different subsections of a single sensor. Each subsection contains a different analyzer to solve for the Stokes parameters. This type of sensor is called a division-of-aperture polarimeter [38], since the aperture of the sensor is subdivided for polarization measurement of the same scene. The advantage is that it requires only one sensor, but the disadvantage is that it is prone to misalignment and can contain a long optics train. Multiple scene sampling on the same array also reduces the effective resolution of the sensor, without the possibility of upsampling through interpolation. The system complexity, from maintaining the optical alignment to the image processing, has precluded them from wider use.

B. Bioinspired Polarization Imaging Sensors

Taking a cue from nature, however, would mate the polarization analyzers directly to the photosensitive element. Fig. 2 (left) shows an example of how nature has evolved polarization-sensitive vision. The compound eye of the mantis shrimp contains a group of individual photo-cells called an ommatidium. Each ommatidium has a cornea that focuses external light. The focused light is filtered through a pigment cell for color sensitivity and passes through a series of photosensitive retinular cells (R-cells). In the mantis shrimp, these cells contain an array of microvilli that can act as polarization filters. The photosensitive R-cells will signal the brain via the optic nerve, and the brain extracts visual information based on input from the array of ommatidia.

Fig 2.

(Left) The compound eye of the mantis shrimp, where ommatidia combine polarization-filtering microvilli with light-sensitive receptors. (Right) A bioinspired CMOS imager constructed with polarization sensitivity, where aluminum nanowires placed directly on top of photodiodes act as linear polarization filters.

Biomimetic approaches have also attempted to replicate the polarization sensitivity present in certain species. Early designs integrated liquid crystals [46] or birefringent crystals [5] directly to pixels. These sensors allowed for full-frame polarization contrast imaging. More advanced polarization sensors integrated filters at multiple orientations, which enabled capture of the first three Stokes parameters [12], [47], [48].

Further advances in nanotechnology and monolithic integration of nanowires with CMOS technology have enabled high-resolution versions of this paradigm [6]. The use of liquid crystal polymers and dichroic dyes has allowed a full Stokes polarimeter [10], [49]. These sensors are capable of capturing polarization information at video frame rates, and their compact realization has allowed them to pertain to remote-sensing applications, such as underwater imaging [21].

Other polarization sensor designs have attempted alternate, more biologically pertinent designs. As octopuses are known to have polarization-sensitive vision [50], a design based on polarization contrast with a resistive network sought to replicate the octopus vision system in silicon [9]. Polarization sensor designs have been developed that utilize asynchronous address event mode to output only when there are large enough changes in polarization contrast [51]. In this work, both the ommatidia functionality and neural processing circuitry have been efficiently implemented in CMOS technology.

Analogous to the microvilli in the mantis shrimp vision system [52], which function as polarization-filtering elements, bioinspired polarization sensors use pixel-matched aluminum nanowire polarization filters at 0° , 45° , 90° , and 135° , arrayed in a 2-by-2 grid called a superpixel [6], [14] (see Fig. 2, right). These filters are fabricated to be 70 nm wide and 200 nm tall and have a horizontal pitch of 140 nm. The filters are deposited postfabrication of the CMOS imager through an interference lithography process, matching the pixel pitch of the imager array of 7.4 μm by 7.4 μm. Maintaining an air gap between these filters allows for a higher extinction ratio than does embedding the filters within a layer of silicon dioxide [16].

With the maturity of nanofabrication techniques, many interesting optical designs have become feasible. For example, metamaterial surfaces acting as achromatic quarter-wave plates [18] or as high-extinction ratio polarization filters [15] can further advance the field of polarization imaging when integrated with an array of imaging elements. These advances will bring the complete imaging system design closer to biology in terms of sensitivity and selectivity to both spectral and polarization information. Foundries such as TowerJazz Semiconductor (Migdal Haemek, Israel), Dongbu HiTek (Bucheon, Korea), LFoundry (Avezzano, Italy), and TSMC (Hsinchu, Taiwan) already offer specialized CMOS fabrication processes explicitly optimized for image sensors. However, polarization-filtering capabilities are not included in regular image sensor fabrication. The key would be to integrate these emerging optical fabrication techniques with these specialized CMOS fabrication technologies at the foundry level for optimal optical performance and high yield. With such an integrated solution, future polarization imaging designs could incorporate low-power analog circuitry that mimics neural circuitry, leading to sparse on-chip computation.

C. Bioinspired Current-Mode Imaging Sensor With Polarization Sensitivity

We have designed a bioinspired polarization imaging sensor by combining CMOS imaging technology with nano-fabrication techniques to realize linear polarization filters.

In this bioinspired vision system, the photosensitive elements are monolithically integrated with aluminum nanowires, or microvilli, acting as linear polarization filters. The bioinspired photosensitive element is based on a current-mode CMOS imaging paradigm. The signal from the diode is linearly converted into a current inside the pixel, and the image is then formed from each of the independent pixels.

Circuitry on the pixel and for readout is presented in Fig. 3. The pixel consists of a charge transfer transistor (M1), reset transistor (M2), transconductance amplifier (M3), and select transistor (M4). Through a series of switching multiplexers, the output of the pixel connects either to a reset voltage V_reset or to the readout current conveyor. This bus-sharing methodology eliminates the need for two separate buses to separately connect the drain of the readout transistor and the output current bus, which reduces the pixel pitch. The transconductance amplifier (M3), also known as the readout transistor, is biased to operate in the linear mode. This ensures a linear relationship between an output drain current and input photo-voltage applied at the gate of transistor M3. The linearity is critical in correcting threshold offset mismatches between readout transistors via a technique known as correlated double sampling (CDS).

Fig. 3.

Current-mode pixel schematic and peripheral readout circuitry of the imaging sensor. The pixel's readout transistor operates in the linear mode, allowing for high linearity between incident photons on the photodiode and output current from the pixel.

Current-mode image sensors rely on current conveyors to copy currents from the pixels to the periphery while providing a fixed reference voltage to the input node, that is, to the drain node of the pixel's readout transistor (M3). The classic current conveyor design [53] uses four transistors, two n-channel (NMOS) and two p-channel (PMOS) metal-oxide-semiconductor transistors, in a complementary configuration. The design is compact, but the output impedance is limited, and the transistors are subject to nonlinearity due to channel length modulation. Furthermore, the voltage at the input terminal of the current conveyor (i.e., the voltage at the drain node of the pixel's readout transistor) can vary as much as 20% for the typical input current from a pixel. A single transistor design [54] improves settling time and power consumption but decreases linearity of the output current.

Because the polarization information conveyed in the S₁ and S₂ parameters is based on the linear difference in pixel intensities, pixel linearity is crucial to accurate polarization measurement. Alternate current conveyor designs use an operational amplifier with a transistor in the feedback path. The conveyor has high linearity and can be used for novel current-mode designs [55], but at the cost of increased power consumption and area.

To improve the performance of the output current conveyor, a regulated cascoded structure for the current conveyor is used. Since all transistors in the current conveyor operate in the saturation mode, the potentials on the gates of transistors M13 and M14 are set by a biasing current. Since the gate potential of M13 (M14) and drain potential of M15 (M16) are the same, the channel length modulation effect is eliminated between the two branches, and the two drain currents are the same. Furthermore, the impedance of the output branch is increased due to the regulated cascode structure by a factor of (g_m * r_o)², where g_m is the transconductance and r_o is the small signal output impedance. The high output impedance of the output branch is important when supplying a current to the next processing stage. This improved performance does come at a cost of increase in chip area compared with the aforementioned implementations.

The row-parallel current conveyors set the reference voltage on the output bus and copy the current from the pixel to the output branch, using transistor M20 to switch along the pixels in the column. The current conveyors are implemented by connecting two current mirrors in a negative feedback configuration. Transistors M11–M16 form a PMOS-regulated cascode current mirror connected with an NMOS-regulated cascode current mirror composed of transistors M5–M8. Transistors M13 and M14 operate in the saturation region, and the gate-to-source potentials are set by a reference current source of 1 μA. Hence, the drain nodes of transistors M15 and M16 are at the same potential. Transistors M11 and M12 provide negative feedback to transistors M13 and M14, respectively, ensuring that all transistors remain in the saturation mode of operation. Since transistors M15 and M16 have the same source, gate, and drain potential, the drain currents flowing through these two transistors are the same.

Transistors M7 and M8 pin the drain voltage of transistors M5 and M6 because the bias current through these transistors sets the gate voltage on each, respectively. Since the currents are the same flowing through transistors M5 and M6, and since the gate and drain potentials are the same for these transistors, the drain potential is the same for these transistors. Therefore, the drain potential on transistor M5 is set to V_ref.

The readout transistor in the pixel (M3) is designed to operate in the linear current mode by ensuring that the drain potential of the M3 transistor is lower than the gate potential by a threshold during the entire mode of operation. This is achieved by setting the V_ref bias potential to 0.2 V and resetting the pixel, which sets the gate voltage of M3 to 2.7 V. Since the threshold voltage of the transistor is ~0.6 V, the lower limit on the gate of M3 transistor is set to 0.7 V in order to operate in the linear mode. The output current from transistor M3 is described by

$$I\text{photo}={\mu }_n{C}_{ox}\frac{W}{L}\left((V_{\text{photo}}-V_{\mathrm{TH},\mathrm{M}1})V_{\mathrm{ref}}-\frac{V_{\mathrm{ref}}^2}{2}\right).$$ (10)

In (10), μ_n is the mobility of electrons, C_ox is the gate capacitance, and V_th is the threshold voltage of the transistor. The current conveyor holds V_ref on the drain of the readout transistor M3. By keeping V_ref constant, the output current is linear with respect to the photovoltage.

The pixel timing is shown in Fig. 4. During FD Reset, reset transistor M2 and select transistor M4 are activated. With these transistors activated, setting the voltage on the Out node of the pixel to V_reset drives the floating diffusion node V_fd to the reset potential. After resetting the floating diffusion, the reset value can be read out during Reset Readout for difference double sampling. During the Pixel to FD stage, the charge transfer transistor M1 activates, placing the integrated photovoltage onto the floating diffusion. After turning M1 off, readout of all the pixels in the row takes place. M1 reactivates during Pixel Reset, after which the Out switches back to V_reset, and M2 reactivates, pulling the photodiode up to the reset potential. All three switch transistors turn off, and the readout proceeds to the next column.

Fig. 4.

Timing diagram for operating a current-mode pixel. The timing information is provided from digital circuitry placed in the periphery of the imaging array.

The pixel's layout is implemented in a 180-nm-feature CMOS image sensor process with pinned photodiode capabilities. Fig. 5 shows a schematic of the pixel. The charge transfer transistor is highly optimized to allow full transfer of all charges from the photodiode capacitance to the floating diffusion, with the node heavily shielded for light sensitivity. This node is capable of holding electron charges with no significant losses for over 5 ms at an intensity of 60 μW/cm².

Fig. 5.

Cross section of the pinned photodiode together with the reset, transfer, readout, and select transistors. The diode is an n-type diode on a p-substrate with an insulating barrier between. The readout transistor operates as a transconductor, providing a linear relationship between accumulated photo charges and an output current.

IV. SIGNAL PROCESSING ALGORITHMS FOR BIOINSPIRED POLARIZATION SENSORS

The recent introduction of bioinspired polarization image sensors has opened up several research areas in signal processing dealing with how best to reconstruct polarization images from measured data. In this section, we highlight three such research areas: 1) calibration of optical performance due to defects at the nanoscale; 2) spatial interpolation for increased polarization accuracy; and 3) processing to visually interpret polarization information.

A. Calibration of Bioinspired Polarization Sensors

Calibration of bioinspired polarization sensors aims to correct imperfections and variations of the pixelated polarization filters due to their nanofabrication. Variations in the dimensions of aluminum nanowires cause the optical properties of the pixelated polarization filters (namely, transmission and extinction ratios) to vary by as much as 20% across an imaging array composed of 1000 by 1000 pixels [56]. Fig. 6 presents a scanning electron microscope (SEM) image of nanowire pixelated polarization filters, where dimensional variations, as well as damage such as cracks, can be clearly observed. Better nano-fabrication instruments can partially mitigate these problems, at considerable expense, but will not completely eliminate them. Thus, we take a mathematical approach, using mathematical models of the optics and imaging electronics to compensate for nonidealities occurring at the nanoscale [56].

Fig. 6.

SEM image of pixelated polarization filters fabricated via interference lithography followed by reactive ion etching. Variations between individual nanowires lead to variation of the optical response of pixelated filters.

Each pixel–filter pair's response is modeled as a first-order linear system according to

$$I=\left(\begin{array}{cccc}\hfill g\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill \end{array}\right)\cdot \mathbf{M}\cdot {\overrightarrow{S}}_{\mathrm{in}}+d=\overrightarrow{A}\cdot {\overrightarrow{S}}_{\mathrm{in}}+d.$$ (11)

The measured value I is the product of the top row of the filter's Mueller matrix M with the photodiode's conversion gain g and the Stokes vector of the incident light ${\overrightarrow{S}}_{\mathrm{in}}$, plus the photodiode's dark offset d. In order to correct for errors in the 4-D analysis vector $\overrightarrow{A}$, at least four measurements must be considered simultaneously. The typical case is to assume that ${\overrightarrow{S}}_{\mathrm{in}}$ is uniform across each superpixel and thus treat each superpixel as a unit

$$\overrightarrow{I}=\mathbf{A}\cdot {\overrightarrow{S}}_{\mathrm{in}}+\overrightarrow{d}.$$ (12)

In this case, $\overrightarrow{I}$, A, and $\overrightarrow{d}$ are the vertical concatenation of each of the superpixel's constituent pixels I, $\overrightarrow{A}$, and d, respectively.

The parameters A and $\overrightarrow{d}$ can be learned for each superpixel by measuring $\overrightarrow{I}$ with n known values of ${\overrightarrow{S}}_{\mathrm{in}}$ and performing a least squares fit as per

$$\left(\mathbf{A}\overrightarrow{d}\right)=({\overrightarrow{I}}_1\cdots {\overrightarrow{I}}_n){\left(\begin{array}{ccc}\hfill {\overrightarrow{S}}_{in,1}& \hfill \cdots \hfill & {\overrightarrow{S}}_{\mathrm{in},n}\hfill \\ \hfill 1& \hfill \hfill & 1\hfill \end{array}\right)}^{+}.$$ (13)

A minimum of five measurements must be taken, but increasing n will reduce the impact of noise on the parameters.

Once the parameters are learned, the incident Stokes vector can be reconstructed via

$${\overrightarrow{S}}_{in}\approx {\mathbf{A}}^{+}\cdot (\overrightarrow{I}-\overrightarrow{d}).$$ (14)

However, if the intent is to use more sophisticated reconstruction methods such as interpolation, then the parameters can instead be used to transform the measurement into what an ideal superpixel would measure

$${\overrightarrow{I}}_{\text{ideal}}\approx {\mathbf{A}}_{\text{ideal}}{\mathbf{A}}^{+}\cdot (\overrightarrow{I}-\overrightarrow{d})=\mathbf{G}\cdot (\overrightarrow{I}-\overrightarrow{d}).$$ (15)

This technique can correct for variations in the filters’ transmission and extinction ratios, orientation angles, and even retardance as necessary. Reductions in reconstruction error from 20% to 0.5% have been achieved with this mathematical model [56]. Fig. 7 shows the difference in visual quality between uncalibrated and calibrated reconstructions of the DoLP. This calibration method not only reduces the reconstruction errors but also eliminates the fixed-pattern noise present from both filter nanofabrication and sensor integrated circuit fabrication.

Fig. 7.

Uncalibrated (left) and calibrated (right) DoLP images of a moving van. Spatial variation in the optical response of individual polarization pixels is removed using a matrix-type calibration scheme. This results in a more detailed and accurate DoLP (top) and AoP (bottom), as can be seen by the emergence of the trees in the background. Refer to Video 1 in the supplementary material.

B. Interpolation of Polarization Information

A second image processing challenge is interpolating the correct polarization component from its neighbors, as the DoFP array subsamples the image. Similar to the case with color, many interpolation algorithms may be used, from simple bilinear interpolation to more complex cubic spline methods, each with varying degrees of accuracy [57], [58]. An example is shown in Fig. 8. Because of the pixelated filters, edges, such as the white spots on the dark fish, can cause erroneous DoLP and AoP readings. Processing the image using bicubic interpolation greatly reduces these false polarization signatures.

Fig. 8.

Importance of interpolation. Edge artifacts cause false polarization signatures in both DoLP (inset, top right) and AoP (inset, bottom right). Use of interpolation, in this instance bicubic, significantly reduces these artifacts (inset, center column) and results in greater accuracy. The data were taken with an underwater imaging setup at Lizard Island Research Station in Australia. Refer to Video 2 in the supplementary material.

The correlated nature of the polarization filter intensities does allow for some new interpolation methods specific to polarization. Some examples of these methods are Fourier transform techniques [59], interpolation techniques based on local gradients [60], polarization correlations between neighboring pixels [61], and Gaussian processes [62].

The performance of these different interpolation methods is usually evaluated both quantitatively and visually. Mean square error (MSE) and the modulation transfer function (MTF) [57], [58], [60] are regular quantitative ways to measure the performance of an interpolation method. MSE measures the difference in interpolated results compared with a known or generated ground truth image. This allows evaluation of the optical artifacts introduced during the interpolation step. The MTF, which measures the spectrum of the point spread function, gives an indication of the spatial fidelity of the sensor. When used as an evaluator for interpolation techniques, it demonstrates how well the given technique recovers spatial frequencies beyond simple decimation. In spatially bandlimited images, full recovery is possible using a fast Fourier transform technique. In the more general case, small, uniformly applied interpolation kernels, such as bilinear- or bicubic-based interpolation, perform worse than edge-detection-based [60] or local-prediction-based [62] interpolation methods in terms of MSE. But they have less computational complexity because they are separable filters, which allows them to process images with fewer mathematical operations for real-time display (i.e., 30 frames/s at 1-megapixel spatial resolution).

The signal processing challenges for this new class of bioinspired polarization imaging sensors are as important as the actual imaging hardware (electronics and optics) design. Polarization data generated from these sensors without proper signal processing can lead to erroneous conclusions, as can be seen in Fig. 8. In this example, high polarization patterns across the fish are due to pixelation of the polarization filters in the imager and are not observed across the fish if the data are properly processed. Similar artifacts can be observed when imaging cells and tissues, as described in Section VI. In order for this class of sensors to live up to its full potential, signal processing algorithms have to be developed with understanding of the underlying structure of the sensor.

C. Processing to Visually Interpret Polarization Information

Since the human eye is polarization insensitive, displaying polarization information has posed a serious hurdle and has impeded the advancement of polarization research. Displaying the four Stokes parameters can often lead to an overwhelming amount of information presented to an end user. Measurements of the degree and angle of polarization combine the information from the four Stokes parameters and capture two important aspects of the light field: the amount of polarization and the major axis of oscillation, respectively. These two parameters can be viewed separately or combined into a single image using hue-saturation-value (HSV) transformation, greatly simplifying the presented information [63], [64]. Nevertheless, displaying polarization information is still a challenging problem. Further research on displaying polarization information is needed and will be a key factor for further advancing the field of polarization and bridging polarization research to non-optics and non-engineering fields.

V. OPTICAL AND ELECTRICAL CHARACTERIZATION OF SENSORS

Because of the infancy of the bioinspired polarization imaging sensor, a detailed opto–electronic performance evaluation of these sensors has to be systematically developed. The performance of these sensors depends on many optical and electronic parameters. Light intensity impinging on the sensor plays a role, as the underlying sensor may be limited by dark noise at low intensities and shot noise at higher intensities. Wavelength influences the performance of both the nanowire polarizers and the sensor, as the sensor has a defined quantum efficiency, and the filters’ transmission properties are wavelength dependent. Focus can also be an issue, as the possibility exists of divergent light transmitting through a filter being detected through a neighboring pixel. The aperture size (i.e., varying the F-number) also impacts the divergence angle of the incident light. A detailed system performance evaluation, such as the one proposed in [65], which includes an evaluation for different intensities, wavelengths, divergence, and polarization states, can serve as an illustrative testing methodology.

The bioinspired sensor described in Section III-C was given a series of electrical and optical tests to characterize its performance. For the electrical tests, a set of narrowband light-emitting diodes (LEDs) (OPTEK OVTL01L-GAGS) were placed flush to an integrating sphere (Thorlabs IS200). The light was then collimated with an aspheric condensing lens (Thorlabs ACL2520) before reaching the sensor. The intensity of the light was changed by altering the current through the LEDs with a constant direct current (dc) power supply (Agilent E3631A). The reference optical intensity was measured at the focal plane of the sensor with a calibrated photodiode (Thorlabs S120VC). Fig. 9(a) shows a diagram of the setup.

Fig. 9.

(a) Setup for electrical characterization. The integrating sphere/aspheric lens combination creates a uniform field. (b) Setup for polarization characterization, using the same water-immersion lens, submerged in saline, as used for neural recording experiments.

For the polarization characterization, to better calibrate for the optics used in the neural recording experiments presented in Section VI, the same integrating sphere/LED combination was used as the light source. A rotating polarization element (Newport 10LP-Vis-B mounted in a Thorlabs PRM1Z8 stage) was used to generate input linearly polarized light of a known AoP. The sensor used a 10× water-immersion lens (Olympus UMPLFLN10XW) submerged in a glass dish of water to view the flat field generated from the light source. Fig. 9(b) shows a diagram of the setup.

A. Electrical Characterization of the CMOS Image Sensor

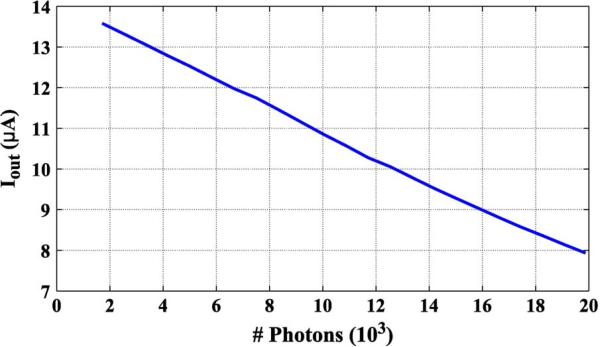
Fig. 10 shows the output current measured as a function of the incident light intensity. The current shows a linear response with respect to the incident light, with 99% linearity in the range. This primarily results from the current conveyor. The regulated cascode structure helps eliminate channel length modulation while also maintaining a steady voltage reference. Fig. 11 shows the signal-to-noise ratio (SNR) of the current-mode sensor. The maximum SNR for our sensor is 43.6 dB, consistent with the shot noise limit based on the pixel well-depth capacity. Fig. 12 shows a histogram of image intensities. The fixed-pattern noise for room light intensity is 0.1% from the saturated level, comparable to voltage-mode imaging sensors. Also, due to the low currents and small array size, bus resistance variation remains minimal.

Fig. 10.

Measured output current from a pixel versus the number of incident photons on the photodiode.

Fig. 11.

SNR of the current-mode imaging sensor as a function of the number of incident photons.

Fig. 12.

Histogram of all responses of pixels in the imaging array to a uniform illumination at room light intensity. The fixed pattern noise of the current-mode imaging sensor

B. Polarization Characterization of the Sensor

The sensor was tested for polarization sensitivity. To improve polarization sensitivity, a Mueller matrix calibration approach was used [56]. Fig. 13 shows the pixel response to polarized light after calibration. Malus's law (16) describes the intensity of light seen through two polarizers offset at θ_i degrees

$$I=I_0{\cos }^2{\theta }_i.$$ (16)

The pixels in the polarization sensor show nearly the same response. The more uniform response after calibration also manifests in a more linear AoP than the raw measurement, as depicted in Fig. 14.

Fig. 13.

Optical response to four neighboring pixels to incident linearly polarized light. As the angle of polarization of the incident light is swept from 0° to 180°, the pixels follow Malus's law for polarization.

Fig. 14.

Measured angle of polarization as a function of the incident light angle of polarization for our bioinspired polarization imager.

VI. BIOMEDICAL APPLICATIONS FOR BIOINSPIRED POLARIZATION IMAGING SENSORS

The emergence of bioinspired polarization imaging sensors has enabled rapid advancements in several biomedical areas. In this section, three biomedical applications are covered: 1) label-free optical neural recording; 2) soft tissue stress analysis; and 3) in vivo endoscopic imaging for flat lesion detection.

A. Optical Neural Recording With Polarization

Imaging sensors have greatly advanced the field of neuroscience, especially through the use of fluorescent imaging techniques. These techniques have enabled the in vivo capture of neural activity from large ensembles of neurons over wide spatial areas. With Ca²⁺ probes or voltage-sensitive dyes, neuronal action potentials trigger a corresponding optical change. This may change the optical intensity, as when a photon is released upon a transition from an excited state to a ground state. It may also change the spectrum of light during neural activation [66]. Although fluorescent imaging has enabled a tremendous success in the neuroscience field, a number of problems impede further elucidation of neural activity. Many calcium markers require input excitation in the high-energy ultraviolet (UV) spectrum, which can cause cell damage over time. Additionally, fluorescent signals may be directly toxic to the cell, or indirectly toxic by interacting with nearby molecules during excitation [67]. Fluorescent signals also decrease in intensity over time, after repeated excitation and emission cycles, a process called photo-bleaching. Further, some structures in the cell intrinsically fluoresce, overwhelming the measurement of any weaker desired signals.

Two-photon excitation techniques mitigate some of these deficiencies. This technique requires the simultaneous excitation of two low-energy photons to produce a higher energy fluorescent photon. Two-photon excitation typically focuses a high-power pulsed laser at the recording image plane. Doing so reduces the background, as a signal requires the simultaneous excitation of two photons, thus increasing the SNR of the neural recording. Additionally, tightly focusing the input beam to increase spot intensity also significantly reduces background photobleaching. Since the excitation wavelength is usually in the near-infrared, two-photon techniques allow imaging deeper into tissue than single-photon techniques that require UV. These fluorescent techniques, however, can still result in photobleaching over time, reducing the potential for long-term recording experiments.

Alternate optical techniques exist for measuring neural activity. These methods capture the intrinsic changes of light scattered from neural cells without the use of molecular reporters. Because these techniques rely only on intrinsic signals, they will not result in photobleaching after repeated stimulus cycles, allowing for the possibility of long recording periods. Since the signals are optical, they also do not require the introduction of potentially destructive electrophysiology probes for measurement.

State-of-the-art techniques for using polarization to measure neural activity are based on in vitro observation of the birefringence change during stimulus. Isolated neural cells are placed between two crossed polarizers and are given an electrical stimulus while optical changes are recorded. During an action potential, the birefringence of the neuron changes, thus causing an intensity change through the crossed polarizer. Initial experiments were performed on squid giant axons, with the SNR of early detection methods limiting them to cultured neurons [68], [69]. More recent experiments have been able to go beyond cultured neurons and use those extracted from lobster (Homarus americanus) and crayfish (Orconectes rusticus) to show birefringence change during action potentials [70]. Further experiments on the lobster nerve show that the reflection of s-polarized light off the nerve through a p-polarized filter also exhibits an optical intensity change during an action potential propagation [71]. Since the birefringence changes, it is also possible to use circularly polarized light [72] to detect action potentials. However, all of these in vitro methods have relied on isolated nerves, with most of these methods employing only a single photodetector. A polarization sensor that has multiple detectors, like the one presented here, could simultaneously capture populations of neurons in vivo.

Reflectance

From the theory covered in Section II-B, unpolarized light reflecting off of an object or tissue becomes polarized based on the incident angle and index of refraction. Therefore, if the incident lighting conditions remain the same but the index of refraction changes, this change manifests as a change in the reflected polarization state of light. Neurons during an action potential show a change in the index of refraction [73] and thus should also show a change in the reflected polarization.

Detection of this change can be hindered in the presence of scattering, which causes a decrease in intensity in the direction of propagation. Since neurons typically lay within tissue, the small intrinsic changes in optical intensity that accompany an action potential can be lost. Polarization signals can be more robust to scattering, as evidenced by the use of polarization to see farther in hazy environments [40]. This can be true in tissue as well, with the polarization signal persisting longer through multiple scattering events [74]. This means that detection of the intrinsic polarization signal change might be possible.

If a neuron resides in tissue, then unpolarized light will scatter on entrance to the tissue, reflect off of the neuron, and scatter back toward the camera. The light will be partially polarized upon reflection, and although this polarized reflection will scatter during propagation back to the sensor, as a polarized reflection it will be less affected by the scattering, making detection possible with a real-time polarimeter.

Polarization Imager

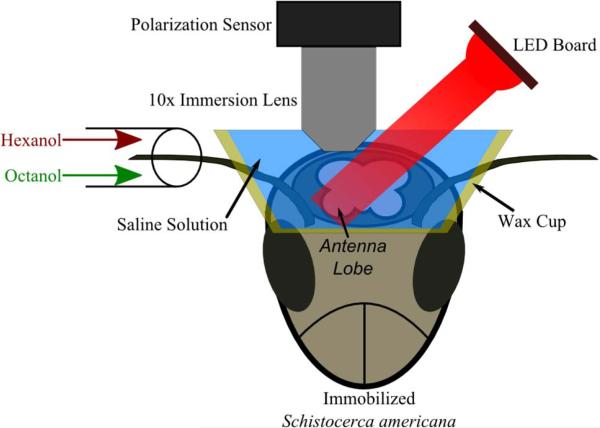
Fig. 15 shows the setup for optical neural capture [75]. Optical neural activity was obtained from the antennal lobe of the locust (Schistocerca americana). The experiment required exposing the locust brain. To ensure the locust's viability, a wax cup formed a watertight seal around the exposed area, holding a saline solution [76]. To minimize motion artifacts, the locust was immobilized on a floating optical table. Odors in airflow were introduced to the locust through a plastic tube placed around the antenna at a constant rate of 0.75 L/min. The two odors used in the experiment, 1% hexanol and 1% 2-octanol, were both diluted in mineral oil. During the stimulation period, odors were introduced at a rate of 0.1 L/min. The airflow is aspirated through a charcoal filter at the same rate of flow around the antenna.

Fig. 15.

Experimental setup for in vivo polarization-based optical neural recording.

To image in vivo the locust's olfactory neurons, the bio-inspired current-mode CMOS polarization sensor was attached through a lens tube to an Olympus UMPLFLN10XW water-immersion objective with 10× magnification. The objective was placed in the saline solution and was focused on the surface of the antennal lobe area of the brain closest to the odor tube. As the focus is on the surface, the frame rate of the sensor in these experiments (20 frames/s) allows detection of the aggregate response of populations of surface neurons. The light source used for the optical recording was a custom circuit board containing ten 625-nm center-wavelength LEDs, powered by a constant-current power supply. A microcontroller synchronized the video frames and a trigger used for introduction of the odor stimuli.

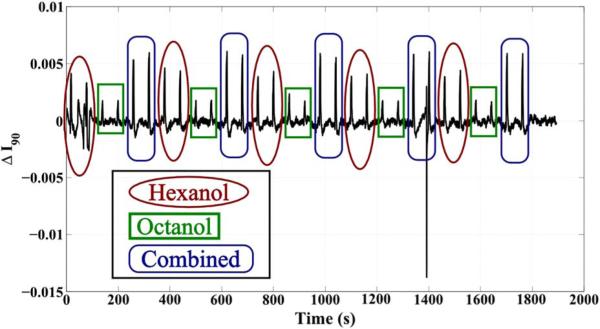
We used two different stimulation protocols for two different experiments. In the first experiment, odors were introduced for 4-s puffs at 60-s intervals. The odors were interspersed as two puffs of hexanol, two puffs of 2-octanol, and two puffs of both odors combined. The sequence was repeated five times. The second experiment used the same 4-s puffs in 60-s increments, but in this case the odors are introduced consecutively as ten hexanol puffs, ten 2-octanol puffs, and ten combined puffs.

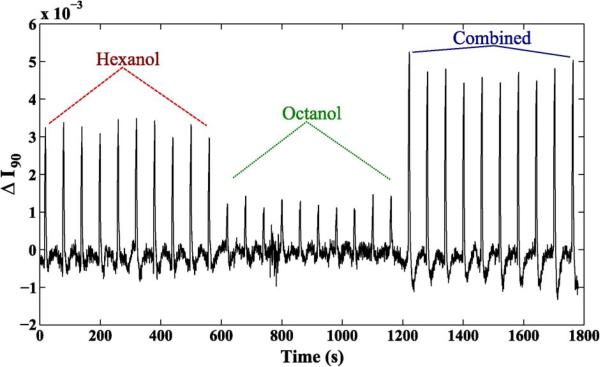
The data were filtered using a zero-phase bandpass filter to eliminate high-frequency noise and low-frequency drift. To improve the SNR of the neural signal, the data were also spatially filtered from an 11 × 11 region of pixels within the antennal lobe. Fig. 16 shows the results of the second, 10-puff experiment. The average change for each puff of hexanol was 0.38% ± 0.02%; 2-octanol, 0.15% ± 0.02%; and combined odors, 0.45% ± 0.03%. The stronger response for hexanol over 2-octanol is consistent with electrophysiological data. This trend persisted even for highly interspersed sequences in the first, two-puff experiment (Fig. 17): the average change for hexanol was 0.36% ± 0.06%; for 2-octanol, 0.16% ± 0.04%; and for the combined odor, 0.54% ± 0.02%.

Fig. 16.

In vivo measurements from a population of neurons in the locust's antennal lobe. The locust antenna was exposed to series of ten puffs of hexanol, octanol, or both combined, with each puff lasting for 4 s, followed by 56 s of no stimulus.

Fig. 17.

In vivo measurements from a population of neurons in the locust antennal lobe to highly interspersed odors during the first experiment, comprising two puffs per odor exposure.

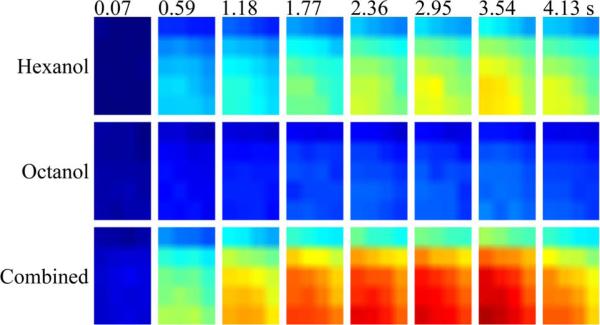
Fig. 18 presents 2-D maps of the neural activation pattern during stimulus presentation with the second protocol. The top row is the neural response to a hexanol puff, the middle row is the neural response to a 2-octanol puff, and the last row shows the neural response to a combination puff of both odors. The eight different images per row depict the neural activity at a particular time interval indicated at the top of each image.

Fig. 18.

Spatial activation of neural activity across the locust's antennal lobe. Each 2-D map is a dorsal view, with the left as lateral, right as medial, top as caudal, and bottom as rostral. The eight images per row represent neural activity at particular time intervals indicated at top of each column. Refer to Video 3 in the supplementary material.

The activation maps show a response that spreads from the portion of the lobe closest to the antenna, and the source of odor, outward through the rest of the antennal lobe. The images show some similarity to the response dynamics observed in the population neural activity. The maps show the measurement of the scattering of light changes from the activation of populations of neurons. It has been previously shown that these changes are proportional to the change in voltage potential during activation [69].

This new class of bioinspired polarization imaging sensors is opening unprecedented opportunities in the advancement of the knowledge in neuroscience. The possibility of recording neural activity from a large population of neurons with high temporal fidelity can help in understanding how information is processed in the olfactory system or other sensory systems in the brain. Such questions as how the primary coding dimensions, time and space, are used in biological signal processing can possibly be answered. These imaging sensors can ultimately lead to implantable neural recording devices based on measuring the optical intrinsic signals. The monolithic integration of optical filters with CMOS imaging arrays makes this sensor architecture the only viable solution for implantable devices in animal models, allowing the study of neural activity in awake, freely moving animals.

B. Real-Time Measurement of Dynamically Loaded Soft Tissue

The bioinspired polarization imager allows for real-time measurement of dynamically loaded tissue [77]. Measuring the alignment of collagen fibers gives insight into the anisotropy and homogeneity of the tissue's micro-structural organization and enables characterization of structure–function relationships through correlation of alignment data with measured mechanical properties under different loading conditions. Traditional measurements involve applying a fixed amount of force to the tissue and then rotating crossed polarizers on either side of the tissue. The structure of collagen fibers (i.e., long and thin) creates optical birefringence along the direction of the alignment of each fiber, which causes transmitted illumination through the crossed polarizers. Rotation of the crossed polarizers through 180° enables detection of the angles of maximum and minimum transmitted illumination, which correspond to the alignment direction of the collagen fibers.

This imaging method is a standard technique for analysis of tissue alignment; however, the time required for rotation of the polarizers precludes real-time measurement of dynamically loaded tissue. Further, errors are introduced using this method, as the force applied to the tissue may not remain constant during the time of rotation (and image acquisition). This leads to inaccuracy in the polarization measurements for the collagen fiber alignment and orientation.

The bioinspired polarization imager does not require the rotation of any polarization analyzing components and thus can be used to make real-time (i.e., 30 frames/s) measurements of dynamically loaded tissue. This modality requires the use of transmitted circularly polarized light through the tissue, which has a DoLP of 0. The birefringence of the tissue introduces a phase delay between the transmitted x/y field components, causing the circularly polarized light to become more linearly polarized as it passes through the tissue. In fact, the amount of phase retardance ϕ between x and y is the inverse sine of the DoLP

$$\begin{array}{cc}\hfill \mathrm{DoLP}& =\frac{\sqrt{S_1^2+S_2^2}}{S_0}=\frac{\sqrt{({\sin }^{2}2\theta +{\cos }^{2}2\theta ){\sin }^2\varphi }}{1}\hfill \\ \hfill & =\sin \varphi .\hfill \end{array}$$ (17)

The AoP of the transmitted light corresponds to the alignment of the tissue. The alignment of the fiber θ corresponds to the fast axis of a linear retarder. Thus, if the tissue is rotated with respect to the sensor, computing the AoP shows the alignment of the fiber

$$\mathrm{AoP}=\frac{{\tan }^{-1}\left(\frac{S_2}{S_1}\right)}{2}=\frac{(90°-2\theta )}{2}=\theta -45°.$$ (18)

Since the AoP shows the alignment, and the DoFP polarimeter captures the AoP at real-time speeds, the DoFP polarimeter is also capable of computing the spread in the AoP, which shows the spread in the fiber alignment. The AoP spread is an indicator of the relative strength or weakness of the tissue, as smaller spreads in the fiber alignment generally correlate with stronger tissue along the principal fiber direction.

This technique was evaluated using a thin section (~300 μm) of bovine flexor tendon, which was selected as a representative soft connective tissue of highly aligned collagen fibers. The tendon was secured to tissue clamps and loaded using a computer-controlled linear actuator, which precisely measures the force applied to the tendon using a six-degree-of-freedom sensor. A linear polarizer was placed at 45° with respect to a broadband quarter-wave plate to generate circularly polarized light. We used a standard 16-mm fixed-focus lens with our DoFP polarimeter [6] to measure the light transmitted through the tendon. The tissue was cyclically loaded at 1 Hz, with a displacement amplitude of 1 mm.

Fig. 19 shows an example of the tendon under strain. The images on the left demonstrate that the DoLP is maximal when the tissue is subject to the highest force. The image on the right shows the AoP with the angle mapped to the hue in the HSV color space. The graphs at the bottom chart the change in retardance (left) and the spread of the AoP (right) in the central portion of the tissue. Both curves follow the 1-Hz loading, showing that the method is capable of real-time capture of the tissue dynamics.

Fig. 19.

Bovine flexor tendon under cyclic load. (Left) DoLP (top) and change in retardance (bottom) over time. (Right) AoP (top), which corresponds to the collagen alignment, and spread in alignment angle (bottom). Refer to Video 4 in the supplementary material.

This imaging method opens up the possibility of using even more complex loading protocols that require high-speed, real-time measurements (e.g., step and impulse forces), much faster cyclic loading, or high-speed observation of tissue failure. This can lead to better understanding of the mechanical properties of connective tissues, yield insight into structure–function relationships in health and disease, and provide guidance for novel development of orthopedic structures and devices.

C. Real-Time Endoscopy Imaging of Flat Cancerous Lesions in a Murine Colorectal Tumor Model With The Bioinspired Polarization Imager

Flat depressed cancerous and precancerous lesions in colitis-associated cancer have been associated with poor clinical outcomes. The current gold standard diagnostic regime involves using a color endoscope that is incapable of capturing flat lesions, which are abundant in this patient population. With about 50%–80% of these lesions going undetected using color endoscopy, there is much room for improvement. Use of targeted molecular markers in optical imaging [78] has demonstrated that they have a unique ability to accumulate in both precancerous and cancerous lesions, making them a strong candidate for visual enhancement. The major drawback is the uncertainty in the lack of signal in other visually suspicious regions that could be dysplastic or cancerous. Investigation and validation of these require biopsy and external analysis.

Polarization provides a possible complementary channel to aid in online and in vivo diagnosis. Since dysplastic and cancerous regions are structurally different from those of normal tissue, observation of the reflected polarization signature could provide detection that does not require biopsy and histological analysis. Cancerous and dysplastic tissues typically contain higher densities of scattering agents, causing them to exhibit a greater level of depolarization compared with neighboring healthy tissue. Detecting this polarization in vivo during an endoscopy is made possible by the development of a sensor capable of real-time measurement of polarization, such as the bioinspired, fully integrated sensors showcased here.

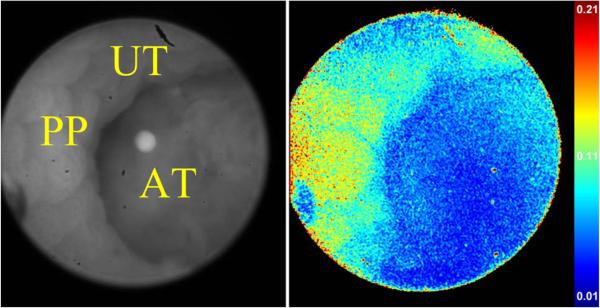
We have tested the use of a complementary fluorescence/polarization endoscope in mice with colorectal tumors induced through the azoxymethane–dextran sodium sulfate (AOM–DSS) protocol [19]. We topically applied LS301, a fluorescent dye with emission in the near-infrared, on suspect regions in the mouse colon. These regions were visually inspected using a Karl Storz Hopkins rod endoscope, to which we could attach a fluorescence-sensitive CCD camera (Fluoro Vivo) or the bioinspired polarization sensor [6]. Guided by the fluorescent signals, we used the polarization sensor to image suspected regions of the colon. In the example shown in Fig. 20, we were able to detect the tumor region by its lower DoLP compared with both the Peyer's patch and uninvolved tissue. From the various samples, we found that both tumors (0.0414 ± 0.0142) and flat lesions (0.0225 ± 0.0073) showed lower DoLP signatures than nearby surrounding uninvolved tissue (0.0816 ± 0.0173 and 0.0924 ± 0.0284, respectively). These signatures were verified using fluorescence, and further validated with histology.

Fig. 20.

DoLP image from in vivo endoscopy of mouse colon. AT: adenomatous tumor; PP: Peyer's patch; UT: uninvolved tissue. Refer to Video 5 in the supplementary material.

The integration of nanowire polarization filters with an array of CMOS imaging elements generates a compact imaging system capable of providing polarization information with high spatial and temporal fidelity. This compact polarization imaging sensor is the only one to date that can be integrated in the front tip of flexible endos-copes. Such integration can lead to unprecedented imaging capabilities for early detection of cancerous tissues in humans. To achieve this goal, advancements in nano-fabrication techniques and nanomaterials, in signal processing and information display, and in system-level instrumentation development would be required, together with a multidisciplinary approach to improve diagnosis of cancerous and precancerous lesions.

VII. CONCLUSION

In this paper, we have presented a bioinspired CMOS current-mode polarization imaging sensor based on the compound eye of the mantis shrimp. The shrimp's eye contains groups of individual photocells called ommatidia. Each ommatidium combines polarization-filtering micro-villi with light-sensitive receptors. The same approach has been taken in constructing a CMOS imager with polarization sensitivity, with aluminum nanowires acting as linear polarization filters, placed directly on top of photodiodes.

The realization of this new class of polarization imaging sensors has opened up new research areas in signal processing and several new applications. Because of defects in the nanostructures that are used to realize the polarization filters, mathematical modeling is necessary to calibrate these sensors. The calibration routine is based on Mueller matrix modeling of individual pixels’ optical response and combines machine learning techniques to find optimal parameters to correct the optical response of the filters.

Interpolation is another key signal processing area that is currently in its infancy for polarization sensors. This technique needs to be further developed to increase the accuracy of the captured polarization information. The success of these low-level signal processing algorithms will be key for the overall success of these bioinspired polarization sensors.

We have used this class of imaging sensors in three biomedical areas: label-free optical neural recording, dynamic tissue strength analysis, and early diagnosis of flat cancerous lesions in a murine colorectal tumor model. The real-time imaging capabilities of polarization information complemented with high spatial fidelity have enabled the early diagnosis of cancerous tissue in murine models, studying of tissue dynamics that were not possible before, and real-time optical neural recordings, along with many potential future applications. ■

Biography

Timothy York (Member, IEEE) received the B.S.E.E. and M.S.E.E degrees from Southern Illinois University, Edwardsville, IL, USA, in 2002 and 2007, respectively. Currently, he is working toward the Ph.D. degree in computer engineering at Washington University in St. Louis, St. Louis, MO, USA.

He worked as a Computer Engineer for the U.S. Air Force from 2006 to 2009. His current work focuses on polarization image sensors and their applications, especially in the field of biomedical imaging.

Mr. York is a member of the International Society for Optics and Photonics (SPIE).

Samuel B. Powell is working toward the Ph.D. degree in the Department of Computer Science and Engineering, Washington University in St. Louis, St. Louis, MO, USA.

His work has focused on the calibration of division-of-focal-plane polarimeters and, more recently, the development of the hardware and software for an underwater polarization video camera for marine biology applications.

Shengkui Gao received the B.S. degree in electrical engineering from Beihang University, Beijing, China, in 2008 and the M.S. degree in electrical engineering from the University of Southern California, Los Angeles, CA, USA, in 2010. Currently, he is working toward the Ph.D. degree in computer engineering at Washington University in St. Louis, St. Louis, MO, USA.

His research interests include imaging sensor circuit and system design, mixed-signal VLSI design, polarization related image processing and optics development.

Lindsey Kahan is an undergraduate at Washington University in St. Louis, St. Louis, MO, USA, studying mechanical engineering and materials science.

Tauseef Charanya received the B.S. degree in biomedical engineering from Texas A&M University, College Station, TX, USA, in 2010. Currently, he is a biomedical engineering graduate student at Washington University in St. Louis, St. Louis, MO, USA.

He is a cofounder of a medical device incubator at Washington University in St. Louis named IDEA Labs. His research interests include endoscopy, surgical margin assessment tools, and fluorescence and polarization microscopy methods.

Mr. Charanya is a member and serves as the President of the WU Chapter of the International Society for Optics and Photonics (SPIE).

Debajit Saha received the M.S degree from the Indian Institute of Technology, Bombay, India and the Ph.D. degree for his work on the role of feedback loop in visual processing from Washington University in St. Louis, St. Louis, MO, USA.

He is currently a Postdoctoral Fellow at the Biomedical Engineering Department, Washington University in St. Louis, working on understanding the functional roles of neural circuitry from systems point of view. His research interests include olfactory coding, quantitative behavioral assay, and application of rules of biological olfaction in biomedical sciences.

Nicholas W. Roberts, photograph and biography not available at the time of publication.

Thomas W. Cronin received the Ph.D. degree from Duke University, Durham, NC, USA, in 1979.

He is a Visual Ecologist, currently in the Department of Biological Sciences, University of Maryland Baltimore County (UMBC), Baltimore, MD, USA, where he studies the basis of color and/or polarization vision in a number of animals ranging from marine invertebrates to birds and whales. He spent three years as a Postdoctoral Researcher at Yale University, New Haven, CT, USA, before joining the faculty of UMBC.

Justin Marshall, photograph and biography not available at the time of publication.

Samuel Achilefu received the Ph.D. degree in molecular and materials chemistry from University of Nancy, Nancy, France and completed his postdoctoral training at Oxford University, Oxford, U.K.

He is a Professor of Radiology, Biomedical Engineering, and Biochemistry & Molecular Biophysics at Washington University in St. Louis, St. Louis, MO, USA. He is the Director of the Optical Radiology Laboratory and of the Molecular Imag ing Center, as well as Co-Leader of the Oncologic Imaging Program of Siteman Cancer Center.

Spencer P. Lake received the Ph.D. degree in bio-engineering from the University of Pennsylvania, Philadelphia, PA, USA.

He is an Assistant Professor in Mechanical Engineering & Materials Science, Biomedical Engineering and Orthopaedic Surgery at Washington University in St. Louis, St. Louis, MO, USA, and directs the Musculoskeletal Soft Tissue Laboratory. His research focuses on biomechanics of soft tissues, with particular interest in the structure- function relationships of orthopaedic connective tissues.

Baranidharan Raman received the B.Sc. Eng. degree (with distinction) in computer science from the University of Madras, Chennai, India, in 2000 and the M.S. and Ph.D. degrees in computer science from Texas A&M University, College Station, TX, USA, in 2003 and 2005, respectively.

He is an Assistant Professor with the Department of Biomedical Engineering, Washington University, St. Louis, MO, USA. From 2006 to 2010, he was a joint Post-Doctoral Fellow with the National Institutes of Health and the National Institute of Standards and Technology, Gaithersburg, MD, USA. His current research interests include sensory and systems neuroscience, sensor-based machine olfaction, machine learning, biomedical intelligent systems, and dynamical systems.

Dr. Raman is the recipient of the 2011 Wolfgang Gopel Award from the International Society for Olfaction and Chemical Sensing.

Viktor Gruev received the M.S. and Ph.D. degrees in electrical and computer engineering from The Johns Hopkins University, Baltimore, MD, USA, in May 2000 and September 2004, respectively.

After finishing his doctoral studies, he was a Postdoctoral Researcher at the University of Pennsylvania, Philadelphia, PA, USA. Currently, he is an Associate Professor in the Department of Computer Science and Engineering, Washington University in St. Louis, St. Louis, MO, USA. His research interests include imaging sensors, polarization imaging, bioinspired circuits and optics, biomedical imaging, and micro/nanofabrication.