Direct spectroscopic evidence for a hydride bridge in the Ni–R form of [NiFe] hydrogenase has been obtained using iron-specific nuclear resonance vibrational spectroscopy. This article focuses on the long and strenuous experimental journey to search for and identify this first spectroscopic evidence for a hydride in Ni–R.
Keywords: nuclear resonance vibrational spectroscopy, NRVS, ultra-weak signal, [NiFe] hydrogenase, Ni–R, Ni–H–Fe wag mode, iron hydride
Abstract
Direct spectroscopic evidence for a hydride bridge in the Ni–R form of [NiFe] hydrogenase has been obtained using iron-specific nuclear resonance vibrational spectroscopy (NRVS). The Ni–H–Fe wag mode at 675 cm−1 is the first spectroscopic evidence for a bridging hydride in Ni–R as well as the first iron-hydride-related NRVS feature observed for a biological system. Although density function theory (DFT) calculation assisted the determination of the Ni–R structure, it did not predict the Ni–H–Fe wag mode at ∼675 cm−1 before NRVS. Instead, the observed Ni–H–Fe mode provided a critical reference for the DFT calculations. While the overall science about Ni–R is presented and discussed elsewhere, this article focuses on the long and strenuous experimental journey to search for and experimentally identify the Ni–H–Fe wag mode in a Ni–R sample. As a methodology, the results presented here will go beyond Ni–R and hydrogenase research and will also be of interest to other scientists who use synchrotron radiation for measuring dilute samples or weak spectroscopic features.
1. Introduction
Molecular hydrogen (H2) is a zero-emission energy carrier and is one of the best alternative fuels for the future, especially in urban areas with stricter environmental requirements. Hydrogenase (H2ase) enzymes catalyze the bidirectional reaction of 2H+ + 2e− ⇌ H2 (Jugder et al., 2013 ▸; Kim & Cha, 2013 ▸) and thus have attracted interest for potential applications in H2 production in addition to their importance in biological sciences (Mertens & Liese, 2004 ▸; Cammack et al., 2001 ▸; Heinekey, 2009 ▸; Tard & Pickett, 2009 ▸; Yang et al., 2011 ▸; Fritsch et al., 2013 ▸; Simmons & Artero, 2013 ▸; Matsumoto et al., 2013 ▸). While both diiron ([FeFe]) and nickel–iron ([NiFe]) H2ases possess high catalytic activity (Evans et al., 2013 ▸; Armstrong, 2009 ▸; Shafaat et al., 2013 ▸; Lubitz et al., 2014 ▸), the latter are attractive practically since they exhibit greater O2-tolerance (Guiral et al., 2006 ▸; Evans et al., 2013 ▸; Lauterbach et al., 2015 ▸; Armstrong et al., 2009 ▸).
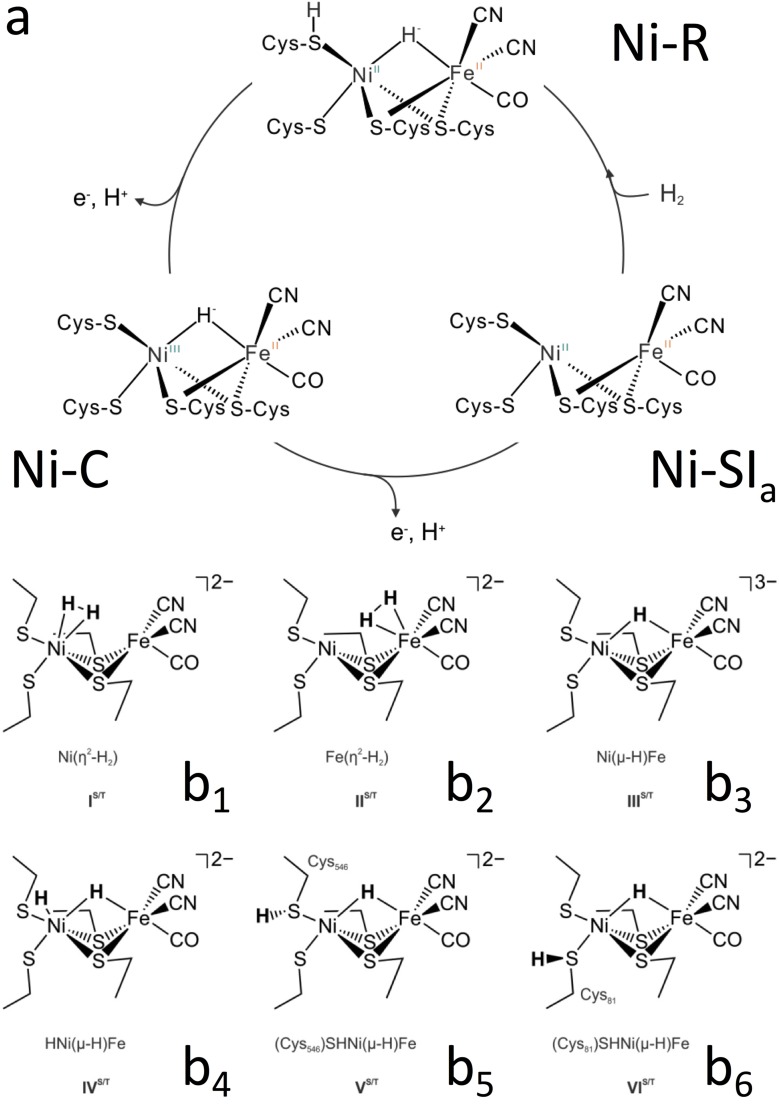
[NiFe] H2ase contains several Fe–S clusters and one NiFe active site, in which Fe is coordinated by one CO and two CN ligands (Kamali et al., 2013 ▸; Lubitz & Ogata, 2013 ▸; Shafaat et al., 2013 ▸; Lauterbach et al., 2015 ▸). The Ni is coordinated to the protein matrix by four cysteinyl thiolates (S), two of which serve as bridging ligands to Fe. In addition to these two S ligands, there could be a third ligand to bridge the two metal atoms in several enzymatic states; for example, a hydroxide ligand in the oxidized inactive forms (Ni–A and Ni–B) (Dole et al., 1997 ▸; Gu et al., 2003 ▸; Gastel et al., 2005 ▸; Volbeda et al., 2015 ▸; Barilone et al., 2015 ▸) and a possible hydride (Ni–H–Fe) in the active forms Ni–C and Ni–R (Dole et al., 1997 ▸; Amara et al., 1999 ▸; Brecht et al., 2003 ▸; Foerster et al., 2003 ▸) (Fig. 1a ▸). Understanding this bridging hydride will be useful in elucidating the Ni–R structures from the proposed candidates [e.g. in Figs. 1(b 1)–1(b 6) ▸], and the possible mechanism for H2 binding and cleavage at the H2ases’ active site. For example, via a density function theory (DFT) calculation, the structures in Figs. 1(b 5) and 1(b 6) ▸ are believed to be the most likely candidates in the real Ni–R. Information about the mechanism in turn could be useful for better producing H2 in the future.
Figure 1.
Schematic diagram of the [NiFe] H2ases’ catalytic cycle (a) and six examples of proposed possible structures for the [NiFe] H2ases’ Ni–R state (b 1–b 6) (Ogata, Kramer et al., 2015 ▸).
Despite progress in characterization of H2ases by crystallography, infrared (IR) spectroscopy (Lubitz et al., 2014 ▸; Fontecilla-Camps et al., 2007 ▸; De Lacey et al., 2007 ▸) and other X-ray spectroscopies (Wang et al., 2000 ▸; Wang, Patil, Gu et al., 2001 ▸; Wang, Patil, Ralston et al., 2001 ▸), questions remain about the detailed molecular and electronic structure of various intermediates and inhibited species. These highly debated questions include the nature or even the existence of a hydride bridge (Ni–H–Fe) in Ni–R (Lubitz & Ogata, 2013 ▸). Recent high-resolution crystallography demonstrated that the electron density as a hydride was detected at the bridging position between Ni and Fe (Ogata, Nishikawa & Lubitz, 2015 ▸). Ni–R represents a special challenge for spectroscopic studies for a number of reasons: (i) it is EPR (electron paramagnetic resonance) silent; (ii) the Raman spectroscopy presents a problem due to its photoreactivity; and (iii) IR spectroscopy for hydride bands is extremely difficult to observe (Jayapal et al., 2008 ▸; Lubitz & Ogata, 2013 ▸). Thus there has been no progress in traditional vibrational spectroscopy so far and the existence of Ni–H–Fe in Ni–R is still speculation from a spectroscopic point of view. It is sometimes inferred by extrapolation from the hydride in the EPR active Ni–C species (Brecht et al., 2003 ▸).
Nuclear resonance vibrational spectroscopy (NRVS) scans an extremely monochromatic (∼1 meV) X-ray beam through the nuclear resonance (at 14.4 keV for 57Fe), and measures the corresponding creation or annihilation of phonons (Seto et al., 1995 ▸; Sturhahn et al., 1995 ▸; Yoda et al., 2001 ▸, 2012 ▸). It is a relatively new X-ray spectroscopy that became available due to the development of third-generation synchrotron sources and advanced X-ray optics. It has several distinguished advantages in comparison with traditional vibrational spectroscopic techniques such as IR and Raman spectroscopies (Smith et al., 2005 ▸; Kamali et al., 2013 ▸; Pelmenschikov et al., 2011 ▸). In the past ten years, this technique has revealed/resolved Fe–S/P/Cl and Fe–CO/CN/NO vibrational modes inside various inorganic complexes and iron enzymes and has become an excellent pin-point tool in recent years to study iron-specific inorganic and bioinorganic systems (Smith et al., 2005 ▸; Xiao et al., 2005 ▸; Cramer et al., 2007 ▸; Tinberg et al., 2010 ▸; Do et al., 2011 ▸; Kamali et al., 2013 ▸). In addition, Fe–H-related NRVS features have also been resolved in several inorganic complexes (Bergmann et al., 2003 ▸; Pelmenschikov et al., 2011 ▸).
Via a series of careful and strenuous measurements, we have revealed the first direct spectroscopic evidence for Ni–H–Fe in a 57Fe-labeled Ni–R form of Desulfovibrio vulgaris Miyazaki F (or DvMF) [NiFe] H2ase using 57Fe-specific NRVS. While its biochemical science and theoretical simulations have been presented and discussed recently (Ogata, Kramer et al., 2015 ▸), the measurement details, especially the strenuous experimental journey leading to the successful observation of the weak Ni–H–Fe wag mode, is the focus of this publication. It is not a simple or straightforward matter at all to observe the Ni–H–Fe in a [NiFe] H2ase sample, and the task will face great difficulties due to the following two aspects: (i) a Fe–H-related bending or wagging mode has a much weaker NRVS signal than Fe–CO (Pelmenschikov et al., 2011 ▸) while Fe–CO in NiFe H2ase is already rather weak (Kamali et al., 2013 ▸; Ogata, Kramer et al., 2015 ▸); (ii) as will be discussed in detail later, its real energy position is far from either model complexes or theoretical predictions and was virtually unknown before it was observed experimentally. This article evaluates all the matters related to whether the feature is observable, where to search for a Fe–H-related feature, whether the observation is reliable, and how the experiments identify the observed 675 cm−1 peak as a Fe–H-related feature.
2. Experimental details
The Ni–R NRVS spectra were recorded at SPring-8 beamlines BL09XU (Yoda et al., 2001 ▸) and BL19LXU (Yabashi et al., 2001 ▸; Takahashi et al., 2001 ▸) in Japan.
2.1. BL09XU
BL09XU is a dedicated nuclear scattering beamline, and its instrumentation and properties have been discussed in detail elsewhere (Yoda et al., 2001 ▸). In summary, it has a Si(111) double-crystal high-heat-load monochromator (HHLM) producing 14.4 keV radiation with ∼1.0 eV resolution, followed by a high-energy-resolution monochromator (HRM) [Ge(422) × 2Si(975)] producing 14.4 keV radiation with 0.8 meV resolution. The beam flux was ∼1.4 × 109 photons s−1 at 0.8 meV energy resolution. The beam size was about 0.6 mm (height) × 1 mm (width). BL09XU has a dedicated NRVS measurement system, including a 2 × 2 avalanche photodiode (APD) detector array, a set of data-acquisition electronics and a control computer with data-acquisition software.
It also has a dedicated liquid-helium (LHe) flow cryostat for measuring NRVS at a cryogenic temperature for air- or temperature-sensitive samples, such as H2ases. The samples were maintained with LHe at 6–9 K (sensor reading). However, due to the extremely short distance from the samples’ surface to the APD array, a cold-finger cryostat has to be used instead of a more efficient gas exchange cryostat (Dong et al., 2013 ▸). The real sample temperatures were much higher than 6–9 K, e.g. 50–70 K (Wang et al., 2012 ▸). This standard NRVS setup has been used in many NRVS measurements in the past and their details are discussed elsewhere (Cramer et al., 2007 ▸; Pelmenschikov et al., 2011 ▸; Wang et al., 2012 ▸, 2014 ▸).
2.2. BL19LXU
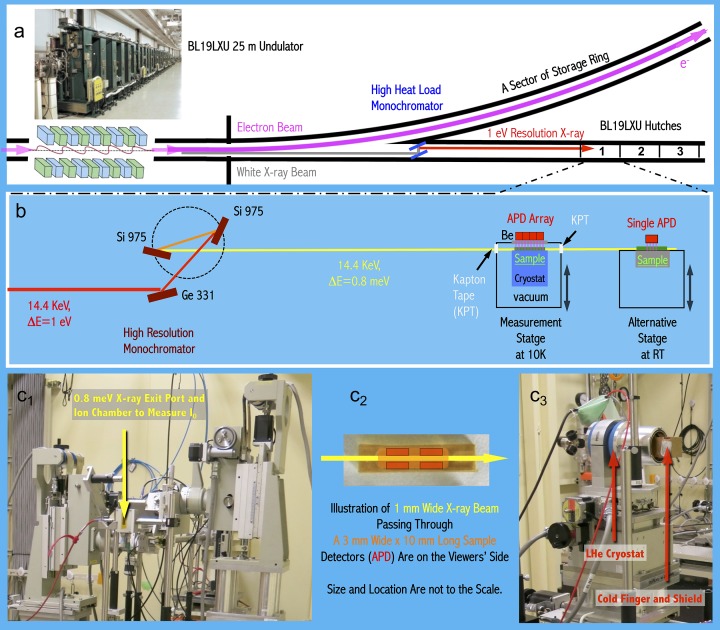
BL19LXU (Yabashi et al., 2001 ▸; Takahashi et al., 2001 ▸) provides the fundamental beam in the 7.2–18 keV energy region, covering 57Fe nuclear resonance at 14.4 keV. As shown in Fig. 2(a) ▸, it has a 25 m-long undulator (Hara et al., 2002 ▸) instead of the usual 5 m-long undulator at SPring-8. Therefore its HHLM provides ∼2.5 × 1014 photons s−1 at 14.4 keV, i.e. about five times higher than the beam intensity at BL09XU (5 × 1013 photons s−1 after HHLM). This beamline has many advanced applications and publications over a broad area from time-resolved measurements to weak feature observations (Tanaka et al., 2011 ▸; Inada et al., 2013 ▸). It is also a good choice for NRVS measurements on weak vibrational features, which requires high beam intensity.
Figure 2.
An illustrative diagram of BL19LXU (a) and of the mobile NRVS apparatus moved into its experimental hutch 1 (b). The top-left photograph insert shows the 25 m-long undulator inside BL19LXU (Goto et al., 2000 ▸), and the bottom panels are (from left to right) a photograph of the HRM station (c 1), an illustration of the sample/X-ray beam and APD detector positions (c 2), and a photograph of the main NRVS measurement station (c 3).
However, BL19LXU is not a dedicated nuclear scattering beamline and it does not have a fixed HRM and NRVS measurement station. We thus have fabricated a mobile system (Fig. 2b ▸) which consists of a HRM, a LHe cryostat, a 2 × 2 APD detector array, a rack of associated electronics, and a control computer with data-acquisition software. While these items are duplicates of those used at BL09XU, they need to be integrated into BL19LXU’s experimental hutch 1 within about 36 h (including optimization time). Therefore, BL19LXU has similar HHLM and HRM as those at BL09XU, and provided 14.4 keV radiation with 0.8 meV resolution, which is suitable for NRVS measurement. The beam size was also 0.6 mm (height) × 1 mm (width), the same as that at BL09XU. After the HRM, a maximum 4.2× higher beam flux was recorded in comparison with that for BL09XU. However, owing to various practical limitations as well as using a moved-in HRM and NRVS apparatus, the ratio in NRVS counts per second (cts/s) for the two beamlines is 2.5–3.4× instead, while for BL09XU the cts/s is stable. For example, in comparison with the BL09XU standard, the BL19LXU beam time for measuring the two Ni–R in H2/H2O (NiR-H for short) samples in this study has a BL19/BL09 cts/s ratio of 2.6, while that for measuring the Ni–R in D2/D2O (NiR-D for short) has a ratio of 3.
2.3. NRVS measurements
The NRVS spectra were measured using a published procedure (Cramer et al., 2007 ▸; Seto et al., 1995 ▸; Sturhahn et al., 1995 ▸; Yoda et al., 2001 ▸), with a step size of 0.28 meV at BL09XU and 0.27 meV at BL19LXU. The difference is due to minor difference in energy scales for the different beamlines; the raw step sizes before the energy calibrations were both 0.295 meV. The 14.4 keV beam with an energy resolution of 0.8 meV was scanned through the defined energy region; the delayed nuclear fluorescence and Fe K α fluorescence from 57Fe were detected with the 2 × 2 APD array, processed by the electronics, and stored/displayed via the control computer. The scanning region covered from −30 meV (−240 cm−1) to 70–125 meV (560–1000 cm−1) depending on the different samples used and the different search cases.
NRVS spectral analysis was performed using the PHOENIX software package (Sturhahn et al., 1995 ▸), where the observed raw NRVS spectra (cts) were calibrated to the nuclear resonance peak position, normalized to I 0, summed and converted to the single-phonon 57Fe partial vibrational density of states (PVDOS for abbreviation). The spectral conversion was optimized when the observed Stokes/anti-Stokes imbalance matched the imbalance calculated using the entered temperature as a parameter. The real sample temperatures were thus obtainable with the measured NRVS’s Stokes/anti-Stokes imbalance (Wang et al., 2012 ▸).
The energy position for each scan was calibrated by aligning the elastic peak to zero during the NRVS spectral analysis with PHOENIX. The energy scales were usually calibrated with a standard sample of [57FeCl4][NEt4] with a prominent peak at 380 cm−1. It was measured inside the regular NRVS measurement chamber at cryogenic temperature. Alternatively, the energy scales can also be calibrated with 57Fe metal powder at the quick-switch calibration stage at the back of the main measurement stage (Wang et al., 2013 ▸). It has a clear peak at 287 cm−1 at room temperature.
The background noise level (dark current cts/s) was estimated prior to (and sometimes during) each beam time by tuning the HRM’s energy position to about −100 meV or about −800 cm−1 (in reference to the resonance elastic energy), where no vibrational peak is present. The ‘signal’ was accumulated for either 500 s in total or five consecutive 100 s to obtain an average cts/s. For almost all the beam times, the dark current was 0.03 cts/s for our NRVS measurement system at BL09XU and at BL19LXU.
2.4. Scan parameters
Since the relative strength of NRVS transitions varies dramatically and since it is necessary to emphasize one region of interest (e.g. for searching for Ni–H–Fe), the scans were divided into segments with different data collection times (seconds per point, or s/p). In general, 1–3 s/p was used for the range from −240 to 400 cm−1 (covering the Fe–S region), then 5–10 s/p for the Fe–CN and Fe–CO region from 400 to 620 cm−1. A longer scanning time (10–30 s) was used for the candidate Ni–H–Fe searching region (e.g. at 620–770 cm−1). This practice is used for the NRVS measurements at both BL09XU and BL19LXU, but the exact timing for different beam times varied a little. The scan details will be discussed again in the Results and discussions section.
To compare the NRVS data from BL09XU and BL19LXU, we re-scale the BL19LXU counting time based on its maximum cts/s versus the standard maximum cts/s at BL09XU and create BL09XU equivalent seconds, e.g 10 s/p at BL19LXU corresponds to 26 or 30 equivalent s/p at BL09XU [corresponding to a cts/s ratio of 2.6 for measuring NiR-H and 3 for measuring NiR-D]. NiR-H was measured once at BL09XU and twice at BL19LXU with an equivalent BL09XU time of 10 × 680 = 680 s/p, 20 × 24 × 2.6 = 1248 s/p and 15 × 12 × 2.6 = 468 s/p, respectively, in total 2396 s/p (with a percentile of 28%, 52% and 20%). NiR-D was measured three times at BL09XU and once at BL19LXU, equivalent to 3980 BL09XU s/p [= (40 × 20) + (30 × 30) + (36 × 30) + 20 × 20 × 3 = 2780 + 400 × 3 = 3980] in the same region. More s/p was used for NiR-D because more time should be used to conclude that there is no signal than to find a weak signal.
2.5. DvMF H2ase Ni–R preparation
Cells were cultivated using a minimal medium supplemented with 57FeSO4. Fermentation was carried out in a 10 l glass fermenter under anaerobic conditions, and the [NiFe] H2ase expressed was isolated and purified as described earlier (Ogata et al., 2005 ▸). For preparing NiR-H (NiR-D), the as-isolated [NiFe] H2ase was transferred from 25 mM Tris-HCl (pH = 7.4) buffer to 100 mM MES (pH = 5.0 or pD = 5.0) and was then purged with 1.2 bar H2 (or 1.3 bar D2) for more than 8 h. The solutions were then loaded into NRVS cells under anaerobic conditions. The final H2ase samples had a concentration of about 4 mM.
Fourier transform IR (FTIR) spectra were recorded on a Bruker IFS66v/S FTIR spectrometer to ensure the samples were in their supposed states (Ni–R1: one of the subforms of Ni–R). It was measured in transmission mode in a sealed IR cell at room temperature and with a 2 cm−1 energy resolution.
2.6. Model complexes and NRVS
NRVS or the Fe–H/D-related bending positions for several Fe–H/D-containing complexes are cited in this study. These complexes include (Bergmann et al., 2003 ▸; Pelmenschikov et al., 2011 ▸; Crossland et al., 2009 ▸; Schilter et al., 2012 ▸): (i) [57FeH(D)6][MgBr(thf)2]4 (or Fe57FeH6/D6 for short); (ii) 57Fe(H/D)(CO)(dppe)2, dppe = 1,2-bis(diphenylphosphino)ethane (or H/DFeCO); (iii) trans-[57Fe(DMeOPrPE)2(N2)H]+ {DMeOPrPE = 1,2-bis[bis(methoxypropyl)phosphino]ethane} (or HFeN2); (iv) [(μ,k2-bdt-H)(μ-PPh2)(μ-H)57Fe2(CO)5][OTf] (or FeHFe); (v) [(dppe)Ni(μ-pdt)(μ-H)*Fe(CO)2(Ph3P)]+ (* = nature abundant, dppe = 1,2-Ph2PCH2CH2PPh2, pdt2− = −SCH2CH2CH2S−) (or NiH*FeX); (vi) [(dppe)Ni(μ-pdt)(μ-H/D)57Fe(CO)3]+ (or NiH/DFe).
In addition, [57FeCl4][NEt4] and metal 57Fe were used as calibration samples for energy scales (Smith et al., 2005 ▸; Wang et al., 2013 ▸).
3. Results and discussion
3.1. Ni–R NRVS summary
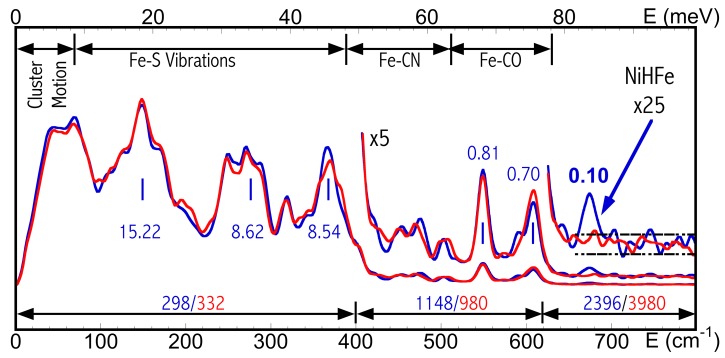
The overall NRVS spectra for DvMF NiR-H (blue) and NiR-D (red) are presented in Fig. 3 ▸ as an introduction for the signal levels for each vibrational feature.
Figure 3.
NRVS-derived PVDOS for DvMF NiR-H (blue) and NiR-D (red) (Ogata, Kramer et al., 2015 ▸). The middle blue labels indicate the signal level (cts/s) for different vibrational features for NiR-H. The bottom labels show the total time (s) measured for each energy regions for NiR-H (blue) and NiR-D (red).
The NRVS spectra include the very low energy intensities from the backbone motion, the 100–400 cm−1 peaks for Fe–S cluster vibrations, the 420–530 cm−1 peaks for Fe–CN modes, the 530–630 cm−1 peaks for Fe–CO modes (Lauterbach et al., 2015 ▸; Kamali et al., 2013 ▸) and a weak but clear peak at 675 cm−1, which are assigned to the Ni–H–Fe wag mode (Ogata, Kramer et al., 2015 ▸). In Fig. 3 ▸, the top bars indicate different vibrational regions while the bottom bars illustrate the total time (s) used to measure the NiR-H (blue text) and NiR-D (red text) in each region. The blue text in the middle shows the signal level (cts/s) for each of the various signature peaks. While these middle blue numbers illustrate the signal level (cts/s) for NiR-H, both NiR-H and NiR-D have about the same signal level. As illustrated, Fe–CO/CN features have a much lower cts/s than the Fe–S features while the Ni–H–Fe has an even lower cts/s in comparison with the weak Fe–CN/CO peaks. This provides readers with a basic idea of how weak the Ni–H–Fe peak in Ni–R is.
Although a DFT calculation assisted the determination of the Ni–R structure from a dozen candidates [including the six in Figs. 1(b 1)–1(b 6) ▸] (Ogata, Kramer et al., 2015 ▸), the existence of Ni–H–Fe at 675 cm−1 for NiR-H (blue) and its absence for NiR-D (red) provided a critical observation reference for the DFT calculations, not the other way around. Without this successful observation, various DFT and normal mode analysis calculations all actually predicted Ni–H–Fe-related modes in Ni–R at a position higher than 760 cm−1.
3.2. Is Ni–H–Fe observable?
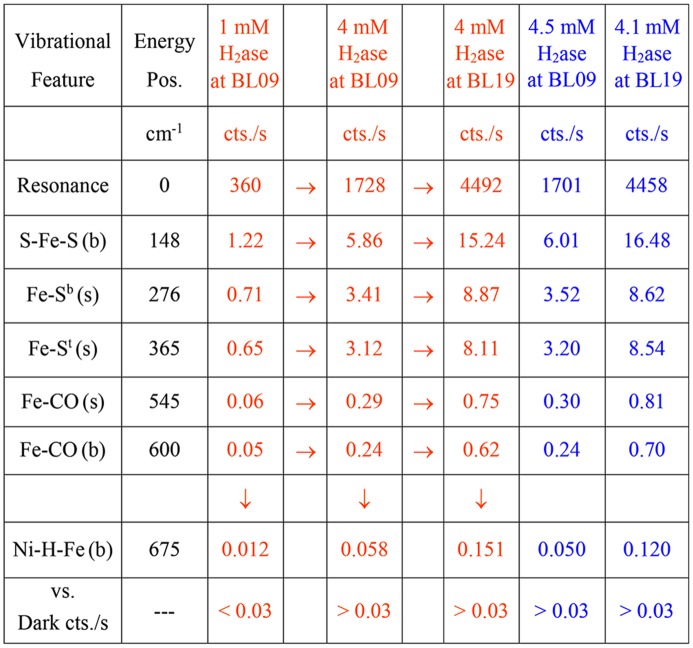
It is important to first know whether the Ni–H–Fe in a Ni–R is observable or not. As per the NRVS statistics at BL09XU between 2006 and 2010, when the HRM’s energy resolution is at 0.9 meV, 1 mM of 57Fe sample produced a 30 cts/s signal in the elastic peak (Wang et al., 2014 ▸). Examples of NRVS signal levels for various hypothetical H2ase samples are illustrated in Fig. 4 ▸, using 30 cts/s per 1 mM 57Fe. The first two columns describe vibrational feature names and their vibrational energy positions, and the third column presents the NRVS signals for a hypothetical 1 mM H2ase (or 12 mM 57Fe) sample, which is similar to the H2ase measured in the past (Kamali et al., 2013 ▸). It has 360 cts/s in the resonance peak, 0.7–1.2 cts/s for the Fe–S peaks (at 150–380 cm−1), and 0.06 cts/s signal for Fe–CO (at 600 cm−1). It is worthwhile mentioning that the then weak Fe–CO features were successfully observed with a 1 mM H2ase sample in the past (Kamali et al., 2013 ▸).
Figure 4.
NRVS spectral signal levels for various vibrational features. The letters ‘(s)’ and ‘(b)’ stand for stretching and bending modes, respectively. The orange-colored columns are for hypothetical cases while the blue-colored columns are for real measurement cases. There are arrows between columns 3, 4 and 5 because columns 4 and 5 are all based on column 3 (1 mM at BL09).
On the other hand, the Ni–H–Fe was too weak to be observed under previous conditions (1 mM H2ase concentration), so we have to estimate its potential cts/s (the numbers below the ‘↓’ in Fig. 4 ▸) based on the NRVS ratio between Ni–H–Fe and Fe–CO in available complexes, e.g. ∼1/5 for NiHFe (Fig. 5b). A value of 0.012 cts/s is estimated for Ni–H–Fe in 1 mM NiR-H at BL09XU; it is under the dark cts/s level (0.03 cts/s) and is not observable under the given circumstances.
Since the completion of the NRVS measurements for Kamali et al.’s publication (Kamali et al., 2013 ▸), further progress has been made to increase the potential NRVS signal level (cts/s). The major advance is the samples’ concentration increasing from ∼1 mM to ∼4 mM, which puts the Ni–H–Fe feature at a hypothetical level of 0.012 × 4 = 0.048 cts/s. Some other minor improvements also contribute to the increase of cts/s: (i) BL09XU’s HRM advanced from 0.9 meV to 0.8 meV energy resolution with almost the same level of beam intensity, which led to an increase in peaks’ cts/s [maximum = (0.9/0.8) = 112.5%]; (ii) due to better control of the sample temperature during the NRVS measurement (Wang et al., 2012 ▸), we are able to move the sample even closer to the APD. It is difficult to estimate the real movement of the sample position but we obtained about 10% signal level increase in cts/s due to sample position alternation while still maintaining the sample temperature below 70 K. These two points thus mean all the NRVS peaks have ×1.2 height. The estimated Ni–H–Fe is then about 0.048 × 1.2 = 0.058 cts/s, which is comparable with the Fe–CO feature for 1 mM H2ase in the previous measurement (Kamali et al., 2013 ▸) and thus becomes observable. Column 4 in Fig. 4 ▸ (not counting the narrow columns showing the arrow symbols) shows the estimated cts/s for a hypothetical 4 mM H2ase, which will be measured at the improved BL09XU (×1.2).
Then, how much time is needed to reveal such a weak peak (0.058 cts/s) with a reasonable signal-to-noise ratio (S/N)? In a previous publication (Wang et al., 2014 ▸) we have concluded that a 10 mM 57Fe sample has ∼1 cts/s in the Fe–S region and 100 s/p is thus enough for a S/N = 1001/2 = 10. Using the same principle, we estimated that 500 s/p on Ni–H–Fe can lead to 0.058 × 500 = ∼29 pure cts and S/N = 291/2 = ∼5.4. Although dark-current cts/s limits the best possible S/N, as will be discussed in detail later, an as-high-as-possible statistical S/N is still required and thus 500 s/p is a kind of realistic minimum time required to achieve a reasonable S/N for a weak feature like Ni–H–Fe. As a reference, the very weak Fe–CO features for the oxidized and the reduced 1 mM H2ase were observed with 580 and 2180 s/p total scanning time at BL09XU in the previous publication (Kamali et al., 2013 ▸). The 500 s/p scanning time means, for example, 25 × 20 s/p, leading to about 24 h or more beam time for one measurement with one Ni–H–Fe search.
3.3. Where to search For Ni–H–Fe?
Knowing where to search for the Ni–H–Fe signal is as important as (if not more important than) knowing it is observable. This is especially true for searching Ni–H–Fe in Ni–R, which requires long (e.g. 24 h or more) beam times for each search.
Since no NRVS features for iron hydrides or iron deuterides in a real iron enzyme have been published before this work, we used NRVS for a series of iron hydride/deuteride complexes and their Fe–H-related vibrational positions (Fig. 5 ▸) as a starting point to discuss the possible location of the Ni–H–Fe mode in Ni–R. The NRVS FeH6 (blue)/FeD6 (red) spectra were among the first NRVS spectra obtained for chemical complexes (Bergmann et al., 2003 ▸). Their features include: the X–Fe–H/X–Fe–D bending modes at 790/572 cm−1 and the Fe–D stretching at 1124 cm−1 (Fig. 5a ▸). Later on, many other iron-hydride-containing complexes were published or evaluated, e.g. the (H/D)FeCO model complexes have the X–Fe–H/X–Fe–D at 740/620 cm−1, respectively (Pelmenschikov et al., 2011 ▸). We noticed that the X–Fe–D bending peak for this complex is close to the Fe–CO peak at 560 cm−1. The NiHFe complex is used to model [NiFe] H2ases’ active site and it mimics the structure for the [NiFe] center with very minor structural differences (Barton et al., 2009 ▸; Shafaat et al., 2012 ▸). Its Ni–H–Fe wag mode is at 758 cm−1 (Fig. 5b ▸). Its Ni–D–Fe mode mixes into the Fe–CO features at 550–630 cm−1 and cannot be resolved (Fig. 5b ▸). Note that the peak at 711 cm−1 is mainly related to Ni–D stretching (mixed with Fe) per DFT calculation (Ogata, Kramer et al., 2015 ▸). It is not Fe–D-related bending, which is mixed into the Fe–CO features.
Figure 5.
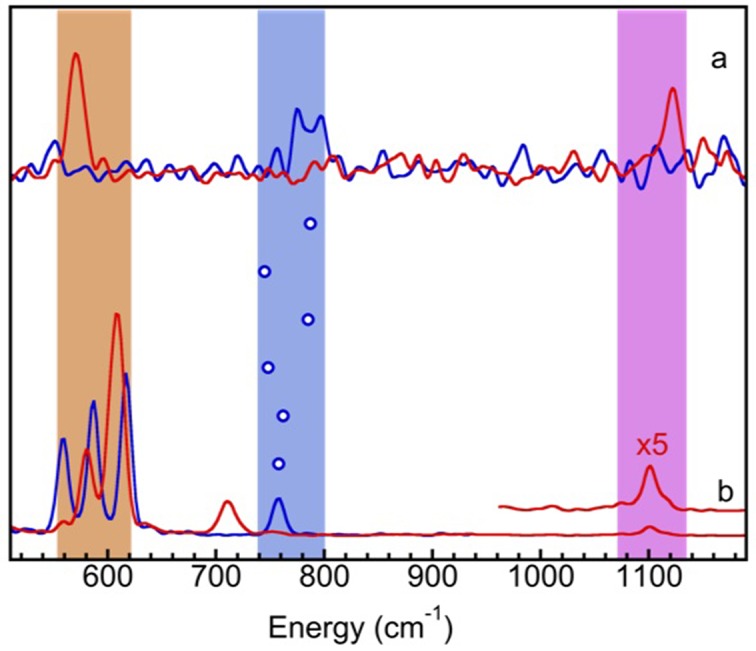
NRVS observed PVDOS for (a) [FeH6] (blue)/[FeD6] (red); (b) NiHFe (blue)/NiDFe (red) model complexes. The blue circles indicate the Fe–H-related bending-mode centroids for (from top down) FeH6, HFeCO, HFeN2, FeHFe, NiH*FeX and NiHFe, while the shaded areas are for Fe–D-related bending (orange), Fe–H-related bending (blue) and Fe–D-related stretching (purple).
The NRVS feature most relevant to Ni–R’s Ni–H–Fe is the X–Fe–H or Ni–H–Fe feature in various complexes. The energy positions of these Fe–H-related bending modes for FeH6, HFeCO, HFeN2, FeHFe, NiH*FeX and NiHFe (refer to §2 for the full names of these complexes) are illustrated in Fig. 5 ▸ with the blue open circles between the traces in Fig. 5(a) ▸ and the traces in Fig. 5(b) ▸. The blue shaded area highlights the possible Fe–H-related bending energies while the orange (purple) area indicates the Fe–D bending (stretching) mode regions.
From these Fe–H/D complexes we have learned the following:
(i) Although Fe–D-related bending has more intensity than Fe–H-related bending, it may mix with Fe–CO and become unresolvable. Therefore, for Fe–CO-containing complexes, the Fe–H-related bending mode has the highest observable NRVS peak among all of the Fe–H/D-related stretching and bending modes. It has about 1/4–1/6 intensity in comparison with that of Fe–CO.
(ii) The Fe–H-related bending mode positions span from 740 to 790 cm−1 for the examined iron hydride complexes, including those whose spectra are not shown here. One thus should first search the 740–790 cm−1 region for the possible Ni–H–Fe mode in Ni–R. Unfortunately, several searches over an extended region of 720–840 cm−1 were unsuccessful.
DFT was also used to make a prediction about the possible position of this critical vibrational peak. However, all of the earlier DFT calculations as well as normal mode analyses (before the Ni–H–Fe was finally observed experimentally) pointed to a region with energies higher than 760 cm−1; some of them suggested a region higher (or much higher) than 800 cm−1 and we experimentally searched up to 125 meV (or 1000 cm−1), but did not find anything. Each of these ‘likely’ Ni–H–Fe regions was searched one to two times but led to no success at all.
Although 620–720 cm−1 became the only region not searched with a great investment of beam time, the idea to search in this region was not at all popular at the time, because all the model complexes and theoretical calculations pointed to a much higher energy position. For example, the Ni–R model complex NiHFe has its Ni–H–Fe at 758 cm−1, 140 cm−1 higher than its highest-energy Fe–CO peak at 617 cm−1, while Ni–R has a similar Fe–CO peak position at 609 cm−1. Then the question arose: should we perform a thorough search in this unlikely but unsearched region? We did, and found the Ni–H–Fe at 675 cm−1.
3.4. Observing Ni–H–Fe at 675 cm−1
As searching in the 620–720 cm−1 region was still not a mainstream opinion at that time, we first performed a balance measurement between acquiring a perfect Fe–CO spectrum and searching for Ni–H–Fe with a 4.5 mM NiR-H sample at (improved) BL09XU. Therefore an even scanning time of 10 s/p was used between 400 and 740 cm−1 instead of spending more time (e.g. 20–30 s) in the Ni–H–Fe region. Nevertheless, via 68 such scans (with a total scanning time of 680 s/p) a weak but positive peak at 675 cm−1 was observed for the first time as shown in Fig. 6(a) ▸, with the raw NRVS spectrum at the top and the converted PVDOS at the center (×10) and the bottom (×1). We noticed that the 675 cm−1 energy position is much lower than any of the previous DFT or normal mode analyses ‘predicted’ theoretical energy positions. It is actually still at least 32 cm−1 lower than the lowest current DFT value, which is at 707 cm−1 [model VI in Fig. 1(b 6) ▸] (Ogata, Kramer et al., 2015 ▸). The observed cts/s for various Fe–S, Fe–CO and Ni–H–Fe in Ni–R are documented in Fig. 4 ▸ [column 6 (not counting the columns showing ‘→’)].
Figure 6.
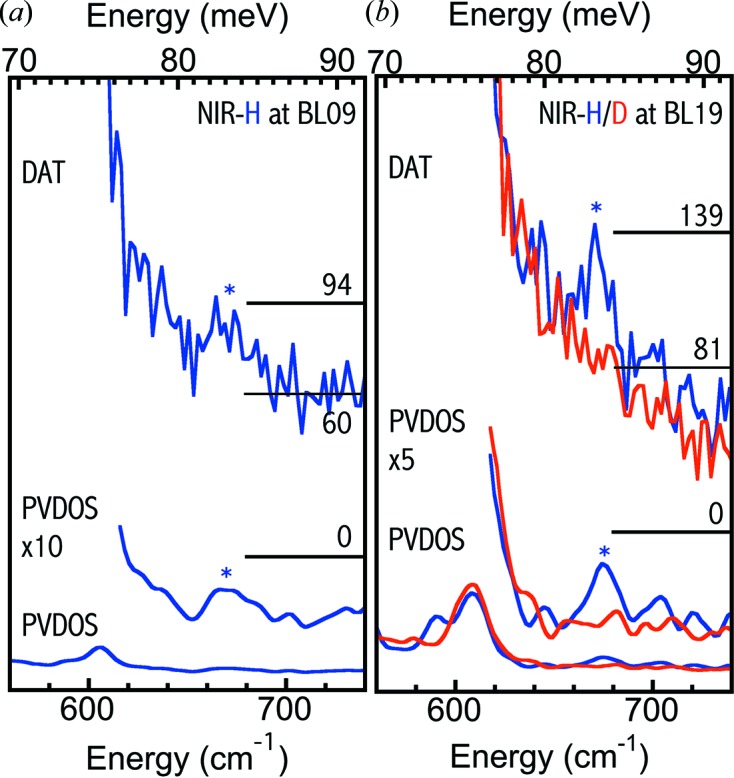
(a) One set (680 s/p) of raw NRVS (top) and PVDOS [bottom and middle (×10)] for NiR-H (blue) measured at BL09XU. (b) One set (480 s/p) of raw NRVS (top) and the PVDOS [bottom and middle (×10)] for NiR-H/D (blue/red) obtained at BL19LXU. Note that the NiR-D raw NRVS has been rescaled in order to match the NiR-H baseline (due to different measurement times).
Even after this successful observation, the disputes did not disappear completely. The first argument was that the observed peak at 675 cm−1 was still too weak. The second argument attributed this peak to a Fe–CO-related feature, rather than to a Fe–H-related peak. However, there is no such Fe–CO sub-feature in the mimic complex NiHFe (Ogata, Kramer et al., 2015 ▸). To clarify the second issue, we examined three NiR-D samples at BL09XU under similar experimental conditions. These NRVS measurements on NiR-D took 106 scans in total (= 40 + 30 + 36) and 2780 total s/p [= (40 × 20) + (30 × 30) + (36 × 30)], but concluded no peak in the same region. This suggests that the peak at 675 cm−1 is related to a Fe–H vibrational mode.
In order to resolve the first issue (to repeat the observation and to improve the spectral S/N) and to further clarify the second issue, two samples of NiR-H and one sample of NiR-D were re-measured at BL19LXU, which has a higher beam intensity and more NRVS cts/s than BL09XU. A similar pair of NRVS and PVDOS for NiR-H (blue, 24 scans, 480 s/p) and for NiR-D (red, 20 scans, 400 s/p) are compared in Fig. 6(b) ▸, illustrating much clearer evidence for the existence and the Fe–H-related nature for the 675 cm−1 peak.
3.5. Signal levels
From Fig. 4 ▸ (column 6 for one measurement at BL19 and column 7 for one measuremnt at BL19, not counting the columns with the arrow symbols), the observed weak Ni–H–Fe wagging mode is 27–29 parts per million in intensity in comparison with the nuclear resonance peak, or ∼0.8% in comparison with the Fe–S feature at 150 cm−1. Compared with Fe–CO (s), this ratio is about 14.8–16.6%, or, equivalently, Ni–H–Fe:Fe–CO ≃ 1:6–1:7. For such a weak signal, the APD’s dark-current noise (instrument error) defines the best possible S/N because the instrumental error bar cannot be averaged lower with more signal statistics. Therefore a low (0.03 cts/s) dark current is the most important foundation for a successful observation of weak Ni–H–Fe. An estimated signal level for Ni–H–Fe for a hypothetical 4 mM NiR-H but measured at BL19LXU, which has 2.6 times more cts/s, is listed in column 5 of Fig. 4 ▸: the hypothetical Ni–H–Fe signal = ∼0.15 cts/s. The real signal level for a 4.1 mM NiR-H at BL19 is listed in column 7: Ni–H–Fe = 0.12 cts/s for measurement 1 [and 0.13 cts/s for measurement 2 (not listed)]. In comparison with the hypothetical case (column 5), the real measurement (column 7) of Ni–H–Fe has a slightly lower cts/s level although the corresponding Fe–CO has a higher cts/s level. This is because Ni–H–Fe:Fe–CO is about 1:6 for NiR-H (Fig. 3 ▸) as opposed to 1:4.5 for the NiHFe complex (Fig. 5b ▸), which was used for the hyperthetical calculations.
NiR-H was measured once at BL09XU (680 s) and twice at BL19LXU (480 + 180 s). The signal level at BL09XU is estimated at (94 − 60)/680 = 0.05 cts/s, leading to a S/N = 0.05/0.03 ≃ 1.7 and a not-so-clear NRVS (Fig. 6a ▸). Meanwhile the signal level for measurement 1 at BL19LXU (Fig. 6b ▸) is (139 − 81)/480 = 0.12 cts/s, corresponding to a S/N = 0.12/0.03 = 4, a much clearer observation for the Ni–H–Fe at 675 cm−1. The signal level for measurement 2 at BL19LXU is about 0.13 and S/N = 4.3. The total equivalent BL09XU s/p (as defined in the experimental section) for NiR-H in the Ni−Fe−H region is 2396 s and the averaged signal level is ∼0.1 cts/s. Assuming as-high-as-possible statistics, this leads to S/N = 3.3. As the real statistics are not infinite, the real S/N is slightly lower than 3.3.
NiR-D was measured three times at BL09XU and once at BL19LXU, equivalent to 3980 BL09XU s/p in the same region (versus 2396 s for NiR-H). As there is no peak, there is no meaning to estimating the signal level or S/N for NiR-D. However, a more equivalent s/p was used for NiR-D because more time should be used to conclude that there is no signal than to find a weak signal.
Fig. 7 ▸ summarizes three PVDOS for NiR-H and four PVDOS for NiR-D in the region around 675 cm−1. Again, all NiR-H PVDOS show a clear peak around 675 cm−1 while none of those for NiR-D show a peak in the same region, providing solid evidence that the observed 675 cm−1 peak is real and is related to Fe–H bending and not to a Fe–CO feature.
Figure 7.
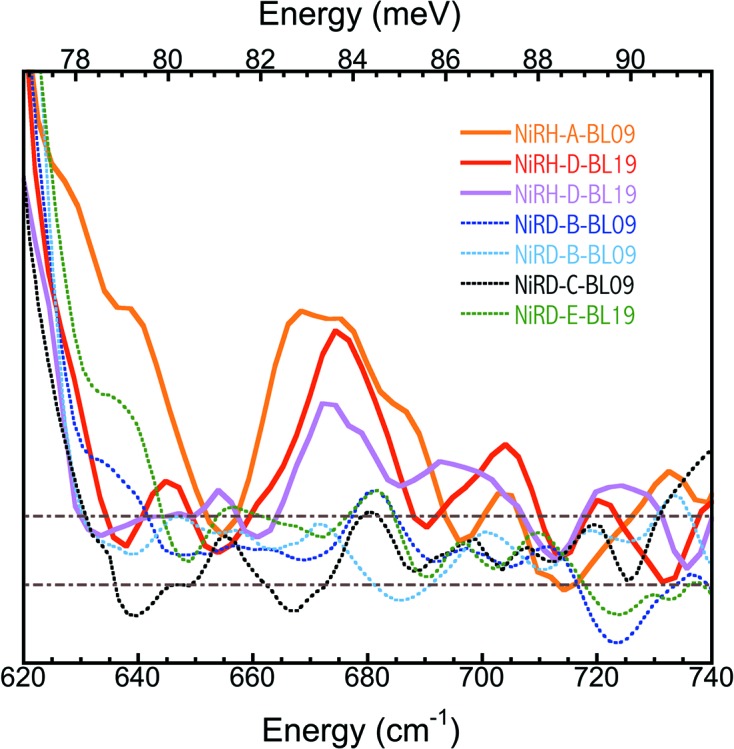
PVDOS for three NiR-H (solid curves) and four NiR-D (dotted curves). In the legends, the front letters indicate sample type (NiR-H or NiR-D), the middle letter marks the beam time sequence, and the last letters/numbers record the beamline at which the particular measurement was made.
3.6. Monitoring samples’ integrity
There are several experimental conditions which make this work successful and a super-concentrated (∼4 mM) and almost pure Ni–R sample (most in Ni–R1, a subform of Ni–R) is one of the most important conditions but is also difficult to realise. We proceed with exchange pH of the buffer (7.4 → 5.0) and with a longer period (more than 8 h) of H2/D2 reduction. Monitoring samples’ integrity can never be more important than under these circumstances. The following three steps were used to monitor the samples’ integrity:
(i) NiR-H/D were first checked with FTIR at the sample preparation laboratory before sending to SPring-8 for NRVS measurements, as shown in Fig. 8(a) ▸. The Ni–R form is known to have up to three isoelectronic forms, Ni–R1, Ni–R2 and Ni–R3. These subforms are distinguishable by FTIR and differ in their protonation states but they are all Ni–R. The NiR-H (blue) sample comprised 84% Ni–R1 (νCO = 1946 cm−1), 16% NiC (at 1962 cm−1) and a trace amount of Ni–R2 (νCO = 1933 cm−1). The NiR-D (red) comprised almost 100% Ni–R1.
Figure 8.
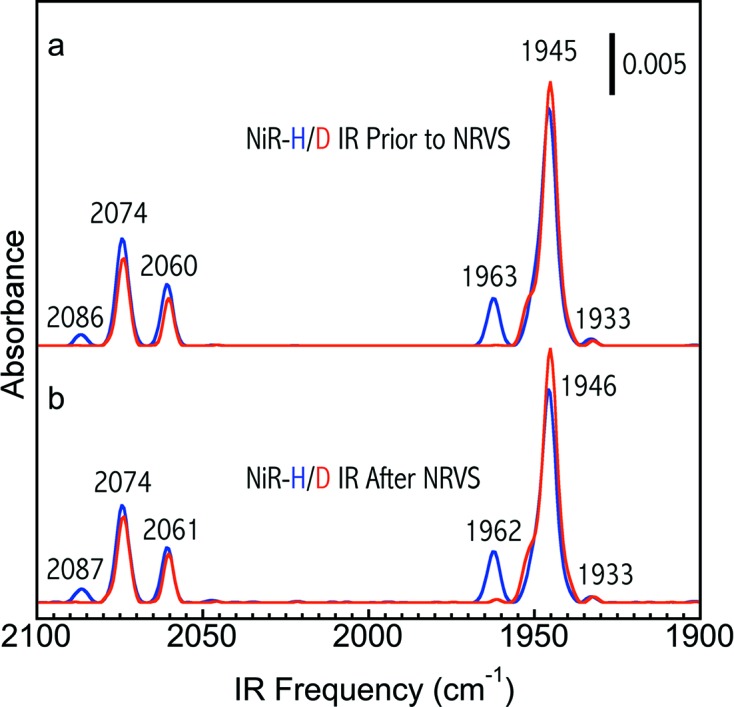
FTIR spectra for one pair of particular NiR-H (blue) and NiR-D (red) samples collected (a) before sending to and (b) after returning from the NRVS measurements.
(ii) NiR-H/D after NRVS measurements were also collected and checked with FTIR and both IR spectra [blue for NiR-H and red for NiR-D in Fig. 8(b) ▸] show little change in comparison with those measured before sending for NRVS experiments (Fig. 8a ▸), confirming the integrity of the samples for the whole NRVS measurement.
(iii) Immediately prior to a NRVS measurement, in situ NRVS measurement in a sample’s Fe–S region was another way of carrying out a last-minute check, as shown in Fig. 9 ▸. For example, the light blue curve shows one example of many good Ni–R samples measured in this study (e.g. for those used in Fig. 7 ▸), while the black curve shows one bad (unexpectedly oxidized) ‘Ni–R’ sample. The green and red spectra are the established NRVS for the oxidized and reduced DvMF H2ase (Kamali et al., 2013 ▸). Although such an identified reduced state may not be a Ni–R, the real control over the samples’ integrity is via the FTIR measurements prior to and following the NRVS experiments, as shown in Fig. 8 ▸. This in situ examination was used only as a handy check that the sample was not oxidized (e.g. Fig. 9 ▸, black curve) before investing a long beam time on the sample.
Figure 9.
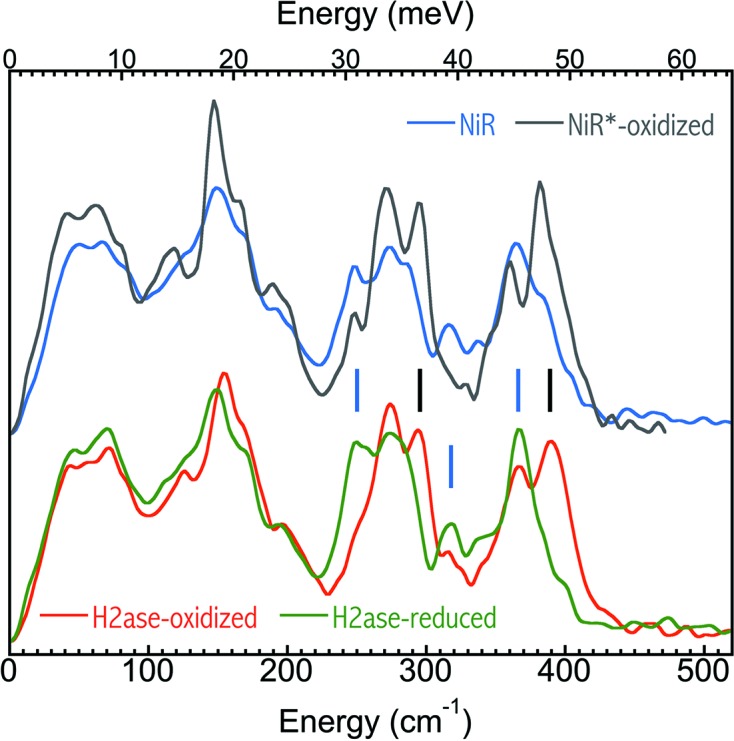
The first two-scan averaged NRVS spectra for a good Ni–R sample (light blue) and a bad (unexpectedly oxidized) Ni–R sample versus the established NRVS spectra for the oxidized (red) and reduced (green) DvMF H2ase (Kamali et al., 2013 ▸).
There are a lot of features in the Fe–S region which can be used to characterize the oxidation states of NiFe H2ase, including the peaks between 340 and 460 cm−1 (Kamali et al., 2013 ▸). At BL09XU (Fig. 4 ▸, column 4), a hypothetical 4 mM DvMF H2ase sample will have 3–6 cts/s in its Fe–S region, and three regular 5 s/p scans will produce 45–90 total cts or a statistical S/N of 6.7–9.5. As the dark current is much smaller in comparison with the Fe–S signal cts/s, the statistical S/N is close to the real S/N. Then a S/N of 7–9 should be sufficient to resolve the samples’ oxidation states. At BL19LXU, in principle, one scan is enough, but we usually took two 3 s/p scans in order to check the repeatability.
3.7. Miscellaneous issues
We noticed that the low dark cts/s of the APD array (i.e. 0.03 cts/s) stays the same at BL19LXU, which has a higher beam intensity than BL09XU. If this dark-current level increases at BL19LXU, the increased cts/s will become less meaningful. We also noticed that the higher beam intensity at BL19LXU does not lead to higher sample temperatures (Wang et al., 2012 ▸) during the NRVS measurement. This again illustrates the conclusion in our previous publication, which suggested that the hike in the samples’ temperatures in comparison with the sample base is mainly due to thermal radiation from the room-temperature window near the samples rather than from the X-ray irradiation (Wang et al., 2012 ▸).
As the HRM is inside the same hutch as the NRVS measurement chamber, entering the hutch can disturb the hutch temperature and the performance of the HRM. A sample change or other regular operation, which lasts ∼30 min, will lead to a system recovery time of about 2 h. In the case of an emergency entry for ∼1 min, the system can be recovered in about 20–30 min. As mentioned earlier, the energy scale can be calibrated either normally or with a quick-switch calibration procedure (Wang et al., 2013 ▸). For concentrated NiR-H/D samples, the Fe–S peak at 365 cm−1 (Fig. 9 ▸) can also be used as a calibration reference because of its high signal level.
3.8. Looking for Fe–H/D stretching modes
The Fe–H or Fe–D stretching modes will have no overlaps with any possible NRVS peaks in the same regions and will allow a straightforward experimental identification of the hydride. However, in reference to the model complexes and DFT calculations (Ogata, Kramer et al., 2015 ▸), Fe–D has 1/5 of the intensity of Ni–H–Fe (see Fig. 5 ▸) while Fe–H has 1/15 of that of Ni–H–Fe (not shown in Fig. 5 ▸), presenting further challenges. Under the current experimental conditions, all these peaks are still not observable unless significant improvements in beam intensity, sample concentration and/or measurement solid angles are made. Different improvements and tests are underway. From the NiDFe complex, the 711 cm−1 Ni–D stretching bending peak (mixed with Fe) has about the same intensity as Ni–H–Fe. However, it could be mixed with Fe–CO and is not observable in Ni–R (Ogata, Kramer et al., 2015 ▸).
4. Conclusions
This publication has presented the strenuous experimental journey to discover the first spectroscopic evidence for the existence of a bridging hydride in a [NiFe] H2ase’s Ni–R. The observed weak Ni–H–Fe wagging mode has 27–29 parts per million in intensity in comparison with the nuclear resonance peak, or ∼0.8% in comparison with a Fe–S feature. Improved sample concentration, increased photon flux and ultra-low noise level in the APD detectors all set the foundation for a possible NRVS measurement of the weak Ni–H–Fe. The decision and insistence on searching in the then unlikely energy region of 620–720 cm−1 was the key step towards successful observation of the Ni–H–Fe at 675 cm−1. The existence/non-existence of the 675 cm−1 peak for NiR-H/NiR-D identified the peak as a Fe–H-related feature experimentally. The Ni–H–Fe feature at 675 cm−1 provided a critical observed reference for DFT calculations and thus served as a key in the DFT determination of the Ni–R structures (Ogata, Kramer et al., 2015 ▸). The experimental science discussed here will also have a much broader impact beyond Ni–R and even beyond [NiFe] H2ases. It will be of interest to other scientists who use synchrotron radiation for measuring dilute samples and/or weak spectroscopic features in general.
Acknowledgments
This work was funded by NIH (GM-65440) and DOE Office of Biological and Environmental Research (both to Professor Stephen P. Cramer at UC Davis). We also thank Professor Cramer for his overall support to this research. The work was also supported by BMBF (03SF0355C), EU/Energy Network project SOLAR-H2 (FP7 contract 212508), DFG-funded Cluster of Excellence RESOLV (EXC1069) and Max Planck Society (HO and WL). Use of SPring-8 is supported by JASRI (via proposals 2012A0032-2013B0032 and 2014B1032) and RIKEN (via proposals 20120107 and 20130022).
References
- Amara, P., Volbeda, A., Fontecilla-Camps, J. C. & Field, M. J. (1999). J. Am. Chem. Soc. 121, 4468–4477. [DOI] [PubMed]
- Armstrong, F. A. (2009). Photosynth. Res. 102, 541–550. [DOI] [PubMed]
- Armstrong, F. A., Belsey, N. A., Cracknell, J. A., Goldet, G., Parkin, A., Reisner, E., Vincent, K. A. & Wait, A. F. (2009). Chem. Soc. Rev. 38, 36–51. [DOI] [PubMed]
- Barilone, J. L., Ogata, H., Lubitz, W. & van Gastel, M. (2015). Phys. Chem. Chem. Phys. 17, 16204–16212. [DOI] [PubMed]
- Barton, B. E., Whaley, C. M., Rauchfuss, T. B. & Gray, D. L. (2009). J. Am. Chem. Soc. 131, 6942–6943. [DOI] [PMC free article] [PubMed]
- Bergmann, U., Sturhahn, W., Linn, D. E., Jenney, F. E., Adams, M. W. W., Rupnik, K., Hales, B. J., Alp, E. E., Mayse, A. & Cramer, S. P. (2003). J. Am. Chem. Soc. 125, 4016–4017. [DOI] [PubMed]
- Brecht, M., van Gastel, M., Buhrke, T., Friedrich, B. & Lubitz, W. (2003). J. Am. Chem. Soc. 125, 13075–13083. [DOI] [PubMed]
- Cammack, R., Frey, M. & Robson, R. (2001). Editors. Hydrogen as a Fuel: Learning from Nature. New York: Taylor & Francis.
- Cramer, S. P., Xiao, Y., Wang, H., Guo, Y. & Smith, M. C. (2007). Hyperfine Interact. 170, 47–54.
- Crossland, J. L., Young, D. M., Zakharov, L. N. & Tyler, D. R. (2009). Dalton Trans. 2009, 9253–9259. [DOI] [PubMed]
- De Lacey, A. L., Fernández, V. M., Rousset, M. & Cammack, R. (2007). Chem. Rev. 107, 4304–4330. [DOI] [PubMed]
- Do, L. H., Wang, H., Tinberg, C. E., Dowty, E., Yoda, Y., Cramer, S. P. & Lippard, S. J. (2011). Chem. Commun. 47, 10945–10947. [DOI] [PMC free article] [PubMed]
- Dole, F., Fournel, A., Magro, V., Hatchikian, E. C., Bertrand, P. & Guigliarelli, B. (1997). Biochemistry, 36, 7847–7854. [DOI] [PubMed]
- Dong, W., He, P., Wang, J., Zhou, Z. & Wang, H. (2013). Infrared Phys. Technol. 56, 51–56.
- Evans, R. M., Parkin, A., Roessler, M. M., Murphy, B. J., Adamson, H., Lukey, M. J., Sargent, F., Volbeda, A., Fontecilla-Camps, J. C. & Armstrong, F. A. (2013). J. Am. Chem. Soc. 135, 2694–2707. [DOI] [PubMed]
- Foerster, S., Stein, M., Brecht, M., Ogata, H., Higuchi, Y. & Lubitz, W. (2003). J. Am. Chem. Soc. 125, 83–93. [DOI] [PubMed]
- Fontecilla-Camps, J. C., Volbeda, A., Cavazza, C. & Nicolet, Y. (2007). Chem. Rev. 107, 4273–4303. [DOI] [PubMed]
- Fritsch, J., Lenz, O. & Friedrich, B. (2013). Nat. Rev. Microbiol. 11, 106–114. [DOI] [PubMed]
- Gastel, M. van, Stein, M., Brecht, M., Schröder, O., Lendzian, F., Bittl, R., Ogata, H., Higuchi, Y. & Lubitz, W. (2005). J. Biol. Inorg. Chem., 11, 41–51. [DOI] [PubMed]
- Goto, S., Ishikawa, T., Kitamura, H. & Takahashi, S. (2000). SPring-8 Annual Report pp. 30–35. SPring-8, Hyogo, Japan.
- Gu, W., Jacquamet, L., Patil, D. S., Wang, H.-X., Evans, D. J., Smith, M. C., Millar, M., Koch, S., Eichhorn, D. M., Latimer, M. & Cramer, S. P. (2003). J. Inorg. Biochem. 93, 41–51. [DOI] [PubMed]
- Guiral, M., Tron, P., Belle, V., Aubert, C., Leger, C., Guigliarelli, B. & Giudici-Orticoni, M. (2006). Int. J. Hydrogen Energy, 31, 1424–1431.
- Hara, T., Yabashi, M., Tanaka, T., Bizen, T., Goto, S., Marechal, X. M., Seike, T., Tamasaku, K., Ishikawa, T. & Kitamura, H. (2002). Rev. Sci. Instrum. 73, 1125–1128.
- Heinekey, D. M. (2009). J. Organomet. Chem. 694, 2671–2680.
- Inada, T., Namba, T., Asai, S., Kobayashi, T., Tanaka, Y., Tamasaku, K., Sawada, K. & Ishikawa, T. (2013). Phys. Lett. B, 722, 301–304. [DOI] [PubMed]
- Jayapal, P., Robinson, D., Sundararajan, M., Hillier, I. H. & McDouall, J. J. W. (2008). Phys. Chem. Chem. Phys. 10, 1734–1738. [DOI] [PubMed]
- Jugder, B. E., Welch, J., Aguey-Zinsou, K. F. & Marquis, C. P. (2013). RSC Adv. 3, 8142–8159.
- Kamali, S., Wang, H., Mitra, D., Ogata, H., Lubitz, W., Manor, B. C., Rauchfuss, T. B., Byrne, D., Bonnefoy, V., Jenney, F. E. Jr, Adams, M. W. W., Yoda, Y., Alp, E., Zhao, J. & Cramer, S. P. (2013). Angew. Chem. Int. Ed. 52, 724–728. [DOI] [PMC free article] [PubMed]
- Kim, J. Y. H. & Cha, H. J. (2013). Korean J. Chem. Eng. 30, 1–10.
- Lauterbach, L., Wang, H., Horch, M., Gee, L. B., Yoda, Y., Tanaka, Y., Zebger, I., Lenz, O. & Cramer, S. P. (2015). Chem. Sci. 6, 1055–1060. [DOI] [PMC free article] [PubMed]
- Lubitz, W. & Ogata, H. (2013). Encyclopedia of Biological Chemistry, edited by W. J. Lennarz and M. D. Lane, pp. 562–567. London: Academic Press.
- Lubitz, W., Ogata, H., Rüdiger, O. & Reijerse, E. (2014). Chem. Rev. 114, 4081–4148. [DOI] [PubMed]
- Matsumoto, T., Kim, K., Nakai, H., Hibino, T. & Ogo, S. (2013). Chem. Cat. Chem. 5, 1368–1373.
- Mertens, R. & Liese, A. (2004). Curr. Opin. Biotechnol. 15, 343–348. [DOI] [PubMed]
- Ogata, H., Hirota, S., Nakahara, A., Komori, H., Shibata, N., Kato, T., Kano, K. & Higuchi, Y. (2005). Structure, 13, 1635–1642. [DOI] [PubMed]
- Ogata, H., Kramer, T., Wang, H., Schilter, D., Pelmenschikov, V., van Gastel, M., Neese, F., Rauchfuss, T. B., Gee, L. B., Scott, A. D., Yoda, Y., Tanaka, Y., Lubitz, W. & Cramer, S. P. (2015). Nat. Commun. 6, 7890. [DOI] [PMC free article] [PubMed]
- Ogata, H., Nishikawa, K. & Lubitz, W. (2015). Nature, 520, 571–574. [DOI] [PubMed]
- Pelmenschikov, V., Guo, Y., Wang, H., Cramer, S. P. & Case, D. A. (2011). Faraday Discuss. 148, 409–420. [DOI] [PMC free article] [PubMed]
- Schilter, D., Nilges, M. J., Chakrabarti, M., Lindahl, P. A., Rauchfuss, T. B. & Stein, M. (2012). Inorg. Chem. 51, 2338–2348. [DOI] [PMC free article] [PubMed]
- Seto, M., Yoda, Y., Kikuta, S., Zhang, X. W. & Ando, M. (1995). Phys. Rev. Lett. 74, 3828–3831. [DOI] [PubMed]
- Shafaat, H. S., Rüdiger, O., Ogata, H. & Lubitz, W. (2013). Biochim. Biophys. Acta, 1827, 986–1002. [DOI] [PubMed]
- Shafaat, H. S., Weber, K., Petrenko, T., Neese, F. & Lubitz, W. (2012). Inorg. Chem. 51, 11787–11797. [DOI] [PubMed]
- Simmons, T. R. & Artero, V. (2013). Angew. Chem. Int. Ed. 52, 6143–6145. [DOI] [PMC free article] [PubMed]
- Smith, M. C., Xiao, Y. M., Wang, H. X., George, S. J., Coucouvanis, D., Koutmos, M., Sturhahn, W., Alp, E. E., Zhao, J. Y. & Cramer, S. P. (2005). Inorg. Chem. 44, 5562–5570. [DOI] [PubMed]
- Sturhahn, W., Toellner, T. S., Alp, E. E., Zhang, X., Ando, M., Yoda, Y., Kikuta, S., Seto, M., Kimball, C. W. & Dabrowski, B. (1995). Phys. Rev. Lett. 74, 3832–3835. [DOI] [PubMed]
- Takahashi, S., Aoyagi, H., Mochizuki, T., Oura, M., Sakurai, Y., Watanabe, A. & Kitamura, H. (2001). Nucl. Instrum. Methods Phys. Res. A, 467–468, 758–761.
- Tanaka, Y., Uozaki, Y., Nozaki, K., Ito, K., Yamasaki, K., Terauchi, H., Takahashi, I. & Ishikawa, T. (2011). J. Phys. Conf. Ser. 278, 012018.
- Tard, C. & Pickett, C. J. (2009). Chem. Rev. 109, 2245–2274. [DOI] [PubMed]
- Tinberg, C. E., Tonzetich, Z. J., Wang, H., Do, L. H., Yoda, Y., Cramer, S. P. & Lippard, S. J. (2010). J. Am. Chem. Soc. 132, 18168–18176. [DOI] [PMC free article] [PubMed]
- Volbeda, A., Martin, L., Barbier, E., Gutiérrez-Sanz, O., De Lacey, A., Liebgott, P., Dementin, S., Rousset, M. & Fontecilla-Camps, J. (2015). J. Biol. Inorg. Chem. 20, 11–22. [DOI] [PubMed]
- Wang, H., Alp, E., Yoda, Y. & Cramer, S. (2014). Methods in Molcular Cell Biology, Vol. 1122, Metalloproteins, edited by J. C. Fontecilla-Camps and Y. Nicolet, pp. 125–137. New Jersey: Humana Press.
- Wang, H., Patil, D. S., Gu, W., Jacquamet, L., Friedrich, S., Funk, T. & Cramer, S. P. (2001). J. Electron Spectrosc. Relat. Phenom. 114–116, 855–863.
- Wang, H., Patil, D. S., Ralston, C. Y., Bryant, C. & Cramer, S. P. (2001). J. Electron Spectrosc. Relat. Phenom. 114–116, 865–871.
- Wang, H. X., Ralston, C. Y., Patil, D. S., Jones, R. M., Gu, W., Verhagen, M., Adams, M., Ge, P., Riordan, C., Marganian, C. A., Mascharak, P., Kovacs, J., Miller, C. G., Collins, T. J., Brooker, S., Croucher, P. D., Wang, K., Stiefel, E. I. & Cramer, S. P. (2000). J. Am. Chem. Soc. 122, 10544–10552.
- Wang, H., Yoda, Y., Dong, W. & Huang, S. D. (2013). J. Synchrotron Rad. 20, 683–690. [DOI] [PMC free article] [PubMed]
- Wang, H., Yoda, Y., Kamali, S., Zhou, Z.-H. & Cramer, S. P. (2012). J. Synchrotron Rad. 19, 257–263. [DOI] [PMC free article] [PubMed]
- Xiao, Y. M., Wang, H. X., George, S. J., Smith, M. C., Adams, M. W. W., Jenney, F. E., Sturhahn, W., Alp, E. E., Zhao, J. O., Yoda, Y., Dey, A., Solomon, E. I. & Cramer, S. P. (2005). J. Am. Chem. Soc. 127, 14596–14606. [DOI] [PubMed]
- Yabashi, M., Mochizuki, T., Yamazaki, H., Goto, S., Ohashi, H., Takeshita, K., Ohata, T., Matsushita, T., Tamasaku, K., Tanaka, Y. & Ishikawa, T. (2001). Nucl. Instrum. Methods Phys. Res. A, 467–468, 678–681.
- Yang, J. Y., Bullock, M., DuBois, M. R. & DuBois, D. L. (2011). MRS Bull. 36, 39–47.
- Yoda, Y., Imai, Y., Kobayashi, H., Goto, S., Takeshita, K. & Seto, M. (2012). Nucl. Instrum. Methods Phys. Res. A, 206, 83.
- Yoda, Y., Yabashi, M., Izumi, K., Zhang, X. W., Kishimoto, S., Kitao, S., Seto, M., Mitsui, T., Harami, T., Imai, Y. & Kikuta, S. (2001). Nucl. Instrum. Methods Phys. Res. A, 467–468, 715–718.