Erroneous Arrhenius: Modified Arrhenius model best explains the temperature dependence of ectotherm fitness

Abstract

The initial rise of fitness that occurs with increasing temperature is attributed to Arrhenius kinetics, in which rates of reaction increase exponentially with increasing temperature. Models based on Arrhenius typically assume single rate-limiting reaction(s) over some physiological temperature range for which all the rate-limiting enzymes are in 100% active conformation. We test this assumption using datasets for microbes that have measurements of fitness (intrinsic rate of population growth) at many temperatures and over a broad temperature range, and for diverse ectotherms that have measurements at fewer temperatures. When measurements are available at many temperatures, strictly Arrhenius kinetics is rejected over the physiological temperature range. However, over a narrower temperature range, we cannot reject strictly Arrhenius kinetics. The temperature range also affects estimates of the temperature dependence of fitness. These results indicate that Arrhenius kinetics only apply over a narrow range of temperatures for ectotherms, complicating attempts to identify general patterns of temperature dependence.

Introduction

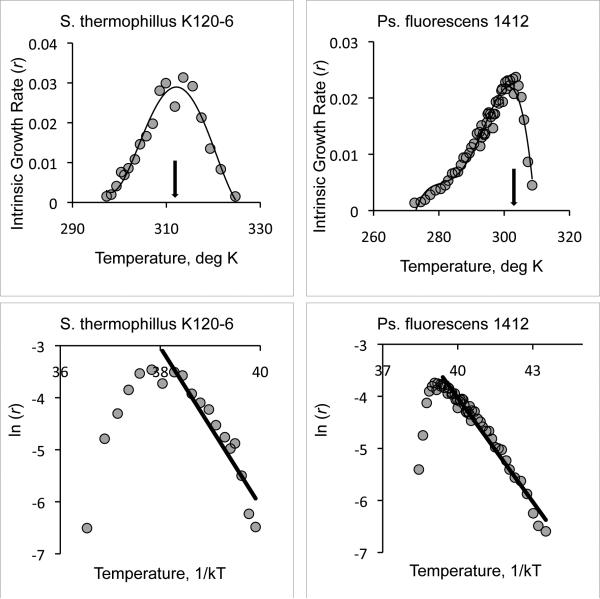
Temperature affects all biological rate processes, from molecular kinetics to population growth. At the level of whole-organism performance, rates of locomotion, growth, development and fitness have a predictable dependence on temperature. Performance increases gradually with increasing temperature, reaches a maximum at the optimal temperature, T_opt, then declines rapidly with further increases of temperature (Huey and Stevenson 1979; Huey and Hertz 1984; Huey and Kingsolver 1989). This pattern is illustrated in Figure 1 (top panel) for the temperature-dependence of fitness (intrinsic rate of population growth, r) for the bacteria Staphlococcus thermophilius and Pseudomonas fluorescens (modified from Ratkowsky et al. (2005) Figure 2). The initial rise of fitness that occurs with increasing temperature is attributed to Arrhenius kinetics, in which rates of reaction exponentially increase with increasing temperature (Arrhenius 1915). The decrease in fitness that occurs above T_opt is attributed to higher temperatures making proteins overly flexible, reducing substrate affinity by disrupting the active site and ultimately leading to denaturation of critical proteins (Fields 2001; Hochachka and Somero 2002).

Figure 1.

Representative microbial thermal reaction norms (adapted from Ratkowsky et al. 2005, Figure 2). Top row, the intrinsic growth rate of two microbes is shown as a function of temperature. Arrows indicate the optimal temperature of each microbe (respectively, 313K and 300K, where K is degrees Kelvin). Temperature below the optimal temperature (to the left of the arrow) would be considered part of the physiological temperature range. Bottom row, the natural log of growth rate is shown as a function of 1/kT. The solid black line is the linear regression performed per the Arrhenius equation (eq. [1]). The linear slopes are −1.22 and −0.66 eV for S. thermophilius and Ps. fluorescens respectively.

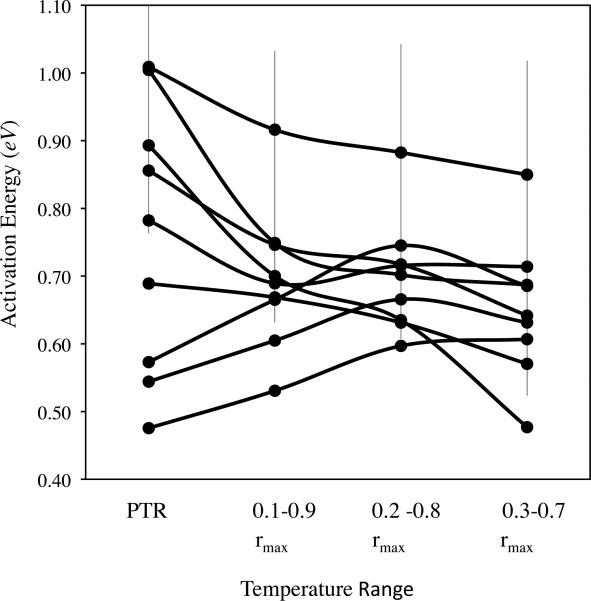
Figure 2.

Linear slopes (activation energy estimates) as a function of temperature range for microbial species. These data are for the species from Ratkowsky et al. (2005). PTR represents the physiological temperature range and includes temperatures greater than 0°C and less than T_opt. For species (Escherichia coli, Listeria monocytogenes and Streptococcus thermophilus) where there was more than 1 dataset, error bars are shown for the standard deviation in the slope estimate.

The Arrhenius equation has been used in many models for rates of metabolism, growth, development, and fitness. These models assume that these rates depend on a rate-limiting reaction(s). Some models use the Arrhenius equation without modification (Gillooly et al. 2001; Savage et al. 2004), while others do modify the Arrhenius equation to allow for thermal denaturation of the rate-limiting enzyme(s) (Schoolfield et al. 1981; Ratkowsky et al. 2005). Using only the Arrhenius equation (Arrhenius 1915), the intrinsic rate of population growth (r) over temperatures below T_opt, the physiological temperature range (PTR), is

$$\ln \left(r\right)=\frac{-E}{kT}$$ (1)

where k is the Boltzmann constant, T is temperature (in Kelvin), and E is the activation energy parameter (in electron Volts) for the rate-limiting reaction(s). The Arrhenius equation thus predicts a linear relationship between ln(r) and (kT)⁻¹ for temperatures within the PTR.

The Arrhenius model has recently been extended to incorporate the scaling effects of body mass (M) on rates of metabolism, individual growth, and fitness (intrinsic rate of population growth) (Gillooly et al. 2001; Savage et al. 2004). This model predicts the temperature dependence of mass-scaled fitness:

$$\ln \left(r{M}^{1∕4}\right)=\frac{-E}{kT}$$ (2)

where M is the mass of an individual in micrograms. Equation [2] predicts that mass-scaled population growth rates [ln(rM^1/4)] are linearly dependent on inverse temperature (kT)⁻¹ with a slope given by -E. A second prediction of the model is that across diverse taxa, this activation energy parameter, E, should have an average, or universal value of 0.6 eV. As a result this model is sometimes called the universal temperature dependence (UTD) model. These predictions apply within some “physiologically relevant temperature range” (PTR) (Savage et al. 2004) : temperatures below the optimal temperature but excluding low temperatures at which growth rate is negative.

A critical assumption of the Arrhenius and UTD models is that the probability that the rate-limiting enzyme(s) is in its active conformation is 100% and does not vary within the PTR (Schoolfield et al. 1981; Gillooly et al. 2001; Ratkowsky et al. 2005). If the probability that the rate-limiting reaction is in active form declines at high or low temperatures within the PTR (Schoolfield et al. 1981; Ratkowsky et al. 2005), then this will make the relationship between ln(r) and (kT)⁻¹ concave (curved downwards) rather than linear. As a result there are two key empirical questions to consider. Is the relationship between ln(r) and inverse temperature (kT)⁻¹ linear or concave within the PTR? Is the slope of this relation constant across diverse organisms, suggesting a single universal value for activation energy E (Savage et al. 2004)? The second question has been explored empirically by several authors (Savage et al. 2004; Frazier et al. 2006; Lopez-Urrutia and Moran 2007; Knies et al. 2009) including a thorough analysis of data for metabolic rates and developmental rates in insects (Irlich et al. 2009). The first question, and its implications for estimates of activation energy, has not been systematically explored: This is the goal of our paper.

Previously, the UTD model predictions have been tested by combining growth rate data for multiple species or taxa, each having intrinsic growth rate measures at only a few temperatures (eg (Gillooly et al. 2001; Savage et al. 2004; Irlich et al. 2009). However, the predictions of the UTD model can best be assessed for individual species with measurements of intrinsic growth rate measures at many temperatures below the optimal temperature (T_opt). For example, from Ratkowsky et al. (2005), S. thermophilius and Ps. fluorescens have 13 and 42 growth rate measures below their respective T_opt of 313K and 300K (Figure 1). At temperatures below T_opt of each species (within the PTR), equation [1] predicts a negative and linear relationship between ln(r) and (kT)⁻¹. A visual assessment within the PTR suggests a relatively linear relationship for Ps. fluorescens, but a concave relationship for S. thermophilus (Figure 1, bottom row). It is unclear which pattern is true for most organisms. If most organisms do not show a linear relationship between ln(r) and (kT)⁻¹ for temperatures less than T_opt, it may be that this predicted linear relationship still holds over a narrower range of temperatures.

Here, we assess how well the Arrhenius model assumed by UTD (eqs. [1-2]) described data for intrinsic rate of population growth (fitness, r) for individual species or genotypes at temperatures within the physiological temperature range (PTR). We use two sources of data: microbes for which there are many measured temperatures (Ratkowsky et al. 2005); and diverse plankton, algae and insect species for which there are relatively few measured temperatures for each species (Savage et al. 2004). The specific questions we focus on are: (i) Is the temperature dependence of (mass-scaled) fitness linear or concave below T_opt?; (ii) How might non-linearity impact our estimates of the slope?; (iii) Can we define operationally a more restricted temperature range within the PTR for which the slope is linear?; and (iv) Are there differences among species in the slope within this PTR over which equation [1] applies?

Methods

Datasets

We consider data for clonal growth rate (r) for microbes (Ratkowsky et al. 2005). This includes 35 datasets for 9 microbial species, each with growth rate measures at many (mean of 24) temperatures over a broad range (mean of 32.4 °C). We restrict our analyses to temperatures within the PTR (Savage et al. 2004) by excluding low temperatures at which growth rate is negative, and high temperatures above the optimum temperature. To identify the optimum temperature (T_opt) in a consistent, quantitative, and unbiased manner, we first determine whether a 3^rd or 4^rth order polynomial best describes the temperature dependence of fitness of each dataset, based on the small-sample Aikake Information Criterion (AIC) (Burnham and Anderson 2002). T_opt is then defined for each dataset as the temperature at which r is maximized when evaluated with the AIC best model (as shown in Figure 1, top row). Because the thermal reaction norm is expected to become nonlinear near T_opt (Ratkowsky et al. 2005), we also choose a narrower range of temperatures within the PTR. These narrower temperature ranges are determined by identifying temperatures at which the growth rate is some fraction of the maximum growth rate (r_max), where r_max is the growth rate at T_opt.

We also reanalyze the data from Savage et al. (2004), which have relatively few measurements (mean of 4) for each species. Savage et al. (2004) considered the UTD model of intrinsic rate of population growth (mass scaled growth rate) (eq. [2]) for unicellular organisms with nonoverlapping generations (unicellular algae and protists), multicellular organisms with nonoverlapping generations (plankton and insects), and multicellular organisms with overlapping generations (vertebrates: mammals and fish). Savage et al. (2004) excluded low temperatures at which growth rate is negative and high temperatures at which growth rate is clearly rapidly declining. Savage et al. (2004) fit eq. [2] to each class of organisms and so estimated the activation energy for each class of organisms. However, this approach obscures deviations of individual species from the linear model predicted by eq. [2]. Therefore, from the Supplemental Material in Savage et al. (2004), we consider only species with growth rate measures at 4 or more temperatures within the PTR, which eliminated the data for all vertebrate species. This requirement ensured that we could statistically evaluate non-linear patterns between ln(r) and (kT)⁻¹. After these exclusions, there were 13 species with sufficient data for analysis, including 5 plankton species, 3 algal species, and 5 insect species.

For each dataset, we calculate the best-fit line and best-fit second-degree polynomial for the relationship between either ln(r) and 1/kT (eq. [1]) or ln(rM^1/4) and 1/kT (eq. [2]). For the Ratkowsky et al. (2005) analysis, we used an F test and small-sample AIC (Burnham and Anderson 2002) to determine whether the second-degree polynomial is a significantly better fit than the linear model. We report only the F test results, unless the tests disagreed. For the Savage et al. (2004) analysis, the small sample sizes precluded use of the small-sample AIC and so an F test was used to determine the best-fit model. For each dataset, we also determined whether the best-fit second-degree polynomial was concave up or down by taking the second derivative of this function.

Permutations

To assess the effect of number of measurements on ability to reject the linear model and to make the number of measurements for each dataset in Ratkowsky et al. (2005) comparable to those in Savage et al. (2004), we also analyzed the Ratkowsky et al. (2005) datasets in another way. For each Ratkowsky et al. (2005) dataset with N measurements in the PTR, we generated $\left(\begin{array}{c}N-2\hfill \\ 2\hfill \end{array}\right)$ permutations, each of which maintained the original PTR range, but decreased the number of measurements to 4: one at the minimum of the PTR, one at the maximum of the PTR, and two at intervening temperatures. For each permutation, we used an F test as above, to determine whether the second-degree polynomial is a significantly better fit than the linear model. As in the Savage et al. (2004) analysis, we could not use the small-sample AIC here because of the small sample size.

Results

The linear Arrhenius model (eq. [1]) is a poor fit to the 35 datasets from Ratkowsky et al. (2005). Over the PTR (mean of 25.2°C; range of 13.1-32.9 °C), the second-degree polynomial is a significantly (F test, p < 0.05) better fit to 34 of 35 datasets (97%) and is concave down (second-derivative < 0) for all the datasets. As the temperature range examined was reduced, the number of data sets best-fit by a second degree polynomial became smaller (Table 1). For example, when the temperature range is 0.1-0.9 of r_max (mean of 17.6 measurements) then the second-degree polynomial is a significantly better fit to 91% of datasets. But this fraction drops to 57% (AIC: 54%) for 0.2-0.8 of r_max (mean of 12.9 measurements) and to 26% (AIC: 16%, 5/31) when the temperature range is restricted to temperatures at which r is 0.3-0.7 of r_max (mean of 8.31 measurements). Figure A1 depicts a representative comparison of the full PTR and the temperature range which r is 0.3-0.7 of r_max for 10 datasets. At the temperature range (0.3-0.7 r_max) when a majority (26 of 35) of datasets are fit better by the linear model, the average temperature range is 7.6°C and the average number of measurements is 8.3 (as compared to 25.2 °C and 24.1 respectively for the average PTR). Across all datasets, the mean slope declines from 0.89 for the full PTR to 0.71 when the temperature range is restricted to temperatures at which r is 0.3-0.7 of r_max (Figure 2).

Table 1.

EFFECT OF TEMPERATURE RANGE ON ESTIMATION OF ACTIVATION ENERGY FOR MICROBIAL SPECIES FROM RATKOWSKY ET AL. (2005)

TEMPERATURE RANGE	MEAN TEMPERATURE RANGE (°C)	MEAN NUMBER OF TEMPERATURES	MEAN ACTIVATION ENERGY (eV)	LINEAR MODEL IS BEST FIT
PTR	25.15	24.06	0.89	1/35
0.1 -0.9 rmax	17.64	17.6	0.77	4/35
0.2 -0.8 rmax	12.23	12.9	0.75	15/35
0.3-0.7 rmax	7.64	8.31	0.71	24/35

The change in the linear slope that accompanies a decreasing temperature range is not the same for all the bacteria species. For 6 of 9 species, including the 3 species with the greatest number of datasets (Escherichia coli, Listeria monocytogenes and Streptococcus thermophilus), the slope of linear fit decreases as temperature range is narrowed. For 3 of 9 species, the slope of linear fit increases as temperature range is narrowed. These results suggest that restricting the temperature range within the PTR does cause the slope estimates to become more similar, but it is unclear whether the estimates converge towards a common value (Figure 2).

The number of temperatures at which growth rate is measured impacts whether or not the linear Arrhenius model is rejected. By restricting each dataset from Ratkowsky et al. (2005) to just 4 temperatures and sampling all possible 4-temperature samples for each dataset, each dataset rejects the linear model in an average of only 25% (range: 1.5-41%) of its permutations.

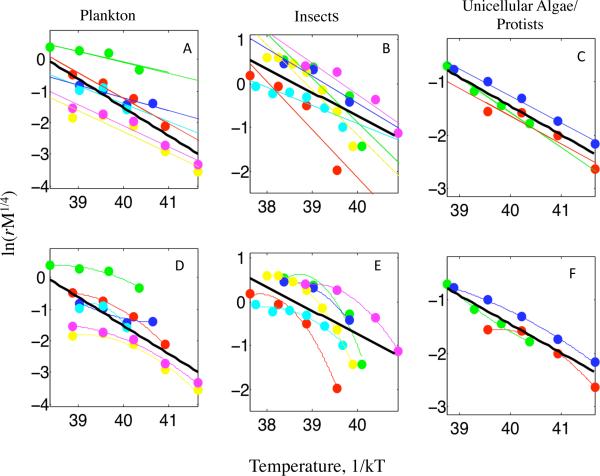
The Savage et al. (2004) data have fewer measurements (range: 4-7) for each species making it difficult to assess the fit of the linear UTD model (eq. [2]) (Figure 3). For 11 of the 13 species, the best- fit second-degree polynomial is concave down (second derivative < 0). However, for only 4 of the 13 species, the second degree polynomial is a significantly better fit (F test, p < 0.05) than a linear model for the dependence of ln(rM^1/4) on (kT)⁻¹.

Figure 3.

Linear UTD model fit to diverse organisms. The 3 types of organisms in Savage et al. (2004) are each shown in a panel. A-C. The top row of each panel is the shows the best fit line to each species and the species data points. The best-fit line to the combined species data is shown in black. D-F. The bottom row of each panel shows the best-fit polynomial of degree 2 for each species. The best-fit line to the combined species data is still shown in black.

Discussion

Microbiologists and entomologists have long recognized the limitations of applying the Arrhenius equation to data for growth and developmental rates. Ratkowsky et al. (1982) pointed out that population growth rates for microbes were concave down rather than linear when plotted in the Arrhenius manner. We found that significant negative curvature, concavity, occurs in most datasets for temperature below T_opt for the 9 microbial species from Ratkowsky et al. (2005). We found concavity also occurs in the majority of species from Savage et al. (2004), including algal, protist, and insect species, though significant concavity was detected in only 4 of the 13 species presumably due to lack of statistical power in these datasets.

The linear relation predicted by Arrhenius-based models for growth rate as a function of inverse temperature is only true when 100% of the rate-limiting enzyme is in an active form. The UTD model prediction (eq. [2]) follows Arrhenius in assuming the probability of enzyme being in the active form is high (~1) and constant over some temperature range (the PTR). The concavity that we observe violates these model predictions and can be accounted for by incorporating a probability of activation as a function of temperature (Schoolfield et al. 1981; Ratkowsky et al. 2005)). Models that estimate the probability of activity as a function of temperature for rates of growth or differentiation show that the fraction of active enzyme is not 100%, and is not constant at temperatures below T_opt. Rather, these models find support for enzyme inactivation occurring at the lower and upper end of the PTR and it is only in the intermediate range of the PTR that enzyme activation is at or near 100% (Schoolfield et al. 1981; van der Have and de Jong 1996; Ratkowsky et al. 2005).

Other factors may also contribute to the non-linearity observed here. If the Arrhenius model is a purely probabilistic description of reaction kinetics, then one might expect increasing variation in growth rate towards the extremes of any line fitted through the data, generating random variation in the degree and direction of curvature. However, we detected negative concavity in all microbial datasets and in 11 of 13 of the Savage et al. (2004) datasets: in no case did we detect significant curvature (upwards) concavity. This pattern is inconsistent with a probabilistic interpretation of Arrhenius. Second, the rate-limiting enzyme may not be saturated by substrate across all temperatures in the PTR. To produce the downwards concavity that we see in nearly all the datasets, the probability of rate-limiting enzymes being saturated would have to decline towards the extremes of the PTR. We are not aware of data that address this hypothesis.

The assumption that Arrhenius governs growth rates below T_opt is particularly problematic when, as in most cases, only a handful of temperatures are evaluated (Savage et al 2004). In this case, it is not clear what is being estimated by the activation energy (slope) term used to describe the temperature sensitivity of growth rate of different groups. It is also not clear that there is a single common slope (Terblanche et al. 2007). One potential solution to this problem of concavity is to define a restricted range of temps below T_opt within which the linear model holds. But identifying this range operationally is a challenge and still requires measurements at many temperatures. Our results clearly show that the choice of the temperature range can strongly affect the estimated slope (Figure 2 and Table 1). We find that the linear model is generally better than the concave model only over a very narrow range within the PTR—8°C on average—limiting the generality of this model. Even when a restricted range for PTR is used (in which linearity applies), there is substantial variation in estimated slopes (Table 1: 0.5-0.9 eV) among species of microbes. They do cluster around the predicted value of 0.6-0.7eV. This may indicate that there is a universal temperature dependence, but only over a narrow range of a species PTR, because of high and low temperature inactivation of critical enzyme(s). We are unable to eliminate the possibility that at the narrowest temperature range (0.3-0.7 r_max), the linear model is not rejected by many of the datasets because the number of measurements is too few (mean of 8.31, range of 4-23).

Evidence from enzyme and physiological studies also challenges the assumption of a universal E based on Arrhenius. Studies of enzyme kinetics suggest that enzymes from cold-adapted species tend to have a lower E than orthologs from warm-adapted species. This reduction in activation energy for cold-adapted enzymes will increase rates of reaction and may be one mechanism of adaptation to cold temperatures (Feller and Gerday 1997; Lonhienne et al. 2000; Fields et al. 2002; Feller 2003). For multicellular animals, metabolic fluxes may be limited by oxygen supply such that no single enzyme is rate-limiting across the entire physiological temperature range, altering the temperature-dependence of organismal rate processes (Portner et al 2006).