In Silico Investigation of Angiogenesis with Growth and Stress Generation Coupled to Local Extracellular Matrix Density

Abstract

Mechanical interactions during angiogenesis, i.e., traction applied by neovessels to the extracellular matrix and the corresponding deformation, are important regulators of growth and neovascularization. We have previously designed, implemented, and validated a coupled model of angiogenesis in which a discrete microvessel growth model interacts with a continuous finite element mesh through the application of local remodeling sprout stresses (Edgar et al. in Biomech Model Mechanobiol, 2014). However, the initial implementation of this framework does not take matrix density into account when determined these remodeling stresses and is therefore insufficient for the study of angiogenesis within heterogeneous matrix environments such as those found in vivo. The objective of this study was to implement sensitivity to matrix density in the active stress generation within AngioFE in order to allow the study of angiogenic growth within a heterogeneous density environment. We accomplished this by scaling active sprout stresses relative to local matrix density using a scaling factor previously determined from experimental data. We then exercised the new functionality of the model by simulating angiogenesis within four different scenarios: homogeneous density, a narrow gap model, and matrix density gradient, and a construct subjected to repeated loading/unloading and preconditioning. These numerical experiments predicted heterogeneous matrix density in the initially homogeneous case, the closure and alignment of microvessels along a low-density gap, the formation of a unique cap-like structure during angiogenesis within a density gradient, and the alignment of microvessels in the absence of applied load due to preconditioning. The result of these in silico investigations demonstrate how matrix heterogeneity affects neovascularization and matrix deformation and provides a platform for studying angiogenesis in complicated and multi-faceted mechanical environments that microvessels experience in vivo.

INTRODUCTION

A vasculature is an essential component of native and engineered tissue health. Uncontrolled or insufficient blood vessel growth causes and/or complicates a spectrum of diseases, including ischemia, atherosclerosis, and cancer.^1,19,35 Neovascularization, the establishment of a new vasculature in cell and tissue constructs, remains a significant challenge in tissue engineering and improving neovascularization is a means to therapeutically improve tissue vascularity.^4,36,37 Sprouting angiogenesis, the formation of new blood vessels from an existing vasculature, is a key process in neovascularization and leads to the expansion of an existing vascular network by creation of new vascular components. Vascular density and network topology vary amongst different tissues facilitating the unique function of the tissue.³⁸ While there are many factors that control angiogenesis, little is known as to the how the mechanical microenvironment influences the topology of a growing vasculature.^11,40

Mechanical interactions are important regulators of growth and neovascularization. During angiogenesis, endothelial cells of sprouting neovessels move into the extracellular space, applying traction to and migrating along the extracellular matrix (ECM).⁴⁴ Therefore, the mechanical properties of the matrix stromal environment including composition, stiffness, density, and boundary conditions control these mechanical interactions. Previous experimental studies have demonstrated how changes in the mechanical microenvironment affect angiogenic growth.^{5,7,13,15,23,41,43,47} Using an organ culture model of angiogenesis based on isolated microvessel fragments in a type I collagen gel, we have previously demonstrated that constraining the deformation of the matrix can induce vascular alignment.^7,43 Numerous studies using a variety of cell and organ cultures embedded in different types of biopolymer substrates have demonstrated that matrix density regulates the rate of angiogenic growth and sprouting.^{5,13,15,23,41,47} However, current fabrication methods associated with these experimental models often only permit the study of simplified environments and manipulation of conditions at the global level. Therefore, these techniques often do not provide sufficient means to study the outcome of angiogenesis in more complex microenvironments.

Computational modeling can facilitate the testing of scenarios and hypotheses that are beyond the limitations of current experimental techniques in a systematic manner. However, applying traditional methods in computational biomechanics to a process such as angiogenesis is challenging due to the intricate and discontinuous geometry of microvascular networks. To overcome these challenges we have designed, implemented, and validated a coupled computational model of angiogenesis (AngioFE) in which a discrete model of the sprouting, elongation and anastomosis of angiogenic microvessels is coupled to a continuum representation of ECM mechanics.^11,12 Local density and directionality of the ECM directly influence the growth of the discrete neovessels.^10,13 The neovessels interact with a continuum finite element (FE) representation of the ECM by generating active stresses at the tips of the neovessel sprouts.^11,12 This model has previously been used to demonstrate the mechanism by which mechanical boundary conditions exert global control over the orientation of the vascular network in 3D vascularized constructs.¹² This implementation used microvessel position and orientation to calculate active stress within the matrix. However, there is growing experimental evidence that local matrix density modulates traction forces and active matrix stresses during cellular migration.^{15,22–24,41}

The objective of this study was to extend the capabilities of AngioFE to allow simulation of growth within a heterogeneous density environment. This new capability of the model was then used to simulate angiogenesis under homogeneous density conditions and three different mechanical microenvironments than resembled different stromal conditions that can be found in vivo and cannot be easily studied using experimental techniques. This was accomplished by making the active stresses generated by the growing neovessels dependent on ECM density. We have previously examined the effect of heterogeneous ECM density on angiogenic growth using our discrete growth model,¹³ but these studies lacked any coupling between growth and matrix mechanics. The resulting modeling framework provides an enhanced platform for the study of the complicated interplay between angiogenic growth and matrix mechanics, with the capability to investigate the role of complex heterogonous mechanical environments such as those found in vivo.

MATERIALS AND METHODS

Overview of AngioFE

AngioFE is a modeling framework that consists of a discrete microvessel model simulating angiogenic growth^10,13 coupled to a continuous FE model of matrix mechanics.^11,12 The development of this framework was motivated by in vitro organ culture experiments of angiogenesis.¹⁸ In these experiments, isolated microvessel fragments consisting of endothelial cells, associated perivascular cells, and the native basement membrane were seeded within a type I collagen gel (Fig. 1a). During culture, neovessel sprouts form within these initial fragments which elongate, branch, and anastomoses with other microvessels, forming a new microvascular network (Fig. 1b). In previous studies we have examined the impact of construct boundary conditions,^27,43 ECM density,¹² and preexisting vascular organization⁷ on subsequent neovessel outgrowth and vascular topology.

FIGURE 1.

Organ culture model of angiogenesis using isolated microvessel fragments within a collagen gel. (a) An initial microvessel fragment within a type I collagen matrix imaged using two-photon microscopy. Endothelial cells and pericytes are shown in green while collagen fibrils are shown in red. Scale bar 20 µm. (b) Angiogenic growth within unconstrained constructs shown in images of different cultures fixed at different time points after initial feeding. Cultures were imaged using confocal microscopy and fluorescently labeled endothelial cells. Neovessels sprouts from parent vessels at around Day 2–3 of culture and by Day 6 a well-established vascular network exists within the construct. Scale bar 200 µm.

The coupling between the discrete and continuous models occurs in several ways. The discrete growth model uses local ECM field information stored at the nodes of the mesh and interpolated to the growth model using FE shape functions. Active sprout stress fields are then applied to the mesh to represent the stress that vessels generate in the matrix during remodeling and growth. These active stress fields are calculated based on sprout position and orientation within the discrete growth model. Nonlinear FE analysis is then used to solve for the deformation based on a mixture constitutive model that homogenizes vascular properties over the mesh using the vascular volume fraction. Lastly, the kinematic solution predicted by FE analysis is then used to update microvessels and regulatory ECM field information within the growth model prior to simulating the next growth step, completing the coupling.

Discrete Growth Model

Angiogenic growth was modeled using discrete representations of microvessels within a background FE mesh that represented the ECM as described previously.^10–13 Briefly, ECM properties such as fibril orientation and density were stored at the nodes of the mesh and interpolated at any point within the mesh using the FE shape functions. Values for initial ECM fibril orientation (θ) and density (ρ) were prescribed at the mesh nodes. Microvessels were represented as a discrete collection of end-to-end line segments. Initial microvessel fragments (i.e., line segments) were seeded throughout the mesh with a random position and orientation. Both ends of each initial segment were designated as active growth tips, and a segment with an active growth tip was referred to as a sprout. Neovessel elongation (i.e., growth) was modeled by the addition of new line segments at each active sprout location. Local ECM information was interpolated to the sprout locations using the FE shape functions, and this information was used to determine the properties of these new segments. ECM fibril orientation was used to determine the orientation of the segment (net direction of growth) and ECM density was used to determine the length of the segment (net amount of growth). If a new segment encountered an external boundary of the mesh, then that new segment was truncated at the intersection point and the active sprout tip was deactivated. Branching and anastomosis were modeled using methods described previously.^10–13

Coupling Angiogenic Growth with Matrix Mechanics

After each growth step, active sprout stresses representing the stress in the matrix generated by neovessel sprouts was assigned to each sprout location. The nonlinear finite element software FEBio³² was then called to solve for the deformation based on the constitutive model, applied loading, and boundary conditions. The total stress within the construct was given by the sum of the active stress component and the passive stress response. The passive stress response was determined using a mixture material model that included a microvessel component and an ECM component as previously described.^10–13 The contribution of each component was weighted by the vascular volume fraction in order to account for the changes in the stress response that occur as the construct becomes progressively vascularized.

The final step in the model involved using the kinematic solution predicted by FEBio to update the growth model into the current configuration to complete the coupling between neovessel growth and matrix deformation (Fig. 2a). Nodal displacement was interpolated to the microvessel positions and used to update vessel position and orientation into the current configuration. ECM fibril orientation was represented using free vectors and updated into the current configuration using the deformation gradient tensor, and ECM density was updated into the current configuration based on the conservation of mass using the volume change of the deformation.

FIGURE 2.

Stress generation and coupled growth with matrix deformation in AngioFE. (a) Schematic of the coupling between the discrete growth model and the nonlinear FE software FEBio. (clock-wise) First, growth was simulated using the current ECM field. Active sprout stress fields were applied then to the mesh at each sprout location. FEBio was then called to solve for the resulting deformation, and the kinematic information predicted by FEBio was used to update vessels and the ECM into the current configuration. (b) When calculating the stress field at a certain position x, a distance vector r was created running from x to the location of the sprout tip. The active stress at this location due to that sprout tip was calculated based on the distance away from the sprout, ‖r‖, and, the angle formed between r and the direction of the sprout, v. (c) A density scaling factor v was calculated according to Eq. (3) and used to scale the amount of active stress generated by neovessel sprouts depending on local ECM density. This factor was calculate using a previously determined three-parameter exponential function and had a value of 1.0 and ρ = 3.0 mg/mL.

Active Sprout Stresses

Previously, active sprout stress was determined using only the position and orientation of the individual sprout. In this study, our goal was to include sensitivity of the active stress mechanism to ECM density to al- low simulation of the effects of growth and matrix mechanics within a heterogonous matrix environment. The active stress field σ_s(x) at a position x due to a particular sprout location at x_s was calculated based on the following equations,

$$\mathit{r}(\mathit{x})=\Vert \mathit{r}\Vert \hat{\mathit{r}}={\mathit{x}}_s-\mathit{x},$$ (1)

$${\mathit{\sigma }}_s(\mathit{x})=\mathit{v}(\rho )a{e}^{-b\Vert r\Vert }{\text{cos}}^N\left(\frac{\psi }{2}\right)\hat{\mathit{r}}\otimes \hat{\mathit{r}},$$ (2)

where r was the distance vector between x_s and x. The exponential term in this equation caused sprout stresses to be localized around the sprout tip, while the cosine power term gives the field directionality. The angle ψ was measured between the sprout orientation vector v and the distance vector r (Fig. 2b). The parameter a scaled the magnitude of the sprout stress, while b determined the range and N controlled the angular width. The total stress field in the construct was then determined by superimposing the contributions from all sprouts within the domain.

The density scaling factor v was calculated using a previously-described three-parameter exponential function, with coefficients determined from experimental data and calculated based on local collagen density interpolated at x¹³ (Fig. 2c):

$$\mathit{v}(\rho )=5.1605e^{-0.5112\rho (\mathit{x})}-0.16.$$ (3)

This scaling factor was previously obtained using measuring the total vascular length of vascular networks cultured at different matrix densities to determine the factor by which total vascular length (and overall neovascularization) changes as matrix density changes.¹³ In our previous study, we used this scaling factor to scale neovessel growth rate and branch formation within our discrete growth model, which was found to give valid predictions of experimental morphometric data of vascular networks cultured at different matrix densities.¹³ Given that our hypothesis is that the morphometrics of angiogenesis such as growth rate and branch formation are directly regulated by the ability of neovessels to deform and remodel the matrix, we propose that using this same scaling factor to regulate the amount of cell-generated stress with respect to matrix density will lead to realistic predictions of the relationship between angiogenic growth, matrix deformation, and matrix density. In addition to scaling active stress generation, neovessel growth and branching rate were also scaled relative to local matrix density using the same scaling factor v as previously described.¹³

Numerical Experiments

We designed four numerical experiments to exercise the new features of AngioFE. All simulations took place within a FE meshed domain measured 7.5 × 5.0 × 0.5 mm with an element spacing of 250 µm in each direction, similar to previous studies.¹³ Displacement was fully constrained at the node located at the origin (lower left bottom corner) and all external surfaces were prescribed as traction-free. All parameters for the model were set at values used in a previous study,¹² with the exception of the sprout stress magnitude a which was increased by 50% to 5.58 µPa in order to cause the same amount of deformation we achieved without density scaling. Without increasing this parameter, simulations with density scaling contracted less than what we found before because stress decreases as the matrix contracts and density increases. The mesh was seeded with N_^frag initial fragments (based on a seeding density of 50,000 fragments/ml similar to a previous study⁴³) using the same random seed number in each experiment, and growth was simulated for 6 days, the length of our previous vascularized construct experiments.^12,43 Vascular orientation was quantified using WinFiber3D³¹ by collecting the distribution of angles that microvessels formed with respect to the x-axis, and ECM fibril orientation was quantified using a custom MATLAB script.

The first simulation incorporated random ECM fibril orientation, and homogeneous ECM density and stiffness (ρ = 3.0 mg/mL as used in previous experiments^7,13,43). The second experiment was designed to represent a narrow gap of low-density collagen surrounded by regions of higher density collagen. This experiment is similar to the process of wound healing, during which angiogenic neovessels from the surrounding healthy tissue invade the granulated tissue and establish a new microvascular network.⁴² The wound clot, composed of fibrin and fibronectin, is much less stiff than the surrounding native tissue which is primarily composed of collagen.^9,42 This was modeled by creating a narrow “gap” of low-density collagen (ρ = 3.0 mg/mL) by generating two discrete cylindrical (radius = 4.0 mm) regions of high density (ρ = 6.0 mg/mL) at the upper right and lower left corners. This gap had a maximum width of 900 µm.

The third experiment involved angiogenesis in a continuous ECM density gradient running along the long-dimension (x) of the domain, dropping from ρ = 8.0 mg/mL on the left to ρ = 1.0 mg/mL on the right. Mechanical gradients such as this are often found in biological tissues at the interface of layers with different composition and mechanical properties. In the final experiment, we modeled angiogenesis within an environment with periodic loading and relaxation, to model the mechanical loading experienced by tissues such as muscle, ligament, tendon, arteries/ veins, and the heart. This periodic loading changes the orientation of microvessels and ECM fibrils and can induce anisotropy as fibers in the material are “preconditioned.” In this experiment, angiogenesis was simulated for 7 days. Displacement in the x-direction was constrained to zero along the left face of the mesh (normal to −x) and an external traction along the x-direction was applied to the right face (normal to +x). This external traction ramped up from 0.0 to a value of t_ex = 2.0 MPa between Day 3–Day 4 and Day 6–Day 7. At the conclusion of the simulation, Green–Lagrange (G–L) strain along each coordinate axis (E_xx, E_yy, E_zz) was measured at the midline node of the right face along the top surface at a position of (x, y, z) = (7.5, 2.5, 0.5) µm.

RESULTS

Homogeneous Experiment

Predicted growth and neovascularization were consistent with what we have reported in previous efforts (Fig. 3, Supplementary Material: “1—homogeneous simulation.avi”).^12,13 Active stress created in the matrix by neovessel sprouts drove the mesh to contract inward towards its geometric center. The maximum strain in each direction within the gel at Day 6 was E_xx = −0.20, E_yy = −0.19, and E_zz = −0.10. These strain values were less than what we’ve previously measured in unconstrained vascularized constructs at Day 6 (E_xx = −0.40, E_yy = −0.37, and E_zz = −0.33⁴³), but the initial size and aspect ratio of the domain in these simulations is quite different than our previous experiments.^12,43 Strain was not equal along each direction as contraction was dependent on the initial aspect ratio of the mesh. Simulations with meshes of uniform dimensions produced isotropic strain (data not shown). Microvessels were randomly aligned at Day 6, with a slight alignment along the z-axis due to reduced strain along this direction. The ECM density, initially set to a homogenous value of 3.0 mg/mL, became heterogeneous by Day 6 and reached a maximum of 5.31 mg/mL after the contraction (Fig. 1c).

FIGURE 3.

Homogeneous experiment: angiogenesis simulated within a homogeneous ECM density field (3.0 mg/mL) and a randomly oriented ECM fibril field. All external faces of the mesh were traction-free. (a) Initial seeding of microvessel fragments at Day 0. (b) Final vasculature at Day 6. (c) Heterogeneous ECM density field (mg/mL) at Day 6. Scale bar 2 mm.

Narrow Gap Experiment

Microvessels in this simulation vascularized the 3.0 mg/mL gap region but did not grow into the high-density regions (Fig. 4, Supplementary material: “2—narrow gap simulation.avi”). Vessels were able to contract the matrix within the gap region but not within the high density region, causing an increase in matrix density along the gap-high density region interface to 7.81 mg/mL. The contraction of the matrix within the gap region caused the gap to close, pulling the two stiffer regions closer together and narrowing the maximum width of the gap from 900 to 734.1 µm. The 3rd principal strain within the gap was oriented across the gap, running between the two stiff regions, and reached a value of −0.22 along this direction (Fig. 4d).

FIGURE 4.

Narrow gap experiment: angiogenesis simulated within a low-density gap (3.0 mg/mL) that lies within the gap in between two high-density zones (6.0 mg/mL). The ECM fibril field was randomly oriented and all surfaces were traction-free. The top panel displays ECM density (mg/mL) at Day 0 (a) and Day 6 (b). (c) Final microvasculature at Day 6. Scale bars 2 mm. (d) Magnification of the center of the mesh at the gap region. The border of the high density regions are denoted by the yellow dashed line. The black arrows indicate the direction of 3rd principal G–L strain, which reached a maximum of −0.22 within the gap. Scale bar 500 µm.

Density Gradient Experiment

Matrix contraction varied along the density gradient due to the addition of density-sensitivity scaling to active sprout stresses (Fig. 5, Supplementary material: “3—density gradient simulation.avi”). The matrix contracted inward along y- and z-directions in the low density regions, but the stiffness gradient along x prevented contraction along this direction. The construct narrowed within the low-density regions and this narrowing decreased while moving up the density gradient, resulting in the formation of a cap-like structure. The contraction of the low-density regions increased matrix density in these regions up to 1.51 mg/mL. Vascular density was high at the right side of the mesh and decreased along the x-axis due to the density gradient (Fig. 5b). The contraction of the lower density regions further increased vascular density by condensing vessels together.

FIGURE 5.

Density gradient experiment: Angiogenesis was simulated in an ECM density gradient along the long-axis running from 8.0 mg/mL on the left to 1.0 mg/mL on the right. The ECM fibril field was randomly oriented and all surfaces were traction-free. (a) Deformed geometry and ECM density (mg/mL) at Day 6. (b) Final microvasculature at Day 6.

Preconditioning Experiment

In the final simulation (Fig. 6, Supplementary material: “4—preconditioning simulation.avi”), the gel contracted similarly to the homogeneous experiment until traction was applied at Day 3. The applied traction caused the mesh to extend along the x-direction and to contract laterally. After the applied traction was released at Day 4 (Fig. 6a), the construct continued to contract laterally but did not contract along the loading direction. Traction was then again applied at Day 6, which caused the gel to further extend along the x-direction and contract laterally until Day 7 (Fig. 6b). Loading in this simulation was divided into three different sections: the first loading period between Days 3 and 4, the relaxation period between Day 4 and Day 6, and the second loading period between Day 6 and Day 7 (Fig. 6c). G–L strain along the loading direction (E_xx) decreased until Day 3 and then increased to a value 0.08 over the first loading period, after which E_xx essentially remained constant over the relaxation period and then reached a final value of 0.14 at Day 7 (Fig. 6d). Strain along the y-direction (E_yy) slowly decreased to −0.02 until Day 3, and then decreased by −0.14 over the first loading period between Days 3 and 4. Strain continued to decrease by −0.05 during the 2-day relaxation period, and reached a final value of −0.28 at Day 7 (Fig. 6e). Strain along the z-direction displayed a similar trend to E_yy (data not shown). ECM density in this simulation reached a maximum of 5.63 mg/mL. The loading scenario in this case led to distinct changes in microvessel alignment (Fig. 6f). Vessels began randomly oriented at Day 0 (Fig. 6 F black line) but became slightly aligned along the x-direction after the first loading period at Day 4 (Fig. 6f, red line). During the relaxation period between Day 4 and Day 6, the construct continued to contract laterally, further aligning vessels along the loading direction (Fig. 6f, blue line). Afterwards, vessels were further aligned along the loading direction after the final loading period at Day 7 (Fig. 6f, green line).

FIGURE 6.

Preconditioning experiment: angiogenesis simulated within a homogeneous ECM density field (3.0 mg/mL) and a randomly oriented ECM fibril field. Displacement in the x-direction was constrained along the left external face (normal to −x) and an external traction was applied along the x-direction on the right external face (normal to +x). Predicted microvasculature at (a) Day 4, and (b) Day 7. Scale bar 2 mm. (c) Loading curve for external traction applied to the right surface of the mesh. The applied traction was ramped up from 0 to a value of t_ex between Day 3–4 and Day 6–7. G–L strain was measured throughout time at the midline of the right surface of the mesh along the x-direction (d) and the y-direction (e). (f) Distribution of the angle microvessels formed with respect to the x-axis at Day 0 (black), the end of the first loading period at Day 4 (red), the start of the second loading period at Day 6 (blue), and at the end of the second loading period and simulation at Day 7 (green). The high percentage of vessels oriented at acute angles with respect to x indicates alignment along this direction.

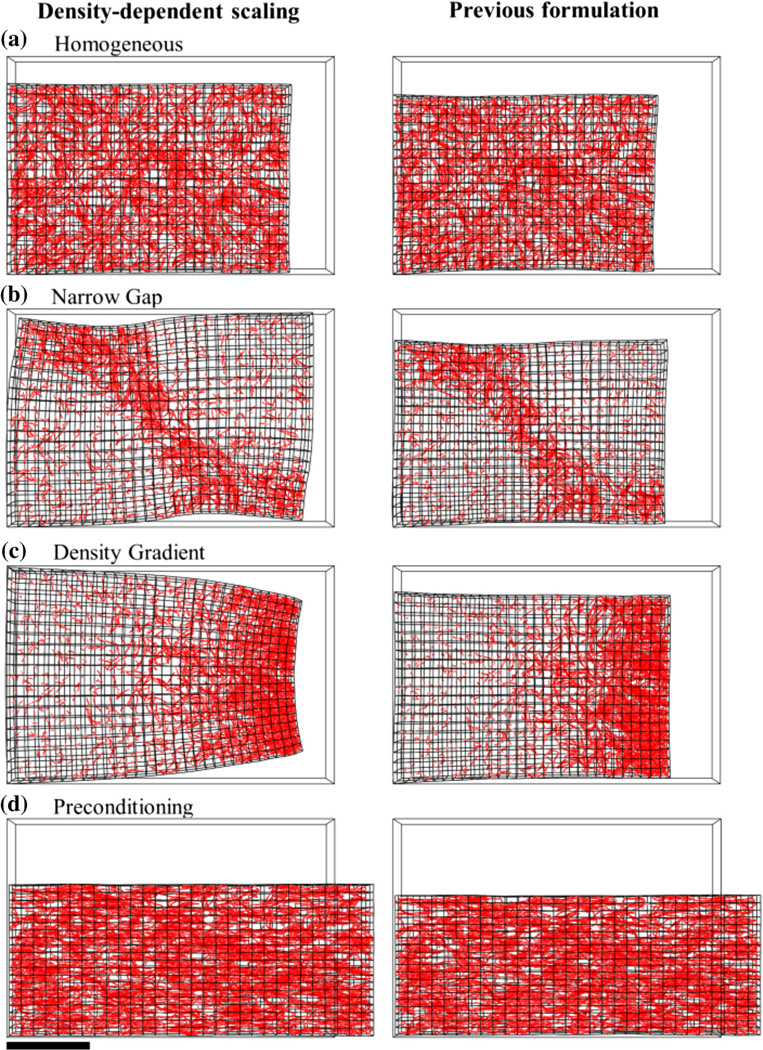
Simulations of these three microenvironments using the improved framework with density-dependent scaling of active stress generation produced different results than simulations using our previous formulation (Fig. 7). In the homogeneous experiment, results from the previous formulation were very similar to those from the updated formulation, reaching larger final strain values at Day 6 E_xx = −0.25, E_yy = −0.25, and E_zz = −0.13 (Fig. 7a, right). Without the inclusion of density-dependent scaling in the previous formulation, construct deformation in the narrow gap and density gradient experiments were very similar to the homogenous case, even though the vascular networks within the constructs at Day 6 differed greatly between the two (Figs. 7b and 7c). Results of the preconditioning experiment using the previous formulation were similar to results using the updated formulation (Fig. 7d), with the construct reaching a larger final strain values along the y-direction at Day 6, E_yy = −0.32, while reaching the same final strain value along the x-direction.

FIGURE 7.

Comparison of results from the updated formulation of the model with density-dependent scaling of active sprout stress and results from the previous formulation.¹² The vascular networks resulting from the updated formulation and previous formulation were similar in each case, although construct deformation differed greatly. (a) Simulations of a homogeneous experiment at Day 6. The results from the previous formulation were similar to those of the updated formulation. In the previous formulation contraction of the construct was increased as a result of the lack of density-dependent scaling. Construct deformation in the narrow gap experiment (b) and density gradient experiment (c) was very similar to the results of the homogenous experiment using the previous formulation, although the heterogeneous matrix in both these cases led to vastly different vascular networks. (d) Construct deformation in the preconditioning experiment was similar using the previous formulation compared to the updated formulation. The construct reached the same amount of strain along the x-direction, but lateral contraction was slightly increased in the previous formulation. Scale bar 2 mm.

DISCUSSION

This study examined the effects of density-dependent cell-generated stress within the ECM on predictions of angiogenesis in a coupled model of angiogenic growth and matrix mechanics. We coupled the composition to the mechanical properties of the ECM by scaling the amount of active stress generated by each neovessel sprout relative to local ECM density, effectively increasing the stiffness of the ECM and reducing the ability of neovessel to remodel their surroundings as density increased. Previous efforts have measured an increase in total traction force applied by endothelial cells as collagen density increases as measured using 2D traction force microscopy, but no corresponding increase in total traction stress (traction force normalized by projected cell area) was observed, and in some cases a decrease in traction stress as collagen density increased was found.²⁴ Furthermore, the multicellular neovessels studying in our experiments and represented in our model may exhibit a fundamentally different relationship between phenotype and neovessel behavior and matrix density. It is our hypothesis that although neovessels may generate more force in response to this increase and ECM density, this increased traction is not enough to overcome the increase in matrix stiffness that accompanies this density increase, resulting in a matrix that is more difficult for neovessel sprouts to deform and remodel and thus inhibiting angiogenic outgrowth.

This updated framework has several new capabilities not available in previous implementations.¹² First, the new framework allows us to model matrix stiffening in vascularized constructs as the matrix is contracted. In our previous mathematical formulation of the model, microvessels applied the same stress to the matrix regardless of current local matrix density. If simulations were allowed to continue indefinitely, the matrix would eventually be collapsed down to a point, which is not physically realistic. This total collapse of the matrix would occur due to (1) the vascularized constructs are modeled as a composite of compressible hyperelastic materials (Poisson’s ratio v = 0.0) with viscoelasticity that dissipates passive stress within the matrix, and (2) the lack of dependence on ECM material properties such as density (i.e., stiffness) when calculating active sprout stresses.¹² We have observed that matrix contraction as a function of time asymptotes in these vascularized constructs and microvessels do not possess the ability to contract the matrix indefinitely.^13,27,43 Including the density scaling factor v into Eq. (2) causes stress to decrease (i.e., stiffness increases) as the matrix contracts and density increases. Calculating the scaling factor according to Eq. (3) causes stress to drop to zero around a matrix density of 7.0 mg/mL, which is consistent with our experimental model as we have yet to see significant growth and matrix deformation in matrix densities higher than 6.0 mg/mL in our previous efforts.¹³

Additionally, by using local ECM density to scale active stress generation in the model, we also provide the means to simulate growth in a matrix environment of heterogeneous density. While the first experiment involved growth within an initially homogenous ECM density field, the narrow gap and density gradient experiments employed a heterogeneous matrix density field. Without the inclusion of density-dependent scaling in the sprout stress mechanisms, the deformation of the matrix in all three of these cases was similar even though vascular growth was very different in each case. The previous formulation of the model predicted more contraction of the vascularized construct, as the increased density caused by the contraction results in a decrease in the active stress generated within the construct over time in the updated formulation. The active stress generated in the matrix depends on several factors including the force generated by the cytoskeleton of endothelial cells, the adhesion of the cells to ECM components, and the structure and mechanical properties of the matrix. As the density of the matrix increases, cells respond by increasing force generation^6,29 and increasing the number of adhesion sites,⁴⁸ while the increased density results in a matrix with increased fibril density, more inter-fibril cross-links, and increased mechanical stiffness.^25,39,45 These changes in cellular behavior and matrix structure reduce the ability of neovessels to generate stress and remodel the matrix, which in turn reduces angiogenic outgrowth and network formation.^{13,22,23,41,47} In our updated modeling framework, we account for these effects by scaling active stress generation and the rate of neovessel growth and branching relative to local matrix density, presenting a more realistic model that is capable of predicting angiogenesis for a wider variety of matrix conditions than previous formulations.

The final three experimental cases (narrow gap, density gradient, preconditioning) demonstrate how heterogeneity and complexity of the matrix environ- ment can lead to the formation of different vascular topologies and deformed geometry during angiogenesis. In the narrow gap experiment, two large regions of high density matrix with a low density region between them were simulated. These conditions are similar to a soft fibrin wound clot surrounding by the stiffer native tissue^9,42 and also resemble structures such as the loose connective tissue fascia that lie between adjacent stiffer muscle bodies.^2,21 Microvessels growing parallel to the gap had the highest rate of growth, while vessels growing transverse to the gap soon encountered the high density zones and experienced a dramatic reduction in outgrowth. This caused vessels to become slightly aligned along the gap as neovessel growth in this direction was more favored. Furthermore, the contraction of the matrix in the gap, pulling the stiffer bodies closer together and closing the gap. This contraction increased vascular density in the gap region, and the anisotropic nature of this contraction caused vessels to further align parallel to the gap.

Mechanical gradients in density and material properties, such as the one generated for the density gradient experiment, are present in numerous tissues in vivo, most commonly found at interfaces between tissue layers with differing physical properties. Gradients of mechanical properties such as stiffness, density, porosity, and anisotropy can be found at the interface as dense cortical bone transitions to a low density trabecular bone,^28,46 between layers of differing mineral composition in the periodontium,¹⁶ between layers in the artery,¹⁷ and at the transition of soft tissues to bone at locations of tendon and ligament insertion sites.^20,30,33 The results of the density gradient demonstrate the effects that mechanical gradients have on angiogenic growth and matrix deformation. Microvessel growth in the direction down the gradient or transverse to the gradient was more robust than up the gradient. Thus, the resulting vascular network was slightly oriented along these directions. The creation of a density gradient within the construct resulted in the inhomogeneous deformation of the matrix. The construct was relatively un-deformed in the high-density regions on the left and contraction increased along the x-axis. At the bottom of the gradient, neovessel contracted the surface of the gel inward and creation of the “cap” caused microvessels to align perpendicular to the x-direction at the cap surface. Vascular density was high in this region due to both the increased growth and deformation which condensed microvessels in this region.

The final simulation presented an example of the complex interplay between angiogenic growth, external loading, and tissue mechanical properties during neovascularization that might occur in vivo in tissues with repeated loading–unloading cycles such as orthopedic and cardiac tissue. The fiber distribution material model used to represent the ECM allows for strain-induced anisotropy and alignment of material fibers during deformation. Therefore, the first loading period (Day 3–4) causes the initially isotropic fiber distribution to become skewed in the x-direction as the matrix is deformed, causing the matrix to stiffen along that direction as fibers are re-aligned. This behavior is similar to the “preconditioning” of fibrous tissues like ligaments and tendons in which effects of entropy changes in aligning fibers are removed by using applied load to orient fibers along the loading direction.³⁴ The applied load during the first loading period of this simulation causes microvessels and fibers to align along the loading direction. As a result, E_xx does not decrease after during the relaxation period between Day 4 and Day 6 because the preconditioned fibers prove too stiff for the neovessel to contract against (Fig. 6d). However, this same preconditioning causes the lateral directions to “soften” as the material moves from an isotropic response to something that resembles transverse anisotropy with the tension-only fiber component of the ECM constitutive model aligned along the loading direction. This results in a large decrease in E_yy during the relaxation period as the lateral directions are much more susceptible to contract after preconditioning (Fig. 6e). During the relaxation period, the construct is essentially constrained along the loading direction due to the preconditioning and free to deform laterally. This causes vessels to align along the x-axis, similar to what we have seen previously in the uniaxial constraint of vascularized constructs during growth.^12,27,43 In fact, the majority of vessel alignment in this simulation occurs during the relaxation period when no external traction is being applied (Fig. 6f). This pronounced alignment results from both the lateral contraction of the gel (while constrained along x) and neovessel growth along preconditioned fibrils aligned along the loading direction during the first loading period.

This study presents the capabilities of AngioFE to simulate angiogenesis in a variety of mechanical environments: homogeneous density, discrete density heterogeneity (narrow gap), continuous density heterogeneity (density gradient), and applied load/unloading (preconditioning). Although there are a variety of cell culture and organ culture models of angiogenesis, there is a lack of experimental evidence as to how angiogenic microvessels respond to complex 3D matrix environments such as the conditions included in this study, mostly due to a lack of fabrication methods to perform the necessary experiments. Our updated simulation framework provides the capabilities to overcome these experimental limitations and predict angiogenesis within these complex microenvironments using a previously-validated framework, but the lack of experimental evidence also means that full validation of the updated framework remains incomplete.

Although the simulations presented here incorporated relatively simple domains, these types of matrix conditions could be combined to better resemble the environments in which angiogenesis takes place in vivo. For example, angiogenesis within a tendon-bone insertion site could be modeled by creating discrete mechanical regions for the bone and tendon, a gradient region connecting the two representing the insertion site, and subjecting the domain to repeated loading/unloading as a tendon would experience in vivo. These new capabilities in AngioFE allow us to model and study angiogenesis in complex physiological environments with a unique approach not found in other modeling frameworks.

Even with these new features, our modeling framework remains simplified. Besides mechanical factors, angiogenesis is regulated by a variety of soluble (e.g., angiogenic peptides) and insoluble (e.g., matrix haptogens) stimuli.^8,14 Additionally, mRNA levels for proteolytic enzymes (matrix metalloproteases MMP) increase during the culture of these vascularized constructs,²⁶ and MMP levels undoubtedly affect the matrix’s density and vulnerability to cellular remodeling. Certainly, gradients of these biochemical factors in the tissue environment can influence the extent and direction of neovessel growth during angiogenesis. Undoubtedly, these patterned biochemical signals would work in concert with matrix deformation and related mechanical factors in determining vascular topology. The consequence of such a dynamic interplay is not known, particularly in situations where a biochemical signal may be bound to a matrix fibril, which is in turn influenced by tissue deformation and matrix turnover. Extending our computational framework to incorporate these chemical signals, including the spatial gradients that may be present would provide us with a conceptual foundation from which to further investigate these complex questions. The capability to couple phenomena such as solute transport, convection, and chemical reactions with tissue mechanics has been recently added to the FEBio framework,³ and these new capabilities should prove useful coupling these addition factors with AngioFE to further enhance our investigative ability to study the multi-faceted regulation of angiogenesis and neovascularization.