A large-scale circuit mechanism for hierarchical dynamical processing in the primate cortex

Abstract

We developed a large-scale dynamical model of the macaque neocortex, which is based on recently acquired directed- and weighted-connectivity data from tract-tracing experiments, and which incorporates heterogeneity across areas. A hierarchy of timescales naturally emerges from this system: sensory areas show brief, transient responses to input (appropriate for sensory processing), whereas association areas integrate inputs over time and exhibit persistent activity (suitable for decision-making and working memory). The model displays multiple temporal hierarchies, as evidenced by contrasting responses to visual versus somatosensory stimulation. Moreover, slower prefrontal and temporal areas have a disproportionate impact on global brain dynamics. These findings establish a circuit mechanism for “temporal receptive windows” that are progressively enlarged along the cortical hierarchy, suggest an extension of time integration in decision-making from local to large circuits, and should prompt a re-evaluation of the analysis of functional connectivity (measured by fMRI or EEG/MEG) by taking into account inter-areal heterogeneity.

Introduction

The receptive field is a central concept in Neuroscience, defined as the spatial region over which an adequate stimulus solicits rigorous response of a neuron (Sherrington, 1906). In the primate visual cortical system the receptive field size of neurons progressively enlarges along a hierarchy (Hubel and Wiesel, 1962; Hubel, 1988; Wallisch and Movshon, 2008). As a result, higher areas can integrate stimuli over a greater spatial extent, which is essential for such functions as size-invariance of object recognition in the ventral (“what”) stream for visual perception (Kobatake and Tanaka, 1994).

Accumulating evidence suggests that the brain also displays a hierarchy in the temporal domain. This allows neurons in higher areas to respond to stimuli spread over a greater temporal extent and to integrate information over time, while neurons in early sensory areas rapidly track changing stimuli. In human studies, preserving the short timescale structure of stimuli while scrambling long timescale structure changes responses in association areas but not early sensory areas (Hasson et al., 2008; Lerner et al., 2011; Honey et al., 2012; Gauthier et al., 2012; Stephens et al., 2013). Notably, using ECoG, Honey et al. (2012) found that cortical areas sensitive to long time structure in the stimulus also show slower decays in their temporal autocorrelation (and hence slower dynamics), and Stephens et al. (2013) made a similar observation with fMRI. In the macaque, Murray et al. (2014) found a hierarchical organization in the timescales of spontaneous fluctuations of single neurons across 7 cortical areas, and an area’s timescale was well-predicted by its position in the anatomical hierarchy of Felleman and Van Essen (1991). Similarly, temporal correlations in neural activity reveal slower decay rates in the frontal eye fields than area V4 (Ogawa and Komatsu, 2010), the timescales of reward memory lengthen from parietal to dorsolateral prefrontal to anterior cingulate cortex (Bernacchia et al., 2011), and, more generally, persistent activity after a brief stimulus can last for seconds, even across inter-trial intervals, in association areas (Amit et al., 1997; Histed et al., 2009; Curtis and Lee, 2010). Finally, normative theories of predictive coding suggest that a hierarchy of timescales would allow animals to form a nested sequence of predictions about the world (Kiebel et al., 2008).

What underlying neurobiological mechanisms might give rise to such a range of temporal dynamics? For example, spatial patterns of convergence can produce increasing receptive field sizes in the visual hierarchy. Are there basic anatomical motifs that produce a hierarchy of timescales?

Here we report a large-scale circuit mechanism for the generation of a hierarchy of temporal receptive windows in the primate cortex. This hierarchy naturally emerges in a dynamical model based on a recent quantitative anatomical dataset containing directed and weighted connectivity for the macaque neocortex (Markov et al., 2011, 2013b, 2014a; Ercsey-Ravasz et al., 2013). The data were obtained using the same experimental conditions and measures, ensuring a consistent database (Kennedy et al., 2013), and include both the number of projections between areas and their laminar origins. Based on a separate anatomical study (Elston, 2000; Elston et al., 2011), we introduced heterogeneity across cortical areas in the form of a gradient of excitatory connection strengths. Strong recurrent excitation has been proposed as a mechanism by which prefrontal cortex could implement “cognitive-type” computations, like information integration and memory-related delay activity; we hypothesized that differences in recurrent excitation might allow the generation of a temporal hierarchy.

The model thus incorporates anatomically-constrained variation in both within-area and inter-areal connectivity, and enables us to probe the interplay of local microcircuitry and long-range connectivity that underlies a hierarchy of timescales. Using different sensory inputs we demonstrate the existence, in our model, of multiple dynamical hierarchies subserved by a single integrated global and local circuit. We then investigate the implications of local circuit heterogeneity for macroscopic dynamics measured by functional connectivity (i.e. correlations in activity across areas). Here we find a disproportionate role for slow dynamics in the prefrontal and other association cortices in shaping resting-state functional connectivity. This role is not predicted by long-range connections, suggesting that interpretations of brain imaging data will need to be revised to account for inter-areal heterogeneity.

While we have used the model to investigate the origin of a hierarchy of timescales, it can be a platform for future models relating connectivity to dynamics and the functions of cortical areas. Most statistical analyses of connectivity (Bullmore and Sporns, 2009; Sporns, 2014) and computational models (Ghosh et al., 2008; Deco and Corbetta, 2011; Honey et al., 2007, 2009; Deco et al., 2014) have lacked comprehensive high-resolution data, relying either on collating qualitative tract-tracing data across disparate experiments and conditions or on diffusion tensor imaging (DTI), which is noisy and cannot reveal the direction of a pathway. Moreover, such models typically treat cortical areas as identical nodes in a network, distinguished by connection patterns but not by local properties or computational capabilities. While this approach is reasonable for certain purposes, it is doubtful that functional specialization of cortical areas can be elucidated without considering heterogeneity. Our model provides a framework to explore how dynamical and functional specialization can emerge from inter-areal pathways coupled with local circuit differences.

Results

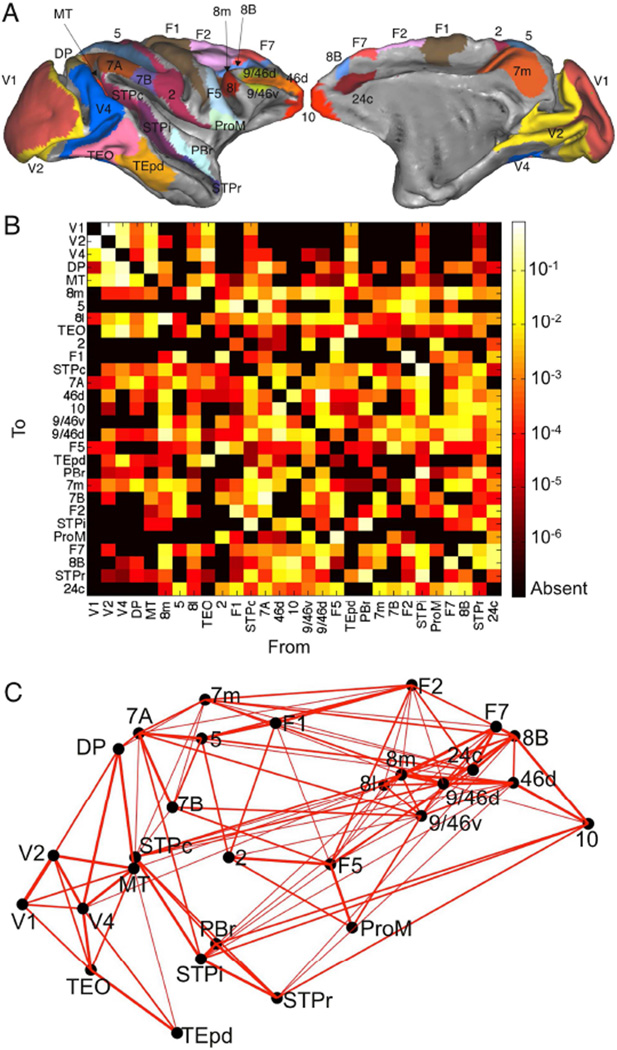
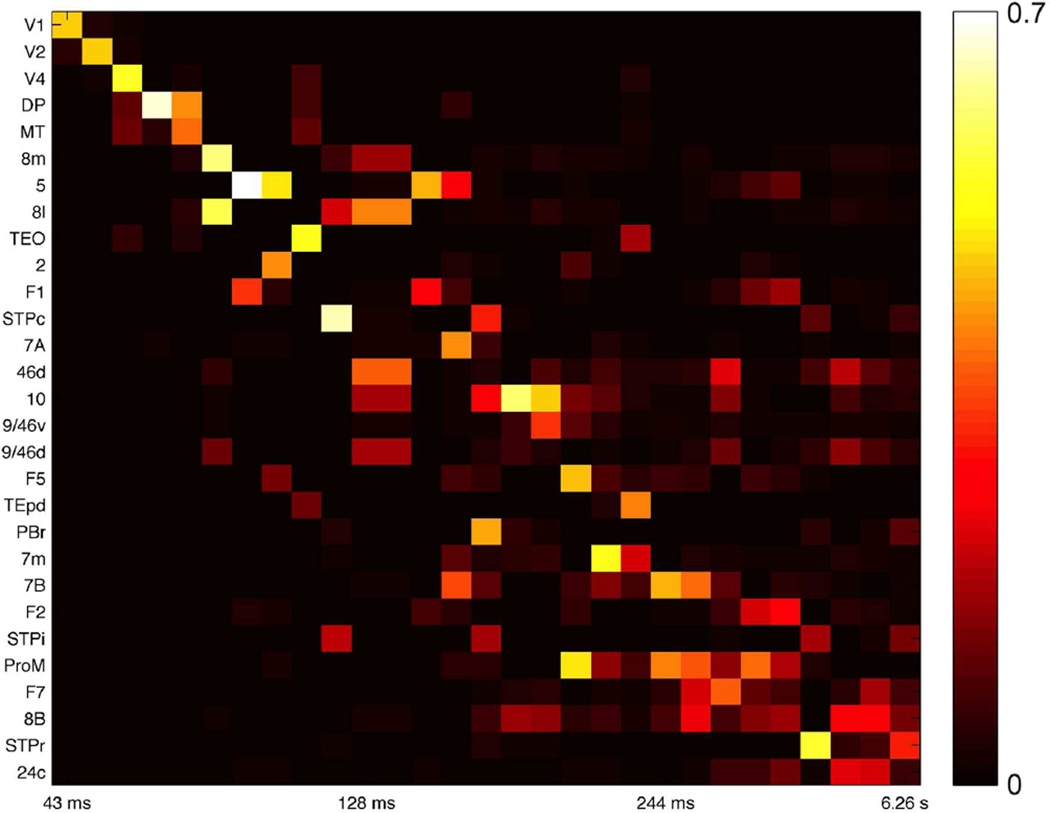
We developed the model in three steps. First, we used recent connectivity data for the macaque neocortex (Markov et al., 2014a), designed to overcome the limitations of collated anatomical data sets, and collected by the same group under similar conditions, with quantitative measures of connectivity. The connectivity weights are directionally specific and cover 29 widely-distributed cortical areas, with 536 connections whose strengths span five orders of magnitude (Figure 1). The presence or absence of all projections in this network has been established; thus there are no unknown pathways.

Figure 1.

The network consists of 29 widely-distributed cortical areas. (A) Lateral (left) and medial (right) plots of the macaque cortical surface with areas in color. Plots generated with Caret (Van Essen et al., 2001). (B) Connection strengths between all 29 areas. The strength of the projection from area A to area B is measured by the Fraction of Labeled Neurons or FLN (see Experimental Procedures and Table S1). (C) Three dimensional positions of areas along with strongest connections between them (FLN > 0.005). Connection strength is indicated by line width.

Second, each cortical area was described by a threshold-linear recurrent network with interacting excitatory and inhibitory populations and calibrated by the neurophysiology of the primary visual cortex (Binzegger et al., 2009), but rescaled as described below. This is a highly simplified description of the dynamics of an area and ignores most within-area variability. In particular, note that the model is large-scale in that it addresses macroscopic cortical dynamics but is not large-scale in the sense of having millions of neurons or very high-dimensional activity. However, this level of complexity allows us to parsimoniously capture essential requirements for a hierarchy of timescales. We extend our results in Figure 7, and suggest further extensions in the Discussion.

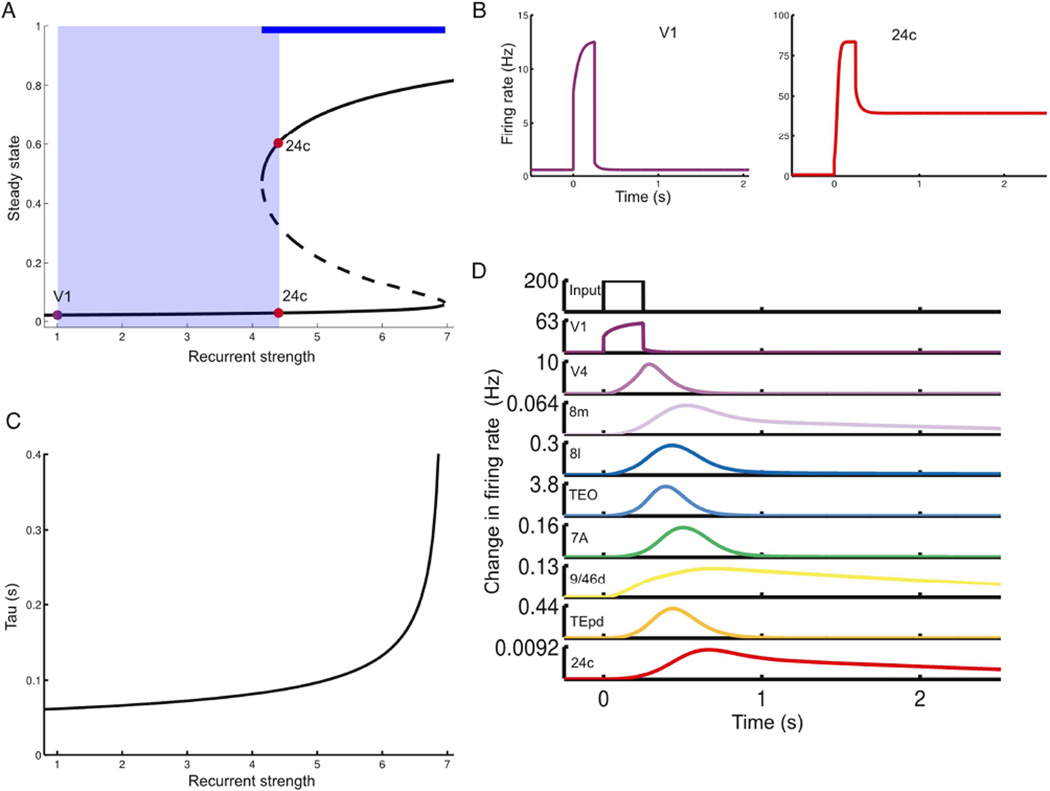
Figure 7.

Hierarchy of timescales in a nonlinear model. (A) Possible steady-states (bifurcation diagram) for an area as a function of recurrent strength (normalized by value at V1). Stable steady-states are shown with solid lines. Areas with comparatively low recurrent strength display only a single steady-state. Increasing the recurrent strengths leads to a regime with a high-activity steady-state. The dashed line is an unstable intermediate steady-state. The thick blue line shows the parameter range supporting bistability, while the light blue shaded region indicates the range used for areas in the model. Steady-states shown as fractional activation of NMDA conductance. (B) Response of disconnected areas to a strong pulse of input. As in (A), V1 only shows a single stable state, while area 24c shows sustained delay activity. (C) The timescales of responses to a small perturbation serve as a probe of the recurrent strength of a local area. These timescales are much smaller than those in response to a larger input but emerge from the same underlying gradient in recurrent strengths. (D) Response of connected network to a brief pulse of input to area V1. As in Figure 3, the input is propagated up the hierarchy, slowing down as it proceeds. Note that the input is not strong enough to switch any area into the high-activity stable state.

Third, we hypothesized that the local microcircuit is qualitatively canonical (Douglas and Martin, 1991), i.e. the same across areas, but that quantitative inter-areal differences are crucial in generating the timescales of areas. Specifically, the number of basal dendritic spines on layer 3 pyramidal neurons increases sharply from primary sensory to prefrontal areas (Elston, 2000; Elston et al., 2011). Taking spine count as a proxy for excitatory synapses per pyramidal cell, we introduced a gradient of excitatory input strength across the cortex. We modeled this by scaling the strength of excitatory projections in an area according to the area’s position in the anatomical hierarchy described below.

Gradient of excitation along the cortical hierarchy

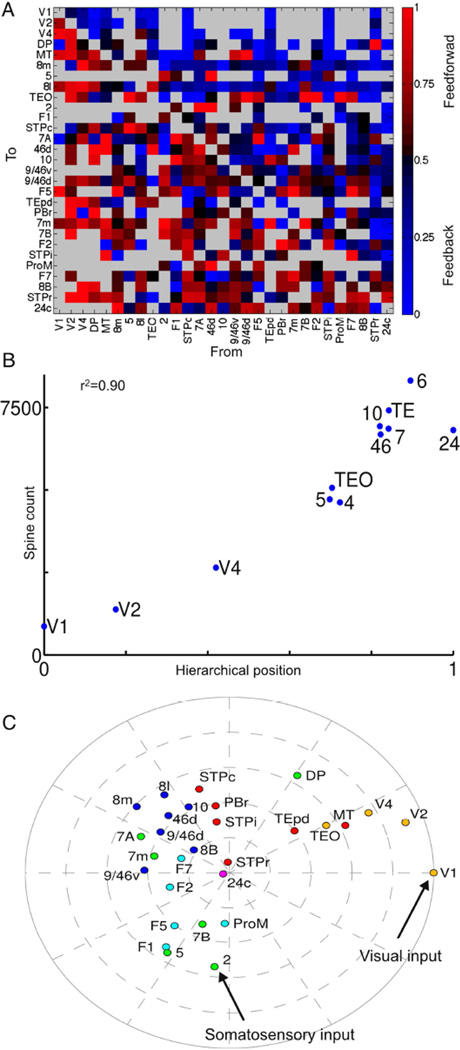
The laminar pattern of inter-areal projections can be used to place cortical areas in a hierarchy: neurons mediating feedforward connections from one area to another tend to originate in supragranular layers of the source area, whereas feedback projections tend to originate in infragranular layers (Felleman and Van Essen, 1991; Barbas and Rempel-Clower, 1997). This was quantified by Barone et al. (2000), who observed that the fraction of projecting neurons located in the supragranular layers of the source area defines a hierarchical distance between two areas; this allowed them to reproduce the hierarchy of Felleman and Van Essen (1991) using data from connections to only two areas (V1 and V4).

The laminar data included with this paper (see Table S1) contain hierarchical distance measured this way for all pairs of cortical areas included in the model (Fig. 2A). We follow the approach of Markov et al. (2014b), and use these to estimate each area’s position in an underlying hierarchy. We found that an area’s position in this anatomical hierarchy is strongly correlated with counts of spines on pyramidal neurons in that area (Elston, 2007). This allowed us to introduce a systematic gradient of excitatory connection strength per neuron along the cortical hierarchy, and to explore how such heterogeneity interacts with the pattern of long-range projections to produce large-scale dynamics.

Figure 2.

Hierarchical organization of the cortex. (A) Fraction of neurons in a projection originating from the supragranular layers of the source area (SLN). Areas are arranged by hierarchical position. Thus most feedforward projections (SLN>0.5) lie below the diagonal and most feedback projections (SLN < 0.5) lie above the diagonal. Absent projections shown in grey. (B) Hierarchical position of an area is well-correlated with the number of spines on pyramidal neurons in that area (Elston, 2007). For details on area labels in this panel see Supplemental Experimental Procedures. (C) Two-dimensional plot of areas determined by long-range connectivity and hierarchy. The distance of an area from the edge corresponds to its hierarchical position, while the angular distance between two areas is inversely related to their connection strength. Areas are colored by cortical lobe. See also Figure S1, and Table S1 for the data.

As a visual and conceptual aid, in Figure 2C we use a two-dimensional embedding to plot hierarchy and connectivity for the 29 areas. The angle between two areas reflects connection strength (closer areas have stronger connections), and the distance of an area from the center reflects hierarchy (higher areas closer to the center). The low-dimensional embedding is approximate but captures broad features of cortical organization and provides intuitive understanding of the model’s behavior. It suggests two hierarchical streams of sensory input originating in area V1 (primary visual cortex) and area 2 (part of primary somatosensory cortex) respectively, and converging on densely-connected association areas. We next explored the response of the network to these sensory inputs.

Response to visual inputs

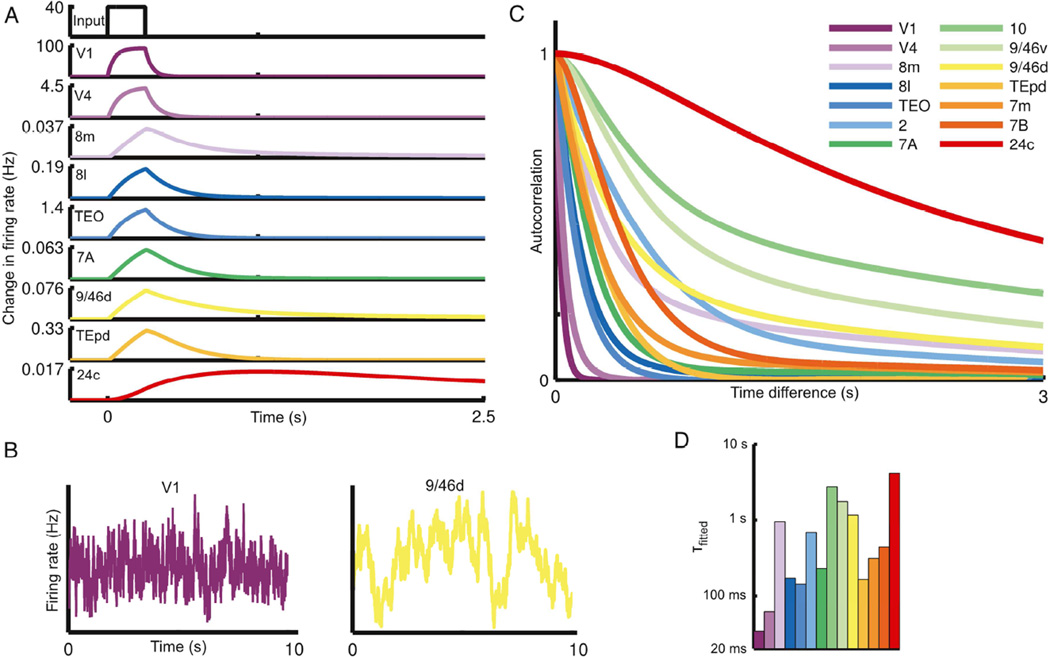
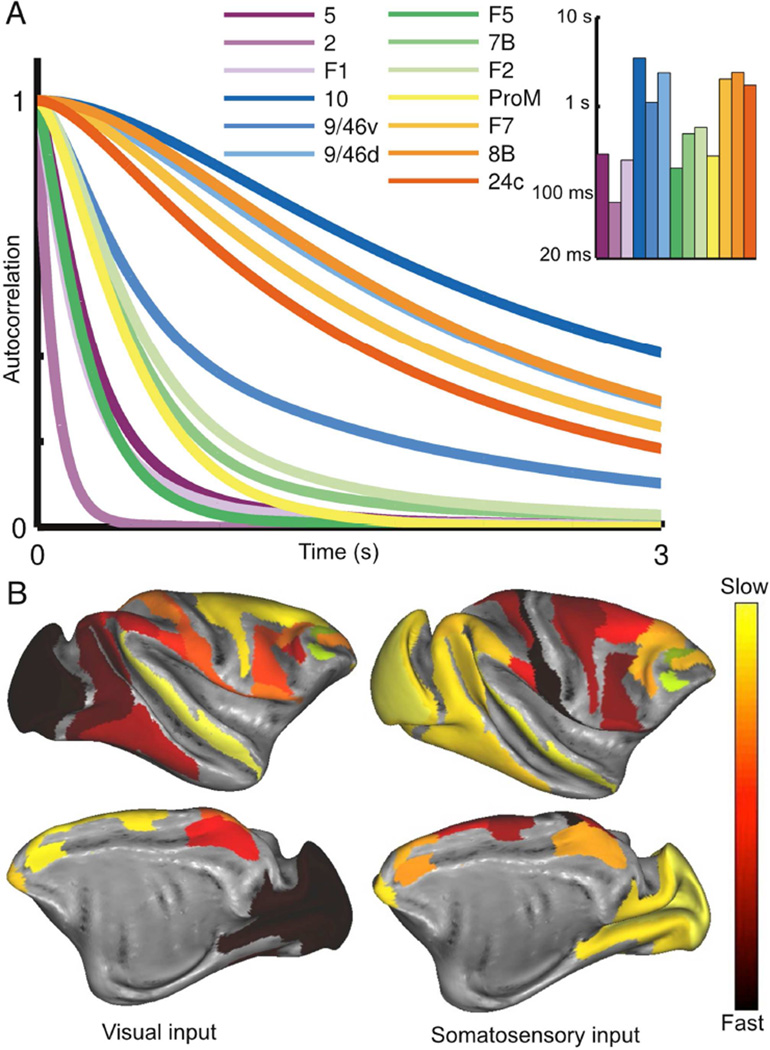
We simulated the response of the network to a pulsed input to primary visual cortex (area V1). The response is propagated up the visual hierarchy, progressively slowing as it proceeds (Fig. 3A). Early visual areas, such as V1 and V4, exhibit fast, short-lived responses. Prefrontal areas, on the other hand, exhibit slower responses and longer integration times, with traces of the stimulus persisting several seconds after stimulation. As with the response to a pulse of input, white-noise input is integrated with a hierarchy of timescales: the activity of early sensory areas shows rapid decay of autocorrelation with time whereas cognitive areas are correlated across longer periods (Figs. 3B and C). Thus, a hierarchy of widely disparate temporal windows or timescales emerges from this anatomically-calibrated model system.

Figure 3.

The network shows a hierarchy of timescales in response to visual input. (A) A pulse of input to area V1 is propagated along the hierarchy, displaying increasing decay times as it proceeds. In all panels, areas are arranged (and colored) by position in the anatomical hierarchy. (B) Traces contrasting the activity of area V1 and dorsolateral prefrontal cortex in response to white-noise input to area V1. (C) Autocorrelation of area activity in response to white-noise input to V1. The autocorrelation decays with different time constants in different areas, showing a functional hierarchy ranging from area V1 at the bottom to prefrontal areas at the top. (D) The dominant time constants in various areas of the network, extracted by fitting exponentials to the autocorrelation (colors as in C). Time constants tend to increase along the hierarchy but depend on the influence of long-range projections (for example, contrast area 8m with area TEpd). See also Figures S2 and S3.

To quantitatively compare areas, we fit single or double exponentials to the decay of each area’s autocorrelation function (see Figure S2 for plots of the fits). These fits capture a dominant characteristic timescale for each area in our model in response to visual stimulation. The time constants from the fits are plotted in Figure 3D, with areas ordered by position in the anatomical hierarchy. As can be seen from the bar plot, the dominant timescale of an area tends to increase along the hierarchy (i.e. left to right), suggesting an important role for a gradient of excitation in generating the temporal hierarchy.

Nevertheless, an area’s timescales are not entirely determined by its hierarchical position, and the plotted timescales do not increase monotonically with hierarchy. To gain some intuition for the role of long-range projections in the model, consider area 8m (part of the frontal eye fields), which is low in the hierarchy and would show a rapid decay of correlation in the absence of long-range projections (far-right panel of Figure 5A) but instead demonstrates long timescales in the model (and in the empirical observations of Hasson et al. (2008)). As can be seen from Figure 2C, area 8m participates in a strongly-connected core of prefrontal and association areas (Ercsey-Ravasz et al., 2013; Markov et al., 2013b), allowing it to show long timescales that emerge from inter-areal excitatory loops (these timescales are strongly attenuated in the absence of feedback projections). The shared slower timescales are particularly characteristic of prefrontal areas in our model (see Figure S2, especially areas best fit by two timescales). Conversely, while area TEpd is high in the hierarchy it does not participate in this core and is instead strongly-coupled to ventral stream visual areas. Thus, it reflects the faster timescales of visual input.

Figure 5.

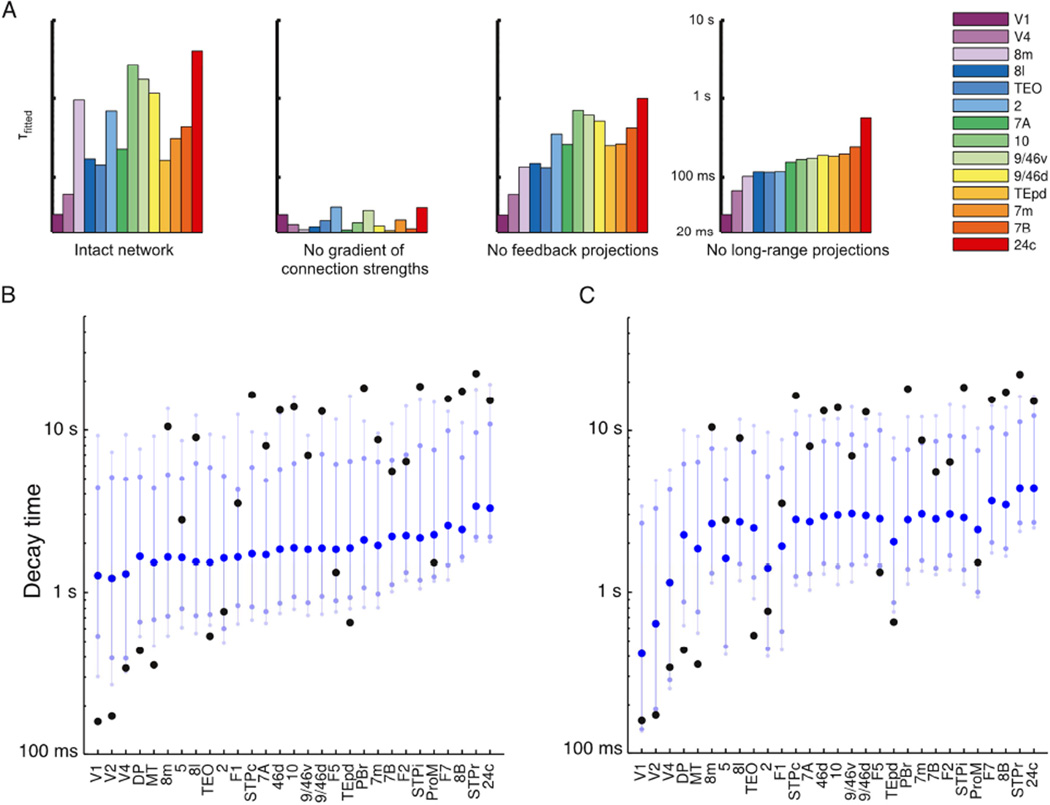
Role of local and long-range projections in determining timescales. (A) Time-constants fit to network activity after removing gradient of excitation or long-range projections. Far left: time constants for intact network. Center left: network with no gradient of excitatory synapses across areas. Center right: network with feedback projections lesioned. Far right: network with all long-range projections lesioned. (B) Effect of scrambling long-range connectivity on resting-state network dynamics, measured by the time taken for an area’s activity to return to 5% of baseline after a 250 ms pulse of input. Distribution of timescales when all connection strengths are randomly permuted. Dark blue, lighter blue and very light blue circles indicate median value, 10th to 90th percentiles and 5th to 95th percentiles respectively. Intact network shown in black, for comparison. Timescales for scrambled networks are much more similar to each other (compare black to blue), and fast visual areas show the greatest disruption. (C) Distributions when only non-zero connection strengths are permuted, thus preserving the connectivity pattern but not strengths.

Multiple functional hierarchies

The response to visual input reveals an ascending hierarchy of timescales in the visual system. We next stimulated primary somatosensory cortex (area 2), which is weakly connected to the visual hierarchy and strongly connected to other somatosensory and motor areas (Fig. 2C). As previously, input propagates up a hierarchy of timescales (Fig. 4A). However, the somatosensory response uncovers a different dynamical hierarchy to visual stimulation. Primary somatosensory cortex shows the fastest timescale, followed by primary motor cortex (area F1) and somatosensory association cortex (area 5). Parietal and premotor areas show intermediate timescales and, as with visual stimulation, prefrontal areas show long timescales. Visual areas demonstrate much weaker responses than before, and are mostly driven by top-down projections from association areas. Thus, in the absence of direct input they reflect the slower timescales of a distributed network state. In Figure 4B, we contrast time-constants for visual and somatosensory stimulation across areas.

Figure 4.

The response to somatosensory input reveals a different functional hierarchy subserved by the same anatomical network. (A) Autocorrelation of activity for areas that show strong responses to input to area 2 (part of primary somatosensory cortex). Area labels are arranged according to position in the underlying anatomical hierarchy. Inset: time constants fitted to the autocorrelation function for each area. (B) Timescales in response to visual (left) and somatosensory input (right) shown with lateral (top) and medial (bottom) views of the cortex. See also Figure S4.

An area’s timescales emerge from a combination of local circuit properties, the specificity of long-range projections, and the particular input to the network. Our model allows us to examine the contribution of each. These can be intuitively summarized by noting that each area in Figure 2C shows timescales approximately determined by its distance from the periphery (hierarchical position), proximity to the central clusters (long-range connectivity) and distance from the source of input.

Role of local and long-range projections

To further dissect the contributions of local and long-range projections, we examined time constants in response to visual input after removing either differences in local microcircuitry or inter-areal projections. In the second panel of Figure 5A, we show that the range of timescales is drastically reduced in the absence of differences in the microcircuit across areas. Moreover, there is no longer a relationship to an area’s position in the anatomical hierarchy. Thus, while differences in long-range inputs and outputs to each area are significant, they are insufficient to account for disparate timescales and local heterogeneity is needed.

In the third panel of Figure 5A, we show the effect of removing long-range feedback projections, and for the far right panel we remove all long-range projections and stimulate individual areas separately. The range of time-constants is lower, reflecting the propensity of slow areas to form long-range excitatory loops with each other. More significantly, once long-range projections are removed an area’s time-constant simply reflects its position in the hierarchy.

We extend our investigation of the role of long-range projections by contrasting the resting-state response (i.e., equal white-noise input to all areas) of the intact network to networks where long-range connections are scrambled while preserving the gradient of excitation. A number of these networks show responses that are poorly-fit by exponentials, so we measure timescale non-parametrically as the time after pulse offset for activity to decay to within 5% of baseline. In Fig. 5B, we show that scrambling almost entirely removes the hierarchy of timescales, further confirming that a gradient of excitation alone is insufficient to separate timescales.

The connectivity data show specificity both in which projections exist and in their strengths, and both connection probability and strength decay exponentially with inter-areal distance (Markov et al., 2011, 2013b, 2014a; Ercsey-Ravasz et al., 2013). In Fig. 5C we preserve network topology (i.e. which areas are connected), but scramble the strengths of non-zero projections. Here the separation of timescales is strongly attenuated for most areas, suggesting that specificity in projection strengths and not just network topology is required for the timescales we see.

Localized eigenvectors and separated timescales

The model for a single area is threshold-linear, meaning we ignore nonlinearities besides the constraint that firing rates be positive. This allowed us to explore the genesis of separated timescales with linear systems analysis. The activity of a linear network is the weighted sum of characteristic activity patterns, called eigenvectors (Rugh, 1995). Each eigenvector evolves on a timescale given by a corresponding eigenvalue, and is differently driven by different inputs.

The eigenvectors of the linearized network are localized: those with short timescales are broadly concentrated around sensory areas and those with long timescales are concentrated at frontal areas (Fig. 6). In general, if an eigenvector is small at a node then its amplitude at that node in response to input will also be small, and the corresponding timescale will be weakly expressed. Thus localization means that for most inputs network dynamics will be dominated by rapid timescales at sensory areas and slower timescales at cognitive areas. In previous theoretical work, we have shown how localized eigenvectors can arise in networks with gradients of local properties and produce a diversity of timescales (Chaudhuri et al., 2014).

Figure 6.

Eigenvectors of the network coupling matrix are weakly localized, corresponding to segregated temporal modes. Each column shows the amplitude of an eigenvector at the 29 areas, with corresponding timescale labeled below. The 29 slowest eigenvectors of the system are shown.

Extension to nonlinear dynamics and multistability

The threshold-linear local circuit let us highlight the requirements for a hierarchy of timescales and provide intuition from linear systems theory. Moreover, many systems can be linearly approximated, and neural responses are often near-linear over a wide range of inputs (Wang, 1998; Chance et al., 2002), making linear and threshold-linear models useful for neural circuits (Dayan and Abbott, 2001).

Nevertheless, linear models show limited dynamics and cannot capture features such as persistent activity or multistability, which are thought to be important for cognitive capabilities in higher areas (Wang, 2013). We thus replaced our local circuit with a firing rate (“mean-field”) version of a spiking network with more realistic synaptic dynamics (Wang, 2002; Wong and Wang, 2006). When isolated, an area in this network can display qualitatively different regimes (Figure 7A). For relatively weak recurrent connections, an area shows a single stable state. As recurrent excitation is increased, there is a transition to a regime with two stable states, with low and high firing rates that correspond to a resting state and a self-sustained persistent activity state. In this regime, an area can integrate inputs over time and maintain activity in the absence of a stimulus. Such dynamical regimes have been proposed to underlie “cognitive-type” computations such as working memory and decision-making (Wang, 2002, 2013).

With this model for each area in the large-scale network, we introduced the previous gradient of excitation. Consequently, sensory areas show single stable states while areas further up the hierarchy can also show persistent activity when driven by strong inputs (Figure 7B). Small perturbations are insufficient to shift the state of a node but take longer to decay away in areas further up the hierarchy (Figure 7C).

For small inputs the network response resembles the threshold-linear model: a brief input to V1 is propagated up the hierarchy, with rapid decays in sensory areas and slow decays in association areas (Figure 7D). Thus, the previous results extend to a nonlinear model with a larger dynamical repertoire. Exploring the complex dynamical behaviors that this network can show is beyond the scope of this paper, but one interesting consequence of the extended model is that the timescales of small fluctuations around baseline predict the ability of an area to show much longer timescales in response to larger inputs (Figure 7C, and see Discussion), as observed in Honey et al. (2012) and Murray et al. (2014).

Functional connectivity

We now investigate the implications of local heterogeneity for network organization as measured by correlations in resting-state activity (resting-state functional connectivity). In our model, frontal and association areas reflect a slowly varying network state, and we hypothesized that this state should strongly shape functional connectivity.

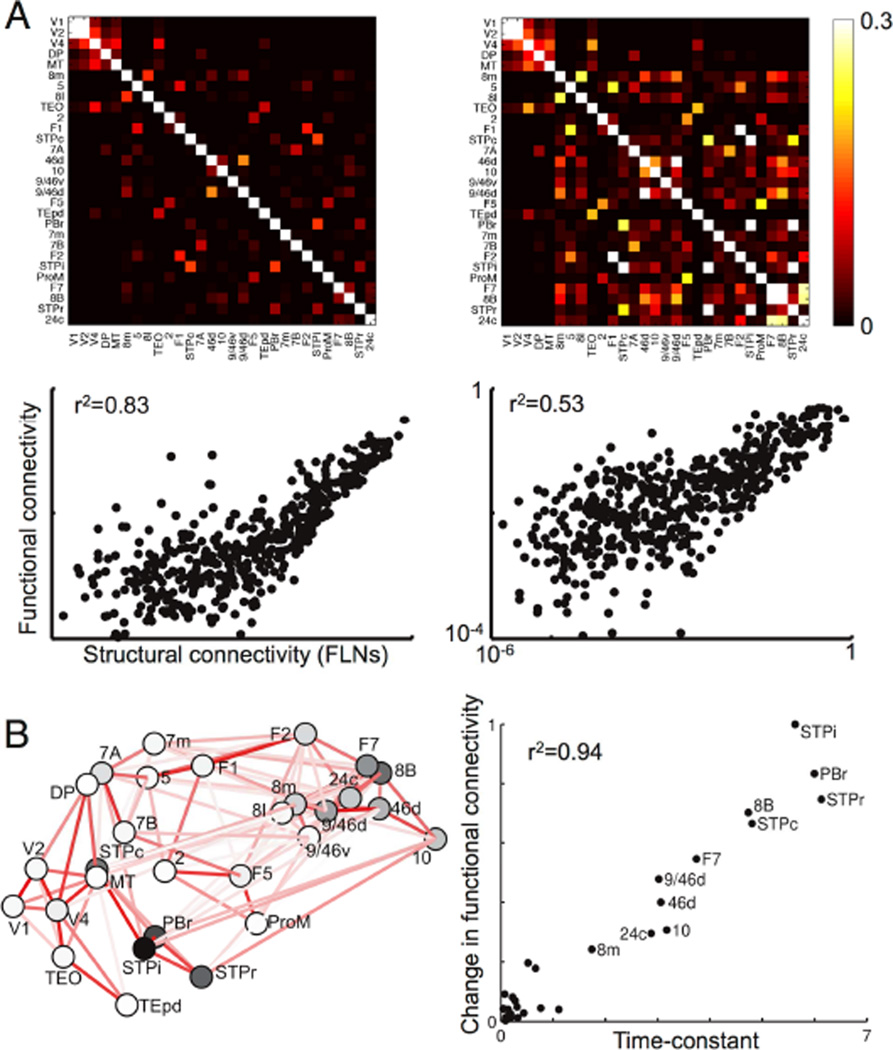
In Figure 8A we show functional connectivity in our threshold-linear model with heterogeneity in local area properties, or without it (as typically assumed in models relating functional to anatomical connectivity). The inclusion of a gradient of local excitation reduced the correlation (r²) between functional and anatomical connectivity from 0.83 to 0.53 (Figure S6 shows results using a BOLD kernel (Boynton et al., 1996)).

Figure 8.

Functional connectivity depends on local microcircuitry. (A) Functional connectivity for two networks with identical long-range connectivity. The network on the left has the same properties at each area, while that on the right has a gradient of local recurrent strengths. Top panel: correlations in area activity for uncorrelated background input to each area. Bottom panel: functional connectivity (correlation) vs. structural connectivity (FLN) for non-zero projections. The network with a gradient of local recurrence has enhanced functional connectivity for slow areas, and a smaller overall correlation between functional and anatomical connectivity (showing that long-range connections alone cannot predict global brain activity patterns). (B) Effect of lesioning areas, one at a time, on functional connectivity. Left panel: Darker areas are those with a greater influence on resting-state functional connectivity. Right panel: The effect of lesioning an area on functional connectivity is well-correlated with the time constant of spontaneous fluctuations in that area. See also Figures S5 and S6.

Multiple studies find that the strength of an anatomical connection between areas (“structural connectivity”) partially predicts correlations in neurophysiological signals from those areas (functional connectivity), but there are significant differences (Hagmann et al., 2008; Honey et al., 2009; Damoiseaux and Greicius, 2009; Honey et al., 2010; Deco and Corbetta, 2011; Deco et al., 2014). Our results also suggest that inter-areal connections are insufficient to predict functional connectivity. However, we find that heterogeneity in local connectivity could help account for the previously unexplained variance.

In our model slower frontal and temporal areas in particular show enhanced functional connectivity. Consequently, areas with slow timescales play a predominant role in the network, as shown by “lesioning” individual areas (Figure 8B, left panel). For the simple case of identical input to each area, the effect of lesioning an area is well predicted by the time constant of intrinsic fluctuations (Figure 8B, right panel). Note that areas most important for functional connectivity are not simply those at the highest positions in the hierarchy (i.e., with the most recurrent connections), and hierarchy alone poorly predicts impact on functional connectivity (r²=0.18). For instance, the caudal superior temporal polysensory region (STPc) and the rostral parabelt (PBr) are at intermediate hierarchical positions but have strong connections to other parts of STP (darker lines in Figure 8B) forming a cluster that shapes functional connectivity. In general, areas combining intermediate to high hierarchical position and strong connections to slow areas have the strongest influence on global activity patterns.

Discussion

The main findings of this work are threefold. First, it establishes a circuit mechanism for a hierarchy of temporal receptive windows, which has received empirical support in recent human (Hasson et al., 2008; Lerner et al., 2011; Honey et al., 2012; Gauthier et al., 2012; Stephens et al., 2013) and single-unit monkey experiments (Murray et al., 2014). The model extends time integration in decision-making from local circuits (Wang, 2008) to a large-scale system across multiple timescales (Hasson et al., 2015). Second, inter-areal heterogeneity implies that areas cannot be treated as identical nodes of a network and slow dynamics in association areas can play a disproportionate role in determining the pattern of functional connectivity. This suggests that functional connectivity analyses be revised. And third, this is the first large-scale dynamical model of the macaque cortex based on weighted and directed connectivity and incorporating heterogeneity across areas.

The ability to integrate and hold information across time is critical for cognition. On the other hand, the brain must rapidly and transiently respond to changing stimuli. Complex behavior thus requires a multitude of coexisting timescales. We demonstrate how such timescales (or temporal receptive windows) naturally emerge in a model of primate cortex, built with quantitative anatomical data. Our work reveals multiple functional hierarchies converging on a slow distributed network of densely-connected frontal and other association areas.

A long-standing observation is that strong recurrent connections can produce slower dynamics (Wang, 2008), and we show how this basic anatomical motif can interact with the pattern of long-range connections to produce a hierarchy of timescales. The hierarchies we observe with different stimuli thus emerge from a combination of heterogeneity in excitatory connection strengths across areas and the profile of long-range connectivity (which is highly specific to each area (Markov et al., 2013a)), and neither alone can predict an area’s timescales. For example, while differences in local recurrence play a crucial role in generating timescales, the correlation between anatomical hierarchy and timescale is relatively weak (r²=0.25, 0.14, 0.22 in the visual, somatosensory and resting-state conditions respectively). Moreover, areas can show quite different timescales in response to different inputs: as seen in Figure 4B, even early visual areas with relatively weak recurrence can have slower timescales. To characterize the dependence of timescales on local and long-range properties, we first removed the gradient of local properties and observed that the hierarchy of timescales vanishes. Separately, we preserved the local properties of areas and either removed (Fig. 5A, right panels) or scrambled the long-range projections both globally and while preserving network topology (Fig. 5B and C).

It will be important to further probe the interaction of local and long-range connectivity. This will require additional anatomical and physiological data, and our model can be a platform to explore the consequences of these data for large-scale dynamics. For example, following the finding of Markov et al. (2011) that the proportion of local to long-range synapses is roughly conserved across areas, we have chosen to scale both local and long-range projections by an area’s position in the hierarchy. Nevertheless, local and long-range synapses may have different strengths and properties and may differentially target cell types and dendritic locations. Relatedly, long-range inputs may be differentially gated depending on task demands and the local circuit regime. Conversely, in the nonlinear model, long-range input can shift the dynamical regime of the local circuit: an area that lacks persistent activity when isolated may show persistent activity in the presence of a weak long-range control signal. These interactions can provide the network with an enhanced computational repertoire.

To examine timescales in the clearest way possible, we modeled individual areas with a threshold-linear rate model, where time constants are mathematically well defined. However, the results hold for a nonlinear local circuit with multiple stable states. Note that this work did not focus on the latency of neural responses (Schmolesky et al., 1998; Bullier, 2001), for which a spiking model is needed. Nevertheless, single neurons in the monkey cortex display slow responses during stimulus presentation as shown in the model; for example, in decision tasks prefrontal and parietal neurons can show quasi-linear ramping with a time constant that may appear effectively infinite (Smith and Ratcliff, 2004; Gold and Shadlen, 2007; Wang, 2008; Brunton et al., 2013). Thus the model is the simplest that is adequately designed to reveal a hierarchy of timescales in the cortex.

We systematically introduced heterogeneity into our model by assigning each cortical area a hierarchical position determined by its pattern of feedforward and feedback projections. A priori, there is no reason why excitatory input would vary systematically along this anatomical hierarchy. However, we find that hierarchical position correlates very strongly with the number of spines per neuron in an area (Fig. 2B). This suggests an underlying cortical organizational principle, which could be explored in future (see Scholtens et al. (2014) for a similar observation and Barbas and Rempel-Clower (1997) and Hilgetag et al. (2002) for correlation of hierarchy with lamination and relative density of an area).

There are no systematic measurements of the timescales of areas in response to different stimuli, but recent studies have compared temporal responses and integration timescales across areas and report a hierarchical organization (Hasson et al., 2008; Ogawa and Komatsu, 2010; Lerner et al., 2011; Bernacchia et al., 2011; Honey et al., 2012; Gauthier et al., 2012; Stephens et al., 2013; Murray et al., 2014). Notably, Honey et al. (2012) connected a functional hierarchy in the timescales of preferred stimuli to a dynamical hierarchy in the timescales of correlation in network activity, and found autocorrelation timescales similar to those we model (in particular, see Fig. 6 of Honey et al. (2012)). Similarly, Murray et al. (2014) found that autocorrelation traces were well-described by exponentials, the hierarchical ordering of areas they observe agrees with our model, and the timescales of small fluctuations in that study are close to the intrinsic time-constants of areas in the model (i.e., in the absence of long-range projections such as Fig. 5A, far right panel).

Our model has several testable predictions. Though there are multiple combinations of local time constants and network connection strengths that could produce a particular set of observed timescales, the model suggests that timescales of small fluctuations should reflect the intrinsic properties of areas (far right panel of Fig. 5A), while larger responses should reflect time constants that emerge from the entire system (far left panel of Fig. 5A). In the model, slow network timescales are driven by strongly-connected frontal and temporal areas, corresponding to a slowly varying global state. Inactivating these areas should decrease slow dynamics in connected areas lower in the hierarchy. The differential responses to visual and somatosensory input suggest that when a particular input is not involved in a task, the corresponding sensory areas better reflect slow changes in global cortical state. This may explain decreases in low-frequency ECoG power (i.e. slow modes) when a subject engages in a task (He et al., 2010; Honey et al., 2012), as well as the observation of Stephens et al. (2013) that, despite fast timescales in response to visual input, early visual areas have slow timescales during auditory processing. Finally, we predict that areas with longer timescales, such as prefrontal and superior temporal areas, can shape functional connectivity to a greater degree. This highlights the importance of incorporating heterogeneous local dynamics in studying the determinants of functional connectivity and, intriguingly, suggests that functional connectivity might be used to probe local properties. While there is some evidence that frontal and association areas show enhanced functional connectivity (Sepulcre et al., 2010) and of a correlation between enhanced functional connectivity and slow timescales (Baria et al., 2013), it would be interesting to use functional imaging to better understand the link between functional connectivity and response timescales (for example, as determined by the approach of Hasson et al. (2008); Lerner et al. (2011); Honey et al. (2012); Gauthier et al. (2012)). The link between slow timescales and enhanced functional connectivity might also explain observations that functional connectivity is greater at low frequencies (Salvador et al., 2005). Moreover, since distant areas tend to lack strong direct connections their functional connectivity will be primarily driven by slow distributed network modes and will be further biased towards low frequencies, as previously observed (Salvador et al., 2005).

We mostly used a threshold-linear model for local areas, but the hierarchy of timescales holds when areas are modeled by a nonlinear microcircuit, similar to one proposed as a model for general “cognitive-type” computations (Wang, 2002, 2013). Depending on connectivity and input parameters, such networks show a single stable state, multistability with persistent firing, or continuous slow fluctuations between metastable states. While we do not explore this broader range of behaviors, note that in the nonlinear model the timescales of small fluctuations around baseline predict an area’s ability to show much longer timescales in response to larger inputs. This can be seen by comparing the timescales of Figure 7C with the steady-states of Figure 7A, and by contrasting responses to large and small perturbations in Figures 7B and D (also note that timescales in response to large perturbations tend to be slower than those from small perturbations even if the area is not bistable). This may explain why the timescales of spontaneous fluctuations in an area (on the order of hundreds of milliseconds) correlate with its sensitivity to temporal structure in stimuli across seconds (Honey et al., 2012) as well as with slow drifts in baseline neural activity and the timescales of reward memory (Murray et al., 2014).

Our model is parsimonious, designed to capture a basic mechanism underlying a hierarchy of timescales, and can be extended in several ways. First, the local area model could be made more complex, and an interesting direction is using the SLNs to incorporate a laminar structure. Second, in our model activity propagates along the hierarchy with significant attenuation. This attenuation can be substantially decreased by changing model parameters (M. Joglekar & X.-J. Wang, personal communication), and may also be removed by synchronous firing (Diesmann et al., 1999) or more sophisticated feedback projections (Moldakarimov et al., 2015). Third, we only consider cortico-cortical connections. While these form the major input to a cortical area (Markov et al., 2011), subcortical projections will play an important role. For example, incorporating thalamo-cortical projections would allow us to more realistically model input and may help set network state and gate inter-areal interactions, while neuromodulators such as acetylcholine might modulate the excitability of local populations and enhance information transmission at other synapses. Fourth, as a first step we used two global parameters to scale long-range connection strengths but emerging data relating long-range anatomy and physiology should be incorporated. Fifth, extensions should include other inter-areal heterogeneities, such as in interneuron types and densities (Medalla and Barbas, 2009) and in neuromodulatory signaling (Hawrylycz et al., 2012). For example, it would be interesting to model the higher numbers of dopaminergic projections to prefrontal areas. Finally, while we have focused on how areas are able to accumulate incoming information on different timescales, processing input requires synthesizing it with previous input. Future work should explore how different areas in our model integrate information from more realistic time-varying stimulation such as a movie or a song and to probe how these responses change when the correlation structure of the input is disrupted (for example, by scrambling).

In conclusion, we report a novel, quantitatively-calibrated, dynamical model of the macaque cortex with directed and weighted connectivity. The identification of a specific circuit mechanism for a hierarchy of timescales (temporal receptive windows) represents a key advance towards understanding specialized processes and functions of different (from early sensory to cognitive-type) cortical areas. Our findings demonstrate the importance of heterogeneity in local areal properties, as well as the specific profile of long-range connectivity, in sculpting the large-scale dynamical organization of the brain.

Experimental Procedures

Anatomical data

Connectivity data are from an on-going project to quantitatively measure all connections between cortical areas in the macaque (Markov et al., 2014a). Inter-areal connection strengths are measured by counting projecting neurons labeled by retrograde tracer injections and normalizing by the total number of neurons labeled in the injection, yielding a fractional weight or FLN (Fraction of Labeled Neurons) for each pathway:

$$FL{N}_{B\to A}=\frac{\#\mathit{\text{neurons projecting to area A from area B}}}{\mathit{\text{total neurons projecting to area A from all areas}}}$$

So far, 29 areas have been injected and we use the subnetwork consisting of these areas. The presence or absence of all connections is known bidirectionally, and 66% of possible connections exist, with widely varying strengths.

We also use data on the fraction of neurons in each projection that originate in the upper layers of the source area (SLN, for Supragranular Layer Neurons (Markov et al., 2014b)) defined as

$$SL{N}_{B\to A}=\frac{\#\mathit{\text{supragranular neurons projecting to area A from area B}}}{\#\mathit{\text{neurons projecting to area A from area B}}}$$

Data are in Table S1.

Hierarchy and connectivity embedding

To extract the hierarchy, we follow observations from the visual system that the fraction of projections originating in the supragranular layers of the source area (the SLN) measures hierarchical distance between the source and target areas (Felleman and Van Essen, 1991; Barone et al., 2000; Markov et al., 2014b). We use a generalized linear model to assign hierarchical values to areas such that the differences in hierarchical values predict the SLNs (similar to the method in Markov et al., 2014b).

For Figure 2C, we compute angles θ_i such that the angular distances between areas A_i and A_j correspond to dissimilarity measured as −Log(FLN(A_i, A_j)). We then plot the areas on a polar plot with θ(A_i)=θ_i and $R(A_i)=\sqrt{1-h_i}$.

See the Supplemental Experimental Procedures and Figure S1 for an expanded discussion of the hierarchy and the circular embedding.

Model architecture

Each area consists of an excitatory and an inhibitory population described by

$${\tau }_E\frac{d}{dt}{\nu }_E^i=-v_E^i+{\beta }_E{[(1+\eta h_i)(w_{EE}{v}_E^i+{\mu }_{EE}\sum _{j=1}^{N}FL{N}_{ij}{v}_E^j)-w_{EI}{v}_I^i+I_{\mathit{\text{ext}},E}^i]}_{+}$$

$${\tau }_I\frac{d}{dt}{\nu }_I^i=-v_I^i+{\beta }_I{[(1+\eta h_i)(w_{IE}{v}_E^i+{\mu }_{IE}\sum _{j=1}^{N}FL{N}_{ij}{v}_E^j)-w_{II}{v}_I^i+I_{\mathit{\text{ext}},I}^i]}_{+}$$

${\nu }_E^i$ is the firing rate of the i-th excitatory population, with intrinsic time constant τ_Ε, couplings w_EE and w_EI from the local excitatory and inhibitory population, and external input $I_{\mathit{\text{ext}},E}^i$ (both stimulus input and any noise we add to the system). The inhibitory population has corresponding parameters τ_I, w_IE, w_II and $I_{\mathit{\text{ext}},I}^i$. The f-I curves are threshold linear, with slope β_E and β_Ι. FLN_ij is the FLN from area j to area i. μ_EE and μ_IE control the strengths of long-range input to the excitatory and inhibitory populations, and do not vary between connections: all specificity comes from the FLNs. η scales both local and long-range excitatory inputs to an area by its position in the hierarchy, h_i. We set τ_E=20 ms, τ_I=10 ms, β_E=0.066 Hz/pA, β_I=0.351 Hz/pA, w_EE=24.3 pA/Hz, w_IE=12.2 pA/Hz, w_EI=19.7 pA/Hz, w_II=12.5 pA/Hz, μ_EE=33.7 pA/Hz, μ_IE=25.3 pA/Hz and η=0.68. For more details see Supplemental Experimental Procedures.

We mostly ignore inter-areal conduction delays, but see Figure S3 for a network with conduction delays.

Pulse input, autocorrelation and fitted time constants

For Figures 3, 4, 5 and 8, we choose the background input for each area so that the excitatory and inhibitory populations have rates of 10 and 35 Hz respectively.

In Figure 3A, V1 receives a 250 ms pulse of input that drives its rate to 100 Hz. For the remaining panels of this figure and Figure 5A, the stimulus to V1 is white-noise with a mean of 2 Hz and a standard deviation of 0.5 Hz. The other areas receive a small amount of background input (standard deviation on the order of 10⁻⁵), but are primarily driven by long-range input propagating out from area V1. For Figure 4, the currents are the same except that area 2 receives the stimulus rather than V1.

For each area we extract time constants by fitting both one and two exponentials to the part of the autocorrelation function that decays from 1 to 0.05. If the sum of squared errors of the single exponential fit is less than 8 times that of the double exponential, then we report that time-constant. Otherwise we use the sum of time-constants from the double exponential fit, with each weighted by its amplitude. Fits in response to V1 and area 2 input and for resting state activity are shown in Figures S2, S4 and S5.

For Figure 4B, we map the time-constants logarithmically to a heat map and plot them using Caret (Van Essen et al., 2001).

Functional connectivity

To highlight the effect of intrinsic hierarchy, in Fig. 8A we contrast a network without hierarchy with a network that has a gradient of local excitatory connections but, unlike in the remaining figures, no gradient in the long-range projection strengths (thus these networks have the same long-range connection strengths and differences emerge from local properties). We replace $(1+\eta h_i)(w_{EE}{\nu }_E^i+{\mu }_{EE}{\sum }_{j=1}^{N}FL{N}_{ij}{\nu }_E^j)$ with $(1+\eta h_i)w_{EE}{\nu }_E^i+{\mu }_{EE}{\sum }_{j=1}^{N}FL{N}_{ij}{\nu }_E^j$ for the excitatory population, and similarly for the inhibitory population. For Figure 8B we use the same network as elsewhere, so that all incoming excitatory projections are scaled by an area's hierarchical position.

We calculate functional connectivity as the correlation matrix of area activity in response to equal white-noise input to all areas. For Figure 8B we determine this correlation matrix analytically (see Supplemental Experimental Procedures). The effect of lesioning an area, A, is measured as ‖C_l,A−C_rs,A‖/‖C_rs,A‖, where C_l,A is the correlation matrix after lesioning A, C_rs,A is the intact correlation matrix without the row and column corresponding to A, and the double lines indicate the norm. The values are then scaled to lie between 0 and 1.

Nonlinear network

The nonlinear single area model is a variant of a model proposed in Wong and Wang (2006) as an approximation to a spiking network with AMPA, GABA and NMDA synapses (Wang, 2002). Each area is described by:

$${\nu }_E^i=\phi ((1+\eta h_i)(w_{EE}{s}_N^i+{\mu }_{EE}\sum _{j=1}^{N}FL{N}_{ij}{s}_N^j)-w_{EI}{v}_I^i+I_{\mathit{\text{ext}},E}^i)$$

$${\tau }_N\frac{d}{dt}{s}_N^i=-s_N^i+\gamma {\tau }_N(1-s_N^i)v_E^i$$

$${\tau }_I\frac{d}{dt}{\nu }_I^i=-v_I^i+{\beta }_I{[(1+\eta h_i)(w_{IE}{s}_N^i+{\mu }_{IE}\sum _{j=1}^{N}FL{N}_{ij}{s}_N^j)-w_{II}{v}_I^i+I_{\mathit{\text{ext}},I}^i]}_{+}$$

ν_E and ν_I are excitatory and inhibitory firing rates, s_N is a gating variable corresponding to NMDA synapses (with decay timescale τ_N) and φ is a simplified f-I curve from Abbott and Chance(2005). We set τ_N=60 ms, τ_I=10 ms, γ=0.641, w_EE=250.2 pA, w_EI=8.110 pA/Hz, w_IE=303.9 pA and w_II=12.5 pA/Hz.

For Figures 7A–C we remove long-range connections and characterize an isolated area. The bifurcation diagram of Figure 7A shows network steady-states as we vary the hierarchy scaling (i.e., 1+ηh_i), while Figure 7C shows the slowest timescale of the Jacobian around the low firing state.

For Figure 7B we set η=3.4 and give a 100 Hz pulse of input for 250 ms to the two disconnected areas at opposite ends of the hierarchy (V1 and 24c). For Figure 7D we consider a connected network, with long-range projections only targeting excitatory subpopulations, for simplicity, and set μ_EE=125.1 pA. We give a 200 Hz pulse of input to area V1 for 250 ms.

Highlights.

• -Large-scale model of the macaque cortex with a gradient of synaptic excitation
• -Sensory areas show fast responses while cognitive areas show slow integrative activity
• -Multiple temporal hierarchies in the same anatomical network
• -Functional connectivity analysis needs to incorporate inter-areal heterogeneity