Fibronectin Fibrillogenesis Facilitates Mechano-dependent Cell Spreading, Force Generation, and Nuclear Size in Human Embryonic Fibroblasts

Abstract

Cells respond to mechanical cues from the substrate to which they are attached. These mechanical cues drive cell migration, proliferation, differentiation, and survival. Previous studies have highlighted three specific mechanisms through which substrate stiffness directly alters cell function: increasing stiffness drives 1) larger contractile forces; 2) increased cell spreading and size; and 3) altered nuclear deformation. While studies have shown that substrate mechanics are an important cue, the role of the extracellular matrix (ECM) has largely been ignored. The ECM is a crucial component of the mechanosensing system for two reasons: 1) many ECM fibrils are assembled by application of cell-generated forces, and 2) ECM proteins have unique mechanical properties that will undoubtedly alter the local stiffness sensed by a cell. We specifically focused on the role of the ECM protein fibronectin (FN), which plays a critical role in de novo tissue production. In this study, we first measured the effects of substrate stiffness on human embryonic fibroblasts by plating cells onto microfabricated pillar arrays (MPAs) of varying stiffness. Cells responded to increasing substrate stiffness by generating larger forces, spreading to larger sizes, and altering nuclear geometry. These cells also assembled FN fibrils across all stiffnesses, with optimal assembly occurring at approximately 6 kPa. We then inhibited FN assembly, which resulted in dramatic reductions in contractile force generation, cell spreading, and nuclear geometry across all stiffnesses. These findings suggest that FN fibrils play a critical role in facilitating cellular responses to substrate stiffness.

Graphical Abstract

Introduction

Over the past decade, there has been an incredible focus on cell mechanosensing: the ability of cells to sense and respond to the mechanical properties of their surroundings^1–9. Studies have demonstrated that cell mechanosensing can have profound effects on cell fate, cell survival and cell migration. Several groups have demonstrated that substrate stiffness can mediate differentiation of stem cells or progenitor cells^10–12. Leight, et al. have shown that substrate stiffness can affect TGF-β1 signaling, promoting apoptosis on softer substrates while mediating EMT on stiffer substrates¹³. Several studies have demonstrated that cells preferentially migrate from softer surfaces to stiffer surfaces, a phenomenon known as durotaxis^14–17. Additionally, there is evidence that mechanosensing plays a significant role in disease progression including cancer^18–20 and fibrosis^21–22.

There are three physical changes that occur at the cellular scale in response to substrate stiffness. First, as substrate stiffness increases, cells generate larger forces and increase their cytoskeletal stiffness^{11, 23–26}. Second, cells spread to larger sizes as a function of substrate stiffness^26–27. (It is worth noting that several studies suggest that these two effects are not independent^28–29.) Third, a subset of actin filaments are anchored to the nucleus³⁰, and as such, several studies have suggested that substrate stiffness sensing may alter tension on the nuclear membrane, driving changes at the transcription level^31–33.

Despite many groundbreaking studies that detail the mechanical interactions of cells and their underlying substrate, there is one component of the system that has largely been ignored in these systems: the extracellular matrix (ECM). While the interconnected relationship between matrix composition and tissue stiffness is well appeciated^34–35, and that changes in ECM deposition and stiffness drive pathological events^{19, 21, 36}, the role of the ECM in modulating mechanosensing events, particularly cell traction force generation, cell size, and nuclear morphology, has not been elucidated. In the current study, we have specifically focused on the role of fibronectin in these events. Fibronectin (FN) is an ECM protein found at high concentrations in a soluble form in blood plasma, and is assembled by cells into elastic, insoluble fibrils^37–40. These fibrils form the primordial ECM, and are the first matrix proteins assembled by cells during wound healing and embryonic tissue development^41–44.

Assembly of FN fibrils is mediated primarily by cell attachment via α₅β₁ integrins. Actomyosin forces stretch FN, revealing a hypothesized cryptic FN-FN binding site. Soluble FN binds to the stretched FN via the 70 kDa N-terminus of the molecule⁴⁵. The process repeats, driving assembly of the insoluble fibrils. Assembly of FN fibrils can be inhibited by addition of soluble 70 kDa fragment⁴⁵; addition of a partial Type III FN domain⁴⁶; or addition of a bacterially derived 49 amino acid peptide from S. pyogenes (FUD)⁴⁷. In the current study, we have inhibited FN assembly through the use of FUD, which has been shown to effectively inhibit FN assembly both in vitro^48–49 and in vivo⁵⁰ wihtout affecting cell adhesion.

There is good reason to envision a role for FN fibrils in mediating cell-substrate mechanical interactions. First, FN fibrillogenesis requires application of cell-derived contractile forces; in the absence of RhoA-mediated contractility, no FN fibrils are assembled^51–52. Thus, the application of traction forces to a substrate often results in assembly of FN, provided there is sufficient soluble FN available. Second, these fibrils have unique mechanical properties that will influence the local stiffness sensed by cells: previous studies have demonstrated that FN fibrils are extremely elastic and can be maximally stretched to fourfold their resting length^53–56. The role of cell-derived FN fibrils in mediating mechanosensing has not been investigated. Given that: a) cells generate differential contractile forces in response to substrate stiffness, and b) contractile forces drive FN fibrillogenesis, we hypothesize fibronectin fibrillogenesis facilitates cellular response to substrate stiffness (in contrast to prevailing theories in which substrate stiffness drives modifications in ECM assembly).

Materials and Methods

Cell culture and Reagents

Human embryonic fibroblasts (WI-38) were a gift from Dr. Lewis Romer (Johns Hopkins University, Baltimore, MD) and were maintained in high glucose DMEM (Sigma Aldrich, St. Louis, MO) +10% fetal bovine serum (Quality Biological, Gaithersburg, MD) and 1% penicillin/streptomycin (Life Technologies, Carlsbad, CA) under standard culture conditions. Y27632 was purchased from Sigma Aldrich.

Fabrication of Microfabricated Pillar Arrays

MPAs were fabricated using a two-step casting process from a silicon wafer master mold as previously described ^57–59. Briefly, a two dimensional pattern of each pillar geometry was created on a chrome-coated quartz mask (Nanofilm, Westlake Village, CA) using a direct-write laser mask writer (microPatternGenerator 101, Heidelberg Instruments, Heidelberg, Germany). A silicon wafer was cleaned and spin-coated with SU-8 5 to generate a photoresist layer. Pillars were fabricated at heights of 4, 5, 6, 7 and 9 μm. The photoresist-coated wafer was then brought into contact with the quartz mask and exposed to UV light using a mask aligner (MA56, Karl Suss, Garching, Germany) and developed to remove unexposed areas. The wafer was then submerged in Isopropyl Alcohol to terminate the development process and allowed to air dry. Finally the wafer was hard baked at 200 °C for 30 minutes to strengthen the features. This resulted in a wafer with positive features (that is, pillars). A negative mold was fabricated from the silicon wafer master. PDMS was first prepared at a 10:1 ratio of Sylgard 184 (Corning) elastomer base to curing agent. The PDMS was mixed thoroughly for 5 minutes, and the resulting mixture was desiccated to remove any air bubbles. The master wafer was brought into contact with the PDMS and cured at 110 °C for 10 minutes. The master wafer was gently removed and the PDMS negative was completely cured by incubation at 110 °C for 18 hours. Negative molds were exposed to oxygen plasma for 2 minutes and then incubated with trichloro(1H,1H,2H,2H-perfluorooctyl)silane vapor (Sigma Aldrich, St Louis, MO), overnight in order to aid release of subsequent PDMS substrates. To fabricate MPAs from the negative molds, PDMS was again prepared at a ratio of 10:1 Sylgard 184 elastomer base to curing agent. Desiccated PDMS was added to 25mm coverslips, and negative molds were placed face down in the PDMS and tapped down to ensure PDMS completely filled the mold. MPAs were then cured at 110 °C for 18 hours. Coverslips were removed from the oven and the negative was gently peeled away from the coverslip to produce an MPA.

Preparation of MPAs for cell plating

To facilitate cell attachment and imaging, MPAs were prepared as previously described^{57, 59–60}. Briefly, a PDMS stamp is made from 30:1 base:curing agent. This stamp was rinsed in EtOH, dried, and incubated with 50 μg/ml human recombinant FN at room temperature for 1 hr. The stamp was then rinsed and dried with N2 before being brought into conformal contact with a MPA substrate that had been exposed to UV ozone for 5 minutes. This resulted in a layer of FN microcontact printed onto the top surface of the MPA pillars. MPAs were then rinsed in increasingly more dilute EtOH, and then placed into a solution of 0.5 μg/ml FITC-labeled BSA for 1 hour to facilitate visualization of the pillars. MPAs were subsequently rinsed in sterile PBS and incubated for one hour in 1% F-127 Pluoronics in PBS. This inhibits cell attachment to sides and bases of pillars. Fibroblasts adhere to the tops of the pillars, contract, and deflect the pillars at each cell-pillar attachment site. To measure deflections, an image was acquired at both the top (deflected position) and bottom (undeflected position) for each cell. Images were analyzed by an original Matlab code that calculates the centroid of each pillar in its deflected and undeflected states and determines pillar deflection. Force per pillar is calculated from the deflection of each pillar, provided the modulus of elasticity (E) of PDMS, moment of inertia (I) and height of the pillar (L) are known. These values are calculated as previously described^{57, 59–60}.

Immunofluorescence

MPAs were fixed and permeabilized with 0.5% Trition-X 100 (Sigma-Aldrich) and 3% paraformaldehyde. The triton solution was removed after 2 minutes via aspiration, and samples were incubated an additional 20 minutes in 3% paraformaldehyde. Cells were labeled with AlexaFluor555 phalloidin (Invitrogen, City, State) to label F-actin and polyclonal anti-FN (Abcam, Waltham, MA) followed by AlexaFluor647 goat anti-rabbit secondary to identify FN. Cell nuclei were labeled with DAPI. Focal adhesions were labeled with polyclonal anti-vinculin (Sigma-Aldrich). MPAs were mounted onto a cover glass with Fluoromount-G^™ and inverted. Immunofluorescence images were taken on a Zeiss Axiovert inverted fluorescence microscope equipped with a CCD camera (Zeiss, Oberkochen, Germany). ZEN software was used to collect and export images (Zeiss, Oberkochen, Germany).

Expression and Purification of FUD

The cDNA for the functional upstream domain of F1 adhesin, a gift originally from Dr. Deane Mosher (University of Wisconsin, Madison, WI), was cloned into a pET15b HisTag expression vector that also contained the Maltose Binding Protein by Dr. Tomoo Ohashi and Dr. Harold Erickson (Duke University, Durham, NC), who graciously gifted the resulting MBP-FUD plasmid. This plasmid was transformed in C41 competent Escherichia coli cells and grown on ampicillin-resistant LB agar plates overnight. Individual colonies were selected and amplified in LB containing 0.1 mg/ml ampicillin. Cultures were grown to an A600 of 0.5, at which point protein expression was induced with 0.5 mM IPTG (Sigma-Aldrich, St. Louis, MO). Cultures were incubated overnight at room temperature to facilitate protein expression. Poly-histidine-tagged protein was purified from bacterial lysates by running over a cobalt resin column (Thermo Scientific, Waltham, MA) using standard protein purification techniques. Protein was eluted from the column with 0.2 M imidazole, and subsequently exchanged using a PD10 buffer exchange column (GE Healthcare Sciences, Buckinghamshire, UK). Protein concentration was quantified on a Nanodrop Spectrophotometer (Thermo Scientific, Waltham, MA).

Image Processing and Data Analysis

Cell traction forces were calculated by an original Matlab code as described above. For each cell, total cell traction force magnitude was calculated by summing the magnitude of each deflected pillar beneath a cell (determined by overlay of the actin image). To normalize data for cell size, total traction force was divided by the number of pillars occupied by the cell. Cell area and nuclear area were quantified using an original Matlab analysis code that reads in immunofluorescence images, converts images to a binary mask using an opening and closing by reconstruction technique, and calculates relevant morphometric analyses, including size, major and minor axis, eccentricity, and solidity (described in results in more detail). Similarly, FN fibrils and vinculin-continaing focal adhesions were measured by converting immunofluorescence images into a binary mask and conducting morphometric analysis, including area, number, length, and width. For all data sets in the paper, data were acquired for at least 10 cells. Statistical significance was determined using either an unpaired, two-tailed student t-test or a one-way ANOVA, depending on the experiment; significance was indicated by a p value of less than 0.05.

Results and discussion

Effects of substrate stiffness on FN fibrillogenesis

It is well established that substrate stiffness plays a profound role in cell function; however, most existing studies have failed to account for the contribution of ECM fibrils in this process. Because we know that fibroblasts readily assemble FN fibrils, and that these fibrils are highly elastic, we hypothesized that FN may be integral to modulating responses to substrate stiffness (Fig. 1). To investigate this, we first examined how FN fibrillogenesis was altered in response to varying substrate stiffness. WI-38 embryonic fibroblasts were plated onto MPAs of increasing height. WI-38s have been well-studied in the literature, are representative of a stereotypical fibroblast morphology, and were used in early work identifying FN fibrils ^61–63.

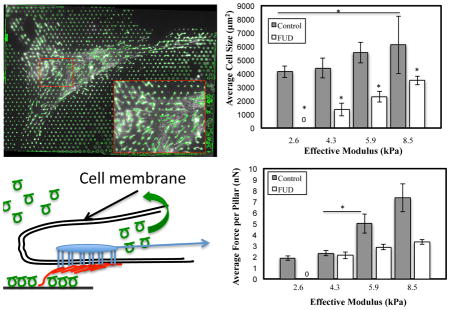
Figure 1. Mechanism of FN fibril formation.

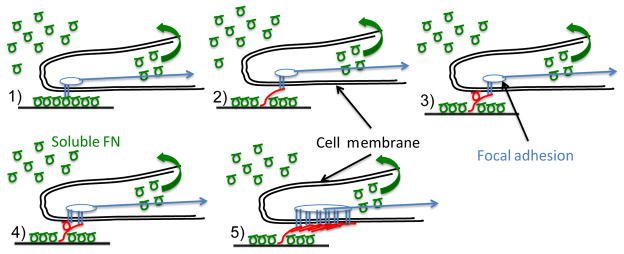
Soluble FN (green circles) is present in serum at high concentration. Assembly of insoluble fibrils proceeds through the following steps: (1) Soluble FN binds to the cell surface via transmembrane integrins (this may also be pre-coated onto in vitro surfaces). (2) Actomyosin forces stretch FN into an extended conformation that (3) facilitates the binding of a second FN molecule. (4) Subsequent integrin binding occurs at the new FN molecule; (5) The process continues until an insoluble, elastic FN fibril is formed. These fibrils act as an intermediate spring between substrate and cell, and as such may alter mechanotransduction responses.

MPAs were fabricated with heights of 4, 5, 6, 7, and 9 microns, which correspond to shear bending stiffnesses of 142.8, 73.1, 42.3, 26.7, and 12.5 nN/μm, respectively. Heights were confirmed by SEM imaging, and shear bending stiffnesses were calculated using the bending equation:

$$k=\frac{3EI}{L^3}$$

where E is the elastic modulus of PDMS, I is the cross-sectional moment of inertia, and L is the height of the pillars. MPAs had diameters of 2.2 μm and a center-to-center spacing of 5 μm. Many studies of substrate stiffness use hydrogels with a measurable, homogenous elastic modulus. For comparison, we have calculated an effective stiffness for each MPA, which is a function of both individual pillar bending stiffness and pillar spacing. This effective stiffness was calculated using the methodology previously developed and described in the lab of Dr. Nathan Sniadecki⁶⁴. The effective moduli for the 5 geometries were 13.3, 8.5, 5.9, 4.3, and 2.6 kPa, respectively.

MPAs not only allow for control of substrate stiffness and quantification of cell traction forces; they also serve as a scaffold for cell-derived FN fibrils⁵². FN fibrillogenesis was probed by morphometric analysis of FN immunofluorescence images (Fig. 2A). FN image thresholding was first conducted as described above; this resulted in a binary image of FN fibrils (shown as a green outline overlay in Fig. 2B). This binary image was then processed using an original author-written morphometric package in Matlab, which calculates the area, minor axis, and major axis of each assembled fibril. These data were averaged over an entire cell to calculate mean values per MPA pillar. Average fibril area per MPA pillar was calculated for each substrate stiffness (Fig. 3A), and data indicate a decrease in fibril area as a function of stiffness. To further quantify fibrillogenesis as a function of substrate stiffness, we performed a second analysis in which we calculated the percentage of cell-occupied pillars that possessed an assembled fibril. This metric allows us to probe the prevalance of FN fibrils: while the area metric indicates an average assembled area, it is possible that a few large fibrils would skew this value. In contrast, the percentage of pillars with an FN fibril metric indicates the prevalence of assembly throughout the cell. To calculate this value, we examined the major axis length of fibrils from each pillar beneath a cell. Any fibril with a major axis length greater than 1.5 times the diameter of a pillar was considered to be “fibril positive”. The percentage of fibril-positive pillars was then calculated relative to the total number of cell-occupied pillars. These data are presented as a function of substrate stiffness in Fig. 2B. These data indicate that FN fibrillogenesis is relatively constant across stiffnesses ranging from 2–6 kPa, and then decrease at effective moduli above 6 kPa.

Figure 2. Representative output images from microfabricated pillar arrays (MPAs).

(A) Fibronectin immuno-fluorescence image shows assembled fibrils extending from fibronectin-stamped pillars. (B) Traction forces are represented by arrows; pillar deflections beneath cell (red arrows) are significantly larger than pillars not contacted by the cell (blue arrows). (C) Image of the base of the pillars indicates undeflected positions, whereas (D) image of the free end of the pillars indicates the deflected positions. Inset shows overlay of top and bottom images; difference in centroid indicates pillar deflection. Scale bar = 20 microns.

Figure 3. FN fibrillogenesis as a function of substrate stiffness.

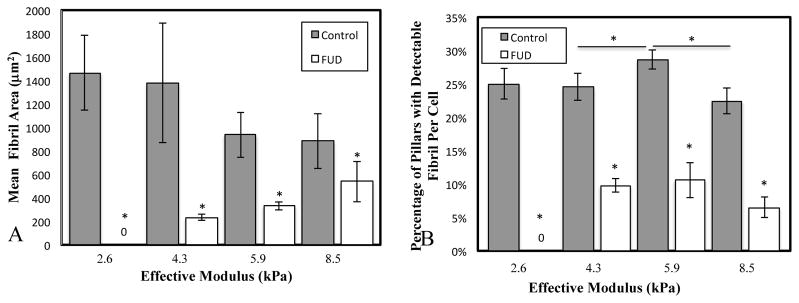
Cells were grown on MPAs of varying stiffness, and the resulting FN fibrillogenesis was quantified via two metrics: A) the mean fibril area per MPA pillar per cell, and B) the percentage of pillars that contained a detectable fibril. *p < .05, N > 10 cells for each condition.

Inhibition of FN Fibrillogeneis

FN fibril assembly is a dynamic process that occurs in response to cell-applied force. To determine the effect of FN fibrillogenesis on substrate stiffness-mediated cellular events, we inhibited FN assembly using a 49-aa peptide containing the functional upstream domain (FUD) of the F1 adhesion protein from S. Pyogenes. FUD blocks FN fibrillogenesis by binding to the Type I modules of FN in the N-terminal 70 kDa fragment⁴⁷. Treatment with FUD does not affect secretion of soluble FN into the media nor does it affect binding of cells to FN via β₁ integrin receptors⁴⁷. Cells were plated onto MPAs of varying stiffness and incubated with 50 nM of FUD for 24 hours, at which point cells were fixed, labeled, and imaged (Fig. S1). Morphometric analysis of the FUD-treated cells indicate that FN assembly is significantly inhibited across all substrate stiffnesses, as indicated by both the FN area metric (Fig. 3A) and the percent fibril occupancy metric (Fig. 3B).

Effects of FN Fibrillogenesis and Substrate Stiffness on Force Generation and Cell Size

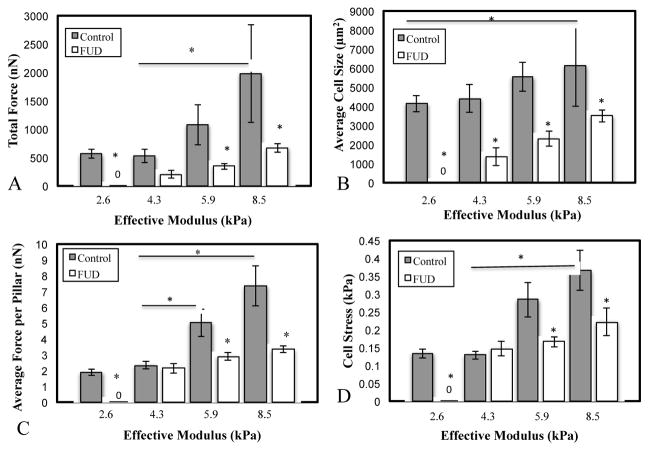
Previous studies have shown that traction forces increase as a function of substrate stiffness ^{25–26, 65–66}. We sought to determine if FN fibrils played a role in modulating these effects. WI-38s were plated onto MPAs for 24 hours, with or without 50 nM of FUD, and were then subsequently fixed and labeled as described above. Traction forces were calculated from pillar deflections as described above using an original Matlab analysis code. Force magnitudes were summed for each pillar beneath a cell to calculate the total magnitude of cell-generated force per cell (nN) (Fig. 4A). Total cell force increased as a function of stiffness. Treatment with FUD led to a significant reduction in traction force at all stiffnesses. On 2.6 kPa pillars, FUD-treated cells attached, but generated no measureable forces. Previous studies have also shown that cell size increases with increasing substrate stiffness ^{26, 65}. Cell size was calculated from actin immunofluorescence images, and increased as a function of stiffness (Fig. 4B). Treatment with FUD showed a significant reduction in cell size across all substrate stiffnesses.

Figure 4. Quantification of cell traction forces and cell size as a function of stiffness and FN fibrillogenesis.

Cells were plated onto MPAs of varying stiffness and exhibited (A) an increase in total cell force and (B) a small but insignificant increase in cell size as a function of stiffness. Treatment with the FN fibrillogenesis inhibitor FUD significantly reduced both. To assess whether force changes were simply a function of impaired spreading, two normalized metrics were used: C) the average force per pillar per cell and D) the cell stress (force per unit cell area). In both metrics, FUD treatment showed significant inhibition of the normalized force on stiffer surfaces. *p < .05. N > 10 cells per condition.

Because cell size increased with substrate stiffness and was inhibited by FUD, it was possible that observed changes in total cell force were simply a function of changes in cell size. To account for this, we normalized cell traction force in two ways: first, we calculated the average traction force per pillar beneath each cell (Fig. 4C), as well as the cell “stress”: the force per unit area (Fig. 4D). Both metrics indicated that the normalized force was roughly the same on the softer surfaces (2.6 and 4.3 kPa) but was significantly reduced on stiffer surfaces (5.9 and 8.5 kPa) when FN assembly was inhibited. Representative images of cells for each condition in Fig. 4 are shown in Fig. S2.

As a comparison, force was directly inhibited in cells by incubating with the Rho Kinase inhibitor, Y27632 (Figure 5). Results showed that the total force per cell was reduced to comparable levels in both Y27632-treated and FUD-treated cells (Figure 5A). When normalized for cell size, the force per pillar was reduced comparably on stiffer substrates (Figure 5B). However, the inhibitory effects of FUD were less than the inhibitory effects of Y27632 on softer substrates. FN assembly was inhibited in the Y27632 samples, as has previously been reported ⁵²

Figure 5. Comparative effects of force inhibition and FN fibrillogenesis inhibition.

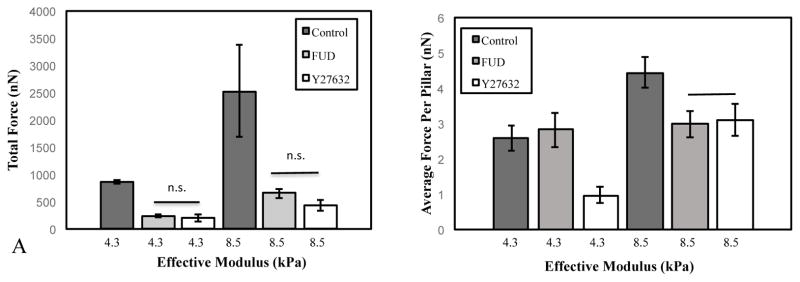
Effects of FN fibrillogenesis inhibition on force generation were compared to inhibition with the Rho Kinase inhibitor Y27632, which inhibits myosin activity and contractility. Inhibition with either FUD or Y27632 showed similar effects on total force per cell. The effects of Y27632 were more pronounced on soft (4.3 kPa) micropillars relative to FN fibril inhibition. On stiffer (8.5 kPa) pillars, FUD and Y27632 had similar effects.

While previous studies have demonstrated that FUD does not affect cell attachment and/or β₁ integrin ligation, we investigated whether FUD was disrupting initial attachment in our system and driving observed differences at the later time points. To investigate this, we probed cell spreading and FN assembly at 3 hours after plating; at this early time point, FN assembly is typically minimal, and as such, FUD treatment should result in no discernible differences in cell size or traction forces. Results indeed show only minimal FN assembly at 3 hours in both the FUD and control cases (Fig. 6A), with a significant increase in FN fibrillogenesis in the 24 hr control case relative to the 24 hr FUD case (Fig. 6B). Cell size at 3 hours showed no significant difference between FUD treatment and control, indicating that FUD-treated cells were able to attach and spread to an equivalent size at time points prior to FN assembly.

Figure 6. FUD has no effect on initial attachment and spreading.

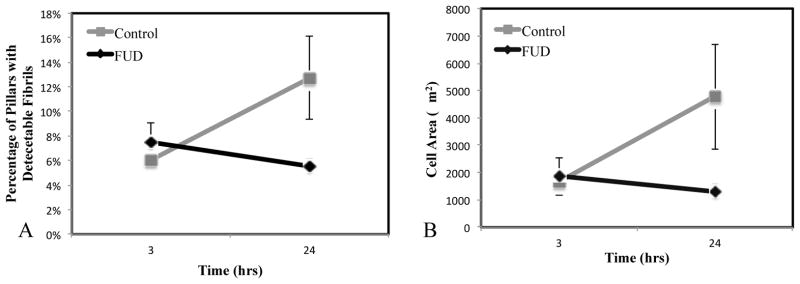
To ensure that FUD was not disrupting cell attachment and spreading, cells were analyzed at 3 hours post-plating, which is prior to FN fibril formation. (A) Mean fibronectin area is identical for both populations (this indicates the area of stamped fibronectin), whereas it increases in the control case at 24 h. (B) Cell area is identical and 3h in both FUD and control cases, but is significantly different by 24 h. Error bars represent standard error. N > 10 cells.

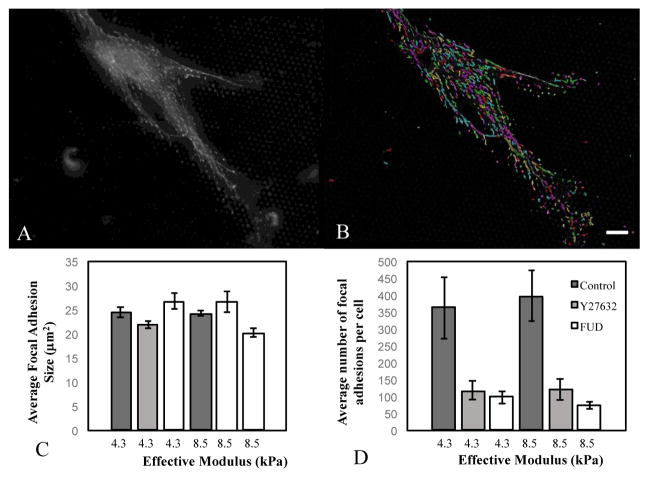
It is possible that the effects of inhibiting FN fibrillogenesis are mediated through alterations in focal adhesion dynamics. To probe this, we labeled cells on either soft (4.3 kPa) or stiff (8.5 kPa) pillars and immunofluorescently labeled the focal adhesion protein vinculin (Figure 7). Vinculin images were processed through an author-written image processing program to determine average number and size of adhesions (Figure 7A, B). Substrate stiffness, Y27632, or FUD had no statistically significant effect on the average focal adhesion size (Fig. 7C). However, inhibiting contractile force with Y27632 or FN fibrillogenesis with FUD significantly reduced the total number of focal adhesions on both soft (4.3 kPa) and stiff (8.5 kPa) substrates (Fig. 7D). These data suggest that responses to substrate stiffness may be mediated by altering the number of adhesions beneath a cell. Representative vinculin images from each condition are shown in Fig. S3.

Figure 7. Effect of FN fibrillogenesis and contractile force on focal adhesion size and count.

Cells were plated on either soft (4.3 kPa) or stiff (8.5 kPa) micropillar arrays and incubated with Y27632 or FUD. (A) Focal adhesions were imaged using antibodies against vinculin, and (B) were analysed using an author-written image processing algorithm (outlines show detected adhesions). (C) Average focal adhesion area and (D) total number of adhesions per cell were calculated for each condition. Error bars represent standard error. N > 100 focal adhesions. Scale bar = 20 microns.

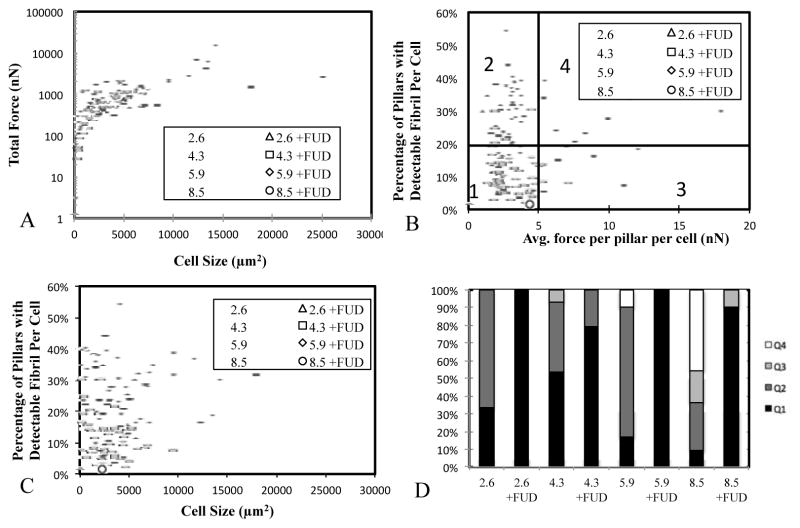
The observed increases in cell size and cell traction forces as a function of FN fibrillogenesis suggest a complex interaction between these three events. We sought to examine these complex relationships further. The relationship of total traction force to cell size was examined for both control cells and FUD-treated cells on all stiffnesses (Fig. 8A). Results suggest a power-law relationship between the two. FUD-treated cells (open circles) are constrained to the lower portion of this curve, suggesting that the presence of FN fibrils creates a permissive environment for cells to continue along the increasing force/size function.

Figure 8. Relationship between force, cell area, and FN fibrillogenesis.

(A) Total cell force and cell size can be related be a power law function regardless of stiffness or FUD treatment; treatment with FUD shifts the relationship to lower values. (B) Fibril/force relationship was divided into quadrants and suggest an optimal force for FN fibrillogenesis. (C) Fibrillogenesis shows no correlation with cell size. (D) Quantification of quadrants indicates a predominance of cells in Q2 on intermediate stiffnesses. FUD treatment leads to a predominance of Q1 cells.

We also examined the relationship between traction forces and FN fibril size. While an intuitive assumption would be that because traction forces are required for fibril formation, a linear relationship exists between the two (that is, a larger cell traction force results in a larger FN fibril), previous studies have shown that this linear correlation does not exist ⁵². To further probe this relationship, we examined fibril size vs average force per FUD MPA pillar on a per-cell basis (each data point in Fig. 9B represents a single cell). Data suggest an intermediate force range (2–5 nN per pillar) that facilitates FN fibrillogenesis. At larger or smaller forces, cells assemble less fibrils. This may explain observations in Fig. 3 in which we observed an optimum (intermediate) stiffness for FN fibrillogenesis. To further quantify these relationships, we separated the data into four quadrants: low force and low FN fibrillogenesis (Q1), low force and high FN fibrillogenesis (Q2), high force and low FN fibrillogenesis (Q3) and high force and high FN fibrillogenesis (Q4). The percentage of cells in each quadrant was determined for each condition (Fig. 9D). Results demonstrate that on intermediate stiffness surfaces, cells exhibit a predominance of low force/high FN fibrils (Q2) that decreases on softer or stiffer surfaces. On all stiffnesses, FUD treatment led to a predominance of low force/low FN (Q1) cells.

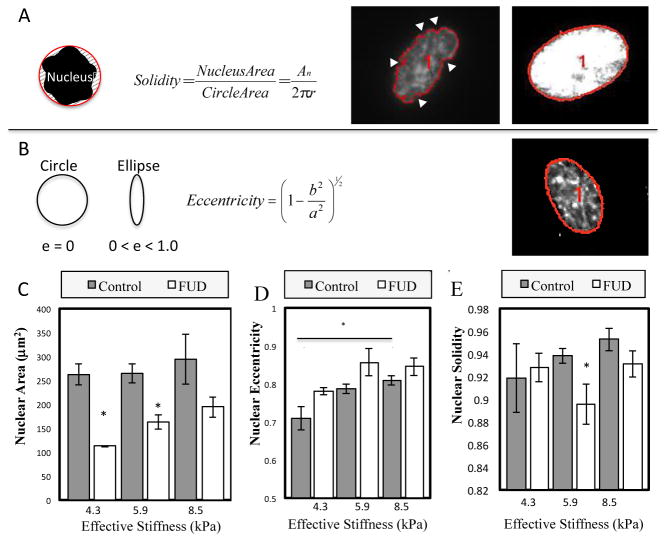
Figure 9. Effects of substrate stiffness and FN fibrillogenesis on nuclear morphology.

Changes in nucleus area, solidity and eccentricity were measured on cells grown on MPAs of increasing stiffness. (A) Solidity is defined as the ratio of nuclear area to the enclosing convex polygon area. Lower solidity indicates an invaginated nucleus (white arrows). (B) Eccentricity quantifies the elongation of the nucleus. A value closer to one is a more eccentric nucleus. (C) Nuclear area is roughly constant across stiffnesses, but is inhibited by FN fibril inhibition. (D) Eccentricity increases as a function of stiffness, and is not altered by FN inhibition. (E) Solidity increases with increasing stiffness and is inhibited on stiffer substrates. p < 0.05, N > 10 cells per condition.

Effects of FN fibrillogenesis and substrate stiffness on nuclear morphology

Given recent interest in nuclear shape changes in response to substrate stiffness^{31–33, 67–68}, we performed a morphometric analysis of nuclear geometry in WI-38s on varying stiffness MPAs. Nuclear solidity, eccentricity, and size were calculated (Fig. 9A). No statistically significant differences were seen in cell size (Fig. 9C). However, there was a statistically significant increase in nuclear eccentricity (Fig. 9D), which indicates a transition from a rounded shape to a more elongated, ovoid shape. Although not significant, there was a positive correlation between nuclear solidity and substrate stiffness (Fig. 9E). Nuclear solidity is a measure of the “smoothness” of the nuclear shape: a highly invaginated nuclear membrane will yield a low solidity value, and vice versa. This indicates that the profile of the nucleus is smoother on stiffer surfaces, which may indicate higher contractile forces on the nuclear membrane. When treated with FUD, cells exhibited significant decreases in nuclear size (Fig. 9C). Nuclear eccentricity was unaffected (Fig. 9D), while nuclear solidity decreased only on 5.9 kPa substrates (Fig. 9E).

Discussion

In the current work we have demonstrated that human embryonic fibroblasts respond to substrate stiffness by increasing contractile forces, spreading to larger sizes, and altering the nuclear morphology from a folded shape to a smoother, elongated shape. We have also shown that fibroblasts respond to substrate stiffness by assembling FN fibrils to varying degrees, with an optimal stiffness of approximately 6 kPa. Inhibition of FN fibrillogenesis with the Functional Upstream Domain of S. Pyogenes F1 adhesin resulted in nearly complete inhibition of fibrillogenesis, and also resulted in significant inhibition of stiffness-induced traction force, spreading, and nuclear morphological changes. These data indicate an important role for FN fibrillogenesis in mechanosensitive cellular events.

While the importance of the relationships between cell size, substrate stiffness, and contractile force generation has been well-explored^{26, 52, 69–70}, the role of FN fibrils (and other ECM components) has not been explored, despite the facts that fibrillar assembly processes requiring cellular traction forces is well understood^51–52 and these fibrils engage in a major role for establishing the mechanical properties of tissue in vivo. While previous studies have demonstrated that contractile forces play a key role in driving FN fibril formation^{52, 71}, we believe that this is the first study to show the inverse: FN fibrils allow for generation of larger traction forces and increased cell spreading, which may form a positive feedback loop leading to increased fibrillogenesis.

How does FN fibrillogenesis facilitate increased spreading and larger contractile forces? We hypothesize that these events are a function of the elasticity of the FN fibrils and/or the fibrillar geometry of the fibrils. Previous studies have demonstrated that FN fibrils are extremely elastic; they can be stretched to a length greater than fourfold their resting length, and removal of applied cell traction forces results in a recoil of the fibril back to its resting length⁵⁴. The possibility exists that this elasticity alters the mechanical environment at the leading edge of the cell. This potentially explains some apparent discrepancies between experimental data and computational models of the cell/substrate interface. Chan and Odde have previously demonstrated a mechanistic model of the interaction between the actomyosin machinery and the external substrate⁷². Their results demonstrated that on stiffer surfaces, cells theoretically exhibit a force-limiting phenomena, which they refer to as “frictional slippage”, where exceedingly large forces yield frequent rupture of integrin bonds at the cell surface due to substrate inelasticity, and thus create an environment in which cells cannot maintain large traction forces over a significant duration of time. Their predictions are well-supported by filopodial dynamics, but appear to be in conflict with experiments that demonstrate cells generating larger forces on stiffer surfaces^{11, 25}. We hypothesize that the presence of elastic fibrils creates an environment in which integrin bonds are not ruptured, thus overcoming the frictional slippage schema. In support of this, another study has indicated a correlation between large forces and FN fibrils at the cell periphery⁵². While the conclusions of this work were that larger forces drove the assembly of FN fibrils, it is equally plausible that the presence of the fibrils allowed cells to generate larger forces.

Another possible explanation for the role of FN fibrils in cell spreading, traction force generation and nuclear geometry is the 3-dimensional nanotopography of the fibrils. Numerous studies have documented the role that nanotopography plays in mechanical force generation and substrate stiffness-driven cellular events^73–76. Large FN fibrils have a diameter of approximately 500 nm, whereas smaller fibrils are in the range of 50–100 nm. Hence, the fibrils potentially facilitate larger force generation and cell spreading by presenting a curved surface on the micron scale.

It is also of interest that substrate stiffness does not affect FN fibrillogenesis in a linear fashion, but instead shows an optimal, intermediate stiffness. This is consistent with previous work that has shown that FN fibrillogenesis is inhibited under situations that either increase or decrease cellular contractile forces⁵². An optimal stiffness may differ depending on tissue type or it may be conserved across tissues. This will be an interesting line of future inquiry.

Conclusions

We conclude that this study elucidates a key player in the mechanical interaction between cells and substrate, namely the presence of FN fibrils. Our findings indicate that assembly of FN fibrils facilitates cell spreading and traction force generation, as well as changes in nuclear morphology. These findings could be critical to an improved understanding of several disease states in which ECM assembly, increased stiffness, and increased contractile forces have been implicated, including cancer¹⁹ and fibrosis²².

Insight, innovation, integration.

Cells respond to the stiffness of the underlying substrate, which is referred to as mechanosensing: increasing substrate stiffness leads to increased cell spreading, traction force generation, and nuclear size. An overlooked aspect of this process is the assembly of extracellular matrix fibrils, a cellular process that controls tissue rigidity in vivo. We investigate the role of these fibrils in regulating the cellular response to stiffness; the novel insight described in this work is that fibrils comprised of the ECM protein fibronectin contribute significantly to the mechanosensing response. The innovation is the use of a unique inhibitor of fibronectin assembly in conjunction with microfabricated substrates that allow for the control of substrate stiffness while also quantifying cell force, size, and fibronectin assembly. The integration of cell biology, microfabrication, and engineering analysis of traction forces is an essential component of discovering these new insights.