Band-pass processing in a GPCR signaling pathway selects for NFAT transcription factor activation

Abstract

Many biological processes are rhythmic and proper timing is increasingly appreciated as being critical for development and maintenance of physiological functions. To understand how temporal modulation of an input signal influences downstream responses, we employ microfluidic pulsatile stimulation of a G-Protein coupled receptor, the muscarinic M₃ receptor, in single cells with simultaneous real-time imaging of both intracellular calcium and NFAT nuclear localization. Interestingly, we find that reduced stimulation with pulses of ligand can give more efficient transcription factor activation, if stimuli are timed appropriately. Our experiments and computational analyses show that M₃ receptor-induced calcium oscillations form a low pass filter while calcium-induced NFAT translocation forms a high pass filter. The combination acts as a band-pass filter optimized for intermediate frequencies of stimulation. We demonstrate that receptor desensitization and NFAT translocation rates determine critical features of the band-pass filter and that the band-pass may be shifted for different receptors or NFAT dynamics. As an example, we show that the two NFAT isoforms (NFAT4 and NFAT1) have shifted band-pass windows for the same receptor. While we focus specifically on the M₃ muscarinic receptor and NFAT translocation, band-pass processing is expected to be a general theme that applies to multiple signaling pathways.

Introduction

Appropriate timing is crucial for proper development and maintenance of physiological functions^1–5. Timing information is relayed through modular interaction of signaling motifs in complex signaling pathways^6–8. Cellular responses are typically studied for step changes in ligand concentrations, although in nature stimuli are often periodic or fluctuate over frequencies ranging from milliseconds to days^9–13. A majority of these rhythmic as well as arrhythmic stimuli lead to oscillations in second messengers (e.g. calcium, cAMP, PKA, MAPK)^14–18. Among these, the effect of frequency modulation of calcium oscillations on downstream transcription factor activation has been extensively studied using calcium-clamped cells^19,20. However, the more physiologically relevant ligand-induced calcium oscillations and downstream signaling are less well-understood. Using pulsatile ligand stimulation of a G-Protein coupled receptor (GPCR), we provide new insights into how cell surface receptor activation leads to calcium signaling and activation of a downstream transcription factor, NFAT (Nuclear Factor of Activated T-Lymphocytes).

The M₃ muscarinic acetylcholine receptor is a GPCR expressed in many locations²¹. Ligand-induced activation of the receptor signals through the common G-protein-PLC-IP₃ pathway that couples to the calcium-calcineurin pathway to induce NFAT nuclear translocation (Fig. 1A). Calcium-dependent calcineurin-NFAT signaling plays key roles in T-cell activation, in insulin secretion^22,23 and in regulating neonatal beta cell development²⁴. In this work, we employ pulsatile stimulation of M₃ receptors and simultaneous measurement of cytoplasmic calcium and NFAT nuclear translocation in single cells using a computer-controlled microfluidic device²⁵. Using computational modeling, we delineate the temporal modulation of GPCR (M₃ receptor)-induced Ca²⁺ oscillations and Ca²⁺-induced NFAT nuclear localization. Microfluidic experiments and mathematical modeling are used in combination to determine the model parameters that control the temporal coding of downstream signaling.

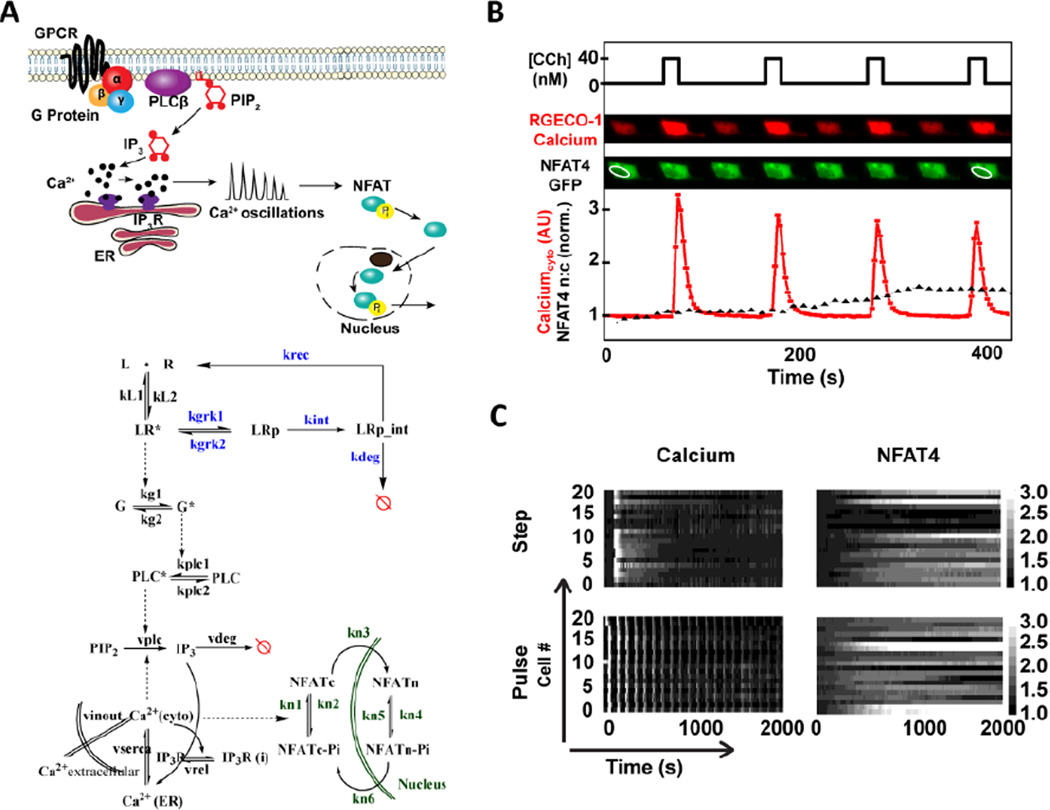
Fig. 1. Simultaneous observation of calcium and NFAT4 dynamics in single cells under step and pulsatile ligand stimulation.

A) GPCR (Muscarinic M₃)-calcium-NFAT pathway showing calcium oscillations leading to NFAT nuclear localization (top). The mathematical model incorporates receptor (R) – ligand (L) binding; phosphorylated (LRp) and active (LR*) complexes; receptor internalization, recycling and degradation; G-protein-PLC-IP3 pathway leading to the release of intracellular calcium; and calcium-calcineurin pathway for NFAT4 nuclear translocation (bottom). Red circle with a line indicates degradation. Some important rate constants are shown. Model equations and parameter values are available in the Text.S2, ESI†) Simultaneous observation of intracellular calcium concentration and NFAT4 in single cells under pulsatile ligand stimulation. C) Calcium and NFAT4 dynamics for a population of cells (20 cells) under step and pulsatile ligand stimulation shows signalling amid cell-to-cell variability.

A common expectation in receptor-mediated signaling is that greater agonist stimulation will lead to greater activation of downstream signals until saturation of processes occurs. Indeed, ligand stimulation of M₃ muscarinic receptor with higher ligand concentrations leads to faster calcium oscillations and overall larger calcium release. Here, we demonstrate, however, that reduced overall ligand exposure, if delivered as pulses of ligand, can give more efficient transcription factor activation. The optimal stimulation timing is achieved when the rest period between stimulations is sufficiently long to allow receptors to recover from stimulus-triggered desensitization, while being sufficiently short that downstream signaling cascades can be actively maintained. We also show that when using pulsatile stimulation, receptor desensitization and the dynamics of downstream signaling combine to form a band-pass regime of frequencies for which the signaling is significantly enhanced as compared to a step change in ligand stimulation. Critical factors that determine this optimal stimulation frequency are the rate constants for receptor desensitization and NFAT translocation. As an example, we show that the two NFAT isoforms (NFAT4 and NFAT1) have distinguishable band-pass windows for the same receptor.

Results

Simultaneous observation of calcium and NFAT4 dynamics in single cells under step and pulsatile ligand stimulation

We measured calcium and NFAT4 responses simultaneously in single HEK293 cells for a step change or pulsatile ligand stimulation using microfluidics (Fig. S1 A, ESI†)²⁶. Oscillatory cell signaling circuits under external periodic stimulation get entrained to the stimulatory input, a phenomenon commonly described as phase locking^26,27. Using pulsatile ligand inputs with varying concentration (C), pulse duration (D) and pulse rest period (R) (Fig. S1 B, ESI†), we tested the hypothesis that different pulsing patterns will alter intracellular calcium release and the amount of NFAT4 nuclear translocation. Cytoplasmic calcium was quantified with RGECO1 sensor transiently transfected in stable M₃ receptor expressing HEK293 cells and responses were induced by the cholinergic agonist carbachol (CCh) (Fig. S2, ESI†). NFAT4 nuclear localization was quantified in the same cells by measuring the ratio of nuclear to cytoplasmic intensities of transiently transfected NFAT4-GFP (Fig. S3, ESI†). Simultaneous observation of calcium and NFAT4 dynamics under step and pulsatile stimulation was performed at the single cell level in microfluidic device that can provide time-varying ligand stimulation (Fig. 1B).

A step change in ligand stimulation leads to a concentration-dependent calcium frequency response in cells exhibiting calcium oscillations, with high cell-to-cell variability as expected²⁸ (Fig. 1C and Fig. S2, ESI†). Pulsatile stimulation results in calcium oscillations that are phase-locked at the specific frequency of ligand stimulation (Fig. 1C, bottom panel) and are more sustained than those elicited by step stimulation. For each of the cells under step or pulsatile stimulation, NFAT4 nuclear translocation was observed and quantified amidst cell-to-cell variability (Fig. 1C, right panels). Thus our experimental set-up can measure the time-resolved phase-locked calcium response and corresponding NFAT4 nuclear translocation in single cells.

Experiments and simulations show distinct GPCR-calcium-NFAT4 pathway dynamics in response to step and pulsatile ligand stimulation

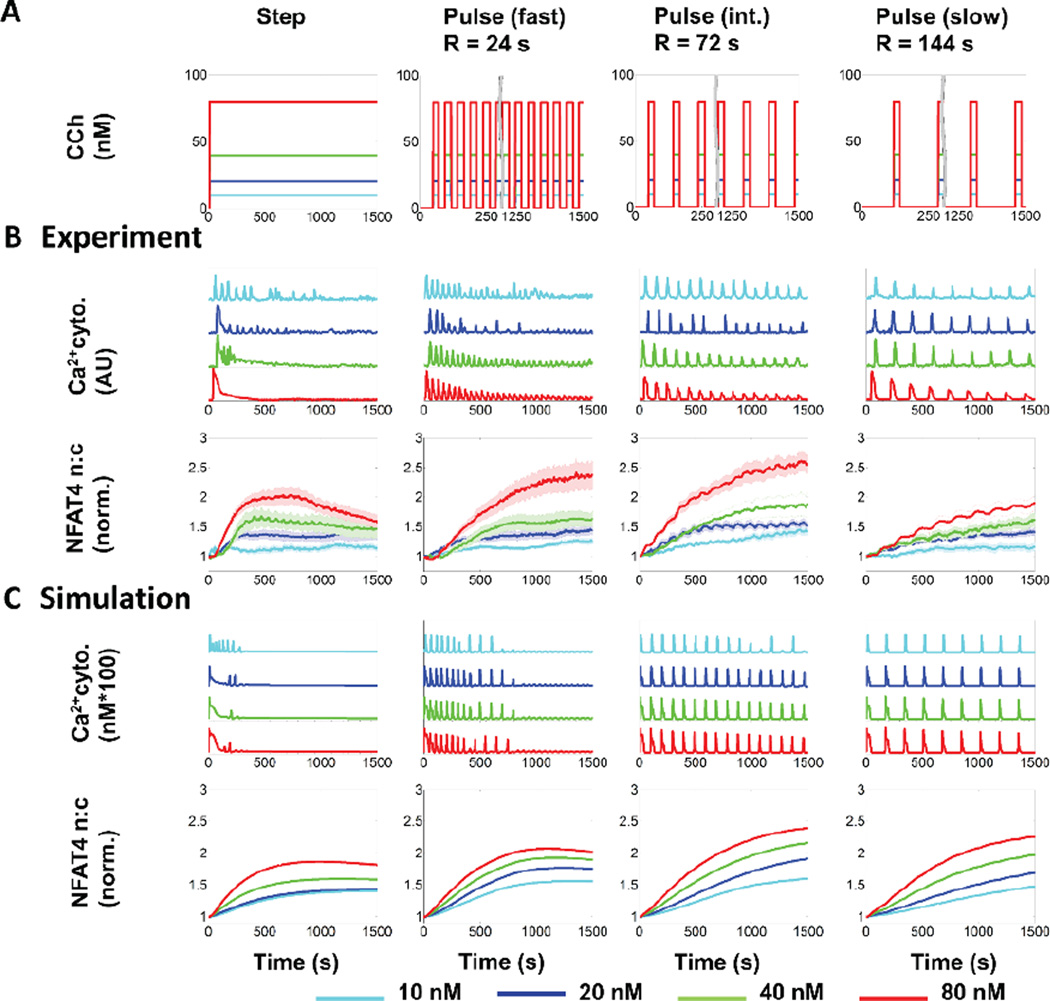
We performed a frequency response analysis of GPCR-calcium-NFAT4 signaling with varying ligand concentration (C) and rest period (R) values and developed our mathematical model to capture the characteristic features elicited by both step and pulsatile stimulation (Fig. 2). The time-dependent responses for cytoplasmic calcium and NFAT4 nuclear translocation were generated for step stimulation and for three different pulse stimulation conditions, i.e., fast (corresponding to R = 24 s), intermediate (R = 72 s) and slow (R = 144 s) (Fig 2A). Responses in this GPCR-calcium-NFAT4 pathway to step and various pulsatile stimulations were distinct (Fig. 2B). Step simulation with CCh produced strong calcium response at the outset of stimulation, resulting in either oscillations (at lower concentrations) or peak-and-plateau responses (at higher concentrations), but also resulted in rapid decay of the peak amplitude and/or frequency over time. Pulsatile stimulation produced phase-locked calcium responses as expected^26,27. However, calcium oscillations elicited by faster ligand pulses decayed rapidly over time, whereas oscillations elicited by slower ligand pulses were more sustained. The corresponding NFAT4 responses exhibited a sustained time course reaching their maxima at different time points for step and various pulse conditions. A step change in ligand concentration stimulation led to a rapid (~ 500 s) attainment of the maximum NFAT response, followed by a slow decay. In contrast, slow pulsatile ligand stimulations led to a gradual accumulation of nuclear NFAT4.

Fig. 2. Step and pulsatile dynamics of GPCR-calcium-NFAT4 pathway.

A) Step and pulsed stimulation with carbachol (CCh) performed in microfluidic experiments and simulations. The concentrations of CCh are as indicated in the colour coded key. Pulse duration (D) was 24 s. B) CCh-induced time courses of cytosolic calcium (representative single cell traces) and NFAT4 nuclear translocation (population averages) by step (left column) and pulse (fast (R=24 s), intermediate (R=72 s) and slow (R=144 s)) stimulation in HEK293 cells stably expressing M3 receptor. Population averages are mean +/− S.E.M. for n > 20 cells from 3 sets of experiments. C) CCh-induced calcium and NFAT4 nuclear translocation in the mathematical model, which captures the characteristic features of both calcium and NFAT4 translocation response.

For a quantitative and mechanistic understanding of the distinct frequency responses of calcium and NFAT4 under step and pulsatile conditions, we developed a mathematical model based on both literature data and our own microfluidic experiments. Our mathematical model is comprised of two modules – GPCR-induced calcium oscillations and calcium-induced NFAT4 nuclear translocation (Fig. 1A and Text S1, ESI†). Most calcium mathematical models exhibit continuous oscillations without decay in frequency or amplitude when subjected to step ligand stimulation, in contrast to our own experimental observations and literature data^29–31. One model that does offer an explanation for frequency and amplitude decay³² doesn’t explain the phase locking behavior we observe. Building upon Jovic et al³³, we incorporated receptor phosphorylation and receptor internalization followed by receptor recycling or degradation to reproduce our observed calcium response at various frequencies and concentrations of stimulation (Text S2, ESI†). Our mathematical model captures characteristic features of the calcium-NFAT4 signaling under step and pulsatile ligand stimulation (Fig 2C).

Slower ligand pulses lead to more sustained calcium response, but intermediate frequency pulses lead to a maximum NFAT4 response

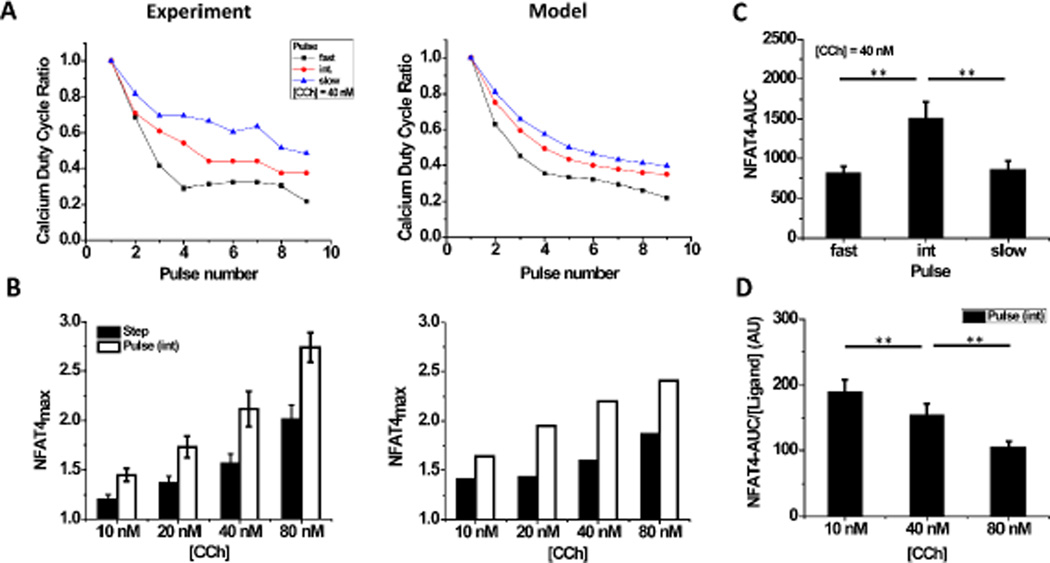
The sustained calcium oscillations and distinct NFAT4 responses that we observed under pulsatile ligand input allowed us to determine how calcium and NFAT4 dynamics depend upon the input ligand concentration and pulse frequency. We find that fast ligand pulses (R = 24 s) lead to less sustained calcium signaling as evident from a faster decay of the calcium duty cycle ratio (n), defined here as the ratio of the ‘area under the curve’ (AUC) of the nth calcium pulse to that of the first pulse. In contrast, slow ligand pulses lead to more sustained calcium signaling (higher duty cycle ratio) (Fig. 3A, Fig. S4, ESI†). Our mathematical model also captures this characteristic feature of the calcium response for all ligand concentrations and pulse frequencies tested (Fig. 3A, Fig. S4, ESI†). The measured NFAT4 responses were compared by determining the maximum of the normalized NFAT4 curve of nuclear to cytoplasmic ratio (NFAT4_max) that each cell attained under various step and pulsatile ligand stimulation conditions. Surprisingly, NFAT4_max was greater for stimulation at intermediate ligand pulse frequency (R = 72 s) than for a step change in ligand concentration for each of the ligand concentrations tested, in experiments and in the model (Fig. 3B). Further, NFAT4_max for intermediate ligand pulse frequencies was greater than for the slow or fast ligand pulse frequencies (Fig. S5 A, ESI†).

Fig. 3. Ligand pulse frequency affects calcium duty cycle and NFAT4 response.

A) The calcium duty cycle ratio (ratio of the calcium-AUC of the nth pulse to that of the first one) decreases with consecutive stimulations. The decay is greater for faster ligand pulses than for slower pulses. Duty cycle in experiments (left) was calculated from population-averaged data for each pulse condition, and the mathematical model shows similar trends (right). [CCh] = 40 nM. B) Greater NFAT4 translocation under pulsatile stimulation (R = 72 s) for all ligand concentrations in the experimental regime (left), with a similar trend predicted by the mathematical model (right). C) NFAT4-AUC was calculated from experimental data for three pulse frequencies at [CCh] = 40 nM (mean +/− S.E.M., n > 20 single cells for three different sets of experiments), and shows that maximum NFAT4 nuclear translocation occurs at an intermediate frequency. D) NFAT4-AUC per unit ligand was calculated from experimental data for intermediate frequency pulse. Ligand efficiency is greater at low ligand concentrations. Results for other pulse frequencies and the model are shown in Fig. S5. (**: P < 0.01 based on t-test for statistical data).

The non-monotonic dependence of NFAT4 translocation on ligand pulse frequency was further explored by calculating NFAT4-AUC for each cell. For a ligand concentration of 40 nM, we find that the NFAT4-AUC is maximum for intermediate rest period (R = 72 s) as compared to both a shorter and longer rest period (Fig. 3C). When the rest period is fixed and only the ligand concentration is varied, we find the NFAT4-AUC significantly increases at high concentrations (Fig. S5 B, ESI†). The common notion that calcium oscillations are frequency modulated leads to the hypothesis that at the same calcium oscillation frequency, NFAT4 output should be the same regardless of concentration of ligand used to elicit that response. Our results suggest that both the frequency of calcium oscillations and the ligand-concentration dependent calcium duty cycle play important roles in signal transduction, and hence the GPCR-calcium-NFAT4 signaling is both frequency and amplitude modulated. We also determined a “ligand efficiency”, or total NFAT4-AUC per unit ligand at intermediate ligand pulse frequency. The ligand efficiency decreases with increasing concentrations of ligand (Fig. 3D). Taken together, our experiments and model support that although slower ligand pulses lead to a high fidelity calcium response, an intermediate frequency range for ligand pulses results in maximum NFAT4 activation.

A modular combination of high-pass and low-pass filter works as a band pass filter in GPCR-Calcium-NFAT signalling

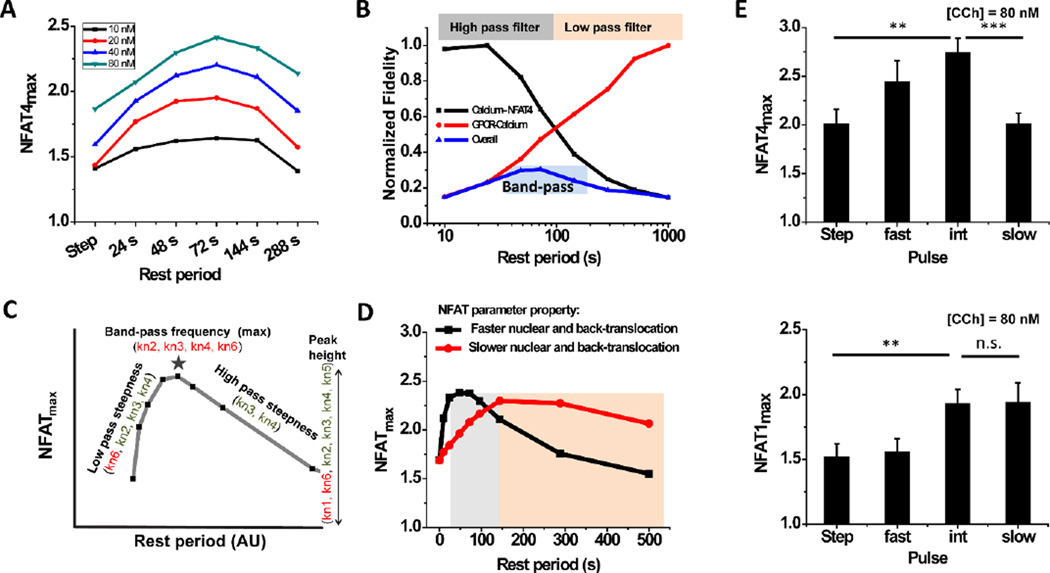
When NFAT4_max is calculated for a range of concentration (C) and rest period (R) values using the mathematical model, the greatest value is found for ligand pulses with R values in the range of ~ 50 s – 100 s (Fig. 4A). A qualitative approach to delineate this feature is to calculate the response fidelity of various signaling modules (output response versus various frequencies or rest periods tested, normalized to the maximum of the output), a method adapted from dynamic system analysis³⁴. Shutting down the receptor desensitization module (by imposing parameter values to be zero) results in sustained and non-decaying calcium oscillations, i.e., the mean calcium duty cycle ratio remains ~ 1 for all R. Under such conditions, NFAT4 localization (output) correlates with the input ligand frequencies (Fig 4B, black curve and Fig. S6, ESI†). Calcium-NFAT4 signaling thus works as a high pass filter that allows faster pulsatile stimulations to be transmitted with high fidelity. In contrast, when the receptor dynamics of desensitization, internalization and degradation are included in the mathematical model, we observe amplitude and frequency decay of calcium oscillations leading to rapid calcium duty cycle decay (output) with fast pulse stimulation (Fig. 4B, red curve). Thus, receptor dynamics act as a low-pass filter that allows low frequency ligand pulses to be transmitted to NFAT4 responses with higher fidelity. The combination of low pass (receptor dynamics) and a high pass (calcium-NFAT signaling) filters acts as a band-pass filter (Fig. 4B). The overall fidelity of GPCR-calcium-NFAT4 signaling is estimated by multiplying the impact of both low pass and high pass filters (Fig. 4B, blue curve). The signal fidelity is maximum at intermediate frequencies of ligand stimulation, as we observe for NFAT4_max in our experiments. Taken together, our experimentally-validated mathematical model demonstrates that the band-pass regime is a result of coupling of a low pass filter imposed by receptor dynamics with the high pass filter imposed by calcium-dependent NFAT4 translocation.

Fig. 4. Receptor and NFAT kinetics regulate band-pass behaviour in GPCR-calcium-NFAT signalling.

A) NFAT4max for various rest periods and ligand concentrations calculated from the mathematical model shows band-pass behaviour. B) Turning off receptor desensitization in the model leads to a high-pass calcium-NFAT4 curve (black), while turning it on adds features of rapid calcium duty cycle decay with fast pulse stimulation due to desensitization and degradation (red). Both signalling fidelity curves are normalized with respect to their maximum value. Overall curve (blue) is an empirical multiplication of the two. C) Sensitivity analysis identifies parameters that significantly affect the band-pass characteristic features. Rate constants for: activated NFAT complex formation (kn1); dissociation of NFAT_cyto from the complex (kn2); nuclear translocation of activated complex (kn3); dissociation of NFAT_nuc from the activated complex (kn4); association of NFAT_nuc and calcineurin (kn5); and back-translocation of NFAT_nuc (kn6). D) The band-pass regime shows a shift to the left or right for two different parameter sets. Parameter set 1: kn2 = 0.002 s−1; kn4 = 0.000445 s 1; kn6 = 2*10−4 s−1; Parameter set 2: kn2 = 0.02 s−1; kn4 = 0.0013 s 1; kn6 = 0.25 s−1. Other parameters kn1 = 7.7*10−6 (nM-s) −1; kn3 = 0.001 s−1; kn5 = 4.7*10−5 (nM-s) −1; C = 20 nM, D = 24 s remain same. E) Experiment demonstrating shift in optimum frequency regime for NFAT1max as compared to NFAT4max (n > 20 single cells for three different sets of experiments; **: P <0.01; ***: P <0.005; n.s.: not significant based on t-test for statistical data).

Receptor desensitization and NFAT translocation dynamics are key to the specificity of downstream signalling and specific temporal modulation

The band-pass nature of signal processing raises questions: can the peak location, height, or width of the band-pass curve be modulated? Might different receptors elicit maximal NFAT4 responses at different frequencies of ligand stimulation? To address these questions, we performed a sensitivity analysis on the mathematical model. Partial-rank correlation coefficients (PRCCs) with strong positive or negative correlations were determined for various curve characteristics such as peak-shift and height of the band-pass and steepness of the low-pass and high-pass filters (Table S1, ESI†). The phosphorylation rate constant of the receptor-ligand complex strongly correlates with peak-shift (negative, P <10⁻⁹) and also with peak-height (positive, P <10⁻⁹). The rate constant for recycling of the internalized receptor-ligand complex also contributes significantly to the peak-shift (positive, P <10⁻⁶). Among the parameters linked with calcium-NFAT signaling, the rate constants for NFAT nuclear translocation and for dissociation of the activated nuclear complex contribute significantly to the peak-shift, suggesting that the characteristics of the band-pass regime are determined by both receptor kinetics and NFAT kinetics. Thus the band-pass regime could vary with receptor identity due to different phosphorylation and recycling rate constants and also with calcium-dependent transcriptional factor identity due to different translocation and dissociation rate constants (Fig. 4C, Table S1, ESI†). For example, a rapidly translocating transcription factor will require faster ligand pulses to sustain the signal as it can move in and move out of the nucleus rapidly, while a slowly translocating transcription factor will require slower ligand pulses (Fig. 4D). As an experimental demonstration of this concept, we measured NFAT_max for another isoform of NFAT viz. NFAT1, which is known to have slower nuclear translocation and back-translocation rate constants than NFAT4³⁵. When compared (for [CCh] = 80 nM), we find that the optimum pulse frequency for NFAT1 shifts towards slower pulsatile stimulation (Fig. 4E). Taken together, our model sensitivity analysis and pulsatile experiments with NFAT4 and NFAT1 demonstrate that both receptor and NFAT dynamics play a significant role in downstream signal processing.

Discussion

A better understanding of how rhythmic processes and their appropriate timing enhances and selects for cellular functions is a fundamental problem in biology as well as a practical issue for cell culture application. Here we show that the most efficient NFAT nuclear translocation with muscarinic M₃ receptor stimulation is obtained with “just right” timing of ligand pulses – not too slow or too fast. Time-varying ligand stimulation leads to different downstream responses for different stimulation conditions via band-pass processing of the signal (Fig. 4D). GPCR-calcium-NFAT signaling forms a modular combination of low pass (GPCR signaling) and high pass (calcium-NFAT signaling) filters. Although GPCR kinetics are well-documented, only a few have explored their role as a low pass filter and how they contribute to downstream^3,5,36,37. Our work provides an experimental demonstration of how receptor down-regulation/desensitization may enhance information processing ability of the cells, consistent with the theoretical predictions made by Shankaran et al³⁷.

Infra-slow rhythms in the body which take place in the seconds to minutes time scale are an emerging area of interest for understanding physiological receptor-mediated signal processing^10,38–40. The natural analog of CCh, acetylcholine (ACh), has been observed to have sustained oscillations in the range of ~ 0.2 min – 6 min during nerve stimulation⁴¹. In addition, other neurotransmitters like glutamate and dopamine have been shown to have sustained oscillatory release^42,43. Our work provides an experimental demonstration of how such periodic inputs might have an optimum frequency range for maximized target cell responsiveness, consistent with the theoretical predictions made by Li and Goldbeter⁴⁴. An understanding of how such biological rhythms affect cellular signal processing may facilitate the design of interventions to rationally modulate signaling and may also enable design and use of signaling modules in synthetic biology applications. Most studies focus on either longer or shorter timescales⁹. Our work may motivate investigation into biorhythms at such intermediate timescales.

Our work shows that variations in receptor kinetics (i.e., desensitization, internalization, degradation and recycling) are capable of generating different features for the low-pass filter and thereby affecting the band-pass regime. According to the recent ‘barcode hypothesis’, differences in phosphorylation and arrestin binding may encode for different desensitization, internalization, and recycling kinetics^45,46; different receptors may also have different kinetics. The band-pass concept can be extended to non-GPCR receptors that mediate calcium-dependent transcription factor activation. The low pass filter formed by the receptor motif can determine whether slow ligand pulses would be most efficient (for rapidly down-regulated receptors) or whether fast pulses or a step change of ligand is most efficient (for slowly down-regulated receptors). Thus, T-cell receptors, which are slowly internalized and rapidly recycled⁴⁷, may not require ligand pulses for efficient signaling; a step change in ligand concentration could be sufficient. In contrast, pulsed stimulation can be more efficient than step changes for GPCRs. The band-pass concept might further be applied other second messenger systems, such as cyclic AMP, which undergoes oscillations via GPCR-Gs signaling and activates PKA that leads to phosphorylation of several downstream transcription factors¹⁵. Overall, pulsatile microfluidic analyses add temporal dimensions in the observability space that, when coupled with computational modeling, can delineate the underlying band-pass characteristics of such network motifs. These band-pass characteristics determine ligand pulse frequencies for efficient downstream signaling, and can potentially select for particular downstream responses as well.

Conclusions

Temporal signal processing in receptor mediated pathways is increasingly appreciated as a tool that cells utilize to achieve enhanced activity and selectivity, and to distinguish signal from noise. Despite a few experimental evidences of such signal processing, proper mechanistic understanding based on the underlying kinetics remains largely unknown. To this end, using a microfluidic delivery system with real-time assessment of both cellular calcium levels and nuclear translocation of the Ca²⁺-regulated transcription factors NFAT1 and 4, we are able to evaluate these processes systematically. We obtain counterintuitive results, wherein an intermediate pulsing rate (less overall stimulation) elicits a larger response than is obtained by continuous exposure or frequent pulsing (which both provide greater overall ligand exposure). Furthermore, different stimulation frequencies favour activation of the two different transcription factor isoforms. Operationally, the frequency-dependence of the responses is consistent with the concept of band pass filter. Based on computational modelling of the experimental data, the band pass processing is expected to be a general theme that applies to multiple signalling pathways.

Experimental

Materials

High glucose Dulbecco’s Modified Eagle’s Medium (DMEM) with phenol red, 0.05% Trypsin, 10× HBSS (with Ca²⁺, Mg²⁺), HEPES buffer (1 M), Geneticin and OPTIMEM were obtained from Gibco (life technologies, Grand Island, NY), Fetal Bovine Serum (FBS) was obtained from Gemini Bioproduct (West Sacramento, CA), Lipofectamine 3000 was obtained from Invitrogen (life technologies, Carlsbad, CA), D-Glucose 10% (w/v) from Sigma (St. Louis, MO), Carbachol from Calbiochem (EMD Biosciences, La Jolla, CA), PDMS and curing agent from Dow Corning (Midland, MI). Imaging media (1× HHBSS, pH 7.4) was prepared as described in⁴⁸. CMV-R-GECO1 was a gift from Robert Campbell (Addgene plasmid # 32444)⁴⁹. HA-NFAT4-GFP and HA-NFAT1-GFP were a gift from Anjana Rao (Addgene plasmid # 21664)⁵⁰.

Methods

Cell culture

HEK293 cells stably transfected with human muscarinic acetylcholine M₃ receptor described previously²⁶ were cultured in DMEM with 10% FBS and Geneticin (400 µg ml⁻¹) in T-25 flasks. Transient transfection with R-GECO1 and NFAT4-GFP or NFAT1-GFP was carried out using Lipofectamine 3000 following prescribed protocol.

Microfluidic device

The devices were fabricated based on the computerized microfluidic cell culture system using Braille display as described in²⁵. The chips were filled with laminin (100 µg/ml) and incubated overnight. Subsequently, the chips were washed and incubated with DMEM/10% FBS under sterilized conditions. Cells were seeded in the outlet channel of the device as described in^26,27. The microfluidic setup was used to deliver periodic and step stimulation of carbachol controlled by a custom written software as described in²⁵.

Time lapse imaging and analysis

Cells were imaged with a TE-2000 U Nikon microscope using a 20× Flour objective illuminated by a 100W Hg lamp. Sequential acquisition of R-GECO1 and NFAT-GFP fluorescence was carried out every 5 s using ET572/35 (ex), ET630/50 (em), ET490/20 (ex) and ET535/50 (em) filters respectively (Chroma Technology Corp, Rockingham, VT). The excitation and emission filters were equipped in filter wheels controlled by a Lambda 10−3 Shutter Controller (Sutter Instruments, Novato, CA). MetaFluor Software (Molecular Devices, Downington, PA) was used to select regions of interest (ROIs) in single cells and to determine the area-averaged intensity I(t) both in cytoplasmic region (I(t)_cyto) and in the nuclear region (I(t)_nuc). Calcium response was measured by the ratio I(t)_cyto/I₀ where I₀ corresponds to the basal RGECO1 intensity in the cytoplasmic ROI (Fig. S2, ESI†). NFAT translocation was quantified by determining I(t)_nuc/I(t)_cyto ratio from the GFP fluorescence data (Fig. S3, ESI†).

Mathematical model development and computational analysis

We developed a mathematical model that links step or pulsatile ligand stimulation, receptor/ligand binding, calcium signaling, and NFAT translocation illustrated in Fig. 1A. The model description, reactions and parameter table are provided in Text S2 (ESI†). A system of ordinary differential equations (ODEs) was generated for the model and solved in MATLAB (MathWorks Incorp) with the ode15s stiff solver.

Characterization of Ca²⁺ signaling and NFAT4 translocation

Intracellular calcium responses were characterized in terms of the varying ligand pulse parameters (Concentration (C) and Rest periods (R)). The ligand pulse duration (D) for which each pulse translates into a single calcium spike, i.e. without resulting in either no response at all or in multiple peaks, lies in the range ~ 16 s to ~ 32 s²⁶. D was kept constant at 24 s in this study. We quantify the oscillation decay by defining calcium duty cycle ratio, which is the AUC of each calcium spike relative to the first spike and is thus an indicator of how the calcium response decays over time upon various pulsatile conditions.

$$\mathit{\text{Calcium Duty Cycle Ratio}}(\mathit{C}\mathit{D}\mathit{R}(\mathit{n}))=\frac{\mathit{\text{Calcium}}-\mathit{A}\mathit{U}\mathit{C}\mathit{\text{of}}\mathit{n}\mathit{t}\mathit{h}\mathit{\text{pulse}}}{\mathit{\text{Calcium}}-\mathit{A}\mathit{U}\mathit{C}\mathit{\text{of the first pulse}}}$$

Extent of NFAT nuclear translocation was characterized using a standard procedure described in literature³⁵ by determining the maximum of NFAT nuc/cyto ratio (NFAT_max) attained under a pulsatile condition. MATLAB codes were written to determine the values of CDR(n) and NFAT_max for both experimental and in silico data. AUC values for the time-course was determined for single cell traces by integrating the NFAT nuc/cyto ratio over time as follows:

$$\mathit{N}\mathit{F}\mathit{A}\mathit{T}-\mathit{A}\mathit{U}\mathit{C}={\int }_{\mathit{t}=\mathbf{0}\mathit{s}}^{\mathit{t}=\mathit{t}\mathit{\text{max}}\mathit{s}}\mathit{N}\mathit{F}\mathit{A}{\mathit{T}}_{\mathit{\text{curve}}}\mathit{d}\mathit{t}$$

where tmax is the time when NFAT nuc/cyto attains its maximum. Nuclear export of NFAT (back-translocation) follows a first order decay kinetics, consistent with other studies^20,35. Therefore, total NFAT-AUC is approximately proportional to the AUC calculated up to tmax. Time integrals were determined for the data sets using trapezoidal function in MATLAB. Statistical tests for determining the significance of the experimental data was performed with t-test for comparison of NFAT_max for different pulse conditions.

Sensitivity analysis of the model

We used Latin Hypercube Sampling (LHS) and Partial-Ranked Correlation Coefficients (PRCC) to explore the mathematical model parameter space and identify those parameters which significantly contribute to the particular characteristics of the temporal signal processing in GPCR-calcium-NFAT signaling. MATLAB code for LHS-PRCC analysis was taken from Marino et al⁵¹. Parameters related to GPCR-ligand binding kinetics and calcium-NFAT kinetics were varied over two logs by sampling from a uniform distribution using LHS. PRCC along with significance value was determined for each parameter against particular curve characteristics (Table S1, ESI†).