Demonstration of Nonlinearity Bias in the Measurement of the Apparent Diffusion Coefficient in Multicenter Trials

Abstract

Purpose

Characterize system-specific bias across common magnetic resonance imaging (MRI) platforms for quantitative diffusion measurements in multicenter trials.

Methods

Diffusion weighted imaging (DWI) was performed on an ice-water phantom along the superior-inferior (SI) and right-left (RL) orientations spanning ±150 mm. The same scanning protocol was implemented on 14 MRI systems at seven imaging centers. The bias was estimated as a deviation of measured from known apparent diffusion coefficient (ADC) along individual DWI directions. The relative contributions of gradient nonlinearity, shim errors, imaging gradients and eddy currents were assessed independently. The observed bias errors were compared to numerical models.

Results

The measured systematic ADC errors scaled quadratically with offset from isocenter, and ranged between −55% (SI) and 25% (RL). Nonlinearity bias was dependent on system design and diffusion gradient direction. Consistent with numerical models, minor ADC errors (±5%) due to shim, imaging and eddy currents were mitigated by double echo DWI and image co-registration of individual gradient directions.

Conclusion

The analysis confirms gradient nonlinearity as a major source of spatial DW bias and variability in off-center ADC measurements across MRI platforms, with minor contributions from shim, imaging gradients and eddy currents. The developed protocol enables empiric description of systematic bias in multicenter quantitative DWI studies.

Introduction

Diffusion weighted imaging (DWI) is an inherently quantitative magnetic resonance imaging (MRI) technique widely utilized in clinical applications and for research evaluating efficacy of tumor treatment (1–4). The most common summary measure of quantitative DWI is the apparent diffusion coefficient (ADC) that reports on the mean diffusivity of water which is modulated by the cellularity of the imaged tissue (5,6). The ADC is derived from two or more DWI measurements assuming mono-exponential signal decay with increasing diffusion weighting, b-value. The clinical utility of ADC as a radiological marker for tissue response to treatment (2,4,7) and/or lesion characterization (8–11) is being assessed through multicenter oncology trials (12–14). For such studies it is imperative that the sources of technical variability are characterized (and controlled) (15–17) so that measured changes due to biology are interpretable relative to systematic error (18–20). Eliminating bias in ADC measurements can reduce requisite subject numbers (and associated trial costs), and help avoid inconclusive findings from underpowered studies (18–20).

Previous multi-scanner quality control studies have demonstrated excellent reproducibility of ADC measurements acquired at magnet isocenter (21,22) using a temperature-controlled (ice-water) phantom (variability < 3%). Away from the isocenter, large ADC errors (> 20%) due to gradient nonlinearity (GNL) bias were detected on some clinical systems (21–23). Although both systematic bias and random errors are known to contribute to measurement variability (15,24,25), the detected platform-specific spatial bias in diffusion weighting (i.e., deviation from the specified b-value) (26,27) can exceed random measurement noise many-fold (21–23), thereby confounding ADC values obtained by different scanner platforms in multicenter studies (14,20,28). Characterization and removal of the detected spatial DW bias is a prerequisite for establishing confidence levels of the derived ADC metric in clinical oncology applications (12,14).

Systematic deviations from nominal diffusion weighting (26,27) are not routinely corrected on clinical MRI systems, even though platform-dependent gradient characteristics are utilized by vendor engineers to spatially (un)warp images so that distance and geometry are faithfully represented (29,30). Evaluation of emerging DW bias correction methods developed by the research community (23,26,27,31) requires a uniform protocol for independent characterization of systematic errors across the relevant clinical MRI platforms. Additionally, the relative contributions to the actual (incorrect) diffusion-weighting by multiple sources (including GNL (26), imaging gradients (32), imperfect shim, concomitant fields (33), and eddy currents (34)) need to be assessed to develop and implement efficient platform-specific correction strategies. For quantitative assessment of these contributions, a comprehensive model for b-value bias combining multiple sources of gradient imperfection is required.

Conventional approaches for quantitative 3D characterization of individual gradient systems often rely on a set of platform-specific (and application-specific) phantoms and tedious procedures (29,35) that are not suited for uniform multicenter cross-platform implementation. In contrast, the diffusion phantom approach is well adapted for the multi-platform setting typical of clinical oncology trials (21,22). The equivalence of GNL characteristics obtained via ADC bias measurement on an ice-water phantom (31) to those measured using a geometric distortion phantom (29) or predicted by spherical harmonics model based on gradient design (26,27) has been demonstrated for select systems (21,23,31). This approach enables direct quantitative investigation of systematic GNL bias impact on inter-platform ADC variability for multicenter trials. Furthermore, the diffusion phantom method allows for comprehensive empiric evaluation of both GNL and non-GNL sources of b-value bias for direct comparison with numerical models.

The characterization of platform-dependent bias in diffusion weighting leading to systematic ADC errors that deteriorate inter-system reproducibility was addressed in this study by the Data Acquisition Working Group of the NCI-sponsored Quantitative Imaging Network (QIN) (13,36), established to improve the role of quantitative imaging for oncology trails. This Working Group developed a uniform diffusion phantom test protocol for data acquisition and analysis to objectively characterize the systematic DW bias across diverse and commonly used clinical MRI platforms. The proposed empirical procedure was implemented on representative scanners from three major vendors at seven QIN member institutions. Empirical measurements were corroborated by numerical models of b-value bias. Results of the analysis and their implications for multisite clinical trials utilizing quantitative diffusion imaging are described in this manuscript.

Methods

A single phantom with support stage (Supporting Material: Figures S1–S5) and scan instructions was shipped to seven QIN centers, where it was prepared and scanned onsite. The resulting DWI data acquired on 14 MRI scanners were uploaded for analysis by a single center. All data were in Digital Image Communication in Medicine (DICOM) format (37) and data analysis was automated using routines developed in Matlab 7 (Mathworks, Natick MA).

(1) Diffusion Phantom and DWI acquisition

The ice-water phantom consisted of a 260 mm long, thin-walled, capped polyethylene tube (diameter: 29 mm) filled with distilled water (0.17L) and immersed in another container filled with an ice-water bath (3.8L Nalgene jar, Sup. Mat.: Fig. S1). The ~20-fold larger volume of ice-water bath facilitated rapid thermal equilibration of the inner tube, and sustained temperature over the full scanning session on a given system (21). Maintaining the phantom at a controlled temperature of (0.0±0.5)°C provided the universal ADC standard with a known (published) diffusion coefficient of (1.100±0.011)×10⁻³ mm²/s (38). A plastic stage was built to control phantom anterior-posterior (AP) elevation in the magnet bore (Sup. Mat.: Figures S3, S4). The phantom was scanned using head first, supine positioning. Initial AP elevation of the measurement tube was assessed on the first locator series, acquired with no superior-inferior (SI) and right-left (RL) offsets from isocenter (Sup. Mat.: Schema I). The vertical height of the phantom stage was then adjusted to set the AP location of the center of the measurement tube to within ±10 mm of AP = 0 for all subsequent series. Extended off-center measurements were performed by repositioning the phantom on the stage to +70 mm, 0mm and −70mm offsets for both RL and SI phantom orientations (Sup. Figs. S3,S5). Extended AP offset measurements were not performed due to redundancy with RL orientations expected from cylindrical symmetry of the studied horizontal-bore gradient systems (26,29,31). Axial (AX) multislice DWI scans with nominal b = 0, 750 and 1500 s/mm² were acquired for all phantom positions. Additional sagittal (SAG) acquisitions were performed on several systems when the phantom was oriented in the RL direction (Table 1). To characterize individual gradient channels (here defined as, G_X – RL gradient, G_Y – AP gradient, and G_Z – SI gradient), the phantom was scanned using diffusion gradients applied along the primary magnet axes (X, Y, Z). The recommended key scanning parameters are listed in Supporting Table S1 (Sup. Mat.).

Table 1.

Details of scanning systems used in the study

Log#	Vendor	Model	Field	L/d (m/m)	Seq.Var.	RLb	SIb	AP(at RL= 0/120mm)c	TE (ms) RL/SI
1	Philips	Ingenia	3T	1.64/0.7	SSE	AX,SAG	AX	5/5	115
2	Siemens	Verio	3T	1.73/0.7	DSE	AX,SAG	AX	−2/−20	134
3	GEa	HDxt-W	1.5T	1.72/0.6	SSE	AX,SAG	AX	35/37	110
4	GEa	HDxt-Z	1.5T	1.72/0.6	SSE	AX,SAG	AX	7/3	75
5	Siemens	Trio	3T	2.13/0.6	DSE	AX,SAG	AX	−5/−25	156
6	Siemens	Trio	3T	2.13/0.6	DSE	AX	AX(p5,6)d	−5/−30	103
7	Siemens	Espree	1.5T	1.25/0.7	DSE	AX,SAG	AX	−5/−20	135
8	Philips	Achieva	3T	1.6/0.6	SSE	AX	AX(p6)d	15/12	130
9	GE	Explorer	3T	1.7/0.6	SSE	AX	AX	13/5	99
10	Philips	Ingenia	3T	1.64/0.7	SSE	AX	AX	10/10	116/125
11	GE	Excite	1.5T	1.72/0.6	S/DSE	AX,SAG	AX	10/5	96/110
12	Siemens	Skyra	3T	1.73/0.7	SSE	AX	AX	−15/−30	158
13	Siemens	Espree	1.5T	1.25/0.7	DSE	AX	AX	−35/−57	169
14	Siemens	Skyra	3T	1.73/0.7	DSE	AX	AX	−15/−33	175/161

“SSE”: single spin-echo; “DSE”: double spin-echo; “AX”: axial; “SAG”: sagittal; “L/d”: gantry bore length (m) / bore diameter (m)

^asame system with two gradient settings (labeled “W”hole and “Z”oom).

^bimage acquisition plane (AX/SAG) for specific phantom alignment direction in the magnet (RL/SI);

^capparent AP elevation of the phantom at RL offset 0 mm and 120 mm;

^dmissing phantom SI-scans (“positions”, see Sup. Mat., Table S1);

DWI data were acquired on 14 MRI scanners (ten different models) from three major vendors (Siemens (Erlangen, Germany), Philips (Best, Netherlands), GE (Waukesha, WI)) at two fields (five 1.5T and nine 3.0T systems). The system information and scanning parameters (derived from DWI DICOM header) are summarized in Table 1. Half of the systems had a bore diameter of 0.7 m and the other half – 0.6 m. Bore length varied over a broader range from 1.25m to 2.13m, with the majority of systems (10) falling between 1.55m and 1.75m. A GE Signa HDxt scanner that provided two gradient settings (labeled “W”hole and “Z”oom) is listed as two separate systems (#3 and #4 in Table 1). Four system models (out of ten different platforms) were duplicated by different sites. Seven systems provided AX and SAG scans for the RL phantom orientation. Four systems exceeded recommended TE (≤130ms, Sup. Table S1), while all systems used the recommended TR ≥10s. The applied spin echo sequence variant (single spin-echo (SSE) versus double spin-echo (DSE), Table 1) was confirmed by individual sites with their vendor application scientists. Seven systems used SSE, six systems confirmed DSE, and one system (#11) ran both sequence variants. Additionally, SSE versus DSE was run on a scanner of the same model (#12 and #15) by two different sites, respectively. Two systems did not perform select SI offset measurements (“positions”, Sup. Mat., Fig. S5), and one system (not listed in Table 1) did not provide images for each individual diffusion direction, and thus were excluded from corresponding direction or offset specific analysis.

(2) ADC analysis

Centralized data analysis was performed by a single site to derive the ADC from native DWI images using a mono-exponential fit between pairs of acquired b = 0 and b > 0 s/mm² values. The ADC was calculated for the three separate DWI directions to characterize each individual gradient channel. The applied diffusion gradient direction in magnet coordinates was derived from the DICOM header (to assign to specific gradient channel). Only one vendor utilized “public” DICOM tags (37) for DW direction [0018, 9089] and b-value [0018, 9087] conditions. Diffusion direction and b-value information for the other two vendors had to be extracted from “private” DICOM tags, with one vendor using special tags for X, Y, Z (versus oblique) DWI gradients, as described in the corresponding DICOM conformance statement. The information on DWI image post-processing (e.g., spatial filtering) was not available from the DICOM header, but was confirmed by individual sites to exclude optional filtering (as required by the study protocol, Sup. Mat.).

To correct for channel-specific b > 0 s/mm² image distortion induced by eddy currents (34), two-dimensional full-affine co-registration to the b = 0 s/mm² image was performed for DWI data that exhibited substantially different (in excess of 5 mm) phantom tube displacements and/or misshaping for different gradient channels (DWI directions). For systems with significant initial distortions, the co-registration efficiency was assessed by visual inspection of consistent phantom tube position and shape for all DWI directions of each given image slice prior to ADC map generation. Co-registration of major distortions improved resulting ADC map uniformity (reduced histogram width) for systems with high eddy current distortions on select gradient channels.

ADC was calculated on a pixel-by-pixel basis, and the mean value was measured from 10mm-diameter circular ROIs (~90 pixels) manually placed in the middle of the ice-water tube on the b=0 image, avoiding areas with susceptibility artifacts (e.g., near air bubble or near edges) and non-uniform signal (e.g., severe geometric distortions). Typically, 20–30 offsets (ROIs) were defined for each phantom position to cover a spatial extent of ±150 mm with a total of approximately 50 non-overlapping ADC measurements along the SI and RL orientations for individual gradient channels. Measurement uncertainty was estimated as 2×SD (95% confidence level (18)) of the ADC pixel noise within an ROI. Uncertainty analysis across systems provided a baseline sensitivity threshold for detection of systematic bias.

(3) Systematic bias evaluation

For all measured offsets, the fractional bias error for ADC was estimated as a normalized deviation from the published (“pub”) value of 1.1 × 10⁻³ mm²/s (38), using the equation (ADC-ADC_pub)/ADC_pub. For the mono-exponential phantom medium (ice-water), the measured fractional ADC bias was equivalent to bias in b-value (i.e., DW bias). Bias statistics across systems were characterized by mean, standard deviation (SD), median and ranges. ADC bias dependence on offset, x, was fit to a 4^th order polynomial in Matlab: c₀+c₁x+c₂x²+c₃x³+c₃x⁴. For a majority of the studied platforms, a 2^nd order fit was indistinguishable from a 4^th order for ADC bias along SI. However, at remote RL offsets, ADC measurements for five systems exhibited higher order features, therefore, a 4^th order fit was used for all systems for consistent analysis. The goodness of fit was characterized by the norm of residuals (NR). For uniform comparison of relative bias curvature, asymmetry and offset contributions, the fit coefficients were scaled (to common ADC units of 10⁻³ mm²/s) by: 10⁻³ (mm) for c₁ (original units of mm/s), and 10⁻⁶ (mm²) for c₂ (original units of 1/s). A representative offset of ±120 mm from isocenter was chosen to estimate bias magnitude across systems to ensure (by inspection) that bias for all systems exceeded their corresponding ROI noise at least two-fold both for RL and SI orientations.

The relative gradient nonlinearity (GNL) bias contribution was assessed from c₂, and its magnitude (for cross-platform analysis), using the average fractional bias measured at ±120 mm for the available data from 14 systems with RL and 13 systems with SI measurements, Table 1. GNL AP characteristics were implicitly inferred from the cylindrical symmetry of gradient channels (26,29,31) for the studied horizontal-bore systems: G_X(AP) = G_Y(RL), G_Y(AP) = G_X(RL), G_Z(AP) = G_Z(RL). The similarity of GNL designs for the four duplicate system models (Table 1) was quantified by mean distance between measured average fractional bias of corresponding channels and orientations: $\frac{1}{6}{\sum }_i^{(\mathit{XYZ})(\mathit{RL},\mathit{SI})}\sqrt{{(GN{L}_i^{\mathit{sysA}}-{\mathit{GNL}}_i^{\mathit{sysB}})}^2}$. The relative bias asymmetry was estimated from c₁, and its magnitude, by the mean difference between measured fractional biases at ±120 mm provided for 14 systems (RL) and 12 systems (SI), Table 1. The c₀-coefficient was used to evaluate mean ADC shift (from the known ice-water value) close to the isocenter. The Pearson correlation coefficient, R, across systems was used to find the dependent variables among measured/fit quantities and acquisition parameters. The assignment of dominant physical bias sources was performed on the basis of the highest correlation with the measured bias characteristics (nonlinearity, asymmetry and shift). Third and fourth order fit coefficients, c₃ and c₄, were not correlated to physically meaningful parameters, and corresponding analysis was omitted. For a qualitative description of observed bias trends, numerical models for DW-bias (i.e., non-uniformity of the b-value) were built for SSE and DSE sequence variants using established theory (Appendix) to include GNL (30) as well as the second-order gradient imperfections (32–34). Note that these models for b-value bias are distinct from geometric distortions (not analyzed here) of DW images by the same sources.

The magnitudes of the second-order gradient imperfections were assessed from independent empiric measurements. Imperfect shim (causing background gradients, G_BG) was evaluated from the apparent (measured) versus actual (isocenter) region-of-interest (ROI) elevation (AP) as a function of (and normalized by) the offset (Table 1). ROI location accuracy was 2–3 mm (approximately 1–2 pixels). Cross-terms between the diffusion gradients, G_DW, and the imaging gradients, G_IM, were measured from the difference in ADC bias near isocenter for the DWI gradient along the slice direction with respect to other DWI directions. Eddy current contribution was analyzed by comparison of ROI noise (histogram width) from ADC maps generated for individual DW gradient directions with and without the b > 0 s/mm² images co-registered to the b = 0 s/mm² image. A proof-of-concept, empiric GNL bias correction was performed as described in (31). Channel-specific SI and RL nonlinearity “scalars” for diagonal elements of system nonlinearity tensor, L_ii, were measured directly from ADC/ADC_pub~5% (31). Trace-ADC correctors for the isotropic DWI phantom were approximated by the channel-average GNL as a function of the offset, $C_{\mathit{av}}(x)=\frac{1}{3}{\sum }_i^{\mathit{XYZ}}{L}_{\mathit{ii}}^2(x)$. Ten individual GNL correctors were built for the non-duplicate system models (Table 1). Same corrector was used for the duplicate models. The numeric correctors were applied to remove the measured offset-dependent b-value bias as, ADC_c=ADC(x)/C_av(x).

Results

Offset-dependent ADC measurements for the ice-water phantom along RL and SI orientations, performed for the individual gradient channels (G_X, G_Y, G_Z) and the trace DWI of all systems, provided independent estimates of the ROI noise, the mean ADC value at isocenter (constant fit coefficient, c₀), the dependence of ADC asymmetry on offset direction (linear fit coefficient, c₁), and the ADC bias curvature (quadratic fit coefficient, c₂). Typical ADC measurements are illustrated for a representative system in Figure 1a. Nearly quadratic offset dependence is observed for all gradient channels, with positive deviations from known ADC value away from isocenter along RL, and negative deviations along SI, qualitatively consistent with GNL. Direction average (trace ADC) fit dependence on the offset is illustrated by the solid black curves. Since typical ADC measurements are performed by combining three orthogonal DWI directions, the deviation of trace ADC from the known value for ice-water directly quantifies the bias error of a given system. Deviation from symmetry at positive versus negative offsets from the isocenter is detected for the specific gradient directions (e.g., G_X (blue) along SI, Fig.1a), reflecting the contribution of non-GNL bias sources. For offsets less than ±40mm from the isocenter, the mean measured ADC values for all gradient directions of this system are within ROI measurement uncertainty (±2%, error-bars) from the known ADC of ice-water (solid horizontal line).

Figure 1.

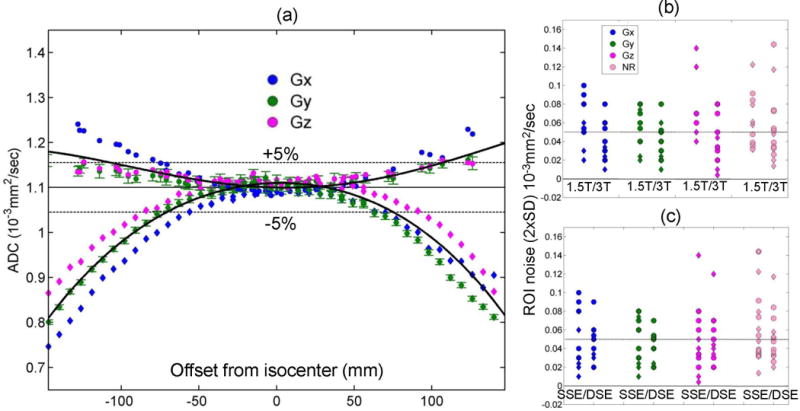
(a) The measured ADC of water at 0°C is plotted for the individual diffusion gradient channels (G_X: blue, G_Y: green, G_Z: magenta) of one representative MRI scanner as a function of the offset from isocenter along the RL (circles) and the SI (rhombi) phantom orientation; the average (trace) ADC for the three channels is also shown (solid black curves). The known (unbiased) ice-water ADC value (solid line) ±5% deviation (dashed lines) is shown for reference. Error bars (illustrated only for G_Y (green) channel for clarity) represent one standard deviation (SD) of measurement noise within each ROI. The 2×SD noise averaged over all offsets is shown on the same scale as the norm of residuals (NR, pink symbols) of the trace-ADC fit for both acquisition orientations (RL: circles, SI: rhombi) of each gradient channel (legend) versus field strength (b) and sequence variant (c). Dotted horizontal lines in (b) and (c) mark mean ADC noise level across systems.

To establish the level of significance for different contributors to ADC bias with respect to ROI noise, the measurement error statistics was analyzed for all studied systems. The analysis of the ROI noise (2×SD measurement uncertainties) averaged over all offsets is shown in Figs.1b,c for individual gradient directions along with the norm of residuals (NR) for the trace (channel-average) ADC fit. The trace-ADC uncertainties (not shown) are reduced by averaging of three channel-specific measurements $(\sim 1/\sqrt{3})$, and thus would always be below the noise level of the individual channels (Fig.1b,c). As is evident from Fig.1b,c, NR provides a more conservative error envelope for the direction-dependent ROI noise. The observed measurement uncertainty was relatively independent of the sequence variant and b-value. The RL measurement errors were negatively correlated to TE and field strength (R = −0.54, −0.64; P = 0.036, 0.01, respectively), and positively correlated (R = 0.55, P = 0.034) to NR for the fit. Three outliers (ROI noise > 0.1 × 10⁻³ mm²/s) were observed for G_Z -channels of the systems with higher eddy current contribution or with large areas where ice had melted (thermal equilibrium was not assured).

The significant channel-specific DWI distortions due to eddy currents (Methods) were observed to correlate both with broader ROI histograms and the jitter in the mean ADC measurements for adjacent ROIs at some offsets (e.g., Fig.1a, G_X (SI >100mm)), leading to an increase in apparent NR. Co-registration to the b = 0 s/mm² image for systems with high eddy current contribution (Methods) effectively reduced ROI noise (pixel histogram width) by half and alleviated mean jitter between the adjacent ROIs. The observed average ROI noise (Fig.1b,c) was higher at 1.5T than at 3.0T and along RL versus SI (0.06 versus 0.04) × 10⁻³ mm²/s, and was tighter for the DSE compared to the SSE sequence variant (SD: 0.02 versus 0.03) × 10⁻³ mm²/s. Suppression of eddy-current artifacts in DWI images by DSE acquisition was further confirmed empirically for the system that ran both SSE and DSE variants (Table 1). Average noise for individual gradient channels fell within trace-fit NR (Figs.1b,c, last column), indicating that the main source of fit error was measurement uncertainty. Mean ROI noise across systems was 0.05 (±0.03) × 10⁻³ mm²/s (dotted line in Figs.1b,c).

Figure 2 illustrates two physical sources of the mean ADC bias (deviation from ice-water value) at the isocenter (zero offset): (i) phantom AP-elevation (Figs.2a,b) and (ii) imaging gradients on the slice-select channel (Figs.2c,d). For all systems, the detected AP ROI elevation near isocenter ranged between (−35 and +35) ±3 mm (median of 5 mm) (Table 1). Physical AP elevation of the phantom correlated with the concerted shift of ADC curves for multiple gradient channels (e.g., G_X and G_Y, Fig.2a,b). The relative shift of an ADC curve for the slice-select channel with respect to the other gradient directions (Fig.2c,d), observed for SAG versus AX acquisition (Table 1), supplied direct empirical measurement of imaging gradient contribution to ADC bias (e.g., +2% shift between G_X and G_Z curves in Fig.2c,d). For all systems that performed SAG versus AX scans for RL phantom orientation (Table 1), this measurement confirmed that imaging gradients contributed a small (< 3%) error for the diffusion gradient along slice direction. Note that the combined (minor) bias contribution from phantom positioning error and imaging gradients fell within mean ROI noise (5%, Fig.1b,c) across the studied scanner systems at isocenter.

Figure 2.

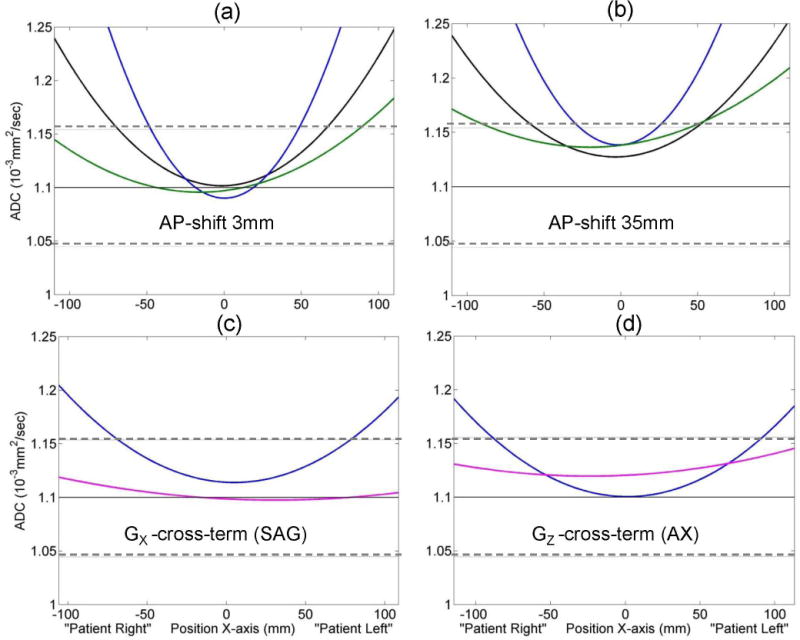
Vertical offset in measured ADC value is illustrated for individual system gradient channels (G_X: blue, G_Y: green) and the trace (black) due to phantom positioning error (AP-elevation) in (a) versus (b), and due to cross-terms between diffusion and imaging gradients on slice-select channel (G_X: blue, G_Z: magenta) for sagittal (c) versus axial (d) scans. Solid horizontal lines mark the unbiased (known) ice-water ADC value. Dashed horizontal lines mark ±5% deviation. Head first, supine positioning was used for “Patient RL” direction assignment.

Figures 3a,b summarize the offset-dependent bias (as fractional deviation from published value) for the trace-ADC fit of all studied systems (Table 1: 14 for RL orientation, and 13 for SI) when using the b = 1500 s/mm². (No significant differences were observed for fits that used the b = 750 s/mm²; the data is not shown.) Note that the change of presentation scale (for this and following figures) to fractional bias units makes interpretation of the observed systematic ADC errors equivalent to the DW bias in b-value (Methods). The detected bias for all scanners exceeded ROI measurement error (Fig.1b,c) for offsets from isocenter greater than 40 mm. For individual systems, the largest (negative) bias (up to −55%) was observed along SI (Fig.3b), with RL showing comparatively less bias (up to +25%, Fig.3a). At the 120 mm offset, mean SI bias across systems was −20% (±20%, 2×SD), while RL was +7% (±15%, 2×SD), indicating relatively high variability (2×SD exceeding the mean bias) among systems for the measurements away from isocenter.

Figure 3.

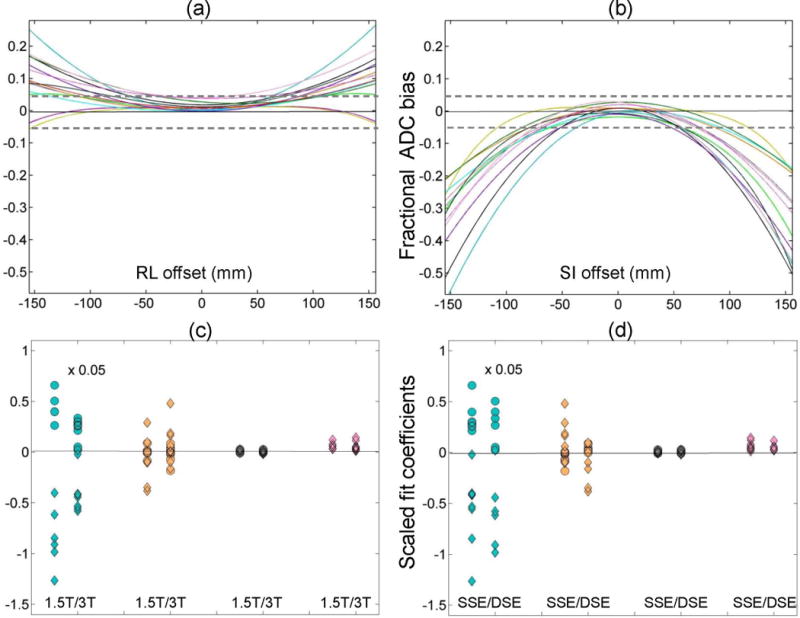
Fractional trace-fit ADC bias for the ice-water phantom is plotted for all measured systems (Table 1) as a function of RL offset (a) and SI offset (b). Dashed horizontal lines mark ±5% error. The corresponding scaled fit coefficients (left-to-right: quadratic, linear and constant) and the fitted norm of residuals are plotted as a function of field (c) and sequence variant (d) for the RL orientation (circles) and SI orientation (rhombi). Note that the linear and quadratic fit coefficients are scaled by 10⁻³ and 10⁻⁶, respectively, for uniform presentation (as described in Methods). Additional scaling by 0.05 was applied to quadratic coefficient to aid visualization.

The relative contributions of bias curvature, asymmetry and constant shift from ice-water value are illustrated in Figure 3c,d for c₀, and scaled c₁ and c₂ fit coefficients with respect to NR (that provides ROI noise envelope, Fig. 1c,d). The constant shift coefficient (c₀=0.02±0.01) was less than a half of NR, independent of field and sequence variant, indicating good agreement among ADC measurements across systems close to isocenter. This coefficient was also significantly correlated (R = 0.83, P = 10⁻⁴) to the measured all-channel ADC shift (due to phantom AP elevation, Table 1, c, Fig.2a,b), confirming that the major source of ADC error at isocenter was due to differences in the AP location of the phantom. The next largest bias effect, which exceeded NR (and ROI noise, Fig.1b,c), was explained by the linear fit coefficient, ₁, (Fig.3c,d) that was significantly anti-correlated (R = −0.8, P = 3·10⁻⁴) to RL bias asymmetry at ±120 mm (Methods). The average (absolute) asymmetry among the scanners was about 3-fold higher and changed sign for SI orientation compared to RL. This fit coefficient was nominally independent of field, but spread over a wider range among the SSE (compared to DSE) scanners (Fig. 3d). Finally, the major source of offset-dependent bias among the systems was explained by the c₂ coefficient (note ×20 scale in Fig. 3c,d). This coefficient was highly correlated (R > 0.9, P < 10⁻⁵) to average fractional bias along both SI (negative bias, rhombi) and RL (positive bias, circles), and exhibited higher values for 1.5T systems (Fig.3c).

To directly quantify the relative magnitude of the two dominant bias contributors for individual gradient directions (nonlinearity and asymmetry), the corresponding correlates of c₂ and c₁ fit coefficients (average fractional bias and bias asymmetry at ±120 mm) were plotted in Figure 4 and analyzed as a function of field and sequence variant. For off-center measurements, the GNL bias accounted for the bulk of the observed ADC error (compared to constant shift and asymmetry) independent of sequence variant, but dependent on gradient channel and field (Fig.4a,b). The highest nonlinearity (>|0.2|) was observed for G_X (SI and RL) and G_Y (SI) of the 1.5T scanners. For an individual gradient channel, the bias along SI offset (rhombi) was twice the RL bias (circles). The channel-average nonlinearity along RL orientation was significantly anti-correlated (R = −0.73, P = 0.002) to the system bore length (Table 1). Nearly zero RL nonlinearity bias was observed for all channels of the two long-bore 3T systems of the same model (Fig.4). A high correlation (|R| > 0.7, P < 0.005) was also observed between the system aspect ratio (bore-length to bore-diameter, Table 1) and the G_Z-channel nonlinearity along RL (R < 0) and SI (R > 0). Duplicate system models (Table 1) exhibited nominally indistinguishable GNL characteristics for all channels, with the (channel and orientation) average percent-difference in GNL bias falling within the corresponding measurement SD: (0.6±1.8)% (#1,10); (1.6±1.7)% (#5,6); (1.4±3.3)% (#7,13); and (1.3±3.3)% (#12,14). The most linear channel among the scanners was G_Z, and the channel-specific GNL bias was more consistent among 3T scanners (Fig. 4a). Overall these results provide the strong evidence that GNL contribution to diffusion weighting bias is predictable from gradient system design.

Figure 4.

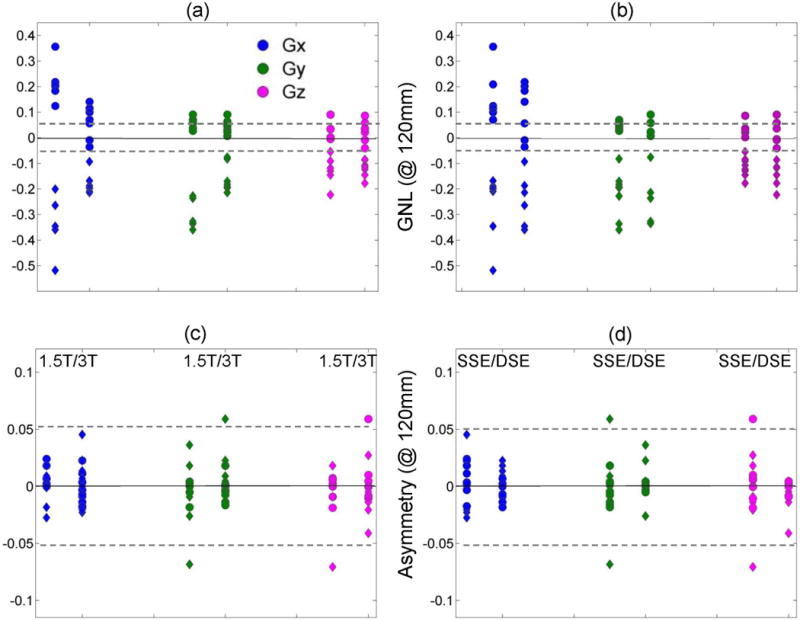
The channel-specific (G_X: blue, G_Y: green, G_Z: magenta) fractional gradient nonlinearity (GNL) bias and average bias asymmetry error measured at ±120 mm are plotted versus field strength (a and c, respectively) and sequence variant (b and d, respectively). Data are shown for all 14 MRI scanners along the RL orientation (circles), as well as, for available (Table 1) 13 and 12 scanners along SI (rhombi) for GNL and asymmetry, respectively. The dashed horizontal lines mark ±0.05 bias error.

The average bias asymmetry error among the channels (Fig.4c,d) was within ±0.03 (2×SD) and nominally independent of the field or offset direction. The asymmetry errors among systems were reduced for DSE, most effectively (~1/2) for G_Z and G_Y (Fig.4d). Independent measurement of ROI drift (AP) at 120 mm (RL) with respect to isocenter directly reported on shim accuracy and was significant (−15 to −20 mm) for six systems by the same vendor, while generally less than 5 mm for all other scanners (Table 1). Remarkably, the systems with poor shim were almost exclusively using DSE (0.85 correlation) that apparently lessened their observed bias asymmetry. Different asymmetry was observed for duplicate gradient models, reflecting independence of shim errors from general gradient channel design (GNL errors).

Numerical simulations of different contributions to bias in diffusion weighting (b-value: Appendix, Figure 5a,b) predicted that minor bias errors (due to shim and imaging gradients) would be mitigated by DSE, while major GNL bias persisted. Figs.5c,d show the ROI-offset (stars), quadratic G_Y bias (blue) and SI asymmetry (green) measured for two systems (from different QIN centers) with the same gradient model using SSE and DSE (Table 1). The extent of ROI AP-drift (stars) confirmed that both systems had similar significant shim imperfections. These resulted in a noticeable DW bias asymmetry for SSE, which was corrected by DSE. Another system showing significant bias contribution from the imaging gradients for SSE (not shown) was also corrected by DSE, consistent with the prediction from the numerical model (Fig. 5a,b). No significant contribution to b-value bias was predicted (or detected) from eddy-currents and concomitant gradients. The GNL model of a representative system (supplied by a vendor) was consistent with the measured channel-specific DW bias and showed that the expected b-value offsets due to observed AP positioning errors among systems (±35mm, Table 1) would be within 3%. Feasibility of empiric GNL (b-value) correction for the phantom ADC data, presented in Fig.3(a,b), is demonstrated in Sup. Mat. Fig. S6. This empiric correction removed 80–90% of the total original ADC error and effectively reduced both cross-platform variability and individual system bias to ±3% for RL and SI offsets within ~120 mm. The residual error, amplified for a few systems at the remote offsets, |x|>120mm, confirmed contribution of non-GNL bias sources.

Figure 5.

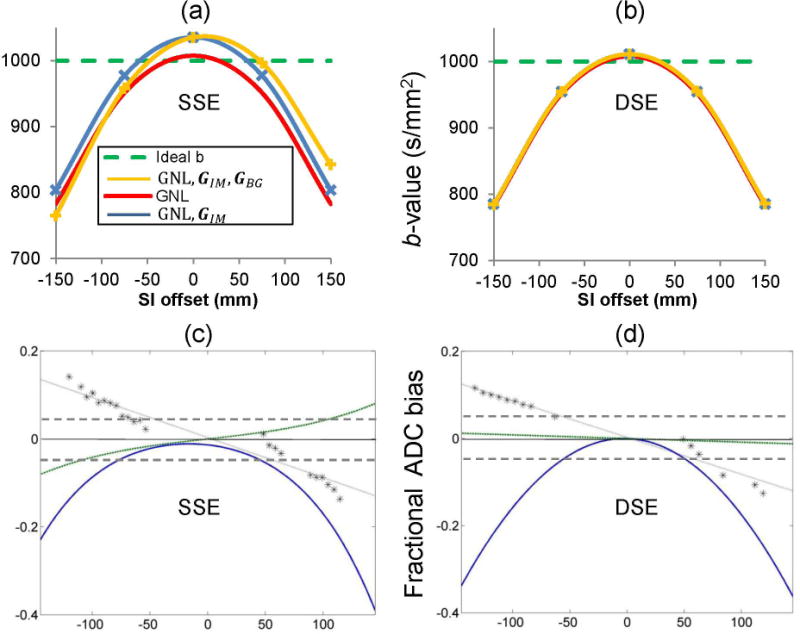
Effect of sequence variant on b-value bias of G_Y-channel in presence of gradient nonlinearity (GNL), imaging gradients (G_IM) and background gradients (G_BG) theoretically predicted for SSE (a) and DSE (b); and ADC bias measured by two scanners of the same model that used SSE (c) and DSE (d), respectively. Similar shim error (G_BG) for both scanners (c, d) is detected from an apparent ROI drift (stars), normalized by the SI-offset and fit to a sloped (dotted) line. Nearly linear bias asymmetry trend (green), obtained as mean difference between fit values at positive and negative SI-offsets from the isocenter, is over-plotted above the quadratic fit (blue) for the observed fractional ADC bias. Note negligible bias asymmetry predicted and observed for DSE (b, d). The dashed horizontal lines in (c) and (d) mark ±0.05 bias error.

Discussion

Consistent with the previous findings (21,22), high ADC agreement with published value (within 3%) was achieved close to isocenter (offset < 40mm) by all systems, with bias not exceeding the measurement error (mean ROI noise of 5%). The dominant sources of amplified random ROI noise were eddy-currents, lower field and longer TE. In the small offset range, the minor (systematic) ADC bias contributions (<3%) were mainly due to phantom positioning errors (AP elevation) and/or cross-terms with imaging gradients on slice-select channel (32). At larger offsets (> 40 mm) bias scaled nearly quadratically with the offset and exceeded the ROI noise. This offset-dependent bias led to both spatially dependent error of the measured ADC for a single system and increased variability among the systems due to different gradient characteristics. The major contribution to the DW bias was from the systematic nonlinearity in the gradients. ADC measurements at the same location (e.g., SI = 120mm) by different systems showed variations of 15–20% (2×SD), while ADC of the same (phantom) anatomy at ±120 mm deviated from the value at isocenter (and published value) by an average bias error of −20% (SI) to +7% (RL). The empiric correction of the major GNL bias in the phantom ADC has reduced both cross-platform variability and bias error range down to ±3% (below ROI noise) for the RL and SI offsets of up to ±120 mm.

Minor second-order bias contributions due to shim, imaging and eddy currents were virtually independent of gradient design. As expected from the physical origin of the effect, the shim-related bias was most pronounced along the main magnetic field direction (SI), while the imaging gradients contributed bias terms for the slice-select channel exclusively. Consistent with the prediction of a numerical model (Appendix), application of the DSE acquisition effectively suppressed bias due to shim and imaging gradients. For three systems, the errors due to eddy-currents on G_Z-channels along RL or SI exceeded (otherwise small) GNL error. With the exception of the outliers, the absolute measurement uncertainty was small enough (2×SD < 7%) to allow confident characterization of ADC bias away from isocenter. Consistent with the analytical model (Appendix), the numerically predicted eddy-current contribution to b-value bias was negligible (even for the systems with significant eddy-current artifacts). DSE acquisition or co-registration of diffusion images from individual DWI directions to the b = 0 s/mm² image for SSE acquisition alleviated the eddy current effects and reduced ROI noise (histogram width).

The proposed measurement protocol allowed quantitative description of the major nonlinearity bias for individual gradient channels across diverse scanner platforms in a multicenter setting. GNL was virtually independent of sequence variant and had the dominant contribution to systematic ADC bias, not correctable by acquisition or co-registration. Among the studied systems, the widest inconsistencies (20% spread from 20% mean bias) for off-center trace-ADC measurements were observed due to GNL for 1.5T magnets. This finding may be related to the older gradient design of the sampled 1.5T systems (rather than lower field). Direction-specific nonlinearity was dominated by G_X-channel contribution for all systems and was higher at 1.5T. The most linear channel across all systems was the G_Z gradient. For the typical ADC measurements of isotropic media, systematic error would be an average of the direction-specific bias.

GNL characteristics were highly correlated to bore geometry and nearly identical (within measurement error) for systems of the same model supporting the premise that related DW imperfections could be corrected using model-specific gradient design parameters (23,26,27). When these parameters are unknown, empiric off-line correction of GNL bias, based on (presently) measured system-specific nonlinearity characteristics, is also possible (31). However this would require diffusion direction and nominal b-value information, currently not uniformly stored in “public” DICOM tags (37). Use of non-public tags for DWI acquisition parameters should be discouraged in view of multicenter studies that need to characterize and correct for GNL bias. The described measurements were performed along linear offsets, RL (SI, AP = 0) and SI (RL, AP = 0), and the results should not be extrapolated to arbitrary locations within the magnet bore. There may be spatial regions for the systems where the ADC deviations are larger than detected. The orthogonal (X, Y, Z) DWI gradients were used to characterize individual channel performance along primary gradient directions, which does not provide information on cross-channel gradients (L_i≠j, Appendix). These spurious gradients can be substantial, depending on the gradient design (26,29,30).

As a result of the findings presented here, a set of guidelines has been proposed and tested for multisite evaluation of scanners and minimizing ADC errors to correct for gradient design imperfections on individual platforms by vendors. For multisite clinical trials, the proposed practical QC protocol should be implemented to characterize the scanners and develop on-site correction strategies, independently (31) or with the vendor assistance (23,27). For large FOV scans (typically used for body applications) or off-center anatomies (e.g., breast, kidney) in multicenter trials, platform-specific GNL correction practices are strongly recommended. The measured channel-specific bias characteristics can be utilized to benchmark correction efficiency across the studied systems using tools developed by the research community (26,27,31). This study has demonstrated the feasibility of empiric DW-bias correction, based on an approximation for diagonal elements of the nonlinearity tensor (31), which is readily available for research purposes. Ultimately, for clinical trials, the GNL bias in diffusion weighting is best corrected “on-line” by manufacturers, based on known (comprehensive) gradient design characteristics (23).

In conclusion, the implemented protocol for evaluating DW bias allows independent characterization of gradient channels and determination of the dominant sources of ADC error both for individual gradient systems and across a diverse set of imaging platforms for multicenter trials. The results confirm gradient nonlinearity as a significant source of bias in ADC maps. Additional (minor) sources of bias are due to shim, eddy currents and imaging cross-terms. Importantly, these sources of DW bias are not currently corrected on clinical scanners regardless of vendor platform. The presence of systematic bias will not affect variability for the same anatomy scanned by the same platform at the same location relative to isocenter, other than that the actual measured ADC value will be biased (but consistent). However, without bias correction, ADC variability in multicenter studies is expected to be significant due to both different system designs and scan locations. Minor bias in b-value is mitigated by twice-refocused spin-echo acquisition, while dominant nonlinearity bias (same origin as geometric distortions) can be corrected using platform-specific gradient design information.

Supplementary Material

Supp Material

Supporting Schema I: Schematic of height adjustment such that center of tube is at A/P=0 as achieved in (b) showing axial survey scan for R/L tube axis orientation; (c) “Phantom Positions 1,2,3” R/L offset scans; (d) “Phantom Positions 4,5,6” S/I offset scans.

Supporting Figure S1: Preparation of ice-water bath for the phantom.

Supporting Figure S2: The assembled phantom in insulating foam pocket (a) and (b) is placed on stage in a scanner (c).

Supporting Figure S3: The phantom and stage on a scanner table: (a) the stage with the phantom guides and green cross-tape marking its center; (b) the phantom on stage in RL orientation, position 1; (c) the full experimental assembly with an anterior coil.

Supporting Figure S4: Phantom on stage positioning: (a) position 1: 0mm offset in RL orientation. The stage is resting flat on a table before adjustment of AP elevation (ruler); (b) stage elevation is adjusted with the screw; (c) position 2: right offset +70mm.

Supporting Figure S5: Phantom positioning for SI orientation scans: (a) position 4: 0 mm offset; (b) position 5: superior +70mm offset; (c) position 6: inferior −70mm offset.

Supporting Figure S6: Residual fractional bias is plotted as a function of RL (a) and SI (b) offsets after empiric GNL correction was applied to the original data in Fig.3(a,b). Dashed horizontal lines mark ±5% error.

Supporting Table S1 (Sup. Mat.): Key acquisition parameters (allowed ranges).

Appendix

The diffusion weighting b-value was obtained as an Euclidian norm of b-matrix, b_k = ‖b_k, calculated by numerical time-integration of k^th-direction gradient waveform, G_k(τ) = (G_kX,G_ky,G_kZ)^T, whose coordinates indicate active gradient channel elements at time τ, according to (32,39): ${\mathit{b}}_k={\gamma }^2{\displaystyle {\int }_0^{TE}dt}{\displaystyle {\int }_0^t{\mathit{G}}_k(\tau )d\tau }{\displaystyle {\int }_0^t{\mathit{G}}_k^T(\tau \prime )d\tau \prime }$. Here γ is the gyromagnetic ratio and TE is the echo time for the spin echo DWI sequence. In addition to idealized combination (32), G_ID = G_DW + G_IM, of imaging, G_IM, and diffusion gradients, G_DW = ‖G_DW‖ u, where u_k = (u_kX,u_ky,u_kZ)^T, ‖u‖ = 1, u^Tu = 1 defines DW direction, the gradient waveforms were expanded to include spatially-dependent, r = (x,y,z)^T, contributions from gradient nonlinearity tensor (26), $L_{\mathit{ij}}(\mathit{r})=\frac{\partial B_z^{g_i}}{\partial r_j\Vert {\mathit{G}}_{io}\Vert }$, G_io=G_i(r₀); background gradients due to imperfect shim, G_BG = ∇B_o; concomitant gradients (33), ${\mathit{G}}_{CF}=\nabla {\Vert {\mathit{G}}_{\mathit{xyz}/2}^{ID}\times \mathit{r}\Vert }_{z=0}^2/2B_0$; G_j/2 ≡ G_j/2; and eddy current distortions (34), ${\mathit{G}}_{\mathit{EC}}=\frac{\partial {\mathit{G}}^{ID}}{\partial t}\otimes [a_1\mathit{exp}(-t/{\tau }_1)+a_2\mathit{exp}(-t/{\tau }_2)]/(a_1+a_2)$. These resulted in the combined gradient waveform: G_k(τ,r) = L(r)G^ID + G_BG(r) + G_EC(r) + G_CF(r). In this model the nonlinearity tensor, defined by gradient channel design, operates only on the G^ID term, since other terms do not directly generate currents in the gradient channels.

An example of the combined gradient waveforms generated for DSE and SSE sequence variants on the G_Y channel at ±150 mm (SI) is shown in Figure A1. The waveform polarity is reversed after TE/2 (32) to implicitly account for the effect of the spin echo RF pulses (39). The relative contribution of the individual gradient imperfections into b-value bias was evaluated by percent deviation of simulated value from ideal (input b = 1000 s/mm²) in the presence of a specific (additive) bias source. Based, on the average values observed for the studied systems, the simulation parameters were set to: TE=100ms, B₀=3T, τ₁=0.5ms, τ₂=2ms, a₁ = a₂ = 1, G_BG=±0.3mT/m, G_IM=18.8mT/m. With these characteristics, the contributions of G_CF and G_EC were negligible, accounting for less than 0.02% and 0.5% of the b-value bias, respectively, while G_IM and G_BG produced minor detectible errors of 3–5%, and GNL stood out as the major contributing bias factor of up to 20% at remote offsets from isocenter.

Figure A1.

Gradient waveforms for G_Y channel illustrating contributions of spurious gradients (blue trace) due to nonlinearity, background and chronic fields, imaging, and eddy currents compared to idealized waveforms (black traces) for SSE (a) and DSE (b) sequence variants at r=±150 mm (SI). Red vertical bars mark the time of implicit RF pulses, and green bar corresponds to TE.