A Gauge Invariant Multiscale Approach to Magnetic Spectroscopies in Condensed Phase: General Three-Layer Model, Computational Implementation and Pilot Applications

Abstract

Analytical equations to calculate second order electric and magnetic properties of a molecular system embedded into a polarizable environment are presented. The treatment is limited to molecules described at the self consistent field (SCF) level of theory, including Hartree–Fock theory as well as Kohn-Sham density functional theory (DFT) and is extended to the Gauge-Including Atomic Orbital method (GIAO). The polarizable embedding is described by means of our already implemented polarizable QM/MM methodology, where the polarization in the MM layer is handled by means of the fluctuating charge (FQ) model. A further layer of description, i.e, the polarizable continuum model, can also be included. The FQ(/PCM) contributions to the properties are derived, with reference to the calculation of the magnetic susceptibility, the NMR shielding tensor, EPR g-tensors and hyperfine couplings.

I. INTRODUCTION

The accurate calculation of spectroscopic and response properties is, nowadays, among the most important tasks of computational chemistry. The framework of response theory, both linear and nonlinear, has been subject of huge developments in the last few decades and has been extended to different properties and to different quantum mechanical (QM) methodologies. It is in fact possible, using well attested methodologies, to compute spectroscopic observables for small- or medium-sized molecules in gas phase with great accuracy; however, to reproduce experimental results it is often mandatory to take into account the effects due to the chemical environment surrounding the molecule. While the increasing availability of computational power, combined with state-of-art linear scaling techniques and efficient implementations, make possible to treat quantum-mechanically systems composed of hundreds or thousands of atoms, a full QM treatment of a significant portion of the environment is not convenient. A proper description of a complex system composed by a molecule and its surroundings requires in fact a statistical averaging of the results, as the number of accessible energy minima can be huge: a meaningful computation would therefore require a very high number of barely feasible simulations.

A well known, effective strategy to address these issues is represented by focused models, where the system is partitioned into a chemically interesting core - e.g., the solute in a solution, a chromophore in a biological matrix - and the environment, which perturbs the core, modifying its properties. While a level of theory as high as required is retained for the core, the environment is introduced into the model in a more approximate way. Two popular alternatives of such approaches are to consider the environment as a structureless continuum, as in the Polarizable Continuum Model¹ (PCM), or to treat it by retaining its atomistic resolution, but describing it via molecular mechanics (MM).

Both alternative strategies can be effectively coupled together to overcome the respective limitations: in the last few years, we have developed in our laboratory a combined QM/MM/PCM model^2–4 which employs a polarizable, fluctuating charge (FQ) based force field for the atomistic portion and the Conductor-like approximation of the PCM to take into account long range interactions and to provide suitable boundary conditions. For such a model, which in the following will be referred to as QM/FQ/PCM, linear response equations have been derived and implemented, as well as first and second analytical derivatives with respect to geometrical and electric perturbations.^3,4

In this contribution, we focus on the extension of this model to magnetic properties with a procedure assuring gauge-invariance of the computed results.

The FQ/PCM contributions to first and second order properties will be derived and implemented, giving access to the computation of parameters of interest for magnetic resonance spectroscopies,⁵ such as nuclear magnetic resonance (NMR) and electron spin resonance (ESR).^6–9 Due to the formal analogy between QM/FQ/PCM and PCM,² we will generalize to our model the approach by Cammi and coworkers.^10,11. To the best of our knowledge, this paper reports on the first development and implementation of a polarizable QM/MM/PCM Hamiltonian for gauge-invariant magnetic response and spectroscopic properties.

The paper is organized as follows. In section II the QM/FQ/PCM model is briefly introduced, with particular emphasis on both static and frequency dependent response equations for a generic perturbation. In section III, the response equations will be specialized to electric and magnetic perturbations and the polarizable embedding contributions will be derived explicitly. Finally, in section IV some pilot applications will be discussed.

II. THEORY

Notation

We will use the bold font to indicate vectors and matrices as a whole, while we will use the normal font for their elements. For instance, P refers to the density matrix, whose elements are P_μν. q is the vector composed of all of the FQs, while the i-th charge is q_i and F is the representation matrix of the Fock operator in some basis set. If a quantity is both a matrix (i.e., with respect to the atomic basis set) and a vector (i.e., with respect to the charges manifold), we will use the bold font when we deal with the whole vector irrespectively of the matrix attribute. As an example, we will denote with V_μν the vector made of the matrices V_μν,i, so that, for instance

$${\mathbf{q}}^{†}{\mathbf{V}}_{\mu \nu }=\sum _i{q}_i{V}_{\mu \nu ,i}$$

We will use the accent ~ to denote quantities including a FQ contribution: for instance, $\tilde{\mathbf{F}}$ will be the FQ corrected Fock matrix. Finally, we will use superscripts to denote analytical derivatives and put them between parentheses when we mean only the explicit contributions (i.e., the partial derivative). The fluctuating charge model represents the polarization of a classical, atomic system by endowing each atom with a charge, whose value depends on the environment^12–14 according to the electronegativity equalization principle^15,16 A convenient formulation of this theory is to define the FQs as the ones minimizing the following functional:

$$F(\mathbf{q},\lambda )=\sum _{\alpha ,i}{q}_{\alpha i}{\chi }_{\alpha i}+\frac{1}{2}\sum _{\alpha ,i}\sum _{\beta ,j}{q}_{\alpha i}{J}_{\alpha i,\beta j}{q}_{\beta j}+\sum _{\alpha }{\lambda }_{\alpha }(\sum _i{q}_{\alpha i}-Q_{\alpha })={\mathbf{q}}^{†}\chi +\frac{1}{2}{\mathbf{q}}^{†}\mathbf{Jq}+{\lambda }^{†}\mathbf{q}$$

where the Greek indexes α and β run on molecules and the Latin ones on the atoms of each molecule. The χ vector collects the atomic electronegativities, and the J matrix represents the interaction kernel between the FQs. This functional has a precise chemical meaning: differences in electronegativities create a flow of charge; on the other hand, to polarize the various atoms it is necessary to spend some energy (because of their hardness) and the interaction between the charges needs to be taken into account to reach the equilibrium. In eq. 1, a set of Lagrangian multipliers λ_α is used to impose charge conservation constraints; by introducing a compact notation (see ref. 2), the stationarity conditions read

$${\mathbf{Dq}}_{\lambda }=-{\mathbf{C}}_Q$$ (1)

where C_Q is a vector containing atomic electronegativities and total charge constraints, whereas q_λ is a vector containing charges and Lagrange multipliers. The D is composd by the J matrix and the Lagrangian blocks.

To couple the FQ model with a QM description of some portion of the system, it is possible to exploit a variational approach:^2–4,17,18 a global, variational energy functional of both the FQs and the electronic density can be written as the sum of functional in eq.1, a variational expression for the QM energy and a positive interaction term, such as the Coulomb interaction between the FQs and the core’s density of charge:

$$E_{\mathrm{QM}∕\mathrm{MM}}=\sum _{i=1}^{N_q}\Phi [{\rho }_{\mathit{QM}}]\left({\mathbf{r}}_i\right)q_i$$ (2)

Φ[ρ_QM](r_i) is the electrostatic potential due to the QM density of charge at the i-th FQ placed at r_i:

$$\Phi [{\rho }_{\mathit{QM}}]\left({\mathbf{r}}_i\right)\stackrel{\mathit{def}}{=}{V}_i\left(\mathbf{P}\right)=V_i^N\left(\mathbf{P}\right)+V_i^e\left(\mathbf{P}\right)=\sum _{\zeta =1}^{N_n}\frac{Z_{\zeta }}{\mid {\mathbf{r}}_i-{\mathbf{R}}_{\zeta }\mid }-{\int }_{R^3}d\mathbf{r}\frac{{\rho }^{\mathit{el}}\left(\mathbf{r}\right)}{\mid {\mathbf{r}}_i-\mathbf{r}\mid }$$ (3)

where the ζ-labeled sum runs over the N_n QM nuclei, whose position we call R_ζ (see ref. 3 for a more detailed discussion of the coupling). Notice that, by expanding the electronic density in a suitable basis set {χ_ν}, the second term of the potential becomes

$$V_i^e\left(\mathbf{P}\right)=-\sum _{\mu \nu }{P}_{\mu \nu }{\int }_{R^3}d\mathbf{r}\frac{{\chi }_{\mu }\left(\mathbf{r}\right){\chi }_{\nu }\left(\mathbf{r}\right)}{\mid {\mathbf{r}}_i-\mathbf{r}\mid }=\sum _{\mu \nu }{P}_{\mu \nu }{V}_{\mu \nu ,i}$$ (4)

where the “uncontracted” potential V_μν is introduced and the double sum runs on the atomic orbitals. We will assume that a Self Consistent Field (SCF) level of theory, including modern density functional theory, is used for the QM portion. The global functional then reads:

$$\mathcal{E}[\mathbf{P},\mathbf{q},\lambda ]=\text{tr}\mathbf{hP}+\frac{1}{2}\text{tr}\mathbf{PG}\left(\mathbf{P}\right)+{\mathbf{q}}^{†}\chi +\frac{1}{2}{\mathbf{q}}^{†}\mathbf{Jq}+{\lambda }^{†}\mathbf{q}+{\mathbf{q}}^{†}\mathbf{V}\left(\mathbf{P}\right)$$ (5)

where h and G are the usual one- and two-electron matrices.

By imposing the stationarity conditions taking into account the proper constraints, a modified set of Fock equations is obtained, defined in terms of the QM/FQ Fock matrix:

$${\tilde{F}}_{\mu \nu }=\frac{\partial \mathcal{E}}{P_{\mu \nu }}=h_{\mu \nu }+G_{\mu \nu }\left(\mathbf{P}\right)+{\mathbf{q}}^{†}{\mathbf{V}}_{\mu \nu }$$ (6)

and a new set of equations for the FQs, where, with respect to eq. 1, a new source term arises:

$${\mathbf{Dq}}_{\lambda }=-{\mathbf{C}}_Q-\mathbf{V}\left(\mathbf{P}\right)$$ (7)

The inclusion of a further layer treated by means of the PCM approach (in particular, we will refer to the conductor-like PCM^19–22) is easily achieved by redefining the charges and the D matrix so as to include PCM contributions, i.e.

$$\left(\begin{array}{cc}\hfill \mathbf{D}\hfill & \hfill {\Omega }^{†}\hfill \\ \hfill \Omega \hfill & \hfill \mathbf{S}∕f\left(\epsilon \right)\hfill \end{array}\right)\left(\begin{array}{c}\hfill {\mathbf{q}}_{\lambda }\hfill \\ \hfill \sigma \hfill \end{array}\right)=\left(\begin{array}{c}\hfill -\mathbf{C}\hfill \\ \hfill 0\hfill \end{array}\right)$$ (8)

where S and Ω represent the Coulomb interaction of the PCM charges with themselves and with the FQs, respectively, and f(ε) = ε/(ε − 1) is an empirical factor accounting for the dielectric nature of the medium. In addition, a PCM contribution σ^†V_μν is to be added to q^†V_μν in eq. 6. Because the inclusion of PCM does not add anything to the theoretical framework but only makes the notation more cumbersome, in the following we will only deal with the QM/FQ contributions, and therefore we will assume tacitly that slight modifications are to be implemented to include the PCM layer. Further details on the coupling of the PCM with the FQ model can be found elsewhere.^2,3

Second order response properties can be analytically derived by calculating the second derivatives of the variational QM/MM energy. Let x, y be two generic perturbations (i.e., electric or magnetic field components, or nuclear coordinates). Under the general assumption that the basis functions depend on the perturbation, the second derivatives of the SCF/FQ energy are:⁴

$$\begin{array}{c}{\mathcal{E}}^{\mathit{xy}}=\sum _{\mu \nu }\left[h_{\mu \nu }^{\mathit{xy}}+\frac{1}{2}{G}_{\mu \nu }^{\left(\mathit{xy}\right)}\left(\mathbf{P}\right)+{\mathbf{q}}^{†}{\mathbf{V}}_{\mu \nu }^{\mathit{xy}}\right]P_{\mu \nu }-\text{tr}{\mathbf{WS}}^{\mathit{xy}}-\text{tr}{\mathbf{W}}^y{\mathbf{S}}^x\hfill \\ \hfill +\sum _{\mu \nu }\left[h_{\mu \nu }^x+G_{\mu \nu }^{\left(x\right)}\left(\mathbf{P}\right)+{\mathbf{q}}^{†}{\mathbf{V}}_{\mu \nu }^x\right]P_{\mu \nu }^y+\sum _{\mu \nu }{\mathbf{q}}^{y†}{\mathbf{V}}_{\mu \nu }^x{P}_{\mu \nu }\hfill \end{array}$$ (9)

In eq.9, we can distinguish between explicit contributions, i.e., the ones that involve the evaluation of integral derivatives, or expectation values of derivatives of operators, and response contributions, i.e., the ones that involve the derivatives of the density matrix. In order to compute these latter, response equations, namely the Coupled Perturbed Hartree Fock (CPHF) equations, need to be solved:

$$\left(\begin{array}{cc}\hfill \tilde{\mathbf{A}}\hfill & \hfill \tilde{\mathbf{B}}\hfill \\ \hfill \tilde{\mathbf{B}}\hfill & \hfill \tilde{\mathbf{A}}\hfill \end{array}\right)\left(\begin{array}{c}\hfill \mathbf{X}\hfill \\ \hfill \mathbf{Y}\hfill \end{array}\right)+\left(\begin{array}{c}\hfill {\tilde{\mathbf{Q}}}_X\hfill \\ \hfill {\tilde{\mathbf{Q}}}_Y\hfill \end{array}\right)=0$$ (10)

Here, as previously shown:^3,4

$${\tilde{A}}_{\mathit{ia},\mathit{jb}}=({ϵ}_a-{ϵ}_i){\delta }_{\mathit{ij}}{\delta }_{\mathit{ab}}+\langle \mathit{aj}\Vert \mathit{ib}\rangle -{\mathbf{V}}_{\mathit{ia}}^{†}{\mathbf{D}}^{-1}{\mathbf{V}}_{\mathit{jb}}$$ (11)

$${\tilde{B}}_{\mathit{ia},\mathit{jb}}=\langle \mathit{ab}\Vert \mathit{ij}\rangle -{\mathbf{V}}_{\mathit{ia}}^{†}{\mathbf{D}}^{-1}{\mathbf{V}}_{\mathit{bj}}$$ (12)

$${\tilde{Q}}_{\mathit{ia}}={\tilde{F}}_{\mathit{ia}}^{\left(x\right)}-G_{\mathit{ia}}\left(S_{\mathit{oo}}^x\right)-\tilde{\mathbf{F}}{S}_{\mathit{ia}}^x+{\mathbf{V}}_{\mathit{ia}}^{†}{\mathbf{D}}^{-1}\mathbf{V}\left({\mathbf{S}}_{\mathit{oo}}^x\right)$$ (13)

and

$${\tilde{F}}_{\mu \nu }^{\left(x\right)}=h_{\mu \nu }^x+G_{\mu \nu }^{\left(x\right)}\left(\mathbf{P}\right)+{\mathbf{q}}^{†}{\mathbf{V}}_{\mu \nu }-{\mathbf{V}}_{\mu \nu }^{†}{\mathbf{D}}^{-1}{\mathbf{V}}^{\left(x\right)}\left(\mathbf{P}\right)=h_{\mu \nu }^x+G_{\mu \nu }^{\left(x\right)}\left(\mathbf{P}\right)+{\mathbf{q}}^{†}{\mathbf{V}}_{\mu \nu }^x+{\mathbf{V}}_{\mu \nu }^{†}{\mathbf{q}}^{\left(x\right)}$$ (14)

Hence, in general, three types of FQ contributions are present:

1. Explicit contributions:

   $${\mathbf{q}}^{†}{\mathbf{V}}^{\left(\mathit{xy}\right)}+{\mathbf{q}}^{\left(x\right)†}{\mathbf{V}}^{\left(y\right)}$$
2. Contributions to the explicit Fock matrix derivatives:

   $${\mathbf{q}}^{†}{\mathbf{V}}_{\mu \nu }^x+{\mathbf{q}}^{\left(x\right)†}{\mathbf{V}}_{\mu \nu }$$
3. Contribution to the CPHF matrix:

   $$-{\mathbf{V}}_{\mathit{ia}}^{†}{\mathbf{D}}^{-1}{\mathbf{V}}_{\mathit{jb}}$$

In case a PCM layer is present, such terms are modified as follows:

1. Explicit contributions:

   $${\mathbf{q}}^{†}{\mathbf{V}}^{\left(\mathit{xy}\right)}+{\mathbf{q}}^{\left(x\right)†}{\mathbf{V}}^{\left(y\right)}+{\sigma }^{†}{\mathbf{V}}^{\left(\mathit{xy}\right)}+{\sigma }^{\left(x\right)†}{\mathbf{V}}^{\left(y\right)}$$
2. Contributions to the explicit Fock matrix derivatives:

   $${\mathbf{q}}^{†}{\mathbf{V}}_{\mu \nu }^x+{\mathbf{q}}^{\left(x\right)†}{\mathbf{V}}_{\mu \nu }+{\sigma }^{†}{\mathbf{V}}_{\mu \nu }^x+{\sigma }^{\left(x\right)†}{\mathbf{V}}_{\mu \nu }$$
3. Contribution to the CPHF matrix:

   $$-{\left(\begin{array}{c}\hfill {\mathbf{V}}_{\mathit{ia},\mathit{FQ}}\hfill \\ \hfill {\mathbf{V}}_{\mathit{ia},\mathit{PCM}}\hfill \end{array}\right)}^{†}{\left(\begin{array}{cc}\hfill \mathbf{D}\hfill & \hfill {\Omega }^{†}\hfill \\ \hfill \Omega \hfill & \hfill \mathbf{S}∕f\left(\epsilon \right)\hfill \end{array}\right)}^{-1}\left(\begin{array}{c}\hfill {\mathbf{V}}_{\mathit{jb},\mathit{FQ}}\hfill \\ \hfill {\mathbf{V}}_{\mathit{jb},\mathit{PCM}}\hfill \end{array}\right)$$

If the external perturbation depends on time, as the case of an oscillating electric field, the response equations need to be generalized to the frequency dependent case. Frequency dependent CPHF equations (FD-CPHF), also known as time-dependent SCF equations, need to be solved and the proper transition densities are to be used to compute the desired properties:

$$\left(\begin{array}{c}\hfill {\tilde{\mathbf{Q}}}_X\hfill \\ \hfill {\tilde{\mathbf{Q}}}_Y\hfill \end{array}\right)+\left(\begin{array}{cc}\hfill \tilde{\mathbf{A}}-\omega \mathbf{I}\hfill & \hfill \tilde{\mathbf{B}}\hfill \\ \hfill \tilde{\mathbf{B}}\hfill & \hfill \tilde{\mathbf{A}}+\omega \mathbf{I}\hfill \end{array}\right)\left(\begin{array}{c}\hfill \mathbf{X}\hfill \\ \hfill \mathbf{Y}\hfill \end{array}\right)=0$$ (15)

III. ELECTRIC AND MAGNETIC PERTURBATIONS

The calculation of electric, magnetic or vibrational properties requires the evaluation of the perturbed density matrix and, possibly, of the perturbed FQs (and PCM charges). We will now give more details on the response equations for electric and magnetic perturbations. Geometrical perturbations have already been extensively discussed elsewhere⁴. Consistently with the definition of a focused model²³, we will assume in the following the electromagnetic field to interact directly with only the QM portion of the system, and the FQs to be affected by the perturbation only through the response of the molecule. In the case of a magnetic field, as it will be discussed in section III A, this is justified by the classical nature of the FQs; on the other hand, in principle the interaction with an electric field can also induce a response in the classical layer of the system. Such an interaction (see appendix A for a complete derivation) introduces two effects: a direct contribution to the property (i.e., to the polarizability or to other first order properties with respect to the electric field) and an additional term, which enters response equations, and which can be seen as a local field contribution, i.e. a term which accounts for the interaction between the Maxwell field and the environment.²⁴ It is worth remarking here that the direct contribution to the property does not arise from the geometrical rearrangement or by the orientation of the classical system, but from its pseudo-electronic properties, which are introduced by means of the polarizability of the force field. Such a contribution is highly dependent on the parametrization and, especially for pure electronic properties such as the polarizability, of ambiguous physical interpretation; however, in case of properties which can be computed as mixed derivatives, such as IR absorption intensities, such contributions can deserve further exploration. A similar discussion, only focused on nuclear perturbations, can be found in ref.⁴. The local field term introduces in the model the fact that the field experienced by the QM core embedded in the classical environment does not coincide with the Maxwell field, but the one that results from the interaction of the electric field with the environment. Such an effect has been thoroughly analyzed in the framework of continuum solvation models^1,25–30 and will be subject of a future communication. We end this discussion by pointing out that common experimental protocols for the measurement of properties of solvated systems, exploit solvents which are transparent in the spectral region involved in the measurement: in other words, the effect of the solvent is to modify the properties of the solute without directly interacting with the probing fields. This is consistent with our model, which discards the direct interaction between the fields and the environment, whereas it retains all the interactions between the core and the classical part through the full inclusion of the interaction Hamiltonian in the computation of response properties.

By starting with these premises, in the presence of an external electric field E and by assuming the FQ to be affected by the field only through the response of the QM molecule, a perturbation term must be added to the energy functional:

$$V^{\mathit{ele}}=-\mu \cdot \mathbf{E}=-({\mu }^n-\sum _{\mu \nu }{P}_{\mu \nu }{\mathbf{M}}_{\mu \nu })\cdot \mathbf{E}$$

where M_μν = ⟨χ_μ∣r∣χ_ν⟩ are dipole integrals. An electric perturbation hence gives rise to a contribution to the mono-electronic part of the Fock operator of the system:

$$h_{\mu \nu }^{\mathit{ele}}={\mathbf{M}}_{\mu \nu }\cdot \mathbf{E}$$

The second derivatives of the energy with respect to the electric field, that correspond to the static polarizability, reduce to

$${\mathcal{E}}^{\mathit{xy}}={\alpha }_{\mathit{xy}}=\sum _{\mu \nu }{M}_{\mu \nu }^x{P}_{\mu \nu }^y$$ (16)

From eq. 16 it follows that no explicit FQ contributions to the polarizability are involved. The right-hand side of the CPHF equations becomes:

$${\tilde{Q}}_{\mathit{ia}}^{\mathit{ele}}={\tilde{F}}_{\mathit{ia}}^{\left(x\right)}={\mathbf{M}}_{\mathit{ia}}$$ (17)

Again, there is no FQ contribution to this term. The right-hand side of the CPHF equations is real: hence, Q_X = Q_Y and it is possible to reduce the response equations to a problem of half dimension solving for X + Y together. By summing the CPHF equations, one gets

$$(\tilde{\mathbf{A}}+\tilde{\mathbf{B}})(\mathbf{X}+\mathbf{Y})+2\mathbf{Q}=0$$ (18)

which can be used together with $(\tilde{\mathbf{A}}+\tilde{\mathbf{B}})(\mathbf{X}-\mathbf{Y})=0$. Notice that a FQ contribution is present in the orbital rotation Hessian $\tilde{\mathbf{A}}+\tilde{\mathbf{B}}$.

A. Magnetic perturbations

In the presence of a static magnetic field, which we will assume be given by the sum of a homogeneous magnetic field B and of a field produced by the magnetic moment m_X of the nucleus X at position R_X, four perturbation terms appear in the Fock operator:

$$h_{\mu \nu }^{\left(10\right)}=-\frac{i}{2c}\langle {\chi }_{\mu }\mid (\mathbf{r}\times \nabla )\cdot \mathbf{B}\mid {\chi }_{\nu }\rangle$$ (19)

$$h_{\mu \nu }^{\left(01\right)}=-\frac{i}{c}\langle {\chi }_{\mu }\mid \frac{{\mathbf{m}}_X\cdot (\mathbf{r}-{\mathbf{R}}_X)}{{\mid \mathbf{r}-{\mathbf{R}}_X\mid }^3}\mid {\chi }_{\nu }\rangle$$ (20)

$$h_{\mu \nu }^{\left(11\right)}=\frac{1}{2c^2}\langle {\chi }_{\mu }\mid \frac{(\mathbf{B}\times \mathbf{r})\cdot [{\mathbf{m}}_X\times (\mathbf{r}-{\mathbf{R}}_X\left)\right]}{{\mid \mathbf{r}-{\mathbf{R}}_X\mid }^3}\mid {\chi }_{\nu }\rangle$$ (21)

$$h_{\mu \nu }^{\left(20\right)}=\frac{1}{8c^2}\langle {\chi }_{\mu }\mid (\mathbf{B}\times \mathbf{r})\cdot (\mathbf{B}\times \mathbf{r})\mid {\chi }_{\nu }\rangle$$ (22)

Here, we have imposed the Coulomb Gauge and have used minimum coupling to introduce the magnetic field. Notice that, in principle, a fifth term is present,¹⁰ i.e.

$$h_{\mu \nu }^{\left(02\right)}=\frac{1}{2c^2}\langle {\chi }_{\mu }\mid \frac{[{\mathbf{m}}_X\times (\mathbf{r}-{\mathbf{R}}_X\left)\right]\cdot [{\mathbf{m}}_X\times (\mathbf{r}-{\mathbf{R}}_X\left)\right]}{{\mid \mathbf{r}-{\mathbf{R}}_X\mid }^6}\mid {\chi }_{\nu }\rangle$$ (23)

However, such a term is relative to the interaction between the electrons and the nuclear magnetic moments,¹⁰ and is not relevant to this work. Therefore, we will not consider it.

Working with London Orbitals^31,32, the basis functions depend on the perturbation and none of terms in eq. 9 can be neglected. Before considering the explicit derivatives, and in particular, magnetic susceptibility and NMR shielding tensors, let us examine the magnetic response equations. The magnetic right-hand side for the isolated system is:

$$Q_{\mathit{ia}}^{\mathit{mag}}=h_{\mathit{ia}}^{\left(x\right)}+G_{\mathit{ia}}^{\left(x\right)}\left(\mathbf{P}\right)-G_{\mathit{ia}}\left(S_{\mathit{oo}}^x\right)-\mathbf{F}{S}_{\mathit{ia}}^x$$ (24)

where

$$h_{\mathit{ia}}^{\left(x\right)}=\langle {\varphi }_i^x\mid h\mid {\varphi }_a\rangle +\langle {\varphi }_i\mid h\mid {\varphi }_a^x\rangle -\frac{i}{2c}\langle {\varphi }_i\mid (\mathbf{r}\times \nabla )\mid {\varphi }_a\rangle$$

The Q is pure imaginary, and hence Q_X = −Q_Y: again, it is possible to transform the CPHF equation in a simpler problem, solving for X − Y. By subtracting the response equations

$$(\mathbf{A}-\mathbf{B})(\mathbf{X}-\mathbf{Y})+2\mathbf{Q}=0$$ (25)

which can be used together with (A − B)(X + Y) = 0. Notice the absence if any FQ response contribution in the magnetic Hessian A − B. The possible perturbed charges would be, as well as the perturbed density, imaginary: this is of course in contradiction with the semiclassical nature of the QM/MM(/PCM) model.^10,11 Hence, all the terms involving the perturbed charges will be discarded: only FQ contributions where the unperturbed charges interact with the perturbed potential are admitted. The contribution to the right-hand side for the QM/FQ response equation will be

$${\tilde{Q}}_{\mathit{ia}}^{\mathit{mag}}=h_{\mathit{ia}}^{\left(x\right)}+G_{\mathit{ia}}^{\left(x\right)}\left(\mathbf{P}\right)+{\mathbf{q}}^{†}{\mathbf{V}}_{\mathit{ia}}^x-G_{\mathit{ia}}\left(S_{\mathit{oo}}^x\right)-\mathbf{F}{S}_{\mathit{ia}}^x$$ (26)

where

$$V_{j,\mathit{ia}}^x=\langle {\varphi }_i^x\mid {\widehat{V}}_j\mid {\varphi }_a\rangle +\langle {\varphi }_i\mid {\widehat{V}}_j\mid {\varphi }_a^x\rangle$$

Again, the FQ contribute only indirectly to the magnetic response.

Once we have all the tools to calculate magnetic properties, the magnetic susceptibility, i.e. the second derivative of the energy with respect to the magnetic field, is given by:

$$\begin{array}{cc}\hfill {\chi }_{\mathit{xy}}=\frac{{\partial }^2\mathcal{E}}{\partial B_x\partial B_y}& =\sum _{\mu \nu }\left[h_{\mu \nu }^{\mathit{xy}}+\frac{1}{2}{G}_{\mu \nu }^{\left(\mathit{xy}\right)}\left(\mathbf{P}\right)+{\mathbf{q}}^{†}{\mathbf{V}}_{\mu \nu }^{\mathit{xy}}\right]P_{\mu \nu }-\text{tr}{\mathbf{WS}}^{\mathit{xy}}-\text{tr}{\mathbf{W}}^y{\mathbf{S}}^x\hfill \\ \hfill & +\sum _{\mu \nu }\left[h_{\mu \nu }^x+G_{\mu \nu }^{\left(x\right)}\left(\mathbf{P}\right)+{\mathbf{q}}^{†}{\mathbf{V}}_{\mu \nu }^x\right]P_{\mu \nu }^y\hfill \end{array}$$ (27)

An explicit FQ contribution arises, namely

$${\mathbf{q}}^{†}{\mathbf{V}}^{\mathit{xy}}\left(\mathbf{P}\right)$$

where

$$V_j^{\mathit{xy}}\left(\mathbf{P}\right)=\sum _{\mu \nu }{P}_{\mu \nu }\left(\langle {\chi }_{\mu }^{\mathit{xy}}\mid {\widehat{V}}_j\mid {\chi }_{\nu }\rangle +\langle {\chi }_{\mu }^x\mid {\widehat{V}}_j\mid {\chi }_{\nu }^y\rangle +\langle {\chi }_{\mu }^y\mid {\widehat{V}}_j\mid {\chi }_{\nu }^x\rangle +\langle {\chi }_{\mu }\mid {\widehat{V}}_j\mid {\chi }_{\nu }^{\mathit{xy}}\rangle \right)$$

The NMR shielding tensor, which is defined as the second derivative of the energy with respect to the magnetic field and the nuclear magnetic moment, can be calculated as:

$${\sigma }_{\mathit{xy}}^X=\frac{\partial \mathcal{E}}{\partial B_x\partial m_y}=\text{tr}({\mathbf{Ph}}^{B_x{m}_y}+{\mathbf{P}}^{B_x}{\mathbf{h}}^{m_y})$$ (28)

In eq.28 there is no explicit FQ contribution, because none of the FQ-related quantities depend on the nuclear magnetic moment.

Another magnetic property which can be computed after solving the magnetic CPHF equations, is the ESR g tensor, which can be seen as the sum of four contributions:³³

$$g_{\alpha \beta }=g_e{\delta }_{\alpha \beta }+\Delta g^{\mathrm{RMC}}{\delta }_{\alpha \beta }+\Delta g_{\alpha \beta }^{\mathrm{GC}}+\Delta g_{\alpha \beta }^{\text{OZ/SOC}}$$

The first contribution is isotropic and equals the g value of the free electron,g_e. The second term is also isotropic and is due to the relativistic mass correction. The third one is a diamagnetic correction; both the second and third terms are first order, and can be computed starting from the spin density matrix. The fourth contribution to the g tensor is a second order property that can be calculated as the second derivative of the energy with respect to the external magnetic field and the magnetic moment of the electron. Note that in solution molecular motions lead to full averaging of the tensor components, so that only its trace $(g_{\mathit{iso}}=\frac{1}{3}\mathit{Tr}(g))$ can be measured.

IV. VALIDATION OF A CLASSICAL QM/MM/PCM MODEL FOR MAGNETIC PROPERTIES

In semi-classical models the interaction between the environment and the QM electronic density is seen as the classical, purely electrostatic interaction of two charge densities. This means that exchange, dispersion, effects due to the delocalization of the electronic density, and other purely QM contributions are completely neglected. In the calculation of electric properties, such as the polarizability and related quantities (including excitation energies), it is often reasonable to assume that electrostatic effects dominate the interaction of a molecule with its chemical surroundings. In the case of magnetic properties, this assumption is less justified. Exchange effects, repulsion, and dispersion, possibly coupled to the generation of induced currents in the environment can be relevant. In our QM/FQ/PCM method, repulsion and dispersion terms are treated classically; they can be formulated quantum-mechanically, by extending to the QM/FQ/PCM what already proposed for the PCM Hamiltonian,³⁴ and recently extended to energy derivatives.^35,36 Such a treatment goes beyond the scope of this work, however it will the subject of future investigations. An alternative procedure consists in extending the QM treatment of - at least - the first neighbors of the QM core. However, the expansion of the QM region has some issues. First, the computational cost is highly dependent on the size of the QM region (i.e., on the number of basis functions), which means that the computation can easily become barely feasible. Second, some properties are extensive with respect to the size of the QM portion: the spurious contributions due to the explicit presence of a portion of the environment are difficult to interpret and can only be eliminated through a thorough statistical averaging; this means that also cluster models may be difficult to employ. On the other hand, if a strong electrostatic interaction between the core and the environment is present, for instance in case of hydrogen bonds or highly polar environments, the other effects can be less relevant and classical models might be adequate for the calculation of magnetic properties.

In order to show the potentialities of our approach, and shed light on the aforementioned issues, we will report on two second order properties (namely NMR shieldings and ESR gtensor) and a first order property (i.e. ESR isotropic hyperfine constants). As a test case for NMR parameters, we have chosen diazines in aqueous solution (see Figure 1), as described with the PCM and by means of small clusters, composed by a diazine and two H-bonded water molecules. This latter approach was previously proven to effectively reproduce the NMR properties of pyrimidine, pyrazine and pyridazine.³⁷ Here, the water molecules are treated at the QM level (QM), at the classical, non-polarizable MM level (QEq) and at the FQ level (FQ), with and without the PCM embedding (/PCM). Among the various solvent representations, we will take as reference the QM/PCM one and we will treat the QM portion at the Kohn-Sham DFT level of theory, using the popular B3LYP functional and the 6-311++G(2df,2pd) basis set. Non-polarizable QM/MM calculations were done by using the QEq charges¹⁶ and QM/FQ calculations were performed by using the parameters given by Rick et al.¹² The geometries of both the isolated molecule and the cluster were optimized at the B3LYP/6-311++G(2df,2pd) level of theory.

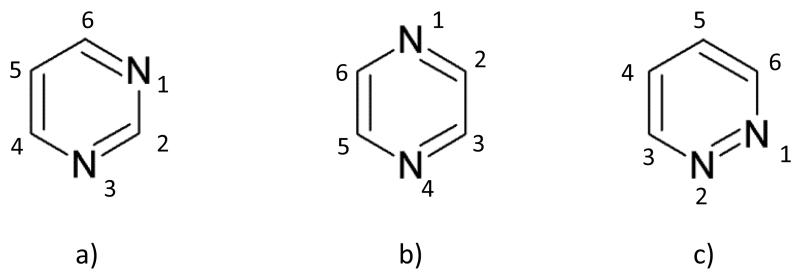
FIG. 1.

Scheme and atom numbering of diazines: a) pyrimidine; b) pyrazine; c) pyridazine.

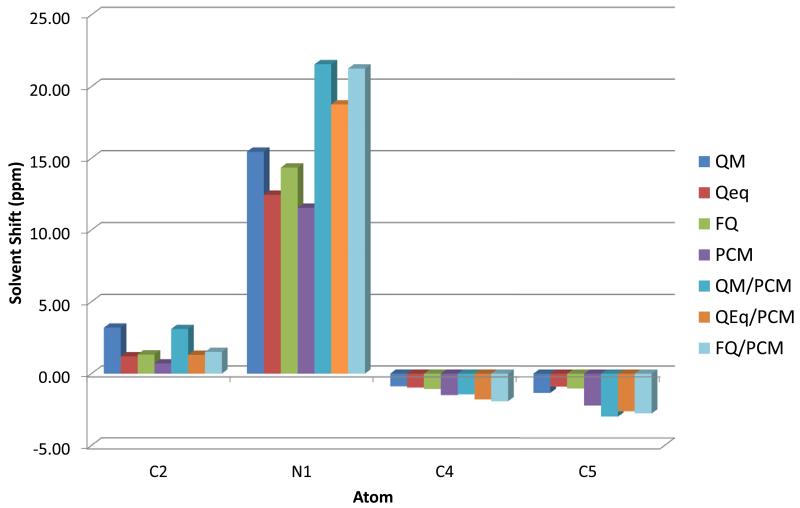
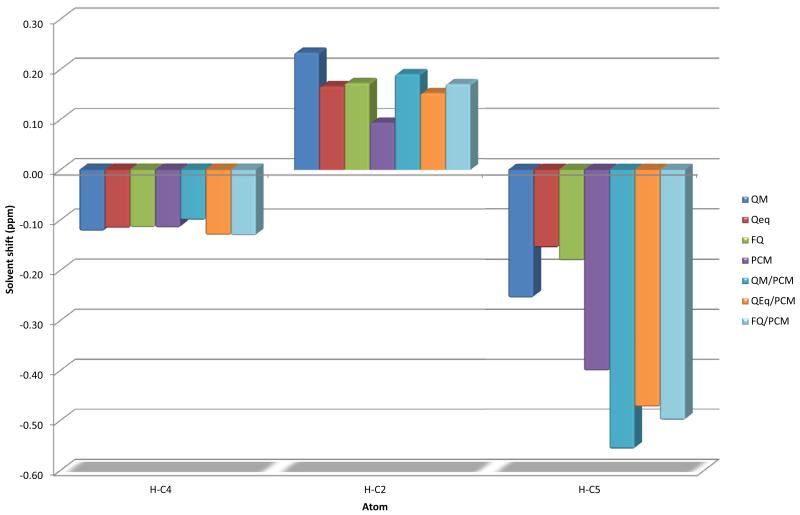
A pictorial view of pyrimidine absolute NMR chemical shifts in vacuo and vacuo-to-solvent shifts obtained with various models is given by figures 2 and 3 (see Supplemental Material for the raw data)³⁸. Notice that as both the molecule and the cluster have C_2v symmetry, only non-equivalent atoms are reported.

FIG. 2.

Solvent shift on NMR chemical shifts for pyrimidine heavy atoms

FIG. 3.

Solvent shift on NMR chemical shifts for pyrimidine hydrogen atoms

The largest solvent effect is observed, as expected, for the nitrogen atom involved in the H-bond (N1). FQ data are always close to QM ones and the FQ/PCM model performs very well, with a RMS error of less than 1 ppm with respect to QM/PCM, which is taken as reference. It is interesting to notice that the error for the N1 atom is particularly small for the FQ(/PCM) model, whereas other models usually give larger deviations: this is a relevant point in supporting the capabilities of the QM/FQ model to describe hydrogen bonded systems. Notice how the interplay between short and long range effects is crucial for a good description of environmental effects: the results obtained with any cluster model and the continuum are the most accurate.

By focusing on the performance of the polarizable and non-polarizable QM/MM approaches, we first notice that both the polarizable and electrostatic embedding schemes introduce in the description of magnetic properties similar contributions, because no response terms are present. The differences between the results are therefore ascribed to the (small) differences between the charges obtained with the QEq and FQ models. Besides the differences due to the parametrization, the polarizable force field is more flexible: while in the QEq approach the whole system is modeled by classical charges, in the QM/FQ model the charges are equilibrated to the QM density.

Moving to the the other diazines, namely pyrazine (C_2h) and pyridazine (C_2v), calculated data are reported in tables I and II. Once again, the results of the FQ/PCM approach are in very good agreement with the full QM treatment.

TABLE I.

Absolute chemical shifts (ppm) of pyrazine in vacuo and solvent shifts (ppm) as obtained with different solvent representations. For the cluster approaches, two explicit water molecules are included at the QM, classical MM and FQ levels of theory, respectively, possibly including the PCM embedding (/PCM). The RMS and Max errors are reported with respect to QM/PCM.

Atom	Vacuum	QM	QEq	FQ	PCM	QM/PCM	QEq/PCM	FQ/PCM
C	31.74	0.54	0.13	0.09	−0.98	−0.07	−0.71	−0.78
N	−114.48	13.54	10.77	12.99	9.38	21.38	18.07	22.26
H	22.88	−0.06	−0.03	−0.04	−0.12	−0.14	−0.13	−0.13
RMS	-	4.54	6.13	4.85	6.95	-	1.95	0.65
MAX	-	7.85	10.61	8.40	12.00	-	3.32	0.88

TABLE II.

Absolute chemical shifts (ppm) of pyridazine in vacuo and solvent shifts (ppm) as obtained with different solvent representations. For the cluster approaches, two explicit water molecules are included at the QM, classical MM and FQ levels of theory, respectively, possibly including the PCM embedding (/PCM). The RMS and Max errors are reported with respect to QM/PCM.

Atom	Vacuum	QM	QEq	FQ	PCM	QM/PCM	QEq/PCM	FQ/PCM
C2	25.82	0.07	−0.14	−0.20	−2.24	−1.04	−1.79	−1.85
C3	55.94	−3.21	−1.83	−2.14	−4.45	−7.40	−5.68	−6.44
N1	−212.27	36.85	25.76	29.49	28.98	60.00	47.11	54.89
H-C3	22.16	0.01	0.00	0.01	−0.03	0.04	0.01	0.03
H-C2	24.40	−0.26	−0.17	−0.20	−0.50	−0.71	−0.59	−0.66
RMS		10.53	15.52	13.85	13.94	-	5.82	2.35
MAX		23.14	34.24	30.51	31.01	-	12.89	5.11

In the previous discussion we have taken the QM/PCM results as benchmark for the other models. In order to evaluate the quality of this solvent representation, we will compare the solvent shifts obtained with such a model to experimental data. We will take as reference data for calculating solvent shifts those in cyclohexane solution: as it has been shown by Mennucci,³⁷ such an environment is correctly modeled by the PCM. Computed shifts for the nitrogen atoms of the various diazines are reported in table III, together with experimental ones.³⁹ The agreement with the experiment is good.

TABLE III.

Calculated and experimental nitrogen NMR chemical shifts from cyclohexane to water. Experimental data are taken from ref. 39.

Molecule	Calc	Exp
Pyridazine	46.57	41.55
Pyrimidine	12.73	16.84
Pyrazine	17.90	16.85

A further proof of the quality of the cluster model can be obtained by comparing the results with the ones obtained by averaging several snapshots obtained from a MD trajectory. Such a simulation has been carried out in the NPT ensemble (300 K, 1 bar); for each snapshot a sphere centered on the solute of radius 16.5 Å was cut and embedded into a spherical PCM cavity of radius 18 Å (more details on the MD simulation protocol can be found in ref. 40). A QM/FQ/PCM calculation has been performed on each snapshot: the averaged results (with standard deviations) are reported in table IV, together with QM/FQ/PCM data obtained for the pyrimidine–water cluster. No major difference is observed, especially for the N1 atom, thus confirming the validity of the cluster approach for such a system. In addition, standard deviations are generally very low.

TABLE IV.

Absolute chemical shifts (ppm) of pyrimidine in water as obtained with a cluster approach and as an average over an MD simulation.

Atom	Cluster	MD
C2	15.86	13.67±0.53
N1	−56.83	−56.52±1.04
C4	16.90	16.70±0.42
C5	54.79	56.10±0.5
H-C4	22.48	22.57±0.05
H-C2	22.17	22.10±0.04
H-C5	23.80	23.94±0.05

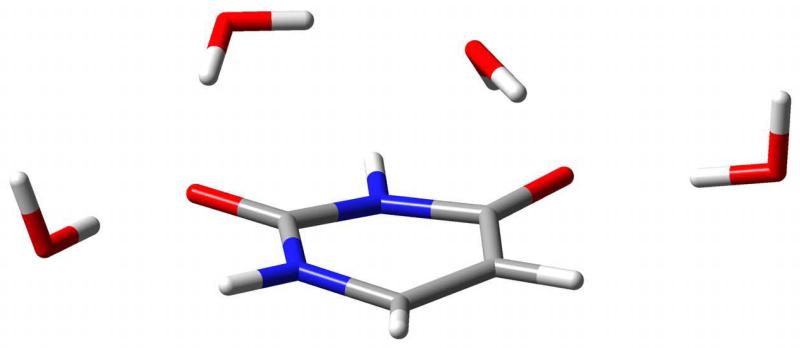
A similar analysis can be performed for ESR spectroscopy. As a test case, we have chosen the anion radical of uracil. Such a system has been recently studied and it has been shown that it is mainly represented by one canonical conformation.^41–43 A pictorial view of the Uracil-water complex is given in figure 4. The geometries of the radical and of the radical–water cluster were optimized at the B3LYP/aug-N07D^44,45 both in vacuo and including the PCM embedding; the ESR parameters were calculated using the B3LYP functional and the purposely tailored EPR-III basis set.⁴⁶ The results are reported in table V. Environmental effects on the g tensor are quite small and reproduced, at least qualitatively, by the different models. However, the difference among full QM and different flavors of QM/MM approaches strongly suggests that non-electrostatic contributions (especially Pauli repulsion) cannot be neglected. The situation is different for the hyperfine couplings: here environmental effects are more relevant, but dominated by electrostatic contributions. As a consequence, a remarkable agreement with full QM computations is observed for the QM/FQ model. It is also noteworthy that bulk solvent effects cannot be neglected and first-shell solvent effects require an atomistic model in view of strong specific (H-bond) contributions. Therefore, only a full QM/FQ/PCM approach is satisfactory, whereas cluster or pure PCM approaches suffer from significant limitations, although for opposite reasons.

FIG. 4.

Uracil-water complex optimized geometry.

TABLE V.

Isotropic hyperfine coupling constants (MHz) of the uracil radical anion in vacuo and solvent shifts as obtained with different solvent representations. For the cluster approaches, four explicit water molecules are included at the QM, classical MM and FQ levels of theory, respectively, possibly including the PCM embedding (/PCM). The RMS and Max errors are reported with respect to QM/PCM. The isotropic g_iso – 2 values are also reported for each model (×10⁻³).

Atom	Vacuum	QM	QEq	FQ	PCM	QM/PCM	QEq/PCM	FQ/PCM
N	−0.29	0,26	0.26	0.26	−0.21	−0.09	−0.16	−0.10
C	97.54	−22.49	−23.47	−23.20	−16.31	−34.75	−34.99	−34.97
C	4.41	−8.40	−8.08	−8.16	−26.90	−5.89	−5.66	−5.71
H	−7.41	2.29	2.52	2.44	−8.81	3.90	4.01	3.93
H	−7.11	−25.14	−24.41	−24.63	3.70	−35.06	−34.99	−35.02
C	1.82	−21.92	−19.82	−20.43	6.70	−25.88	−24.82	−25.03
N	−10.08	12.65	12.44	12.49	−0.10	13.35	13.31	13.31
O	1.56	−1.77	−1.84	−1.82	0.69	−2.05	−2.11	−2.09
H	−5.58	4.22	3.03	3.31	0,28	7.50	6,78	6.92
C	−4.02	17.88	15.34	15.91	0.03	22.72	21.04	21.31
H	−0.38	−6.00	−5.66	−5.72	−0.05	−5.45	−5.08	−5.09
O	−0.67	−9.33	−9.75	−9.73	−3.72	−9.30	−9.66	−9.63
RMS	-	5.07	5.48	5.36	18.98	-	0.64	0.53
MAX	-	12.26	11.28	11.55	38.76	-	1.68	1.42
giso	3.21	3.18	3.22	3.21	3.24	3.19	3.24	3.23

V. CONCLUSIONS AND PERSPECTIVES

In this paper we have reported on analytical equations to calculate second order electric and magnetic properties of molecular systems, treated at the HF or Kohn-Sham DFT level, embedded into a polarizable environment. Notably, our procedure is able to assure gauge invariance of the results, by extension to the Gauge-Including Atomic Orbital method (GIAO). The results of the test cases reported for NMR shieldings and ESR constants show that in any case our QM/FQ/PCM method gives results close to a full QM approach. However, our results are not intended to generally state the capability of QM/MM models to accurately describe environmental effects on magnetic properties. In some cases, non electrostatic effects can play a prominent role and, in such a case, classical models are not adequate. On the other hand, several chemically interesting systems are characterized by very strong electrostatic interactions: in these cases, QM/MM approaches can be a viable compromise between accuracy and computational cost to afford the computation of magnetic properties of large systems embedded in complex environments (solution, proteins). In particular, in this paper we have tested our procedure against solvated systems. However, our approach is not limited to such kind of environments, and can be applied also to bounded systems partitioned in a QM/MM fashion. Also, our procedure, can be easily extended to mixed electric/magnetic properties, i.e. chiral properties and spectroscopies, for which preliminary investigations carried out in our lab have given very promising results.⁴⁷

Appendix A. Coupling the QM FQ model with the External Electric Field

In this appendix, we will derive the response equations for electric perturbation assuming that also the classical portion of the system interacts directly with the perturbing electric field and give some further remarks on why we choose to neglect such a contribution. For ease of notation, we will call this picture “strong coupling”, in opposition with the “weak coupling” picture described in section III, where the classical portion interacts only indirectly with the field.

In the presence of an external electric field F, the energy functional of the coupled QM/FQ system becomes

$$\mathcal{F}(\mathbf{P},\mathbf{q},\lambda ;\mathbf{F})=\text{tr}\mathbf{hP}+\frac{1}{2}\text{tr}\mathbf{PG}\left(\mathbf{P}\right)+\frac{1}{2}{\mathbf{q}}^{†}\mathbf{Jq}+\chi \mathbf{q}+\lambda \mathbf{q}+{\mathbf{q}}^{†}\mathbf{V}\left(\mathbf{P}\right)-\mu \cdot \mathbf{F}$$

where μ is the dipole moment of the total system:

$$\mu ={\mu }^{\mathit{QM}}+{\mu }^{\mathit{MM}}=\sum _{\zeta =1}^{N_a}{Z}_{\zeta }{\mathbf{R}}_{\zeta }-\text{tr}\mathbf{M}+\sum _{j=1}^{N_q}{q}_j{\mathbf{R}}_j$$

From this definition, it is possible to derive the polarizability of the system as the second derivative of the energy with respect to the electric field:

$${\alpha }_{\alpha \beta }=\frac{{\partial }^2\mathcal{F}}{\partial F_{\alpha }\partial F_{\beta }}=-\frac{\partial {\mu }_{\alpha }^{\mathit{QM}}}{\partial F_{\beta }}-\frac{\partial {\mu }_{\alpha }^{\mathit{FQ}}}{\partial F_{\beta }}={\alpha }_{\alpha \beta }^{\mathit{QM}}+{\alpha }_{\alpha \beta }^{\mathit{FQ}}$$

The QM contribution to the polarizability depends on the response density matrix

$${\alpha }_{\alpha \beta }^{\mathit{QM}}=\text{tr}\frac{\partial }{\partial F_{\beta }}{M}_{\alpha }$$

which can be obtained by solving the electric CPHF equations (or, if the field is oscillating, the frequency-dependent CPHF equations)

$$(\tilde{\mathbf{A}}+\tilde{\mathbf{B}})(\mathbf{X}+\mathbf{Y})+2\mathbf{Q}=0$$ (A1)

where the right-hand side contains not only the dipole integrals (see section III), but also a contribution arising from the response of fluctuating charges. In fact, the derivative of the interaction operator, i.e.,

$$\frac{\partial ({\mathbf{q}}^{†}{\mathbf{V}}_{\mu \nu })}{F_{\beta }}={\mathbf{V}}_{\mu \nu }\frac{\partial \mathbf{q}}{F_{\beta }}$$

will contain two different terms which we will now derive. The FQ equations in the presence of an electric field are

$$\sum _{k=1}^{N_q}{J}_{\mathit{jk}}{q}_k=-{\chi }_j-V_j\left(\right)-{\lambda }_{\left(j\right)}+{\mathbf{R}}_j\cdot \mathbf{F}$$

where λ_(j) is the Lagrangian multiplier that enforces the total charge constraint on the molecule which the atom j belongs to; the perturbed FQ equations can be obtained by further differentiating with respect to the field:

$$\sum _{k=1}^{N_q}{J}_{\mathit{jk}}\frac{\partial q_k}{\partial F_{\beta }}=-V_j{(}^{F_{\beta }})+R_{j,\beta }$$

The contribution involving the derivatives of the density matrix is the one included in the definition of the modified response matrices $\tilde{\mathbf{A}}$ and $\tilde{\mathbf{B}}$, the second one has to be added to the right-hand side and can be considered a local field contribution. Finally, the FQ contribution to the polarizability can be assembled after solving the coupled perturbed equations:

$${\alpha }_{\alpha \beta }^{\mathit{FQ}}=\sum _{j=1}^{N_q}\frac{\partial q_j}{\partial F_{\beta }}{R}_{j,\alpha }$$

In the weak coupling scheme, the interaction of the FQs with the electric field is neglected, i.e., the term −μ^MM · F is dropped. This means that the polarizability will arise only from the response of the QM density to the electric field and not by the polarization of the FQs. Notice that, as already stated in section III, “polarization of the FQs”, in a response theory framework, means alteration of the magnitude of the FQs as an effect of the presence of the field and not the geometrical reorganization of the classical portion of the system (i.e., the alignment of the dipoles). This latter effect, the inclusion of which would be mandatory in a MD simulation in the presence of a static field, is indeed a “nuclear effect”, in the sense that it depends on the displacement of the classical portion in the space as a response to the field and not (or only in a minor proportion) an “electronic effect”, that is a rearrangement of its electronic density.

In our model, a polarizable force field is used to mimic the electronic component of the charge density of the environment and a contribution to the polarization arises in the response theory meaning, that is, as a rearrangement of the (polarizable) density of charge of the system. Hence, the contribution that we neglect in the weak coupling picture can be regarded as the electronic density contribution of the environment to the property. The are several reasons why the weak interaction scheme is not only consistent with the definition of a focused model, but also physically well justified. As a first, the key assumption of focused model is that the properties of the whole system are determined mainly by the core and perturbed by the presence of the environment. That is, they arise by the response of the system which is modeled in terms of the core’s Hamiltonian and the interaction operator, but not of the environment Hamiltonian. This is also the reason why a much cheaper description is used in focused models for the environment. The weak interaction picture corresponds exactly to this assumption: it is the core that responds to the external perturbation and the environment, by interacting with the core (and not, directly, with the perturbation) affects such a response. Notice that, especially when one is interested in properties that are extensive with the size of the system, the weak coupling provides an excellent strategy to avoid the spurious contributions arising from the extensivity, which can otherwise be removed only be means of a thorough statistical averaging.

A more physical justification to this assumption is provided by the normal experimental setup of properties measures. Let us use solvation as an example: if one wants to measure some property of a molecule in solution, one will assume that the solvent does not give a signal in the same range of the solute. To make a more specific example, when one measures a frequency-dependent property, one will be careful to choose a solvent which does not absorb at the wavelengths used in the experiment. In other words, in common experimental conditions, the direct interaction of the environment with the external fields is negligible.

Nevertheless, some further investigation on the influence of the interaction of the classical environment with the perturbing electric field on the system’s response properties is required and will be object of a future communication.