Consequences of Misspecifying the Number of Latent Treatment Attendance Classes in Modeling Group Membership Turnover within Ecologically-Valid Behavioral Treatment Trials

Abstract

Historically, difficulties in analyzing treatment outcome data from open enrollment groups have led to their avoidance in use in federally-funded treatment trials, despite the fact that 79% of treatment programs use open enrollment groups. Recently, latent class pattern mixture models (LCPMM) have shown promise as a defensible approach for making overall (and attendance class-specific) inferences from open enrollment groups with membership turnover. We present a statistical simulation study comparing LCPMMs to longitudinal growth models (LGM) to understand when both frameworks are likely to produce conflicting inferences concerning overall treatment efficacy. LCPMMs performed well under all conditions examined; meanwhile LGMs produced problematic levels of bias and Type I errors under two joint conditions: moderate-to-high dropout (30–50%) and treatment by attendance class interactions exceeding Cohen's d ≈.2. This study highlights key concerns about using LGM for open enrollment data: treatment effect overestimation and advocacy for treatments that may be ineffective in reality.

Introduction

It is well-known among substance abuse treatment researchers and practitioners alike that the majority of psychosocial interventions for the treatment of drug abuse and alcoholism treatment are delivered in group settings. In spite of the widespread use of therapy groups in substance abuse and alcoholism treatment, there has been a relative dearth of rigorous empirical research of group therapy for substance abuse (Weiss, Jaffe, de Menil & Cogley, 2004). Indeed, standing in stark contrast to the way treatment is delivered in community practice (see Klostermann, Fals-Stewart, & Morgan-Lopez, 2008), the portfolio of federally-funded research on psychosocial interventions for substance abuse has been dominated by studies of interventions delivered in a one-on-one counseling format (NIDA, 2003).

In response to the lack of research on group therapy, both NIDA and NIAAA sought to stimulate group therapy research by (a) the release of specific Requests for Applications (RFAs) which were explicitly geared towards group therapy research (e.g., RFA-DA-04-008; NIDA/NIAAA, 2003a) or b) including group research into updates of Program Announcements (PAs) that had been previously released (e.g., PA-03-126; NIDA/NIAAA, 2003b). As a result, there have been more research studies funded that have focused on group therapy for substance abuse, yet many well-founded concerns remain about the ecological validity (i.e., the match between treatment research designs and treatment-in-practice) of many currently-funded group-based trials (Morgan-Lopez & Fals-Stewart, 2007, 2008; Weiss et al., 2004).

Closed versus open enrollment groups

The majority of recently-funded group treatment trials use closed-enrollment groups, yet 79% of all substance abuse treatment programs¹ in the US use open-enrollment groups for treatment delivery (Klosterman et al., 2008); this discrepancy between the use of closed groups in practice and the use of open groups (or even individual therapies) in treatment research is at the heart of the ecological validity problem in substance abuse treatment research (Morgan-Lopez & Fals-Stewart, 2007). As described elsewhere (Morgan-Lopez & Fals-Stewart, 2006a, 2008), closed enrollment groups are formed with a core set of members and are designed to remain intact for a limited period of time. The typical length of closed treatment groups corresponds directly to the length of the prescribed treatment (e.g., if the treatment protocol calls for 6 sessions of treatment, the group only runs for 6 sessions and is disbanded thereafter) and, though membership dropout is usually inevitable, no new members are added after a specific point (usually after the initial session). However, in open enrollment groups, members can join the group at any point in time; coupled with graduations, termination and dropout, membership in open enrollment groups is in a state of constant flux.

Closed groups have the benefit of being easier to handle analytically because the nature of non-independence (i.e., nesting) of repeated measures from the same patients over time within therapy groups is clear (i.e., the composition of the group does not “change” over time; Morgan-Lopez & Fals-Stewart, 2006a). However, closed groups are neither practical nor economical for clinical practice (i.e., patients must wait until the requisite number of group members are available before they can begin treatment) nor do they reflect the reality of how treatment programs operate in general (Morgan-Lopez & Fals-Stewart, 2008). Data generated from open enrollment groups, on the other hand, have historically been difficult to analyze (at least in a statistically defensible manner) because membership turnover gradually changes the group composition over time; in fact, complete turnover in membership in open enrollment groups (nay times over for groups that run for extended periods of time) is the norm rather than the exception. Many treatment researchers who have proposed open enrollment group studies have faced significant criticisms in grant and/or manuscript review in part because of analytic (Morgan-Lopez & Fals-Stewart, 2006a) and logistical difficulties (Weiss et al., 2004) in executing open enrollment treatment trials. In the absence of resolutions to either set of these challenges, substance abuse treatment researchers have largely eschewed group therapy research to sidestep these issues (Morgan-Lopez & Fals-Stewart, 2006a, 2008).

Modeling group membership turnover

Among the substance abuse and alcoholism treatment studies that have used groups, irrespective of whether open or closed enrollment was used, there have been three primary approaches to handle group-level nesting in the presence of membership turnover (Morgan-Lopez & Fals-Stewart, 2006a, 2008): a) ignore group-level nesting (e.g., Fals-Stewart, Marks & Schafer, 1993), b) model group-level nesting in a conventional fashion, but assume that the continual addition (i.e., new admissions) and subtraction (i.e., dropout, termination, graduation) of members has no impact on group interdependence or treatment effects (e.g., Fals-Stewart, O'Farrell & Birchler, 2004) or c) model group-level dependency as session-specific (i.e., treat each session as a new “group”, irrespective of any overlap in group membership from session-to-session; Fals-Stewart, Cordova et al., 2005).

Approach “a” is well-known for increasing the likelihood of Type I errors in group-administered interventions (Baldwin et al., 2005; Hox, 2002; Snijders & Bosker, 1999). Approach “b” is ideal for contexts where group membership remains constant throughout the life of the study (Bryk & Raudenbush, 1992) but has been shown in at least one recent study to potentially lead to Type I errors with respect to treatment effect estimates when membership turnover is not accounted for (Morgan-Lopez & Fals-Stewart, 2007). Finally, approach “c” has been shown to be overly conservative, possibly leading to Type II errors (Fals-Stewart, Klostermann, Hoebbel & Kennedy, 2004).

One recently-developed approach, group-clustered latent class pattern mixture modeling (LCPMMs; Lin, McCulloch & Rosenheck, 2004; Muthén, Jo & Brown, 2003; Roy, 2003), provides a framework that more closely represents the process of turnover in group membership than traditional methods (e.g., group-clustered latent growth models) or even conventional pattern mixture models (Morgan-Lopez & Fals-Stewart, 2007). LCPMMs were primarily intended to model non-ignorable missing data, where the probability of missingness is related to the values of variables that are missing, even after conditioning on variables that are non-missing (e.g., dropout due to drug relapse in drug treatment studies; see Schafer & Graham, 2002). Morgan-Lopez and Fals-Stewart (2007) showed that LCPMMs can be structured to handle turnover in group membership under the following conceptual assumptions: that (a) there are hidden subpopulations (i.e., latent classes) within treatment groups, (b), the hidden populations are characterized by the joint variation in treatment attendance patterns and treatment outcomes and (c) that, as membership changes, the proportion of treatment group members from each patient subtype (e.g., consistent attenders, dropouts, irregular attendees) fluctuates from session-to-session and throughout the course of the trial.

In a recently reported trial comparing open enrollment group therapy (called Getting Along) to individual therapy for alcoholism, Morgan-Lopez and Fals-Stewart (2007) found that under conventional (group-clustered) longitudinal growth modeling (gLGM), group therapy was superior to individual therapy in reducing alcohol use over time through termination of treatment; yet under (group-clustered) latent class pattern mixture modeling no overall¹ differences between the two conditions were observed. These contrasting results highlight the most important aspect of the modeling issues in group therapy research; the choice of approach matters and, in this particular case (and probably many others), it matters greatly. Further study is required in order to see if it is the case that gLGMs are overly liberal or gLCPMMs are overly conservative³ when used to model membership turnover in treatment outcome studies.

Motivation for the Present Study

In this article, we describe a statistical simulation study comparing gLCPMMs and gLGMs on their relative accuracy in treatment effect estimation and inference. This study is motivated by our interest in understanding the practical consequences (e.g., biased treatment effects, incorrect inferences) of selecting an analysis that is potentially sub-optimal (i.e., group-clustered LGM⁴) for modeling rolling group data; however, there may be circumstances when both approaches produce equivalent results, unbiased estimates and correct inferences the expected proportion of the time (i.e., 95%). Delineating the circumstances under which these approaches produce convergent and divergent results is not only of significant importance to those who are now doing some form of group therapy research, but also to those who will be moving their programmatic lines of research in this direction as interest in ecologically-valid group therapy research grows.

Method

Primer on Statistical Simulation

Prior to describing the simulation study, we felt it appropriate to familiarize readers with the execution of simulation studies in general. Statistical simulation studies, also commonly referred to as Monte Carlo studies (Muthén & Muthén, 2002), at their root, are investigations where sample data are artificially generated (and subsequently analyzed) from a population with known parameters (e.g., variances, regression coefficients); this process is designed to mimic the analogous process in “real” studies, where we take a sample of individuals from a population, collect data on the sample, and analyze their data to estimate population parameters based on the sample at hand.

The fundamental difference between simulated data and real data (aside from the artificial data versus real data distinction) is that the true population parameters will always be unknown in real data, but are known and manipulable by the researcher conducting the simulation. This point of unknown population parameters in studies with real data, though familiar to anyone who has taken an introductory undergraduate statistics course, cannot be overemphasized with respect to simulation studies. In a real treatment outcome study, one can never know how close the sample estimates of interest (e.g., the treatment effect estimate) are to the corresponding true population parameters (e.g., the true treatment effect). However in simulation studies, because the population parameters are known, the estimates from a series of simulated samples can be directly compared to the true values in the population using many different metrics (Collins, Schafer & Kam, 2001; MacKinnon et al., 2002, 2004; Morgan-Lopez & MacKinnon, 2006).

Simulations can be conducted in general statistical packages such as SAS and SPSS or in many “model-specific” packages (e.g., Mplus, EQS, or LISREL in structural equation modeling). The key technical component of statistical packages that have simulation facilities is the random number generator, which allows artificial “variables” to be generated across a specified number of observations (i.e., artificial cases) under a specified population model; in many programs, these variables can be generated from a number of different distributions including normal (e.g., SAS rannor function), uniform (e.g., SAS ranuni) poisson (e.g., SAS ranpoi) just to name a few. Random number generation allows simulation modelers to generate the stochastic components of a model; the stochastic components of a model (e.g., predictor variables, residuals) are any components that vary across a particular set of units (e.g., individual cases, groups of cases). For example, in a simple regression model, the lone predictor “X” is a stochastic component, as the value of X, by definition, varies across individuals. The error term in a regression model is also stochastic; the residual terms vary across individuals as well. However, the regression coefficient in simple regression is the same for all individuals, or fixed.

In a very basic simulation model, three components are necessary: (a) specification of the number of observations to be generated (i.e., the simulated sample size); (b) generation of stochastic terms from a known distribution which vary across observations (e.g., predictors and residual terms) and (c) specification of fixed terms that do not vary across observations (e.g., intercepts, regression coefficients). The simulated data of sample size N can then be analyzed in the same way a real data set would be analyzed. This process of “generate-then-analyze” can be repeated K times and would be a direct analog to the process of replicating a real treatment outcome study K times with successive new samples of size N. In simulation studies, given the possibility of comparing the sample estimates from each artificial sample to population parameters (in a way that cannot be done with real studies), simulation researchers can assess a number of properties of study designs and estimation procedures. For example, for a given statistical model, population parameter and sample size, a researcher can study the proportion of times the estimate of a key parameter is significantly different from 0 across K artificial samples, each of size N (i.e., statistical power; see MacKinnon et al., 2002; Muthén & Muthén, 2002) or the discrepancy between a population parameter and the average estimate of that parameter across K artificial samples (i.e., parameter estimate bias; see Collins et al., 2001; Morgan-Lopez & MacKinnon, 2006a). Many other indicators of statistical performance can be examined across an infinite number of conditions (e.g., sample size, effect size, (im)proper model specification) in simulation studies; in fact simulations are used more as the rule rather than the exception in a number of different areas (e.g., quantitative psychology) and are even used frequently as a method for determining power in NIH grant submissions (Muthén & Muthén, 2002).

Hypothetical Context for the Simulation

The simulation is set within the hypothetical context of a study of the comparison of two treatments for alcoholism (N = 150), which we will call “Treatment A” (focal treatment condition) and “Treatment B” (comparison condition/TAU). Treatment A is a group-administered treatment where there are three rolling treatment groups, each of which can have between 3 and 9 members on any given week. Treatment B is an individually-administered therapy. Both treatment protocols call for 6 weeks of treatment. The trial period lasts for 21 weeks, with open enrollment into each group (or into individual therapy) lasting from weeks 1 through 16 (i.e., no new admissions after week 16).

Model Overview

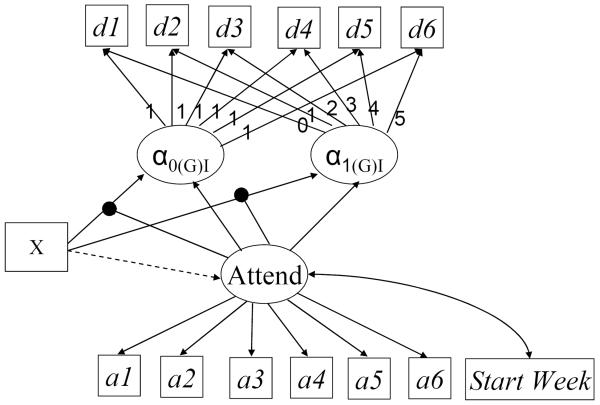
In this simulation study, the focal population model is a 3-Class, six timepoint (group-clustered) LCPMM model as shown in Figure 1, which is directly linked to our hypothetical treatment outcome study. The gLCPMM is both a special case of the general mixture SEM model which handles both continuous latent (e.g., growth parameters) and categorical latent (e.g., latent classes) variables (Muthén, 2002) and an extension of classical pattern mixture models for non-ignorably missing data (Hedeker & Gibbons, 1997; Schafer, 2003).

Figure 1.

Latent Class Pattern Mixture Model. Attend = Latent Attendance Class Variable. d₁-d₆ = Observed simulated outcome variable (e.g., past week substance use) from person weeks 1-6. a₁-a₆ = Binary indicators of treatment attendance from weeks 1-6. StartWeek = The week that the trial was in when individual i joined the trial (ranges from trial week 1 to trial week 16). X = Treatment condition (Open Enrollment Group = 1; Individual Therapy = 0). α_0GI = estimated level of the outcome at time = 0 (i.e., baseline). α_1(G)I = estimated rate of per week change in the outcome from weeks 1-6. Paths from “Attend” to the growth parameters (i.e., α_0(G)I, α_1(G)I) indicate that the conditional means of the growth parameters vary across attendance class. Paths from “Attend” to the X → growth parameter links (as connected by the “dots”) indicate that the treatment effects vary across attendance classes.

The focal point of the gLCPMM model is a categorical latent variable (called “Attend” in Figure 1) which represents membership in one of a finite number of latent classes (e.g., Attend = 1, 2…..C). This variable captures the fact that multiple hidden subpopulations may exist within our treatment outcome data. In gLCPMMs, as used for open enrollment group treatment outcome analyses (e.g., Morgan-Lopez & Fals-Stewart, 2007), differences among multiple hidden subpopulations, if there is indeed more than one subpopulation, manifest themselves in between-class differences among three sets of variables (see Figure 1).

First, differences across classes can manifest themselves in differences in the probabilities of treatment attendance on a₂ through a₆, which are binary indicators of whether each patient showed up for treatment at time t (0 = no-show, 1 = show) beyond the initial session for each person; these patterns over time may show consistently high probabilities of attendance for one class (i.e., consistent attenders) or steeply decreasing probabilities of attendance for another class (i.e., dropouts). Second, differences may emerge on the distributions of the timing of treatment entry (i.e., “Start Week”) which may show (a) fluctuations over time in the proportions of patients from each sub-population and (b) be indicative of variation in the makeup of treatment groups that is dependent on calendar time (Morgan-Lopez & Fals-Stewart, 2007, 2008). Finally, differences across classes may emerge on differences in the impact of the treatment condition (“Tx A v. Tx B”) on growth over time in the outcome (i.e., β_I, treatment effects on alcohol use).

For example, in Morgan-Lopez and Fals-Stewart (2007), different attendance classes produced different patterns of treatment attendance (i.e., proxy for missingness) over time, and within each of these attendance patterns, a different pattern of findings emerged with regard to treatment effects for alcohol use (i.e., group treatment was better for erratic attendees, individual treatment was better for those who would eventually dropout); in this case, gLCPMMs also present opportunities for latent moderator effects to emerge from class-specific estimates of treatment efficacy.

If there is more than one class, the growth parameters (i.e., conditional growth parameter means, treatment effects) from each class are averaged and weighted by the class proportions and standard errors are calculated using the delta method (see Hedeker & Gibbons, 1997, p.74–76, Morgan-Lopez & Fals-Stewart, 2007, p.593) in order to estimate the overall treatment effect.

Population Parameters

Several of the key population parameters that were manipulated in the simulation, are loosely related to parameter estimates from the LCPMM exemplar illustrated in Morgan-Lopez and Fals-Stewart (2007). These include (a) class-specific treatment effect sizes, b) the probabilities of missingness/attendance at time t (conditional on attendance class), c) the attendance class proportions and (d) the signs of the class-specific treatment effects. Various combinations of these factors were mixed-and-matched to examine the impact of purposeful (mis)specification of the number of classes (i.e., 1-class, 2-class), relative to the number of classes that exist in the population (i.e., 3), in analyzing open enrollment treatment data on the accuracy of treatment effect estimation under a variety of population scenarios. The improper specification of the single-class model is key, because it is directly analogous to the decision that behavioral treatment researchers make if they were to analyze open enrollment group data with conventional LGM. Until recently, LGM was the best and only choice that behavioral treatment researchers had (i.e., group-clustered growth models) in modeling treatment outcome data from open enrollment groups. Though initial evidence suggests that this approach may not be optimal for open enrollment data, it is clear that, in many cases, the treatment research community was “doing the best they c(ould) with what they ha(d)” (Morgan-Lopez & Fals-Stewart, 2007, p.591).

Attendance Patterns

The attendance patterns (i.e., probabilities for a₂ through a₆) for each of the three classes are described as follows: (a) Consistent Attenders: set to fluctuate between 74% and 93% probability of “attendance” across Weeks 2 through 6 of treatment; (b) Dropouts: set to have a constant decrease in the probability of attendance from 43% at Week 2 to 11% by Week 6; and (c) Erratics: probabilities of attendance were 20% for Week 2, 90% for Week 3, 20% for Week 4, 70% for Week 5 and 90% for Week 6. It is noted that if a 0 is generated for any given case in a simulated sample, based on the conditional probabilities of time t attendance in the population, then the corresponding value on the outcome (Y_T) was set to missing.

Class-Specific Treatment Effects

Class-specific population treatment effects, defined as mean differences in growth over time on the outcome variable across the two treatment conditions (i.e., Tx A v. Tx B → β_(G)I), corresponded to r²s of .01, .14 and .43; these correspond directly to the class-specific r²s observed in Morgan-Lopez and Fals-Stewart (2007). These r² values were converted to regression coefficients via covariance algebra (see Appendix A); the r²s of .01, .14 and .43 corresponded to regression coefficients of |.263|, |.815| and |1.73|.

Class Proportions

The proportions of the population from each attendance class (i.e., Consistents, Dropouts, Erratics) varied across each combination and could be set to 50%, 30% or 20%.

Cross-matching of Population Parameters

Class-specific treatment effects and class proportions were cross-matched under each attendance class; this cross-matching produced a total of 36 possible treatment effect/class proportion combinations

Sign of Class-Specific Treatment Effect

Based on limited pilot simulation work (Morgan-Lopez & Fals-Stewart, 2006b) and observations from real data (Morgan-Lopez & Fals-Stewart, 2007), we observed that there was a greater possibility of distortion of overall treatment effect estimates when the class-specific treatment effects were opposite in sign (e.g., treatment A is more efficacious for one class, treatment B is more efficacious for another). As a result, the 36 treatment effect/class proportion combinations were crossed with 7 treatment effect sign combinations (see Table 2) which produced a grand total of 252 possible combinations.

Random subset of combinations

In lieu of an examination of each of the 252 possible combinations, a random subset of 36 of these combinations (see Table 1) was examined in this simulation study; 18 of these were randomly selected from the 36 “all positive sign” set of combinations while the other 18 were randomly selected from the remaining larger set of 216 overall combinations. We aimed to balance coverage of a reasonable range of population conditions against computational burden.

Table 1.

Cross-Matching of Simulation Parameters

Combination	C%	Cγ	E%	Eγ	D%	Dγ	Weighted-Average γ
1	50%	1.73	30%	.263	20%	.815	1.1069
2	50%	.815	30%	1.73	20%	.263	.9791
3	50%	.815	30%	.263	20%	1.73	.8324
4	50%	1.73	20%	.263	30%	.815	1.1621
5	50%	.815	20%	.263	30%	1.73	.9791
6	50%	.263	20%	1.73	30%	.815	.722
7	50%	.263	20%	.815	30%	1.73	.8135
8	30%	1.73	50%	.815	20%	.263	.9791
9	30%	.815	50%	1.73	20%	.263	1.1621
10	30%	.263	50%	1.73	20%	.815	1.1069
11	30%	.263	50%	.815	20%	1.73	.8324
12	20%	1.73	50%	.815	30%	.263	.8324
13	20%	.263	50%	1.73	30%	.815	1.1621
14	20%	.263	50%	.815	30%	1.73	.9791
15	20%	1.73	30%	.815	50%	.263	.722
16	20%	.815	30%	.263	50%	1.73	1.1069
17	20%	.263	30%	1.73	50%	.815	.9791
18	20%	.263	30%	.815	50%	1.73	1.1621
19	50%	−.263	30%	1.73	20%	.815	.5505
20	50%	−.815	20%	.263	30%	1.73	.1641
21	30%	−.263	50%	.815	20%	1.73	.6746
22	50%	.263	20%	−1.73	30%	.815	.0300
23	30%	.263	20%	−1.73	50%	.815	.1404
24	20%	1.73	30%	−.815	50%	.263	.2330
25	20%	−.815	50%	−1.73	30%	.263	−.9491
26	20%	−1.73	30%	−.815	50%	.263	−.459
27	20%	−1.73	30%	−.263	50%	.815	−.0174
28	50%	.815	30%	1.73	20%	−.263	.8739
29	30%	.815	20%	.263	50%	−1.73	−.5679
30	20%	.263	30%	.815	50%	−1.73	−.5679
31	50%	−.815	30%	.263	20%	−1.73	−.6746
32	20%	−1.73	30%	.815	50%	−.263	−.233
33	20%	−1.73	30%	.263	50%	−.815	−.6746
34	50%	1.73	20%	−.815	30%	−.263	.6231
35	20%	1.73	30%	−.815	50%	−.263	−.0300
36	20%	.815	30%	−1.73	50%	−.263	−.4875

Notes. C = Completers. E = Erratics. D = Dropouts. γ = regression parameter for the treatment effect on growth over time on the outcome.

For instance, it was estimated that an analysis of each of 250 replications (i.e., simulated datasets) for one combination would take a total of 6.75 hours⁵ in running 1-class (15 minutes), 2-class (2 hours) and 3-class (4.5 hours) LCPMMs in succession on the same dataset(s). Based on this estimate, completion of an analysis of all 252 combinations would take 71 days if each analysis was run continuously with manual restarting of the analysis in Mplus, irrespective of the time of day (or night) that the previous analysis terminated. Even if simulated data from two full combinations per day were analyzed from start-to-finish (requiring ≈ 14 hours of computing time per day) it would still require over four months to complete.

In addition to the challenges outlined above, we also concluded that a random subset of the possible combinations would still provide reasonable variability in the combinations of population parameters (i.e., treatment effect sizes/signs, class proportions). This strategy is in the same spirit as the fractional factorial design, used when the interest is in examining a selected subset of all possible combinations of several independent variables in an experiment where resources are conserved and lower-order interaction effects of interest (e.g., 2-way interactions) can still be examined (Box, Hunter & Hunter, 2005).

Constants across conditions

Although several key factors were manipulated in the simulation study, there were a number of factors that were held constant across simulation conditions. As noted earlier, for each combination of treatment effect sizes/class proportions, there were always three classes in the population and each simulated dataset (250 per combination) had a sample size of 150. This was done to roughly represent the median sample size in behavioral treatment outcome studies. Group-level population variance components were set such that the group-level accounted for a) 4% of the variability in the intercept, α_(G)I (i.e., an intercept ICC of .04) and b) 1% of the variability in the slope, β_(G)I (i.e., a slope ICC of .01). Individual-level variance components for the intercept and slope were set to 1 in the population. Finally, the distributions for the week of trial entry variable were generated to be consistent with what was observed in Morgan-Lopez and Fals-Stewart (2007). The week of trial entry variable was generated from a uniform distribution with values ranging from 1–16 for the consistent attenders class and the dropout class. For the Erratics class, week of trial entry variable was generated from a bimodal distribution where the two modes were 1 and 16.

Simulation heuristics

First, simulated data were generated in SAS v9 under a 3-class latent class pattern mixture population structure, with population values for the class-specific treatment effects/signs and class proportions set based on the particular combination; 250 replications were generated, each with N = 150. Once generated, each of the 250 datasets was analyzed in Mplus v4.21 in the External Montecarlo analysis framework (Muthén & Muthén, 1998–2006, p.275) under maximum likelihood estimation for non-normal data and/or non-independent observations (Asparouhov, 2004; Yuan & Bentler, 2000). Each dataset was analyzed under three different scenarios: (a) correctly analyzed as a 3-class gLCPMM; (b) incorrectly analyzed as a 2-class gLCPMM (which still accounts for turnover in membership and non-ignorable missingness but estimates too few classes); and (c) incorrectly analyzed as a single-class gLCPMM (analogous to a conventional gLGM model and assumes that membership turnover is irrelevant and data are missing-at-random). The parameter estimates and parameter covariances from each set of analyses were saved; for 2- and 3-class LCPMMs, the weighted averaged treatment effect estimates and standard errors were calculated using the delta method (see Hedeker & Gibbons, 1997, p.74–76, Morgan-Lopez & Fals-Stewart, 2007, supplemental materials available at http://dx.doi.org/10.1037/0022-006X.75.4.580.supp).

Results

Analysis of Simulation Results

Simulation outcomes

Two outcome variables were calculated from the output of the analysis of simulation data, with a focus on discrepancies between the population values and sample estimates of the weighted averaged treatment effect (WATE): standardized bias and confidence interval coverage.

Bias in simulation studies generally refers to the discrepancy between a known population parameter and the average estimate of that parameter across K simulated samples (see, for example, Muthén & Muthén, 1998–2006, p.281). However, whether bias is “small” or “large” in impact is dependent on the size of the “overall level of uncertainty” in estimating the parameter (Collins et al., 2001, p.340). To put bias on a more interpretable metric, Collins and her colleagues (2001) developed the standardized bias measure, 100 × (â − α)/ SE, where in this study â is the mean of the WATE estimates across all 250 replications per condition, α is the population WATE for the condition and SE is the standard deviation of the simulated distribution of the WATE estimates across the 250 replications; this measure capture the bias in relation to the overall level of sample-to-sample variability in estimating the treatment effect. Using the criteria outlined in Collins et al., (2001), standardized bias exceeding ±40% was considered problematic (i.e., severe under/overestimation of the WA treatment effect).

A second outcome variable of interest is confidence interval coverage. Coverage is defined as the proportion of times that a statistical method (e.g., 1-, 2- and 3-class LCPMM) produces confidence intervals that contain the population parameter (e.g., the true weighted averaged treatment effect in the population), irrespective of the actual inference made from the analysis; coverage rates are the direct inverse of Type I error. Optimal methods should produce confidence intervals that contain the true population parameter 95% of the time (just as the Type I error rate should ideally be .05), with coverage rates at or below 90% (Type I error rates above .10) considered problematic (Collins et al., 2001). A robustness interval of 92.5–97.5% coverage (Bradley, 1978) was used to indicate empirical coverage rates that did not deviate meaningfully from 95%.

General Simulation Results Summary

Three-class models

When simulation data were properly analyzed as a three-class LCPMM model, none of the 36 treatment effect by class proportion combinations yielded confidence interval coverage rates below 90% for the weighted-averaged overall treatment effect nor did any of the combinations yield standardized bias rates that exceeded ±40%. Two out of the 36 combinations had coverage values that fell outside of the robustness interval (i.e., fell between 90.1–92.4%) but did not fall below 90%. It was also noted that, although the models generally produced accurate estimates and inferences (as expected), the models produced anywhere from 0 to a maximum of 6.4% non-converged models (16 out of 250) across all combinations; this suggests that there is a small risk of not being able to get a proper solution in 3-class LCPMMs with sample sizes of N = 150.

Two-class models

Even when simulation data were purposefully mis-analyzed under two-class LCPMM models, none of the 36 treatment effect by class proportion combinations yielded confidence interval coverage rates below 90% for the weighted-averaged overall treatment effect nor did any of the combinations yield standardized bias rates that exceeded ±40%. Five out of the 36 combinations had coverage values that fell outside of the robustness interval (i.e., fell between 90.1–92.4%) but did not fall below 90%. There was also a maximum of 3.2% (8/250) non-converged solutions under the 2-class framework.

Single-class models

When simulation data, generated under a 3-class LCPMM population model were analyzed under a single-class model (analogous to conventional growth modeling) only 15 out of the 36 combinations (41.6%) of the combinations examined had confidence interval coverage rates for the treatment effect within the specified robustness interval. Thirty-three percent (12/36) of the combinations examined yielded coverage rates below 90% (i.e., Type I error rates above .10); in fact, problematic coverage values ranged as low as 69.6% (i.e., Type I error rate of 31.4%). The other 9 combinations had coverage rates that fell out outside the robustness interval but not below 90% coverage. Fifty-eight percent of the combinations (21/36) examined produced standardized bias values that exceeded ±40%.

Analysis of Single-Class Simulation Results

It was clear from the summary of simulation results that specifying a single-class analysis for simulated rolling group data when multiple classes exist in the population can lead to biased estimates and higher-than-acceptable rates of Type I errors in many cases. Although the majority of the conditions examined in this study produced high rates of over/under-estimation of treatment effects and poor confidence interval coverage rates, there were some combinations of class-specific treatment effects and class proportion/class type matches that produced minimal bias and acceptable coverage rates even when the analysis was misspecified. As a result, we analyzed the outcomes of the simulation in order to account for variability in the impact of model misspecification; in other words, we were interested in answering the question “When does choosing LGM to analyze data generated under the LCPMM model lead to greater problems analytically?”

It was suspected that combinations where the discrepancies between the three class-specific treatment effects were small would have been most likely to produce standardized bias values and confidence interval coverage rates that were acceptable. In fact, this would be consistent with Hedeker and Mermelstein's (2000) assertion that, when data are missing-at-random, the treatment effect does not differ appreciably across the cause of (or patterns of) missingness. This may suggest that, the more similar the treatment effects are across attendance classes (i.e., as treatment X class interaction effects approach 0), the closer these data are to MAR and thus not need a non-ignorable missingness model such as LCPMM. So, at least a priori, we anticipated that as the size of the discrepancies between class-specific treatment effects (in essence, treatment x class interaction effects) were large, bias and coverage rates (under the single-class LCPMM/LGM) would be worse.

However, upon visual inspection of a table of simulation results, it appeared that the following combinations of factors seemed to produce low coverage/high bias when simulation data were (mis)analyzed under a single-class framework: a) heavy missingness (dropout class ≥ 30%) and “high” treatment effect discrepancies between the Completers Class and the other two classes. As a result, these two factors (along with size of the Completers class) were examined as predictors of bias and coverage in order to quantify the conditions under which model misspecification has little-to-no impact on treatment effect estimation and when it has a large impact on treatment effect estimates.

Key Predictors

Proportion of the Dropout Class

The dropout class proportions could take values of 20%, 30% or 50%, consistent with the corresponding condition as shown in Table X.

Proportion of the Completers Class

The completers class proportions could also take on values of 20%, 30% or 50%, consistent with the corresponding condition as shown in Table 1.

Treatment Effect Discrepancy

The treatment effect discrepancy (TED) measure is a contrast comparing the Completers treatment effect against the average treatment effect of the other two class types (e.g., Erratics, Dropouts) in a Cohen's D effect size metric. To capture this, we first calculated the absolute value of the difference between the completers' treatment effect and the average treatment effect in the other two classes (only for the results from datasets where the estimation procedure converged on an admissible 3-class solution) as follows:

$$\mid {\gamma }_{\mathit{Completers}}-\left(\frac{{\gamma }_{\mathit{Erratics}}+{\gamma }_{\mathit{Dropouts}}}{2}\right)\mid$$ (1)

We then derived and calculated the standard error for this discrepancy measure (See Appendix B) for each dataset, calculated the z-test value for the discrepancy measure and then converted the t-test value to a Cohen's D effect size based on the formula found in Rosenthal and Rosnow (1991).

Outcomes

Although the predictors listed above correspond to measures derived from the three-class models, the outcomes (standardized bias, coverage) correspond to the results from the single-class models. The two outcome variables were a) (the absolute value of) standardized bias from the single-class analysis and b) confidence interval coverage from the single-class analysis. The three-class discrepancy measures and dropout class proportions were merged with the single-class bias and coverage outcomes based on identification with the same simulated dataset (note that the bias and coverage measures from the single-class datasets that produced non-converged solutions under three-class analysis were dropped from this analysis). The logic underlying these analyses is “Given the size of the treatment effect differences across classes and size of the dropout class when a dataset is analyzed properly with three classes, how problematic is it to analyze the same dataset with the wrong method (single-class analysis)?” Simulation results were analyzed under the generalized linear mixed modeling framework, as the 8700+ datasets were nested within the 36 study combinations. Variability in standardized bias was examined under SAS Proc MIXED and variability in coverage was examined in SAS Proc GLIMMIX. It is noted that, because standardized bias is a summary measure across all replications, the value does not vary from datasetto-dataset within each of the combinations under study; however, coverage varies from dataset-to-dataset within a combination.

Standardized Bias

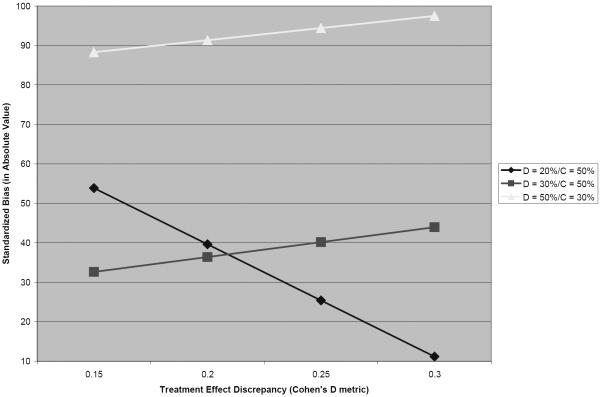
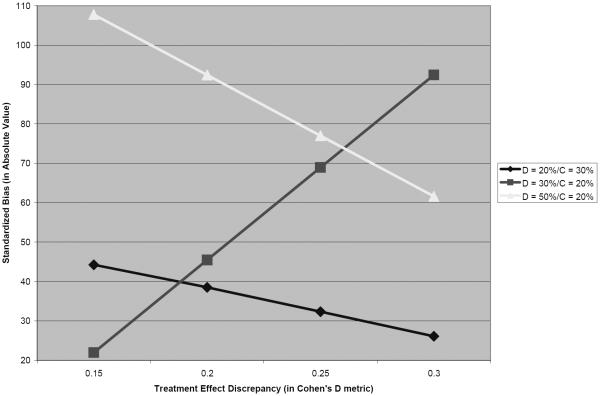
There was a 3-way interaction effect between Dropout Class proportion x Completer Class proportion X TED on standardized bias, b = 602.56 (23.97), t = 25.14, p<.0001. The predicted values of standardized bias (in absolute value) were calculated and plotted (see Figures 2 and 3) across the ranges of Dropout Class proportion (20–50%) and a range TED values in Cohen's D metric; the figures are separated based on a) the highest possible proportion for the Completers class (Figure 2) and b) the lowest possible proportion for the Completers class (Figure 3).

Figure 2.

Treatment Effect Discrepancy by Dropout Class Proportion Interaction: Standardized Bias (When the Completers Class Size is Highest).

Figure 3.

Treatment Effect Discrepancy by Dropout Class Proportion Interaction: Standardized Bias (When the Completers Class Size is Lowest).

Based on the plot in Figure 2, bias appears to be more pronounced as the size of the Dropout class gets larger when the Completers class is as large as possible. When the dropout class is 50% of the population, predicted bias exceeds more than twice the level of bias that is considered problematic by Collins and colleagues (2001), irrespective of the size of the treatment effect discrepancy across classes (within the range of TED values studied); in general, bias did not exceed problematic levels when the Dropout class consisted of ≤ 30% of the population.

The general trend was similar when the Completers class was as small as possible (relative to the sizes of other two classes; Figure 3); bias was severe when the Dropout class was 50% of the population though, oddly, it appeared to decrease as the treatment effect discrepancy increased. When the Dropout class was 20% of the population, bias was generally lower than 40% across the range of TED values studied. However, when the Dropout class was 30% of the population (and the Completers = 20%/Erratics = 50%), bias increased sharply as the size of the discrepancy between treatment effects across classes increased.

Confidence Interval Coverage

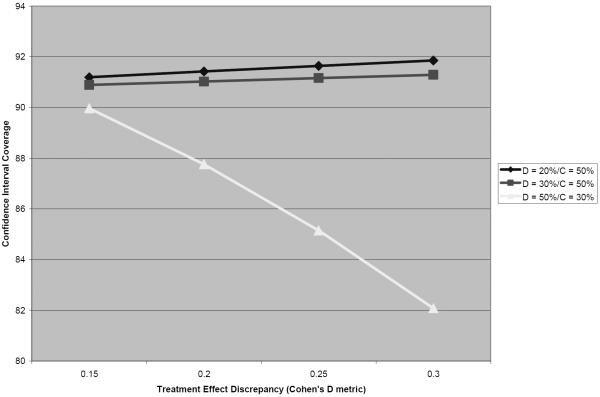
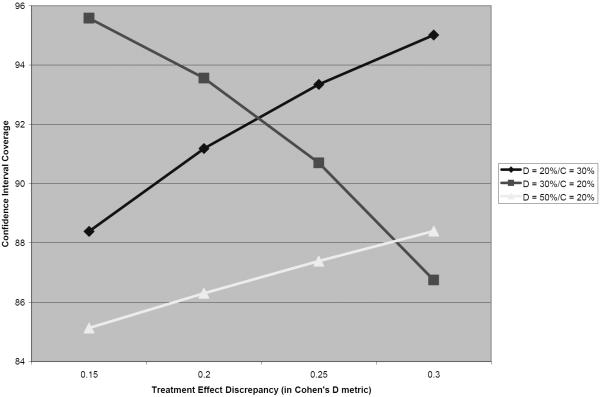
There was a 3-way interaction effect between Dropout Class proportion x Completer Class proportion X TED on confidence interval coverage, b = −18.56 (9.22), t = −2.04, p=.04. The predicted proportions for CI coverage were calculated and plotted (see Figures 4 and 5) across the ranges of Dropout Class proportion (20–50%) and a range of TED values in Cohen's D metric; the figures are separated based on a) the highest possible proportion for the Completers class (Figure 4) and b) the lowest possible proportion for the Completers class (Figure 5).

Figure 4.

Treatment Effect Discrepancy by Dropout Class Proportion Interaction: Confidence Interval Coverage (When the Completers Class Size is Highest).

Figure 5.

Treatment Effect Discrepancy by Dropout Class Proportion Interaction: Confidence Interval Coverage (When the Completers Class Size is Lowest).

Based on the plot in Figure 4, coverage does not drop below 90% when the Dropout class ≤ 30% of the population (and the Completers class is as large as possible), irrespective of the size of the discrepancy in treatment effects across classes. However, when the Dropout class was 50% of the population (and Completers = 30%/Erratics = 20%), CI coverage rates dropped to a rate of well below was is acceptable as the size of the TED increased; in fact, when the TED approached a Cohen's D of .3, the Type I error rate approached a rate of four times (.18) the rate that a researcher would believe he/she was operating under when incorrectly specifying a single-class model.

The general trend for coverage was different when the Completers class was as small as possible (relative to the sizes of other two classes; Figure 5); coverage was consistently below 90% across the range of TED under study when the dropout class was 50% of the population, though (again, unexpectedly) it appeared to increase as the treatment effect discrepancy increased. When the Dropout class was 20% of the population, coverage rates increased as the TED values increased. However, when the Dropout class was 30% of the population (and the Completers = 20%/Erratics = 50%), coverage rates decreased sharply as the size of the discrepancy between treatment effects across classes increased.

Discussion

Oveview of findings

The results from this study indicate that, when multiple-class LCPMM data are analyzed under conventional growth modeling, there is a non-trivial risk of observing (a) problematic discrepancies between the true treatment effect and the estimated treatment effect within a sample, and (b) making incorrect inferences concerning the sample treatment effect; in fact, bias and coverage reached problematic levels across the majority of conditions examined in this study. However, our interest was in understanding the variation in bias and coverage when we analyzed 3-class open enrollment data under LGM, as there were conditions where selecting the wrong analytic framework still led to accurate estimates and inferences.

Implications

Thus, here are some of the general conclusions, and with them, recommendations for when treatment researchers need to be careful about using conventional growth models for modeling data from open enrollment group therapy trials:

• 1)Heavy dropout is problematic when the size of the differences in treatment effects across classes exceeds Cohen's D = .15.

Under conditions 50% dropout and attendance class by treatment interaction effects that exceed a Cohen's D of .15, we found that bias and coverage reached problematic rates across the entire range of treatment effect discrepancies (TED) under study. When the Completers class was the next largest class (30%), the findings were more clear cut and consistent with expectations: a) standardized bias never decreased below 88%, which is more than twice the acceptable level of bias (see Figure 2) and b) confidence interval coverage dropped to the point where the Type I error rate could reach above three times the rate (18%) a researcher would believe s/he was operating under (5%) (Figure 4).When the Erratics class was the next largest class (30%), findings were somewhat counterintuitive: as the treatment effect discrepancy increased, standardized bias decreased (Figure 3) and coverage rates increased, though within the range of TEDs studied, both were still in the problematic range based on model predicted values.

• 2)Moderate dropout (30%) in combination with increasing TEDs across classes can be problematic

When moderate dropout existed in our simulated open enrollment trial data, bias and coverage was problematic under the following combination of circumstances: when the TED increased and when the Erratics class was the largest class in the population (50%). Steep increases in standardized bias (Figure 3) and steep decreases in confidence interval coverage (Figure 5) occur under moderate dropout as the TED increases (if the Erratics class is the largest class); however, bias and coverage are not problematic when moderate dropout exists and the Completers class is the largest class (Figures 2 and 4).

• 3)Strange findings are possible when there is a great deal of intermittent treatment attendance

The results from this study were generally intuitive when the Erratics class was not the largest class. In this situation, the consequences of selecting the incorrect analysis framework were greater as the treatment effect discrepancy increased so long as the Erratics class was the smallest class (see Figures 2 and 4). However, as the Erratics class size was larger, some conditions look better as the treatment effect discrepancies looked worse relative to the predicted values of standardized bias and confidence interval coverage (Figures 3 and 5). Further complicating matters is the fact that, under the combinations where the Erratic class was 50% of the population, the observed coverage values never drop below 90%, regardless of a) the size of the treatment effect discrepancy or b) the sizes of the other two classes, a phenomenon requiring further study among quantitative methodologists interested in the behavior of latent class pattern mixture models in general.

At first glance, these results related to high levels of intermittent attendance may be seen as irrelevant, because the likelihood of the emergence of such a pattern in substance abuse treatment may generally be considered low. In Morgan-Lopez and Fals-Stewart (2007), the Erratics class only composed of 12% of the sample, and the majority of those patterns occurred during specific points of the calendar year that are intuitively related to intermittent attendance (e.g., the Winter holiday season). However, it may be premature to suggest that intermittent attendance by patients cannot occur in larger proportions and may be population-specific. For example, there tends to be a relatively high proportion of women who have comorbid substance abuse disorders and PTSD symptoms who attend treatment intermittently because they choose to modulate the amount of re-exposure to the trauma during treatment by consciously limiting the number of sessions they attend consecutively (Hien, D.A., personal communication, 17 June 2007).

• 4)When in doubt, execute LCPMM and conventional LGM if treatment effect discrepancies occur across attendance classes

The practice of sensitivity analysis in modeling data that has some form of non-ignorable missingness is not new (Schafer & Graham, 2002) and such a recommendation is in order for the present context. As we have shown, there may be some clear and identifiable conditions where divergent inferences are more likely between the two approaches than others. The primary conditions where diverging inferences may be anticipated are when treatment effect discrepancies are observed across attendance classes that are between small and medium in effect size (e.g., Cohen's D ≈ .2) and moderate-to-heavy dropout is expected; other situations where conflicting inferences would occur between LCPMM and LGM are much less clear. As such, it is probably prudent to examine open enrollment treatment data under both frameworks in order to get a sense for the level of impact of missingness that may be conditionally related to unobserved values of the outcome of interest (i.e., alcohol/drug use) and membership turnover on estimates of treatment efficacy.

There may be some temptation on the part of substance abuse treatment researchers to dismiss these findings and suggest that the conditions under study in this simulation work may not represent the reality of treatment research and practice settings (i.e., “I don't need to worry about this, so I'll stick to LGM”). This line of thinking may be correct if investigators can be reasonably assured that they can (a) mitigate dropout from their studies successfully and, more importantly, and (b) be reasonably certain that their treatment effects will be exactly the same for patients who show up consistently for treatment and for those who are prone to dropping out. However, experts on missing data in clinical trial contexts (Schafer & Graham, 2002) and subsequent empirical work with data from open enrollment groups (Morgan-Lopez & Fals-Stewart, 2007) suggest that those assumptions may be tenuous at best.

Limitations

Although this study gives some initial clues into the consequences of model misspecification on treatment effect estimation in open enrollment trial data, this study was purposefully limited in scope. However, these limitations do have some impact on how this study should be viewed more globally. Because all possible combinations of class-specific treatment effects, attendance class proportions and treatment effect signs were not examined correlations between predictors in the analysis of simulation data may have contributed to some distortions in predicted values (Pedhazur, 1991). Although the overall trends in relation to the factors examined in the study may be generally valid, the predicted values represented in Figures 2–5 would be estimated more accurately in the absence of correlations between predictors (i.e., had the study been a full factorial design).

Also, a number of key factors were not manipulated that could serve as moderators of the effects observed in this study, the clearest one being sample size. We used a sample size of 150 for all simulated datasets which is representative of the median N for behavioral substance abuse treatment trials, which typically range between Ns of 80 to 400. However, smaller samples may see a more severe impact of model misspecification on bias and coverage rates and, because of the large number of parameters in LCPMMs, may be subject to greater likelihood of non-converged solutions that were observed in this study.

Finally, this study was constructed based on class-specific treatment effects from one of the few published studies to examine LCPMMs as an option for modeling the impact of group membership turnover on treatment effect estimation in open enrollment group trials (Morgan-Lopez & Fals-Stewart, 2007), although the key focus of the simulation study was the á posteriori examination of the effect sizes for the differences between those class-specific treatment effects. Because this area of treatment methodology research is in its infancy, the literature offered us no additional clues as to which parameters to use other than those which we ourselves have published. However, methodologists, particularly those who may be generally interested in research on LCPMMs (an area that is underdeveloped) may consider focusing on manipulating the size of the discrepancies between treatment effects (i.e., the sizes of the treatment x class interaction effects) rather than manipulating the class-specific treatment effects (i.e., manipulating the within-class treatment main effects).

Conclusion

The federal funding agencies charged with the caretaking of the substance abuse and alcoholism treatment research portfolio in the United States (i.e., NIDA, NIAAA) have recognized and, to their credit, attempted to eliminate (NIAAA/NIDA, 2003a, 2003b) the gap between the predominant use of open enrollment groups for behavioral treatment conducted in community settings and their scant use in the designs of behavioral treatment research trials. The logistical and methodological difficulties accounting for those gaps have been well documented and have served to stymie grant applications with ecologically-valid designs (all things equal). Changes over time in group membership structure have been cited as the top analytic concern in the development and evaluation of open enrollment therapy trials (NIDA, 2003); recent advances in modeling non-ignorable missing data via latent class pattern mixture models (Lin et al., 2004; Muthén et al., 2003; Roy, 2003) have shown promise in handling the problem of turnover in group membership in ways that conventional longitudinal growth models cannot (Morgan-Lopez & Fals-Stewart, 2007, 2008). With these advances has come the recognition that the choice of analysis is critical to making sound inferences about the efficacy of group treatments; we illustrated this in the context of a single dataset in the evaluation of an open enrollment group therapy trial for men with a primary diagnosis of alcoholism (Morgan-Lopez & Fals-Stewart, 2007) and, in this article have identified conditions where treatment researchers should be most concerned about the choice of analytic framework for the evaluation of their respective open enrollment group trials. It is our desire that these continuing advances will free up behavioral treatment researchers to defensibly analyze data they currently have from open enrollment groups or encourage them to submit grants on new and/or empirically-supported therapies that incorporate open enrollment groups in the ultimate hope of bridging the gap between how treatment research is designed and conducted and how substance abuse and alcoholism treatment are implemented in practice.

Appendix A

Converting Regression Coefficients to R² values

Consider the following mixture SEM, structured as a K-class latent class pattern mixture model:

$$\sum _{K=1}^{K}P({\mathit{Attend}}_{ik}=1)(a_{it}=1\mid {\mathit{Attend}}_{ik})(d_{it}\mid {\mathit{Attend}}_{ik})$$

where the probability of membership in attendance class K is:

$$P({\mathit{Attend}}_{ik}=1)=\frac{e^{{\alpha }_{ck}}}{\sum _{K=1}^K{e}^{{\alpha }_{ck}}}$$

captured by an intercept-only (i.e., unconditional) multinomial logit model for class membership (Muthén & Muthén, 1998–2004, p.29), the probability of a_it conditional on membership in Attendance Class K (i.e., the probability that patient i will show up for treatment at time t, given membership in attendance class K) is captured in the following logit model:

$$P(a_{it}=1\mid {\mathit{Attend}}_{ik})=1-\frac{1}{1-e^{-(\tau -a^{\ast })}}$$

Finally, the distribution of the outcome variable, d_it takes the following form:

$$(d_{it}\mid {\mathit{Attend}}_{ik})~N({\mu }_i,{\Sigma }_i)$$

Where the mean structure of d_it (conditional on class membership) is:

$${\mu }_i=v+\Lambda ({\alpha }_K+{\Gamma }_K{\chi }_i)$$

And the covariance structure for d_it is:

$${\Sigma }_i=\Lambda \Psi {\Lambda }^{\prime }+\Theta$$

The mean and covariance structure take on the same form (within each attendance class) as the standard confirmatory factor analysis model, which is then structured to model linear growth over time in d_it.

The level-1 (within-patient) model (within each class) would be:

$${\mathrm{d}}_{\mathrm{it}}={\alpha }_{0\mathrm{i}}+{\alpha }_{1\mathrm{i}}\left({\text{Time}}_{\mathrm{T}}\right)+{\epsilon }_{\mathrm{ti}}$$

The level-2 (between-patient) model would be:

$$\begin{array}{cc}\hfill & {\alpha }_{0\mathrm{i}}={\alpha }_{00}+{\mathrm{g}}_{0\mathrm{i}}\hfill \\ \hfill & {\alpha }_{1\mathrm{i}}={\alpha }_{10}+{\Gamma }_{11}\left(\text{Treatment}\right)+{\mathrm{g}}_{1\mathrm{i}}\hfill \end{array}$$

Note that there is not an explicit 3^rd level for variation between treatment groups; instead, standard errors for the model parameters are corrected for non-independence due to third-level clustering of observations using robust ML estimation (Yuan & Bentler, 2000).

Our focus is on the converting r² values from Morgan-Lopez and Fals-Stewart (2007) to a regression parameter (Γ₁₁) in the between-patient model capturing the impact of the treatment condition on variation in growth over time on d_it (i.e., α_1i). If:

$${\alpha }_{1\mathrm{i}}={\alpha }_{10}+{\Gamma }_{11}\left(\text{Treatment}\right)+{\mathrm{g}}_{1\mathrm{i}}$$

then the total variance of α_1i (based on the rules of covariance algebra) equals:

$$V\left({\alpha }_{1\mathrm{i}}\right)={{\Gamma }_{11}}^2\text{V(Treatment)}+\mathrm{V}\left({\mathrm{g}}_{1\mathrm{i}}\right)$$

In this case, the r² of interest is defined as the proportion of variance in the slope-over-time in the outcome α_1i that is accounted for by the treatment condition (relative to the total variance in α_1i).

$${\mathrm{r}}^2=\frac{{{\Gamma }_{11}}^{2}V\left(Treatment\right)}{{{\Gamma }_{11}}^{2}V\left(Treatment\right)+V\left(g_{1i}\right)}$$

If the V(Treatment) = .25 (as it would with equal Ns in the treatment and comparison conditions) and V(g_1i) is set to variance 1, and the r² of interest is .43 (for example), then solving for Γ₁₁ yields a regression coefficient of |1.73|.

Appendix B

Delta Method Standard Errors and Cohen's D values for the Difference between the Completers Class Treatment Effect and the Average Treatment Effect in the Other Two Classes

The delta method is used to derive the variance of functions (e.g., sums, products, sums of products) of normally distributed random variables (e.g., regression coefficients). The asymptotic distribution of the estimator (i.e., f(θ')) is given by (Bishop et al., 1975, p.493):

$$\mathrm{L}\left[{\mathrm{n}}^{1∕2}\right(\mathrm{f}\left(\theta ’\right)-\mathrm{f}\left(\theta \right)\left)\right]\to \mathrm{N}\{\theta ,((\partial \mathrm{f}∕\partial \theta )\Sigma \left(\theta \right)(\partial \mathrm{f}∕\partial \theta )’\left)\right\}$$ (1)

Where f(θ') is a single function of interest, ∂f/∂θ is a vector of partial derivatives and Σ(θ') is a covariance matrix among all parameters that appear in the function f(θ). The function of interest in the present case is the difference between the Completers treatment effect and the average of the treatment effects in the Dropout and Erratics classes (i.e. the treatment effect discrepancy measure (TED) in absolute value):

$$\theta =\mid {\gamma }_{Completers}-\left(\frac{{\gamma }_{Erratics}+{\gamma }_{Dropouts}}{2}\right)\mid$$ (2)

The partial derivatives of the function (θ) with respect to each parameter are as follows:

$$\frac{\partial f}{\partial {\gamma }_{Completers}}=1,\frac{\partial f}{\partial {\gamma }_{Erratics}}=-.5;\frac{\partial f}{\partial {\gamma }_{Dropouts}}=-.5$$

The covariance matrix among the treatment effect estimates from the three classes are pre- and post-multiplied by the vector of partial derivatives of the functions of interest:

$$\left[\begin{array}{ccc}\hfill 1\hfill & \hfill -.5\hfill & \hfill -.5\hfill \end{array}\right]\left[\begin{array}{ccc}\hfill {{\sigma }^2}_C\hfill & \hfill {\sigma }_{EC}\hfill & \hfill {\sigma }_{DC}\hfill \\ \hfill {\sigma }_{CE}\hfill & \hfill {{\sigma }^2}_E\hfill & \hfill {\sigma }_{DC}\hfill \\ \hfill {\sigma }_{CD}\hfill & \hfill {\sigma }_{ED}\hfill & \hfill {{\sigma }^2}_D\hfill \end{array}\right]\left[\begin{array}{c}\hfill 1\hfill \\ \hfill -.5\hfill \\ \hfill -.5\hfill \end{array}\right]$$

Where C = completers, E = erratics, and D = dropouts. The square root of this new quantity is the standard error for the TED. The standard error is:

$$\sqrt{}{{\sigma }^2}_{\mathrm{C}}-{\sigma }_{\mathrm{CE}}-.5{\sigma }_{\mathrm{CD}}+.25{{\sigma }^2}_{\mathrm{E}}+.5{\sigma }_{\mathrm{DE}}+.25{{\sigma }^2}_{\mathrm{D}}$$

The z-test for significance of the TED is:

$$\frac{\mid {\gamma }_{Completers}-\left(\frac{{\gamma }_{Erratics}+{\gamma }_{Dropouts}}{2}\right)\mid }{\sqrt{}{{\sigma }^2}_{\mathrm{C}}-{\sigma }_{\mathrm{CE}}-.5{\sigma }_{\mathrm{CD}}+.25{{\sigma }^2}_{\mathrm{E}}+.5{\sigma }_{\mathrm{DE}}+.25{{\sigma }^2}_{\mathrm{D}}}$$

This value is then converted to a Cohen's D effect size using the formula in Rosnow and Rosenthal (1991): 2z/√(df), where the degrees of freedom equal the sample size.