Surface EMG Decomposition Based on K-means Clustering and Convolution Kernel Compensation

Abstract

A new approach has been developed by combining the K-mean clustering (KMC) method and a modified convolution kernel compensation (CKC) method for multi-channel surface electromyogram (EMG) decomposition. The KMC method was first utilized to cluster vectors of observations at different time instants and then estimate the initial innervation pulse train (IPT). The CKC method, modified with a novel multi-step iterative process, was conducted to update the estimated IPT. The performance of the proposed K-means clustering - Modified CKC (KmCKC) approach was evaluated by reconstructing IPTs from both simulated and experimental surface EMG signals. The KmCKC approach successfully reconstructed all 10 IPTs from the simulated surface EMG signals with true positive rates (TPR) of over 90% with a low signal-to-noise ratio (SNR) of −10dB. Over 10 motor units were also successfully extracted from the 64-channel experimental surface EMG signals of the first dorsal interosseous (FDI) muscles when a contraction force was held at 8 N by using the KmCKC approach. A ‘two-source’ test was further conducted with 64-channel surface EMG signals. The high percentage of common MUs and common pulses (over 92% at all force levels) between the IPTs reconstructed from the two independent groups of surface EMG signals demonstrates the reliability and capability of the proposed KmCKC approach in multi-channel surface EMG decomposition. Results from both simulated and experimental data are consistent and confirm that the proposed KmCKC approach can successfully reconstruct IPTs with high accuracy at different levels of contraction.

I. INTRODUCTION

ENCOURAGED by highly successful achievements [1-7] in the decomposition of indwelling electromyograms (EMG) signals, various approaches have been developed over the past years to decompose surface EMG signals into their constituent motor unit action potential (MUAP) trains [8-10]. However, surface EMG signal decomposition presents many technical challenges [10], e.g. shape changes across different action potentials from each motor unit (MU), similarities of shape at various times among the action potentials of different MUs, the large dynamic range of amplitudes present among the action potentials of different interested MUs, and the overlap of action potentials from different MUs. These phenomena may also present together to make the surface EMG decomposition task even more difficult.

Recently, multi-channel amplifiers and high-density surface electrode grids which can partially solve aforementioned problems have become available for the non-invasive recording of human motor units [11]. Subsequently, a variety of techniques, including pattern recognition and blind source separation (BSS), that are capable of handling the multi-channel surface EMG data have also been developed [12-14]. Kleine et al. [15] investigated the importance of two-dimensional (2D) spatial filters in decomposing surface EMG signals, and the presented results demonstrate that the proposed 2D spatial filtering approach can detect the firing times of MUs with a high level of accuracy, but has difficulty in separating MUs with identical MUAP shapes. Gazzoni et al. [16] utilized a classification and template matching segmentation technique to extract and classify single MUAPs and further investigated the anatomical and physiological properties of the detected MUs. The main limitation of this method is that it is difficult to obtain complete firing patterns due to the superposition of MUAPs. Garcia et al. [17] modeled surface EMG signals as an instantaneous mixture of MUAP trains in order to separate MUs and claimed that they could successfully solve overlaps of MUAPs, even at 60% maximum voluntary contraction (MVC), by combining the preprocessing filters, independent component analysis (ICA), and template-matching techniques. Holobar and Zazula proposed both a convolution kernel compensation (CKC) method [18] and latterly a gradient convolution kernel compensation method (GCKC) [19] to handle convolution mixtures of innervation pulse trains (IPTs). The CKC method estimates the IPTs directly without calculating the unknown mixing matrix, and results show that over 30 concurrently active MUs can be extracted from multi-channel surface EMG signals with good quality [19]. This CKC method, however, is mainly applied in the case of relatively low force contractions for better results [20, 21]. The GCKC method has been demonstrated in previous studies to perform with high accuracy and noise robustness in decomposing surface EMG signals [19], but it has a requirement for the length of the signal to converge when a certain gradient-based update rule is utilized [22].

In the present study, a new hybrid surface EMG decomposition approach (KmCKC) was successfully developed by combining the K-means clustering (KMC) method and the CKC method modified with a novel multi-step iteration strategy to further improve the efficiency, noise robustness and accuracy of multi-channel surface EMG decomposition.

II. METHODS

A. K-means Clustering Method, Data Model, and Convolution Kernel Compensation

The KMC method is employed in the proposed KmCKC approach for data clustering. If a set of data and the number of clusters were given, the data would be repeatedly put into different groups by the KMC by evaluating a distance function. The clustering criterion adopted in the KMC is the distance between two elements within the same group. A two-stage iterative algorithm [23] is used also to minimize the sum of point-to-center distances over all clusters.

Given a linear time-invariant (LTI) multi-input multi-output (MIMO) system, the equation of CKC model can be stated as [18-19, 24]:

$$X\left(n\right)=H\stackrel{‒}{s}\left(n\right)+e\left(n\right)$$ (1)

where X (n) = [x₁ (n),..., x_M (n)]^T is the group of M convolution observations and x_j (n) is the n-th sample of the j-th observation. e(n) = [e₁(n),...,e_M (n)]^T is a vector of temporally and spatially zero mean white noise.

$$\stackrel{‒}{s}\left(n\right)={[s_1\left(n\right),s_1(n-1),\dots ,s_1(N-P+1),\dots ,s_N\left(n\right),s_N(n-1),\dots ,s_N(n-P+1)]}^T$$

is an extended form of N sources, s(n) = [s₁(n),...,s_N(n)]^T, and H is the mixing matrix, which consists of all of the channel responses h_ij = [h_ij (0),...,h_ij (P – 1)] (the j-th source in surface EMG signals appearing in the i-th measurement) of length P samples.

In order to improve the knowns-to-unknowns ratio, the model (1) is extended with K-1 delayed repetitions of each original observation [18, 19]:

$$\overline{X}\left(n\right)={[x_1\left(n\right),x_1(n-1)\dots x_1(n-K+1),\dots ,x_M\left(n\right),x_M(n-1)\dots x_M(n-K+1)]}^T.$$

Adopting the extended form X̄ (n) and the model from (1), an activity index of global pulse train can be written as [18, 19]:

$$\gamma \left(n\right)={\overline{X}}^T\left(n\right)C_{\overline{X}\overline{X}}^{-1}\overline{X}\left(n\right)$$ (2)

where C_{X̄ X̄} stands for the correlation matrix of the extended and observations X̄ (n), and ^T and ⁻¹ stand for transpose and inverse, respectively. Suppose the pre-multiplying vector X̄ (n₀) is fixed in (2) to the sampling time n₀, and the expression can be rewritten as [18]:

$$s_{n0}\left(n\right)={\overline{X}}^T\left(n_0\right)C_{\overline{X}\overline{X}}^{-1}\overline{X}\left(n\right)$$ (3)

It has been proven that if only the j-th source is active in time instant n₀, s_n0(n) yields the estimation of the innervation pulse train of the j-th source [18]:

$$s_{n0}\left(n\right)\approx {\stackrel{‒}{s}}_j\left(n\right)$$ (4)

A solution can then be achieved via (3) for the decomposition of a linear and convolution mixture of IPTs.

In order to improve s_n0(n), X̄ (n₀) in (3) is replaced with the average value C_X̄sj [18],

$$C_{\overline{X}sj}=\frac{1}{card\left({\phi }_n\right)}\sum \overline{X}\left({\phi }_n\right)$$ (5)

where φ = {n0, n1 ,..., n_m} denotes a set of firing times of the j-th MU, and card(φ_n) denotes the cardinal number of φ_n.

B. KmCKC Method

A pulse train s_n0 was first estimated using time instant n₀ according to (3), where a pulse was randomly selected and denoted by n₁ – the time of its occurrence [18]. Then a new pulse train s_n1 is obtained by using (3). According to [18], there should be one pulse train denoted by s_j which is active in pulse train s_n1. Some of the time instants (usually 30-60 time instants) associated with the highest peaks can then be selected from s_n1 and denoted by φ_nc = {n_c1, n_c2, ...,n_ck}, where these instants are usually generated by one or more MUs. The observations X̄ (n) corresponding to φ_nc can then be classified into groups (usually 2-4 groups are classified) by using the KMC. The group which contains the largest number of elements will be selected and the time instants in this group will be denoted by , where most of time instants in φ_nv = {n_v1, n_v2, ...,n_vn}, where most of time instants in φ_nv should be fired by one MU in general. Then an initial pulse train ${\widehat{\stackrel{‒}{s}}}_{j0}$ can be estimated from the observations X̄ (n) corresponding to φ_nv. Usually the initially estimated pulse train is not acceptable in cases with a low signal to noise ratio (SNR). Hence, the multi-step iteration as described below is necessary to improve the pulse train. The detailed algorithm steps are depicted below.

Step 1

Compute the correlation matrix of observations C_{X̄ X̄} and the associated inverse matrix.

Step 2

Compute γ(n) and $n_0=\underset{\arg }{median\left(\right(\gamma \left(n\right))}$ with (2) and compute s_n0 with (3) [18]; find the maximum value in s_n0, its time of occurrence n₁, and reconstruct s_n1 according to (3). Identify k time instants corresponding to the highest peaks in s_n1, denoted by φ_nc = {n_c1, n_c2, ...,n_ck}.

Step 3

X̄(n_ci ), n_ci ε φ_nc are clustered into groups by using the KMC method. The group which contains the largest number of elements, denoted by φ_nv = {n_v1, n_v2, ...,n_vn}, is then selected. According to (5), the observations X̄(n) over all time instants from φ_nv can be averaged as $C_{\overline{X}sj0}=\frac{1}{card\left({\phi }_{nv}\right)}\sum \overline{X}\left({\phi }_{nv}\right)$. An initial pulse train is estimated as ${\widehat{\stackrel{‒}{s}}}_{j0}=C_{\overline{X}sj0}^T{C}_{\overline{X}\overline{X}}^{-1}\overline{X}\left(n\right)$ by using C_X̄sj0 to replace X̄(n₀) in (3).

Step 4

Find r different highest peaks in ${\widehat{\stackrel{‒}{s}}}_{j0}$ and their time of occurrence φ_nu = {n_u1, n_u2, ..., n_ur}. Average as X̄(φ_nu) as $C_{\overline{X}sj1}=\frac{1}{card\left({\phi }_{nu}\right)}\sum \overline{X}\left({\phi }_{nu}\right)$ and a new pulse train can be estimated as ${\widehat{\stackrel{‒}{s}}}_{j1}=C_{\overline{X}sj1}^T{C}_{\overline{X}\overline{X}}^{-1}\overline{X}\left(n\right)$ according to (3) and (5).The r + Np (Np ≥ 1) highest peaks in , ${\widehat{\stackrel{‒}{s}}}_{j1}$ denoted by φ_nq = {n_q1, n_q2, ..., n_qp}, and their times of occurrence are continually found, and is averaged X̄(φ_nq) is averaged as $C_{\overline{X}sj2}=\frac{1}{card\left({\phi }_{nq}\right)}\sum \overline{X}\left({\phi }_{nq}\right)$ . The pulse train is then updated as ${\widehat{\stackrel{‒}{s}}}_{j2}=C_{\overline{X}sj2}^T{C}_{\overline{X}\overline{X}}^{-1}\overline{X}\left(n\right)$ and r is set to r+Np.

Step 5

Repeat step 4 for h times, until finally the j-th pulse train ${\widehat{\stackrel{‒}{s}}}_{j(h+1)}=C_{\overline{X}sj(h+1)}^T{C}_{\overline{X}\overline{X}}^{-1}\overline{X}\left(n\right)$ is obtained.

Step 6

Set γ(d) = 0, ∀ d ε φ_nv [18].

Step 7

Repeat steps 2-6 for N_mdl times (usually depending on the maximum number of motor units that can be extracted). Finally, the IPTs are classified into groups for each specific MU.

C. Simulated Surface EMG Signals

1) Test 1: Test with Signals Generated by a Random Mixing Matrix

Ten trails were conducted in this test with the number of sources N being set to 10, and N_mdl in step 7 from section II.B was set to 150. All the simulated signals were generated with the same protocol as described in [18], but the mean interpulse interval (IPI) of each input pulse train was set to 100 samples, parameter τ was set to 10 samples and the number of observations M was set to 25. The number of delayed repetitions K was set to 9 [18] so that the number of extended IPTs was 190 and the number of observations was 250. Each generated signal was corrupted by Gaussian zero-mean noises with the SNRs being set to −10dB, −5dB, 0dB, 5dB and 10dB, respectively. The number of highest peaks r was set to 10 and the number of time instants (Np) added in each iteration step was also set to 10, while the number of iteration steps h (step 5 in section II. B) was set to 20.

2) Test 2: Test with Synthetic Surface EMG Signals

Synthetic surface EMG signals were generated by using a planar volume conductor model as described in [25]. The intracellular action potential of a muscle fiber was modeled as a current tripole (impulse amplitudes: I1 = 24.6 A/m², I2 = −35.4 A/m², I3 = 10.8 A/m²; distances between poles: a = 2.1 mm, b = 6.9 mm) [26].

A grid of 8×8 electrodes with a 5-mm inter-electrode distance in both directions was assumed in the study for recording surface EMG signals. These surface EMG signals were sampled at a frequency of 2,000 Hz. Ten simulation trails were performed by assuming 10 different active MUs, where the number of fibers, position of the active MUs, discharging patterns, and conduction velocity were all generated randomly in each trail. The surface EMG signals were corrupted by additive Gaussian zero-mean noises with different SNRs varying from 0 to 20 dB, and the number of delayed repetitions of each original observation was set to 9 [18,19].

D. Experimental Surface EMG Signals of the First Dorsal Interosseous (FDI) Muscles

1) Test 3: Test with Experimental Multi-channel EMG Signals

The experimental surface EMG signals were collected from the first dorsal interosseous (FDI) muscles of three adult subjects. The study protocol was approved by the Institutional Review Board (IRB) of Northwestern University (Chicago, USA). Subjects were seated upright in a mobile Biodex chair (Biodex, Shirley, NY). A standard 6 degrees-of-freedom load cell (ATI Inc, Apex, NC) setup and procedures for minimizing spurious force contributions from unrecorded muscles as described in [27] were used to accurately record the isometric contraction force of the FDI muscles during index finger abduction. Surface EMG signals were recorded from the FDI muscles with a Refa amplifier (TMS International BV, The Netherlands) using a flexible 2-dimensional 64-channel (individual recording probes were 1.2 mm in diameter in 8 × 8 formation, with a center-to-center probe distance of 4 mm) surface electrode array (TMS International BV, The Netherlands). The skin over the tested muscle was carefully prepared with gentle abrasion and a small amount of absorbable conductive electrode cream [28]. The electrode array was attached to the FDI muscle with a double adhesive sticker and further secured with medical tapes. The maximum voluntary contraction (MVC) was first measured; after that, each subject was asked to generate an isometric contraction force of the FDI muscles at different contraction levels at 2N, 4N, 6N and 8N, respectively. Multiple trials were performed at each force level in which the subject was asked to maintain the force as stable as possible for up to 10s. The signals were sampled at 2 kHz per channel, with a band pass filter setting at 10 - 500 Hz.

III. RESULTS

A. Simulated Surface EMG Signals

1) Test 1 Results

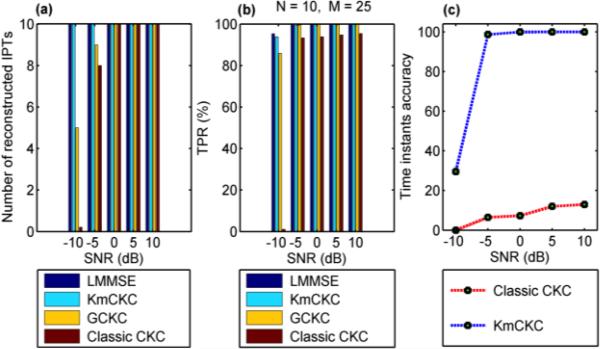
Fig. 1(a) shows the number of reconstructed IPTs and Fig. 1(b) shows the true positive rate (TPR) [20] achieved by the linear minimum mean square error (LMMSE) estimator [18], KmCKC, GCKC and classic CKC respectively at different noise levels. Parameters utilized in the KmCKC method and the corresponding computation times in this test are listed in Table I, where Ls is the number of samples in each channel's signal, tc is the computing time, and r, Np, h and N_mdl refer to the steps 4, 5 and 7 in the section II. B. The same amount of IPTs were reconstructed by all the four decomposition methods with SNRs over 0 dB, but the KmCKC method achieved a higher TPR than either the GCKC or classic CKC methods. All the 10 assumed IPTs were successfully reconstructed by the KmCKC method when the SNR is set to −5dB or −10dB, while both the GCKC and classic CKC methods failed to achieve such results. These results demonstrate that the proposed KmCKC method is robust to noise. Note that the LMMSE estimator assumes prior information that is known in the computer simulation, but is not available in experimental EMG signals. Therefore the LMMSE method stands for an ideal solution here but is not practicable in reality – the LMMSE results are listed here only as a reference.

Fig. 1.

Compares the performance of difference decomposition methods with the simulated surface EMG signals. (a) shows the number of reconstructed IPTs, (b) shows TPR and (c) shows the accuracy of the time instants of the reconstructed IPTs, achieved by different decomposition methods at different noise levels. The results are obtained by averaging the 10 simulation trails (Test 1).

TABLE I.

PARAMETERS USED AND COMPUTING TIMES IN THE IMPLEMENTATION OF THE KMCKC METHOD IN THE 3 TESTS (TESTS 1-3)

Signal	Nmdl	r	Np	h	Ls	tc (s)
Test 1	150	10	10	20	20000	37.3
Test 2	200	5	5	7	6001	9.4
Test 3	350	5	5	40	27001	339.4

Let TIA denote the accuracy of time instants, TIT denote the total number of correctly identified time instants that were fired by one MU before estimating the final pulse train (e.g. For KmCKC, TIT stands for the total number of correctly identified time instants in step 5 used to calculate C_X̄sj(h+1) ; whereas for CKC, TIT stands for the total number of correctly identified time instants in a common set Ψ_j in step 5 [18]), and TIW denote the total number of time instants fired by this MU, then TIA can be given as

$$TIA=\frac{TIT}{TIW}\times 100\%$$ (6)

Note that TIA is an important parameter to decide the quality of reconstructed IPTs, and TPR is a parameter utilized to measure the accuracy of time instants that are correctly identified after obtaining the final pulse train. Fig. 1(c) shows the average time instant accuracy achieved by the KmCKC and classic CKC, respectively, at different noise levels. It can be seen that the time instant accuracy of the IPTs reconstructed by the KmCKC reaches about 100% for all SNRs over −5dB. The time instant accuracy of the reconstructed IPTs does drop to about 30% when the SNR is set to −10dB, but overall the KmCKC approach offers higher time instant accuracy than the classic CKC at all noise levels.

It can also be seen that the performance of the KmCKC approach is similar to that of the LMMSE estimator. Please note that the original IPTs were delayed by samples in the range of [1, 10] to achieve better results when the LMMSE estimator was implemented. When the classic CKC was implemented, the number of n_r, denoted by N_nr, was selected from 200-300 [18], as it would not improve results to further increase the number of n_r beyond this value. A threshold Thp was set to determine the number of pulses in the product of (11) of [18]. The parameter R was set to 4 and the number of combinations (n₃, n₄, ..., n_R-1), denoted by Nc, contributing the number of pulses exceeding the threshold J in the common set Ψ_j was selected from 60-400 [18]. The main decomposition loops (steps 2-8 in Fig.1 of [18]) were performed 20 times with different parameters chosen from the above range in order to best fit the parameters for the classic CKC. The results were compared and the values that could reconstruct the greatest number of IPTs were selected, the main decomposition loops were then performed 300 times to obtain the final results (it again would not improve the results any more to further increase the number of main decomposition loops). The number of main decomposition loops and the number of iterations were set to 500 and 40, respectively, to estimate ĉ_tjX in (5) of [19] when the method of GCKC was implemented. The scalar function f (t) = (1 3)t³ was used as in (9) of [19]. The IPT was considered as real when its TPR was greater than 75%.

2) Test 2 Results

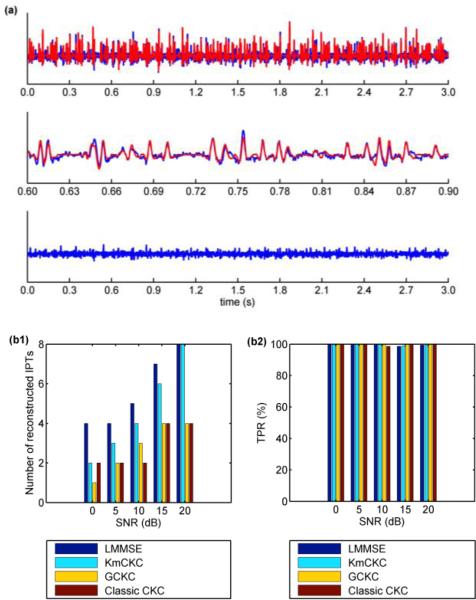
The sum of MUAP trains reconstructed by KmCKC from one typical channel of the synthetic surface EMG signals and the associated residual are shown in Fig. 2(a). Fig. 2(b1) shows the number of reconstructed IPTs and Fig. 2(b2) shows the TPRs achieved by the LMMSE estimator, KmCKC, GCKC, and classic CKC respectively. Parameters utilized in the KmCKC approach and the computing time are listed in Table I. The implementation of the classic CKC method in this test is similar to its implementation in Test 1, but the main decomposition loops were performed 350 times. The parameters used in the GCKC method in this test are the same as in Test 1. Results show that the number of reconstructed IPTs achieved by all four of the decomposition methods increases as the SNR goes up. A maximal reconstructed IPT number of 4 is achieved by the classic CKC and GCKC methods when the SNR is increased to 15 dB, but does not increase further when the SNR is further increased to 20 dB. This phenomenon seems hint that only the MUs contributing Significantly to the surface EMG signals can be identified by the classic CKC and GCKC methods. The maximal reconstructed IPT number of 8 achieved by the KmCKC demonstrates a superior level of performance in reconstructing MUs.

Fig. 2.

(a) The top panel represents the sum of the MUAP trains (red lines) reconstructed by the KmCKC method compared to the raw signals (blue lines) in one typical channel from the synthetic surface EMG signals with SNR=20dB, the middle panel shows an expanded segment of the raw signal, and the bottom panel represents the residual after subtraction of reconstructed MUAP trains from the raw surface EMG signals. (b1) shows the number of reconstructed IPTs and (b2) shows the TPR of the reconstructed IPTs achieved by different decomposition methods at different noise levels. The results are averaged over 10 simulation trails (Test 2).

B. Experimental Surface EMG Signals

1) Test 3 Results

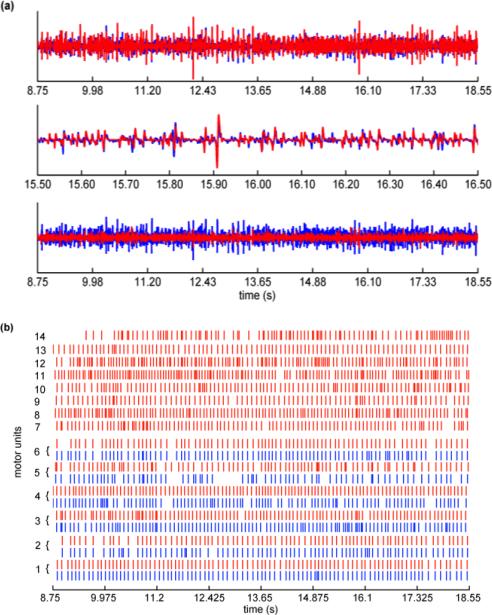
Parameters utilized in the KmCKC method and the computing time are listed in Table I. Note that the implementation the classic CKC method in this test is similar to the implementation in Test 1, but the main decomposition loops were performed 400 times. The parameters used in the GCKC method in this test are the same as the parameters used in the Test 1. The sums of the MUAP trains extracted by KmCKC and the residual after the subtraction of these extracted MUAP trains from the raw surface EMG signals of the FDI muscles are shown in Fig. 3(a). Fig. 3(b) shows the MUs identified by the classic CKC and KmCKC methods. Results show that both the KmCKC and classic CKC can identify the first six MUs, but the last eight MUs can only be identified by the KmCKC approach. The number of MUs extracted by the KmCKC, GCKC, and classic CKC methods corresponding to different force levels of contraction of three subjects are reported in Table II, where N_MU-64 denotes the number of MUs extracted from all 64 channels. Overall the number of MUs identified by the KmCKC increases with the increasing contraction force, but the number of MUs identified by the classic CKC is reduced.

Fig. 3.

(a) The top panel shows the sum of the MUAP trains (red lines) extracted by the KmCKC method compared to the raw surface EMG (blue lines) recordings from FDI muscles (Subject B) in one typical channel, the middle panel shows an expanded segment of the signal, and the bottom panel shows the residual (red lines) after subtraction of extracted MUAP trains from the raw surface EMG compared to the raw surface EMG (blue lines). (b) shows MU firing patterns identified by the KmCKC (red lines) and classic CKC (blue lines) from surface EMG signals of the FDI muscles, the isometric constant force of contraction was held at 10% MVC (Test 3).

TABLE II.

EXPERIMENTAL SURFACE EMG DECOMPOSITION RESULTS (MEAN ± STD. DEV.) ACHIEVED FROM DIFFERENT NUMBERS OF CHANNELS AT DIFFERENT FORCE LEVELS OF CONTRACTION (TEST 3)

Method	Parameters	Contraction force
		2N	4N	6N	8N
CKC	NMU-64	4.7±1.5	5.7±2.5	3.3±2.3	2.7±2.5
GCKC	NMU-64	5.7±2.5	8.0±0	5.7±4.0	6.7±2.3
KmCKC	NMU-64	10.7±4.2	10.7±1.5	10.7±3.1	12.7±0.6
	NMU-48	7.7±2.8	10.5±1.2	8.2±2.3	8.3±1.6
	NMUG1	6.7±2.5	9.3±1.5	8.0±1.7	5.7±2.1
	NMUG2	6.7±1.5	8.0±1.0	7.3±2.5	6.0±2.6
	NCOMMU	5.7±2.5	7.7±0.6	6.3±2.1	5.0±2.6
	PCOMPUL (%)	92.2±5.6	92.2±5.4	94.3±4.2	97.0±4.1
	NMU-16	3.3±1.6	4.2±1.2	3.7±1.9	2.5±1.5

Experimental multi-channel surface EMG recordings from the three subjects were also utilized to validate the performance of the proposed KmCKC method in surface EMG decomposition by using the ‘two source’ approach. Surface EMG channels were divided into two independent groups: channels with odd channel numbers formed one group and channels with even channel numbers formed the other group. The number of MUs extracted from all channels for each independent group (denotes by N_MUG1 and N_MUG2 respectively), the number of common MUs extracted from the two independent groups (denotes by N_COMMU), and the percentage of common pulses generated by the common MUs (denotes by P_COMPUL) are reported in Table II. It is not surprising that the number of extracted MUs decreases significantly when the number of channels drops by half, especially in the case of high-force contractions. The fact that the percentage of common MUs and common pulses are still very high even when the number of MUs extracted is reduced demonstrates the reliability of the proposed KmCKC method in multi-channel surface EMG decomposition. In addition, to study the effect of number of channels on the decomposition performance, the first and last 16 channels as well as the first and last 48 channels were used to decompose sEMG signals respectively. These results are also presented in Table II, where N_MU-16 and N_MU-48 denotes the number of MUs extracted from 16 channels and 48 channels respectively.

IV. DISCUSSION

There are two innovations in the proposed KmCKC approach compared to the classic CKC and the GCKC. One innovation is the employment of the KMC method in step 3, while the other is the use of the novel multi-step iteration approach in steps 4-5 in the proposed KmCKC approach.

Since the MUAPs generated by the same MU have a certain degree of similarity in multi-channel surface EMG signals, the firing times of the same MU can be clustered by using the KMC method via evaluating a distance function. The firing times of different MUs are often mixed into a single group if a small number of groups is clustered by KMC in step 3 (section II.B) and a large number of time instants in φ_nc is identified in step 2 (section II.B). Therefore, the number of clustered groups and time instants should ensure that the time instants in one group are fired by the same MU as completely as possible. In general, 30-60 time instants are identified in φ_nc and 2-4 groups are clustered by KMC.

If the quality of the multi-channel surface EMG signals is good, as with signals generated in the case of low force muscle contraction with high SNR, the IPTs can be satisfactorily reconstructed even when steps 4 and 5 are skipped. In the case of complex surface EMG signals, such as the signals generated with high force level of contraction, the time instants fired by the same MU may not be clustered into one group successfully by using the KMC method, which means the IPTs cannot be satisfactorily reconstructed by only using the KMC method. In this case, the multi-step iteration approach proposed in the steps 4-5 is needed to improve the initial pulse train ${\widehat{\stackrel{‒}{s}}}_{j0}$.

It is critical to obtain a satisfactory correlation matrix C_X̄sj in (5) for all the CKC methods, including the classic CKC, the GCKC and the proposed KmCKC methods, in order to achieve good decomposition results. The C_X̄sj2 estimation approach proposed in the KmCKC is novel, where C_X̄sj2 is calculated as an arithmetic mean of X̄(φ_nq) in each iteration step. Once an IPT is estimated, the time instants corresponding to the highest peaks in the IPT, which are usually fired by the same MU [18], will be used to update the original IPT to form a new one. The quality of the new IPT will be improved when compared to the previous one, and new time instants corresponding to the highest peaks in the new IPT fired by the same MU will be identified. The new IPT will be updated by combining the new time instants with the previous ones. In this way the IPT will be iteratively updated and the quality of the IPT will be significantly improved after such a multi-step iteration process. In the tests conducted in this study, nearly all of the IPTs could be reconstructed after 10-30 iteration steps. Clearly the C_X̄sj estimating process employed in the proposed KmCKC methods is different from the existing CKC methods, including the classic CKC and GCKC methods. The feature that the IPTs can be gradually improved by the iterative process in steps 4-5 of the proposed C_X̄sj estimating approach help to select more time instants fired by the same MU, and thereby push its performance to better approximate the performance of the LMMSE method. This then leads to its superior performance when compared to the GCKC and classic CKC methods in terms of the number of reconstructed MUs and TPRs, which is demonstrated in Fig. 1, Fig. 2(b1-b2), Fig. 3(b) and Table II.

Fig. 1(c) shows that the time instant accuracy of the IPTs reconstructed by the KmCKC approach is as low as approximately 30% when a low SNR of −10 dB is considered. The time instant accuracy of 30% presented in Fig. 1(c) is an average value over all of the reconstructed IPTs, meaning that some of the reconstructed IPTs have time instant accuracies lower than 30% while others have time instant accuracies higher than 30%. It is surprising that the TPR of some reconstructed IPTs is still above 90%, even the time instant accuracy is lower than 5%. This may indicate that some time instants that do not belong to the same IPT will be helpful to improve C_X̄sj for obtaining better results. The proposed method also demonstrates better noise robustness in test 1 when compared to the test 2. This is mainly because some of the signal components generated by smaller or deeper motor units are often considered as noise with low SNR (Fig. 2(b1-b2)).

The ‘two source’ method was employed in the present study to further evaluate the performance of the proposed KmCKC with experimental EMG signals. The high percentage of common MUs observed by the KmCKC method from the two independent groups of signals demonstrates its reliability in multi-channel surface EMG decomposition (Table II). Results also show that the number of reconstructed MUs significantly decreases as the number of surface EMG channels decreases. Therefore, it is important to increase the number of surface EMG channels in order to satisfactorily decompose surface EMG signals in cases of high force contraction.

V. CONCLUSIONS

In conclusion, a new KmCKC approach has been developed by combining a modified CKC method and the K-mean clustering method for multi-channel surface EMG decomposition. The KMC is performed as an initial step to cluster the time instants fired by the same MU and the classic CKC, which is modified with a novel multi-step iterative process, is performed to update the IPTs iteratively. These two innovations lead to the superior performance of the proposed KmCKC method in decomposing multi-channel surface EMG signals when compared to the GCKC method and classic CKC method in terms of the decomposition accuracy and robustness against noise. The present promising simulation and experimental results suggest that the proposed KmCKC method can be expected to accurately and efficiently decompose multi-channel surface EMG signal from different levels of contraction.