Skip to main content
PMC home page
The Journal of Experimental Biology logoLink to The Journal of Experimental Biology
. 2015 Oct;218(19):3150–3159. doi: 10.1242/jeb.121673

Timing matters: tuning the mechanics of a muscle–tendon unit by adjusting stimulation phase during cyclic contractions

Gregory S Sawicki 1,*, Benjamin D Robertson 1, Emanuel Azizi 2, Thomas J Roberts 3
PMCID: PMC4631775  PMID: 26232413

ABSTRACT

A growing body of research on the mechanics and energetics of terrestrial locomotion has demonstrated that elastic elements acting in series with contracting muscle are critical components of sustained, stable and efficient gait. Far fewer studies have examined how the nervous system modulates muscle–tendon interaction dynamics to optimize ‘tuning’ or meet varying locomotor demands. To explore the fundamental neuromechanical rules that govern the interactions between series elastic elements (SEEs) and contractile elements (CEs) within a compliant muscle–tendon unit (MTU), we used a novel work loop approach that included implanted sonomicrometry crystals along muscle fascicles. This enabled us to decouple CE and SEE length trajectories when cyclic strain patterns were applied to an isolated plantaris MTU from the bullfrog (Lithobates catesbeianus). Using this approach, we demonstrate that the onset timing of muscle stimulation (i.e. stimulation phase) that involves a symmetrical MTU stretch–shorten cycle during active force production results in net zero mechanical power output, and maximal decoupling of CE and MTU length trajectories. We found it difficult to ‘tune’ the muscle–tendon system for strut-like isometric force production by adjusting stimulation phase only, as the zero power output condition involved significant positive and negative mechanical work by the CE. A simple neural mechanism – adjusting muscle stimulation phase – could shift an MTU from performing net zero to net positive (energy producing) or net negative (energy absorbing) mechanical work under conditions of changing locomotor demand. Finally, we show that modifications to the classical work loop paradigm better represent in vivo muscle–tendon function during locomotion.

KEY WORDS: Muscle–tendon interaction, Muscle stimulation phase, Work loop, Elastic energy storage and return, Terrestrial locomotion

Summary: During cyclic contractions of a muscle–tendon unit, the timing of muscle stimulation onset determines whether the muscle acts like a force producing strut, energy generating motor or energy absorbing brake.

INTRODUCTION

During locomotion, skeletal muscles are recruited to generate force and perform a diverse set of mechanical actions (Dickinson et al., 2000). Muscle performance is strongly influenced by its mechanical state and neural activation (Hill, 1925, 1938; Gordon et al., 1966; Josephson, 1999). The timing and magnitude of activation dictates the context in which muscle forces will generate or absorb mechanical energy (Josephson, 1993, 1999; Ahn and Full, 2002). When activated during a period of shortening, skeletal muscle functions as a motor by performing positive work (Josephson, 1985, 1999; Dickinson et al., 2000). When active during lengthening, however, muscle functions as a brake by performing negative work and dissipating mechanical energy (Josephson, 1985, 1999; Dickinson et al., 2000). Finally, within a relatively compliant muscle–tendon unit (MTU), the muscle can be active and isometric (i.e. at constant length), generating high forces to act as a strut while energy is cycled in series elastic elements (Ettema, 1996a, 2001; Roberts et al., 1997; Dickinson et al., 2000).

The neuromechanical factors that ultimately determine the amount of force or work produced by active skeletal muscle are its force–length (F–L) and force–velocity (F–V) properties (Hill, 1925, 1938; Gordon et al., 1966), the magnitude and timing of muscle activation (Josephson, 1985; Stevens, 1996; Dickinson et al., 2000) and environmental factors, such as externally applied loads or strain patterns (Josephson, 1985). Sinusoidal length changes similar to those observed during steady locomotion (e.g. walking, running, swimming, flying) provide a useful paradigm for probing how the mechanical state of active muscle ultimately governs cyclic force and power production in a functional task. This sort of ‘work loop’ experiment allows for exploration and understanding of how activation kinetics, as well as F–L and F–V dynamics, govern the mode of operation (motor, brake or strut) of a muscle depending on when it is stimulated along its length trajectory (Josephson, 1985, 1999; Ahn, 2012). One limitation of the ‘work loop’ paradigm is the potential inaccuracy when extrapolating from isolated muscles to isolated MTUs. Changes in length applied directly to a MTU may not reflect the length and/or velocity of the underlying muscle fascicles (contractile elements or CEs), especially if there is considerable series compliance from elastic tissues (series elastic elements or SEEs). This decoupling can make it difficult to resolve the relative contribution of the CEs and SEEs to the mechanical behavior of the MTU.

Recent muscle-level studies of terrestrial gait have observed that in the distal, more compliant MTUs of many species, including humans, CEs (i.e. active muscle) are in fact used as a strut to allow the SEEs (i.e. tendon, aponeurosis) within MTUs to stretch and recoil during cyclic limb motions (Roberts et al., 1997; Biewener et al., 1998; Fukunaga et al., 2001; Ishikawa et al., 2005; Takeshita et al., 2006; Dean and Kuo, 2011; Farris and Sawicki, 2012; Farris et al., 2013). In other words, CE length changes are decoupled from MTU trajectories via SEE compliance, and CE–SEE interaction is ‘tuned’ to cycle large amounts of energy in tendons and aponeuroses while the CE itself remains relatively isometric (Robertson and Sawicki, 2014). This ‘tuned’ pattern facilitates length change dynamics suitable for high CE force production, which, in turn, require relatively smaller active volumes of muscle to generate force during each stride (Roberts et al., 1997; Gabaldon et al., 2008).

Our understanding of the patterns of neural control necessary to tune CE and SEE interactions to allow for effective force production is limited. Multiple in vitro work loop studies exploring the role that tendon compliance plays in gait have relied on mathematical models of the SEE in order to decouple CE and MTU trajectories in the absence of direct muscle level measurements (Ettema et al., 1990; Ettema, 1996a, 2001; Lou et al., 1999; Barclay and Lichtwark, 2007; Lichtwark and Barclay, 2010, 2012). For example, Ettema (1996a) integrated a mathematical model with experimental data to conclude that effective elastic energy storage and release in an SEE is strongly dependent on the timing of muscle stimulation during a MTU stretch–shorten cycle, and that SEE compliance can significantly affect muscle-level energetics without having a dramatic effect on MTU force production. While there is no doubt that mathematical models of MTUs provide a useful avenue for examining the interaction between CE and SEE, they do have limited ability to capture some aspects of the dynamics of force generation in both muscle and tendon. In fact, multiple studies have shown that model-based predictions of muscle force production are flawed for active contractions during non-isokinetic (i.e. variable length/velocity) conditions (Caiozzo and Baldwin, 1997; Sandercock and Heckman, 1997; Lou et al., 1998; Lichtwark and Wilson, 2005). This is further complicated by incomplete models of biological tendons, which do not capture their tendency to dissipate energy over a stretch–shorten cycle (Bennet et al., 1986; Lieber et al., 1991; Maganaris and Paul, 2000).

List of symbols and abbreviations

Acycle

amplitude of the sinusoidal MTU length change cycle

CE

contractile element, or muscle fascicles

Dforce

active force duty factor, % of MTU length change cycle period when the muscle is actively producing force

Dstim

stimulation duty factor, % of MTU length change cycle period that stimulus pulse train is ‘on’

L0

muscle fascicle rest length

MTU

muscle–tendon unit

SEE

series elastic element, or tendon and aponeurosis

tpulse

duration of each individual pulse within a stimulus pulse train

φnet zero

muscle stimulation phase that generates net zero MTU mechanical work

φstim

muscle stimulation phase, or time of muscle stimulation onset expressed as a % of the MTU length change cycle (with 0% representing minimum and 50% representing maximum length, respectively)

ωcycle

frequency of the sinusoidal MTU length change cycle

ωpulse

frequency of individual pulses within a stimulus pulse train

The purpose of the present study was to use a novel, in vitro muscle–tendon work loop approach to probe how the temporal aspects of neural control influence muscle–tendon interaction within a relatively compliant MTU. We extended the work loop approach by including independent measurements of both CE and MTU length in order to make observations that did not rely on model estimates for CE or SEE force production. Using direct measurements of CE length from sonomicrometry in conjunction with externally applied cyclic length changes via a servo-controlled ergometer, we examined how the onset timing of muscle stimulation within an MTU length change cycle (i.e. muscle stimulation phase, φstim) relates to the ‘tuned’ muscle–tendon interaction observed within compliant MTUs during steady speed terrestrial gait (Fig. 1). We expected that the relationship between overall MTU net work and muscle stimulation phase, φstim, would follow the same trends previously observed in work loop experiments using direct measurements from CE only (Josephson, 1999) and a combination of empirical measures and model-based estimates from whole MTUs (Ettema, 1996a). First, we hypothesized that there would be a φstim that would generate net zero work over a MTU length change cycle. We refer to the stimulation phase leading to net zero work as (φstim=φnet zero). Second, we expected that muscle stimulation with onset that occurred earlier in the MTU length change cycle (φstim<φnet zero) would generate net negative work while muscle stimulation onset that occurred later in the cycle (φstim>φnet zero) would generate net positive work. Finally, we expected that the muscle stimulation phase resulting in net zero work for the MTU over a length change cycle (φstim=φnet zero) would be ‘tuned’, allowing the CE to operate isometrically with all positive and negative work resulting from cycling of elastic energy in the SEE.

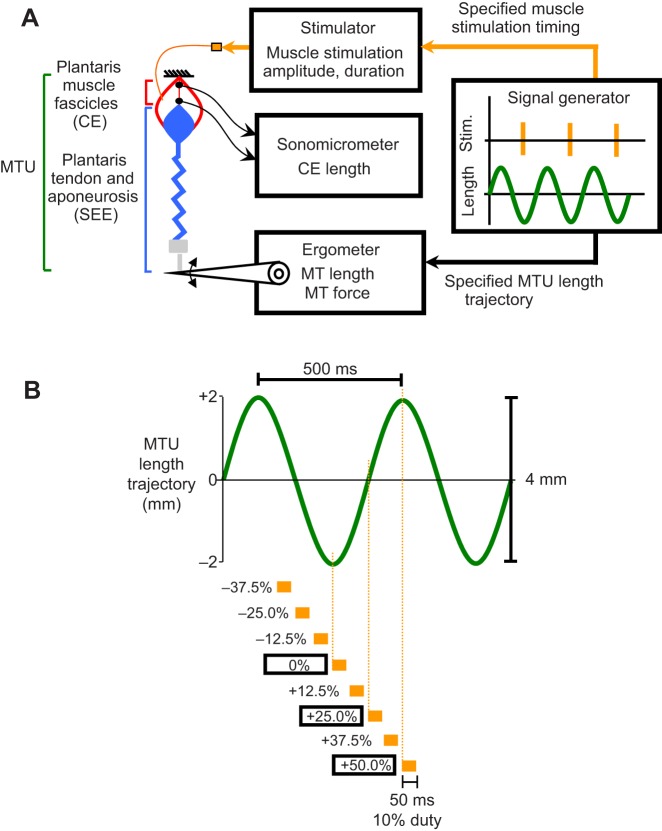
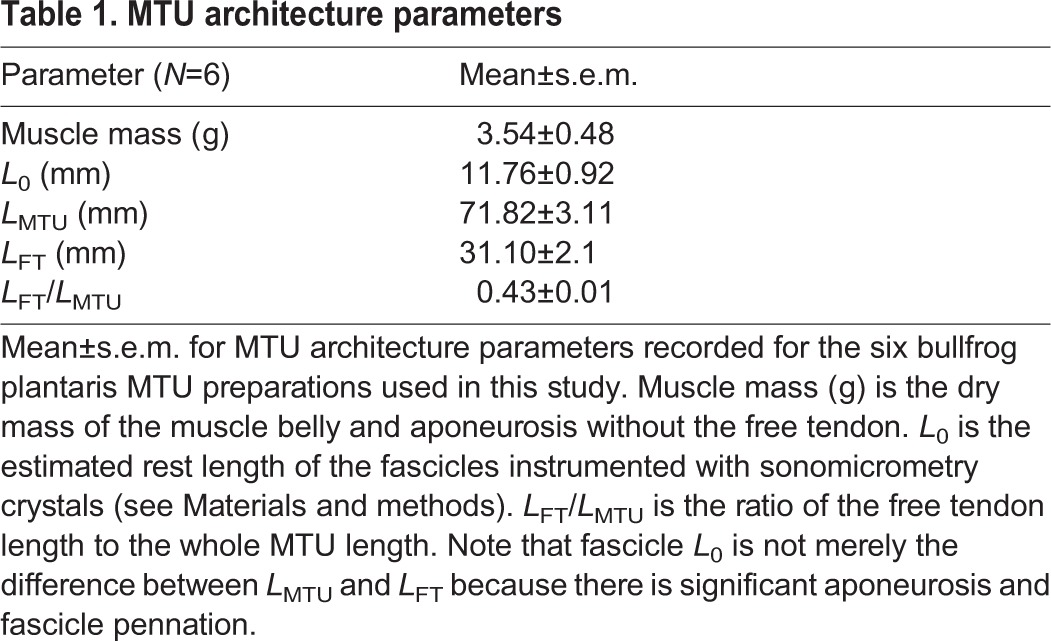
Fig. 1.

Fig. 1.

Open in a new tab

Schematic of muscle–tendon unit work loop experimental apparatus and protocol. (A) Schematic of experimental MTU work loop preparation. A bullfrog plantaris MTU was attached using an aluminium clamp and steel cable to an ergometer and driven through sinusoidal length change cycles while an electrical stimulus was applied to the sciatic nerve over set time periods during a cycle. Sonomicrometry was used to directly measure the length change of the muscle fascicles (CEs) within the MTU. (B) Schematic showing the imposed MTU length change trajectory (frequency 2 Hz, amplitude 4 mm, positive is lengthening) (green) and the set of conditions for onset timing and duration of muscle stimulation (orange) explored in this study. The onset timing of muscle stimulation (i.e. muscle stimulation phase) was defined with respect to the MTU length change cycle, with 0% referring to MTU minimum length (i.e. ‘bottom dead center’) and 50% referring to MTU maximum length (i.e. ‘top dead center’). We tested muscle stimulation phases spanning from −37.5% to +50% and stimulus always had a 50 ms duration (i.e. 10% duty) (orange).

RESULTS

All results reported here are taken from trials where cyclic length changes were applied to the MTU with a cycle frequency (ωcycle) of 2 Hz (i.e. cycle period=500 ms) and an amplitude (Acycle) of 4 mm with an initial (minimum) MTU length corresponding to a CE length of 1.2L0 (Figs 1 and 3). Key metrics characterizing the muscle–tendon architecture of preparations used in this study can be found in Table 1.

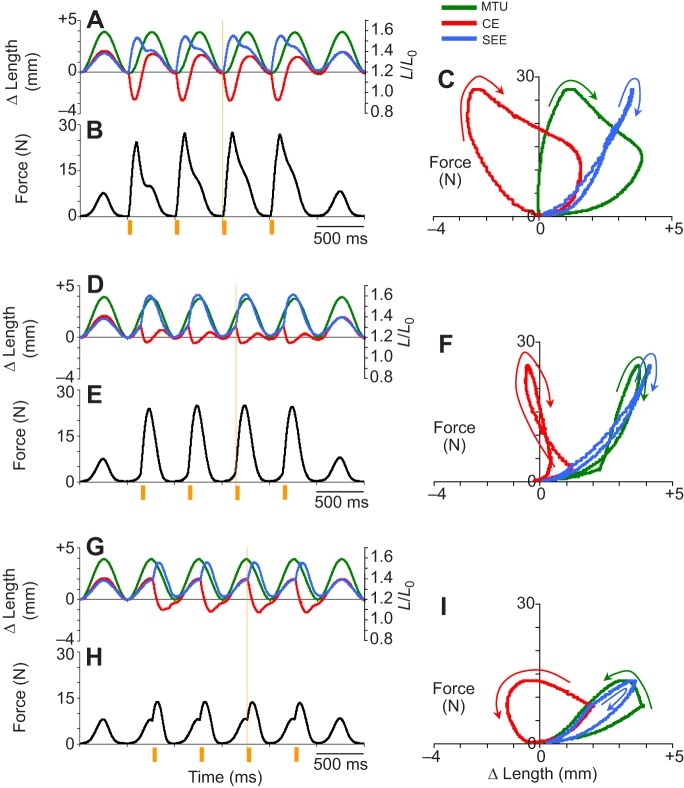
Fig. 3.

Fig. 3.

Open in a new tab

Work loop dynamics for the MTU, CE and SEE for different stimulation phases. Cyclic contraction dynamics observed for (A–C) 0%, (D–F) +25% and (G–I) +50% muscle stimulation phase. Each condition was subjected to six cycles of MTU shortening/lengthening. Plots of length change, Δ length (left axis) and CE strain (right axis) versus time (A,D,G), force versus time (B,E,H) and average work loop dynamics (force versus Δ length) (C,F,I) for stretch–shorten cycles where stimulation was applied are shown for each condition. Dynamics for the MTU, CE and the SEE are displayed where appropriate. Orange bars beneath plots of force versus time (B,E,H) indicate timing (i.e. phase) and duration (duty=10% or 50 ms) of muscle stimulation. Note that electrical stimulation is only applied in the middle four cycles, with the first and last stretch–shorten cycles occurring in the absence of stimulation (i.e. passively). Work loops traveling clockwise generate net negative work over a cycle [e.g. CE and MTU with muscle simulation phase=0% (C)]; work loops traveling counter clockwise generate net positive work over a cycle [e.g. CE and MTU with muscle simulation phase=50% (I)].

Table 1.

MTU architecture parameters

graphic file with name jexbio-218-121673-i1.jpg

Open in a new tab

Peak force

For all experimental conditions explored, peak force was recorded for each cycle of strain/stimulation (Figs 2 and 3) and was averaged within (N=4 cycles) and between (N=6 subjects) preparations to determine an average peak force (Fig. 4A). The highest peak force was observed at 12.5% muscle stimulation phase (Fig. 2 and Fig. 4A), and minimum values were recorded for stimulation phase of −37.5% (Fig. 4A). Peak forces were significantly different from the 25% phase (Tukey's; P<0.05) at −50%, −37.5%, −25% and 50%, and in no-stimulation conditions (Fig. 4A).

Fig. 2.

Fig. 2.

Open in a new tab

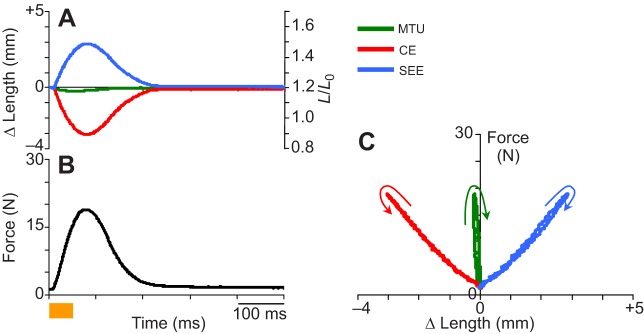
Data snapshot from a typical ‘fixed-end’ contraction cycle. (A) Length change of muscle–tendon unit (MTU), muscle fascicle (CE) and series elastic tissue (SEE) versus time, starting with muscle stimulation onset. Left axis is absolute length and right axis is strain with respect to fascicle rest length L0. (B) Force versus time. The orange bar under this axis indicates onset/offset and duration (50 ms) of the applied electrical stimulation. (C) Work loop dynamics observed in a typical ‘fixed-end’ contraction. Note significant internal shortening and lengthening of CE and SEE, respectively when CE is activated and MTU length is held constant.

Fig. 4.

Fig. 4.

Open in a new tab

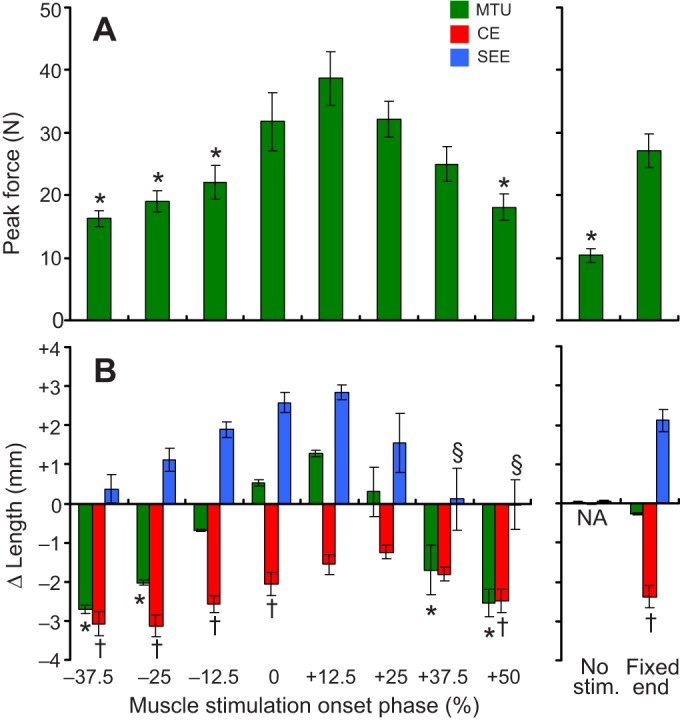
MTU component force and length change versus stimulation phase. (A) Mean peak force observed during active stretch–shorten cycles for all muscle stimulation phase conditions (left), as well as no stimulation (i.e. passive length change) and ‘fixed-end’ conditions (i.e. no MTU length change, right). (B) Mean length change observed from the onset of muscle stimulation to the end of active muscle fascicle (CE) shortening for the MTU, CE and SEE. Negative is shortening. Values significantly different (Tukey's; P<0.05) from the +25% muscle stimulation phase condition are indicated by * for MTU, † for CE and § for SEE. Values are means±s.e.m. No stim., no stimulation.

Length change trajectories following muscle stimulation

All conditions showed significant decoupling of the change in length of the CE from that of the MTU (Figs 2 and 3). Decoupling was particularly obvious immediately following stimulation; when the rapid rise in force resulted in SEE stretch and significant shortening of the CE, regardless of the direction of length change of the MTU. CE shortening following stimulation onset was observed for all conditions (Figs 2 and 3) and was minimal at 25% muscle stimulation phase (Fig. 3D and Fig. 4B).

Length change dynamics observed immediately following onset of muscle stimulation were of particular interest in this study because it is during this period that active force production tends to decouple MTU trajectory from CE and SEE strain (Fig. 3). All conditions, except for 12.5% stimulation phase had CE shortening excursions significantly greater than those in the 25% stimulation phase (Tukey's; P<0.05) (Fig. 4B). The greatest MTU force output and largest SEE stretch during the period of active CE shortening was observed at 12.5% stimulation phase (Fig. 4B). SEE strains were significantly less at 37.5% and 50% compared with 25% stimulation phase (Tukey's; P<0.05).

Mechanical power output

We were not only concerned with how force development influenced decoupling of CE/MTU dynamics, but also the role it played in generating mechanical work and power over a stretch–shorten cycle. Mechanical power was defined as positive during segment shortening (i.e. positive velocity), and was calculated as the product of force and velocity versus time as follows:

graphic file with name jexbio-218-121673-e1.jpg (1)

where Inline graphic is mechanical power, v□ is velocity and the □ symbol acts as a placeholder for a subscript of CE, SEE or MTU depending on the MTU component for which power was computed (Fig. 5).

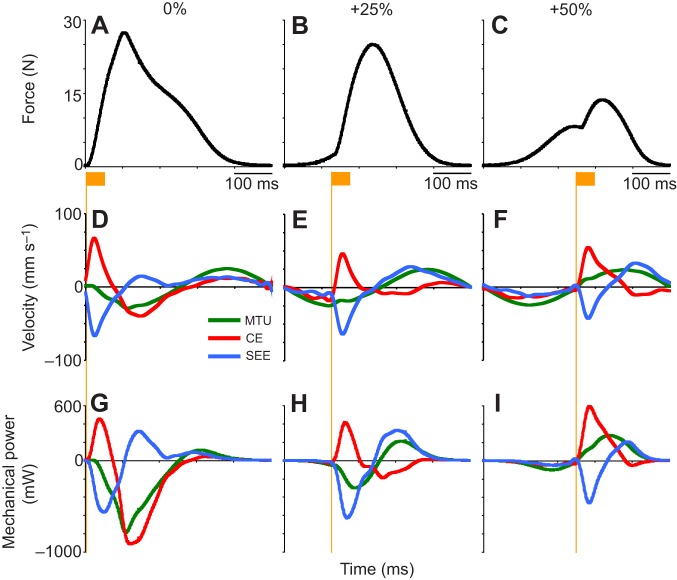
Fig. 5.

Fig. 5.

Open in a new tab

MTU component force, velocity and power versus time for different stimulation phases. (A–C) Force versus time for the 0% (A), +25% (B) and +50% (C) muscle stimulation phase conditions (left to right). The orange bar indicates the timing and duration of electrical stimulation. (D,F) Velocity versus time for the 0% (D), 25% (E) and 50% (F) muscle stimulation phase conditions. Positive is shortening. (G–I) Mechanical power versus time (s) for the 0% (G), +25% (H) and +50% (I) muscle stimulation phase conditions. Velocity and mechanical power are shown for the whole MTU, the CE and SEE. Note that in all conditions, muscle stimulation onset results in significant CE shortening/mechanical power generation while the SEEs lengthen/absorb mechanical energy to varying degrees.

In every dynamic condition, onset of muscle stimulation was followed by rapid force development, shortening and positive power production by the CE, regardless of whether the MTU was shortening or lengthening. During MTU lengthening, positive power production by the CE was associated with negative power (energy storage) from the SEE. Energy stored in the SEE has two possible fates. It can be returned externally to the motor, as positive MTU power, or it can do work on the CE to lengthen active muscle fibers. The extent to which work done by the CE on the SEE could be returned externally varied, depending on the phase of stimulation (Fig. 5). Under some conditions (e.g. 0% phase), all of the energy stored in the SEE was released to do work on the CE, rather than contributing to MTU power.

Decoupling of CE and MTU mechanics

Because we expected there to be some decoupling between CE and whole MTU length change dynamics, we computed a Pearson product-moment correlation coefficient to compare time-averaged CE and MTU velocities over a stretch–shorten cycle. r values were computed as follows:

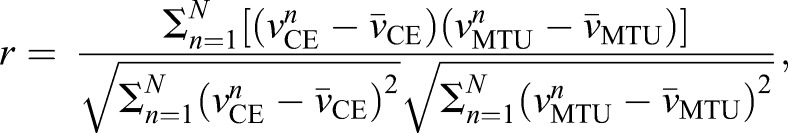graphic file with name jexbio-218-121673-e2.jpg (2)

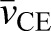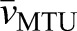where the coefficient n corresponds to a single discrete sample within a given period, N is the total number of samples recorded over a stretch–shorten cycle (Tcycle=500 ms, sample rate=1000 Hz, N=500 for all data presented here), and Inline graphic and Inline graphic are the average CE and MTU velocities, respectively, over a stretch–shorten cycle. A value of 1 indicates a perfect correlation, 0 is completely uncorrelated and −1 indicates perfect inverse correlation. We note that, although this approach serves well in the current study as a simple way to quantify the relative amount of decoupling between MTU and CE dynamics, it may not generalize to situations that are not as highly controlled in terms of the frequency and amplitude of the overall change in MTU length, timing of the muscle stimulation phase and regularity of the data sampling frequency. For example, when comparing signals that may have variation in sampling frequency, the correlation coefficient is prone to errors resulting from clustering of data in certain regions of the curves that could bias the measure.

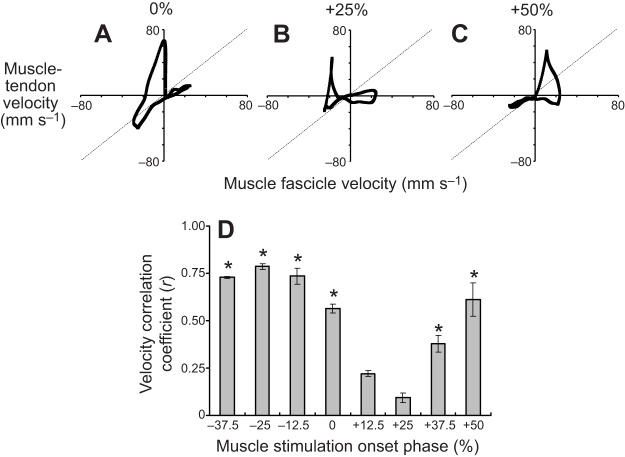
The r values computed based on CE versus MTU velocities were between 0 and 1 (i.e. positively correlated) for all conditions examined (Fig. 6). A minimum mean r value of 0.09 was observed for the 25% stimulation phase condition (Fig. 6B), which was significantly lower than all other stimulation phase conditions except for 12.5% (Tukey's P<0.05) (Fig. 6D).

Fig. 6.

Fig. 6.

Open in a new tab

Decoupling of MTU and CE length change dynamics. (A–C) MTU velocity (vMTU) versus muscle fascicle velocity (vCE) for the 0% (A), +25% (B) and +50% (C) muscle stimulation phase conditions. The dashed diagonal line indicates a trajectory where vCE=vMTU. (D) Mean Pearson product-moment correlation coefficient (r) value comparing instantaneous MTU and CE velocities. Lower r values indicate greater degree of decoupling between MTU and CE length change trajectories. The * symbol indicates an r value significantly different (Tukey's; P<0.05) from that observed for the +25% stimulation phase condition.

Net, positive and negative mechanical work

To examine how the muscle stimulation phase influenced average positive, negative and net mechanical work produced over a stretch–shorten cycle for the MTU and its components (CE, SEE) we computed:

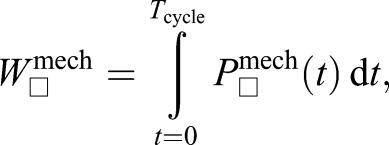graphic file with name jexbio-218-121673-e3.jpg (3)

where W□mech is net mechanical work over a full MTU stretch–shorten cycle, starting with t=0, the time of muscle stimulation onset and ending at Tcycle=500 ms later (Fig. 1); and □ is a place holder for CE, SEE or MTU subscripts. To compute positive and negative work over a cycle, we simply integrated only the positive or negative region of instantaneous mechanical power curve. Holding with convention from previous literature, we have defined positive work as mechanical energy produced, while negative work indicates energy absorbed by the element of interest.

The MTU produced approximately zero net work with onset of muscle stimulation at 25% of the MTU length change cycle (i.e. φstim=φnet zero=25%) (Fig. 3F, Fig. 5H and Fig. 7A). Because net work over the course of an entire MTU length change cycle must be due to the CE, net work in the CE and MTU were nearly identical in all muscle stimulation phase conditions (Fig. 7A). Even in the condition with nearly zero net work (i.e. φstim=φnet zero=25%), we did not observe ‘tuned’, strut-like isometric behavior of the CE. Instead, at 25% stimulation phase, the CE underwent an appreciable change in length following stimulation (Fig. 3D and Fig. 4B) and thus generated and absorbed substantial but equal amounts of mechanical energy (Fig. 5H and Fig. 7B,C).

Fig. 7.

Fig. 7.

Open in a new tab

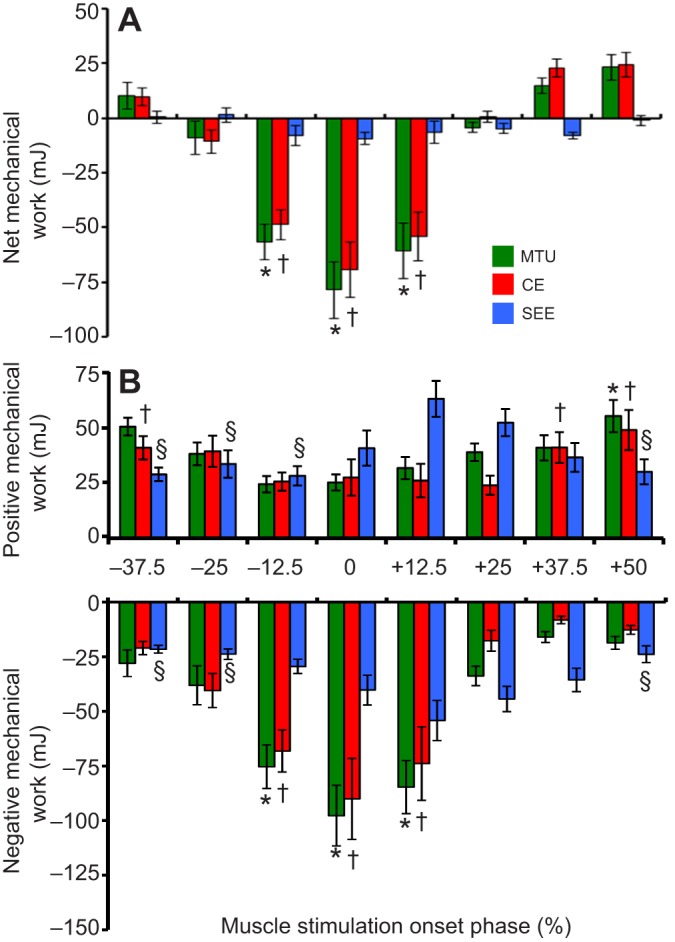
MTU component net, positive and negative work versus stimulation phase. (A–C) Mean±s.e.m. net (A), positive (B) and negative (C) mechanical work performed over a full stretch–shorten cycle for the MTU, CE and SEE. Net MTU work output shifts from absorption to generation as muscle stimulation phase increases from −25 to +50%. Mechanical work values significantly different (Tukey's; P<0.05) than those observed in the +25% muscle stimulation phase condition are marked with * for MTU, † for CE and § for SEE.

When muscle stimulation onset occurred earlier in the MTU length change cycle than for conditions of net zero work (φstim<φnet zero=25%), the MTU and CE generated net negative work (Fig. 3C, Fig. 5G and Fig. 7A). Maximal energy absorption by the MTU and CE occurred for 0% stimulation phase. Muscle stimulation phases ranging from −12.5% to +12.5% of the MTU length change cycle generated significantly more net negative CE and MTU work than at 25% stimulation phase (Tukey's; P<0.05) (Fig. 7A). We note that, as expected, SEE net work was small and ∼zero or negative for all conditions studied here because passive tissues can only store and return mechanical energy with small losses (Fig. 7A).

For muscle stimulation onset that occurred later in the MTU length change cycle than net zero work conditions (φstim>φnet zero=25%), the MTU and CE generated net positive work (Fig. 3I, Fig. 5I and Fig. 7A). Maximal net positive MTU and CE work per cycle was observed at 50% muscle stimulation phase; however, none of the conditions generated net positive work that was significantly different from the 25% stimulation condition (Tukey's; P≥0.05) (Fig. 7A).

DISCUSSION

While the mechanical roles of elastic elements during terrestrial gaits are well understood, the role that neural control plays in governing them is not. Therefore, we used a novel in vitro MTU work loop approach to determine how MTU, CE and SEE mechanics are modulated by the timing of muscle stimulation within a cyclical MTU strain trajectory (i.e. muscle stimulation phase). We specifically focused on elucidating the role of neural control in shaping muscle–tendon interaction dynamics which produced zero net MTU work, conditions akin to steady-speed terrestrial locomotion.

We hypothesized that: (1) there would be an onset timing of muscle stimulation relative to the MTU length change cycle that resulted in net zero MTU work over a stretch–shorten cycle (φstim=φnet zero); and that (2) muscle stimulation timed earlier (φstim<φnet zero) would result in net negative MTU work, while muscle stimulation timed later (φstim>φnet zero) would result in net positive MTU work. Our data supported these hypotheses (Fig. 7A). We note that, despite significant decoupling of CE and whole MTU dynamics observed here (Fig. 6), φnet zero for a compliant MTU occurred at a similar muscle stimulation phase as has been previously observed for isolated muscles without significant series elastic tissues (Josephson, 1985, 1999).

Our final hypothesis was that (3) the muscle stimulation phase resulting in net zero work (φstim=φnet zero) would be ‘tuned’ so that all positive and negative work produced by the MTU would be the result of elastic energy storage and return in the SEE, with little to no positive/negative mechanical work output from active muscle (CE). This hypothesis was not supported because the CE produced non-negligible amounts of both positive and negative work over a stretch–shorten cycle for the φstim=φnet zero≈25% condition (Fig. 7B).

A coordination rule for net zero work: aligning active muscle force with symmetric MTU stretch–shorten cycles

Under conditions specific to this study (i.e. MTU length change cycle duration=500 ms, muscle stimulation duration=50 ms) we found that an onset of muscle stimulation (i.e. stimulation phase) of ∼25% resulted in net zero MTU work over a cycle (φnet zero=25%). To begin to generalize our findings beyond the specific conditions of this study, we observed the force and length change dynamics of the MTU with respect to muscle stimulation timing (Fig. 3D,E) and devised a qualitative rule for zero net work as follows: employ stimulation timing and duration so that there is a symmetrical MTU stretch–shorten cycle during the period of active muscle force production. These conditions can be summarized mathematically by a simple equation relating the onset of muscle stimulation (i.e. stimulation phase) that yields net zero work (φnet zero) to the duration of active muscle force production (Dforce) for a given stimulus pattern, both expressed as a percentage of the cycle period of the MTU length change:

graphic file with name jexbio-218-121673-e4.jpg (4)

In this formulation, 0% phase is the time of minimum MTU length (i.e. ergometer bottom dead center) and 50% phase is the time of peak MTU length (i.e. ergometer top dead center) (Fig. 1). For the experiments presented here, 50 ms of muscle stimulation resulted in a duration of active muscle force of ∼250 ms (Fig. 2). Since the cycle period for a 2 Hz MTU length change pattern is 500 ms (Fig. 1), the duration of active muscle force production as a percentage of the length change cycle period Dforce was ∼250 ms/500 ms×100 or 50%. Using Eqn 4, Dforce=50% yields an estimate for the onset of muscle stimulation timing (i.e. stimulation phase) that would lead to net zero MTU work over the cycle; φnet zero=25%. This estimate is in good agreement with the experimental observation of net zero MTU work (Fig. 7A) in this study, as the 25% stimulation phase condition aligns active force onset/offset with MTU stretching and shortening (Figs 3 and 5) to facilitate effective elastic energy storage/return in the SEE (Fig. 3, Fig. 5 and Fig. 7B,C) and net MTU mechanical power output of ∼0 (Fig. 7A). We expect that this relationship (Eqn 4), albeit very simple, could provide a useful initial framework for relating neural control (stimulation amplitude, phase and duty) and mechanics of muscle–tendon systems during cyclic contractions. Future work will focus on elucidating the influence of sub-maximal muscle activation and MTU architecture on Dforce to expand the utility of Eqn 4 to conditions even closer to ‘real-world’ locomotion.

Challenges of achieving ‘tuned’ isometric force production in muscle–tendon systems

During steady-speed terrestrial locomotion, compliant MTUs at distal joints (e.g. the ankle) cyclically lengthen and shorten from step to step. This creates an opportunity for optimally coordinating muscle activation timing and amplitude to ‘tune’ muscle–tendon interaction for maximal performance. For example, if muscles are activated with timing and amplitude that supplies a rigid force producing strut (i.e. ‘tuned’ to be nearly isometric), they can allow elastic tissues to stretch and recoil during limb segment lengthening and shortening in order to cycle the energy required for steady gait. Because of the intrinsic force–length and force–velocity relationships, strut-like muscle-level dynamics are particularly well suited for high force production, reducing the volume of active muscle required to meet force demands and ultimately increasing the economy of locomotion (Roberts et al., 1997; Gabaldon et al., 2008).

Our results suggest that, even in the presence of highly compliant elastic tissues in series with muscle fascicles, tuning the CE for strut-like force production (i.e. near isometry) during cyclic contractions is challenging. Contrary to our third hypothesis, the net zero work condition (φnet zero=25%) resulted in significant length changes of the CE. That is, the net zero work condition was accomplished not by isometric force production by the CE, but by significant and approximately equal amounts of positive and negative work (Fig. 7B,C). Shortening work occurred early in the period of force production, as the CE shortened against the SEE and lengthening work occurred when the SEE recoiled against the CE. Although this pattern represented the most decoupled CE/MTU behavior (Fig. 6), it was far from the ‘ideal’ of an isometric CE strut supporting the cyclic stretch and recoil of tendon.

Why is isometric muscle behavior difficult to achieve under the conditions of our experiment? One likely issue is the combination of asymmetric muscle activation/deactivation dynamics (Zajac, 1989) and a symmetric/sinusoidal strain pattern. In general, muscle force onset occurs more rapidly than offset (Fig. 2). When symmetric patterns of MTU strain are applied to a muscle with asymmetric force onset/offset, some muscle shortening and lengthening is going to be required to match passive forces in SEEs. One possible approach to addressing this asymmetric force output is to apply an asymmetric strain pattern. Marsh and co-workers have demonstrated that when asymmetric strains are applied, it is possible to maximize power output from muscle alone (Askew and Marsh, 1997; Girgenrath and Marsh, 1999). With this in mind, we attempted to design an ergometer controller that would apply the required MTU strain pattern to keep CE length constant during muscle activation/deactivation using real-time sonomicrometry measurements as feedback (Sawicki and Roberts, 2009). The resulting MTU strain pattern was highly asymmetric and the length of the CE remained more isometric than shown in the current study. However, it was still not possible to achieve ‘perfect’ isometry as we could not avoid internal CE shortening against the SEE early in the supramaximal contractions of the compliant MTU. We note that animals probably use dynamically changing moment arms (Carrier et al., 1994) and pennation angles (Azizi et al., 2008), combined with differential sub-maximal motor-unit recruitment patterns (Holt et al., 2014) that can be modulated by reflex feedback (Maas and Lichtwark, 2009) to help ‘dial in’ nearly perfect strut-like muscle action during real-world locomotion.

Modulating muscle stimulation phase to meet changing mechanical demands during locomotion

Gait on level ground at constant speed requires no net mechanical work, but most terrestrial animals experience terrain that imposes varying mechanical demands (e.g. slowing down, speeding up, going up- or downhill). The decoupling of MTU and CE by SEEs may afford considerable advantages during unsteady locomotion, including: (1) limiting negative work absorbed by CE when active during MTU lengthening (Roberts and Azizi, 2010); (2) amplifying positive work by allowing muscle to operate at velocities for optimal power output during MTU shortening (Lichtwark and Barclay, 2010); and (3) providing a rapid means of mechanical feedback (i.e. ‘preflex’) following environmental perturbation (Daley and Biewener, 2006; Biewener and Daley, 2007). Our results support previous research suggesting that locomotion tasks involving net generation or absorption of mechanical energy may be accessible by adjusting timing of muscle stimulation relative to the pattern of MTU strain (Ettema, 1996a, 2001; Lichtwark and Wilson, 2005; Lichtwark and Barclay, 2010, 2012). We observed that slight changes in muscle stimulation onset phase from the φnet zero (i.e. 25%±12.5%) resulted in near maximal values of net positive or negative work, respectively (Fig. 7A). Our data are consistent with previous studies by Ettema (1996a) and Lichtwark and Barclay (2010), which varied frequency, phase and stimulation duty in a compliant MTU. Both of these studies emphasized the importance of proper muscle stimulation timing to either effectively store and return energy in series tendon (Ettema, 1996a) or maximize efficiency in shortening for performing positive work (Lichtwark and Barclay, 2010). Shifting muscle activation phase could provide a potentially simple neural mechanism for altering compliant MTU function to produce net negative (braking or moving downhill), net zero (constant speed) or net positive (acceleration or moving uphill) mechanical work output.

Benefits of direct muscle-level measurements in MTU work loop experiments

The most novel aspect of this study was the use of implantable sonomicrometry for direct measurement of muscle-level mechanics during dynamic work loop experiments. Previous work loop studies of MTU mechanics have relied on model-based approximations of SEE force–length behavior to dissect CE from SEE length changes. Ettema left the biological SEE intact, approximated SEE stiffness under high force conditions, and assumed perfect elasticity (i.e. all energy stored in SEE must be returned) to calculate the contribution of the SEE (Ettema et al., 1990; Ettema, 1996a,b). Multiple studies, however have demonstrated that biological tendons exhibit non-linear force–length behavior at low strains (Lichtwark and Wilson, 2007), and that volumetric changes in active muscle can change elastic properties of aponeurosis/SEE (Azizi and Roberts, 2009). Tendons will also dissipate some energy over a stretch–shorten cycle (Fig. 7A) (Bennet et al., 1986; Lieber et al., 1991; Maganaris and Paul, 2000). Lichtwark and Barclay avoided many of these pitfalls by removing the tendon altogether and replacing it with elastic strips of latex with well-defined linear stiffness (Lichtwark and Barclay, 2010, 2012). While this is an excellent approach to studying the effect of series compliance on muscle level function, it lacks many of the aforementioned mechanical features of biological tendons that might have a subtle but significant impact on CE mechanics. Despite this, findings presented here confirm the previous experimental observations of Lichtwark and colleagues (Lichtwark and Wilson, 2007; Lichtwark and Barclay, 2010, 2012) without the need for any sort of model-based approximation and further highlight that SEE compliance can have a profound impact on CE contractile dynamics.

Limitations of the classical work loop approach and future directions

While work loops have proved to be an effective means of exploring how strain trajectories and neural activation influence muscle-level mechanics and energetics (Ahn, 2012), they depart from muscle function during ‘real-world’ locomotion in significant ways (Marsh, 1999). During locomotion, muscle strain trajectories are not a pre-existing phenomenon to which neural activation patterns can be applied. Rather, they are an emergent behavior resulting from active muscle force, transmitted through mechanical lever systems (i.e. biological moment arms) and interaction with an inertial-gravitational load (Marsh, 1999; Richards and Clemente, 2012; Robertson and Sawicki, 2014). To understand the dynamic interplay of all of these factors, and the role that they play in generating stable/efficient MTU mechanics observed in gait, trajectory must not be imposed (Robertson and Sawicki, 2014).

During locomotion in the ‘real-world’, the dynamic interactions between MTUs of the limb and the load of the body serve to couple muscle stimulation frequency and phase. Thus, future work should focus on simulating a dynamic inertial environment (i.e. mechanical advantage, gravitational load) that can freely interact with a biological MTU undergoing cyclic stimulation (Sheppard et al., 2009; Farahat and Herr, 2010; Robertson and Sawicki, 2014). With direct, real-time measurements of both fascicle-level dynamics via sonomicrometry and muscle force from the ergometer as we have done in the current study, we could simulate spindle organ (i.e. length/velocity) and/or Golgi tendon (i.e. force) afferent feedback. By varying muscle stimulation intensity (via rate-coding) as a function of simulated feedback within and between muscle stimulation pulses, it may be possible to begin systematically exploring how environment dynamics, as well as feed-forward and feed-back neural control processes (e.g. reflexes) govern the influence of muscle activation on the mechanics and energetics of muscle–tendon interaction (Stevens, 1996; Farahat and Herr, 2010; Richards and Clemente, 2012).

MATERIALS AND METHODS

Animal subjects

Six adult bullfrogs (Lithobates catesbeianus Shaw 1802) with body masses ranging from 214 to 373 g, were purchased from a licensed vendor and housed in the Brown University Animal Care facility in a large tank of shallow water with free access to a terrestrial platform. Subjects were fed large, vitamin-enriched crickets ad libitum twice weekly. Before use in experimental procedures, animals were given a minimum acclimation period of 1 week. Prior to their use in any experimental preparation, frogs were anesthetized and euthanized by double pithing. All animal procedures were approved by Brown University Institutional Animal Care and Use Committee.

In vitro sample preparation

A single limb from each subject was removed just below the hip, the skin was removed and the limb was placed in a bath of oxygenated amphibian Ringer's solution (100 mmol l−1 NaCl, 2.5 mmol l−1 KCl, 2.5 mmol l−1 NaHCO3, 1.6 mmol l−1 CaCl2, 10.5 mmol l−1 dextrose) and kept at room temperature (∼22°C) during dissection. All muscles were completely removed except the plantaris longus (PL) MTU, which serves as the primary ankle extensor, and is known to be both compliant (i.e. high ‘fixed-end’ compliance and SEE/MTU length ratio), and a major source of power output during jumping. Caution was taken during removal of proximal muscles to ensure the sciatic nerve remained intact. The PL muscle was left intact at its proximal insertion point (the knee joint), and freed from the ankle and tibia/fibula, with great care taken to preserve series aponeurosis and free tendon up to its distal insertion point at the toes.

Following dissection, a bipolar electrode cuff constructed from two silver wires and plastic tubing (7 mm length, 1.5 mm inner diameter) was carefully placed over the free (but intact) sciatic nerve just proximal to the PL insertion point at the knee and connected to a Grass S48 stimulator (Grass Technologies, West Warwick, RI, USA). Sonomicrometry transducers (1 mm diameter, Sonometrics Inc., London, Ontario, CA, USA) were implanted along a superficial, proximal muscle fascicle of the PL muscle and sutured in place to provide direct measurement of fascicle (CE) length change (i.e. decoupled from whole MTU length change) (Fig. 1).

Intact sections of femur and tibia were securely mounted on acrylic bolted at the bottom of a chamber with continuously circulating oxygenated Ringer's solution maintained at room temperature (22°C). The distal end of the free tendon was placed in a custom friction clamp attached to a servomotor (310 B-LR, Aurora Scientific Inc., Cambridge, MA, USA) via a rigid stainless steel cable (stiffness≈94.1 N mm−1) (Fig. 1).

Measurement of MTU, CE and SEE force, length, velocity and mechanical power

MTU force and length were recorded from the servomotor and CE length was recorded using sonomicrometry (Fig. 1) and a 16-bit A/D converter (National Instruments USB-6251, Austin, TX, USA) sampling at 1000 Hz. Data were processed and analyzed using custom MATLAB software (MathWorks Inc., Natick, MA, USA). Raw data (MTU force, MTU length, CE length) were smoothed using a 4th order Butterworth, zero-lag filter with low pass cut-off frequency of 25 Hz. In all trials, we subtracted the length change of the stainless steel cable connecting the ergometer and the MTU, by subtracting 1/94.1 mm N−1 of force to get the true length change of the MTU.

To compute the velocity of the MTU and the CE we took the first derivative of the smoothed servomotor and sonomicrometry length change data, respectively. The length change and velocity of the SEEs was computed by simply subtracting the CE from the MTU length or velocity, respectively (e.g. Figs 2, 3 and 5). We note that this approach implies that ΔLMTU(t)=ΔLCE(t)+ΔLSEE(t) and vMTU=vCE(t)+vSEE(t), which assumes that CEs and SEEs reside along the same geometrical axis as the whole MTU. Finally, we computed mechanical power (mW) by multiplying instantaneous MTU force (N) and velocity (mm s−1) for the MTU and each of its component parts (i.e. CE and SEE; e.g. Fig. 5). We note that, because fascicles rotate while they shorten or lengthen and we did not record fascicle pennation angle, we could not estimate length changes of the CE along the long axis of the MTU/SEE. As a result, our length change measurements using sonomicrometry crystals implanted in fascicles are likely to be an underestimate of the CE length change along the MTU/SEE long axis (Azizi et al., 2008; Azizi and Roberts, 2014). These underestimates in CE length change and velocity will lead to overestimates in calculated SEE length change and velocity and therefore tend to attribute too much MTU mechanical power to the SEE and too little to the CE.

Estimation of muscle rest length for calculating dynamic strain

Normalized CE strains reported throughout (e.g. Figs 2 and 3) are based on the absolute length at which the muscle developed 1 N of passive tension, and previous experimental observation that this passive force occurs at a CE length of 1.2L0, so that:

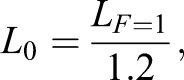graphic file with name jexbio-218-121673-e5.jpg (5)

where L0 is the length at which isometric muscle produces peak active forces, LF=1 is the absolute length of the CE under 1 N of passive force and 1.2 is the strain at which bullfrog muscles of similar size develop a passive force of 1 N (Azizi and Roberts, 2010).

‘Fixed-end’ contractions

Prior to any dynamic work loop conditions, ‘fixed-end’ contractions were performed by holding the ergometer position constant to impose an MTU length that resulted in 1 N of passive tension (CE length≈1.2L0), and then applying four stimulation trains at a frequency (ωstim) of 2 Hz with a duty factor (Dstim) of 10% (i.e. 50 ms). Each stimulation train consisted of pulses with a duration (tpulse) of 0.2 ms and a pulse frequency (ωpulse) of 100 Hz. The average peak force from the four ‘fixed-end’ contractions was recorded. Data showing a snapshot of a typical ‘fixed-end’ trial is shown in Fig. 2. The small amount of MTU shortening in these trials reflects the fact that we accounted for the ∼0.011 mm N−1 of compliance of the stainless steel cable used to attach the distal tendon to the ergometer arm. We note that the amount of muscle strain against internal stretch of the series elastic tissues, or ‘fixed-end’ compliance of this preparation was ∼0.30, which is in line with the value reported for the human gastrocnemius muscles (Narici et al., 1996; Biewener and Roberts, 2000; Roberts, 2002), indicating that the bullfrog plantaris is a convenient scaled-down model for human plantarflexors.

A second set of ‘fixed-end’ contractions was performed at the conclusion of all dynamic work loop conditions. Peak force values from the second set of ‘fixed-end’ contractions were compared with those for the first to be sure that muscle fatigue or damage due to trauma or low levels of oxygenation in deep portions of the tissue did not play a significant role in observed dynamics. For the six experimental preparations reported, the final peak force was ≥80% of the initial value, so factors negatively impacting force production were considered to be a non-factor and data were used for further analysis.

Work loop experiments

Cyclic length changes were applied to the MTU with a cycle frequency (ωcycle) of 2 Hz (i.e. cycle period=500 ms), and an amplitude (Acycle) of 4 mm with an initial (minimum) MTU length corresponding to a CE length of 1.2L0 (Figs 1 and 3). The MTU preparation was subjected to six cycles of shortening and lengthening, with the first and last cycle occurring in the absence of any muscle stimulation (Fig. 3). For the middle four cycles, muscle stimulation was driven via direct nerve stimulation with a specified onset timing that was different in each condition. More specifically, we defined the onset timing of muscle stimulation (i.e. muscle stimulation phase) with respect to the MTU length change cycle, with 0% referring stimulation onset at MTU minimum length (i.e. ‘bottom dead center’), and 50% referring to MTU maximum length (i.e. ‘top dead center’). We tested muscle stimulation phases ranging from −37.5% to 50% in 12.5% increments, always using a 50 ms pulse train duration (i.e. duty factor, Dstim=10%) (Fig. 1). Stimulation was delivered in a pulse train, with each individual pulse having period tpulse=0.2 ms and pulses delivered with frequency ωpulse=100 Hz. The order of muscle stimulation phase conditions was randomized in all in vitro preparations to minimize fatigue effects on averaged data.

Statistical analysis

To determine the influence of muscle stimulation phase on observed MTU mechanical performance, a two-factor analysis of variance (ANOVA) with subject (i.e. repeated measures) and muscle stimulation phase as the independent variables. We performed ANOVA analyses for all dependent variables of interest (Fig. 4A,B; Fig. 6D and Fig. 7A–D), with α=0.05. For dependent variables where we found a significant main effect (P<0.05), we report results from a post hoc Tukey's honestly significant difference (HSD) test, indicating which conditions were significantly different (P<0.05) from the 25% muscle stimulation phase condition. All values are reported as means±s.e.m.

Footnotes

Competing interests

The authors declare no competing or financial interests.

Author contributions

G.S.S. and T.J.R. conceived of the study; G.S.S., E.A. and T.J.R. constructed the experimental apparatus and designed the experimental protocol; G.S.S. and E.A. carried out experiments, G.S.S. and B.D.R. analyzed the data, G.S.S. and B.D.R. drafted the manuscript, G.S.S., B.D.R., E.A. and T.J.R. edited the manuscript. All authors gave final approval for publication.

Funding

This research was supported by the National Institutes of Health [F32 AR055847 to G.S.S., AR055295 to T.J.R.]. Deposited in PMC for release after 12 months.

References

  1. Ahn A. N. (2012). How muscles function--the work loop technique. J. Exp. Biol. 215, 1051-1052. 10.1242/jeb.062752 [DOI] [PubMed] [Google Scholar]
  2. Ahn A. N. and Full R. J. (2002). A motor and a brake: two leg extensor muscles acting at the same joint manage energy differently in a running insect. J. Exp. Biol. 205, 379-389. [DOI] [PubMed] [Google Scholar]
  3. Askew G. N. and Marsh R. L. (1997). The effects of length trajectory on the mechanical power output of mouse skeletal muscles. J. Exp. Biol. 200, 3119-3131. [DOI] [PubMed] [Google Scholar]
  4. Azizi E. and Roberts T. J. (2009). Biaxial strain and variable stiffness in aponeuroses. J. Physiol. 587, 4309-4318. 10.1113/jphysiol.2009.173690 [DOI] [PMC free article] [PubMed] [Google Scholar]
  5. Azizi E. and Roberts T. J. (2010). Muscle performance during frog jumping: influence of elasticity on muscle operating lengths. Proc. Biol. Sci. 277, 1523-1530. 10.1098/rspb.2009.2051 [DOI] [PMC free article] [PubMed] [Google Scholar]
  6. Azizi E. and Roberts T. J. (2014). Geared up to stretch: pennate muscle behavior during active lengthening. J. Exp. Biol. 217, 376-381. 10.1242/jeb.094383 [DOI] [PMC free article] [PubMed] [Google Scholar]
  7. Azizi E., Brainerd E. L. and Roberts T. J. (2008). Variable gearing in pennate muscles. Proc. Natl. Acad. Sci. USA 105, 1745-1750. 10.1073/pnas.0709212105 [DOI] [PMC free article] [PubMed] [Google Scholar]
  8. Barclay C. J. and Lichtwark G. A. (2007). The mechanics of mouse skeletal muscle when shortening during relaxation. J. Biomech. 40, 3121-3129. 10.1016/j.jbiomech.2007.03.024 [DOI] [PubMed] [Google Scholar]
  9. Bennet M. B., Ker R. F., Imery N. J. and Alexander R. M. (1986). Mechanical properties of various mammalian tendons. J. Zool. 209, 537-548. 10.1111/j.1469-7998.1986.tb03609.x [DOI] [Google Scholar]
  10. Biewener A. A. and Daley M. A. (2007). Unsteady locomotion: integrating muscle function with whole body dynamics and neuromuscular control. J. Exp. Biol. 210, 2949-2960. 10.1242/jeb.005801 [DOI] [PMC free article] [PubMed] [Google Scholar]
  11. Biewener A. A. and Roberts T. J. (2000). Muscle and tendon contributions to force, work, and elastic energy savings: a comparative perspective. Exerc. Sport Sci. Rev. 28, 99-107. [PubMed] [Google Scholar]
  12. Biewener A. A., Konieczynski D. D. and Baudinette R. V. (1998). In vivo muscle force-length behavior during steady-speed hopping in tammar wallabies. J. Exp. Biol. 201, 1681-1694. [DOI] [PubMed] [Google Scholar]
  13. Caiozzo V. J. and Baldwin K. M. (1997). Determinants of work produced by skeletal muscle: potential limitations of activation and relaxation. Am. J. Physiol. 273, C1049-C1056. [DOI] [PubMed] [Google Scholar]
  14. Carrier D. R., Heglund N. C. and Earls K. D. (1994). Variable gearing during locomotion in the human musculoskeletal system. Science 265, 651-653. 10.1126/science.8036513 [DOI] [PubMed] [Google Scholar]
  15. Daley M. A. and Biewener A. A. (2006). Running over rough terrain reveals limb control for intrinsic stability. Proc. Natl. Acad. Sci. USA 103, 15681-15686. 10.1073/pnas.0601473103 [DOI] [PMC free article] [PubMed] [Google Scholar]
  16. Dean J. C. and Kuo A. D. (2011). Energetic costs of producing muscle work and force in a cyclical human bouncing task. J. Appl. Physiol. 110, 873-880. 10.1152/japplphysiol.00505.2010 [DOI] [PMC free article] [PubMed] [Google Scholar]
  17. Dickinson M. H., Farley C. T., Full R. J., Koehl M. A. R., Kram R. and Lehman S. (2000). How animals move: an integrative view. Science 288, 100-106. 10.1126/science.288.5463.100 [DOI] [PubMed] [Google Scholar]
  18. Ettema G. J. (1996a). Mechanical efficiency and efficiency of storage and release of series elastic energy in skeletal muscle during stretch-shorten cycles. J. Exp. Biol. 199, 1983-1997. [DOI] [PubMed] [Google Scholar]
  19. Ettema G. J. C. (1996b). Contractile behaviour in skeletal muscle-tendon unit during small amplitude sine wave perturbations. J. Biomech. 29, 1147-1155. 10.1016/0021-9290(96)00014-0 [DOI] [PubMed] [Google Scholar]
  20. Ettema G. J. C. (2001). Muscle efficiency: the controversial role of elasticity and mechanical energy conversion in stretch-shortening cycles. Eur. J. Appl. Physiol. 85, 457-465. 10.1007/s004210100464 [DOI] [PubMed] [Google Scholar]
  21. Ettema G. J., Huijing P. A., van Ingen Schenau G. J. and de Haan A. (1990). Effects of prestretch at the onset of stimulation on mechanical work output of rat medial gastrocnemius muscle-tendon complex. J. Exp. Biol. 152, 333-351. [DOI] [PubMed] [Google Scholar]
  22. Farahat W. A. and Herr H. M. (2010). Optimal workloop energetics of muscle-actuated systems: an impedance matching view. PLoS Comput. Biol. 6, e1000795 10.1371/journal.pcbi.1000795 [DOI] [PMC free article] [PubMed] [Google Scholar]
  23. Farris D. J. and Sawicki G. S. (2012). Human medial gastrocnemius force-velocity behavior shifts with locomotion speed and gait. Proc. Natl. Acad. Sci. USA 109, 977-982. 10.1073/pnas.1107972109 [DOI] [PMC free article] [PubMed] [Google Scholar]
  24. Farris D. J., Robertson B. D. and Sawicki G. S. (2013). Passive elastic exoskeletons reduce soleus muscle force but not work in human hopping. J. Appl. Phys. 115, 579-585. 10.1152/japplphysiol.00253.2013 [DOI] [PubMed] [Google Scholar]
  25. Fukunaga T., Kubo K., Kawakami Y., Fukashiro S., Kanehisa H. and Maganaris C. N. (2001). In vivo behaviour of human muscle tendon during walking. Proc. Biol. Sci. 268, 229-233. 10.1098/rspb.2000.1361 [DOI] [PMC free article] [PubMed] [Google Scholar]
  26. Gabaldon A. M., Nelson F. E. and Roberts T. J. (2008). Relative shortening velocity in locomotor muscles: turkey ankle extensors operate at low V/V(max). Am. J. Physiol. Regul. Integr. Comp. Physiol. 294, R200-R210. 10.1152/ajpregu.00473.2007 [DOI] [PubMed] [Google Scholar]
  27. Girgenrath M. and Marsh R. L. (1999). Power output of sound-producing muscles in the gray tree frogs Hyla versicolor and Hyla chrysoscelis. J. Exp. Biol. 202, 3225-3237. [DOI] [PubMed] [Google Scholar]
  28. Gordon A. M., Huxley A. F. and Julian F. J. (1966). The variation in isometric tension with sarcomere length in vertebrate muscle fibres. J. Physiol. 184, 170-192. 10.1113/jphysiol.1966.sp007909 [DOI] [PMC free article] [PubMed] [Google Scholar]
  29. Hill A. V. (1925). Length of muscle, and the heat and tension developed in an isometric contraction. J. Physiol. 60, 237-263. 10.1113/jphysiol.1925.sp002242 [DOI] [PMC free article] [PubMed] [Google Scholar]
  30. Hill A. V. (1938). The heat of shortening and the dynamic constants of muscle. Proc. R. Soc. Lond. B Biol. Sci. 126, 136-195. 10.1098/rspb.1938.0050 [DOI] [PubMed] [Google Scholar]
  31. Holt N. C., Wakeling J. M. and Biewener A. A. (2014). The effect of fast and slow motor unit activation on whole-muscle mechanical performance: the size principle may not pose a mechanical paradox. Proc. Biol. Sci. 281, 20140002 10.1098/rspb.2014.0002 [DOI] [PMC free article] [PubMed] [Google Scholar]
  32. Ishikawa M., Komi P. V., Grey M. J., Lepola V. and Bruggemann G.-P. (2005). Muscle-tendon interaction and elastic energy usage in human walking. J. Appl. Physiol. 99, 603-608. 10.1152/japplphysiol.00189.2005 [DOI] [PubMed] [Google Scholar]
  33. Josephson R. K. (1985). Mechanical power output from striated muscle during cyclic contraction. J. Exp. Biol. 114, 493-512. [Google Scholar]
  34. Josephson R. K. (1993). Contraction dynamics and power output of skeletal muscle. Annu. Rev. Physiol. 55, 527-546. 10.1146/annurev.ph.55.030193.002523 [DOI] [PubMed] [Google Scholar]
  35. Josephson R. K. (1999). Dissecting muscle power output. J. Exp. Biol. 202, 3369-3375. [DOI] [PubMed] [Google Scholar]
  36. Lichtwark G. A. and Barclay C. J. (2010). The influence of tendon compliance on muscle power output and efficiency during cyclic contractions. J. Exp. Biol. 213, 707-714. 10.1242/jeb.038026 [DOI] [PubMed] [Google Scholar]
  37. Lichtwark G. A. and Barclay C. J. (2012). A compliant tendon increases fatigue resistance and net efficiency during fatiguing cyclic contractions of mouse soleus muscle. Acta Physiol. 204, 533-543. 10.1111/j.1748-1716.2011.02361.x [DOI] [PubMed] [Google Scholar]
  38. Lichtwark G. A. and Wilson A. M. (2005). Effects of series elasticity and activation conditions on muscle power output and efficiency. J. Exp. Biol. 208, 2845-2853. 10.1242/jeb.01710 [DOI] [PubMed] [Google Scholar]
  39. Lichtwark G. A. and Wilson A. M. (2007). Is Achilles tendon compliance optimised for maximum muscle efficiency during locomotion? J. Biomech. 40, 1768-1775. 10.1016/j.jbiomech.2006.07.025 [DOI] [PubMed] [Google Scholar]
  40. Lieber R. L., Leonard M. E., Brown C. G. and Trestik C. L. (1991). Frog semitendinosis tendon load-strain and stress-strain properties during passive loading. Am. J. Physiol. 261, C86-C92. [DOI] [PubMed] [Google Scholar]
  41. Lou F., Curtin N. A. and Woledge R. C. (1998). Contraction with shortening during stimulation or during relaxation: how do the energetic costs compare? J. Muscle Res. Cell Motil. 19, 797-802. 10.1023/A:1005455505056 [DOI] [PubMed] [Google Scholar]
  42. Lou F., Curtin N. A. and Woledge R. C. (1999). Elastic energy storage and release in white muscle from dogfish scyliorhinus canicula. J. Exp. Biol. 202, 135-142. [DOI] [PubMed] [Google Scholar]
  43. Maas H. and Lichtwark G. A. (2009). Is muscle-tendon unit length a valid indicator for muscle spindle output? J. Physiol. 587, 13-14. 10.1113/jphysiol.2008.165555 [DOI] [PMC free article] [PubMed] [Google Scholar]
  44. Maganaris C. N. and Paul J. P. (2000). Hysteresis measurements in intact human tendon. J. Biomech. 33, 1723-1727. 10.1016/S0021-9290(00)00130-5 [DOI] [PubMed] [Google Scholar]
  45. Marsh R. L. (1999). How muscles deal with real-world loads: the influence of length trajectory on muscle performance. J. Exp. Biol. 202, 3377-3385. [DOI] [PubMed] [Google Scholar]
  46. Narici M. V., Binzoni T., Hiltbrand E., Fasel J., Terrier F. and Cerretelli P. (1996). In vivo human gastrocnemius architecture with changing joint angle at rest and during graded isometric contraction. J. Physiol. 496, 287-297. 10.1113/jphysiol.1996.sp021685 [DOI] [PMC free article] [PubMed] [Google Scholar]
  47. Richards C. T. and Clemente C. J. (2012). A bio-robotic platform for integrating internal and external mechanics during muscle-powered swimming. Bioinspir. Biomim. 7, 016010 10.1088/1748-3182/7/1/016010 [DOI] [PubMed] [Google Scholar]
  48. Roberts T. J. (2002). The integrated function of muscles and tendons during locomotion. Comp. Biochem. Physiol. A Mol. Integr. Physiol. 133, 1087-1099. 10.1016/S1095-6433(02)00244-1 [DOI] [PubMed] [Google Scholar]
  49. Roberts T. J. and Azizi E. (2010). The series-elastic shock absorber: tendons attenuate muscle power during eccentric actions. J. Appl. Physiol. 109, 396-404. 10.1152/japplphysiol.01272.2009 [DOI] [PMC free article] [PubMed] [Google Scholar]
  50. Roberts T. J., Marsh R. L., Weyand P. G. and Taylor C. R. (1997). Muscular force in running turkeys: the economy of minimizing work. Science 275, 1113-1115. 10.1126/science.275.5303.1113 [DOI] [PubMed] [Google Scholar]
  51. Robertson B. D. and Sawicki G. S. (2014). Exploiting elasticity: modeling the influence of neural control on mechanics and energetics of ankle muscle-tendons during human hopping. J. Theor. Biol. 353, 121-132. 10.1016/j.jtbi.2014.03.010 [DOI] [PubMed] [Google Scholar]
  52. Sandercock T. G. and Heckman C. J. (1997). Force from cat soleus muscle during imposed locomotor-like movements: experimental data versus Hill-type model predictions. J. Neurophysiol. 77, 1538-1552. [DOI] [PubMed] [Google Scholar]
  53. Sawicki G. S. and Roberts T. J. (2009). Isometric force production requires asymmetric muscle-tendon length trajectory. In 33rd Annual Meeting of American Society of Biomechanics. State College, PA: ASB. [Google Scholar]
  54. Sheppard P., Sawicki G. S. and Roberts T. J. (2009). Power Augmentation in a Compliant Muscle-Tendon System. In 33rd Annual Meeting of American Society of Biomechanics. State College, PA: ASB. [Google Scholar]
  55. Stevens E. D. (1996). The pattern of stimulation influences the amount of oscillatory work done by frog muscle. J. Physiol. 494, 279-285. 10.1113/jphysiol.1996.sp021490 [DOI] [PMC free article] [PubMed] [Google Scholar]
  56. Takeshita D., Shibayama A., Muraoka T., Muramatsu T., Nagano A., Fukunaga T. and Fukashiro S. (2006). Resonance in the human medial gastrocnemius muscle during cyclic ankle bending exercise. J. Appl. Physiol. 101, 111-118. 10.1152/japplphysiol.01084.2005 [DOI] [PubMed] [Google Scholar]
  57. Zajac F. E. (1989). Muscle and tendon: properties, models, scaling, and application to biomechanics and motor control. Crit. Rev. Biomed. Eng. 17, 359-411. [PubMed] [Google Scholar]

Articles from The Journal of Experimental Biology are provided here courtesy of Company of Biologists

RESOURCES