Functional connectivity changes detected with magnetoencephalography after mild traumatic brain injury

Abstract

Mild traumatic brain injury (mTBI) may affect normal cognition and behavior by disrupting the functional connectivity networks that mediate efficient communication among brain regions. In this study, we analyzed brain connectivity profiles from resting state Magnetoencephalographic (MEG) recordings obtained from 31 mTBI patients and 55 normal controls. We used phase-locking value estimates to compute functional connectivity graphs to quantify frequency-specific couplings between sensors at various frequency bands. Overall, normal controls showed a dense network of strong local connections and a limited number of long-range connections that accounted for approximately 20% of all connections, whereas mTBI patients showed networks characterized by weak local connections and strong long-range connections that accounted for more than 60% of all connections. Comparison of the two distinct general patterns at different frequencies using a tensor representation for the connectivity graphs and tensor subspace analysis for optimal feature extraction showed that mTBI patients could be separated from normal controls with 100% classification accuracy in the alpha band. These encouraging findings support the hypothesis that MEG-based functional connectivity patterns may be used as biomarkers that can provide more accurate diagnoses, help guide treatment, and monitor effectiveness of intervention in mTBI.

Highlights

• •We analyzed resting state connectivity profiles in 31 mTBI patients and 55 controls.
• •We quantified frequency-specific connectivity couplings using phase-locking values.
• •Normal control networks showed dense local and sparse long-range connections.
• •TBI patient networks showed sparse local and dense long-range connections.
• •Tensor subspace analysis could classify subjects with 100% accuracy in the α band

1. Introduction

Traumatic brain injury is a major cause of sustained morbidity and disability both in the military and civilian populations (Tarapore et al., 2013). In the case of mild traumatic brain injury (mTBI), an initial brief change in mental state or consciousness is typically followed by postconcussion symptoms (Cassidy et al., 2004), such as headaches, fatigue, and dizziness, which usually emerge on the day of injury and persist for at least the first few days thereafter (Boccaletti et al., 2006). In most patients cognition recovers and symptoms resolve within 3 months; however, up to 25% of patients (Sigurdardottir et al., 2009) suffer residual symptoms, long-term impairment, and sometimes disability (Levin, 2009). In a large percentage of patients mTBI is difficult to diagnose because of the absence of apparent external injuries and obvious focal brain lesions in conventional computed tomography (CT) or magnetic resonance imaging (MRI) scans (Tarapore et al., 2013), although mTBI-related morphological changes at a microscopic level have been recently reported using MRI (Pasternak et al., 2014; Sasaki et al., 2014). There is a large body of literature for the accurate classification of TBI. A common practice is to classify TBI as mild, moderate, or severe based on the level of consciousness assessed using the well-known Glasgow Coma Scale (GCS, Teasdale and Jennet, 1974). Some studies have attempted to classify TBI and predict long-term outcome based on CT findings (Zhu et al., 2009) or the amount of exosomes released in the peripheral circulation due to injury (Taylor and Taylor, 2014).

One mechanism by which TBI is thought to affect cognition and behavior is through changes in functional connectivity (Castellanos et al., 2010; Martino et al., 2011). Functional brain connectivity refers to temporally correlated activity in spatially distinct brain regions and is believed to mediate neural communication among these regions (Aertsen et al., 1989; Salvador et al., 2005).

Several imaging studies have demonstrated the existence of a network of functionally connected brain regions that support a default mode of brain function (Guskiewicz et al., 2005). Changes in brain activity caused by focal lesions result in abnormal interactions among local and remote brain regions that are functionally connected (Quigley et al., 2001; Van Cappellen van Walsum et al., 2003), and these changes are reflected on the configuration of the default brain network. Thus, functional connectivity analysis offers a unique opportunity to quantify changes in neurophysiological processes that correlate well with clinical symptoms (Huang et al. 2009, Huang et al. 2012; Lewine et al., 2007).

The literature shows several examples of pathological alterations, including increase (Van Dellen et al., 2012) and decrease (Sharp et al., 2014) of functional connectivity using different modalities (Congedo et al. 2010, Rubinov, and Bullmore 2013), which provide evidence that a balance in the synchronization level in healthy controls is required for optimal brain function. Several brain connectivity studies in clinical populations focus on the description of topological differences with control group employing various synchronization measures, network metrics and statistics (Sporns, Tononi, and Kötter 2005, Guggisberg et al. 2008 Micheloyannis et al., 2006; Shiver et al., 2012; Stam et al., 2007; Bassett et al., 2009; Bullmore and Sporns, 2009; Castellano et al., 2010; Dimitriadis et al., 2013b; Bigler, 2013). In the area of brain injury in particular, during the last two decades there has been a growing effort to characterize the structural and functional effects of mTBI using the full range of neuroimaging methods (see the excellent review by Eierud et al., 2014), and various biomarkers have been proposed based on functional MRI (fMRI) and diffusion tensor imaging (DTI) (Kou et al., 2010; Hunter et al., 2012; Bigler, 2013). Among these methods, MEG plays a special role because it measures neuromagnetic fields resulting from primary neuronal currents that are not subject to the distortion induced by the variable conductance of brain tissues (Tarapore et al., 2013). Of particular interest are recordings of resting state MEG (de Pasquale et al. 2012, Mantini et al. 2011, Qian et al. 2013) because they require no training or experience with cognitive tasks, and they impose minimal demands on a patient, which is especially important after brain injury. Thus, resting state MEG is particularly suitable for detecting changes in functional connectivity networks in patients with mTBI compared to matched controls.

One of the very first studies using resting-state MEG as a possible neurophysiological biomarker for mTBI provided clear evidence that analysis of functional connectivity patterns could be a valuable tool for early detection of mTBI (Zouridakis et al., 2012). Other studies showed abnormal slowing in brain areas affected by TBI (Huang et al., 2014) and reduced overall functional connectivity in TBI patients compared to controls (Tarapore et al., 2013). In particular, using resting-state MEG and low-frequency source imaging, Huang et al. (2012) showed 87% and 100% accuracy in detecting abnormalities in mild and moderate TBI, respectively. Furthermore, Lewine et al. (1999) used MRI and MEG to examine postconcussive symptomatology and were able to discriminate between healthy adults and individuals with resolved mTBI. Another MEG study attempting to characterize system complexity and potential neural network damage found reduced complexity in multiple brain areas in mTBI subjects relative to healthy controls (Luo et al., 2013). Other studies further demonstrated that decreased connectivity in resting-state MEG may persist for years after mTBI, even in mild TBI cases (Castellanos et al., 2011), but the abnormally reduced connectivity might improve over time across serial MEG scans, suggesting neuroplasticity during recovery from TBI (Tarapore et al., 2013).

Continuing our earlier attempt (Zouridakis et al., 2012) to understand how mTBI affects communication in the human brain network, the present study extends our previous work in several ways: first, we employ a much larger sample of patients and controls, 31 mTBI patients and 50 normal controls, compared to only 10 and 10, respectively; second, we use the phase locking value estimator and graph theory to compute functional connectivity graphs (FCGs), whereas in the earlier study we used Granger causality as the estimator; and third, we follow a tensor-based instead of vector-based approach for subject classification. Here we consider FCGs as second-order tensors, which, after dimensionality reduction, are used for subject classification, whereas the earlier study considered the Granger connectivity matrices as one-dimensional vectors and used them for subject classification; and fourth, we performed the analysis in several frequency bands, instead of only one, based on recent studies that found differences in FCGs across frequency bands (Ηillebrand et al., 2012; Engel et al., 2013).

The remainder of this paper is structured as follows: Section 2 describes the data and the detailed analysis procedure, Section 3 presents the classification results, Section 4 is devoted to discussing our findings, and Section 5 summarizes some concluding remarks.

2. Methods

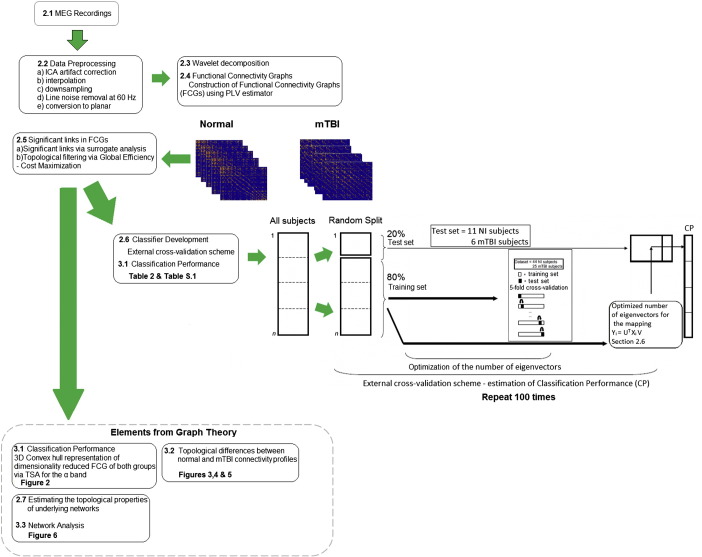
The overall methodology employed in this study is outlined in Fig. 1 and includes the following steps: data collection, preprocessing, wavelet decomposition, computation of functional connectivity graphs (FCGs), selection of significant links, feature extraction, optimization of the number of features, designing a classifier, evaluating its performance, and assessing the topological properties of the FCGs. Each step is described in detail in the following sections.

Fig. 1.

Various steps of the proposed analysis procedure.

2.1. Subjects and recording procedure

The present project is part of a larger study of mTBI, supported by the Department of Defense (DoD). The definition of mTBI used in this study followed the guidelines of DoD (Assistant Secretary, 2007) and the American Congress of Rehabilitation Medicine (Kay T., 1993). This work was approved by the Institutional Review Boards (IRBs) at the participating institutions and the Human Research Protection Official's (HRPO) Review of Research Protocols for DoD. All procedures were compliant with the Health Insurance Portability and Accountability Act (HIPAA).

Subjects included in this analysis included a group of mTBI subjects from the DoD project and a group of age-matched normal controls drawn from a database that was being assembled as a normative data repository at UTHSC-Houston. The mTBI group consisted of 31 right-handed mTBI participants (29.33 ± 9.2 years of age). Subjects were recruited from the Emergency Departments (EDs) of two Level 1 trauma centers and one Level III community hospital in a large ethnically diverse southwestern metropolitan area. Subjects were recruited by healthcare professionals (RN, MD, EMT-P) who had clinical experience with brain injury patients, knowledge of research, and excellent interpersonal and problem-solving skills. Screening occurred through review of data in the EDs' electronic healthcare system (EHS), consultation with ED staff, and subject interviews. Special permission was obtained from the institutional IRBs to administer the Galveston Orientation and Amnesia Test (GOAT) (Levin et al., 2008) prior to obtaining informed consent to identify cognitive impairment that would preclude provision of informed consent. All subjects showed GOAT scores of 75 or greater and so have provided informed consent.

The inclusion criteria for all subjects in the DoD project included age 18–50 years, injury occurring within the preceding 24 h, and no requirement for hospitalization for the injury for which the participant was enrolled. For mTBI subjects, the inclusion criteria also required the presence of a head injury (documented in medical records and/or verified by witnesses), Glasgow Coma Scale (GCS) (Teasdale and Jennett, 1974) score 13–15, loss of consciousness <30 min including 0 min, post-traumatic amnesia <24 h including 0 min, and a negative head computed tomography (CT) scan. The exclusion criteria included a score on the Abbreviated Injury Scale (AIS) >3 for any body part, history of significant pre-existing disease (e.g., psychotic disorder, bipolar disorder, post-traumatic stress disorder (PTSD) diagnosed by a psychiatrist or psychologist, past treatment for alcohol dependence or substance abuse), blood alcohol level >80 mg/dL at the time of consent, documentation of intoxication, left-handedness, and contraindications for MRI (including claustrophobia and pregnancy). Previous head injury requiring hospitalization or ED treatment was also an exclusion criterion. The demographics of mTBI subjects and the location of injury are given in Table 1.

Table 1.

Subject demographics, location, and mode of impact (MOI) for the mTBI group.

Subject	Age at injury	Gender	Primary MOI	Primary MOI type	Primary MOI location	Location	Side
1	21.7	M	Auto pedestrian	Laceration — no sutures	Head	F, C
2	42.0	M	Motor vehicle	Abrasion	Head	P
3	22.1	M	Motor vehicle	Tenderness	Head	O
4	43.1	M	Motor vehicle	Tenderness	Head	F, C
5	34.6	M	Fall raised surface	Abrasion	Head	T
6	42.3	F	Assault	Bruising	Head	P
7	20.3	M	Motor vehicle	Bruising	Head	T	L
8	24.0	F	All-terrain vehicle	Laceration — no sutures	Head	Fa, F, C
9	24.9	M	Sports-related	Laceration — with sutures	Head	Fa, F, C	L, M, R
10	24.4	F	Motor vehicle	Bruising	Head/face		L
11	43.7	F	Motor vehicle	Tenderness	Head	P, T	L
12	36.3	M	Blow to head	Tenderness	Head	O
13	49.1	M	Motorcycle	Contusion	Head	F, C, O
14	43.3	F	Fall standing	Laceration — no sutures	Head	F, C	L
15	23.3	F	Fall standing	Laceration — with sutures	Head		L
16	33.4	M	Fall raised surface	Laceration — no sutures	Head	Fa, F, C
17	27.3	M	Auto pedestrian	Tenderness	Head/face	Fa, F, C	R
18	49.8	F	Fall moving object	Laceration — with sutures	Head	Fa, T	R
19	25.3	M	Fall	Abrasion	Head		R
20	27.7	M	Fall moving object	Abrasion	Head	P
21	20.5	M	Motor vehicle	Bruising	Head	Fa, F, C
22	27.0	F	Auto pedestrian	Bruising	Head	P, T	L
23	22.6	F	Motor vehicle	Contusion	Head	F, C
24	34.8	M	Assault	Contusion	Head	F, C
25	20.3	M	Sports-related	Contusion	Head/face	Fa	B
26	43.8	F	Fall standing	Contusion	Head	O
27	28.8	F	Motor vehicle	Contusion	Head	F, C, O
28	27.8	M	Assault	Contusion	Head	Fa, F, C	B
29	24.7	F	Assault	Contusion	Head	Fa, F, C
30	22.8	F
31	19.3	M	Assault	Contusion	Head	O

The control group (group N) consisted of 55 right-handed age-matched normal subjects (29.25 ± 9.1 years of age). Previous hospitalization for mTBI, history of neurologic disorder, schizophrenia, bipolar disorder, substance abuse, and extensive dental work and implants incompatible with MEG were also the exclusion criteria for the control subjects. The research protocol for the control group also received IRB approval, and all participants provided written informed consent.

Subjects were asked to lie down and remain as still as possible during the recording procedure with eyes closed. Approximately 10 min of resting state MEG activity was recorded from each subject. Data collection in this large multicenter study involved two different MEG scanners, a 248-channel whole-head Magnes WH3600 system (4D Neuroimaging Inc., San Diego, CA) featuring axial gradiometer sensors, and a 306-channel Elekta Neuromag system (Elekta AB, Stockholm, Sweden) featuring 204 planar gradiometers and 102 magnetometers. To make the recordings from various projects of the larger study comparable, all data collected with axial gradiometers were transformed to planar gradiometer field approximations using the sincos method implemented in Fieldtrip (Oostenveld et al., 2011). Planar gradiometers have maximum sensitivity to superficial cortical sources directly under them (Hämäläinen, 1995), which makes them less sensitive to artifacts and distant disturbances.

2.2. Data preprocessing

The MEG multichannel recordings were preprocessed using Matlab (The MathWorks, Inc., Natick, MA, USA) and Fieldtrip (Oostenveld et al., 2011). Axial gradiometer data were originally collected at a sampling rate of 1017.25 Hz and bandpassed between 0.1–200 Hz using hardware filters, whereas the planar gradiometer data were collected at 1000 Hz and bandpass filtered via software between 0.1–200 Hz. Artifact reduction was performed based on independent component analysis (ICA) as implemented in the EEGLAB toolbox (Delorme and Makeig, 2004). The extended Informax algorithm (Delorme et al., 2007a; Onton et al., 2006; Romero et al., 2008) was used to remove components associated with eye, muscle, and cardiac artifactual activity (Dimitriadis et al. 2010, Dimitriadis et al. 2012). In addition to visually inspecting the time course and topographical layout of all ICs, we estimated their kurtosis and skewness values. Components reflecting cardiac activity were recognized from their typical rhythmic pattern in the time domain and their widespread topography. ICs related to muscle activity were identified based on statistical measures (kurtosis higher than a predefined threshold, kurt_thr = 12, determined empirically), spectral characteristics (increased energy in the frequency range between 20–60 Hz), and topographies encompassing temporal brain areas (Delorme et al., 2007b; Dimitriadis et al. 2010, Dimitriadis et al. 2012). Artifactual ICs were zeroed, whereas the remaining ICs were used to generate artifact-free signals that were back-projected to the original MEG sensor space via the inverse ICA transformation.

Occasionally, activity from a bad sensor was replaced with the interpolated activity of its immediate neighbors after applying ICA to avoid introducing dependencies in the recordings. Line noise was removed using a notch filter at 60 Hz. This interpolation procedure was necessary for five control and two mTBI subjects for at most four MEG sensors.

2.3. Wavelet decomposition

MEG signal oscillations in specific frequency bands were studied using wavelet transform analysis (Mallat, 2008). After preprocessing, all data were further lowpass filtered and decimated by a factor of six, giving an effective sampling rate of 166 Hz, which constrained the frequency bands of the wavelet transform to roughly conform to the classical frequency bands (Βassett et al., 2009). Decimation was used to reduce the processing time, while the new sampling rate was higher than twice the minimum rate required by the Nyquist theorem to avoid distortion of the MEG signals in the effective range of frequencies of interest (1–60 Hz). Each frequency band was isolated by applying the maximum overlap discrete wavelet transform to each time series (Daubechies, 1992) using the Daubechies 5 wavelet in line with previous work (Βassett et al., 2009). Thus, wavelet scale 1 (30–60 Hz) roughly corresponded to the classical low-γ band, scale 2 (15–30 Hz) to β, scale 3 (8–15 Hz) to α, scale 4 (4–8 Hz) to θ, and scale 5 (1–4 Hz) to δ.

2.4. Functional connectivity graphs

We constructed FCG by quantifying the coupling between pairs of sensors using the phase locking value (PLV) as an estimator (Lachaux et al., 1999), separately for each frequency band. PLV is defined as

$$PLV=\frac{1}{N}\Vert \sum _{t=1}^N{e}^{j\theta \left(t\right)}\Vert$$ (1)

where θ(t) is the difference in phase between the two time series and N is the number of samples. PLV estimates the variability of this phase difference over time. If the phase difference varies by a little, PLV is close to one; otherwise it is close to zero. PLV can assess phase relationships between two signals but it cannot detect any causal relationships (lags or delays) between the signals. To construct intra-frequency functional connectivity matrices, we calculated the PLV between the time series in each frequency band for all possible pairs of sensors to create the weights matrix FCG. Through this process, we created 5 such connectivity matrices (δ, θ, α, β, and γ) per subject.

2.5. Significant links in FCGs

For each subject, the aforementioned procedures yielded a fully connected, weighted, symmetric FCG representing the mutual influences among all cortical regions. The maximum number of possible undirected connections in a network with k nodes is N_max = k(k − 1) / 2. When k = 248, the corresponding N_max = 30,628, and the FCG is extremely dense. Therefore, it must be filtered so that the pattern of the most significant connections can emerge. We performed two kinds of filtering based on statistical analysis and graph theory principles.

For statistical filtering a surrogate data method (Lachaux et al., 1999) with multiple realizations was used to select the most significant FCG values at the 99% confidence level. Generating 200 surrogates from the original time series was enough to reveal significant interactions (Lachaux et al., 1999). Surrogates were obtained by randomizing the phase of the original signals while keeping their spectral profile intact to remove all temporal correlations (Theiler, 1992). After computing the surrogate PLVs, we assigned a p-value to each connection in the FCG matrix by estimating the proportion of surrogate PLV values that were higher than the observed values (Theiler et al., 1992). To correct the effects of multiple comparisons, p-values were adjusted using the false discovery rate (FDR) method (Benjamini and Hochberg, 1995). A threshold of significance q was set such that the expected fraction of false positives was restricted to q ≤ 0.01 (Dimitriadis et al., 2012; Ioannides et al., 2012).

Graph theory-based analysis (Bullmore and Sporns, 2009; Bassett and Bullmore, 2009; He and Evans, 2010; Stam, 2010) was used to capture the structure of the neural system under investigation and the relationship between separation and integration of neural populations. Small-word structures are characterized by a dense network of local connections and a limited number of long-range connections that provide efficient communication between distant nodes. Efficiency in information transmission between nodes is measured as the inverse of the shortest distance between the nodes, while the average of all pair-wise efficiencies represents the global efficiency of the graph. The function cost relates to the energy expenditure needed for a network to maintain its efficiency, and it is given by the ratio of existing connections divided by the total number of possible pairwise connections in a network. Global cost efficiency is defined as the global efficiency E at a given cost C minus the cost (E − C), which typically has a positive maximum value at some cost C_max, for an economical small-world network. Importantly, this metric of network topology is independent of arbitrary, investigator-specified thresholds. Instead, the cost efficiency curve is estimated over a wide range of thresholds, and the behavior of the curve is summarized by its maximum value, which occurs at a data-driven connection density or cost C (Bassett et al., 2009)1

The physical distance among the MEG sensors was used to separate the local from the long-range connections. For each sensor, we computed its neighbors of order one, two, three, and four, i.e., neighbors in all directions that were one, two, three, and four steps away, based on the topographical layout of the MEG sensors (Zouridakis et al., 2012).

2.6. Classifier development

To optimize the performance and generalizability of our methodology (Hastie et al., 2003), we implemented a true external cross-validation procedure by splitting the data into two subsets: a training set that included 80% of the subjects (44 N and 25 mTBI) and was used for designing the classifier and a test set that included the remaining 20% of the subjects (11 N and 6 mTBI) and was used for assessing the classifier performance. As a metric, we used the correct classification rate, which was defined as the proportion of subjects in the test set for which the correct label was predicted. The entire cross-validation procedure was repeated 100 times to avoid any adaptation effects, and the average value of the correct classification rate was used to compute the overall accuracy of the procedure. The optimum number of feature to represent the data was determined using only the training dataset in a five-fold cross-validation procedure as described in Fig. 1. Test subjects were removed from the analysis at the very beginning of the procedure, prior to feature selection and five-fold cross validation. Thus, test subjects were treated as a truly external dataset.

2.6.1. Feature extraction: tensor subspace analysis

Most of the previous studies in this area represent FCGs as vectors in a high-dimensional space (Shen et al., 2010; Pollolini et al., 2010; Richiardi et al., 2011). The main limitation of this approach (and the related feature extraction algorithms) is that it overlooks the inherent form of FCGs. Each FCG has a natural tabular representation and hence it can be thought of as a second-order tensor. The relationship between the row and column vectors of the associated matrix might be important for deriving a suitable low-dimensional representation (projection), especially when the number of available connectivity patterns is small. To overcome the limitations of previous approaches, in this study we treated FCGs as tensors and resorted to tensor subspace analysis (TSA) (He and Cai, 2005) as the most appropriate feature extraction algorithm. In our formulation, the tensor form was given by (subjects × sensors × sensors) (Dimitriadis et al. 2013a, Dimitriadis et al. 2015).

FCGs from individual subjects were represented based on a recent methodology that blends ideas from multi-linear algebra and manifold data learning (He and Cai, 2005). Briefly, given a set of FCGs sampled from the space of functional connectivity patterns, we approximated the underlying manifold by first building an adjacency graph that captured the proximity relationships among the connectivity patterns, and then derived a tensor subspace that faithfully represented these relationships. TSA provided an optimal linear approximation to the FCG manifold.

2.6.2. Feature selection: tensor space dimensionality reduction

Mathematically, an FCG $X\in {\Re }^{n_1\times n_2}$ of size n₁× n₂, where n₁ and n₂ denote the dimensions of a second order tensor (in our case, n₁ and n₂ are equal to the number of MEG sensors), can be thought of as a second order tensor in the tensor space ℜ^n₁ ⊗ ℜ^n₂. Then, the generic problem of linear dimensionality reduction in the second order space is expressed as follows: given a set of m tensors $X_1,\mathrm{...},X_m\in {\Re }^{n_1}\otimes {\Re }^{n_2}$, find two transformation matrices U and V of size (n₁×l₁) and (n₂×l₂), respectively, that map these m tensors to a new set of tensors $Y_1,\mathrm{...},Y_m\in {\Re }^{l_1}\otimes {\Re }^{l_2}$, where Y_i=U^TX_iV, l₁< n₁, and l₂< n₂, such that each new tensor Y_i represents uniquely a tensor X_i in the original set. The method is of particular interest in the special case when X₁, X₂, …, X_m ∈ M, where M is a nonlinear sub-manifold embedded in ${\Re }^{n_1}\otimes {\Re }^{n_2}$. Traditional linear dimensionality reduction algorithms, such as principal component analysis and linear discriminant analysis, find first-order mappings from ℜⁿ to ℜ^l with l < n, but TSA finds a second-order mapping from ${\Re }^{n_1}\otimes {\Re }^{n_2}$ to ${\Re }^{l_1}\otimes {\Re }^{l_2}$ with l₁< n₁ and l₂ < n₂.

2.6.3. Optimal linear embedding

The “true” domain of FCGs most probably forms a nonlinear sub-manifold embedded in the ambient space of second order tensors (Lu et al., 2013). Using TSA, we attempted to find a linear subspace approximation to the sub-manifold in the sense of local isometry using a technique that is the tensorial counterpart of the locality preserving projection (He et al., 2005).

Given a set of m tensors {X_i}_i = 1:m, where each tensor is the tabular version of a single FCG having the group membership as class label (N or mTBI), TSA starts by building an (m × m) weight matrix S that represents the nearest neighbor graph G among the tensors. The value of m is given by the total number of subjects in the training dataset. The elements of S_ij are given by

$${\text{S}}_{\text{ij}}=\left\{\begin{array}{c}\text{exp(}{\text{−||X}}_{\text{i}}{\text{ − X}}_{\text{j}}{\text{||}}^{\text{2}}/\text{r}\text{) Condition 1 }\\ \text{ 0 otherwise}\end{array}\right\}$$ (2)

where the exponential is known as the heat kernel and is employed with the Frobenius norm (Golub and van Loan, 1996), r is a control parameter usually referred to as radius of influence, and Condition 1 states that tensors X_i and X_j share the same class label and each of them is among the k-nearest neighbors of the other, while the indices i and j vary across the m tensors (m equals the number of subjects in the training dataset). Then TSA seeks two transformation matrices U and V which, when applied to each tensor, result in a mapping that preserves the neighborhood relationship encoded in graph G. Mathematically, this is formulated in the following optimization problem,

$$\underset{U,V}{\min }{\sum _{ij}\Vert U^T{X}_{i}V-U^T{X}_{j}V\Vert }^2{S}_{ij\text{.}}$$ (3)

Denoting with D a diagonal matrix with elements $D_{ii}={\sum }_j{S}_{ij}$, the above problem is reformulated as two coupled problems of eigenvector analysis (He et al., 2005):

$$\begin{array}{l}(D_U-S_U)\text{v}=\lambda D_U\text{v}\\ D_U={\sum }_i{D}_{ii}{X}_i^{T}U{U}^T{X}_i\text{, }{S}_U={\sum }_{ij}{S}_{ij}{X}_i^{T}U{U}^T{X}_j\end{array}$$ (4)

$$\begin{array}{l}(D_V-S_V)\text{u}=\lambda D_V\text{u}\\ D_V={\sum }_i{D}_{ii}{X}_{i}V{V}^T{X}_i^T{S}_V={\sum }_{ij}{S}_{ij}{X}_i^{}V{V}^T{X}_j^T\text{.}\end{array}$$ (5)

The optimal matrices U and V can be obtained by iteratively computing the generalized eigenvectors of Eq. (4) and Eq. (5) after initializing U with the identity matrix. TSA detects the intrinsic local geometric structure of the tensor space by learning the topology of a new tensor subspace of lower dimension. The objective function in Eq. (3) incurs a heavy penalty if neighboring points X_i and X_j are mapped far apart. Therefore, minimizing Eq. (3) ensures that when the original tensors X_i and X_j are close, the new tensors Y_i = U^T X_iV and Y_j = U^T X_jV will be close as well.

The dimensionality of the reduced tensors Y_i, i.e., the number of eigenvectors used for mapping Y_i = U^T X_i V, was optimized using a five-fold cross-validation procedure that achieved maximum separation between the N and mTBI groups. Specifically, we randomly partitioned the training dataset into five equal sized subsets and used four subsets for building a k-nearest neighbor (k-NN) classifier (Altman, 1992) and one subset for testing its performance. The overall classification performance was obtained by averaging the results across the five folds. The number of neighbors k and the heat parameter were set in a similar way.

2.7. Classifier testing

Our methodology employed the so-called extreme learning machine (ELM) classifier (Huang et al., 2006), an emerging learning technique that provides efficient unified solutions to generalized feed-forward networks, including single- and multi-layer neural networks. We chose this relatively new classification procedure because of its computational elegance and fast-learning capabilities, which lead to improved performance compared to other learning algorithms, like back propagation neural networks, radial basis function networks, and support vector machines (Kim et al., 2009). The proposed scheme combined tensor subspace analysis with extreme learning machine classification and it was thus denoted as TSA+ELM2.

For comparison purposes, we used two additional popular classifiers as a baseline: the k-NN algorithm with the Frobenius norm (Horn and Mathias, 1990) as a measure of similarity, and a support vector machine (SVM) with a linear kernel (Cortes and Vapnik, 1995). Furthermore, to demonstrate the superiority of the proposed tensorial approach, we considered FCGs as vectors with or without feature extraction. The FCG tensors were first vectorized, i.e., converted to high dimensional vectors by traversing the corresponding matrices in a systematic way, and then their dimensionality was reduced using linear discriminant analysis (LDA; Fisher, 1936) for feature extraction. The dimensions kept by LDA were selected to optimize classification performance of the two groups. Therefore, our analysis employed various combinations of approach (TSA, LDA, and vectorial) and classifier (ELM, k-NN, and SVMs).

After selecting a classifier/approach combination, and optimizing it using the training data, the classifier was validated using the test data as follows: each FCG in the test set was compared against FCGs of known group membership (normal or mTBI) developed from the training dataset. The FCG was finally assigned to the group with which it had the highest similarity.

2.8. Topological properties of underlying brain networks

Following the significant link selection procedure described previously, the resulting FCGs were described using the well-known topological metrics of global and local efficiency defined for weighted graphs. The global efficiency GE of a network is given by

$${}_{GE=\frac{1}{N}\sum _{i\in N}\frac{1}{N-1}\sum _{j\in N,j\ne i}{\left(d_{ij}\right)}^{-1}}$$ (6)

where N represents the total number of nodes in the network and d_ij is the shortest path length between nodes i and j. GE is the inverse of the harmonic mean of paths between nodes and reflects the overall efficiency of parallel information transfer in the network (Achard and Bullmore, 2007; Latora and Marchiori, 2001). On the other hand, local efficiency LE is a measure of fault tolerance in the network and is defined as

$${}_{LE=\frac{1}{N}\sum _{\text{i}\in \text{N}}nodal\_L{E}_i\text{ =}\frac{1}{N}\sum _{i\in N}\frac{\sum _{j,h\in G_{i,j,h\ne i}}{\left(d_{jh}\right)}^{-1}}{k_i(k_i-1)}}$$ (7)

where k_i corresponds to the functional neighbors of the ith node, N represents the total number of nodes in the network, and d_ij is the shortest path length between nodes i and j. LE indicates how well subgraphs exchange information when a particular node is eliminated (Achard and Bullmore, 2007).

To identify cost-efficient functional networks, the same link selection procedure was applied to the average FCGs, independently for each frequency band and group. Statistical analyses were performed using the Wilcoxon rank sum test (p < 0.001).

3. Results

3.1. Classification performance

Table 2 summarizes the classification performance obtained for various combinations of approach (vectorial, LDA, and TSA) and classifier (k-NN, ELM, and SVMs). For TSA, the parameters used were as follows, weight mode: Ηeat Kernel, neighbor mode: 10, supervised learning, and number of dimensions: 6 (Dimitriadis et al. 2013a, Dimitriadis et al. 2015). For the k-NN algorithm we used majority voting. For each of the three classifiers (k-NN, ELM, and linear SVM), the corresponding dimensions kept by LDA in each frequency band were as follows, δ: (5, 6, 5), θ: (6, 6, 5), α: (6-6-5), β: (7-6-7), and γ: (6-6-5).

Table 2.

Average classification performance (CP%) over five frequency bands using vectorized, tensorial, and LDA FCG representations with k-NN, ELM, and linear SVM classifiers.

(a) k-NN classifier
Frequency Band	LDA treatment of vectorized FCGs (LDA + k-NN)			Tensorial treatment of FCGs (TSA + k-NN)			Vectorized FCGs (k-NN)
CP%	Sensitivity %	Specificity %	CP%	Sensitivity %	Specificity %	CP%	Sensitivity %	Specificity %
δ	77.65	73.05	75.34	82.15	79.45	80.45	67.35	71.65	71.45
θ	78.23	75.75	78.65	85.30	81.40	82.34	70.35	71.47	68.08
α	80.45	76.45	74.55	87.34	82.78	83.30	71.65	71.36	70.09
β	79.45	74.30	75.38	83.50	80.87	81.54	67.05	72.08	71.28
γ	77.59	73.45	75.76	83.34	78.25	80.85	68.28	72.38	70.26
(b) ELM classifier
Frequency Band	LDA treatment of vectorized FCGs (LDA + ELM)			Tensorial treatment of FCGs (TSA + ELM)			Vectorized FCGs (ELM)
CP%	Sensitivity %	Specificity %	CP%	Sensitivity %	Specificity %	CP%	Sensitivity %	Specificity %
δ	80.45	74.68	74.28	96.48	95.22	96.02	68.85	71.25	70.95
θ	80.25	78.28	78.64	97.64	95.05	96.12	72.77	71.15	70.75
α	82.27	78.65	76.45	100	100	100	73.03	68.75	70.14
β	81.25	75.25	77.36	97.85	95.34	96.32	69.09	69.64	70.32
γ	78.38	73.58	76.30	96.58	100	97.85	70.05	69.88	69.78
(c) Linear SVM
Frequency Band	LDA treatment of vectorized FCGs (LDA + k-NN)			Tensorial treatment of FCGs (TSA + k-NN)			Vectorized FCGs (k-NN)
CP%	Sensitivity %	Specificity %	CP%	Sensitivity %	Specificity %	CP%	Sensitivity %	Specificity %
δ	81.37	73.75	77.45	94.05	92.15	93.23	70.32	70.23	69.73
θ	82.46	78.86	79.68	93.32	90.73	93.12	74.42	72.76	70.23
α	83.93	78.24	77.27	94.26	93.62	92.12	75.63	73.27	72.83
β	82.88	75.68	76.83	93.10	91.91	90.34	70.05	69.83	69.35
γ	80.34	74.95	77.32	91.23	92.34	92.81	71.07	70.63	69.76

As it can be seen in Table 2, the proposed classification scheme of TSA+ELM provided clear separation of the two groups, in all frequency bands, with high sensitivity and specificity. In particular, in the α band normal controls and mTBI patients could be separated with 100% classification accuracy. The combination of LDA + k-NN showed reduced classification accuracy (approximately 80% across all frequency bands) compared to TSA + kNN (Table 2a). On the other hand, the ELM classifier showed improved performance compared to k-NN (Table 2b) in all cases. Using the SVM classifier with TSA resulted in decreased performance compared to ELM classifier (Table 2c). However, the use of the SVM classifier improved performance for both the LDA and vectorial approaches compared to the ELM classifier (Table 2c).

To demonstrate visually the ability of the proposed TSA+ELM scheme to absolutely separate mTBI patients from normal controls in the α frequency band, we computed a three-dimensional representation for the FCGs, each of which was originally described by a vector of 36 dimensions (in TSA each dimension of the second order tensor was 6, thus the total number of dimensions needed for the vector representation was 6 × 6 = 36). We estimated the pair-wise similarity between all possible pairs of vectors A and B across all subjects using cosine similarity (CoS), which was given by

$$\mathit{CoS}\left(A,B\right)=\frac{A\cdot B}{‖A‖‖B‖}=\frac{{\displaystyle \sum _{i=1}^N{A}_i{B}_i}}{\sqrt{{\displaystyle \sum _{i=1}^N{A}_i^2}}\sqrt{{\displaystyle \sum _{i=1}^N{B}_i^2}}}$$ (8)

CoS(A,B) measures the cosine of the angle between vectors A and B, and thus it is a judgment on their orientation, not on their magnitude. The final CoS estimates were tabulated in a matrix with dimensions 86 × 86 (since 86 is the total number of subjects in the two groups). By employing multidimensional scaling (Borg and Groenen, 2003), a well-known dimensionality reduction technique, we were able to project the original multidimensional matrix onto a set of three-dimensional points. Finally, we estimated the convex hull (Borst et al., 1999) of the 3D points corresponding to each group. The results are shown in Fig. 2, which shows complete separation of the two groups and also illustrates their variance.

Fig. 2.

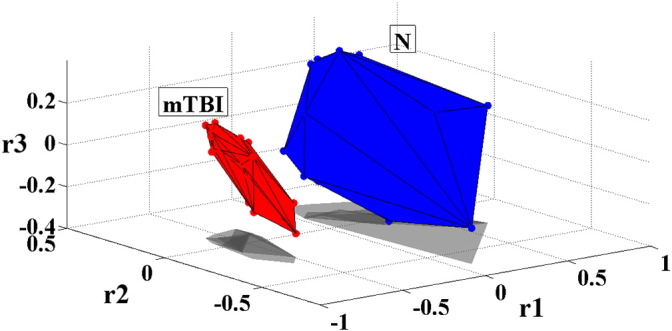
Separation of normal controls (N) from patients (mTBI) in the α frequency band using the proposed methodology: convex hull of points obtained after projecting the functional connectivity graphs of both groups in 3D space.

3.2. Topological differences between normal and mTBI connectivity profiles

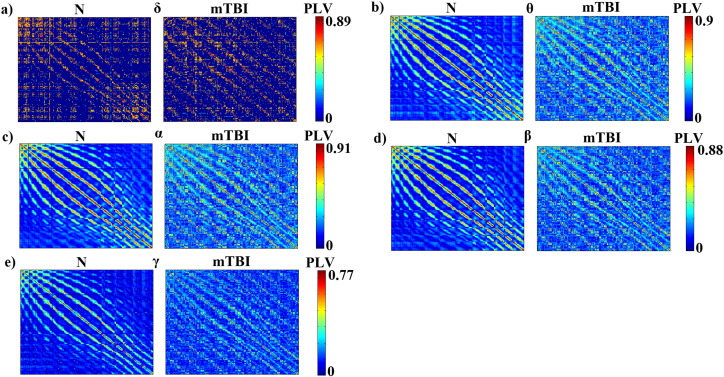
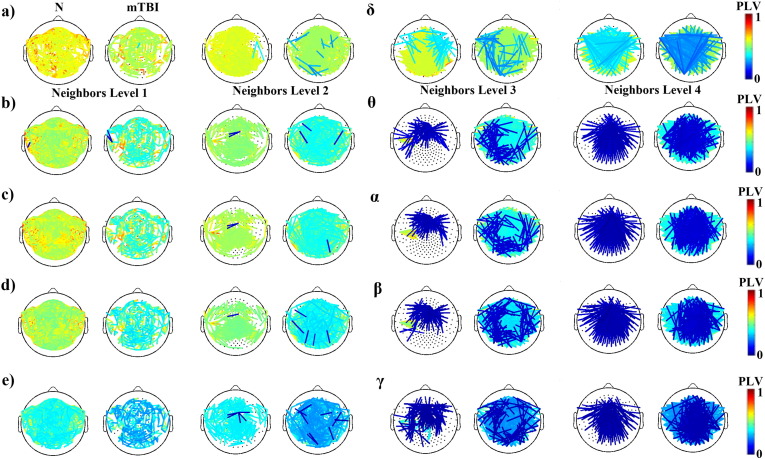
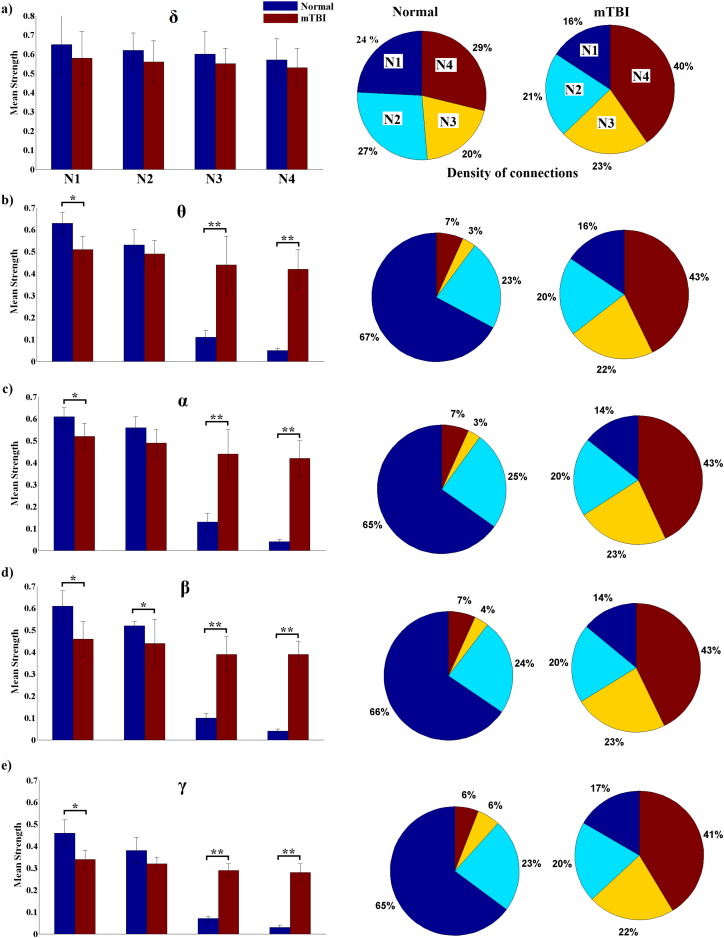
Fig. 3 illustrates the average functional connectivity patterns for each frequency band and group after applying the cost–efficiency thresholding scheme. As it can be seen in Fig. 3, Fig. 4, the functional connectivity profile of the control group exhibited a consistent network with stronger local connections (level 1 and 2 neighbors) whereas the mTBI group showed a variable network with stronger distant connections (level 3 and 4 neighbors). Across most frequencies, with the exception of the δ band, in the N group more than 80% of the total number of connections was distributed locally (level 1 and 2 neighbors), whereas in the mTBI group, more than 60% of the connections were shared between distant sensors (level 3 and 4 neighbors). Additionally, from θ to γ, the N group exhibited significantly stronger connections locally, whereas the mean strength of distant connections was significantly higher in the mTBI group (see Fig. 5).

Fig. 3.

Functional connectivity patterns for normal controls (N) and patients (mTBI) computed at various frequency bands (δ, θ, α, β, and γ).

Fig. 4.

Topographical illustration of connections according to neighbor level for normal controls (N) and patients (mTBI) computed at various frequency bands (δ, θ, α, β, and γ).

Fig. 5.

Mean strength values and density (%) of connections (pie-charts) for each neighbor level in both groups and across frequency bands (*p < 0.001, **p < 0.001 × 10⁴ Wilcoxon rank sum test. N1, N2, N3, and N4 correspond to neighborhood level 1, 2, 3, and 4, respectively).

Furthermore, as Fig. 5 shows, when long-range connections were compared across subjects, the N group exhibited mostly central-to-central or central-to-peripheral connections, especially in the θ to γ frequency bands, whereas the mTBI group showed connections involving primarily peripheral locations, practically bypassing fronto-central and centro-parietal brain regions.

3.3. Network analysis

In all frequency bands, global efficiency (GE) values were in general higher in normal controls compared to mTBI patients, but without reaching significance (p^δ = 0.61, p^θ = 0.57, p^α = 0.61, p^β = 0.83, and p^γ = 0.76). In contrast, local efficiency (LE) values were significantly higher (p < 0.001) in the N group compared to the mTBI in all frequency bands, except for θ (Fig. 6).

Fig. 6.

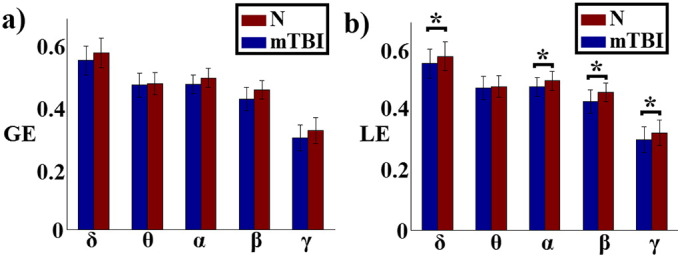
Global (GE) and local (LE) efficiency in normal controls (N) and patients (mTBI) at various frequency bands (*p < 0.01, Wilcoxon rank sum test).

4. Discussion

In this study we used PLV estimation and graph theory to investigate topological differences in the functional connectivity networks of mTBI patients and normal controls computed from resting-state MEG. Our results showed that normal subjects exhibited the typical “small world” configuration, i.e., a dense network of local connections and a limited number of long-range connections. Level 1 and 2 neighbors accounted for more than 80% of the total number of connections and, on average, they were significantly stronger compared to the ones seen in mTBI subjects. In contrast, mTBI subjects showed sparse arrangements of weak local connections and a large number of stronger distant connections. Level 3 and 4 neighbors covered more than 60% of their connectivity profiles and the average strength was significantly higher compared to the control group (Fig. 4, Fig. 5). However, these long-range connections in the mTBI group involved primarily peripheral locations, whereas in the controls, long-range links connected frontal-to-central or central-to-peripheral locations. These findings echo the results of our earlier study (Zouridakis et al., 2012). Marked differences between the two groups were seen in all frequency bands, except for δ, where the connection strength and sensor location were not significantly different between the two groups, at any neighborhood level.

As an extension of our earlier work, in the present study we proposed a novel approach that features two improvements: estimation of functional connectivity graphs based on the PLV estimator and a multivariate tensorial treatment of these graphs. As Table 2 shows, the ELM classifier provided 100% classification accuracy in the α frequency band and more than 96% accuracy in the rest of the frequency bands studied. This new approach provided a more accurate “connectomic” biomarker to characterize mTBI, instead of the typical univariate estimates, like relative power. This can be clearly seen in Table S1 in the Supplementary material, where we provide a detailed analysis based on relative power.

Our findings of frequency-specific differences between the two groups match current research on spontaneous activity. A number of studies used MEG source localization (de Pasquale et al., 2010; Brookes et al., 2012; Hipp, Engel, and Siegel 2011, Hipp et al. 2012; Hillebrand et al., 2012; Bardouille and Boe, 2012; Marzetti et al., 2013) to explore two different modes of intrinsic coupling, namely phase coupling between band-limited oscillations and coupling between aperiodic fluctuations of signal envelopes (Hipp et al., 2012). There is now evidence that the former is more sensitive to functional changes due to injury even in the absence of structural damage, as in the case of mTBI, while the latter can quantify functional abnormalities when structural damage predominates (Ηipp et al., 2012). These studies used various connectivity estimators, including power correlations (de Pasquale et al., 2010; Brookes, Woolrich, and Barnes 2012, Brookes, Woolrich, and Barnes 2012; Hipp et al., 2012), phase coherence (Hipp et al., 2011; Bardouille and Boe, 2012), phase lag index (Hillebrand et al., 2012), and imaginary coherence (Marzetti et al., 2013). Thus, our findings of δ band differences between the two groups using the PLV estimator are in line with the current literature.

In terms of topology, even though our analysis was performed at the sensor level, our findings follow closely the results of studies that explored frequency-dependent networks at the source level (Hillebrand et al., 2012). In general, the brain areas that are part of the default-mode network showed a dense network of connections extended over the entire brain for low frequencies and a more anatomically constrained network for higher frequencies (Buzsaki, G. and Draguhn, 2004; Fox and Raichle, 2007; Florin and Baillet, 2015). We found that, in the range of high frequencies, both the number (80% of total connections) and strength of local connections were higher in the control group, whereas in the δ band there were fewer (only 20%) and weaker connections. Additionally, we showed local topological differences with higher local efficiency for controls compared to mTBI subjects in the δ band, which resulted in 96.48% classification accuracy and partially matched previous findings of abnormal brain activity in mTBI patients in the δ band (Huang et al. 2009, Huang et al. 2012).

Nevertheless, despite the very interesting results obtained, the present study has some limitations. For instance, we estimated FCGs at the sensor level, although some studies have applied source reconstruction methods to identify activation patterns at the source level (Huang et al. 2009, Huang et al. 2012; Hillebrand et al., 2012). Even though we cannot interpret the activation patterns in terms of intracranial cortical locations, we are still able to describe statistically significant differences in the connectivity patterns of mTBI and control subjects using surface brain regions. Another potential criticism of the present study could be attributed to volume conduction effects, i.e., the transmission of electromagnetic fields from a primary intracranial source through biological tissue towards the measurement sensors resulting in distorted recordings. Although these effects can be reduced using connectivity estimators that are robust to volume conduction, such as the phase lag index (Hillebrand et al., 2012) and imaginary coherence (Marzetti et al., 2013), or through orthogonalization preprocessing (Hipp et al., 2012), we decided not to employ any correction, since the absence of correlation between power and connectivity profiles in all frequency bands (see the Supplementary material) was a strong argument that a common source did not alter the functional connectivity patterns; otherwise, a common source would have changed also the signal power. Furthermore, any possible volume conduction effects would be common to both groups, but we were looking only for differences between the two groups. Finally, some details on subject demographics are incomplete, as Table 1 shows, making it difficult to establish correlations between lesion locations and connectivity patterns for every participant in the study.

The present study has focused on the development of noninvasive biomarkers that can be used to uniquely characterize mTBI patients and normal controls. It follows a general trend in current research in the area of neuroinformatics, where the big challenge for the next decade is the development and deployment of a large database with pre-computed brain connectivity profiles and derived network metrics (e.g., a “Connectome database”) in both healthy and mTBI subjects (Sporns, 2012). This would allow recording resting-state MEG in the laboratory, estimating the related connectivity maps in both sensor and source space, querying the Connectome database, and visualizing the results in a laboratory PC (Akil et al., 2011; Iakovidou et al. 2013b, Iakovidou et al. 2013a). Understanding brain function and visualizing the human Connectome are slowly becoming a reality (Human Brain Project, Europe and USA)3. In the near future, computational approaches applied to connectomics will undergo rapid expansion, especially with shared neuroimaging resources, and complex network analysis and modeling (Jirsa et al., 2010; Sporns, 2012), and may be helpful in designing optimal recovery strategies following traumatic brain injury (Irimia et al., 2012).

5. Conclusions

The proposed methodology can estimate patterns of brain activation in the form of connectivity networks that are highly consistent and can uniquely characterize subject groups using resting state MEG, a noninvasive modality with superior temporal resolution over other neuroimaging techniques. Furthermore, resting state recordings are easy to obtain, as they do not require engagement from the subject, which makes such tests suitable for all sorts of patient types and age groups, including children. These encouraging findings support the hypothesis that functional connectivity patterns may be used as general biomarkers for predicting a subject's brain state (Dimitriadis et al. 2013a, Dimitriadis et al. 2015), for detecting various brain diseases (Dimitriadis, 2015), and for developing image-based tools that can provide more accurate diagnosis, help guide treatment, and monitor the effectiveness of intervention in mTBI patients.

Appendix A. Supplementary data

Supplementary material.