A robust and effective time-independent route to the calculation of Resonance Raman spectra of large molecules in condensed phases with the inclusion of Duschinsky, Herzberg-Teller, anharmonic, and environmental effects

Abstract

We present an effective time-independent implementation to model vibrational resonance Raman (RR) spectra of medium-large molecular systems with the inclusion of Franck-Condon (FC) and Herzberg-Teller (HT) effects and a full account of the possible differences between the harmonic potential energy surfaces of the ground and resonant electronic states. Thanks to a number of algorithmic improvements and very effective parallelization, the full computations of fundamentals, overtones, and combination bands can be routinely performed for large systems possibly involving more than two electronic states. In order to improve the accuracy of the results, an effective inclusion of the leading anharmonic effects is also possible, together with environmental contributions under different solvation regimes. Reduced-dimensionality approaches can further enlarge the range of applications of this new tool. Applications to imidazole, pyrene, and chlorophyll a1 in solution are reported, as well as comparisons with available experimental data.

1 Introduction

Resonance Raman spectroscopy (RR) has received much attention in recent years and has found applications in many areas such as analytical chemistry¹ and the study of metal complexes² and biological systems.^3–5 The first distinguishing feature that RR shows with respect to non-resonant Raman is the so-called resonance enhancement:⁶ the intensity of the scattered radiation is 10³-10⁶ higher than the intensity of the regular Raman signal. This property facilitates experimental measurements and, in most cases, also causes the resulting spectrum to be free from any “contamination” arising from the non-resonant Raman signal, which has a much smaller intensity. Resonance enhancement is also responsible for granting RR spectroscopy other peculiar features. Since it is due to the interaction of the incoming radiation with an electronic transition of the system, a RR spectrum carries information about the excited state(s). Traditionally, the methods of choice to study excited-state properties of molecules are UV-vis absorption and fluorescence spectroscopies. Both these methods have two disadvantages: first, because of the naturally short lifetime of some excited states, and because of the inhomogenous broadening caused by the environment, the band-width of most electronic transitions is usually very broad, especially in the case of molecules in solution; this “dilutes” the information that could be extracted from the spectrum, and it is usually difficult to record vibrationally resolved electronic spectra, even though the band-shape may be dominated by the vibronic structure. In RR, the band-width only depends on the initial and final states,⁶ which both belong to the ground state potential energy surface (PES), therefore the peaks’ width is comparable to the case of a non-resonant Raman spectrum. Another advantage of RR over traditional one-photon spectroscopies is that it is a vibrational spectroscopy, whence it is much easier to extract structural information about the system. A second consequence of the resonance enhancement is that only the molecular vibrations that are affected by the electronic transitions (in particular those vibrations that involve atoms close to the chromophore) will be visible in the spectrum because all other vibrational modes will not benefit from the enhancement and will have negligible intensity. This property is heavily exploited in the study of biological macromolecules,^4,5 in which one may tune the incident radiation’s frequency to one particular chromophore within the system, obtaining information about the corresponding region of the macromolecule; if a regular Raman or infra-red spectrum is recorded, the high number of vibrational transitions of the molecule will produce an “overcrowded” spectrum which would be difficult to interpret.

All such characteristic features of RR have stimulated the research in this field, both experimentally⁶ and theoretically,⁷ but there is still much work to be done in both areas. In this contribution we present our work on the time-independent (TI) calculation of RR spectra⁸ within a general-purpose quantum chemistry program, with an emphasis on the computational applicability and scaling of the method with respect to system size. The implementation was designed as an integrated module in the multi-frequency virtual spectrometer under development in our group;⁹ in this way it can take advantage of the various features already present such as the handling of large systems through reduced-dimensionality schemes, the modeling of the solvation environment, and anharmonicity. The present work is organised as follows: after an introduction on the theoretical framework of RR, the inclusion of anharmonicity and of environmental effects is discussed. As an illustration of the versatility and reliability of our procedure, we analyze the spectra of three different systems: imidazole, pyrene, and chloropyll a1.

2 Resonance Raman scattering cross-section

Raman scattering can be formally thought as a two-photon phenomenon where an incident electromagnetic radiation is inelastically scattered by the system, which can either absorb (Stokes scattering) or release (anti-Stokes scattering) energy. The ability of a molecular system to give rise to Raman scattering is related to its transition polarizability tensor¹⁰ between two different vibrational states belonging to the same electronic level. The Raman cross-section can be easily computed once the transition polarizability is known. For isotropic media it can be expressed as a combination of three isotropic invariants corresponding to the mean isotropic polarizability, the symmetric anisotropy, and the antisymmetric anisotropy, defined as¹¹ (summation over repeated indices is implied):

$$a^2=\frac{1}{9}\mathfrak{R}{\alpha }_{aa}^{\mathrm{s}\ast }{\alpha }_{bb}^{\mathrm{s}}{g}^2=\frac{1}{2}\mathrm{Re}(3{\alpha }_{ab}^{\mathrm{s}\ast }{\alpha }_{ab}^{\mathrm{s}}-{\alpha }_{aa}^{\mathrm{s}\ast }{\alpha }_{bb}^{\mathrm{s}})d^2=\frac{3}{2}\mathfrak{R}{\alpha }_{ab}^{\mathrm{a}\ast }{\alpha }_{ab}^{\mathrm{a}}$$ (1)

where α^s and α^a are the symmetric and antisymmetric components of the polarizability tensor. For example, in the case of 90 degrees scattering with an incident radiation of frequency ω perpendicularly polarized with respect to the scattering plane, and an unpolarized scattered radiation,¹² we have:

$${\sigma }^{\prime }(\pi ∕2,\mid {\mid }^{\mathrm{s}}+{\perp }^{\mathrm{s}},{\perp }^{\mathrm{i}})=\frac{{\omega }_{\mathrm{s}}^4}{c^4}\frac{45a^2+7g^2+5d^2}{45}$$ (2)

where ω_s = ω−ω_fi is the angular frequency of the scattered radiation. These expressions are general, and are applicable to both the resonant and non-resonant cases. One important difference, however, is that the non-resonant transition polarizability is symmetric, giving a vanishing contribution from the d² term. There are several methods for the calculation of the RR polarizability, with different levels of approximations. The theoretical framework of RR can be traced back to the work of Placzek,¹³ who obtained sum-over-state formulas for the Raman transition polarizability in the resonant and non-resonant cases starting from the perturbation expansion of the wavefunction, and later Albrecht¹⁴ who gave separate expressions for the various contributions of the polarizability arising from the expansion of the transition dipole moments. The RR polarizability can then be written as a sum-over-state expression as follows:¹⁰

$${\tilde{\alpha }}_{\alpha \beta }=\frac{1}{\hslash }\sum _{m^{\prime }}\frac{\langle f\mid {\mu }_{\alpha }\mid m^{\prime }\rangle \langle m^{\prime }\mid {\mu }_{\beta }\mid i\rangle }{{\omega }_{mi}-\omega -i\gamma }$$ (3)

where 〈f| and |i〉 represent the final and initial vibrational states respectively, ω_mi = ω_m − ω_i is the energy difference between the middle and initial state, μ_α and μ_β are the cartesian components of the transition dipole moments between the ground and excited electronic states, γ is the excited state’s phenomenological damping constant, and the (infinite) summation runs over all vibrational states m′ belonging to the excited state PES. An equivalent expression for the RR polarizability can be obtained in the time domain:^15–17

$${\tilde{\alpha }}_{\alpha \beta }=\frac{i}{\hslash }{\int }_0^{\infty }\langle f\mid {\mu }_{\alpha }{\mathrm{e}}^{-i{\widehat{H}}^{\prime }t∕\hslash }{\mu }_{\beta }\mid i\rangle {\mathrm{e}}^{i({\omega }_i+\omega )t-\gamma t}\mathrm{d}t$$ (4)

Both the time-dependent and the time-independent expressions require a model for the ground and excited PESs, and for the transition electric dipole moment. Usually the harmonic approximation is invoked for both states, but even though a geometry optimization followed by a harmonic analysis can be routinely performed for the ground state with most electronic structure methods, the same task may prove to be much more difficult in the case of an excited state, and often requires a numerical differentiation of the energy gradient, which is much more time consuming. For this reason, further approximations are often invoked and most calculations of RR spectra assume that both states have the same normal modes and harmonic frequencies, and differ only in the equilibrium geometry, this assumption being known as the independent mode displaced harmonic oscillator¹⁸ (IMDHO) model. The latter model has been extensively used to compute RR spectra,^19–24 based on either the time-dependent or the time-independent formulations. Additional methods used for the calculation of RR spectra can be derived by further manipulation of the time-dependent expression, which can be viewed as an equation for the motion of the starting vibrational wavepacket on the excited state PES. Under short-time dynamics conditions,^15–17 it is possible to write the relative RR peak intensity as a ratio between the excited-state gradients calculated along the normal modes under consideration.^25–28 The latter method is the simplest one for computing RR spectra and requires neither a sum-over-state calculation, nor the evaluation of a half-Fourier transform. Following an alternative treatment, which also relies on the short-time dynamics approximation, it is possible to evaluate the RR spectrum by computing the geometrical derivative of the complex electronic polarizability under resonance conditions using linear response theory,^29–34 similarly to what is commonly done to compute frequency-dependent non-resonant Raman intensities, but with the additional complication that the finite lifetime of the excited state must be included in the calculation to avoid the singularities that appear in the undamped linear response equation. It should be clear from this brief discussion that there is currently a profusion of widely different methods that are used to compute RR spectra, each based on different assumptions and presenting its own challenges and advantages, and there are also a few works in the literature that have attempted to compare them against each other and also with respect to experimental data.^20,35,36 However, the majority of RR spectra calculations present in the literature still relies on the IMDHO model to describe the excited-state PES. This provides a rather unbalanced description of the two states involved since a geometry optimization followed by a full harmonic analysis is performed for the ground state, whereas only the gradients are usually computed for the excited state. If the excited state’s normal modes are computed, the integrals which appear in the TI or TD polarizability expressions cannot be straightforwardly computed since the harmonic wavefunctions of the two PESs are expressed in different basis sets. In order to solve this problem, in the case of semi-rigid molecules without large-amplitude motions,³⁷ the excited state normal modes can be related to the ones of the ground state via an affine transformation known as the Duschinsky relation:³⁸

$${\mathit{Q}}^{\prime }=\mathbf{J}\mathit{Q}+\mathit{K}$$ (5)

Where Q and Q′ are the ground and excited state normal modes respectively, and J and K are the Duschinsky matrix and the shift vector. By means of the Duschinsky relation it is possible to write down explicit equations that allow the calculation of RR intensities both in the TI and TD frameworks.^8,39–41 As already pointed out, the most straightforward way to compute the Duschinsky matrix is to perform a geometry optimization followed by a vibrational analysis for both states. This method is often called Adiabatic Hessian (AH),⁴² but it is not the only way to obtain a meaningful description of the excited state normal modes. Indeed, the vibrational analysis for the excited state may also be performed at the ground state equilibrium geometry and the shift vector can be extrapolated from the gradient, a method known as Vertical Hessian (VH).^42,43 If the harmonic approximation is exact then the two methods are equivalent, otherwise the choice of using one or the other depends on whether one needs a better description of the vertical region or the minimum of the excited PES. If the Duschinsky rotation is ignored and excited-state frequencies are not computed, the simplified methods known as Vertical Gradient (VG) and Adiabatic Shift (AS) are obtained; in the first one, only the excited-state gradient at the ground-state equilibrium geometry is computed, whereas for the second one the excited-state geometry is optimized, but the shape of the PES is then assumed to be the same as in the ground state.

2.1 Time-Independent calculation of the RR polarizability

In this work, we chose the time-independent approach for the calculation of the RR polarizability tensor. The transition dipole moments that appear in equation 3 can be expanded in a Taylor series with respect to the excited-state normal modes around the molecule’s equilibrium geometry. Keeping only the terms up to the second order in the polarizability we obtain:

$$\begin{array}{cc}\hfill \tilde{\alpha }=\frac{1}{\hslash }& \sum _{m^{\prime }}[{\overrightarrow{\mu }}_0{\overrightarrow{\mu }}_0\frac{\langle f\mid m^{\prime }\rangle \langle m^{\prime }\mid i\rangle }{{\omega }_{mi}-\omega -i\gamma }\phantom{]}+\hfill \\ & +\sum _a\left({\overrightarrow{\mu }}_a{\overrightarrow{\mu }}_0\frac{\langle f\mid Q_a^{\prime }\mid m^{\prime }\rangle \langle m^{\prime }\mid i\rangle }{{\omega }_{mi}-\omega -i\gamma }+{\overrightarrow{\mu }}_0{\overrightarrow{\mu }}_a\frac{\langle f\mid m^{\prime }\rangle \langle m^{\prime }\mid Q_a^{\prime }\mid i\rangle }{{\omega }_{mi}-\omega -i\gamma }\right)+\hfill \\ & +\sum _{ab}({\overrightarrow{\mu }}_a{\overrightarrow{\mu }}_b\frac{\langle f\mid Q_a^{\prime }\mid m^{\prime }\rangle \langle m^{\prime }\mid Q_b^{\prime }\mid i\rangle }{{\omega }_{mi}-\omega -i\gamma }\phantom{)}+{\overrightarrow{\mu }}_0{\overrightarrow{\mu }}_{ab}\frac{\langle f\mid m^{\prime }\rangle \langle m^{\prime }\mid Q_a^{\prime }{Q}_b^{\prime }\mid i\rangle }{{\omega }_{mi}-\omega -i\gamma }+\hfill \\ & +{\overrightarrow{\mu }}_{ab}{\overrightarrow{\mu }}_0\frac{\langle f\mid Q_a^{\prime }{Q}_b^{\prime }\mid m^{\prime }\rangle \langle m^{\prime }\mid i\rangle }{{\omega }_{mi}-\omega -i\gamma })]\hfill \end{array}$$ (6)

where ${\overrightarrow{\mu }}_a$ and ${\overrightarrow{\mu }}_{ab}$ are the transition dipole moment first and second derivatives with respect to the normal modes. This way of writing the expansion of the polarizability allows to draw a parallel with the non-resonant Raman polarizability, which is expanded directly in a Taylor series up to at least the first order (and more, whenever anharmonicity effects are considered). The zeroth and first order dipole expansion terms that appear in the resonant case are commonly referred to as Franck-Condon (FC), and Herzberg-Teller (HT), therefore the terms that appear in the polarizability expression can be classified as mixed FC-FC, FC-HT, etc. terms, which can be considered the different orders in the expansion of the RR polarizability in the normal modes. The full second order of the polarizability contains a HT-HT term, and two FC-D2 terms (where D2 refers to the second order derivative of the transition dipole moment). In this work we stop the dipole expansion up to the HT terms, therefore the polarizability contains all FC-FC, FC-HT, and HT-HT terms. Note that in these expressions the dipole moments are expanded with respect to the excited state normal modes (all quantities referring to the excited electronic state are denoted by an apex). This choice allows for a simplification of the formulas to calculate the required Herzberg-Teller integrals and, if HT can be considered a good approximation, the two approaches are equivalent. The inclusion of HT terms is especially crucial in the case of symmetry-forbidden transitions, or transitions with a very low oscillator strength, while their inclusion may be forgone in the case of strongly allowed transitions.

The integrals that appear in equation 6 can be computed recursively.^44–46 The time-independent formulation of the RR polarizability has been implemented within the Gaussian suite development version⁴⁷ by taking advantage of the features previously developed for one-photon spectra calculation,^48,49 and in particular for one-photon absorption (OPA) which requires the very same transition integrals as RR. As already mentioned, the time-independent scheme requires a truncation of the summation in equation 6 in order to be of any use. There is in principle an infinite number of middle states 〈m′|, therefore we need to screen them to select beforehand the states that are expected to give the greatest contribution to the dipole integrals. We have accomplished this by using a class-based method, described in Refs.^42,48–51. The convergence of each Raman peak’s calculation can be gauged by evaluating the expression obtained by neglecting the denominator contribution in equation 6 both numerically and analitically, as described in Ref.⁸. Alternative methods for the screening of integrals have also been proposed.^52–54 While the prescreening method attempts to reduce the number of middle states that need to be included in the calculation, their number can still be significant, and does scale with the size of the system. Fortunately each middle state contributes independently to the total sum-over-state, therefore equation 6 can be implemented in an effective parallel way, allowing us to apply our procedure to systems of medium and large size, without the need to introduce further approximations. More specifically, the middle states are separated into “classes” of excitations according to the number of simultaneously excited modes, and the contribution of a class is computed before moving to the next. Within each class, the calculation is split between all available processors, using a shared-memory Open Multi-Processing (OpenMP) protocol, and each processor treats a different family of middle states 〈m′|, where by family we intend a set of states with the same simultaneously excited oscillators, hence differing only by the number of non-null quanta for each mode. The number of states belonging to a class grows very rapidly with the class order, which makes it the bottleneck of the calculation. Parallelizing the latter step can speed up the calculation almost linearly with the number of processors. Additonally, each Raman peak can be computed independently of the others, therefore the evaluation of the different band intensities can also be parallelized if multiple machines are available.

The TI formulation has a few advantages. Since the recursion formulas used to compute the FC integrals are completely general, it is possible to compute the intensity of overtone and combination bands up to any order and the computational cost for a combination band is not significantly higher with respect to a fundamental band (though the raw number of possible combinations grows rapidly with the maximum allowed quantum number and with system size). This also allows the straightforward inclusion of temperature effects in the calculation, since this requires to select a finite number of different initial states according to their Boltzmann population. Finite temperature spectra may contain a greater number of bands, whose computation can also be parallelized. The efficient implementation of FC integral calculation, along with the parallelization of the code, allows us to apply the TI picture with the Duschinsky and temperature effects to systems of medium-large size. Note that as the size of the system increases and we wish to keep intact the level of theory (i.e. inclusion of Duschinsky mixing) the actual RR spectrum calculation will never be the bottleneck of the whole computation since the excited-state vibrational analysis is by far the most demanding step (see section 8 for a specific example). The applicability of our method can therefore be extended to ever-larger systems by reducing the cost of the latter step, e.g. by using a more a ordable basis set or even by estimating the second derivatives using semi-empirical methods, or running the various steps involved in the numerical differentiation on separate machines.

3 Anharmonicity effects

Even though peaks’ intensities carry information about the excited electronic state of the system, RR can still be considered a vibrational spectroscopy since the transition involves two vibrational states belonging to the same PES. While a harmonic description of the ground-state PES to model vibrational spectroscopies can give good qualitative results, inclusion of anharmonic effects is often needed to achieve sufficient accuracy to allow a direct comparison with experimental results. This is especially true in the case of RR because peak positions are determined by the energies of the vibrational states, and it has been shown^55–57 that anharmonicity can have huge effects, resulting in shifts of as much as 150 cm⁻¹ for C-H stretchings, and, more crucially, anharmonicity can affect the ordering of the vibrational modes, which can lead to erroneous peak assignments. The anharmonicity of the PES also affects spectroscopic intensities, as demonstrated in many works in the case of infra-red and vibrational circular dichroism spectra.^55,58–62 In the case of non-resonant Raman spectroscopy, the inclusion of anharmonic contributions on the intensities calls for both an anharmonic description of the PES, and the inclusion of additional terms in the Taylor expansion of the Raman polarizability as a function of the normal modes of vibration up to the third order (the so-called electrical anharmonicity).⁵⁵ In the TI picture of RR the transition dipole moment is instead expanded as a Taylor series, giving rise to Franck-Condon, Herzberg-Teller, and possibly higher terms, so the inclusion of anharmonicity rests on the sole description of the vibrational states. An additional challenge faced in the case of RR is the fact that intensities rely on an accurate description of the excited state PES in addition to the ground-state one, and if performing a complete harmonic vibrational analysis for an excited state can itself be quite demanding, going beyond the harmonic approximation can prove to be truly herculean, unless the excited state can be computationally treated like a ground state, e.g. whenever it has a different symmetry or spin multiplicity with respect to the “true” ground state, or in cases like photon-induced ionizations where an electron is removed from the system. Anharmonicity effects can be included at different levels of approximation and with different methods.^63,64 In this work we used our implementation^65–68 of second order vibrational perturbation theory (VPT2) which can provide an accurate description of both anharmonic vibrational energies and wavefunctions. In VPT2 the perturbed wavefunctions are expressed as linear combinations of harmonic states, and in order to use this kind of expression in calculation of Franck-Condon integrals, we would have to perform a large number of computations for each RR peak, with a prohibitive computational cost, bar for the smallest molecules. Because we are interested in applying our methodology to medium-large sized systems, we choose instead to limit the treatment of anharmonicity effects to the vibrational energies, which are employed in equation 6, in place of the harmonic ones, with no additional computational cost for the vibronic part. As already pointed out, computing the excited-state anharmonic frequencies with a full VPT2 treatment is computationally too expensive, and can only be done in conjunction with an electronic structure method for which analytical second derivatives of the excitation energy are available. We choose instead to use the ground-state anharmonic frequencies to estimate the excited-state ones, following the scheme proposed by some of us.⁶⁴ Since in general the excited-state normal modes differ from the ground-state ones, the anharmonic shifts computed for the latter cannot be directly applied to the former. To solve this problem we compute the scaling factors between the harmonic ground-state energies and their anharmonic counterparts and then use the Duschinsky transformation to estimate the corresponding scaling factors for the excited state. The estimated excited state anharmonic frequencies can then be written as:⁶⁴

$${\omega }_b^{\prime \mathrm{anh}}=\left(\sum _a{J}_{ba}^2\frac{{\omega }_a^{\mathrm{anh}}}{{\omega }_a^{\mathrm{harm}}}\right){\omega }_b^{\prime \mathrm{harm}}$$ (7)

Empirical scaling factors are commonly used to estimate anharmonicity effects for the ground state, and in fact they have also been used in the context of RR calculations.^25,69–71 Computing the scaling factors using vibrational perturbation theory, as opposed to using empirical ones, poses no transferability problems and is therefore much more suited for the estimation of the excited-state frequencies. The excited-state anharmonic frequencies are then inserted into equation 6 along with the ground-state ones, ands are also used in the recursion formulas used to compute the Franck-Condon integrals. It is worth noting that anharmonic frequencies are systematically lower than their harmonic counterparts, therefore if anharmonicity effects were included only in the ground state vibrational energies, the denominators in equation 6 would increase, leading to systematically lower absolute intensities. Because the anharmonicity shift tends to be much higher for higher-energy modes, this effect is also heterogenous along the spectrum, leading to an error in the relative intensities, in addition to the absolute ones. It is therefore crucial that anharmonicity effects be included for both electronic states.

This method of treating the anharmonicity of excited states can be validated by applying the full VPT2 treatment to excited states which, because of symmetry or other reasons, require no TDDFT response calculations. It should be noted that our vibronic method is not applicable in cases where there is a very large change in geometry and normal modes of the excited state with respect to the ground state’s because in that case the Duschinsky transformation is not sufficient to faithfully describe the relation between the two sets of normal modes. To summarize, our method for estimating anharmonic frequencies in the excited state seems suitable for those systems for which the vibronic spectrum can be computed in this framework. To support our claim, we computed the anharmonic frequencies of imidazole in its ground singlet state, and in its first triplet (T₀) and ionized (D₀) states. We then computed the Duschinsky matrix and the anharmonic shifts for the T₀ and D₀ states using equation 7 and compared the results.

While this method of treating anharmonic effects exonerates us from the calculation of high-order geometric derivatives of the excitation energy, computing the anharmonic frequencies for the ground state alone is still very demanding, and scales unfavorably with system size. Fortunately, RR spectroscopy can benefit greatly from the use of a reduced-dimensionality scheme. Usually one is only interested in a specific region of the spectrum, therefore it is not necessary to compute the anharmonic frequencies of the normal modes which lie outside of it. Computationally, this means that the energy Hessian need only be computed after displacing the molecular geometry along the selected normal modes rather than the full ensemble, with a proportional saving in computational time. Unless the modes that are not included in the anharmonic treatment are very strongly anharmonic and strongly coupled to the selected modes, the discarded terms contribute marginally to the anharmonic correction, and can safely be eliminated, so peak positions are almost unaffected.^72,73 In addition, a very small effect on the computed RR intensities can be expected because the harmonic frequencies will be used in place of the anharmonic ones for the non-selected modes in equation 6. In our examples, the effect of anharmonicity on intensities is not very big, therefore we can safely apply our reduced dimensionality scheme in the most complex cases.

4 Environmental effects on resonance Raman spectra

Though some reports of RR spectra of molecules in the gas phase exist,^74–77 RR spectral measurements are most often performed on molecules in solution or more complex environments. The connection between the RR spectral response and the molecular environment is in fact so strong that RR measurements have been used to evaluate solvent reorganization energies associated with the electronic transition.^78–80 The most evident environmental effect on the spectrum is the change in the positions of the peaks, related to the change in the vibrational energies, which can be quite significant.⁵⁶ This change is one of the consequences of the change in the PESs and, by extension, in the vibrational wavefunctions that enter equation 3, causing a change in the intensity of the peaks, as well as their positions. Therefore we need a suitable computational protocol able to model the effects of the environment on all these parameters, having the capability of accurately calculating the energies, geometries, frequencies and vibrational wavefunctions of the system. While these requirements can be met by means of numerical algorithms, there are other issues which have to be solved before the model can be considered suitable for modeling RR spectroscopy. By limiting ourselves to solvated systems (similar considerations also apply to generic systems composed of a core molecule interacting with an external environment), it should be taken into account that RR scattering is a dynamical process. Therefore, the response of the solvent to the core system interacting with the external field will occur at different timescales, depending on the different degrees of freedom of the solvent molecules surrounding the core system. This results in both homogeneous and inhomogenous broadening effects of the spectral response caused by the presence of the solvating environment.⁸¹ The component of the solute-solvent interaction that acts at the polarizability level can be modeled by including an additional time-dependent dephasing term in the exponent of equation 4, and if this is simplified by a constant term, there is a resulting increase in the observed value for the damping constant γ that appears in equation 3, so it can no longer be attributed solely to the finite life-time of the excited electronic state. The choice of an appropriate value for the damping constant to be used in the spectrum simulation should therefore take into account the experimental conditions. In addition, the spectral peaks will also be broadened because of the presence of the solvent, and this latter effect can be empirically considered by using an arbitrarily chosen lineshape, such as a Gaussian or Lorentzian distribution function.

Coming back to the modeling of solvent effects on PESs, vibrational wavefunctions, and electronic excited states, a possible strategy consists in performing QM calculations within the framework of the Polarizable Continuum Model (PCM),^82,83 which has been used in the past to model solvent effects in the context of RR spectroscopy.^{8,21,26,84–88} PCM is a so-called focused model, which treats the solvent as a continuum polarizable dielectric medium that hosts the solute molecule, treated quantum mechanically, within a molecule-shaped cavity. The presence of the polarizable continuum alters the solute electronic density, via an effective solvent-dependent term in the molecular Hamiltonian, which in turn affects the solvent response, until self-consistency, which finally results in mutual solute solvent polarization effects. Besides such direct effects on the molecular electronic wavefunction, the presence of the continuum dielectric also alters the solute PES, i.e. its equilibrium geometry, vibrational frequencies and normal modes, resulting in a change in RR peaks’ positions, but it also affects all excited state properties required in RR calculations (i.e. transition dipole moments, excited state forces, etc.).

PCM has been extensively used to model solvent effects on both vibrational and electronic spectroscopies thanks to the development of algorithms to include solvent contributions in the different terms entering equation 3.

The peculiar nature of RR as a mixed vibrational-electronic property calls for care when considering the solvent time evolution, in order to correctly account for the dynamical aspects of the solute-solvent interaction,⁸⁹ which differ if purely electronic,^90,91 vibrational^57,92 or mixed electronic/vibrational phenomena^89,93 are considered.

In the simple case of electronic absorption spectra, a possible (and most often used) partition of the solvent response to the electronic changes in the solute assumes the solvent electronic degrees of freedom to quickly equilibrate to the time-evolving solute electronic density, whereas the rest stay equilibrated to the unaltered ground state solute charge density, thus resulting in a non-equilibrium solute-solvent regime.^89–91 The same also applies to vibrational spectroscopies,^57,92 however the partition of the solvent response has to be done differently, because both the electronic and vibrational solvent degrees of freedom can, in this case, follow the solute charge density evolving in time. This formally results in a different definition of the non-equilibrium solvation regime.^57,61,94

Unlike simple one-photon (electronic or vibrational) absorption, RR is at the same time a vibrational and an electronic phenomenon, therefore the definition of the physically consistent solvation regime to be used in the calculation of the RR polarizability is to be done with care.⁸⁹ By adopting a time-dependent picture, the RR polarizability can be seen as originating from the evolution in time of the starting vibrational wavepacket on the excited state PES. Therefore, depending on the timescale of such an evolution, it might be assumed that some of the solvent’s nuclear degrees of freedom remain static. To simulate such behavior within the PCM framework, extension of the vibrational non-equilibrium approach^92,95 to excited states, within the further account of electronic non-equilibrium effects would be necessary. Such a model has never been proposed so far. In this paper, in order to partially account for such effects we will assume the PCM cavity to stay fixed, i.e. the geometrical arrangement of the solvent stay equilibrated to the solute equilibrium geometry. This implies the PCM cavity geometric derivatives to be discarded in the evaluation of excitation energy gradients and/or Hessians. As far as the ground state is concerned, we will instead make use of the aforementioned vibrational non-equilibrium regime^57,92 It is worth remarking that the use of a fixed cavity cannot completely freeze the solvent’s nuclear degrees of freedom, because the nuclear solvent response, which contributes to the PCM excited state computed properties, is evaluated within the nuclear equilibrium regime. A further approximation which we will exploit in the following consists of performing a numerical differentiation of the (electronic) non-equilibrium excitation energy, where each atom is displaced along each cartesian coordinate first in the positive and then in the negative direction, and the derivative is then computed numerically. The PCM cavity is also kept fixed. A univocal assessment of the (nuclear+electronic) solvation regime to be exploited in modeling RR spectra is far from trivial. Therefore, in the following we will compare three different approaches to compute the parameters required for a RR calculation:

1. Equilibrium solvation: all solvent degrees of freedom are equilibrated with the solute. Both ground state and excitation properties are computed in this manner and the PCM cavity is mobile.

2. Fixed cavity: the PCM cavity is kept fixed in the calculation of all energy derivatives, for both the ground state and excitation properties, where the former are computed under the vibrational non-equilibrium regime, and the latter are computed in the electronic equilibrium solvation regime.

3. Non-equilibrium: in addition to keeping the cavity fixed, the vertical excitation energy is computed under (electronic) non-equilibrium conditions, and is numerically differentiated.

The choice of the solvation regime should also be coherent with the treatment of the excited-state PES: in an adiabatic scheme, where the excited-state geometry is optimized and the PCM cavity is displaced along with it during the optimization, the equilibrium solvation should be selected. The other two regimes can be used in vertical treatments (VG or VH). In order to apply the other two solvation regimes to adiabatic schemes, the excited-state geometry optimization must also be performed with a fixed PCM cavity.

5 Computational details

All DFT, RR, and vibronic absorption calculations were performed using a development version of the Gaussian suite of quantum chemistry programs.⁴⁷ The B3LYP^96,97 functional is adopted for imidazole and chlorophyll a1, while PBE0⁹⁸ is used in the case of pyrene, following previous studies establishing this functional as appropriate for this system.⁸⁷ Some test computations on pyrene were also performed with the CAM-B3LYP⁹⁹ and the M06-2X¹⁰⁰ functionals. The basis set was chosen taking each system’s size and consequent computational cost of each task into account. For imidazole the aug-cc-pVTZ¹⁰¹ was used for all calculations, for pyrene and chlorophyll a1 the ground state harmonic frequencies were computed with the double-zeta SNSD basis set¹⁰² whereas anharmonic effects and excited state frequencies were computed with the smaller 6-31G* basis set.

Solvent effects were taken into account using the Polarizable Continuum Model (PCM).^82,83 The PCM cavity was built using a system of interlocking spheres with the following radii expressed in Ångstroms: 1.443 for hydrogen, 1.926 for carbon, and 1.830 for nitrogen, 1.7500 for oxygen, and 1.5105 for magnesium, each multiplied by a factor of 1.1. The solvents’ static and optical dielectric constants used are ε₀ = 78.36 and ε_∞ = 1.78 for water, ε₀ = 35.69 and ε_∞ = 1.81 for acetonitrile, and ε₀ = 32.61 and ε_∞ = 1.77 for methanol.

All Complete Active Space Self-Consistent Field (CASSCF) and Multi-State Complete Active Space Second-Order Perturbation Theory (MS-CASPT2)¹⁰³ calculations were performed using the MOLCAS package (version 7.8).^104–106

6 Imidazole in aqueous solution

Imidazole was chosen for its role in biological systems and because its small size and solubility in water allow for a very extensive analysis of the various contributions to the final spectra and of the different levels of approximation involved. For our study, we focused on the very bright π − π* transition, which appears around 210 nm. Because this transition is strongly allowed,¹⁰⁷ we performed our calculations at the FC level.

6.1 Anharmonicity effects

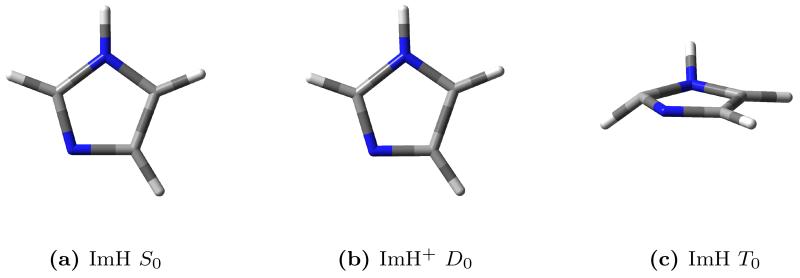
As already mentioned, imidazole is an ideal candidate to illustrate our method for treating anharmonicity effects in RR spectroscopy. We performed the full VPT2 anharmonic analysis^65–68 for imidazole in its ground S₀ state and first triplet state T₀, and for the radical cation ImH⁺ in the lowest energy D₀ state. The calculations in each case involve a geometry optimization (see figure 1 for the three optimized geometries), followed by the calculation of harmonic force constants (to obtain the normal modes of vibration), and finally the numerical differentiations of the energy Hessian.

Figure 1.

Optimized structures of imidazole (singlet), imidazole cation (doublet), and imidazole (triplet).

From the harmonic analysis of the three species, it is possible to compute the Duschinsky matrix and shift vector that relate the normal modes of the cation and the triplet to the normal modes of the singlet. Using equation 7 the anharmonic frequencies of the ground singlet state were used to estimate the anharmonic frequencies of the cation and triplet, which were compared to their VPT2 counterparts to assess the validity of our scaling scheme. The results are reported in table 1. The anharmonic frequencies obtained with the Duschinsky method are in excellent agreement with the VPT2 ones in the case of the doublet cation, with an average deviation of 0.4% and a maximum deviation of 1.1% for normal mode 15. A much larger deviation is observed in the case of the triplet state, with deviations as high as 43% for the first normal mode. This behavior can be explained from the observation of the optimized structures (figure 1). The optimized structure for the triplet state presents a significant piramidalization of two atoms in the ring, resulting in a different molecular symmetry. The normal modes of the triplet state are poorly described in terms of the singlet state normal modes using a simple affine transformation such as the Duschinsky relation, leading to a very dense Duschinsky matrix (see Supporting Information for a pictorial representation of the Duschinsky matrices), with many elements of significant magnitude for each row (or column). In this case our vibronic model is not applicable. From these results it is reasonable to suggest that this method of estimating anharmonic frequencies rests upon the same assumptions behind the vibronic model itself, i.e. there should be a limited structural deformation associated with the electronic transition.

Table 1.

Comparison between VPT2 anharmonic frequencies and the ones estimated with the anharmonic scaling scheme based on the Duschinsky transformation. ImH denotes neutral imidazole, ImH⁺ is the radical cation. Note that the optimized structure for the triplet state of imidazole has a different symmetry with respect to the singlet; the symmetry labels therefore do not apply in this case.

		ImH S0 (Cs)		ImH+ D0 (Cs)				ImH T0 (C1)
#	Sym	Harm	VPT2	Harm	VPT2	Dusch.	% dev	Harm	VPT2	Dusch.	% dev
1	A″	540	533	496	491	487	0.78	201	137	196	43.14
2	A″	647	633	544	531	534	0.73	404	328	394	20.15
3	A″	683	673	707	690	694	0.70	467	392	455	16.00
4	A″	743	724	799	778	781	0.42	599	545	586	7.42
5	A′	827	810	825	806	810	0.57	736	611	719	17.80
6	A″	885	864	890	872	871	0.20	809	775	793	2.25
7	A′	908	895	923	907	908	0.14	832	801	815	1.86
8	A″	946	932	936	917	913	0.42	914	865	892	3.14
9	A′	1073	1049	964	942	944	0.26	916	871	895	2.75
10	A′	1093	1069	1043	1018	1021	0.24	1008	966	982	1.72
11	A′	1144	1121	1125	1105	1100	0.47	1049	1025	1024	0.05
12	A′	1159	1133	1212	1186	1184	0.21	1107	1074	1080	0.58
13	A′	1286	1261	1265	1242	1237	0.45	1262	1232	1229	0.25
14	A′	1363	1323	1295	1270	1267	0.22	1305	1271	1272	0.11
15	A′	1427	1389	1416	1365	1380	1.12	1358	1317	1322	0.40
16	A′	1499	1470	1453	1415	1421	0.41	1396	1346	1366	1.45
17	A′	1556	1524	1539	1494	1506	0.79	1541	1507	1501	0.37
18	A′	3242	3115	3235	3112	3109	0.09	3110	2988	2984	0.13
19	A′	3244	3118	3241	3116	3115	0.04	3180	3054	3055	0.05
20	A′	3272	3145	3248	3124	3122	0.05	3230	3083	3105	0.69
21	A′	3652	3484	3565	3399	3401	0.07	3467	3223	3325	3.17

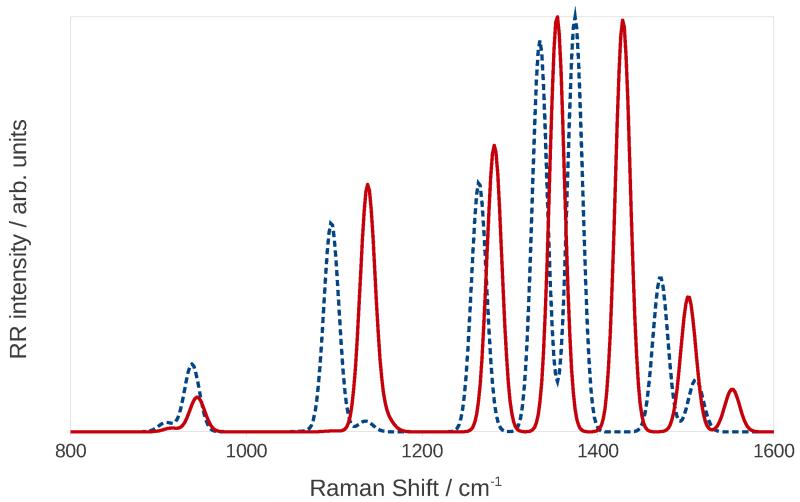
Figure 2 shows the harmonic and anharmonic RR spectra calculated for an incident wavelength of 224 nm, a damping of 500 cm⁻¹, and with peaks convoluted with Gaussian functions with a half-width at half maximum (HWHM) of 10 cm⁻¹. The spectra were scaled to have the same maximum intensity to compare them more easily. As expected, anharmonic bands are systematically redshifted with respect to the harmonic ones, and there is also a significant difference in the computed relative peak intensities. Notice also that in the anharmonic spectrum there is a very small peak at 1136 cm⁻¹ which, in the harmonic spectrum, is obscured by the intense peak close to it. We finally note that imidazole is a small system, i.e. it has a limited number of vibrational modes, thus the resulting spectrum is relatively simple. In case of more complex systems, the combination of peak displacements and changes in relative intensities can potentially lead to notable differences in the bandshapes.

Figure 2.

Harmonic (continuous red line) and anharmonic (dashed blue line) RR spectra of imidazole in water.

6.2 Effect of the solvation regime

As pointed out previously, solvent effects can be crucial in RR spectroscopy, and the choice of the solvation regime is of particular relevance. Because of water’s high polarity, the distinction between equilibrium and non-equilibrium solvation can have very dramatic consequences on spectroscopic properties. As already pointed out in section 4, for RR, as well as vibrationally resolved absorption and fluorescence spectra, it is necessary to make a distinction between electronic and vibrational non-equilibrium solvation, depending on which degrees of freedom of the solvent are allowed to relax and thus remain at equilibrium with the solute evolving with a timescale characteristic of the spectroscopic phenomenon. In the framework of a time-dependent picture, the vibronic structure characteristic of any electronic excitation and the RR response arise from the evolution of the initial vibrational wavepacket on the excited state PES, which may last long enough to allow for the relaxation of the solvent’s electronic (and, possibly, nuclear) degrees of freedom. The choice of the most appropriate solvation regime depends on the system and is by no means trivial. We have investigated the effect of the different approaches on RR and vibrationally resolved OPA spectra of imidazole in water by performing the calculations under the three distinct conditions described in section 4. First we considered the solvent in full equilibrium with the system, both in its electronic and nuclear degrees of freedom, then we considered the effect of keeping the PCM cavity fixed (where the vibrational non-equilibrium regime is employed in the computation of the harmonic or anharmonic vibrational ground state frequencies and normal modes), and finally we performed the calculation with the addition of electronic non-equilibrium effects on excited state properties. Note that we also included anharmonicity effects in all cases.

Electronic and nuclear non-equilibrium affects the computed spectra at different levels. Keeping the PCM cavity fixed only influences the calculation of the gradients (and, if required, Hessian and higher order derivatives) of the ground state energy and excitation energy that are used to model the PESs. Conversely, under equilibrium conditions, it is necessary to include in the derivatives additional terms accounting for the displacement of the cavity. This effect does not change the vertical energy or dipole strength of the transition (the latter accounted for by the FC terms), since neither involves any geometrical derivatives, but affects the shape of the excited-state PES and the HT and higher terms in the Taylor expansion of the dipole moments. It should be clear that the question of the vibrational non-equilibrium does not arise in the modeling of one-photon spectroscopies (e.g. absorption and fluorescence) unless one is interested in the vibronic bandshape, but is always present in the case of RR, for which even the simplest computational models require the calculation of the excited state gradient. Electronic non-equilibrium has a more dramatic effect, as it influences the calculated vertical excitation energies and can even affect the order of the excitations. Figure 3 shows the computed vibronic OPA spectra, the RR excitation profile (i.e. a plot of the RR intensity against the incident frequency at a fixed Raman shift) corresponding to the 8th normal mode (an in-plane bending motion, see the Supporting Information for a pictorial representation of the normal modes mentioned throughout the article), and the RR spectrum, under the three solvation regimes discussed in section 4. All spectra were computed at the Vertical-Gradient Franck-Condon (VG|FC) level, with the inclusion of anharmonic effects. Each band in the vibronic OPA spectrum was convoluted with a Gaussian function with a HWHM of 150 cm⁻¹, while the peaks in the RR spectra were convoluted with Gaussian functions with a HWHM of 10 cm⁻¹. The RR and RR excitation profile spectra employ a value for the damping constant of 500 cm⁻¹. All spectra are shown in arbitrary units. The RR spectra were computed for an incident wavelength of 224 nm and, since we are more interested in comparing relative intensities rather than absolute ones, they were subsequently scaled to have the same maximum intensity.

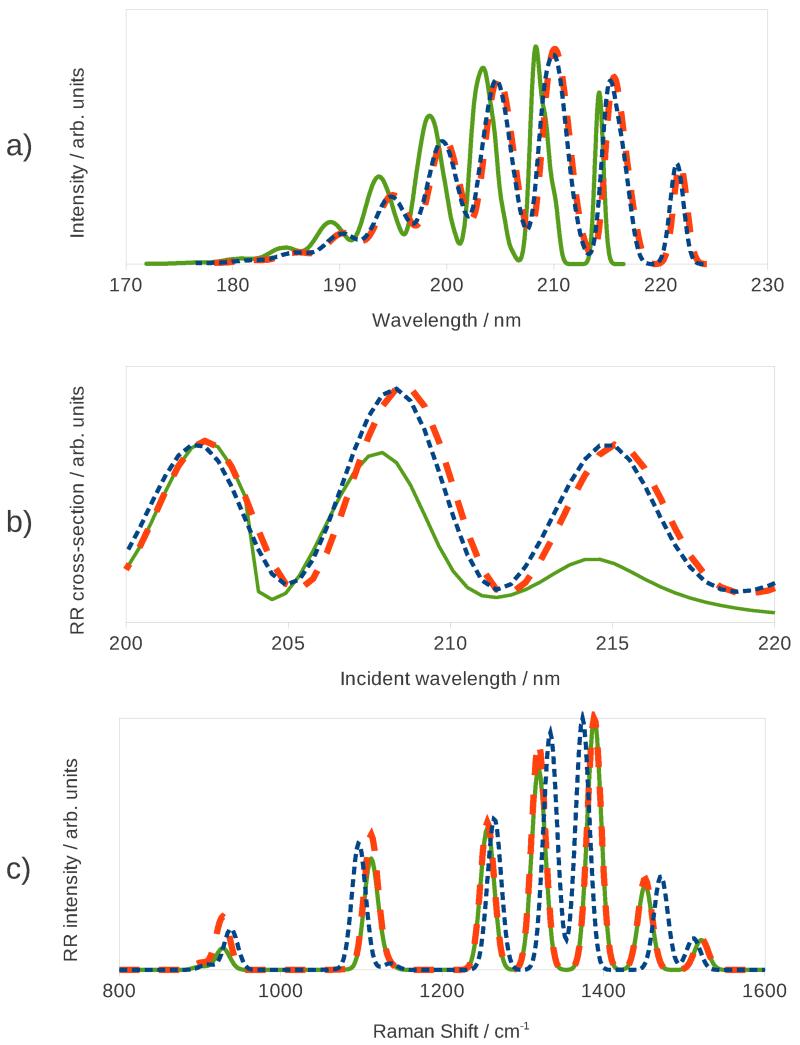
Figure 3.

UV-Vis (Top panel), RR excitation profile (middle panel), and RR spectra (bottom panel) of imidazole in water calculated with three different solvation regimes: equilibrium solvation (finely dashed blue line), fixed cavity (dashed orange line), and non-equilibrium (continuous green line).

All three vibronic OPA spectra show a similar convolution; the lowest energy band corresponds to the 0-0 transition, while the other bands arise mainly from the superposition of different peaks corresponding to transitions from the vibrational ground state to a combination of normal modes 11, 13, 14, and 15 in the excited state PES. The spectra show that there is only a slight change when the PCM cavity is held fixed (dashed orange line), and the resulting spectrum is almost superimposed to the spectrum obtained with a mobile cavity. The position of the peaks is expected to be almost identical in the two cases, as keeping the cavity fixed does not directly affect the vertical transition energy. The same behavior is observed in the case of the RR excitation profile. The RR spectrum instead shows a much more pronounced difference: the position of the peaks is heavily influenced by the solvation regime employed to compute the ground state anharmonic frequencies, with a smaller yet clearly discernible effect on relative intensities. A much larger change can be observed in the case of the electronic non-equilibrium: in this case the vertical transition energy is blueshifted by about 1500 cm⁻¹ (roughly 7.5 nm) and both the OPA spectrum and the RR excitation profile appear translated. In addition, the relative intensities of the absorption peaks are affected by the variation of the solvation regime, and the same behavior is observed in the excitation profile. The change in both intensity patterns is a consequence of the change in the computed excited-state forces under the two different solvation regimes. The RR spectrum shows a very different behavior, as there is very little change with respect to the fixed-cavity regime. The position of the peaks is a property of the ground state, therefore it is not influenced by the way excitation properties are calculated, and while a small change in the intensity pattern is noticeable, it is by no means as significant as in the case of the RR excitation profile, though this depends upon the chosen incident wavelength.

These results greatly highlight the nature of RR spectroscopy as a mixed electronic-vibrational phenomenon which is heavily influenced by the environment and the choice of solvation regime.

6.3 Comparison with experiment

So far we have analyzed the effect of anharmonicity and solvation environment employing the simplest model for the vibronic transition (VG|FC). Before comparing our results with experimental data we needed to study the effect of Duschinsky mixing on the spectrum. To do so we compared the anharmonic (VH|FC) RR spectrum with the (VG|FC) one represented as a dashed orange line in figure 3 (whithin the fixed-cavity solvation regime). The results are represented in figure 4 a. Of course, peak positions are unaffected by the introduction of Duschinsky mixing, but relative intensities experience significant changes.

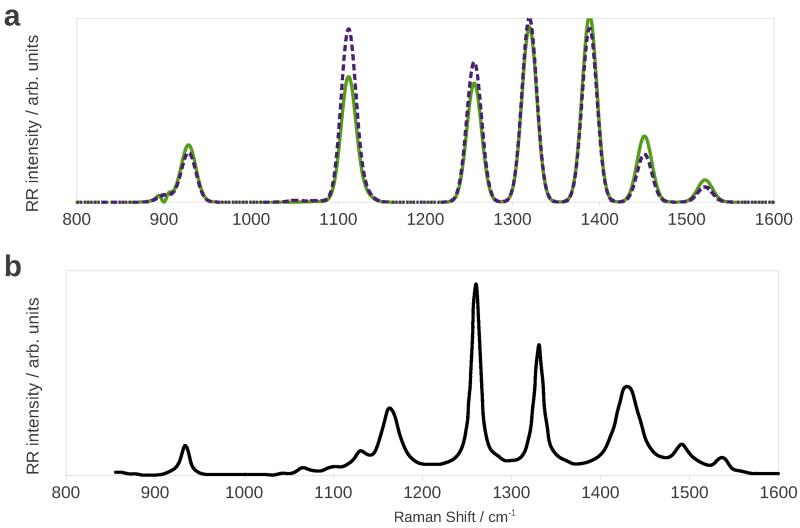
Figure 4.

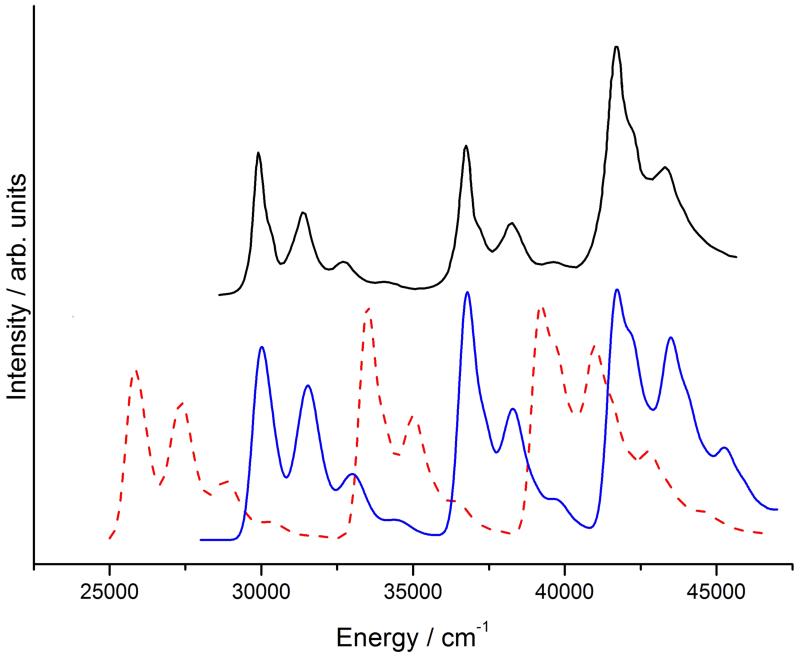
Calculated VG|FC (top, solid green line) and VH|FC (top, dashed purple line) RR spectra, and experimental¹⁰⁸ (bottom, black line) RR spectrum of imidazole in water.

The comparison with experiment is complicated by the great number of parameters involved. First, one has to choose an incident frequency and a suitable damping constant, which can assume a wide range of different values. The incident frequency may be chosen to differ from the calculated vertical energy by the same amount as the experimental laser frequency differs from the measured absorption maximum.⁸⁷ If the absorption spectrum is very broad this method may not be very precise. Note also that a lower damping constant may cause the spectrum to depend more strongly upon the chosen incident frequency.⁸ In addition, the solvation regime greatly affects both the vertical transition energy and the RR intensity pattern. The comparison may be greatly facilitated if both the experimental RR spectrum and RR excitation profile are available. We compare our results with experimental one by Balakrishnan et al,¹⁰⁸ (see figure 4b), who measured the RR spectrum at an excitation wavelength of 229 nm, which corresponds to the very start of the absorption band of imidazole. The comparison of the experimental spectrum with the calculated VH one (figure 4a) shows that peak positions are reproduced well enough to permit an assignment. The band that appears around 1100 cm⁻¹ is enhanced with respect to the experimental one, while the one at 1260 cm⁻¹ has a lower than expected intensity, otherwise the agreement is fairly good, and the VH spectrum shows a better agreement with experiment than the VG one, owing to the effect of Duschinsky mixing. The small peaks between 1050 cm⁻¹ and 1150 cm⁻¹ are in-plane bending motions of the C-H bonds;¹⁰⁸ they are not visible in the theoretical spectrum because of their negligible calculated intensity or because they are obscured by the higher-intensity peak at 1100 cm⁻¹. One possible source of errors may be that imidazole in water can form hydrogen bonds with solvent molecules, whose effect is not fully captured by our implicit solvation model. A way to overcome this limitation is to use atomistic models for the environment, such as the QM/FQ/PCM model we have recently implemented.^109–111 Because the experimental incident frequency is on the tail of the absorption bandshape there may also be contamination from the non-resonant Raman spectrum.

7 Pyrene in acetonitrile solution

The RR spectra of pyrene (D_2h symmetry) and its derivatives have been previously studied both experimentally¹¹² and theoretically.^87,113,114 In this contribution we wish to draw upon the previous work by some of us⁸⁷ and expand it by including anharmonicity and non-equilibrium solvent effects in the spectrum calculation. The interesting property of the RR spectra of pyrene is the interference between different excited states. Contrary to what happens in the case of OP spectra, in RR the contributions from different electronic states must be added at the amplitude (polarizability) level rather than at the intensity level (the Raman cross section is quadratically dependent on the polarizability). The result is that the total spectrum is not simply the sum of the spectra arising from the different electronic states. The three excited states that should be taken into consideration are, in order of increasing energy, the 1B_1u, 2B_2u, and 2B_1u states.^87,112 In the case of pyrene calculations we chose the intermediate solvation regime, with ground state harmonic and anharmonic frequency calculations performed with vibrational non-equilibrium effects, and we kept the cavity fixed in all calculations involving the excited states. We performed a ground state geometry optimization followed by a normal mode calculation at the PBE0/SNSD¹⁰² level of theory. We also optimized the ground-state geometry and computed the anharmonic vibrational frequencies using the smaller 6-31G* basis set in order to obtain them at a reduced computational cost. The PBE0/SNSD harmonic frequencies were combined with the PBE0/6-31G* anharmonic shifts to obtain the anharmonic vibrational energies to be used in the subsequent RR calculations. The PBE0/6-31G* level of theory was also used for all excited-state calculations, and the model chosen for the excited PESs is AH, which requires a geometry optimization followed by harmonic frequency calculations. All RR spectra were computed using a damping constant of 500 cm⁻¹ and the RR peaks were convoluted with Gaussian functions with a HWHM of 15 cm⁻¹.

As already pointed out, it is not essential to accurately reproduce the excitation energy to compute a RR spectrum because the incident frequency used in the calculation can be easily adjusted to compensate for this error. However, whenever multiple states are involved it may be crucial to correctly reproduce the energy difference between the states. For example, a spectrum may contain peaks which are enhanced by resonance with different electronic states, and if the energy difference between those states is overestimated, it may be impossible to find an incident frequency for which all peaks are visible. A comparison between the experimental and theoretical vibronic absorption spectrum can be used to check the reliability of the chosen electronic structure model. Moreover, if the vibronic resolution is clearly visible in the experimental spectrum, the latter can be used to extract the energy of the 0-0 transitions for each electronic state, and those energies can then be employed in the calculation of the RR spectra. This is the case of pyrene, whose experimental and calculated vibronic absorption spectra are shown in figure 5. While the bandshapes are correctly reproduced, the calculated spectrum is not merely shifted with respect to the experimental one because the energy of the 1B_1u state is underestimated by a larger amount with respect to the 2B_2u, and 2B_1u states. To compensate for this error we therefore shifted the energy of each state individually before computing the RR spectra and excitation profiles.

Figure 5.

Experimental (top black line) and calculated (bottom lines) vibronic absorption spectra of pyrene in acetonitrile. The dashed red line is the unshifted spectrum (PBE0/SNSD band positions), the continuous blue line is the shifted spectrum according to the experimental transition energies.

We also checked whether other DFT functionals or a multireference method would yield better results. We therefore computed the vertical excitation energies using the CAM-B3LYP⁹⁹ and M06-2X¹⁰⁰ functionals with the SNSD basis set, as well as by MS-CASPT2¹⁰³ with the ANO basis set with the contraction 4s3p1d for carbon atoms, and 2s1p for hydrogen atoms.^115,116 A full valence π space which comprised 16 electrons distributed in 16 orbitals (16,16) was used. The DFT calculations included solvent effects by means of PCM, while the MS-CASPT2 calculations were performed for the molecule in the gas phase, so we also computed the excitations with PBE0 without PCM, to estimate the solvent shift. The PBE0/SNSD ground state optimized geometry was used in all cases. The calculated vertical transition energies cannot be directly compared with the energy of the 0-0 transition obtained from the experimental spectrum, though their difference can be estimated theoretically from the vibronic spectrum calculated with the PBE0 functional, giving 2690 cm⁻¹ for the 1B_1u state, 2188 cm⁻¹ for the 2B_2u state, and 2967 cm⁻¹ for the 2B_1u state. These values were then subtracted from the calculated vertical excitation energies. Table 2 summarizes the results. M06-2X gives the best results for the excitation energies, however it has been shown that it is less reliable for calculation of harmonic frequencies,¹¹⁷ therefore we still preferred to use PBE0 to compute all spectra because, as shown in figure 5 and in the analysis by Avila Ferrer et al.⁸⁷ this functional gives a very good description of the shape of the PESs. The MS-CASPT2 results do not show a significant improvement with respect to the TDDFT ones, though they lack a description of solvation effects which, as can be seen from the comparison of the gas-phase and acetonitrile solution results obtained for PBE0, give a large contribution.

Table 2.

Energies of the 0-0 transitions (in cm⁻¹) computed with different methods, and their experimental counterparts.¹¹² PBE0_(g) denotes gas-phase excitation energies, while all other TDDFT results include solvent effects.

State	MS-CASPT2	PBE0(g)	PBE0	CAM-B3LYP	M06-2X	Exp112
1B1u	25688	27333	25773	27219	27700	29940
2B2u	36180	35271	33761	35944	35931	36765
2B1u	41469	40768	38328	39527	39902	41667

Often the resolution of the experimental spectrum is not sufficient to clearly identify the energy of the 0-0 transition (especially if the states are very close in energy and their spectra overlap). In that case it may be useful to perform additional calculations with different electronic structure methods to estimate the energy differences between the excited states.

To show the effect of the excitation-energy shift and of anharmonicity on the RR spectrum we computed the harmonic and anharmonic spectra using the PBE0/SNSD excitation energy, as well as the anharmonic spectrum calculated using the excitation energies from experiment. We chose an incident frequency of 42000 cm⁻¹ (238 nm) to compute the latter spectrum, and an incident frequency of 39500 cm⁻¹ (253 nm) to compute the two former ones (in order to adjust the energy of the 2B_1u state without touching the energy differences, as would be normally done). The incident energy is at the edge of the 2B_1u band in the experimental spectrum in figure 5, so it is affected by interference with the lower-energy 2B_2u state. Figure 6 shows the results. As in the case of imidazole, anharmonicity causes a redshift of all bands, as well as minor intensity changes. The spectrum computed using the experimental excitation energies shows an additional change in intensity, especially visible for the band that appears around 1700 cm⁻¹. This kind of effects are not very big in the case of pyrene because there is quite a large separation between the three electronic states, but they may be more relevant in cases where the energy difference between the states is grossly overestimated or underestimated by the chosen electronic structure method.

Figure 6.

Calculated harmonic (bottom red line) and anharmonic (middle green line) RR spectra obtained using the PBE0/SNSD excitation energies, and anharmonic spectrum (top blue line) obtained using the experimental excitation energies of pyrene in acetonitrile.

8 Chlorophyll a1 in methanol solution

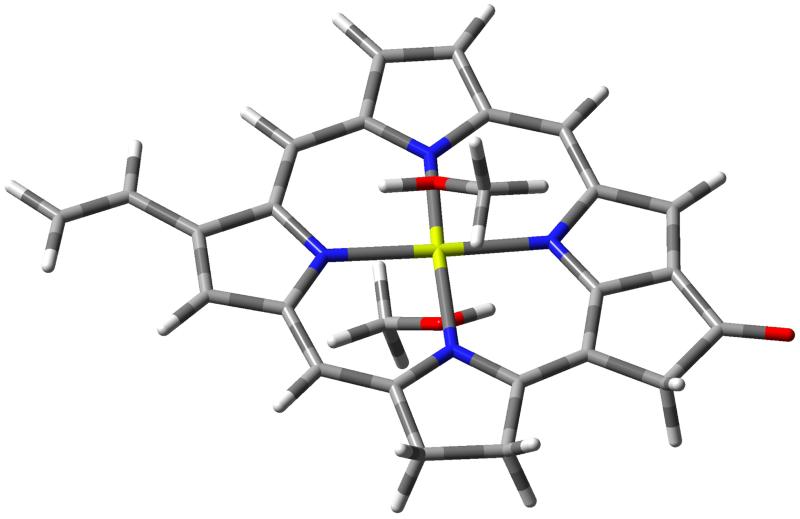
To illustrate how our approach can be applied to larger systems we computed the RR spectrum of chlorophyll a1 (ChlA1, figure 7), a large system of 46 atoms that is often used as a model for chlorophyll a, a pigment found at the heart of the biological machinery responsible for photosynthesis.¹¹⁸ RR spectroscopy has already proved to be an invaluable tool in the study of multichromophoric systems, such as those involved in photosynthesis, thanks to the possibility of tuning the incident frequency to selectively excite the different chromophores.^119,120 In this work we studied the influence of a solvent on the RR spetrum, postponing the case of more complex environments, such as proteins, to future works. We also compared our results with the experimental ones by Hanf et al.¹²¹ who measured the RR spectrum of protochlorophyllide a (PChlide) in methanol solution. PChlide has an identical π structure to chlorophyll a1, but with additional alkylic substituents which do not significantly alter the shape of the absorption spectrum. We calculated the RR spectrum of ChlA1 in methanol solution with the inclusion of Duschinsky mixing, Herzberg-Teller, solvent, and anharmonicity effects combined (anharmonic AH|FCHT model with equilibrium solvation). The RR spectrum was calculated for the bright Soret band which appears at about 420 nm in the experimental spectrum,^122,123 and the solvation regime chosen in this case is the equilibrium one. Since the magnesium atom at the center of the ring is expected to be hexacoordinated, with one solvent molecule on either side of the ring, to overcome the limitations of the continuum solvent model we explicitly added these solvent molecules to the part of the system treated quantum-mechanically.

Figure 7.

Structure of chlorophyll a1 with two additional methanol solvent molecules.

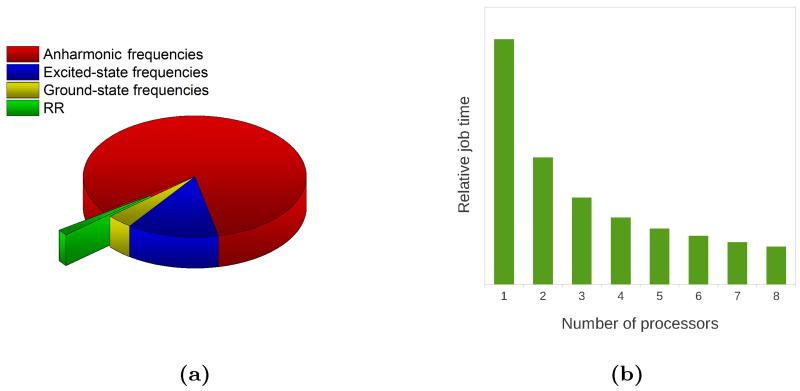
We first note that the dimensionality of the system requires great care in the choice of the computational level. The most demanding step in our calculations is by far the evaluation of ground state anharmonic frequencies, which is accomplished by displacing the molecular geometry along each normal mode in the positive and negative directions, computing the energy Hessian at each step, and obtaining the numerical third and semi-diagonal fourth energy derivatives. The computational cost of this approach scales unfavorably with system size (even though the calculations can be done in parallel if multiple machines are available). Similarly to what was reported for pyrene, we employed the SNSD¹⁰² basis set to compute the harmonic frequencies while resorting to the smaller 6-31G* basis set to compute the anharmonic shifts. In the case of ChlA1, even with the smaller basis set, the full anharmonic calculation is computationally too expensive so, to further reduce its cost, we resorted to a reduced-dimensionality approach,^72,73 limiting the evaluation of the required anharmonic derivatives to the normal modes in the 1100-1800 cm⁻¹ region, and thus restricting the computed RR spectrum as well. The reduced-dimensionality approach is especially useful for the calculation of anharmonic RR spectra because it is always possible to focus on the frequency region in which the final RR spectrum is to be computed, while for vibronic OP spectra this is not possible. Restricting the calculation to a smaller region also saves time in the subsequent TI-RR spectrum calculation, though it must be emphasized that, notwithstanding the large number of peaks and the great number of states included in the TI expression for each peak, this is still the cheapest step in the overall calculation. To present this last point in deeper detail we show in figure 8a the relative computational times for each step leading to the final spectrum. Note that, even with a reduced-dimensionality approach, the most expensive step is by far the calculation of anharmonic frequencies, followed by the calculation of excited state frequencies. Anharmonicity and Duschinsky effects can sometimes be ignored, but the calculation of ground state frequencies is essential for vibrational spectroscopies and it is still more expensive than the final spectrum calculation. Note in addition that in figure 8a we report the time needed to obtain the RR spectrum in the selected spectral region with the inclusion of first overtones and combination bands (the calculation of the fundamental bands only is in fact so cheap that it would not be visible in the reported pie chart). Thanks to our parallel implementation we are able to compute the RR spectrum of medium-large systems with a reasonable cost, and the limiting factor is represented by all other steps that are necessary to define the two PESs. Figure 8b shows the relative computational time required for the TI-RR spectrum calculation as a function of the number of processors used. The computational gain is close to the maximum theoretically possible: with 8 processors the computational time is reduced to 15.4% (as opposed to ⅛=12.5%).

Figure 8.

(a) Relative computational cost of the different steps leading to the final RR spectrum of ChlA1. Ground state frequencies (SNSD basis set) are in blue, anharmonic shifts (6-31G* basis set) are in orange, excited state frequencies (6-31G* basis set) are in yellow, and the final RR spectrum between 1100 and 1800 cm⁻¹, up to the first overtones and 1+1 combination bands is in green. (b) Relative cost of the RR spectrum calculation with increasing number of processors.

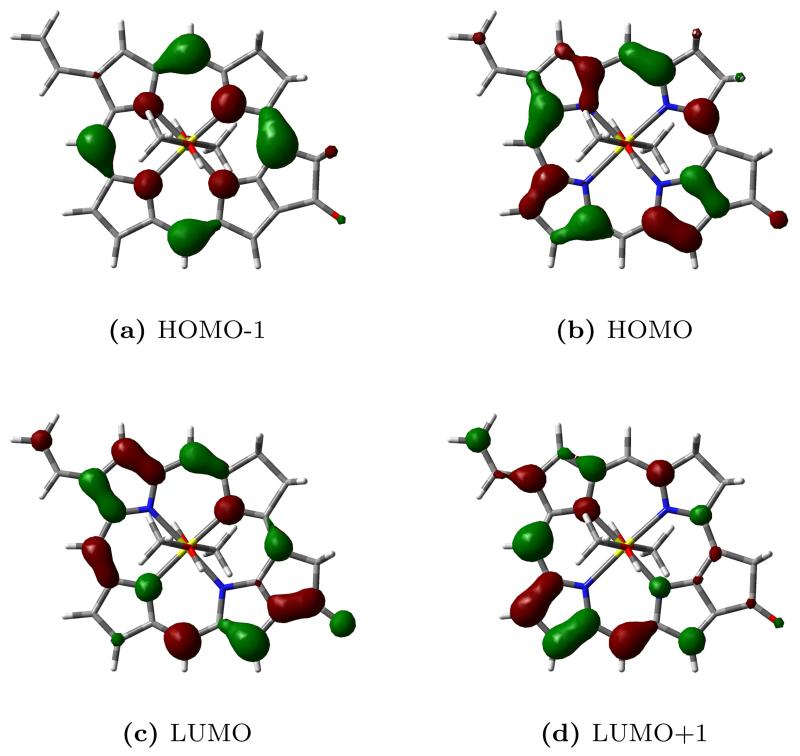
Before computing the RR spectrum, we simulated the vibronic bandshape of the UV-vis absorption spectrum in order to assess the quality of our approach for the specific system. A TD-DFT vertical excitation energy calculation reveals that the band we are interested in is a superposition of two different π − π* excited states, S₃ (HOMO-1–LUMO+1) and S₄ (HOMO–LUMO+1). The S₁ (HOMO–LUMO) and S₂ (HOMO-1–LUMO) states, have lower intensity and calculated vertical excitation wavelengths of 637 nm and 618 nm respectively. Figure 9 shows a graphical representation of the Kohn-Sham orbitals involved in the transitions.

Figure 9.

Kohn-Sham orbitals of chlorophyll a1.

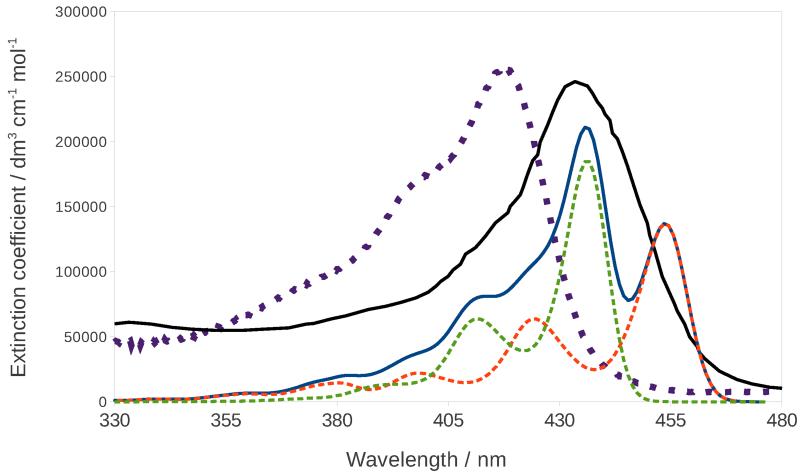
Figure 10 shows the comparison between the experimental spectra of PChlide¹²¹ and ChlA1¹²² and the calculated vibronic spectrum of ChlA1, which was obtained by convoluting each peak with a Gaussian function with a HWHM of 250 cm⁻¹. For both electronic states that appear in the calculated spectrum, the band with highest intensity corresponds to the 0-0 transition, and both show a similar vibronic progression, which is due to the excitation of several very diffuse in-plane bending motions. The experimental spectra of PChlide and ChlA1 show a similar band-shape which justifies the use of the latter as a model for the former in the calculation of the RR spectrum. The calculated band-shape reproduces experiment fairly well, even though DFT predicts the two excited states to be further apart than they would appear from the experimental spectrum. The calculated spectrum almost overlaps with the experimental PChlide one, with the maximum appearing at 434 nm and 437 nm in the experimental and calculated spectrum, respectively, whereas the maximum of the experimental ChlA1 spectrum appears at 417 nm. Overall, the chosen model seems appropriate for the description of our system.

Figure 10.

Calculated (continuous blue line) and experimental¹²² (dotted purple line) absorption spectra of ChlA1 in methanol. The continuous black line is the experimental absorption spectrum of PChlide,¹²¹ and the dashed orange and green lines are the calculated absorption spectra for the S₃ and S₄ states respectively.

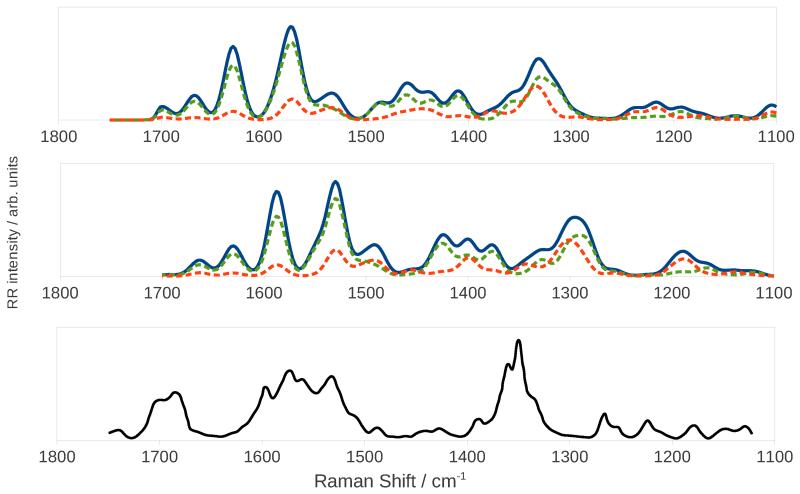
Figure 12 shows the calculated and experimental¹²¹ RR spectra. The calculations were performed with an incident frequency of 24550 cm⁻¹ (407 nm), and a damping constant of 500 cm⁻¹. The experimental spectrum of PChlide was also recorded with a 407 nm incident radiation. Because the calculated ChlA1 UV-vis spectrum overlaps with the experimental PChlide one, we did not need to apply any shift to the incident frequency. The peaks were convoluted with Gaussian functions with a HWHM of 10 cm⁻¹. The top and middle panels show the harmonic and anharmonic spectra, respectively. As already reported for imidazole, the effect of anharmonicity mainly consists of a redshift of all bands but, because the shift is different for each peak, the convoluted spectrum also shows some clearly visible differences in the bandshape. Figure 12 also shows the separate contribution of each excited state: the S₄ state gives a greater contribution, as is expected from its greater intensity in the absorption spectrum and from the fact that it lies closer to the incident frequency. The S₃ state still gives a non-negligible contribution thanks to the fact that the tail in its absorption spectrum reaches the value of the incident frequency. As explained above, the total spectrum is not simply the sum of the two separate spectra because of interference effects acting at the polarizability level. We also computed the spectrum with the inclusion of overtones and combination bands of up to two quanta transitions, but we found that they all have negligible intensities resulting in an almost identical spectrum (see Supporting Information).

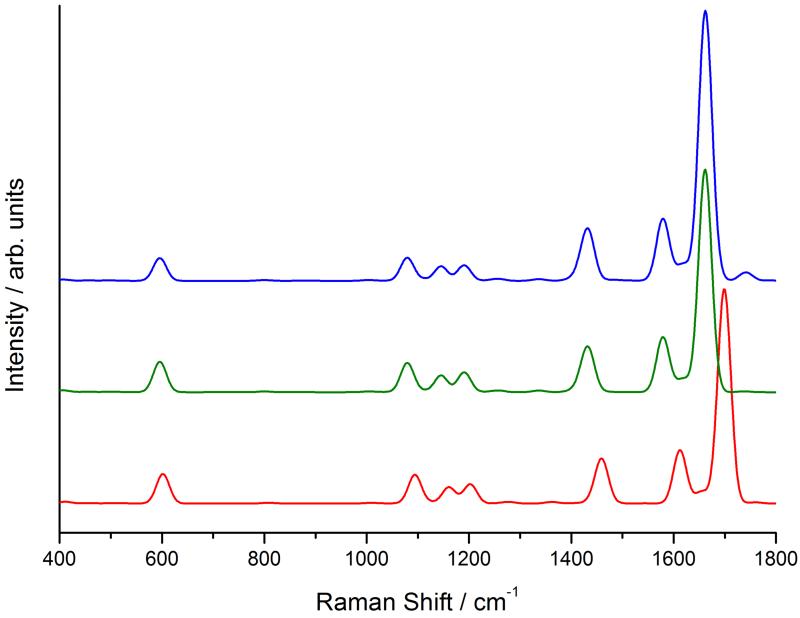
Figure 12.

Harmonic (top panel) and anharmonic (middle panel) RR spectra of ChlA1 in methanol. The continuous blue line is the total spectrum, the dashed orange and green lines the spectra for the S₃ and S₄ states respectively. The bottom panel shows the experimental RR spectrum of PChlide.¹²¹

The bottom panel in figure 12 shows for comparison the experimental spectrum of PChlide recorded with a 407 nm laser frequency.¹²¹ The experimental spectrum shows a strong band around 1360 cm⁻¹ which the authors assign to C-C breathing vibrations of the porphyrin, a band around 1570 cm⁻¹ assigned to C=C stretching vibrations, and one at 1700 cm⁻¹ assigned to the C=O bending of the ciclopentanone ring. These features are all reproduced in the calculated spectrum, though with notable differences. The computed frequencies are lower than the experimental ones, causing a shift of the whole spectrum. The 1400 cm⁻¹ zone in the computed spectrum shows a few bands of significant intensities, which correspond to very diffuse C=C bendings, that are not observed in the experimental spectrum. The high-intensity peaks that appear between 1500 and 1600 cm⁻¹ in the anharmonic calculated spectrum are due to C=C stretching motions and they are separated by a gap which is not found in the experimental spectrum, but our calculations reveal that there are actually no normal modes with an energy that would place them whithin that gap. These differences may be attributed to the additional side chains of PChlide, which would result in a greater number of peaks.

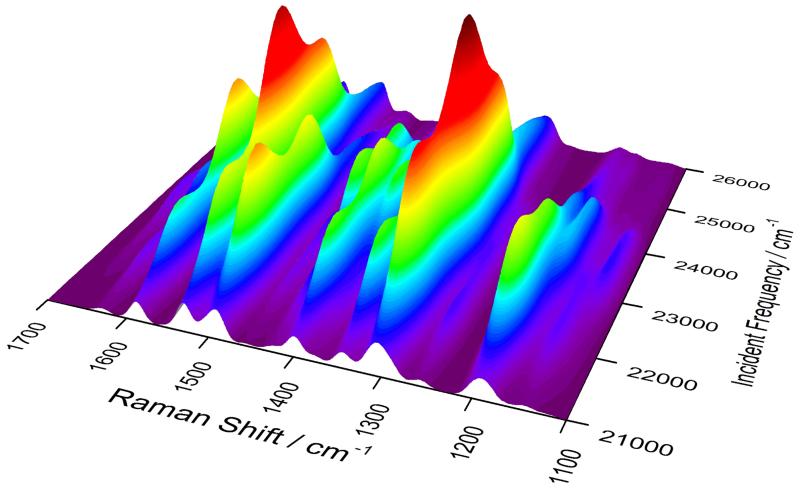
The effect of changing the incident frequency can be grasped by looking at the 3D plot in figure 11, where the axes hold the Raman shift, incident frequency, and spectrum intensity. The behavior of the different bands seems irregular because the two excited states affect the various peaks in different ways, and their large number means that they often overlap to give rise to the visible bands. The potential interpretative power of theoretical calculation is then evident as it can help to unravel complex spectroscopic responses such as RR which, as an additional complication, does not benefit from the simple selection rules valid for non-resonant Raman scattering.

Figure 11.

Calculated 2D-RR spectrum of ChlA1 in methanol, where the spectrum and excitations profiles are shown at the same time.

9 Conclusions and perspectives

In this work we have presented a parallel implementation of the TI calculation of RR spectra with the inclusion of anharmonicity and solvent effects. We have shown that it is possible, by carefully choosing the computational methods and employing appropriate reduced-dimensionality schemes, to coherently include anharmonicity, Duschinsky, and solvent effects in the calculation of RR spectra of medium-to-large sized systems. We have demonstrated that the cost of the calculations required to accurately model the ground-state and excited-state PESs far outweighs the simulation of the final TI-RR spectrum, therefore the best way to extend the applicability of the method to ever-larger systems is to find cheaper means to perform the former tasks. This goal may be accomplished through analytic implementations of excited state energy second derivatives,^124,125 which scale very favorably with system size with respect to their numerical counterparts, and through the use of less expensive methods such as semi-empirical ones, especially for the evaluation of anharmonic frequencies.¹²⁶

With the goal of extending the method to larger and more complex systems, another issue calling for deeper investigations is the choice of internal coordinates for the simultaneous description of electronic states possibly characterized by quite different geometries. Several studies have shown that normal modes built from cartesian coordinates represent the most straightforward and robust choice when small displacements occur. In such circumstances the full adiabatic Hessian (AH) model, possibly including leading anharmonic corrections, shows a remarkable agreement with experiment, provided that the quantum mechanical method chosen to build the PES is accurate enough. When large structural displacements take place between the different electronic states, the situation is more involved, especially if inversions and/or torsions are present.¹²⁷ Recent works suggest that in such circumstances cartesian coordinates face significant difficulties for a correct description of curvilinear displacements and a proper account of the Duschinsky mixing within the AH model, where the PESs of the different electronic states are quadratically expanded around their own equilibrium geometry.^127–129 Although the theory behind the use of internal coordinates is well known¹²⁷ and several works have been published concerning specific systems,^128,129 a general implementation of this model is still lacking and is one of the most important tasks on which our group is concentrating its e orts. On the other hand, the good agreement between the results issuing from the vertical hessian (VH) model and experimental line shapes indicates that this approximation, in which all the normal modes are evaluated at the equilibrium geometry of a single reference electronic state, is a good alternative to deal with systems exhibiting large displacements. The use of this model can be, however, problematic when imaginary frequencies arise.¹³⁰

Motivated by the fact that there is a well-known strong relationship between the RR spectral response and the molecular environment, we have also studied the effect of the solvation regime on the final spectrum. We have employed three different solvation regimes with the intent of modeling the behavior of the different degrees of freedom of the solvent as they either remain fixed or equilibrate with the time-dependent evolution of the starting vibrational wavepacket of the solute that generates the spectral response, according to their characteristic timescales. It should be noted that the different solvation regimes we have considered can be viewed as limiting cases of the real behavior of the solvent: in reality the solvent’s degrees of freedom always start from a non-equilibrium situation, and then, if the lifetime of the vibrational wavepacket on the excited state PES is long enough to allow it, they gradually evolve to re-equilibrate with the solute. Nonetheless, our results show that the change in the solvation regime does have a great influence on the final RR spectrum and excitation profile, which could stimulate more research in this area. In particular, by performing the calculation in the time-dependent picture, it could be possible to model the evolution of the solvent’s polarization more accurately by considering an additional time-dependence of all the terms in the equation caused by the solvent, though the assessment of how the solvent’s evolution affects the excited state PES and the transition moments is far from trivial. The choice of the appropriate solvation regime may be particularly important in the case of more complex environments, such as a chromophore embedded in a protein, which cannot freely rearrange itself to adapt to the evolution of the chromophore. In this case though, implicit solvent models may fail to capture the specificity of the interactions, therefore atomistic models may be more appropriate. A possible strategy to overcome such limitations can be the hybrid multi-scale QM/FQ/PCM scheme^109–111 we have recently proposed, to treat explicit interactions between a molecular system and its environment. An additional limitation of the implicit model used in this work is the absence of non-electrostatic effects in the solvent respose in its basic formulation. Several methods have been proposed to include non-electrostatic effects within the PCM framework,^131–133 though, to the best of our knowledge, none have been applied to RR spectroscopy.