Abstract
Objective
Several longitudinal studies of Alzheimer Disease (AD) report heterogeneity in progression. We sought to identify groups (classes) of progression-trajectories in the population-based Cache County Dementia Progression Study (N=328), and to identify baseline predictors of membership for each group.
Methods
We used parallel-process growth mixture models (GMM) to identify latent classes of trajectories based on MMSE and CDR-sb scores over time. We then used bias-corrected multinomial logistic regression to model baseline predictors of latent class membership. We constructed ROC curves to demonstrate relative predictive utility of successive sets of predictors.
Results
We fit 4 latent classes; class 1 was the largest (72%), and had the slowest progression. Classes 2 (8%) ,3 (11%), and 4 (8%) had more rapid worsening. In univariate analyses, longer dementia duration, presence of psychosis, and worse baseline MMSE and CDR-sb were associated with membership in class 2, relative to class 1. Lower education was associated with membership in class 3. In the multivariate model, only MMSE remained a statistically significant predictor of class membership. ROC AUCs were 0.98, 0.88, and 0.67, for classes 2,3, and 4 relative to class 1.
Conclusions
Heterogeneity in AD course can be usefully characterized using GMM. The majority belonged to a class characterized by slower decline than is typically reported in clinical samples. Class membership could be predicted using baseline covariates. Further study may advance our prediction of AD course at the population level, and in turn shed light on the pathophysiology of progression.
Search Terms: Alzheimer, growth mixture model, trajectory, disease course
Introduction
Alzheimers disease (AD) is prevalent and costly (Wimo, Winblad, Jonsson, 2010; Alzheimer’s Association, Thies, Bleiler, 2011). There is substantial heterogeneity in rates and patterns of progression in AD, with a substantial proportion (25–50%) experiencing relatively slow decline (Cortes et al., 2008; Cortes et al., 2008; Tschanz et al., 2011). We aim to identify classes of patterns of progression, in a population-based cohort study of incident AD, and to determine which baseline characteristics are predictive of these patterns.
AD is characterized by cognitive and functional declines and the presence of neuropsychiatric symptoms, but there is considerable variability in rate of progression both between individuals, and during individual courses of illness (Folstein, Folstein, McHugh, 1975; Aguero-Torres, Fratiglioni, Winblad, 1998; Wilson et al., 2000a; Cortes et al., 2008; Tschanz et al., 2011). In a review of clinic-based samples, average annual rate of decline on the Mini-Mental State Exam (MMSE) (Folstein, Folstein, McHugh, 1975), ranged from 2.7 to 4.3 points per year, but the standard deviations were comparatively large, ranging from 2.4 to 4.3 (Aguero-Torres, Fratiglioni, Winblad, 1998). In the REAL-FR study (Cortes et al., 2008), in a large clinical sample, mean change over two years was 4.57 (0.23) MMSE points, and 4.17 (0.17) points on the Clinical Dementia Rating sum of boxes (CDR-sb) (Hughes et al., 1982). In the Cache County Dementia Progression Study (DPS), mean annual rates of change were 1.53 (2.69) and 1.44 (1.82) points on the MMSE and CDR-sb, respectively (Tschanz et al., 2011). In both of these samples, the authors noted distinct “profiles” or groups, which appeared to differ by rate and pattern of disease progression.
The rate of progression is not constant over the course of AD (Wild and Kaye, 1998; Xie et al., 2009); typically decline is slower in the early stages of the disease. Individuals’ changes in rates of progression over the course of AD are often modeled through the inclusion of a quadratic (time-squared) term (Wilson et al., 2004; Camicioli and Kryscio, 2005; Tschanz et al., 2011). This results in a fitted line which is curved; direction and magnitude of the curvature dictated by the sign and magnitude of the regression coefficient for the quadratic term. Trajectories are therefore characterized by the combination of intercept, slope, and quadratic terms with respect to time, rather than just the mean rate of progression. Growth mixture modeling (GMM), which estimates latent classes of trajectories, allows for the identification of subtypes of patterns of progression (Small and Backman, 2007). For example, it might identify a class of individuals with high baseline MMSE scores but sharply accelerating declines, and another class of individuals who start out with lower baseline but who experience a shallow and steady decline. Because AD is characterized by both cognitive and functional decline, we will model class membership based on patterns of change in both of these domains, simultaneously.
GMM also allows for the modeling of predictors of class membership, and a number of correlates of progression have been identified in the literature. Female sex has been associated with faster decline (Tschanz et al., 2011) but not in all studies (Martins et al., 2005). Earlier age at symptom onset has been associated with faster decline (Jacobs et al., 1994; Wilson et al., 2004) as has higher education (Stern et al., 1999; Andel et al., 2006; Scarmeas et al., 2006). Higher baseline cognitive function has been associated with slower decline (Atchison, Massman, Doody, 2007).
APOE genotype (4/4 homozygosity) has been associated with greater functional (Dal Forno et al., 1996), and cognitive decline (Martins et al., 2005), though these associations have not been found consistently (Growdon et al., 1996; Murphy et al., 1997; Aerssens et al., 2001). Increased neuropsychiatric symptoms, including agitation and wandering (Miller et al., 1993), hallucinations and delusions (Wilson et al., 2000b), and depressive symptoms (Wilson et al., 2002), have been associated with greater decline.
Concurrent, but not baseline, worsened general medical health has been associated with increased decline (Leoutsakos et al., 2012b). Vascular risk factors, including atrial fibrillation, systolic hypertension, and angina have been associated with greater functional and cognitive declines (Mielke et al., 2007), but not in all studies (Regan et al., 2006).
If distinct subtypes of progression trajectories could be identified, and if it were possible to determine, at baseline, which subtype a given individual would express, there would be several important uses for those findings. First, it would improve the precision of forecasts of the burden of AD. Current models are based on mean times of progression from onset to need for skilled nursing care in clinical populations (Brookmeyer et al., 2007). Better understanding of the types of courses and their prevalence would enable refinement of these projections. On an individual level, it could provide more information for long-term financial and caregiver planning. Identifying predictors of each subtype could provide clues to the underlying pathology governing decline. If any of these factors were modifiable, it could lead to advances in the treatment of AD. The goals of this work, therefore, are to identify discrete subtypes (latent classes) of AD progression; we hypothesize that one of these classes will be characterized by comparitively slow decline. Further, we will determine which baseline variable are useful in predicting class membership.
Methods
The Cache County Dementia Progression Study (DPS) is a prospective cohort study of all incident dementia cases identified as part of the Cache County Study on Memory in Aging (CCSMA) (Tschanz et al., 2011). The CCSMA is a longitudinal, population-based cohort which began in 1995 and included 90% of county residents over 65. Nineteen incident AD cases were identified during wave 1, 108 during wave 2 (completed in 1999), 156 during wave 3 (completed in 2003) and 52 during wave 4 (completed in 2007). As part of the DPS, CCSMA participants with incident AD were followed prospectively, approximately every six months, until death, loss-to-follow-up, or the close of the study. Institutional review boards at Utah State, Duke, and Johns Hopkins Universities reviewed and approved all study procedures, and all participants and their next-of-kin provided informed consent.
Details of the methods used in CCSMA and DPS are published elsewhere (Breitner et al., 1999; Lyketsos et al., 2000), but in brief, dementia cases were identified through a multi-stage procedure (Breitner et al., 1999). This included screening with an adapted Modified Mini-Mental State Exam (MMSE) (Teng and Chui, 1987). Screen-positive individuals and a designated subsample were administered an informant-based telephone interview (Kawas et al., 1994). The subsample and participants who still screened positive then underwent a clinical assessment (CA) by a trained nurse and neuropsychological technician which included a physical and neurological exam and a neuropsychological battery (Tschanz et al., 2000). A study geriatric psychiatrist and a neuropsychologist then reviewed the available data and preliminary diagnoses were made using DSM-III-R criteria (American Psychiatric Association, 1987). Individuals with preliminary dementia diagnoses underwent MRI scans and standard laboratory studies for dementia. They were also examined in person by a geriatric psychiatrist or neurologist, and finally a panel with expertise in neurology, geriatric psychiatry, neuropsychology and cognitive neuroscience reviewed all data and assigned diagnoses of possible or probable AD as defined by NINCSD-ADRDA criteria (McKhann et al., 1984).
At wave 1 of the CCSMA, demographics including years of education and sex were collected, as well as APOE genotype from buccal DNA. At each DPS follow-up visit, trained neuropsychological technicians administered the MMSE (Folstein, Folstein, McHugh, 1975), a measure of global cognitive functioning. A trained nurse administered the Clinical Dementia Rating (CDR) (Hughes et al., 1982), a measure of functional ability in six domains on a scale from 0 (no impairment) to 5 (terminal), producing a summed score (CDR-sb) ranging from 0–30. The Neuropsychiatric Inventory (NPI) (Cummings et al., 1994) was administered to caregivers, and measured the presence, frequency, and severity of 12 neuropsychiatric symptoms including delusions, hallucinations, agitation, depression, and apathy. Domain scores are calculated as the product of frequency and severity, range from 0–12, and are summed for the NPI total score.
Statistical Methods
The study sample included 328 subjects with complete data at baseline. Time was measured in years from dementia onset. Growth mixture models (GMMs) allow for the grouping of subjects based on similarities in their patterns of progression over time. Their use implies an assumption that each subject’s scores over time arise from their membership in a latent (unobserved) trajectory class. In a typical mixed effects longitudinal regression model, coefficients for intercept, slope, and quadratic terms would be estimated, and would represent the expected trajectory for the entire sample. Random effects would be used to account for variability in intercept and slope among individuals. In GMM, separate intercept, slope, and quadratic terms are estimated for each latent class, and class membership is a function of all three terms (Muthen and Muthen, 2000; Jung and Wickrama, 2008).
Since AD involves both cognitive and functional declines, we chose to model class membership as a function of both MMSE and CDR trajectories, using parallel process growth mixture models (Gross and Rebok, 2011). Unlike MMSE, higher CDR-sb scores represent worse performance; for ease of interpretation and modeling, we reverse-coded all CDR-sb scores (e.g., a CDR-sb score of 1 was recoded as a 29). Since we expected declines in MMSE and CDR to be correlated, the random effects on intercept and slope for each outcome were allowed to be correlated to each other and with random effects on the other outcome. We fit models with 1–5 classes, and chose the model with the lowest BIC value (Nylund, Asparouhov, Muthen, 2007). Next, we tested our ability to predict membership in each latent class using baseline information, including age at AD onset, sex, education, duration of dementia, presence of 1 or more APOE e4 alleles, history of transient ischemic attack (TIA), history of hypertension, presence of either hallucinations or delusions as measured by the Neuropsychiatric Inventory, MMSE, and CDR-sb (reversed). Using the parallel process GMM parameter estimates, multinomial logistic regression was used to predict class membership in univariate models. For these regressions, age of onset was mean-centered at 84, education was centered at 12, MMSE was centered at mean-22, and CDR-sb (reversed) was mean-centered at 24. We then fit a multivariate model with any predictors that were significantly associated with class membership at α=0.10 in the univariate analyses. It is well known that treatment of latent class membership as an observed variable in such regressions leads to downwardly-biased estimates of regression coefficients (Bolck, A., Croon, M.A., & Hagenaars, J.A., 2004). We used a 3-step bias correction procedure to address this issue (Asparouhov and Muthen, 2013).
Classification utility for each covariate individually, and then for progressively larger sets of covariates, was assessed via ROC (Receiver Operating Characteristic) curves, which plot sensitivity of the linear predictor (from the previous multinomial logistic regression analyses) against 1-sensitivity. Area under the curve (AUC), a measure of classification utility, was calculated for each predictor and set of predictors, for each latent class (Obuchowski, 2003). Latent variable models, including the bias-corrected regression models, were fit using MPLUS v7.11 (Muthen and Muthen, 1998–2007). Further analyses, including ROCs and processing of results, was performed using R v. 2.13 (R Development Core Team, 2008). R code is available from the first author upon request.
Results
Demographics and other characteristics of the 328 subjects are shown in table 1. The majority were female (66%), and white (99%). The mean age at dementia onset was 84.3 (SD=6.4). Mean years of education was 13.2 (SD=3.0), and baseline MMSE, CDR, and NPI were 22.0 (SD=4.6), 5.9 (SD=3.4), and 4.6 (SD=9.3). The mean number of visits was 3.6 (SD=3.0) and the mean years of followup was 3.7 (SD=2.5); the respective medians were 2 visits and 3.1 years.
Table 1.
Sample Characteristics
| Age at Onset (yrs) | 84.3 (6.3)1 | |
| Male (yes/no) | 35 (114)2 | |
| Education (yrs) | 13.2 (3.0) | |
| Dementia Duration (yrs) | 1.64 (1.2) | |
| White (yes/no) | 99 (326) | |
| APOE (yes/no) | 3/4 or 4/4 | 40 (131) |
| Transient Ischemic Attack (yes/no) | 18 (57) | |
| Hypertension (yes/no) | 54 (172) | |
| NPI (Total) | 4.4 (9.0) | |
| NPI Psychosis (yes/no) | 17 (55) | |
| NPI Depression (yes/no) | 23 (75) | |
| NPI Apathy (yes/no) | 16 (52) | |
| MMSE | 22.4 (3.8) | |
| CDR-sb | 5.7 (2.8) | |
| Visits | 3.6 (3.0) | |
| Length of Followup (yrs) | 3.8 (2.5) |
Mean (SD) are displayed for all continuous variables
Percent (count) are displayed for all dichotomous variables (denoted as yes/no)
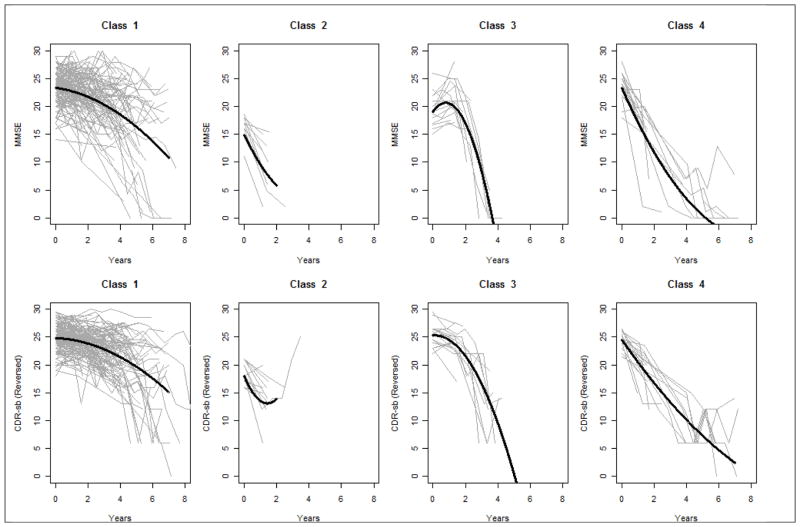
Parallel process growth mixture models were fit to MMSE and CDR scores measured at up to 7 timepoints. BIC statistics were 10679.827 (1-class model), 10550.432 (2-class model), 10200.264 (3-class model), 10184.256 (4-class model), and 10535.020 (5-class model). As such, a 4-class model was chosen. Parameter estimates from this 4-class parallel process GMM are shown in table 2, and fitted and observed trajectories by class are shown in figure 1. Entropy, a measure of classification accuracy was 0.78. As expected, the random effects for each of the trajectories were highly correlated; the correlation between the intercepts for MMSE and CDR-sb was 0.56, and the correlation between the two slopes was 0.91. Class 1 included the majority (72%) of the sample, and was characterized by modest, but steady progression throughout the period of observation. Class 2 included 8% of the sample, and was characterized by poor MMSE and CDR-sb scores at the outset and rapid progression. Class 3 included 11% of the sample and was characterized by little progression in the first 1–2 years, followed by a precipitous change. Class 4 included 8% of the sample, and like class 2, was characterized by steep changes throughout, though these individuals started out with better MMSE and CDR-sb scores. In post-hoc bias-corrected analyses, mean number of visits (3.9, 1.7, 2.5, and 3.4 for classes 1–4, respectively) varied significantly by class (χ2(3) = 73.3, p<0.001.
Table 2.
Parameter Estimates By Latent Trajectory Class
| Class 1 | Class 2 | Class 3 | Class 4 | ||
|---|---|---|---|---|---|
| Prevalence | 0.72 | 0.08 | 0.11 | 0.08 | |
| Baseline | MMSE | 23.350 (0.368)1 | 14.919 (0.820) | 19.098 (1.043) | 23.395 (1.361) |
| CDR2 | 24.838 (0.180) | 17.947 (0.708) | 25.289 (0.650) | 24.574 (0.672) | |
| Rate of decline3 | MMSE | −0.419 (0.259) | −6.234 (2.014) | 3.964 (0.984) | −6.595 (1.212) |
| CDR | −0.149 (0.137) | −6.853 (1.705) | 0.232 (0.742) | −4.194 (1.554) | |
| Change in rate of decline4 | MMSE | −0.198 (0.041) | 0.836 (0.994) | −2.511 (0.316) | 0.401 (0.130) |
| CDR | −0.178 (0.029) | 2.416 (0.636) | −1.040 (0.309) | 0.147 (0.243) |
Parameter estimate (SE)
CDR scores were reverse coded
Slope parameter
Quadratic, or “time squared” parameter
Figure 1.
Fitted and Observed MMSE and CDR-sb1 Trajectories By Class
1CDR-sb has been reverse coded, such that higher scores represent less progression.
Table 3 shows bias-corrected results from univariate logistic regressions of each predictor on membership in each latent class versus class 1 (slow progressors). Tables 3 and 4 shows log odds ratios, rather than odds ratios, in order to facilitate risk calculations. Older age at baseline was associated with greater odds of membership in class 3 (OR: 1.19; 95% CI: 0.99–1.42; p-value=0.059). Greater education was associated with decreased odds of membership in class 3 (OR: 0.73; 95% CI: 0.58–0.92; p-value=0.007). Longer duration of dementia (OR: 1.61; 95% CI: 1.22–2.12; p-value<0.001) and presence of psychosis (OR: 5.19; 95% CI: 2.09–12.85; p-value<0.001) were associated with greater odds of membership in class 2. Higher MMSE was associated with decreased odds of membership in class 2 (OR: 0.31; 95% CI: 0.2–0.47; p-value<0.001) and class 3 (OR: 0.39; 95% CI: 0.27–0.56; p-value=0.001). Better CDR was associated with decreased odds of membership in class 2 (OR=0.29; 95%CI: 0.18–0.47; p-value<0.001).
Table 3.
Parameter Estimates and AUC from Univariate Prediction of Latent Class Membership
| Class 21 | Class 31 | Class 41 | ||||
|---|---|---|---|---|---|---|
| Log Odds Ratio2 | AUC | Log Odds Ratio | AUC | Log Odds Ratio | AUC | |
| Age at Onset | 0.051 (0.048) | 0.57 | 0.171 (0.091) 0.059 | 0.63 | 0.037 (0.087) | 0.54 |
| Male | −0.010 (0.437) | 0.50 | −0.625 (0.924) | 0.54 | −1.606 (2.753) | 0.56 |
| Education | −0.168 (0.104) | 0.60 | −0.316 (0.116) 0.007 | 0.66 | 0.187 (0.136) | 0.57 |
| Dementia Duration | 0.474 (0.142) 0.001 | 0.68 | −0.432 (0.366) | 0.57 | −0.497 (0.296) 0.093 | 0.58 |
| APOE | −0.166 (0.442) | 0.52 | 0.342 (0.727) | 0.52 | −1.318 (2.003) | 0.55 |
| TIA | 0.086 (0.553) | 0.51 | 0.661 (0.790) | 0.53 | −0.459 (1.872) | 0.51 |
| HTN | −0.057 (0.427) | 0.51 | 0.538 (0.813) | 0.53 | 0.167 (1.095) | 0.51 |
| NPI Psychosis | 1.608 (0.465) 0.001 | 0.72 | 0.951 (0.847) | 0.52 | 1.272 (1.043) | 0.59 |
| NPI Depression | 0.665 (0.461) | 0.56 | 0.405 (0.864) | 0.51 | 2.316 (1.477) | 0.62 |
| NPI Apathy | 0.777 (0.475) | 0.57 | −1.322 (2.545) | 0.53 | −3.635 (30.897) | 0.53 |
| MMSE | −1.187 (0.219) <0.001 | 0.97 | −0.949 (0.189) <0.001 | 0.88 | 0.163 (0.181) | 0.56 |
| CDR-sb (reversed) | −1.488 (0.243) <0.001 | 0.99 | 0.363 (0.310) | 0.57 | −0.071 (0.107) | 0.54 |
Log odds ratios with Class 1 as the reference class.
Bias-Corrected Beta (SE) p-value; P-values are shown where p<0.10. Estimates can be translated to odds ratios by exponentiation; 95% confidences intervals for odds ratios can be obtained by constructing the interval for the log odds ratios and the exponentiating the upper and lower bounds.
Table 4.
Logs Odds Ratios from Multivariate Prediction of Class Membership
| Class 2 | Class 3 | Class 4 | |
|---|---|---|---|
| Intercept | −5.801 (1.169) <0.0011 | −4.304 (1.010) <0.001 | −4.572 (1.073) <0.001 |
| Age at Onset | −0.030 (0.069) | 0.110 (0.059) 0.063 | 0.009 (0.087) |
| Education | −0.166 (0.137) | −0.258 (0.120) 0.099 | 0.265 (0.139) 0.057 |
| NPI Psychosis | −0.225 (1.251) | −1.305 (1.473) | 1.957 (1.111) 0.078 |
| MMSE | −1.259 (0.366) 0.001 | −1.056 (0.375) 0.005 | 0.141 (0.174) |
Bias-Corrected Beta (SE) p-value; P-values shown where p<0.10. Estimates can be translated to odds ratios by exponentiation; 95% confidences intervals for odds ratios can be obtained by constructing the interval for the log odds ratios and then exponentiating the upper and lower bounds.
Table 4 shows bias-corrected parameter estimates from a multivariate logistic regression model with age at onset, education, NPI psychosis, and MMSE. CDR-sb was omitted due to colinearity; dementia duration was omitted because the model including dementia duration failed to converge. In the multivariate model, only MMSE was a statistically significant predictor of class membership. Higher MMSE scores were associated with decreased odds of membership in class 2 (OR: 0.28; 95% CI: 0.14–0.58; p-value=0.001), and in class 3 (OR: 0.35; 95% CI: 0.17–0.73; p-value<0.001). Figure 2 shows sequential ROC curves for successively large sets of predictors in the multivariate model. AUCs for the multivariate model were 0.98, 0.88, and 0.67, respectively, for classes 2 through 4 (with class 1 as the reference).
Figure 2.
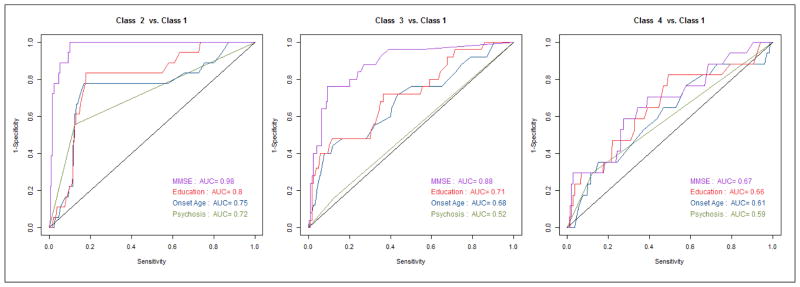
ROC Curves for Successive Sets of Predictors of Latent Class Membership
One can use the coefficients in table 4 to calculate the model-based log odds of class membership for an individual, and from that probability of membership in given class based on a set of baseline variables. For example, consider an individual with dementia onset at age 75, with 12 years of education, no NPI psychosis, and a baseline MMSE of 25. They would have a 99% chance of being a member of class 1, a 1% of being in class 4, and near-zero chances of being in classes 2 or 3. By contrast, that same individual, but with a baseline MMSE of 15, would have a 3% chance of being in class 1, an 80% chance of being in class 2, a 17% chance of being in class 3, and a near-zero chance of being in class 4. A spreadsheet to perform these calculations is available from the first author on request.
Discussion
Growth mixture modeling has been used to model cognitive decline among older adults (Small and Backman, 2007; Leoutsakos et al., 2012a), but to our knowledge this is its first application in incident AD. We demonstrated substantial heterogeneity in course in both cognition and function. It is noteworthy that the majority of people with incident AD belonged to a class characterized by relatively slow progression (0.62, 1.63, and 7.05 expected loss of MMSE points, and 0.33, 1.01, and 5.20 expected CDR-sb points, respectively, at 1, 2, and 5 years). In previously published analyses from DPS, random effects models fit across all participants yielded expected MMSE and CDR-sb losses at 5 years of 8.8 and 6.5, respectively (Tschanz et al., 2011). To paraphrase Stephen Jay Gould, the mean is not the message (Gould, 1985), since most individuals actually declined considerably less.
The progression observed in DPS, even as a whole, is much slower than is typically reported in clinical based samples. For example, a meta-analysis of research clinic samples reported a pooled mean annual rate of loss on the MMSE of 3.3 points (Han et al., 2000). The Kungsholmen project reported mean annual MMSE losses of 2.75 (first three years) and 3.03 (3–7 years). Given that the rate of progression in AD varies over the course of the disease (Camicioli and Kryscio, 2005), it may be better to move away from discussions of annual rates of change (e.g. slopes), and towards predictions of expected loss at set intervals (1,2, and 5 years, for example). This more flexible convention would allow for the communication of the meaning behind non-linear terms, such as quadratic terms, that are now being used more frequently.
We found that it was possible, using a set of baseline predictors, to classify individuals with good accuracy (AUCs ranging from 0.74 to 0.99). Predictably, baseline MMSE and CDR-sb were the most potent predictors. Though baseline total NPI score was not predictive of decline when the sample was analyzed together (Tschanz et al., 2011), presence of psychosis as measured by the NPI delusions and hallucinations domains was predictive of membership in class 2 (a class characterized by steep declines) in univariate models. Canavelli and colleagues looked at clusters of NPI symptoms as predictors of decline in the large ICTUS sample, and found no relationship between these clusters and rate of decline (Canevelli et al., 2013). Presence of neuropsychiatric symptoms has been shown to be predictive of conversion to dementia among those with MCI (Chan et al., 2011; Peters et al., 2013). Male sex was not predictive of class membership in our analyses. This finding is not consistent with other reports that females with AD decline more rapidly (Aguero-Torres et al., 1998; Tschanz et al., 2011). Education was associated with increased odds of membership in class 3 in the univariate analysis; this is consistent with other reports (Stern et al., 1999; Andel et al., 2006; Scarmeas et al., 2006).
We are not aware of any published risk calculators for rate of decline in AD, but a function to predict mortality using data from the PAQUID study has been developed. It uses age at diagnosis, sex, and number of impaired ADLs at baseline, and had an AUC of 0.75. Neither subjective health nor education were predictive in their model (Delva et al., 2013).
There are a number of limitations to our findings which should be noted. First, the use of single, relatively crude measures of cognition (MMSE) and functional decline (CDR-sb) may not have fully captured the nature of participants’ declines. Though population-based, the sample is from a single county in northern Utah whose residents are almost universally of northern or western European descent, who are almost all members of the Church of Jesus Christ of Latter Day Saints. Findings from DPS may not generalize to other populations.
The use of growth mixture modeling, while novel, increases the complexity of the analysis by estimating model parameters for each latent class. Joint modeling of functional and cognitive decline adds a second layer of complexity. This complexity is the likely cause of the convergence failure we experienced for the multivariate model that included dementia duration. Further, because the classes are latent, it is impossible to know with certainty of what class an individual is a member. By modeling predictors of class membership rather than trajectories themselves, our findings are not directly comparable with findings from other observational studies which look at modifiers of a single mean trajectory across all individuals.
The strengths of the study include the population-based sample which includes individuals observed prior to the onset of dementia and throughout the course of their illness. The use of growth mixture modeling is novel and allows for characterization of heterogeneity in dementia course. Jointly modeling both cognition and function acknowledges the inter-relatedness of these two domains.
In conclusion, we demonstrated that heterogeneity in AD course can be modeled as classes of trajectory types, and that most individuals in our sample were members of a class with rates of decline which were less precipitous than the overall mean trajectory previously reported from the DPS study. Subjects could be accurately classified using baseline variables. Few (if any) population-based longitudinal studies of AD are comparable to DPS, making replication of our findings difficult, though such replication is essential. If similar patterns of decline and predictors of those patterns are reported using independent samples, it will be important to use this information to revise current projections of the global burden of AD (Brookmeyer et al., 2007). We note that comparison of predictors of class membership across samples would only be possible if the latent classes of decline themselves were similar. Finally, further study of predictors of class membership could shed light on the underlying neuropathological processes of AD.
Key Points.
There is significant variability in rate of progression both within and between individuals over the course of AD.
We use growth mixture modelling to identify 4 latent classes of progression trajectories
The majority of the cohort were members of a class characterized by slow progression
Predictors of course include age, education, presence of psychosis at baseline, and MMSE and CDR-sb scores at baseline.
Acknowledgments
This work was supported by NIH grants: R01AG21136, R01AG11380, and R01AG18712. The study sponsor had to role in study design, collection, data analysis, report writing, or publication decisions.
References
- Aerssens J, Raeymaekers P, Lilienfeld S, Geerts H, Konings F, Parys W. APOE genotype: no influence on galantamine treatment efficacy nor on rate of decline in Alzheimer’s disease. Dement Geriatr Cogn Disord. 2001;12:69–77. doi: 10.1159/000051238. 51238. [DOI] [PubMed] [Google Scholar]
- Aguero-Torres H, Fratiglioni L, Winblad B. Natural history of Alzheimer’s disease and other dementias: review of the literature in the light of the findings from the Kungsholmen Project. Int J Geriatr Psychiatry. 1998;13:755–66. doi: 10.1002/(sici)1099-1166(1998110)13:11<755::aid-gps862>3.0.co;2-y. [DOI] [PubMed] [Google Scholar]
- Aguero-Torres H, Fratiglioni L, Guo Z, Viitanen M, Winblad B. Prognostic factors in very old demented adults: a seven-year follow-up from a population-based survey in Stockholm. J Am Geriatr Soc. 1998;46:444–452. doi: 10.1111/j.1532-5415.1998.tb02464.x. [DOI] [PubMed] [Google Scholar]
- Alzheimer’s Association. Thies W, Bleiler L. 2011 Alzheimer’s disease facts and figures. Alzheimers Dement. 2011;7:208–244. doi: 10.1016/j.jalz.2011.02.004. [DOI] [PubMed] [Google Scholar]
- American Psychiatric Association. Diagnostic and Statistical Manual of Mental Disorders, DSM-III-R. Washington, D.C: 1987. [Google Scholar]
- Andel R, Vigen C, Mack WJ, Clark LJ, Gatz M. The effect of education and occupational complexity on rate of cognitive decline in Alzheimer’s patients. J Int Neuropsychol Soc. 2006;12:147–152. doi: 10.1017/S1355617706060206. [DOI] [PubMed] [Google Scholar]
- Asparouhov T, Muthen B. Auxiliary Variables in in Mixture Modeling: 3-Step Approaches Using Mplus. MPLUS Web Notes. 2013;15 [Google Scholar]
- Atchison TB, Massman PJ, Doody RS. Baseline cognitive function predicts rate of decline in basic-care abilities of individuals with dementia of the Alzheimer’s type. Arch Clin Neuropsychol. 2007;22:99–107. doi: 10.1016/j.acn.2006.11.006. [DOI] [PubMed] [Google Scholar]
- Boksay I, Boksay E, Reisberg B, Torossian C, Krishnamurthy M. Alzheimer’s disease and medical disease conditions: a prospective cohort study. J Am Geriatr Soc. 2005;53:2235–6. doi: 10.1111/j.1532-5415.2005.00512_4.x. [DOI] [PubMed] [Google Scholar]
- Bolck A, Croon MA, Hagenaars JA. Estimating latent structure models with categorical variables: One-step versus three-step estimators. Political Analysis. 2004;12:3-3-27. [Google Scholar]
- Breitner JC, Wyse BW, Anthony JC, Welsh-Bohmer KA, Steffens DC, Norton MC, Tschanz JT, Plassman BL, Meyer MR, Skoog I, Khachaturian A. APOE-epsilon4 count predicts age when prevalence of AD increases, then declines: the Cache County Study. Neurology. 1999;53:321–31. doi: 10.1212/wnl.53.2.321. [DOI] [PubMed] [Google Scholar]
- Brookmeyer R, Johnson E, Ziegler-Graham K, Arrighi HM. Forecasting the global burden of Alzheimer’s disease. Alzheimers Dement. 2007;3:186–191. doi: 10.1016/j.jalz.2007.04.381. [DOI] [PubMed] [Google Scholar]
- Camicioli R, Kryscio R. Nature throws curveballs: APOE and nonlinear decline in Alzheimer disease. Neurology. 2005;65:1855–1856. doi: 10.1212/01.wnl.0000195338.67756.4b. [DOI] [PubMed] [Google Scholar]
- Canevelli M, Adali N, Cantet C, Andrieu S, Bruno G, Cesari M, Vellas B The ICTUS/DSA Group. Impact of behavioral subsyndromes on cognitive decline in Alzheimer’s disease: data from the ICTUS study. J Neurol. 2013 doi: 10.1007/s00415-013-6893-3. [DOI] [PubMed] [Google Scholar]
- Chan WC, Lam LC, Tam CW, Lui VW, Leung GT, Lee AT, Chan SS, Fung AW, Chiu HF, Chan WM. Neuropsychiatric symptoms are associated with increased risks of progression to dementia: a 2-year prospective study of 321 Chinese older persons with mild cognitive impairment. Age Ageing. 2011;40:30–35. doi: 10.1093/ageing/afq151. [DOI] [PubMed] [Google Scholar]
- Cortes F, Nourhashemi F, Guerin O, Cantet C, Gillette-Guyonnet S, Andrieu S, Ousset PJ, Vellas B. Prognosis of Alzheimer’s disease today: a two-year prospective study in 686 patients from the REAL-FR Study. Alzheimers Dement. 2008;4:22–9. doi: 10.1016/j.jalz.2007.10.018. [DOI] [PubMed] [Google Scholar]
- Cummings JL, Mega M, Gray K, Rosenberg-Thompson S, Carusi DA, Gornbein J. The Neuropsychiatric Inventory: comprehensive assessment of psychopathology in dementia. Neurology. 1994;44:2308–2314. doi: 10.1212/wnl.44.12.2308. [DOI] [PubMed] [Google Scholar]
- Dal Forno G, Rasmusson DX, Brandt J, Carson KA, Brookmeyer R, Troncoso J, Kawas CH. Apolipoprotein E genotype and rate of decline in probable Alzheimer’s disease. Arch Neurol. 1996;53:345–350. doi: 10.1001/archneur.1996.00550040085017. [DOI] [PubMed] [Google Scholar]
- Delva F, Pimouguet C, Helmer C, Peres K, Brechat B, Le Goff M, Jacqmin-Gadda H, Amieva H, Orgogozo JM, Auriacombe S, Berr C, Tzourio C, Barberger-Gateau P, Dartigues JF. A Simple Score to Predict Survival with Dementia in the General Population. Neuroepidemiology. 2013;41:20–28. doi: 10.1159/000346497. [DOI] [PubMed] [Google Scholar]
- Doraiswamy PM, Leon J, Cummings JL, Marin D, Neumann PJ. Prevalence and impact of medical comorbidity in Alzheimer’s disease. J Gerontol A Biol Sci Med Sci. 2002;57:M173–7. doi: 10.1093/gerona/57.3.m173. [DOI] [PubMed] [Google Scholar]
- Folstein MF, Folstein SE, McHugh PR. “Mini-mental state”. A practical method for grading the cognitive state of patients for the clinician. J Psychiatr Res. 1975;12:189–98. doi: 10.1016/0022-3956(75)90026-6. [DOI] [PubMed] [Google Scholar]
- Gould SJ. The Median isn’t the Message. Discover. 1985;6:40. [Google Scholar]
- Gross AL, Rebok GW. Memory training and strategy use in older adults: results from the ACTIVE study. Psychol Aging. 2011;26:503–517. doi: 10.1037/a0022687. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Growdon JH, Locascio JJ, Corkin S, Gomez-Isla T, Hyman BT. Apolipoprotein E genotype does not influence rates of cognitive decline in Alzheimer’s disease. Neurology. 1996;47:444–448. doi: 10.1212/wnl.47.2.444. [DOI] [PubMed] [Google Scholar]
- Han L, Cole M, Bellavance F, McCusker J, Primeau F. Tracking cognitive decline in Alzheimer’s disease using the mini-mental state examination: a meta-analysis. Int Psychogeriatr. 2000;12:231–247. doi: 10.1017/s1041610200006359. [DOI] [PubMed] [Google Scholar]
- Hughes CP, Berg L, Danziger WL, Coben LA, Martin RL. A new clinical scale for the staging of dementia. Br J Psychiatry. 1982;140:566–72. doi: 10.1192/bjp.140.6.566. [DOI] [PubMed] [Google Scholar]
- Jacobs D, Sano M, Marder K, Bell K, Bylsma F, Lafleche G, Albert M, Brandt J, Stern Y. Age at onset of Alzheimer’s disease: relation to pattern of cognitive dysfunction and rate of decline. Neurology. 1994;44:1215–1220. doi: 10.1212/wnl.44.7.1215. [DOI] [PubMed] [Google Scholar]
- Jung T, Wickrama KAS. An Introduction to Latent Class Growth Analysis and Growth Mixture Modeling. Social and Personality Psychology Compass. 2008 doi: 10.1111/j.1751-9004.2007.00054.x. [DOI] [Google Scholar]
- Kawas C, Segal J, Stewart WF, Corrada M, Thal LJ. A validation study of the Dementia Questionnaire. Arch Neurol. 1994;51:901–6. doi: 10.1001/archneur.1994.00540210073015. [DOI] [PubMed] [Google Scholar]
- Leoutsakos JM, Muthen BO, Breitner JC, Lyketsos CG ADAPT Research Team. Effects of non-steroidal anti-inflammatory drug treatments on cognitive decline vary by phase of pre-clinical Alzheimer disease: findings from the randomized controlled Alzheimer’s Disease Anti-inflammatory Prevention Trial. Int J Geriatr Psychiatry. 2012a;27:364–374. doi: 10.1002/gps.2723. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Leoutsakos JM, Han D, Mielke MM, Forrester SN, Tschanz JT, Corcoran CD, Green RC, Norton MC, Welsh-Bohmer KA, Lyketsos CG. Effects of general medical health on Alzheimer’s progression: the Cache County Dementia Progression Study. Int Psychogeriatr. 2012b;24:1561–1570. doi: 10.1017/S104161021200049X. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lyketsos CG, Steinberg M, Tschanz JT, Norton MC, Steffens DC, Breitner JC. Mental and behavioral disturbances in dementia: findings from the Cache County Study on Memory in Aging. The American journal of psychiatry. 2000;157:708–14. doi: 10.1176/appi.ajp.157.5.708. [DOI] [PubMed] [Google Scholar]
- Lyketsos CG, Galik E, Steele C, Steinberg M, Rosenblatt A, Warren A, Sheppard JM, Baker A, Brandt J. The General Medical Health Rating: a bedside global rating of medical comorbidity in patients with dementia. J Am Geriatr Soc. 1999;47:487–91. doi: 10.1111/j.1532-5415.1999.tb07245.x. [DOI] [PubMed] [Google Scholar]
- Martins CA, Oulhaj A, de Jager CA, Williams JH. APOE alleles predict the rate of cognitive decline in Alzheimer disease: a nonlinear model. Neurology. 2005;65:1888–1893. doi: 10.1212/01.wnl.0000188871.74093.12. [DOI] [PubMed] [Google Scholar]
- McKhann G, Drachman D, Folstein M, Katzman R, Price D, Stadlan EM. Clinical diagnosis of Alzheimer’s disease: report of the NINCDS-ADRDA Work Group under the auspices of Department of Health and Human Services Task Force on Alzheimer’s Disease. Neurology. 1984;34:939–44. doi: 10.1212/wnl.34.7.939. [DOI] [PubMed] [Google Scholar]
- Mielke MM, Rosenberg PB, Tschanz J, Cook L, Corcoran C, Hayden KM, Norton M, Rabins PV, Green RC, Welsh-Bohmer KA, Breitner JC, Munger R, Lyketsos CG. Vascular factors predict rate of progression in Alzheimer disease. Neurology. 2007;69:1850–1858. doi: 10.1212/01.wnl.0000279520.59792.fe. [DOI] [PubMed] [Google Scholar]
- Miller TP, Tinklenberg JR, Brooks JO, 3rd, Fenn HH, Yesavage JA. Selected psychiatric symptoms associated with rate of cognitive decline in patients with Alzheimer’s disease. J Geriatr Psychiatry Neurol. 1993;6:235–238. doi: 10.1177/089198879300600410. [DOI] [PubMed] [Google Scholar]
- Murphy GM, Jr, Taylor J, Kraemer HC, Yesavage J, Tinklenberg JR. No association between apolipoprotein E epsilon 4 allele and rate of decline in Alzheimer’s disease. Am J Psychiatry. 1997;154:603–608. doi: 10.1176/ajp.154.5.603. [DOI] [PubMed] [Google Scholar]
- Muthen B, Muthen L. Mplus User’s Guide. Muthen & Muthen; Losa Angeles, CA: 1998–2007. [Google Scholar]
- Muthen B, Muthen LK. Integrating person-centered and variable-centered analyses: growth mixture modeling with latent trajectory classes. Alcohol Clin Exp Res. 2000;24:882–891. [PubMed] [Google Scholar]
- Nylund KL, Asparouhov T, Muthen BO. Deciding on the Number of Classes in Latent Class Analysis and Growth Mixture Modeling: A Monte Carlo Simulation Study. Structural Equation Modeling: A Multidisciplinary Journal 2007 [Google Scholar]
- Obuchowski NA. Receiver operating characteristic curves and their use in radiology. Radiology. 2003;229:3–8. doi: 10.1148/radiol.2291010898. [DOI] [PubMed] [Google Scholar]
- Peters ME, Rosenberg PB, Steinberg M, Norton MC, Welsh-Bohmer KA, Hayden KM, Breitner J, Tschanz JT, Lyketsos CG Cache County Investigators. Neuropsychiatric Symptoms as Risk Factors for Progression From CIND to Dementia: The Cache County Study. Am J Geriatr Psychiatry. 2013 doi: 10.1016/j.jagp.2013.01.049. [DOI] [PMC free article] [PubMed] [Google Scholar]
- R Development Core Team. R Foundation for Statistical Computing. 2008. R: A language and environment for statistical computing. [Google Scholar]
- Regan C, Katona C, Walker Z, Hooper J, Donovan J, Livingston G. Relationship of vascular risk to the progression of Alzheimer disease. Neurology. 2006;67:1357–1362. doi: 10.1212/01.wnl.0000240129.46080.53. [DOI] [PubMed] [Google Scholar]
- Scarmeas N, Albert SM, Manly JJ, Stern Y. Education and rates of cognitive decline in incident Alzheimer’s disease. J Neurol Neurosurg Psychiatry. 2006;77:308–316. doi: 10.1136/jnnp.2005.072306. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Small BJ, Backman L. Longitudinal trajectories of cognitive change in preclinical Alzheimer’s disease: a growth mixture modeling analysis. Cortex. 2007;43:826–834. doi: 10.1016/s0010-9452(08)70682-8. [DOI] [PubMed] [Google Scholar]
- Stern Y, Albert S, Tang MX, Tsai WY. Rate of memory decline in AD is related to education and occupation: cognitive reserve? Neurology. 1999;53:1942–1947. doi: 10.1212/wnl.53.9.1942. [DOI] [PubMed] [Google Scholar]
- Teng EL, Chui HC. The Modified Mini-Mental State (3MS) examination. J Clin Psychiatry. 1987;48:314–8. [PubMed] [Google Scholar]
- Tschanz JT, Welsh-Bohmer KA, Skoog I, West N, Norton MC, Wyse BW, Nickles R, Breitner JC. Dementia diagnoses from clinical and neuropsychological data compared: the Cache County study. Neurology. 2000;54:1290–6. doi: 10.1212/wnl.54.6.1290. [DOI] [PubMed] [Google Scholar]
- Tschanz JT, Corcoran CD, Schwartz S, Treiber K, Green RC, Norton MC, Mielke MM, Piercy K, Steinberg M, Rabins PV, Leoutsakos JM, Welsh-Bohmer KA, Breitner JC, Lyketsos CG. Progression of cognitive, functional, and neuropsychiatric symptom domains in a population cohort with Alzheimer dementia: the Cache County Dementia Progression study. Am J Geriatr Psychiatry. 2011;19:532–542. doi: 10.1097/JGP.0b013e3181faec23. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wild KV, Kaye JA. The rate of progression of Alzheimer’s disease in the later stages: evidence from the Severe Impairment Battery. J Int Neuropsychol Soc. 1998;4:512–516. doi: 10.1017/s1355617798005104. [DOI] [PubMed] [Google Scholar]
- Wilson RS, Gilley DW, Bennett DA, Beckett LA, Evans DA. Person-specific paths of cognitive decline in Alzheimer’s disease and their relation to age. Psychol Aging. 2000a;15:18–28. doi: 10.1037//0882-7974.15.1.18. [DOI] [PubMed] [Google Scholar]
- Wilson RS, Gilley DW, Bennett DA, Beckett LA, Evans DA. Hallucinations, delusions, and cognitive decline in Alzheimer’s disease. J Neurol Neurosurg Psychiatry. 2000b;69:172–177. doi: 10.1136/jnnp.69.2.172. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wilson RS, Li Y, Aggarwal NT, Barnes LL, McCann JJ, Gilley DW, Evans DA. Education and the course of cognitive decline in Alzheimer disease. Neurology. 2004;63:1198–1202. doi: 10.1212/01.wnl.0000140488.65299.53. [DOI] [PubMed] [Google Scholar]
- Wilson RS, Barnes LL, Mendes de Leon CF, Aggarwal NT, Schneider JS, Bach J, Pilat J, Beckett LA, Arnold SE, Evans DA, Bennett DA. Depressive symptoms, cognitive decline, and risk of AD in older persons. Neurology. 2002;59:364–370. doi: 10.1212/wnl.59.3.364. [DOI] [PubMed] [Google Scholar]
- Wimo A, Winblad B, Jonsson L. The worldwide societal costs of dementia: Estimates for 2009. Alzheimers Dement. 2010;6:98–103. doi: 10.1016/j.jalz.2010.01.010. [DOI] [PubMed] [Google Scholar]
- Xie SX, Ewbank DC, Chittams J, Karlawish JH, Arnold SE, Clark CM. Rate of decline in Alzheimer disease measured by a Dementia Severity Rating Scale. Alzheimer Dis Assoc Disord. 2009;23:268–274. doi: 10.1097/WAD.0b013e318194a324. [DOI] [PMC free article] [PubMed] [Google Scholar]