The importance of mechanisms for the evolution of cooperation

Abstract

Studies aimed at explaining the evolution of phenotypic traits have often solely focused on fitness considerations, ignoring underlying mechanisms. In recent years, there has been an increasing call for integrating mechanistic perspectives in evolutionary considerations, but it is not clear whether and how mechanisms affect the course and outcome of evolution. To study this, we compare four mechanistic implementations of two well-studied models for the evolution of cooperation, the Iterated Prisoner's Dilemma (IPD) game and the Iterated Snowdrift (ISD) game. Behavioural strategies are either implemented by a 1 : 1 genotype–phenotype mapping or by a simple neural network. Moreover, we consider two different scenarios for the effect of mutations. The same set of strategies is feasible in all four implementations, but the probability that a given strategy arises owing to mutation is largely dependent on the behavioural and genetic architecture. Our individual-based simulations show that this has major implications for the evolutionary outcome. In the ISD, different evolutionarily stable strategies are predominant in the four implementations, while in the IPD each implementation creates a characteristic dynamical pattern. As a consequence, the evolved average level of cooperation is also strongly dependent on the underlying mechanism. We argue that our findings are of general relevance for the evolution of social behaviour, pleading for the integration of a mechanistic perspective in models of social evolution.

1. Introduction

There is a long tradition in biology of separating proximate and ultimate perspectives when explaining phenotypic variation [1,2]. The proximate perspective is concerned with the mechanisms that directly cause the phenotype (such as neurological and physiological processes), whereas the ultimate perspective is concerned with the emergence of the phenotype through (adaptive) evolution. In concordance with this traditional separation, knowledge about the specific mechanisms underlying phenotypes has long been regarded as inconsequential to the question of how phenotypes are shaped by evolution. Accordingly, evolutionary biologists have a strong focus on the fitness consequences of phenotypic traits, thereby largely disregarding the underlying mechanisms. Conceptualization of evolution is often based on the implicit assumptions that genes interact in a simple way and that there is a one-to-one relationship between genotypes and phenotypes. These assumptions are convenient, as they allow a view of selection as a process directly acting on the genes in the ‘gene pool’ of a population. Although this view has already been criticized as ‘beanbag genetics' more than 50 years ago [3], theoretical approaches to explaining the evolution of phenotypes with an explicit focus on mechanisms are not very prominent even today.

Verbal discussions of the importance of underlying mechanisms for the dynamics and outcomes of evolutionary processes started to emerge in the literature in the 1980s [4]. In particular, the influential book of John Maynard Smith and Eörs Szathmáry on the ‘Major Transitions in Evolution’ [5] clearly showed how crucial genetic and phenotypic architecture are for the course of evolution. This view is now firmly established in the field of ‘evo-devo’ [6,7], where the interplay between (developmental) mechanisms and evolution is at centre stage. Similarly, studies on gene-regulatory networks [8–10] have revealed that network topology strongly affects both the robustness and evolvability of living systems, while recent ‘integrative’ models [11–13] reveal that the mechanisms underlying phenotypic responses can be important for a full understanding of eco-evolutionary processes.

In line with these general developments, there are now strong pleas [14–16] to apply ‘mechanistic thinking’ in evolutionary studies of animal and human behaviour as well. Yet, with some notable exceptions [17–22], models for the evolution of behaviour still tend to make the ‘least constraining’ assumptions on the genetic basis and the physiological and psychological processes underlying behaviour. When the direction and intensity of selection do not change in time and when there is a single optimal behaviour, this may not be problematic. In such a case, one would expect evolution to proceed towards the single optimum, regardless of underlying mechanisms. However, whenever there are multiple equilibria, the situation is no longer so straightforward. And even in relatively simple social contexts, the existence of multiple equilibria is the rule rather than the exception [23–25]. In other words, the question is not that much ‘which strategy is favoured by natural selection’ but rather ‘which equilibrium will be achieved in the course of evolution’ [26–28]. It is conceivable that, in such a context, the mechanisms underlying behaviour may be of evolutionary importance, because mechanisms can affect the probabilities with which phenotypes arise and, hence, the likelihood of alternative evolutionary trajectories.

Here, we study the evolution of behavioural strategies in two types of social interaction without clearly delineated optimal behaviour. Our question is whether, and to what extent, the mechanistic implementation of the available strategies affects the course and outcome of evolution. We consider two prototype models for the evolution of cooperation: the Iterated Prisoner's Dilemma (IPD) game and the Iterated Snowdrift (ISD) game, which have been the subject of hundreds of earlier studies (IPD [24,29–34], ISD [33–37]). In both games, the players have to decide (repeatedly) on whether to cooperate or to defect. For both players, mutual cooperation is more profitable than mutual defection. However, mutual cooperation is not easy to achieve, as defection yields a higher pay-off than cooperation if the other player cooperates. The games differ in their assumption on whether defect (IPD) or cooperate (ISD) yields a higher pay-off against a defector. Following the traditions of evolutionary game theory ([28,38–45], but see [46]), studies of the evolution of strategies in these games have overwhelmingly assumed a one-to-one relationship between genotypes and strategies. Here, we contrast such a one-to-one implementation with a different implementation where selection does not directly act on strategies, but on the architecture (a simple neural network) underlying these strategies. In addition, we consider two genetic mechanisms that determine the probabilities with which the mutation of each strategy yields any other strategy. We will show that the evolutionary dynamics are strongly affected by both the genetic and the behavioural architecture and discuss how the different outcomes can be explained on the basis of the mutational distributions arising from the interplay between genetics and behavioural mechanisms.

2. The model

(a). Games and strategies

Throughout, we will consider a Prisoner's Dilemma (PD) game and a Snowdrift game (SD) with the following pay-off matrices:

The top and bottom rows give the pay-offs of cooperation and defection, respectively, both for when the opponent cooperates (first column) and defects (second column). In the PD, defection always yields a higher pay-off than cooperation, regardless of the action of the opponent. In the one-shot version of this game, mutual defection is therefore the only evolutionarily stable strategy (ESS). In the SD, the highest pay-off is always attained by choosing the opposite action than the opponent. In this case, the one-shot game has an ESS that is characterized by a mixture of cooperation and defection.

We consider iterated versions of both games, for which the determination of all ESSs is much less straightforward than for their one-shot counterparts (see the electronic supplementary material for a game-theoretical analysis). In our simulations, agents repeatedly interact for an indefinite period of rounds; after each round, the game is terminated with probability 1−m. The full strategy space of the iterated game is infinite-dimensional [30]. Here, we confine the strategy space by only allowing individuals to condition their behaviour on the outcome of the previous interaction round. As there are four possible interaction outcomes (mutual cooperation, mutual defection, and both combinations of cooperation and defection), and a strategy always prescribes one of two possible actions for each outcome (cooperation or defection), there are in total 2⁴ = 16 possible strategies (see table 1 for a complete list). We assume that individuals are not perfect; they make both perception errors (with probability ɛ_P, they misinterpret the behaviour of their opponent as the opposite behaviour) and implementation errors (with probability ɛ_I, they perform the opposite behaviour than dictated by their strategy).

Table 1.

An overview of all possible pure strategies that condition their behaviour on the previous interaction. (The four columns on the left show whether the strategy cooperates (1) or defects (0), for each of the four possible outcomes of the previous interaction (from left to right: mutual cooperation, having cooperated while the opponent defected, having defected while the opponent cooperated, and mutual defection). The column on the right shows the name of the strategy that is used to refer to them in the main text. The two middle columns show the percentage of the genotype space that is associated with each strategy for the two different behavioural architectures. These percentages were obtained by generating a large number of genotypes (in the same way as generating a genotype through ‘entire-genome mutation’), and subsequently determining the strategy induced by each genotype (as explained in the electronic supplementary material).)

behaviour				percentage of genotype space
CC	CD	DC	DD	1 : 1 mapping	neural network	strategy name	strategy description
0	0	0	0	6.25	40.35	ALLD	always defects
0	0	0	1	6.25	1.79	desperate	only cooperates after mutual defection
0	0	1	0	6.25	1.75	Acon-D	anti-conventional, shifts after playing opposite of opponent, otherwise defects
0	0	1	1	6.25	1.65	inconsistent	plays opposite of previous move
0	1	0	0	6.25	1.75	con-D	conventional, stays after playing the opposite of opponent, otherwise defects
0	1	0	1	6.25	1.65	ATFT	anti-tit for tat, plays opposite of opponent's last move
0	1	1	0	6.25	0.08	APavlov	win, shift; lose, stay
0	1	1	1	6.25	0.98	hopeless	only defects after mutual cooperation
1	0	0	0	6.25	0.98	grim	only cooperates after mutual cooperation
1	0	0	1	6.25	0.08	Pavlov	win, stay; lose, shift
1	0	1	0	6.25	1.65	TFT	tit for tat, copies opponent's last move
1	0	1	1	6.25	1.75	MNG	Mr Nice Guy, only defects after ‘being cheated’ (playing C while other plays D)
1	1	0	0	6.25	1.65	consistent	repeats its own previous move
1	1	0	1	6.25	1.75	con-C	conventional, stays after playing the opposite of opponent, otherwise cooperates
1	1	1	0	6.25	1.79	willing	only defects after mutual defection
1	1	1	1	6.25	40.35	ALLC	always cooperates

(b). Behavioural and genetic architecture

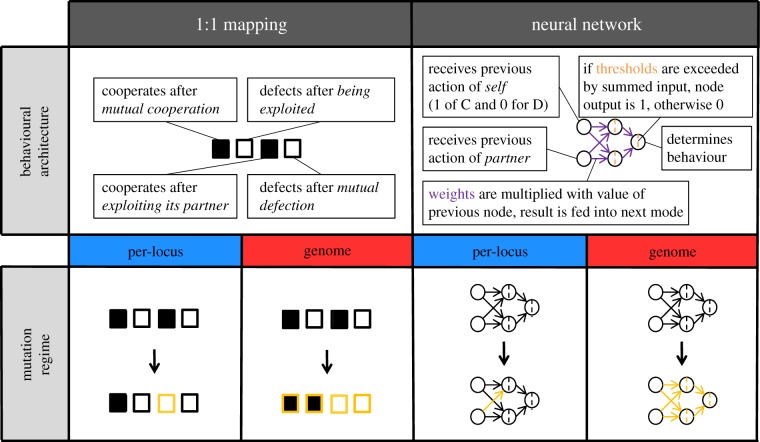
Figure 1 shows a schematic of the behavioural and genetic architectures considered in this study. We consider a ‘1 : 1’ behavioural architecture and an artificial neural network (ANN) architecture, which can both realize the 16 possible strategies presented in table 1. The 1 : 1 architecture is the simplest possible architecture, in which behaviour for each of the four possible outcomes of the previous round is under the direct control of a single gene locus. Each of these four loci can only have two values: 1 (for cooperation) or 0 (for defection). In addition, a separate locus determines an individual's behaviour in the first round; this locus can take on any value of the unit interval, which corresponds to the probability of cooperation in the first round.

Figure 1.

A schematic of the four implementations of the 16 strategies considered in this study. The top row shows illustrations of the two behavioural architectures. In the 1 : 1 architecture, individuals have four gene loci that each determine the behaviour (cooperate or defect) in a given round for one of the four possible outcomes of the previous round. These four loci are represented by boxes (in the example shown, black boxes represent cooperation and white boxes represent defection). In the neural network architecture, individuals have nine loci, determining the (continuous) values of six connection weights (purple) and three thresholds (orange). The network processes the input (the behaviour of ‘self’ or ‘partner’ in the previous round) into an output (cooperate or defect). In the bottom row, the two mutation regimes are illustrated for both behavioural architectures, representing the four implementations considered in this study. Under per-locus mutation, each locus mutates independently (illustrated by single loci turning yellow after the arrow). In case of whole-genome mutation, all loci mutate in the event of a mutation (illustrated by all loci turning yellow after the arrow).

In the neural network architecture ([47]; see figure 1 for a graphical representation; and see the electronic supplementary material for a more detailed explanation), behaviour is determined through a very simple underlying structure that translates an input (the behaviours of ‘self’ and ‘partner’ in the previous interaction round) into an output (cooperation or defection). There are two input nodes, one of which receives the previous own behaviour (0 for defection, 1 for cooperation), and the other receives the previous behaviour of the opponent. The input from both these nodes is fed into two ‘hidden layer’ nodes, multiplied by the weights of the connections between the nodes. Each hidden layer node has a threshold; if the summed input into a hidden layer node exceeds its threshold, its output equals 1, otherwise the output is 0. Both hidden layer nodes are connected to the output node, which also has a threshold. If the total output from the hidden nodes (multiplied with the relevant connection weights) exceeds this threshold, the individual cooperates. If not, the individual defects. This way, six connection weights and three thresholds determine the strategy implemented by the network. Accordingly, the ANN is encoded by nine gene loci (that can take on any real value): one for each connection weight and one for each threshold. In addition, a tenth locus determines an individual's behaviour in the first round (as in the 1 : 1 implementation).

Even under the highly simplifying assumptions on the strategy set and their underlying architectures, there are many ways to implement inheritance. For example, ploidy level and linkage patterns are of considerable importance for the genetic transmission of information on strategies in sexually reproducing organisms. To keep matters as simple as possible, we here only consider asexual populations of haploid individuals. In order to study the effect of genetic factors, we restrict attention to two different mutation regimes. In both regimes, the gene locus determining the behaviour in the first round mutates independently (with probability μ_F), the mutational step size being drawn from a normal distribution with mean 0 and standard deviation σ_F. Under ‘per-locus mutation’, each of the other loci (four loci in case of the 1 : 1 architecture and nine in case of the ANN architecture) has a probability μ_L of giving rise to a mutation, independently of what is happening at the other loci. Under ‘entire-genome mutation’, a mutation event (occurring with probability μ_G) affects all these loci, that is, all these loci mutate at the same time. Under both mutation regimes, mutation is implemented as drawing a random number to replace the current value of the locus (in the 1 : 1 architecture, this is done by drawing 0 or 1 with equal probability; in the neural network architecture, by drawing a number from a normal distribution with mean 0 and standard deviation σ_N).

(c). Simulation set-up and parameters

We simulated a population of 1000 asexual haploid individuals, with discrete and non-overlapping generations. At the start of each generation, pairs of two individuals are formed at random. These pairs interact repeatedly, where a new round always starts with probability m = 0.99 (leading to an average interaction length of 100 rounds). In any given generation, all pairs play the same number of rounds. After the last round of each repeated interaction, individuals reproduce. The probability of reproducing is directly proportional to the pay-off individuals accumulate over the entire repeated interaction. Population size was kept constant. After reproduction, a new cycle starts.

At the beginning of each simulation, the loci of all individuals were initialized at random: initial values for the locus that determines the behaviour in the first round were drawn from a normal distribution with mean 0.5 and standard deviation 0.1; the four binary loci in the 1 : 1 architecture were assigned a 0 or a 1 with equal probability; and the nine loci encoding the connection weights and thresholds in the neural network architecture were assigned values that were drawn from a normal distribution with mean 0 and standard deviation σ_N. Each simulation was run for 100 000 generations. We ran 100 replicate simulations for all four combinations of the two behavioural architectures (1 : 1 and neural network) and the two mutation regimes (per-locus mutation and entire-genome mutation). Resulting cooperation levels and strategy frequencies were calculated by averaging over all interactions in the last generation of each simulation, and then averaging those averages over all replicates.

In all simulations reported here, the perception error ε_P and the implementation error ɛ_I were both set to 0.01; mutation probabilities (µ_L, µ_G and µ_F) were all set to 0.001, and mutational step sizes for all continuous loci (σ_N and σ_F) were set to 0.1. In the electronic supplementary material, we consider different values of these parameters in order to check for the robustness of our results.

3. Results

(a). Effect of architecture on the average cooperation level

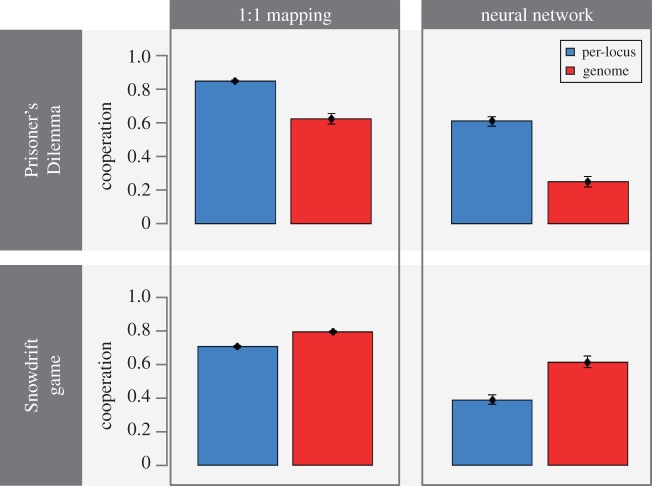
We studied the evolution of cooperation in two games (the ISD and the IPD), with four different implementations (figure 1) of behavioural strategies, reflecting two scenarios concerning the underlying behavioural architecture (1 : 1 versus neural network), and two scenarios concerning the mutation regime (per-locus versus entire-genome). Figure 2 shows that in both games, the evolved cooperation level is strongly affected by both the genetic and the behavioural architecture. In fact, in both games, average cooperation levels were 0.4 or lower for one implementation and 0.8 or higher for another implementation. Cooperation levels were higher for the 1 : 1 architecture when compared with the neural network architecture in all scenarios, but the effect of the mutation regime was different between the two games. In the IPD, per-locus mutation was associated with higher levels of cooperation than whole-genome mutation, whereas the opposite was true in the ISD. To understand the causes underlying these large differences, we next zoom in on the evolutionary dynamics of the 16 strategies that were considered in this study (see table 1 for a complete list and an explanation of strategy names).

Figure 2.

Cooperation levels in the IPD (top) and the ISD (bottom) for all four mechanistic implementations of the 16 strategies. The bars show average cooperation levels over all interactions in the last generation, across all replicates. Error bars show standard error of the mean.

(b). Evolutionary dynamics in the Iterated Snowdrift game

A game-theoretical analysis of the 16 strategies in the ISD reveals that there are three ESSs (see the electronic supplementary material for details). ESS 1 consists of 83.3% con-D (conventional defector, a strategy that sticks with its previous behaviour if it played the opposite as its opponent in the previous round, and defects otherwise), together with 16.7% ALLD. ESS 2 consists of the pure strategy Pavlov. ESS 3 involves three pure strategies: 96.8% MNG (Mr Nice Guy, which always cooperates, except if it cooperated while the interaction partner defected in the previous round), 2.2% inconsistent (which always plays the opposite to its previous move) and 1.0% Acon-D (unconventional defector, a strategy that changes behaviour if it played the opposite as its opponent in the previous round, and defects otherwise).

In our simulations, we recover the three ESSs above. Typically, a simulation stays at one of the ESSs for extensive periods of time, followed by a rapid shift to another ESS. In most simulations across all scenarios, ESS 1 evolved first. In some of the simulations, ESS 1 was invaded by Pavlov, leading to the establishment of ESS 2. In a subset of those cases, ESS 2 was ultimately invaded by MNG, establishing ESS 3. ESS 3 was almost never invaded, but in very rare cases could be followed by a new establishment of ESS 1. The probability of transition between two ESSs and, accordingly, the probability to find the population in any of the three ESSs strongly depends on the behavioural architecture and mutation regime (figure 3): in case of a 1 : 1 architecture, ESS 3 is the dominant state in case of per-locus mutation, while the simulations switch between ESS 2 (attained 81% of the time) and 3 (19%) in case of whole-genome mutation. In case of a neural network architecture, the simulations either end up in ESS 1 (55%) or 3 (45%) in case of per-locus mutation and in ESS 1 (38%) and 2 (62%) in case of whole-genome mutation. In other words, the four implementations differ in their likelihood of attaining each of the ESSs, and this difference is reflected in the average cooperation levels observed in figure 2 (as each ESS induces a different cooperation level; see electronic supplementary material, table S1).

Figure 3.

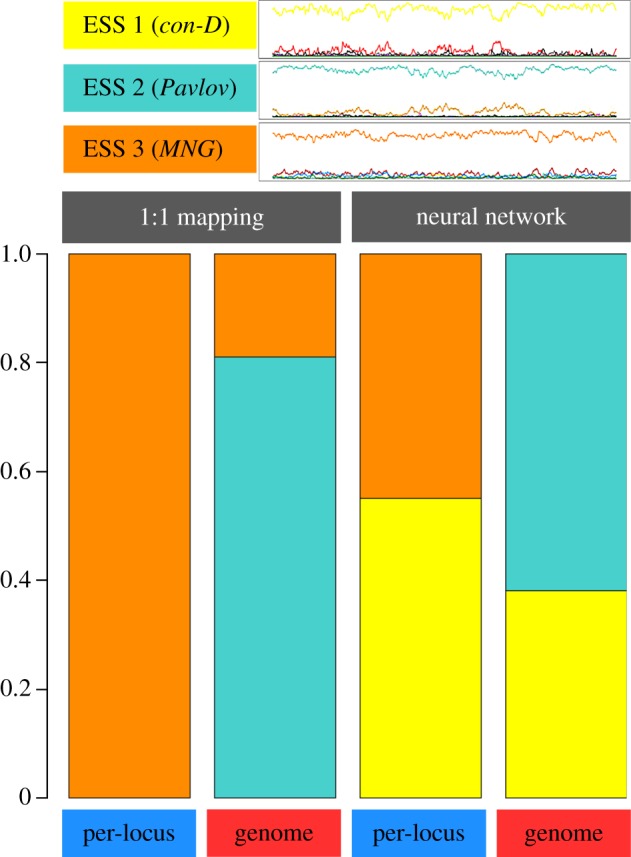
Simulation outcomes in the ISD, for all four mechanistic implementations. The three line graphs (top) show time series (2500 generations) of typical simulation runs, each illustrating the attainment of one of the three ESSs of this game (see the electronic supplementary material, table S1). The bar graphs (bottom) show for each scenario the fraction of 100 replicate simulations for which the last generation was in each of the three ESSs.

Why do the behavioural and the genetic architecture have such a strong effect on the evolutionary outcome? This can be illustrated by considering the transition from ESS 1 to ESS 2. In ESS 1, Pavlov has a slight selective disadvantage when rare, but as soon as it occurs in higher frequencies, it achieves a higher pay-off than the strategies in ESS 1 (because the pay-off of Pavlov against itself is high). Therefore, if Pavlov increases enough against the selection gradient owing to mutation and genetic drift, it can invade, and ESS 2 becomes established. Clearly, the probability that Pavlov results from mutation of the strategies in ESS 1 is a crucial factor in this regard. As shown in table 1 (and explained in the electronic supplementary material), Pavlov occupies a much larger part of the genotype space (6.25%) in the 1 : 1 architecture than in the neural network architecture (0.08%). As a result, Pavlov almost never invades ESS 1 in the neural network architecture, whereas this often happens in the 1 : 1 architecture.

(c). Evolutionary dynamics in the Iterated Prisoner's Dilemma game

A game-theoretical analysis of the 16 strategies in the IPD reveals two ESSs, both containing only a single strategy: ALLD and grim (see the electronic supplementary material for details).

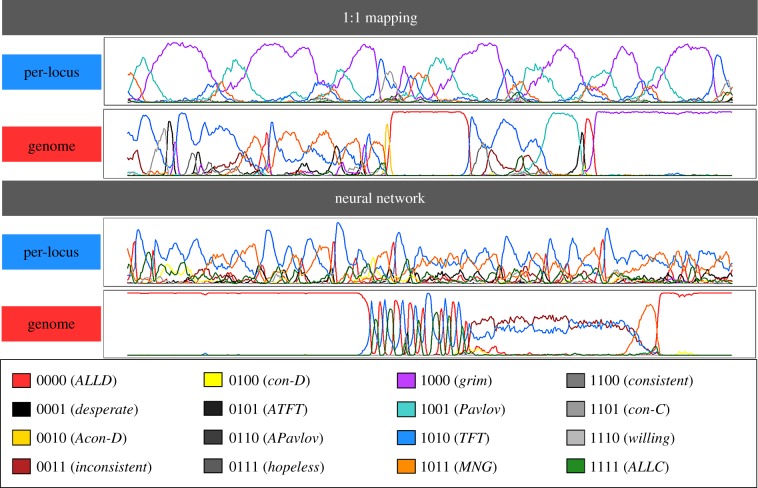
In our simulations, there indeed were extended periods of time in which either ALLD or grim are dominant in the population. However, in most cases, the evolution of strategies was very dynamic and often irregular. This is in line with earlier studies which also conclude that the evolutionary dynamics in an IPD is often chaotic and off-equilibrium [48–50]. Like in the ISD, both the behavioural and the genetic architecture had a strong effect on the evolutionary dynamics (figure 4). In the case of 1 : 1 mapping with per-locus mutation, steady cycles of grim, TFT, MNG and Pavlov were observed for all replicate simulations (this is consistent with earlier findings by Nowak & Sigmund [48]). For whole-genome mutation, the patterns look less consistent (yet highly dynamic), including longer spells of ALLD domination (this explains the relatively low cooperation levels in this scenario). In the neural network architecture, per-locus mutation led to very dynamic yet fairly consistent patterns, mostly involving TFT and MNG, and infrequent ALLD domination spells. Entire-genome mutation typically led to long ALLD domination spells interspersed by short periods with both cyclical dynamics involving various strategies including TFT, ALLC, ALLD, grim, and MNG and non-cyclical coexistence of TFT and inconsistent.

Figure 4.

Time series of typical simulation runs in the IPD, for all four mechanistic implementations. In each case, a time period of 2500 generations is shown. The coloured lines represent the frequencies of the 16 different strategies.

The effect of underlying mechanisms on the evolutionary dynamics can be explained by the fact that different mechanisms induce differences in the ‘mutational distance’ between strategies, that is, the likelihood that a mutation in a strategy gives rise to a given alternative strategy. As an example, consider the extended periods of dominance of grim that were frequently observed. Those periods are typically ended by the invasion of TFT. TFT obtains a slightly worse pay-off against grim than grim obtains against itself. However, TFT does obtain better pay-offs when it happens to be paired with itself. In other words: if TFT can increase enough against the selection gradient because of genetic drift and mutation, it gains a selective advantage and can invade. The probability that this occurs depends on the implementation: in the 1 : 1 architecture with per-locus mutation, a mutation of grim produces TFT with probability 1/4. In the case of whole-genome mutation, this probability is only 1/16—this makes it considerably less likely that TFT obtains appreciable frequencies, and explains the extended spells of grim domination (figure 4) and the lower degree of cooperation (figure 2) in this case.

4. Discussion

Our study demonstrates that behavioural architecture and mutation regime are of considerable importance for the dynamics and outcome of social evolution. In the IPD, we observed three types of dynamic behaviour (predictable cycles; fast and chaotic dynamics; spells of ALLD or grim domination) whose occurrence crucially depended on both behavioural architecture and mutation structure. Likewise, the prevalence of and the transitions between the three ESSs in the ISD were strongly determined by both architecture and mutation structure. In both games, the differences in evolutionary dynamics resulted in substantial differences in the average level of cooperation. These conclusions are not specific to the parameters considered in our simulations; they also hold for different pay-off configurations of both games, and for a lower degree of stochasticity in the simulations (see the electronic supplementary material).

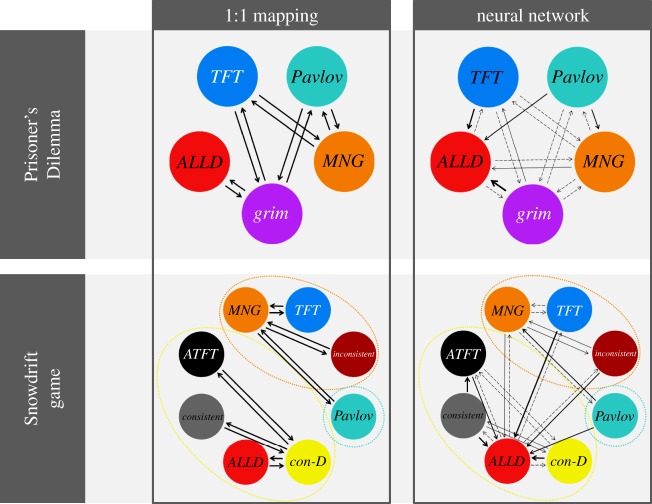
The effect of mechanisms on the evolutionary dynamics was not caused by ‘hard’ constraints (the inability of mechanisms to produce all phenotypes), as all 16 strategies of the game were feasible in all four implementations. Yet, the mechanisms induced some ‘soft’ constraints on evolution, by strongly affecting the probabilities with which strategies arise by mutation (see figure 5 for a schematic overview of mutation probabilities for each scenario considered in this study). Even in case of small mutation rates, the mutational distribution has a strong effect on the type of variation that can be expected to be present in a given situation. Some strategies only gain a selective advantage once they have increased beyond a certain frequency, and mutation probabilities determine the probability that this will happen. In the 1 : 1 architecture considered in this study, each strategy has an equal probability to result from a randomly generated genotype, whereas in the neural network architecture, some strategies (notably ALLD and ALLC) are much more likely to arise owing to mutation than others (table 1). In the case of entire-genome mutation, the strategy of a mutant individual is independent of the strategy of its parent, and mutation probabilities therefore only depend on the behavioural architecture. In the case of per-locus mutation, the parental strategy partly determines the strategy of their mutant offspring.

Figure 5.

Mutational distance between the most relevant strategies in the Prisoner's Dilemma (top) and the ISD (bottom), for both behavioural architectures and the case of per-locus mutation. An arrow pointing from one strategy to another indicates that a mutation of the former strategy has probability of larger than 0.001 to yield the latter strategy. A probability of more than 0.05 is indicated by a solid arrow (the thickness of the arrow is proportional to the probability). In the 1 : 1 model, each strategy can mutate to four other strategies with equal probability, so the arrows in the mutation maps for the 1 : 1 model all represent a probability of 0.25. To calculate these probabilities, we first generated a large number of random genotypes (in the same way as generating a genotype through ‘entire-genome mutation’), and determined their corresponding strategy. Then, for each strategy, we mutated all corresponding genotypes many times, and again determined the resulting strategies.

We are not the first to point out that the genotype–phenotype mapping and the induced mutation structure are important for the course of evolution. In fact, the formal frameworks for modelling evolutionary dynamics can, to a certain extent, take these complexities into account. For example, the ‘canonical equation’ of adaptive dynamics theory includes a mutational covariance matrix [51,52], which characterizes the likelihood that a combination of phenotypic traits (like a conditional strategy) arises and potentially invades the current resident strategy. Likewise, the multivariate selection equation of quantitative genetics [53,54] can be written in a form that it includes a matrix characterizing the covariance in phenotypic traits between parents and offspring [55]. Sean Rice has worked out formally how these covariances arise and determine the course of evolution when phenotypic traits are the outcome of (developmental) mechanisms [55,56]. We are not aware of attempts to actually derive the covariance matrices of adaptive dynamics of quantitative genetics theory on the basis of a concrete mechanistic model. Instead, theoretical studies tend to make simplifying assumptions, such as replacing the covariance matrix by the identity matrix (e.g. [25]). Already in the case of frequency-independent selection and in the absence of stochasticity, assumptions like these are not unimportant, as the covariance structure largely determines which peak of a multi-peaked fitness landscape will be reached.

There are two main reasons why we think that phenotypic covariances and, hence, the mechanisms underlying the development of phenotypes are of particular importance for social evolution. First, selection will virtually always be frequency-dependent in this case. As a consequence, the success of each strategy will strongly depend on the context, and, in particular, on the presence of selectively favoured competitors. Accordingly, a given architecture will contribute to the stability of a given equilibrium if it makes the production of selectively favoured alternatives less likely, and it will have a destabilizing effect if the opposite is the case. Second, in case of social interactions, there are typically many alternative Nash equilibria and ESSs. This is already illustrated in the IPD and the ISD with highly restricted memory considered here. Relaxing the restrictions on the strategy set would lead to a rapid increase in the number of equilibria. In fact, the Folk theorem of game theory [23,57] implies quite generally that in repeated games the set of Nash equilibrium strategies is so large that virtually any ‘reasonable’ outcome (in case of our IPD: any outcome between 0 and 5; in case of our ISD: any outcome between 1 and 5) can be achieved as the average outcome of an equilibrium. But also non-repeated games typically have several (and often a large number of) Nash equilibria and ESSs [58]. In all these cases, it is to be expected that the evolutionary dynamics will be affected in a similar way by mechanisms as in this study.

We have here focused on situations where the evolutionary game dynamics [42] are relatively simple. For the pay-off structure considered, the IPD and the ISG have a small number of ESSs, and these are the only attractors of the replicator equation (see the electronic supplementary material). Accordingly, mechanisms will mainly affect the transition between ESSs, as described above. It is conceivable that mechanisms have an even stronger effect in the presence of limit cycles or other non-equilibrium attractors. Such attractors regularly occur in evolutionary games (such as variants of the Rock–Scissors–Paper game; [59]), and it has been shown that seemingly small differences in the genetic implementation of strategies can have major effects on the evolutionary outcome [60]. In the electronic supplementary material, we show that non-equilibrium attractors can also occur in the IPD (for slightly different pay-off parameters), but a thorough investigation of the interplay of genetic or behavioural architecture and non-equilibrium dynamics is beyond the scope of this study.

Our results should be mainly viewed as proof of principle that mechanisms matter for the course and outcome of social evolution. It would be premature to conclude that one of the four implementations considered in our study is more ‘realistic’ than the others. On purpose, we kept our assumptions on architecture as simple as possible, as this allowed us to develop a sound intuitive understanding of our results (figure 5). Because of this understanding, we are confident that our findings are of general relevance. The development of truly ‘realistic’ models remains a major challenge, as the actual genetic, physiological, neurological and psychological mechanisms behind social behaviour are still largely terra incognita for virtually all organisms and virtually all interaction types. For this reason, it would be premature to abandon the standard 1 : 1 genotype–phenotype mapping assumption in favour of (for example) a neural network implementation. However, whatever the implementation chosen, researchers should be aware that it may have considerable implications for the course and outcome of evolution.

The evolution of social behaviour is often an intricate process, with many feedbacks at work, and many possible outcomes. We have shown that underlying mechanisms are of decisive importance in determining which outcome eventually emerges in evolution. Therefore, it is of importance that we focus more on mechanisms when trying to explain the evolution of social behaviour. Both empirical work focused on understanding mechanisms and theoretical work investigating their importance for the dynamics and course of evolution have a vital role to play in this regard.

Data accessibility

All data are available on Dryad: http://dx.doi.org/10.5061/dryad.5hq6r.

Authors' contributions

P.v.d.B. and F.J.W. designed the study, conducted analyses, drafted the article and gave final approval of the paper. P.v.d.B. conceived of the study and conducted simulations.

Competing interests

We declare we have no competing interests.

Funding

P.v.d.B. was supported by grant no. NWO 022.033.49 of the Graduate Programme of the Netherlands Organisation for Scientific Research.