Chromatic detection from cone photoreceptors to V1 neurons to behavior in rhesus monkeys

Abstract

Chromatic sensitivity cannot exceed limits set by noise in the cone photoreceptors. To determine how close neurophysiological and psychophysical chromatic sensitivity come to these limits, we developed a parameter-free model of stimulus encoding in the cone outer segments, and we compared the sensitivity of the model to the psychophysical sensitivity of monkeys performing a detection task and to the sensitivity of individual V1 neurons. Modeled cones had a temporal impulse response and a noise power spectrum that were derived from in vitro recordings of macaque cones, and V1 recordings were made during performance of the detection task. The sensitivity of the simulated cone mosaic, the V1 neurons, and the monkeys were tightly yoked for low-spatiotemporal-frequency isoluminant modulations, indicating high-fidelity signal transmission for this class of stimuli. Under the conditions of our experiments and the assumptions for our model, the signal-to-noise ratio for these stimuli dropped by a factor of ∼3 between the cones and perception. Populations of weakly correlated V1 neurons narrowly exceeded the monkeys' chromatic sensitivity but fell well short of the cones' chromatic sensitivity, suggesting that most of the behavior-limiting noise lies between the cone outer segments and the output of V1. The sensitivity gap between the cones and behavior for achromatic stimuli was larger than for chromatic stimuli, indicating greater postreceptoral noise. The cone mosaic model provides a means to compare visual sensitivity across disparate stimuli and to identify sources of noise that limit visual sensitivity.

Introduction

Vision begins with the absorption of photons in the outer segments of photoreceptors. Each absorption triggers a complex cascade of chemical reactions that ultimately results in an electrical signal across the photoreceptor cell membrane. Noise in this process places an upper bound on visual sensitivity, because signal processing downstream of phototransduction cannot replace information once it has been lost. For example, a linear filter cannot selectively eliminate noise from frequency bands that contain relevant information without also eliminating the information itself.

The neural representation that provides the basis for perceptual decisions (e.g., about the presence or absence of a visual stimulus) has a signal-to-noise ratio that is inherited from processing stages throughout the visual system. Under some conditions, these processing stages are relatively noise-free, and small modulations of photoreceptor activity produce detectable visual sensations. Under other conditions, photoreceptor activity may modulate over a larger range but fail to produce a sensation, implying substantial downstream noise. These issues, while conceptually clear, are incompletely understood, due largely to a lack of tools to compare photoreceptor noise with perceptual thresholds.

In this study, we focused on low-spatiotemporal-frequency chromatic modulations because this class of stimuli is detected efficiently by humans (Chaparro, Stromeyer, Huang, Kronauer, & Eskew, 1993; Kelly, 1974; Mullen, 1985; Stromeyer, Cole, & Kronauer, 1985; Thornton & Pugh, 1983) and monkeys (Gagin et al., 2014; Lindbloom-Brown, Tait, & Horwitz, 2014; Merigan, 1989). The cones are the first step for both luminance and chromatic vision, so the relatively high sensitivity to color (or conversely, the insensitivity to achromatic stimuli) must be due to postreceptoral processing. Differences in the sensitivity of neurons in the midget and parasol ganglion-cell pathways may underlie this difference in psychophysical sensitivity, at least for stimuli that stimulate the S-cones minimally (Crook, Lee, Tigwell, & Valberg, 1987; Lee, Martin, & Valberg, 1989; Lee, Martin, Valberg, & Kremers, 1993). These issues lead to several questions that form the basis of our study. First, how much noise is added to chromatic signals downstream of the cones? Second, does the amount of added noise depend on the degree of S-cone modulation in a chromatic stimulus? Third, does the chromatic sensitivity of individual V1 neurons approach the limits imposed by the cones? To answer these questions, we compared the behavior of monkeys performing a chromatic detection task to the performance of a statistical ideal observer that had access to a parameter-free model of currents in the cone outer segments. Results from this comparison revealed that the monkeys' sensitivity to chromatic modulations approached that of the ideal observer (within a factor of 3) for all low-frequency, isoluminant stimuli tested, suggesting that these patterns are transmitted through the visual system with particularly high fidelity. We also found that on average, V1 neurons were substantially less sensitive than the population of cones that presumably fed them but only slightly less sensitive than the monkeys.

Methods

Subjects

Two female Macaca mulatta monkeys were used in the V1 recording and behavioral experiments. Behavioral data only were obtained from two others (one male, one female). We obtained isolated retinas of macaque monkeys (M. mulatta, M. nemestrina, and M. fascicularis) through the Tissue Distribution Program of the Washington National Primate Research Center. All procedures conformed to the guidelines provided by the US National Institutes of Health, the University of Washington's Animal Care and Use Committee, and the Association for Research in Vision and Ophthalmology.

Chromatic contrast detection task

Chromatic sensitivity was measured using a contrast detection task described previously (Figure 1A; see also Hass & Horwitz, 2013). On each trial, the monkey was rewarded for detecting a Gabor stimulus, which was the product of a stationary Gaussian window and a sinusoid that translated at 3 Hz. During sessions in which the spiking activity of V1 neurons was recorded, the Gabor stimulus was oriented to evoke a robust spiking response. In other sessions, the Gabor stimulus was oriented horizontally. Monkeys viewed the stimulus binocularly.

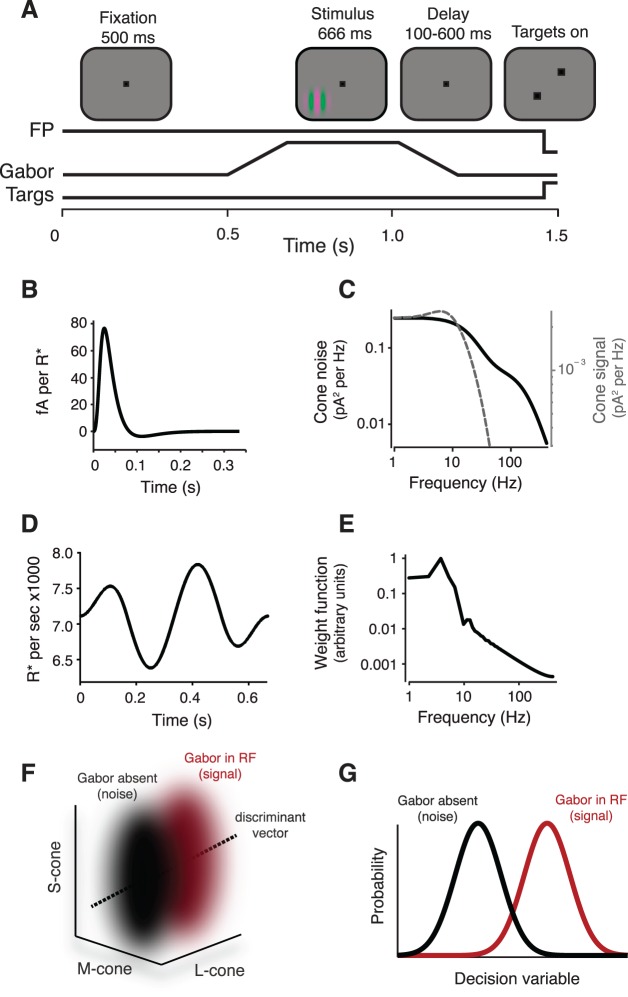
Figure 1.

Overview of the detection task and photocurrent ideal-observer model. (A) Display geometry and event timing in the detection task. Monkeys were required to maintain fixation within a 1° window around a 0.1° fixation point (FP). A drifting Gabor stimulus appeared in one of two mirror-symmetric locations about the fixation point. The contrast of the Gabor increased linearly for 160 ms, was constant for 346 ms, and then decreased linearly over 160 ms. Following a brief delay (100–600 ms), the fixation point disappeared and two choice targets appeared. An eye movement to the choice target located in the direction of the Gabor stimulus triggered a juice reward. (B) The temporal IRF of a modeled cone at the adaptation state induced by the visual display used in the behavioral experiments. The deterministic portion of the model-cone output was calculated as the convolution of the stimulus time series with the IRF. (C) Power spectra of the cone noise (solid) and the IRF (dashed). (D) Example time series for a single stimulus pixel. (E) Amplitude spectrum of the ideal observer's temporal weighting function. Abrupt discontinuities in light due to the refresh rate of the monitor contribute to the jaggedness of this spectrum. (F) Pooled response distributions for Gabor-present (red) and Gabor-absent (black) trial types in a 3-D cone-response space. The discriminant vector was found using linear discriminant analysis. (G) One-dimensional decision variables used by the observer. Projecting the 3-D pooled response distributions onto the discriminant vector produced the 1-D decision variable used by the photocurrent ideal observer. The performance of the model on the detection task was defined by the discriminability between the two distributions of the decision variable as quantified as the area under the receiver operating characteristic curve.

Cone contrasts of the stimuli were calculated using a set of cone fundamentals described later under “Converting the physical stimulus into cone photoisomerizations.” Contrast was defined as the length of a vector in cone-contrast space:

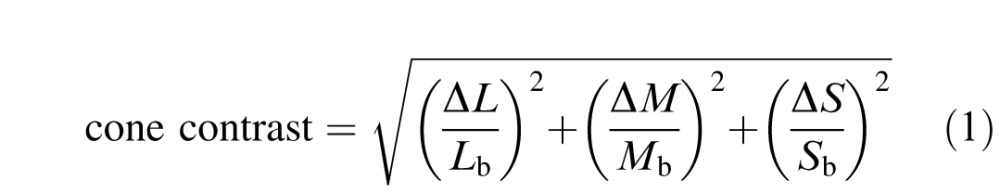where, e.g., ΔL represents the difference in L-cone excitation between the maximum of the Gabor and the background, and L_b represents the L-cone excitation due to the background.

Isodetectability surfaces in cone-contrast space

Isodetectability surfaces were measured iteratively. Each iteration had two phases: (1) Detection thresholds were estimated in three interleaved color directions and (2) new color directions were selected for testing. Each detection threshold was measured using the QUEST adaptive procedure (Watson & Pelli, 1983) and was defined as the contrast necessary to support 82% correct performance, as estimated as the modal value of the QUEST function at the end of the procedure. For Monkey K, each threshold measurement was based on 40 trials; for Monkey S, 93% of thresholds were based on ≥40 trials, and the remainder were based on ≥20 trials. Color directions were selected using an algorithm that has previously been used to characterize neuronal color-tuning functions (Horwitz & Hass, 2012).

We fit detection thresholds in three-dimensional (3-D) cone-contrast space with a surface defined by the following equation:

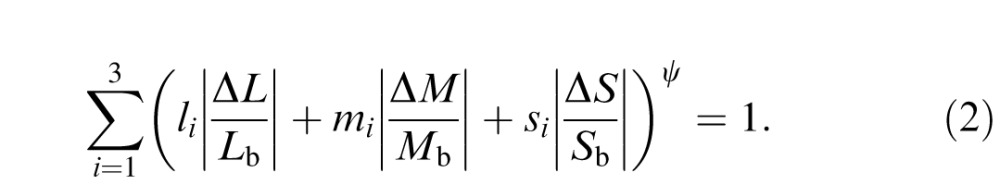This equation is based on a model that assumes that detection is mediated by three statistically independent visual mechanisms that interact via probability summation (Cole, Hine, & McIlhagga, 1993). The coefficients l_i, m_i, and s_i specify the cone weights to the ith visual mechanism. The parameter ψ determines the degree of interaction among the mechanisms. Fitting was performed by minimizing the squared log of the difference between the actual and predicted thresholds.

Neurophysiological recordings

We recorded extracellularly from individual V1 neurons with glass-tipped transdural tungsten microelectrodes (FHC Inc., Bowdoin, ME; Hass & Horwitz, 2013). Single-unit isolation was assessed by stability of the action-potential waveform over the duration of the recording and by the absence of interspike intervals of <1 ms.

We recorded photocurrents of cone photoreceptors in the whole-cell voltage-clamp configuration (Angueyra & Rieke, 2013) and excluded cones that showed marked run-down of light responses during the first 2–3 min of recording or holding currents in darkness smaller than 150 pA (large dark currents correlated well with high light sensitivity). All recorded cones were from peripheral retina (>10° of eccentricity) and were either L- or M-cones, because S-cones were encountered relatively rarely. Recordings from a small sample of S-cones indicate that they behave similarly to L- and M-cones under the conditions of these experiments (data not shown). Twenty of the most sensitive L- and M-cones in our data set were used to construct different parts of the cone model; we assume that the most sensitive cones we encounter most closely reflect in vivo cone responses.

We estimated the impulse response function (IRF) of each cone by reverse correlation of the photocurrent with a truncated Gaussian noise stimulus (standard deviation of 50% contrast, bandwidth 0–60 Hz). Draws from this distribution that fell more than two standard deviations below the mean correspond to negative light intensities (decremental contrasts of >100%) and were rounded up to zero intensity. We fitted the resulting IRF empirically, as described previously (Figure 1B; see also Angueyra & Rieke, 2013). Measurements were made at backgrounds ranging from 4000 and 6500 R*/s, and were broadly consistent with similar measurements made by Cao, Luo, and Yau (2014). Responses to Gaussian white-noise stimuli were well described by a purely linear model, except for extreme current deviations corresponding to infrequent high-contrast events (see Results). Following the linear model with a static nonlinearity increased the accuracy of the predicted currents by less than 4%, as evaluated as an increase in the correlation between nonlinear model prediction and data compared to the purely linear model (n = 6). The kinetics of the modeled cone responses were taken from a single cone whose temporal IRF was representative of those studied.

We estimated cone noise by subtracting the power spectrum of currents recorded in near-saturating light from that in darkness (Figure 1C; average noise from six cones). We did not quantify noise from the same population of cones used to estimate the impulse response, as cones did not recover their dark sensitivity after exposure to near-saturating light. Nevertheless, the noise in darkness (before subtraction) was similar across the two cone populations. To test the key assumptions of our cone model, we stimulated four cones with a low-contrast (20%), 3-Hz tapered-sine stimulus that mimicked the modulations produced by the Gabor stimuli used in the behavioral experiments (see Results).

We assume that noise in the currents across cone outer segments is independent across cones. This assumption is supported by the fact that noise in the outer-segment current is dominated by noise produced within the phototransduction cascade; under conditions where the light response was eliminated in a single recorded cone but not its neighbors, we failed to detect significant current transmission of signals or noise from stimulation of the surrounding cones (Angueyra & Rieke, 2013). Moreover, recordings from pairs of neighboring cones did not reveal strong noise correlations (data not shown). This is also consistent with previous work, showing at most weak transmission of signals between cones in the macaque retina (see Schneeweis & Schnapf, 1999, figure 5).

Constructing the artificial cone mosaic

The model cone mosaic was constructed by dividing the area of the retina stimulated by the Gabor stimulus into regions corresponding to each stimulus pixel. The area of each retinal region was calculated using a reduced-eye model with one nodal point,

where A_ret is the area of a retinal region, θ is the angle of elevation subtended by a single pixel of the Gabor stimulus, and F_post is the distance between the nodal point and the retina, which was set to 12.75 mm (Lapuerta & Schein, 1995; Qiao-Grider, Hung, Kee, Ramamirtham, & Smith, 2007). We assume that each pixel of the Gabor stimulus projects onto the same retinal area regardless of eccentricity. We ignore both blurring of the image as it passes through the eye's optics and eye movements that displace the stimulus on the retina during visual fixations (Banks, Geisler, & Bennett, 1987; Campbell & Gubisch, 1966; Hass & Horwitz, 2011; Martinez-Conde, Macknik, & Hubel, 2004). These assumptions are reasonable for the low-spatial-frequency stimuli we focus on here.

We allocated cone photoreceptors to each retinal region according to the eccentricity dependence of the cone density in the macaque retina (Goodchild, Ghosh, & Martin, 1996; Packer, Hendrickson, & Curcio, 1989):

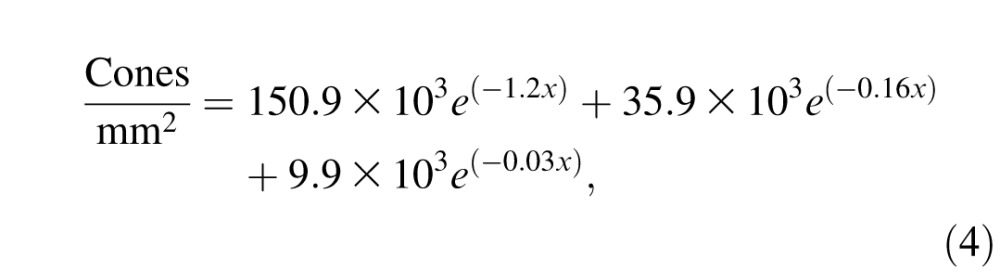where x is the eccentricity (in degrees of visual angle) at the center of each retinal region. After determining the number of cones in each retinal region, we determined their type (i.e., L-, M-, or S-cones). The number of S-cones per degree of visual angle was determined using published estimates of S-cone density in the macaque temporal retina (De Monasterio, McCrane, Newlander, & Schein, 1985),

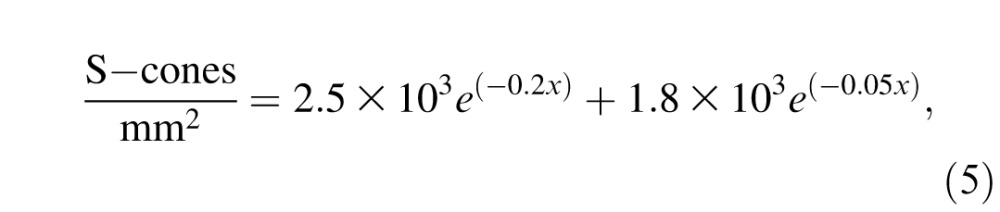and the remaining cones were allocated equally to the L- and M-cone classes (Jacobs & Deegan, 1999). The two monkeys investigated most intensively (Monkeys S and K) had flicker thresholds consistent with a ∼1:1 ratio of L- to M-cones (Lindbloom-Brown et al., 2014). The number of cones computed this way was doubled to account for the fact that the monkeys viewed the stimulus through both eyes. Human subjects performing similar tasks use information from both eyes to detect the stimulus, but appear to combine inputs using a binocular contrast-energy calculation (Legge, 1984a, 1984b). The ideal observer, however, combines signals via linear summation. A detection model using a binocular energy calculation performed nearly as well as the linear ideal observer of the cones that we used (data not shown).

Cones in the model were not assigned specific locations; instead, each pixel-sized region of the retina contained a noninteger number of cones (e.g., 0.18 L-cones, 0.18 M-cones, and 0.04 S-cones at 6° of eccentricity). This approximation precludes us from studying cone responses to finely patterned stimuli; for example, a tiny point of light on a real retina might excite an L-, M-, or S-cone, depending on exactly where it falls, whereas in our model it would always activate all three at once. This mathematical convenience is inconsequential for the class of stimuli we use, which are large with respect to the heterogeneity of real cone mosaics. At 6° of eccentricity, a Gabor with a standard deviation of 0.4° subtends ∼2,100 cones (∼200 S-cones) within two standard deviations in a single eye.

Converting the physical stimulus into cone photoisomerizations

The number of photoisomerizations induced by the Gabor stimulus was quantified as follows. First, we converted the spectral radiance (in units of watts per steradian per square meter) of each monitor phosphor into spectral irradiance (watts per square micrometer) using the formula

where R_(λ) is the emission spectrum of a CRT phosphor measured at its maximum intensity. The number of steradians subtended by the pupil was calculated by dividing pupil area by the square of the eye's diameter. Pupil area (12.6 mm²) was measured using an optical eye tracker (iView X Hi-Speed Primate, SensoMotoric Instruments, Teltow, Germany). The eye's diameter was set to 19 mm following published values (Lapuerta & Schein, 1995; Qiao-Grider et al., 2007). Multiplying by 10⁻¹² converts watts per square meter into watts per square micrometer.

Second, the spectral irradiance of the stimulus was adjusted for preretinal filtering by multiplying irradiance spectra with the lens and macular-pigment transmittance functions:

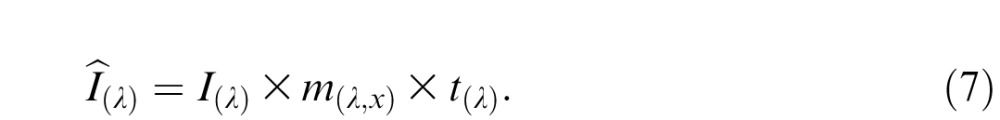The macular-pigment transmittance function m_(λ,x) was calculated by converting the Wyszecki and Stiles (1982) absorbance function into transmittance adjusted for the eccentricity dependence of macular-pigment density:

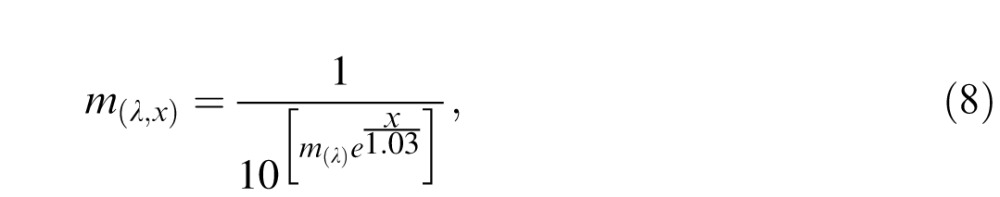where m_(λ) is the macular-pigment absorbance spectrum, which was scaled to have a value of 0.35 at 460 nm at 0° of eccentricity (Snodderly, Auran, & Delori, 1984; Stockman, MacLeod, & Johnson, 1993; Wooten & Hammond, 2005). We calculated m_(λ,x) at a single eccentricity x defined by the center of the Gabor stimulus. The lens transmittance function t_(λ) was based on published estimates of lens optical density (Stockman et al., 1993), scaled to 10% transmittance at 400 nm (Lindbloom-Brown et al., 2014).

Third, we converted spectral irradiance into photon flux:

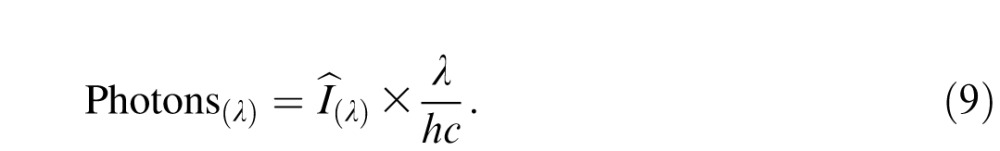The resulting photon spectrum is in units of photons per square micrometer per second. We constructed an absorptance spectrum for each cone type by multiplying the Baylor, Nunn, and Schnapf (1987) cone action spectra A_(λ) by a photopigment optical density of 0.3 (Stockman et al., 1993) and converting absorbance to absorptance via the Beer–Lambert equation:

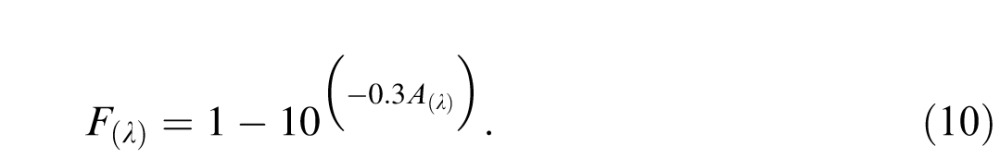The cone absorptance functions were then normalized to have a peak value equal to the cone collecting area (0.6 μm²; see Schnapf, Nunn, Meister, & Baylor, 1990; Schneeweis & Schnapf, 1999).

The last step was to convert the intensities of the red, green, and blue phosphors into cone photoisomerization rates (R* per second) for each of the cone types in response to the neutral gray background. At 5° of eccentricity, where most of our stimuli were placed, the photoisomerization rates produced by the background were L = 7131, M = 6017, and S = 1973 R*/s. For comparison, the activity of modeled rod photoreceptors due to the background was ∼8000 R*/s, which was estimated using the rod action spectrum (Baylor et al., 1984) and published estimates of rod optical density (0.35) and collecting area (1 μm²; Baylor et al., 1984; Schneeweis & Schnapf, 1999).

Calculating the linear photocurrent response

The photocurrent response of each cone was modeled as the sum of a deterministic, linear component and a stochastic, Gaussian noise component. The linear response of a single cone was calculated as the discrete-time convolution between the stimulus time series for a pixel (Figure 1D) and a temporal IRF (Figure 1B):

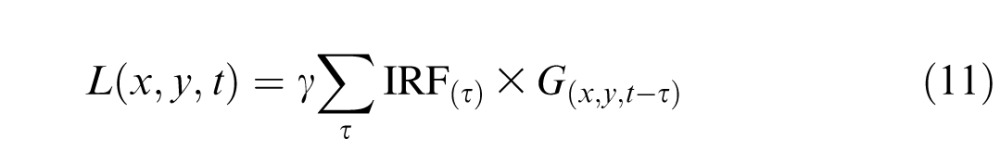where L_(x,y,t) represents the linear response of a single cone in the retinal region defined by the stimulus pixel at location (x, y) at time t, in picoamperes. The variable G_(x,y,t) represents the Gabor stimulus in R* per second. We denote by γ a scale factor that is unique to each cone type and scales the linear response to account for adaptation due to the background; it followed a Weber–Fechner relationship with a half-desensitization constant of 2250 R* and a dark sensitivity of 0.32 pA/R* (Angueyra & Rieke, 2013; note that the half-desensitization constant here corrects a calibration error and hence differs from that originally reported). The Gaussian noise component was shaped to match the measured power spectrum of cone noise (Figure 1C).

Pooling the responses of the cone mosaic

Signals from the modeled cone photoreceptors were summed within each retinal region and then transformed into a decision variable used by an ideal observer to detect the stimulus. We computed the signal component PR_sig of the pooled response by projecting the linear response of the cones onto a spatiotemporal weighting function wt and summing across space and time:

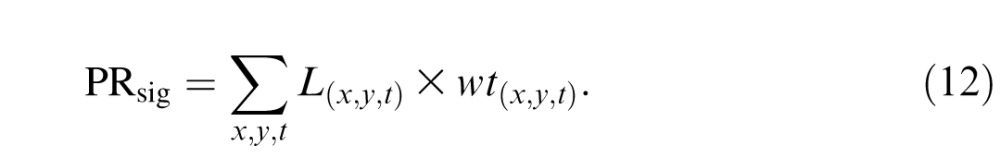This process was repeated for each cone type, yielding a three-element vector that quantifies the signal component of the pooled response.

The spatiotemporal weighting function captures the ideal observer's prior information about the stimulus. The ideal observer was assumed to know the temporal filtering properties of the cones and the spatiotemporal profile of the signal. We provided this information by using a spatiotemporal weighting function that was identical to the linear response of the cones (shifted and scaled to have a mean of 0 and range of ±1 for all cone types). The noise spectrum was not taken into account in making the weighting function, because the noise is approximately constant over the range of frequencies that contain the signal.

The noise component PR_noise of the pooled response was computed as the dot product of the weighting function (Figure 1E) and a noise vector whose temporal statistics were given by the measured cone-noise power spectrum (Figure 1C). We are primarily interested in the sensitivity of the ideal observer across many repeated trials, so instead of computing PR_noise on individual trials, we compute the variance of this quantity across trials. The variance of the dot product of the noise ε onto the weight function wt can be written as

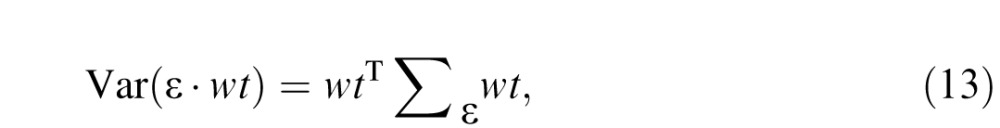where Σ_ε is the covariance matrix of the noise. This matrix multiplication is computationally intensive in the time domain but relatively simple in the Fourier domain, where it can be written as

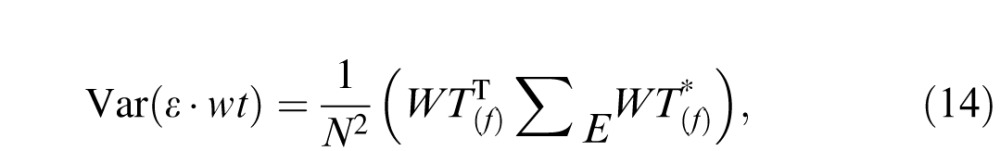with N denoting the number of frequencies, WT the Fourier transform of the weighting function, * complex conjugation, and Σ_E the covariance matrix of the Fourier coefficients, which is a diagonal matrix whose diagonal elements E_(f) correspond to the cone-noise power spectrum (Leon-Garcia, 1994). This expression can be rewritten as the sum of element-wise products:

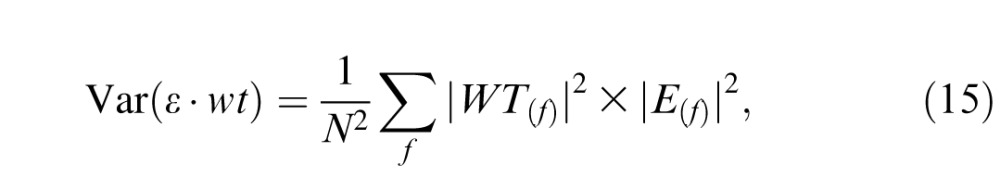where E_(f) is the cone-noise power spectrum. Equation 15 defines the variance of a single cone's response after weighting the response by the spatiotemporal weighting function. Assuming independence across cones, we sum variances within and across retinal subregions to calculate the noise of the pooled response:

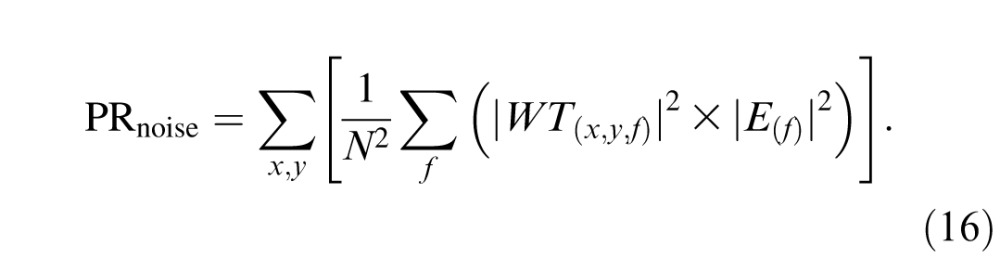Repeating this process for each cone type results in a three-element vector describing the variance of the model's pooled L-, M-, and S-cone responses. Assuming Gaussian cone noise, the distribution of the pooled response is Gaussian and completely specified by its mean PR_sig and variance PR_noise (Figure 1F).

For comparison, we implemented a second ideal-observer model based on cone photon catches rather than outer-segment currents. In this model, the ideal observer based its decisions about the stimulus on the weighted sum of photons absorbed by each cone. The expected number of photon catches per cone was calculated as before—G_(x,y,t) in Equation 11. The actual number of photon catches was assumed to follow a Poisson distribution with this time-varying rate. The photon-observer model differs from the photocurrent model in two key respects: First, it is equally sensitive across temporal frequencies, whereas the photocurrent model is relatively insensitive to high temporal frequencies. Second, variance in photon catches is assumed to be equal to the mean, whereas photocurrent noise is assumed to be additive and independent of the mean.

Ideal-observer analysis on the pooled responses

The performance of the model on the chromatic detection task was calculated using receiver operating characteristic analysis (Britten, Shadlen, Newsome, & Movshon, 1992; Green & Swets, 1966) based on the pooled-response distributions for Gabor-present and Gabor-absent trials. We reduced the 3-D pooled-response distributions to 1-D distributions by projecting onto the linear discriminant vector 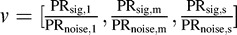, normalized to unit length (Figure 1G). Thus the ideal observer uses a matched filter for color as well as a matched spatiotemporal filter (Equation 12). The mean and variance of these 1-D distributions are

Distributions corresponding to Gabor-present and Gabor-absent trial types were calculated identically, but in the calculation of the Gabor-absent distribution the stimulus—G_(x,y,t) in Equation 11—had a contrast of 0.

On each trial, the ideal observer receives a random draw from the Gabor-present distribution and an independent draw from the Gabor-absent distribution. The trial is answered correctly if the draw from the Gabor-present distribution exceeds the draw from the Gabor-absent distribution. The task of the ideal observer is thus analogous to the monkeys'. The percent correct of the ideal observer was calculated as the area under the receiver operating characteristic curve (Green & Swets, 1966). We used the same method to quantify the sensitivity of V1 neurons, except that in this case the distributions were defined by spike counts recorded across repeated trials. This method does not assume that cone signals are combined linearly in V1. It does assume that spike counts increase stochastically as a function of stimulus contrast and that they are independent across trials.

We repeated this process for multiple stimulus contrasts to derive a neurometric function, and we defined the detection threshold for the model on the basis of the best fitting cumulative Weibull function:

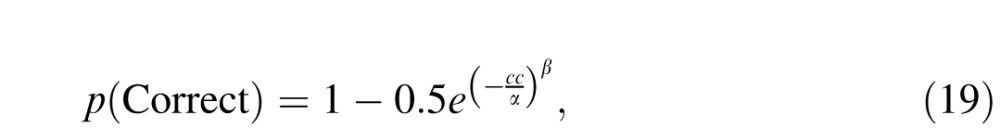where cc is the cone contrast of the stimulus, α is the contrast at detection threshold, and β defines the slope of the neurometric function. The Weibull function was chosen for consistency with our earlier comparison of V1 neuronal and psychophysical chromatic sensitivity (Hass & Horwitz, 2013).

Results

We start by predicting the limits to chromatic sensitivity set by an ideal observer of photocurrents in the cone array. This involves developing a parameter-free, experimentally based model of the cone responses and then using this model to predict responses to near-threshold stimuli. We then compare the predicted thresholds with those measured from monkey behavior and from V1 neurophysiological recordings.

Parameter-free model for responses in the cone array

Cone responses to a low-contrast stimulus were predicted by convolving the stimulus with an IRF and adding Gaussian noise. We describe later how the model parameters were determined and how the model assumptions were tested.

The IRF was determined from photocurrents recorded from individual cones during Gaussian noise stimulation at a background near that used in the behavioral experiments (∼5000 R*/s, where R* denotes photoisomerization; see Methods and Figure 2A). For each cone, the experimental IRF was fitted (Figure 2B, inset) and used as a linear filter to estimate the response to Gaussian noise (Figure 2A, red trace).

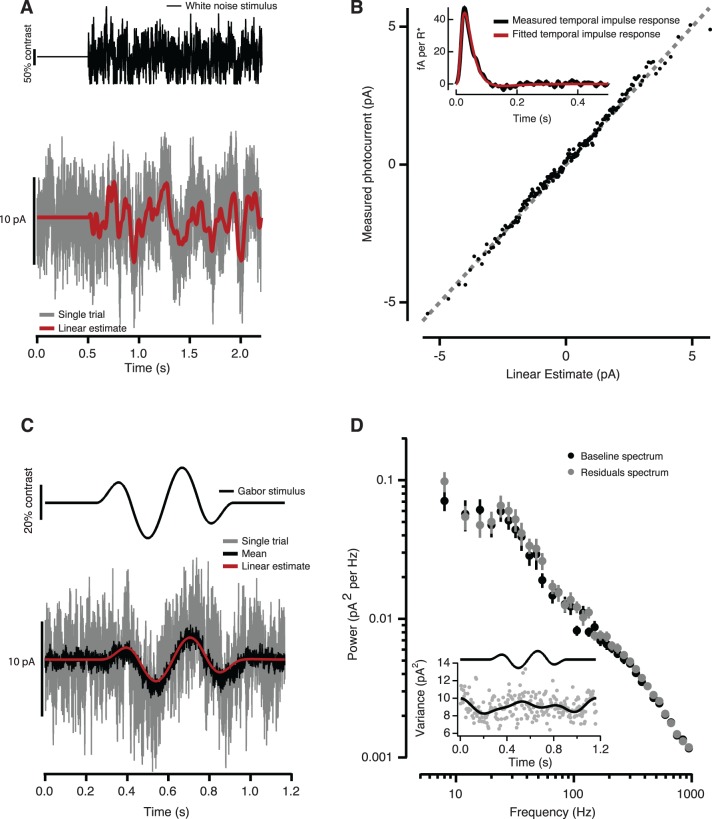
Figure 2.

Determination of the primate cone photocurrent model. (A) Cone photocurrents (example in gray trace) in response to a Gaussian white-noise stimulus (black trace) at a background intensity of 6500 R*/s were used to derive a cone's IRF—see inset in (B)—and to calculate a linear estimate of its response (red trace; see Methods). (B) Relationship between measured currents and linear estimates. Each point corresponds to the mean after averaging over 23 trials and binning for the example cone shown in (A). The unity line (dashed gray), given as reference, shows that a purely linear model provides an accurate estimate of the data—R² = 0.9910 for the cone shown in (A); average for six cones, R² = 0.98. (C) Cone response (gray trace) to a 20% contrast, 3-Hz tapered-sine (emulating the Gabor stimulus used in the V1 recording and behavioral experiments) for the same example cell as in (A) and (B); the mean response over 30 trials (black trace) was again well described by the linear model (R² = 0.930; red trace). (D) Absence of significant stimulus-dependent noise is supported by the lack of covariation between the variance of the residuals and the mean response (inset); the variance of the residuals (gray points) has been low-pass filtered at 5 Hz to ease comparisons (black trace). The power spectrum of the residuals and of noise during baseline for this example cell are nearly identical (points are M ± SEM across trials). No significant differences were found across four cones—spectra integrated across three frequency ranges: low (1–20 Hz), mid (20–100 Hz) and high (100–1000 Hz); paired t tests, all nonsignificant, df = 3; low: p = 0.751, t = 0.347; mid: p = 0.383, t = −1.02; high: p = 0.188, t = −1.70).

To check for systematic deviations between the linear prediction and actual responses, we plotted one against the other. The relationship was well described by the identity line in all cones tested (average coefficient of determination R² = 0.98, n = 6; Figure 2B). Fitting this relationship with nonlinear models improved the correlation between the model predictions and data by at most a few percent (see Methods).

Cones were also stimulated with a 20% contrast tapered-sine, simulating the drifting Gabor stimulus used in the V1 recording and behavioral experiments. The response to this stimulus was small compared to the baseline cone noise but could be uncovered by averaging (Figure 2C). The average measured response agreed well with the response predicted by the convolution with the IRF (R² = 0.93; Figure 2C). Cone responses to high-contrast (≥50%) stimuli showed clear deviations from linearity (data not shown); cone contrasts at behavioral threshold, however, were usually below 20%. Thus, for near-threshold chromatic stimuli, cone signals were close to linear and could be accurately estimated by convolving the stimulus with the IRF.

Noise in the measured cone currents contains contributions from both cellular and instrumental sources, but cellular noise dominates over the range of temporal frequencies of interest (see Methods and Angueyra & Rieke, 2013). To check for stimulus dependence of the noise, we subtracted the average response to repeated trials of the same 20% contrast tapered-sine stimulus from the individual current records. The variance of the resulting residual currents was not significantly correlated with the mean response (M±SD correlation coefficient R = −0.018 ± 0.13, n = 4). This lack of correlation demonstrates that the noise can be modeled as additive under the conditions of our measurements (Figure 2D, inset). The power spectrum of the residual currents closely matched the power spectrum of the currents recorded during a baseline period, as expected from additive, stimulus-independent noise (Figure 2D).

Comparison of 3-D isodetectability surfaces for monkey and model

The cone model described in the previous section provides a means of calibrating and comparing behavioral sensitivity to different stimuli. We focused on chromatic sensitivity. We compared behavioral sensitivity across a broad range of color directions to the limits set by stochastic photon absorptions and by noise in cone outer-segment currents.

We began by considering an ideal observer with access to Poisson-distributed photon absorptions (see Methods). We identified a collection of stimuli that differed in L-, M-, and S-cone contrast but were equally detectable to this photon ideal observer (82% correct). Each of these stimuli can be represented as a point in cone-contrast space, and together these points lie on an isodetectability ellipsoid (Figure 3A). We compared the sensitivity of this ideal observer with the photocurrent ideal observer. The photocurrent ideal observer was less sensitive than the photon ideal observer, so its isodetectability ellipsoid is larger (Figure 3B). As expected, the principal axes of isodetectability ellipsoids for both ideal observers were aligned to the cone axes, because neither model includes postreceptoral interactions. Both ideal observers were relatively insensitive to S-cone-isolating stimuli, because S-cones are rare compared to L- and M-cones. For the photocurrent ideal observer, the insensitivity of the population of S-cones is partially offset by an increase in the sensitivity of individual S-cones due to their relatively unadapted state (the gain of the S-cone signals was ∼2.5 times higher than that of the L- and M-cones under the conditions of our experiments).

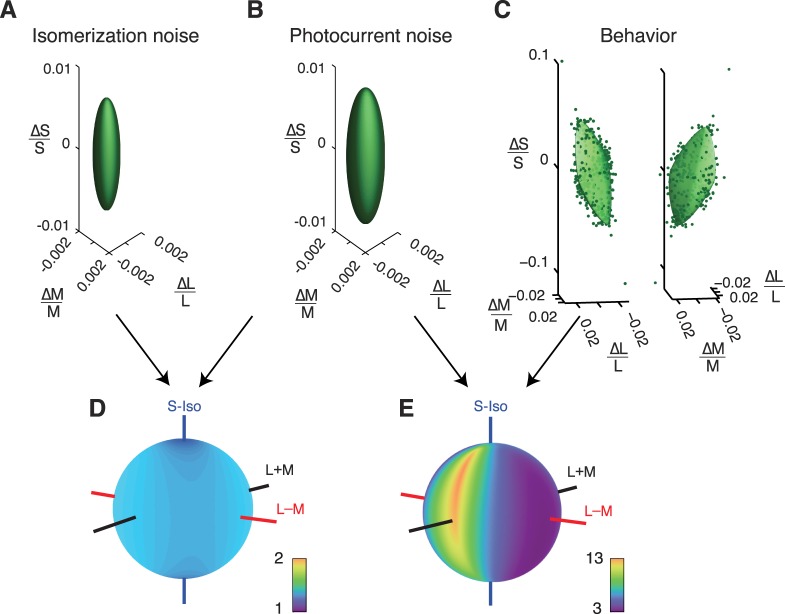
Figure 3.

Isodetectability surfaces in cone-contrast space for two ideal observers (A and B) and one monkey observer (C). The photon ideal observer had access to photon absorptions (A) and the photocurrent ideal observer had access to currents across cone outer segments (B). Two views of the same 3-D data set and fitted surface are shown in (C). The stimulus was a 3-Hz upward-drifting Gabor located 3.5° below and 5° lateral to the fixation point. (D) TRs between the photon ideal observer and the photocurrent ideal observer. (E) TRs between the photocurrent ideal observer and the monkey. Colors in the spherical heat maps represent TRs (arranged on a log scale). Cool colors indicate color directions for which the monkey is only slightly less sensitive than the ideal observer (low TRs). Warm colors indicate color directions in which the monkey is much less sensitive (high TRs). Note the different color scale between (D) and (E). The orientation of the behavioral isodetectability surface in the left panel of (C) matches the orientation of the spherical heat maps in (D) and (E). In (D) and (E) and similar plots in Figure 4, theoretical important color directions are shown as axes through the each sphere. The L − M axis (red) represents lights that do not affect the S-cones and produce L- and M-cone contrasts with identical magnitude and opposite phase. The S-cone-isolating axis (blue) represents lights that do not affect the L- or M-cones. The L + M axis (black) represents lights that do not affect the S-cones and produce L- and M-cone contrasts with identical magnitude and phase. The achromatic direction (L + M + S, not drawn) is at a 45° angle between the L + M and S-cone-isolating axes.

The isodetectability surface measured for a monkey performing a psychophysical task was not oriented along the cone axes (Figure 3C). The distortion of isodetectability surfaces between the photocurrent ideal observer and the monkey shows that sources of noise downstream of the cones degrade the representation of some stimuli more than others.

To compare the visual sensitivity of ideal and actual observers, we calculated threshold ratios (TRs) as a function of color direction. TRs calculated between the photon and photocurrent ideal observers were ∼1.4 in every color direction (Figure 3D), showing that Poisson noise in cone photoisomerization rate accounts for approximately half of the noise in the currents across the cone outer segments under the conditions of these experiments (adding two sources of independent noise with equal amplitudes increases detection threshold by 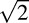≅ 1.4).

TRs calculated between the monkey and the photocurrent ideal observer ranged more broadly, from 3 to 13 (Figure 3E). The low end of this range shows that behavioral sensitivity can be within a factor of 3 of the limits set by the cone photocurrents. TR minima occurred for a broad set of chromatic directions located near the isoluminant plane, as shown by the cool colors along the great circle connecting the S and L − M axes. The TR maximum was between the S and L + M axes, near the achromatic color direction. This shows that under the conditions of this experiment (in particular, when the stimulus had low spatial and temporal frequencies: 0.5 c/°, 3 Hz), the monkey detected chromatic stimuli more efficiently than achromatic stimuli.

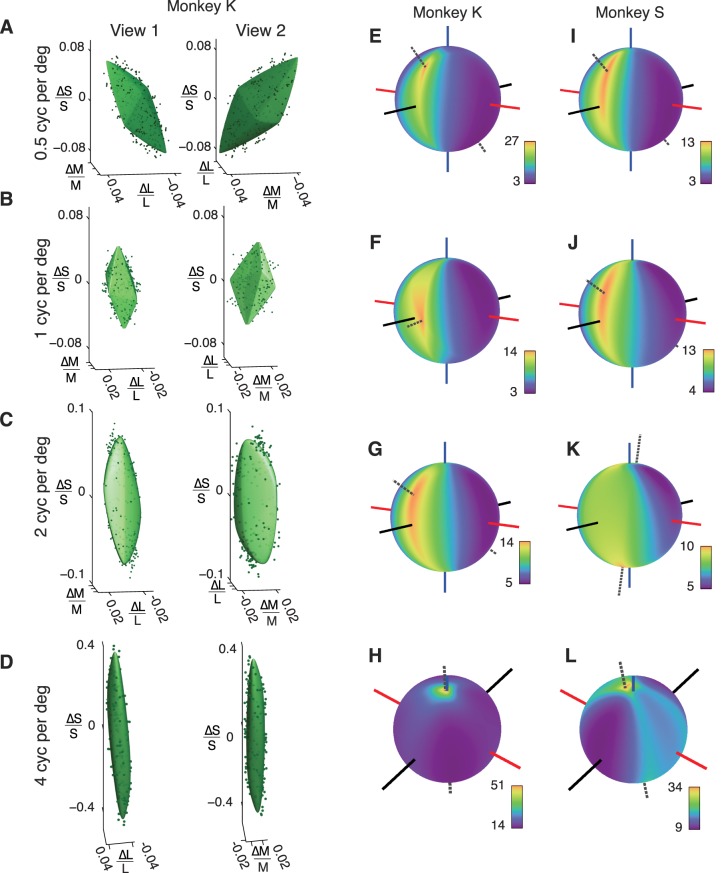
To examine the generality of this result across a broader range of spatial frequencies, we measured isodetectability surfaces for two monkeys at 0.5, 1, 2, and 4 c/° (Figure 4). In every case examined, TR as a function of color direction had a unique, well-defined maximum (dotted lines). The location of this maximum depended on spatial frequency; it lay near the L + M + S (achromatic) color direction at low spatial frequency, near L + M at intermediate spatial frequencies, and near S at the highest spatial frequency tested (4 c/°). It is important to note that the sensitivity of both ideal observers is independent of spatial frequency because neither observer filters the cone responses spatially; therefore, changes in TR with spatial frequency are due entirely to changes in the monkeys' sensitivity. Some of these changes are likely due to optical factors; approximately half of the monkeys' threshold elevation to 4-c/° S-cone-isolating patterns can be attributed to axial chromatic aberration (Flitcroft, 1989; Marimont & Wandell, 1994). Postreceptoral processing of cone signals also surely contributes to the monkeys' spatial-contrast sensitivity (see Discussion). Changes in the ratio of L- to M-cones from 1:1.5 to 1.5:1 had negligible effects on TRs.

Figure 4.

(A–D) Isodetectability surfaces for a monkey observer. Detection data and surface fits from each spatial-frequency condition are shown from two perspectives to ease visualization. The left panel in each part is matched to the rotation of the spherical heat maps in (E–H). Spherical heat maps represent TRs (monkey/photocurrent ideal observer). Dashed line in each panel indicates the direction of the TR maximum. (I–L) Spherical heat maps from a second monkey observer. Data in (I) are replotted from Figure 3E. See the legend to Figure 3 for an explanation of the axes.

Dependence of TR on other stimulus parameters

Although our focus was on chromatic sensitivity, we also explored several other factors known to alter behavioral sensitivity: spatial and temporal frequency and retinal eccentricity. These manipulations explore the range of stimuli for which the monkeys' sensitivity approaches that of the ideal observer. It is impossible to test every stimulus condition, and thus behavioral performance could come even closer to the limits set by the cones for some stimuli. Nevertheless, our study places an upper bound on the minimum threshold difference; we have documented stimulus conditions in which the ideal photocurrent observer is ∼3 times more sensitive than a monkey. Threshold ratios would be smaller by a factor of 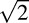if the monkey used information from one eye only (see Methods).

Figure 5A shows thresholds for the monkey and the photocurrent ideal observer as a function of spatial frequency for five color directions. These data appeared in Figure 4, but the representation in Figure 5A highlights aspects of the data that are otherwise difficult to see. Psychophysical thresholds were relatively constant for achromatic stimuli from 0.5 to 4 c/° but increased steeply for isoluminant stimuli over the same range. For all isoluminant stimuli, the relationship between spatial frequency and threshold had approximately the same form: constant from 0.5 to 1 c/° and increasing above 1 c/°.

Figure 5.

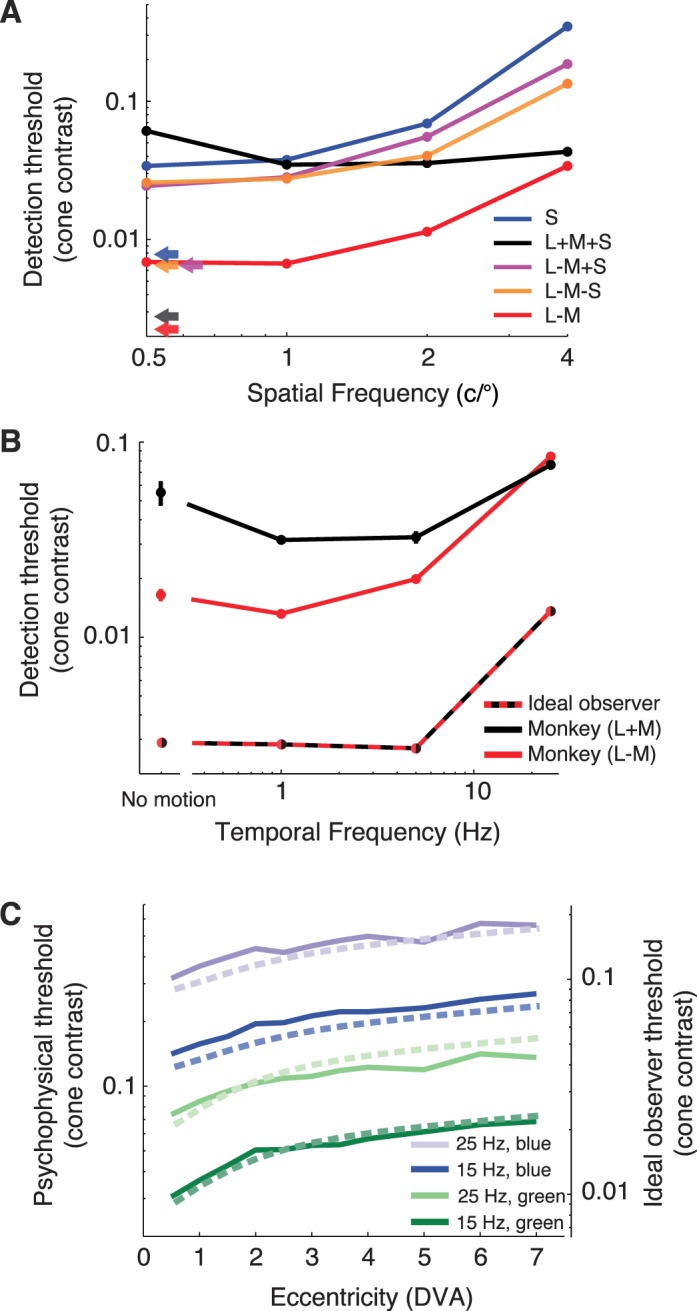
Detection threshold comparisons for the monkey and photocurrent ideal observer. (A) Effects of color and spatial frequency. Data for five color directions from Figure 4 are shown: S (blue), L + M + S (black), L − M + S (magenta), L − M − S (orange), and L − M (red). Ideal-observer thresholds are invariant to spatial frequency (arrows). (B) Effects of temporal frequency and relative phase of L- and M-cone modulation. L- and M-cones modulated in phase to create a luminance modulation (black) and out of phase to create an isoluminant modulation (red). Gabor stimuli had a standard deviation of 0.4° and a spatial frequency of 3 c/° and were 5° away from the fixation point. Error bars are ±1 standard error of the mean and in some cases are smaller than the plotting symbols. Dashed line (black and red bicolored) shows ideal-observer thresholds. (C) Effects of eccentricity, temporal frequency, and phosphor. Stimuli were Gabor patterns with a standard deviation of 0.15° and spatial frequency of 3 c/° that drifted at 15 Hz (saturated curves) or 25 Hz (pale curves), and were defined by modulation of either the green or blue monitor phosphor (green and blue, respectively). S-cones were omitted from the model for this analysis because they contribute little if anything to the detection of flicker under the conditions we used (Eisner & MacLeod, 1980). The ordinate on the left indicates monkey thresholds (solid curves), and the ordinate on the right indicates ideal-observer thresholds (dashed curves). DVA = degrees of visual angle.

Figure 5B shows thresholds as a function of temporal frequency for modulations of the L- and M-cones. Two types of stimuli were used for this comparison: in-phase (L + M) and out-of-phase (L − M) modulations. The information available at the level of the cone mosaic is invariant to the phase of the L- and M-cone modulations, so thresholds for the photocurrent ideal observer are identical for both stimuli and have the same dependence on temporal frequency. At temporal frequencies <15 Hz, the monkey's thresholds were lower for L − M modulations than for L + M modulations. This discrepancy cannot be attributed to differences in the sensitivity of the cones, and so we conclude that substantially more noise is added to the postreceptoral processing of L + M modulations than L − M at these frequencies. At 15 Hz, detection thresholds are matched, implying equivalent levels of noise for L − M and L + M signals at the level of the visual system where psychophysical detection occurs.

We also examined the effect of eccentricity (Figure 5C). Eccentricity dependence in the model comes from macular pigment and cone density. To compare the eccentricity dependence of the model to psychophysical data, we measured a monkey's detection threshold for 15- and 25-Hz drifting Gabor stimuli that varied in retinal eccentricity across blocks of trials. In interleaved trials, the Gabor was a modulation of either the blue or green monitor phosphor. Using two phosphors allowed us to dissociate the influences of macular pigment from cone density (see Methods). The photocurrent ideal observer's thresholds were lower than the monkey's by a factor of ∼3.3, but the dependence of threshold on eccentricity and phosphor were similar for the ideal observer and monkey.

Chromatic-contrast detection and comparison with V1 sensitivity

The analysis of Figure 4 shows that behavioral sensitivity to chromatic stimuli can be within a factor of 3 of the limits imposed by the cones across a broad range of color directions. This gap between the monkeys' sensitivity and that of the cone photocurrent ideal observer indicates that not all of the noise that limits chromatic detection occurs in the cone outer segments—additional noise is added downstream. Results in this section suggest that much of this additional noise is already present in the responses of individual V1 neurons.

We compared the sensitivity of the photocurrent ideal observer, V1 neurons, and the monkey to modulations in four different directions in color space: S-cone isolating, L − M, L − M − S, and L − M + S. The first two are expected to isolate the retinal cone-opponent pathways, and the second two to coactivate them. None of these color directions modulate the L- and M-cones in phase, and we consider them to be approximately isoluminant.

These behavioral and neurophysiological data were collected as part of a previous study (Hass & Horwitz, 2013). In these experiments, the orientation and spatial frequency of the stimulus were tailored to the neuron under study (other stimulus parameters—temporal frequency, duration, and size—were not adjusted). The photocurrent ideal observer's sensitivity does not depend on spatial frequency, but the monkeys' does (see Figures 4 and 5A). Consequently, the monkeys' psychophysical thresholds in the V1-recording experiments usually exceeded the photocurrent ideal observer's by a factor of >3; as spatial frequency increased, so did TRs. Color-only and color-luminance neurons (Johnson, Hawken, & Shapley, 2001) were pooled in this analysis because their chromatic sensitivity was similar (Hass & Horwitz, 2013).

The stimuli used in the V1-recording experiments were designed with respect to human cone fundamentals, not the fundamentals specified in the model. Consequently, cone modulations in the model produced by these stimuli differed subtly from those intended (e.g., the S-cone-isolating stimulus modulated the simulated L-, M-, and S-cones in the ratio 0.05:0.10:0.99). This fact had little effect on the outcome of the analysis. In particular, it did not account for an asymmetry between L − M − S and L − M + S detection described later.

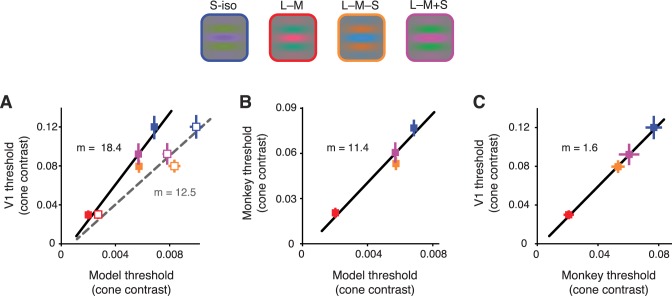
Thresholds for individual V1 neurons were related to thresholds for the photocurrent ideal observer by a factor of 18.4, which indicates that the model was 18.4 times more sensitive than the V1 neurons across these four color directions (Figure 6A). This gap in sensitivity is due in part to cone sampling; the photocurrent ideal observer had access to signals from every cone that was modulated by the stimulus, whereas the V1 neurons had access only to the signals from cones inside their receptive fields. To eliminate this difference, we repeated the analysis using a photocurrent ideal observer that had access only to cones inside the receptive field. For each V1 neuron we recorded, we estimated the receptive-field size by varying the diameter of a circular drifting grating patch from 0.5° to 2° and identifying the grating size that drove the strongest response. V1 receptive fields in our data set averaged 0.9° in diameter (SD = 0.5°), as expected at the eccentricities from which we recorded (Cavanaugh, Bair, & Movshon, 2002). When given access only to the cones inside these receptive fields, the photocurrent ideal observer was 12.5 times more sensitive than the V1 neurons (Figure 6A). With this restriction, the sensitivity relationship between the photocurrent ideal observer and V1 neurons was similar to that between the photocurrent ideal observer and the monkey's behavior (Figure 6B). A direct comparison between the monkeys' thresholds and those of V1 neurons confirmed a close match (Figure 6C). On average, V1 thresholds were a factor of ∼1.6 higher than the monkeys' in all four color directions.

Figure 6.

Sensitivity of the photocurrent ideal observer, individual V1 neurons, and behaving monkeys on the contrast detection task. Upper panel: four color directions in the isoluminant plane defined by the following unit vectors: S-iso (blue symbols) = [0 0 1], L − M (red) = [0.71 −0.71 0], L − M − S (orange) = [0.14 −0.14 −0.98], and L − M + S (magenta) = [0.14 −0.14 0.98]. Small differences between the cone fundamentals used in the V1 experiments and the model caused the simulated cones to modulate in proportions slightly different from these values. In the model, average cone contrasts were S-iso = [0.05 0.10 0.99], L − M = [0.86 −0.50 −0.05], L − M − S = [0.12 −0.19 −0.97], and L − M + S = [0.22 − 0.01 0.97]. The Gabor stimulus had a standard deviation of 0.4° truncated at 3 standard deviations and drifted at 3 Hz. The other parameters of the Gabor (orientation and spatial frequency) were optimized for each V1 neuron. (A) Neurometric thresholds of individual V1 neurons vs. detection thresholds of the ideal observer. Best-fit lines were obtained by orthogonal regression. In one version of the analysis, the ideal observer had access to all of the cones stimulated by the Gabor (closed symbols, slope of fit = 18.4); in another, it had access to just those inside the receptive field (open symbols, slope of fit = 12.5). (B) Average behavioral thresholds for the monkey vs. detection thresholds for the photocurrent ideal-observer model. (C) V1 neurometric thresholds vs. behavioral detection thresholds. All error bars represent ±1 standard error of the mean.

Discussion

The signal-to-noise ratio of currents generated in cone photoreceptor outer segments places an upper bound on photopic sensitivity. Our experiments demonstrate that the chromatic-contrast sensitivity of macaque monkeys can come within a factor of 3 of this limit. In the following, we discuss the noise model used in our analysis of the photocurrent ideal observer and the implications of our results for the neural mechanisms that mediate contrast detection. We consider the assumptions on which the model is based and how violations of these assumptions affect our conclusions. We end with future directions and a proposal for new behavioral and neurophysiological sensitivity measurements that would be particularly informative when compared against the sensitivity of the photocurrent ideal-observer model.

Non-Poisson noise model

An innovation of the photocurrent ideal observer is the incorporation of a non-Poisson noise model. Historically, cone-based ideal-observer models have assumed that noise in phototransduction is primarily caused by stochastic fluctuations in photoisomerizations due to the quantal nature of light (Banks et al., 1987; Geisler, 1989; Sekiguchi, Williams, & Brainard, 1993; Williams, Sekiguchi, & Brainard, 1993; but see Rovamo, Kankaanpää, & Kukkonen, 1999). Under these conditions, the signal-to-noise ratio is invariant with temporal frequency because the power spectra of the impulse response and cone noise are identical. In this case, any frequency dependence of behavior must originate from noise introduced after photon absorption.

Under the conditions of our experiment, cone noise exceeds that produced by Poisson fluctuations in photon absorption by a factor of 1.4. This implies that intrinsic cone noise and extrinsic photon noise impair detection efficiency by similar amounts. We expect that intrinsic cone noise plays a relatively greater role at higher background light levels, because adaptation reduces photon noise while the intrinsic noise is relatively unaffected (Angueyra & Rieke, 2013). We also expect that intrinsic cone noise will be relatively more important at higher temporal frequencies, because the power spectrum of the noise falls off less sharply with frequency than both the flash response and noise due to Poisson fluctuations.

Comparisons with individual V1 neurons

The neural circuits that underlie the detection of low-spatiotemporal-frequency chromatic patterns are equally noisy from the cones to V1 to behavior, irrespective of color direction within the isoluminant plane. In contrast, for stimuli of ≥1 c/°, monkeys and their V1 neurons are more sensitive to L − M − S (orange/cyan) than to L − M + S (lime/magenta) modulations (see Figure 6 and Hass & Horwitz, 2013). This asymmetry is presumably due to processing downstream of the cones. In the lateral geniculate nucleus, S-OFF signals are frequently paired with M-OFF signals, whereas S-ON signals are rarely paired with M-ON signals (Tailby, Szmajda, Buzás, Lee, & Martin, 2008). Moreover, S-OFF midget cells have smaller receptive fields than small bistratified S-ON cells and have stronger antagonistic receptive-field surrounds (Dacey, Crook, & Packer, 2014). One possibility is that S-OFF neurons play a greater role in the detection of high-spatial-frequency chromatic patterns than low-spatial-frequency ones. This would be consistent with a greater psychophysical sensitivity to L − M − S patterns at higher spatial frequencies. Alternatively, the asymmetry may have a cortical basis. Double-opponent V1 neurons respond weakly to uniform colored patches but strongly to chromatic modulations with spatial frequencies ≥1 c/°. Moreover, most double-opponent cells respond more strongly to L − M − S than to L − M + S modulations (Lafer-Sousa, Liu, Lafer-Sousa, Wiest, & Conway, 2012). This asymmetry in V1 may arise de novo in V1, or it may reflect the inheritance of an asymmetry already present in the lateral geniculate nucleus. Whether the asymmetry in L − M − S and L − M + S detection has a cortical or a subcortical basis is an interesting and unanswered question.

The photocurrent ideal observer bases decisions on the pooled output of the cone mosaic, but the ideal observer of V1 considers only individual neurons. Pooling the responses of V1 neurons would increase their collective sensitivity, but the joint distribution of spiking responses among V1 neurons is unknown, and the number of V1 neurons that could meaningfully contribute to a perceptual decision is poorly constrained by available data. Nevertheless, a simple model provides insight into the signal-to-noise ratio of such a pool.

To estimate the signal-to-noise ratio of a pool of weakly correlated V1 neurons, we use the formalism of Zohary, Shadlen, and Newsome (1994). We consider a pool of M neurons, each of which responds with a mean μ and a standard deviation σ to the stimulus. The d′ of the pooled response can be calculated as

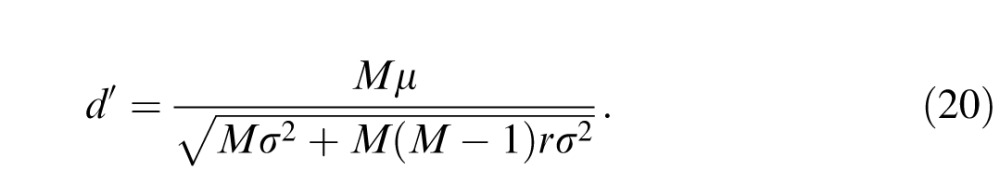If we assume an interneuronal correlation r of 0.2, the d′ of a pool of 10 neurons is 1.9 times higher than an individual neuron's d′ and 1.2 times higher than the monkey's d′ (under the conditions of our experiment, the monkey was 1.6 times more sensitive than an individual V1 neuron; see Figure 6C). The photocurrent ideal observer was ∼11 times more sensitive than the monkey under the conditions of our V1 experiments (Figure 6B) and was therefore ∼9 times more sensitive than this V1 pooling model. As the V1 pool is made larger, the d′ of the pool increases to an asymptote that is 1.4 times higher than the monkey's d′ but still 3.9 times lower than the photocurrent ideal observer's d′. The d′ of the V1 pool is therefore closer to the d′ of the monkey than it is to that of the photocurrent ideal observer, implying a substantial noise source between the cone outer segments and the recorded V1 neurons. This interpretation is consistent with the observation that detection thresholds of monkeys and an ideal observer of V1 population responses differ by a factor of ≤2 (Chen, Geisler, & Seidemann, 2006).

Model assumptions and parameter uncertainty

Responses of modeled cones were based on parameter values that were either measured directly or identified from previous studies. However, not all of the parameters were equally constrained by data. An important question is how changes to the parameters affect the output of the model.

Many of the parameters affect the absolute sensitivity of the photocurrent ideal observer without affecting its spatiotemporal chromatic tuning. Examples of these parameters include the dimensions of the eye, the cone collecting area, the eccentricity dependence of cone density, and the signal-to-noise ratio of individual cones.

The model assumes that photocurrent is linearly related to photoisomerization rate. This assumption is valid for low-contrast (<20%) stimuli. Most of the contrast thresholds reported in this article were below this bound, but S-cone contrast exceeded it in the 4-c/° condition (Figure 4H, L). The monkeys' apparent insensitivity to 4-c/° S-cone modulations might therefore be an artifact due to misestimation of the cone currents produced by this stimulus. This seems unlikely, however, because isodetectability surfaces for both monkeys had similar shapes despite differences in absolute threshold.

More generally, a number of factors could cause the assumptions of the ideal-observer model to inaccurately reflect how cone signals are integrated. We felt these factors were too uncertain to incorporate into our calculations, but they would tend to decrease the ideal observer's sensitivity and hence reduce the TRs.

Spatial and temporal integration

Ideal observers make optimal use of stimulus information, but real observers integrate over finite space and time. The monkeys' spatiotemporal integration window is difficult to estimate because the spatiotemporal limits of our stimuli were soft-edged, and we did not vary them systematically.

High-spatial-frequency chromatic gratings are difficult to detect, particularly in the periphery (R. S. Anderson, Zlatkova, & Beirne, 2002; S. J. Anderson, Mullen, & Hess, 1991; Mullen & Kingdom, 2002; Mullen, Sakurai, & Chu, 2005). We studied chromatic detection at low spatial frequencies (≤4 c/°) and parafoveal eccentricities (∼5°). It is likely that, outside of this range, the monkeys' behavioral sensitivity would fall further below that of the photocurrent ideal observer.

L- and M-cone signals are carried from the eye to the brain predominantly via the midget and parasol pathways. The compression of signals from a large number of cones to a relatively small number of retinal ganglion cells results in information loss through dimensionality reduction. Near the fovea, however, where our stimuli were presented, information is transmitted faithfully from cones to the centers of midget retinal ganglion-cell receptive fields. How much information is lost due to center–surround antagonism depends on the noisiness of neural circuitry and the invertibility of the synaptic mapping from cones to midget ganglion cells. Estimating these losses is challenging without a full spatiotemporal model of primate retinal ganglion cells.

Our stimulus had maximal contrast for 346 ms, which is on the order of a typical intersaccadic interval but is long with respect to the linear temporal integration period of contrast signals under similar conditions (Burr, 1981; Williams et al., 1993). Suboptimal temporal integration, in the retina or beyond, may have contributed to the monkeys' insensitivity relative to the ideal observer. Parasol retinal ganglion cells respond briskly to abrupt luminance changes, accounting for the greater psychophysical sensitivity for high-frequency luminance than chromatic flicker (Lee et al., 1989). The fact that the stimuli we used in this study ramped on and off slowly presumably emphasized contributions of the more sustained midget pathway. Transient stimuli would have increased the monkeys' sensitivity to luminance modulations, potentially narrowing the gap between psychophysical sensitivity and the limits set by the cones.

Future directions

We restricted our analysis primarily to stimulus configurations that we had used in previous V1-recording experiments (Hass & Horwitz, 2013). These stimulus configurations were selected to probe the low-temporal-frequency chromatic sensitivity of V1 neurons, not to test predictions of the cone model. An important future direction is to compare the results of behavioral and neurophysiological experiments to the performance of the cone model over a wider range of stimuli.

The photocurrent model predicts how stimulus detectability should vary with the spectrum and intensity of an adapting light. In the model, the cone's IRF scales with background level, and the noise does not change. The approximations are imperfect (Angueyra & Rieke, 2013; Schneeweis & Schnapf, 1999) but reasonable across the background light levels we probed (2000–8000 R*/s). An open question is whether this model accounts for aspects of visual behavior that are limited by adaptation over greater changes in light level.

The power spectral density of noise in the cone outer segments was nearly flat over the range of temporal frequencies we tested. At higher temporal frequencies, both cone signal and noise are frequency dependent (Figure 1C). How these concomitant changes in signal and noise influence visual perception is an open question. A final future direction is to merge our model with one that includes spatial blurring (Banks et al., 1987; Banks, Sekuler, & Anderson, 1991; Campbell & Gubisch, 1966; Losada, Navarro, & Santamaría, 1993; Sekiguchi et al., 1993; Williams et al., 1993).