Short abstract
Two Poisson-based distances were developed for SAGE data; their application to simulated and experimental mouse retina data show that they are more appropriate and reliable for analyzing SAGE data than other commonly used distances or similarity measures.
Abstract
Serial analysis of gene expression (SAGE) data have been poorly exploited by clustering analysis owing to the lack of appropriate statistical methods that consider their specific properties. We modeled SAGE data by Poisson statistics and developed two Poisson-based distances. Their application to simulated and experimental mouse retina data show that the Poisson-based distances are more appropriate and reliable for analyzing SAGE data compared to other commonly used distances or similarity measures such as Pearson correlation or Euclidean distance.
Background
Serial analysis of gene expression (SAGE) is an effective technique for comprehensive gene-expression profiling. It has been used in studies of a wide range of biological systems [1-5]. Several SAGE analysis methods have been developed, primarily for extracting SAGE tags and identifying differences in mRNA levels between two libraries [2,3,6-11]. However, searching for patterns and grouping transcripts into expression clusters provides additional insight into the biological function and relevance of genes that show different expression. Thus, it is essential to investigate appropriate and reliable clustering methods for analyzing SAGE data.
Successful clustering analysis depends on choosing an appropriate distance or similarity measure [12] that takes into account the underlying biology and the nature of the data. Commonly used measures include the Pearson correlation and Euclidean distance for data with a normal distribution [12]. Those measures have been successful in microarray expression data analysis. However, SAGE data are generated by sampling, which results in 'counts', and are governed by different statistics from those of microarray data. Thus, the distance metrics suitable for measuring dissimilarity of microarray data may not be suitable for SAGE data. In this regard, SAGE data have been poorly exploited owing to a lack of appropriate statistical methods that consider the specific properties of SAGE data.
In this paper, we assume that the tag counts follow a Poisson distribution. This is a natural assumption seeing how SAGE data are generated (see Materials and methods for details). We use the chi-square statistic as a measure of the deviation of observed tag counts from expected counts, and employ it within a K-means clustering [13] procedure. We call this newly developed algorithm PoissonC. To evaluate the PoissonC algorithm, we applied it to a simulated dataset and a set of experimental mouse retinal SAGE libraries. The simulation results demonstrate clear advantages of using the chi-square statistic over Pearson correlation and Euclidean distance when the data are sampled from Poisson distributions. When applied to the mouse retinal SAGE libraries, PoissonC produced clusters of more biological relevance than clusters generated by some other popular clustering methods. This superior performance of PoissonC partially confirms the validity of the Poisson model.
In addition to the chi-square statistic, we also studied the use of the log-likelihood: that is, the logarithm of the joint probability of the observed counts under the expected model as a measure of similarity in the K-means clustering procedure. We call this algorithm PoissonL. The PoissonL algorithm is based purely on the Poisson assumption; thus it would not work well unless the data follow at least an approximate Poisson distribution. PoissonL and other methods, including PoissonC, K-means using Pearson correlation distance (PearsonC), and K-means using Euclidean distance (Eucli), were applied to a set of 143 mouse SAGE tags with known functional annotations. The clustering results show that PoissonL performs the best and PoissonC second (both within 5% error rate). Both PoissonL and PoissonC outperform PearsonC and Eucli. The success of Poisson-based algorithms further confirms the validity of Poisson model.
Although PoissonL performs best, it is also the slowest. It is at least 10 times slower than any of the other algorithms. Thus, PoissonC is more practical and appropriate for large SAGE datasets, providing results comparable to PoissonL but computationally much more efficient. The software of K-means procedure using the above distances and similarity measures is available to researchers at [14].
In this study, we implemented the Poisson-based distances in the K-means procedure to show that the Poisson-based distances perform better than Pearson correlation and Euclidean distance in clustering SAGE data. In addition to K-means, many other popular clustering methods are being used for revealing patterns of gene expression, including hierarchical clustering [15,16], self-organizing maps (SOMs) [17] and model-based cluster methods [18-20]. The Poisson-based distances can be implemented in those clustering procedures as well.
Results
Clustering results of the simulation data
To evaluate the performance of the PoissonC algorithm, we first applied it to simulated data. An illustrative example of the simulated dataset is shown in Table 1, which consists of simulated counts of 20 tags at five time points. All the counts are generated independently from Poisson distributions, and the 20 tags belong to four groups - A, B, C, and D - according to the models they are generated from. The four groups are of size three, four, six, and seven, respectively. The tags from the same group have the same expression profile, and the expression profile is determined by the relative expression across different time points rather than the absolute expression level. For instance, b4 from group B is generated from the Poisson distributions with means μ = (100,300,300,600,100), while other members of group B are generated from the Poisson distributions with mean μ' = (10,30,30,60,10); μ = 10 μ'.
Table 1.
List of simulated data
| Group A | P(0.05)* | P(0.05) | P(0.05) | P(15) | P(150) |
| a1 | 0 | 0 | 0 | 19 | 145 |
| a2 | 0 | 0 | 0 | 13 | 146 |
| a3 | 0 | 0 | 0 | 13 | 154 |
| Group B | P(10) | P(30) | P(30) | P(60) | P(10) |
| b1 | 16 | 33 | 31 | 60 | 12 |
| b2 | 8 | 23 | 23 | 59 | 18 |
| b3 | 11 | 30 | 39 | 76 | 14 |
| b4† | 109 | 306 | 296 | 620 | 93 |
| Group C | P(10) | P(10) | P(10) | P(10) | P(10) |
| c1 | 10 | 11 | 9 | 2 | 11 |
| c2 | 12 | 11 | 10 | 12 | 7 |
| c3 | 4 | 10 | 16 | 14 | 6 |
| c4 | 10 | 8 | 8 | 7 | 12 |
| c5 | 9 | 6 | 9 | 18 | 12 |
| c6‡ | 99 | 84 | 77 | 102 | 106 |
| Group D | P(15) | P(0.05) | P(0.05) | P(0.05) | P(150) |
| d1 | 19 | 0 | 0 | 0 | 154 |
| d2 | 17 | 0 | 0 | 0 | 148 |
| d3 | 12 | 0 | 0 | 0 | 173 |
| d4 | 10 | 0 | 0 | 0 | 148 |
| d5 | 12 | 0 | 0 | 0 | 152 |
| d6 | 15 | 0 | 0 | 0 | 146 |
| d7 | 13 | 0 | 0 | 1 | 149 |
* P(0.05): Poisson distribution with mean 10. †b4 is generated by P(100), P(300), P(300), P(600), P(100). ‡c6 is generated by P(100), P(100), P(100), P(100), P(100).
For comparison, we applied PoissonC, PearsonC and Eucli to the simulated data. The clustering results from different methods are shown in Figure 1. Data were normalized before plotting. For each tag, the count vector (tag frequency in each SAGE library) is rescaled to make the sum of the elements of the count vector equals 1; for example, b4 = (109,306,296,620,93) is rescaled to b4' = b4/θ, where θ = 109 + 306 + 296 + 620 + 93.
Figure 1.
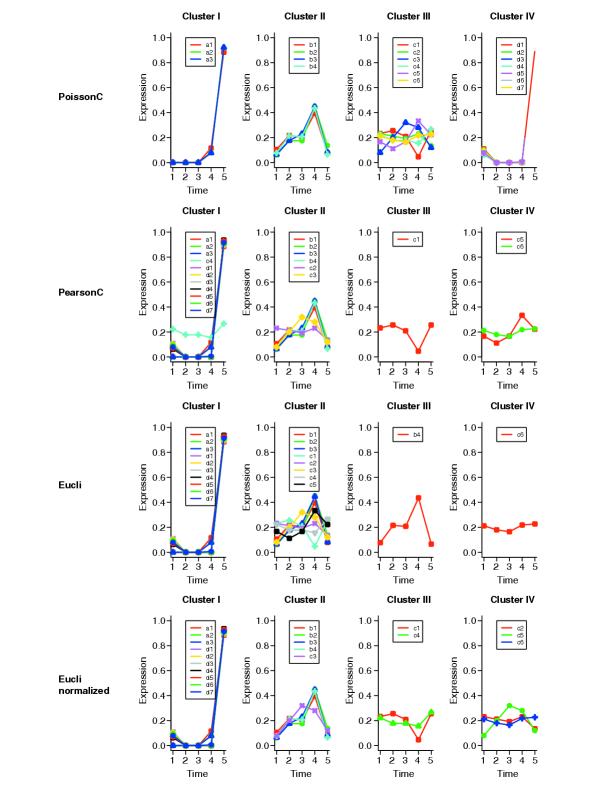
Graphs of clustering results for simulation data. The x-axis represents the different time points; the y-axis represents the expression level scaled as percentage. Data were normalized before plotting. For each tag, the count vector is rescaled to make the sum of the elements of the count vector equal 1. For example, b4 = (109,306,296,620,93) is rescaled to b4' = b4/θ where θ = (109 + 306 + 296 + 620 + 93).
In Figure 1, only PoissonC clustered the tags correctly into four groups. PearsonC and Eucli incorrectly assigned most of the tags to clusters I and II. The poor performance of PearsonC may be due to the fact that the Pearson correlation distance only compares the shape of the curves, but neglects the magnitude of changes. For instance, the Pearson correlation coefficient (PCC) between c4 = (10,8,8,7,12) and c5 = (9,6,9,18,12) is only -0.16 while the PCC between c4 = (10,8,8,7,12) and d1 = (19,0,0,0,154) is 0.89. The Eucli algorithm identified two single-member clusters (III and IV in Figure 1). This is because Euclidean distance takes the difference between data points directly; thus it may be overly sensitive to the magnitude of changes. So, b4 and c6 are clustered alone because of their large magnitudes. To reduce the magnitude effects, we apply Eucli to the normalized data. Data normalization was performed in the same way as we did for plotting. Figure 1 shows that the clustering results on normalized data were cleaner and more accurate than the results on un-normalized data, although there were still many tags incorrectly grouped in clusters I and II.
We performed an additional 100 replications of the above simulation. PoissonC correctly clustered 90 of the 100 replicate datasets. Eucli on normalized data correctly clustered 49 of the 100 datasets while PearsonC or Eucli on un-normalized data never generated correct clusters.
To further test these methods, we applied the different algorithms to a larger simulated dataset containing 2,000 tags with counts at five different time points. Results were similar to those observed for the smaller dataset (data not shown).
Thus, when data are Poisson distributed, the Poisson-based method, PoissonC, is superior to the non-Poisson methods, for example PearsonC and Eucli. The performance of the Eucli algorithm can be improved to some extent when it is applied to normalized data.
Clustering results of experimental SAGE data
To validate our newly developed PoissonC algorithm on experimental SAGE data, we applied PoissonC, PearsonC and Eucli to a set of mouse retinal SAGE libraries. The raw mouse retinal data consists of 10 SAGE libraries (38,818 unique tags with tag counts ≥ 2) from developing retina taken at 2-day intervals, ranging from embryonic day 12.5 (E12.5) to postnatal day 6.5 (P6.5), P10.5 and adult [21]. Of the 38,818 tags, 1,467 with counts equal to or greater than 20 in at least one of the 10 libraries were selected. These 1,467 tags were the potentially most biologically relevant SAGE tags because of their high tag frequencies. These 1,467 tags were grouped into 30 clusters using each of the algorithms, PoissonC, PearsonC and Eucli on original and normalized data. Clusters from each algorithm were compared and analyzed in detail. In general, the patterns revealed by the clusters under different algorithms roughly agreed with each other. SAGEmap (tag to gene mapping) [22] was used to evaluate the biological relevance for all clusters. Analysis of a set of clusters corresponding to mouse photoreceptor genes is presented in Figure 2 as an illustrative example. The comparison statistics are summarized in Table 2.
Figure 2.
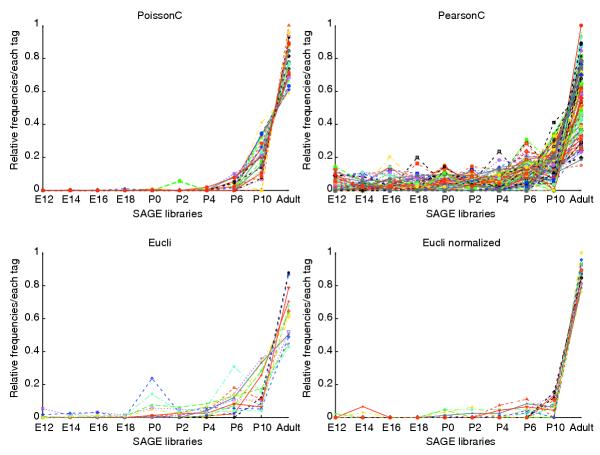
Graphs of clustering results for mouse retinal SAGE data. The x-axis represents the time points of the developing mouse retina SAGE libraries; the y-axis represents the relative frequency for each tag scaled as a percentage. Data were normalized before plotting. Each tag from the 10 libraries was rescaled to make the sum of all 10 tags equal to 1. Different colors represent different tags. See Additional data file 1 for more details.
Table 2.
Statistics of photoreceptor-generated clusters by four different algorithms
| Algorithm | Number of total members | Number of specific genes | Percentage of specific genes | Number of rhodopsin tags |
| PoissonC | 28 | 22 | 78.6 | 5 of 5 |
| PearsonC | 67 | 24 | 35.8 | 2 of 5 |
| Eucli | 12 | 8 | 66.7 | 2 of 5 |
| Eucli on normalized data | 17 | 12 | 70.6 | 2 of 5 |
See Additional data file 1 for more details.
The clusters in Figure 2 show high tag counts in late retinal development, that is, P6, P10 and adult, and their gene-expression pattern correlates with photoreceptor cell differentiation. The cluster generated by PoissonC contains 28 tags, and 78.6% (22 of 28) of those tags mapped to photoreceptor genes, for example rhodopsin, cone opsin and recoverin. Importantly, all five of the 'rhodopsin' tags were grouped together. The clusters generated by PearsonC or Eucli are much noisier. The percentages of photoreceptor-specific genes were 35.8%, 66.7% and 70.6% for PearsonC and Eucli on original and normalized data, respectively (Table 2). Only two of the five rhodopsin tags were correctly grouped by PearsonC or Eucli, or Eucli on normalized data (Table 2).
To test the sensitivity and specificity of PoissonC for clustering SAGE data, four sets of clusters (number of clusters (K) = 25) were generated for the 1,467 tags by each of the different algorithms. Thirty-four tags that showed the most dynamic and cell-specific expression in the mouse neonatal retina (developmental stages P0-P6 [21]) were selected to compare the ability of each of the four algorithms to cluster these 34 'cell-specific' tags into appropriate clusters (see Additional data file). For these 34 tags, PoissonC generated clusters that are most enriched for cell-specific genes (Table 3).
Table 3.
Statistics of the 34 cell-specific genes
| Cell-specific genes | Total | Sensitivity | Specificity |
| PoissonC | |||
| 13 | 50 | 38.2% | 26.0% |
| 1 | 7 | 2.9% | 14.3% |
| 5 | 42 | 14.7% | 11.9% |
| 3 | 68 | 8.8% | 4.4% |
| 3 | 90 | 8.8% | 3.3% |
| PearsonC | |||
| 12 | 86 | 35.3% | 14.0% |
| 3 | 52 | 8.8% | 5.8% |
| 3 | 55 | 8.8% | 5.5% |
| 3 | 75 | 8.8% | 4.0% |
| 3 | 81 | 8.8% | 3.7% |
| Eucli | |||
| 2 | 13 | 5.9% | 15.4% |
| 7 | 77 | 20.6% | 9.1% |
| 12 | 206 | 35.3% | 5.8% |
| 1 | 22 | 2.9% | 4.5% |
| 4 | 142 | 11.8% | 2.8% |
| Eucli on normalized data | |||
| 10 | 48 | 29.4% | 20.8% |
| 5 | 53 | 14.7% | 9.4% |
| 7 | 77 | 20.6% | 9.1% |
| 2 | 24 | 5.9% | 8.3% |
| 2 | 47 | 5.9% | 4.3% |
The numbers in the first column are the numbers of cell-specific genes in a cluster; total, the total number of cluster members; sensitivity, the number of cell-specific genes/34; specificity, the number of cell-specific genes/total number of cluster members. The top five clusters that contain the 34 cell-specific genes are listed. The numbers in bold are the highest percentage in sensitivity and specificity in that method. See Additional data file 2 for more details.
It is impossible to judge the performance of the algorithms on clustering SAGE tags with unknown biological function(s). Many SAGE tags have not been annotated in the current release of SAGEmap (the version used was last updated on 3 April, 2004); for example, 126,111 of the 508,202 mouse tags are RIKEN cDNAs. For the 1,467 mouse retinal SAGE tags, 247 tags are RIKEN cDNAs (with unknown biological function) and 32 tags have no matches with SAGEmap. To compare the clustering algorithms effectively, a subset of 143 SAGE tags all with known biological functions were selected. These 143 tags fall into six clusters on the basis of their biological function(s), cell-type specific gene expression, or timing of gene expression during mouse retinal development.
PoissonC, PoissonL, PearsonC, and Eucli were applied to group these 143 tags in six clusters. Results show that 4, 6 and 14 of the 143 tags were in the incorrect clusters for PoissonL, PoissonC, and Eucli on normalized data, respectively (Table 4). There were too many tags in the incorrect clusters for PearsonC and Eucli on original data to perform a correct statistical study (data not shown). The performance of PoissonL and PoissonC were very close: PoissonL and PoissonC correctly grouped 97.2% (139 of 143) tags and 95.8% (137 of 143), respectively. Both algorithms have an error rate of less than 5% (Table 4).
Table 4.
Comparison of algorithms on 143 tags
| Algorithm | Number of tags in incorrect clusters | Percentage of tags in incorrect clusters |
| PoissonL | 4 | 2.8 |
| PoissonC | 6 | 4.2 |
| Eucli on normalized data | 14 | 9.8 |
| PearsonC | NA | NA |
| Eucli | NA | NA |
Clusters generated by PearsonC and Eucli were too messy.
Discussion
In this study, we have implemented the Poisson-based distances into the K-means procedure and demonstrated that the Poisson-based distances have advantages over the Pearson correlation and Euclidean distance in clustering SAGE data. The poor performance of PearsonC and Eucli may be due to the fact that the Pearson correlation distance only cares about the shape of the curves, but neglects the magnitude of changes, while the Euclidean distance takes the difference between data points directly and may be overly sensitive to the magnitude of changes.
An unsolved issue in K-means clustering analysis is the estimation of K, the number of clusters. If K is unknown, starting with arbitrary random K is a relatively poor method. Hartigan [23] proposed a stage-wise method to determine the K value. However, when sporadic points are present in the dataset, Hartigan's method may fail. The recently introduced method of TightCluster [24] partially solves this problem by a resampling method to sequentially attain tight and stable clusters in order of decreasing stability.
The Poisson-based methods PoissonC and PoissonL are appropriate for clustering analysis of data with Poisson distribution, for example SAGE data, data from the massive parallel signature sequencing (MPSS) profiling [25], and digital gene expression un-normalized EST datasets. MPSS is similar to SAGE in that it is a sampling method that permits quantification of the number of specific mRNAs in an RNA sample.
Conclusions
From the analysis of simulation data and the experimental mouse retinal SAGE data, we demonstrate that the Poisson-based methods, PoissonC and PoissonL, are more appropriate for analyzing SAGE data. The success of PoissonC and PoissonL indicates that an effective method for analyzing large-scale gene-expression data must be based on an understanding of the biological and statistical nature of the experimental data.
Materials and methods
Poisson assumption
In a SAGE experiment, a subset of transcripts from a cell or tissue is sampled for tag extraction. The number of sampled transcripts of a particular type is binomially distributed when the sampling process is random. In this multinomial process, the selection probability of a particular type of transcript at each draw should be very small considering the numerous types of transcripts in a particular cell or tissue. Thus the binomial distribution is well approximated by a Poisson limit [26], and we can assume that the number of sampled transcripts of each type is approximately Poisson distributed.
Probability model
We assume that the count of each tag in a SAGE library is Poisson distributed. These Poisson distributions are independent of each other across different tags and libraries.
Let Yi(t) be the count of tag i in library t, and Yi(t) ~ Poisson(λi(t)θi). The expected count λi(t)θi consists of two factors: θi is the expected sum of counts of transcript i (tag i) over all libraries; λi(t) is the contribution of transcript i in library t to the sum θi expressed in percentage.
when a total of T libraries are considered. So λi(t)θi redistributes the tag counts according to the cluster profile (λ) but keeps the sum of counts across libraries constant.
The goal is to group the transcripts with similar relative expression patterns across different libraries, that is to cluster tags by their λi(t) values. We assume that the tags within a cluster share the same λ = (λ(1),λ(2), ..., λ (T)), and λ uniquely represents the cluster profile. Letting Yi = (Yi(1),..., Yi(T)), we have the following joint likelihood function for a cluster consisting of tags 1, 2, ..., m:
The maximum likelihood estimate of λs and θs are:
For a set of tags assumed to be in the same cluster, we then can estimate the cluster model λ and the total count θ for each tag by formula (2). It is natural to use the joint likelihood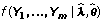 
to evaluate how well the observed counts Y1,...,Ym fit the expected Poisson models. The larger the likelihood is, the more likely that the observed counts are generated from the expected model. Then the tags 1, 2, ..., m share the same pattern of expression. We can also use the chi-square test statistic to evaluate how well the observed tag count fits the estimated cluster model, which is to calculate
.
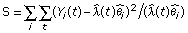The larger the value of S, the less likely that the tags within a cluster share the same pattern of expression. Using the chi-square test statistic, the penalty for deviation from a large expected count is smaller than that for a small expected count. This is consistent with the Poisson probability function 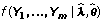, which has the property of mean = variance.
PoissonC/PoissonL algorithm
The K-means cluster algorithm [23] generates good clusters by specifying a desired number of clusters, say, K, and then assigning each object to one of the K clusters in such a way as to minimize a measure of dispersion within clusters. In this work, we modified the K-means clustering algorithm by using the chi-square statistic or the joint likelihood as distance/similarity measures instead of using the Pearson correlation, Euclidean distance or other distances. The PoissonC/PoissonL algorithm is sketched below:
1. All SAGE tags are assigned at random to K sets. Estimate θj for each tag by formula (2).
2. Set cluster centers λk(0) from formula (2). If tag j belongs to cluster k, Yj is expected to be generated from joint Poisson distribution with mean λk(0) θj, the expected counts of tag j. Current iteration i = 0.
3. In the ith iteration, assign each tag j to the cluster with the best fit model.
(a) When the chi-square statistic is used, tag j is assigned to the cluster with minimum
.
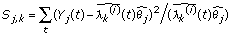(b) When joint likelihood is used, tag j is assigned to the cluster with minimum
.
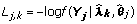4. Set new cluster centers λk(i + 1).
5. Go to step 3 until convergence.
In total, if c(j) denotes the cluster number that tag j is assigned to, the PoissonC or PoissonL algorithm is to minimize the within-cluster dispersion
or
,
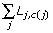respectively.
When data are Poisson distributed, PoissonL is expected to perform better than PoissonC. Experimental SAGE data analysis confirms that PoissonL was slightly better than PoissonC. However, PoissonL is too slow to apply to large datasets.
Implementation
The algorithms are implemented in both C++ and Java. The routines for the EM algorithm for reassigning cluster members are from the work of Michiel de Hoon and colleagues at the Human Genome Center at the University of Tokyo. The algorithm described here is available from [14].
Additional data files
The following additional files are available with the online version of this article: Further details for Figure 2 and Table 2 and a list of 28, 67, 12, and 17 members of the photoreceptor clusters generated by PoissonC, PearsonC, Eucli, and Eucli on normalized data, respectively (Additional data file 1); additional data for Table 3 and a list of the 34 'cell-specific' mouse SAGE tags (Additional data file 2).
Supplementary Material
Further details for Figure 2 and Table 2 and a list of 28, 67, 12, and 17 members of the photoreceptor clusters generated by PoissonC, PearsonC, Eucli, and Eucli on normalized data, respectively
Additional data for Table 3 and a list of the 34 'cell-specific' mouse SAGE tags
Acknowledgments
Acknowledgements
We thank members of the Department of Research Computing at Dana-Faber Cancer Institute and Feng X. Zhao for converting the C++ version of the algorithm to a Java program. S.B. was a Howard Hughes Medical Institute Fellow of the Life Sciences Research Foundation. This research was supported by NSF grant GMS-0204674, NIH grant R01 HG02518-01 to J.S.L; the Howard Hughes Medical Institute, NIH grant EY08064, the Foundation for Retinal Research to C.L.C.; and NIH grant P20 CA96470 to W.H.W.
Contributor Information
Li Cai, Email: lcai@research.dfci.harvard.edu.
Haiyan Huang, Email: hhuang@stat.Berkeley.EDU.
Wing H Wong, Email: wwong@stat.harvard.edu.
References
- Blackshaw S, Fraioli RE, Furukawa T, Cepko CL. Comprehensive analysis of photoreceptor gene expression and the identification of candidate retinal disease genes. Cell. 2001;107:579–589. doi: 10.1016/S0092-8674(01)00574-8. [DOI] [PubMed] [Google Scholar]
- Zhang L, Zhou W, Velculescu VE, Kern SE, Hruban RH, Hamilton SR, Vogelstein B, Kinzler KW. Gene expression profiles in normal and cancer cells. Science. 1997;276:1268–1272. doi: 10.1126/science.276.5316.1268. [DOI] [PubMed] [Google Scholar]
- Velculescu VE, Zhang L, Vogelstein B, Kinzler KW. Serial analysis of gene expression. Science. 1995;270:484–487. doi: 10.1126/science.270.5235.484. [DOI] [PubMed] [Google Scholar]
- Buckhaults P, Zhang Z, Chen YC, Wang TL, St Croix B, Saha S, Bardelli A, Morin PJ, Polyak K, Hruban RH, et al. Identifying tumor origin using a gene expression-based classification map. Cancer Res. 2003;63:4144–4149. [PubMed] [Google Scholar]
- Porter D, Weremowicz S, Chin K, Seth P, Keshaviah A, Lahti-Domenici J, Bae YK, Monitto CL, Merlos-Suarez A, Chan J, et al. A neural survival factor is a candidate oncogene in breast cancer. Proc Natl Acad Sci USA. 2003;100:10931–10936. doi: 10.1073/pnas.1932980100. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Margulies EH, Innis JW. eSAGE: managing and analysing data generated with serial analysis of gene expression (SAGE). Bioinformatics. 2000;16:650–651. doi: 10.1093/bioinformatics/16.7.650. [DOI] [PubMed] [Google Scholar]
- van Ruissen F, Jansen BJ, de Jongh GJ, van Vlijmen-Willems IM, Schalkwijk J. Differential gene expression in premalignant human epidermis revealed by cluster analysis of serial analysis of gene expression (SAGE) libraries. FASEB J. 2002;16:246–248. doi: 10.1096/fj.01-0618fje. [DOI] [PubMed] [Google Scholar]
- Audic S, Claverie JM. The significance of digital gene expression profiles. Genome Res. 1997;7:986–995. doi: 10.1101/gr.7.10.986. [DOI] [PubMed] [Google Scholar]
- Madden SL, Galella EA, Zhu J, Bertelsen AH, Beaudry GA. SAGE transcript profiles for p53-dependent growth regulation. Oncogene. 1997;15:1079–1085. doi: 10.1038/sj.onc.1201091. [DOI] [PubMed] [Google Scholar]
- Man MZ, Wang X, Wang Y. POWER_SAGE: comparing statistical tests for SAGE experiments. Bioinformatics. 2000;16:953–959. doi: 10.1093/bioinformatics/16.11.953. [DOI] [PubMed] [Google Scholar]
- Blackshaw S, Kuo WP, Park PJ, Tsujikawa M, Gunnersen JM, Scott HS, Boon WM, Tan SS, Cepko CL. MicroSAGE is highly representative and reproducible but reveals major differences in gene expression among samples obtained from similar tissues. Genome Biol. 2003;4:R17. doi: 10.1186/gb-2003-4-3-r17. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Quackenbush J. Computational analysis of microarray data. Nat Rev Genet. 2001;2:418–427. doi: 10.1038/35076576. [DOI] [PubMed] [Google Scholar]
- Tavazoie S, Hughes JD, Campbell MJ, Cho RJ, Church GM. Systematic determination of genetic network architecture. Nat Genet. 1999;22:281–285. doi: 10.1038/10343. [DOI] [PubMed] [Google Scholar]
- SAGE data analysis using a Poisson approach http://genome.dfci.harvard.edu/sager
- Eisen MB, Spellman PT, Brown PO, Botstein D. Cluster analysis and display of genome-wide expression patterns. Proc Natl Acad Sci USA. 1998;95:14863–14868. doi: 10.1073/pnas.95.25.14863. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wen X, Fuhrman S, Michaels GS, Carr DB, Smith S, Barker JL, Somogyi R. Large-scale temporal gene expression mapping of central nervous system development. Proc Natl Acad Sci USA. 1998;95:334–339. doi: 10.1073/pnas.95.1.334. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tamayo P, Slonim D, Mesirov J, Zhu Q, Kitareewan S, Dmitrovsky E, Lander ES, Golub TR. Interpreting patterns of gene expression with self-organizing maps: methods and application to hematopoietic differentiation. Proc Natl Acad Sci USA. 1999;96:2907–2912. doi: 10.1073/pnas.96.6.2907. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Li C, Wong WH. Model-based analysis of oligonucleotide arrays: expression index computation and outlier detection. Proc Natl Acad Sci USA. 2001;98:31–36. doi: 10.1073/pnas.011404098. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ramoni MF, Sebastiani P, Kohane IS. Cluster analysis of gene expression dynamics. Proc Natl Acad Sci USA. 2002;99:9121–9126. doi: 10.1073/pnas.132656399. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fraley C, Raftery AE. How many clusters? which cluster method? answers via model-based cluster analysis. Computer J. 1998;41:578–588. [Google Scholar]
- Blackshaw S, Harpavat S, Trimarchi J, Cai L, Huang H, Kuo WP, Fraioli RE, Cho S-H, Yung R, Asch E, et al. Genomic analysis of mouse retinal development. PLoS Biol. 2004. [DOI] [PMC free article] [PubMed]
- SAGEmap http://www.ncbi.nlm.nih.gov/SAGE
- Hartigan J. Clustering Algorithms. New York and London: Wiley; 1975. [Google Scholar]
- Tseng GC, Wong WH. A resampling method for tight clustering: with an application to microarray analysis. Biometrics. 2004.
- Brenner S, Johnson M, Bridgham J, Golda G, Lloyd DH, Johnson D, Luo S, McCurdy S, Foy M, Ewan M, et al. Gene expression analysis by massively parallel signature sequencing (MPSS) on microbead arrays. Nat Biotechnol. 2000;18:630–634. doi: 10.1038/76469. [DOI] [PubMed] [Google Scholar]
- Ewens WJ, Grant GR. Statistical Methods in Bioinformatics. 1. Berlin & Heidelberg: Springer Verlag; 2001. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Further details for Figure 2 and Table 2 and a list of 28, 67, 12, and 17 members of the photoreceptor clusters generated by PoissonC, PearsonC, Eucli, and Eucli on normalized data, respectively
Additional data for Table 3 and a list of the 34 'cell-specific' mouse SAGE tags