Simultaneous determination of sample thickness, tilt, and electron mean free path using tomographic tilt images based on Beer-Lambert law

Abstract

Cryo-electron tomography (cryo-ET) is an emerging technique that can elucidate the architecture of macromolecular complexes and cellular ultrastructure in a near-native state. Some important sample parameters, such as thickness and tilt, are needed for 3-D reconstruction. However, these parameters can currently only be determined using trial 3-D reconstructions. Accurate electron mean free path plays a significant role in modeling image formation process essential for simulation of electron microscopy images and model-based iterative 3-D reconstruction methods; however, their values are voltage and sample dependent and have only been experimentally measured for a limited number of sample conditions. Here, we report a computational method, tomoThickness, based on the Beer-Lambert law, to simultaneously determine the sample thickness, tilt and electron inelastic mean free path by solving an overdetermined nonlinear least square optimization problem utilizing the strong constraints of tilt relationships. The method has been extensively tested with both stained and cryo datasets. The fitted electron mean free paths are consistent with reported experimental measurements. The accurate thickness estimation eliminates the need for a generous assignment of Z-dimension size of the tomogram. Interestingly, we have also found that nearly all samples are a few degrees tilted relative to the electron beam. Compensation of the intrinsic sample tilt can result in horizontal structure and reduced Z-dimension of tomograms. Our fast, pre-reconstruction method can thus provide important sample parameters that can help improve performance of tomographic reconstruction of a wide range of samples.

Introduction

In recent years, cryo-electron tomography (cryo-ET) has emerged as a powerful imaging technique that allows 3D visualization of sub-cellular architecture and macromolecular organization in a near-native and fully frozen-hydrated state. Cryo-ET circumvents the deleterious effects from fixation, dehydration or staining (Frank, 2006; van Heel et al., 2000). This technique bridges the gap of knowledge between cellular architecture revealed by low resolution light microscopy and high resolution structures of macromolecular complexes by single particle cryo-EM.

To prepare samples for cryo-ET, a commonly used technique is plunge freezing in which the sample solution is deposited onto a holey-carbon coated grid, blotted with filter paper, and vitrified by rapidly plunging into a cryogen (e.g. liquid ethane) cooled by liquid nitrogen (Adrian et al., 1984; Dubochet et al., 1988). However, this method has poor control of thickness of the resulted vitreous ice. Another technique for cryo-sample preparation is cryo-sectioning in which the high pressure frozen thick specimen is trimmed using a diamond knife. Unfortunately, previous studies have shown that there is considerable variation in section thickness, especially for thin sections (Luther, 2006). Focused ion beam (FIB) milling has gained considerable acceptance in recent years as a precision section preparation method. However, slice thickness by FIB still has unignorable variations due to differential thermal expansion (Boergens and Denk, 2013), charging (Jones et al., 2014; Schaffer et al., 2007), stage movements (Korte et al., 2011) or ion beam instabilities (Jones et al., 2014).

To obtain a high quality tomogram, it is essential to use volumes with sufficiently large Z-dimension to contain the entire sample. Due to lack of both thickness control during sample preparation and a method for reliable estimation of sample thickness, it is common practice to use a large Z-dimension for 3-D reconstruction. Alternatively, a trial reconstruction of a small region can be used to first determine the thickness before a full reconstruction is performed. However, the poor image contrast and the significant smearing along Z-axis due to missing wedge often render the sample boundaries hard to detect. It is thus desirable to have a method to reliably determine sample thickness to allow 3-D reconstruction with optimal Z-dimension, which will not only eliminate the need for trial reconstruction but also improve the speed of reconstruction by reducing the tomogram volume to the smallest possible Z-dimension. Current methods for thickness measurement include measuring the shift of top/bottom surface projections of a small cylindrical hole through sample in a tilt pair image (Cheng et al., 2006), image contrast between open and sample area (Cheng et al., 2006), and electron energy loss spectroscopy (Cho et al., 2013; Malis et al., 1988). The first method is destructive to the sample while the last two methods rely on an accurately known electron mean free path (Zhang et al., 2012). Unfortunately, the mean free path is dependent on accelerating voltage and sample types, and can vary significantly as shown by drastically different values obtained by experimental measurements for a few sample conditions (Feja and Aebi, 1999; Grimm et al., 1996; Vulovic et al., 2013). Different elemental compositions of the sample, for example, samples stained with heavy metals vs cryo biological samples mostly composed of low atomic number elements, can lead to a large change of mean free path (Langmore and Smith, 1992; Wall et al., 1974). It is desirable to have a convenient method that can reliably estimate the mean free path of every sample.

It is a common assumption in cryo-EM that the specimen plane is horizontal and thus perpendicular to the electron beam. However, unintended sample tilts have often been observed due to multiple factors, including undulation of the carbon support film (Mindell and Grigorieff, 2003), instability of the sample holder mechanics, and insufficient reproducibility of goniometer (Houben and Bar Sadan, 2011). These residual sample tilts were not detectable during data acquisition, which would result in systematic errors to the tilt angles assigned to all images in a cryo-ET tilt series. The residual tilt, if not corrected, will lead to tilted structure in the 3-D tomogram that requires larger Z-dimension to fully contain the structure and larger computing resource for reconstruction. For some specimens, for example, stained sections with gold beads coated on both surfaces, the 3-D geometric model of the fiducial markers obtained from alignment of the whole tilt series can be used to determine/correct the residual sample tilt (Kremer et al., 1996). However, this approach will not be applicable to most cryo-ET samples without markers or with fiducial markers randomly distributed in the sample solution (Hayashida et al., 2014; Winkler and Taylor, 2006)

In this study, we describe a computational approach that can simultaneously estimate sample thickness, tilt and inelastic mean free path using only the tilt images already collected for cryo-ET without need for additional data. This new approach employs a mathematical model derived from the Beer-Lambert law and estimates these parameters as a solution of a multi-variable overdetermined nonlinear least square problem with strong constraints provided by unique geometric relationships among the serial tilts of common structure.

Methods

2.1 Mathematical model for thickness determination

The relationship between sample thickness and beam intensity can be represented by Eq. (1) based on the Beer-Lambert law

$$\frac{d_e}{{\lambda }_{in}}=ln\frac{I_0}{I_{\mathit{exit}}}$$ (1)

where d_e represents the effective thickness which is the distance that the electron beam travels through the specimen, λ_in represents the mean free path for inelastic scattering, I₀ represents the intensity of the incident electron beam on the specimen and I_exit represents the intensity of the electron beam exiting the specimen and hitting the detector. It is obvious that the effective thickness d_e in Eq. (1) varies when the sample is tilted. Assuming the specimen is placed in an arbitrarily tilted plane in 3D space before serial tilting, we define the residual sample tilt γ₀ as the angle between the normal vector of this plane and the Z-axis (i.e. direction of electron beam). Here, the effective thickness d_e for each tilt can be described in Eq. (2) by taking the nominal tilt angles (i.e. intended tilt angles during data collection) and residual sample tilt into consideration (Appendix)

$$d_e=\frac{d_0·cos{\theta }_0}{cos{\gamma }_0·cos({\theta }_0+\theta )}=d_0·\frac{cos{\theta }_0·\sqrt{{tan}^2{\theta }_0+{tan}^2{\alpha }_0+1}}{cos({\theta }_0+\theta )}$$ (2)

where d₀ represent the absolute geometric thickness of the specimen, θ represents the intended tilt angles around Y axis, θ₀ and α₀ represent the residual sample tilt around Y and X axis, respectively, and they can be measured via the corresponding side views of the 3D reconstruction.

Next, the exiting beam intensity I_exit can be expressed as Eq. (3) according to the linear relationship between I_exit and pixel values of images

$$I_{\mathit{image}}=A·I_{\mathit{exit}}+B$$ (3)

where I_image represents the average pixel value of the targeted area in the image, A represents the gain factor of the detector. B represents the average pixel value when no electron hits the detector. Although it should always be zero, we found some corner cases in which the detector is not properly gain-normalized or the image pixel values are shifted post imaging during alignment of the tilt series. To make our method robust for all datasets, this B variable is included in our model as a nuisance parameter.

Hence, we can write our complete mathematical model for each tilt image as Eq. (4) by combining Eqs. (1–3)

$$\frac{d_0}{{\lambda }_{in}}·\frac{cos{\theta }_0·\sqrt{{tan}^2{\theta }_0+{tan}^2{\alpha }_0+1}}{cos({\theta }_0+\theta )}=ln\frac{A·I_0}{I_{\mathit{image}}-B}$$ (4)

In Eq. (4), I_image and θ are known from tilt series. The 7 unknown parameters are I₀, d₀, θ₀, α₀, λ_in, A and B. The 4 parameters of interest in our study are d₀, θ₀, α₀ and λ_in while the remaining three are nuisance parameters. In our case, this is a vastly overdetermined system since the number of equations (the number of selected regions in each image × the number of tilt images) is much larger than the number of unknowns (7) in the model.

2.2 Parameter determination as a constrained nonlinear least square problem

In order to obtain the solution of this overdetermined least square problem, we minimize the scoring function defined in Eq. (5)

$$f(I_0,d_0,{\theta }_0,{\alpha }_0,{\lambda }_{in},A,B)=\sum _{j=1}^N\sum _{i=1}^M{\left[ln\left(\frac{A·I_0}{I_{\mathit{image}}(i,j)-B}\right)-\frac{d_0}{{\lambda }_{in}}·\frac{cos{\theta }_0·\sqrt{{tan}^2{\theta }_0+{tan}^2{\alpha }_0+1}}{cos({\theta }_0+\theta (i))}\right]}^2$$ (5)

where i represents the i^th image in the tilt series, j represents the j^th selected region, M represents the total number of images in the tilt series, N represents the total number of selected regions, and θ(i) represents the intended tilt angle of the i^th image in the tilt series. We would first select N regions of interest in the untilted image, and then track the corresponding areas in all tilts according to tilt geometry. The average pixel value of the j^th region in the i^th tilted image is denoted as I_image (i, j).

Since each unknown variable has its own range that the solution must satisfy, we can estimate the solution of unknowns in Eq. (5) by solving the following constrained nonlinear optimization problem

$$\underset{I_0,d_0,{\theta }_0,{\alpha }_0,{\lambda }_{in},A,B}{min}f(I_0,d_0,{\theta }_0,{\alpha }_0,{\lambda }_{in},A,B)$$ (6)

subject to

$$\begin{array}{l}A·I_0>I_{\mathit{image}}(i,j)-B>0\\ d_0>0\\ {\lambda }_{in}>0\end{array}$$

where f(I₀, d₀, θ₀, α₀, λ_in, A, B) is defined in Eq. (5).

2.3 Implementation

Our approach has been implemented into tomoThickness.py, a single python script for easy usage. We used EMAN2 library functions (Tang et al., 2007) for image IO. numpy/scipy software (Oliphant, 2007; van der Walt et al., 2011) was used to perform nonlinear least square fitting and matplotlib software (Hunter, 2007) was used for plotting. There are many well-developed algorithms and software packages available to solve the constrained nonlinear optimization problem. The global minimization method basin-hopping in scipy.optimize module was used to find solutions to the 7 unknown parameters in less than a minute for each tilt series. Although we have only tested this program on Linux systems, the program should run on all major computer platforms (Linux, Windows and MacOS) since the dependent software packages (python, numpy, scipy, matplotlib, and EMAN2) are all compatible with these platforms. The tomoThickness.py program will be freely downloadable after publication from the authors’ Web site (http://jiang.bio.purdue.edu).

2.4 Test datasets

In this study, we used both stained and cryo tilt series to test the performance of our method. Sindbis virus infected Baby Hamster Kidney fibroblasts (BHK) cells and Flock House Virus infected Drosophila S2 cells were embedded in resin, sectioned and then stained. Tilt series of both samples were acquired on a FEI Titan Krios at 300 kV and were recorded on a Gatan 4K×4K CCD camera at room temperature. Before automated tilt series collection using SerialEM (Mastronarde, 2005), the samples were first pre-irradiated (~10⁴ e/Ų) to stabilize the resin and minimize specimen shrinkage during data collection (Braunfeld et al., 1994). Tilt images were collected from −60° to +60° in 2° increments with constant dose for each tilt and a total dose of 4000 e/Å ². The pixel size was 0.51 nm for the images of Sindbis virus infected Baby Hamster Kidney fibroblasts (BHK) cell sections and 0.404 nm for Flock House Virus infected Drosophila S2 cell sections. One group of cryo-datasets are the images of purified Sindbis virus plunge frozen and imaged at liquid nitrogen temperature. The cryo tilt series were obtained using a FEI Polara TEM at 300 kV, and were recorded on a Tietz 4k×4k CCD. Tilt images were taken from −60° to +60° in 1° increment with constant dose for each tilt and a total dose of 100 e/Å ². The images were 2× binned to 2048×2048 pixels with final pixel size of 0.55 nm. The other group of cryo-datasets are the tilt series of DNP-labeled liposomes and anti-DNP antibody downloaded from EMPIAR (EMPIAR-10009) (Diebolder et al., 2014). This group of datasets were imaged on a FEI Tecnai 200 kV microscope.

The tilt series were aligned using gold fiducial markers with the IMOD software package (Kremer et al., 1996). IMOD was also used for visualization of the tilt series and tomograms (Mastronarde, 1997). The parameters of interest including sample thickness and tilt were verified by examining the corresponding side views of the reconstructed tomogram (Mastronarde, 1997; Venkatakrishnan et al., 2013).

Results

3.1 Tilt dependent variation of image intensity

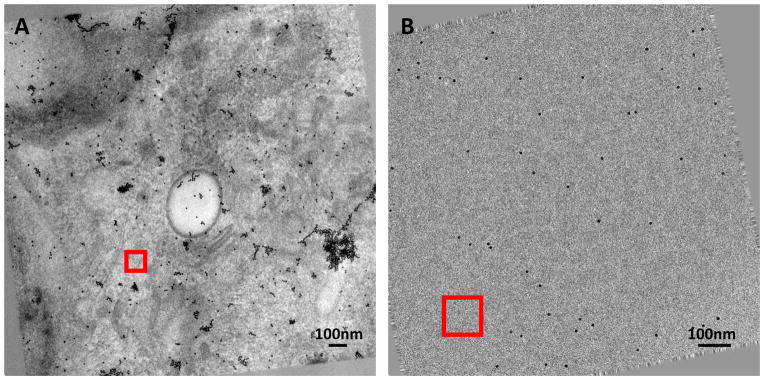
To determine sample parameters using the tilt dependent variation of image intensity, we first selected a region in the zero-tilt image then tracked this region through the aligned stack of tilt series according to the tilt angles. We usually selected regions without extremely dark contents. Fig. 1 shows a region selected for a stained (Fig. 1A) and cryo (Fig. 1B) tilt series, respectively. We calculated the average pixel values in the tracked patches and used them to estimate the sample parameters.

Fig. 1. Zero tilt image of aligned tilt series.

(A) Stained Sindbis virus infected BHK cell section. (B) Plunge-frozen Sindbis virus. The tilt axis is vertical. The red squares indicate regions selected and tracked through the tilt series. The region size is 200×200 pixels.

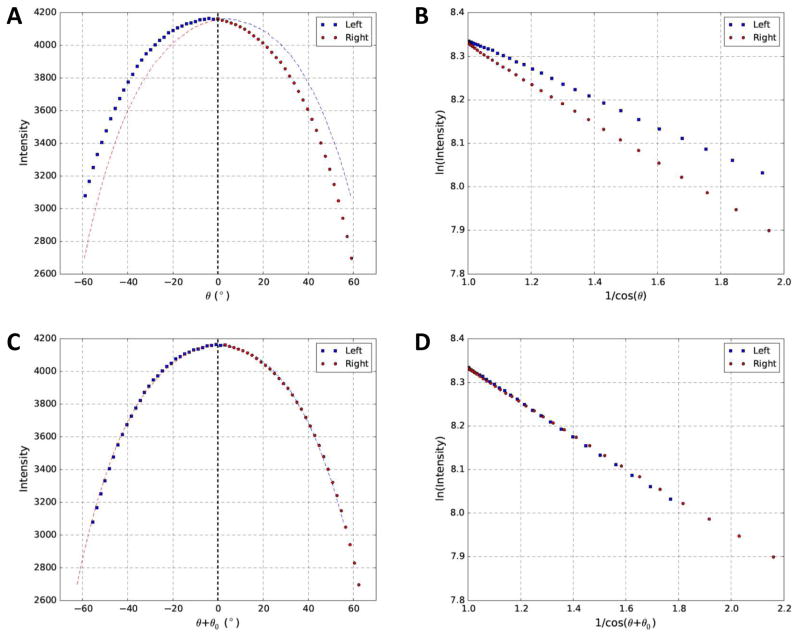
The effective sample thickness is directly associated with the tilt angles. When the specimen is tilted towards larger angles, the effective sample thickness increases, leading to more attenuation of the electron beam passing through specimen and hitting the detector (I_exit in Eq. (1)). The relationship between image intensity and tilt angle of a stained tilt series is shown in Fig. 2A in which the gradual decrease of intensity (i.e. average pixel value, I_image in Eq. (3)) with increasing tilt angle is qualitatively consistent with the theoretical prediction (Eq. (1)). However, close inspection of Fig. 2A revealed that the curve was asymmetric about 0° tilt angle, inconsistent with the expected symmetric shape.

Fig. 2. Relationship between image intensity and tilt angles of a stained dataset before and after correction of residual tilt.

(A) Profile of image intensity and intended tilt angle (θ) for the red square shown in Fig. 1A. (B) Replot of (A) using log of intensity (Y-axis) and 1/cosθ (X-axis). (C) Profile of image intensity and corrected tilt angle (θ+θ₀) after estimation of parameters of interest. (D) Replot of (C) using log of intensity (Y-axis) and 1/cos(θ+θ₀) (X-axis). To provide visual guide for the asymmetric (A) or symmetric (C) distributions about 0° tilt angle, a mirror copy of both sides of 0° tilt angle was also plotted in the opposite side with dash curves in corresponding colors.

Based on Eqs. (1–3) and assuming that residual tilt is 0° (θ₀ = 0°, α₀ =0°) and that there is no linear scaling of pixel values (A=1, B=0), we can obtain Eq. (7):

$$ln(I_{\mathit{exit}})=ln(I_0)-\frac{d_0}{{\lambda }_{in}}·\frac{1}{cos\theta }$$ (7)

From Eq. (7), we expect that log of image intensity will be a linear function of 1/cosθ. To better illustrate the tilt-intensity relationship, we thus replotted Fig. 2A as log of intensity (Y axis) with 1/cosθ (X axis) shown in Fig. 2B. It was obvious that linear relationship did exist. However, the two straight lines representing the left half (blue squares) and right half (red circles) of the curve in Fig. 2A were separated with different slopes. Similar to the curves in Fig. 2A with unexpected asymmetric shape, this line separation was also puzzling as two opposite directions of tilting should result in identical change of effective thickness and overlapping straight lines in the log-linear plots in Fig. 2B and symmetric about 0° tilt in Fig. 2A. Electron beam induced mass loss (Braunfeld et al., 1994) cannot be the cause as smaller slope would be expected for the line corresponding to the right half tilts which were imaged last and would cause less attenuation of the beam after mass loss. We suspected that residual sample tilt caused these unexpected results, which led us to develop the nonlinear least square fitting method reported here to resolve these issues. As shown in results below, residual sample tilt was indeed found to be the cause.

3.2 Determination of sample thickness, tilt and electron mean free path

We applied our nonlinear least square fitting algorithm (Eq. (6)) to the tilt series in order to determine the parameters of interest (sample thickness, tilt and electron mean free path). As shown in Fig. 2C, the plot of intensity became more symmetric about 0° tilt after correcting the tilt angles with residual sample tilt (θ₀ = 3.38°). As shown in Fig. 2D, the two separated lines now converged to a single line after taking the residual sample tilt (θ₀ =3.38°) into account. We thus have confirmed that residual sample tilt was indeed the cause for the asymmetric curve in Fig. 2A and line separation in Fig. 2B. Furthermore, it also demonstrated that our nonlinear least square method could be used to correctly determine the residual sample tilt from a high contrast stained tilt series.

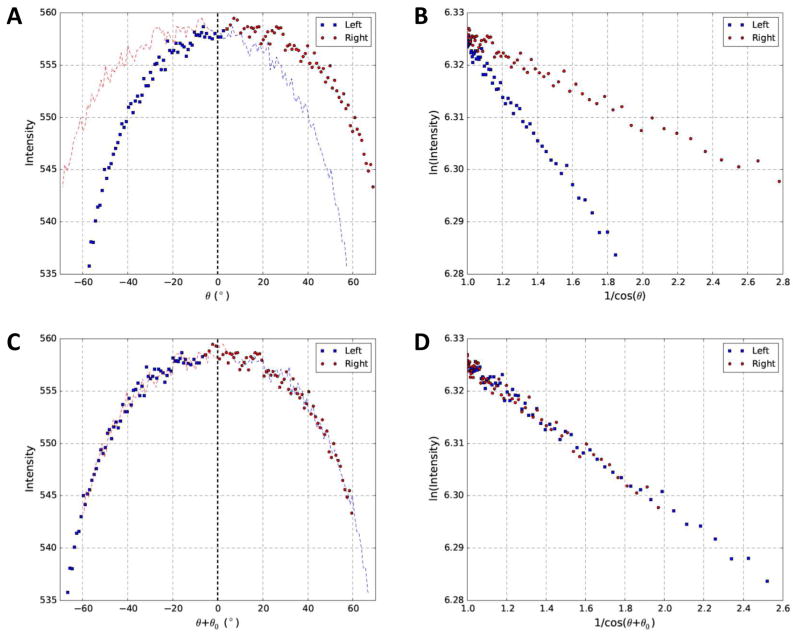
We then applied our method to analyze a cryo tilt series (Fig. 3) which showed similar results with Fig. 2. The cryo dataset was much noisier with lower contrast, as expected, since the signal-to-noise ratio (SNR) of cryo tilt series (Fig. 3) imaged at much lower electron dose is poorer than that for the stained dataset (Fig. 2). Nevertheless, the residual tilt could still be accurately determined to make the curve symmetric (Fig. 3C) and the lines to converge (Fig. 3D).

Fig. 3. Relationship between image intensity and tilt angles of a cryo dataset before and after correction of residual tilt.

(A) Profile of image intensity and intended tilt angle (θ) for the red square shown in Fig. 1B. (B) Replot of (A) using log of intensity (Y-axis) and 1/cosθ (X-axis). (C) Profile of image intensity and corrected tilt angle (θ+θ₀) after estimation of parameters of interest. (D) Replot of (C) using log of intensity (Y-axis) and 1/cos(θ+θ₀) (X-axis). To provide visual guide for the asymmetric (A) or symmetric (C) distributions about 0° tilt angle, a mirror copy of both sides of 0° tilt angle was also plotted in the opposite side with dash curves in corresponding colors.

Our method could use arbitrary number of regions (Eq. (5), N ≥ 1) from the tilt series to estimate a single set of parameters. Fig. S1 and Fig. S2 extended those in Fig. 2 and Fig. 3 and showed curves/lines for two different regions in the corresponding stained and cryo tilt series, respectively. It was evident that the originally separate lines for each region converged after considering a common residual sample tilt parameter for both regions. The converged lines for the two regions remain separate due to the different local sample contents. Together, we showed that our method worked well for both stained and cryo tilt series.

3.3 Cross validation with measurements from 3D tomogram

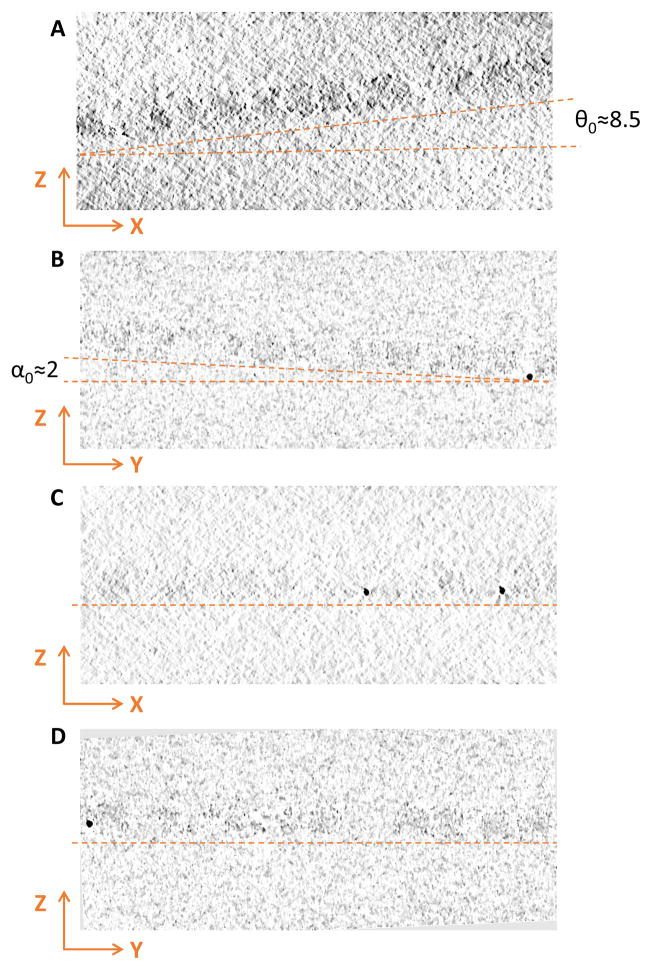
To verify these fitted parameters with independent measurements, we reconstructed both tilt series shown in Fig. 2 and Fig. 3 and manually measured the corresponding parameters from side views of the tomograms. Fig. 4 shows the measured sample tilt θ₀ ≈ 3.3° (Fig. 4A) and α₀ ≈ 0° (Fig. 4B), and thickness d₀ ≈ 170nm, which agree well with the fitting results d₀ =168nm, θ₀=3.38°, α₀ = 0.17°, λ_in =230nm of this stained dataset used in Fig. 2. To further demonstrate that the fitted sample tilt angle is accurate, we modified the tilt angles by adding the fitted θ₀ and then performed reconstruction with the modified tilt angles. In Fig. 4C the sample structure now become horizontal in XZ view, implying that the estimated θ₀ is correct. Similarly, compensating the residual tilt α₀ around X-axis also resulted in horizontal structure in YZ view (Fig. 4D), although α₀ for this tilt series is small and original tomogram without this correction (Fig. 4B) was already visually horizontal.

Fig. 4. Comparison of reconstruction of the stained tilt series shown in Fig. 1A before and after correction of residual tilt.

Sections (A) and (B) are XZ and YZ planes before tilt correction. Sections (C) and (D) are XZ and YZ planes after tilt correction. Note that the sample plane is horizontal after tilt correction (C, D) and the measured thickness is close to fitted value, indicating that the fitted parameters are reliable for stained datasets.

Repeating these tests with the cryo dataset used in Fig. 3 further confirmed that the fitted parameters were also correct. The parameters θ₀ ≈ 8.5° (Fig. 5A), α₀ ≈ 2° (Fig. 5B), and d₀ ≈ 72nm measured from tomogram also matched well with the fitted parameters θ₀ =8.7°, α₀ =2.12°, d₀ =74.64nm, λ_in =356nm and the correction of sample tilt also made the specimen horizontal in XZ (Fig. 5C) and YZ views (Fig. 5D).

Fig. 5. Comparison of reconstruction of the cryo tilt series shown in Fig. 1B before and after correction of residual tilt.

Sections (A) and (B) are XZ and YZ planes before tilt correction. Sections (C) and (D) are XZ and YZ planes after tilt correction. Note that the sample plane is horizontal after local tilt correction (C, D) and the measured thickness is close to fitted value, indicating that the fitted parameters are reliable for cryo datasets.

It is worth pointing out that the fitted inelastic mean free path for vitreous ice λ_in =356nm is very close to the predicted value 350nm in the literature (Vulovic et al., 2013) although no experimental values have been published for λ_in at 300kV. In addition, the fitted λ_in for stained dataset is 230nm which is significantly smaller than that for cryo dataset. While there is no experimentally measured λ_in for stained sections, the reduced value is consistent with expectation: electrons are scattered with much higher probability by the heavy metal materials in the stained sample than by the light atoms in cryo samples (Langmore and Smith, 1992).

3.4 Robustness of basin-hopping optimization method

As described in Section 2.2, we used a basin-hopping method to solve the constrained nonlinear optimization problem. Basin-hopping is a stochastic global optimization algorithm that has been shown to be extremely useful for problems in physics and chemistry. During the iterative search, the basin-hopping algorithm introduces random perturbation of the search variables to escape local minima and find the global minimum efficiently. To test the robustness of our approach, we reran the script 100 times on both stained and cryo datasets. The results in Fig. S3 showed that sample thickness d₀ (Fig. S3A), mean free path λ_in (Fig. S3B), sample tilt (θ₀, α₀ in Fig. S3C and γ₀ in Fig. S3D) could be correctly determined in all runs with little variations among different runs. These results implied that the basin-hopping algorithm employed in our approach can reliably find the global minimum and successfully determine the sample parameters.

3.5 Tests with varying number of regions

We next attempted to examine the robustness of our method with different number sample regions used for fitting (Fig. S4). Different numbers of regions were chosen in the stained tilt series (blue symbols in Fig. S4) and the cryo tilt series (red symbols in Fig. S4) to determine the sample parameters. The fitted parameters, including thickness d₀ (Fig. S4A), mean free path λ_in (Fig. S4B) and sample tilt (θ₀, α₀ in Fig. S4C and γ₀ in Fig. S4D), were plotted in Fig. S4 as a function of the number of regions, respectively. It is evident that our approach is stable with varying number of selected regions for both stained and cryo datasets. It is satisfying to observe that the method could correctly determine the parameters with just one region despite the low SNR of cryo tilt series.

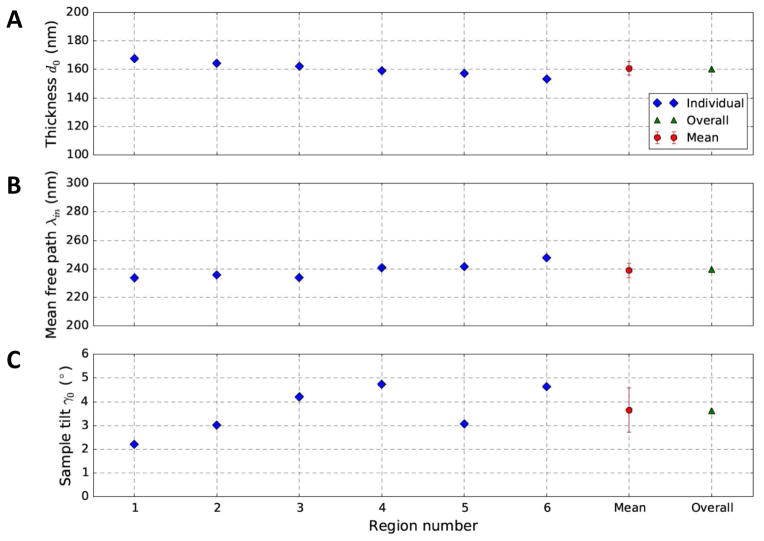
To better understand the overall parameters determined from multiple regions, we investigated the results from individual regions and overall result from multiple regions. As shown in Fig. S5, we chose six regions with different amount of contents (i.e. darkness) from the stained tilt series and plotted the individual results (blue diamonds in Fig. 6) determined independently for each region. The mean (red circles in Fig. 6) of individual fitting results is consistent with the value (green triangle in Fig. 6) determined using all regions simultaneously. The thickness and mean free path values independently determined from different parts of the sample are very consistent with only small scatter (Fig. 6), which demonstrated the robustness of both the optimization algorithm and the non-linear least square formulation of our method. In contrast, the individually fitted sample tilts have larger scatter (Fig. 6C), which might arise from cutting artifact wrinkles in section samples or the nonuniform density distribution in the regions leading to different amounts of apparent tilt added to the actual sample tilt. These results suggest that fitting with multiple regions will help average out local variations and obtain a set of parameters representing the overall sample properties.

Fig. 6. Comparison of the parameters fitted from different regions shown in Fig. S5.

The fitted parameters include thickness d₀ (A), mean free path λ_in (B) and sample tilt γ₀ (C). The blue diamonds represent the parameters determined from individual regions. The red square represents the mean of all blue diamonds. The green triangle represents the overall parameters determined by simultaneously fitting all selected regions. Note that the overall parameters (green triangles) are in agreement with the mean value (red circles), although the individually determined parameters vary slightly from region to region.

In order to further study the robustness of our method in the measurement of sample thickness, we tested one cryo dataset with ice thickness gradient (Fig. S6). In this dataset, the gradient of ice thickness could be observed in the tilt image (Fig. S6A) and in the side view of the tomographic reconstruction (Fig. S6B). We selected 6 ice regions (red boxes in Fig. S6A) along the direction of ice gradient and used our method to estimate the ice thickness of these regions. It is clear that the estimated thicknesses increase smoothly (Fig. S6C), which is consistent with the gradient visible in the 2-D image (Fig. S6A) and the side view of the tomogram (Fig. S6B).

3.6 Cross validation with more experimental tilt series

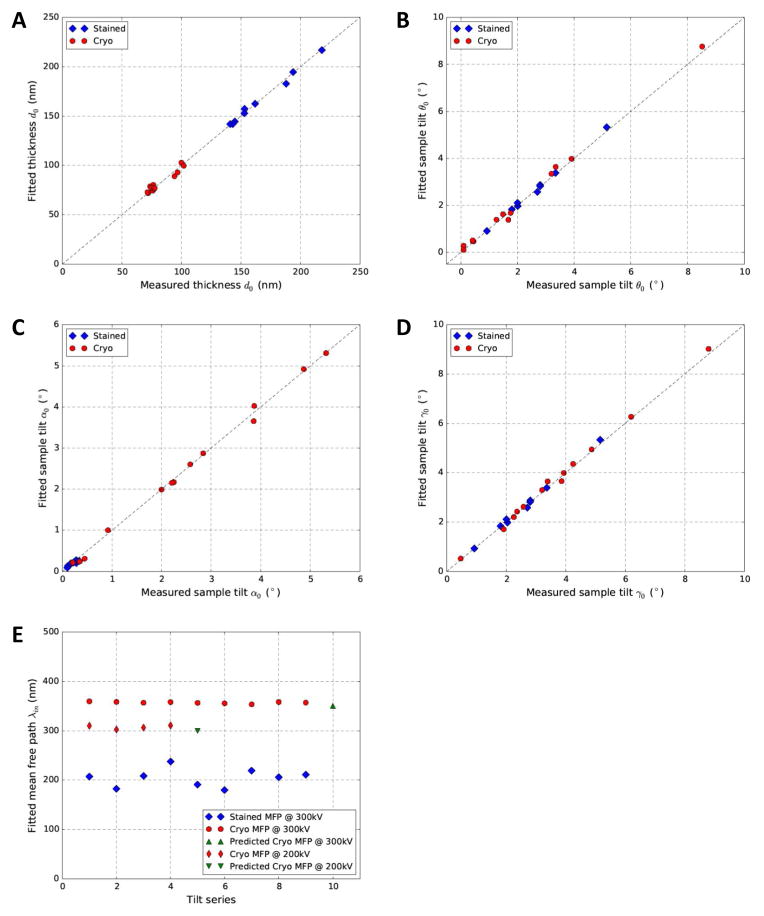
As can be seen from the above results, our approach could reliably determine the sample parameters of both stained and cryo tilt series. We further tested this approach with additional stained and cryo datasets. In Fig. 7A–D, we could see that fitted parameters vs parameters measured from tomograms all tightly clustered on the diagonal lines, suggesting excellent agreement between the two sets of independently derived parameters. Since the mean free path cannot be measured from tomograms and there is no experimental measurement for comparable imaging/sample conditions in literature, we use three indirect evidences to support our fitted mean free paths (Fig. 7E). First, the independently fitted values were self-consistent for different datasets within the same sample groups, stained (blue diamonds), cryo datasets collected at 300kV (red circles) and 200kV (red thin diamonds), respectively. Second, the relative ranking of the values was consistent with the expected larger mean free paths for cryo samples at 300kV (red circles) than those of cryo samples at 200kV (red thin diamonds) and stained samples (blue diamonds). Third, the fitted free path for cryo samples acquired at 300kV (red circles) and 200kV (red thin diamonds) was also consistent with the value 350nm (green point-up triangle) and 300nm (green point-down triangle) extrapolated from experimental measurements of different imaging conditions (Vulovic et al., 2013).

Fig. 7. Cross validation of the parameters fitted by our method (Y-axis) and measured from the 3D tomogram (X-axis) for both stained (blue diamonds) and cryo (red circles) tilt series.

The cross-validated parameters include thickness d₀(A) and sample tilt θ₀ (B), α₀ (C) and γ₀ (D). (E) Plot of fitted mean free path λ_in. The green triangles in (E) represents the predicted mean free paths for 300kV and 200kV electrons through vitreous ice from literature (Vulovic et al., 2013).

Discussion

In this study, we developed a novel computational approach to determine sample thickness, tilt and mean free path for electron tomography by solving a constrained nonlinear least square problem of an overdetermined system. Due to the benefit of an overdetermined system, the resulting parameters from this approach are reliable. The systematic tests with good performance have shown that this approach can provide accurate and robust estimations of these parameters for both stained and cryo tilt series. It is well-established that appropriate thickness of vitreous ice in cryo-sample is crucial for obtaining high quality images (Quispe et al., 2007). Thick ice will result in poor image contrast, while the embedded sample structure may be disturbed due to the contact with the air-water interface if the ice is too thin. Thus, reliable and convenient determination of ice thickness can help evaluation of image quality, selection of good images and improvement of reconstruction resolution. It will also provide feedback to help further improve sample preparation conditions. In addition, an optimal Z-dimension of cryo-tomogram can be predefined based on reliable estimation of the thickness of specimen, allowing a more efficient reconstruction process and obviate the need of visual examination of the thickness in trial reconstruction with poor contrast. Therefore, our method, which is able to reliably and quickly determine the thickness from 2D tilt series before 3D reconstruction, will be a useful tool for cryo-ET studies. By integrating this tool with existing alignment and reconstruction tools, it will help assemble a more automated and efficient high-throughput data processing pipeline for cryo-ET.

Based on our extensive tests with large numbers of stained and cryo samples (Fig. 7B–D), it can be concluded that residual sample tilt occurs unintentionally but commonly during data acquisition in ET. Similar observations were also reported based on iterative alignment of tilt images with projections of tomograms (Winkler and Taylor, 2006). These residual sample tilts, if not correctly determined and corrected, will limit tomogram reconstruction in both computational performance and quality. Combined with the reliable thickness, correction of residual sample tilt can generate a 3D tomogram in a horizontal plane with optimal Z-dimension size, leading to faster speed and smaller 3D volume of reconstruction. For example, it took 3 minutes to reconstruct a 2048×2048×100 tomogram from 137 tilt images using IMOD on a 3.2 GHz CPU computer. If the user has no clue about the correct sample thickness and might just blindly specify a very large number, 200 pixels, for the reconstruction. In this case, the reconstruction of tomogram would take 5 minutes. Since defocus gradient is one of the critical resolution limiting factors in ET (Voortman et al., 2014), accurate tilt angle of each tilt image is essential for accurate determination and correction of defocus gradient, and eventually improvement of the resolution of the tomogram. Our approach is designed to determine residual sample tilt based on the Beer-Lambert law and it can work accurately and robustly without the limitation of current method based on gold beads distribution (Hayashida et al., 2014). Furthermore, it also performs well on low dose cryo tilt series whose residual sample tilt is hard to determine either by fiducial marker model or by visual examination of 3D tomogram with faint top/bottom boundaries due to low contrast and smearing by missing wedge.

Experimental methods are too time-consuming to determine the electron mean free path at a wide range of incident energies of electron and sample conditions. In fact, most reported values from experiments were obtained at low acceleration voltage (≤120kV) and vary among different measurements (Vulovic et al., 2013). It is thus highly desirable to have some means of predicting and verifying the mean free path. The mean free path is a critical parameter in accurate simulation of image formation process in electron microscopy. A model based iterative reconstruction (MBIR) was reported to significantly improve the reconstruction quality according to its applications on electron tomography of inorganic materials (Venkatakrishnan et al., 2013). Since the physical foundation of image formation model in MBIR is the Beer-Lambert law, accurate mean free path is essential for it to obtain an optimal reconstruction. Our method can thus help improve the quality of 3D reconstruction methods like MBIR by providing optimal mean free path value for every sample/imaging condition, instead of reusing a fixed value measured at different conditions.

Supplementary Material

1. Fig. S1. Expansion of plots in Fig. 2 to include two regions for the stained tilt series.

Note that the accurate fitted residual tilt can help converge the two separate lines with different slopes (B) into well-superimposed lines (D).

2. Fig. S2. Expansion of plots in Fig. 3 to include two regions for the cryo tilt series.

Note that the accurate fitted residual tilt can help converge the two separate lines with different slopes (B) into well-superimposed lines (D).

3. Fig. S3. Robustness of basin-hopping global optimization method employed in our approach.

We ran the script 100 times and plotted the fitted parameters, including d₀ (A), mean free path λ_in (B) and sample tilt (θ₀/α₀ in C, γ₀ in D). The tests were performed for both a stained Sindbis virus infected BHK cell section dataset and a cryo dataset of purified Sindbis virus.

4. Fig. S4. Performance with different numbers of regions for both stained (blue symbols) and cryo (red symbols) tilt series.

The plots demonstrate the stability of thickness d₀ (A), mean free path λ_in (B) and sample tilt (θ₀/α₀ in C, γ₀ in D) determined by our method with increasing number of regions used for fitting.

5. Fig. S5. Multiple regions with different contents selected for fitting.

The dataset is same as the one used in Fig. 1A. The fitting results were shown in Fig. 6.

6. Fig. S6. Performance with vitreous ice thickness gradient.

(A) A −60° tilt image of cryo dataset of purified Sindbis virus. The 6 marked regions were used for the test. (B) Side view of the 3-D tomogram with clearly visible thickness gradient. (C) Plot of the estimated sample thickness of the 6 regions shown in (A).

Appendix

Derivation of the expression for effective thickness at tilt angle θ

Assuming the specimen is placed in an arbitrary plane in 3D space before tilting, we define the plane normal vector as n⃗₀= (a,b,c) and the angle between n⃗₀ and Z-axis asγ₀.

The cosine of γ₀ is expressed as

$$cos{\gamma }_0=\frac{c}{\sqrt{a^2+b^2+c^2}}$$ (A.1)

The projection vector of n⃗₀ to XZ plane is

$${\overrightarrow{n}}_{\mathit{projXZ}}=(a,0,c)$$ (A.2)

We define the angle between n⃗_projXZ and Z-axis as θ₀ and the tangent of θ₀ is expressed as

$$tan{\theta }_0=\frac{a}{c}$$ (A.3)

Similarly, the angle between n⃗_projXZ and Z-axis can be defined as α₀ and

$$tan{\alpha }_0=\frac{b}{c}$$ (A.4)

Thus, we can rewrite the cosine of γ₀ by combining Eqs. (A.1), (A.3), (A.4)

$$cos{\gamma }_0=\frac{c}{\sqrt{a^2+b^2+c^2}}=\frac{1}{\sqrt{{(\frac{a}{c})}^2+{(\frac{b}{c})}^2+1}}=\frac{1}{\sqrt{{tan}^2{\theta }_0+{tan}^2{\alpha }_0+1}}$$ (A.5)

Since θ₀ and α₀ can be measured from the side views of tomogram, we can easily get γ₀ from Eq. (A.5).

Next, given that the tilt axis is usually along Y-axis, we define θ as the intended tilt angle around the tilt axis (Y-axis). If we tilt the specimen by θ, the plane normal vector will be

$${\overrightarrow{n}}_{\theta }=R_y(\theta )·{\overrightarrow{n}}_0=\left[\begin{array}{ccc}cos\theta & 0& sin\theta \\ 0& 1& 0\\ -sin\theta & 0& cos\theta \end{array}\right]\left[\begin{array}{c}a\\ b\\ c\end{array}\right]=\left[\begin{array}{c}acos\theta +csin\theta \\ b\\ -asin\theta +ccos\theta \end{array}\right]$$ (A.6)

where R_y(θ) is a rotation matrix which rotates vectors by an angle θ around the Y-axis.

The angle between the new normal vector n⃗_θ and Z-axis is defined as γ_θ and

$$\begin{array}{l}cos{\gamma }_{\theta }=\frac{-asin\theta +ccos\theta }{\sqrt{{(acos\theta +csin\theta )}^2+b^2+{(-asin\theta +ccos\theta )}^2}}\\ =\frac{c}{\sqrt{a^2+b^2+c^2}}·(-\frac{a}{c}sin\theta +cos\theta )\\ =cos{\gamma }_0·(-tan{\theta }_{0}sin\theta +cos\theta )\\ =cos{\gamma }_0·(\frac{1}{cos{\theta }_0})·(cos{\theta }_{0}cos\theta -sin{\theta }_{0}sin\theta )\\ =\frac{cos{\gamma }_0·cos(\theta +{\theta }_0)}{cos{\theta }_0}\end{array}$$ (A.7)

Assuming the geometric thickness of the specimen is d₀, the effective thickness at tilt angle θ can be written in Eq. (A.8) by combining Eqs. (A.5), (A.7)

$$d_e=\frac{d_0}{cos{\gamma }_{\theta }}=d_0·\frac{cos{\theta }_0}{cos{\gamma }_0·cos({\theta }_0+\theta )}=d_0·\frac{cos{\theta }_0·\sqrt{{tan}^2{\theta }_0+{tan}^2{\alpha }_0+1}}{cos({\theta }_0+\theta )}$$ (A.8)