The morphological state space revisited: what do phylogenetic patterns in homoplasy tell us about the number of possible character states?

Abstract

Biological variety and major evolutionary transitions suggest that the space of possible morphologies may have varied among lineages and through time. However, most models of phylogenetic character evolution assume that the potential state space is finite. Here, I explore what the morphological state space might be like, by analysing trends in homoplasy (repeated derivation of the same character state). Analyses of ten published character matrices are compared against computer simulations with different state space models: infinite states, finite states, ordered states and an ‘inertial' model, simulating phylogenetic constraints. Of these, only the infinite states model results in evolution without homoplasy, a prediction which is not generally met by real phylogenies. Many authors have interpreted the ubiquity of homoplasy as evidence that the number of evolutionary alternatives is finite. However, homoplasy is also predicted by phylogenetic constraints on the morphological distance that can be traversed between ancestor and descendent. Phylogenetic rarefaction (sub-sampling) shows that finite and inertial state spaces do produce contrasting trends in the distribution of homoplasy. Two clades show trends characteristic of phylogenetic inertia, with decreasing homoplasy (increasing consistency index) as we sub-sample more distantly related taxa. One clade shows increasing homoplasy, suggesting exhaustion of finite states. Different clades may, therefore, show different patterns of character evolution. However, when parsimony uninformative characters are excluded (which may occur without documentation in cladistic studies), it may no longer be possible to distinguish inertial and finite state spaces. Interestingly, inertial models predict that homoplasy should be clustered among comparatively close relatives (parallel evolution), whereas finite state models do not. If morphological evolution is often inertial in nature, then homoplasy (false homology) may primarily occur between close relatives, perhaps being replaced by functional analogy at higher taxonomic scales.

1. Introduction

What is the nature of the morphological state space? How many possible states are available for a discrete morphological character? Does this number vary within and between clades? These questions are central to the study of morphological evolution: with implications for phylogenetics, ancestral character state reconstruction, inferred rates of evolution, disparity analysis and the search for evolutionary trends. However, they are surprisingly difficult to answer. For some character types, the number of possible character states may be relatively easy to establish, such as four states for DNA or RNA, 20 states for standard amino acids and two states for binary (presence/absence) morphological characters. However, for most multistate morphological characters, the number of possible states is essentially unknown [1]. Most phylogenetic reconstruction methods treat morphological characters much like molecular data and implicitly assume that the potential state space is finite for a given character. In practice, the number of states of a given character that are observed among the studied taxa is usually treated as the number of potential evolutionary states, which is fixed for that character throughout the analysis. This is the basis of both standard multistate parsimony analysis and the n-state generalization of the Jukes–Cantor maximum-likelihood DNA substitution model (in which evolution is modelled using a Markov process), which can be adjusted for morphological data by accounting for invariant characters [2].

However, we might ask whether such assumptions are sufficiently realistic [3]. One pertinent question might be, could more states have possibly been evolved across a given clade than those that are observed among some sampled taxa? For example, if the state space is treated as finite and fixed, reconstructed states among the hypothetical ancestors must be drawn from those observed among the terminal taxa. Initially, this may seem sensible: why assume that ancestors could take states that are not observed among their descendants? Yet the evolution of new states along a lineage is a general prediction of evolutionary trends [4]. Consequently, it is not clear that common phylogenetic assumptions (particularly a fixed morphological state space) are entirely compatible with important evolutionary principles such as character release, adaptive radiation or trends in morphological complexity (see [5–9]). Furthermore, a broad view of macroevolution suggests that the morphological state space has varied considerably throughout the history of life. Striking examples are major transitions in evolution, at which radically new evolutionary possibilities appear to have opened up (notably the evolution of eukaryotic organelles, macroscopic body size, terrestrialization and flight). Such problems also find conceptual parallels in a range of other fields where properties of an underlying state space must be estimated from observed instances [7], including ecology (e.g. estimating true numbers of species in sampled communities [10]) and authorship attribution (e.g. analysing the consistency of word usage between texts [11]).

Here, I aim to explore what the state space for morphological characters might be like, by examining patterns in homoplasy, here defined in a phylogenetic context as the repeated derivation of the same character state on a phylogeny [12]. The rationale is that if the nature and size of the state space can be shown to affect patterns of homoplasy, for example, using evolutionary computer simulations, then patterns of homoplasy observed among real morphological characters may, in turn, reveal something about their potential state space. This analysis thereby aims to clarify and test aspects of our core question, are there limits to evolution?

In 2000, Wagner presented an important study [13], suggesting that the accumulation of homoplasy in morphological characters often shows a saturation or ‘exhaustion’ curve, of derived states plotted against evolutionary steps, which is similar to that of molecular data. This exhaustion curve shows a levelling off of the number of new states as evolution proceeds, suggesting progressive exhaustion of a limited number of potential character states. When contrasted with a number of alternative evolutionary models, including a model of ordered character evolution, Wagner found that the character exhaustion model was the best fit to the observed states: steps curve for half of the 28 surveyed clades.

In 1991, Sanderson conducted a search for ‘homoplastic tendencies’ [14], which might cause homoplasy in morphological characters to be clustered among closely related taxa, a phenomenon which is here referred to as parallelism (following [14], reviewed by [15]). Sanderson's study of four cladistic datasets returned little statistical evidence for non-random clustering, suggesting instead that homoplasy was randomly scattered across the tree. However, he noted that the detection of parallelism was likely to depend on the scale of the analysis and choice of characters, and that data collected specifically for phylogenetic reconstruction may not be representative of morphological evolution as a whole. In line with this, subsequent studies, particularly those exploring the genetic underpinnings of phenotypic homoplasy, have identified convincing examples of parallelism including pale pigmentation in subspecies of pocket mice [15,16], independent eye loss by multiple populations of the Mexican cave-dwelling fish Astyanax fasciatus [15,17], and similar warning colour patterns in butterflies of the genus Heliconius [18]. Such examples also show that very similar phenotypic traits, which may even be underlain by changes in homologous genes (e.g. [18,19]), can reoccur at a variety of taxonomic scales (although this may be more probable between closer relatives). As a result, some authors have suggested that there may be a continuum from parallelisms among very closely related taxa to those of much more distant relatives (with the latter equivalent to ‘convergence’ in some uses of the term) [15]. More widely, we can connect morphological parallelism to comparable scenarios in ecology, as well as other fields. For example, similar patterns of species diversity may be more likely among closely ‘related’ communities (e.g. those in close geographical proximity) [20].

Interestingly, we can also show that these two ideas—parallelism and the nature of the state space—are linked, by considering the patterns of homoplasy predicted by some different models of morphological character evolution.

2. Evolutionary models

2.1. Infinite state space

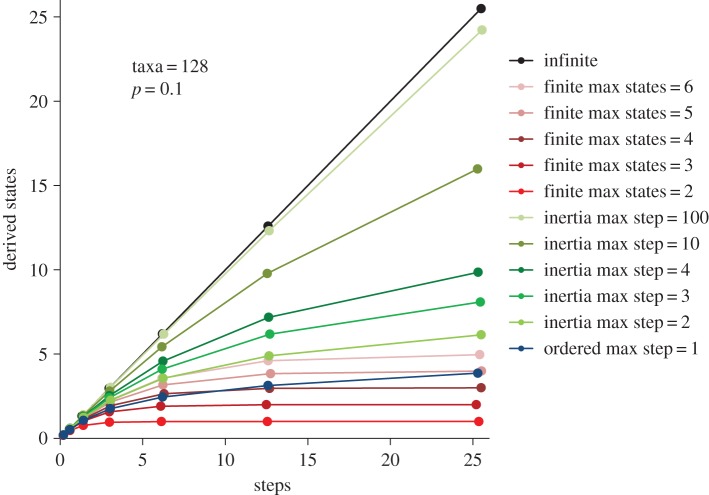
To approximate a truly infinite state space, this evolutionary model uses a very large character state space, which is effectively infinite given the number of taxa in each simulated phylogeny (table 1). Under this model, homoplasy is extremely improbable and in practice did not occur among the computer simulations. Consequently, each evolutionary step produces a new state [1] and the relationship of derived states (M) to the most parsimonious number of steps (S) (the states–steps curve) is linear with a slope of one (figure 1).

Table 1.

Parameters used for computer models of the character state space.

model	lower bound	upper bound	possible states	maximum step size
infinite	−1000000	1000000	2000001	2000000
finite	0	1	2	1
	0	2	3	2
	0	3	4	3
	0	4	5	4
	0	5	6	5
ordered	−1000000	1000000	2000001	1
inertia	−1000000	1000000	2000001	2
	−1000000	1000000	2000001	3
	−1000000	1000000	2000001	4
	−1000000	1000000	2000001	10
	−1000000	1000000	2000001	100

Figure 1.

The average number of derived states (M) versus evolutionary steps (S) per character evolved cumulatively up a phylogeny under different computer models of character evolution (see table 1 for model parameters). Simulations were conducted on perfectly balanced trees with 128 terminal taxa, for 100 characters, with a probability of state change of p = 0.1 on any given branch. Plotted values are the average across 20 independent simulations.

2.2. Finite state space

This model uses a standard Markov matrix specifying a fixed set of potential states (table 1), which applies across a simulated evolutionary tree. As in the infinite states model described above (and indeed all of the evolutionary models used here), the root node in the tree starts with the ancestral state for each character. Then, as speciation proceeds up the tree, characters tend to undergo an increasing number of evolutionary changes. Initially, as new states are derived, both the numbers of states and steps increase (figure 1). However, once a given state has been derived, any subsequent derivations of the same state represent homoplasy. When each potential state has been derived once, any subsequent state changes will be homoplastic. At this point, the curve of states to steps reaches a plateau. Here, the number of evolutionary steps may continue to increase, but no new states can be evolved (figure 1). If, however, the number of potential states is sufficiently large (relative to the number of taxa and rate of state change), evolution may proceed within a finite state space without all of the available states being evolved by all characters. In such cases (e.g. finite spaces with four or more potential states in figure 1), the number of derived states increases more and more slowly but the plateau, which would indicate complete exhaustion of the available states, is not reached.

2.3. Ordered state space

Character state ordering introduces a measure of similarity (or distance) between the states [21]. For a linearly ordered character, the states are treated as an ordinal series, in which the number of evolutionary steps required to move between any pair of states is equal to the difference between them (e.g. a change from state 0 to state 2 requires 2 − 0 = 2 steps). For evolutionary simulations, character state order can be modelled by restricting individual evolutionary changes to those between states that are adjacent on the number line [13]. In other words, the maximum evolutionary step size (the difference between ancestral and descendent states) for a given character on a given branch is one (table 1).

2.4. Inertial state space

In the inertial state space models, introduced here, the total number of potential states is effectively infinite; however, the maximum evolutionary step size is set to a specified value, greater than 1 (table 1). This is an example of the more general concept of a constrained Markov model (e.g. [22]), but used here in a phylogenetic context. The ordered state space (in which the maximum evolutionary step size is 1) is identified as a specific case of an inertial state space.

The aim is to model an effect of phylogenetic inertia, or phylogenetic constraint (terms reviewed by [23]), such that only potential states which are sufficiently similar to the ancestral state can evolve along a given branch of the phylogeny (with the cut-off for similarity specified by the maximum allowed step size). As a result, each node on a phylogenetic tree has a local state space, from which a descendant state may be drawn. As evolution proceeds stochastically up the tree, different lineages on that tree may evolve so that their local state spaces become non-overlapping.

3. Homoplasy and the character state space

From a systematic perspective, multistate morphological characters with an effectively infinite number of states might be highly desirable. This is because random evolutionary trajectories within such spaces are very unlikely to experience homoplasy (figure 1), which can otherwise support misleading phylogenetic groupings (e.g. [24]). However, literature surveys indicate that morphological phylogenies free of homoplasy are seldom, if ever, encountered (e.g. [25]). If homoplasy is indeed ubiquitous, what does this tell us about the morphological state space and the limits on evolution?

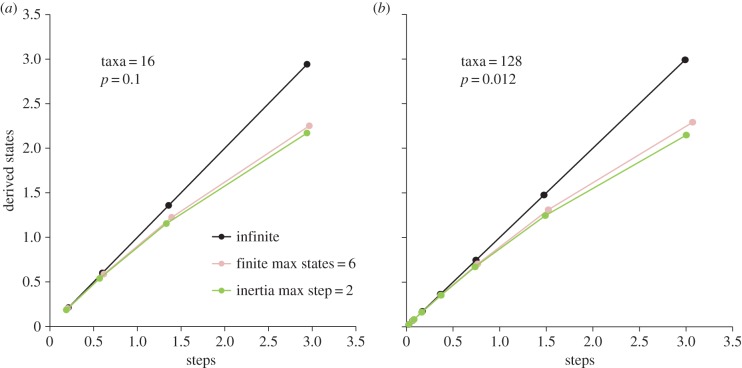
Many authors appear to have taken the occurrence of homoplasy (or the more general phenomenon of evolutionary convergence) as an indication that the number of evolutionary possibilities for a trait is finite, and limited to only a small number of viable alternatives (e.g. see discussion in [26–29]). However, the computer simulations conducted here demonstrate that phylogenetic inertia (the tendency for newly derived states to be comparatively similar to the ancestral state) can also lead to homoplasy (figure 1). This is true even though the overall number of potential states under the inertial model is effectively infinite (and, in this sense, unlimited). Indeed, patterns of state derivation (states–steps curves) can sometimes be identical under these different models, with the proviso that evolution within a finite space has not yet entirely exhausted all of the available states (figure 2).

Figure 2.

The average number of derived states (M) versus evolutionary steps (S) per character under different computer models of character evolution. (a) The effect of a reduced number of taxa (16 compared with 128 for figure 1). (b) The effect of a reduced probability of character states change (0.012 compared with 0.1 for figure 1).

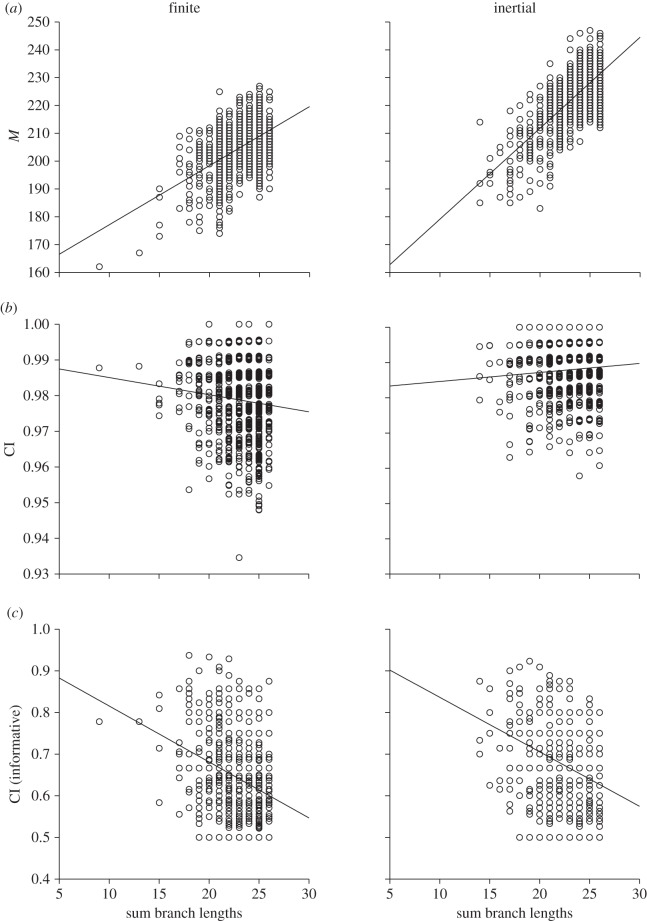
The distinction between finite state spaces and inertial state spaces may seem to be somewhat trivial, as inertial state spaces are locally finite (with potential descendant states determined by the ancestral state and a maximum step size parameter). However, these two classes of model predict distinctly different distributions of homoplasy across evolutionary trees. By sampling small subtrees of four taxa from a larger phylogeny, we can explore patterns of homoplasy across the complete tree. Given combinations of total clade size and rate of state change that capture a sufficiently complete picture of character evolution (figure 3), homoplasy within finite versus inertial state spaces shows different trends. Specifically, as we sample more of a clade's total evolutionary history, characters which evolved within a finite state space show more homoplasy, as measured by the consistency index (CI; figure 3b; table 2) which is the proportion of evolutionary steps that represent uniquely derived states, CI = M/S [30]. By contrast, evolution within inertial state spaces can produce lower levels of homoplasy (again measured by CI) as the phylogenetic distance between sampled taxa increases (figure 3b; table 2).

Figure 3.

Phylogenetic rarefaction plots for simulated character data. Derived states and homoplasy indices measured for four-taxon subtrees sampled from a compete tree of 128 taxa, under a finite state space model (with six states) versus an inertial state space model (with a maximum step size of 2). (a) Numbers of derived states among 100 characters (M). (b) Consistency index (CI) calculated across all characters. (c) Consistency index calculated with parsimony uninformative characters excluded. The x-axis indicates the phylogenetic relatedness of the sampled taxa (total branch length of the sampled subtree). Probability of state change = 0.3. Data points shown for 1000 sampled subtrees.

Table 2.

Statistical results for phylogenetic rarefaction of simulated character data. Correlations between numbers of derived states (M) or homoplasy indices (CI, CI (informative) or RI) and phylogenetic relatedness for four-taxon subtrees sampled across a complete phylogeny of 128 taxa. Simulations were conducted with a probability of state change per branch of 0.3, six potential states for the finite model and a maximum evolutionary step size of 2 for the inertial model. Analyses used 1000 sampled subtrees. Shapiro–Wilk normality tests indicated that numbers of states and homoplasy indices were non-normally distributed (with p < 0.05). Statistically significant correlations (with p < 0.05) are indicated in bold.

model	index	normality test p	normality test W	Spearman's correlation p	Spearman's correlation D	linear correlation p	linear correlation r
finite	M	<0.0001	0.965	<0.0001	95 959 000	<0.0001	0.51159
	CI	<0.0001	0.9767	0.0375	174 570 000	0.0010	−0.1041
	CI (informative)	<0.0001	0.9409	<0.0001	211 330 000	<0.0001	−0.31646
	RI	0.0047	0.9855	<0.0001	211 330 000	<0.0001	−0.31146
inertia	M	<0.0001	0.9529	<0.0001	63 076 000	<0.0001	0.71132
	CI	<0.0001	0.957	0.0006	145 870 000	0.015217	0.076736
	CI (informative)	<0.0001	0.8904	<0.0001	201 900 000	<0.0001	−0.20535
	RI	<0.0001	0.9585	<0.0001	201 900 000	<0.0001	−0.23083
ordered	M	<0.0001	0.965	<0.0001	73 878 000	<0.0001	0.65888
	CI	<0.0001	0.98	0.2316	157 610 000	0.078349	0.055693
	CI (informative)	<0.0001	0.9537	<0.0001	203 180 000	<0.0001	−0.25381
	RI	0.0001	0.9929	<0.0001	203 180 000	<0.0001	−0.24536

However, when we instead calculate a CI after excluding any parsimony uninformative characters, both inertial and finite state spaces show an increase in homoplasy as the phylogenetic distance between sampled taxa increases (figure 3c). This same pattern of increasing homoplasy is indicated by the retention index (RI) [31], which is less sensitive to uninformative characters than the CI [32]. To help make sense of these results, we can also compare the number of sampled states among increasingly distantly related taxa (figure 3a), and note that we see more character states, as well as less homoplasy (as measured by CI), under the inertial model.

Owing to the stochastic nature of character evolution, under all of the models, there is considerable scatter in CI values for individual subtrees. However, the contrasting trends in homoplasy for the finite versus inertial state spaces are statistically significant (with p-values shown in table 2), although there is no significant trend for the ordered state space using comparable parameter values.

We, therefore, observe different patterns of character evolution in finite and inertial state spaces as we consider more distantly related taxa. In both cases, very closely related taxa may not yet show any evolutionary change, as all are likely to retain the ancestral state (giving an invariant or ‘constant’ cladistic character). As speciation proceeds, however, some of the taxa may evolve new character states. When such divergence from the basal ancestral state has occurred, we have opportunities for homoplasy, which happens if a new state is derived independently in two lineages or if a lineage shows divergence followed by subsequent reversal to the ancestral state. In finite state spaces, we essentially remain at this stage in the process of character evolution, and continued state change results first in derivation of all available states (exhaustion), and then toggling between these alternatives. Thus, sampling more distantly related taxa will tend to sample more homoplasy. However, in inertial state spaces, independent phylogenetic lineages may evolve different (and possibly non-overlapping) local state spaces between which homoplasy is improbable or impossible. As a result, sampled subtrees which include more distantly related taxa may show greater numbers of states (figure 3a), including states which are unique among the sampled taxa (a singlet or autapomorphic state). Correspondingly, we may see less homoplasy (as measured by CI) as the sampled lineages drift into different regions of the total state space.

Therefore, in inertial state spaces, homoplasy is especially probable in taxa which are sufficiently distantly related to show divergence from the state of their most recent common ancestor, but close enough to have overlapping sets of potential states. In such cases, homoplasy may be clustered among comparatively close relatives: a phenomenon which corresponds to at least some definitions of parallelism [25], a term which has a long (albeit rather convoluted) history in the evolutionary literature (see [33,34]). By contrast, a tendency towards parallelism is not a prediction for finite state spaces, where homoplasy is possible at any phylogenetic distance (once divergence from the original state of the most recent common ancestor has occurred).

How well do the predictions of either finite or inertial models match real morphological data? Patterns of accumulating homoplasy (exhaustion curves) that have been linked to a finite state space appear to be quite common among cladistic datasets [13]. However, the evolutionary simulations conducted here do show that the states–steps curves for finite models can sometimes look very similar to those of inertial models if a clear exhaustion plateau is not reached (figure 2). Perhaps more usefully, finite and inertial state spaces can produce distinct, opposing trends in homoplasy among sampled subtrees of decreasing relatedness (figure 3), as outlined above.

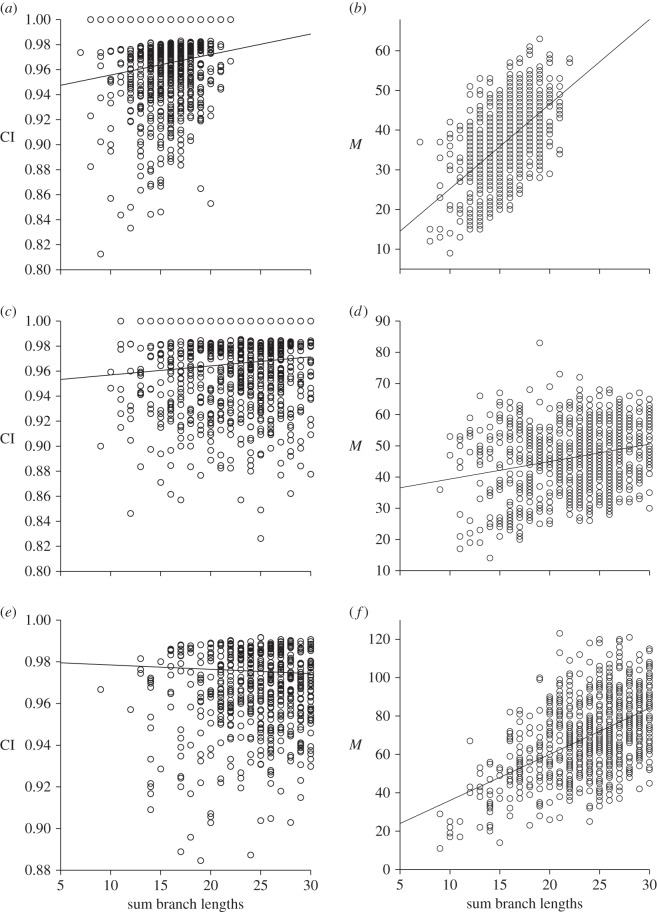
Phylogenetic rarefaction analyses of 10 morphological phylogenies drawn from the cladistic literature (table 3) find two clades (dicynodonts and ptychoparioid trilobites) with statistically significant trends in homoplasy that are characteristic of inertial state spaces. That is, we see decreasing homoplasy, as measured by the CI, when we sub-sample more distantly related taxa (figure 4a,c). One clade (crocodilians) shows a statistically significant (through comparatively weak) trend in homoplasy that is suggestive of a finite state space. Here, more homoplasy is measured (again with the CI) as sampled phylogenetic distance increases (figure 4e). The remaining seven studies show no significant trend in CI among sampled subtrees.

Table 3.

Statistical results for phylogenetic rarefaction of real morphological character data. Correlations between the CI and phylogenetic relatedness for four-taxon subtrees sampled from the complete phylogeny. Analyses used 1000 randomly sampled subtrees. Shapiro–Wilk normality tests indicated that numbers of states and homoplasy indices were non-normally distributed (with p < 0.05). Statistically significant correlations (with p < 0.05) are indicated in bold.

reference	clade	taxa	characters	normality test p	normality test W	Spearman's correlation p	Spearman's correlation D	linear correlation p	linear correlation r
Angielczyk & Kurkin [35]	dicynodonts	28	53	<0.0001	0.8970	0.0019	147 690 000	0.0001	0.1267
Archibald et al. [36]	placental mammals	25	70	<0.0001	0.8801	0.2448	169 250 000	0.5504	−0.0189
Ausich [37]	crinoids	33	25	<0.0001	0.8094	0.6531	158 810 000	0.9101	−0.0036
Bitsch & Bitsch [38]	Mandibulata	35	72	<0.0001	0.9686	0.9603	166 000 000	0.7882	0.0085
Brochu [39]	crocodilians	62	164	<0.0001	0.9062	0.0063	178 990 000	0.1273	−0.0483
Chatterton et al. [40]	proetid trilobites	38	55	<0.0001	0.9483	0.1598	158 340 000	0.1833	0.0421
Cherns [41]	chitons	33	28	<0.0001	0.8950	0.1303	155 450 000	0.1058	0.0512
Cotton [42]	ptychoparioid trilobites	49	97	<0.0001	0.8927	0.0011	147 210 000	0.0011	0.1028
Dietze [43]	ray-fin fishes	50	57	<0.0001	0.9887	0.1336	158 500 000	0.1456	0.0461
Dyke et al. [44]	galliform birds	65	102	0.01705	0.9963	0.1800	159 430 000	0.2259	0.0383

Figure 4.

Phylogenetic rarefaction plots for real morphological character data. Consistency indices (CI) and numbers of derived states (M) measured for 1000 four-taxon subtrees sampled from complete phylogenies. Phylogenies based on reanalysis of published morphological character matrices of (a,b) dicynodonts [35], (c,d) ptychoparioid trilobites [42] and (e,f) crocodilians [39]. See table 3 for statistical results.

This observation of opposing trends in homoplasy (suggesting inertial versus finite state spaces) in different clades may represent genuine biological variation in patterns of character evolution. In support of this, the two clades showing statistically significant inertial trends do have some interesting characteristics. The ptychoparioid trilobites [42], which showed a trend in homoplasy (figure 4c) suggestive of comparatively innovative character evolution (compatible with phylogenetic inertia rather than a finite character state space), were by far the most speciose group of Cambrian trilobites and are thought to represent the main ancestral stock for the post-Cambrian trilobite radiation [42]. So too, the Upper Permian dicynodonts [35], which showed especially clear patterns of decreasing homoplasy (figure 4a) and increasing state derivation (figure 4b) across the phylogeny, represent a period of anomodont therapsid evolution during which the group achieved a height of diversity and morphological variation (disparity) [45]. We can also find clades with trends in homoplasy that suggest a finite set of character states (including the crocodilian study included here, see also [13]).

Interpreted literally, these results might suggest that different clades can show different patterns of character evolution. However, there are also a number of potential biases which may affect the levels of homoplasy measured among cladistic datasets. Notably, when we exclude parsimony uninformative characters (such as constant characters and autapomorphies [46]), the patterns of homoplasy inferred using phylogenetic rarefaction for inertial state spaces cannot be distinguished from those for finite state spaces (e.g. figure 3c). Morphological data matrices, originally intended for cladistic analysis, are often used in subsequent evolutionary meta-analyses because they provide easily accessible data on morphological variation. However, non-random selection of morphological characters may occur as standard during cladistic character analysis. It is possible that systematists may attempt to exclude homoplastic characters, in general [47]. However, the levels of homoplasy inferred for morphological character matrices suggest that, if this attempt has been made, it has often been rather unsuccessful. For example, Sanderson & Donoghue [25] found an average corrected CI of 0.6 among 38 surveyed matrices indicating that, on average, 40% of inferred evolutionary steps were homoplastic. Further to this, character selection for parsimony analysis may favour informative characters in particular (see [2,25]), which might hinder the detection of inertial evolution and exaggerate the extent of character exhaustion. These potential sources of bias for the inference of evolutionary patterns in homoplasy, as well as related phenomena such as disparity and evolutionary rates, may therefore deserve further attention. One potential data source for further analyses might be geometric morphometric descriptions of biological form, which can be contrasted with the phylogenetic signal from other data types (e.g. [48]).

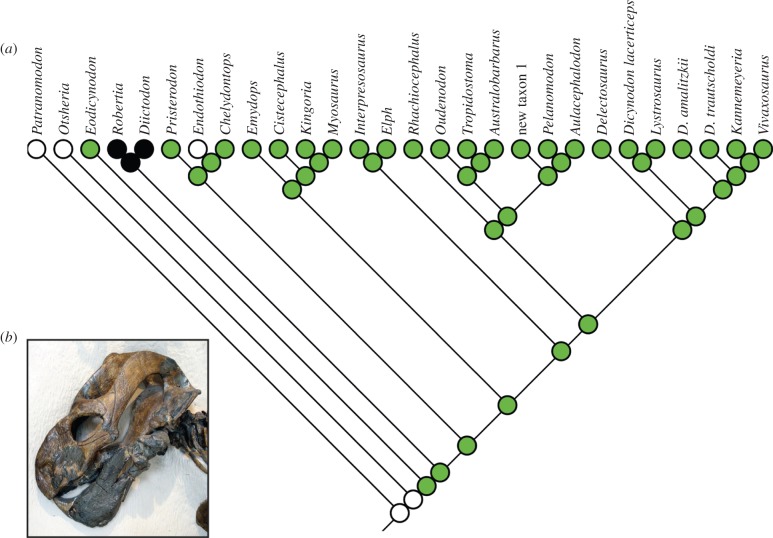
Beyond this, an important implication of the inertial model is that certain character states may be more likely to evolve in parallel among closely related species. Biologically, this might be because some morphological states are more similar to a shared ancestral state and so are comparatively easy to evolve at nodes close to this ancestor, perhaps due to intrinsic genetic and developmental constraints. There may also be reasons for correlated evolution among close relatives that are primarily functional, such as shared features of habitat, climate and ecology (and temporal range within wider evolutionary history). Such factors may also affect multiple distinguishable characters simultaneously because of modulatory, integration and concerted convergence [49–52]. Thinking about the broad sweep of biological diversity, the general principle of parallelism seems plausible. Many, if not all, clades seem to have inherited morphological similarities (such as those referable to the concept of the body plan) which likely affected subsequent evolution. As one example, most dicynodonts share derived chewing adaptations [35], likely affecting many correlated characters of the skull as well as the postcranium and potentially promoting parallel evolution along some lineages during their diversification (figure 5).

Figure 5.

(a) Most parsimonious tree of Permian dicynodonts based on reanalysis of the morphological character matrix of [35]. This tree is a randomly selected example from 54 most parsimonious phylogenies. The evolutionary history of an example character ‘caniniform process’ is indicated by node colours (white, absent; green, present; black, present with anterior notch). This is a most parsimonious character reconstruction inferred using Mesquite [53]. This illustrates an example of diversification of a multistate character, with homoplastic loss of the caniniform process in genus Endothiodon (b). This represents a reversal to the ancestral state held by the comparatively closely related genus Otsheria, and an example of parallel evolution between close relatives. (b) Photograph of a skull of the dicynodont Endothiodon angusticeps at the American Museum of Natural History, sourced from Wikimedia Commons.

According to this view of evolution, the probability of the parallel evolution of highly similar morphological structures (of the sort included in cladistic character matrices) may tend to decline with evolutionary distance, so that we are generally unlikely to see the ‘false homology’ that is homoplasy [54] between very distantly related taxa (although deep homologies are a reminder that genetic-developmental machinery may sometimes be retained over very long evolutionary time scales). Consequently, at very high taxonomic scales the independent evolution of similarity may primarily take the form of functional analogy, or ‘convergence’ as used by Patterson [55], rather than homoplasy (sensu [12,54]).

4. Detailed methods

4.1. Computer simulation methodology

Character evolution was simulated using a Markov process, on a perfectly balanced tree (generally with 128 terminal taxa) and with each branch length set to 1. First, the character state for the root node was set to zero. At each subsequent node, moving up the phylogeny, the character state was either inherited from the immediate ancestor or a state change occurred (according to a specified probability, set to 0.1 for the simulations shown in figure 1). If a state change occurred, the new state was drawn (with equal probability) from a pool of potential discrete states (integers) determined by the evolutionary model considered (table 1) and the corresponding maximum step size (the maximum absolute difference between the ancestral state and the newly derived state). Each time a state change occurred, this was recorded along with the height in the phylogeny of the node at which it occurred. This was used to calculate the total number of evolutionary steps across all characters (S), at each height in the tree. For comparability across evolutionary models, the recorded number of evolutionary steps (S) was calculated as the total number of evolutionary changes (rather than the number of evolutionary steps implied if characters were treated as linearly ordered, for example). After each evolutionary simulation was completed, the simulated characters were then examined to count the cumulative number of states that had been evolved at each height in the tree. This was then used to calculate the number of derived character states, M (the number of character states minus 1).

4.2. Phylogenetic rarefaction

The number of terminal taxa in a phylogeny has a strong effect on the amount of homoplasy we can expect to measure [25,46,56,57]. To avoid this potential bias and to examine distributions of homoplasy across a tree this study used phylogenetic rarefaction to measure homoplasy indices in small, equally sized subtrees (each with four terminal taxa) sampled from a complete phylogenetic tree. In each analysis, 1000 subtrees were sampled from the complete phylogeny. The phylogenetic distance between the sampled taxa was calculated as total branch length of the subtree connecting them (equivalent to the total length of a minimum spanning tree, between the sampled taxa, on the complete phylogeny). For each subtree, the total number of derived states (M), most parsimonious steps (S), extra steps (H), CI and RI were calculated using a heuristic parsimony analysis in PAUP v. 4.0 [58]. In each case, the true phylogenetic topology of the subtree was specified in the nexus file rather than inferred via parsimony analysis. In the case of the computer simulations, true subtree topologies were known because the complete tree topology was specified in the simulation. Phylogenetic rarefaction analyses were also conducted for 10 published morphological character matrices of animal taxa (table 3, most available for download from the Paleobiology Database at https://paleobiodb.org). Here, the complete phylogeny was inferred using a heuristic parsimony analysis, and this tree was used to specify the topology of each sampled subtree. For comparability, all characters were treated as unordered for the purposes of parsimony analysis. Where more than one most parsimonious tree (MPT) was recovered, rarefaction analyses were conducted using one randomly selected MPT.

Competing interests

I declare I have no competing interests.

Funding

This research was supported by Templeton World Charity Foundation grant no. LBAG/143.