Inference and Prediction of Metabolic Network Fluxes

Analyzing metabolic network flux and recent findings in plants highlights future challenges.

Abstract

In this Update, we cover the basic principles of the estimation and prediction of the rates of the many interconnected biochemical reactions that constitute plant metabolic networks. This includes metabolic flux analysis approaches that utilize the rates or patterns of redistribution of stable isotopes of carbon and other atoms to estimate fluxes, as well as constraints-based optimization approaches such as flux balance analysis. Some of the major insights that have been gained from analysis of fluxes in plants are discussed, including the functioning of metabolic pathways in a network context, the robustness of the metabolic phenotype, the importance of cell maintenance costs, and the mechanisms that enable energy and redox balancing at steady state. We also discuss methodologies to exploit 'omic data sets for the construction of tissue-specific metabolic network models and to constrain the range of permissible fluxes in such models. Finally, we consider the future directions and challenges faced by the field of metabolic network flux phenotyping.

The metabolic systems of plants utilize a continual energy stream (i.e. light in the case of photosynthetic tissues and chemical energy in the case of heterotrophic tissues) to drive a complex network of hundreds of chemical reactions away from equilibrium. Ultimately, this leads to the catalyzed biosynthesis of the ordered polymeric biomolecules that make up the biomass of the cells in each tissue and underpins the growth and development of the plant (Smith and Stitt, 2007). To operate on a time scale relevant for life, the system is dependent upon the acceleration of its chemistry by enzymes. Additionally, because of the highly compartmented nature of plant cells, transporter proteins are required to permit the movement of metabolites (i.e. the substrates and products of biochemical reactions) between subcellular compartments. Transporter proteins are also required to bring substrates into cells and to allow the excretion of waste products and other metabolites such as defense compounds. The sum total of expressed genes encoding enzymes and metabolite transporters determines the metabolic capabilities of a cell. In a growing tissue, the net output of this metabolism is anabolic (i.e. leading to the biosynthesis of biomass constituents such as starch, fructans, cell wall, lipid, and protein), but catabolic metabolism is also required. Most importantly, catabolism generates universal energy currencies such as ATP and NAD(P)H, whose turnover is used to provide the energetic driving force for anabolism. Catabolism is also important to allow the turnover of cellular components for regulatory and repair purposes (Linster et al., 2013; Ishihara et al., 2015). The turnover and resynthesis of cellular components, along with the maintenance of electrochemical potentials across membranes, are important facets of metabolism that need to be considered alongside the biosynthesis of macromolecules for growth (Stitt, 2013; Sweetlove et al., 2013).

Metabolism, then, is the entirety of chemical reactions occurring in a biological system. The rate, or flux, of these reactions is dependent upon the activity of the enzymes and transporters present, which in turn is dependent on both the amount of the proteins and the regulatory modifications of their catalytic or transport properties. The concentrations of reactants are also important, affecting the rate and direction of reactions due to enzyme-kinetic and thermodynamic considerations, respectively. As the product of one reaction is the substrate of one or more other reactions, an interconnected network of biochemical pathways is formed in which the reaction rates are mutually dependent. The emergent system-level property of this network as a result of the combined effect of enzyme/transporter amounts, regulation, kinetics, and thermodynamics is a coordinated metabolic steady state in which the concentrations of all metabolites in the system are invariant with time. Thus, to understand the functioning of metabolism, it is necessary to know the fluxes of every active biochemical reaction at a given steady state. This information provides a precise quantification of the metabolic state as an integrated cellular phenotype (Ratcliffe and Shachar-Hill, 2005). More specifically, it allows us to identify which metabolic pathways are active, how active they are, and how their activity is coordinated with other metabolic pathways to form a balanced network. The fluxes can be compared under different states, allowing, for example, the effect of genotype or environment on the metabolic system to be characterized. The resulting integrated view also allows access to important aspects of metabolism, such as energy and redox balancing, that are properties of the system as a whole (Kramer and Evans, 2011; Cheung et al., 2015). Finally, knowledge of system-wide metabolic fluxes is an invaluable tool for guiding efforts to engineer the plant metabolic system, allowing predictions of the ideal network configuration and fluxes for the overproduction of desirable end products (Farré et al., 2014).

In this Update, we will explain the basic principles of estimating and predicting fluxes in metabolic networks. We will also review the progress that has been made in implementing these techniques for the investigation of plant metabolism and the insights that have been obtained. In addition, we will consider a number of areas in which the field is still in a state of development. These include the use of transcriptomic, proteomic, and metabolomic data to develop context-specific models of the metabolic system and approaches to investigate the relationship between fluxes and metabolite levels. We will finish by discussing some key challenges, both experimental and methodological, that need to be addressed in the future if metabolic flux analysis and modeling in plants are to fulfill their considerable potential.

GENERAL PRINCIPLES OF INFERENCE AND THE PREDICTION OF METABOLIC FLUXES

Estimating Flux from Isotopic Labeling Experiments

Metabolic flux analysis (MFA) aims to make simultaneous estimations of the fluxes of multiple reactions in the metabolic network, usually with a focus on a subset of interconnected reactions such as the pathways of central carbon and nitrogen metabolism (Allen et al., 2009a; Kruger and Ratcliffe, 2015). The approach is based upon feeding tissues with stable isotope (usually ¹³C)-labeled substrates and measuring the labeling of intracellular metabolites. One might imagine that the conceptually simplest way to infer fluxes from labeling data is via the rate at which metabolite pools are labeled over time. However, a number of factors considerably complicate the apparently simple relationship between labeling rate and flux. More explicitly, the rate of labeling of a metabolite pool is dependent upon the following: (1) the extent of labeling of the precursor substrate molecule(s) as label propagates through the system; (2) the size of the metabolite pool (a large pool will take longer to become fully labeled than a small one); and (3) the rate of conversion of precursor substrate(s) into the metabolite (the desired flux parameter). In the simple case of an irreversible monomolecular reaction, it is possible to estimate the flux by fitting the reactant labeling profiles to the solution of a single differential equation that describes these relationships, in an approach known as kinetic flux profiling (Yuan et al., 2006, 2008). However, in most cases, the complexity of the network increases the number of parameters that must be considered and the equations are no longer analytically solvable. For example, most reactions involve more than one substrate and form more than one product. Many reactions are reversible in vivo, which complicates the labeling patterns. And the interconnected nature of the network means that there are multiple sources of influx of label into a metabolite pool. The situation is further complicated in plants by the duplication of reactions and metabolite pools in different subcellular compartments.

Given these complexities, most MFA approaches are not based on the analytical solution of equations but rather use numerical approaches to fit fluxes as parameters, to obtain a statistically good match between the modeled and measured labeling patterns for the relevant metabolites. When the rate of labelling is being considered, this is known as isotopically nonstationary metabolic flux analysis (INST-MFA; Wiechert and Nöh, 2013) in recognition of the fact that labeling time courses are used and labeling does not proceed to isotopic steady state. Note that although the system is not at isotopic steady state, it is assumed to remain at metabolic steady state (i.e. the labeling of metabolites changes over time, but the concentrations of the metabolites remain constant). In this way, the reach of the kinetic flux profiling approach can be extended to estimate fluxes in a more complex set of reactions such as the Calvin-Benson cycle (Szecowka et al., 2013; Heise et al., 2014). The labeling information used in these analyses considered only the unlabeled fraction of each metabolite during a labeling pulse chase, but additional constraints on the fluxes can be gained by considering the labeling of fragments of metabolites (using mass spectrometry) or of specific carbon atoms (using NMR). Given labeling time courses of all isotopomers, it is possible to estimate the ratios of fluxes at network branch points of larger metabolic networks (Hörl et al., 2013). More usefully, given quantitative data about the inputs and outputs of the metabolic network (i.e. the rate of substrate utilization and the rates of synthesis of biomass components), it is possible to estimate absolute fluxes of the metabolic network under consideration. Recently, the technique has been implemented successfully in Arabidopsis (Arabidopsis thaliana), a technical and computational tour de force that allowed the quantification of 54 fluxes in illuminated leaves labeled with ¹³CO₂ (Ma et al., 2014). The availability of specialized software, INCA (Young, 2014) and OpenMeBius (Kajihata et al., 2014), will greatly facilitate the implementation of INST-MFA by automatically generating the system of ordinary differential equations that describes the metabolic network under consideration (defined by the user and including information about the carbon transitions between metabolites) and estimating metabolic fluxes by nonlinear optimization of the parameter fit to the labeling time course of the measured isotopomers. The inclusion of metabolite pool size data may improve the accuracy of flux estimates, especially at branch points (Heise et al., 2015).

INST-MFA represents the current state of the art and is the only way to estimate metabolic network fluxes in leaves where ¹³CO₂ is the only physiologically meaningful route for carbon labeling. However, for heterotrophic tissues, it is possible to infer fluxes from the pattern of labeling at isotopic steady state after feeding with positionally ¹³C-labeled substrates such as sugars and amino acids. Fluxes can be accessed from patterns rather than rates of labeling, because the distribution of label from input substrates in which only specific carbon atoms are labeled provides diagnostic information about relative fluxes at branch points in the network. The focus on the pattern of labeling dramatically simplifies the experimental work load (labeling of isotopomers needs to be measured only at a single time point rather than across a time course) and computational burden. The approach is known as steady-state MFA and, like INST-MFA, uses nonlinear fitting of labeling data (in this case to sets of equations describing the carbon transitions between metabolites) and measured input and output fluxes to scale and constrain the fluxes (O’Grady et al., 2012). The main limitation of the technique is that it is restricted to cultured heterotrophic systems in which isotopic steady state can be achieved. That said, steady-state MFA is a mature technique and has been used extensively to analyze flux distributions of seed embryo cultures and heterotrophic cell suspension cultures.

Predicting Flux from Stoichiometric Constraints-Based Modeling

Despite considerable methodological and computational advances, MFA, and particularly INST-MFA, remain low- to medium-throughput techniques (Junker, 2014). Therefore, researchers have increasingly turned to modeling approaches that allow fluxes to be predicted without the requirement for labor-intensive acquisition of isotope labeling data. Arguably the most powerful computational models of metabolic pathways are kinetic models that are based on numerical analysis of differential equations describing changes in metabolite concentrations in terms of rate equations that incorporate the kinetic properties of the relevant enzymes (Rohwer, 2012). However, obtaining reliable values for the enzyme-kinetic parameters (e.g. V_max and K_m) for large numbers of enzymes from the same tissue/cell type is just as experimentally labor intensive as MFA; consequently, kinetic models are usually restricted to relatively small metabolic networks. Instead, for larger networks, a method known as flux balance analysis (FBA) has become widely used. FBA was initially developed for microbial metabolism and allows flux predictions to be made without knowledge of enzyme-kinetic parameters. The central premise of FBA is that natural or artificial selection has imposed optimization drivers on the efficiency or productivity of metabolic networks and, thus, it is possible to predict metabolic behavior (flux) using optimization principles.

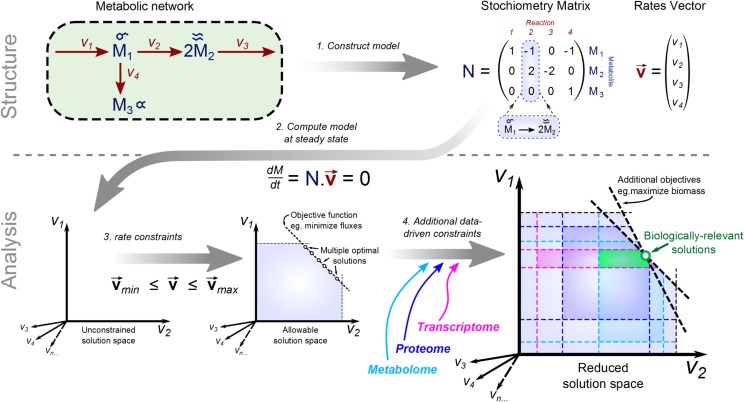
To explain how FBA works, we need to first introduce some basic concepts about the modeling of biochemical reactions and metabolic pools. Each (bio)chemical reaction can be mathematically represented by a matrix capturing the stoichiometric coefficients for each metabolite on the right (producing) and left (consuming) side of the reaction (Fig. 1). The resultant stoichiometric matrix, N, is an accurate representation of the metabolic network, the rows of the stoichiometric matrix corresponding to metabolites and the columns denoting the reactions (Fig. 1).

Figure 1.

Principles and approaches of FBA. The top part illustrates the mathematical encoding of the structure of a metabolic network in the form of a stoichiometry matrix (S) and the activity of the network as a vector of fluxes (v). The bottom part illustrates constraints-based optimization approaches to predict flux distributions in the network by solving the linear set of equations S × v = 0. The unconstrained n-dimensional solution space (shown at left) can be reduced by adding upper and lower bounds for each flux, and a set of solutions that lie within this constrained space can be found that also satisfy an optimization objective (shown in the middle). To reduce this multiple set of feasible flux distributions, additional constraints derived from transcriptomic, proteomic, and metabolomic data can be applied as well as secondary objective functions (shown at right). This allows a smaller set of biologically relevant flux distributions to be obtained.

To use this information to predict metabolic behavior, reaction fluxes need to be introduced. This can be done, as with kinetic modeling, by constructing differential equations that relate changes in metabolite concentrations to reaction flux (Fig. 1). To arrive at a steady-state flux distribution, one has to solve the system of equations, N × v = 0, where v is a vector of reaction fluxes. Since the number of reactions is typically larger than the number of metabolites, the system of linear equations is underdetermined. Such systems usually have infinitely many solutions. However, biological systems operate under additional constraints, aside from the steady state, and these can be used to restrict the feasible space of flux distributions. For instance, some reactions are irreversible; in addition, all reactions are assumed to operate between some (generic) upper and lower flux boundaries. As in MFA, the inputs and outputs of the metabolic system will also be (experimentally) defined (Fig. 1). To further constrain the solution space, one assumes that the biological system optimizes an objective, expressed as a linear combination of the reaction fluxes (Fig. 1). Common objective functions include the maximization of biomass produced per unit of input substrate (Feist and Palsson, 2010) and the minimization of the sum of fluxes, a proxy for the cost of the enzymatic machinery (Sweetlove and Ratcliffe, 2011).

Even with the assumption of optimality, a unique steady-state flux distribution is not usually obtained (Fig. 1). Therefore, the space of flux distributions that result in the optimal value of the assumed objective is explored by means of flux variability analysis, which reveals the range of flux values that a reaction can carry in the optimum. Note that not every combination of values in the range resulting from flux variability analysis is feasible, which implies that not every value may be equally likely to appear in a steady-state flux distribution. In addition, subsequent optimizations for other objectives, such as minimum uptake of substrates and minimum ATP consumption, can be used to further reduce the space of possible distributions (Fig. 1). Another way to reduce the space of feasible flux distributions is to fix some ratio of fluxes to values obtained from measurements (Cheung et al., 2013) or based on insights from other modeling approaches.

The formulation given above indicates that FBA is a linear programming problem. Within the linear programming framework, one can readily investigate the concept of shadow price for a constraint, which essentially quantifies how much change in the objective value results from changing the constraint by one unit. Determining the shadow price for a steady-state constraint for metabolite X then amounts to determining how the imbalance of that metabolite affects the objective. This has recently been termed flux imbalance analysis (Reznik et al., 2013). Therefore, extensions of FBA allow insights to be made as to the effect of changes in metabolite pools on the performance of the biological system.

As indicated above, due to the steady-state assumption and the flux-centered focus, FBA amounts to solving a set of linear equations for the reaction fluxes. However, actual fluxes are integrated outcomes of the activity of available enzymes, their posttranscriptional and allosteric regulation, as well as metabolite levels. Mathematically, each reaction flux v_i is, in fact, described as a nonlinear function of the aforementioned parameters, here denoted by the function v_i(x, p), where p is a set of parameters and x denotes the concentration of metabolites (and enzymes). Each steady-state flux distribution is accompanied by a steady state of metabolite concentrations. The latter can be obtained by solving the system of equations N × v(x, p) = 0, which are often nonlinear for x. Therefore, while the results from FBA are independent of enzyme-kinetic parameters, any predictions about metabolite concentrations in a steady state necessitate the inclusion of specific kinetic rate equations. Despite this, it is still possible to integrate metabolite concentrations into FBA as constraints that further reduce the space of feasible steady-state flux distributions, and this reduction is dependent on the kinetic law used. In addition, this is the principle difference between FBA and kinetic modeling, which integrates the system of differential equations dX/dt = N × v(x, p) to a steady state given initial conditions of metabolite concentrations.

BIOLOGICAL INSIGHTS FROM FLUX ANALYSIS

There is now a substantial body of work in which flux measurements and flux predictions have been made for variety of tissues in a variety of plant species and under a variety of conditions. The studies have mainly focused on the central metabolic network of carbon and nitrogen metabolism as relates to the synthesis of the main biomass components of growing tissues. Recent reviews have provided a comprehensive overview of the findings from such studies (Baghalian et al., 2014; Kruger and Ratcliffe, 2015). Here, we will focus on specific examples that have provided the most significant new insights into metabolic behavior and function.

Metabolic Pathways and Networks

Perhaps the single most important thing that flux studies have demonstrated is that metabolism cannot be fully understood by considering traditional pathways such as glycolysis and the tricarboxylic acid cycle in isolation. Rather, these pathways must be considered as part of a wider network, and it may be necessary to consider the network in its entirety to gain a full understanding of the metabolic state (Marashi et al., 2012). The coordination of the activity of these pathways with the wider network and multiple points of connection via branch points from different intermediates within the pathways means that different sections of the pathways often carry different flux. Thus, it is incorrect to refer to the activity of the tricarboxylic acid cycle or glycolytic flux, since different parts of these pathways are not operating at the same rate. The tricarboxylic acid cycle, for example, can be radically reconfigured into a number of different flux modes, not all of which are cyclic, and this depends on the wider network context (Sweetlove et al., 2010) and environmental conditions (Poolman et al., 2013).

Integrated Metabolic Network Responses

The question, then, is: how does the integrated metabolic system respond to changes in the demands placed upon it? In many cases, the metabolic steady state has proven to be remarkably robust: fluxes in heterotrophic tissues measured by MFA are often invariant under different environmental conditions (Spielbauer et al., 2006; Williams et al., 2008). Naturally, this depends on the nature and magnitude of the altered demand. Small changes in demand, such as an engineered increase in the biosynthesis of secondary metabolites, have no detectable effect on fluxes through central metabolism (Masakapalli et al., 2014). In contrast, changes in the demand for synthesis of the major biomass polymers has been shown to lead to a substantial redistribution of fluxes (Iyer et al., 2008; Schwender and Hay, 2012; Sweetlove et al., 2014). Changes on the supply side are also significant: alteration of the carbon-nitrogen ratio supplied to cultured soybean (Glycine max) embryos led to corresponding changes in the accumulation of oil and protein that were supported by alterations in fluxes of reactions in carboxylic acid metabolism in mitochondria and plastids (Allen and Young, 2013). Nevertheless, in most of these examples, the changes in flux were relatively modest, reflecting the flexibility of the central metabolic network. This also leads to the conclusion that if one is attempting to engineer the biomass composition of crops (e.g. to increase the energy density of bioenergy crops; Vanhercke et al., 2014), a rather more subtle and coordinated engineering of central metabolism may be required than is usually achieved with the sledgehammer of transgenic or mutagenic interventions. Ultimately, it may be preferable to attempt to directly manipulate the controls on biomass demand (Morandini, 2013) and to rely on the inherent plasticity and flexibility of central metabolism to meet the altered demand.

Accounting for the Costs of Metabolism

Whichever way the engineering of biomass is achieved, it will have substantial implications for the energy balance of the engineered system. The computation of detailed metabolic network flux maps has allowed the quantification of energy budgets in plant cells, accounting for all the reactions that produce ATP and those that consume it. Recent FBA models of Arabidopsis that incorporate the energetic costs of all relevant metabolite transport across the plasma membrane and intracellular membranes provide the most complete energy budget calculations (Cheung et al., 2013; Arnold and Nikoloski, 2014). These calculations provide a new perspective on the costs of running a cell. For example, in a heterotrophic Arabidopsis cell, the uptake and metabolic transformation of carbon and nitrogen nutrients to biomass polymers accounts for two-thirds of the ATP budget, the remaining one-third being required for cell maintenance processes. Maintenance processes also consume half of the total NADPH budget. These calculations highlight the substantial expense associated with cell maintenance. It was also shown that a correct accounting for these maintenance costs (in terms of both ATP and NADPH usage) is required for accurate predictions of metabolic fluxes in the catabolic energy transduction pathways (Cheung et al., 2013). Nevertheless, along with recycling of misfire metabolites (Linster et al., 2013), these maintenance processes are something of a black box in modeling terms (Sweetlove et al., 2013). Although new labeling methodologies are being established that would allow some of these turnover parameters to be experimentally constrained (Nelson et al., 2014; Ishihara et al., 2015), a more mechanistic accounting of maintenance in FBA would lead to models with greater predictive power. The calculations of costs can also be extended to account for the costs of synthesizing the enzymatic machinery, something that has been ignored in most flux models. Calculations based on a recent FBA model of Arabidopsis leaf metabolism in the light revealed that the cost of synthesizing and maintaining the pool of Rubisco enzyme is considerable at approximately 0.2 ATP per carboxylation/oxygenation reaction (Arnold and Nikoloski, 2014).

Energy Metabolism in Photosynthetic Tissues

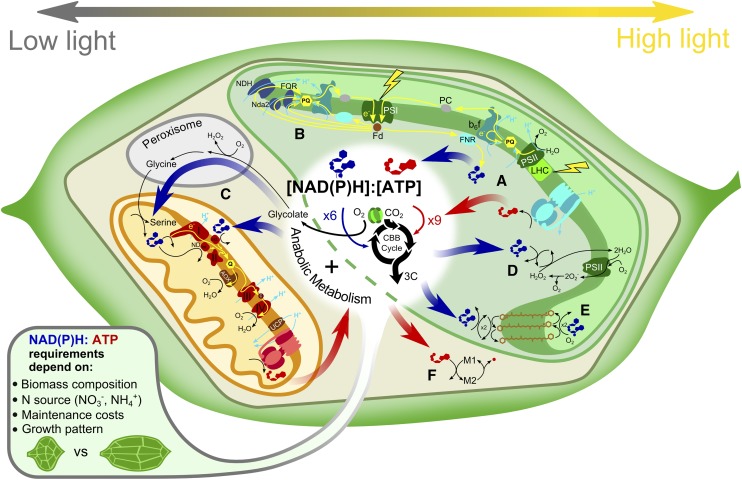
The influx of light energy and its transduction into chemical energy carriers, NADPH and ATP, by the reactions of photosynthesis obviously has a dramatic impact on the energy economy of a plant cell. The benefits of this energy source are seen not just in leaves but can also be observed in the metabolism of green seeds (Chen and Shachar-Hill, 2012). Specifically, the additional NADPH allows the refixation of metabolic CO₂ by Rubisco (Schwender et al., 2004), resulting in spectacularly high carbon conversion efficiencies for green oilseeds in the light (Allen et al., 2009b) in comparison with nongreen oilseeds (Alonso et al., 2007, 2011) or green oilseeds in the dark (Schwender et al., 2006). In photosynthetic tissues, a major challenge is presented by natural variations in light conditions, which lead to variable rates of photosynthetic NADPH and ATP production. This variable energy flux has to be matched to a rather constant energy demand for biosynthesis, maintenance, and metabolite transport. Moreover, even without this variation in light intensity, it is apparent that leaves require mechanisms to rebalance NADPH and ATP, because the ratio of NADPH to ATP produced by photosynthesis does not match the requirements of the Calvin-Benson cycle (Allen, 2003). One mechanism of rebalancing this ratio occurs within the photosynthetic electron transport chain itself: the flow of electrons can be reconfigured from a linear pathway between PSII and PSI to cyclic electron flow around PSI (Allen, 2003; Kramer and Evans, 2011). But there are multiple other mechanisms for NADPH-ATP rebalancing, including the water-water cycle (Miyake, 2010), the conversion of NAD(P)H to ATP by the mitochondrial respiratory chain (Taniguchi and Miyake, 2012), and a variety of other metabolic sinks for ATP/NADPH (Fig. 2). An FBA analysis of photosynthetic cyanobacterial metabolism was recently used to explore some of these alternative pathways (Nogales et al., 2012). It was confirmed that NADPH/ATP rebalancing is required to match the energy demand of the metabolic system as a whole, not just the Calvin-Benson cycle, and the importance of these alternative pathways increased with increasing light intensity. Nine alternative pathways were analyzed (one at a time) and were found to be nonequivalent in terms of quantum yield. Interestingly, photorespiration was found to contribute to energy rebalancing at high light intensities by acting as an ATP sink. Similarly, photorespiration was found to be spontaneously activated at high light in a genome-scale model of rice (Oryza sativa) metabolism (Poolman et al., 2013). These FBA studies suggest that photorespiration is not simply a carbon salvage pathway but also functions as an important energy sink when the plant receives excess light. This FBA prediction was recently confirmed in an INST-MFA analysis of Arabidopsis plants acclimated to high light (Ma et al., 2014). The energy-dissipating role of photorespiration has implications for attempts to transfer C₄ photosynthesis to C₃ plants (Hibberd et al., 2008): for the engineered plants to function properly in high light, it will be essential that alternative energy-dissipating systems have sufficient capacity to replace the role played previously by photorespiration.

Figure 2.

Metabolic pathways for ATP and NAD(P) rebalancing and dissipation in an illuminated leaf. Linear photosynthetic electron flow in the thylakoid (A) generates a fixed stoichiometry of NADPH and ATP that does not match the requirement of the cell’s anabolic metabolism (shown in the middle). Anabolic demands will vary, for example by assimilating ammonium rather than nitrate or depending on the growth phase (cell division or cell expansion). The ratio of NADPH and ATP produced can be adjusted by utilizing cyclic electron flow around PSI, which reduces the production of NADPH relative to ATP (B). Alternatively, the conversion of photorespiratory NADH to ATP by the mitochondrial electron transport chain (C) can be adjusted by the engagement of uncoupling pathways such as the alternative NADH dehydrogenases (ND), the alternative oxidase (AOX), and uncoupling protein (UCP). At high light, there is an excess of energy and both ATP and NADPH must be dissipated. NADPH can be dissipated by the water-water cycle (D) and by pigment cycles such as the xanthophyll cycle (E), while ATP can be dissipated by ATP-consuming futile cycles (F). Flows of electrons and protons are indicated by yellow and cyan lines, respectively. CBB, Calvin-Benson-Bassham; Fd, ferredoxin; FNR, ferredoxin-NADPH oxidoreductase; FQR, ferredoxin-quinone oxidoreductase; LHC, light-harvesting complex; NDH, chloroplast NAD(P)H dehydrogenase; PC, plastocyanin; PQ, plastoquinone; PS, photosystem.

One of the difficulties of analyzing alternative pathways with FBA is that fluxes are predicted using optimization algorithms that, when faced with equivalent alternative pathways, will select a single pathway that best satisfies the optimality criterion. This can be misleading because multiple alternative pathways will often operate simultaneously in planta. A recent methodology that uses reaction weighting factors to account for the differing costs of the enzymatic machinery provides a potential solution (Cheung et al., 2015). Using this approach, the flux space was analyzed in thousands of simulations using different sets of weighting factors for the fluxes, and the averaged results show operation of alternative pathways. By analyzing the flux distributions obtained at different light intensities, it was demonstrated that the roles of alternative pathways varied with light. The importance of mitochondria for energy rebalancing (Taniguchi and Miyake, 2012) was confirmed, with the alternative respiratory pathway becoming more important as light intensity increased. The analysis also highlighted the importance of chloroplastic energy-rebalancing mechanisms at high light in addition to the well-recognized cyclic electron flux and water-water cycle. These include xanthophyll and chlorophyll pigment cycles to dissipate excess NADPH and ATP-consuming futile cycles to dissipate excess ATP (Fig. 2).

BUILDING AND ANALYZING CONTEXT-SPECIFIC METABOLIC MODELS

Genome-scale metabolic networks characterize the entirety of biochemical reactions occurring in a biological system. There is ample evidence that biological systems adapt their metabolism to the conditions in which they operate (e.g. developmental stage, cell type in multicellular organisms, and different environmental conditions). These conditions result in different metabolic contexts in which, typically, only a subset of reactions are active. Therefore, to provide more accurate and more biologically meaningful insights, there is a need to construct context-specific models. This is of particular importance when investigating questions of plant physiology, since context-specific models represent not only the means to understand tissue- and cell-specific metabolism but also the first step in creating interconnected models of metabolism (Bordbar et al., 2011; de Oliveira Dal’Molin et al., 2015).

The existing methods for constructing context-specific models have been classified into three main groups (Robaina Estévez and Nikoloski, 2015) and have been comprehensively compared on a common data set (Machado and Herrgård, 2014). The main aim of these methods is to determine the set of active reactions (i.e. reactions carrying flux) based on the integration of high-throughput data (e.g. transcriptomics, proteomics, and metabolomics) given a genome-scale metabolic network. GIMME (Becker and Palsson, 2008) and GIM³E (Schmidt et al., 2013), from the first group, initially use conventional FBA to optimize for an objective function but then implement a second linear optimization to determine a flux distribution that minimizes the discrepancy to the high-throughput data while maintaining the optimal value from the first step. The second optimization step works by the imposition of user-defined threshold values for the data used to define active reactions and then penalizing reactions whose associated data are under the threshold. The second group of methods, comprising iMAT (Zur et al., 2010) and INIT (Agren et al., 2012), use a mixed integer linear program for the optimization. The binary variables in this formulation select the reaction states (i.e. active or inactive) that are most concordant with the associated data. While iMAT uses data to preclassify reactions of the genome-scale metabolic network into groups of active or inactive reactions, INIT integrates data as a weighting factor for the binary variable. In an extended version, tINIT (Agren et al., 2014), a set of metabolic tasks (i.e. biochemical pathways) that must carry nonzero flux can be added as further constraints. The third group, composed of MBA (Jerby et al., 2010), mCADRE (Wang et al., 2012), and FastCORE (Vlassis et al., 2014), first define a core set of reactions, classified as active in a given context according to experimental data, and then find the minimum set of reactions outside the core required to satisfy the model consistency condition (i.e. all reactions in the model must be able to carry a nonzero flux in at least one of the allowed steady-state distributions). Unlike the methods in the previous two groups, these only extract a context-specific model and do not provide a respective flux distribution.

The first group belongs to the so-called biased methods (within the constraint-based analysis), since the achieved solution depends on the definition of a metabolic objective function to be optimized. In contrast, the second and third groups consist of unbiased methods, since they are independent of objective function (Lewis et al., 2012). The choice of unbiased methods is of particular importance when the metabolic functions to be optimized under a given context may be difficult to obtain and justify; for instance, this is the case when dealing with multicellular organisms, where multiple cell types coexist (cooperate and/or compete) while performing a variety of specialized metabolic functions instead of optimizing a single general function.

Recently, Robaina Estévez and Nikoloski (2015) proposed and tested a fully automated procedure for model extraction and flux prediction without using a priori knowledge of a context-specific function and without any preclassification of reactions in the process of data integration. This is of particular importance when a large number of context-specific models are to be extracted; it is an even more pressing issue for poorly studied organisms or cell types for which no information regarding the context specificity of reactions or metabolic function may be available in the existing databases or from detailed physiological studies.

All of these methods largely depend on integrating transcriptomics and proteomics data to establish bounds on fluxes and, consequently, to reduce the flux space (Fig. 1). The inclusion of flux bounds based on transcript and protein levels has proved to be a useful tool to assess and interpret metabolic behavior between conditions (Töpfer et al., 2013). However, the coordination of several regulatory levels between gene transcription and reaction rates may not result in a direct correspondence between gene expression and fluxes, and this can affect the usefulness of these methods (Machado and Herrgård, 2014). The correspondence between changes in flux and changes in transcript levels in plant tissues was recently investigated (Schwender et al., 2014). ¹³C-MFA flux ratios from two Brassica napus (oilseed rape) accessions were used to constrain fluxes in a larger genome-scale model. The authors then investigated the correspondence between the changes in flux and the changes in transcript levels for the corresponding reactions. They found very little correspondence between these changes, which is in stark contrast to the excellent agreement (coefficient of determination of 0.87 and 0.96 at 75% and 85% of optimal biomass) found in Saccharomyces cerevisiae (Lee et al., 2012). The reason for the low correspondence in the plant study may be due to the fact that the comparison was between fluxes determined under the steady-state assumption, and transcript levels, which, when used directly as proxies for fluxes, may violate the steady-state assumption. A more valid comparison would be between the flux ratios from ¹³C-MFA and the flux ratios from flux distributions satisfying the same set of constraints (e.g. steady state) closest to the transcript levels (or their ratios). Clearly, further methodological developments are needed to effectively reduce the feasible flux space and arrive at physiologically relevant findings.

CONTEXT-SPECIFIC MODELS IN PLANTS

In this section, we review insights obtained from context-specific models in plants. It is notable that the majority of these models have not been assembled following the aforementioned systematic methods for context-specific model extraction but, rather, rely on expert knowledge in selecting the active reactions. In many cases, context specificity has been established using the full genome-scale reaction set, but applying context-specific constraints, and this can be justified for the core reactions of primary metabolism that show little cell- or tissue-type variations in terms of the presence or absence of reactions.

For instance, development-driven changes in biomass composition were considered in modeling of Synechocystis sp. PCC 6803 (Knoop et al., 2013). Similarly, FBA models of Chlamydomonas reinhardtii (Boyle and Morgan, 2009; Chang et al., 2011) included biomass functions for both photoautotrophic and mixotrophic growth. A recently assembled Arabidopsis FBA model includes condition-specific biomass reactions for optimal (light-limited), nitrogen-limited, and carbon-limited conditions (Arnold and Nikoloski, 2014). A similar approach was taken in a multiscale model of barley (Hordeum vulgare) in which models of leaf, stem, seed, and root were interconnected via the phloem and environment to investigate sink-source relationships (Grafahrend-Belau et al., 2013). Time-specific biomass compositions in combination with minimization of the uptake of resources (e.g. CO₂) and minimization of the total flux was used to simulate whole-plant behavior and to obtain tissue-specific steady-state flux distributions followed by FBA. Finally, biomass reactions specific for nine stages of tomato (Solanum lycopersicum) fruit development in combination with the minimization of total flux were used to investigate the temporal redistribution of fluxes in the central metabolism of tomato fruits (Colombié et al., 2015).

In addition, a model used for the exploration of heterotrophic growth of Arabidopsis was updated to a diel metabolic model by dividing the day/night cycle into two phases (day and night), both operating in a steady state (Cheung et al., 2014). The diel model is essentially composed of two copies of the original model with the addition of dummy reactions for the transfer of storage molecules between the two phases as well as enforcing certain values for selected fluxes (e.g. carboxylation-to-oxygenation ratio and photon influx). The model was successful in predicting the carbon and nitrogen storage molecules that accumulate over the day/night cycle and in establishing differences between day and night flux distributions.

Duplicates of a model connected with exchanges of particular metabolites are the usual strategy followed in the field of modeling C₄ metabolism (e.g. maize [Zea mays]; de Oliveira Dal’Molin et al., 2010; Saha et al., 2011) and the transition between C₃ and C₄ metabolism (Mallmann et al., 2014). For instance, C4GEM (de Oliveira Dal’Molin et al., 2010) includes two copies of the same model, with expert-guided alterations to capture the bundle sheath and mesophyll cells, respectively, which exchange molecules through the plasmodesmata. A similar approach is taken in the strategy of Mallmann et al. (2014), where the addition of the photorespiratory CO₂-concentrating mechanism was shown to be a prerequisite for the evolution of C₄ plants (under the constraints on minimizing exchange through the plasmodesmata and fixing additional fluxes from external information).

The approach of Simons et al. (2014) is closer to the methods discussed earlier: transcriptomics data were used to obtain cell type-specific models and combine them in an integrated model of maize that includes pathways from both primary and secondary metabolism. By using the differential behavior from high-throughput data, reactions are switched on/off to investigate flux redistribution between optimal and limiting nitrogen conditions. In addition, flux sums (the total flux passing through a metabolic pool) under the different conditions in combination with appropriate variability analysis are related to the pool sizes assessed experimentally (see “Linking Fluxes to Metabolites” below). Following the MBA method and based on tissue-specific protein expression data from juvenile leaves, open flowers, flower buds, 10-d roots, 23-d roots, siliques, seeds, and cotyledons, as well as cell cultures grown in light and in dark, Mintz-Oron et al. (2012) extracted a model specific for these contexts. The presence of selected metabolites (i.e. three isoprenoid compounds) in different tissues was validated by metabolomics technologies, but no assessment of the correspondence between flux distributions and protein abundance was carried out. Finally, Seaver et al. (2015) extracted an organ-specific model for the maize leaf and tissue-specific models for embryo and endosperm cells by including (similarly to iMAT) a minimal set of reactions required to fill gaps in the network while maximizing the number of flux-carrying reactions associated with highly expressed genes. The models are accompanied by biomass reactions based on measurements under the same conditions, and their validity was tested by comparing the predicted fluxes with those coming from MFA.

While the transcriptome and proteome will continue to be pursued in the context-specific modeling of plant metabolism, largely due to their broad coverage, a drastic reduction in the flux space is more likely to be achieved from the consideration and inclusion of data on metabolite levels.

LINKING FLUXES TO METABOLITES

As stated previously, steady-state flux distributions are obtained by solving a (usually underdetermined) system of linear equations under a set of additional biochemically meaningful constraints. Moreover, in a biological system, a flux distribution is the integrated outcome of the transcription and translation machinery as well as the metabolite pools used as substrates in the reactions. Therefore, a biochemically meaningful flux distribution should correspond to a set of protein abundances (together with adequate active part of the protein pool) and metabolite levels. In other words, the fact that every optimal steady-state flux distribution obtained from FBA and its extensions satisfies the imposed constraints does not necessarily imply that the flux distribution can be associated with biochemically meaningful values for the levels of the other system components. It is due to this requirement, that flux distributions should map to corresponding protein and metabolite levels, that the space of feasible flux distributions can be further constrained by considering respective data sets.

Metabolite levels have been integrated into constraint-based methods with the aim of (1) extraction of context-specific models (e.g. GIM³E); (2) identification of turnover rates and limiting metabolites; (3) prediction of fluxes compatible with a particular kinetic law and thermodynamic principles (Hoppe et al., 2007; Yizhak et al., 2010; Tepper et al., 2013); and (4) prediction of time-resolved flux distributions. The integration of metabolite levels in constraint-based methods and their applications in plant research have already been systematically reviewed elsewhere (Töpfer et al., 2015). Here, we only focus on the most recent plant-related applications of purely structural approaches, namely flux-sum analysis, flux imbalance analysis, and time-resolved expression and metabolite-based (TREM)-flux, which do not require kinetic laws and, thus, maintain the simplicity of FBA.

Flux-sum analysis (Chung and Lee, 2009) determines the flux sum for each metabolite by summing the incoming or outgoing fluxes of the reactions in which the metabolite participates as a product or a substrate, respectively. At steady state, the influx into a metabolite pool equals the efflux from it. However, the steady state does not resolve the magnitude of the total efflux and influx, which can be quantified by the flux-sum approach. Therefore, the flux sum can be used as a descriptor of the turnover rate of a metabolite, with a high flux sum indicating high turnover. Flux sums are used by calculating a basal flux sum for each metabolite based on a flux distribution that maximizes a specific objective, determining the maximum flux sum of individual metabolites irrespective of an objective and using the calculated bounds to manipulate the behavior of flux sums of individual metabolites to investigate their influence on the objective. Simons et al. (2014) recently applied this approach to determine the directional changes of the flux sums of individual metabolites between two different nitrogen conditions in a wild-type maize leaf. These changes were then qualitatively compared with the directional changes in the experimentally measured metabolite levels. Therefore, this study uses the flux sum as a proxy for the metabolic pool size rather than its turnover. Since the flux sum can vary in alternative optima, the authors only considered those metabolites whose ranges for flux sums (normalized by the biomass rate) did not overlap between the compared scenarios.

Flux imbalance analysis explores the sensitivity of metabolic optima to violations of the steady-state constraints (Reznik et al., 2013). The method does not directly integrate metabolite levels but can be used to elucidate the processes that control intracellular metabolites in the cell. The approach is based on the concept of shadow price (see above), which captures the influence of the metabolite’s accumulation or depletion on the optimum of the FBA objective. Thereby, a negative shadow price is considered to imply that the corresponding metabolite is growth limiting. By using data from S. cerevisiae under different nutrient-limiting conditions, the authors showed that the determined shadow prices are negatively associated with the growth limitation of the respective measured intracellular metabolites. Moreover, based on these findings, the authors argued that growth-limiting metabolites cannot exhibit large fluctuations in an uncontrolled manner. Using time-resolved metabolomics data from the metabolic response of Escherichia coli to carbon and nitrogen perturbations, they further demonstrated that metabolites associated with a negative shadow price indeed showed lower temporal variation in comparison with metabolites with zero shadow prices in a perturbed system.

In TREM-flux (Kleessen et al., 2015), the steady-state assumption of the FBA approach is replaced with the requirement that the changes in flux distribution must coincide with the difference of the measured metabolite levels between two consecutive time points while matching global physiological parameters. Therefore, the approach relies on integrating metabolite time-series data with transcriptomics data (using a dynamic variant of the E-flux method). In a genome-scale model reconstruction of C. reinhardtii, TREM-flux was used to predict the metabolic response to rapamycin treatment. The obtained flux distributions over time showed differences in the metabolic responses under varying growth conditions between control and treatment, in line with the findings from closely related organisms. The study showed that the integration of time-resolved unlabeled metabolomics data results in differences in predicted fluxes compared with that obtained under the steady-state assumption and the integration of only transcriptomics data. In addition, the changes in the metabolic pools could not be explained by the reactions predicted not to carry flux in any steady-state assumption, demonstrating the need for the time-resolved variant.

FUTURE DIRECTIONS AND CHALLENGES

The majority of flux studies to date have analyzed fluxes in the metabolic networks of single cell types or single tissues, mainly leaves and usually with reference to a snapshot of developmental time. Clearly, the next step for the field is to integrate metabolic network fluxes into frameworks that connect multiple tissues together in a representation of whole-plant processes and to account for growth and development over time. In principle, this could be done using existing MFA or FBA tissue models, as was recently shown for Arabidopsis (de Oliveira Dal’Molin et al., 2015). However, it is important to realize that most tissue metabolic models are based on the use of average whole-tissue experimental measurements as constraints, such as isotopic label redistribution and biomass composition. Clearly, this will only generate average metabolic flux maps and not the flux maps of the individual cell types. In fact, in the case of MFA, where the labeling patterns are not linearly related to fluxes, the resulting flux map may not even be an accurate average (Kruger and Ratcliffe, 2015). In any case, it would be preferable to have separate flux maps of the different cell types, not averages, so that the tissue structure and varying metabolic demands can be accounted for (Borisjuk et al., 2013).

This is particularly relevant in plant organs because growth is biphasic at the cellular level, with cell division being followed by cell expansion. Cell division and cell expansion impose completely different sets of demands upon the metabolic network and so can be expected to lead to completely different flux maps. In fact, this can be seen in the FBA-predicted network fluxes in tomato fruit at different stages of development, in which network fluxes in fruit at 8 DPA (still in the phase of cell division) are dramatically different from those at later stages of development dominated by cell expansion (Colombié et al., 2015). Tomato fruit are a good system in which to study cell division and cell expansion because the temporal demarcations between them are well established and, also, because sufficient tissue mass accumulates during the cell division phase to make biochemical measurements feasible. This is not the case in organs such as leaves, which are still extremely small when the cell division phase has ended. This means that FBA studies of dicot leaves that use biomass composition as the main constraint on the outputs of the metabolic network are, in fact, only considering this very early stage in development and do not account for the main visible phase of leaf growth, which is driven primarily by cell expansion.

Clearly, more than one temporal phase of leaf development will need to be accounted for. FBA modeling techniques have been developed that can handle multiple time points, including dynamic FBA, in which each time step is solved separately, with the outputs of one time step forming the inputs of the next (Knoop et al., 2013; Kleessen et al., 2015), as well as global methods, in which the different phases are handled simultaneously by the model optimization algorithms (Cheung et al., 2014; de Oliveira Dal’Molin et al., 2015). Accounting for the expansion phase of cell growth will require a consideration of the appropriate experimental measures that can be used as constraints. Given that expansion requires only limited synthesis of new biomass and is instead driven largely by osmotic uptake of water into the vacuole, these will center on the rates of vacuolar transport of ions and metabolites as the source of the osmotic driving force (Lobit et al., 2006). Methods have also been proposed that would allow the determination of isotopic label redistribution in specific cell types to support cell type-specific MFA (Kruger and Ratcliffe, 2015), although the low mass of dividing cells in organs such as roots and leaves would present a considerable sensitivity challenge for this cell type.

It is likely that a large number of metabolic network models will need to be integrated to account for the different populations of cells within tissues and their changing metabolic behavior during time, both at the diel scale and over a longer developmental scale. Fortunately, the optimization algorithms at the heart of FBA are computationally efficient, and such a proliferation of models can be analyzed with standard computer hardware. It is also possible to envisage embedding metabolic network models into multiscale whole-plant models (Baldazzi et al., 2012; Chew et al., 2014), as illustrated by the successful integration of FBA models with an ecophysiological whole-plant model of barley (Grafahrend-Belau et al., 2013). This approach will allow the intracellular behavior of the metabolic network in different tissues and with developmental time to be described in detail. In the barley work, mass balancing demonstrated the requirement for the mobilization of stem carbohydrate stores during grain filling due to the decline of leaf function during senescence. Although this important study represents the first serious attempt to embed FBA metabolic models into a whole-plant model, the definitive parameters with respect to the stem carbohydrate result lie outside of the FBA model. Rather, the prediction was based on calculations of carbon input rates (from a photosynthesis model that includes biophysical representations of gas exchange) and a carbon allocation model based on the growth-maintenance paradigm (Amthor, 2000). The FBA model takes these parameters as input-output constraints and predicts the metabolic network fluxes between them.

It could be argued that it would be more useful in this whole-plant context if FBA models were able to predict the outputs of the metabolic network rather than being constrained by them. A recent FBA model of E. coli shows that it is possible to lift some of the biomass constraints and move toward a more mechanistic form of FBA (O’Brien et al., 2013). In this model, it was assumed that the bacterium requires the biosynthesis of DNA and cell wall in certain proportions in order to grow, but other biomass components such as proteins were not constrained. Instead, the proteome required to support growth was predicted by the model based on the catalytic capacity and protein turnover of the enzymes of the metabolic network. Ultimately, if the remaining biomass demands for cell membranes and cell wall could be coupled to cell geometry and biophysics (Karr et al., 2012), then tissue morphometric considerations would be linked to the metabolic state, and this would allow the full and predictive integration of metabolism with structure-function models of plants.

Finally, methodological advances are necessary to test alternative solutions of constraint-based models, particularly in the case of data integration. This will help further elucidate the relationships between fluxes and other cellular levels on which they depend, including transcription and translation, as well as the levels of the metabolites. In ¹³C-MFA studies, Monte-Carlo sampling is a well-established way to examine the identifiability of flux distribution and to test the statistical differences of fluxes between different cellular scenarios. While some attempts have been made to implement this technique for FBA-based models (Kleessen et al., 2012; Recht et al., 2014), further advances are needed. This is particularly the case for selecting appropriate context-specific models (from the multitude that may match the high-throughput data) that will become more prominent due to the investigation of interconnected cell type-specific models. Ultimately, analogous to the analysis of other cellular phenotypes, these methodological advances will allow statistical testing of the differential behavior of fluxes predicted from modeling attempts.

Glossary

MFA

metabolic flux analysis

INST-MFA

isotopically nonstationary metabolic flux analysis

FBA

flux balance analysis