Factors influencing the assessment of lung function in mice with influenza‐induced lung disease

Abstract

Please cite this paper as: Larcombe et al. (2012) Factors influencing the assessment of lung function in mice with influenza‐induced lung disease. Influenza and Other Respiratory Viruses DOI: 10.1111/irv.12034.

Background  The constant‐phase model (CPM) is commonly fit to respiratory system input impedance (Z _rs) to estimate lung mechanics. Driving signal frequencies and the method of model fitting may influence the results, especially in cases of severe lung disease or under severe bronchoconstriction.

Objective  To illustrate the effects of different CPM fits to Z _rs data using a mouse model of influenza‐induced lung disease.

Methods  BALB/c mice infected with influenza (or control) were challenged with methacholine. The CPM was fitted to Z _rs, measured between 0·25 and 19·625 Hz, using both unweighted and weighted fits. The effect of different lowest frequencies was assessed.

Results and Conclusions  For influenza‐infected mice, the unweighted fit was poor, and airway resistance (R _aw) was often biologically impossible. The weighted fit provided more realistic estimates of R _aw. Different model fits and minimal frequencies had little effect on tissue mechanics.

Introduction

Measurement of lung function forms an important part of the use of animals to model human lung diseases. The effects of respiratory system insults are often obtained through fitting mathematical models, such as the constant‐phase model (CPM), to respiratory system impedance (Z _rs). The CPM partitions low‐frequency input Z _rs into components representing airway mechanics, that is, airway resistance (R _aw) and inertance (I _aw), and a strictly constant‐phase tissue compartment characterized by the coefficients of tissue damping (G) and tissue elastance (H). ¹ The CPM has been validated in a variety of species, ¹ , ² and its sensitivity has been assessed in mice. ³ The relative contributions of the airway and tissue compartments to Z _rs within a given frequency range may change radically if any alterations occur predominantly in either compartment, such that the other compartment will be subjected to estimation bias. This may occur during acute bronchoconstriction where the contributions from the airway may increase markedly or in severe lung disease where the tissue component may dominate. It may be possible to alleviate the estimation bias by studying a more appropriate frequency range or by using different methods for fitting the CPM to Z _rs. ³

We investigated the influence of the frequency content of the driving signal and the method used to fit the CPM to Z _rs on estimates of R _aw, G, and H in mice with influenza‐induced lung disease.

Methods

Eight‐week‐old female BALB/c mice, maintained under specific pathogen‐free conditions and with food and water provided ad libitum, were intranasally inoculated with 10^4·5 plaque‐forming units of influenza A/Mem/1/71 diluted in 50 μl of virus production serum‐free medium (VP‐SFM; Gibco, Mulgrave, Victoria, Australia). Seven mice were infected (mass 17·6 ± 1·1 g), and seven control mice (mass 18·7 ± 0·5 g) received the same volume of the supernatant of uninfected Madin–Darby canine kidney cells diluted in VP‐SFM. Influenza was grown and titrated as previously described. ⁴ This strain replicates to high titres ⁴ and causes significant disease in mice. ⁵

At the peak of infection, ⁶ mice were surgically prepared as described previously. ⁵ Anaesthetized, tracheostomized mice were ventilated using a flexiVent small animal ventilator (SCIREQ, Montreal, Canada) at 450 breaths per min with a tidal volume of 8 ml/kg and a positive end‐expiratory pressure of 2 cm H₂O. Lung volume history was standardized via three slow (16‐s) deep inflations, spaced 1 min apart, to a pressure of 20 cm H₂O and Z _rs measured 1 min after increasing doses (0·1, 0·3, 1, 3, 10, and 30 mg/ml) of aerosolized methacholine (MCh; Sigma‐Aldrich, St. Louis, MO, USA) generated by an ultrasonic nebulizer (DeVilbiss UltraNeb, Somerset, PA, USA). ⁵ , ⁷ We report measurements at baseline (i.e., before any MCh) and after 30 mg/ml MCh.

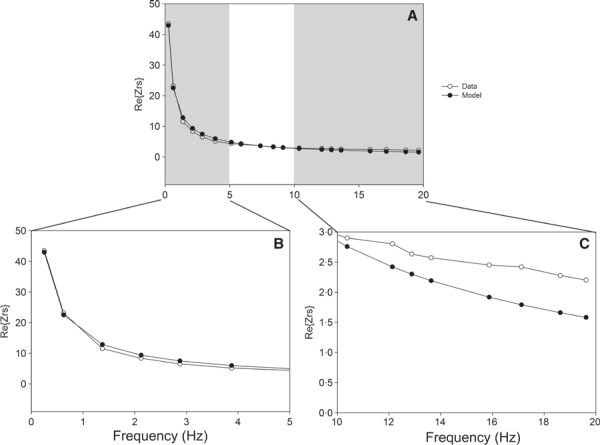
Z_rs was measured using the “Primewave” signal of the flexiVent small animal ventilator, which is comprised of 19 mutually prime sinusoidal frequencies (0·25, 0·625, 1·375, 2·125, 2·875, 3·875, 5·125, 5·875, 7·375, 8·375, 9·125, 10·375, 12·125, 12·875, 13·625, 15·875, 17·125, 18·625, and 19·625 Hz). The CPM ¹ was used to calculate Newtonian resistance (R _n), I _aw, G, and H. Hysteresivity (η) was calculated as G/H. We assumed that the contribution of the lung parenchyma and the chest wall to R _n was insignificantly small ⁸ and hence R _n= R _aw. I _aw values were negligible and are not reported. Z _rs data were imported into custom‐made analysis software (University of Szeged, Hungary) for analysis, which uses a global optimization algorithm ⁹ to fit the CPM to Z _rs. Data were initially analyzed using the complete set of 19 frequencies using an unweighted fitting criterion:

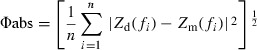where Φ is the fitting error, and Z _d(f _i) and Z _m(f _i) correspond to the measured and model‐predicted impedance value at the ith frequency, respectively. ³ The CPM was then fitted to the measured data using a weighted fitting criterion, where non‐negative weights were incorporated into the fitting criterion:

The weighted fitting criterion scales the contribution of each frequency by the magnitude of the impedance at that frequency, such that model fit is not dominated by frequency points where Z _rs is larger compared to other frequencies. Z _rs data were then adjusted to alter the lowest frequency, and the model was refit using the weighted fitting criterion, such that we had one set of data which was analyzed in six ways;

• 1 Fu_0·25: unweighted fit/0·25–19·625 Hz,
• 2 Fw_0·25: weighted fit/0·25–19·625 Hz,
• 3 Fw_1·375: weighted fit/1·375–19·625 Hz,
• 4 Fw_2·875: weighted fit/2·875–19·625 Hz,
• 5 Fw_3·875: weighted fit/3·875–19·625 Hz, and
• 6 Fw_5·125: weighted fit/5·125–19·625 Hz.

Results

Baseline Lung Function

Applying a weighted CPM fit to Z _rs spectra (compared to an unweighted fit) had the greatest influence on estimates of R _aw at baseline, and this effect was more pronounced for influenza‐infected mice compared to controls (Figure 1). For infected mice, the unweighted fit resulted in the lowest and most variable estimation of R _aw (0·25 ± 0·46 cm H₂O s/ml) for any fitting criterion. This was a reflection of the CPM returning a negative (and biologically impossible) R _aw (−0·53 cm H₂O s/ml) for one of the seven mice in this group when the Fu_0·25 was used. Applying the Fw_0·25 fitting scheme to this measurement resulted in a more biologically realistic R _aw (0·39 cm H₂O s/ml). This skewing of R _aw using the Fu_0·25 criterion had the flow on effect of increasing G for infected mice. Employing a weighted fitting of the CPM for influenza‐infected mice resulted in a reduction in the SD of baseline R _aw and G, regardless of the frequency range used. At baseline, increasing the lowest frequency of the driving signal had little effect on estimates of, or variability in, measurements of R _aw, G, or H beyond the difference made by applying the Fw_0·25 (Figure 1).

Figure 1.

 Box and whisker plots of baseline airway resistance (R _aw), tissue damping (G), tissue elastance (H), and hysteresivity (η) of BALB/c mice, 4 days post‐inoculation with influenza A (B, D, F and H) or control solution (A, C, E and G) using different methods of fitting the constant‐phase model to Z _rs spectra. Note different scales.

Maximum response to MCh (30 mg/ml)

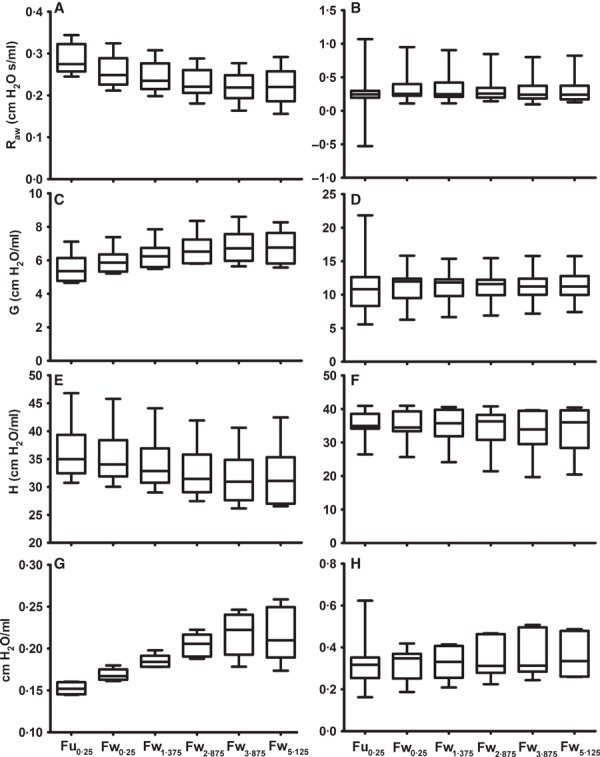
A similar pattern was noted for R _aw after exposure to 30 mg/ml MCh (Figure 2). Again, when using the Fu_0·25 fitting criterion, R _aw for infected mice was underestimated due to three of the seven mice in this group returning a negative estimation of R _aw. Applying the Fw_0·25 fitting scheme resulted in non‐negative estimates of R _aw for two of these mice; however, it was not until the minimum frequency was increased to 1·375 Hz that six of the seven infected mice returned biologically realistic estimates of R _aw (Figure 2). The seventh mouse required a minimum driving signal frequency of 5·125 Hz before a realistic estimate of R _aw was achieved. Considerable alterations in estimates of G and H were also observed when using the Fw_0·25 compared to the Fu_0·25; however, increasing the minimum driving signal frequency beyond 1·375 Hz resulted in little change in these measurements or their variability (Figure 2). Representative impedance spectra and CPM fit for an influenza‐infected mouse after exposure to 30 mg/ml MCh are shown in Figures 3 (Fu_0·25) and 4 (Fw_1·375). These figures illustrate the improved fit of the CPM to Z _rs, particularly in panels C.

Figure 2.

 Box and whisker plots of maximum (after exposure to 30 mg/ml MCh) airway resistance (R _aw), tissue damping (G), tissue elastance (H), and hysteresivity (η) of BALB/c mice, 4 days post‐inoculation with influenza A (B, D, F and H) or control solution (A, C, E and G) using different methods of fitting the constant‐phase model to Z _rs spectra. Note different scales.

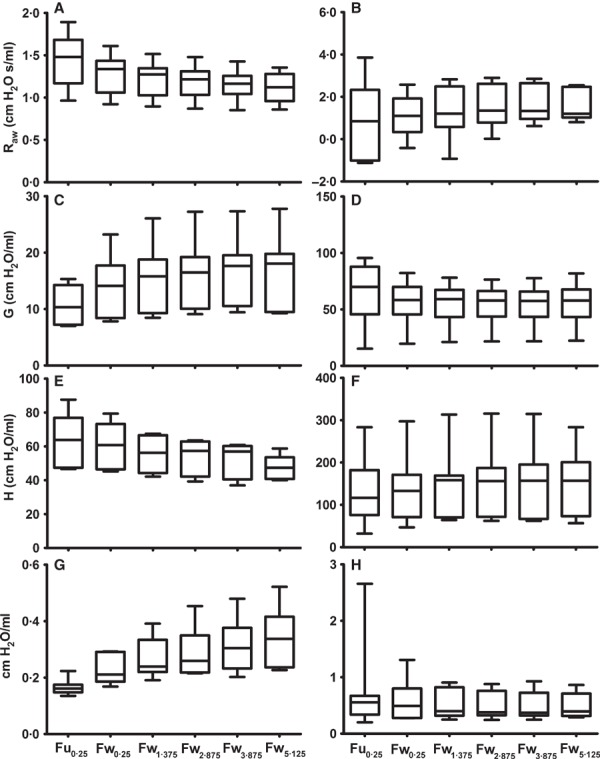
Figure 3.

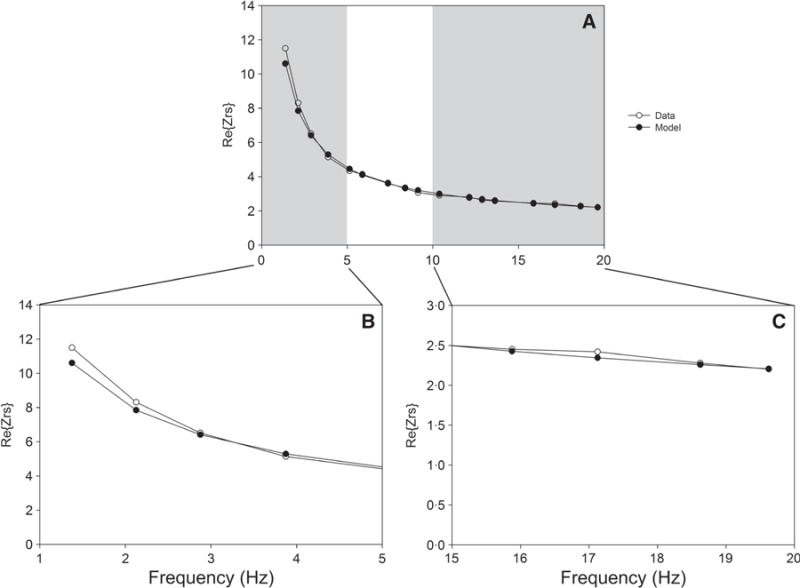
 Representative “real part” of the impedance spectrum and constant‐phase model (CPM) fit for an influenza‐infected mouse after exposure to 30 mg/ml MCh, using the Fu_0·25: unweighted fit/0·25–19·625 Hz criterion. Panel A shows the entire Z _rs, while panels B and C zoom in on either end of the Z _rs. For this individual, R _aw = −0.73 cm H₂O s/ml, G = 47.25 cm H₂O/ml, and H = 90.61 cm H₂O/ml. Open circles represent Z _rs measured at each frequency, and closed circles represent CPM fit. The data shown in Figure 4 are for the same measurement from the same mouse, using an alternative fit criterion.

Figure 4.  Representative “real part” of the impedance spectrum and constant‐phase model (CPM) fit for an influenza‐infected mouse after exposure to 30 mg/ml MCh, using the Fw_1·375: weighted fit/1·375–19·625 Hz criterion. Panel A shows the entire Z _rs, while panels B and C zoom in on either end of the Z _rs. For this individual, R _aw = 0.85 cm H₂O s /ml, G = 37.31 cm H₂O/ml, and H = 121.57 cm H₂O/ml. Open circles represent Z _rs measured at each frequency, and closed circles represent CPM fit. The data shown in Figure 3 are for the same measurement from the same mouse, using an alternative fit criterion.

Discussion

This study illustrates the importance of selecting appropriate settings for the measurement of lung mechanics when applying the CPM to Z _rs spectra. The greatest differences were found when comparing an unweighted (Fu_0·25) fit of the CPM to Z _rs spectra with any of the weighted fitting criteria. Applying a weighted fit of the CPM to Z _rs spectra can improve measures of lung mechanics under acutely bronchoconstricted conditions by preventing undue contributions from the lower frequencies, which have intrinsically larger magnitudes. In severe lung disease, such as that caused by influenza infection, Z _rs may increase even further at low frequencies, and the negative frequency dependence of the real part of Z _rs may strengthen ¹⁰ , ¹¹ , ¹² leading to misestimation of R _aw. We have also shown that selecting different lowest frequencies of the forced oscillation signal can have considerable impacts on the estimation of CPM parameters. Generally, we identified slight differences in the model fit with increasing lowest frequency, up to a point where the potential benefits of the removal of additional low frequencies were outweighed by the loss of degrees of freedom of the model.

Our data show that the frequencies of a forced oscillation technique signal should be carefully selected so that the measured Z _rs as a result of the tissues and airways has an equal “opportunity” to contribute to parameters specified in the model. Selection of an appropriate frequency range is dependent on multiple factors including species and disease state. Under the particular set of circumstances employed in the current study (i.e., mice with influenza), an unweighted fit and frequency range of 1·375–19·625 Hz provided the most realistic measurements. When undertaking studies that apply the CPM to Z _rs spectra, researchers need to be aware that fitting criteria and frequency selection are important. Without previous knowledge of what frequencies are appropriate, a useful starting point may be the selection of the lowest frequency based on the resting respiratory rate of the study species. For example, the laboratory mouse has a resting breathing rate (ƒ_R) ∼80 to 200 breaths per minute. ¹³ Thus, the lower end of the forced oscillatory signal, for an animal this size, should be ∼1·3 to 3·3 Hz. This relationship holds for larger species, such as humans with a resting ƒ_R of 15 breaths per min (0·25 Hz); indeed, many studies on low‐frequency respiratory mechanics in humans select similar frequencies. ¹⁴ , ¹⁵ In saying this, some researchers employ much lower minimum frequencies (e.g., 0·078 Hz) in studies of broncho‐constriction and acute lung injury. ¹⁶ , ¹⁷ The selection of the highest frequency is perhaps not as vital, although they are usually within the medium frequency range (4–40 Hz) ¹⁸ , ¹⁹ , which means that resonance and anti‐resonance phenomena ¹⁹ , ²⁰ are not examined in low‐frequency studies.