Abstract
Objective
Conventional inverse-scattering algorithms for microwave breast imaging result in moderate resolution images with blurred boundaries between tissues. Recent 2D numerical microwave imaging studies demonstrate that the use of a level set method preserves dielectric boundaries, resulting in a more accurate, higher resolution reconstruction of the dielectric properties distribution. Previously proposed level set algorithms are computationally expensive and thus impractical in 3D. In this paper we present a computationally tractable 3D microwave imaging algorithm based on level sets.
Methods
We reduce the computational cost of the level set method using a Jacobian matrix, rather than an adjoint method, to calculate Frechet derivatives. We demonstrate the feasibility of 3D imaging using simulated array measurements from 3D numerical breast phantoms. We evaluate performance by comparing full 3D reconstructions to those from a conventional microwave imaging technique. We also quantitatively assess the efficacy of our algorithm in evaluating breast density.
Results
Our reconstructions of 3D numerical breast phantoms improve upon those of a conventional microwave imaging technique. The density estimates from our level set algorithm are more accurate than those of conventional microwave imaging, and the accuracy is greater than that reported for mammographic density estimation.
Conclusion
Our level set method leads to a feasible level of computational complexity for full 3D imaging, and reconstructs the heterogeneous dielectric properties distribution of the breast more accurately than conventional microwave imaging methods.
Significance
3D microwave breast imaging using a level set method is a promising low-cost, non-ionizing alternative to current breast imaging techniques.
Keywords: level set method, microwave imaging, breast density
I. Introduction
MICROWAVE imaging of the breast is an exploratory imaging modality that offers several potential advantages over x-ray mammography, magnetic resonance imaging (MRI), and provides complementary information to ultrasound. Microwave imaging via inverse scattering involves reconstructing the 3D distribution of the breast dielectric properties from scattered fields measured in the microwave frequency range using an antenna array surrounding the breast. Microwave imaging does not involve painful compression or ionizing radiation, unlike x-ray mammography. The equipment used in microwave imaging is also portable and low-cost; thus, microwave tomography has the potential to be more widely available and cost effective than MRI.
In the microwave frequency range there is a moderate to large contrast between the dielectric properties of different breast tissue types [1], [2]. This contrast reflects both the type and physiological state of the tissue. Hence, the dielectric properties distribution within the breast conveys clinically relevant anatomical and functional information. Reconstructions of the dielectric properties are potentially useful for several clinical applications including density estimation, tumor detection, and treatment monitoring. However, the inverse scattering problem is ill-posed, so microwave imaging performance depends heavily on the algorithm used to reconstruct the dielectric properties of the breast. Many common microwave imaging algorithms are based on iteratively solving a least squares problems with Tikhonov-Philips regularization (e.g. [3]) which results in over-smoothing or blurring of the boundaries between tissues of contrasting dielectric properties.
Level set algorithms [4]–[6] for microwave imaging have yielded high-resolution reconstructions of dielectric properties. An algorithm for imaging several 3D, homogeneous, non-overlapping targets is described in [6], but the only level set algorithms suitable for imaging the spatially complex and heterogeneous tissue structure of the breast are applied to 2D numerical breast phantoms [4], [5]. These 2D level set algorithms have a high computational cost and are impractical for 3D breast imaging. They involve a large number of iterations (over 100) [4], with each iteration requiring multiple runs of a computational electromagnetics simulation that can be time-consuming for large domain sizes [5].
In this paper, we present a computationally feasible level set method for 3D microwave breast imaging. Our algorithm requires only one electromagnetics simulation per iteration and fewer overall iterations than previously proposed level set approaches. The effectiveness of our algorithm is demonstrated by comparing our 3D level set reconstructions of anatomically realistic MRI-derived numerical phantoms [7] to those from the distorted Born iterative method [8].
We quantitatively evaluate the performance of our level set method in the context of breast density estimation – a promising application for microwave imaging. Current imaging modalities for 3D breast density evaluation have shortcomings in terms of accuracy and cost. High volumetric breast density, defined as a large percentage of fibroglandular tissue, is one of the strongest predictors of breast cancer risk [9]. Hence, breast density estimation can play an important role in assessing breast cancer risk, as described by Harvey and Bovbjerg [10], as well as monitoring preventative interventions designed to lower breast density and the consequent cancer risk. We use density estimation as a biologically relevant performance metric for the reconstructions obtained with our level set method. The high resolution images produced by our level set method yields more accurate breast density estimates than those obtained with Tikhonov-regularized Gauss-Newton methods. The accuracy of our density estimates also exceeds that reported previously for mammographic density estimation [11], [12].
The next section presents the physical relevance of the level set technique for representing the dielectric properties of breast tissue. We also introduce a single parameter dispersion model that significantly reduces computational requirements. Our level set model for dielectric properties and the optimization algorithm we use for imaging are presented in Section III. Section IV describes the implementation details of our algorithm and Section V presents the results from our imaging study using numerical phantoms. A discussion of our results is found in Section VI and the conclusions are presented in Section VII. Throughout this work boldface symbols represent vectors or matrices and superscript T represents matrix or vector transpose. The symbol ▽ represents the Fréchet derivative, whereas represents the partial derivative with respect to variable x. A preliminary version of this work was reported in [13].
II. Dielectric Properties of Breast Tissue
Previous studies have shown that there exists a large contrast in the dielectric properties of different types of healthy breast tissues at microwave frequencies [1]. The dielectric properties of fibroglandular tissue, which consists of epithelial and connective tissue, are significantly higher than those of adipose (fatty) tissue. The contrast ratio of fibroglandular tissue to adipose tissue is large in both permittivity and effective conductivity [1]. This contrast in properties suggests using level sets to represent the distinctly different adipose and fibroglandular tissue types.
The microwave inverse scattering problem is ill-posed, as the number of unknowns is much larger than the number of electric field measurements. The ill-posedness of the microwave breast imaging problem is reduced by using a dispersive model for the tissue dielectric properties and making measurements at multiple frequencies. Throughout the frequency range of interest (0.5-3 GHz) the dispersive nature of breast tissue is well-approximated by a single-pole Debye model for the complex permittivity [14]:
| (1) |
The only parameters in the Debye model that are assumed to be spatially varying are Δε, ε∞, and σs. The parameter Δε is the difference between static permittivity (εs) and infinite frequency permittivity (ε∞). The static conductivity of the material is σs. A fixed, spatially invariant relaxation time constant (τ) of 15 ps is used for all tissue types. This Debye model results in three unknown parameters per voxel in the imaging domain.
We further reduce the number of unknowns by exploiting the following linear relationship between the three unknown Debye parameters,
| (2a) |
| (2b) |
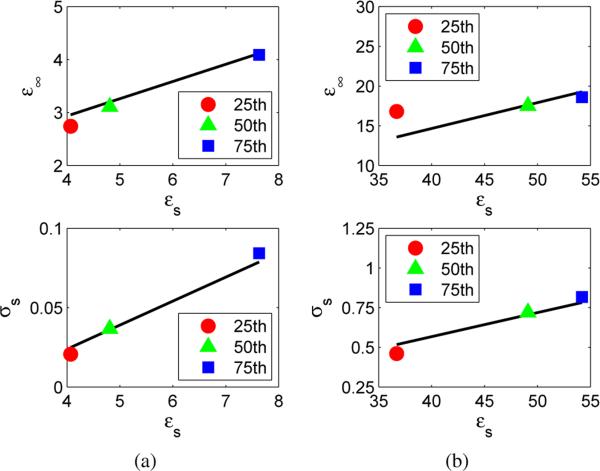
The linear model above well approximates the underlying dispersion curves for both adipose and fibroglandular tissue as demonstrated in Fig. 1. Figure 1 compares the linear relationship in (2) to the Debye parameters that correspond to the 25th, 50th, and 75th percentile values [8] of measured dielectric properties of breast tissue [1]. The resulting linear model reduces the number of unknowns in the imaging problem to one parameter, εs, per voxel. Reduction to a single unknown parameter at each voxel significantly reduces the complexity of the multi-frequency microwave breast imaging problem. Once εs is reconstructed throughout the imaging domain, the frequency dependent dielectric properties of each voxel may be calculated according to the relationship in (2) and the Debye model of (1).
Fig. 1.
Linear Debye-parameter relationship of (2), shown by the black curve, compared to the Debye parameters that correspond to the 25th, 50th, and 75th percentile values [8] of measured dielectric properties [1]. (a) Infinite permittivity and static conductivity versus static permittivity of adipose tissue; (b) Infinite permittivity and static conductivity versus static permittivity of fibroglandular tissue.
III. Level Set Method for Microwave Imaging
A. Mathematical Model for Permittivity
The breast is composed of distinct healthy tissue types, namely adipose (fatty) tissue and fibroglandular tissue. On a microscopic (cellular) scale, there are clear-cut natural boundaries between these different tissues. On a macroscopic scale, these distinct boundaries persist, albeit in a spatially complex manner due to the inherent heterogeneity of the the mammary network. Nevertheless, level sets can accommodate such spatial complexity. Thus level sets are indeed well defined for this problem.
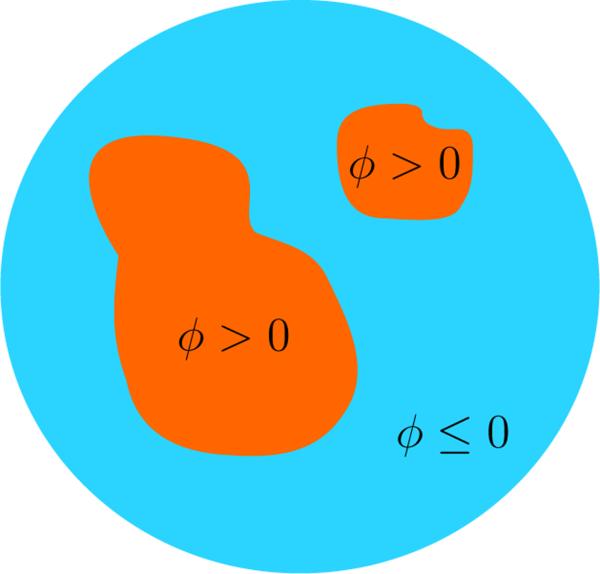
In this paper we use a single level set to represent the distribution of healthy tissue throughout the breast. A level set is a real valued function that is defined everywhere in the imaging domain. An example of a single level set segmenting a domain into distinct regions is shown in Fig. 2, where sections with (ϕ > 0) have dielectric properties that correspond to fibroglandular tissue, and regions with (ϕ ≤ 0) have dielectric properties that correspond to adipose tissue. This representation gives rise to the following model for complex permittivity in the imaging domain, as follows:
| (3) |
Here ϕ(r) is our level set, H(·) is the Heaviside or unit step function, εf(r) is the complex permittivity inside the region corresponding to fibroglandular tissue, and εa(r) is the complex permittivity inside the region corresponding to adipose tissue. The static permittivity in the fibroglandular and adipose regions, and respectively, are used to calculate the complex permittivity in each region by substituting (2) into (1). The level set function segments the imaging domain into arbitrarily shaped regions of fibroglandular and adipose tissue. We note that this inherent segmentation makes breast density estimation a trivial calculation based on the level set function itself. The complex permittivities εf(r) and εa(r) may be spatially varying inside the regions; they may also incorporate any a priori information about the statistical distribution of the dielectric properties of tissue.
Fig. 2.
2D example of a single level set ϕ segmenting a sample domain into distinct regions. Sections with (ϕ > 0) have dielectric properties that correspond to fibroglandular tissue, and regions with (ϕ ≤ 0) have dielectric properties that correspond to adipose tissue.
B. Level Set Optimization
We use an iterative approach to reconstruct the level set and corresponding permittivities of an unknown object from a set of electric fields measured with the unknown object present. The following least squares cost function is used to assess how similar the measured electric field is to the total electric field computed for the reconstructed properties, ε(r):
| (4) |
The location of the receiver for one of the M transmit-receive pairs is denoted by rm, while ωf is one of the F frequencies being used. The residual Ri is defined as the difference between the measured and reconstructed electric fields for a transmit-receive pair at a given frequency.
We iteratively optimize the least squares cost function with respect to ε(r) as follows. An initial guess for ε(r) is made, then a forward solution is computed to obtain the corresponding electric fields. A search direction is identified, based on the difference between the reconstructed and measured electric fields, and is used to update each dielectric properties voxel. The search direction used in other level set based microwave imaging algorithms [4] is based on an adjoint solution [5]. This adjoint solution incurs a considerable computational burden, on the order of another forward simulation.
We avoid this computational cost by calculating the Jacobian matrix instead. The Jacobian matrix of the least squares cost function in (4) is calculated using only the Green's function and total field simulated inside a known permittivity distribution, as derived in [15], as follows:
| (5) |
Here, Gr(r|r′) is the MF × K Green's function matrix, where K is the number of imaging voxels. Each row in this matrix represents the Green's function, as it varies across the K imaging voxels, for a particular channel and freq ωf for a medium with permittivity ε. In the MF × K total field matrix , each row represents the total electric field for a particular channel calculated at each of the K imaging voxels for a specific frequency ωf. The Jacobian matrix for the least squares cost function evaluated for a specific permittivity is the element-by-element multiplication (Hadamard product) of the Green's function matrix and the total field matrix. Each row of the Jacobian matrix is interpreted as the Fréchet derivative of the residuals in (4) with respect to the complex permittivity ε.
The finite-difference time-domain method (FDTD) is used to compute the total electric fields necessary to evaluate the Jacobian at each iteration. The Green's function matrix is calculated from FDTD simulations of the total field [16] assuming each source excitation is a z-directed current source, Iz, of known length, L. Each row in the Green's function matrix is calculated as follows:
| (6) |
This Green's function calculation is described in detail in [8].
The Fréchet derivative of our cost function with respect to permittivity is calculated using the Jacobian matrix from (5) and the cost function in (4) as follows [17]:
| (7) |
Calculating the Fréchet derivative in this manner greatly reduces the computational complexity compared to the adjoint method [18]. Using our method requires only one FDTD simulation, whereas the adjoint method requires two electromagnetics simulations to obtain this derivative at every iteration. Therefore, our method of calculating the derivative using the Jacobian reduces our computational burden by half at every iteration.
The partial derivatives of (3) with respect to ϕ, , and are computed as follows:
| (8a) |
| (8b) |
| (8c) |
where and are derivatives of the complex permittivity in (1) with respect to the static permittivity with the linear model of (2) substituted for the ε∞ and σs parameters.
The partial derivatives of the cost function with respect to the level set parameters are obtained using the chain rule to combine (8) with the Fréchet derivative in (7), as shown below:
| (9a) |
| (9b) |
| (9c) |
These partial derivatives are used to obtain a gradient-based descent optimization approach, as follows:
| (10a) |
| (10b) |
| (10c) |
where n is the iteration number. The step sizes αϕ, , and are chosen independently to control the descent of each parameter while taking into account any a priori information about the tissue types and their structure.
IV. Algorithm Implementation Details
A. Extension Velocity
The partial derivative with respect to the level set is only defined at the boundary between tissue types due to the delta function in (8a). Choosing a suitable region around the boundary to extend the derivative is often referred to as choosing an extension velocity [18]. There are many choices for extension velocities but here we simply extend the derivative to the entire imaging domain. Consequently, the level set function is updated everywhere in the imaging domain at each iteration, according to (10a). The permittivites for the two different regions do not need an extension velocity and are updated everywhere in the imaging domain according to (10b), (10c).
B. Step Size Selection
We determined appropriate step sizes αϕ, , and in (10) based on a priori information about the statistical distribution of dielectric properties for the two tissue types. The step sizes are also chosen to take into account the general behavior of the optimization algorithm. The step size of the level set function αϕ is chosen to allow a fixed percentage of the estimated number of fibroglandular voxels to change from adipose to fibroglandular (negative value to positive value) or vice versa. This step size prevents the algorithm from taking erroneously large steps that add too many fibroglandular or adipose voxels in one step.
The step size for the region corresponding to fibroglandular tissue is larger than the step size for the region corresponding to adipose tissue to account for the larger variation in complex permittivity of fibroglandular tissue than adipose tissue as reported by Lazebnik et al. [1]. These step sizes can be increased or decreased to encourage more or less heterogeneity within tissue types. At each iteration the static permittivity of the fibroglandular region is restricted to the range 20 to 65, and the static permittivity of the adipose region is constrained to be in the range 2 to 10 based on the expected values for the measured tissue properties [1].
C. Multiple Frequency Approach
We use several frequencies independently in our algorithm in a frequency hopping fashion similar to the algebraic reconstruction technique (also known as the Kaczmarz method) [19]. One frequency is used to update every parameter (ϕ, , ) for multiple iterations and then we switch to the next frequency and so forth until the algorithm converges. This strategy of iterating through the frequencies is an attempt to avoid any local minima that might exist at one frequency but not at other frequencies. This approach prevents the steepest descent algorithm from getting stuck in the nearest local minimum associated with any individual frequency. We terminate the iterative process when the change in the cost function is less than 1% of the initial cost, after ensuring that each frequency is given the same number of iterations.
D. Initial Parameter Generation
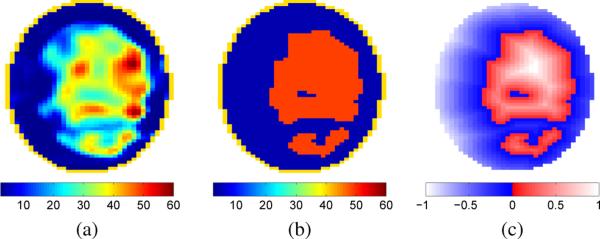
Many different biologically relevant initial guesses may be used with the level set method. The initial guess we chose in this work is based on a distorted Born iterative method (DBIM) reconstruction obtained using the approach outlined in Shea et al. [8]. The boundary of the level set is chosen by thresholding the DBIM reconstruction with the threshold set midway between the 50th percentile for static permittivity of fibroglandular tissue and the 50th percentile for static permittivity of adipose tissue [1]. Inside each region the level set function takes on a value corresponding to the signed Euclidean distance from the boundary. Level set voxels corresponding to fibroglandular tissue assume a value of the Euclidean distance from the boundary, whereas those corresponding to adipose tissue are the negative of the distance to the boundary as shown in Fig. 3. Using the Euclidean distance effectively reduces the likelihood of the algorithm changing voxels in the interior of the two initial guess regions. This strategy was chosen because DBIM reconstructions approximate the rough shape of the different regions well, but tend to blur boundaries, reducing confidence in the initial guess near those boundaries. The initial values for the permittivity in the region corresponding to fibroglandular tissue and adipose tissue are homogeneous and set to the 50th percentiles as reported by Lazebnik et al. [1].
Fig. 3.
(a) Coronal cross section of static permittivity from a DBIM reconstruction. (b) Thresholded version of the DBIM reconstruction where fibroglandular tissue is represented by εs = 49.1 (i.e. red) and adipose tissue is represented by εs = 4.8 (i.e. dark blue). (c) Initial guess of the level set obtained using the DBIM reconstruction. Voxels in the level set are assigned a value based on the distance from the boundary between tissue types, with negative distance used for the region corresponding to adipose tissue.
E. Numerical Phantoms
We tested our level set method using nine MRI-derived numerical breast phantoms from the UWCEM online repository [20]. These 3D phantoms span the four breast density classes defined by the American College of Radiology Breast Imaging Reporting and Data System (BI-RADS) Atlas. The BI-RADS denotes Class 1 as mostly adipose, Class 2 as scattered fibroglandular, Class 3 as heterogeneously dense, and Class 4 as very dense. The phantoms are surrounded by an oil immersion medium and a cylindrical array of 40 dipole antennas, arranged in five rings of eight antennas, as described in Shea et al. [8]. The location of the skin, its thickness, and its dielectric properties were assumed known for all reconstructions. The antennas were excited with an ideal wideband current source, and we record data at four frequencies: 1.0, 1.5, 2.0, and 2.5 GHz. The fields received at the antennas were computed using a 2 mm FDTD grid. Gaussian noise was added to obtain a 30 dB SNR, where SNR is defined as the ratio of total non-monostatic received power to total noise power.
V. Results
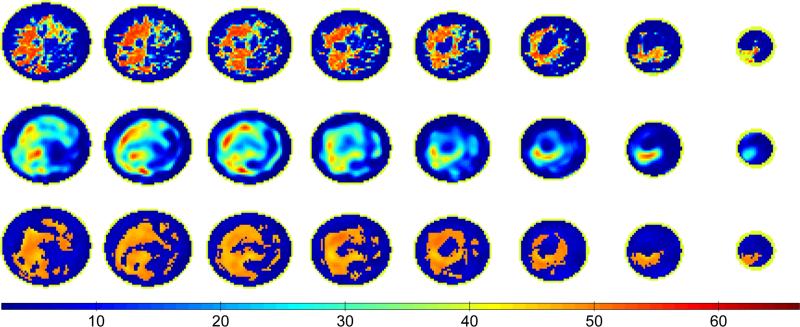
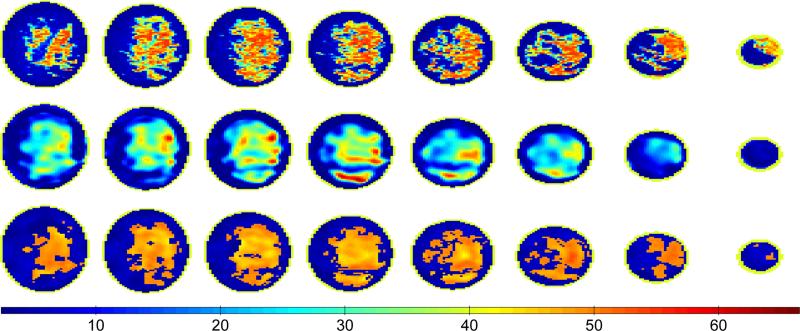
We begin by comparing reconstructions obtained with our level set method to those obtained with the DBIM algorithm. Figures 4 and 5 present reconstructions of Class 3 and Class 4 phantoms, respectively. The first row shows the phantom properties, the second row shows the reconstruction using the DBIM algorithm described in Shea et al. [8], and the third row shows the reconstruction after 80 iterations of our level set method. The cross sections shown represent regions of the breast contained within the span of the rings of the antenna array. The eight coronal cross sections are spaced every 8 mm for both the Class 3 and Class 4 phantom, where the base of the breast phantom is nearest to the first column of images (far left). All the cross sections are of static permittivity. Images of the other Debye parameters (static conductivity and infinite permittivity) are similar due to the linear relationship of (2) and are omitted for brevity.
Fig. 4.
Coronal cross sections of static permittivity from a Class 3 phantom (top) and the corresponding cross sections from the 3D DBIM reconstruction (middle) and the 3D level set method reconstruction (bottom). The coronal cross sections are taken every 8 mm between the top and bottom rings of antennas with the cross sections closest to the phantom base shown at the far left.
Fig. 5.
Coronal cross sections of static permittivity from a Class 4 phantom (top) and the corresponding cross sections from the 3D DBIM reconstruction (middle) and the 3D level set method reconstruction (bottom). The coronal cross sections are taken every 8 mm between the top and bottom rings of antennas with the cross sections closest to the phantom base shown at the far left.
The proposed level set method more accurately reconstructs breast tissue structure than conventional microwave imaging methods. For example the DBIM reconstruction misses fibroglandular tissue in the fifth and sixth columns of Fig. 4 that is accurately reconstructed by the level set method. The level set method also identifies the small regions of fibroglandular tissue extending from the bottom of the large fibroglandular tissue region in the second column of Fig. 5; this feature is not present in the DBIM reconstruction. The average absolute errors of the reconstructed Debye parameters using DBIM and the level set method are shown in Table I for the adipose and fibroglandular regions of the Class 3 and 4 phantoms (Figs. 4 and 5). While the average absolute errors in adipose tissue properties are comparable between the two methods, the absolute error in fibroglandular properties are consistently smaller for the level set method.
TABLE I.
Average absolute error in Debye parameters with the two reconstruction techniques
| DBIM | Level Set Method | ||||||
|---|---|---|---|---|---|---|---|
| ε s | ε ∞ | σ s | ε s | ε ∞ | σ s | ||
| Class 3 | Adipose | 6.3 | 2.3 | 0.09 | 6.3 | 2.1 | 0.09 |
| Fibroglandular | 16.2 | 5.4 | 0.29 | 15.0 | 4.7 | 0.24 | |
| Class 4 | Adipose | 7.2 | 2.7 | 0.11 | 7.2 | 2.4 | 0.11 |
| Fibroglandular | 16.4 | 5.6 | 0.27 | 16.3 | 5.1 | 0.26 | |
Next we compare the density of the phantom to the densities estimated from the DBIM and level set method reconstructions. All three densities are determined by comparing the static permittivity at each voxel to a threshold. Static permittivity is chosen because it exhibits the largest difference between fibroglandular and adipose tissue types. The threshold is chosen to account for the variance in measured static permittivity by fitting Weibull distributions [21] to the adipose and fibroglandular properties, respectively, reported in Lazebnik et al. [1]. The threshold is chosen as the value giving equal area under the two distributions. Adipose tissue was modeled as a Weibull distribution with λ = 7 and K = 1.63, and fibroglandular tissue was modeled as a Weibull distribution with a λ = 51.82 and a K = 4.29. We used the coefficient of determination (R2 value) to assess the fit of these models to the 25th, 50th, and 75th percentiles of the Lazebnik et al. study [1]. The coefficient of determination was 0.91 for the fit to adipose tissue and 0.95 for the fit to fibroglandular tissue. These models lead to a threshold of 18.8 for static permittivity. Any static permittivity values greater than 18.8 were classified as fibroglandular tissue and any values less than or equal to 18.8 were classified as adipose tissue.
The breast density estimates (volumetric percentages) for the nine phantoms of the UWCEM repository [20] are shown in Table II. Applying the static permittivity threshold of 18.8 to the level set method reconstructions gives the exact same density estimate as the level set segmentation itself. This occurs because the level set method reconstruction forces all voxels in the fibroglandular region to have a static permittivity greater than 20 and all voxels in the adipose region less than 10, as noted in Section IV-B.
TABLE II.
Volumetric percent density estimates for the nine phantoms and the two reconstruction techniques
| Breast Density (%) | ||||
|---|---|---|---|---|
| Phantom | Level Set Method | DBIM | ||
| Class 1 | Phantom 1 | 2.6 | 1.6 | 1.7 |
| Phantom 2 | 2.9 | 1.4 | 0.6 | |
| Class 2 | Phantom 1 | 5.0 | 2.8 | 2.1 |
| Phantom 2 | 6.4 | 3.8 | 4.7 | |
| Phantom 3 | 4.5 | 2.9 | 2.6 | |
| Class 3 | Phantom 1 | 29.5 | 28.7 | 36.5 |
| Phantom 2 | 24.2 | 22.9 | 33.2 | |
| Phantom 3 | 23.0 | 19.9 | 25.9 | |
| Class 4 | Phantom 1 | 33.4 | 33.4 | 42.7 |
The quantitative density estimates shown in Table 1 reveal that the level set method outperforms DBIM for the higher density classes, and performs similarly to DBIM for the lower density phantoms. The level set density estimates for the Class 3 and Class 4 phantoms, the two density classes with the highest cancer risk, have an average error of 1.3 percentage points or a 5% relative error. This performance is much better than the average error of 7.1 percentage points or 25% relative error of the DBIM reconstructions. The density estimation performance of our level set method is also better than the 5-10 percentage points [11] or 10-15% relative error [12] reported for mammographic density estimation.
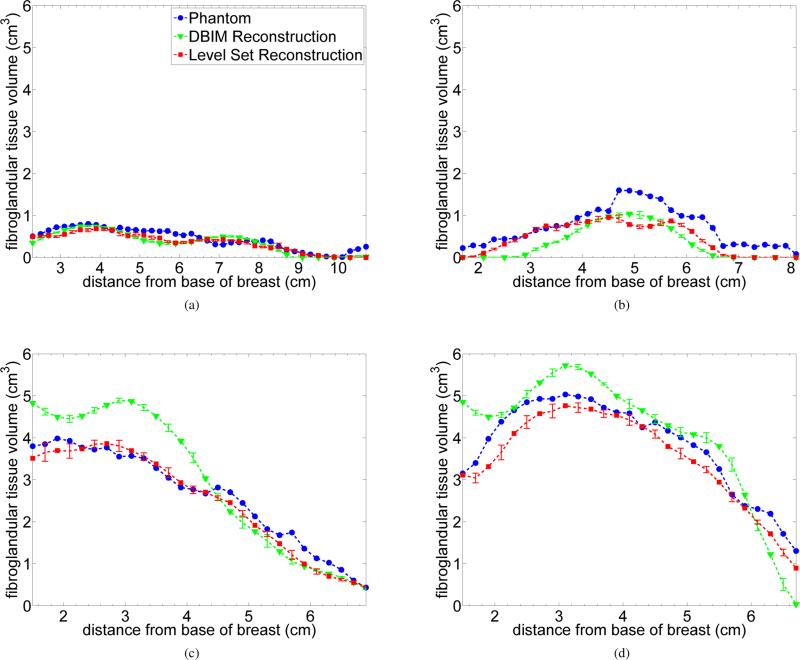
We calculated density estimates in each cross section to further investigate imaging performance and evaluate whether the reconstructed fibroglandular tissue was being spatially localized correctly. Fig. 6 compares the fibroglandular tissue volume in sequential 2 mm cross sections of the phantom to that of DBIM and level set method reconstructions. The error bars in Fig. 6 represent the standard deviation of the density estimates over 10 different noise realizations with the same SNR.
Fig. 6.
Volume of fibroglandular density in 2 mm thick coronal cross sections as a function of cross-section position (distance from the base of the phantom). The markers represent the mean value in the reconstructed cross section. Error bars represent the standard deviation of the estimates over 10 noise realizations. (a) Class 1 phantom, (b) Class 2 phantom, (c) Class 3 phantom, and (d) Class 4 phantom.
The sensitivity of our level set method to errors in the assumed skin properties was also tested. This represents a realistic error that might occur in a clinical application. We introduced 10% error in the dielectric properties of the reconstructed skin properties and compared the density estimates to reconstructions without errors. A 10% error in skin properties resulted in less than a 0.5% change in the overall density estimates reported in Table II. Furthermore, the volume of fibroglandular tissue in individual cross sections changed less than 0.2 cm3 from the mean values shown in Fig. 6. This demonstrates our level set method is robust to noise and assumed skin properties, both of which are potential sources of error in clinical application.
The results shown in Fig. 6 indicate that for the highest density classes (Fig. 6c and Fig. 6d) the level set method accurately reconstructs the tissue throughout the breast. DBIM overestimates the volume of fibroglandular tissue near the base and underestimates it in the apical coronal cross sections. Overall the fibroglandular tissue distribution of the level set method tracks the profile of the phantom confirming the spatial accuracy of the reconstruction.
VI. Discussion
Current level set imaging algorithms for 2D microwave breast imaging have a high computational cost that make them impractical for 3D imaging. Level set algorithms like the one developed by Irishina et al. [4] use an adjoint method [18] that requires two electromagnetics simulations to calculate the Fréchet derivative at each iteration. The algorithm of [4] also follows a staged approach that does not update every parameter at each iteration, which results in a large number of iterations (over 100) in 2D imaging. Our level set method utilizes the Jacobian matrix to calculate the Fréchet derivative which only requires one electromagnetics simulation per iteration, effectively cutting our computational burden in half. Our algorithm also updates every level set parameter each iteration, utilizes frequency hopping across different iterations, and incorporates a priori information to determine step sizes and bounds for the properties of the different tissue regions. This optimization strategy gives our algorithm a faster convergence rate than other level set algorithms and results in fewer iterations (≈80) in 3D imaging.
We selected DBIM as our benchmark instead of other microwave breast imaging algorithms for several reasons. DBIM, a well known technique that is equivalent to the Gauss-Newton algorithm [22], has Tikhonov regularization when implemented using conjugate gradient least squares [23] as described in Shea et al. [8]. It is able to localize coarse features of the breast, which motivates the use of DBIM for generating an initial guess of the level set. Robustness of the level set method to the initial guess was not investigated in this study. Certainly other initial guesses (for example, Kurrant et al. [24]) could be employed for the level set method.
In this study, we used breast density evaluation to quantitatively assess the efficacy of our level set method for 3D microwave imaging. Conventional microwave imaging algorithms often use a minimum norm regularizer to select a unique solution to the ill-posed inverse problem. Minimum norm regularizers are know to blur the tissue structure of the breast and produce misleading density estimates as illustrated by the DBIM results in Table II. This blurring inhibits the detection of small tissue features, especially in regions with less fibroglandular tissue, such as the apical coronal cross sections of the breast. This blurring effect also erroneously extends the size of large tissue features like those near the base of the breast. Both of these effects are apparent in Figs. 6c and 6d, and their impact on the overall density estimate is clearly evident in Table II. Our level set method does not suffer from these blurring effects since it incorporates a priori information about the tissue properties and preserves distinct boundaries between tissues. Requiring the solution to contain two tissue types constrains the set of possible solutions and forces the algorithm to produce physically meaningful results. This results in a more accurate boundary between tissue types. Consequently, our level set method improves upon the reconstructed tissue structure of DBIM and results in better localization and identification of the fibroglandular tissue as shown in Fig. 6 and Table II.
The level set method presented here was formulated with a single level set to accommodate two types of tissue: adipose and fibroglandular tissue. This formulation is relevant to imaging healthy breast tissue, as is the case for breast density estimation. An additional level set can be added to the model in (3) to represent cancerous tissue in a manner similar to that presented by Irishina et al. [4]. This addition would allow the application of the algorithm to tumor detection.
VII. Conclusion
We have developed a level set method that requires fewer iterations and fewer electromagnetics simulations per iteration than other level set based implementations and leads to a feasible level of computational complexity for full 3D imaging. Reconstructions of anatomically realistic numerical breast phantoms demonstrate the ability of the proposed algorithm to reconstruct the tissue structure better than conventional microwave imaging approaches. The entire-breast density estimates as well as the sequence of coronal cross section density estimates demonstrate the high accuracy that our level set method achieves in reconstructing the actual tissue structure of the phantom.
Acknowledgments
This work was supported by the National Institutes of Health under grant R21 CA161369 awarded by the National Cancer Institute and by the National Science Foundation under grant 1128049.
REFERENCES
- 1.Lazebnik M, McCartney L, Popovic D, Watkins CB, Lindstrom MJ, Harter J, Sewall S, Magliocco A, Booske JH, Okoniewski M, Hagness SC. A large-scale study of the ultrawideband microwave dielectric properties of normal breast tissue obtained from reduction surgeries. Phys. Med. Biol. 2007 Apr;52:2637–2656. doi: 10.1088/0031-9155/52/10/001. [DOI] [PubMed] [Google Scholar]
- 2.Lazebnik M, Popovic D, McCartney L, Watkins C, Lindstrom MJ, Harter J, Sewall S, Ogilvie T, Magliocco A, Breslin T, Temple W, Mew D, Booske JH, Okoniewski M, Hagness SC. A large-scale study of the ultrawideband microwave dielectric properties of normal, benign, and malignant breast tissues obtained from cancer surgeries. Phys. Med. Biol. 2007;52:6093–6115. doi: 10.1088/0031-9155/52/20/002. [DOI] [PubMed] [Google Scholar]
- 3.Rubaek T, Meaney PM, Meincke P, Paulsen K. Nonlinear microwave imaging for breast-cancer screening using Gauss-Newton's method and the CGLS inversion algorithm. IEEE Transactions on Antennas and Propagation. 2007 Aug;55(8):2320–2331. [Google Scholar]
- 4.Irishina N, Alvarez D, Dorn O, Moscoso M. Structural level set inversion for microwave breast screening. Inverse Probl. 2010;26:035015. [Google Scholar]
- 5.Dorn O, Miller EL, Rappaport CM. A shape reconstruction method for electromagnetic tomography using adjoint fields and level sets. Inverse Probl. 2000;16:1119–1156. [Google Scholar]
- 6.Hajihashemi MR, El-Shenawee M. Level Set Algorithm for Shape Reconstruction of Non-Overlapping Three-Dimensional Penetrable Targets. IEEE Transactions on Geoscience and Remote Sensing. 2012 Jan;50(1):75–86. [Google Scholar]
- 7.Zastrow E, Davis SK, Lazebnik M, Kelcz F, Van Veen BD, Hagness SC. Development of anatomically realistic numerical breast phantoms with accurate dielectric properties for modeling microwave interactions with the human breast. IEEE Transactions on Biomedical Engineering. 2008 Dec;55(12):2792–2800. doi: 10.1109/TBME.2008.2002130. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Shea JD, Kosmas P, Hagness SC, Van Veen BD. Three-dimensional microwave imaging of realistic numerical breast phantoms via a multiple-frequency inverse scattering technique. Med. Phys. 2010 Aug;37(8):4210–4226. doi: 10.1118/1.3443569. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Kerlikowske K, Ichikawa L, Miglioretti DL, Buist DSM, Vacek PM, Smith-Bindman R, Yankaska B, Carney PA, Ballard-Barbash R. Longitudinal measurement of clinical mammographic breast density to improve estimation of breast cancer risk. J. Natl. Cancer Inst. 2007;99(5):386–395. doi: 10.1093/jnci/djk066. [DOI] [PubMed] [Google Scholar]
- 10.Harvey JA, Bovbjerg VE. Quantitative assesment of mammo-graphic breast density: Relationship with breast cancer risk. Radiology. 2004 Jan;230:29–41. doi: 10.1148/radiol.2301020870. [DOI] [PubMed] [Google Scholar]
- 11.Pawluczyk O, Augustine BJ, Yaffe MJ, Rico D, Yang J, Mawdsley GE. A volumetric method for estimation of breast density on digitized screen-film mammograms. Med. Phys. 2003 Mar;30(3):352–364. doi: 10.1118/1.1539038. [DOI] [PubMed] [Google Scholar]
- 12.van Engeland S, Snoeren PR, Huisman H, Boetes C, Karssemeijer N. Volumetric breast density estimation from full-field digital mammograms. IEEE Transactions on Medical Imaging. 2006 Mar;25(3):273–282. doi: 10.1109/TMI.2005.862741. [DOI] [PubMed] [Google Scholar]
- 13.Colgan TJ, Hagness SC, Veen BDV. 3-D Microwave Imaging using a Level Set Method for Breast Density Evaluation. presented at USNC-URSI National Radio Science Meeting; Boulder, CO. January 2013. [Google Scholar]
- 14.Lazebnik M, Okoniewski M, Booske JH, Hagness SC. Highly accurate debye models for normal and malignant breast tissue dielectric properties at microwave frequencies. IEEE Microwave and Wireless Components Letters. 2007 Dec;17(12):822–824. [Google Scholar]
- 15.Franchois A, Pichot C. Microwave imaging - Complex permittivity reconstruction with a Levenberg-Marquardt method. IEEE Transactions on Antennas and Propagation. 1997 Feb;2(2):203–215. [Google Scholar]
- 16.Cui TJ, Qin Y, Wang G-L, Chew WC. Low-frequency detection of two-dimensional buried objects using high-order extended Born approximations. Inverse Probl. 2004;20:S41–S62. [Google Scholar]
- 17.Nocedal J, Wright S. Nonlinear Optimization. 2nd ed. Springer; New York: 2006. [Google Scholar]
- 18.Dorn O, Lesselier D. Level set methods for inverse scattering. Inverse Probl. 2006;22:R67–R131. [Google Scholar]
- 19.Ladas KT, Devaney AJ. Generalized ART algorithm for diffraction tomography. Inverse Probl. 1991;7(1):109–125. [Google Scholar]
- 20.UWCEM numerical breast phantom repository. [Online] Available: http://uwcem.ece.wisc.edu.
- 21.Papoulis A, Pillai SU. Probablity, Random Variable, and Stochastic Processes. 4th ed. McGraw-Hill; Boston: 2002. [Google Scholar]
- 22.Remis RF, van den Derg PM. On the equivalence of the Newton-Kantorovich and distorted Born methods. Inverse Probl. 2000 Feb;16(1):L1–L4. [Google Scholar]
- 23.Hansen PC. Rank-deficient and Discrete Ill-posed Problems: Numerical Aspects of Linear Inversion. Society for Industrial and Applied Mathematics; 3600 Market Street, Floor 6, Philadelphia, PA 19104: Philadelphia, Pa: 1998. [Google Scholar]
- 24.Kurrant D, Fear E. Regional estimation of the dielectric properties of inhomogeneous objects using near-field reflection data. Inverse Probl. 2012;28:075001, 27. [Google Scholar]