Modeling the Epidemiology of Cholera to Prevent Disease Transmission in Developing Countries

Abstract

Cholera remains an important global cause of morbidity and mortality, which is capable of causing periodic epidemic disease. A number of mathematical models have been developed to help in understanding the dynamics of cholera outbreaks and for use as a tool in planning interventions, including vaccination campaigns. We have explored the utility of models in assessing the spread of cholera in the recent epidemics in Zimbabwe and Haiti. In both instances, a mathematical model was formulated and fitted to cumulative cholera cases to estimate the basic reproductive number ℜ₀, and the partial reproductive numbers reflecting potential differences in environmental-to-human versus human-to-human transmission were quantified. In Zimbabwe, estimated ℜ₀ for the epidemic using aggregated data at the national level was 1.15; in Haiti, it was 1.55. However, when calculated at a provincial/departmental level, estimated basic reproductive numbers were highly heterogeneous, with a range of 1.11 to 2.72 in Zimbabwe and 1.06 to 2.63 in Haiti. Our models suggest that the underlying patterns of cholera transmission varied widely from region to region, with a corresponding variation in the amenability of outbreaks to control measures such as immunization. These data underscore the heterogeneity of transmission dynamics, potentially linked to differences in environment, socio-economic conditions, and cultural practices. They also highlight the potential utility of these types of models in guiding development of public health intervention strategies.

INTRODUCTION

Historical reports of cholera-like illness can be traced back almost a millennium in South Asia (1). Global, pandemic spread of cholera from its ancestral home in Bengal was first documented in 1817, with the beginning of what has been designated as the first pandemic. We are currently in the throes of the seventh pandemic (caused by toxigenic Vibrio cholerae of the El Tor bio-type), which originated almost 50 years ago in the Celebes. In contrast to the earlier six pandemics, at no time in these past 50 years has cholera retreated to its south Asian home. It has instead established endemicity at multiple sites around the globe and continues to trigger major localized epidemics, including the epidemics in Zimbabwe during 2008 to 2009 (2, 3) and the ongoing epidemics in Haiti that began in 2010 (4). These recent epidemics, which were characterized by increased severity and duration, have demonstrated the need for ongoing work to optimize public health responses and develop prevention strategies for this disease.

To better understand the underlying dynamics of these epidemics, we have developed a series of mathematical models of cholera transmission (5, 6). A key element of these models has been the quantifying of the basic reproductive number of disease transmission (ℜ₀) at a regional level, to assess possible geographic differences in transmission dynamics, and to permit better targeting of interventions based on these differences. These models also take into account potential differences in transmission related to what have been characterized as “direct” transmission of the microorganism (direct transmission from human-to-human during the short period of time when the microorganism is “hyper-infectious” after passage in stool) versus “indirect,” or transmission from environment-to-human (7, 8, 9, 10).

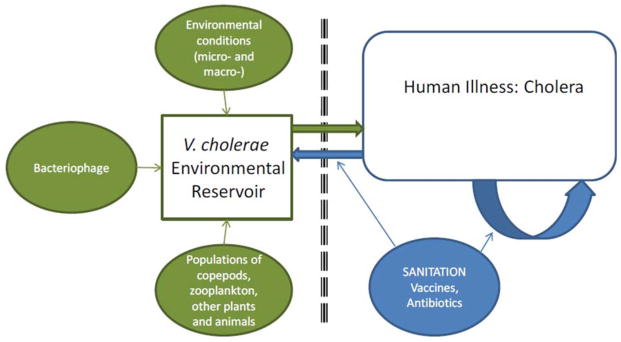
This separation of direct versus indirect transmission pathways is reflected in the conceptual framework shown in Fig. 1 [from Morris (10)]. In this framework, the aquatic, environmental reservoir is critical to long-term maintenance of epidemic V. cholerae. These reservoirs constitute complex biologic systems, with modulation of V. cholerae populations by environmental conditions [the local microenvironment (11, 12)], as well as global macroenvironmental factors, such as the El Niño/Southern Oscillation (ENSO) (13), by predatory bacteriophage populations (14), and by fluctuations in populations of copepods and zooplankton (which may, in turn, be driven by predation by fish) (15), binding to chironomid egg masses, water hyacinth, carriage by birds and mammals, and a host of other variables. However, once the microorganism moves from these sources into human populations, we hypothesize that transmission accelerates, driven by the potential for rapid transmission of hyperinfectious microorganisms to susceptible individuals, with, possibly, a short intervening step in the immediate household environment of the patient (10).

FIGURE 1.

Conceptual framework for cholera transmission. From Morris (10). doi:10.1128 /microbiolspec.VE-0011-2014.f1

Here, we review and compare our modeling studies on cholera for Zimbabwe and Haiti (5, 6) and bring to the fore their implication to the understanding of cholera dynamics and control.

METHODS

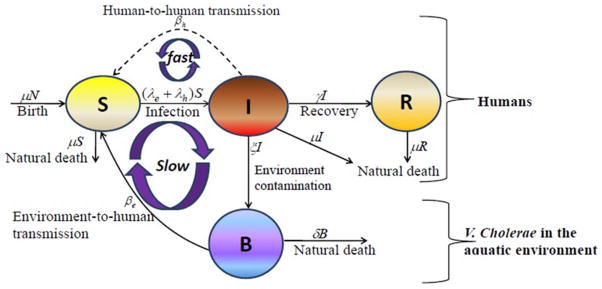
Details regarding the development and application of our models to the epidemics in Zimbabwe and Haiti are reported in Mukandavire et al. (5, 6). In brief, the cholera model compartmentalizes the human population (Fig. 2), of population size N, into susceptibles S, infected I, and recovered R individuals. The concentration of vibrios in contaminated water is denoted by B. Susceptible individuals acquire cholera infection either by ingesting environmental V. cholerae from contaminated aquatic reservoirs (“indirect” transmission, higher infectious dose) or through close contact with infected humans (“direct” transmission, lower infectious dose) at daily per-capita rates ${\lambda }_e=\frac{{\beta }_{e}B}{\kappa +B}$ and λ_h= β_hI, respectively, with the subscripts e and h denoting environment-to-human and human-to-human transmission routes. The constant k is a shape parameter that determines the human infectious dose: when B equals k, the probability of ingestion resulting in human disease is 0.5. β_e and β_h are rates of exposure to V. cholerae from the contaminated environment and through human-to-human interaction, respectively. Infected individuals recover from infection at a rate γ. Infected individuals contribute V. cholerae in the aquatic environment at a daily rate χ and vibrios have a net death rate δ in the environment. The resulting model as a system of coupled stochastic differential equations (6) is as follows.

FIGURE 2.

Model flow diagram. S, susceptibles; I, infected; R, recovered individuals; B, concentration of vibrios in contaminated water. From Mukandavire et al. (6). doi:10.1128 /microbiolspec.VE-0011-2014.f2

$$\{\begin{array}{l}\frac{dS}{dt}=\mathrm{\mu }N-{\beta }_e(1+{\alpha }_1{\xi }_1(t))S\frac{B}{\kappa +B}-{\beta }_h(1+{\alpha }_2{\xi }_2(t))SI-\mu S,\hfill \\ \frac{dS}{dt}={\beta }_e(1+{\alpha }_1{\xi }_1(t))S\frac{B}{\kappa +B}+{\beta }_h(1+{\alpha }_2{\xi }_2(t))SI-(\gamma +\mu )I,\hfill \\ \frac{dR}{dt}=\gamma I-\mu R,\hfill \\ \frac{dB}{dt}=\chi I-\delta B.\hfill \end{array}$$ (1)

Where, α_i for i = 1,2 are real constants and ξ (t)=(ξ₁(t), ξ₂(t)) is the Gaussian white noise process to model environmental stochasticity.

For the Zimbabwe epidemic (5), we fitted the deterministic version of the cholera model system (Eq. 1) to weekly data on numbers of cholera cases reported to the Zimbabwe Ministry of Health and Child Welfare (MoHCW) for the period from November 13, 2008, to July 31, 2009. This is the period with a complete cholera data set for all of the provinces in Zimbabwe and marked the onset of the national epidemic. We obtained this data set from the Epidemiology and Disease Control department in the Ministry of Health and Child Welfare. For Haiti, we used daily data on numbers of hospitalized cases published on the Ministry of Public Health and Population (MSPP) website (16). These data may well be underestimates due to weaknesses in the health systems in Zimbabwe and Haiti. However, despite quality issues surrounding the data sets, they presented the best available platform for quantifying the magnitude of the epidemics.

RESULTS

The basic reproductive number (ℜ₀) is defined as a measure of the average number of secondary cases generated by a primary case. Understanding its magnitude and variation can help to identify cholera “hot spots” and in designing targeted surveillance and intervention programs. In our models, the two transmission routes of cholera are quantitatively described by partial reproductive numbers, ℜ_h and ℜ_e that describe new cases that arise from either the direct human-to-human or the indirect environment-to-human transmission routes, respectively. Estimates for ℜ_e, ℜ_h, and ℜ₀ for the 10 provinces and the whole country of Zimbabwe are given in Table 1. Similar data for Haiti, by department, are shown in Table 2. The plots for the data fitting can be found in Mukandavire et al. (5, 6).

TABLE 1.

Estimates of ℜ_e, ℜ_h, ℜ₀, and minimum vaccination coverages for Zimbabwe

Provinces	Population Size/1000	ℜe	95% CI	% ℜ0	ℜh	95 % CI	% ℜ0	ℜ0	95 % CI	Vaccination Coverage Resulting in ℜ0 <1
Harare	2012.78	0.9	(0.57–1.24)	59.4	0.62	(0.57–0.72)	40.6	1.52	(1.14–1.96)	44
Bulawayo	718.28	0.14	(0.071–0.22)	10.6	1.22	(1.05–1.39)	89.4	1.36	(1.12–1.61)	34
Mashonaland Central	1056.67	0.2	(0.11–0.29)	14.3	1.18	(1.11–1.25)	85.7	1.38	(1.21–1.54)	35
Mashonaland East	1196.77	0.45	(0.31–0.58)	40.4	0.66	(0.58–0.74)	59.6	1.11	(0.90–1.32)	13
Mashonaland West	1300.01	0.32	(0.01–0.62)	16.9	1.54	(1.33–1.76)	83.1	1.87	(1.34–2.38)	59
Midlands	1554.06	0.077	(0.012–0.14)	5.5	1.31	(1.21–1.41)	94.5	1.39	(1.23–1.56)	36
Manicaland	1665.45	0.2	(0.099–0.29)	9.5	1.87	(1.68–2.05)	90.5	2.06	(1.78–2.34)	66
Matebeleland South	693.23	1.44	(0.68–2.2)	52.9	1.28	(0.52–2.04)	47.1	2.72	(1.19–4.24)	81
Matebeleland North	748.32	0.14	(0.036–0.24)	8	1.58	(1.4–1.76)	92	1.72	(1.44–1.99)	53
Masvingo	1401.67	0.25	(0.047–0.46)	15.8	1.36	(1.15–1.56)	84.2	1.61	(1.20–2.03)	49
Zimbabwe [Country]	12347.24	0.2	(0.15–0.25)	17.3	0.95	(0.93–0.98)	82.7	1.15	(1.08–1.23)	17

CI, confidence interval.

TABLE 2.

Estimates of ℛ_e, ℛ_h, ℛ₀, and minimum vaccination coverages for Haiti

Department	Population size/1000	ℜe	SE	% ℜ 0	ℜh	SE	% ℜ 0	ℜ 0	SE	Vaccination coverage resulting in ℜ0 <1
Haiti (Country)	9923.24	0.84	7.00 × 10−1	54.01	0.71	0.29	45.35	1.55	0.41	45.4
Artibonite	1571.02	2.54	2.32 × 10−1	96.70	0.09	0.06	3.30	2.63	0.18	79.5
Centre	678.63	0.58	4.82 × 10−1	42.12	0.79	0.24	57.88	1.37	0.24	34.3
Grande Anse	425.88	0.59	4.31 × 10−1	46.31	0.68	0.09	53.70	1.27	0.35	27.2
Nippes	311.5	0.09	2.84 × 10−4	8.86	0.96	0.21	91.15	1.06	0.21	6.9
Nord	970.5	0.16	7.79 × 10−2	10.24	1.37	0.24	89.76	1.53	0.23	44.4
Nord Ouest	662.78	0.20	2.56 × 10−4	14.26	1.20	0.11	85.74	1.40	0.11	36.4
Nord Est	358.28	0.22	1.43 × 10−3	14.99	1.22	0.21	85.01	1.44	0.21	38.9
Ouest1 (Ouest)	1187.83	0.45	2.04 × 10−4	37.67	0.74	0.06	62.33	1.18	0.06	19.9
Port-au-Prince (Ouest)	2476.79	0.74	3.68 × 10−4	39.27	1.15	0.13	60.73	1.89	0.13	60.5
Sud	704.76	0.21	1.32 × 10−3	14.65	1.23	0.09	85.36	1.44	0.09	39.5
Sud Est	575.29	0.13	2.31 × 10−4	11.11	1.04	0.14	88.89	1.17	0.14	18.3
Ouest	3664.62	0.43	1.78 × 10−3	25.41	1.30	0.30	74.75	1.73	0.30	54.2

Ouest department includes Port-au-Prince and Ouest¹ hospitalized cases. The population estimates were extracted from http://www.citypopulation.de/Haiti.html.

The basic reproduction numbers provide useful guidelines for the prevention and control of cholera. For example, a vaccination program has to achieve a minimum coverage of

$$\mathrm{c}\ge \frac{1-{\mathfrak{R}}_0^{-1}}{1-(1-r)(1-s)}$$

contain a cholera epidemic, where r is the fraction of the vaccinated population who are completely immunized (i.e., with zero susceptibility), and s is the proportional reduction of the susceptibility for those partially immunized. For r = 0 and s = 78% (17, 18), regional vaccination coverages that would have been required to contain the Zimbabwe and Haitian epidemics (Tables 1 and 2) range from about 7% to 82%.

DISCUSSION

The term ℜ₀ plays a critical conceptual role in our understanding of the epidemiology of cholera and other infectious diseases. While acknowledging differences in R₀ that may arise when comparing different models and model assumptions (19), our data underscore the heterogeneity that may be seen in ℜ₀ within a single model as one moves from province to province (or department to department) in the midst of an epidemic. Nonetheless, while there is variability, the ranges from the Zimbabwe and Haiti studies are reasonably close, and, with the exception of the work by Chunara et al. (20), these results are in the same general range as the estimates from other mathematical models of the initial Haitian epidemic (21, 22, 23).

Such heterogeneity may be driven by a number of factors, including environmental factors, socio-economic conditions, and cultural practices. In the absence of more detailed epidemiologic data from these epidemics, it is difficult to identify the specific factors that are operational in each instance. However, at the environmental level, it is interesting to note that in the Zimbabwe model, “indirect” transmission through the environment contributes only a small component (17%) of the total value of ℜ₀ using aggregated country level data. In the Haiti model, in contrast, indirect transmission through the environment was estimated to contribute 54% of the value of ℜ₀ at a national level. When calculated as the average of values across provinces/departments, differences are still apparent, with an average value of 25% for the contribution of the indirect environmental route to ℜ₀ for Zimbabwe and 38% for Haiti. These differences are not unexpected, given that Zimbabwe is land-locked, without the coastline and estuarine areas (present in Haiti) that are known to represent ideal environmental reservoirs for V. cholerae. Interestingly for Haiti, the model also identified Artibonite as a potential disease “hot spot” with ℜ₀ values for outbreaks for surrounding departments slightly higher than those further away.

This regional variability in ℜ₀ has a potential impact on interventions to limit or prevent further cholera transmission. Our models suggest that, even with limited vaccine uptake, there are certain regions where vaccination campaigns could have a greater impact on disease transmission: that is, the model supports regional targeting of vaccination programs. Regions with a greater concentration of cases linked with “indirect” acquisition of V. cholerae from the environment may benefit most from implementation of strategies to improve water sources and community sanitation; in contrast, for those with high levels of direct, person-to-person transmission, a strong emphasis on household hygiene may be important.

While acknowledging the limitations inherent in these and similar models, mathematical models of disease transmission provide a valuable means of assessing the complex set of variables that come into play in cholera epidemiology. They also have the potential for improving our ability to select and target interventions, particularly at a regional level, so that limited resources that may be available in an outbreak situation can be best allocated to prevent spread of this potentially devastating disease.