Abstract
X-ray spectroscopies, when combined in laser-pump, X-ray-probe measurement schemes, can be powerful tools for tracking the electronic and geometric structural changes that occur during the course of a photoinitiated chemical reaction. X-ray absorption spectroscopy (XAS) is considered an established technique for such measurements, and X-ray emission spectroscopy (XES) of the strongest core-to-core emission lines (Kα and Kβ) is now being utilized. Flux demanding valence-to-core XES promises to be an important addition to the time-resolved spectroscopic toolkit. In this paper we present measurements and density functional theory calculations on laser-excited, solution-phase ferrocyanide that demonstrate the feasibility of valence-to-core XES for time-resolved experiments. We discuss technical improvements that will make valence-to-core XES a practical pump–probe technique.
Introduction
Hard X-ray spectroscopies are powerful tools for probing the electronic and geometric structure of molecules in complex or disordered systems1 and have been particularly useful for studying molecules in the solution phase. Unlike UV, VIS, or IR spectroscopic techniques they are element specific, sensitive to the electronic structure and the local arrangements of surrounding atoms of the element being selectively probed. Additionally, in contrast to soft X-ray techniques, they readily penetrate matter and do not require ultrahigh vacuum conditions making in situ or operando measurements feasible.2,3 When combined in a pump–probe scheme with ultrafast lasers, X-ray spectroscopies can be used to track the evolution of structural changes that occur after photoexcitation.4
X-ray absorption spectroscopy (XAS) has been employed for laser pump–X-ray probe studies.5,6 Here the incident X-ray energy is tuned across an inner shell of an element of interest within a molecule, and the transmission, or for dilute samples total fluorescence yield, is measured. Close to the edge energy, in the X-ray absorption near edge structure (XANES) region, the formal valence state and coordination geometry contribute to the spectral shape, and when compared with theoretical models or spectra of reference compounds XANES can provide insight into the chemical environment of the absorbing atom.7 Below the core ionization threshold, in the pre-edge XANES region, resonances due to transitions from inner shell orbitals to unoccupied valence orbitals reveal important insights about the electronic structure of the absorbing atom. Above the edge, in the extended X-ray absorption fine structure (EXAFS) region, scattering of the outgoing photoelectron on neighboring atoms leads to modulations of the absorption which can be analyzed to yield information on the number, type, and distances of coordinating atoms.
X-ray emission spectroscopy (XES) has only recently been used in pump–probe experiments. In nonresonant XES the incident X-ray energy is tuned above an inner shell edge, and the fluorescence emitted as an electron decays from an occupied higher-lying orbital to the core hole is spectrally resolved. The shapes of the different emission lines can yield information about the occupied orbitals,8 complementing information gained from XAS about unoccupied orbitals. The need for a wavelength-dispersive spectrometer and a smaller detected signal makes XES more challenging than XAS to incorporate into a pump–probe experiment, and consequently it has been implemented only in the past few years. Laser-pump, X-ray-probe XES experiments have so far focused on studies of transition metal coordination complexes, measuring the core-to-core emission lines Kα due to 2p → 1s transitions and the Kβ1,3 and its satellite, Kβ′, due to 3p → 1s transitions. These spectra are sensitive to the unpaired electrons in the metal 3d orbitals, those that determine spin state, through means of the intra-atomic exchange interaction between the unpaired electron in the 2p (for Kα) or 3p (for Kβ) core-hole final state and the unpaired metal 3d valence electrons.9,10 Other details of the metal ion’s chemical environment often do not have an appreciable impact on the core-to-core XES lineshapes, which makes Kα and Kβ spectroscopy a very powerful probe of spin state. In most cases a quantitative value for the total spin momentum of the transition metal ion can be obtained from core-to-core XES spectra.9,11−14 Exceptions are where strong covalency or charge transfer additionally modify the line shape.15,16 The first laser-pump, X-ray-probe XES experiment17 measured the iron Kα1 core-to-core emission line to study laser-induced spin-state switching in the [Fe(bpy)3]2+ molecule in an aqueous solution. The laser excitation induced a spin transition of the central iron ion, from low spin (singlet) to high spin (quintet), that was detected as a broadening of the Fe Kα line shape, in agreement with static reference spectra and theoretical simulations. Subsequent experiments improved dramatically on the data quality by using a high-repetition-rate pump–probe scheme that used more of the available synchrotron X-ray flux.18,19 In this way the weaker iron Kβ1,3 spectrum, which shows more conspicuous sensitivity to spin state,11 was also obtained with good signal-to-noise18 as well as 1s2p resonant X-ray emission (RXES) spectra.19 The [Fe(bpy)3]2+ molecule was investigated with finer time resolution at the Linac Coherent Light Source (LCLS)20 where by comparison of the transient core-to-core Kβ spectra with those from statically measured reference samples it was found that the complex passed through a triplet state before reaching the quintet. Core-to-core Kβ measurements have also been carried out at the LCLS to follow changes in the valence electron pairing of manganese in photosystem II, which in this case correspond to oxidation state changes.21
On the high energy tail of the transition metal core-to-core Kβ1,3 line lies the valence-to-core (vtc) region which contains the Kβ2,5 and Kβ″ lines. This region has not yet been utilized in a pump–probe experiment although it has potential to reveal a great deal of additional information about molecular structure, complementing that obtained from XAS and core-to-core XES. The intensity of the features are several tens of times weaker than those of the core-to-core Kβ lines, making this region a challenge to measure. The valence-to-core region has recently sparked a good amount of interest,22−24 reflecting an awareness of the potential utility of this region and progress in the availability of theoretical calculations. The vtc XES features of transition metal complexes have been shown to be dominated by dipole transitions to the metal 1s orbital from valence molecular orbitals that are predominantly ligand s or p in character but that contain sufficient metal p mixing to make the cross section appreciable. In this way vtc XES probes directly valence molecular orbitals, those that undergo photoinitiated dynamics. This is in contrast to core-to-core XES which probes the changes that take place in valence orbitals indirectly. Vtc XES has been shown to overcome a limitation that is present in EXAFS spectroscopy, specifically discrimination of ligands containing the light atoms C, N, or O,25−29 which is of importance in areas such as catalysis.24 Additionally vtc XES has sensitivity to detect chemical changes in the ligands (e.g., protonation).30−32
A tremendous strength of vtc XES is that the spectral features can be sufficiently modeled considering only one-electron transitions within ground-state density functional theory (DFT), without the need for the inclusion of multiplet structure, core hole, or multielectron excitations that are necessary to model core-to-core XES or L- and M-edge XANES spectra.23,33−37 This has aided experimentalists in extracting useful information about molecular orbitals from measured spectra, especially since it has been implemented in a user-friendly quantum chemistry software package, ORCA.23 Additionally, this relative ease of modeling has particular utility for time-resolved measurements as it could help to identify transient species formed after photoexcitation. The transient spectrum measured in a laser-pump, X-ray-probe experiment is a mixture of the spectra from the ground-state molecule and one or more photoproducts. In order to extract structural information about the transient photoproducts the signal from each component needs to be separated. The “fingerprinting” or linear combination fitting (LCF)38 approach in XANES spectroscopy, where linear combinations of reference spectra are fit to an unknown spectrum to determine the fraction of each species present, has long been used to determine the composition of mixed samples. Yet a challenge for studying laser-initiated chemical reactions is the lack of knowledge about the spectral shapes of the often short-lived photoproducts that are generated as the reaction proceeds. Reference samples are often not available. Calculated XANES spectra can be used in place of measured reference spectra, but the complexity of the XANES edge shape, being dependent on a combination of electronic and geometric factors which may not be precisely known, can lead to ambiguity. In the pre-edge region, the spectral features reflect 3d electronic structure and can be an important means to identify particular products; yet, often resonances can be quite small when due predominantly to quadrupolar transitions, and they fall within the tail of the K-edge making them somewhat difficult to precisely resolve experimentally, particularly when masked by the signals of other species. Calculated vtc spectra, which have been shown to exhibit substantial spectral variation for different species, like XANES, compared with experimental spectra could provide additional feedback that when used in conjunction with XANES and core-to-core XES could produce the desired species identification and perhaps even the fractions of each species.
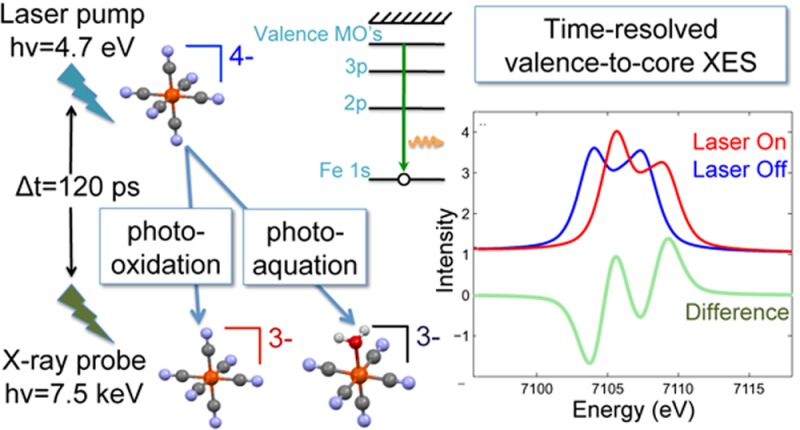
To our knowledge no laser pump, X-ray probe vtc XES studies have been reported. A major hurdle is the fact that vtc emission lines are hundreds of time weaker than the strongest XES lines, the Kαs. However, MHz pump–probe methods developed now at several synchrotrons are enabling flux demanding techniques by utilizing a larger fraction of the available X-rays.39−44 In this paper, we demonstrate the feasibility of vtc XES using synchrotron X-rays, presenting measurements of a well-known, symmetric, and very stable transition metal complex in a water solution after laser excitation. The molecule chosen was ferrocyanide, [FeII(CN)6]4–, which is known to undergo two common photoinitiated reactions: photooxidation and photoaquation.45,46 At the laser excitation used, 266 nm, the dominant reaction is photooxidation. Here a photon promotes an electron into a charge-transfer-to-solvent (CTTS) manifold that yields an ejected electron along with the oxidized parent ion, ferricyanide [FeIII(CN)6]3–. In the photoaquation reaction the light excites the iron ion to the lowest singlet ligand field state, 1T1g, which eventually leads to detachment of a CN– ligand and substitution by H2O producing [FeII(CN)5H2O]3–. Previous X-ray measurements of ferrocyanide have used XAS to study its ground-state structure47,48and in laser-pump, X-ray-probe studies to understand its photoexcited dynamics.49,50
In this paper we present laser-pump, X-ray-probe XES measurements. Time-resolved core-to-core XES spectra of laser-excited [FeII(CN)6]4– are presented and compared to a statically measured spectrum of [FeIII(CN)6]3–, the photooxidation photoproduct which is expected to be the primary photoproduct contributing to the time-resolved spectra. Calculated valence-to-core spectra of ground-state [FeII(CN)6]4– and of [Fe(CN)5NO]2– are compared to statically measured spectra demonstrating the ability of theory to capture experimental details and to highlight the potential use as fingerprints to aid identification of and quantify amounts of transient species present after photoexcitation, even when such species differ only by one ligand. Measured vtc XES spectra of [FeII(CN)6]4– and [FeIII(CN)6]3– are presented along with our first measurement of time-resolved vtc XES of laser-excited [FeII(CN)6]4–. Finally we discuss technical developments that will enable full utilization of this technique.
Experimental and Theoretical Methods
Measurements were carried out at beamline 7ID-D at the Advanced Photon Source.51 The setup includes a high-repetition-rate laser and X-ray microprobe and is similar to that used in previous experiments.18,19,39 X-rays and laser are spatially overlapped at a fast-flowing liquid jet. The jet is 100 μm thick, ∼6 mm wide, and produced by circulating fluid with a gear pump through a sapphire nozzle. The flow speed is 6.5 m/s. The X-ray spot size (7 μm fwhm × 4 μm fwhm) was smaller than the laser spot size (30 μm fwhm × 25 μm fwhm) in order to probe only the volume with the highest excitation fraction. The hybrid singlet storage ring mode was used, where a single electron bunch with 16 mA circulates the ring at 271.6 kHz, separated by 1.594 μs on each side from a train of close-spaced bunches containing 86 mA. Only the singlet pulse was used for the pump–probe experiments. The signal from the detector was electronically gated to isolate the singlet pulse signal from that due to the other bunches. The singlet provided 3 × 1011 photons/s at 7.5 keV, the X-ray energy used, and its pulse duration of 120 ps fwhm determined the temporal resolution of the measurement. For the static measurements, all bunches were used corresponding to a flux of 2 × 1012 photons/s. The laser repetition rate was 135.8 kHz so that the laser pulses overlapped every other X-ray singlet pulse. Counts from the laser-overlapped X-ray pulses (“laser-on”) and nonoverlapped X-ray pulses (“laser-off”) were tallied independently but simultaneously in the same experimental scan. The detected signals were normalized to a measure of the incident X-ray flux. The laser wavelength was 266 nm, and the pulse duration was 10 ps. The incident power on the sample was 275 mW corresponding to a laser pulse energy of 2 μJ and fluence of ≈130 mJ/cm2. The flow speed of the jet was set so that an area defined by the laser fwhm was cleared in the 3.7 μs between X-ray pulses. This ensured that the “laser-off” counts were due to a fresh ground-state sample rather than contaminated by longer lived photoproducts.
The emission spectrometer consisted of a spherically bent Si(531) analyzer crystal, positioned relative to the sample on a 1 m Rowland circle. The analyzer focused Bragg-reflected radiation onto an APD detector. A 1 mm slit in front of the APD reduced the background. The analyzer crystal was rotated, while the detector was translated to record an emission spectrum at a fixed incident X-ray energy. The energy resolution was determined by scanning the elastic scattering at 7060 and 7108 eV. At both energies an overall bandwidth slightly less than 1 eV was found.
Aqueous solutions were prepared by dissolving high purity K4[Fe(CN)6]·3H2O and K3[Fe(CN)6], purchased from Sigma-Aldrich, in distilled water. The concentration was 0.05 M for all time-resolved measurements and 0.4 M for the static measurements. A volume of 750 mL was circulated through the liquid jet and was replaced with a fresh volume periodically to prevent contamination of the signal from irreversible photoproducts.
The static measurement on Na2[Fe(CN)5NO]·2H2O was obtained with a similar Rowland-circle spectrometer at the Inelastic Scattering (ID16) beamline of the European Synchrotron Radiation Facility. As the sample degraded in the X-ray beam, sets of consecutive X-ray absorption spectra were taken to determine the time scale of the decay. For the emission scans the flat pellet sample was moved along its face, orthogonal to the beam during the data collection at a speed sufficient to avoid effects of decay in the spectra.
The calculations of the vtc XES spectra were carried out with the ORCA 3.0.0 quantum chemistry program package.52 The structures of the [FeII(CN)6]4–, [FeIII(CN)6]3–, [FeII(CN)5(NO)]2–, and [FeII(CN)5(H2O)]3– complexes were optimized using the standard B3LYP53−55/TZVP56 DFT method. Modifications of the electronic structure due to the solvent were approximated with the conductor-like screening model (COSMO)57 which treats the solvent as a dielectric continuum that surrounds a molecular cavity containing the solute. In the present case with water being the solvent the relative permittivity used was ϵr = 80.4. The vtc X-ray emission spectra were computed in a quasi-one-electron approach;23 this includes the calculation of transition energies as the differences of core and valence orbital energies (ΔE = εval – εcore) as well as the determination of the emission oscillator strengths, f, of the electric dipole transitions utilizing the formula
| 1 |
Here ψI and ψF are the initial and final electronic states involved in the emission process, respectively, and D̂ is the electric dipole moment operator.23 Spin–orbit coupling was included in these computations by the application of the spin–orbit mean field (SOMF) operator.58 The numerical integration accuracy was set to 7.0 for the Fe atom in order to achieve a more accurate description. A pseudo-Voigt profile broadening was applied to account for the Lorentzian core-hole lifetime broadening and the Gaussian experimental broadening. The widths, 1.4 eV for the Lorentzian and 1.5 eV for the Gaussian, were chosen to best match the experimental spectrum.
Results and Discussion
Measurements of iron core-to-core (3p → 1s) Kβ emission spectra of aqueous [FeII(CN)6]4– are shown in Figure 1. The spectra consist of a main peak, Kβ1,3, and a small and broad shoulder to lower energy, Kβ′. If unpaired 3d electrons are present in the ion, the intra-atomic exchange interaction between the unpaired 3p core electron in the XES final state and the unpaired 3d valence electrons transfers intensity into the Kβ′ region.9 A higher spin state, and therefore stronger exchange interaction, produces more intensity in the Kβ′ shoulder and a shift of the Kβ1,3 peak to higher energy.10,11,59 This higher energy shift can be seen in the spectra of the [FeII(CN)6]4– and [FeIII(CN)6]3– reference samples in Figure 1(a). The [FeII(CN)6]4– Kβ1,3 main-line peak at ∼7057 eV shifts to ∼7058 eV in the [FeIII(CN)6]3– spectrum, reflecting the change of spin state from S = 0 to S = 1/2. Additionally, a subtle increase in the Kβ′ shoulder is observed. Being highly covalent compounds, the Kβ lineshapes of [FeII(CN)6]4– and [FeIII(CN)6]3– are somewhat more complex than described here.60,61 However, details such as the effects of back-bonding on the core-to-core lines are beyond the scope of this paper.
Figure 1.
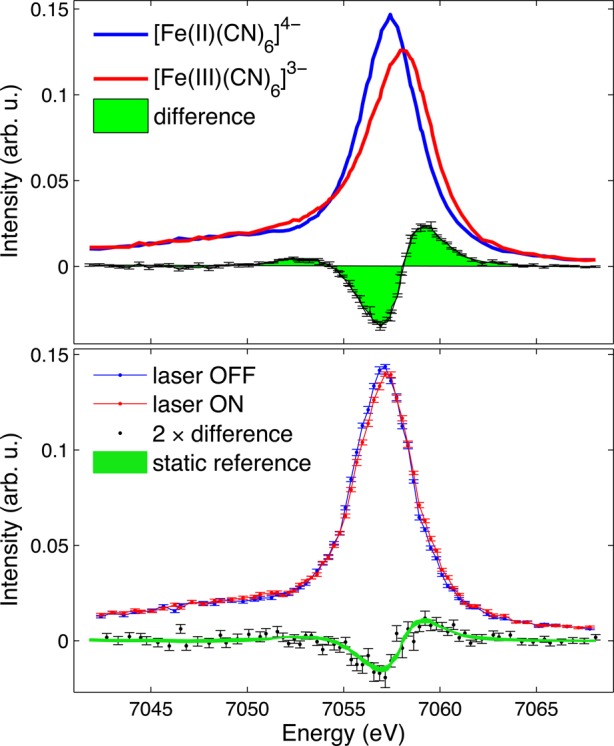
Measured iron core-to-core (3p → 1s) Kβ emission spectra. Static measurements on 0.4 M aqueous [FeII(CN)6]4– (blue) and [FeIII(CN)6]3– (red) reference samples are shown in the top panel along with the difference between these spectra. The time-resolved spectrum on 0.05 M aqueous [FeII(CN)6]4– pumped with 266 nm light, measured 120 ps after laser excitation is shown in the bottom panel. The difference between laser-on and laser-off is compared to the scaled difference between the reference samples in the top panel.
Our time-resolved Kβ measurement of ferrocyanide is shown in Figure 1(b). The laser-on curve is collected at a delay of 120 ps after excitation with 266 nm light. 120 ps is the delay between laser pump and X-ray probe where maximum changes between the laser-on and laser-off spectra were observed. This time delay corresponds to the pulse duration of the X-ray singlet pulses in the hybrid singlet operating mode and indicates the limit of our temporal resolution. On this time scale excitation to the ligand field states and subsequent CN– dissociation or hydrated electron formation are too fast to be resolved. Our measured transient signals are due to the presence of the photoproducts that result from these initial dynamics. The difference between laser-on and laser-off is small but clearly observed given the small statistical uncertainties. We compare the transient difference to the difference between the [FeII(CN)6]4– and [FeIII(CN)6]3– reference samples and find the agreement is consistent with our expectation that [FeIII(CN)6]3– would be the dominant photoproduct formed. However, such an observation does not exclude the possibility that other photoproducts are contributing to the transient signal. The core-to-core Kβ’s insensitivity to details of the absorbing ion’s chemical environment except for the number of unpaired electrons makes it a powerful probe of spin state but also means that the spectra of different chemical species with the same or close spin momentum on the transition metal ion will look very similar. In the present case photoaquation is known to occur alongside the photo-oxidation reaction although with a much smaller quantum yield.45,46 The photoaquated product [FeII(CN)5H2O]3–, while not expected to undergo a spin change, could contribute to the difference signal to some extent due to changes in the metal–ligand covalency.15 Additionally, the presence of an intermediate species such as [FeII(CN)5]3– which may have a different spin state from [FeII(CN)6]4– could also contribute to the difference signal but is not distinguishable. Separating contributions from multiple photoproducts in core-to-core Kβ emission spectra is a challenge and makes obtaining useful spin-state information for products involved in photoinduced chemical reactions difficult.
Roughly 50 eV to higher energy, on the tail of the core-to-core Kβ1,3 spectrum, is the vtc region which exhibits more sensitivity to the chemical environment of the absorbing metal ion and hence more spectral variation for different chemical species than core-to-core Kβ. Measured and calculated vtc spectra of aqueous [FeII(CN)6]4– are shown in the top panel of Figure 2. The intensity is considerably weaker than that for the core-to-core Kβ1,3 fluorescence, with a peak count rate of 130 counts per second as compared to 4200 counts per second. The features of the Kβ2,5 spectrum are due to dipole transitions to the Fe 1s core from molecular orbitals that are primarily ligand 2p in character but mixed with some Fe 4p and, for molecules lacking inversion symmetry, Fe 3d.23 The intensity of the spectral features is related to the amount of Fe np mixing with the ligand valence orbitals. A greater amount of Fe np character leads to stronger lines.23 The calculated spectrum reproduces the experimental features well. The energy and intensity of the main transitions contributing along with representations of the molecular orbitals involved are shown. The calculated spectrum was shifted by 150 eV to match the experimental spectrum. It can be seen that the molecular orbitals that are probed are those concentrated on the ligands and that have dominantly p character.
Figure 2.
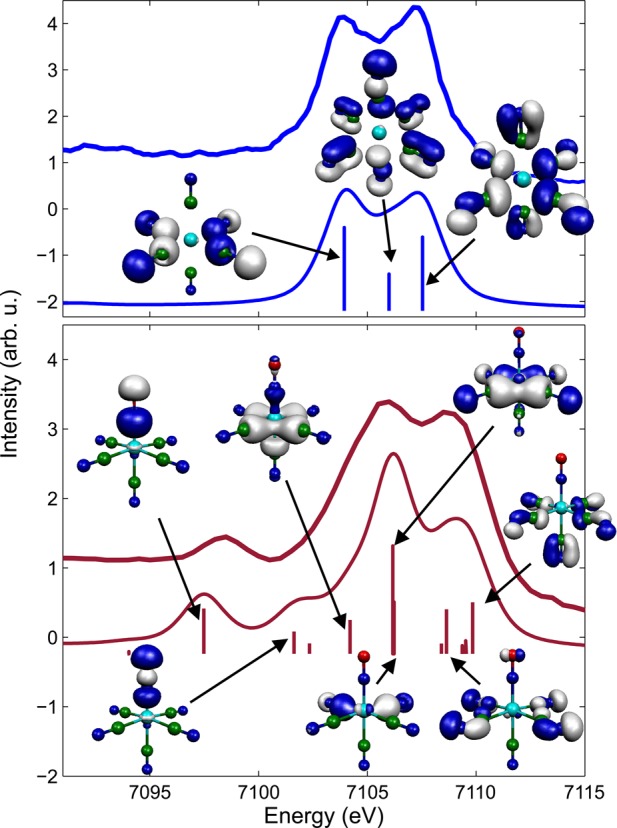
Measured iron valence-to-1s core XES compared with DFT-simulated spectrum. (top) Measured vtc XES of 0.4 M aqueous [Fe(CN)6]4– and the calculated spectrum for the same ion. (bottom) Spectrum of sodium nitroprusside, in solid form, and calculations for the [Fe(CN)5(NO)]2– ion. Representations of the main contributing molecular orbitals are shown.
For comparison, and to demonstrate this region’s sensitivity to ligand environment, measured and calculated vtc spectra of sodium nitroprusside are shown in the bottom panel of Figure 2. [Fe(CN)5(NO)]2– is very similar to [Fe(CN)6]4–, being low spin and having an iron oxidation state of +2, but differs in that it has a NO+ ligand in place of a CN– ligand. This difference can be seen to have a dramatic impact on the vtc spectrum. In particular, a distinct peak at 7098 eV is present. Kβ″ satellite peaks, such as this, have been shown to be due to transitions from ligand 2s orbitals.23,26 This can be seen to be the case here from the calculation which indicates that the peak involves a molecular orbital concentrated on the N donor atom of the ligand with s character. The energy of the satellite peak depends on the ligand’s 2s binding energy and can be used to identify the type of ligand. Since the intensity of this feature is correlated with the metal–ligand distance, this peak is large in the [Fe(CN)5(NO)]2– because of the short Fe–N bond length (1.66 Å). The spectrum of [Fe(CN)6]4– has a Kβ″ satellite peak as well, but it is very small and broad, therefore not as apparent above the background in our data. The [Fe(CN)5(NO)]2– Kβ2,5 region is shifted to higher energy relative to the [Fe(CN)6]4– spectrum. As demonstrated in ref (23) the vtc spectrum is sensitive to the effective nuclear charge on the metal, decreasing in energy upon reduction. Here the negatively charged CN ligand has been replaced by a positively charged NO ligand leading to an effective charge difference of +2 and a corresponding shift of the vtc spectrum to higher energy.
Our first measurement of time-resolved vtc XES is shown in the top panel of Figure 3. These four data points are the difference between laser-on and laser-off 120 ps after 266 nm excitation of 50 mM aqueous [FeII(CN)6]4–. Each data point results from a total of 2 h integration. The emission spectrometer was cycled through the four emission energies sitting at each for 2 min at a time. These points are compared to the difference between static measurements of 0.4 M aqueous [FeII(CN)6]4– and [FeIII(CN)6]3–. As the dominant photoproduct is expected to be [FeIII(CN)6]3– it is encouraging that the time-resolved points lie close to this difference signal. However, the photoaquated product [FeII(CN)5H2O]3– is also expected to be present. This complex is unstable and difficult to measure alone in a static measurement, so to determine its vtc spectrum we turn to calculations. The lower panel of Figure 3 shows calculated spectra for [FeII(CN)6]4–, [FeIII(CN)6]3–, and [FeII(CN)5H2O]3–. The [FeII(CN)6]4– and [FeIII(CN)6]3– spectra are in excellent agreement with the experimental spectra. The [FeIII(CN)6]3– spectrum is shifted to higher energy with respect to the [FeII(CN)6]4– spectrum due here also to the change in the effective nuclear charge on the metal. The calculated [FeII(CN)5H2O]3– spectrum is very similar to the [FeII(CN)6]4– spectrum, exhibiting only a loss of signal amplitude. This stems from the fact that the Fe–O distance is rather large in the [FeII(CN)5H2O]3– complex (2.19 Å as opposed to 1.92 Å for the Fe–C distance in the Fe–CN bonds), leading to little overlap of the O 2s and 2p orbitals with the Fe center and therefore negligible contribution to the signal. In effect the spectrum is due to five CN ligands as opposed to six, and therefore the intensity of the signal is less. The symmetry of [FeII(CN)5H2O]3– is distorted relative to [FeII(CN)6]4–, and this difference in geometrical arrangement of the CN ligands around the Fe center does not appear to influence the shape of the spectra, similar to findings in ref (23).
Figure 3.
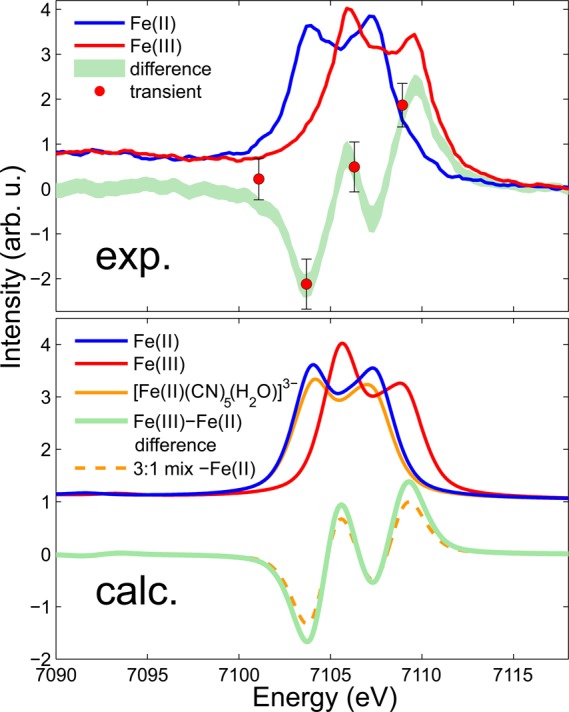
Valence-to-core emission spectra of [FeII(CN)6]4– (blue) and [FeIII(CN)6]3– (red). Measured spectra of the compounds in aqueous solution are shown in the top panel. DFT calculated spectra are shown in the bottom panel along with a third possible species, the photoaquated product [FeII(CN)5H2O]3–. The differences between the [FeII(CN)6]4– and [FeIII(CN)6]3– spectra are shown in green. The red data points are the difference between laser-on and laser-off, 120 ps after 266 nm laser excitation of [FeII(CN)6]4–. The amplitude of the points has been scaled to show the agreement with the reference difference signal.
The difference spectra shown in the lower panel of Figure 3 are the difference between [FeII(CN)6]4– and [FeIII(CN)6]3–, to be compared to the measured difference signal in the top panel, and the differences assuming both [FeIII(CN)6]3– and [FeII(CN)5H2O]3– are present. For the latter the relative amounts of [FeIII(CN)6]3– and [FeII(CN)5H2O]3– are taken to be 3:1. This has been estimated from literature values for the quantum yields for the two reactions: ϕ = 0.52 for the photoaquation reaction at 266 nm as reported by Shirom and Stein45,46 and ϕ ≈ 0.19 for the photoaquation reaction which is our estimated extrapolation from the quantum yield reported at 254 nm.62 Detection of the presence of the [FeII(CN)5H2O]3− product based on this valence-to-core measurement alone is difficult due to the similarity of its spectral shape to that of the ground state molecule. However, combined with XANES valuable information can be obtained. The XANES spectra of [FeII(CN)6]4−, [FeIII(CN)6]3−, and [FeII(CN)5H2O]3− will differ due to their different geometries, valence states, and 3d electronic structure. Because the spectral shape is known from static measurements, the fraction of [FeIII(CN)6]3− present can be directly determined from the XANES measurement. Given this fraction, the contribution of [FeIII(CN)6]3− to the measured valence-to-core difference signal can be removed and the remaining signal amplitude will yield the fraction of [FeII(CN)5H2O]3−. The fractions obtained from these techniques can then be used as valuable input for EXAFS or X-ray diffuse scattering analysis.18
To be able to extract meaningful information more time-resolved data points are obviously needed. We estimate that a factor of 5 to 25 times more points (with improved statistics) could constitute a definitive time-resolved vtc spectrum. This would be 20 to 100 points which in the present case would correspond to 1–0.2 eV per point, the latter being more than enough resolution to distinguish features similar to those of Figure 2. Straightforward improvements to increase the fluorescence detection efficiency along with the incident X-ray flux will make collection of such time-resolved vtc spectra possible. The spectrometer used for our measurements consists of one 10 cm diameter crystal analyzer. The reflective portion is 8.6 cm in diameter which subtends a small solid angle of 0.006 sr, or 0.05% of 4π. Detection efficiency can be improved simply by adding crystal analyzers. Such multicrystal spectrometers have been implemented at, for example, the ESRF,63,64 the Swiss Light Source,65 the APS,66 the Stanford Synchrotron Radiation Lightsource,67 and the LCLS.68 However, as the number of analyzers increases, so does the complexity and size of the setup, and care must be taken to not add too much to an already technically challenging experiment.
More substantial gain can be made by increasing the incident X-ray flux. Our measurements were carried out with a monochromatic beam, with 0.005% bandwidth (corresponding to ∼0.35 eV centered at 7 keV) and ∼106 photons/pulse, but monochromaticity is not necessary for emission spectroscopy. The X-ray photon energy only need be a few hundred electronvolts above the absorption edge which makes vtc XES compatible with pink beam. Such broad bandwidth beams, with bandwidths on the order of 1%, are provided by many synchrotron beamlines, including Sector 7 at the APS, as well as by the self-amplified spontaneous emission (SASE) radiation from X-ray free electron lasers (XFELs). At Sector 7 pink beam operation could provide approximately 2 orders of magnitude more photons/pulse at a MHz repetition rate. Comparably, at the LCLS, 1012 photons/pulse in a 70 eV bandwidth at 7 keV is available, but at a lower repetition rate of 120 Hz, leading to a similar number of photons per second. As the fluorescence scales directly with incident flux, incorporating pink beam at Sector 7 could lead to a 100 times increase in signal.
Lastly, an increase in flux can be achieved by increasing the repetition rate of the pump–probe measurement to use more of the available X-ray flux. The 135.8 kHz repetition rate used in this work was dictated by the hybrid singlet operating mode and the need to have a fresh sample for each laser-pump, X-ray-probe cycle. The laser-on and laser-off data collected at this rate are a result of only 15% of the available X-ray flux. The maximum rate to ensure sample refresh is dependent on our laser and X-ray spot sizes as well as the flow speed of the liquid jet. In 24 bunch mode given our jet parameters and spot sizes, our maximum pump–probe repetition rate is approximately 300 kHz. Our laser system is already capable of matching the repetition rate of the APS X-rays so it is this rate that limits the efficient use of X-ray flux. However, developments in faster flowing, stable, liquid jets could enable higher repetition rate experiments. A factor of 5 in flow speed already brings measurements into the MHz regime. Jets capable of 30 m/s flow speeds are presently in use for soft X-ray experiments.69−71
In total, it can be seen that the increase in signal needed to make time-resolved valence-to-core spectroscopy feasible is well within reach with technical improvements that are already available.
Conclusion
Valence-to-core XES promises to be a powerful addition to the X-ray toolbox for understanding the geometrical and electronic structures of intermediates produced as a solution-phase chemical reaction occurs. The decreased signal strength compared to XAS or core-to-core XES makes it challenging, but we argue that the technical capabilities to make it a practical time-resolved technique are available. The information that can be supplied by valence-to-core XES with the use of straightforward theoretical models is complementary to that of XANES, EXAFS, and core-to-core XES and can, for instance, help identify the presence of photoproducts and quantify their amounts, disentangle the contributions to the XANES spectra, and provide the photoproduct fraction needed for EXAFS analysis.
Acknowledgments
This project was supported by the European Research Council via contract ERC-StG-259709, the ’Lendület’ (Momentum) Program of the Hungarian Academy of Sciences, and the European XFEL. Z.N. acknowledges support from the Bolyai Fellowship of the Hungarian Academy of Sciences. W.G., T. A., A.G., and C. B. acknowledge funding by the Deutsche Forschungsgemeinschaft via SFB925 and by the Hamburg Centre of Ultrafast Imaging. Work by A.M.M., G.D., L.Y., E.P.K., and S.H.S was supported by the U.S. Department of Energy (DOE), Office of Science, Basic Energy Sciences (BES), under Contract No. DE-AC02-06CH11357. This research used resources of the Advanced Photon Source, a U.S. Department of Energy (DOE) Office of Science User Facility operated for the DOE Office of Science by Argonne National Laboratory under Contract No. DE-AC02-06CH11357.
The authors declare no competing financial interest.
References
- de Groot F. High-Resolution X-ray Emission and X-ray Absorption Spectroscopy. Chem. Rev. 2001, 101, 1779–1808. [DOI] [PubMed] [Google Scholar]
- Boubnov A.; Carvalho H. W. P.; Doronkin D. E.; Günter T.; Gallo E.; Atkins A. J.; Jacob C. R.; Grunwaldt J.-D. Selective Catalytic Reduction of NO Over Fe-ZSM-5: Mechanistic Insights by Operando HERFD-XANES and Valence-to-Core X-ray Emission Spectroscopy. J. Am. Chem. Soc. 2014, 136, 13006–13015. [DOI] [PubMed] [Google Scholar]
- Safonova O. V.; Florea M.; Bilde J.; Delichere P.; Millet J. M. M. Local Environment of Vanadium in V/Al/O-Mixed Oxide Catalyst for Propane Ammoxidation: Characterization by In Situ Valence-to-Core X-ray Emission Spectroscopy and X-ray Absorption Spectroscopy. J. Catal. 2009, 268, 156–164. [Google Scholar]
- Milne C. J.; Penfold T. J.; Chergui M. Recent Experimental and Theoretical Developments in Time-Resolved X-ray Spectroscopies. Coord. Chem. Rev. 2014, 277–278, 44–68. [Google Scholar]
- Bressler C.; Chergui M. Molecular Structural Dynamics Probed by Ultrafast X-Ray Absorption Spectroscopy. Annu. Rev. Phys. Chem. 2010, 61, 263–282. [DOI] [PubMed] [Google Scholar]
- Chen L. X.; Zhang X.; Shelby M. L. Recent Advances on Ultrafast X-ray Spectroscopy in the Chemical Sciences. Chem. Sci. 2014, 5, 4136–4152. [Google Scholar]
- Glatzel P.; Smolentsev G.; Bunker G. The Electronic Structure in 3d Transition Metal Complexes: Can We Measure Oxidation States?. J. Phys.: Conf. Ser. 2009, 190, 012046. [Google Scholar]
- Glatzel P.; Bergmann U. High Resolution 1s Core Hole X-ray Spectroscopy in 3d Transition Metal Complexes–Electronic and Structural Information. Coord. Chem. Rev. 2005, 249, 65–95. [Google Scholar]
- Rovezzi M.; Glatzel P. Hard X-ray Emission Spectroscopy: A Powerful Tool for the Characterization of Magnetic Semiconductors. Semicond. Sci. Technol. 2014, 29, 023002. [Google Scholar]
- Peng G.; deGroot F. M. F.; Haemaelaeinen K.; Moore J. A.; Wang X.; Grush M. M.; Hastings J. B.; Siddons D. P.; Armstrong W. H. High-Resolution Manganese X-ray Fluorescence Spectroscopy. Oxidation-State and Spin-State Sensitivity. J. Am. Chem. Soc. 1994, 116, 2914–2920. [Google Scholar]
- Vankó G.; Neisius T.; Molnár G.; Renz F.; Kárpáti S.; Shukla A.; de Groot F. M. F. Probing the 3d Spin Momentum with X-ray Emission Spectroscopy: The Case of Molecular-Spin Transitions. J. Phys. Chem. B 2006, 110, 11647–11653. [DOI] [PubMed] [Google Scholar]
- Vankó G.; Rueff J.-P.; Mattila A.; Németh Z.; Shukla A. Temperature- and Pressure-Induced Spin-State Transitions in LaCoO3. Phys. Rev. B 2006, 73, 024424. [Google Scholar]
- Rueff J.-P.; Shukla A. Inelastic X-ray Scattering by Electronic Excitations Under High Pressure. Rev. Mod. Phys. 2010, 82, 847–896. [Google Scholar]
- Vankó G.; de Groot F. M. F. Comment on “Spin Crossover in (Mg,Fe)O: A Mössbauer Effect Study with an Alternative Interpretation of X-ray Emission Spectroscopy Data. Phys. Rev. B 2007, 75, 177101. [Google Scholar]
- Pollock C. J.; Delgado-Jaime M. U.; Atanasov M.; Neese F.; DeBeer S. Kβ Mainline X-ray Emission Spectroscopy as an Experimental Probe of Metal-Ligand Covalency. J. Am. Chem. Soc. 2014, 136, 9453–9463. [DOI] [PMC free article] [PubMed] [Google Scholar]
- De Groot F., Kotani A.. Core Level Spectroscopy of Solids; CRC: Boca Raton, FL, 2008; Vol. 6. [Google Scholar]
- Vankó G.; Glatzel P.; Pham V.-T.; Abela R.; Grolimund D.; Borca C. N.; Johnson S. L.; Milne C. J.; Bressler C. Picosecond Time-Resolved X-Ray Emission Spectroscopy: Ultrafast Spin-State Determination in an Iron Complex. Angew. Chem., Int. Ed. 2010, 49, 5910–5912. [DOI] [PubMed] [Google Scholar]
- Haldrup K.; et al. Guest-Host Interactions Investigated by Time-Resolved X-ray Spectroscopies and Scattering at MHz Rates: Solvation Dynamics and Photoinduced Spin Transition in Aqueous Fe(bipy)32+. J. Phys. Chem. A 2012, 116, 9878–9887. [DOI] [PubMed] [Google Scholar]
- Vankó G.; et al. Spin-State Studies with XES and RIXS: From Static to Ultrafast. J. Electron Spectrosc. Relat. Phenom. 2013, 188, 166–171. [Google Scholar]
- Zhang W.; et al. Tracking Excited-State Charge and Spin Dynamics in Iron Coordination Complexes. Nature 2014, 509, 345–348. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kern J.; et al. Taking Snapshots of Photosynthetic Water Oxidation Using Femtosecond X-ray Diffraction and Spectroscopy. Nat. Commun. 2014, 5, 4371. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gallo E.; Glatzel P. Valence to Core X-ray Emission Spectroscopy. Adv. Mater. 2014, 10.1002/adma.201304994. [DOI] [PubMed] [Google Scholar]
- Lee N.; Petrenko T.; Bergmann U.; Neese F.; DeBeer S. Probing Valence Orbital Composition with Iron Kβ X-ray Emission Spectroscopy. J. Am. Chem. Soc. 2010, 132, 9715–9727. [DOI] [PubMed] [Google Scholar]
- Bauer M. HERFD-XAS and Valence-to-Core-XES: New Tools to Push the Limits in Research with Hard X-rays?. Phys. Chem. Chem. Phys. 2014, 16, 13827–13837. [DOI] [PubMed] [Google Scholar]
- Delgado-Jaime M. U.; Dible B. R.; Chiang K. P.; Brennessel W. W.; Bergmann U.; Holland P. L.; DeBeer S. Identification of a Single Light Atom within a Multinuclear Metal Cluster Using Valence-to-Core X-ray Emission Spectroscopy. Inorg. Chem. 2011, 50, 10709–10717. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bergmann U.; Horne C. R.; Collins T. J.; Workman J. M.; Cramer S. P. Chemical Dependence of Interatomic X-ray Transition Energies and Intensities -A Study of Mn Kβ″ and Kβ2,5 Spectra. Chem. Phys. Lett. 1999, 302, 119–124. [Google Scholar]
- Swarbrick J. C.; Kvashnin Y.; Schulte K.; Seenivasan K.; Lamberti C.; Glatzel P. Ligand Identification in Titanium Complexes Using X-ray Valence-to-Core Emission Spectroscopy. Inorg. Chem. 2010, 49, 8323–8332. [DOI] [PubMed] [Google Scholar]
- Safonov V. A.; Vykhodtseva L. N.; Polukarov Y. M.; Safonova O. V.; Smolentsev G.; Sikora M.; Eeckhout S. G.; Glatzel P. Valence-to-Core X-ray Emission Spectroscopy Identification of Carbide Compounds in Nanocrystalline Cr Coatings Deposited from Cr(III) Electrolytes Containing Organic Substances. J. Phys. Chem. B 2006, 110, 23192–23196. [DOI] [PubMed] [Google Scholar]
- Lancaster K. M.; Roemelt M.; Ettenhuber P.; Hu Y.; Ribbe M. W.; Neese F.; Bergmann U.; DeBeer S. X-ray Emission Spectroscopy Evidences a Central Carbon in the Nitrogenase Iron-Molybdenum Cofactor. Science 2011, 334, 974–977. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Smolentsev G.; Soldatov A. V.; Messinger J.; Merz K.; Weyhermüller T.; Bergmann U.; Pushkar Y.; Yano J.; Yachandra V. K.; Glatzel P. X-ray Emission Spectroscopy To Study Ligand Valence Orbitals in Mn Coordination Complexes. J. Am. Chem. Soc. 2009, 131, 13161–13167. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lassalle-Kaiser B.; et al. Experimental and Computational X-ray Emission Spectroscopy as a Direct Probe of Protonation States in Oxo-Bridged MnIV Dimers Relevant to Redox-Active Metalloproteins. Inorg. Chem. 2013, 52, 12915–12922. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chandrasekaran P.; Chiang K. P.; Nordlund D.; Bergmann U.; Holland P. L.; DeBeer S. Sensitivity of X-ray Core Spectroscopy to Changes in Metal Ligation: A Systematic Study of Low-Coordinate, High-Spin Ferrous Complexes. Inorg. Chem. 2013, 52, 6286–6298. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pollock C. J.; DeBeer S. Valence-to-Core X-ray Emission Spectroscopy: A Sensitive Probe of the Nature of a Bound Ligand. J. Am. Chem. Soc. 2011, 133, 5594–5601. [DOI] [PubMed] [Google Scholar]
- Gallo E.; Lamberti C.; Glatzel P. Investigation of the Valence Electronic States of Ti(IV) in Ti Silicalite-1 Coupling X-ray Emission Spectroscopy and Density Functional Calculations. Phys. Chem. Chem. Phys. 2011, 13, 19409–19419. [DOI] [PubMed] [Google Scholar]
- Delgado-Jaime M. U.; DeBeer S.; Bauer M. Valence-to-Core X-Ray Emission Spectroscopy of Iron-Carbonyl Complexes: Implications for the Examination of Catalytic Intermediates. Chem.—Eur. J. 2013, 19, 15888–15897. [DOI] [PubMed] [Google Scholar]
- Beckwith M. A.; Roemelt M.; Collomb M.-N.; DuBoc C.; Weng T.-C.; Bergmann U.; Glatzel P.; Neese F.; DeBeer S. Manganese Kβ X-ray Emission Spectroscopy As a Probe of Metal-Ligand Interactions. Inorg. Chem. 2011, 50, 8397–8409. [DOI] [PubMed] [Google Scholar]
- Bordage A.; Papai M.; Sas N. S.; Szlachetko J.; Nachtegaal M.; Vanko G. On the Sensitivity of Hard X-ray Spectroscopies to the Chemical State of Br. Phys. Chem. Chem. Phys. 2013, 15, 11088–11098. [DOI] [PubMed] [Google Scholar]
- Gaur A.; Shrivastava B. D.; Joshi S. K. Copper K-edge XANES of Cu(I) and Cu(II) Oxide Mixtures. J. Phys. Conf. Ser. 2009, 190, 012084. [Google Scholar]
- March A. M.; Stickrath A.; Doumy G.; Kanter E. P.; Krässig B.; Southworth S. H.; Attenkofer K.; Kurtz C. A.; Chen L. X.; Young L. Development of High-Repetition-Rate Laser Pump/X-ray Probe Methodologies for Synchrotron Facilities. Rev. Sci. Instrum. 2011, 82, 073110. [DOI] [PubMed] [Google Scholar]
- Lima F. A.; et al. A High-Repetition Rate Scheme for Synchrotron-Based Picosecond Laser Pump/X-ray Probe Experiments on Chemical and Biological Systems in Solution. Rev. Sci. Instrum. 2011, 82, 063111. [DOI] [PubMed] [Google Scholar]
- Stebel L.; Malvestuto M.; Capogrosso V.; Sigalotti P.; Ressel B.; Bondino F.; Magnano E.; Cautero G.; Parmigiani F. Time-Resolved Soft X-ray Absorption Setup Using Multi-Bunch Operation Modes at Synchrotrons. Rev. Sci. Instrum. 2011, 82, 123109. [DOI] [PubMed] [Google Scholar]
- Wu B.; Zhu D.; Acremann Y.; Miller T. A.; Lindenberg A. M.; Hellwig O.; Stöhr J.; Scherz A. Observations of Laser Induced Magnetization Dynamics in Co/Pd Multilayers with Coherent X-ray Scattering. Appl. Phys. Lett. 2011, 99, 252505. [Google Scholar]
- Kozina M.; Hu T.; Wittenberg J. S.; Szilagyi E.; Trigo M.; Miller T. A.; Uher C.; Damodaran A.; Martin L.; Mehta A. Measurement of Transient Atomic Displacements in Thin Films with Picosecond and Femtometer Resolution. Struct. Dyn. 2014, 1, 034301. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Navirian H.; Shayduk R.; Leitenberger W.; Goldshteyn J.; Gaal P.; Bargheer M. Synchrotron-Based Ultrafast X-ray Diffraction at High Repetition Rates. Rev. Sci. Instrum. 2012, 83, 063303. [DOI] [PubMed] [Google Scholar]
- Shirom M.; Stein G. Excited State Chemistry of the Ferrocyanide Ion in Aqueous Solution. I. Formation of the Hydrated Electron. J. Chem. Phys. 1971, 55, 3372–3378. [Google Scholar]
- Shirom M.; Stein G. Excited State Chemistry of the Ferrocyanide Ion in Aqueous Solution. II. Photoaquation. J. Chem. Phys. 1971, 55, 3379–3382. [Google Scholar]
- Westre T. E.; Kennepohl P.; DeWitt J. G.; Hedman B.; Hodgson K. O.; Solomon E. I. A Multiplet Analysis of Fe K-Edge 1s → 3d Pre-Edge Features of Iron Complexes. J. Am. Chem. Soc. 1997, 119, 6297–6314. [Google Scholar]
- Penfold T. J.; Reinhard M.; Rittmann-Frank M. H.; Tavernelli I.; Rothlisberger U.; Milne C. J.; Glatzel P.; Chergui M. X-ray Spectroscopic Study of Solvent Effects on the Ferrous and Ferric Hexacyanide Anions. J. Phys. Chem. A 2014, 118, 9411–9418. [DOI] [PubMed] [Google Scholar]
- Reinhard M.; Penfold T. J.; Lima F. A.; Rittmann J.; Rittmann-Frank M. H.; Abela R.; Tavernelli I.; Rothlisberger U.; Milne C. J.; Chergui M. Photooxidation and Photoaquation of Iron Hexacyanide in Aqueous Solution: A Picosecond X-ray Absorption Study. Struct. Dyn. 2014, 1, 024901. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lee T.; Jiang Y.; Rose-Petruck C. G.; Benesch F. Ultrafast Tabletop Laser-Pump-X-ray Probe Measurement of Solvated Fe(CN)64–. J. Chem. Phys. 2005, 122, 084506. [DOI] [PubMed] [Google Scholar]
- Dufresne E. M.; Adams B.; Arms D. A.; Chollet M.; Landahl E. C.; Li Y.; Walko D. A.; Wang J. Time-Resolved Research at the Advanced Photon Source Beamline 7-ID. AIP Conf. Proc. 2010, 1234, 181–184. [Google Scholar]
- Neese F. The ORCA Program System. WIREs Comput. Mol. Sci. 2012, 2, 73–78. [Google Scholar]
- Lee C.; Yang W.; Parr R. G. Development of the Colle-Salvetti Correlation-Energy Formula into a Functional of the Electron Density. Phys. Rev. B 1988, 37, 785–789. [DOI] [PubMed] [Google Scholar]
- Becke A. D. Density-Functional Thermochemistry. III. The Role of Exact Exchange. J. Chem. Phys. 1993, 98, 5648–5652. [Google Scholar]
- Stephens P. J.; Devlin F. J.; Chabalowski C. F.; Frisch M. J. Ab Initio Calculation of Vibrational Absorption and Circular Dichroism Spectra Using Density Functional Force Fields. J. Phys. Chem. 1994, 98, 11623–11627. [Google Scholar]
- Schäfer A.; Huber C.; Ahlrichs R. Fully Optimized Contracted Gaussian Basis Sets of Triple Zeta Valence Quality for Atoms Li to Kr. J. Chem. Phys. 1994, 100, 5829–5835. [Google Scholar]
- Klamt A.; Schuurmann G. COSMO: A New Approach to Dielectric Screening in Solvents with Explicit Expressions for the Screening Energy and its Gradient. J. Chem. Soc., Perkin Trans. 2 1993, 799–805. [Google Scholar]
- Heß B. A.; Marian C. M.; Wahlgren U.; Gropen O. A Mean-Field Spin-Orbit Method Applicable to Correlated Wavefunctions. Chem. Phys. Lett. 1996, 251, 365–371. [Google Scholar]
- Glatzel P.; Weng T.-C.; Kvashnina K.; Swarbrick J.; Sikora M.; Gallo E.; Smolentsev N.; Mori R. A. Reflections on Hard X-ray Photon-In/Photon-Out Spectroscopy for Electronic Structure Studies. J. Electron Spectrosc. Relat. Phenom. 2013, 188, 17–25. [Google Scholar]
- Hocking R. K.; Wasinger E. C.; de Groot F. M. F.; Hodgson K. O.; Hedman B.; Solomon E. I. Fe L-Edge X.A.S. Studies of K4[Fe(CN)6] and K3[Fe(CN)6]: A Direct Probe of Back-Bonding. J. Am. Chem. Soc. 2006, 128, 10442–10451. [DOI] [PubMed] [Google Scholar]
- Lundberg M.; Kroll T.; DeBeer S.; Bergmann U.; Wilson S. A.; Glatzel P.; Nordlund D.; Hedman B.; Hodgson K. O.; Solomon E. I. Metal-Ligand Covalency of Iron Complexes from High-Resolution Resonant Inelastic X-ray Scattering. J. Am. Chem. Soc. 2013, 135, 17121–17134. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Emschwiller M. G.; Legros J. L’Hydrolyse Photochimique des Solutions de Ferrocyanure de Potassium: Influence de la Frequence, de l’Intensite d’Irradiation et de la Concentration sur le Rendement Quantique. Compt. Rend. 1965, 261, 1535. [Google Scholar]
- Bergmann U.; Glatzel P. X-ray Emission Spectroscopy. Photosynth. Res. 2009, 102, 255–266. [DOI] [PubMed] [Google Scholar]
- Verbeni R.; Pylkkänen T.; Huotari S.; Simonelli L.; Vankó G.; Martel K.; Henriquet C.; Monaco G. Multiple-element spectrometer for non-resonant inelastic X-ray spectroscopy of electronic excitations. J. Synchrotron Radiat. 2009, 16, 469–476. [DOI] [PubMed] [Google Scholar]
- Kleymenov E.; van Bokhoven J. A.; David C.; Glatzel P.; Janousch M.; Alonso-Mori R.; Studer M.; Willimann M.; Bergamaschi A.; Henrich B.; Nachtegaal M. Five-Element Johann-Type X-ray Emission Spectrometer with a Single-Photon-Counting Pixel Detector. Rev. Sci. Instrum. 2011, 82, 065107. [DOI] [PubMed] [Google Scholar]
- Gog T.; et al. Momentum-Resolved Resonant and Nonresonant Inelastic X-ray Scattering at the Advanced Photon Source. Synchrotron Radiat. News 2009, 22, 12–21. [Google Scholar]
- Sokaras D.; Weng T.-C.; Nordlund D.; Alonso-Mori R.; Velikov P.; Wenger D.; Garachtchenko A.; George M.; Borzenets V.; Johnson B.; Rabedeau T.; Bergmann U. A Seven-Crystal Johann-Type Hard X-ray Spectrometer at the Stanford Synchrotron Radiation Lightsource. Rev. Sci. Instrum. 2013, 84, 053102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Alonso-Mori R.; Kern J.; Sokaras D.; Weng T.-C.; Nordlund D.; Tran R.; Montanez P.; Delor J.; Yachandra V. K.; Yano J. A Multi-Crystal Wavelength Dispersive X-ray Spectrometer. Rev. Sci. Instrum. 2012, 83, 073114. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Suljoti E.; Garcia-Diez R.; Bokarev S. I.; Lange K. M.; Schoch R.; Dierker B.; Dantz M.; Yamamoto K.; Engel N.; Atak K.; Kühn O.; Bauer M.; Rubensson J.-E.; Aziz E. F. Direct Observation of Molecular Orbital Mixing in a Solvated Organometallic Complex. Angew. Chem., Int. Ed. 2013, 52, 9841–9844. [DOI] [PubMed] [Google Scholar]
- Charvat A.; Lugovoj E.; Faubel M.; Abel B. New Design for a Time-of-Flight Mass Spectrometer with a Liquid Beam Laser Desorption Ion Source for the Analysis of Biomolecules. Rev. Sci. Instrum. 2004, 75, 1209–1218. [Google Scholar]
- Lange K. M.; Kothe A.; Aziz E. F. Chemistry in Solution: Recent Techniques and Applications Using Soft X-ray Spectroscopy. Phys. Chem. Chem. Phys. 2012, 14, 5331–5338. [DOI] [PubMed] [Google Scholar]


