Stem-Loop V of Varkud Satellite RNA Exhibits Characteristics of the Mg²⁺ Bound Structure in the Presence of Monovalent Ions

Abstract

The Varkud Satellite RNA contains a self-cleaving ribozyme that has been shown to function independently of its surroundings. This 160 nucleotide ribozyme adopts a catalytically active tertiary structure that includes a kissing hairpin complex formed by stem-loop I and stem-loop V (SLV). The five-nucleotide 5′-rUGACU loop of the isolated SLV has been shown to adopt a Mg²⁺-dependent U-turn structure by solution NMR. This U-turn hairpin is examined here by molecular dynamics simulations in the presence of monovalent and divalent ions. Simulations confirm on an all-atom level the hypotheses for the role of the Mg²⁺ ions in stabilizing the loop, as well as the role of the solvent exposed U₇₀₀ base. Additionally, these simulations suggest the Mg²⁺-free stem-loop adopts a wide range of structures, including energetically favorable structures similar to the Mg²⁺-bound loop structure. We propose this structure is a “gatekeeper” or precursor to Mg²⁺ binding when those ions are present.

Introduction

The Varkud Satellite (VS) ribozyme is a catalytic RNA which performs cleavage and ligation of a phosphodiester bond, and it requires Mg²⁺ for tertiary structure formation and catalysis.¹⁻³ Though there is no available structure of the complete ribozyme, several of the four hairpin loops and internal stems and junctions have been characterized by NMR.⁴⁻⁷ Stem-loop V (SLV) undergoes a Mg²⁺-dependent conformational change which allows it to orient the substrate stem-loop I (SLI) via Watson–Crick base pairing in a kissing-loop interaction.^3,8

The structure and dynamics of SLV were examined by NMR revealing a Mg²⁺-dependent conformational switch of the loop conformation (shown in Figure 1a,b).^4,5 The Mg²⁺-dependence is particularly interesting since it illustrates a role for divalent ions in the association of SLI with SLV.^1,2 SLV is a six base pair stem capped by a five-membered loop with the sequence 5′-U₆₉₆G₆₉₇A₆₉₈C₆₉₉U₇₀₀-3′ and it forms a canonical U-turn motif in the presence of Mg²⁺. The structural features of a U-turn motif include a UNR sequence (where N is any nucleotide and R is a purine); a Y:A, Y:Y, or G:A loop-closing base pair (Y is pyrimidine); a sharp turn of the backbone α torsion angle 3′ to the U; a hydrogen bond from U 2′ OH to R N7 (Figure 1c,d); a hydrogen bond from U NH3 to the phosphate oxygen 3′ to R (Figure 1e,f); and stacking of the U with the R 5′ phosphate group (Figure 1e,f). These canonical features are illustrated in molecular graphics images of the experimental structures in the presence and absence of Mg²⁺ in Figure 1 panels c, d, e, and f, respectively. In a monovalent ion environment (-Mg²⁺ or MgFree), SLV is described as a noncanonical or “loose” U-turn motif, and these characteristic intermolecular interactions range from weak to nonexistent.⁴ In a divalent ion environment these interactions are able to form and stabilize a more compact loop.⁵ It has been proposed that Mg²⁺ stabilizes the U-turn of SLV and neutralizes the electronegative charges in the loop, making it easier for the substrate SLI to bind.⁵

Figure 1.

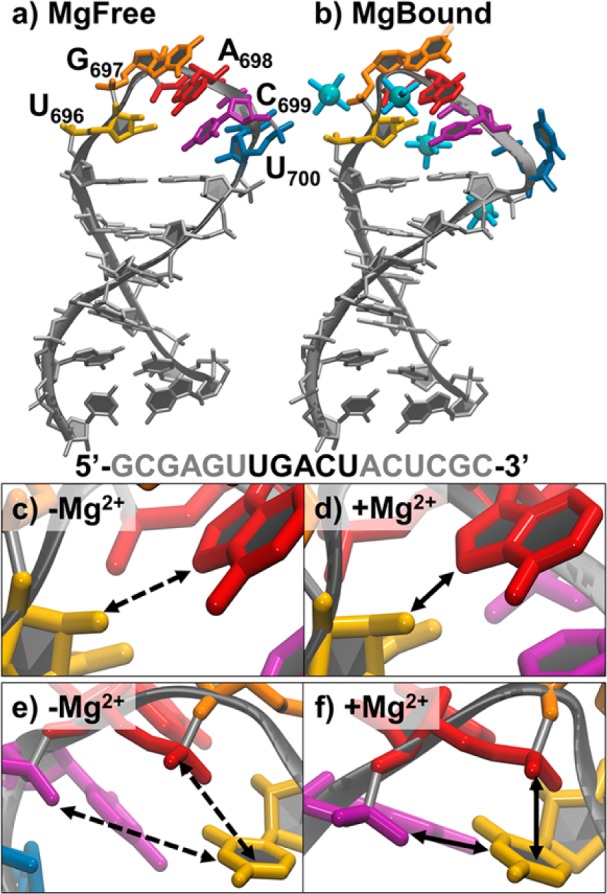
NMR structures and U-turn characteristics of SLV. (a) The MgFree most representative structure determined by NMR (1TBK). Bases of the five-membered U-turn are labeled and shown in color. (b) The MgBound most representative structure determined by NMR (1YN2). Bases of the five-membered U-turn are shown in the same color as part a, and hexahydrated Mn²⁺ are shown as blue spheres. The primary sequence is shown with the bases of the U-turn in black. Close ups of the characteristic U-turn hydrogen bond between the 2′ OH of U₆₉₆ (yellow) and the N7 of A₆₉₈ (red) (c) in the absence of Mg²⁺ and (d) in the presence of Mg²⁺. Close ups of the characteristic U-turn hydrogen bond between the 3′ phosphate of A₆₉₈ (shown in purple here as the 5′ phosphate of C₆₉₉) and the N3 of U₆₉₆, and stacking of 5′phosphate of A₆₉₈ with the U₆₉₆ base in the (e) absence and (f) presence of Mg²⁺. Solid lines indicate a favorable interaction (stacking or hydrogen bonding) is present and dashed lines indicate absence of interaction.

The experimental evidence outside of NMR includes kinetic and thermodynamic characterization of SLI and SLV. A focus on the solvent exposed U₇₀₀ base showed that mutation to another base maintained the enzymatic rate of the wild type U, but deleting the base reduces k_cat/K_M.⁹ Similarly, mutating U₇₀₀ to C showed no change in binding affinity for SLI, but deletion of U₇₀₀ reduced the binding affinity.⁸ This led to the hypothesis that U₇₀₀ contributes to the enthalpic stability of SLV by donating a phosphate group that coordinates a Mg²⁺ ion, and that the solvent exposed nature of the base would contribute to increased entropy in the monovalent (unbound) environment.

SLV is a rich source of information about Mg²⁺-dependent structural changes in small RNA molecules, and so is of particular interest for molecular dynamics (MD) simulations. Nucleic acid force fields lag behind those for proteins, in part due to the high charge density and high flexibility of the nucleic acid backbone.¹⁰ In RNA—which adopts many types of structures beyond a simple duplex—capturing the dynamic aspects, coupled with the long time scales over which these conformational changes can occur, is particularly challenging.¹¹⁻¹³ However, recent modifications, some specific to RNA, have brought force fields into better alignment with experimental data.¹⁴⁻¹⁶

Here we use MD simulations to provide atomic-level detail into the dynamics of ion association with SLV. We show computational evidence supporting the current hypotheses for the role of Mg²⁺ ions in stabilizing SLV, as well as the role of the U₇₀₀ base. Additionally, we show that the dynamics of the unbound SLV (in a monovalent ion environment) adopt U-turn characteristics similar to the canonical U-turn characteristics of the Mg²⁺-bound conformation, though admittedly not identical to the NMR structure. We propose the SLV RNA in the presence of monovalent ions samples a dynamic and wide range of structures, including a “gatekeeper” structure which is a precursor to Mg²⁺ binding, adopting structural features which are more similar to the bound loop than to the excess of unbound conformations.

Experimental Methods

A flowchart of the simulation protocol is provided in the Supporting Information as Supporting Figure 1. A summary of simulations is provided in Table 1. Starting structures for simulations were taken from the first model of the NMR ensembles of SLV: 1TBK (MgFree) and 1YN2 (MgBound).^4,5 Structures were solvated with TIP3P water in an octahedral box.¹⁷ The RNA, without the ions that were present in the pdb file, was placed with a buffer of 12 Å of water, resulting in the addition of ∼5800 water molecules. For the MgBound systems eight Mg²⁺ ions were added back to neutralize the system charge, and five additional MgCl₂ molecules were added to generate an ∼40 mM excess Mg²⁺ concentration. For the MgFree systems 16 Na⁺ ions were added to neutralize the system charge and six additional NaCl molecules were added to generate an ∼50 mM excess Na⁺ concentration. All ion initial positions were randomized with placement at least 6 Å from the RNA and at least 4 Å from each other by swapping positions with random water molecules. Joung–Cheatham parameters were used for monovalent ions and Allner et al. parameters were used for Mg²⁺.^18,19

Table 1. Summary of MD Simulations Performed in This Work.

starting RNA structure	ions added	nomenclature	figure
Rerefinement
1TBK models 2–11	20 Na+, 4 Cl–	rerefined MgFree ensemble	Figure 2b
Long MD Simulations −10 × 250 ns Simulations for Each System
1TBK model 1	20 Na+, 4 Cl–	n/a	Supporting Figure 2
rerefined 1TBK, all 10 models	20 Na+, 4 Cl–	MgFree + 50 mM NaCl	Figure 2b; Figure 3c,g; Figure 4, blue; Figure 6, red
1YN2 model 1	20 Na+, 4 Cl–	MgBound + 50 mM NaCl	Figure 3a,e
1YN2 model 1	12 Mg2+, 4 Cl–	MgBound + 40 mM MgCl2	Figure 3b,f; Figure 4, black and red; Figure 6, black
rerefined 1TBK, all 10 models	12 Mg2+, 4 Cl–	MgFree + 40 mM MgCl2	Figure 3d,h
Replica Exchange Simulation: 48 replicas × 1.2 μs per Replica
rerefined 1TBK, model 1	20 K+, 4 Cl–	MgFree + 50 mM KCl	Figure 6, blue

Simulations were carried out using the Amber12 and developmental versions of the Amber14 suite of programs^20,21 using the GPU (CUDA) version of PMEMD with SPFP (a mixed single/fixed precision model on the GPU).²² The ff12 force field for nucleic acid simulations was used, combining ff99 + parmbsc0 modifications + chiOL3 modifications for RNA.^14,23−25 Periodic boundary conditions were used in all simulations, and the particle mesh Ewald method, with default parameters, was used to handle electrostatic interactions with a 9 Å cutoff for direct interactions.²⁶

As presented in the PDB, the original NMR structures of SLV ± Mg²⁺ were described by an ensemble of 10 structures consistent with the NMR constraints. Our initial simulations used model 1 of each ensemble as a starting structure, and to evaluate experimental variability, 10 simulations were produced from that model 1, with different initial velocities (via randomized random number generator seeds using the ig = −1 option in AMBER) as well as different randomized initial ion positions.²⁷ Minimization and equilibration procedures were the same as previously used.²⁸ In brief, the initial minimization of coordinates and heating to 300 K were followed by successive rounds of minimization and equilibration performed with decreasing positional restraints (from 5 kcal mol^–1 Å^–2) on the RNA. The system was determined to be equilibrated when the potential energy, density, and pressure of the system stabilized.

Unrestrained production MD simulation runs of 250 ns were begun from these equilibrated systems, and the properties of the RNA and ions were measured from this portion of the trajectory. Production runs were constant volume and temperature; temperature was set to 300 K and regulated using the Langevin algorithm with a collision frequency of 5 ps^–1.²⁹ Bonds to hydrogen were constrained using the SHAKE algorithm, allowing use of a 2 fs time step.³⁰

The instability of the SLV RNA in 50 mM NaCl simulations described above led us to rerefine the 1TBK NMR structure in explicit solvent using the published NMR restraint data. Rerefinement simulations were carried out in 50 mM NaCl, with equilibration as described above for models 2 through 11 of the original ensemble (10 structures total). In addition to positional restraints, NMR experimental NOE distance restraints were applied to the RNA. Reported NMR restraints in DYANA format were translated into Amber format using the makeDIST_RST program, totaling 553 restraints; 527 distance restraints with a force constant of 20 kcal mol^–1 Å^–2 and 26 torsion angle restraints with a force constant of 500 kcal mol^–1 rad^–1 were used throughout equilibration and rerefinement unless otherwise noted. Equilibration was performed as previously described. Restrained simulations were run for 20 ns at constant temperature and pressure. Temperature was regulated using a Langevin thermostat and a 1 ps^–1 collision frequency.²⁹ The pressure coupling time constant was set to 5 ps. The position of the center-of-mass of the molecule was reset to zero every 10 ps.

To analyze the ensemble of 10 SLV structures in the restrained rerefined simulations, the CPPTRAJ analysis program from AmberTools was used to cluster the structures with a hierarchical agglomerative algorithm on all heavy atoms using an epsilon value of 1.0 Å with a sieve of 5 frames (Supporting Script 1).^31,32 The representative structure from the largest cluster in each of the 10 trajectories was minimized using 1000 steps of steepest descent followed by 1000 steps of conjugate gradient, with restraints intact to allow structures to relax with respect to the NMR restraints. Each minimized structure was subsequently subjected to heating and annealing over 4 ns, followed by 6 ns restrained NPT dynamics (Supporting Script 2). During this step coupling to the heat bath was lowered to 0.5 ps. Temperature was increased linearly from 300 to 700 K over 1 ns, held constant at 700 K for 1 ns, and then reduced linearly to 300 K over 2 ns. The NMR restraints were lowered to 80% of their strength for the first 1.5 ns, and then linearly increased to 100% over the next 500 ps, and remained at 100% strength for the duration of the simulation. Average structures were generated from the last 6 ns of the trajectory.

The new average structures were used to start a second series of 250 ns unrestrained production runs. Production MD simulation runs were performed for every model in the new ensemble, with constant pressure and volume. Temperature was set to 300 K and regulated using the Langevin algorithm with a collision frequency of 5 ps ^–1.²⁹ Bonds to hydrogen were constrained using the SHAKE algorithm, allowing use of a 2 fs time step.³⁰

We did not rerefine the NMR structures where Mg²⁺ was present, since model 1 from 1YN2 was stable in the 10 initial 250 ns simulations. To separate the representative structures present in the bimodal distribution of Mg²⁺-bound SLV RNA, kmeans clustering was used to group structures into two clusters from all snapshots with an RMSD to the MgBound reference below 2.5 Å (Supporting Script 5). Clustering was performed on the heavy atoms of residues U₆₉₅ to A₇₀₁, including the loop and its closing base pair (Supporting Script 6).

Temperature replica exchange MD simulations were performed to enhance the sampling space accessible to the MgFree RNA in the presence of monovalent ions. Model 1 of the MgFree NMR ensemble 1TBK was solvated with TIP3P water in an octahedral box.¹⁷ The RNA was placed with a buffer of 9 Å of water, resulting in the addition of 3953 water molecules. Sixteen K⁺ ions were added to neutralize the system charge and six additional KCl molecules were added to generate an ∼50 mM excess K⁺ concentration. All initial ion positions were randomized with placement at least 6 Å from the RNA and at least 4 Å from each other by swapping positions with random water molecules. Joung–Cheatham parameters were used for monovalent ions.¹⁸

Simulations were carried out using the Amber12 and developmental versions of the Amber14 suite of programs^20,21 using the GPU (CUDA) version of PMEMD with SPFP (a mixed single/fixed precision model on the GPU).²² The ff12 force field for nucleic acid simulations was used, which combines ff99 + parmbsc0 modifications + chiOL3 modifications for RNA.^14,23−25 Simulations were run with Watson–Crick restraints on the stem (residues 690–694 and 702–706), enhancing sampling of the five loop residues and closing base pair only (residues 695–701), and allowing a smaller solvent box. The restraints were enforced during minimization and equilibration using a force constant of 20 kcal mol^–1 Å^–2. Minimization and equilibration were performed as previously described.²⁸

For the T-REMD simulations, 48 temperatures spanning 277 to 400 K were carried out in the NVT ensemble using the pmemd.cuda.MPI module of AMBER 14.³³ The Langevin thermostat was used to regulate temperature with a collision frequency of 5 ps^–1.²⁹ The particle mesh Ewald method, with default parameters, was used to handle electrostatic interactions with a 9 Å cutoff for direct interactions.²⁶ The “ig = −1” option was set to generate random seeds for each restart, avoiding synchronization effects.²⁷ Exchanges were attempted every 1 ps. Repartitioning of the solute hydrogen masses to 3.07 au was performed by decreasing the mass on atoms to which the H is bonded by a respective amount, allowing a 4 fs time step.³⁴ SHAKE was used to constrain bonds to hydrogens.³⁰ Each replica was run for ∼1.2 μs.

Results were plotted using Grace or Microsoft Excel. The sorting of replica trajectories and all analysis was performed using CPPTRAJ and visualized in VMD. Grid density analysis was performed for Mg²⁺ ions, and the histogram of the ions was calculated with a grid spacing of 0.5 Å and normalized by ion density (Supporting Script 3). Hydrogen bond analysis was performed setting the cations as solvent acceptors and the entire RNA as solvent donors, using a distance cutoff of 4.5 Å (Supporting Script 4).

Results

Simulations of MgFree SLV Deviate from the NMR Structure

The NMR structure of SLV in 50 mM NaCl found that the canonical U-turn characteristics were absent, although stacking of G₆₉₇A₆₉₈C₆₉₉ was observed. Ten 250 ns length-independent MD simulations were carried out in 50 mM NaCl, starting from model 1 of the NMR ensemble (1TBK), each with a different random starting velocity as well as different randomized ion positions. The all-residue RMSD for each simulation was calculated with reference to the model 1 starting structure; Supporting Figure 2 shows that the heavy atom RMSD can be attributed mainly to flexibility seen in the loop region, since the stem RMSD remains consistently around 2.5 Å for the duration of the simulations. The base stacking of the G-A-C triplet was disrupted, and the G₆₉₇ alpha torsion angle of 116° was not stable (Supporting Figure 3). To test the influence of that torsion angle on the loop structure, it was restrained in a separate 100 ns length MD simulation that started from model 1. The resulting trajectory did not show an improvement in the stability of the loop structure, however, and its RMSD from the starting structure was not reduced suggesting that deviation from the extreme alpha angle of 116° was not the root cause of instability of the loop structure (Supporting Figure 4).

Overall, the resulting MD simulation structures were more compact with respect to the much extended initial NMR ensemble. Supporting Figure 5 shows decreased major groove distances across the loop and stem compared to the same distances in the NMR ensemble. We hypothesize this is due to the inclusion of an electrostatic component in the force field that was absent during the original refinement. To better understand the structure, we rerefined the original MgFree (1TBK) structure using the NMR data in the presence of explicit solvent, counterions, the excess ion environment, and with a proper treatment of the electrostatics.

Rerefinement Results in Two Distinct Conformations Which Equally Satisfy NMR Restraints and Have Properties of the MgBound NMR Ensemble

The NMR structure was originally refined in vacuo with XPLOR using a simplified version of the CHARMM force field that omitted the attractive van der Waals and the proper electrostatic contributions.⁴ We have previously seen that using explicit water and ions, together with more complete force field parameters (that is, with electrostatic and attractive van der Waals force field components included in addition to explicit solvent and counterions) can improve refinement of structures from NMR data.^28,35 Each of the 10 structures in the MgFree NMR ensemble was rerefined as described in the Experimental Methods. From each of the final 6 ns of restrained simulations, which started from each of the rerefined structures, a new average structure was calculated. These minimized average structures make up the “new” rerefined NMR ensemble, and are shown in Figure 2. Deviations from the experimental restraints were calculated using the sander module in AMBER (employing the pencut = −1 input flag for analyzing all restraints), and are shown in Table 1. The members of the rerefined ensemble are in good agreement with the experimental distance and torsion restraints, and are more similar to their minimized average structure, suggesting that the structure determination was more consistent.

Figure 2.

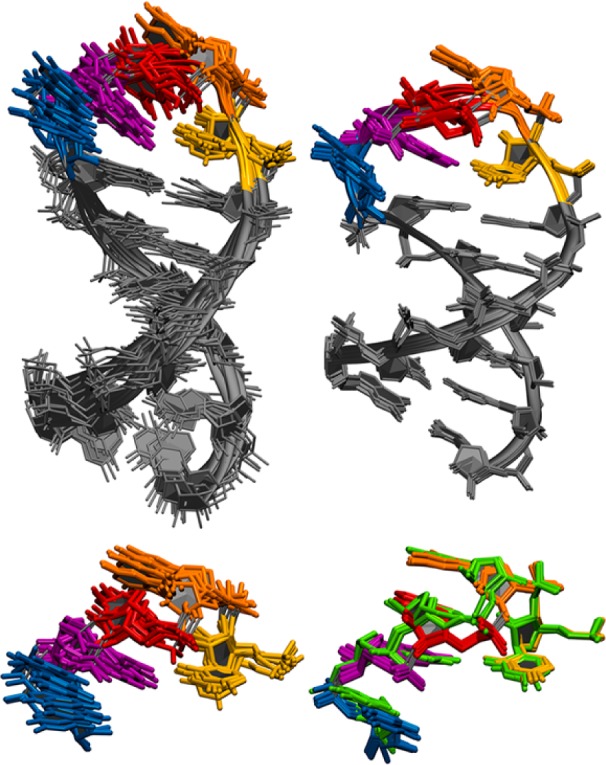
Rerefinement of SLV in 50 mM NaCl. Top: Original NMR ensemble (left, models 1–10 from pdb 1TBK) and minimized average structures from the rerefined NMR ensemble (right). Loop resides U₆₉₆ to U₇₀₀ in color. Bottom: U-turn loop residues in the original ensemble (left) and after rerefinement (right). Each ensemble is RMS fit on all heavy atoms. Three of the rerefined average minimized structures deviate from the rest of the ensemble and are highlighted green.

The rerefined ensemble contains two main conformations, shown in Figure 2, bottom right, and described in Table 2. Conformation 1 is the dominant conformation, adopted by 70% of the final ensemble, and Conformation 2 is the less dominant conformation, adopted by 30% of the final ensemble (Figure 2, highlighted in green). The characteristic U-turn features of the original NMR ensemble, the original MgBound NMR ensemble (1YN2), the rerefined ensemble, and Conformations 1 and 2 are reported in Table 3. Conformation 1, with its G₆₉₇ α torsion angle of 139°, is more comparable to the original NMR structure with its G₆₉₇ α torsion angle of ∼116°, while Conformation 2 adopts a more canonical U-turn α torsion angle of 154°, closer to the MgBound ensemble. For perspective, most canonical U-turns adopt α torsion angle values from 160° to 170° (Supporting Table 1). An exception is HIV-1 A-rich hairpin loop which adopts an average α torsion value of 135°, which is very similar to the rerefined value of Conformation 1.

Table 2. NOE and RMSD Analyses for SLV Ensembles with Na⁺ Ions.

total no. of restraints =553	original NMR	rerefinement
Deviation from Experimental Restraints
NOE (Å)	0.00029 ± 0.0004a	0.0013 ± 0.0002
torsion (deg)	0.0082 ± 0.0051	0
number of NOE deviations	16.9 ± 2.9	11.2 ± 2.0
number of NOE deviations >0.1 Å	0	2.4 ± 0.8
number of torsion deviations	2.7 ± 1.7	0
number of torsion deviations >0.5 Å	0	0
RMS Deviation from Ideal Geometry
bonds (Å)	0.0096 ± 0	0.068 ± 0.003
angles (deg)	1.70 ± 0.01	2.89 ± 0.07
Heavy Atom RMSD to Minimized Average Structure
overall (690–706, 690–705) (Å)	1.11 ± 0.14, 1.38 ± 0.57	0.46 ± 0.16, 0.56 ± 0.39
stem (690–295,701–706) (Å)	0.80 ± 0.08	0.21 ± 0.02
loop (696–700) (Å)	0.73 ± 0.08	0.43 ± 0.16

^aRecalculated using the SANDER program in AMBER12.

Table 3. U-turn Characteristics of NMR Ensembles.

U-turn characteristic:	original MgFree ensemble	original MgBound ensemble	rerefined MgFree ensemble	Conf. 1	Conf. 2
G697 alpha (deg)	116 ± 7	167 ± 34	151 ± 10	139 ± 4	153 ± 8
G697/A698 stacking (Å)	3.6 ± 0.2	4.2 ± 0.4	3.7 ± 0.1	3.7 ± 0.0	3.7 ± 0.1
A698/C699 stacking (Å)	3.7 ± 0.3	3.8 ± 0.2	3.6 ± 0.1	3.7 ± 0.0	3.6 ± 0.0
U696 N3–A698 5′phosphate stacking (Å)	not stacked: 4.2 ± 0.3	stacked: 4.2 ± 0.6	4.2 ± 0.7	4.0 ± 0.1	5.2 ± 0.2
U696 2′OH–A698 N7 h-bond (Å)	3.4 ± 0.3	2.5 ± 0.2	3.6 ± 0.6	3.8 ± 0.1	3.1 ± 0.2
U696 H3 – A698 3′phosphate h-bond (Å)	8.8 ± 0.3	5.1 ± 0.7	8.0 ± 0.5	8.0 ± 0.3	8.9 ± 0.6

Another characteristic feature of U-turns is the hydrogen bond between U 2′ OH and R N7 on the minor groove side of the loop (refer to Figure 1c,d). In SLV, this hydrogen bond between U696 2′ OH and A698 N7 is present in Conformation 2 at an average heavy atom distance of 3.1 Å, which is within error bars of the original MgBound NMR ensemble. While Conformation 1 maintains a similar geometry, it samples a longer average distance of 3.8 Å, which is more similar to the original MgFree NMR ensemble. Another attribute of U-turns is the stacking of U with the 5′ phosphate group of R. In SLV, both with and without Mg²⁺ present, these U696 and A698 5′ phosphate distances are 4.2 Å, and remain this average distance in the rerefined ensemble. However, Conformation 1 consistently adopts lower distances of 4.0 Å at which stacking interactions may occur, similar to the MgBound NMR ensemble. Conformation 2 adopts longer distances of 5.2 Å at which no stacking would occur, as in the MgFree original NMR ensemble. What we conclude from this rerefinement is that the MgFree SLV RNA can adopt some canonical U-turn characteristics and equally fulfill the experimental NMR restraints.

MD Simulations Show a Gatekeeper Conformation of MgFree SLV Enables Mg²⁺ Binding

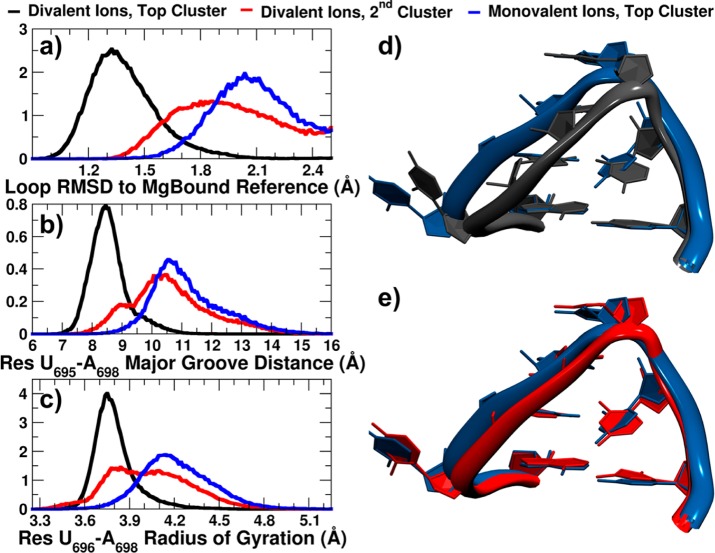
To understand the differences in dynamics of SLV when Mg²⁺ ions are either present or absent, we ran four sets of independent simulations, starting from MgBound or MgFree SLV RNA structures in the presence of monovalent or divalent ions. We started from model 1 of the MgBound NMR ensemble (MgBound starting structure) or each model of the rerefined MgFree ensemble (MgFree starting structure), and ran 10 250–300 ns length MD simulations in either 40 mM MgCl₂ or 50 mM NaCl. The RMSD correlation plots shown in Figure 3 measure the deviation from the MgBound loop (x-axis) and MgFree loop (y-axis), and are colored by the number of structures adopting a particular RMSD value. Below each correlation plot is a 1-dimensional histogram which shows each of the 10 simulations’ RMSD to the MgBound loop (x-axis). From the 1-dimensional histograms it is apparent that there is a bimodal distribution of the SLV RNA structures in the presence of 40 mM MgCl₂ with peaks centered on 1.3 and 2.0 Å. In contrast, there is a single broad distribution of SLV RMSDs to the MgBound loop structures in the presence of 50 mM NaCl centered on 2.0 Å. The SLV RNA prefers the same conformational minima when the ion environment is the same, despite the conformation of the starting structure. Interestingly, the 2-dimensional correlation plots show that in the presence of Mg²⁺, the population of lower 1.3 Å RMSD structures are directly accessible only from the 2.0 Å structures. In this way, the 2.0 Å structure is a gatekeeper, or an intermediate structure in the path to the Mg²⁺ bound loop. In the absence of Mg²⁺, the simulations show the loop populates many structures, but this gatekeeper structure represents the most populated structure. However, in the presence of Mg²⁺, the loop populates a more restricted set of structures. The gatekeeper structure is still populated, but the RNA is able to form a structure more similar to the MgBound reference with the Mg²⁺ ions present. The RNA is sampling structures that are close to the folded loop structure (i.e., the gatekeeper structure at 2.0 Å RMSD to the MgBound reference), but Mg²⁺ is required to stabilize the U-turn in its final form (i.e., at 1.3 Å RMSD to the MgBound reference).

Figure 3.

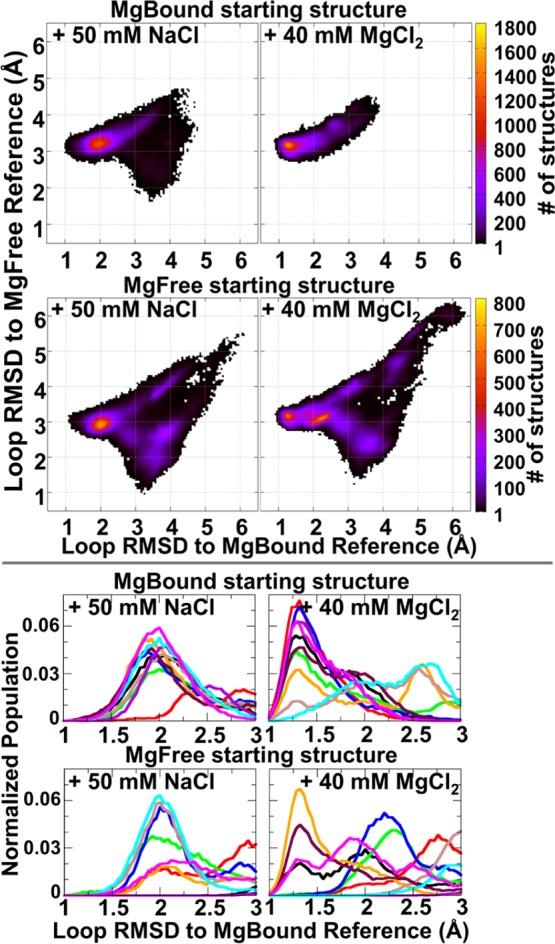
Histograms of loop RMSD to the MgBound reference structure. Top: 2-dimensional histograms of loop RMSD to the MgBound (x-axis) and MgFree (y-axis) reference structures, defined here as model 1 of 1YN2 and the average structure of the rerefined ensemble, respectively. Color range indicates the number of structures in each bin. Data collected from independent 250–300 ns MD simulations for each of 10 systems. Each system started from the MgBound reference or each member of the rerefined MgFree ensemble (labeled MgBound or MgFree, respectively), in a divalent ion environment (+ 40 mM MgCl₂) or monovalent ion environment (+ 50 mM NaCl). Bottom: 1-dimensional histogram graphs of the loop RMSD to the MgBound reference structure are close-ups of the 1.0 to 3.0 Å region of the larger plot.

We wanted to compare the 2.0 Å representative structures found in the presence and absence of Mg²⁺ to the low 1.3 Å representative structure preferred, and only seen, when Mg²⁺ is present. To do so we only considered structures with RMSDs to the MgBound loop below 2.5 Å, and split each of these structure sets by RMSD similarity into two clusters using the kmeans algorithm in CPPTRAJ (Supporting Scripts 3 and 4). Figure 4a shows the RMSD from the MgBound loop distribution for the top cluster from divalent ion simulations (black), representing the 1.3 Å structure, the top cluster from monovalent ion simulations (blue), representing the 2.0 Å gatekeeper structure, and the second cluster from divalent ion simulations (red), representing the 2.0 Å gatekeeper structure observed in simulations with Mg²⁺ present. The distance across the major groove of the loop (Figure 4b), represented by a phosphate–phosphate distance of residues U₆₉₅ to A₆₉₈, shows a shorter distance is sampled by the top divalent ion cluster, and slightly longer distances are sampled by the second cluster and the top cluster in the absence of Mg²⁺. Similarly, the radius of gyration (Figure 4c) of the UNR U-turn residues is smaller in the top divalent ion cluster, indicating a tighter U-turn in the presence of Mg²⁺. The other two clusters sample a larger radius of gyration. The representative structures for the top clusters in divalent and monovalent ions are shown overlapped in Figure 4d, and again demonstrate the more compact U-turn of the loop in the presence of divalent ions. The representative gatekeeper structures from 2.0 Å are overlapped in Figure 4e, and show a very similar looser U-turn structure.

Figure 4.

Differences in top clusters populated in monovalent and divalent ion environments. Normalized histograms of (a) loop RMSD to MgBound reference structure, (b) major groove distance, measured from phosphate atom of residue U₆₉₅ to phosphate atom of residue A₆₉₈, (c) radius of gyration of residues U₆₉₆, G₆₉₇, and A₆₉₈ phosphate groups’ center of mass. Overlap of representative structures’ loop regions from (d) top clusters from divalent (black) and monovalent (blue) ion simulations, (e) top cluster of monovalent ion simulations (blue) and second most populated cluster of divalent ion simulations (red) (gatekeeper structures). RNA was fit on stem base pair U₆₉₅–A₇₀₁.

The overall similarity between these structures can be assessed by how well they fit the MgBound NMR restraints. Table 4 shows the results of this analysis for each structure in the three clusters compared to the original MgBound NMR ensemble. Though the top cluster from the divalent ion environment showed the best fit to experiment with an 0.01 Å NOE deviation, the second divalent ion cluster and top monovalent ion cluster’s deviation of 0.02 Å were still remarkably small and very similar to each other. A detailed analysis of deviations in the loop NOEs can be found in Supporting Table 2, and shows that different NOEs are violated by each cluster. Specifically, the less compact gatekeeper loop structure had violations involving residues U₆₉₆, G₆₉₇, and A₆₉₈, again reflecting the less tight U-turn conformation.

Table 4. Top Clusters Populated in Monovalent and Divalent Ion Environments Equally Satisfy MgBound NMR Restraints.

total no. of restraints = 488	original MgBound NMR (1YN2)	top cluster, divalent ion environment	top cluster, monovalent ion environment	2nd cluster, divalent ion environment
Deviation from Experimental Restraints
NOE (Å)	0.004 ± 0.002	0.01 ± 0.08	0.02 ± 0.13	0.02 ± 0.11
torsion (deg)	0.037 ± 0.010	0.11 ± 0.51	0.07 ± 0.34	0.06 ± 0.28
Heavy Atom RMSD to Minimized Average Structure
overall (690–706) (Å)	1.11 ± 0.14	4.22 ± 0.39	3.70 ± 0.53	4.03 ± 0.53
stem (690–295,701–706) (Å)	0.63 ± 0.19	2.24 ± 0.22	2.22 ± 0.27	2.32 ± 0.27
loop (696–700) (Å)	0.64 ± 0.01	1.39 ± 0.19	2.07 ± 0.21	1.95 ± 0.27

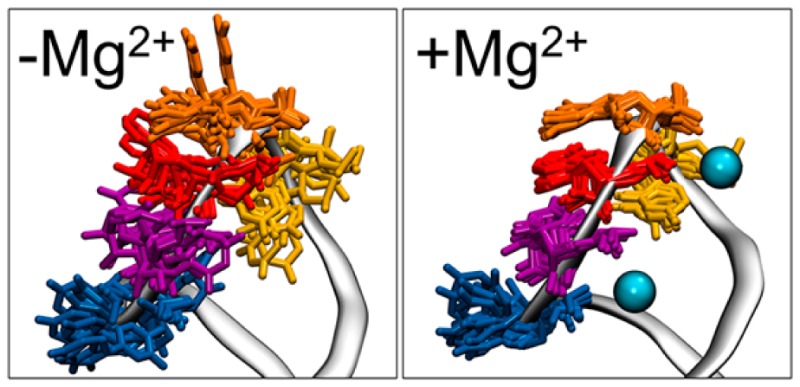
Density-based grid analysis was performed on each cluster of the divalent ion simulations to understand the different influence Mg²⁺ had on the more compact and less compact U-turn. The localization of the top 10% of Mg²⁺ ion density is reported in Figure 5 and Table 5. Figure 5 shows a significant amount of density coordinating the phosphates of the UNR motif residues. The association of Mg²⁺ in this region explains the ability of the U-turn to preferentially adopt compact structures, since charged phosphate groups are shielded from each other by the localized charge density of the Mg²⁺ ion. Interestingly, the localization of associated Mg²⁺ did not change in the second cluster from divalent ion simulations (gatekeeper structure), despite the less-compact nature of the U-turn (Supporting Figure 6). What did change was the percent occupancy, or residence time, of the associated Mg²⁺, which was far lower for most residues in the second less compact structure (and is reported in Table 5). We hypothesize that this is a result of imperfect clustering, and is a combination of Mg²⁺ ions binding and leaving rather than remaining bound for any length of time. Table 5 also identifies that the majority of density is localized in previously described binding sites 1 and 3.⁵ In the simulations starting from MgFree + 40 mM MgCl₂, Mg²⁺ binding in sites 1 and 3 correlates with RNA sampling the MgBound conformation, while binding in sites 2 and 4 does not (Supporting Figure 7). Supporting Table 3 details the percent occupancy of all atoms considered part of binding sites 1–4, and all of these sites have nonzero occupancy in the simulations.⁵ Additionally, this table shows the average distance between Mg²⁺ ions and their RNA hydrogen-bond acceptors is around 4.0 Å in each case, indicating that the Mg²⁺ ions associate with the RNA through interactions with first shell water molecules and do not directly chelate RNA phosphate oxygen atoms.

Figure 5.

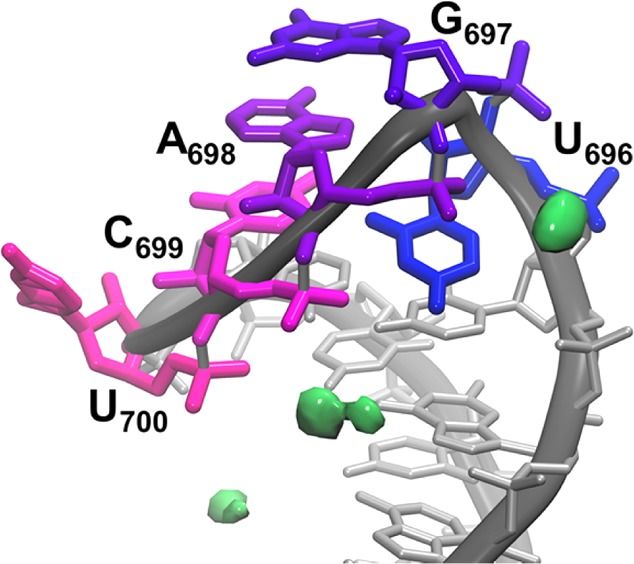
Localization of top 10% of Mg²⁺ ion density (shown in green) in the top cluster from the divalent ion environment MD simulations.

Table 5. Atoms with Mg²⁺ Ion Occupancy over 10%.

residue and atom	percent occupancy in top cluster from divalent ion environment (%)	percent occupancy in 2nd cluster from divalent ion environment (%)	part of established binding site?
U695 O4	16.9	20.5	3
U696 OP2	43.4	15.1	1
G697 OP2	5.3	14.6	no
A698 OP2	32.1	18.6	1
C699 OP1	14.1	13.2	3
C699 OP2	23.1	9.2	3
A701 OP2	10.9	9.3	no

To gain insight into the motion the SLV RNA undergoes to adopt its characteristic conformations in the presence and absence of Mg²⁺, principal component (PC) analysis was performed on three trajectories: the combined 10 simulations in the presence of monovalent ions, the combined 10 simulations in the presence of divalent ions, and the 300 K replica from temperature replica exchange molecular dynamics (T-REMD). The T-REMD was run starting from the rerefined MgFree structures in the presence of 50 mM KCl, without Mg²⁺ ions. Because of the enhanced sampling exchanges performed in T-REMD, the conformational space sampled was much larger than the 10 noninteracting simulations combined. PC projections were calculated for the combined trajectories of all systems, and each individual system was independently projected along the top two PCs, shown in Figure 6. The lowest frequency motions described by the PCs are considered relevant to function, with the higher frequency modes describing more local fluctuations.³⁶ It is apparent that the PC space sampled by the divalent ion simulations (black) is more limited than the space sampled by an equivalent amount of simulation with monovalent ions (red). The T-REMD samples a much wider range of PC space (blue) than either set of simulations. Additionally, it is important that the PC space sampled by the divalent ion simulations overlaps with that sampled by the monovalent ion simulations. This indicates that the SLV RNA is not sampling new conformational space or dynamics in the presence of Mg²⁺ ions, but rather that Mg²⁺ ions serve to limit the dynamics and conformations adopted by the SLV RNA loop.

Figure 6.

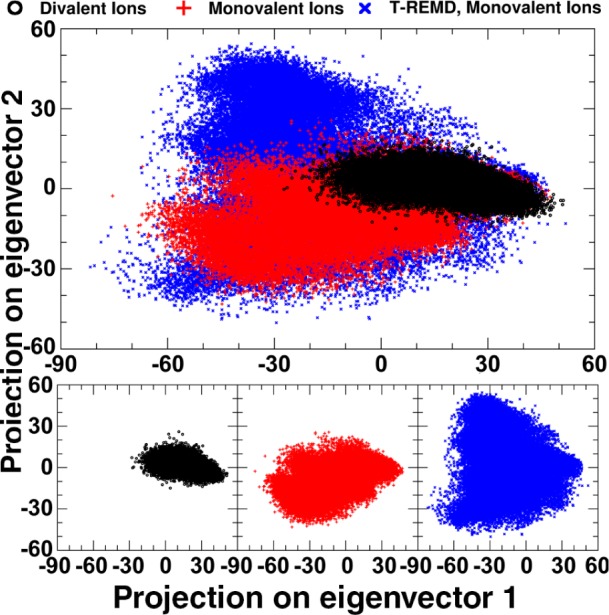
Principal Component Analysis of SLV with monovalent or divalent ions. Ten MD simulations starting from each member of the rerefined ensemble, MgFree + 50 mM NaCl (red), ten MD simulations starting from MgBound + 40 mM MgCl₂ (black), and the 300 K replica from T-REMD simulations of MgFree +50 mM KCl were combined and common principal components were calculated. The PC projection along modes 1 and 2 for each set of simulations are shown above, overlapped, as well as individually. The PC projections for divalent ions (black) overlap well with the two sets of simulations performed in a monovalent ion environment (red and blue).

Evidence Supporting the Proposed Role of the U₇₀₀ Base

The U₇₀₀ base has been proposed to play a significant role in the dynamics of SLV RNA.⁸ In the presence of Mg²⁺, the base contributes a phosphate group to a Mg²⁺ binding site, increasing the enthalpic stability of the MgBound SLV RNA.⁹ Here, we confirm this contribution of U₇₀₀ in our divalent ion simulations. Specifically, Figure 5 shows Mg²⁺ density localized around both the 5′ and 3′ phosphate groups of the U₇₀₀ backbone and Table 5 and Supporting Table 3 contain the measured percent occupancies (note that the 3′ phosphate of U₇₀₀ is equivalent to the 5′ phosphate of A₇₀₁ and is represented as such in the analysis). It was also suggested that the U₇₀₀ base could increase the dynamics of the unbound loop, providing an entropic advantage for SLI recognition.⁹Figure 7 shows the RMS fluctuations for each residue of SLV RNA in the presence and absence of Mg²⁺. The highest fluctuations in the absence of Mg²⁺ ions can be seen in residue U₇₀₀, and the largest change upon Mg²⁺ association is seen in the same residue.

Figure 7.

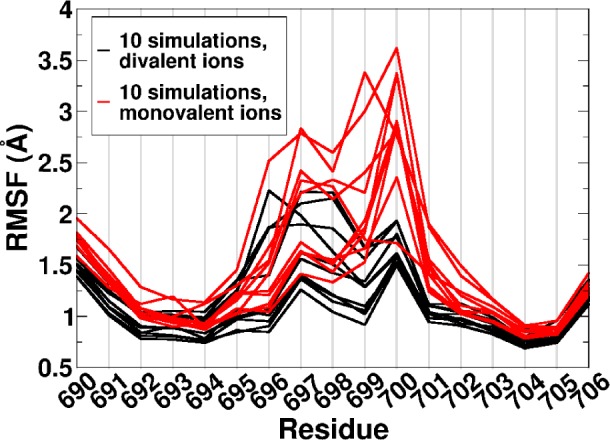
Per residue RMS fluctuations of SLV with monovalent or divalent ions. The RMS fluctuations per residue for 10 MD simulations of MgFree + 50 mM NaCl (red), 10 MD simulations of MgBound + 40 mM MgCl₂ (black) are shown. U-turn residues are 696–700.

Discussion

The Varkud satellite ribozyme SLV participates in a tertiary structure interaction that aligns the catalytic site of the RNA with its intramolecular cleavage site. In the isolated ribozyme, SLV forms a kissing complex with the loop of SLI, anchoring SLI to the ribozyme body, so the properties of SLV that allow its three GAC nucleotides to form base pairs with SLI are essential for a productive interaction. The NMR solution structure of SLV was solved based on interpretations of the NMR observables measured with and without divalent ions, and here we revisit those structures with MD simulations to describe its molecular processes in more detail.

Rerefinement of the SLV structure ensemble with a more complete description of the NMR solution environment (including ∼50 mM excess NaCl) suggested that the structures separate into two main loop conformations, each of which equally fulfill the experimental NMR restraints. These conformations have characteristics of noncanonical and canonical U-turn loops. Each conformation adopts some characteristics of the MgBound NMR ensemble, as shown in Table 3, though a single conformation does not adopt all representative U-turn characteristics.

MD simulations starting from each solution NMR structure (MgFree and MgBound) were performed in both a divalent and monovalent ion environment. Despite the starting structure, the simulations with divalent ions populated a bimodal distribution of low RMSDs to the MgBound loop, with peaks centering around 1.3 and 2.0 Å, and the simulations with monovalent ions populated a peak at 2.0 Å RMSD from the MgBound loop and did not sample lower RMSD structures. Analysis of the representative clusters in the presence of Mg²⁺ and in a monovalent ion environment show that Mg²⁺ binding is required for access to the lower 1.3 Å RMSD. Additionally, the similarity of the monovalent ion cluster and the second cluster of the divalent ion simulations tell us that this structure acts as a gatekeeper for accessing the final Mg²⁺-bound structure.

Though the subtle differences in populated structures are an influence of Mg²⁺ binding, analysis of the overall dynamics using principal components shows that the low frequency modes of motion for the SLV RNA in the presence of divalent ions is a subset of the projection seen for monovalent ions. Instead of shifting the SLV RNA to a previously unseen structure, Mg²⁺ ions instead limit the conformational ensemble and stabilize loop characteristics which are already present in the monovalent ion ensemble.

Molecular dynamics simulations have traditionally struggled to adequately describe RNA structure and dynamics, since they remain extremely sensitive to solution environment and subtle force field parameters that guide nonbonded interactions. Here, we present evidence which both qualitatively and quantitatively matches experiment. Our improved description of the ion environment adequately reproduces the subtle conformational shift seen in multiple experiments of SLV RNA.

Conclusions

Using molecular dynamics simulations of SLV RNA in the presence of divalent and monovalent ions, we are able to confirm experimental hypotheses on an all-atom level. We show that the U-turn prefers a more compact structure in the presence of Mg²⁺, effectively neutralizing the electronegative charges of the loop phosphate groups. We confirm the proposed role of the U₇₀₀ base as a contributor to Mg²⁺ binding site, and as a means to increase entropy of the unbound loop (and therefore conformational search space for its substrate SLI) in a monovalent ion environment. Additionally, we show SLV RNA preferentially samples a “gatekeeper” conformation in the absence of Mg²⁺, which is a conformational substate leading to Mg²⁺ binding and formation of the tight U-turn structure.

Supporting Information Available

The Supporting Information is available free of charge on the ACS Publications website at DOI: 10.1021/acs.jpcb.5b05190.

• Additional data, input files, analysis scripts and simulation flowchart (PDF)

• Rerefined ensemble coordinates (PDB)

The authors declare no competing financial interest.