Abstract
Microtubules (MTs) are cylindrical polymers of αβ-tubulin that display pseudo-helical symmetry due to the presence of a lattice seam of heterologous lateral contacts. The structural similarity between α- and β-tubulin makes it difficult to computationally distinguish them in the noisy cryo-EM images, unless a marker protein for the tubulin dimer, such as kinesin motor domain, is present. We have developed a new data processing protocol that can accurately determine αβ-tubulin register and seam location for MT segments. Our strategy can deal with difficult situations, where the marker protein is relatively small or the decoration of marker protein is sparse. Using this new seam-search protocol, combined with movie processing for data from a direct electron detection camera, we were able to determine the cryo-EM structures of MT at 3.5 Å resolution in different functional states. The successful distinction of α- and β-tubulin allowed us to visualize the nucleotide state at the E-site and the configuration of lateral contacts at the seam.
1. Introduction
Microtubules (MTs) are cylindrical polymers assembled from αβ-tubulin heterodimers, which pack head-to-tail to form polar protofilaments (PFs) that run along the wall of the cylinder. Around 13 PFs associate laterally to form a hollow tube. α- and β-tubulin have similar structures, and each contains a GTP binding site located at the longitudinal interface (Lowe et al., 2001; Nogales et al., 1998a). The GTP bound at the N-site (non-exchangeable) in α-tubulin is always buried at the intradimer interface and mainly plays a structural role (Menendez et al., 1998), while the GTP bound at the E-site (exchangeable) in β-tubulin is exposed in the unassembled tubulin dimer and is hydrolyzed within the MT lattice over time (Nogales et al., 1999). The GTP hydrolysis occurring at the E-site of βtubulin is fundamentally linked to a hallmark behavior of MTs termed dynamic instability (Mitchison and Kirschner, 1984), by which MTs undergo stochastic switching between phases of growth and shrinkage.
The dynamic properties of MTs are highly regulated by a number of MT-associated proteins (MAPs). End-binding proteins (EBs) are the central hub of a network of MT plus-end tracking proteins (+TIPs) that selectively localize to growing MT ends and mediate the interactions with various cellular structures, such as kinetochores, the endoplasmic reticulum or the cell cortex (Akhmanova and Steinmetz, 2008; Galjart, 2010). Recently, studies by Surrey and colleagues suggested that EBs autonomously track the MT growing ends by recognizing a specific nucleotide-dependent state of MT that is best mimicked in vitro by a GTPγS-bound MT lattice (Maurer et al., 2011). Cryo-EM studies of GTPγS MT decorated with Mal3 (EB homolog in S. pombe) (Maurer et al., 2012) or human EB3 (Zhang et al., 2015) revealed that the CH domain of EBs simultaneously interact with four tubulin subunits on the MT outer surface, at the inter-dimer interfaces and between two neighboring PFs.
Both in vivo and in vitro, the most common forms of MT have pseudo-helical symmetry, i.e. ignoring the subtle differences between α- and β-tubulin, the MT can be seen as 3-start helix of tubulin monomers (Fig. 1A). Along the 3-start helix, tubulin subunits are associated via homotypic lateral interactions, i.e., α-α or β-β contacts, except for a single site or “seam”, where α-β contact occurs (Mandelkow et al., 1986). The presence of this seam breaks the helical continuity along the 3-start helix. In order to obtain the true structure of a MT and draw meaningful biological conclusions based on important local regions, such as the nucleotide at the E-site, it is critical to determine the αβ-tubulin register and seam location for each MT segment. This task is a challenging due to the similarity between α- and β-tubulin, especially at low resolution, which usually drive image alignment in data processing. This problem can be surmounted using a marker MAP that binds every tubulin dimer, such as a kinesin motor domain, so that α-and β-tubulin can be distinguished in the noisy cryo-EM images, even at low resolution (Kikkawa, 2004; Metoz and Wade, 1997; Sosa and Milligan, 1996).
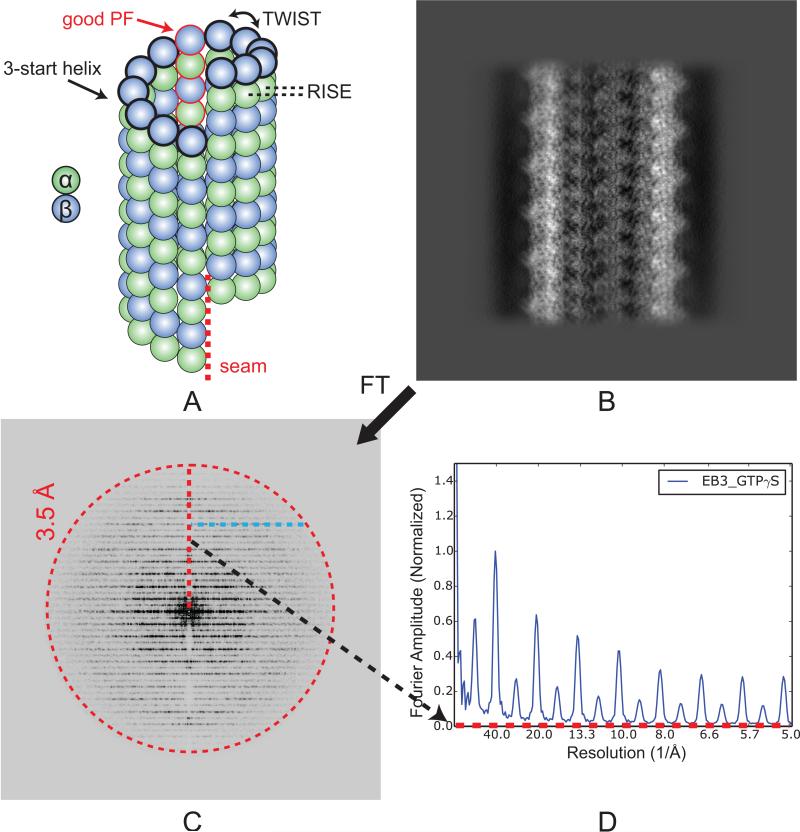
Fig. 1.
Layer line profile for 3D reconstructions of MTs. (A) Architecture of a 13-PF, 3-start helix MT showing the seam. The tubulin with black thick outlines depicts the 3-start helix, with helical parameters (TWIST and RISE) indicated. The PF with red outlines is the good PF in our data processing scheme. (B) Projection of the EB3-GTPγS MT reconstruction after applying pseudo-helical symmetry, along the direction perpendicular to the MT axis. (C) 2D Fourier transform of (B). The red, dashed circle at 3.5 Å resolution indicates the low pass filter applied to the 3D reconstruction. (D) 1D layer line profile of (C). The x-axis corresponds to the red dashed line in (C). The y-axis is the averaged amplitude over all pixels with the same y coordinate (cyan dashed line in (C)), from the central meridian line to a certain resolution shell.
Recently, the Iterative Helical Real Space Reconstruction (IHRSR) method (Egelman, 2000) has been applied to kinesin-decorated MTs with a seam to obtain structures at sub-nanometer (Sindelar and Downing, 2007) or even higher resolution (~5 Å) (Alushin et al., 2014; Shang et al., 2014). This approach determines the seam location for each MT segment based on the cross-correlation values between the raw images and projections of a reference model. In the case of MT well decorated with kinesin, a consensus seam location can be typically obtained for the majority of the segments from the same MT. However, in situations where the kinesin decoration is sparse or the protein marker is relatively small, such as for doublecortin (Liu et al., 2012) or the CH domain of Mal3 (Maurer et al., 2012) or EB3 (Zhang et al., 2015), a simple projection matching based method often fails to find a clear peak of cross-correlation values for a certain MT segment across all the candidate seam locations or ultimately fails to reach a consensus seam location for segments from the same MT.
Here we present a general MT data processing protocol that includes two new seam-search strategies specifically designed to utilize the signal in the raw images originating from the ~80Å tubulin dimer repeat. Using this seam-search protocol, combined with movie for data from a direct electron detector, we have recently determined cryo-EM structures of MTs at 3.5 Å resolution in six different states (Zhang et al., 2015), including kinesin decorated GMPCPP and GDP MTs, EB3 decorated GTPγS, GMPCPP and GDP MTs, as well as EB3 and kinesin co-decorated GTPγS MT. We refer to these six MT structures as GMPCPP-K (K stands for kinesin decoration), GDP-K, EB3-GTPγS, EB3-GMPCPP, EB3-GDP and EB3-GTPγS-K MTs. Due to the effect of EB3 on the MT lattice, all MTs obtained by coassembly with EB3 are almost exclusively 13-PF MTs, while other PF numbers co-exist for MTs polymerized in the absence of EB3.
2. Methods
2.1 Cryo-EM data collection
Microtubule samples with either kinesin or EB3 decoration were prepared as previously described (Alushin et al., 2014; Zhang et al., 2015). Cryo-EM grids were mounted onto a 626 side-entry cryo-transfer holder (Gatan) and transferred into a Titan microscope (FEI) operated at an accelerating voltage of 300 kV. The microscope was carefully aligned to minimize astigmatism and coma (Glaeser et al., 2011). The sample was imaged under parallel illumination conditions, with a beam diameter of ~2 μm on the specimen. A defocus range from −1.2 to −3.5 μm was used. All cryo-EM images were recorded on a K2 Summit direct electron detector camera (Gatan) at a nominal magnification of 27,500×, corresponding to a calibrated pixel size of 1.32 Å. The camera was operated in counting mode, with a dose rate of ~8 electrons/pixel/s on the camera. A total exposure time of 6 s, corresponding to an accumulative dose of 27.6 electrons/Å2 on the specimen, was fractionated into 20 movie frames, with 0.3 s exposure time and a dose of 1.37 electron/Å2 for each frame. The data were collected semi-automatically using the Leginon software suite (Suloway et al., 2005). Drift correction for movie frames was performed using the UCSF motioncorr program (Li et al., 2013). The parameters of the contrast transfer function (CTF) were estimated from the drift-corrected micrographs using CTFFIND4 (Rohou and Grigorieff, 2015).
2.2 General workflow for MT reconstruction
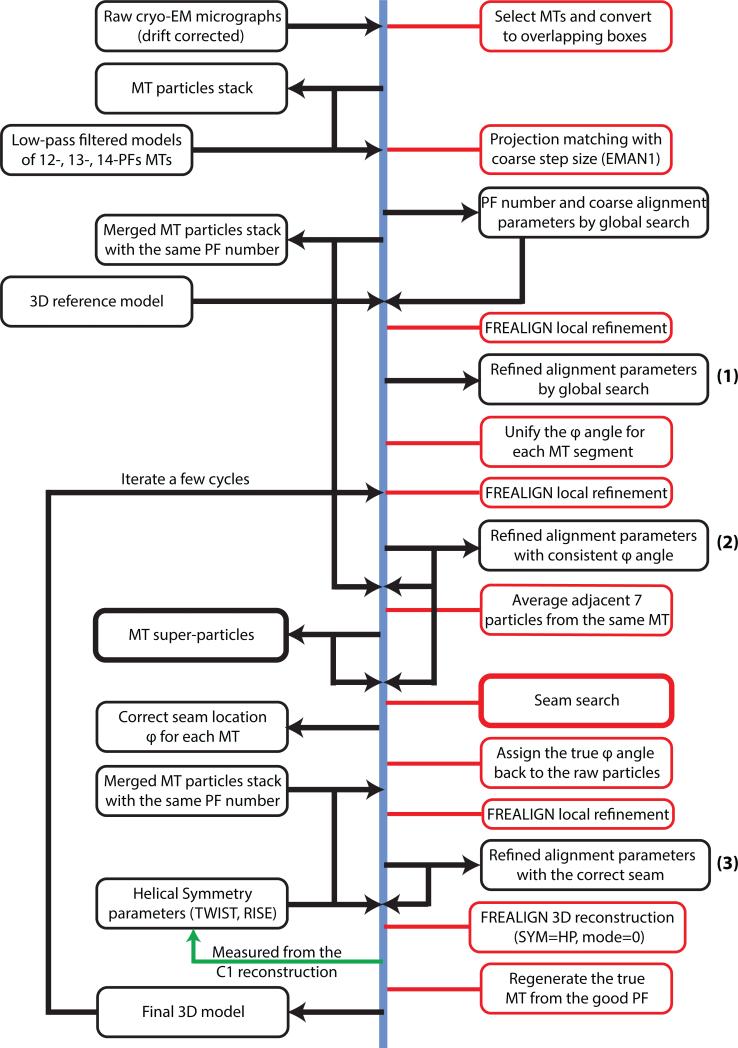
Our general MT reconstruction strategy (Fig. 2) uses the IHRSR algorithm, with modifications specific for MTs (Alushin et al., 2014; Sindelar and Downing, 2007). First, MT segments are manually selected from the drift-corrected micrographs using the APPION image processing suite (Lander et al., 2009). The MT selections are converted to overlapping boxes (512 × 512 pixels) for particle extraction. The non-overlapping region between adjacent boxes is set to be 80 Å, which corresponds approximately to the tubulin dimer repeat. As a result, each MT particle contains ~13 or 14 unique tubulin dimers (asymmetric units) in the non-overlapping region. The raw particle stacks are then compared to projections of low-passed filtered MT models having 12, 13, 14 and 15 PFs, in order to determine the initial global alignment parameters and PF number for each MT particle. This multi-reference alignment (MSA) is carried out using EMAN1 (Ludtke et al., 1999), with a coarse angular step size of 4° while making projections. Subsequently, MT particles with the same PF number are merged and further refined in FREALIGN version 9 (Grigorieff, 2007; Lyumkis et al., 2013). Only local refinement is performed (mode 1 in FREALIGN), followed by 3D reconstruction (mode 0 in FREALIGN) assuming either pseudo-helical symmetry (SYM = HP) (see later for details concerning the special case of the MT) or no symmetry (C1) (SYM = 0). The only difference is whether each raw particle is used only once (C1) or 13 times (HP) during the reconstruction step. The locally refined alignment parameters are also used to determine the seam location for each MT (see Sections 3.1 and 3.2).
Fig. 2.
General protocol for MT data processing. Images, 3D structures and associated metadata are in black rectangles, while human or computer operations are in red rectangles.
The helical parameters (TWIST and RISE) for the 3-start helix of tubulin monomers (Fig. 1A) are precisely measured using the hsearch_lorentz program (Egelman, 2000) from the C1 reconstruction obtained with FREALIGN. We find that these helical parameters are quite robust with respect to the initial model (see Section 3.5). Due to the presence of the seam, application of pseudo-helical symmetry using FREALIGN (SYM = HP) results in a MT reconstruction that contains only one “good” PF (Fig. 1A) for which there is no mismatch of α- and βtubulin after the helical symmetrization (Alushin et al., 2014; Sindelar and Downing, 2007). Using a customized python script, this good PF is cut out from the reconstruction by applying a wedge-shaped mask, and is then used to regenerate the true MT structure with a seam, based on the helical symmetry for the 3-start helix. In the case of EB-bound MT structures, an additional soft-edged cylindrical mask, whose axis is located at the seam location, is applied to remove the majority of the EB densities at the seam. This pseudo-helical structure serves as the reference model for the next round of refinement in FREALIGN.
In addition to the drift-correction performed on the entire micrograph (Li et al., 2013), we attempt to track the independent movement of each MT particle during the 20 movie frames recorded. Movie data processing for individual particle has become a standard practice in the cryo-EM field (Bai et al., 2013; Campbell et al., 2012), and it was critical for us to obtain the final 3.5 Å resolution MT structures. In practice, we find that the signal for a MT particle from four consecutive movie frames (corresponding to a dose of 5.5 electron/Å2) is minimally required for accurate alignment in FREALIGN. As a result, we split each MT particle into four “sub-particles”, each containing signal from four consecutive movie frames (frames 2-5, 6-9, 10-13, and 14-17 out of a total of 20 frames, with the first one being omitted due to particularly large beam-induced movement, and the last ones due to radiation damage). After independent local refinement of these sub-particles, including local translational and rotational searches, a final 3D reconstruction is done in FREALIGN using all four sets of sub-particles, resulting in further resolution improvement.
The 2D Fourier transform (FT) of a projection of the MT reconstruction (along the direction perpendicular to the MT axis) (Fig. 1B) shows the characteristic layer line pattern at ~40 Å spacing for undecorated MTs and additional layer lines at ~80 Å spacing for MT decorated with kinesin or EB3 (Fig. 1C) (Amos and Klug, 1974; Metoz and Wade, 1997). We find it very useful to examine the plots of layer line profiles of a MT 3D reconstruction (Fig. 1D), by averaging the amplitudes over all the pixels with the same y-coordinate in the FT of the 2D projection, from the central meridian line to a certain resolution shell (Fig. 1C, cyan line). We use these layer line profiles at different data processing stages for assessment and comparison purposes. Due to the very small helical supertwist (see description in Section 2.3) for 13-PF and 14-PF MTs, the peaks in the layer line profiles are typically very sharp, allowing clear separation of peaks for MT reconstructions with slightly different axial lattice spacing. To allow direct comparison between different reconstructions, we normalize the amplitude profile so that the amplitude of the 40 Å layer line (corresponding to the tubulin monomer repeat) is always 1.
2.3 The five alignment parameters of a raw MT particle and the idea of “super-particle”
To orient a raw MT particle image with respect to the 3D reference model, five alignment parameters are needed: x, y translations (shx, shy) and three Euler angles (Ψ, θ, φ, FREALIGN convention). In the context of a helical object, Ψ is the in-plane rotation, θ is the out-of-plane tilt, and φ is the azimuthal angle around the MT axis (Table 1). It is usually easy to determine the Ψ and θ angles by projection matching, and any misalignments can be identified using internal restraints, i.e., particles from the same filament have very similar Ψ and θ angles, and θ should be close to 90°. For a helical object, the shx and shy are related to the φ angle by the simple formulas:
| (1) |
| (2) |
where (TWIST,RISE) are the helical parameters that define the rotation and translation needed to align one subunit to the next one along the helical path. In the general IHRSR algorithm it is desirable to adjust the alignment parameters by expressing the majority of x, y translations as φ changes using Eq. (1-2), so that the residual x, y translations are within half the RISE (Sachse et al., 2007). However, this operation is not valid for a MT, and must be turned off (by specifying SYM = HP in FREALIGN v9, instead of SYM = H), since a MT is not a true helix but rather a C1 object due to the presence of the seam. In other words, unlike a helical object with multiple symmetrically equivalent φ angles, each MT particle has only one unique φ that defines the seam location.
Table 1.
The definition of the three Euler angles in the context of a helical object.
| Name (FREALIGN convention) | Equivalent in EMAN convention | Definition in the context of a helical object |
|---|---|---|
| Ψ | phi | In-plane rotation |
| θ | alt | Out-of-plane tilt |
| φ | az | Azimuthal angle around the helical axis |
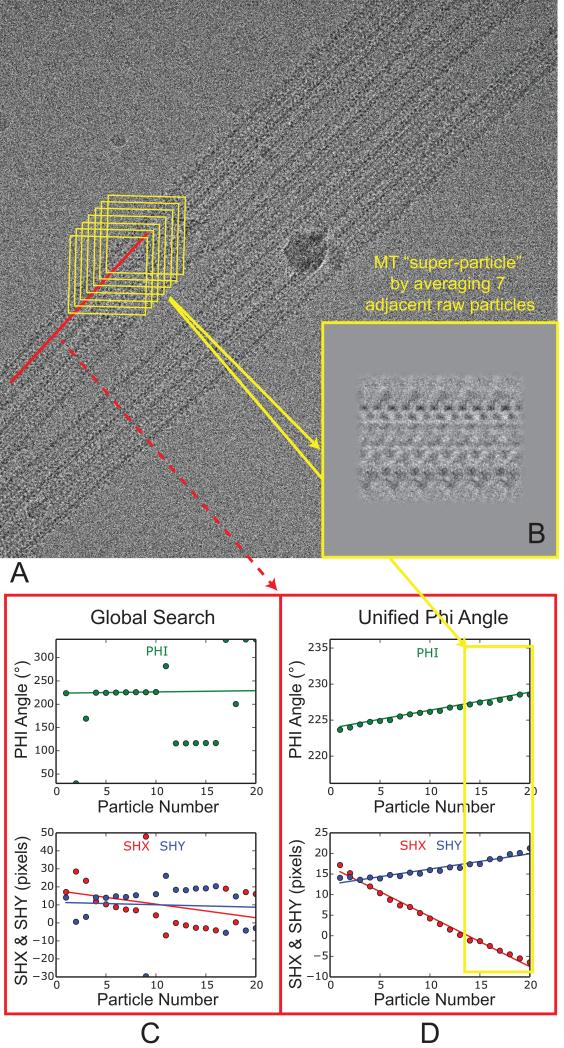
Because in a MT protofilaments (PFs) run approximately parallel to the MT axis, neighboring MT particles boxed from the same MT typically correspond to similar views. On the other hand, due to the fact that the PFs do not run exactly parallel to the MT axis, MTs exhibit a helical supertwist that generates the classical moiré patterns seen over long distances (Chretien et al., 1996; Mandelkow and Mandelkow, 1985). In the case of 13-PF MT, this supertwist is minimal, so the plot of φ angles of all the particles from the same MT within an image follows a straight line with a slope close to zero. The slope is larger for MTs with other PF numbers, e.g. 12 or 14. By dividing a MT into short segments, e.g. every seven neighboring MT particles (Fig. 3A, yellow boxes), the views of these particles are similar enough to allow local averaging, which greatly improves the signal-to-noise ratio (SNR). We refer to the averaged particles as a “super-particles”. In this way, every MT in an image can be represented by only a few non-overlapping super-particles, which can be treated as raw MT particles to perform standard projection matching. When computing each super-particle, the possible curvature of the MT within the image plane was largely corrected by using the measured Ψ angle (in-plane rotation) for each raw MT particle.
Fig. 3.
Procedure to compute MT super-particles. (A) A typical cryo-EM image of EB3-GTPγS MT, after drift correction. The red line corresponds to one MT selection, which was cut into overlapping boxes in yellow. The non-overlapping region between adjacent boxes is set to be 80 Å, which corresponds approximately to the tubulin dimer repeat. (B) The insert shows an averaged MT super-particle from the seven particles in the yellow boxes in (A). (C) Plots of φ angle and x, y translations (shx and shy) for all the 19 particles from the same MT (red line in (A)). (D) Plots of φ angle and x, y translations for the same set of particles after enforcing a consistent φ angle (unifying φ). This set of alignment parameters (φ, shx and shy) were used to compute three non-overlapping MT super-particles. One of them, calculated from the seven particles (indicated by the yellow rectangle), is shown in (B).
Due to the structural similarity between α- and β-tubulin, global search often assigns inconsistent φ angles (different views) for particles from the same MT (Fig. 3C). Based on the dependence of shx and shy on the φ angle (Eq. (1-2)), directly averaging these raw particles using their original shx and shy will lead to blurred super-particle images. To obtain the proper shx and shy for individual particles needed to compute the ‘shiny’ super-particle images, one simply needs to modify their alignment parameters so that all the raw particles from the same MT have consistent φ angles, i.e. plot of φ follows a smooth line (Fig. 3D). In practice, we first pick the consensus (most common) φ after global search, e.g., φ around 228° in Fig. 3C, then try to make the φ angle of each raw particle as close to the consensus φ as possible, by adding/subtracting multiple integer of the TWIST, and adjust the shx and shy based on the change of φ, using Eq. (1-2). Note that, for the purpose of computing shiny super-particle images, this self-consistent φ doesn't have to correspond to the true seam location, because changing the φ angles for every raw particle by the same amount won't change the appearance of the super-particle image, only causing additional shifts. We always do another round of local refinement in FREALIGN after this rough adjustment of alignment parameters using mathematic equations (Fig 2). Typically, after this “unifying-φ” step, the plot of shx or shy also follows a smooth line (Fig. 3D).
To determine the true φ angle (seam location), lets consider the case of a 13-PF MT. Assuming the polarity is correctly determined in the first place (so that Ψ is not off by ~180°), due to the similarity between α- and β-tubulin there are approximately 26 (2×13) local minima when trying to orient a raw MT particle to the 3D reference. The factor of two is due to the ambiguity when shifting the particle along the MT axis by the monomer repeat of ~40 Å, while the factor of 13 is due to the 13-fold ambiguity when rotating the φ angle by 27.7° (the TWIST angle between adjacent PFs, Fig. 1A). After the global search and the unifying-φ step, the set of alignment parameters obtained usually corresponds to one out of the 26 possible local minima. Using Eq. (3-6), which are special cases of Eq. (1-2), one can easily generate 26 different sets of alignment parameters corresponding to the 26 local minima, and use them to identify the true seam location (see Section 3.1 and 3.2).
| (3) |
| (4) |
| (5) |
| (6) |
where n is an integer between −6 and 6.
3. Results
3.1 Determining the seam location using 40Å monomer shifts
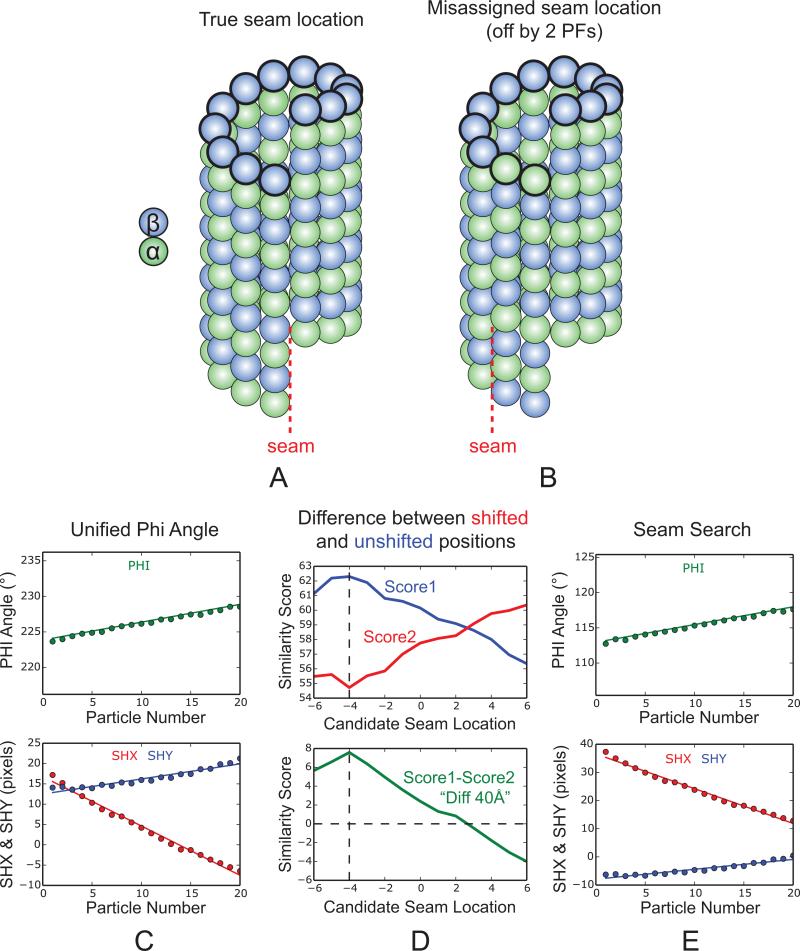
We have developed a seam-search protocol that compares each super-particle, both at 40Å-shifted and unshifted locations, with corresponding projections of the reference model along 13 different directions defined by (θ, φ), with φ being the 13 candidate seam locations. In practice, we run 26 parallel local refinements in FREALIGN, each time starting from a different set of alignment parameters that corresponds to one of the 26 local minima. Considering the scenario where the assigned φ angle happens to be the true seam location, shifting the particle along the MT axis by 40 Å (the tubulin monomer repeat) would result in a much worse similarity score with respect to the 3D reference, since α- and β-tubulin would be out of register for all the 13 PFs. However, if the assigned φ angle is off by a few PFs, e.g. by two PFs as shown in Fig. 4B, by shifting the particle 40 Å along the axis, two out of 13 PFs will actually be in register with the 3D model. The worst scenario is that the initial assignment of φ is off by six PFs, in which case the difference in similarity score between the 40 Å-shifted and unshifted positions (referred to as “DIFF40Å”) is close to zero. As a result, the plot of DIFF40Å across all the 13 candidate seam locations should resemble a bell shape, with the peak corresponding to the true seam location (the case in Fig. 4D was off by four PFs). The seam location determined using the super-particle is then assigned back to the corresponding raw particles, and their shx and shy are adjusted accordingly. After that we do another round of local refinement in FREALIGN (Fig. 4E), followed by 3D reconstruction.
Fig. 4.
Principles behind the seam-search approach using the 40 Å monomer shift. (A) Structure of a 13-PF, 3-start MT with a seam. (B) Structure of the same MT as shown in (A) but rotated around the axis by two PFs. This scenario corresponds to a raw MT particle with a misassigned seam location (off by two PFs). (C) Plots of φ angle and x, y translations (shx and shy) after the unifying φ step, same as Fig.3D. (D) Seam-search results for the EB3-GTPγS MT state obtained by comparing the differences in similarity scores between the 40Å-shifted (red) and unshifted (blue) versions of a MT super-particle (Fig. 3B) and 13 projections of the reference model, projected along different candidate seam locations (denoted by the x-axis). The plot of DIFF40Å indicates that the initial seam assignment is off by four PFs. The black dashed line marks the true seam location (x=−4), while x=0 indicates the originally assigned seam location. (E) Plots of φ angle and x, y translations after seam-search. The true seam location determined in (D) is assigned back to the corresponding raw particles, and their shx and shy are adjusted according to the change in φ, followed by another round of local refinement in FREALIGN.
This seam-search approach takes advantage of the fast local refinement in FREALIGN. First, the program quickly finds one of the 26 local minima from the starting point obtained by initial global search with a coarse angular step size. Then, it searches only within the neighborhood of the other 25 local minima, thus greatly reducing the search space. In addition, the use of MT super-particles rather than raw particles further speeds up the computation by ~ 7-fold, as well as producing improved accuracy due to the higher SNR. In this way, the very expensive process of exhaustive search is reduced to a more feasible task, i.e., the whole seam-search procedure for one dataset (~3,400 super-particles, box size 512 × 512 pixels) can be done in less than one day using a single 8-core desktop computer.
3.2 Seam-search using a simulated map of EB3 alone
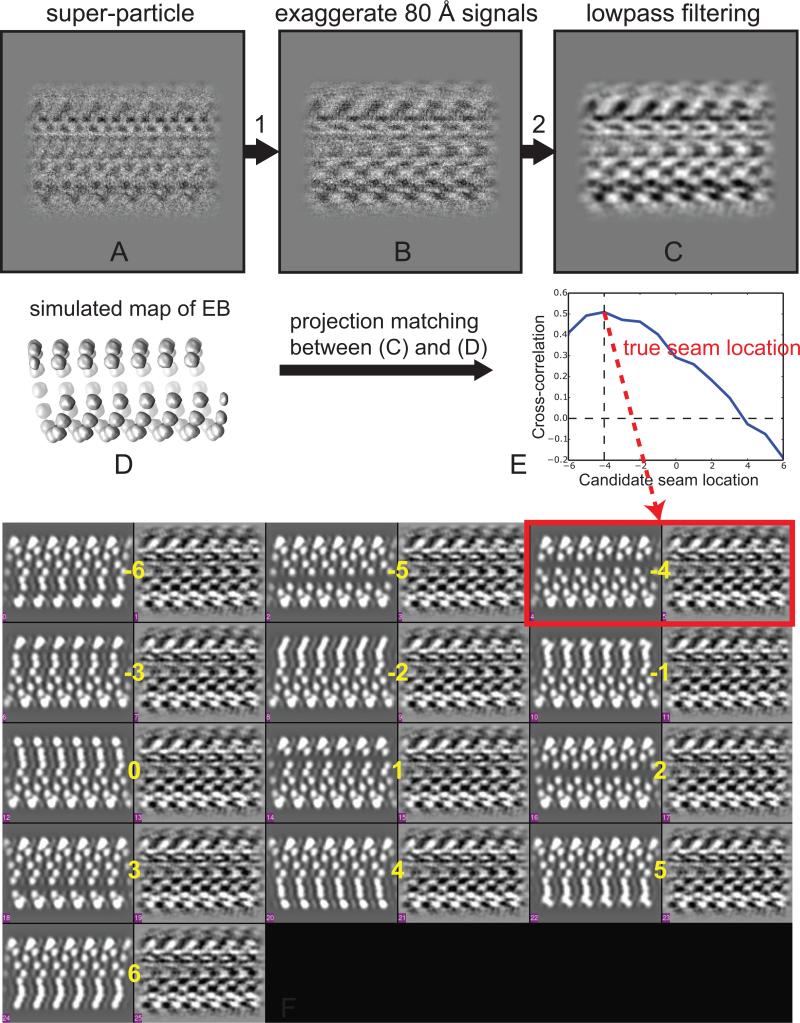
In the previous seam-search approach, all the local refinements are done using a scoring function weighted across all frequencies, which is necessary for accurate alignment. In theory, however, most of the information needed to determine the seam location is contained in the 80 Å layer line and its higher orders, which reflect the presence of the marker protein (kinesin or EB3 in the present case) binding with a tubulin dimer repeat. Signals at other frequencies are much less relevant and may bias the seam-search results, especially signal from the dominant 40 Å layer line. For this reason, we keep the original alignment parameters from local refinement using all frequencies (see Section 3.1), but modify both super-particle images and reference projections in a way to mainly focus on the signal originated from the 80 Å repeat, and re-compute the similarity scores. For the super-particle images (Fig. 5A), we multiply the amplitude of the 80 Å layer line by a factor of 2 and the amplitude of the 40 Å layer line by a factor of 0.2 (Fig. 5B). The resulting images are low-pass filtered to 20 Å to reduce the noise and aid visual comparison (Fig. 5C). For the projections, we replace the original 3D reference model with a map simulated from EB molecules alone, at the same positions as in the experimental MT map (Fig. 5D). Due to the presence of a seam, the 13 projections show different signatures, thus allowing us to identify the true seam location even visually (Fig. 5F). The computed cross-correlation coefficients between the modified super-particle images (at 40Å-shifted and unshifted locations) and the simulated projections (along 13 candidate seam locations) show a clear peak that corresponds to the true seam location (Fig. 5E) and agrees with the seam position suggested by visual comparison (Fig. 5F, red box).
Fig. 5.
Principle behind our seam-search approach using a simulated map of EB alone. (A) MT super-particle, same one as in Fig. 3B. (B) Modified super-particle of (A), by multiplying the amplitude of the 80 Å layer line by a factor of 2, and multiplying the amplitude of the 40 Å layer line by a factor of 0.2. (C) The image in (B) with a 20 Å low-pass filter applied. (D) A simulated map of EB alone, at the positions observed in the experimental MT map. (E) Seam-search result of the EB3-GTPγS MT. The y-axis is the computed cross-correlation coefficient between the modified super-particle image (C) and projections of the simulated map of EB alone (D), along 13 candidate seam locations (denoted by the x-axis). The plot shows a clear peak that corresponds to the true seam location, at x= −4. (F) Visual display of the seam-search results in (E), showing 13 pairs of projection (left) and image (right), which correspond to the 13 different candidate seam locations (marked by yellow numbers from −6 to 6). Note each super-particles image have proper translations applied, based on Eq. (1-2). One can visually identify the true seam location (highlighted in the red box) by the best match of densities among these 13 pairs. The result matches the seam assignment in (E).
By allowing direct visual inspection, this second seam-search approach was developed to validate the results obtained using the first method (see Section 3.1). In practice, we found that both approaches give very consistent results. As an example, for the EB3-GTPγS MT dataset, 88.5% of the MT segments (each corresponding to a MT super-particle) have consistent seam assignments (within +/−1PF) for the two seam-search approaches. The inconsistency of the remaining 11.5% is mostly caused by misaligned particles that produce blurred MT super-particles. In our general data processing workflow, we usually use the first seam-search approach since it is easier to implement.
3.3 The seam-search protocol improves the distinction of α- and β-tubulin in the symmetrized reconstructions
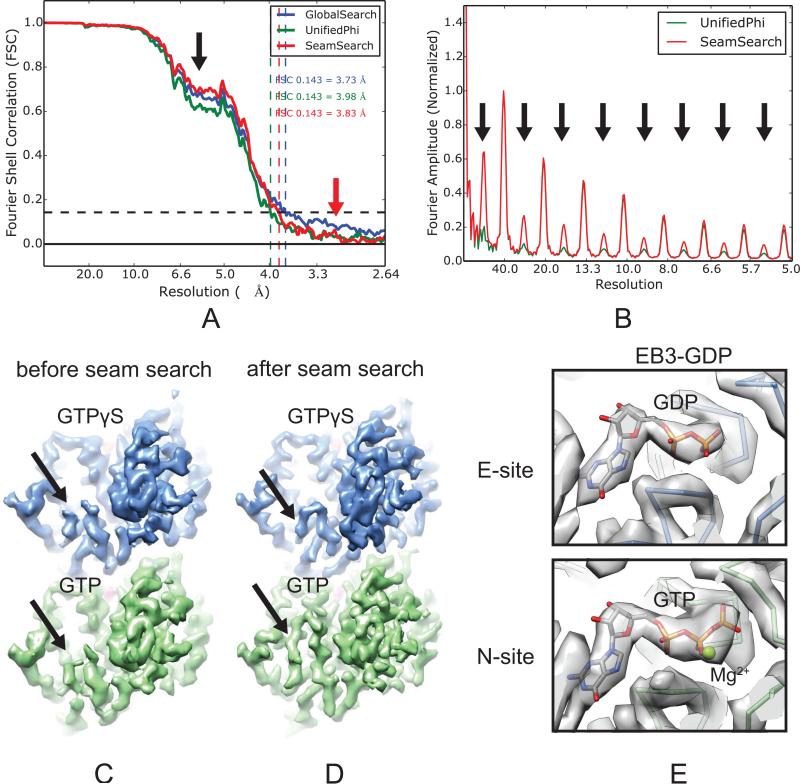
We compared the 3D reconstructions using the locally refined alignment parameters at three different data processing stages (as indicated in Fig. 2): (1) after global search, (2) after unifying the φ angles, and (3) after seam-search. Due to the structural similarity between α- and β-tubulin, and the way FREALIGN applies pseudo-helical symmetry (see Discussion), it was not surprising that our seam-search protocol did not significantly improve the overall resolution of the symmetrized reconstruction, as reported by the plot of Fourier Shell Correlation (FSC) curves (Fig. 6A). This plot, however, shows an interesting fact concerning MT data processing: before the unifying-φ step, the FSC curve (Fig. 6A, blue curve) has a more elevated baseline (Fig. 6A, red arrow) due to noise correlation between the two half maps (see Discussion). On the other hand, the plot shows a significant improvement at low resolutions after seam-search (Fig. 6A, black arrow). Most importantly, comparison of the layer line profiles (see Section 2.2) of these three reconstructions clearly shows that after the seam-search there is a significant boost of signal for the 80 Å layer line and its higher orders (Fig. 6B, black arrows), originated from the EB3 densities, as well as subtle differences between α- and β-tubulin at high resolution.
Fig. 6.
The seam-search protocol improves the distinction of [g302]- and β-tubulin in the symmetrized MT reconstructions. (A) Plot of FSC curves of symmetrized reconstructions of the EB3-GTPγS MT state at three different data processing stages. (B) Layer line profile of the reconstruction before and after seam-search. (C and D) Cryo-EM densities of the EB3-GTPγS MT before (C) and after (D) seam-search, showing the difference in the S9-S10 loop between α- and β-tubulin (black arrows). α- and β-tubulin are colored green and blue, respectively. (E) Cryo-EM densities and atomic models for the EB3-GDP MT showing the difference of nucleotides bound at the E-site (GDP) and the N-site (GTP and Mg2+).
A closer look at the fine details that distinguish α- and β-tubulin in the density map further confirms the success of our seam-search protocol. First, the cryo-EM densities of all our MT reconstructions after seam-search clearly resolve the differences in the S9-S10 loops (this loop contains an insertion in α-tubulin) (Fig. 6D, black arrows). These differences appeared averaged out in the reconstructions before seam-search (Fig. 6C, black arrows). In addition, the densities for the nucleotides in the EB3-GDP MT map show clear differences between the GDP at the E-site (after hydrolysis) and the GTP and the coordinating Mg2+ ion at the N-site (Fig. 6E).
3.4 The seam-search protocol improves the distinction of α- and β-tubulin in the C1 MT reconstructions
In our data processing protocol, due to the pseudo-helical symmetrization step used to reach higher resolution, the true seam configuration is lost. However, the seam information is present in a C1 reconstruction using the same set of alignment parameters. The main difference is that each raw particle is used only once instead of 13 times during the reconstruction step. Compared to the symmetrized reconstruction, which has more tolerance for errors in seam assignment (see Discussion), the C1 reconstruction is more sensitive to errors in seam location assignment.
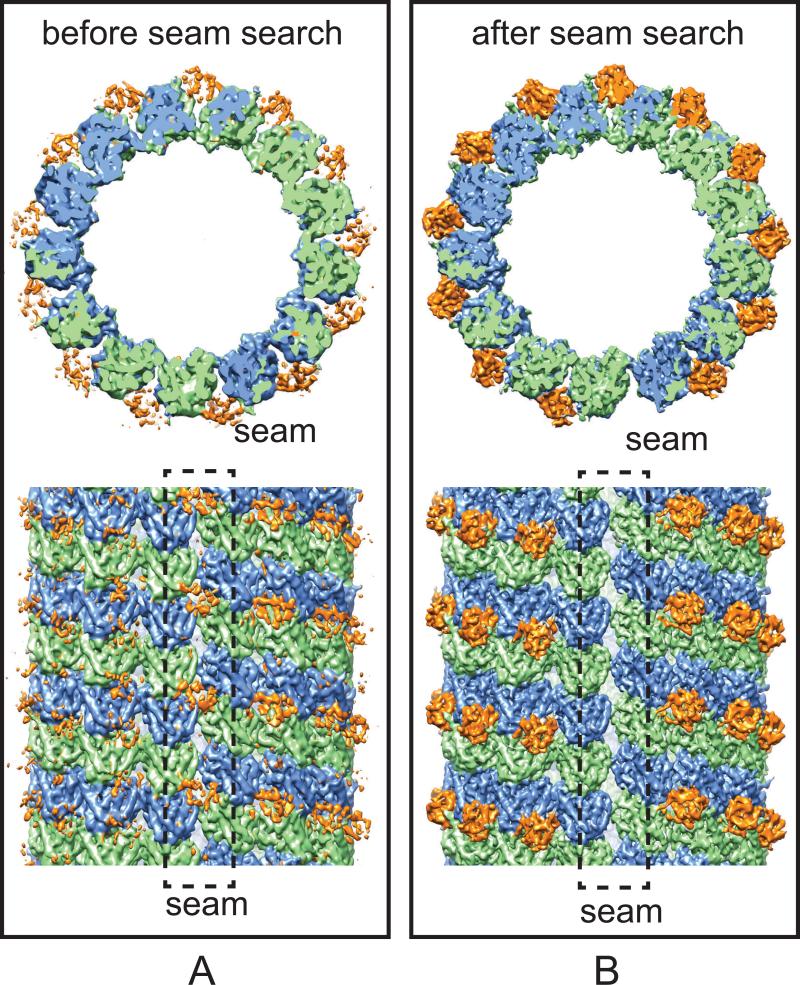
As shown in Fig. 7, the C1 reconstruction of the EB3-GTPγS MT dataset after the seam-search clearly show that EB3 binds to the MT lattice with a tubulin dimer repeat, but not to the seam, where the EB binding pocket across protofilaments is not preserved (Fig. 7B). In contrast, the C1 reconstruction before the seam-search shows “phantom” EB3 densities between two real EB3 binding sites (near the intra-dimer interface), as well as at the seam location (Fig. 7A). After identifying the correct seam location, we were able to obtain a C1 MT reconstruction at an unprecedented resolution of ~4 Å, using the ~80,000 overlapping particles resulting from merging all the data for the EB3-bound states (EB3-GTPγS, EB3-GDP and EB3-GMPCPP states), whose structures turned out to be very similar. This resolution allowed us, for the first time, to build an atomic model for the true seam configuration (Zhang et al., 2015).
Fig. 7.
The seam-search protocol improves the distinction of α- and β-tubulin in the C1 MT reconstructions. (A and B) Cryo-EM densities of the C1 reconstructions of the EB3-GTPγS MT before (A) and after (B) seam-search. α-tubulin, β-tubulin and EB3 are colored green, blue and orange, respectively. The black dashed boxes marked the MT seam where EB3 does not bind (as is apparent in (B), but that appears partially occupied when the seam is misaligned, as in (A).
Since the seven MT particles used to calculate a super-particle span only a short MT segment, this approach not only applies to the 13-PF MTs, which have minimal supertwist, but also works well for MT that display clear moiré patterns (Chretien et al., 1996; Mandelkow and Mandelkow, 1985), such as 12- or 14-PF MTs. The seam-search protocols led to similar improvements for the 14-PF GMPCPP-K and GDP-K MTs. Comparison of the C1 reconstructions for these MTs with their symmetrized reconstructions revealed that in both cases the two PFs across the seam are slightly opened up compared with the others engaged in non-seam lateral contacts (Zhang et al., 2015). This finding strongly suggests that the seam is a weak point in the MT architecture, and likely the first place to break during MT depolymerization.
3.5 Robustness of the measured helical parameters
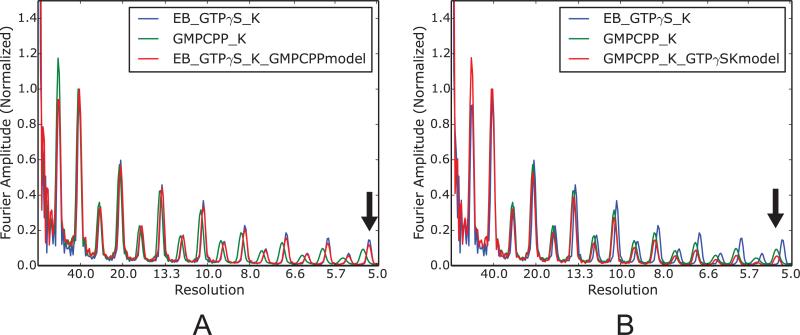
Model bias is a well-known potential problem in single particle analysis (Rosenthal and Henderson, 2003), especially for structures with helical symmetry (Egelman, 2014). In our MT data processing protocol, the helical parameters (twist and rise for the 3-start helix) for each MT state were precisely measured from corresponding C1 reconstruction. The results for our six MT structures in different states fall into two discrete groups, corresponding to an extended lattice (tubulin dimer repeat ~83.2 Å) and a compacted lattice (tubulin dimer repeat ~81.6 Å) (Zhang et al., 2015). Although during the C1 reconstruction no helical symmetry is applied, our measurements may be potentially biased by the intrinsic helical symmetry present in the reference model used to align the raw particles. In order to address this concern, we deliberately used a wrong reference model to align the MT particles, e.g., we used the model of 13-PF GMPCPP-K MT (extended lattice) to align the dataset of 13-PF EB3-GTPγS-K MT (compacted lattice), and vice versa. This analysis showed that the measured helical parameters are quite robust and insensitive to the helical symmetry present in the reference model, which is likely due to the high SNR in the raw MT images obtained with a direct detector. Due to the simple geometric relationship between the helical twist and the tubulin dimer repeat distance, this robustness is also reflected in the comparison of layer line profiles (Fig. 8A, 8B). One caveat of our analysis is that the helical symmetry or lattice geometry present in the reference could not be too far away from the true solution, or otherwise the structural refinement will not converge (a typical phenomena for the helical reconstruction by IHRSR method (Egelman, 2014)).
Fig. 8.
Robustness of the measured MT helical parameters. (A) Layer line profiles for the 13-PF GMPCPP-K and EB3-GTPγS-K MTs, and for the reconstruction obtained using the EB3-GTPγS-K dataset with the 13-PF GMPCPP-K MT as the reference model. (B) Layer line profiles for the 13-PF GMPCPP-K and EB3-GTPγS-K MTs, and for the reconstruction obtained using the 13-PF GMPCPP-K MT dataset with the EB3-GTPγS-K MT as the reference model. The black arrow indicates that the axial lattice spacing in the reconstruction is not biased by the wrong reference model (same in (A)).
4. Discussion
We have observed that overall resolution of our MT reconstruction does not improve significantly after our seam-search protocol, unless the initial seam assignments are dramatically off or the αβ-tubulin registers are mostly wrong. This is due to two reasons. First, α- and β-tubulin are indeed very similar, thus, averaging αβ-tubulin will still improve overall resolution, especially in intermediate resolution range. The second reason has to do with the way FREALIGN applies pseudo-helical symmetry (by specifying SYM = HP). Take the 13-PF MT as an example, in the reconstruction step, the program inserts the 2D FT of each raw particle into the 3D Fourier space exactly 13 times, in its initial position and 12 rotated positions with an angular step size of ~27.7° (the TWIST angle between adjacent PFs). The phases for each Fourier component are also adjusted to account for the x, y translations. Of the 12 rotations, six are done clockwise and six counterclockwise, rather than applying them unidirectionally, so as to minimize error propagation of the helical parameters (TWIST and RISE). In the worst possible case, a given φ angle for a MT particle can be off by six PFs, either in the clockwise or counterclockwise direction. Even that, after the 13 insertions into 3D Fourier space, this particle will make six positive and six negative contributions to the tubulin dimer located in the good PF, which ultimately will be the only density used to regenerate the whole MT density map. As a result, in our specific data processing scheme, adding a MT particle with misassigned seam location will still make some constructive contribution to the final reconstruction in terms of α/β distinction, as long as the αβ tubulin register for most of the PFs are consistent with the reference model. For this reason, compared with the symmetrized reconstruction, the C1 reconstruction, which inserts each particle into the 3D Fourier space only once instead of 13 times, will be more sensitive to the errors in seam assignment.
In our data processing protocol, after the unifying-φ step, the plots of the five alignments parameters (Ψ, θ, φ, shx and shy) should all follow smooth lines (Fig. 3D). These internal restraints are very helpful in identifying misaligned particles (those for which refinement failed to find any of the 26 local minima). Similar to a previous protocol (Sachse et al., 2007), by discarding or rescuing the outliers, the alignment errors could be reduced to a minimum for the entire dataset, a hard-to-achieve goal for traditional single particle datasets of individual complexes. The unifying-φ step is also critical to minimize the correlation of noise when computing FSC between reconstructions from two halves of the dataset, which are typically split based on odd and even particles. In the IHRSR method there is usually significant overlap between two consecutive odd and even particles. Noise correlation would occur if the same tubulin dimer in a raw particle image contributed to the same tubulin dimer in both odd and even maps. Due to the way we box overlapping MT particles (see Section 2.2), the odd and even particles are offset by ~80 Å, corresponding to one “turn” of ~13 tubulin dimers. Consider a helical turn of 13 tubulin dimers (as shown in Fig. 1A, tubulin dimers with black outlines) in the odd particle image. During the pseudo-helical symmetrization step, these 13 dimers will contribute only to one tubulin dimer at the good PF of the odd map (referred to as position N). Due to the 80 Å shift along the MT axis between the odd and the even particles (see Section 2.2), the same 13 dimers in the even particle (assuming they are in the overlap region) will contribute only to a different tubulin dimer on the good PF of the even map (referred to as position N+1), if the φ angle assignments are consistent between these two particles. Otherwise, during the helical reconstruction step, some of these 13 dimers could contribute to the tubulin at position N in the even map, where these 13 dimers also make contribution to the odd map, thus causing noise correlation.
Interestingly, our preliminary results suggest that our seam-search protocol using 40Å monomer shifts also works well on undecorated MTs, probably by picking up the subtle differences between α-to-β and β-to-α distances along each PF (Zhang et al., 2015), and/or the weak signal at higher resolution that distinguishes α- and β-tubulin.
The present resolution of 3.5 Å for MT reconstructions allowed us, for the first time, to refine atomic models directly into the cryo-EM densities. This accomplishment has led to new biological insight that illuminates the mechanistic origin of MT dynamic instability and its regulation by EB proteins (Zhang et al., 2015). However, similar to other cryo-EM structures at high-resolution, most side-chain densities for acidic residues (glutamates and aspartates) in our MT maps are missing, presumably due to radiation-induced decarboxylation of acidic residues (Allegretti et al., 2014; Weik et al., 2000). Our attempt to use sub-particles extracted from only the first two frames (corresponding to a dose of 2.7 electron/Å2) lead to a 3D reconstruction (for the EB3-GTPγS-K MT) at a resolution of 4.2 Å. However, it did not recover these missing side-chain densities. This absence limits our detailed understanding of some critical interactions, such as those at the nucleotide binding site. For example, hydrolysis within the MT lattice is thought to be catalyzed by E254 in α-tubulin (Anders and Botstein, 2001; Nogales et al., 1998a; Nogales et al., 1998b; Oliva et al., 2004), whose side chain density is unfortunately invisible in our structures, as are those for key aspartates involved in Mg2+ ion coordination. It is possible that special buffer conditions could minimize the radiation damages on acidic residues. Alternatively, higher camera frame rates combined with better drift-correction software that can align frames with extremely low electron dose may be helpful to recover information from the very first frame, when the radiation damage is minimal and higher resolution is better preserved. Currently this information is largely lost in our data due to the particularly large beam-induced drift within the first one or two frames.
Ultimately, higher resolution will still be needed in order to understand better the details pertaining to nucleotide hydrolysis, allostery and the binding effects of anti-mitotic drugs, such as taxol, in the context of the intact MT. There is obvious room for improvement, starting with a better cryo-EM sample preparation. Very thin ice has been suggested to be the key to reach sub-3 Å resolution (Bartesaghi et al., 2015; Campbell et al., 2015), and it should be possible to optimize further the ice thickness in our samples without compromising MT integrity. In addition, significant improvement in the reduction of beam induced movement using gold EM grids (Russo and Passmore, 2014) could preserve more of the high-resolution information that is otherwise lost during the time of an individual frame, especially during the very early exposure. Lastly, resolution of MT cryo-EM reconstructions may be ultimately limited by disorder within the MT lattice that can only be partially ameliorated biochemically and thus may require the development of new image processing schemes to detect and compensate for these deformations from a perfect MT lattice.
Acknowledgements
We thank Greg Alushin and Gabriel Lander for developing the python script to apply pseudo-helical symmetry and for stimulating discussions. We thank Robert Glaeser for the use of the Titan microscope, Anchi Cheng and Tom Houwelling for assistance with Leginon installation and APPION data processing, and Alexis Rohou and Nikolaus Grigorieff for guidance in the use of FREALIGN. We are also thankful to Nikolaus Grigorieff for his comments on the manuscript. This work was funded by a grant from NIGMS (GM051487 to E.N.). E.N. is a Howard Hughes Medical Institute investigator.
Footnotes
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
Program Access
All the python scripts for our new seam-search protocols are publically available at http://GitHub.com, under the “nogaleslab” repositories.
References
- Akhmanova A, Steinmetz MO. Tracking the ends: a dynamic protein network controls the fate of microtubule tips. Nature reviews. Molecular cell biology. 2008;9:309–322. doi: 10.1038/nrm2369. [DOI] [PubMed] [Google Scholar]
- Allegretti M, Mills DJ, McMullan G, Kuhlbrandt W, Vonck J. Atomic model of the F420-reducing [NiFe] hydrogenase by electron cryo-microscopy using a direct electron detector. Elife. 2014;3:e01963. doi: 10.7554/eLife.01963. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Alushin GM, Lander GC, Kellogg EH, Zhang R, Baker D, Nogales E. High-resolution microtubule structures reveal the structural transitions in alphabeta-tubulin upon GTP hydrolysis. Cell. 2014;157:1117–1129. doi: 10.1016/j.cell.2014.03.053. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Amos L, Klug A. Arrangement of subunits in flagellar microtubules. Journal of cell science. 1974;14:523–549. doi: 10.1242/jcs.14.3.523. [DOI] [PubMed] [Google Scholar]
- Anders KR, Botstein D. Dominant-lethal alpha-tubulin mutants defective in microtubule depolymerization in yeast. Molecular biology of the cell. 2001;12:3973–3986. doi: 10.1091/mbc.12.12.3973. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bai XC, Fernandez IS, McMullan G, Scheres SH. Ribosome structures to near-atomic resolution from thirty thousand cryo-EM particles. Elife. 2013;2:e00461. doi: 10.7554/eLife.00461. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bartesaghi A, Merk A, Banerjee S, Matthies D, Wu X, Milne JL, Subramaniam S. 2.2 A resolution cryo-EM structure of beta-galactosidase in complex with a cell-permeant inhibitor. Science. 2015;348:1147–1151. doi: 10.1126/science.aab1576. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Campbell MG, Veesler D, Cheng A, Potter CS, Carragher B. 2.8 A resolution reconstruction of the Thermoplasma acidophilum 20S proteasome using cryo-electron microscopy. Elife. 2015;4 doi: 10.7554/eLife.06380. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Campbell MG, Cheng A, Brilot AF, Moeller A, Lyumkis D, Veesler D, Pan J, Harrison SC, Potter CS, Carragher B, Grigorieff N. Movies of ice-embedded particles enhance resolution in electron cryo-microscopy. Structure. 2012;20:1823–1828. doi: 10.1016/j.str.2012.08.026. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chretien D, Kenney JM, Fuller SD, Wade RH. Determination of microtubule polarity by cryo-electron microscopy. Structure. 1996;4:1031–1040. doi: 10.1016/s0969-2126(96)00110-4. [DOI] [PubMed] [Google Scholar]
- Egelman EH. A robust algorithm for the reconstruction of helical filaments using single-particle methods. Ultramicroscopy. 2000;85:225–234. doi: 10.1016/s0304-3991(00)00062-0. [DOI] [PubMed] [Google Scholar]
- Egelman EH. Ambiguities in helical reconstruction. Elife. 2014;3 doi: 10.7554/eLife.04969. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Galjart N. Plus-end-tracking proteins and their interactions at microtubule ends. Current biology : CB. 2010;20:R528–537. doi: 10.1016/j.cub.2010.05.022. [DOI] [PubMed] [Google Scholar]
- Glaeser RM, Typke D, Tiemeijer PC, Pulokas J, Cheng A. Precise beam-tilt alignment and collimation are required to minimize the phase error associated with coma in high-resolution cryo-EM. J Struct Biol. 2011;174:1–10. doi: 10.1016/j.jsb.2010.12.005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Grigorieff N. FREALIGN: high-resolution refinement of single particle structures. J Struct Biol. 2007;157:117–125. doi: 10.1016/j.jsb.2006.05.004. [DOI] [PubMed] [Google Scholar]
- Kikkawa M. A new theory and algorithm for reconstructing helical structures with a seam. Journal of molecular biology. 2004;343:943–955. doi: 10.1016/j.jmb.2004.08.051. [DOI] [PubMed] [Google Scholar]
- Lander GC, Stagg SM, Voss NR, Cheng A, Fellmann D, Pulokas J, Yoshioka C, Irving C, Mulder A, Lau PW, Lyumkis D, Potter CS, Carragher B. Appion: an integrated, database-driven pipeline to facilitate EM image processing. J Struct Biol. 2009;166:95–102. doi: 10.1016/j.jsb.2009.01.002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Li X, Mooney P, Zheng S, Booth CR, Braunfeld MB, Gubbens S, Agard DA, Cheng Y. Electron counting and beam-induced motion correction enable near-atomic-resolution single-particle cryo-EM. Nat Methods. 2013;10:584–590. doi: 10.1038/nmeth.2472. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Liu JS, Schubert CR, Fu X, Fourniol FJ, Jaiswal JK, Houdusse A, Stultz CM, Moores CA, Walsh CA. Molecular basis for specific regulation of neuronal kinesin-3 motors by doublecortin family proteins. Mol Cell. 2012;47:707–721. doi: 10.1016/j.molcel.2012.06.025. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lowe J, Li H, Downing KH, Nogales E. Refined structure of alpha beta-tubulin at 3.5 A resolution. Journal of molecular biology. 2001;313:1045–1057. doi: 10.1006/jmbi.2001.5077. [DOI] [PubMed] [Google Scholar]
- Ludtke SJ, Baldwin PR, Chiu W. EMAN: semiautomated software for high-resolution single-particle reconstructions. J Struct Biol. 1999;128:82–97. doi: 10.1006/jsbi.1999.4174. [DOI] [PubMed] [Google Scholar]
- Lyumkis D, Brilot AF, Theobald DL, Grigorieff N. Likelihood-based classification of cryo-EM images using FREALIGN. J Struct Biol. 2013;183:377–388. doi: 10.1016/j.jsb.2013.07.005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mandelkow EM, Mandelkow E. Unstained microtubules studied by cryo-electron microscopy. Substructure, supertwist and disassembly. Journal of molecular biology. 1985;181:123–135. doi: 10.1016/0022-2836(85)90330-4. [DOI] [PubMed] [Google Scholar]
- Mandelkow EM, Schultheiss R, Rapp R, Muller M, Mandelkow E. On the surface lattice of microtubules: helix starts, protofilament number, seam, and handedness. The Journal of cell biology. 1986;102:1067–1073. doi: 10.1083/jcb.102.3.1067. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Maurer SP, Bieling P, Cope J, Hoenger A, Surrey T. GTPgammaS microtubules mimic the growing microtubule end structure recognized by end-binding proteins (EBs). Proceedings of the National Academy of Sciences of the United States of America. 2011;108:3988–3993. doi: 10.1073/pnas.1014758108. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Maurer SP, Fourniol FJ, Bohner G, Moores CA, Surrey T. EBs recognize a nucleotide-dependent structural cap at growing microtubule ends. Cell. 2012;149:371–382. doi: 10.1016/j.cell.2012.02.049. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Menendez M, Rivas G, Diaz JF, Andreu JM. Control of the structural stability of the tubulin dimer by one high affinity bound magnesium ion at nucleotide N-site. The Journal of biological chemistry. 1998;273:167–176. doi: 10.1074/jbc.273.1.167. [DOI] [PubMed] [Google Scholar]
- Metoz F, Wade RH. Diffraction by Helical Structures with Seams: Microtubules. J Struct Biol. 1997;118:128–139. [Google Scholar]
- Mitchison T, Kirschner M. Dynamic instability of microtubule growth. Nature. 1984;312:237–242. doi: 10.1038/312237a0. [DOI] [PubMed] [Google Scholar]
- Nogales E, Wolf SG, Downing KH. Structure of the alpha beta tubulin dimer by electron crystallography. Nature. 1998a;391:199–203. doi: 10.1038/34465. [DOI] [PubMed] [Google Scholar]
- Nogales E, Downing KH, Amos LA, Lowe J. Tubulin and FtsZ form a distinct family of GTPases. Nature structural biology. 1998b;5:451–458. doi: 10.1038/nsb0698-451. [DOI] [PubMed] [Google Scholar]
- Nogales E, Whittaker M, Milligan RA, Downing KH. High-resolution model of the microtubule. Cell. 1999;96:79–88. doi: 10.1016/s0092-8674(00)80961-7. [DOI] [PubMed] [Google Scholar]
- Oliva MA, Cordell SC, Lowe J. Structural insights into FtsZ protofilament formation. Nature structural & molecular biology. 2004;11:1243–1250. doi: 10.1038/nsmb855. [DOI] [PubMed] [Google Scholar]
- Rohou A, Grigorieff N. CTFFIND4: Fast and accurate defocus estimation from electron micrographs. J Struct Biol. 2015 doi: 10.1016/j.jsb.2015.08.008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rosenthal PB, Henderson R. Optimal determination of particle orientation, absolute hand, and contrast loss in single-particle electron cryomicroscopy. Journal of molecular biology. 2003;333:721–745. doi: 10.1016/j.jmb.2003.07.013. [DOI] [PubMed] [Google Scholar]
- Russo CJ, Passmore LA. Electron microscopy: Ultrastable gold substrates for electron cryomicroscopy. Science. 2014;346:1377–1380. doi: 10.1126/science.1259530. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sachse C, Chen JZ, Coureux PD, Stroupe ME, Fandrich M, Grigorieff N. High-resolution electron microscopy of helical specimens: a fresh look at tobacco mosaic virus. Journal of molecular biology. 2007;371:812–835. doi: 10.1016/j.jmb.2007.05.088. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Shang Z, Zhou K, Xu C, Csencsits R, Cochran JC, Sindelar CV. High-resolution structures of kinesin on microtubules provide a basis for nucleotide-gated force-generation. Elife. 2014;3:e04686. doi: 10.7554/eLife.04686. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sindelar CV, Downing KH. The beginning of kinesin's force-generating cycle visualized at 9-A resolution. The Journal of cell biology. 2007;177:377–385. doi: 10.1083/jcb.200612090. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sosa H, Milligan RA. Three-dimensional structure of ncd-decorated microtubules obtained by a back-projection method. Journal of molecular biology. 1996;260:743–755. doi: 10.1006/jmbi.1996.0434. [DOI] [PubMed] [Google Scholar]
- Suloway C, Pulokas J, Fellmann D, Cheng A, Guerra F, Quispe J, Stagg S, Potter CS, Carragher B. Automated molecular microscopy: the new Leginon system. J Struct Biol. 2005;151:41–60. doi: 10.1016/j.jsb.2005.03.010. [DOI] [PubMed] [Google Scholar]
- Weik M, Ravelli RB, Kryger G, McSweeney S, Raves ML, Harel M, Gros P, Silman I, Kroon J, Sussman JL. Specific chemical and structural damage to proteins produced by synchrotron radiation. Proceedings of the National Academy of Sciences of the United States of America. 2000;97:623–628. doi: 10.1073/pnas.97.2.623. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhang R, Alushin GM, Brown A, Nogales E. Mechanistic Origin of Microtubule Dynamic Instability and Its Modulation by EB Proteins. Cell. 2015;162:849–859. doi: 10.1016/j.cell.2015.07.012. [DOI] [PMC free article] [PubMed] [Google Scholar]