Modelling the distribution of leaf nitrogen is central to specify photosynthetic parameters and simulate canopy photosynthesis using leaf gas exchange models. Nitrogen distribution depends both on soil nitrogen availability and within-canopy light distribution. We propose the use of a set of empirical relationships with measurable parameters to dynamically account for it. The model was assessed on alfalfa canopies under contrasting N nutrition levels. It proved able to predict nitrogen distribution and daily patterns of photosynthesis from leaf to whole canopy for a large range of situations.
Keywords: Light, Medicago sativa, nitrogen distribution, nitrogen nutrition index, photosynthesis, transpiration, upscaling, within-canopy variability
Abstract
Modelling the spatial and temporal distribution of leaf nitrogen (N) is central to specify photosynthetic parameters and simulate canopy photosynthesis. Leaf photosynthetic parameters depend on both local light availability and whole-plant N status. The interaction between these two levels of integration has generally been modelled by assuming optimal canopy functioning, which is not supported by experiments. During this study, we examined how a set of empirical relationships with measurable parameters could be used instead to predict photosynthesis at the leaf and whole-canopy levels. The distribution of leaf N per unit area (Na) within the canopy was related to leaf light irradiance and to the nitrogen nutrition index (NNI), a whole-plant variable accounting for plant N status. Na was then used to determine the photosynthetic parameters of a leaf gas exchange model. The model was assessed on alfalfa canopies under contrasting N nutrition and with N2-fixing and non-fixing plants. Three experiments were carried out to parameterize the relationships between Na, leaf irradiance, NNI and photosynthetic parameters. An additional independent data set was used for model evaluation. The N distribution model showed that it was able to predict leaf N on the set of leaves tested. The Na at the top of the canopy appeared to be related linearly to the NNI, whereas the coefficient accounting for N allocation remained constant. Photosynthetic parameters were related linearly to Na irrespective of N nutrition and the N acquisition mode. Daily patterns of gas exchange were simulated accurately at the leaf scale. When integrated at the whole-canopy scale, the model predicted that raising N availability above an NNI of 1 did not result in increased net photosynthesis. Overall, the model proposed offered a solution for a dynamic coupling of leaf photosynthesis and canopy N distribution without requiring any optimal functioning hypothesis.
Introduction
A close positive relationship exists between the nitrogen (N) content and photosynthetic capacity of leaves (Field and Mooney 1986; Evans 1989; Hikosaka 2004). Such a relationship is the cornerstone of various approaches proposed to upscale leaf gas exchange models to the whole canopy level (Kull and Jarvis 1995; Leuning 1995; De Pury and Farquhar 1997; Sinoquet et al. 2001; Evers et al. 2010). Indeed, it has been shown that the within-canopy variability of photosynthetic parameters can be fully specified at a given time by measurements of the spatial distribution of leaf N (Harley et al. 1992; Le Roux et al. 1999; Braune et al. 2009). Changes in leaf N concentration with canopy depth, and the effects of leaf age and leaf light microclimate, have been identified as major sources of spatial variation (Evans 1989). They have been studied extensively in several species and different modelling approaches enable to account for it.
Following the optimization theory, several authors first sought to model N distribution in order to maximize canopy photosynthesis (Charles-Edwards 1981; Field 1983; Hirose and Werger 1987). The outcome was models predicting a leaf N concentration, which paralleled radiation extinction (Kull and Jarvis 1995; Sands 1995). However, there is no a priori reason for N distribution to follow such a pattern. On the contrary, empirical observations have consistently indicated that the exponential fall in leaf N with increasing depth into the canopy occurs in most canopies at a slower rate than light extinction (Hirose and Werger 1987; Lemaire et al. 1991; Anten et al. 1995; Moreau et al. 2012). Alternatively, empirical relationships between light extinction and leaf N have been used to mimic a local light acclimation and model leaf N distribution by considering potential departures from the light gradient (Sellers et al. 1992; Anten et al. 1995; Prieto et al. 2012). The approach is usually based on a coefficient of N allocation (kN) that shapes the N profile with respect to relative light extinction (I/I0), and a reference leaf N concentration at the top of the canopy (Nup):
| (1) |
Leaf N distribution is not solely a function of light and age, however. It is also dependent on mineral N availability (Hikosaka et al. 1994; Lötscher et al. 2003), N demand to support plant growth and more generally on the N status of plants (i.e. the relative satisfaction of plant N demand, Lemaire and Gastal 1997). The N demand of a plant at any time in its cycle is generally defined as the amount of N necessary to sustain maximum plant growth. Nitrogen demand is tightly related to the standing crop mass. On a mass increment basis, it decreases as biomass increases, resulting in an apparent dilution of plant N concentration with plant growth (Greenwood et al. 1990; Gastal et al. 2015). Canopy N content and leaf N distribution, thus, respond not only to changes in the fertilization rate (Bélanger et al. 1992; Dreccer et al. 2000) but also to all factors that affect the plant growth rate (e.g. temperature and CO2 concentration; Pettersson and McDonald 1994). Empirical plant N status indices have been developed to account for both aspects and help to diagnose crop N requirements. For instance, the nitrogen nutrition index (NNI) was assessed on plants as different as C3 annual crops (e.g. Justes et al. 1994; Colnenne et al. 1998), C4 grasses (Plénet and Lemaire 1999) and perennial forage plants (Lemaire et al. 1984, 1985). This is based on the concept of critical N dilution that can be applied in dynamic terms and is able to account for temporal changes in the N nutrition of crops (e.g. STICS crop model, Brisson et al. 2009).
Modelling the effect of the interaction between light acclimation and N limitations on the distribution of leaf N and photosynthetic characteristics has received comparatively less attention (Thornley 1998). One challenge is that light acclimation is a local process driven by the leaf light microclimate (Evans 1989; Hikosaka et al. 1994), whereas N demand, plant N status and N allocation are defined at the whole-plant scale (Givnish 1988; Lemaire and Gastal 1997; Kull 2002; Gastal et al. 2015). Empirical relationships between light extinction and leaf N generally refer to static canopies at a given developmental stage, and their parameters need to be adjusted between years, sites or N treatments (Prieto et al. 2012). To date, dynamic coupling with plant growth has, thus, mainly been achieved using approaches based on the optimal distribution theory (Johnson et al. 2010). Some studies demonstrated a significant relationship between canopy NNI and the kN and Nup parameters (Lötscher et al. 2003; Farruggia et al. 2004; Gastal et al. 2015). These relationships could be tested to make predictions of photosynthetic parameters under contrasting N availabilities without any a priori assumptions regarding optimal functioning of the canopy. Such a model would offer a solution to dynamically simulate the interactions between light and N based on parameters that can be directly measured.
During this study, we developed and assessed a model coupling an empirical canopy N distribution model with a leaf gas exchange model derived from Farquhar et al. (1980). The distribution of leaf N content per unit area (Na) was related to leaf light irradiance and to the canopy NNI. The objectives were to determine whether such an empirical approach to leaf N distribution could be used to specify spatial and temporal changes in leaf gas exchange under fluctuating light and N availability. Alfalfa was chosen as a model species because its leaf N distribution has already been described extensively under non-limiting N and because this species presents limited age dependency of leaf characteristics (Lemaire et al. 1991, 2005; Evans 1993).
Methods
Model description
Canopy N distribution model
We assumed that spatial and temporal variations in leaf N content per unit area (Na) within the canopy and in the course of plant growth can be deduced from leaf light exposure and plant N status. The effect of relative leaf irradiance on relative Na was taken into account using Eq. (1) with the two parameters Nup and kN. The effect of N limitation was assumed to affect whole-canopy N content in leaves by modulating these two parameters. The NNI was considered to account for the effect of canopy N status (integrating the effects of soil mineral N and nodule fixation on internal N availability). At a given time, NNI was defined as:
| (2) |
where Nm represents the actual plant N concentration and Nc the critical plant N concentration (g N 100 g−1 plant) corresponding to its mass W (given by equation Nc = 4.8W−0.33 in alfalfa, Lemaire et al. 1985). When NNI is close to 1, the plant N status is considered as near optimum. Departures from 1 indicate deficiency (NNI < 1; the intensity of deficiency is then equal to 1 − NNI) or excess N (NNI > 1, the intensity of excess is then equal to NNI − 1). Following Farruggia et al. (2004), a linear response of Nup to NNI was considered:
| (3) |
where represents the N content of leaves exposed to incoming photosynthetically active radiation for a NNI of 1 and a2 represents the dependency of upper leaf N content on plant N status. Similarly, the coefficient of N distribution relative to the light gradient was assumed to depend on NNI:
| (4) |
where represents the allocation coefficient for a NNI of 1 and a3 represents the dependency of this coefficient on plant N status.
Leaf gas exchange model
The leaf gas exchange model is described in details in Prieto et al. (2012) and has originally been assessed on grapevine. It combines the biochemical photosynthetic model developed by Farquhar et al. (1980) with a semi-empirical stomatal conductance model that was originally proposed by Ball et al. (1987) and then modified by Leuning (1995). All the equations, variables and parameters are presented in Tables A1–A3. The coupling of this leaf gas exchange model with the previously presented canopy N distribution model was performed through the dependency of the principal photosynthesis parameters (value of Vcmax, Jmax, triose phosphate utilization rate (TPU) and Rd at 25 °C) to Na. A linear relationship was assumed [Eq. (A9)] (Harley et al. 1992; Le Roux et al. 1999; Braune et al. 2009).
Model calibration
Three experiments were carried out at the INRA Lusignan research station, France (46.43N, 0.18E), to calibrate this model and assess the impacts of light, N nutrition and leaf age on the distribution of leaf photosynthetic parameters in alfalfa (Medicago sativa). The three experiments were based on the same cultivars (cv. ‘Orca’ as a regular N fixing material, and cv. ‘Agate NF’ as a non-N2-fixing material, Barnes et al. 1990).
Experiment 1
The first experiment was performed in a growth chamber between March and June 2010. All plants were grown in 1.5-L pots (10 × 20 cm cylindrical pots) filled with an N-free substrate (fine quartz sand, 0.8–1.4 mm mesh). The pots were arranged in a quincunx and two plants were transplanted into each pot, resulting in a planting density of ∼230 plants m−2. Three canopies comprising 81 pots each (i.e. 162 plants each) were grown under contrasting N availabilities at 22 °C/17 °C (day/night) under a 14-h photoperiod. The incident photosynthetic photon flux density (PPFD) was ∼400 µmol m−2 s−1. Each canopy was surrounded by a row of border plants grown under the same conditions. Two of these canopies were sown using the ‘Orca’ cultivar and were ferti-irrigated every 4 h (daily amount of 200 mL pot−1) with either a complete nutrient solution (N+, 8 mmol N) or a low N nutrient solution (N−, 0.5 mmol N). The N concentration of the N+ solution was non-limiting for growth and prevented the nodulation of alfalfa roots. With the N− solution however, nodulation and N fixation did occur in the Orca cultivar (with natural strains of rhizobium, since the plants were not inoculated). The third canopy was sown with the ‘Agate NF’ cultivar grown with the N− nutrient solution, so that N fixation could not compensate for low mineral N availability. In order to induce a size hierarchy into the canopy, and to decorrelate the vertical position of leaves from their age, alternate rows were sown with a 17-day delay in each canopy. The study focussed on the initial growth period (no defoliation). Two samplings were performed in order to characterize the leaf N distribution. The plants were at the 12th visible leaves stage (40 days after the first sowing) and beginning of bloom stage (58 days after the first sowing), based on development of the Orca-N+ canopy. At each date, eight pots (16 plants) were collected from the centre of each canopy.
Experiment 2
The second experiment was performed outdoors between April and August 2009 using the ‘Orca’ cultivar. The average incident PPFD was ∼725 µmol m−2 s−1. All plants were grown in individual 1-L pots (5 × 52 cm cylindrical pots), resulting in a plant density of 460 plants m−2. The canopy was made up of 100 study pots surrounded by 3 rows of border plants grown under the same conditions. All pots were filled with a growing medium that comprised sterile potting mix sand and clay-sandy-loam soil from a field in Lusignan (1 : 1 : 1, v/v). They were ferti-irrigated three times a day with the N+ nutrient solution. At the end of the second regrowth (beginning of bloom stage), 20 plants were sampled from the centre of the canopy for the characterization of leaf N distribution. The plants in this canopy had previously been shown to be highly size structured (Baldissera et al. 2014).
Experiment 3
The third experiment was carried out in a greenhouse between February and June 2012 using the ‘Orca’ cultivar. The average incident PPFD was ∼540 µmol m−2 s−1. All plants were grown in 1.1-L pots (10 × 10 × 11 cm) filled with an N-free substrate (fine quartz sand, 0.8–1.4 mm mesh). A single plant was transplanted into each pot, resulting in a density of 100 plants m−2. Just after transplantation, the seedlings were inoculated with a solid commercial preparation for the coating of alfalfa seeds (Sinorhizobium meliloti, strain 2011, Becker Underwood). The pots were automatically ferti-irrigated five times a day with a complete nutrient solution devoid of mineral N (N0, 0 mmol N). The nutrient solution was sampled weekly to determine the absence of and and ensure that N fixation was the only source of N supplied to the alfalfa plants. The experimental design consisted of 4 contiguous blocks of 49 pots each. At the end of the initial growth period (mid-bloom stage), four plants were sampled from the centre of each block in order to characterize the leaf N distribution.
Measurement of canopy N distribution and NNI
At each sampling date specified in the three experiments, each plant was separated into stems, flowers (when present) and leaves. The leaves were subdivided into 10 cm strata from the bottom to the top of the plant. The leaf area into each strata was determined using an LI-3100 planimeter (LI-COR, Lincoln, NE, USA). Plant samples were dried at 60 °C for 2 days, weighed to determine the dry mass and finally ground in a vibrating ball mill (MM400, Retsch GmbH and Co., Haan, Germany). Each sample was analysed with an elemental analyser to determine the N content (model EA 1108, Carlo Erba Instruments, Milan, Italy). For each canopy, the leaf area index (LAI) was calculated as the average leaf area of the collected plant multiplied by the plant density. The NNI was calculated as the ratio between the canopy N concentration (Nm) and the critical N concentration (Nc, Eq. 2).
Leaf photosynthetic capacity
In Experiments 1–3, gas exchanges were measured using the same procedure with a portable Licor 6400 photosynthesis system (LI-6400, LI-COR). The photosynthetic parameters were determined through the response of A to the internal CO2 concentration (Ci) at the sub-stomatal level (A–Ci curves). Different levels of Ci were obtained by modifying the ambient CO2 concentration (Ca) in the leaf measurement chamber. The A–Ci curves were determined as proposed by Long and Bernacchi (2003). Each Ca step was maintained for 5 min in order to record stable values. The three parameters (Vcmax, Jmax and TPU) were estimated simultaneously by fitting the Farquhar model to the whole A–Ci curve according to the procedure proposed by Sharkey et al. (2007). All curves were determined at 1500 µmol m−2 s−1 of PPFD, while the leaf temperature was controlled at 25 °C and the vapour pressure deficit (VPD) between the leaf and the air was kept at 1 ± 0.5 kPa. Night respiration was estimated at the end of the night on a subsample of leaves that had previously been used for photosynthesis measurements (A–Ci curves). A different leaflet from the same leaf was used. Night respiration was considered to be equal to day respiration (Rd).
In each of the canopies studied, leaves were sampled at three to four levels from the bottom to the top of the canopy, just before the plants were collected to assess canopy N content and leaf N distribution. Measurements were made on the central leaflet of primary leaves. A total of 102 A–Ci curves were analysed over the 3 experiments (70, 20 and 12 for Experiments 1, 2 and 3, respectively).
Stomatal conductance
In Experiment 2, the daily evolution of leaf transpiration was recorded on leaves with contrasting positions within the canopy. Measurements were carried out during a series of sunny and cloudy days in summer. The parameters of the stomatal conductance model [Eq. (A10)] were estimated using the data obtained during a period which cumulated ∼5 days of measurements.
Leaf traits
For each of the leaves on which A–Ci curves were determined, the leaf age was calculated by the thermal time difference (in °Cd) between the date of measurement and the date of leaf appearance. Thermal time was calculated from the daily integration of air temperatures minus the base temperature (5 °C). Immediately after the gas exchange measurements, the three leaflets were collected and scanned (Konica Minolta C352/C300, Konica Minolta Sensing, Osaka, Japan). The leaf area was determined using image analysis (ImageJ software, http://rsbweb.nih.gov/ij/). The leaves were then dried at 60 °C for 2 days, weighed to determine the dry mass and then ground in a vibrating ball mill (MM400, Retsch GmbH and Co.). Leaf samples were analysed with an elemental analyser (model EA 1108, Carlo Erba Instruments) to determine their N concentration. The specific leaf area (SLA, m2 g−1), leaf N content per unit dry mass (%) and leaf N content per unit of area (Na, g N m−2) were then calculated.
Determination of local light conditions
In Experiment 1, the PPFD values at the top of the canopy and at the leaf level (for each leaf used for the A–Ci characterizations) were measured using a portable LI-189 quantum meter (LI-COR). In addition, in all the canopies studied, the vertical distributions of leaf area measured at each sampling date were used to compute light extinction and average PPFD levels corresponding to each leaf stratum, using the RATP model (Sinoquet et al. 2001). A leaf angle distribution was derived from measurements of alfalfa architecture in Experiment 3 (see Barillot et al. 2011 for details).
Assessment of the leaf gas exchange model at the leaf level
A separate experiment was carried out between March and June 2011 according to the same design as Experiment 1. A data set of 10 leaves was used to assess the ability of the model to predict leaf N from canopy NNI and local leaf irradiance. These leaves were collected from the Orca-N+ and Orca-N− treatments (NNI values of 1.1 and 0.9, respectively) at the beginning of the bloom stage. To evaluate the ability of the model to simulate responses to rapid changes in environmental conditions, the sampled plants were placed outdoors and daily evolutions of the leaf gas exchange were recorded. Measurements were taken during sunny and cloudy days on leaves at different heights within the canopies. On very cloudy days, the plants were placed under a shelter to protect the material from the rain. A total of 14 days were analysed. The incident PPFD, leaf temperature, VPD and Ca were measured.
Assessment of the leaf gas exchange model at the whole-canopy level
The behaviour of the leaf gas exchange model when upscaled to the whole-canopy level was also assessed. The leaf N distribution was simulated for contrasting canopies (i.e. LAI values of 1.5, 3 and 5 m2 m−2) at NNI values ranging from 0.3 to 1.4. Leaf area was assumed to be distributed homogeneously into eight vertical strata, and the leaf N concentration in each stratum was assumed to be acclimated to the relative light irradiance integrated over the day. A leaf angle distribution was derived from measurements of alfalfa architecture in Experiment 3 (see Barillot et al. 2011 for details). The light distribution within the canopy was calculated hourly using the RATP model (Sinoquet et al. 2001). Simulations were performed for contrasting days in the series used for validation at the leaf level. Net photosynthesis was calculated within each stratum and then summed to determine aboveground whole-canopy net gas exchanges.
Statistical analyses
Statistical analyses were performed using R software (https://www.r-project.org/). Curve fittings were realized with the nls procedure for Eq. 2 and with the lm procedure for linear regressions (Eqs 3 and 4). Analyses of covariance (ANCOVAs, lm procedure) were used to test for the effects of continuous and categorical variables simultaneously and to compare the slopes and intercepts of linear relationships between N concentration and photosynthetic parameters.
Predicted and measured values of leaf N concentration and net photosynthesis were compared using the root mean square error (RMSE) and bias (Bias) of the model, calculated as follows:
| (5) |
| (6) |
where si and mi are the ith simulated and measured values, respectively, and n is the number of observations.
Results
Impact of NNI on the relationship between leaf irradiance and leaf N
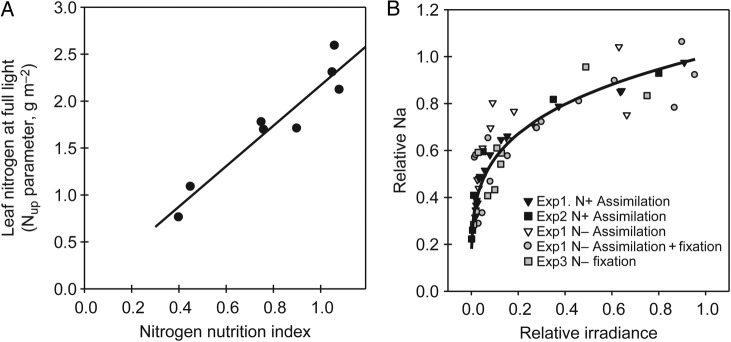
The relationship between Na and relative leaf irradiance was markedly affected by the N nutrition of the plants. Table 1 summarizes the parameters obtained by fitting Eq. 1 to the different N nutrition situations studied. Parameter Nup was the most affected, ranging from ∼2.4 g m−2 under N+ treatments to 0.8 g m−2 in N− plants reliant on mineral N assimilation alone. It related linearly to the NNI of the plant stand (Fig. 1A; Eq. 3). Variations in Nup, thus, reflected variations in N nutrition and internal N availability. By comparison, parameter kN, which accounted for N allocation with respect to relative leaf irradiance, displayed little variation. For kN = 1, the N gradient parallels the light gradient within the canopy. All observed values were clearly inferior to unity (<0.5), indicating a more-than-proportional N allocation to leaves with high irradiance and making the N concentration decrease more slowly than relative irradiance. Most kN values were within the narrow range between 0.2 and 0.3 (except for one 0.09) with no clear relation to NNI. A single kN parameter (0.25) enabled us to fit the normalized Na distributions (Fig. 1B).
Table 1.
Canopy characteristics and N distribution parameters determined during the different experiments and N treatments studied. Parameters were obtained by fitting Eq. 1 to the N content measured in leaves separated in 10-cm strata. Standard errors are indicated in brackets.
| Experiment | Nutrient solution | N acquisition mode | LAI | Nup | kN | r2 |
|---|---|---|---|---|---|---|
| 1 | N+ | Assimilation | 5.1 | 2.12 (0.075) | 0.23 (0.013) | 0.95 |
| 1 | N+ | Assimilation | 2.6 | 2.31 (0.106) | 0.24 (0.020) | 0.96 |
| 2 | N+ | Assimilation | 8.1 | 2.59 (0.123) | 0.21 (0.021) | 0.96 |
| 1 | N− | Assimilation | 1 | 1.09 (0.259) | 0.20 (0.088) | 0.64 |
| 1 | N− | Assimilation | 0.7 | 0.76 (0.130) | 0.09 (0.312) | 0.20 |
| 1 | N− | Assimilation + fixation | 3.3 | 1.77 (0.134) | 0.15 (0.033) | 0.87 |
| 1 | N− | Assimilation + fixation | 2.1 | 1.69 (0.072) | 0.29 (0.031) | 0.94 |
| 3 | N0 | Fixation | 2.0 | 1.71 (0.181) | 0.24 (0.054) | 0.75 |
Figure 1.
Relationships between (A) canopy NNI and leaf N concentration at the top of the canopy (Nup = 2.15 × NNI + 0.02, r2 = 0.91), and (B) relative leaf irradiance and leaf N concentration relative to the leaf N concentration at the top of the canopy (kN = 0.247; r2 = 0.73).
The effect of leaf age on Na distributions was also assessed [see Supporting Information—Figs S1 and S2]. Due to an upward age gradient in alfalfa canopies, leaf nitrogen per unit area was related to both leaf age and local irradiance when considered separately. A multiple regression analysis confirmed the dominant effect of relative irradiance (t-value = 5.11; P < 10−6), but showed a non-significant impact of leaf age per se and no interaction with irradiance (t-value = 1.54; P > 0.12 for the age term).
The canopy N distribution model was parameterized on the basis of these relationships (a2 = 2.15, a3 = 0 and ). Supporting Information—Figure S3 shows the change in leaf N concentration as a function of relative leaf irradiance and NNI as predicted by this model.
Parameters of the photosynthetic and stomatal conductance model
Parameters TPU25 and were related linearly to Na (Fig. 2). The range of values observed for the different leaf parameters varied significantly between experiments, in relation to the minimum and maximum values taken by Na (i.e. up to 2.8, 2, 1.8 and 1.1 g N m−2 in canopies relying on the N+ solution, N− solution and fixation, and fixation only and N− solution only, respectively). The range of variations in Na values resulted from both the N nutrition of plants and leaf-to-leaf variations in the light microclimate. However, a single relationship was found for each parameter between P25 and Na, independently of the N nutrition. No significant difference in the slopes (ANCOVA, t-value <0.91; P > 0.38 for interaction terms between P25 and Na) and intercepts (ANCOVA, t-value <0.31, P > 0.75) were found between the N treatments. A larger dispersion of the points within the ‘N+-assimilation’ data set was observed. This was due to a difference between indoor and outdoor Na values as shown by slightly higher intercepts in Experiment 2 (ANCOVA, t-value < −3.84, P < 0.001 for the intercept term).
Figure 2.
Relationship between the values of photosynthetic parameters at a leaf temperature of 25 °C and leaf N concentration (Na) across the different experiments and N treatments studied. Linear relationships were found for (A, , r2 = 0.86), (B, , r2 = 0.83), TPU25 (C, TPU25 = 6.72Na − 0.72, r2 = 0.78) and (D, , r2 = 0.77), respectively.
An unique set of measurements from Experiment 2 was used to determine the stomatal conductance parameters (a1, Do). It contained leaves from different positions within the canopy and days with contrasting meteorological conditions. Parameter values are presented in Table A2.
Quantitative assessment of the N distribution model
Figure 3 compares the simulated Na values (Eqs 1 and 3) with values measured on leaves at various heights within canopies grown under low and high N availability (NNI ranging from 0.45 to 1.1). Most inter-leaf variance in Na values was explained by the N distribution model (r2 = 0.85). The model error remained low (RMSE = 0.28 g N m−2), but a significant positive bias was observed. Predicted values of Na appeared to be slightly higher on average (Bias = +0.20 g N m−2), particularly in leaves at an intermediate height within the canopy.
Figure 3.

Relationship between leaf N concentrations (Na) observed at various positions within the canopy and the corresponding values simulated. Open and filled symbols indicate canopies grown with N− and N+ nutrient solutions, respectively.
Quantitative assessment of the leaf gas exchange model
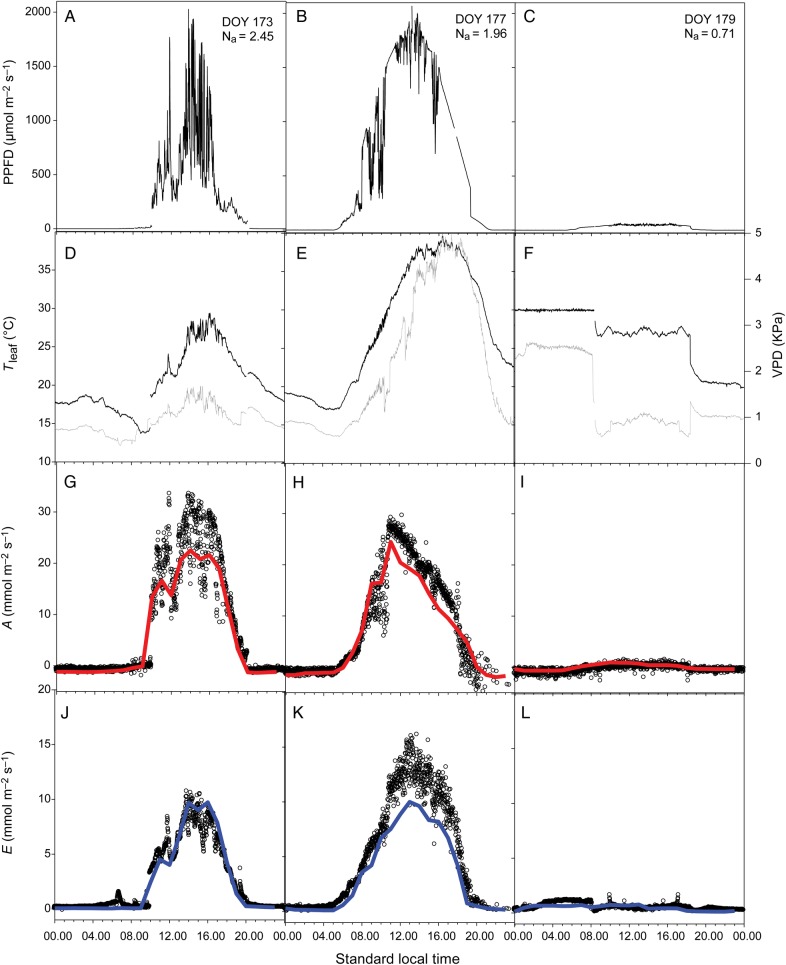
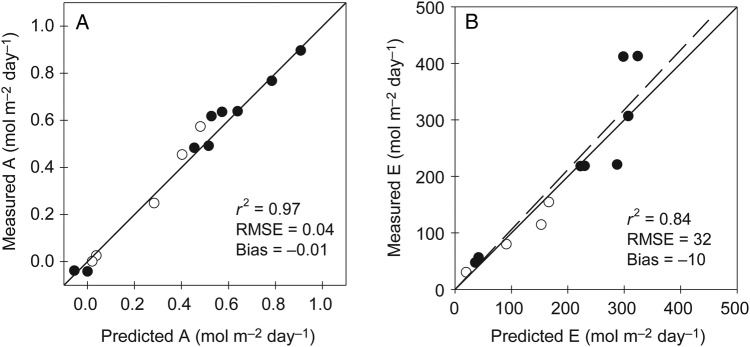
The photosynthesis and transpiration sub-models were further assessed using directly measured leaf Na. In a first step, the photosynthetic parameters were calculated using measured Na as an input. The gas exchange model was then run to simulate the daily patterns of A and E in a range of contrasting leaves (taken from various heights within canopies grown under low and high N availability). The model correctly predicted the diurnal patterns of A and E in various leaves under contrasting environmental conditions (Fig. 4). Cumulated over a day, the relationship between the observed and simulated values of A and E did not differ significantly from the 1 : 1 line (Fig. 5; P < 0.05). The model accurately estimated the diurnal patterns of A and its variation associated with climatic scenarios and leaves under high or low N status (RMSE = 0.04, no significant bias). The predictions also agreed satisfactorily for E, but the model errors were greater. Significant discrepancies were observed on E predictions for leaves with a high N content on sunny days (e.g. day of the year (DOY) 177 for a leaf at 1.96 g N m−2, Fig. 4H). An underestimation of transpiration of up to 20 % was observed under such conditions. This bias did not result from unpaired temporal predictions at a particular time of the day, but from a general underestimation throughout the day.
Figure 4.
Measured instantaneous PPFD at the leaf level (A–C), leaf temperature (black) and VPD (grey, D–F), and the measured (open circles) and predicted (solid line) net photosynthesis (G–I), and transpiration rates (J–L), for three leaves in Lusignan in 2011. DOY, day of the year.
Figure 5.
Comparison of measured and predicted values of daily net photosynthesis (A) and transpiration rates (B). Dashed lines: regressions between measured and predicted values; solid lines: 1 : 1 relationships. Open and filled symbols indicate leaves from canopies grown with N− and N+ nutrient solutions, respectively.
Model predictions of the whole-canopy response to N availability
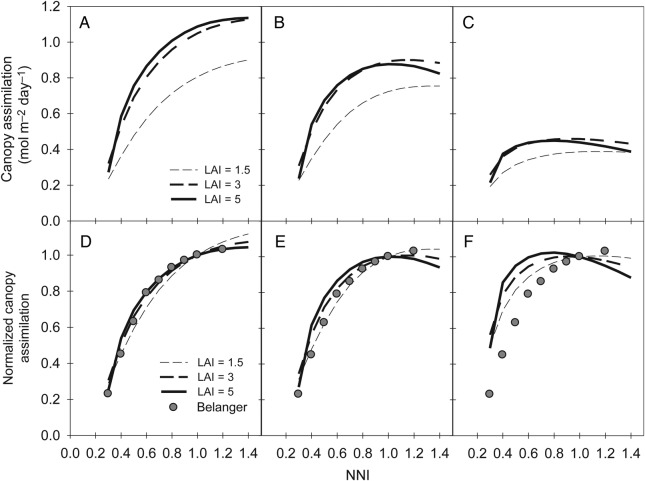
The behaviour of the model integrated at the whole-canopy level was assessed for canopies growing under a range of N availabilities. Examples of daily integrated canopy assimilation are presented in Fig. 6 for three contrasting days (DOY 176, 177 and 157 with an average PPFD decreasing from 709 to 610 and to 263 µmol m−2 s−1 and average air temperatures of 20.1, 26.3 and 17.9 °C, respectively). All canopies presented a saturating response curve to N availability. As expected, canopy assimilation was lower during cloudy days (Fig. 6A–C). Canopies with a LAI lower than that required for canopy closure (LAI below 3 m2 m−2) always displayed a lower assimilation rate per unit of soil area. Further increasing the LAI after canopy closure (LAI above 3 m2 m−2) did not improve canopy assimilation. The threshold at which canopy assimilation ceased to respond to N availability was very close to an NNI value of 1 for closed canopies during sunny and moderately cloudy days (Fig. 6D and E) and for open canopies during very cloudy days (Fig. 6F). Slight shifts of threshold were predicted, depending on the canopy LAI and light availability. Open canopies appeared to be more able to valorize high N availability and displayed delayed thresholds (e.g. at an NNI of ∼1.2 on sunny days). In contrast, dense canopies presented anticipated thresholds that were particularly apparent on cloudy days.
Figure 6.
Simulations for three contrasting days of whole-canopy net assimilation in response to changes in the canopy NNI and LAI (A–C) and their corresponding responses normalized by the assimilation rate at an NNI value of 1 (D–F). Grey circles in the lower panels represent the relative reduction in radiation use efficiency measured by Bélanger et al. (1992) in response to NNI.
Discussion
A simple empirical model to link leaf N distribution with plant N status and light distribution
To date, modelling the interaction between N limitations and light acclimation has been tackled using ‘goal seeking’ or optimal distribution theory (Chen et al. 1993; Thornley 1998; Johnson et al. 2010). Our study demonstrated how a combination of empirical relationships might be a promising option for this purpose too. The strategy proposed is based on modulation of the Nup and kN parameters used in the empirical distribution model as a function of plant N status (NNI). A linear relationship was found between Nup and NNI over the range of alfalfa canopies studied. Similar results had previously been reported in different grass species, where the relationship was shown to be stable under contrasting growth conditions and canopy structures (Farruggia et al. 2004; Gastal et al. 2015). In these species, Nup has even been used as a routine proxy to facilitate the determination of NNI in the field (Louarn et al. 2015; Maamouri et al. 2015). The second parameter in the empirical relationship, kN, was shown to be independent of NNI during the present study. Depending on the species, however, contradictory results have been reported concerning the effect of N limitation on kN. In some cases, limited effects have been observed (Sinclair and Shiraiwa 1993; Sadras et al. 2012), whereas in others, a steeper N gradient has been found in N-stressed plants (Dreccer et al. 2000; Milroy et al. 2001). Moreau et al. (2012) suggested that the size of the canopy (indirectly reduced by N stress), rather than a direct NNI effect, might explain the steeper gradient in N-limited wheat canopies. In line with our results, Lemaire et al. (1991) did not show any variation of kN in alfalfa canopies at contrasting developmental stages. Different types of plant architecture may affect N reallocation strategies and contribute to explaining these differences in the kN response. Some species, such as alfalfa or sunflower (Archontoulis et al. 2011), are made up of leaves distributed in different strata along the vertical light gradient, and may adjust more efficiently than long-leaf species (such as grasses or cereals) in which each leaf may simultaneously experience light conditions from the bottom to the top of the canopy. In those cases, the parameter a3 representing the dependency of kN on plant N status (Eq. 3) is likely to take values different from zero.
Assumptions and potential limitations of the leaf N distribution model
Species differ in the plasticity of their leaf traits and in the within-canopy variation of photosynthetic characteristics (Niinemets et al. 2015). The present model assumes that the distribution of leaf N is mainly driven by two factors: the light gradient within the canopy and the plant N status. No significant age effects were recorded in alfalfa, as previously shown in several other species (Evans 1993; Hikosaka et al. 1994). This is not a general feature however, and many plant species display age-dependent leaf traits, such as decreasing SLA in ageing leaves for instance. This can alter the light–Na relationship and limit the validity of our model (Prieto et al. 2012). In their recent review, Niinemets et al. (2015) distinguished two main groups of species: a first group with high rates of canopy development and leaf turnover, exhibiting highly dynamic light environments, active change photosynthetic characteristics by N reallocation among leaves, and a second group made up of species with slow leaf turnover exhibiting a passive Na acclimation response, primarily determined by the acclimation of leaf structure. The proposed model appears clearly best suited to the first group of species because they are less susceptible to leaf ageing effects.
Another limitation of empirical models is their validity out of their domain of calibration. Other environmental factors, such as water stress (Errecart et al. 2014), extreme temperatures or extreme light environments (as shown by the indoor/outdoor effect in our data set), can affect leaf growth and leaf traits. In some cases, this is likely to imply a reassessment model parameter values. Finally, the two-parameter model used [Eq. 1, see Supporting Information—Table S1] could present a lack of flexibility in some species. This formalism was previously used on other crops (Moreau et al. 2012; Sadras et al. 2012), but studies comparing a large number of species have generally relied on three-parameter models because they presented an overall better fit (Lötscher et al. 2003; Niinemets et al. 2015).
The N acquisition mode did not affect the photosynthetic parameters
Our study confirmed in alfalfa a linear relationship between Farquhar photosynthetic parameters (P25) and leaf N per unit leaf area (Field 1983; Evans 1989) and showed that it holds true for leaves in different canopies grown under contrasting mineral N availabilities. Acclimation to light and plant N status both affected the N concentration of leaves, but the Na–P25 relationships remained unchanged, as shown previously (Braune et al. 2009). In addition, our study examined the effects of the N acquisition mode in legumes, comparing fixing and non-fixing genotypes of alfalfa under different N nutrition statuses. There was no significant impact of the N acquisition mode on the Na–P25 relationships. We thus showed that, contrary to the whole-plant level (Gosse et al. 1986), no extra cost to carbon acquisition was associated with N fixation at the leaf level (Boller and Heichel 1984). No gain, associated with an extra carbon sink, was observed either. Overall, the Na–P25 relationships established during this study on a perennial forage legume displayed slopes (e.g. SNa of the relationship at 53 µmol g N−1 s−1) that were intermediate between those of cereals (60 and 63 µmol g N−1 s−1 for wheat and barley, respectively; Müller et al. 2005; Braune et al. 2009) and those of C3 trees and vines (e.g. ∼30 and 38 µmol g N−1 s−1 in walnut tree and grapevine, respectively; Le Roux et al. 1999; Prieto et al. 2012). This positioning was consistent with other productive grassland species (e.g. 36–50 µmol g N−1 s−1 reported for cocksfoot and red clover; Wohlfahrt et al. 1998).
Performance of the leaf gas exchange model at the leaf and whole-canopy levels
The gas exchange model correctly estimated daily cumulated values of net assimilation (A) and transpiration (E) at the leaf level and their diurnal patterns. Model errors, however, were greater with respect to transpiration. This might partly be related to the absence of a direct relationship between the leaf N and stomatal conductance parameters considered in the model. Indeed, the scaling parameter a1 has been shown to increase for leaves with a very low N concentration (Braune et al. 2009). In our case, however, discrepancies in E mainly concerned the top leaves under high N availability. An alternative explanation might be a less robust parameterization of the stomatal conductance model. Leaves from a single experiment were used, covering a more limited range of environmental conditions than that encountered in the validation data set (in terms of VPD in particular). Future work will incorporate the response to water deficit in the model, which should enable the refinement of this parameterization.
When upscaled at the whole-canopy level, the gas exchange model coupled with the N distribution model displayed interesting properties regarding the response to N availability. The relationship between N and the assimilation rate switched from a linear function at the leaf level to a saturating function at the whole-canopy scale. Above a certain threshold, the model predicted that an increase in N did not result in increased canopy assimilation. Such a point had previously been reported during numerous experiments comparing a broad range of N fertilization rates (Justes et al. 1994; Lemaire and Gastal 1997), and it defines the critical N concentration on which NNI calculations are based. Remarkably, such behaviour emerged from our canopy-integrated model. Furthermore, the NNI value corresponding to this transition happened to be very close to 1 during sunny and moderately cloudy days. This complied with the theoretical definition of NNI, which states that a value of 1 corresponds to the critical N concentration. The threshold was predicted to be lower during cloudy days. However, as in practice, the critical N concentrations are determined from cumulated values of biomass production, and critical N is likely to be primarily driven by sunny days (accounting for most biomass accumulation) rather than cloudy days.
No direct measurements were carried out to quantitatively assess the gas exchange model on alfalfa canopies. However, the simulated plateau values were consistent with previous studies measuring the daily net carbon exchange in closed canopies of alfalfa under non-limiting N. For instance, Heichel et al. (1988) reported net rates of 1.17, 0.81 and 0.45 mol CO2 m−2 day−1 in a 2.7 LAI canopy during days with average PPFD values of 1100, 700 and 400 µmol m−2 s−1, respectively (corresponding roughly to the light conditions prevailing during the 3 days shown in Fig. 6). Similarly, Woodward and Sheehy (1979) reported rates ranging from 0.27 to 1.39 mol CO2 m−2 day−1 after canopy closure during a spring regrowth. As in these two studies, the model outputs concerned the net aboveground carbon exchange of N fertilized alfalfa (with presumably limited N fixation). Allocation to the root system and to the respiration of roots and nodules needs to be implemented in future versions of the model in order to account for a potential cost of N fixation in terms of the carbon balance at the canopy level (Gosse et al. 1986). Root growth and respiration indeed represent a substantial share of carbohydrate use in fixing alfalfa (Thomas and Hill 1937; Layzell et al. 1981).
Fewer references were available to compare the response induced by N limitation. We, thus, compared the simulation results with those relative to regular non-fixing C3 plants and found a relative reduction in the net assimilation rate measured by Bèlanger et al. (1992) in a range of tall fescue canopies (Fig. 6). The simulated response curve of dense canopies on sunny and moderately cloudy days appeared to be particularly close to the measured curve, suggesting a good ability of the upscaled leaf model to capture the N stress response of a whole canopy.
Conclusions
Overall, the set of empirical relationships introduced in this article to distribute leaf N was simple and effective at predicting leaf N concentration in response to light and plant N status. The leaf gas exchange model proved accurate and produced consistent predictions in terms of whole-canopy assimilation under contrasting soil N availability scenarios. Even if the genericity of the coupled model still needs to be challenged in a broader range of species, this work constitutes a further step towards models that can bridge local acclimation to light with N acquisition and global N nutrition status, without presuming an optimal carbon gain or N distribution. Such a model relies on parameters that can all be directly measured and may help us to infer and better understand the differences in N use efficiency observed between species or genotypes.
Sources of Funding
This study received support from the Regional Council for Poitou-Charentes (http://www.poitou-charentes.fr) and INRA's Environment and Agronomy Division (INNI and TransfertN projects).
Contributions by the Authors
G.L., E.L. and J.P. contributed to model development. G.L. and E.F. designed the experiments and conducted measurements. They performed data analyses with the help of S.Z. All of the authors contributed to writing the manuscript.
Conflict of Interest Statement
None declared.
Supporting Information
The following additional information is available in the online version of this article –
Figure S1. Impact of leaf ageing and relative leaf irradiance on the specific leaf area and leaf nitrogen concentration per unit area in alfalfa.
Figure S2. Relationship between leaf age and the residuals of the fit of Eq. 1 to leaf nitrogen concentration.
Figure S3. Variations in leaf nitrogen concentrations predicted for alfalfa as a function of the nitrogen nutrition index of the canopy and the relative leaf irradiance.
Table S1. Comparison of two- and three-parameter models to account for distribution of leaf nitrogen concentrations with respect to relative irradiance in alfalfa.
Acknowledgements
We thank JoAnn Lamb, USDA, St Paul, MN for supplying us with the AgateNF lucerne seeds. We also would like to thank H. Bobille, S. Denis, A. Eprinchard, L. Fernandez, N. Moynet, A. Philiponneau, E. Rivault, N. Romero and J.P. Terrasson for their assistance with the experiments.
Appendix
Table A1.
Equations for the photosynthesis and stomatal conductance models.
| Equation | Description | No. |
|---|---|---|
| Photosynthesis model | ||
| Net photosynthetic rate (µmol CO2 m−2 s−1) | (A1) | |
| Carboxylation rate (µmol CO2 m−2 s−1) | (A2) | |
| RUBISCO-limited photosynthetic rate | (A3) | |
| RuBP regeneration-limited photosynthetic rate | (A4) | |
| TPU-limited photosynthetic rate | (A5) | |
| Electron transport rate, dependence on the radiance level | (A6) | |
| Arrhenius function, temperature dependence for Kc, Ko, Γ* and Rd | (A7) | |
| Arrhenius function, temperature dependence for Vcmax, Jmax and TPU | (A8) | |
| Nitrogen dependence function for Vcmax, Jmax, TPU and Rd at 25 °C | (A9) | |
| Stomatal conductance model | ||
| Stomatal conductance | (A10) | |
| CO2 partial pressure at the leaf surface | (A11) | |
| Ci value by coupling A and gs | (A12) | |
Table A2.
Symbols, values and units of different parameters, variables and constants used in the photosynthetic and stomatal conductance models. 1Values taken from Schultz (2003). 2Values taken from Harley et al. (1992). 3Constant used for measurement in the leaf chamber of the LcPro (ADC Lcpro, BioScientific Ltd, Hoddesdon, Hertfordshire, UK).
| Symbol | Value | Unit | Description |
|---|---|---|---|
| Photosynthesis model | |||
| α | 0.201 | µmol CO2 µmol photon−1 | Photochemical efficiency or initial quantum yield |
| Γ* | – | Pa | Compensation point for CO2 in the absence of mitochondrial respiration |
| A | – | µmol CO2 m−2 s−1 | Net photosynthetic rate |
| Ac | – | µmol CO2 m−2 s−1 | RUBISCO-limited photosynthetic rate |
| Aj | – | µmol CO2 m−2 s−1 | Electron transport rate-limited photosynthetic rate |
| Ap | – | µmol CO2 m−2 s−1 | Triose phosphate utilization-limited photosynthetic rate |
| c | – | – | Scaling constant |
| Ca | – | Pa | Ambient CO2 partial pressure |
| Ci | – | Pa | Intercellular CO2 partial pressure |
| ΔHa | – | kJ mol−1 | Enthalpy of activation |
| ΔHd | 2002 | kJ mol−1 | Enthalpy of deactivation |
| Kc | – | Pa | Michaelis–Menten constant of RUBISCO for CO2 |
| Ko | – | kPa | Michaelis–Menten constant of RUBISCO for O2 |
| J | – | µmol electron m−2 s−1 | Electron transport rate |
| Jmax | – | µmol m−2 s−1 | Maximum electron transport rate |
| Na | – | g m−2 | Area based N content |
| Namin | – | g m−2 | Minimum value of Na at which P25 → 0 |
| O | 21 | kPa | Oxygen partial pressure |
| P25 | – | µmol m−2 s−1 | Value of Vcmax, Jmax, TPU or Rd at 25 °C |
| PPFD | – | µmol m−2 s−1 | Photosynthetic photon flux density |
| R | 0.00831 | kJ mol−1 K−1 | Universal gas constant for perfect gases |
| Rd | – | µmol m−2 s−1 | Mitochondrial respiration in light |
| ΔS | 0.6352 | kJ mol−1 | Entropy term |
| SNa | – | µmol g−1 s−1 | Slope of the relationship between Na and Vcmax, Jmax, TPU or Rd |
| Tleaf | – | °C | Leaf temperature in degrees Celsius |
| Tk | – | Kelvin degrees | Leaf temperature in Kelvin |
| TPU | – | µmol m−2 s−1 | Triose phosphate utilization rate |
| Vc | – | µmol m−2 s−1 | Carboxylation rate |
| Vo | – | µmol m−2 s−1 | Oxygenation rate |
| Vcmax | – | µmol m−2 s−1 | Maximum rate of RUBISCO carboxylation |
| Stomatal conductance model | |||
| Cs | – | Pa | CO2 partial pressure at the leaf surface |
| gb | 2.3573 | mol m−2 s−1 | Boundary layer conductance |
| gs | – | mmol m−2 s−1 | Stomatal conductance |
| go | 0.020 | mmol m−2 s−1 | Residual stomatal conductance when A → 0 |
| VPD | – | kPa | Water VPD |
| Do | 2.86 | kPa | Empirical factor assessing stomata sensitivity to VPD |
| a1 | 12.5 | – | Empirical stomatal conductance factor |
Table A3.
Values of c (scaling constant), enthalpies of activation (ΔHa) describing the temperature response for parameters of the photosynthesis model. 1Values taken from Bernacchi et al. (2001). 2Values taken from Bernacchi et al. (2003). 3Values taken from Harley et al. (1992).
| Parameter | Value at 25 °C | c | ΔHa (kJ mol−1) |
|---|---|---|---|
| Vcmax | – | 26.351 | 65.331 |
| Jmax | – | 17.72 | 43.92 |
| TPU | – | 21.463 | 53.13 |
| Rd | – | 18.721 | 46.391 |
| Γ* | 42.751 | 19.021 | 37.831 |
| Kc | 404.91 | 38.051 | 79.431 |
| Ko | 278.41 | 20.301 | 36.381 |
Literature Cited
- Anten NPR, Schieving F, Werger MJA. 1995. Patterns of light and nitrogen distribution in relation to whole canopy carbon gain in C3 and C4 mono- and dicotyledonous species. Oecologia 101:504–513. 10.1007/BF00329431 [DOI] [PubMed] [Google Scholar]
- Archontoulis SV, Vos J, Yin X, Bastiaans L, Danalatos NG, Struik PC. 2011. Temporal dynamics of light and nitrogen vertical distributions in canopies of sunflower, kenaf and cynara. Field Crops Research 122:186–198. 10.1016/j.fcr.2011.03.008 [DOI] [Google Scholar]
- Baldissera TC, Frak E, de Faccio Carvalho PC, Louarn G. 2014. Plant development controls leaf area expansion in alfalfa plants competing for light. Annals of Botany 113:145–157. 10.1093/aob/mct251 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ball MC, Woodrow IE, Berry JA. 1987. A model predicting stomatal conductance and its contribution to the control of photosynthesis under different environmental conditions. In: Biggins J, ed. Progress in photosynthesis research. Netherlands: Springer, 221–224. [Google Scholar]
- Barillot R, Louarn G, Escobar-Gutiérrez AJ, Huynh P, Combes D. 2011. How good is the turbid medium-based approach for accounting for light partitioning in contrasted grass-legume intercropping systems? Annals of Botany 108:1013–1024. 10.1093/aob/mcr199 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Barnes D, Heichel G, Vance C, Peaden R. 1990. Registration of ‘ineffective agate’ and ‘ineffective saranac’ non-N2-fixing alfalfa germplasms. Crop Science 30:752–753. [Google Scholar]
- Bélanger G, Gastal F, Lemaire G. 1992. Growth analysis of a tall fescue sward fertilized with different rates of nitrogen. Crop Science 32:1371–1376. 10.2135/cropsci1992.0011183X003200060013x [DOI] [Google Scholar]
- Bernacchi CJ, Singsaas EL, Pimentel C, Portis AR Jr, Long SP. 2001. Improved temperature response functions for models of Rubisco-limited photosynthesis. Plant, Cell and Environment 24:253–259. 10.1111/j.1365-3040.2001.00668.x [DOI] [Google Scholar]
- Bernacchi CJ, Pimentel C, Long SP. 2003. In vivo temperature response functions of parameters required to model RuBP-limited photosynthesis. Plant, Cell and Environment 26:1419–1430. 10.1046/j.0016-8025.2003.01050.x [DOI] [Google Scholar]
- Boller BC, Heichel GH. 1984. Canopy structure and photosynthesis of alfalfa genotypes differing in nodule effectiveness. Crop Science 24:91–96. 10.2135/cropsci1984.0011183X002400010021x [DOI] [Google Scholar]
- Braune H, Müller J, Diepenbrock W. 2009. Integrating effects of leaf nitrogen, age, rank, and growth temperature into the photosynthesis-stomatal conductance model LEAFC3-N parameterised for barley (Hordeum vulgare L.). Ecological Modelling 220:1599–1612. 10.1016/j.ecolmodel.2009.03.027 [DOI] [Google Scholar]
- Brisson N, Launay M, Mary B, Beaudoin N. 2009. Conceptual basis, formalisations and parameterization of the STICS crop model. QUAE Editions, Collection “Update Science and Technologies”, Versailles, FR. 297 pp. [Google Scholar]
- Charles-Edwards DA. 1981. The mathematics of photosynthesis and productivity. Academic Press, London, 127 pp. [Google Scholar]
- Chen JL, Reynolds JF, Harley PC, Tenhunen JD. 1993. Coordination theory of leaf nitrogen distribution in a canopy. Oecologia 93:63–69. 10.1007/BF00321192 [DOI] [PubMed] [Google Scholar]
- Colnenne C, Meynard JM, Reau R, Justes E, Merrien A. 1998. Determination of a critical nitrogen dilution curve for winter oilseed rape. Annals of Botany 81:311–317. 10.1006/anbo.1997.0557 [DOI] [Google Scholar]
- De Pury DGG, Farquhar GD. 1997. Simple scaling of photosynthesis from leaves to canopies without the errors of big-leaf models. Plant, Cell and Environment 20:537–557. 10.1111/j.1365-3040.1997.00094.x [DOI] [Google Scholar]
- Dreccer MF, Van Oijen M, Schapendonk AHCM, Pot CS, Rabbinge R. 2000. Dynamics of vertical leaf nitrogen distribution in a vegetative wheat canopy. Impact on canopy photosynthesis. Annals of Botany 86:821–831. 10.1006/anbo.2000.1244 [DOI] [Google Scholar]
- Errecart PM, Agnusdei MG, Lattanzi FA, Marino MA, Berone GD. 2014. Critical nitrogen concentration declines with soil water availability in tall fescue. Crop Science 54:318–330. 10.2135/cropsci2013.08.0561 [DOI] [Google Scholar]
- Evans JR. 1989. Photosynthesis and nitrogen relationships in leaves of C3 plants. Oecologia 78:9–19. 10.1007/BF00377192 [DOI] [PubMed] [Google Scholar]
- Evans JR. 1993. Photosynthetic acclimation and nitrogen partitioning within a lucerne canopy. I. Canopy characteristics. Australian Journal of Plant Physiology 20:55–67. 10.1071/PP9930055 [DOI] [Google Scholar]
- Evers JB, Vos J, Yin X, Romero P, Van der Putten PEL, Struik PC. 2010. Simulation of wheat growth and development based on organ-level photosynthesis and assimilate allocation. Journal of Experimental Botany 61:2203–2216. 10.1093/jxb/erq025 [DOI] [PubMed] [Google Scholar]
- Farquhar GD, Von Caemmerer S, Berry JA. 1980. A biochemical model of photosynthetic CO2 assimilation in leaves of C3 species. Planta 149:78–90. 10.1007/BF00386231 [DOI] [PubMed] [Google Scholar]
- Farruggia A, Gastal F, Scholefield D. 2004. Assessment of the nitrogen status of grassland. Grass and Forage Science 59:113–120. 10.1111/j.1365-2494.2004.00411.x [DOI] [Google Scholar]
- Field C. 1983. Allocating leaf nitrogen for the maximization of carbon gain: leaf age as a control on the allocation program. Oecologia 56:341–347. 10.1007/BF00379710 [DOI] [PubMed] [Google Scholar]
- Field CB, Mooney HA. 1986. The nitrogen/photosynthesis relationship in wild plants. In: Givnish TJ, ed. On the economy of plant form and function. Cambridge, UK: Cambridge University Press, 25–55. [Google Scholar]
- Gastal F, Lemaire G, Durand JL, Louarn G. 2015. Quantifying crop responses to nitrogen and avenues to improve nitrogen-use efficiency. In: Sadras VO, Calderini D, eds. Crop physiology—applications for genetic improvement and agronomy, 2nd edn London, UK: Academic Press, Elsevier, 161–206. [Google Scholar]
- Givnish TJ. 1988. Adaptation to sun and shade: a whole-plant perspective. Australian Journal of Plant Physiology 15:63–92. 10.1071/PP9880063 [DOI] [Google Scholar]
- Gosse G, Varlet-Grancher C, Bonhomme R, Chartier M, Allirand JM, Lemaire G. 1986. Production maximale de matière sèche et rayonnement solaire intercepté par un couvert végétal. Agronomie 6:47–56. 10.1051/agro:19860103 [DOI] [Google Scholar]
- Greenwood DJ, Lemaire G, Gosse G, Cruz P, Draycott A, Neeteson JJ. 1990. Decline in percentage N of C3 and C4 crops with increasing plant mass. Annals of Botany 66:425–436. [Google Scholar]
- Harley PC, Thomas RB, Reynolds JF, Strain BR. 1992. Modelling photosynthesis of cotton grown in elevated CO2. Plant, Cell and Environment 15:271–282. 10.1111/j.1365-3040.1992.tb00974.x [DOI] [Google Scholar]
- Heichel GH, Delaney RH, Cralle HT. 1988. Carbon assimilation, partitioning and utilization. In: Hanson AA, Barnes DK, Hill RR, eds. Alfalfa and alfalfa improvement. Madison, WI: American Society of Agronomy, 195–228. [Google Scholar]
- Hikosaka K. 2004. Interspecific difference in the photosynthesis-nitrogen relationship: patterns, physiological causes, and ecological importance. Journal of Plant Research 117:481–494. 10.1007/s10265-004-0174-2 [DOI] [PubMed] [Google Scholar]
- Hikosaka K, Terashima I, Katoh S. 1994. Effects of leaf age, nitrogen nutrition and photon flux density on the distribution of nitrogen among leaves of a vine (Ipomoea tricolor Cav.) grown horizontally to avoid mutual shading of leaves. Oecologia 97:451–457. 10.1007/BF00325881 [DOI] [PubMed] [Google Scholar]
- Hirose T, Werger MJA. 1987. Maximizing daily canopy photosynthesis with respect to the leaf nitrogen allocation pattern in the canopy. Oecologia 72:520–526. 10.1007/BF00378977 [DOI] [PubMed] [Google Scholar]
- Johnson IR, Thornley JHM, Frantz JM, Bugbee B. 2010. A model of canopy photosynthesis incorporating protein distribution through the canopy and its acclimation to light, temperature and CO2. Annals of Botany 106:735–749. 10.1093/aob/mcq183 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Justes E, Mary B, Meynard J-M, Machet JM, Thelier-Huché L. 1994. Determination of a critical nitrogen dilution curve for winter wheat crops. Annals of Botany 74:397–407. 10.1006/anbo.1994.1133 [DOI] [Google Scholar]
- Kull O. 2002. Acclimation of photosynthesis in canopies: models and limitations. Oecologia 133:267–279. 10.1007/s00442-002-1042-1 [DOI] [PubMed] [Google Scholar]
- Kull O, Jarvis PG. 1995. The role of nitrogen in a simple scheme to scale up photosynthesis from leaf to canopy. Plant, Cell and Environment 18:1174–1182. 10.1111/j.1365-3040.1995.tb00627.x [DOI] [Google Scholar]
- Layzell DB, Pate JS, Atkins CA, Canvin DT. 1981. Partitioning of carbon and nitrogen and the nutrition of root and shoot apex in a nodulated legume. Plant Physiology 67:30–36. 10.1104/pp.67.1.30 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lemaire G, Gastal F. 1997. N uptake and distribution in plant canopies. In: Lemaire G, ed. Diagnosis of the nitrogen status in crops. Heidelberg: Springer, 3–43. [Google Scholar]
- Lemaire G, Salette J, Sigogne M, Terrasson J-P. 1984. Relation entre dynamique de croissance et dynamique de prélèvement d'azote pour un peuplement de graminées fourragères. I.—Etude de l'effet du milieu. Agronomie 4:423–430. 10.1051/agro:19840503 [DOI] [Google Scholar]
- Lemaire G, Cruz P, Gosse G, Chartier M. 1985. Etude des relations entre la dynamique de prélèvement d'azote et la dynamique de croissance en matière sèche d'un peuplement de luzerne (Medicago sativa L.). Agronomie 5:685–692. 10.1051/agro:19850803 [DOI] [Google Scholar]
- Lemaire G, Onillon B, Gosse G, Chartier M, Allirand JM. 1991. Nitrogen distribution within a lucerne canopy during regrowth: relation with light distribution. Annals of Botany 68:483–488. [Google Scholar]
- Lemaire G, Avice J-C, Kim T-H, Ourry A. 2005. Developmental changes in shoot N dynamics of lucerne (Medicago sativa L.) in relation to leaf growth dynamics as a function of plant density and hierarchical position within the canopy. Journal of Experimental Botany 56:935–943. 10.1093/jxb/eri084 [DOI] [PubMed] [Google Scholar]
- Le Roux X, Grand S, Dreyer E, Daudet FA. 1999. Parameterization and testing of a biochemically based photosynthesis model for walnut (Juglans regia) trees and seedlings. Tree Physiology 19:481–492. 10.1093/treephys/19.8.481 [DOI] [PubMed] [Google Scholar]
- Leuning R. 1995. A critical appraisal of a combined stomatal-photosynthesis model for C3 plants. Plant, Cell and Environment 18:339–355. 10.1111/j.1365-3040.1995.tb00370.x [DOI] [Google Scholar]
- Long SP, Bernacchi CJ. 2003. Gas exchange measurements, what can they tell us about the underlying limitations to photosynthesis? Procedures and sources of error. Journal of Experimental Botany 54:2393–2401. 10.1093/jxb/erg262 [DOI] [PubMed] [Google Scholar]
- Lötscher M, Stroh K, Schnyder H. 2003. Vertical leaf nitrogen distribution in relation to nitrogen status in grassland plants. Annals of Botany 92:679–688. 10.1093/aob/mcg188 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Louarn G, Pereira-Lopès E, Fustec J, Mary B, Voisin A-S, De Faccio Carvalho PC, Gastal F. 2015. The amounts and dynamics of nitrogen transfer to grasses differ in alfalfa and white clover-based grass-legume mixtures as a result of rooting strategies and rhizodeposit quality. Plant and Soil 389:289–305. [Google Scholar]
- Maamouri A, Louarn G, Gastal F, Béguier V, Julier B. 2015. Effects of lucerne genotype on morphology, biomass production and nitrogen content of lucerne and tall fescue in mixed pastures. Crop and Pasture Science 66:192–204. [Google Scholar]
- Milroy SP, Bange MP, Sadras VO. 2001. Profiles of leaf nitrogen and light in reproductive canopies of cotton (Gossypium hirsutum). Annals of Botany 87:325–333. 10.1006/anbo.2000.1344 [DOI] [Google Scholar]
- Moreau D, Allard V, Gaju O, Le Gouis J, Foulkes MJ, Martre P. 2012. Acclimation of leaf nitrogen to vertical light gradient at anthesis in wheat is a whole-plant process that scales with the size of the canopy. Plant Physiology 160:1479–1490. 10.1104/pp.112.199935 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Müller J, Wernecke P, Diepenbrock W. 2005. LEAFC3-N: a nitrogen-sensitive extension of the CO2 and H2O gas exchange model LEAFC3 parameterised and tested for winter wheat (Triticum aestivum L.). Ecological Modelling 183:183–210. 10.1016/j.ecolmodel.2004.07.025 [DOI] [Google Scholar]
- Niinemets Ü, Keenan TF, Hallik L. 2015. A worldwide analysis of within-canopy variations in leaf structural, chemical and physiological traits across plant functional types. New Phytologist 205:973–993. 10.1111/nph.13096 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pettersson R, Mcdonald AJS. 1994. Effects of nitrogen supply on the acclimation of photosynthesis to elevated CO2. Photosynthesis Research 39:389–400. 10.1007/BF00014593 [DOI] [PubMed] [Google Scholar]
- Plénet D, Lemaire G. 1999. Relationships between dynamics of nitrogen uptake and dry matter accumulation in maize crops. Determination of critical N concentration. Plant and Soil 216:65–82. 10.1023/A:1004783431055 [DOI] [Google Scholar]
- Prieto JA, Louarn G, Perez Peña J, Ojeda H, Simonneau T, Lebon E. 2012. A leaf gas exchange model that accounts for intra-canopy variability by considering leaf nitrogen content and local acclimation to radiation in grapevine (Vitis vinifera L.). Plant, Cell and Environment 35:1313–1328. 10.1111/j.1365-3040.2012.02491.x [DOI] [PubMed] [Google Scholar]
- Sadras VO, Lawson C, Montoro A. 2012. Photosynthetic traits in Australian wheat varieties released between 1958 and 2007. Field Crops Research 134:19–29. 10.1016/j.fcr.2012.04.012 [DOI] [Google Scholar]
- Sands PJ. 1995. Modelling canopy production. II. From single-leaf photosynthesis parameters to daily canopy photosynthesis. Australian Journal of Plant Physiology 22:603–614. 10.1071/PP9950603 [DOI] [Google Scholar]
- Schultz HR. 2003. Extension of a Farquhar model for limitations of leaf photosynthesis induced by light environment, phenology and leaf age in grapevines (Vitis vinifera L. cvv. White Riesling and Zinfandel). Functional Plant Biology 30:673–687. 10.1016/0034-4257(92)90102-P [DOI] [PubMed] [Google Scholar]
- Sellers PJ, Berry JA, Collatz GJ, Field CB, Hall FG. 1992. Canopy reflectance, photosynthesis, and transpiration. III. A reanalysis using improved leaf models and a new canopy integration scheme. Remote Sensing of Environment 42:187–216. 10.1016/0034-4257(92)90102-P [DOI] [Google Scholar]
- Sharkey TD, Bernacchi CJ, Farquhar GD, Singsaas EL. 2007. Fitting photosynthetic carbon dioxide response curves for C3 leaves. Plant, Cell and Environment 30:1035–1040. 10.1111/j.1365-3040.2007.01710.x [DOI] [PubMed] [Google Scholar]
- Sinclair TR, Shiraiwa T. 1993. Soybean radiation-use efficiency as influenced by nonuniform specific leaf nitrogen distribution and diffuse radiation. Crop Science 33:808–812. 10.2135/cropsci1993.0011183X003300040036x [DOI] [Google Scholar]
- Sinoquet H, Le Roux X, Adam B, Ameglio T, Daudet FA. 2001. RATP: a model for simulating the spatial distribution of radiation absorption, transpiration and photosynthesis within canopies: application to an isolated tree crown. Plant, Cell and Environment 24:395–406. 10.1046/j.1365-3040.2001.00694.x [DOI] [Google Scholar]
- Thomas MD, Hill GR. 1937. The continuous measurement of photosynthesis, respiration, and transpiration of alfalfa and wheat growing under field conditions. Plant Physiology 12:285–307. 10.1104/pp.12.2.285 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Thornley JHM. 1998. Dynamic model of leaf photosynthesis with acclimation to light and nitrogen. Annals of Botany 81:421–430. 10.1006/anbo.1997.0575 [DOI] [Google Scholar]
- Wohlfahrt G, Bahn M, Horak I, Tappeiner U, Cernusca A. 1998. A nitrogen sensitive model of leaf carbon dioxide and water vapour gas exchange: application to 13 key species from differently managed mountain grassland ecosystems. Ecological Modelling 113:179–199. 10.1016/S0304-3800(98)00143-4 [DOI] [Google Scholar]
- Woodward FI, Sheehy JE. 1979. Microclimate, photosynthesis and growth of lucerne (Medicago sativa L.). II. Canopy structure and growth. Annals of Botany 44:709–719. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.