Inhibitory Actions Unified by Network Integration

SUMMARY

Cortical function is regulated by a strikingly diverse array of local-circuit inhibitory neurons. We evaluated how optogenetically activating somatostatin- and parvalbumin-positive interneurons subtractively or divisively suppressed auditory cortical cells’ responses to tones. In both awake and anesthetized animals, we found that activating either family of interneurons produced mixtures of divisive and subtractive effects and that simultaneously recorded neurons were often suppressed in qualitatively different ways. A simple network model shows that threshold nonlinearities can interact with network activity to transform subtractive inhibition of neurons into divisive inhibition of networks, or vice versa. Varying threshold and the strength of suppression of a model neuron could determine whether the effect of inhibition appeared divisive, subtractive, or both. We conclude that the characteristics of response inhibition specific to a single interneuron type can be “masked” by the network configuration and cellular properties of the network in which they are embedded.

INTRODUCTION

Synaptic inhibition shapes the response properties of every neuron in the auditory cortex (AC), either directly (through synaptic inhibition onto the examined neuron [De Ribaupierre et al., 1972; Volkov and Galazjuk, 1991; Wehr and Zador, 2003; Kaur et al., 2004]) or indirectly (by inhibiting the cells that synapse onto it [Wang et al., 2000, 2002; Foeller et al., 2001]). Within the AC, the numerous subtypes of inhibitory interneurons show a remarkable diversity in their anatomical, electrical, and molecular properties (reviewed in Markram et al., 2004; Freund and Katona, 2007; Ascoli et al., 2008; DeFelipe et al., 2013). Each subtype expresses its own unique combination of ion channels and receptors, targets specific cell types and cellular compartments, and has its own laminar organization. This implies that the different sources of intracortical inhibition may provide multiple, selective mechanisms for modulating different aspects of cortical information processing (Vu and Krasne, 1992; Miles et al., 1996). Much effort has been expended to relate interneuron types and their specializations to their specific computational roles.

One common, conceptually straightforward framework models the effects of synaptic inhibition as a linear transformation with a divisive (scaling) and a subtractive (shifting) component (Chance and Abbott, 2000; Doiron et al., 2001; Mitchell and Silver, 2003; Prescott and De Koninck, 2003; Hao et al., 2009). In this view, the essential question is whether the suppression that an interneuron type provides is predominantly divisive or predominantly subtractive (Atallah et al., 2012; Lee et al., 2012; Wilson et al., 2012). This framework has been applied to visual cortex by several groups with seemingly conflicting results (Atallah et al., 2012, 2014; Lee et al., 2012, 2014; Wilson et al., 2012; El-Boustani and Sur, 2014; Xue et al., 2014), producing an ongoing debate regarding whether separate functions of division and subtraction can be assigned to different populations of interneuron and whether those assignments are fixed. Indeed, evidence from a variety of physiological and modeling studies has converged to produce clear predictions regarding which interneuron types will implement divisive versus subtractive suppression (Vu and Krasne, 1992; Miles et al., 1996; Hao et al., 2009; Jadi et al., 2012). Yet the majority of this work has been carried out in single neurons or single-neuron models. Due to the densely interconnected nature of cortical networks, changes in inhibition may significantly affect the activity of other neurons in the network (Tsodyks et al., 1997; Hasenstaub et al., 2007; Ozeki et al., 2009), raising the possibility that an interneuron’s overall effect on neural processing may differ from its direct effect on individual targets.

To address this issue, we studied the effects of activation of two types of interneuron in mouse primary AC on basic auditory response properties. We evaluated the resulting changes in response properties within a threshold-linear suppression framework and designed a simple model to evaluate our results in the context of a larger cortical network.

RESULTS

We evaluated the effects of activating the two most numerous families of cortical interneuron, those expressing somatostatin (Sst) and those expressing parvalbumin (Pvalb). Sst is expressed in roughly 25% of cortical inhibitory interneurons, including interneuron subtypes that avoid synapsing onto excitatory neurons’ somata and instead form contacts on their (mainly distal) dendrites (Kawaguchi and Kubota, 1997, 1998); these synapses are electrotonically isolated both from the proximal dendrites (on which feedforward synapses are made), from the cell body (at which signals from different dendritic branches are integrated), and from the axon initial segment (Vu and Krasne, 1992; Miles et al., 1996; Hao et al., 2009; Jadi et al., 2012). Thus, the standard prediction, based on single-cell studies, is that at the soma or axon initial segment (the site of action potential generation), Sst+ cells’ activation will produce a change in current, but not a change in conductance; this would produce subtractive but not multiplicative effects on responsiveness to excitatory synapses closer to the cell body (Blomfield, 1974; Sturgill and Isaacson, 2015). In contrast, Pvalb is expressed in roughly ~50% of cortical inhibitory interneurons, including subtypes whose axons form “baskets,” enfolding the soma in a dense net of inhibitory synapses, or “chandeliers,” enfolding the axon initial segment (DeFelipe et al., 1989; Hendry et al., 1989; Kawaguchi and Kubota, 1998). Because these synapses are electrotonically close to the site of action potential generation, their activation effectively changes somatic conductance (as well as membrane potential), and their activation is thus predicted to produce divisive or mixed subtractive/divi-sive effects on cells’ responsiveness (Tuckwell, 1986; Holt and Koch, 1997; Borg-Graham et al., 1998; Chance and Abbott, 2000; Mitchell and Silver, 2003).

In order to compare the effects of Pvalb+ versus Sst+ neuron activation in an interconnected network, we produced mice in which Sst+ or Pvalb+ interneurons could be optogenetically activated by crossing strains that express Cre-recombinase under control of Sst or Pvalb promoters (Taniguchi et al., 2011) with a strain in which expression of ChR2-eYFP is Cre dependent (Ai32) (Madisen et al., 2012). In Ai32 × Sst-Cre mice (“Ai32/ Sst”), GFP and Pvalb did not colocalize (Figure 1A), while in Ai32 × Pvalb-Cre mice (“Ai32/Pvalb”), GFP and Pvalb did co-localize (Figure 1H). This is consistent with expression patterns established by numerous groups (Cardin et al., 2009; Sohal et al., 2009; Cardin et al., 2010; Kerlin et al., 2010; Taniguchi et al., 2011; Adesnik et al., 2012; Kvitsiani et al., 2013; Pfeffer et al., 2013) who found low (<10%) levels of misexpression within the cortex.

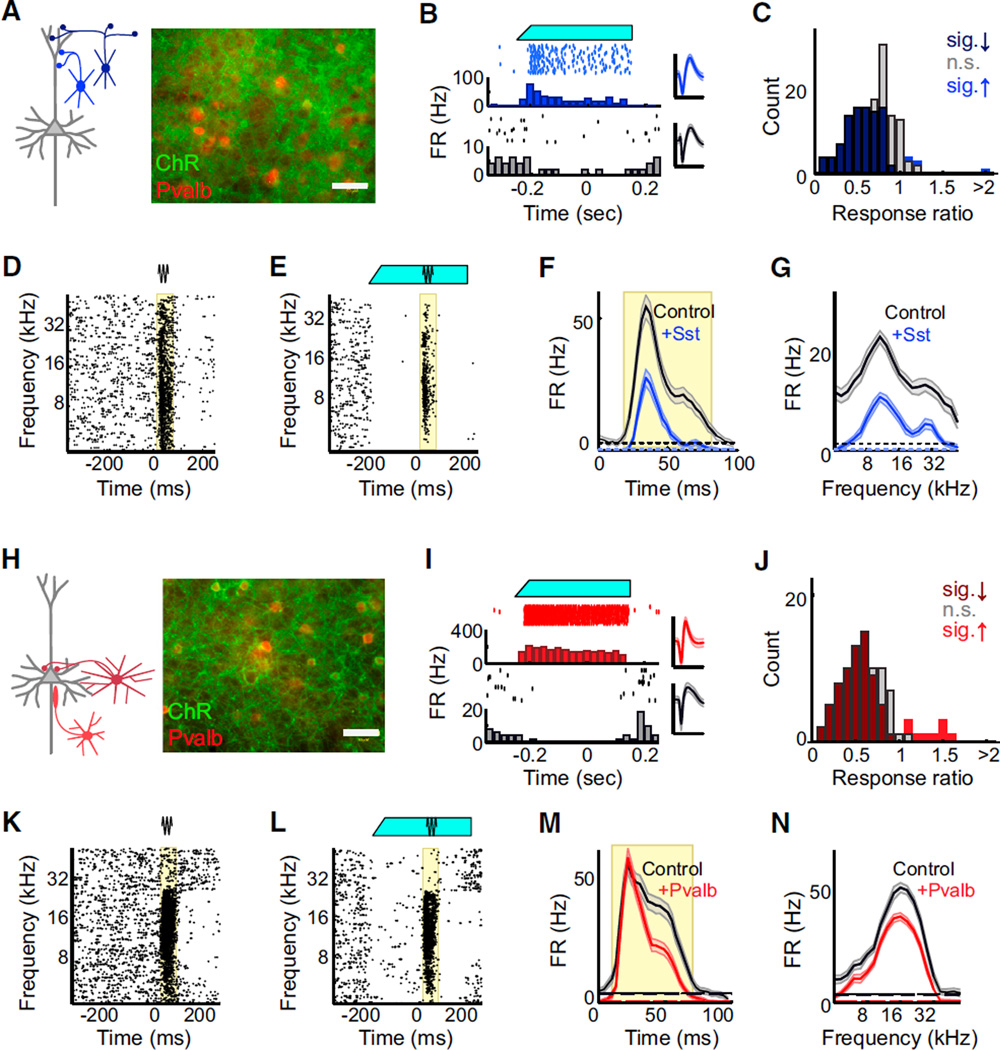
Figure 1. Optogenetic Activation of Sst+ and Pvalb+ Interneurons in A1.

(A) Left: schematic of prominent connections from Sst+ interneurons (blue) onto the dendrites of a pyramidal neuron (gray). Right: immunofluores-cent labeling of Pvalb (red) did not co-localize with ChR2 (green) when Cre-dependent ChR2 was expressed in Sst-Cre mice (“Ai32/Sst”). Scale bar: 50 µm.

(B) Blue light illumination of the cortical surface (top, cyan) of anesthetized Ai32/Sst mice increased the activity of some units (middle/blue: rasters, PSTH, and spike waveform for an example light-activated unit), while suppressing activity of others (bottom/ black: rasters, PSTH, andwaveform for anexample light-suppressed unit). Scale bar: 2 ms.

(C) Distribution of light effects on tone-evoked firing rate in anesthetized Ai32/Sst mice. Dark blue bars: units for which light significantly reduced activity (n = 76 of 145 units), light blue bars: units for which light significantly increased activity (n = 3 of 145 units), gray bars: units for which light did not significantly change activity (n = 66 of 145 units), as determined by a rank-sum test between control and light-activation trials, α = 0.05.

(D and E) Raster of tone-evoked firing for a representative unit without (D) and with (E) light (cyan bar). Black and cyan lines: periods of tone and light stimuli. Yellow region: times during which firing rate was significantly elevated above baseline (rank-sum test, α = 0.001 following multiple comparisons correction).

(F) Aggregate PSTHs of spikes across all tones on trials without light (black) versus with light (blue). Dashed line: baseline firing rate. Yellow region: time range during which firing rate was significantly elevated above baseline (rank-sum test, α = 0.001). Data are represented as mean ± SEM.

(G) FTP of spike counts during the response region (yellow) on trials without light (black) versus with light (blue). Dashed line: baseline firing rate. Data are represented as mean ± SEM.

(H) Left: schematic of prominent connections from Pvalb+ interneurons (red) onto perisomatic regions of a pyramidal neuron (gray). Right: immunofluorescent labeling of Pvalb (red) co-localized with ChR2 (green) when Cre-dependent ChR2 was expressed in Pvalb-Cre mice (“Ai32/Pvalb”).

(I–N) Corresponding to (B)–(G): example waveforms, responses, and effect distributions from recordings in Ai32/Pvalb rather than Ai32/Sst mice.

We then used linear 16-channel silicon probes to record the responses of isolated single units across the auditory cortical layers to pure-tone acoustic stimulation with and without blue-light illumination of the cortical surface. In Ai32/Sst mice under ketamine-xylazine anesthesia, blue-light illumination of the cortical surface suppressed spontaneous activity in most units (Figures 1B and 1C) but caused a small subset of units—putative Sst+ interneurons—to substantially increase their firing rates (p < 0.05 in 7 of 250 units from 23 animals). Similarly, in Ai32/ Pvalb mice under ketamine-xylazine anesthesia, blue-light illumination of the cortical surface suppressed spontaneous and evoked activity in most units (Figures 1I and 1J) but caused a small subset of units—putative Pvalb+ interneurons—to substantially increase their firing rates (p < 0.05 in 6 of 154 units from 11 animals).

We set light levels to ~40 µW to produce visually apparent suppression of tone-evoked multiunit activity. Among the tone-responsive units recorded (Ai32/Sst: n = 145 of 250, Ai32/ Pvalb-Cre: n = 91 of 154), the majority showed reduced responses to tones during optical stimulation (Ai32/Sst: 76 of 145 decreased, 3 increased, 66 no significant change; Ai32/ Pvalb: 63 of 91 decreased, 9 increased, 19 no significant change). We then computed temporal profiles of the tone response with and without blue-light illumination (Figures 1D, 1E, 1K, and 1L). From the firing rate over time for all tested tones (the cumulative peri-stimulus time histogram [cPSTH]), we identified the time period with significant response over baseline activity (Figures 1F and 1M, significant response period in red). We constructed iso-intensity frequency tuning profiles (FTPs) by measuring the firing rate during that time period as a function of stimulus frequency (Figure 1G and 1N).

Activating Either Sst+ or Pvalb+ Neurons Produces a Mixture of Divisive and Subtractive Suppression

In a threshold-linear response framework, when neurons’ responses are described in terms of canonical “tuning curves” relating their synaptic or sensory inputs to their spiking outputs, other factors such as synaptic inhibition are then characterized in terms of their effects on the scale or offset of these curves (Figure 2A). A factor may be described as subtractive (green) if it provides a constant bias to all responses—in other words, if it results in equal changes in all parts of the tuning curve, subject to thresholding. Conversely, a factor may be described as divisive (purple) if it changes the overall gain of neural re-sponses—in other words, if it has absolutely greater effects on the processing of stimuli that normally evoke stronger responses. Plotting a straight-line fit of the control versus the suppressed responses to each stimulus (Figure 2B) allows us to evaluate whether suppression in a given neuron is well described by this linear framework, and if so, the extent to which its suppression is divisive, subtractive, or a mixture of both. In a subtractively suppressed neuron, this best-fit line will have a slope of 1 and a y-intercept significantly less than 0, while in a divisively suppressed neuron, the best-fit line will have a slope significantly less than 1 and a y-intercept not significantly different from 0.

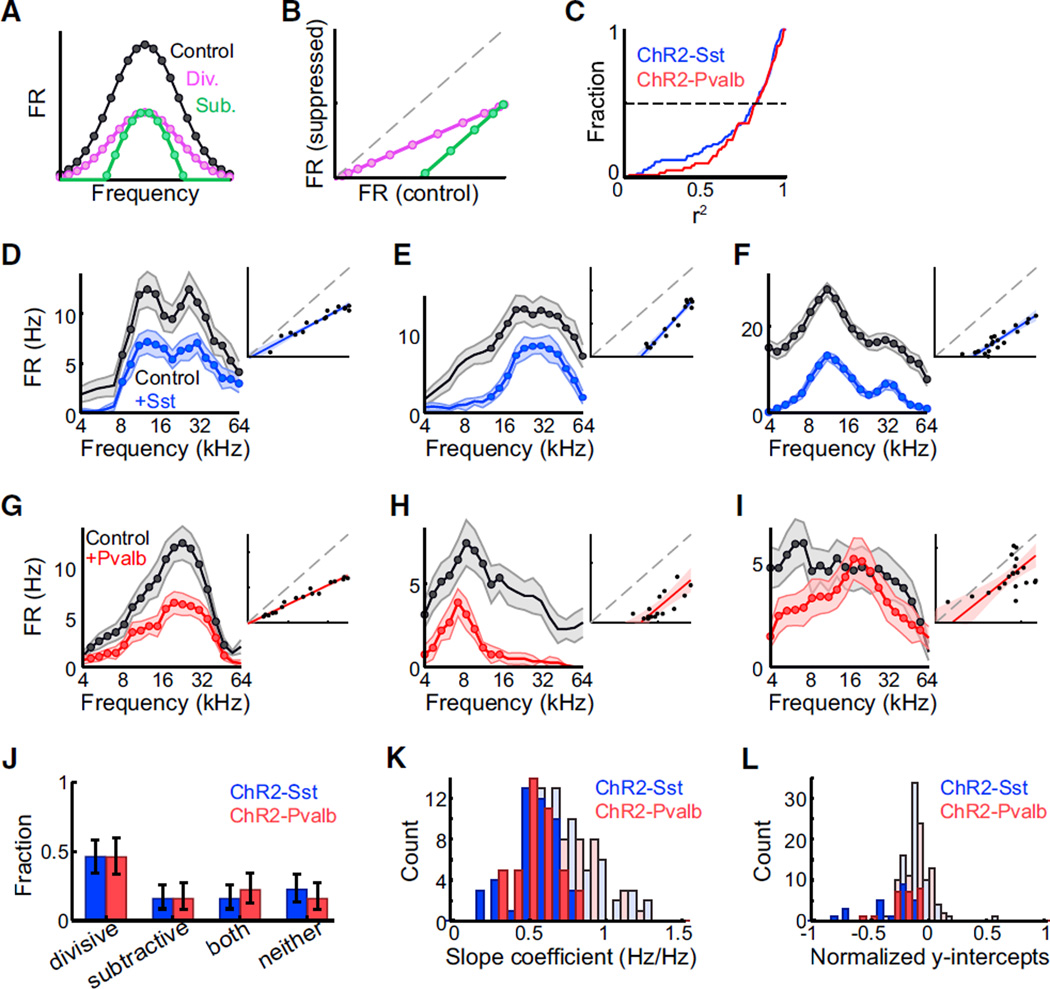
Figure 2. Sst+ and Pvalb+ Interneuron Activation Cause Similar Linear Suppression of Tone-Evoked Firing in Anesthetized Mice.

(A) Schematic: control (black), divisively suppressed (purple), and subtractively suppressed (green) responses as a function of stimulus frequency.

(B) Schematic: divisively (purple) or subtractively (green) suppressed responses as a linear function of the unsuppressed response, for stimuli evoking firing rates above baseline in both conditions.

(C) Cumulative distribution of r² values (i.e., quality of linear fit) in Ai32/Sst (blue) and Ai32/Pvalb (red) mice shows that a linear fit accounts for a high proportion of the total variance of suppression. Dashed line: median. Ai32/Sst: n = 76 units. Ai32/ Pvalb: n = 63 units.

(D–I) Activating Sst+ (blue) or Pvalb+ (red) in-terneurons leads to various forms of suppression in individual units: units in (D) and (G) are divisively suppressed, with slopes < 1, y-intercepts ≥ 0; (E) and (H) are subtractively suppressed, with slopes ≥ 1, y-intercepts<0;(F)isboth divisively and subtractively suppressed; and (I) is neither divi-sively nor subtractively suppressed. The data in the response curves are represented as mean ± SEM. The data in the regression plots are represented as lines of best-fit with 95% confidence intervals.

(J) Similar proportions of cells were divisively and subtractively suppressed by activation of Sst+ (blue) or Pvalb+ (red) interneurons (g-test p = 0.54). Error bars: 95% confidence intervals (Bernoulli distributions). Ai32/Sst: n = 76 units, Ai32/Pvalb: n = 63 units.

(K) Distributions of best-fit slope coefficients (i.e., relative strength of divisive suppression) when activating Sst+ or Pvalb+ interneurons. Dark bars: units in which slope was significantly less than unity (n = 47 of 57 Ai32/Sst, n = 43 of 63 Ai32/Pvalb). Distributions were not significantly different (rank-sum p = 0.19 for all units, rank-sum p = 0.44 for units with significant slopes only).

(L) Distributions of best-fit y-intercept coefficients (i.e., relative strength of subtractive suppression) when activating Sst+ or Pvalb+ interneurons. Dark bars: units in which intercept was significantly less than 0 (n = 24 of 76 Ai32/Sst, n = 24 of 63 Ai32/Pv). Distributions were not significantly different (rank-sum p = 0.61 for all units, p = 0.20 for units with significant intercepts only).

We applied this analysis to all auditory-responsive units for which light significantly suppressed the firing rate in the cPSTH. We observed that these linear components accounted for a high proportion of the total variance of suppression in both Ai32/Pvalb and Ai32/Sst mouse strains (Figure 2C), implying that suppression of individual neurons evoked by either Sst or Pvalb neurons can be described in a linear framework. However, in both strains, we observed a mixture of divisive, sub-tractive, and mixed suppression. Approximately half of units showed only divisive but not subtractive suppression (slope < 1, intercept not significantly less than 0 in Ai32/Sst: n = 35 of 76 units; Ai32/Pvalb: n = 27 of 63 units; Figures 2E and 2H). Of the remainder, some showed only subtractive but not divisive suppression (slope not significantly less than 1, intercept significantly less than 0 in Ai32/Sst: n = 12 of 76 units; Ai32/ Pvalb: n = 11 of 63 units; Figure 2F and 2I); some showed both divisive and subtractive suppression (slope significantly less than 1, intercept significantly less than 0 in Ai32/Sst: n = 13 of 76 units; Ai32/Pvalb: n = 16 of 63 units; Figure 2G); and in some units, neither subtractive nor divisive components were significant (Ai32/Sst: n = 16 of 76 units; Ai32/Pvalb: n = 9 of 63 units; Figure 2J). The proportions of suppression types observed (divisive, subtractive, both, or neither) when activating Sst+ interneurons were not significantly different from that observed when activating Pvalb+ interneurons (g-test p = 0.54).

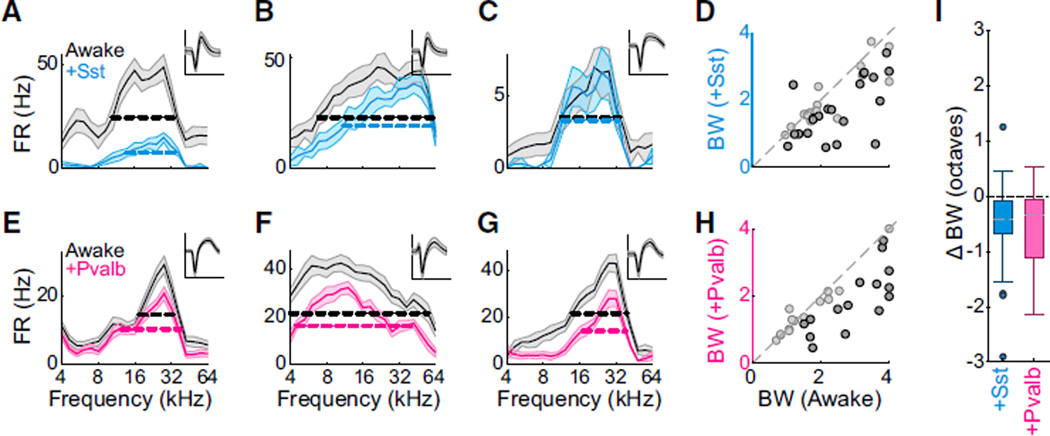
Activating Either Sst+ or Pvalb+ Neurons Reduces Response Bandwidths

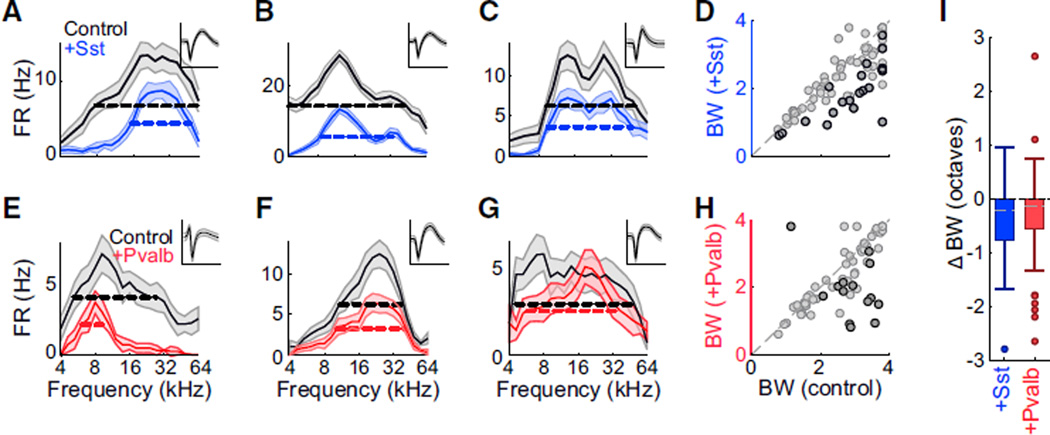
Consistent with this, the effects of Sst+ and Pvalb+ activation on the frequency bandwidth of the FTPs were on average similar. In anesthetized mice, activation of either Pvalb+ or Sst+ interneu-rons typically reduced other units’ frequency tuning bandwidths (Figures 3A, 3B, 3E, and 3F), although some units showed unchanged or even increased bandwidths despite an overall reduction in firing rate (Figures 3C and 3G). Across the populations, activating either Sst+ or Pvalb+ interneurons significantly narrowed bandwidths (median ± MAD: Ai32/Sst: control: 2.8 ± 0.7 octaves, activation: 2.3 ± 0.7 octaves, sign-rank p < 0.001; Ai32/Pvalb: control: 2.8 ± 0.6 octaves, activation 2.0 ± 0.7 octaves, sign-rank p < 0.001; Figures 3D and 3H). The distribution of bandwidth changes when activating Sst+ interneurons was not significantly different from that observed when activating Pvalb+ interneurons (rank-sum p = 0.63, Figure 3I).

Figure 3. Sst+ and Pvalb+ Interneuron Activation Have Similar Effects on Response Bandwidths in Anesthetized Mice.

(A–C) FTPs for three representative units (A, B,and C) recorded in anesthetized mice without (black) and with (blue) activation of Sst+ interneurons. Data are represented as mean ± SEM. Dashed lines: bandwidths at half-height. Inset: unit’s mean waveform ± SD. Scale bar: 2 ms.

(D) Half-height bandwidths with versus without activation of Sst+ interneurons across the population of n = 76 units. Dark circles: units for which bandwidth change was significant (bootstrap test, n= 20 of 76 units). Light circles: units for which bandwidth change was not significant (n = 56 of 76 units).

(E–H) Corresponding to (A)–(D): representative units and group data showing the effect of Pvalb+ neuron activation (red) on FTP bandwidth in n = 63 units in anesthetized mice (n = 14 of 63 units significant).

(I) Box-and-whisker summary of the effects of Sst+ versus Pvalb+ interneuron activation on half-height bandwidths shows significant bandwidth reduction (sign-rank p < 0.001) that was not significantly different between groups (rank-sum p = 0.63).

Simultaneously Recorded Neurons Can Show Divergent Types of Suppression

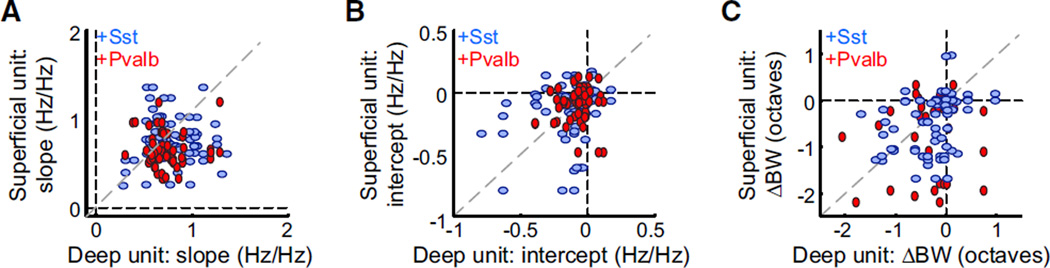
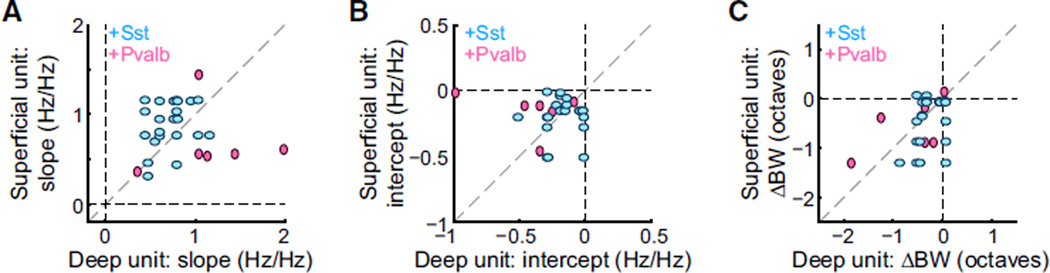
These results demonstrate that activation of either type of inhibitory network could produce subtractive, divisive, or mixed inhibition of sensory responses in their targets. Furthermore, we observed that even within a single recording, activation of Sst+ or Pvalb+ interneurons could produce diverse effects. For each pair of simultaneously recorded light-suppressed neurons (Figure 4), we compared the effect of interneuron activation on the change in slope of the input-output relationship (i.e., the strength of multiplicative suppression), the change in y-inter-cept (i.e., the strength of subtractive suppression), and the change in FTP bandwidth (Figure 4C). None of these parameters were substantially correlated (Figure 4A, slope: Ai32/Sst: n = 77, r² < 0.01, p = 0.67; Ai32/Pvalb: n = 56, r² < 0.01, p = 0.94; Figure 4B, y-intercept coefficients: Ai32/Sst: n = 77, r² = 0.06, p = 0.04; Ai32/Pvalb: n = 56, r² < 0.01, p = 0.67; Figure 4C, bandwidth: Ai32/Sst: n = 78, r² = 0.13, p = 0.001; Ai32/Pvalb: n = 53, r² < 0.01, p = 0.88). This shows that neurons within a cortical column are not equally affected by broad interneuron activation and that the resulting changes in the network are not uniform across columns.

Figure 4. Activating Sst+ or Pvalb+ Interneurons Can Suppress Simultaneously Recorded Neurons in Divergent Ways.

Correlations of slope coefficients (A), y-intercepts (B), and differences in bandwidths (C) for pairs of neurons simultaneously recorded on the same probe. (A given unit may be represented more than once if it was recorded simultaneously with more than one other unit.) Ai32/Sst: blue, Ai32/ Pvalb: red.

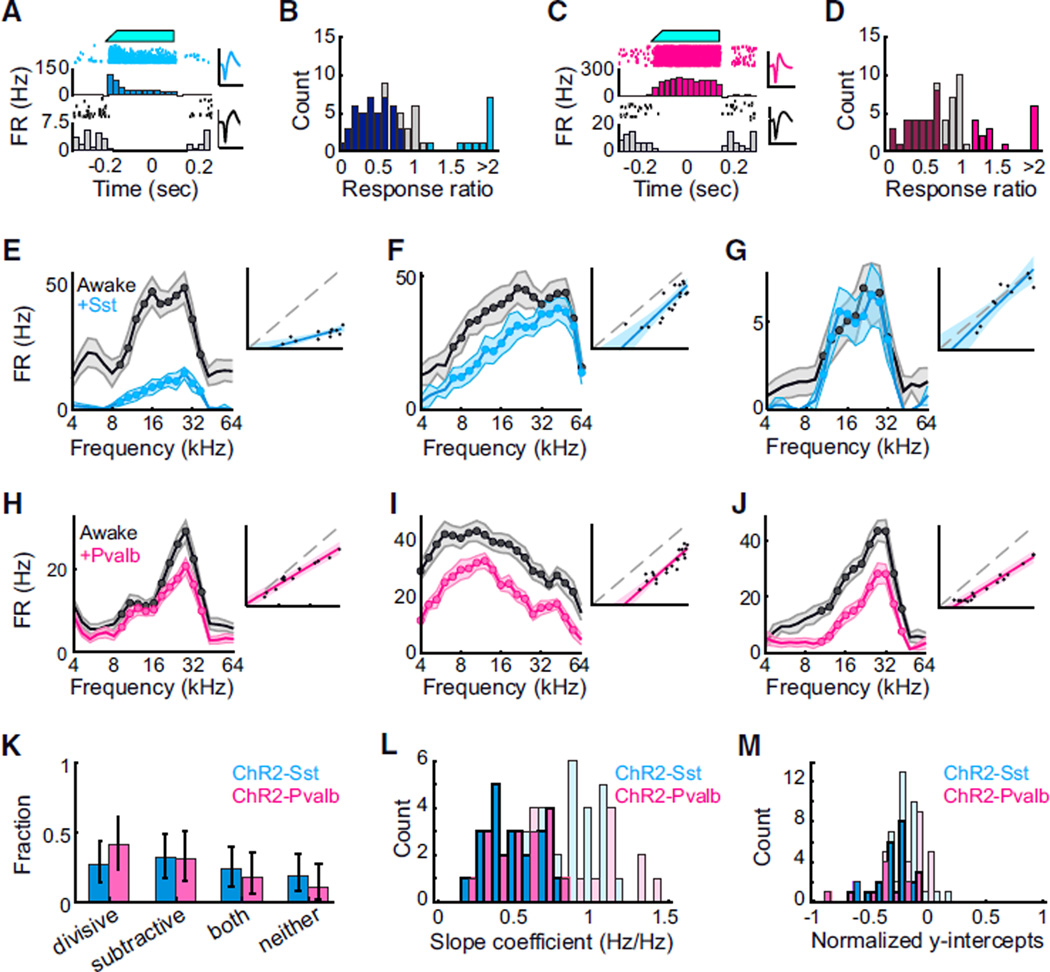
Inhibition Produces a Mixture of Divisive and Subtractive Suppression in Awake Mice

We performed similar experiments in awake head-fixed mice mounted on a stationary treadmill. As in the anesthetized condition, we observed that blue-light illumination of the cortical surface suppressed spontaneous and evoked activity in most units (p < 0.05 in n = 38 of 69 units from Ai32/Sst mice, and in n = 29 of 67 units from Ai32/Pvalb mice), while causing a small fraction of units (putative Sst+ or Pvalb+ interneurons) to increase their firing (Figures 5A–5D). Among significantly suppressed units, we observed that the majority of response variance could be described in a linear framework (median r² = 0.73 ± 0.17 for n = 38 units recorded in awake Ai32/Sst mice, median r² = 0.81 ± 0.17 for n = 29 units recorded in awake Ai32/Pvalb mice). As in anesthetized mice, we classified suppression as divisive, subtractive, mixed, or nonlinear depending on the slope and intercept of the best-fit lines relating suppressed to control responses. We observed all four types of suppression in response to activation of both Sst+ and Pvalb+ interneurons (Figures 5E–5M; divisive: n = 10 of 38 units [Ai32/Sst] versus n = 12 of 29 units [Ai32/Pvalb]; subtractive: n = 12 of 38 units [Ai32/Sst] versus n = 9 of 29 units [Ai32/Pvalb]; mixed: n = 9 of 38 units [Ai32/Sst] versus n = 5 of 29 units [Ai32/Pvalb]; neither: n = 7 of 38 units [Ai32/Sst] versus n = 3 of 29 units [Ai32/Pvalb]). These proportions were not significantly different from one another (g-test p = 0.531). Consistent with this, we observed that both Sst+ and Pvalb+ interneuron activation typically reduced other units’ frequency tuning bandwidths (Figures 6A– 6H; 2.0 ± 0.8 octaves to 1.6 ± 0.7 octaves [Ai32/Sst]; 2.2 ± 1.0 octaves to 1.6 ± 0.7 octaves [Ai32/Pvalb]). The distribution of bandwidth changes observed when activating Sst+ interneurons was not significantly different from that observed when activating Pvalb+ interneurons (rank-sum p = 0.84, Figure 6I). Finally, although we recorded relatively few pairs, we observed that during a single awake recording, activation of Sst+ or Pvalb+ inter-neurons generally suppressed simultaneously recorded neurons in dissimilar ways (Figure 7; slope: Ai32/Sst: n = 23 pairs among n = 15 cells, r² = 0.05, p = 0.28; Ai32/Pvalb: n = 6 pairs among n = 9 cells, r² = 0.01, p = 0.83; y-intercept coefficients: Ai32/ Sst: n = 23 pairs, r² = 0.002, p = 0.83; Ai32/Pvalb: n = 6 pairs, r² = 0.10, p = 0.53; bandwidth: Ai32/Sst: n = 23 pairs, r² = 0.09, p = 0.18; Ai32/Pvalb: n = 6 pairs, r² < 0.34, p = 0.23).

Figure 5. Sst+ and Pvalb+ Interneuron Activation Cause Similar Linear Suppression of Tone-Evoked Firing in Awake Mice.

(A) Blue light illumination of the cortical surface (top, cyan) of awake Ai32/Sst mice increased the activity of some units (middle/light blue: rasters, PSTH, and spike waveform for an example light-activated unit) while suppressing activity of others (bottom/black: rasters, PSTH, and waveform for an example light-suppressed unit). Scale bar: 2 ms.

(B) Distribution of light effects on tone-evoked firing rate in awake Ai32/Sst mice. Dark blue bars: units for which light significantly reduced activity (n = 38 of 69 units), light blue bars: units for which light significantly increased activity (n = 17 of 69 units), gray bars: units for which light did not significantly change activity (n = 14 of 69 units), as determined by a permutation test between control and light-activation trials, α = 0.05.

(C) Blue light illumination of the cortical surface (top, cyan) of awake Ai32/Pvalb mice increased the activity of some units (middle/pink: rasters, PSTH, and spike waveform for an example light-activated unit) while suppressing activity of others (bottom/black: rasters, PSTH, and waveform for an example light-suppressed unit). Scale bar: 2 ms.

(D) Distribution of light effects on tone-evoked firing rate in awake Ai32/Pvalb mice. Dark pink bars: units for which light significantly reduced activity (n = 29 of 67 units), light pink bars: units for which light significantly increased activity (n = 16 of 67 units), gray bars: units for which light did not significantly change activity (n = 22 of 67 units), as determined by a permutation test between control and light-activation trials, α = 0.05.

(E–J) Activating Sst+ (blue) or Pvalb+ (red) interneurons in awake mice leads to various forms of suppression in individual units: units in (E) and (H) are divisively suppressed, with slopes < 1, y-intercepts ≥ 0; (F) and (I) are subtractively suppressed, with slopes ≥ 1, y-intercepts < 0; (J) is both divisively and subtractively suppressed; and (G) is neither divisively or subtractively suppressed. The data in the response curves are represented as mean ±SEM. The data in the regression plots are represented as lines of best-fit with 95% confidence intervals.

(K) Similar proportions of cells are divisively and subtractively suppressed by activation of Sst+ (blue) or Pvalb+ (red) interneurons. Error bars: 95% confidence intervals (Bernoulli distributions).

(L) Distributions of best-fit slope coefficients (i.e., relative strength of divisive suppression) when activating Sst+ (blue) or Pvalb+ (pink) interneurons. Dark bars: units in which slope was significantly less than unity (n = 19 of 38 Ai32/Sst, n = 17 of 29 Ai32/Pvalb). Distributions are not significantly different (rank-sum p = 0.58 for all units; p = 0.46 for units with significant slopes).

(M) Distributions of best-fit y-intercept coefficients (i.e., relative strength of subtractive suppression) when activating Sst+ or Pvalb+ interneurons. Dark bars: units in which intercept was significantly less than 0 (n = 21 of 38 Ai32/Sst, n = 14 of 29 Ai32/Pvalb). Distributions are not significantly different (rank-sum p = 0.472 for all units; for units with significant intercepts, p = 0.45).

Figure 6. Sst+ and Pvalb+ Interneuron Activation Have Similar Effects on Response Bandwidths in Awake Mice.

(A–C) FTPs for three representative units (A, B, C) recorded in awake mice without (black) and with (light blue) activation of Sst+ interneurons. Data are represented as mean ± SEM. Dashed lines: bandwidths at half-height. Inset: unit’s mean waveform ± SD. Scale bar: 2 ms.

(D) Half-height bandwidths with versus without activation of Sst+ interneurons across the population of n = 38 units. Dark circles: units for which bandwidth change was significant (bootstrapped signrank test, n = 21 of 38 units). Light circles: units for which bandwidth change was not significant (n = 17 of 38 units).

(E–H) Corresponding to (A)–(D): representative units and group data showing the effect of Pvalb+ neuron activation (pink) on FTP bandwidth in n = 29 units (15 significant, 14 non-significant) in awake mice.

(I) Box-and-whisker summary of the effects of Sst+ versus Pvalb+ interneuron activation on half-height bandwidths shows significant bandwidth reduction (sign-rank p < 0.0005) that was not significantly different between groups (rank-sum p = 0.84).

Figure 7. In Awake Mice, Activating Sst+ or Pvalb+ Interneurons Can Suppress Simultaneously Recorded Neurons in Divergent Ways.

Correlations of slope coefficients (A), y-intercepts (B), and differences in bandwidths (C) for pairs of neurons simultaneously recorded on the same probe. (A given unit may berepresented more than once if it was recorded simultaneously with more than one other unit.) Ai32/Sst: cyan, Ai32/Pvalb: pink.

Divisive and Subtractive Suppression of Input Neurons Can Produce Similar Effects in a Convergent, Non-linear Network

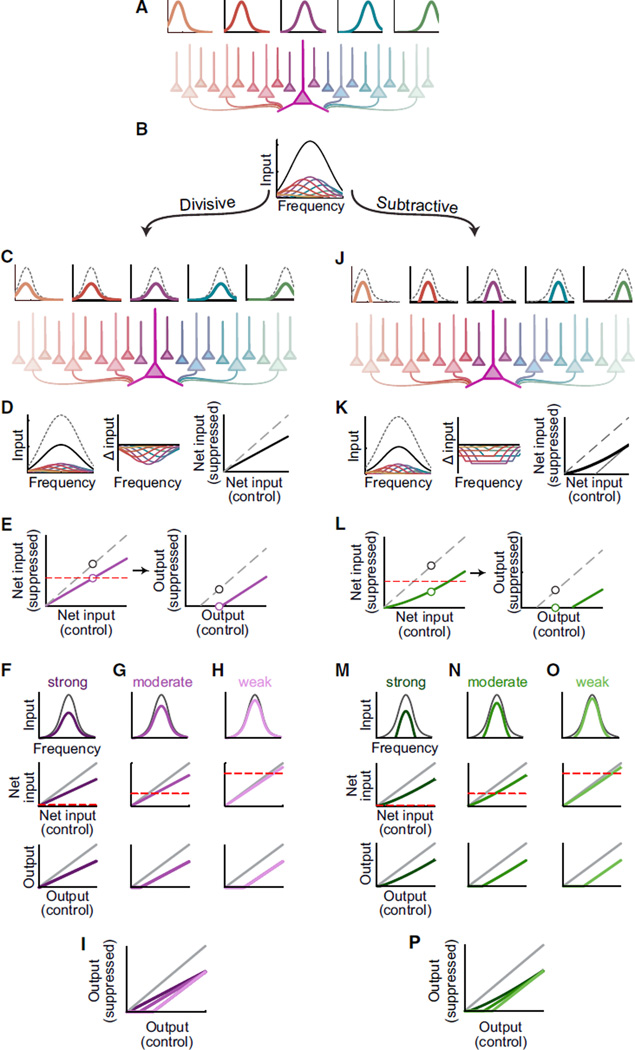
The seeming functional equivalency between Pvalb+ and Sst+ interneuron activation produces an apparent contradiction: how can Pvalb+ and Sst+ neurons cause similar effects on processing at the level of neural populations, when previous work has clearly demonstrated that these two neuron types have distinctly different effects on processing in individual cells? Cortical neurons are densely interconnected. This implies that activating inhibitory networks will have both first- and second-order effects on processing in a given neuron: first, inhibition will directly change the way that an individual neuron transforms inputs into outputs; but in addition, it will indirectly alter processing by changing the activity of many of the inputs the neuron receives. We modeled the consequences of these indirect effects on downstream neurons. As one example, consider a simple model in which a target neuron is driven by a population of input neurons, each tuned to different frequencies, organized along the tonotopic axis (Figure 8A). These inputs are connected to the downstream neuron by a connectivity function, in which neurons with more similar tuning will be more strongly interconnected. The net drive to the downstream neuron is equal to the convolution of the inputs’ tuning curves with the connectivity function (Figure 8B). The total drive is then transformed into spiking output through a threshold non-linearity. How will divisive versus subtractive suppression of the input neurons propagate through this network to affect the target neuron?

Figure 8. Linear Suppression Types May Be Obscured by Network Properties.

(A) Neurons tuned to different frequencies (top) are connected to a downstream neuron (large purple neuron in the center) by a connectivity function that weakens with distance (shading).

(B) The contributions of many tuned input neurons (colors) are summed by the downstream neuron, producing a center-peaked tuning curve (black).

(C) Schematic similar to (A) in which input neurons are divisively suppressed (dashed versus color).

(D) Left: sum (black) of individually suppressed inputs (color) is divisively suppressed compared to control (dashed). Center: decreases in contributions from each input (color) as a function of frequency. Right: input strength comparison for divisively suppressed inputs (black) versus control (dashed).

(E) Divisive suppression (purple, left) can appear subtractive (right) when spiking threshold (dashed red) limits observable output.

(F–I) Variations in suppression strength and threshold can cause divisive suppression of inputs to produce primarily divisive (F), subtractive (H), or mixed (G) suppression of the spiking output (overlaid in I).

(J–P) Similar to (C)–(I) but for subtractive suppression. Note that because firing rates cannot be negative, subtractively suppressed inputs are not uniformly suppressed (H, center). As a result (H, right), the sum of subtractively suppressed inputs (thick black) differs from theoretical subtractive suppression (thin gray).

If the input neurons are divisively suppressed (Figure 8C, top) while leaving the network connectivity unchanged (Figure 8C, bottom), divisive suppression of the inputs will divisively suppress the net drive because the net drive is a linear function of the contributions of the input neurons. A given neuron’s net drive (Figure 8D, left) will be most strongly suppressed near the center of its tuning profile (Figure 8D, center) and for frequencies evoking the strongest response (Figure 8D, right). Perhaps coun-terintuitively, subtractive suppression of the input neurons (Figure 8J) also produces stronger suppression near the center of the cell’s tuning curve. Because firing rates cannot be negative, subtractive suppression hasagreater effectatthe center of each input neuron’s tuning profile (Figure 8K); because of the connectivity function, this non-linear effect is passed on most strongly to the sum of inputs at the downstream neuron’s preferred frequency. The result is that the target neuron is most strongly suppressed at its best frequencies, just as when the inputs are divisively suppressed (Figure 8K, far right). This implies that both divisive and subtractive mechanisms operating at the level of single cells can produce divisive-like suppression of the net drive to a neuron embedded in the network.

These divisive-like changes in net drive can acquire subtrac-tive-like qualities as they pass through the output neuron’s threshold nonlinearity (Figures 8E–8I). Intuitively, this occurs because suppressing a cell’s inputs, without changing the cell’s own firing threshold, causes many of its weaker or non-preferred inputs to fall below threshold (“iceberging”). Although this does not manifest as pure subtraction (i.e., the input-output relationships retain the altered slope), depending upon the overall magnitude of suppression, the apparent strength of subtractive suppression may besubstantial (Figure 8E). Thus, even inhibitory mechanisms with clear subtractive or divisive effects on integration in individual neurons can produce mixed subtractive/divisive effects on integration in a convergent network, consistent with our observation that either Pvalb+ or Sst+ activation can suppress responses subtractively, divisively, or both. Indeed, combined local variations of threshold and degree of suppression can produce a wide range of joint divisive and subtractive suppression effects in a broadly connected network, consistent with our observation that activation of a single type of inter-neuron could have divergent effects on neurons recorded at the same time. By varying two properties of the model neuron (its threshold and the overall strength of suppression of its inputs), we could shift the observed output suppression from being mainly subtractive, to being mainly divisive or mixed, irrespective of whether the inputs were suppressed divisively or subtractively (Figures 8F–8I, 8M–8P, and S2–S4).

DISCUSSION

We evaluated the effects of activating somatostatin- and parval-bumin-positive interneurons by comparing the degree to which they subtractively or divisively suppressed auditory cortical cells’ responses to tones of different frequencies. Both in awake and anesthetized mice, we found that activating either population of interneurons produced a mixture of divisive and subtractive effects, that the mixtures of divisive and subtractive effects caused by activating either population of interneurons were similar, and that the variability in suppression types was not due to variations across experiments because the suppression types in simultaneously recorded neurons was not strongly correlated.

In the context of subtractive versus divisive inhibition, the standard argument is that axons from Pvalb+ interneurons form synapses onto the somata, axon initial segments, and proximal dendrites of pyramidal neurons (Kawaguchi and Kubota, 1993, 1997, 1998; Tama´s et al., 1997). Because action potentials are generated near the soma, activating inhibitory conductances near the soma decreases the effective input resistance and thus divisively scales the magnitude of depolarization evoked by a particular synaptic conductance. This means that proportionately larger input currents are necessary to reach threshold (Vu and Krasne, 1992; Jadi et al., 2012) and yields an overall divisive suppression of firing rates. In contrast, axons from Sst+ interneurons form synapses onto dendrites and frequently onto distal dendrites (Kawaguchi and Kubota, 1997, 1998; Wang et al., 2004; Silberberg and Markram, 2007). Because dendrites are electrotonically distant from the site of action potential generation, activating inhibitory conductances only in the dendrites will not substantially decrease the effective input resistance for more proximally delivered excitation. Because dendritic inhibition does not decrease somatic resistance, dendritic inhibition would be predicted to subtractively suppress the firing rate (Vu and Krasne, 1992; Jadi et al., 2012). Under many conditions, somatic and dendritic inhibition have been confirmed to provide divisive and subtractive suppression, respectively, to single pyramidal neurons in vitro (Miles et al., 1996; Hao et al., 2009). Based on the relationship between suppression type, synapse location, and the morphology of Pvalb+ and Sst+ interneurons, the standard prediction would be that activating Pvalb+ and Sst+ interneurons should implement divisive and subtractive forms of suppression, respectively.

However, we observed that activating either Pvalb+ or Sst+ neurons could modify other neurons’ sensory responses in diverse ways including primarily subtractive, primarily divisive, or mixed. To explain this observation, we note that cortical neurons are densely interconnected: the majority of cortical neurons receive the majority of their inputs from intracortical or feedback connections rather than from feedforward thalamocortical projections (Benshalom and White, 1986; Abeles, 1991). Thus, although changes in inhibitory tone may have the predicted linear effect on neurons’ responses to any particular current or conductance, they also change the firing properties of the majority of these neurons’ converging/recurrent inputs and may thus have effects on responses qualitatively different from those predicted by single-neuron models. As one example of such a mechanism, we used a simple network model to show that threshold nonlinearities can interact with inhibition to transform subtractive inhibition of neurons into divisive inhibition of networks, or vice versa. Varying just two properties of the model neuron (its threshold and the overall strength of suppression of its inputs) could cause the apparent linear effect of inhibition to be divisive, subtractive, or both (Figure 8). The character of suppression in higher-order neurons was determined by their intrinsic properties and connections, regardless of whether the suppression in first-order neurons was divisive or subtractive— in other words, the characteristics of response inhibition specific to a single interneuron type can be “masked” by the network configuration and cellular properties of the network in which they are embedded. Note that this second-order effect of inhibitory activity on excitatory tuning is merely one among many mechanisms by which this “masking” phenomenon may emerge. Additional sources of obfuscation are abundant in the cortical literature. For example, many types of interneuron are themselves tuned and receive organized excitation from local cortical networks (Thomson et al., 2002; Holmgren et al., 2003; Yoshimura and Callaway, 2005; Stokes and Isaacson, 2010; Moore and Wehr, 2013; Lee et al., 2014); manipulations that change the tuning of cortical excitation will themselves change the tuning of cortical interneurons, producing third- and higher-order effects. In addition, many types of cortical interneurons selectively inhibit one another; activation of one type may thus reduce the inhibition originating from others, producing complex changes in activity and tuning (Jiang et al., 2013; Lee et al., 2013; Pi et al., 2013; Xu et al., 2013; Fu et al., 2014). It is thus likely that similar masking phenomena will be observed in any network of appreciable complexity. This may explain how we can observe such similar distributions of linear suppression types in vivo, even though activating Pvalb+ or Sst+ interneurons produces easily distinguishable forms of suppression in vitro. The similarity of the data in the anesthetized and the awake preparation, despite the fact that some of the optogenetic parameters (light strength, optical fiber diameter) were not identical between the two conditions, suggests that this masking may be relatively robust. However, we note that in this experiment both populations of interneurons were activated in a nonselective and temporally diffuse manner; it is likely that during normal brain operation, functional differences between interneuron types will emerge from differences in their response properties and temporal dynamics.

Our second main observation was that even within a single columnar recording, activation of a given type of inhibitory neuron could produce diverse effects on other cells’ suppression and tuning behavior. The responses of neurons recorded at the same time in a single penetration were often modulated by inhibition in dissimilar ways (for instance, primarily subtractive versus primarily divisive). This variability is unlikely to be an artifact of animal-to-animal variability in the experimental preparation, because the characteristics of suppression in simultaneously recorded cells were not strongly correlated (Figure 4), and it is unlikely to be associated only with a specific anesthetic condition because we observed it in awake animals as well. This indicates that even in the same global network, local subnetworks of neurons with different intrinsic or connectional properties can selectively and differentially interpret the inhibition provided by a given population of interneurons. In our example model, varying overall suppression strength (e.g., proportion of suppressed versus unaffected inputs) and threshold could alter the observed balance between divisive and subtractive suppression (Figures 8 and S2–S4). This suggests that the neuron-to-neuron variability that we observed may be explained by neuron-to-neuron differences in biophysical properties and network connectivity.

These results may provide context to the ongoing debate regarding the functional roles of different types of cortical interneuron. Studies in primary visual cortex (V1) have produced diverse and even apparently irreconcilable findings regarding the effects of activating Sst+ and Pvalb+ interneurons on single unit responses. Various studies have shown that Pvalb+ neurons’ activation may change other neurons’ sensory responses divisively, while Sst+ neurons’ activation produces subtractive changes; that Pvalb+ neurons subtractively suppress sensory responses, while Sst+ neurons divisively suppress sensory responses; that both populations of interneurons produce divisive changes; or that a single population of interneurons can produce both divisive and subtractive changes (Atallah et al., 2012,2014; Lee et al., 2012, 2014; Wilson et al., 2012; El-Boustani and Sur, 2014; Xue et al., 2014). Here, we demonstrate the critical, and occasionally counterintuitive, role of network interactions in determining the systems-level effects of neuron-level manipulations. We have demonstrated that non-linear networks readily obscure linear suppression type and that inhibition of neurons’ excitatory inputs provides a parsimonious explanation for the complex and apparently contradictory consequences of activating Sst+ or Pvalb+ interneurons in auditory cortex. Our current results provide experimental and theoretical support for a mechanism by which either type of interneuron may induce either type of change in responsiveness when the multi-layered or recurrent nature of cortical networks is taken into account.

EXPERIMENTAL PROCEDURES

Animals

All experiments were approved by the Institutional Animal Care and Use Committee at the University of California, San Francisco. We targeted Sst+ and Pvalb+ cells using Sst-Cre and Pvalb-Cre knockin lines (JAX strains 013044 and 008069, respectively); these strains have been demonstrated to drive expression in Sst+ and Pvalb+ interneurons of the cortex and hippocampus with minimal (<10%) leak (Taniguchi et al., 2011). We crossed these Cre lines to the AI32 line (JAX strain 012569), which encodes the light-gated depolarizing cation channel channelrhodopsin-2 (ChR2), conjugated to eYFP, after a floxed stop cassette under the CAG promoter. Only 6- to 12-week-old mice heterozygous for both genes were used in these experiments.

Histology

Adult mice were deeply anesthetized with a mixture of ketamine and xylazine and perfused transcardially with 4% paraformaldehyde (PFA) in PBS (0.1 M, pH 7.4). The brains were removed and post-fixed overnight in the same fixative. The brains were transferred to a solution of 30% sucrose 0.1 M PBS until the brain sank to the bottom of the flask. Coronal sections were cut at 40 mm thickness using a freezing microtome and placed into a cryo-protective solution (30% ethylene glycol, 30% glycerol, in 0.1 M PBS). The slices were washed in PBS solution three times for 10 min, then rinsed in 0.25% Triton X-100/0.1 M PBS three times for 10 min, then incubated in blocking solution (0.25% Triton X-100 and 10% normal donkey serum in 0.1 M PBS) for 2 hr, and incubated overnight at 4°C in the primary antibody diluted in 0.25% Triton X-100, 10% normal donkey serum, in 0.1 M PBS. The primary antibodies used were as follows: chicken-anti-GFP (1:500, Aves Lab) and rabbit-anti-parvalbumin (1:1,000, Swant). The sections were then rinsed in blocking solution of 5% normal donkey serum, 0.25% Triton in 0.1 M PBS three times for 10 min. The sections were incubated, in the same blocking buffer for 2 hr, with secondary antibodies as follows: donkey-anti-chicken-Alexa 488 (1:200, Jackson ImmunoResearch) and donkey-anti-rabbit-Alexa 594 (1:200, Jackson ImmunoResearch). The sections were then rinsed in 0.1 M PBS three times for 10 min, mounted on gelatin-subbed slides, and allowed to dry. The slides were then dehydrated and defatted by the following sequence of washes: 50% ethanol, 2 min, 70% ethanol, 2 min, 95% ethanol, 5 min, 100% ethanol, 10 min, 100% ethanol, 10 min, xylenes, 10 min, xylenes, 10 min. The sections were promptly coverslipped using Krystalon mounting medium (EMD Millipore) and dried overnight. Digitized images were obtained with a Nikon DS-Fi1 digital camera (Nikon Instruments) on a Nikon ECLIPSE 90i microscope (Nikon Instruments) using a 10 × objective.

In Vivo Anesthetized Recordings

Mice were anesthetized with a mixture of ketamine and xylazine, supplemented with dexamethasone, atropine, and bupivacaine. The skin and bone over right auditory cortex were removed and the brain kept moist with silicone oil. A cisternal drain was performed to reduce brain swelling. Primary auditory cortex (A1) was identified by using multiunit recordings of responses to tones of different frequencies and intensities to identify the short-latency (<12 ms) tonotopically organized auditory region caudal to the main frequency reversal. Recordings were made using a 16 site linear probe (50 mm spacing, Neuronexus), inserted perpendicular to the cortical surface to a depth of ~750 µm. Stimuli consisted of randomly ordered 50 ms tones of various frequencies (4 kHz to 64 kHz, 0.2 octave spacing, 1 s interstimulus interval) near 55 dB SPL± 5dB) presented through a free-field high-frequency speaker (ES1, TDT).

On randomly interleaved trials, the penetration site was illuminated with blue light. Light was delivered through a 105-µm-diameter fiber optic connected to a 470 nm LED (Mightex) or 473 nm laser (OLS Laser Systems), positioned at the cortical surface just above the probe. Recordings were performed with a light power near 40 µW (range 25 to 100 µW), which typically suppressed firing to about 50% of control in 65%–75% of units (Ai32/Sst: n = 102 of 156 cells significantly suppressed, mean 0.58 ± 0.12; Ai32/Pvalb: n = 80 of 103 cells significantly suppressed, mean 0.51 ± 0.20; Figure S1). The light began 250 ms before the tone onset with a 50 ms linear ramp and remained on for 400 ms. Each stimulus was presented 10–40 times with and without light. Responses were amplified and digitized continuously with a 16-channel recording system (TDT) at 24,414 Hz. Events in the recordings that crossed a 4 SD threshold were collected, sorted using KlustaKwik, and reviewed and merged manually to select single units.

In Vivo Awake Recordings

1–5 days prior to recording, a custom metal headplate with an opening over the temporal skull was affixed to the skull with dental adhesive. On the day of recording, mice were anesthetized with isoflurane supplemented with subcutaneous lidocaine, given a subcutaneous injection of carprofen as a post-operative analgesic, and allowed to recover for 1–3 hr. A craniotomy (~2 mm) centered over auditory cortex was performed, and the opening was filled with silicone elastomer. After 1–3 hr of recovery, animals were placed in a head holder on a free-spinning spherical treadmill (modified from Niell and Stryker, 2010) and the silicone plug was removed. Auditory stimulation, optical stimulation, and electrophysiological recording were performed as in the anesthetized recordings, with the following exceptions: (1) some auditory stimulus sets included pairs of tones separated by 50 ms as well as single tones; for this reason, only the first 50 ms of response (i.e., the period prior to the second tone) was analyzed. (2) Light was delivered through a 400 mm fiber optic connected to a 470 nm LED, using a light power near 15 mW, which typically suppressed firing to about 50% of control in 50% of units (Ai32/Sst: n = 43 of 69 cells significantly suppressed, mean 0.50 ± 0.21; Ai32/Pvalb: n = 29 of 67 cells significantly suppressed, mean 0.54 ± 0.21).

Data Analysis

Data were analyzed in MATLAB (MathWorks). Event rasters for each unit were constructed around each tone and used to produce cPSTHs and frequency tuning profiles (FTPs). The cPSTH for each unit was taken to be the firing rate in 3 ms time bins from 0 to 99 ms after tone onset, pooled across all tones but separated into light on or light off trials. The firing rate in each time bin was compared against the time bins in the 100 ms preceding the tone by a ranksum test with α = 0.001 (after Bonferroni-adjusted multiple comparisons corrections). The first significantly different bin was taken to be the response onset, the last significantly different bin was taken to be the response termination, and the difference between onset and offset was taken to be the response duration.

The FTP for each unit was defined to be the firing rate during the period between response onset and termination, as a function of frequency. Band-widths were calculated as half-height above baseline in the smoothed FTP (produced by averaging adjacent bins). The overall percent suppression was calculated as the percent change in spike count during the time period of the response, averaged across all stimulus conditions. Linear suppression was characterized by using standardized major axis regression to relate the firing rates in the light-on and light-off conditions. Only frequencies that elicited a significant response in both light-on and light-off conditions were included in this analysis. (Major axis regression was necessary to account for the measurement variance on both the x and y axis, which ordinary least-squares regression does not [Sokal and Rohlf, 2012].) Units were deemed to show significant divisive or subtractive suppression if the regression slope was significantly less than one, or the y-intercept was significantly less than zero, respectively.

Significance of regression parameters was determined based on a t test of the parameter distribution as in Sokal and Rohlf (2012) with α = 0.05. For all other metrics, we performed bootstrap analysis to determine whether the changes observed in individual units were significant: we repeatedly (500 times) randomly reassigned trials to the light-off and light-on conditions and recalculated the response metric for each reassignment. Effects were deemed significant if the observed effects were less than 2.5% or greater than 97.5% of the bootstrap-calculated distribution of effects. Unless otherwise noted, tests of whether light significantly affected a population of units were sign-rank tests; tests of whether continuous parameters were differently distributed between groups were rank-sum tests; tests of whether similar proportions of units were significantly affected by light were performed using Fisher’s exact test, except when testing for significant differences in the distributions of linear suppression types (proportional, absolute, both, neither), for which a g-test was used.

Model

We assumed a population of N frequency-tuned input neurons I_n,, each with a Gaussian tuning curve, systematically varying in their center frequency:

$$I_n(f)=e^{-\left(\frac{{(f-n)}^2}{2*{\sigma }_I^2}\right)}.$$

These input neurons are connected to the target neuron by a center-weighted (Gaussian) connectivity function W:

$$W(x)=e^{-\left(\frac{x^2}{2*{\sigma }_W^2}\right)}.$$

The target neuron’s total drive I_net, as a function of frequency, is then

$$I_{\mathit{\text{net}}}(f)=\sum _n{I}_n(f)*W(n).$$

The target neuron is assumed to be threshold linear (i.e., its firing rate is proportional to its input, except that subthreshold inputs produce a firing rate of zero). Its output O is calculated by thresholding its total input against a threshold T:

$$O_T(f)=\text{max}(0,I_{\mathit{\text{net}}}(f)-T).$$

When input neurons are partially suppressed, each input neuron’s activity is calculated as:

$$I_n^{\mathit{\text{supp}}}(f)=\text{max}(0,m*I_n^{\mathit{\text{ctrl}}}(f)-b).$$

Here m and b represent the strengths of divisive and subtractive inhibition, respectively. The target neuron’s net drive, output, and change in responsiveness are then calculated as:

$$I_{\mathit{\text{net}}}^{\mathit{\text{supp}}}(f)=\sum _n{I}_n^{\mathit{\text{supp}}}(f)*W(n)$$

$$O_T^{\mathit{\text{supp}}}(f)=\text{max}(0,I_n^{\mathit{\text{supp}}}(f)-T)$$

$$\mathrm{\Delta }O(f)=O_T^{\mathit{\text{ctrl}}}(f)-O_T^{\mathit{\text{supp}}}(f).$$

Highlights.

• Activation of Sst or Pvalb cells causes diverse mixtures of division and subtraction

• Simultaneously recorded neurons can show qualitatively different suppression

• Network interactions can mask subtractive inhibition as divisive, and vice versa

• In active networks, optogenetic effects must be interpreted with extreme caution