Evaluating Differential Effects Using Regression Interactions and Regression Mixture Models

Abstract

Research increasingly emphasizes understanding differential effects. This article focuses on understanding regression mixture models, which are relatively new statistical methods for assessing differential effects by comparing results to using an interactive term in linear regression. The research questions which each model answers, their formulation, and their assumptions are compared using Monte Carlo simulations and real data analysis. The capabilities of regression mixture models are described and specific issues to be addressed when conducting regression mixtures are proposed. The article aims to clarify the role that regression mixtures can take in the estimation of differential effects and increase awareness of the benefits and potential pitfalls of this approach. Regression mixture models are shown to be a potentially effective exploratory method for finding differential effects when these effects can be defined by a small number of classes of respondents who share a typical relationship between a predictor and an outcome. It is also shown that the comparison between regression mixture models and interactions becomes substantially more complex as the number of classes increases. It is argued that regression interactions are well suited for direct tests of specific hypotheses about differential effects and regression mixtures provide a useful approach for exploring effect heterogeneity given adequate samples and study design.

A typical study in the social sciences starts with a straightforward research question, such as “what is the average relationship between parenting practices and a child’s social skills?” This assessment is often followed by a secondary question such as “does the relationship between parenting and social skills vary based on a child’s ethnicity and sex?” This assessment of effect heterogeneity is motivated by the question, “does the relationship between social skills and parenting differ across children?” This is an important question, as it recognizes the complexity underlying human behavior and social interactions and allows the research to further explore the “main effect” found in answer to the primary question (Aiken & West, 1991; Cohen, Cohen, West, & Aiken, 2003). Note that we use the word “effect” to mean a statistical association without any assumptions concerning patterns of cause–effect.

Although the use of multiplicative interaction terms in the general linear model (henceforth referred to as regression interactions) is a well-known approach for assessing differential effects, only a few examples of newer methods such as regression mixture models currently exist in the social sciences (Dyer, Pleck, & McBride, 2012; Kaplan, 2005; Lanza, Kugler, & Mathur, 2011; B. O. Muthén & Asparouhov, 2009; Schmeige, Levin, & Bryan, 2009; Van Horn et al., 2009; Van Horn et al., 2012). This article aims to clarify the role of regression mixtures for assessing differential effects. The article includes two studies, the first focuses on clarifying how regression mixture models assess differential effects by comparing them with regression interactions. The questions each model answers and assumptions of the different models are compared and their unique roles in finding differential effects are examined. Simulations are used to show how regression mixtures and regression interaction results are related. The second study describes issues specific to the use of regression mixture models and includes an illustration of the use of both methods with applied data.

Study 1: How Regression Mixtures Work

In many areas of the social sciences, heterogeneity in the effects of predictors on outcomes is expected (Bauer, 2011). Developmental theories such as ecological systems theory (Bronfenbrenner, 1977, 1989) posit the presence of individual differences in effects as well as outcomes resulting from complex processes. For example, genes and environments are believed to interact such that biological variation and temperamental characteristics shape individual behavior within a given environment (Belsky, Hsieh, & Crnic, 1998). Individuals who are highly responsive to their contexts may be vulnerable to negative environmental influences but also may thrive in positive environments and show stronger responses to interventions (Blair, 2002; Klein Velderman, Bakersman-Kranenburg, Juffer, & van IJzendoorn, 2006). Thus, individual differences may be conceptualized as a high biological sensitivity to context (Boyce, 2007; Boyce & Ellis, 2005) or a differential susceptibility to environmental influences (Belsky, 2005). Theory and empirical research often lead to the expectation that differential effects will be complex and are unlikely to be characterized by a single variable.

We define differential effects as existing when the relationship of a predictor, x, to an outcome, y, differs across subsets of individuals. Assessment of differential effects typically starts with evaluating the main effect of x on y and then exploring whether the effect varies as a function of a third variable (z), which is identified a priori. This is parsimonious and effective when one reliably measured predictor, z, is available to explain the differential effect. However, this approach is limited when differential effects are more complex (Bauer, 2011; Boyce et al., 1998), such as those suggested by many theories. Differential effects could be a function of multiple predictors, imperfectly measured variables, and the form or strength of the relationship could vary across levels of these variables. Additional approaches for examining effect heterogeneity could increase the chances of finding them when present.

We propose a broad evaluation of differential effects with emphasis on heterogeneity in “the effect” of interest, instead of the more typical approach which examines differential effects as a secondary aim. The idea is simple: Begin with the expectation that the relationship of interest may be heterogeneous across respondents. An immediate implication is that research questions about main effects include hypotheses about effect heterogeneity; investigators should specify, based on the theory(ies) guiding their research, whether they expect the effects to be substantially the same across all respondents or if differences are likely to be evidenced. An advantage of starting with specific hypotheses about differential effects is that the study design can be adapted to increase the likelihood of detecting these differential effects. This can be done, for example, by including reliable measures of hypothesized predictors of heterogeneity and by ensuring adequate power for estimating differential effects. Expecting differential effects from the beginning of a study also has implications for analyses. First, statistical models should be used to examine specific hypotheses about the variables or groups responsible for heterogeneous effects. Second, the expectation that effects may differ suggests the use of additional statistical methods that allow for the exploration of unspecified heterogeneity.

In our example examining the relationship of parenting with social skills, we would hope to see hypotheses about the average effects expected and the heterogeneity likely to exist in these effects or a justification why homogeneous effects are expected. Where existing literature does not support strong hypotheses about differential effects it may provide broad guidelines to focus the search on key variables that may explain effect heterogeneity. For instance, there is evidence that what is considered best parenting differs as a function of culture and sex and hence it is sensible to expect that effects of parenting may also differ between these groups. This approach allows the study design to be modified so hypotheses can be better tested, such as by including reliable measures of the hypothesized predictors of effect heterogeneity.

The implication of finding differential effects depends on the magnitude of differences in the effects found. Take an extreme case of two equally sized groups, where for one group there is a positive effect of parenting and for the second group there is an equally strong negative effect of parenting. The average or “main effect” of parenting is zero and clearly describes the relationship for either subgroup inadequately. In such cases the average effect is misleading (Richters, 1997; von Eye & Bogat, 2006) as it suggests no relationship between parenting and social skills, when, in fact, the relationship is present and the direction is counter to the hypothesis for half of the population. A more typical finding is moderate differences in magnitude of an effect (Murray, Farrington, & Sekol, 2012) that qualify and add nuance to, rather than supplant, the main effect. The possibility of differential effects which substantively change the interpretation of the main effects suggests that evaluation of effect heterogeneity should be a primary step in the research process.

Formulation of Regression Interactions

Differential effects are traditionally assessed using interactions terms in a regression model. Let y_i and x_i be the observed value for a continuous outcome, y, and a predictor, x, for individual i, respectively, where i = 1, . . ., n. Note that extending these models to other outcomes is possible, a continuous outcome is used here for simplicity. A typical model is

$$y_i={\mathrm{\beta }}_0+{\mathrm{\beta }}_1{x}_i+{\mathrm{\epsilon }}_i,$$

where β₀ and β₁ are the regression parameters to be estimated, The random error, ε_i, is usually assumed to be normally, independently and identically distributed with a mean of zero and a constant variance; that is, ${\mathrm{\epsilon }}_i{~}^{\mathrm{i}.\mathrm{i}.\mathrm{d}.}\mathrm{N}(0,{\mathrm{\sigma }}^2)$, which also implies that random errors are homoscedastic with the same variance across all levels of x. Additional key assumptions are that the relationship is linear such that the expected change in y is the same for any one unit change in x and that random errors are uncorrelated with the predictor. Violations of any one of these assumptions can lead to distorted inference about the association between x and y (Cohen et al., 2003; Graybill, 1976).

In the standard approach for modeling differential effects, a third variable thought to relate to differential effects, z, is introduced, along with a multiplicative interaction term, xz, such that

$$y_i={\mathrm{\beta }}_0+{\mathrm{\beta }}_x{x}_i+{\mathrm{\beta }}_z{z}_i+{\mathrm{\beta }}_{\mathrm{xz}}{x}_i{z}_i+{\mathrm{\epsilon }}_i$$

Figure 1 represents this model in path diagram form with squares indicating observed variables; the circle around the random error, ε, indicates that it is unobserved; the triangle indicates a constant in the model. Including an interaction term allows for the heterogeneity in the effects of x on y with regards to the predictor z. This approach makes no distinction between a model were the effects of x on y differ as a function of z, and the one where the effect of z on y differs as a function of x (Kraemer, Kierman, Essex, & Kupfer, 2008). Equivalently formulating this model as

Figure 1.

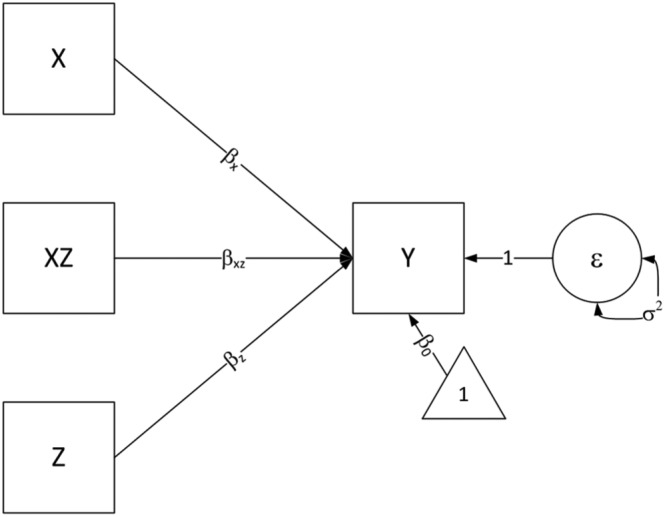
Path diagram of a linear regression with x, z, and the interaction terms between x and z, xz, predicting to y.

$$y_i=({\mathrm{\beta }}_0+{\mathrm{\beta }}_z{z}_i)+({\mathrm{\beta }}_x+{\mathrm{\beta }}_{\mathrm{xz}}{z}_i)x_i+{\mathrm{\epsilon }}_i,$$

highlights another feature of interactions: the differential effect of x on y is itself linear such that the effect of x on y changes in the same way for every one unit increase in z. Traditional regression interactions allow for the detection of effect heterogeneity but require that heterogeneity is a linear function of an observed and reliably measured predictor of heterogeneity. For testing specific hypotheses about heterogeneity the interaction model is natural—it provides a direct test for linear effect heterogeneity.

Formulation of Regression Mixture Models

Several novel exploratory methods to find differential effects exist. One method uses random forests (Breiman, 2001) with the focus on an interaction term to search for interactions among a large number of covariates (Su, Meneses, & McNees, 2011). Another alternative is regression mixture models, which fall under the broad category of finite mixture models. A mixture model uses a categorical latent variable, sometimes called a latent class variable, to describe the underlying structure (mean and covariance) in observed data (MacLachlan & Peel, 2000; Magidson & Vermunt, 2004). It assumes that the observed structure from the overall population can be explained by a mixing of subpopulations, each with a distinct distribution of the variables. The measurement model for a latent class variable contains the number of classes (mixture components), the prevalence of each class (mixing weight), and distributional features by which the classes are distinguished, for example, means and variances. In its simplest form, the distribution of a continuous variable is a mixture of normally distributed latent classes with equal variances, but class-specific means. However, finite mixture models have been applied to much more complex settings, including multivariate continuous and categorical outcomes (Magidson & Vermunt, 2004). They have also been applied in modeling the distributional structure of latent factors (Vermunt & Van Dijk, 2001) or the distribution of growth factors in a latent growth curve model (B. O. Muthén & Shedden, 1999; Xu & Hedeker, 2001).

Consider a sample of n individuals measured on a continuous random variable, where y_i is the observed value on y for subject i. The probability density function of y is modeled as a mixture of a finite number of K classes, represented by a categorical latent variable, C, where C = 1, . . ., K. The value of K is specified a priori but the mixing weights (i.e., the class prevalences in the population), π₁, . . ., π_K, are not known in advance. These proportions are constrained to be positive (π_K > 0 for all k) and must sum to 1 $(\sum _{k=1}^K{\mathrm{\pi }}_k=1)$. The probability density function of y, f_Y(·) is expressed as a weighted sum of conditional (i.e., class-specific) probability density functions, $f_{Y|k}(·)=\mathrm{Pr}(Y|C=k)$:

$$f(y|\mathrm{\phi })=\sum _{k=1}^K({\mathrm{\pi }}_k·f_k(y_k|{\mathrm{\theta }}_k)),$$

where $\mathrm{\phi }=(\mathrm{\pi },\mathrm{\Theta })$ denotes the vector of all unknown parameters to be estimated; π = π₁, π₂, . . ., π_k, which represents the probability of membership in class k; and Θ = θ₁, θ₂, . . ., θ_k consists of a set of estimated parameters which describe the probability density for each of the k classes. It is usually assumed that the component distributions are from the same parametric family and, more specifically, the component distributions are most often assumed to be normal in which case θ_k includes the means and variances for class k. Maximum likelihood estimates for all the elements of ϕ can be obtained via the expectation–maximization algorithm (B. O. Muthén & Shedden, 1999). Note that the assumption of within-class normality is a particularly strong assumption because of its impact on parameter estimation (Bauer & Curran, 2003a, 2003b, 2004). It is further assumed that observations are independent, and if the resulting classifications are to be substantively interpreted the model implicitly assumes that differences in the population can be reasonably represented by discrete unobserved classes.

It is possible to simultaneously include predictors of class membership in the model used to estimate ϕ. Consider a set of Q covariates, where z_iq is the observed value of z_q for individual i, then the probability of class membership is expressed as a multinomial regression given by

$$\mathrm{Pr}(c_i=k|{\mathbf{z}}_i)=\frac{\exp ({\mathrm{\alpha }}_k+\sum _{q=1}^Q{\mathrm{\gamma }}_{\mathrm{qk}}{z}_{\mathrm{iq}})}{\sum _{s=1}^K\exp ({\mathrm{\alpha }}_s+\sum _{q=1}^Q{\mathrm{\gamma }}_{\mathrm{qs}}{z}_{\mathrm{iq}})},$$

where class K is designated as the reference class with ${\mathrm{\alpha }}_K={\mathrm{\gamma }}_K=0$. Predictors of class membership can be interpreted as explaining the heterogeneity captured by latent classes.

Latent classes may have two underlying interpretations. It is possible that individuals differ qualitatively and the latent classes correspond to “true” subpopulations present within the larger population—a direct use of mixture modeling. Another possibility is that rather than representing “true” subpopulations, latent classes may approximate a nonnormal continuous distribution using a set of discrete categories—an indirect use of mixture modeling (Titterington, Smith, & Makov, 1985). Thus, classes could indicate either qualitative and/or quantitative differences across individuals (Bauer & Curran, 2003a, 2003b). Interpretation of the latent classes should be based on this knowledge and, if classes are to be interpreted as representing qualitative differences, further evidence for the validity of those classes should be provided (B. O. Muthén, 2003; Van Horn et al., 2009). For the purposes of this article both direct or indirect latent classes are useful.

In regression mixture models, the latent class variable is used to capture discrete population heterogeneity in effects (regression weights) of one or more predictor variables, x, on an outcome variable, y. The method first emerged in the economics literature in the form of switching regression models (Quandt, 1972; Quandt & Ramsey, 1978), and was further developed and applied in statistical and marketing fields, primarily as a means to understand market segmentation and other facets of consumer behavior (Bai, Yao, & Boyer, 2012; Bartolucci & Scaccia, 2005; Cleaver & Wedel, 2001; Desarbo, Jedidi, & Sinha, 2001; Grewal, Chandrashekaran, Johnson, & Mallapragada, 2013; Jedidi, Ramaswamy, DeSarbo, & Wedel, 1996; Sarstedt, 2008; Wedel & DeSarbo, 1994, 1995). Regression mixtures have only recently begun to be applied to a broader range of areas. The formulation for a regression mixture model builds on the standard mixture model by adding class specific regression weights. Regression mixtures expand Equation (4) by modeling the conditional distribution of a random variable, y, given some value of a predictor variable x, $f_{Y|x}(·)=\mathrm{Pr}(Y|X=x)$, described by a mixture of K components, each with a conditional distribution, $f_{Y|x,k}(·)=\mathrm{Pr}(Y|X=x,C=k)$, described by a normal linear regression model. That is,

$$f(y|\mathrm{\phi })=\sum _{k=1}^K({\mathrm{\pi }}_k·f_k(y_k|{\mathrm{\theta }}_k)),$$

where

$$f_k(y_k|{\mathrm{\theta }}_k)=\frac{1}{\sqrt{2{\mathrm{\pi \sigma }}_k^2}}\exp \left\{\frac{-{[y_i-({\mathrm{\beta }}_{0k}+{\mathrm{\beta }}_{\mathrm{xk}}{x}_i)]}^2}{2{\mathrm{\sigma }}_k^2}\right\}$$

This model can be alternately expressed in the more familiar structural equation form:

$$y_{\mathrm{ik}}={\mathrm{\beta }}_{0k}+{\mathrm{\beta }}_{\mathrm{xk}}{x}_{\mathrm{ik}}+{\mathrm{\epsilon }}_{\mathrm{ik}},$$

where y_ik is the value for a continuous outcome variable, y, x_ik is the value for the predictor variable, x, and ε_ik is the random error for individual i in class k with k = 1, . . ., K, i = 1, . . ., n, and ${\mathrm{\epsilon }}_{\mathrm{ik}}~\mathrm{N}(0,{\mathrm{\sigma }}_k^2)$. The path diagram representation for this model is shown in Figure 2. The latent class variable, C, may influence the intercept parameter for y, the regression parameter for y on x, and the random error. C, in turn, is modeled as a function of a set of predictor variables, z.

Figure 2.

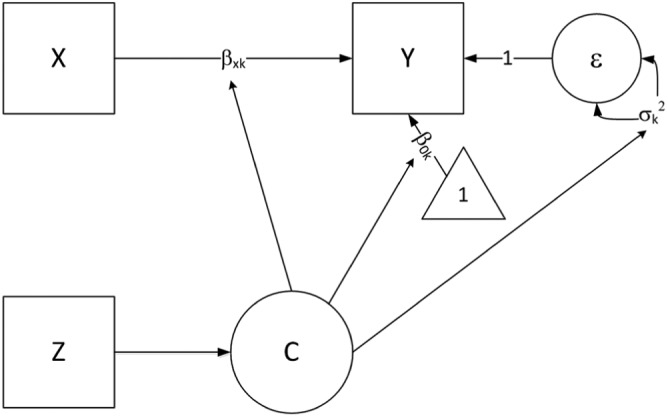
Path diagram of a regression mixture model with x predicting y and z predicting membership in the latent classes, C.

The regression mixture model assumes that the effect of x on y is linear in the parameters (although class-specific linear associations between x and y can correspond to a nonlinear association between x and y in the overall population); observations are independent; x is measured without error (error in predictors of the latent classes does not bias estimates of differential effects although it will result in underestimates of the effects of the predictors on latent classes); and error terms are normal within each latent class. Like the interaction model, regression mixture models do not make any assumptions about the distribution of the predictors (x and z). The regression mixture model does not assume equal residual variance in each latent class, but heavily relies on the assumption that errors are normal; violation of this assumption can seriously bias parameter estimates (Van Horn et al., 2012). Three different approaches, discussed in detail in Study 2, have shown promise for reducing this bias.

Regression mixture models have several potential strengths. First, they are identified without the inclusion of any predictors of the individual differences in the association between x and y. Thus, they can be used to explore a data set for evidence of classes of respondents characterized by differential effects, including the presence of classes characterized by heterogeneous effects that were not specified. Even when predictors of heterogeneity are thought out a priori, it is unlikely that all such predictors will be identified or included in a study. Regression mixtures can thus provide new insights that can be further explored. Second, the method can provide evidence of different classes that would otherwise be difficult to detect, especially if not hypothesized in advance. This is illustrated in Figure 3 with a scatter plot of a hypothetical sample consisting of a mixture of two classes where in one class x has a strong positive relationship with the outcome whereas in the second class, the relationship is much weaker. In a real data set, only the individual data points and not class membership or the effects in each class, would be observed; there would be little obvious evidence for the existence of differential effects. Third, in a typical regression interaction, when predictors of differential effects (z) are unreliable the interaction term is downward biased (Aiken & West, 1991). We will show that regression mixtures provide a method for solving this problem through the inclusion of a latent class variable for capturing differential effects predicted by z. Fourth, when the processes that lead to heterogeneous classes are complex (e.g., multiple predictors with multiway interactions), regression mixtures can help clarify the heterogeneity.

Figure 3.

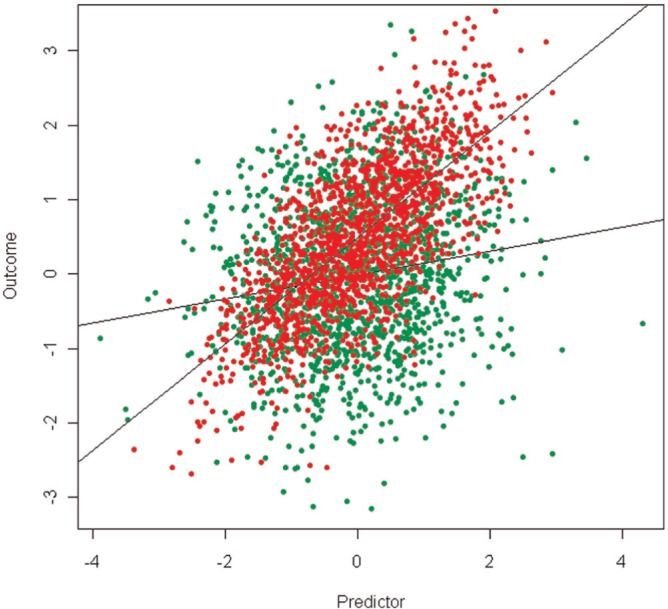
Example scatter plot of data from a two-class mixture with class-specific distributions for the predictor and class-specific regression parameters for the conditional mean and variance–covariance structure of the outcome.

Comparison of Regression Interactions and Regression Mixture Models

Comparing statistical interactions and regression mixtures provides insight into the types of differential effects identified by each. Take the simplest interaction where the effect of x on y differs across levels of a binary variable, z. This could, for example, be that the effect of parenting on social skills differs between boys and girls. Testing this model using an interaction term requires that parenting, social skills, and sex all be measured. The test of differential effects can then be achieved through a model such as SocialSkills_i = β₀+β₁ (Parenting) +β₂ (Female) +β₃ (Parenting * Female) +ε_i, where the regression weight β₀ is the mean level of social skills when all other variables equal 0, the weight β₁ is the linear relationship of parenting with social skills for males (with female coded “1” when the student is female and “0” when male), β₂ is the mean difference between females and males in social skills when parenting equals 0, β₃ captures differences between females and males in the linear relationship of parenting with social skills, and ε_i represents individual deviation from the conditional population mean value. The coefficient for the interaction, β₃, tests whether the relationship between parenting and social skills differs between boys and girls. This model requires that all differential effects must be explicitly modeled.

Analyzed with a regression mixture model, the model specification would be SocialSkills_ik = β_0k+β_1k (Parenting) +ε_ik within each class, k. Sex (z) is not needed and typically only enters the analysis later as a predictor of class membership. We suggest that the model is run in two steps, first without any predictors of C and then with key predictors of differential effects included. If sex is the sole determinant of differential effects of parenting, then two classes will be identified and, when included as a predictor of C, sex will perfectly predict class membership. It would follow that C is equal to z with the only difference being that C is not observed. The main effects of sex are in the between-class differences in β₀, and the sex-specific effects of parenting will be reflected in between-class differences in β₁. When sex is the sole cause of differential effects, the interaction and the regression mixture model lead to equivalent results.

The regression mixture model differs from the interaction model when (a) more than two classes are found, (b) class membership is not perfectly related to sex, (c) residual variances differ for boys and girls, and/or (d) sex is not perfectly measured. If more than two classes are identified, then sex cannot be the only variable responsible for differences in the effects of parenting as sex typically only has two levels. Similarly, the finding that sex does not perfectly predict the latent class variable means that sex is not the sole determinant of differential effects. This could be due to measurement error in the assessment of sex, or to contributions of other variables such as gender roles. In regression mixture models, C represents the subgroups that show differential effects. The predictors of C, one or more z variables, are rarely perfect predictors. Regression mixtures allow great flexibility in the types of subgroups that can be identified (if they exist). For example, if there is an interaction between multiple predictors each of the components of C, say k, would represent one or more specific combinations of values on these multiple predictors rather than a subgroup defined on a single predictor z, as in the interaction approach.

Comparing the assumptions of regression interaction and regression mixture models provides additional insights. The assumptions are quite comparable on their face, each assumes the model is linear in the parameters, residuals are normal, predictors are measured without error, observations are independent, and predictors are uncorrelated with the error terms. One difference is that residual variances are not assumed to be the same in each class in a regression mixture model whereas they typically are assumed to be constant in a regression interaction, although approaches such as sandwich estimators can relax this assumption (Huber, 1967). Estimated regression parameters for interaction models are generally robust to the assumption that residual variances are equal across levels of predictor variables; however, when the assumption is violated it will lead to inaccurate estimates of variances and therefore effect sizes for the interactions in each group if the effect size is based on estimates of the residual variance. For example, if the residual variance is 0.9 in one group and 0.5 in another group, in the interaction model, the residual variance will be estimated as 0.7 (given equal group sizes) for both groups resulting in overestimation of the effect size in the first group and underestimation in the second group. Although the assumptions are similar for both models, the effects of violating the assumptions are not necessarily similar. Regression interaction models are quite robust to the effects of violating the assumption of normal residuals with effects mostly limited to standard errors rather than parameter estimates (Cohen et al., 2003) whereas nonnormality within classes has serious impacts on parameter estimates obtained from regression mixture models (Van Horn et al., 2012). Although each model assumes that predictors are measured without error, violating this assumption leads to an imperfect relationship between z and C in a mixture model rather than an underestimation of the interaction term.

These approaches also differ in sample size requirements. Although tests for interaction term coefficients have lower power (and thus require larger samples) than the tests for main effects in a regression model (Aiken & West, 1991), the sample size requirements for regression mixture models, when perfect predictors of latent classes are not included, are expected to be even larger than those for regression interactions. One simulation study found that under conditions like those encountered in marketing research where differences in multiple regression weights are assessed simultaneously and where the R² values for different effects range from .60 to .98, the correct number of classes can be reliably found with sample sizes as small as 200 to 400 respondents so long as the smallest classes contained 20% or more of the population (Sarstedt & Schwaiger, 2008). A second study evaluating the performance of negative binomial regression mixtures found large bias in some model parameters with samples of less than 2,000 under most conditions (Park, Lord, & Hart, 2010). This study concluded that required sample size is dependent on the degree of class separation. When there is high class separation because of large mean differences between classes or by very strong effect sizes for the regression weights in each class, then the negative binomial regression mixture can be effective with samples as small as 300; with low class separation much higher samples are needed. In the social sciences, effect sizes are typically much smaller than those examined in the Sarstedt and Schwaiger study, and when the focus of regression mixtures is strictly on differential effects class separation is likely to be very weak. More research is needed in this area, but we suspect that in the social sciences regression mixtures should be considered a large sample technique.

The types of inferences which can be drawn also differ between the two methods. When used with cross sectional data neither interaction nor regression mixture models provide strong support for causal hypotheses about process given that neither x nor z proceed y in time (Cohen et al., 2003). Changes to study design including use of longitudinal data and randomization can greatly strengthen the types of causal inferences that can be made using statistical interactions. However, regression mixtures rely on assumptions about the conditional distribution of the outcome for the estimation of differential effects. In essence, the latent classes function as an unobserved z that is identified by the conditional distribution of the outcome and therefore cannot be isolated from the outcome. In our view, this means that results of regression mixture models are inherently exploratory and, compared with interaction models, are not well suited for testing hypotheses about specific interactions and are less able to allow strong causal conclusions even with longitudinal data or a randomized study design.

To summarize, although in some cases regression interactions and regression mixture models will yield very similar results, there are many circumstances in which results will be different. Both have strengths and limitations and are therefore best viewed as playing complimentary roles in the search for differential effects. Regression interactions provide a direct test for whether the effects of x on y differ as a function of a third variable, z, or, equivalently, whether the effects of z on y differ as a function of x. Regression mixture models provide a more global exploration for discrete classes of respondents characterized by heterogeneity in the effects of x on y. Regression mixtures may also be useful in assessing more focused questions about differential effects when predictors are not reliably measured and when those effects are a function of multiple variables or a complex function of a few variables.

Study 1 Aims

As the use of regression interactions for finding differential effects is already well understood, this study uses simulations to more fully describe regression mixture models and compare them with statistical interactions rather than to test performance under many conditions. The first aim of the simulations is to illustrate the ability of regression mixture models to identify discrete differential effects in the presence of a simple interaction when the effect of one predictor on an outcome differs between two classes. Thus, we simulate data using a regression interaction model and estimate a regression mixture model. The predictor of differential effects (z in the interaction model) is not included in the regression mixture analyses and so the research question could be phrased as “can regression mixture models detect simple effect heterogeneity, without predictors of differential effects?” The effect size and differences between classes in intercepts (which in the regression interaction model corresponds to a main effect of the predictor of differential effects) is varied between simulations. We hypothesize that regression mixtures are able to find two classes that accurately capture the differential effects in the population. We also hypothesize that as class separation increases (i.e., larger differences between classes in effect sizes and main effects), classification accuracy—measured by the entropy statistic (Ramaswamy, Desarbo, Reibstein, & Robinson, 1993) with values of 1 indicating no uncertainty about individual’s classification using highest posterior probabilities—will increase and model performance will improve.

The second aim is to demonstrate the inclusion of predictors of differential effects into the regression mixture model, and compare the results with the results of an interaction model. We focus on the case where differential effects are not perfectly predicted as is the case when the predictor is not reliably measured or an imperfect proxy for the predictor of differential effects is included. We hypothesize that the regression mixture model will find the true effects and accurately describe their relationship to the predictor. We hypothesize that the interaction model will identify the presence of differential effects, but will underestimate the size of the differences.

The third aim is to examine the ability of regression mixture models to detect a moderating factor when differential effects are more complex (more than two groups) as is likely in many applied scenarios. Specifically this aim assesses the presence of three groups of individuals who differ in the effects of a set of predictors on an outcome and where the size of the groups differs.

The outcome of each aim is to demonstrate the ability of regression mixture models to find the correct number of classes, and, given that the correct number of classes is found, to show that the parameter estimates for each class match those in the population. For the second aim an additional outcome is to demonstrate the ability of the interaction model to find a significant differential effect, and to examine bias in the estimates of differential effects obtained with the interaction.

Method

Study 1 uses Monte Carlo simulations. Data were generated using R (R Development Core Team, 2010), with 1,000 simulations for each condition and a sample size of 3,000 subjects. We used a sample of 3,000 in this study because our preliminary evidence suggests that regression mixture models are best thought of as a large sample technique. This is a sample size which is available in many public data sets (such as the one used for Study 2) and is a reasonable starting point for estimating these models. Regression mixture models were run in Mplus version 6 (L. K. Muthén & Muthén, 2010). We examined whether regression mixture models can detect the true number of classes, the true effect sizes, and the correct proportion of respondents in each class. Latent class enumeration is based on the bootstrapped likelihood ratio test (BLRT; McLachlan & Peel, 2000) and the Bayesian information criterion (BIC; Schwarz, 1978), which have both been shown to be effective for latent class enumeration (Nylund, Asparauhov, & Muthén, 2007). The BIC appears to be especially effective when used with regression mixture models and large samples (George, Yang, Van Horn, et al., 2013; Van Horn et al., 2012). For all models we used 96 randomly perturbed sets of start values with the 24 with the best likelihood after 10 iterations run until convergence.

One problem when using simulations with finite mixtures is label switching (McLachlan & Peel, 2000; Sperrin, Jaki, & Wit, 2010), in which the class labeled 1 in some simulations receives the label 2 in other results. In order to report the model parameters for each class across simulations, it is necessary to sort the results so that the first and second class remain substantively the same from replication to replication. We used an identifiability constraint where the class with the stronger effect of x on y was always Class 1. This creates a potential bias if, across simulations, the distributions of classes with the high slope and low slope overlap. For Aims 1 and 2 we found good separation (complete separation in nearly all cases) in the distribution of the regression weights for Class 1 and Class 2 across simulations suggesting negligible bias.

Results

Aim 1: To Illustrate the Use of Regression Mixture Models for Detecting Simple Discrete Interactions

For the simple interaction model, data were generated under four conditions that varied in the main effect of the predictor (present or not) and the size of the interaction. We choose moderate and large interactions. In preliminary analyses testing smaller effect sizes (r = .50 and r = .70 in different classes), we did find evidence for differential effects in most simulations, but the number of spurious results increased. We contend that a difference between classes in correlations of .20 and .70 is the minimum that should be detectable by regression mixtures if they are to be considered useful for finding differential effects. This represents a weak correlation in one class and a strong correlation in the other which would lead to substantively different conclusions in many applied areas. Differences in the main effects of z are important because they contribute to the definition of the latent classes and thus may improve model performance. Having no main effect of z provides a stringent test of the ability of regression mixtures to detect differential effects when class separation is only due to differential effects.

The differential effect was characterized by a binary variable (z) with 1,500 cases in each level. Both the predictor (x) and the random error term (ε) were generated from a standardized normal distribution and y was then created as a function of the linear equation: y = β₀+β₁x+β₂z+β₃xz+ε. β₀ was 0 for all analyses. β₁ was 0 and β₃ was 0.70 for models with a large interaction effect, and β₁ was 0.20 and β₃ was 0.50 for models with a medium interaction effect. The β₂ term was 0 in the model without main effects of the z and 0.50 (Cohen’s d = 0.50, Cohen, 1992) in the model including a medium main effect. In this case, z and C are equal and the true model in terms of a regression mixture has two latent classes differing in the effects of x on y and, in the case of a main effect of z, the y intercept.

Successive regression mixture models with one, two and three classes were estimated for each simulation. In each model y was regressed on x with class-specific intercepts, regression weights, and error variances (Mplus code for the two-class model is included in the appendix). For each simulation, the number of classes indicated by the data was established by choosing the model with the lowest BIC and the model with the most classes where the BLRT p value was less than .05. Using either the BIC or the BLRT the models performed quite well at detecting the correct number of classes. The BLRT chose the correct two-class model over both the one- and three-class models in between 92% and 95% of the simulations, and the BIC chose the correct model in more than 98% of the simulations except when there was no intercept difference for the moderate effect, in which case the BIC chose the correct model in 83% of the simulations. We expected worse performance for the model with less class separation (moderate interaction and no main effect), and the best performance for the model with more class separation (a strong interaction and a moderate main effect). A chi-square test evaluating the probability of choosing the correct model across conditions found support for this hypothesis using the BIC (χ² = 7.82, df = 1)but not the BLRT (χ² = 0.41, df = 1). Across the simulation conditions average entropy ranged from .14 to .18, indicating that the models do a poor job of correctly classifying individuals despite finding the correct number of classes.

An examination of estimated model parameters (see Table 1) shows that on average the models recover the true effects very well. The median and mean parameter estimates are always very close to the true values, and the 25th and 75th percentiles show that the results of most simulations fall within a small range around the true values. Some problems are evident in the minimum and maximum values, which sometimes are quite discrepant from the true values. For a few simulations the observed results are not a good representation of how the data were generated. Results for the conditions with the greatest separation between classes are closer to the population values than those with less separation. Regression weights under the main effect/strong interaction condition had a mean absolute difference from the population values of 0.15, whereas simulations from the no main effect/moderate interaction condition had a mean absolute difference of 0.35.

Table 1.

Parameter Estimates Across Simulations With Varying Effect Sizes.

	No main effect/moderate interaction								Main effect/moderate interaction
	True value	Mean	SD	SE	Minimum	25%	75%	Maximum	True value	Mean	SD	SE	Minimum	25%	75%	Maximum
Class 1 intercept	0.00	−0.03	0.03	0.04	−0.49	−0.05	−0.01	0.04	0.00	−0.02	0.09	0.07	−0.93	−0.05	0.04	0.16
Class 2 intercept	0.00	0.03	0.14	0.04	−0.04	0.01	0.04	3.13	0.50	0.50	0.05	0.05	0.35	0.47	0.54	0.66
Class 1 slope	0.20	0.18	0.12	0.08	−1.62	0.13	0.25	0.45	0.20	0.19	0.06	0.06	−0.16	0.15	0.23	0.34
Class 2 slope	0.70	0.71	0.07	0.06	0.44	0.66	0.75	0.99	0.70	0.70	0.05	0.05	0.51	0.67	0.73	0.91
Class 1 proportion	0.50	0.60	0.08		0.50	0.54	0.65	1.00	0.50	0.57	0.05		0.50	0.53	0.60	0.86
	No main effect/strong interaction								Main effect/strong interaction
	True value	Mean	SD	SE	Minimum	25%	75%	Maximum	True value	Mean	SD	SE	Minimum	25%	75%	Maximum
Class 1 intercept	0.00	−0.03	0.03	0.04	−0.17	−0.04	−0.01	0.04	0.00	0.00	0.05	0.05	−0.20	−0.04	0.03	0.16
Class 2 intercept	0.00	0.03	0.03	0.04	−0.04	0.01	0.04	0.16	0.50	0.50	0.04	0.04	0.38	0.48	0.53	0.64
Class 1 slope	0.00	−0.01	0.08	0.07	−0.31	−0.06	0.05	0.20	0.00	0.00	0.06	0.06	−0.18	−0.04	0.04	0.18
Class 2 slope	0.70	0.70	0.05	0.05	0.55	0.67	0.73	0.88	0.70	0.70	0.04	0.04	0.57	0.68	0.73	0.88
Class 1 proportion	0.50	0.56	0.05		0.50	0.52	0.59	0.76	0.50	0.55	0.03		0.50	0.52	0.57	0.70

Note. The mean is the average parameter estimate across all 500 simulations, the SD is the standard deviation of the parameter estimate, and the SE is the median estimated standard error for the parameter estimate. The SE is not directly available for the class proportions.

Aim 2: To Demonstrate the Inclusion of Predictors of Differential Effects Into Regression Mixture Models

If the predictor of differential effects is known rather than unknown, then the traditional interaction approach is a more direct and parsimonious test of that particular differential effect because the latent classes do not need to be estimated. These analyses show what happens when an imperfect predictor of differential effects is available such that z and C are related but not equal. To simplify, analyses were run only for the model with a moderate interaction term and a main effect of class membership as described above (for Class 1, the model is y = 0 + 0.2 *x+ε, and for Class 2, the model is y = 0.5 + 0.7 *x+ε), the only change was the inclusion of a binary predictor variable z that predicted class membership with 50% accuracy (the predictor correctly predicted the class in 50% of the cases while in the remaining 50% of the cases are either incorrectly predicted or correct by chance). Analyses were run for the regression mixture model as described above, but where z is now included as a covariate predicting class membership. Analyses were compared with results of the regression interaction model which included the interaction between x and z.

Model convergence is often an issue with regression mixture models. To evaluate for local maxima models are typically run many times with multiple sets of start values (we used 96 randomly perturbed set of start values with 24 runs until convergence) and the result with the best log likelihood (LL) ratio is selected (Hipp & Bauer, 2006; McLachlan & Peel, 2000). Two types of problems can arise: the best LL ratio statistic may not be replicated across multiple starts or the model with the best LL value can fail to converge to a proper solution. While all two-class models converged, 2.2% of three-class models did not produce a solution at all and an additional 58.8% of the three-class models did not converge to a replicated solution (the best LL value was not replicated within 1 unit across at least two random sets of start values). Results showed that, using the BIC as the reference, the regression mixture model was able to correctly identify the presence of two versus one and three classes in 98.4% of the simulations, while the BLRT was able to correctly identify two classes in 78.8% of the simulations. Because of the superior performance of the BIC we focus on it for the remainder of the study.

The parameter estimates (reported in Table 2) show that the regression mixture models perform very well in recovering these discrete differential effects. The only difference in results from analyses without a class predictor, in Table 1, is that the variability of the intercepts for both classes is increased. This is likely because of the additional uncertainty arising from including the class predictor. The other additional model parameters are the intercept and slope for the prediction of latent class membership. The slope for the effects of z shows that there is a very strong relationship between the imperfectly measured z variable and the latent class that corresponds to observed odds of 9.12, indicating that the odds of being in Class 1 are 9 times greater when z equals 1 than when z equals 0. This corresponds closely with the true odds ratio for C given z of 9.00 determined by the method described above for generating z as a function of C with 50% accuracy. In sum, when imperfect predictors of discrete differential effects are present and differential effects can be adequately captured by latent classes, regression mixtures are able to both find differential effects and to identify that those effects are partially (but not completely) a function of the predictor.

Table 2.

Parameter Estimates Across Simulations for the Main Effect and Moderate Interaction Model With Predictors of Differential Effects.

	Regression mixture model with a main effect and strong interaction
	True values	Mean	SD	SE	Minimum	25%	75%	Maximum
Class 1 intercept	0.00	−0.01	0.05	0.19	−0.22	−0.04	0.03	0.14
Class 2 intercept	0.50	0.50	0.03	0.23	0.39	0.47	0.52	0.60
Class 1 slope	0.20	0.19	0.05	0.05	−0.01	0.16	0.23	0.33
Class 2 slope	0.70	0.70	0.04	0.04	0.60	0.67	0.72	0.80
Class 1 proportion	0.50	0.49	0.06		0.30	0.46	0.53	0.70
Predicting Class 1 (logistic regression)
Intercept	3.00	3.34	0.45	0.60	1.68	2.92	3.72	7.10
Slope of Z	−2.20	−2.25	0.36	0.34	−3.83	−2.46	−1.99	−1.36
	Interaction model: Y = β0+β1X+β2Z+β3XZ
	True values	Mean	SD	SE	Minimum	25%	75%	Maximum
Class 1 intercept (β0)	0.00	0.12	0.02	0.02	0.04	0.11	0.14	0.21
Class 2 intercept (β0+β2)	0.50	0.38	0.02	0.04	0.30	0.36	0.39	0.44
Class 1 slope (β1)	0.20	0.32	0.03	0.02	0.25	0.31	0.34	0.40
Class 2 slope (β1+β3)	0.70	0.57	0.02	0.04	0.50	0.56	0.59	0.64
Class 1 proportion	na	na	na	na	na	na	na	na

Note. Five hundred simulations were conducted for each condition. The proportions are not applicable (na) for the interaction model because Z is known and not an estimated parameter.

Analyses were also conducted evaluating the use of interaction terms when differential effects were imperfectly predicted. Results (see Table 2) show that the estimates of intercepts and slopes from the interaction model are both shrunken toward each other and differential effects are substantially underestimated as hypothesized. In conclusion, although the sampling distribution for the model parameters is tighter for the interaction model, this model provides estimates of differential effects because of the measured variable z. In cases where z is unreliably measured or is a poor proxy for the categorical variable that actually predicts differential effects, these estimates will not correspond well with the differential effects that actually exist.

Aim 3: To Illustrate the Use of Regression Mixture Models With Complex Interactions

In the previous examples, the regression mixture approach was used to identify two subgroups of respondents with differential effects of a predictor. In that case, we compared these approaches when differential effects were the function of a single unobserved, or imperfectly measured, moderating variable, and thus the latent classes derived from the regression mixture model were equivalent to a potentially observed variable (Z equals C). In more complex models, regression mixtures do not always have a one-to-one correspondence with a GLM equation even if the moderating variables causing the differential effects were fully observed. Take for example a situation where there are two predictors of an outcome and three classes representing differences in the effects of the predictors. In our example, 50% of the respondents are in C₁ which is defined as Y = 0 + 0X₁+ 0X₂+e; 25% of the respondents are in C₂ where the response is Y = .5 + .2X₁+ .8X₂+e; and the remaining 25% of respondents are in C₃ where the response is Y = −.5 + .7X₁+ .3X₂+e. To show the link between regression mixtures and interactions, assume that we have two binary Z variables which are perfect measures of the latent classes such that when Z₁ is 1 and Z₂ is 0 the respondent is in C₁, when Z₁ is 0 and Z₂ is 1 then the respondent is in C₂, and when both Z₁ and Z₂ are 1 then the respondent is in C₃. Intuitively this should map onto the three-way interaction model:

$$Y=B_0+B_1{Z}_1+B_2{Z}_2+B_3{Z}_1{Z}_2+B_4{X}_1{Z}_1+B_5{X}_1+B_6{X}_1{Z}_2+B_7{X}_1{Z}_1{Z}_2+B_8{X}_2+B_9{X}_2{Z}_1+B_{10}{X}_2{Z}_2+B_{11}{X}_2{Z}_1{Z}_2+e.$$

However, because the data have only three classes, one of the Z₁×Z₂ combinations (in this case, it is Z₁ = 0 and Z₂ = 0), are not represented in the data and the above model is not uniquely estimable without dropping one of the terms for X₁ and one of the terms for X₂. For example, the above figure can be perfectly represented by an equation without a three-way interaction term: Y = 1 − 1Z₁− .5Z₂+ .5X₁+ .5X₁Z₁+ .7X₁Z₂+ 0.5X₂− 0.5 *X₂Z₁+ 0.3 *X₂Z₂. Alternatively, another term, such as one of the two-way interactions could be dropped and a unique solution found. To fully reproduce Equation (9) with regression mixtures and binary Z variables, it would be necessary for there to be four latent classes representing differential effects. Where it is possible to perfectly predict latent classes from a regression mixture model, it is also possible to map the regression mixture onto an interaction model. However, this mapping is only straightforward and intuitive in the simple case where there are only two classes. With more than two classes there may be multiple interaction models that lead to the same results such that simplifying assumptions must be made.

To demonstrate the performance of regression mixtures for finding more complex differential effects simulations were run under the model described above. One-, two-, three-, and four-class models were compared; the BLRT selected the true three-class model in 92% of the simulations. The BIC selected the three-class model in 99% of the simulations. In this case, regression mixtures do a good job of finding the presence of differential effects. We next examined the parameter estimates for the true three-class model (see Table 3). The median and mean values across all simulations deviate from the true population values by at most .01. The range from the 25th to 75th percentiles is also quite tight in all cases and the standard errors indicate a high degree of precision in the parameter estimates. As demonstrated by the minimum and maximum values, there is nearly complete separation between classes for all parameter estimates except for the slope of X₂ for Classes 1 and 3. The standard errors appear reasonable with fairly tight sampling distributions for all parameters.

Table 3.

Parameter Estimates Across Simulations for the Complex Moderation Model.

	Minimum	25%	50%	75%	Maximum	Mean	SD	SE
Class 1 intercept	−0.15	−0.03	0.00	0.03	0.23	0.00	0.05	0.05
Class 2 intercept	−0.72	−0.55	−0.50	−0.45	−0.25	−0.50	0.07	0.07
Class 3 intercept	0.30	0.47	0.51	0.54	0.73	0.50	0.05	0.05
Class 1 slope X1	−0.26	−0.04	0.00	0.03	0.16	−0.01	0.05	0.05
Class 2 slope X1	0.13	0.26	0.30	0.34	0.50	0.30	0.05	0.05
Class 3 slope X1	0.65	0.77	0.80	0.83	0.98	0.80	0.05	0.05
Class 1 slope X2	−0.27	−0.04	0.00	0.03	0.15	−0.01	0.05	0.05
Class 2 slope X2	0.44	0.66	0.70	0.74	0.90	0.70	0.06	0.06
Class 3 slope X2	0.06	0.17	0.20	0.23	0.35	0.20	0.05	0.04
Class 1 size	0.00	0.45	0.49	0.53	0.69	0.49	0.06
Class 2 size	0.10	0.22	0.25	0.29	0.98	0.26	0.05
Class 3 size	0.02	0.23	0.25	0.28	0.38	0.25	0.04

Note. Mean is the average parameter estimate across all imputations, SD is the standard deviation of the parameter estimate across simulations, and SE is the median estimated standard error for the parameter estimate.

Conclusion: Study 1

The first study aimed to clarify the role that regression interactions and regression mixtures have in assessing differential effects. Simulations for Aim 1 showed that when effects differ across discrete groups and when model assumptions are met, regression mixtures and regression interactions produce the same results. While these two approaches work very differently, the types of differential effects they both examine are similar in kind. In this case, the primary difference between regression mixtures and a regression interaction approach is that regression mixtures do not require that the predictor of the differential effects be included in the model. While this is not a logical approach for examining specific hypotheses about predictors of differential effects, it is a useful approach for exploring for effect heterogeneity beyond specific hypotheses. The second set of simulations showed another potential use of regression mixtures: examining differential effects with imperfect predictors of heterogeneity. We envision this being used as a follow-up when discrete differential effects are found with a regression interaction. The regression mixture approach is capable of both finding differential effects that are corrected for unreliability in the predictors and identifying the relationship of the measured predictor with the actual differential effects. The final set of simulations showed that when the models are more complicated such as what happens with multiple predictors and multiple latent classes, the one-to-one relationship between regression mixtures and interactions is not always so clear. We argue that there are times when regression mixtures may more clearly identify heterogeneous effects that are difficult to correctly uncover with interactions. In our example, the analyst would have probably found the correct model because there was one combination of Zs (0, 0) that was not represented in the data. However, if there was some error in Z such that this combination did appear in the data then the interaction model would not get to the right differential effects.

In summary, the first study showed that regression mixtures and regression interactions are both answering the same fundamental research question: Do the effects of a predictor on an outcome differ? However, the models approach the problem from different perspectives. Regression interactions take a confirmatory approach: examining differential effects as a linear function of interacting variables identified a priori. Regression mixtures work by exploring for evidence of effects which differ across discrete but unobserved classes. The trade-off for the global exploration of the regression mixture is a strong reliance on model assumptions and the need for large sample sizes. We believe that exploratory approaches to finding heterogeneity have a role to play as scientists increasingly focus on refining theories about human behavior and identifying heterogeneity in the effects they are investigating.

Study 2: Application of Regression Mixtures

Because regression mixture models are quite new in the social sciences little knowledge currently exists on the process of estimating these models. This study reviews the recommendations available from the limited existing literature on best practices in estimating regression mixtures and then illustrates the use of these models by examining heterogeneity in the effects of the Parenting Dimensions Inventory (PDI)—a global measure of parenting that assesses nurturance, responsiveness, being nonrestrictive, and consistency—on children’s social skills while controlling for child sex and ethnicity.

Distributional assumptions are integral in the estimation of mixture models in general (Bauer & Curran, 2003a) and regression mixtures in particular (Van Horn et al., 2012); addressing violations of distributional assumptions is in some respects an intractable problem because when within-class normality is assumed, a nonnormal distribution implies the presence of additional latent classes. However, three alternative parameterizations of the model have been proposed which have more flexible assumptions about within-class error distributions: the use of an ordered logistic regression link function (George, Yang, Van Horn, et al., 2013; Van Horn et al., 2012), using a skew normal residual distribution (Liu & Lin, 2014), and “differential effects sets” in which additional latent classes are included to approximate nonnormality in errors (George, Yang, Jaki, et al., 2013). The former two approaches are particularly geared toward moving away from the assumption of within-class normality and allow for investigating the number of classes and the general direction of differential effects whereas the latter approach uses additional classes to capture nonnormality.

A second key issue in using regression mixtures is the sample size requirements of these methods. As discussed in the introduction, the limited existing research in this area suggests that when class separation is weak regression mixtures may require large samples (Sarstedt & Schwaiger, 2008); however, this research was conducted using negative binomial models and did not address conditions likely to be found in the social sciences. More research is needed in this area, but it appears that large samples are to be advised.

A third applied issue that arises in estimating regression mixtures is the inclusion of predictors of latent classes. Because of the concern that regression mixture results may be unstable if covariates are misspecified, we propose that the safest approach is to first conduct latent class enumeration and identification of differential effects in models without covariates predicting latent class membership (although direct effects of key covariates on the outcome may be included). Covariate effects on latent classes can be included as a second step and substantive differences in the latent classes should be carefully examined. When estimates of differential effects change dramatically we are inclined to be suspicious of the original result; ongoing research is examining what covariate relationships are likely to lead to substantive changes in latent classes. A related issue concerns modeling the relationship between latent classes and the predictor (X) variable. The models presented above assume that the mean of X is constant across latent classes. Suggestions for relaxing this assumption include modeling the regression of the latent classes on X (B. O. Muthén & Asparouhov, 2009) or including X as an indicator of the latent classes (Ingrassia, Minotti, & Vittadini, 2012). Research examining modeling the relationship between X and latent classes in regression mixtures shows that misspecifying the model by failing to include this relationship rarely results in serious problems with class enumeration or assessment of differential effects (Lamont, Vermunt, & Van Horn, 2014). Because including this relationship increases model complexity we suggest first estimating the model without the relationship between X and the latent classes and then testing the final model with this relationship included, again looking for substantive changes in estimates of differential effects.

The main additional suggestion we have is that while these models are exploratory they are best conducted within some theoretical framework and focused on a particular differential effect. We suggest focusing on a small number of effects for which there is a rational for expecting heterogeneity in the population. Where differential effects are identified we suggest testing alternative model parameterizations to show that the effects remain stable when model assumptions are changed. The inclusion of key covariates based on initial theory can help better understand the heterogeneity that is found and provide a basis for replication. If strong predictors of class membership are found, replication of the results using regression interactions in an independent, but potentially much smaller, sample is highly recommended. Current research is investigating methods for obtaining residuals and conducting model diagnostics with regression mixtures.

Application of Regression Mixtures to Examining Differential Effects of Parenting

The issues raised above are demonstrated with an applied example examining differences in the relationship between parenting and children’s social skills. As with any study, the search for differential effects should be guided by theory. In this example, many prominent developmental theories suggest not only that poor parenting behaviors (e.g., low warmth, low responsiveness, and high intrusiveness or hostility) are associated with children’s adjustment difficulties (Campbell, Shaw, & Gilliom, 2000; Chorpita & Barlow, 1998; Rubin, Burgess, Dwyer, & Hastings, 2003) but also that the relationship between parenting and child adjustment will differ between children. Effects may be dependent on contextual and individual characteristics of both the parent and child (Belsky, 2005). Given that some empirical research indicates that parenting differs for boys and girls (Lytton & Romney, 1991), and for families of different ethnicities or races (Deater-Deckard & Dodge, 1997a, 1997b), in this example we examined whether or not the effects of parenting differs as a function of sex and ethnicity. The use of regression mixtures allows for an assessment of whether there is heterogeneity unaccounted for by these demographic variables.

Method

Data are from the National Head Start-Public School Transition Demonstration Study, a 30-site, 5-year, longitudinal intervention study (for a full description, see C. T. Ramey, Ramey, & Phillips, 1996; S. L. Ramey et al., 2001). The intervention evaluated by the Transition Study demonstrated no effects on children’s social skills outcomes or the family environment (S. L. Ramey et al., 2001), consequently we ignored treatment condition in these analyses. Clustering was also ignored. Because all predictors were measured at the individual level and intraclass correlation coefficients are modest, the design effect (Neuhaus & Segal, 1993) was estimated to be 1.02 indicating no meaningful effect of clustering on standard errors. The Transition study included 30 sites in different states and two cohorts of families of kindergartners who were followed through third grade. Data were collected from 1992 through 1997. Because our purpose was to demonstrate regression mixtures using a simple model, this study used cross-sectional analyses to examine differential effects of family resources in the third grade data (collected in 1996 for Cohort I and 1997 for Cohort II). The sample enrolled children who were formerly in the Head Start program and their peers from the same classrooms when they entered kindergarten. Data from 6,305 third grade students and their families were included in most analyses; however, because local sites were given the option to administer the PDI, data for this measure were available for only 5,425 students. Reported demographics for children were 50% female, 33% African American, 48% White/non-Hispanic, 6% Hispanic, and 13% reported “Other” racial or ethnic group. Average family income was below the federal poverty line, and median parent education level was a high school diploma (31% did not have a diploma).

Measures

Parenting was assessed using the abbreviated PDI (Slater & Power, 1987). Student social skills were measured using parent ratings of the Social Skills Rating System (Gresham & Elliott, 1990). The current study used a second-order factor score for Social Skills composed of four subscales: Cooperation, Assertion, Responsibility, and Self-Control. Based on previous psychometric analyses a modified version of the original factor structure was used that included 24 of the original 38 items (see, Van Horn, Atkins-Burnett, Ramey, Snyder, & Karlin, 2007). Reliability for the subscales was generally adequate although the parent report version of Responsibility has a coefficient alpha less than .70. Parent ratings obtained 4 weeks apart demonstrated a test–retest reliability of .87 for Social Skills.

Results

The second step in estimating a regression mixture model, after establishing theoretical support for differential effects, is to examine the distribution of the outcome variable conditional on any covariates from a one-class model. A density plot of the residuals from a regression analyses where the Social Skills Rating System was predicted by the covariates with an overlay of a normal density was examined (see Figure 4). The finite mixture approach used here assumes that any nonnormality in this plot is due to the presence of mixtures in the data. Thus, although we did not assume that the plot is normal, in practice high levels of skew were likely to mean that the normality assumption was problematic. In this case, the distribution of the outcome closely matched a normal distribution and so we proceeded with the assumption of normal within-class residuals. Otherwise we would have used an alternative model.

Figure 4.

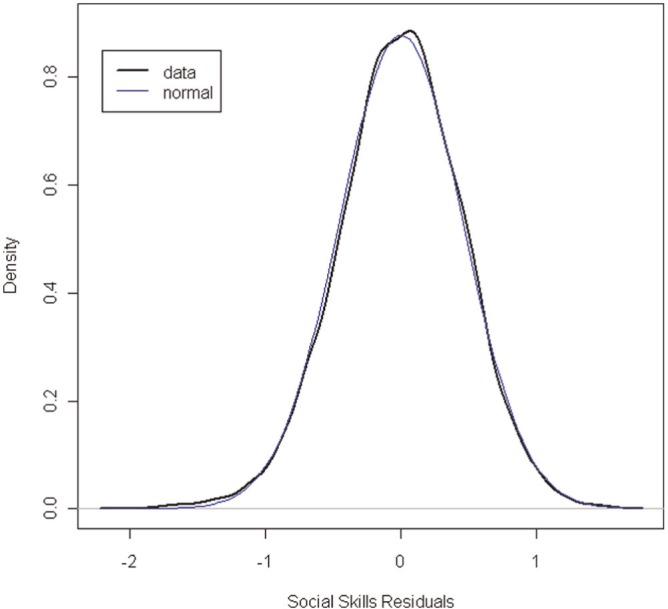
Density plot of residuals for the effects of parent ratings of social skills with a normal overlay.

The third step in the process is to specify the within-class regression mixture model which was

$$\begin{array}{l}{\mathrm{SocialSkills}}_{ik}={\mathrm{\beta }}_{0k}+{\mathrm{\beta }}_{1k}{\mathrm{PDI}}_{ik}+{\mathrm{\beta }}_2{\mathrm{ChildSex}}_{ik}+{\mathrm{\beta }}_3{\mathrm{Black}}_{ik}\\ +{\mathrm{\beta }}_4{\mathrm{Hispanic}}_{ik}+{\mathrm{\beta }}_5{\mathrm{White}}_{ik}+{\mathrm{\epsilon }}_{ik}\end{array}$$

Only the intercept, the effect of PDI, and the error term were allowed to vary between classes. Multiple classes may represent differences in intercepts or differences in the effects of parenting on the outcome between classes. The variance of the error term was allowed to vary between classes because we expected that if the effects of PDI were greater in some classes there would be less error in those classes. Model complexity is substantially increased by estimating class-specific variances; however, research shows that incorrectly fixing variances to be constant across classes can lead to serious bias in parameter estimates (Kim et al., 2014).

To determine the number of classes supported by the data we estimated multiple models, each with one additional class. Table 4 presents fit criteria and the percentage of respondents in each class for the one- through four-class models, as well as a more constrained three-class model, which will be described later. One challenge in mixture models is to find the solution which optimally fits the data, balancing gains in the log likelihood value and decreasing parsimony for increasing complex models. Because the likelihood function with finite mixtures is typically unbounded and usually quite complex, local maximum may lead to selection of a solution which is not optimal. It is recommended to run the model with multiple starting values for each parameter, choosing the solution with the best LL value, ideally this solution should be replicated multiple times across different starting values (Masyn, 2013). In this example, each analysis used 200 different starting values, with 50 run to convergence, with the exception of the four-class model, all the 50 final LL values were replicated. In this case, we ran 100 starts to convergence, 21 converged to the same lowest value. LL values for the remaining runs were within 12 units of the lowest and checks of those different solutions showed no substantive differences. When too many classes are selected in a regression mixture model, we find that it is commonly difficult to obtain stable model results. In our experience with simulated data, lack of convergence is actually evidence of model misspecification. These results clearly indicated the three-class solution using both the BLRT and the BIC. Furthermore, the smallest class in the four-class solution included less than 1% of the sample, suggesting that the additional class was composed of unusual observations. While it may be possible to reliably identify small classes with large samples, in regression mixture models we are reluctant to give much weight to small classes. A reasonable cutoff is to require classes to be interpreted to contain greater than 10% of the respondents, a number recommended (although not tested) by others as well (Leisch & Gruen, 2010).

Table 4.

Latent Class Enumeration for the Regression of Social Skills on Parenting.

Classes	One class	Two class	Three class	Four class	Three class constrained
Log likelihood	−3,418	−3,366	−3,330	−3,317	−3,330
No. of parameters	7	11	15	19	14
BIC	6,896	6,827	6,790	6,797	6,781
p-BLRT	n/a	.00	.00	.53	n/a
Entropy	1.00	0.55	0.49	0.61	0.49
Percentage Class 1	100	85	72	73	72
Percentage Class 2		15	15	15	15
Percentage Class 3			13	12	13
Percentage Class 4				1

Note. p-BLRT is the p value for the bootstrap likelihood ratio test (BLRT) where the null hypothesis is that the k− 1 class model fits better than the k class model. n/a indicates that the BLRT was not available for that model. The last rows indicate the percentage of respondents in each class, with classes ordered from highest to lowest. BIC = Bayesian information criterion.

Note that the three-class model had the lowest entropy value. In our view entropy should not be considered a criterion for class enumeration in regression mixture models. The reasons for this can be illustrated by Figure 3; high levels of entropy would require little overlap between individuals in Class 1 and Class 2. If the classes were defined primarily by differences in the effects of a predictor on an outcome, there would often be little separation between the two classes and entropy would be low. This does not indicate model failure, rather it indicates that while the models may do a good job of finding differential effects they should not be considered reliable for classifying individuals. The inclusion of covariates may dramatically improve entropy and the utility of regression mixtures for classification.

After selecting the number of classes supported by the data, the next step is to determine what distinguishes latent classes. While our results supported a three-class solution, it is instructive to examine the parameters from both the two- and three-class models in Table 5. The primary parameters of interest for each class were the intercepts and slopes of PDI. For the two-class model the largest class, containing 85% of the respondents, had a slightly negative intercept and a positive effect of parenting on social skills. The smaller class, containing 15% of the children, had a positive intercept indicating that students in this class on average have higher social skills than those in the first class, and the effects of parenting in this class were zero. For the three-class solution, the first two classes had nearly identical parameter estimates to those in the two-class solution. However, now there was an additional class, with a lower intercept and where the effects of parenting are virtually identical to that in the larger class with a positive effect of parenting. Given the low entropy, it was difficult to verify this, but it appears as though Class 1 from the two-class solution is split in two; the effects of parenting remain the same in both classes, they differ only in their intercepts. This was an example of a “differential effects set,” one of the methods which has been shown effective for modeling nonnormal error distributions (George, Yang, Jaki, et al., 2013). Together, the two classes with similar regression weights captured one population of students in which the effects of parenting were positive and in which the error distribution is not normal. Model estimation can be greatly simplified by constraining the effects of parenting to be the same in two classes. Model fit (see Table 4) was slightly improved in this simplified solution as model parameters remain virtually identical for the constrained model (see Table 5), and since there were now just two differential effects in the model it became easier to include predictors of the differential effects. This approach demonstrated what should be the next step in estimating regression mixtures, testing for the effects of distributional assumptions. While differential effects sets are able to find differential effects in nonnormal data (George, Yang, Jaki, et al., 2013), we also transformed the outcome into an ordinal variable and ran an ordinal logistic regression model which has also been shown to be effective with nonnormal error distributions (George, Yang, Van Horn, et al., 2013). The two-class ordinal logistic regression model showed very similar effect patterns and similar class sizes to those found above; however, the BIC and adjusted BIC slightly favored the one-class over the two-class models. Because the two-class results were very similar we take this as an example of low power for the BIC with ordinal logistic regression when there are minimal intercept differences. A final step in assessing model stability was including a relationship between the predictor (PDI in this case) and the latent classes in the model. In this case, including PDI as a predictor of latent classes resulted in no changes in the other model parameters; if the other parameters had changed we would have investigated the possibility of a nonlinear relationship between PDI and social skills.

Table 5.

Estimates for the Two- and Three-Class Regression Mixtures of Social Skills on Parenting.

	Two classes		Three classes		Three classes—constrained
	Parameter	SE	Parameter	SE	Parameter	SE
Effect of covariates (equal across classes)
Black	−0.011	0.012	−0.014	0.012	−0.014	0.012
Hispanic	0.039	0.021	0.038	0.020	0.038	0.020
White	−0.026	0.011	−0.027	0.011	−0.027	0.011
Female	0.083	0.012	0.083	0.012	0.083	0.012
Class 1 intercept	−0.098	0.015	−0.047	0.028	−0.047	0.028
Class 1 PDI	0.216	0.009	0.213	0.010	0.214	0.008
Class 1 residual variance	0.182	0.005	0.130	0.011	0.130	0.010
Class 2 intercept	0.413	0.049	0.491	0.037	0.490	0.036
Class 2 PDI	−0.003	0.023	0.020	0.019	0.021	0.019
Class 2 residual variance	0.087	0.012	0.077	0.008	0.077	0.008
Class 3 intercept	n/a		−0.494	0.101	−0.487	0.079
Class 3 PDI	n/a		0.219	0.035	0.214	0.008
Class 3 residual variance	n/a		0.221	0.025	0.221	0.025

Note. In the three-class constrained model the slopes for PDI are constrained to be the same in Classes 1 and 3.

Once differential effects are found and reasonable model stability is established, most regression mixture analyses will focus on predicting the latent classes. This is done by including covariates (which were also included as within-class control variables in Equation (10) as predictors of latent class membership in Equation (5). In this case, since the effects of parenting were different between Class 2 and Classes 1 and 3, we added just one logistic regression into the equation to predict membership in Class 2, with predictors chosen based on existing theory:

$$\mathrm{Pr}(c_i=2|\mathrm{co}{v}_i)=\frac{1}{1+e^{-(\mathrm{\alpha }+{\mathrm{\gamma }}_1\mathrm{blac}{\mathrm{k}}_i+{\mathrm{\gamma }}_2\mathrm{hispani}{\mathrm{c}}_i+{\mathrm{\gamma }}_3\mathrm{whit}{\mathrm{e}}_i+{\mathrm{\gamma }}_4\mathrm{femal}{\mathrm{e}}_i)}}.$$

The regression mixture model was re-estimated with these predictors now included. Because all parts of the model are jointly estimated and predictors of class membership can strongly affect estimated class probabilities, it is possible the model results can change. Before interpreting prediction of classes we first compared the differential effects with those observed in Table 6. Only minor changes resulted from the inclusion of predictors; substantial changes in differential effects would have raised questions about model stability and caused us to investigate whether the original results were because of a model misspecification. We recommend great caution in interpreting model results where there is evidence of instability. The only class predictor for which the confidence interval did not contain zero was the effect code for White students (γ = −0.879, SE = 0.435); the odds of a White student being in the high intercept class with no effect of parenting are reduced by 0.415 as compared with the average student.

Table 6.

Comparison of Regression Interactions and Regression Mixture Models.

Regression interactions	Regression mixtures
Research questions
Tests hypotheses about heterogeneity in an effect because of an a priori identified predictor	Explores for any evidence of discrete heterogeneity in effects
Types of heterogeneity identified
DTiscrete or continuous heterogeneity that is a linear funciton of a predictor	Discrete heterogeneity in effects
Model assumptions
Normal residuals—Affects standard errors	Normal residuals—Affects parameter estimates
Errors and independent and constant across all predictors	Errors and independent and constant across x variables
Relationships are linear	Relationships are linear
All predictors are measured without error	x Variables are measured without error
	z Variables need to be measured without error for the relationship between z and latent classes to be unbiased
Sample size required
Moderate samples required	Large samples required

Regression Interaction Model

For comparison the same data were analyzed using a regression interaction model with parent ratings of social skills regressed on the PDI total score, child sex, effect codes for child ethnicity, and all two-way interactions between PDI and child sex and ethnicity. As with the regression mixture model, the interaction model (with df = [9, 5415]), showed no significant main effects of ethnicity. The main effect of being female (b = 0.085, SE = 0.012) was very similar to the main effect in the regression mixture model. The overall effect of parenting in the interaction model (b = 0.199, SE = 0.011) was in between the two different effects found in the regression mixture model, but as expected was much closer to the estimates from the two classes containing 85% of the sample. The main effects appeared to be consistent across the two approaches.

The interactions between parenting and being female and being White were found to be nonsignificant in this model, whereas the interaction between parenting and being African American was significant and negative (b = −0.030, SE = 0.015) and the interaction between parenting and being Hispanic was close to significant (b = −0.052, SE = 0.028). On initial inspection these results looked different from the regression mixture results where only the effect of being White on class membership was significant. However, because of the effect coding the substantive interpretation was the same: in the regression mixture model White students were less likely to be in the class with no effects of parenting, and in the interaction model the effects of parenting were reduced for Black and Hispanic students as compared with the average student. These apparently different findings had a similar substantive meaning.

The interesting comparison between the two approaches is that while the results were consistent, the interaction model suggested that differential effects were small and that the effects of parenting were positive for all students, just slightly less so for Black and Hispanic children. The regression interaction estimates the effects of parenting to be .17 for Black students and .15 for Hispanic students, confidence intervals for both estimates exclude zero and were very close to the average effects of parenting (approximately .20); thus, the interaction model showed that differences between ethnic groups in the effect of parenting is a matter of degree, rather than qualitative differences. The regression mixture model on the other hand showed a small group of students for whom there were no effects of parenting on social skills; these students were more likely to be African American, Hispanic, or some other ethnicity. As expected based on the simulations, results were similar, but the interaction model estimates the differential effects to be of lower magnitude than does the regression mixture model. An explanation for this is that the variables included in the interaction did not account for all the differential effects.

Conclusion: Study 2

While regression mixture models are understood in theory, there is still much to learn about the applied use of these models. This study provided some guidance from existing research but there is still much work to be done to understand when regression mixtures are effective at finding differential effects, step-by-step recommendations for how to use the models, and methods for diagnosing model performance. The most general concern is that regression mixture results are because of artifacts in the data (i.e., outliers, distributional assumptions, and nonlinear relationships) rather than differential effects. This study reviewed some of the specific issues which existing research has suggested are important to consider in conducting regression mixture models. In general, we suggest that two especially important principles are (a) understanding how it is that regression mixtures find differential effects is likely to lead to more robust application of the method and (b) assessing the stability of results across different models (i.e., those with different link functions, including and excluding key covariates, and replication with alternative data sets) should increase the confidence placed in differential effects found.

The application of regression mixture models in this study suggested the presence of a small group of children whose parents rated their social skills higher than other children, and for whom, in contrast to the other children, there was no relationship between parenting and social skills. These results appeared stable across different models, and were partially explained by the inclusion of ethnicity as a predictor of the differential effects. However, additional heterogeneity remained after the inclusion of ethnicity as a predictor. One possible interpretation of these results is that there is a group of children who are highly socially adaptable; and, for this group of children, parenting has no additional impact. Another interpretation of these findings may be that either the social skills or parenting measures have some culturally specific components that would suggest they are not equally relevant for all families (Deater-Deckard & Dodge, 1997a, 1997b). Yet a third interpretation is that there is a group of parents whose response to the Social Skills Rating System is driven by social desirability; thus, their children are rated highly and those ratings are unrelated to reports of parenting. In this case, evidence for heterogeneous effects leads to more questions than answers. We expect that this will often be the case, because heterogeneity in effects have rarely been studied, exploratory methods to search for differential effects are likely to lead to heterogeneity being found where it was not previously hypothesized. Ideally, the finding of unexplained heterogeneity in effects would lead to an examination of additional predictors of those effects and to the further development of and test of theory, in this case about what may be responsible for a small group of students who are not affected by parenting.

In practice, it is appropriate to use statistical interactions to evaluate focused hypotheses about differential effects and then use regression mixtures to further explore the data and possibly provide additional guidance on the interpretation of the effects found. In this case, interactions show that the effects of parenting on social skills were substantively the same for boys and girls and across ethnic groups although the effects different somewhat in magnitude. Regression mixtures answer a different question, testing for evidence of classes differentiated by the effects of parenting. Results suggest the presence of a small class of students for whom there is no effect of parenting, and show that this differs from the rest of the population in ethnicity. We expect that these results will lead to more focused theories about effect heterogeneity which can in turn lead to the use of regression interactions to test these specific hypotheses. Together the results shed light on the complexity of differential effects of parenting.

Discussion

Understanding of differential effects is best facilitated by a comprehensive and systematic approach from the beginning of the research process. This article has suggested a process for doing so that includes developing hypotheses based on theory for the types of effect heterogeneity expected, designing studies to include reliable measures of predictors of effect heterogeneity and adequate power, using interactions to test for specific differential effects, and using exploratory methods to examine for heterogeneity not accounted for by the model. We see this as a process which is facilitated by the use of analytic methods for testing specific hypotheses about differential effects, most commonly regression interactions, as well as exploratory methods for identifying differential effects empirically. In many areas of research in the social sciences there are few tests of effect heterogeneity and inadequate theory to focus these tests on specific predictors. Exploratory analyses are a useful tool for building theories of heterogeneity and for finding differential effects which would otherwise be missed.

In many ways regression mixtures are similar to regression interactions in their approach to finding differential effects, but there are also differences, as summarized in Table 6. The most obvious difference between the two approaches is that regression mixtures do not require the predictor of differential effects to be measured. Thus, these models focus on an exploration of discrete heterogeneity in the effects of a predictor on an outcome. Strengths of this exploratory approach include the ability to deal with unreliability in predictors of differential effects, better understanding of complex interactions in certain cases, and the ability to find evidence for differential effects when the predictors are not observed. We see regression mixtures as complimenting the use of statistical interactions: Interactions are efficient for testing focused questions about differential effects whereas regression mixtures can be used to better understand the interactions found and to explore for evidence of other discrete heterogeneity. The applied example was a good illustration of this point. Although the different models yielded similar results, the functional interpretation was quite different with regression mixtures finding substantively different and more nuanced effects that raised additional questions that invite further exploration.

One limitation of regression mixtures is that they are only well suited for finding differential effects when there are a small number of typical functions that capture differences in the effects of the predictor(s) on the outcome(s). Regression interaction models are ideal for finding both discrete and continuous differential effects when the predictors are measured. However, exploratory methods for finding differential effects which are not discrete are currently very limited. More work is needed to understand the types of nondiscrete differential effects that regression mixtures are able to capture. Other limitations include the need for larger samples and the restricted inferences inherent in exploratory analyses.

Appendix

Mplus Code for the Two-Class Regression Mixture Model

• title: a latent class model assuming cross-sectional data;

• data: file = sim1.dat;

• variable:

• NAMES = X Y Group;

• USEVARIABLES = X Y;

• CLASSES = c(2);

• analysis:

• type=mixture;

• starts=100 20;

• lrtbootstrap=100;

• lrtstarts=20 10 20 10;

• processors=8 (STARTS);

• model:

• %overall%

• Y on X*0;  ! Starting value of 0 for the effect of X on Y in Class 1 is 0

• Y*1;  ! Variance of Y is started at 1 in Class 1

• ‘%c#2%

• Y on X*0.7; ! Starting value for the regression weight in Class 2 is .7

• Y*.714;  ! Starting value for the error variance of Y in class 2 is .714

• save:

• RESULTS

• Output:

• TECH14;