Convergence and Stability of a Class of Iteratively Re-weighted Least Squares Algorithms for Sparse Signal Recovery in the Presence of Noise

Abstract

In this paper, we study the theoretical properties of a class of iteratively re-weighted least squares (IRLS) algorithms for sparse signal recovery in the presence of noise. We demonstrate a one-to-one correspondence between this class of algorithms and a class of Expectation-Maximization (EM) algorithms for constrained maximum likelihood estimation under a Gaussian scale mixture (GSM) distribution. The IRLS algorithms we consider are parametrized by 0 < ν ≤ 1 and ε > 0. The EM formalism, as well as the connection to GSMs, allow us to establish that the IRLS(ν, ε) algorithms minimize ε-smooth versions of the ℓ_ν ‘norms’. We leverage EM theory to show that, for each 0 < ν ≤ 1, the limit points of the sequence of IRLS(ν, ε) iterates are stationary point of the ε-smooth ℓ_ν ‘norm’ minimization problem on the constraint set. Finally, we employ techniques from Compressive sampling (CS) theory to show that the class of IRLS(ν, ε) algorithms is stable for each 0 < ν ≤ 1, if the limit point of the iterates coincides the global minimizer. For the case ν = 1, we show that the algorithm converges exponentially fast to a neighborhood of the stationary point, and outline its generalization to super-exponential convergence for ν < 1. We demonstrate our claims via simulation experiments. The simplicity of IRLS, along with the theoretical guarantees provided in this contribution, make a compelling case for its adoption as a standard tool for sparse signal recovery.

I. Introduction

Compressive sampling (CS) has been among the most active areas of research in signal processing in recent years [1], [2]. CS provides a framework for efficient sampling and re-construction of sparse signals, and has found applications in communication systems, medical imaging, geophysical data analysis, and computational biology.

The main approaches to CS can be categorized as optimization-based methods, greedy/pursuit methods, coding-theoretic methods, and Bayesian methods (see [2] for detailed discussions and references). In particular, convex optimization-based methods such as ℓ₁-minimization, the Dantzig selector, and the LASSO have proven successful for CS, with theoretical performance guarantees both in the absence and in the presence of observation noise. Although these programs can be solved using standard optimization tools, iteratively re-weighted least squares (IRLS) has been suggested as an attractive alternative in the literature. Indeed, a number of authors have demonstrated that IRLS is an efficient solution technique rivalling standard state-of-the-art algorithms based on convex optimization principles [3], [4], [5], [6], [7], [8]. Gorodnitsky and Rao [3] proposed an IRLS-type algorithm (FOCUSS) years prior to the advent of CS and demonstrated its utility in neuroimaging applications. Donoho et al. [4] have suggested the usage of IRLS for solving the basis pursuit de-noising (BPDN) problem in the Lagrangian form. Saab et al. [5] and Chartrand et al. [6] have employed IRLS for non-convex programs for CS. Carrillo and Barner [7] have applied IRLS to the minimization of a smoothed version of the ℓ₀ ‘norm’ for CS. Wang et al. [8] have used IRLS for solving the ℓ_ν -minimization problem for sparse recovery, with 0 < ν ≤ 1. Most of the above-mentioned papers lack a rigorous analysis of the convergence and stability of the IRLS in the presence of noise, and merely employ IRLS as a solution technique for other convex and non-convex optimization techniques. However, IRLS has also been studied in detail as a stand-alone optimization-based approach to sparse reconstruction in the absence of noise by Daubechies et al. [9].

In [10], Candès, Wakin and Boyd have called CS the “modern least-squares”: the ease of implementation of IRLS algorithms, along with their inherent connection with ordinary least-squares provide a compelling argument in favor of its adoption as a standard algorithm for recovery of sparse signals [9].

In this work, we extend the utility of IRLS for compressive sampling in the presence of observation noise. For this purpose, we use the Expectation-Maximization (EM) theory for Normal/Independent (N/I) random variables and show that IRLS applied to noisy compressive sampling is an instance of the EM algorithm for constrained maximum likelihood estimation under a N/I assumption on the distribution of its components. This important connection has a two-fold advantage. First, the EM formalism allows to study the convergence of IRLS in the context of the EM theory. Second, one can evaluate the stability of the IRLS as a maximum likelihood problem in the context of noisy CS. More specifically, we show that the said class of IRLS algorithms, parametrized by 0 < ν ≤ 1 and ε > 0, are iterative procedures to maximize ε-smooth approximations to the ℓ_ν ‘norms’. We use EM theory to prove convergence of the algorithms to stationary points of the objective, for each 0 < ν ≤ 1. We employ techniques from CS theory to show that the IRLS(ν, ε) algorithms are stable for each 0 < ν ≤ 1, if the limit point of the iterates coincides with the global minimizer (which is trivially the case for ν = 1, under mild conditions standard for CS). For the case ν = 1, we show that the algorithm converges exponentially fast to a neighborhood of the stationary point, for small enough observation noise. We further outline the generalization of this result to super-exponential convergence for the case of ν < 1. Finally, through numerical simulations we demonstrate the validity of our claims.

The rest of our treatment begins with Section II, where we introduce a fairly large class of EM algorithms for likelihood maximization within the context of N/I random variables. In the following section, we show a one-to-one correspondence between the said class of EM algorithms and IRLS algorithms which have been proposed in the CS literature for sparse recovery. In Sections IV and V, we prove the convergence and stability of the IRLS algorithms identified previously in Section III. We derive rates of convergence in Section VI and demonstrate our theoretical predictions through numerical experiments in Section VII. Finally, we give concluding remarks in Section VIII.

II. Normal/Independent random variables and the Expectation-Maximization algorithm

A. N/I random variables

Consider a positive random variable U with probability distribution function p_U(u), and an M-variate normal random vector Z with mean zero and non-singular covariance matrix Σ. For any constant M-dimensional vector μ, the random vector

$$Y=\mu +U^{-1/2}Z$$ (1)

is said to be a normal/independent (N/I) random vector [11]. N/I random vectors encompass large classes of multi-variate distributions such as the Generalized Laplacian and multi-variate t distributions. Many important properties of N/I random vectors can be found in [12] and [11]. In particular, the density of the random vector Y is given by

$$p_Y(y)=\frac{1}{{(2\pi )}^{M/2}{\mid \mathrm{\sum }\mid }^{1/2}}exp\left(-\frac{1}{2}\kappa \left({(y-\mu )}^T{\mathrm{\sum }}^{-1}(y-\mu )\right)\right),$$ (2)

with

$$\kappa (x):=-2ln\left({\int }_0^{\infty }{u}^{M/2}{e}^{-ux/2}{p}_U(u)du\right)$$ (3)

for x ≥ 0 [11].

N/I random vectors are also commonly referred to as Gaussian scale mixtures (GSMs). In the remainder of our treatment, we use the two terminologies interchangeably.

Eq. (2) is a representation of the density of an elliptically-symmetric random vector Y [13]. Eq. (3) gives a canonical form of the function κ(·) that arises from a given N/I distribution. However, when substituted in Eq. (2), not all κ(·) lead to a distribution in the GSM family, i.e., to random vectors which exhibit a decomposition as in Eq. (1). This will be important in our treatment because we will show that IRLS algorithms which have been proposed for sparse signal recovery correspond to specific choices of κ(x) which do lead to GSMs. In [14], Andrews et al. give sufficient and necessary conditions under which a symmetric density belongs to the family of GSMs. In [11], Lange et al. generalize these results by giving sufficient and necessary conditions under which a spherically-symmetric random vector is a GSM (note that any elliptically-symmetric density as in Eq. (2), with non-singular covariance matrix, can be linearly transformed into a spherically-symmetric density). The following theorem gives necessary and sufficient conditions under which a given choice of κ(x) leads to a density in the N/I family.

Proposition 1 (Conditions for a GSM)

A function f(x) : ℝ ↦ ℝ is called completely mono-tone iff it is infinitely differentiable and (−1)^kf^(k)(x) ≥ 0 for all non-negative integers k and all x ≥ 0. Suppose Y is an elliptically-symmetric random vector, with representation as in Eq. (2), then Y is a N/I random vector iff κ′(x) is completely monotone.

We refer the reader to [11] for a proof of this result.

B. EM algorithm

Now, suppose that one is given a total of P samples from multi-variate N/I random vectors, y_i, with mean and covariances μ_i(θ) and Σ_i(θ) respectively, for i = 1, 2, · · ·, P, all parametrized by an unknown parameter vector θ. Let

$${\delta }_i^2(\theta ):={(y_i-{\mu }_i(\theta ))}^T{\mathrm{\sum }}_i^{-1}(\theta )(y_i-{\mu }_i(\theta ))$$ (4)

for i = 1, 2, · · ·, P. Then, the log-likelihood of the P samples, parametrized by θ, is given by:

$$L\left({\{y_i\}}_{i=1}^P;\theta \right)=-\frac{1}{2}\sum _{i=1}^P\left\{\kappa \left({\delta }_i^2(\theta )\right)+ln\mid {\mathrm{\sum }}_i(\theta )\mid \right\}.$$ (5)

An Expectation-Maximization algorithm for maximizing the log-likelihood results if one linearizes the function κ(x) at the current estimate of θ. This is due to the fact that

$${{\kappa }^{\prime }(x)|}_{{\delta }_i^2(\theta )}=\mathbb{E}\{U\mid y_i,\theta \}$$ (6)

and hence linearization of κ(x) at the current estimate of θ gives the Q-function by taking the scale variable U as the unobserved data [15], [11]. If θ^(ℓ) is the current estimate of θ, then the (ℓ + 1)^th iteration of an EM algorithm maximizes the following Q-function:

$$Q\left(\theta \mid {\theta }^{(\ell )}\right)=-\frac{1}{2}\sum _{i=1}^P\left\{{\kappa }^{\prime }\left({\delta }_i^2({\theta }^{(\ell )})\right){\delta }_i^2(\theta )+ln\mid {\mathrm{\sum }}_i(\theta )\mid \right\}.$$ (7)

Maximization of the above Q-function is usually more tractable than maximizing the original likelihood function.

The EM algorithm is an instance of the more general class of Majorization-Minimization (MM) algorithms [16]. The EM algorithm above can also be derived in the MM formalism, that is, without recourse to missing data or other statistical constructs such as marginal and complete data likelihoods. In [11], Lange et al. take the MM approach (without missing data) and point out that the key ingredient in the MM algorithm is the κ(·) function, which is related to the missing data formulation of the algorithm through Eq. (6).

III. Iterative Re-weighted Least Squares

In this section, we define a class of IRLS algorithms and show that they correspond to a specific class of EM algorithms under GSM assumptions.

A. Definition

Let x ∈ ℝ^M be such that |{x_i : x_i ≠ 0}| ≤ s, for some s < M. Then, x is said to be an s-sparse vector. Consider the following observation model

$$b=Ax+n$$ (8)

where b ∈ ℝ^N, with N < M is the observation vector, A ∈ ℝ^N×M is the measurement matrix, and n ∈ ℝ^N is the observation noise. The noisy compressive sampling problem is concerned with the estimation of x given b, A and a model for n. Suppose that the observation noise n is bounded such that ||n||₂ ≤ η, for some fixed η > 0. Let := {x : ||b − Ax||₂ ≤ η}. Let w ∈ ℝ^M such that w_i > 0 for all i = 1, 2, · · ·, M. Then, for all x, y ∈ ℝ^M, the inner-product defined by

$${\langle x,y\rangle }_w:=\sum _{i=1}^M{w}_i{x}_i{y}_i$$ (9)

induces a norm ${\Vert x\Vert }_w^2:={\langle x,x\rangle }_w$.

Definition 2

Let ν ∈ (0, 1] be a fixed constant. Given an initial guess x⁽⁰⁾ of x (e.g. the least-squares solution), the class of IRLS(ν, ε) algorithms for estimating x generates a sequence ${\{x^{(\ell )}\}}_{\ell =1}^{\infty }$ of iterates/refined estimates of x as follows:

$$x^{(\ell +1)}:=arg\underset{x\in \mathcal{C}}{min}{\Vert x\Vert }_{w^{(\ell )}}^2,$$ (10)

with

$$w_i^{(\ell )}:=\frac{1}{{\left({\epsilon }^2+{\left(x_i^{(\ell )}\right)}^2\right)}^{1-\nu /2}}$$ (11)

for i = 1, 2, · · ·, M and some fixed ε > 0.

Each iteration of the IRLS algorithm corresponds to a weighted least-squares problem constrained to the closed quadratic convex set , and can be efficiently solved using the standard convex optimization methods. The Lagrangian formulation of the IRLS has a simple closed form expression which makes it very appealing for implementation purposes [4]. Moreover, if the output SNR is greater than 1, that is, ||n||₂ ≤ η < ||b||₂, then 0 is not a feasible solution. Hence, the gradient of ${\Vert x\Vert }_w^2$ is non-vanishing over . Therefore, the solutions lie on the boundary of , given by ||b−Ax||₂ = η. Such a problem has been extensively studied in the optimization literature in its dual form, for which several robust and efficient solutions exist (See [17] and references therein). Finally, note that when η = 0, the above algorithm is similar to the one studied by Daubechies et al. [9]. Throughout the paper, we may drop the dependence of IRLS(ν, ε) on ν and ε, and simply denote it by IRLS, wherever there is no ambiguity.

B. IRLS as an EM algorithm

Consider an M-dimensional random vector y ∈ ℝ^M with independent elements distributed according to

$$p_{Y_i}(y_i)=\frac{1}{\sqrt{2\pi }}exp\left(-\frac{1}{2}\kappa \left({(y_i-x_i)}^2\right)\right)$$ (12)

for some function κ(x) with completely monotone derivative. Note that y is parametrized by θ := (x₁, x₂, · · ·, x_M)^T ∈ . The Q-function of the form (7) given the observation y = 0 ∈ ℝ^M is given by:

$$Q\left(x\mid x^{(\ell )}\right):=-\frac{1}{2}\sum _{i=1}^M{\kappa }^{\prime }\left({\left(x_i^{(\ell )}\right)}^2\right)x_i^2$$ (13)

Identifying ${\kappa }^{\prime }\left({\left(x_i^{(\ell )}\right)}^2\right)$ with $w_i^{(\ell )}$ in Eq. (10), we have

$${\kappa }^{\prime }(x)=\frac{1}{{\left({\epsilon }^2+x\right)}^{1-\nu /2}}$$ (14)

for x ≥ 0. It is not hard to show that κ′(x) is completely monotone [11] and hence, according to Proposition 1, κ(x) given by

$$\kappa (x)=\kappa (0)+{\int }_0^x\frac{1}{{\left({\epsilon }^2+t\right)}^{1-\nu /2}}dt=\kappa (0)+{\left({\epsilon }^2+x\right)}^{\nu /2}$$ (15)

defines an N/I univariate random variable with density given by Eq. (12). The log-likelihood corresponding to the zero observation is then given by

$$L(x):=-\frac{1}{2}\sum _{i=1}^M{\left({\epsilon }^2+x_i^2\right)}^{\nu /2}$$ (16)

Therefore, the IRLS algorithm can be viewed as an iterative solution, which is an EM algorithm [11], for the following program:

$$\underset{x\in \mathcal{C}}{min}{f}_{\nu }(x):=\sum _{i=1}^M{\left({\epsilon }^2+x_i^2\right)}^{\nu /2}.$$ (17)

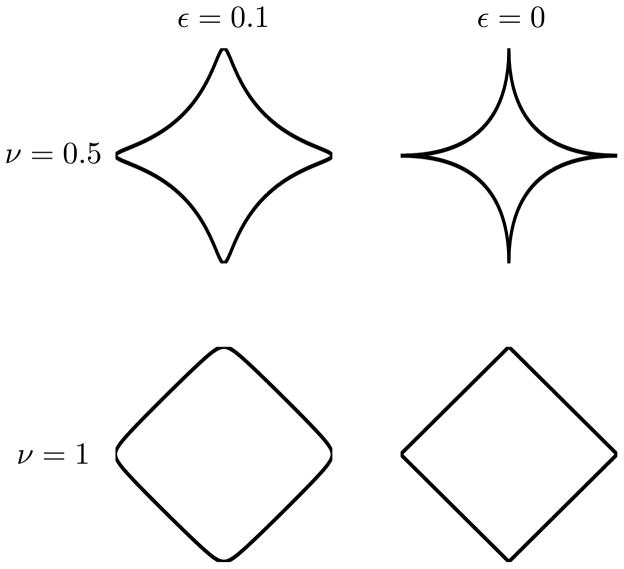
Note that the above program corresponds to minimizing a ε-smoothed version of the ℓ_ν ‘norm’ of x (Figure 1) subject to the constraint ||b − Ax||₂ ≤ η, that is

Fig. 1.

Level sets of ℓ_ν balls and their ε-smooth counterparts, which the IRLS(ν, ε) algorithm maximizes subject to fidelity constraints on the signal reconstruction.

$$\underset{x\in \mathcal{C}}{min}\sum _{i=1}^M{\mid x_i\mid }^{\nu }$$ (18)

The function f_ν (x) has also been considered in [9] in the analysis of the IRLS algorithm for noiseless CS. However, the above parallel to EM theory can be generalized to any other weighting scheme with a completely monotone derivative. For instance, consider the IRLS algorithm with the weighting:

$$w_i^{(\ell )}=\frac{1}{\epsilon +\left|x_i^{(\ell )}\right|}$$ (19)

for some ε > 0. Using the connection to EM theory [11], it can be shown that this IRLS is an iterative solution to

$$\underset{x\in \mathcal{C}}{min}\left\{{\Vert x\Vert }_1-\epsilon \sum _{i=1}^{M}ln\left(\epsilon +\mid x_i\mid \right)\right\}$$ (20)

which is a perturbed version of ℓ₁ minimization subject to ||b − Ax||₂ ≤ η.

IV. Convergence

The convergence of the IRLS iterates in the absence of noise have been studied in [9], where the proofs rely on the null space property of the constraint set. The connection to EM theory allows to derive convergence results in the presence of noise using the rich convergence theory of EM algorithms.

A. Convergence of IRLS as an EM Algorithm

It is not hard to show that the EM algorithm provides a sequence of iterates ${\{x^{(\ell )}\}}_{\ell =0}^{\infty }$ so that sequence of log-likelihoods ${\{L(x^{(\ell )})\}}_{\ell =1}^{\infty }$ converges. However, one needs to be more prudent when making statements about the convergence of the iterates ${\{x^{(\ell )}\}}_{\ell =0}^{\infty }$. Let denote a, non-empty, closed, strictly convex subset of ℝ^N. Let : ℝ^M ↦ ℝ^M be the map

$$\mathcal{M}(z):=\underset{x\in \mathcal{C}}{argmin}{\Vert x\Vert }_{w(z)}^2$$ (21)

for all z ∈ ℝ^M, where

$$w_i(z):=\frac{1}{{\left({\epsilon }^2+z_i^2\right)}^{1-\nu /2}},\text{for}i=1,2,\cdots ,M.$$ (22)

Results from convex analysis [18] imply the following sufficient and necessary optimality condition for x^* ∈ , the unique minimizer of ${\Vert x\Vert }_{w(z)}^2$ over :

$${\langle x^{\ast },x-x^{\ast }\rangle }_{w(z)}\ge 0,\text{for}\text{all}x\in \mathcal{C}.$$ (23)

Moreover, continuity of ${\Vert x\Vert }_{w(z)}^2$ in x and z implies that is a continuous map [19]. We prove this latter fact formally in Appendix A. The proof of convergence of the EM iterates to a stationary point of the likelihood function can be deduced from variations on the global convergence theorem of Zangwill [20] (See [19] and [21]). For completeness, we present a convergence theorem tailored for the problem at hand:

Theorem 3 (Convergence of the sequence of IRLS iterates)

Let x⁽⁰⁾ ∈ and ${\{x^{(\ell )}\}}_{i=0}^{\infty }\in \mathcal{C}$ be a sequence defined as x^(ℓ+1) = (x^(ℓ)) for all ℓ. Then, (i) x^(ℓ) is bounded and ||x^(ℓ) − x^(ℓ+1)||₂ → 0, (ii) every limit point of ${\{x^{(\ell )}\}}_{\ell =1}^{\infty }$ is a fixed point of , (iii) every limit point of ${\{x^{(\ell )}\}}_{\ell =0}^{\infty }$ is a stationary point of the function $f_{\nu }(x):={\sum }_{i=1}^M{\left({\epsilon }^2+x_i^2\right)}^{\nu /2}$ over , and (iv) f_ν(x^(ℓ)) converges monotonically to f_ν(x^*), for some stationary point x^*.

Proof

(i) is a simple extension of Lemmas 4.4 and 5.1 in [9], where one substitutes 〈x^(ℓ+1), x^(ℓ) − x^(ℓ+1)〉_w(x^(ℓ)) ≥ 0 for the optimality conditions at each iterate ℓ.

(ii) From (i), ${\{x^{(\ell )}\}}_{\ell =0}^{\infty }$ is a bounded sequence. The Bolzano-Weierstrass theorem establishes that ${\{x^{(\ell )}\}}_{\ell =0}^{\infty }$ has at least one convergent subsequence. Let x^(ℓ_k) → x̄ be one such convergent sub-sequence:

$$\underset{k\to \infty }{lim}{x}^{({\ell }_k+1)}=\underset{k\to \infty }{lim}{x}^{({\ell }_k)}=\overline{x},$$ (24)

Since x^(ℓ_k+1) = (x^(ℓ_k)), the continuity of the map implies that

$$\overline{x}=\underset{k\to \infty }{lim}{x}^{({\ell }_k+1)}=\mathcal{M}\left(\underset{k\to \infty }{lim}{x}^{({\ell }_k)}\right)=\mathcal{M}(\overline{x}).$$ (25)

Therefore, x̄ is a fixed point of the mapping .

(iii) To establish (iii), we will show that the limit point of any convergent subsequence {x^(ℓ_k)}_k of ${\{x^{(\ell )}\}}_{\ell =0}^{\infty }$ satisfies the necessary conditions of the stationary points of the minimization of $f_{\nu }(x):={\sum }_{i=1}^M{\left({\epsilon }^2+x_i^2\right)}^{\nu /2}$ over . Note that x̄ = (x̄) if and only if 〈x̄, x − x̄〉_w(x̄) ≥ 0 for all x ∈ . Moreover,

$$\begin{array}{ll}{\langle \overline{x},x-\overline{x}\rangle }_{w(\overline{x})}=\sum _{i=1}^M\frac{1}{{\left({\epsilon }^2+{\overline{x}}_i^2\right)}^{1-\nu /2}}{\overline{x}}_i(x_i-{\overline{x}}_i)\hfill & =\frac{2}{\nu }\sum _{i=2}^M\frac{\nu {\overline{x}}_i}{\underset{{(\nabla f_{\nu }(\overline{x}))}_i}{\underbrace{2{\left({\epsilon }^2+{\overline{x}}_i^2\right)}^{1-\nu /2}}}}(x_i-{\overline{x}}_i)\hfill \\ \hfill & =\frac{2}{\nu }\langle \nabla f_{\nu }(\overline{x}),x-\overline{x}\rangle .\hfill \end{array}$$ (26)

Note that 〈∇f_ν(x̄), x − x̄ 〉 ≥ 0 is the necessary condition for a stationary point x̄ of f_ν(x) over the strictly convex set [18]. Finally, (iv) follows from the continuity of ${\Vert x\Vert }_{w(z)}^2$ in x and z, and convexity of (See Theorem 2 of [21]). This concludes the proof of the theorem.

B. Discussion

Note that Theorem 3 implies that if the minimizer of f_ν(x) over is unique, then the IRLS iterates will converge to this unique minimizer. Moreover, by Theorem 5 of [21], the limit points of IRLS lie in a compact and connected subset of the set {x : f_ν (x) = f_ν(x^*)}. In particular, if the set of stationary points of f_ν(x) is finite, the IRLS sequence of iterates will converge to a unique stationary point. However, in general the IRLS is not guaranteed to converge (i.e. the set of limit points of the sequence of iterates is not necessarily a singleton).

There are various ways to choose ε adaptively or in a static fashion. Daubechies et al. [9] suggest a scheme where ε is possibly decreased in each step. This way f_ν(x) provides a better approximation to the ℓ_ν norm. Saab et al. [5] cascade a series of IRLS with fixed but decreasing ε, so that the output of each is used as the initialization of the next.

The result of Theorem 3 can be generalized to incorporate iteration-dependent changes of ε. Let ${\{{\epsilon }^{(\ell )}>0\}}_{\ell =1}^{\infty }$ be a sequence such that lim_ℓ→∞ε^(ℓ) = ε̄ ≥ 0. It is not hard to show that Theorem 3 holds for such a choice of {ε^(ℓ)}, by defining $f_{\nu }(x):={\sum }_{i=1}^M{({\overline{\epsilon }}^2+x_i^2)}^{\nu /2}$, if ε̄ > 0. Let x̄ be a limit point of the IRLS iterates. Then, if ε̄ = 0 and T_x̄ := supp(x̄) ⊆ {1, 2, · · ·, M}, then the results of parts (iii) and (iv) of Theorem 3 holds for minimization of $f_{\nu }(x):={\sum }_{i\in T_{\overline{x}}}{\mid x_i\mid }^{\nu }={\Vert x_{T_{\overline{x}}}\Vert }_{\nu }^{\nu }$ over $\mathcal{C}\cap \{x:x_{T_{\overline{x}}^c}=0\}$. This general result encompasses both the approach of Daubechies et al. [9] (in the absence of noise), and Saab et al. [5] as special cases. The technicality under such iteration-dependent choices of ε arises in showing that x̄ is the fixed point of the limit mapping (z), which can be established by invoking the uniform convergence of $arg{min}_{x\in \mathcal{C}}{\Vert x\Vert }_{w^{(\ell )}(z^{(\ell )})}^2$ to (x̄) for any given subsequence {z^(ℓ)} converging to x̄. A formal proof is given in Appendix B. For simplicity and clarity of presentation, the remaining results of this paper are presented with the assumption that ε > 0 is fixed.

V. Stability of IRLS for noisy CS

Recall that f_ν(x) is a smoothed version of ${\Vert x\Vert }_{\nu }^{\nu }$. Hence, for 0 < ν ≤ 1, the global minimizer of f_ν(x) over is expected to be close to the s-sparse x, given sufficient regularity conditions on the matrix A [8], [5]. Bounding the distance of this minimizer to the s-sparse x provides the desired stability bounds. For ν = 1, f₁(x) is strictly convex. Therefore the solution of the minimization of f₁(x) over the convex set is unique [18]. Hence, the IRLS iterates will converge to the unique minimizer in this case. However, for ν < 1, the IRLS iterates do not necessarily converge to a global minimizer of f_ν(x) over . In practice, the IRLS is applied with randomly chosen initial values, and the limit point with the highest log-likelihood is chosen [7].

Recall that the matrix A ∈ ℝ^N×M is said to have Restricted Isometry Property (RIP) [22] of order s < M with constant δ_s ∈ (0, 1), if for all x ∈ ℝ^M supported on any index set T ⊂ {1, 2, · · ·, M} satisfying |T| ≤ s, we have

$$(1-{\delta }_s){\Vert x\Vert }_2^2\le {\Vert Ax\Vert }_2^2\le (1+{\delta }_s){\Vert x\Vert }_2^2.$$ (27)

The following theorem establishes the stability of the minimization of f_ν(x) over in the noisy setting:

Theorem 4

Let b = Ax+n be given such that x ∈ ℝ^M is s-sparse. Let m be a fixed integer and suppose that A ∈ ℝ^N×M satisfies

$${\delta }_m+{\left(\frac{s}{m}\right)}^{1-2/\nu }{\delta }_{m+s}<{\left(\frac{s}{m}\right)}^{1-2/\nu }-1.$$ (28)

Suppose that ||n||₂ ≤ η and let := {x : ||b − Ax||₂ ≤ η}. Let ε > 0 be a fixed constant. Then, the solution to the following program

$$\overline{x}=arg\underset{x\in \mathcal{C}}{min}\sum _{i=1}^M{\left({\epsilon }^2+x_i^2\right)}^{\nu /2}$$ (29)

satisfies

$${\Vert \overline{x}-x\Vert }_2^{\nu }\le C_1{\eta }^{\nu }+C_2{s}^{\nu /2}{\epsilon }^{\nu }$$ (30)

where C₁ and C₂ are constants depending only on ν, s/m, δ_m and δ_m+s.

Proof

The proof is a modification of the proof of Theorem 4 in [5], which is based on the proof of the main result of [23]. Let T₀ := {i : x_i ≠ 0}. Let S ⊆ {1, 2, ···, M}. We define

$$f_{\nu }(x_S):=\sum _{i\in S}{\left({\epsilon }^2+x_i^2\right)}^{\nu /2}.$$ (31)

Let x̄ be a global minimizer of f_ν(x) over and let h := x̄ − x. It is not hard to verify the following fact:

$$f_{\nu }(h_{T^c})\le f_{\nu }(h_T).$$ (32)

The above inequality is the equivalent of the cone constraint in [23]. Moreover, it can be shown that

$$f_{\nu }(x_S)\le s^{1-\nu /2}\left({\Vert x_S\Vert }_2^{\nu }+s^{\nu /2}{\epsilon }^{\nu }\right)$$ (33)

for any x ∈ ℝ^M and S ⊆ {1, 2, ···, M} such that |S| ≤ s. By dividing the set $T_0^c$ into the sets T₁, T₂, ··· of size m, sorted according to decreasing magnitudes of the elements of $h_{T_0^c}$ , it can be shown that

$${\Vert h_{T_{01}^c}\Vert }_2^{\nu }\le \frac{f_{\nu }(h_{T_0})}{{(2/\nu -1)}^{\nu /2}{m}^{1-\nu /2}}\le \frac{1}{{(2/\nu -1)}^{\nu /2}}{\left(\frac{s}{m}\right)}^{1-\nu /2}\left({\Vert h_{T_{01}}\Vert }_2^{\nu }+s^{\nu /2}{\epsilon }^{\nu }\right),$$ (34)

where T₀₁ := T₀ ∪ T₁. Also, by the construction of and the hypothesis of the theorem about A, one can show that [5], [23]:

$${(2\eta )}^{\nu }\ge {\Vert Ah\Vert }_2^{\nu }\ge \left\{{(1-{\delta }_{m+s})}^{\nu /2}-{(1+{\delta }_m)}^{\nu /2}{\left(\frac{s}{m}\right)}^{1-\nu /2}\right\}{\Vert h_{T_{01}}\Vert }_2^{\nu }$$ (35)

Combining Eqs. (34) and (35) with the fact that ${\Vert h\Vert }_2^{\nu }\le {\Vert h_{T_{01}}\Vert }_2^{\nu }+{\Vert h_{T_{01}^c}\Vert }_2^{\nu }$, yields.

$${\Vert h\Vert }_2^{\nu }\le C_1{\eta }^{\nu }+C_2{s}^{\nu /2}{\epsilon }^{\nu }$$ (36)

where

$$C_1=2^{\nu }\frac{1+\frac{1}{{(2/\nu -1)}^{\nu /2}}{\left(\frac{s}{m}\right)}^{1-\nu /2}}{{(1-{\delta }_{m+s})}^{\nu /2}-{(1+{\delta }_m)}^{\nu /2}{\left(\frac{s}{m}\right)}^{1-\nu /2}}$$ (37)

and

$$C_2=\frac{1}{{(2/\nu -1)}^{\nu /2}}{\left(\frac{s}{m}\right)}^{1-\nu /2}.$$ (38)

Remark

Note that the result of Theorem 4 can be extended to compressible signals in a straightforward fashion [5]. Moreover, as it will be shown in the next section, the hypothesis of Eq. (28) can be relaxed to the sparse approximation property developed in [24], with a similar characterization of the global minimizer under study.

VI. Convergence Rate of IRLs for noisy CS

In presenting our results on the convergence rate of IRLS in presence of noise, it is more convenient to employ a slightly weaker notion of near isometry of the matrix A developed in [24]. This is due to the structure of the IRLS algorithm, which makes it more convenient to analyze the convergence rate in the ℓ₁ sense, and as it becomes clear shortly, the sparse approximation property is the more appropriate choice of regularity condition on the matrix A.

A. Sparse approximation property and its consequences

We say that a matrix A has the sparse approximation property of order s if

$${\Vert x_S\Vert }_2\le D{\Vert Ax\Vert }_2+\frac{\beta }{\sqrt{s}}{\Vert x_{S^c}\Vert }_1$$ (39)

for all x ∈ ℝ^M, where S is an index set such that |S| ≤ s, and D and β are positive constants. Note that RIP of order 2s implies sparse approximation property [24], but the converse is not necessarily true. The error bounds obtained in Theorem 4 can be expressed in terms of D and β in a straightforward fashion [24]. A useful consequence of the sparse approximation property is the reverse triangle inequality in presence of noise:

Proposition 5

Let A satisfy the sparse approximation property of order s with constants β < 1 and D. Let x₁, x₂ ∈ := {x : ||b − Ax||₂ ≤ η} and suppose that x₁ is s-sparse. Then, we have:

$${\Vert x_2-x_1\Vert }_1\le \frac{4D}{1-\beta }\sqrt{s}\eta +\frac{1+\beta }{1-\beta }({\Vert x_2\Vert }_1-{\Vert x_1\Vert }_1).$$

Proof

Let T be the support of x₁. Then, we have:

$$\begin{array}{l}{\Vert {(x_2-x_1)}_{T^c}\Vert }_1\le {\Vert x_{2T^c}\Vert }_1+{\Vert x_{1T^c}\Vert }_1\\ ={\Vert x_2\Vert }_1-{\Vert x_{2T}\Vert }_1\\ \le {\Vert x_2\Vert }_1-{\Vert x_1\Vert }_1+{\Vert {(x_2-x_1)}_T\Vert }_1\end{array}$$ (40)

The sparse approximation property implies that

$${\Vert {(x_2-x_1)}_T\Vert }_1\le \sqrt{s}D{\Vert A(x_2-x_1)\Vert }_2+\beta {\Vert {(x_2-x_1)}_{T^c}\Vert }_1$$ (41)

Moreover, ||A(x₂ − x₁)||₂ ≤ 2η, by the construction of . Hence, combining Eqs. (40) and (41) yield:

$${\Vert {(x_2-x_1)}_T\Vert }_1\le \frac{2D}{1-\beta }\sqrt{s}\eta +\frac{\beta }{1-\beta }({\Vert x_2\Vert }_1-{\Vert x_1\Vert }_1),$$ (42)

which together with Eq. (40) gives the statement of the proposition.

The above reverse triangle inequality allows to characterize the stability of the IRLS in the ℓ₁ sense. This is indeed the method used by Daubechies et. al [9] in the absence of noise. Let x̄ be the minimizer of f₁(x) over . Then, it is straightforward to show that

$${\Vert \overline{x}\Vert }_1\le f_1(\overline{x})\le f_1(x)\le {\Vert x\Vert }_1+M\epsilon$$ (43)

Combining the above inequality with the statement of Proposition 5 yields:

$${\Vert \overline{x}-x\Vert }_1\le \frac{4D}{1-\beta }\sqrt{s}\eta +\frac{1+\beta }{1-\beta }M\epsilon$$ (44)

Note that the above bound is optimal in terms of η up to a constant, since ${\Vert \eta \Vert }_1\le \sqrt{N}{\Vert n\Vert }_2=\sqrt{N}\eta$, and in fact ||n||₁ may achieve the value of $\sqrt{N}\eta$.

B. Convergence rate of the IRLS

Let ${\{x^{(\ell )}\}}_{\ell =0}^{\infty }$ be a sequence of IRLS iterates that converge to a stationary point x̄, for ν = 1. We have the following theorem regarding the convergence rate of IRLS:

Theorem 6

Suppose that the matrix A satisfies the sparse approximation property of order s with constants D and β. Suppose that for some ρ < 1 we have

$$\mu :=\frac{\beta (1+\beta )}{1-\rho }<1.$$ (45)

and let R₀ be the right hand side of Eq. (44), so that ||x̄ − x||₁ ≤ R₀. Assume that

$$\underset{i\in T}{min}\mid x_i\mid >R_0.$$ (46)

Let

$$e^{(\ell )}:=x^{(\ell )}-\overline{x}.$$ (47)

Then, there exists a finite ℓ₀ such that for all ℓ > ℓ₀ we have:

$${\Vert e^{(\ell +1)}\Vert }_1\le \mu {\Vert e^{(\ell )}\Vert }_1+R_1$$ (48)

for some R₁ comparable to R₀, which is explicitly given in this paper.

Proof

The proof of the theorem is mainly based on the proof of Theorem 6.4 of [9]. The convergence of the IRLS iterates implies that e^(ℓ) → 0. Let T be the support of the s-sparse vector x. Therefore, there exists ℓ₀ such that

$${\Vert e^{({\ell }_0)}\Vert }_1\le \rho \underset{i\in T}{min}\mid {\overline{x}}_i\mid .$$ (49)

Clearly the right hand side of the above inequality is positive, since

$$\underset{i\in T}{min}\mid {\overline{x}}_i\mid \ge \underset{i\in T}{min}\mid x_i\mid -R_0>0$$ (50)

by hypothesis. Following the proof method of [9], we want to show (by induction) that for all ℓ > ℓ₀, we have

$${\Vert e^{(\ell +1)}\Vert }_1\le \mu {\Vert e^{(\ell )}\Vert }_1+R_1$$ (51)

for some R₁ that we will specify later. Consider e^(ℓ+1) = x^(ℓ+1) − x̄. The first order necessary conditions on x^(ℓ+1) give:

$$\sum _{i=1}^M\frac{x_i^{(\ell +1)}}{\sqrt{x_i^{{(\ell )}^2}+{\epsilon }^2}}({\overline{x}}_i-x_i^{(\ell +1)})\ge 0.$$ (52)

Substituting x^(ℓ+1) by x̄ + e^(ℓ+1) yields

$$\sum _{i=1}^M\frac{{\mid e_i^{(\ell +1)}\mid }^2}{\sqrt{x_i^{{(\ell )}^2}+{\epsilon }^2}}\le -\sum _{i=1}^M\frac{e_i^{(\ell +1)}{\overline{x}}_i}{\sqrt{x_i^{{(\ell )}^2}+{\epsilon }^2}}$$ (53)

We intend to bound the term on the right hand side. First, note that

$$\left|\sum _{i\in T}\frac{e_i^{(\ell +1)}{\overline{x}}_i}{\sqrt{x_i^{{(\ell )}^2}+{\epsilon }^2}}\right|\le \frac{1}{1-\rho }{\Vert e_T^{(\ell +1)}\Vert }_1,$$ (54)

since

$$\left|\frac{{\overline{x}}_i}{\sqrt{x_i^{{(\ell )}^2}+{\epsilon }^2}}\right|\le \frac{\mid {\overline{x}}_i\mid }{\mid x_i^{(\ell )}\mid }\le \frac{\mid {\overline{x}}_i\mid }{\mid {\overline{x}}_i+e_i^{(\ell +1)}\mid }\le \frac{1}{1-\rho }$$

by hypothesis. Moreover, the sparse approximation property implies that

$$\begin{array}{ll}{\Vert e_T^{(\ell +1)}\Vert }_1\le \sqrt{s}D{\Vert {Ae}^{(\ell +1)}\Vert }_2+\beta {\Vert e_{T^c}^{(\ell +1)}\Vert }_1\hfill & \le \sqrt{s}D{\Vert A(x^{(\ell +1)}-\overline{x})\Vert }_2+\beta {\Vert e_{T^c}^{(\ell +1)}\Vert }_1\hfill \\ \hfill & \le 2D\eta \sqrt{s}+\beta {\Vert e_{T^c}^{(\ell +1)}\Vert }_1,\hfill \end{array}$$ (55)

thanks to the tube constraint ||b − Ax||₂ ≤ η. Hence, the left hand side of Eq. (54) can be bounded as:

$$\left|\sum _{i\in T}\frac{e_i^{(\ell +1)}{\overline{x}}_i}{\sqrt{x_i^{{(\ell )}^2}+{\epsilon }^2}}\right|\le \frac{1}{1-\rho }\left(2D\sqrt{s}\eta +\beta {\Vert e_{T^c}^{(\ell +1)}\Vert }_1\right).$$ (56)

Also, we have:

$$\left|\sum _{i\in T^c}\frac{e_i^{(\ell +1)}{\overline{x}}_i}{\sqrt{x_i^{{(\ell )}^2}+{\epsilon }^2}}\right|\le \underset{i\in T^c}{max}\left\{\frac{e_i^{(\ell +1)}}{\sqrt{x_i^{{(\ell )}^2}+{\epsilon }^2}}\right\}{\Vert {\overline{x}}_{T^c}\Vert }_1\le \frac{{\Vert e^{(\ell +1)}\Vert }_{\infty }}{\epsilon }{\Vert {\overline{x}}_{T^c}\Vert }_1:={\gamma }^{(\ell )}{\Vert {\overline{x}}_{T^c}\Vert }_1$$ (57)

Note that γ^(ℓ) → 0, since e^(ℓ) → 0. Therefore, we have

$$\left|\sum _{i=1}^M\frac{{\mid e_i^{(\ell +1)}\mid }^2}{\sqrt{x_i^{{(\ell )}^2}+{\epsilon }^2}}\right|\le \frac{1}{1-\rho }\left(2D\sqrt{s}\eta +\beta {\Vert e_{T^c}^{(\ell +1)}\Vert }_1\right)+{\gamma }^{(\ell )}{\Vert {\overline{x}}_{T^c}\Vert }_1$$ (58)

An application of the Cauchy-Schwarz inequality yields:

$$\begin{array}{l}{\Vert e_{T^c}^{(\ell +1)}\Vert }_1^2\le \left(\sum _{i\in T^c}\frac{{\mid e_i^{(\ell +1)}\mid }^2}{\sqrt{x_i^{{(\ell )}^2}+{\epsilon }^2}}\right)\left(\sum _{i\in T^c}\sqrt{x_i^{{(\ell )}^2}+{\epsilon }^2}\right)\\ \le \left(\sum _{i\in T^c}\frac{{\mid e_i^{(\ell +1)}\mid }^2}{\sqrt{x_i^{{(\ell )}^2}+{\epsilon }^2}}\right)\left(\sum _{i\in T^c}(\mid e_i^{(\ell )}\mid +\mid {\overline{x}}_i\mid +\epsilon )\right)\\ \le \left(\frac{1}{1-\rho }(2D\sqrt{s}\eta +\beta {\Vert e_{T^c}^{(\ell +1)}\Vert }_1)+{\gamma }^{(\ell )}{\Vert {\overline{x}}_{T^c}\Vert }_1\right)\left({\Vert e^{(\ell )}\Vert }_1+{\Vert {\overline{x}}_{T^c}\Vert }_1+M\epsilon \right).\end{array}$$ (59)

Hence,

$${\Vert e_{T^c}^{(\ell +1)}\Vert }_1\le \frac{\beta }{1-\rho }{\Vert e^{(\ell )}\Vert }_1+\left(\frac{\beta }{1-\rho }+{\gamma }^{(\ell )}\frac{1-\rho }{\beta }\right){\Vert {\overline{x}}_{T^c}\Vert }_1+\frac{\beta }{1-\rho }M\epsilon +\frac{2D}{\beta }\sqrt{s}\eta .$$ (60)

First, note that γ^(ℓ) is a bounded sequence for ℓ > ℓ₀. Let γ₀ be an upper bound on γ^(ℓ) for all ℓ > ℓ₀. We also have:

$${\Vert {\overline{x}}_{T^c}\Vert }_1={\Vert {(\overline{x}-x)}_{T^c}\Vert }_1\le {\Vert \overline{x}-x\Vert }_1\le R_0$$ (61)

Now, we have:

$$\begin{array}{ll}{\Vert e^{(\ell +1)}\Vert }_1\le {\Vert e_T^{(\ell +1)}\Vert }_1+{\Vert e_{T^c}^{(\ell +1)}\Vert }_1\hfill & \le (1+\beta ){\Vert e_{T^c}^{(\ell +1)}\Vert }_1+2D\sqrt{s}\eta \hfill \\ \hfill & \le \frac{\beta (1+\beta )}{1-\rho }{\Vert e^{(\ell )}\Vert }_1+R_1\hfill \end{array}$$ (62)

where

$$R_1:=(1+\beta )\left(\frac{\beta }{1-\rho }+{\gamma }_0\frac{1-\rho }{\beta }\right)R_0+\left(\frac{(4\beta +2)}{\beta }\right)D\sqrt{s}\eta +\left(\frac{\beta }{1-\rho }M\right)\epsilon$$ (63)

This concludes the proof of the theorem.

C. Discussion

Eq. (62) implies that $lim{sup}_{\ell \to \infty }{\Vert e^{(\ell )}\Vert }_1\le {\left(1-\frac{\beta (1+\beta )}{1-\rho }\right)}^{-1}{R}_1$. Therefore, the IRLS iterates approach a neighborhood of radius ${\left(1-\frac{\beta (1+\beta )}{1-\rho }\right)}^{-1}{R}_1$ (in the ℓ₁ sense) around the stationary point x̄ exponentially fast. Note that the radius of this neighborhood is comparable to the upper bound on the distance of x̄ to the s-sparse vector x (in the ℓ₁ sense) given by R₀. Hence, it is expected that with relatively few iterations of IRLS, one gets a reasonable estimate of x (Indeed, numerical studies in Section VII-C confirm this observation). Although the bound of the theorem holds for all ℓ > ℓ₀, it is most useful when (1 − μ)⁻¹ R₁ is less than ρ min_i∈T |x̄_i|. A sufficient condition to guarantee this is that ${min}_{i\in T}\mid x_i\mid \ge R_0+\frac{1}{\rho (1-\mu )}{R}_1$, which gives an upper bound on the noise level η and ε.

It is straightforward to extend the above theorem to the case of ν < 1. As shown in [9], the local convergence of ${\Vert e^{(\ell )}\Vert }_{\nu }^{\nu }$ in the case of ν < 1 and in the absence of noise is super-linear, with exponent 2 − ν. It is not hard to show that in the presence of noise, one can recover the super-linear local convergence with exponent 2 − ν. We refer the reader to Theorem 7.9 of [9], which can be extended to the noisy case with the respective modifications to the proof of Theorem 6.

VII. Numerical Experiments

In this section, we use numerical simulations to explore and validate the stability and convergence rate analyses of the previous sections. In particular, we compare ℓ₁-minimization to f_ν(·)-minimization, in both cases in the presence of noise, for different values of ν, ε, and signal-to-noise ratio (SNR).

A. Experimental set-up

For fixed ν, ε and η,

1. Select N and M so that A is an N × M matrix; sample A with independent Gaussian entries.

2. Select 1 ≤ S < M/2.

3. Select T₀ of size S uniformly at random and set x_j = 1 for all j ∈ T₀, and 0 otherwise.

4. Make b = Ax + n, where each entry of n is drawn uniformly in (−α, α), for some α that depends on η; find the solution x̄ to the program of Eq. (18) by IRLS.

5. Compare x̄ to x.

6. Repeat 50 times.

For each ν, ε and η, we compare the program solved in Step 4 to solving the program of Eq. (19) for ν = 1(ℓ₁-minimization). We solve each IRLS iteration, as well as the ℓ₁-minimization problem, using CVX, a package for specifying and solving convex programs [25], [26].

Remark

Modulo some constants, both η and ε appear in the same proportion in the stability bound derived in Theorem 3. Intuitively, this means that, the higher the SNR (small η), the smaller the value of ε one should pick to solve the program. In our experiment, we start with a fixed ε for the smallest SNR value (5 dB), and scale this value linearly for each subsequent value of the SNR. In particular, we use $\epsilon (\text{SNR})=\epsilon (5)\frac{\eta (\text{SNR})}{{\eta }^{(5)}}$, where we use the loose notation η(SNR) to reflect the fact that each choice of SNR corresponds to a choice of η, and vice versa. In summary, our experimental set-up remains the same, except for the fact that we choose values of ε which depend on η.

B. Analysis of Stability

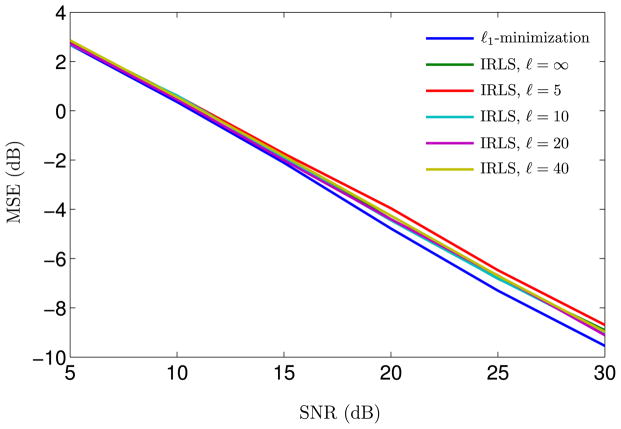
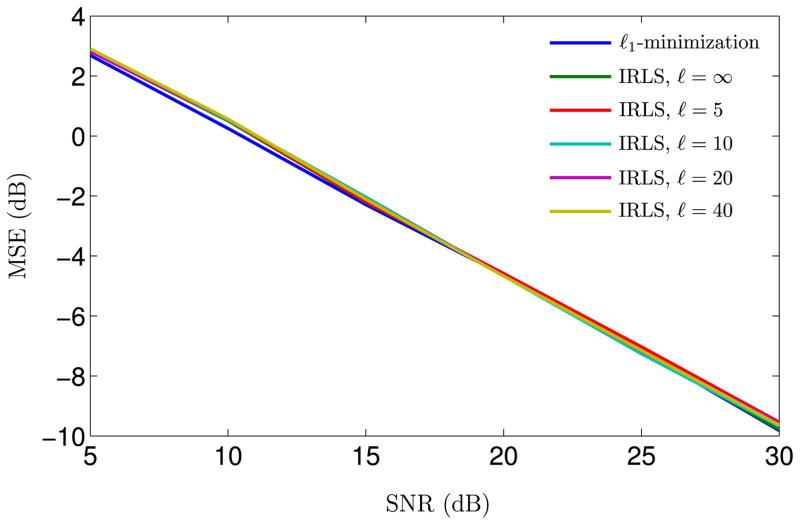
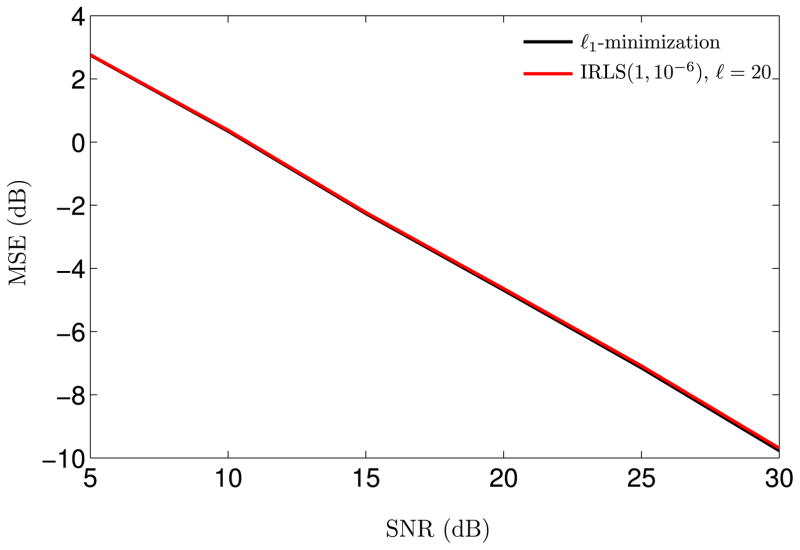
Figures 2 and 3 demonstrate the stability of IRLS for ε = 10⁻⁴, respectively for choices of ν = 1 and ν = 1/2. Figure 2 shows (as expected) that the stability of IRLS is comparable to that of ℓ₁-minimization for ν = 1 and small ε. Moreover, only a few number of IRLS iterations are required to reach a satisfactory value of the MSE. These observations also apply to Figure 3, which further highlights the sparsifying properties of f_ν(·)-minimization for ν < 1. Indeed, the MSE achieved for ν = 1/2 are smaller than those achieved for ν = 1. Figure 4 shows that the approximation to the ℓ₁-norm improves as one decreases the value of ε. In all three figures, we can clearly identify the log-linear dependence of the MSE as a function of η, which is predicted by the bound we derived in Theorem 4.

Fig. 2.

Mean square error (20 log₁₀ ||x̄ − x||₂) as a function of ℓ and SNR, for ν = 1 and ε(5) = 10⁻⁴. The figure shows that the stability of IRLS compares favorably to that of ℓ₁-minimization. More importantly, only a few number of IRLS iterations are required to reach a satisfactory value of the MSE.

Fig. 3.

Mean square error (20 log₁₀ ||x̄ − x||₂) as a function of ℓ and SNR, for ν = 1/2 and ε(5) = 10⁻⁴. This figure highlights the sparsifying properties of f_ν(·)-minimization by IRLS for ν < 1. As in the previous figure, only a few number of IRLS iterations are required to reach a satisfactory value of the MSE.

Fig. 4.

Mean square error (20 log₁₀ ||x̄ − x||₂) as a function of ℓ and SNR, for ν = 1 and ε(5) = 10⁻⁶. The figure shows that, as one decreases ε, the approximation to the ℓ₁-norm improves.

C. Convergence rate analysis

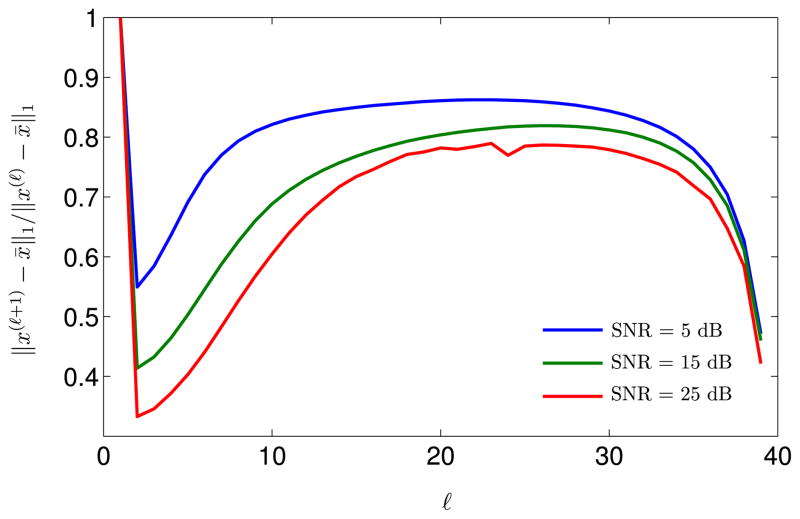
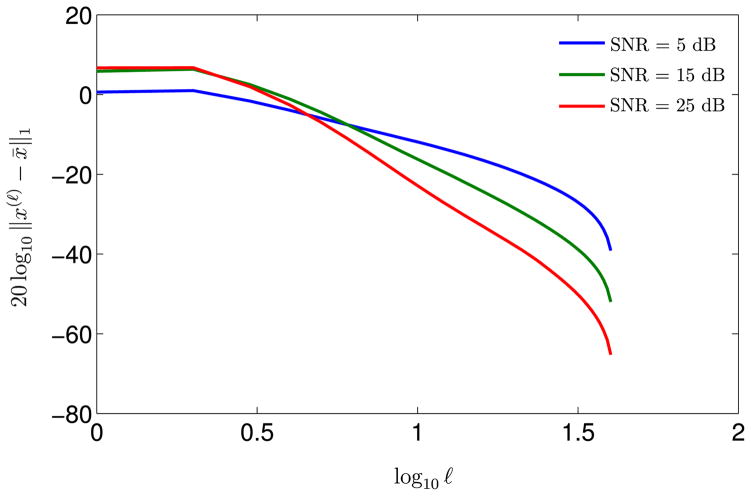
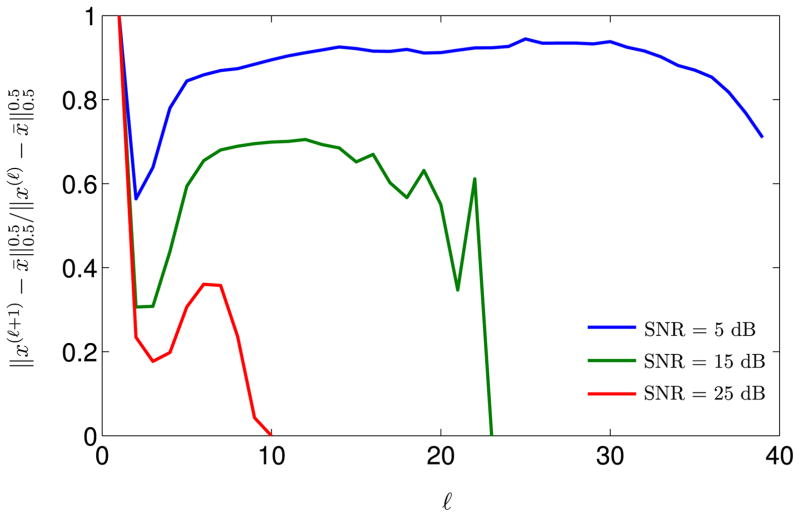
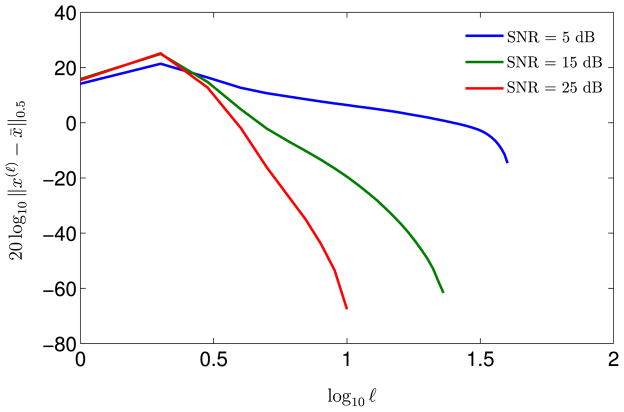
Figure 5 shows that the IRLS algorithm for f₁(·)-minimization converges exponentially fast to a neighborhood of the fixed-point of the algorithm. Moreover, the larger the SNR, the faster the convergence. These two observations are as predicted by the bound of Theorem 6. Figure 6 shows an alternate depiction of these observations in the log scale. Figure 7 shows that the IRLS algorithm for f_1/2(·)-minimization converges super-exponentially fast to a neighborhood of the fixed-point of the algorithm. As observed in Figure 5, the larger the SNR, the faster the convergence. Figure 8 shows an alternate depiction of these observations in the log scale.

Fig. 5.

Ratio ||x^(ℓ+1) − x̄||₁/||x^(ℓ) − x̄||₁ as a function of ℓ and SNR, for ν = 1 and ε(5) = 10⁻⁴. The figure shows that the IRLS converges with a relatively small number of iterations (ℓ).

Fig. 6.

20 log₁₀ ||x^(ℓ) − x̄||₁ as a function of log₁₀ ℓ and SNR, for ν = 1 and fixed ε(5) = 10⁻⁴. The figure shows that the IRLS converges with a relatively small number of iterations (ℓ).

Fig. 7.

Ratio ${\Vert x^{(\ell +1)}-\overline{x}\Vert }_{0.5}^{0.5}/{\Vert x^{(\ell )}-\overline{x}\Vert }_{0.5}^{0.5}$ as a function of ℓ and SNR, for ν = 0.5 and fixed ε(5) = 10⁻⁴. The figure shows that the IRLS converges with a relatively small number of iterations (ℓ).

Fig. 8.

20 log₁₀ ||x^(ℓ) − x̄||_0.5 as a function of log₁₀ ℓ and SNR, for ν = 0.5 and fixed ε = 10⁻⁴. The figure shows that the IRLS converges with a relatively small number of iterations (ℓ).

VIII. Discussion

In this paper, we provided a rigorous theoretical analysis of various iteratively re-weighted least-squares algorithms which have been proposed in the literature for recovery of sparse signals in the presence of noise [3], [4], [5], [6], [7], [8], [9]. We framed the recovery problem as one of constrained likelihood maximization using EM under Gaussian scale mixture assumptions. On the one hand, we were able to leverage the power of the EM theory to prove convergence of the said IRLS algorithms, and on the other hand, we were able to employ tools from CS theory to prove the stability of these IRLS algorithms and to derive explicit rates of convergence. We supplemented our theoretical analysis with numerical experiments which confirmed our predictions.

The EM interpretation of the IRLS algorithms, along with the derivation of the objective functions maximized by these IRLS algorithms, are novel. The proof of convergence is novel and uses ideas from Zangwill [20] which, in a sense, are more general than the proof presented by Daubechies [9] in the noiseless case. We have not presented the proof in the most general setting. However, we believe that the key ideas in the proof could be useful in various other settings involving iterative procedures to solve optimization problems. The proof of stability of the algorithms is novel; it relies on various properties of the function f_ν(·), along with techniques developed by Candés et al. [23]. The analysis of the rates of convergence is novel and makes interesting use of the sparse approximation property [24], along with some of the techniques introduced in [9].

Although we have opted for a fairly theoretical treatment, we would like to emphasize that the beauty of IRLS lies in its simplicity, not in its theoretical properties. Indeed, the simplicity of IRLS alone makes it appealing, especially for those who do not possess formal training in numerical optimization: no doubt, it is easier to implement least-squares, constrained or otherwise, than it is to implement a solver based on barrier or interior-point methods. Our hope is that a firm theoretical understanding of the IRLS algorithms considered here will increase their adoption as a standard framework for sparse approximation.

Appendix A. Continuity of (z)

The proof of Theorem 3 relies on the continuity of (·) as a map from ℝ^M into . We establish continuity by showing that for all z_n → z as n → ∞, (z_n) → (z). We will show that every convergent subsequence of (z_n) converges to (z). Since is non-empty, there exists x̄ ∈ such that

$${\Vert \mathcal{M}(z_n)\Vert }_{w(z_n)}^2\le {\Vert \overline{x}\Vert }_{w(z_n)}^2\le \frac{{\Vert \overline{x}\Vert }_2^2}{{\epsilon }^{\nu }}.$$ (64)

On the other hand, z_n is bounded because it is convergent. This implies that there exists B such that max_i |z_ni| ≤ B, so that ${\Vert \mathcal{M}(z_n)\Vert }_{w(z_n)}^2\ge \frac{1}{{({\epsilon }^2+B^2)}^{1-\nu /2}}{\Vert \mathcal{M}(z_n)\Vert }_2^2$. Therefore,

$${\Vert \mathcal{M}(z_n)\Vert }_2^2\le \frac{{({\epsilon }^2+B^2)}^{1-\nu /2}}{{\epsilon }^{\nu }}{\Vert \overline{x}\Vert }_2^2,$$ (65)

so that (z_n) is uniformly bounded. Therefore, there exists a convergent subsequence of (z_n). Now, let (z_nk) be any convergent subsequence, and let 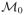be its limit. By definition of (z_nk) and results from convex optimization [18], for each n_k, (z_nk) is the unique element of satisfying

$$\langle \frac{\mathcal{M}(z_{n_k})}{{({\epsilon }^2+z_{n_k}^2)}^{(1-\nu /2)}},x-\mathcal{M}(z_n)\rangle \ge 0,\text{for}\text{all}x\in \mathcal{C}.$$ (66)

Taking limits and invoking continuity of the inner-product, we obtain

$$\langle \frac{{\mathcal{M}}_0}{{({\epsilon }^2+z^2)}^{(1-\nu /2)}},x-{\mathcal{M}}_0\rangle \ge 0,\text{for}\text{all}x\in \mathcal{C}.$$ (67)

Continuity of (·) follows from the fact that (z) is the unique element of which satisifies

$$\langle \frac{\mathcal{M}(z)}{{({\epsilon }^2+z^2)}^{(1-\nu /2)}},x-\mathcal{M}(z)\rangle \ge 0,\text{for}\text{all}x\in \mathcal{C}.$$ (68)

Therefore, 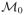= (z), which establishes the continuity of (·).

Appendix B. Iteration-dependent choices of ε

Let ${\{{\epsilon }^{(\ell )}>0\}}_{\ell =1}^{\infty }$ be a non-increasing sequence such that lim_ℓ→∞ ε^(ℓ) = ε̄ ≥ 0. In this case, the mapping must be substituted by the mapping 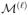ℝ^M ↦ ℝ^M:

$$M^{(\ell )}(z):=\underset{x\in C}{argmin}{\Vert x\Vert }_{w^{(\ell )}(z)}^2$$ (69)

for all z ∈ ℝ^M, where

$$w_i^{(\ell )}(z):=\frac{1}{{({\epsilon }^{{(\ell )}^2}+z_i^2)}^{1-\nu /2}},\text{for}i=1,2,\cdots ,M.$$ (70)

The main difference in the proof is in part (ii), where it is shown that x̄ is a fixed point of the mapping . We consider two cases: 1) ε̄ > 0 and, 2) ε̄ = 0.

Case 1

Suppose that ε̄ > 0 and that {x^(ℓ_k)}_k is a converging subsequence of the IRLS iterates with the limit x̄. Since the sequence {x^(ℓ)} is bounded, there exists an L, such that for all ℓ > L, all the iterates x^(ℓ) lie in a bounded and closed ball B₀ ⊂ ℝ^M. Moreover, let

$$\mathcal{M}(\overline{x}):=\underset{x\in \mathcal{C}}{argmin}\sum _{i=1}^M\frac{x_i^2}{{\left({\overline{\epsilon }}^2+{\overline{x}}_i^2\right)}^{1-\nu /2}}.$$ (71)

Clearly, (x̄) is bounded (since the true vector x ∈ is bounded). Let B ⊂ ℝ^M be a closed ball in ℝ^M such that B₀ ⊆ B and (x̄) ∈ B. Then, we have

$$\begin{array}{ll}\overline{x}=\underset{k\to \infty }{limsup}{x}^{({\ell }_k+1)}\hfill & =\underset{k\to \infty }{limsup}{\mathcal{M}}^{({\ell }_k)}\left(x^{({\ell }_k)}\right)\hfill \\ \hfill & =\underset{k\to \infty }{limsup}\underset{x\in \mathcal{C}}{argmin}{\Vert x\Vert }_{w^{({\ell }_k)}(x^{({\ell }_k)})}^2\hfill \\ \hfill & =\underset{k\to \infty }{limsup}\underset{x\in \mathcal{C}\cap B}{argmin}{\Vert x\Vert }_{w^{({\ell }_k)}(x^{({\ell }_k)})}^2\hfill \end{array}$$ (72)

Now, recall that

$${\Vert x\Vert }_{w^{({\ell }_k)}(x^{({\ell }_k)})}^2=\sum _{i=1}^M\frac{x_i^2}{{\left({\epsilon }^{{({\ell }_k)}^2}+x_i^{{({\ell }_k)}^2}\right)}^{1-\nu /2}}$$ (73)

It is easy to show that the function ${\Vert x\Vert }_{w^{({\ell }_k)}(x^{({\ell }_k)})}^2$ is uniformly convergent to

$${\Vert x\Vert }_{w^{({\ell }_k)}(x^{({\ell }_k)})}^2\to \sum _{i=1}^M\frac{x_i^2}{{\left({\overline{\epsilon }}^2+{\overline{x}}_i^2\right)}^{1-\nu /2}}$$ (74)

for all x ∈ B. To see this, note that

$$\left|\frac{x_i^2}{{\left({\epsilon }^{{({\ell }_k)}^2}+x_i^{{({\ell }_k)}^2}\right)}^{1-\nu /2}}-\frac{x_i^2}{{\left({\overline{\epsilon }}^2+{\overline{x}}_i^2\right)}^{1-\nu /2}}\right|\le x_i^2\left(L_{{\epsilon }^{({\ell }_k)}}\mid x_i^{({\ell }_k)}-{\overline{x}}_i\mid +L_{{\overline{x}}_i}\mid {\epsilon }^{({\ell }_k)}-\overline{\epsilon }\mid \right)$$ (75)

where L_t denotes the Lipschitz constant of the function (x² + t²)^ν/2−1. Since ε^(ℓ_k), ε̄ > 0, the Lipschitz constants are uniformly bounded. Moreover, since x ∈ B, then each $x_i^2$ is bounded, hence the uniform convergence of the function ${\Vert x\Vert }_{w^{({\ell }_k)}(x^{({\ell }_k)})}^2$ is implied. Given the uniform convergence, a result from variational analysis (Theorem 7.33 of [27]) establishes that

$$\underset{k\to \infty }{limsup}\underset{x\in \mathcal{C}\cap B}{argmin}{\Vert x\Vert }_{w^{({\ell }_k)}(x^{({\ell }_k)})}^2\subseteq \underset{x\in \mathcal{C}\cap B}{argmin}{\Vert x\Vert }_{w(\overline{x})}^2$$ (76)

where $w_i(\overline{x}):={({\overline{\epsilon }}^2+{\overline{x}}_i^2)}^{\nu /2-1}$. Note that the minimizer of ${\Vert x\Vert }_{w(\overline{x})}^2$ over the convex set ∩ B is unique. Therefore, the above inclusion is in fact equality. Hence,

$$\overline{x}=\underset{x\in \mathcal{C}\cap B}{argmin}{\Vert x\Vert }_{w(\overline{x})}^2=\underset{x\in \mathcal{C}}{argmin}{\Vert x\Vert }_{w(\overline{x})}^2=\mathcal{M}(\overline{x})$$ (77)

by the construction of B. The rest of the proof remains the same by substituting ε̄ for ε.

Case 2

Suppose that ε̄ = 0 and that supp(x̄) =: T ⊆ {1, 2, ···, M}. In this case, if T ≠ {1, 2, ···, M}, the limit lim_ℓ→∞ 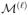(z) does not exist. Hence, the proof technique used for Case 1 does no longer hold. However, with a careful examination of the limiting behavior of the mapping 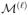(z), we will show that x̄ is a fixed point of the mapping:

$${\mathcal{M}}_T(z):=\underset{x\in \mathcal{C}\cap \{x:x_{T^c}=0\}}{argmin}\sum _{i\in T}\frac{x_i^2}{{\mid z_i\mid }^{2-\nu }}$$ (78)

for |z_i| > 0 for all i ∈ T. Due to the closedness of , x̄ ∈ . So, the set ∩ {x : x_T^c = 0} is non-empty. If this set is a singleton {x̄}, then x̄ is clearly the fixed point. If not, then there exists z ∈ ∩ {x : x_T^c = 0} such that z ≠ x̄. Then, the necessary conditions for each minimization at step ℓ_k gives:

$$\sum _{i=1}^M\frac{x_i^{({\ell }_k+1)}}{{\left({\epsilon }^{{({\ell }_k)}^2}+x_i^{{({\ell }_k)}^2}\right)}^{1-\nu /2}}(z_i-x_i^{({\ell }_k+1)})\ge 0.$$ (79)

First consider the terms over T. We have:

$$\underset{k\to \infty }{lim}\sum _{i\in T}\frac{x_i^{({\ell }_k+1)}}{{\left({\epsilon }^{{({\ell }_k)}^2}+x_i^{{({\ell }_k)}^2}\right)}^{1-\nu /2}}(z_i-x_i^{({\ell }_k+1)})=\sum _{i\in T}sgn({\overline{x}}_i){\mid {\overline{x}}_i\mid }^{\nu -1}(z_i-{\overline{x}}_i)$$ (80)

Next, consider the terms over T^c:

$$\underset{k\to \infty }{lim}\sum _{i\in T^c}\frac{-{\left(x_i^{({\ell }_k+1)}\right)}^2}{{\left({\epsilon }^{{({\ell }_k)}^2}+x_i^{{({\ell }_k)}^2}\right)}^{1-\nu /2}}=\underset{k\to \infty }{lim}\sum _{i\in T^c}-{\mid {\overline{x}}_i\mid }^{\nu }=0$$ (81)

Hence, we have:

$$\underset{k\to \infty }{lim}\sum _{i=1}^M\frac{x_i^{({\ell }_k+1)}}{{\left({\epsilon }^{{({\ell }_k)}^2}+x_i^{{({\ell }_k)}^2}\right)}^{1-\nu /2}}(z_i-x_i^{({\ell }_k+1)})=\sum _{i\in T}sgn({\overline{x}}_i){\mid {\overline{x}}_i\mid }^{\nu -1}(z_i-{\overline{x}}_i)\ge 0$$ (82)

which is the necessary and sufficient condition for x̄ being a fixed point of 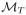(z) over all z ∈ ∩ {x : x_T^c = 0}. Similar to the proof the Theorem 3, it can be shown that x̄ satisfies the necessary optimality conditions for the function:

$$f_{\nu }^T(z):=\sum _{i\in T}{\mid z_i\mid }^{\nu }={\Vert z_T\Vert }_{\nu }^{\nu }$$ (83)

over the set ∩ {x : x_T^c = 0}. This concludes the proof. Note that the case of ε̄ = 0 is not favorable in general. Carefully chosen sequences {ε^(ℓ)} as in [9] together with the assumption that the s-sparse vector x ∈ is unique, can result in convergence of the IRLS to the true s-sparse x. However, for general sequences of {ε^(ℓ)} with lim_ℓ→∞ ε^(ℓ) = 0, this is not necessarily the case.