Abstract
The role of mechanics in degenerative joint disease of the temporomandibular joint (TMJ) is largely unknown. Objectives were to: 1) develop an empirical model to relate variables of cartilage mechanics and tractional forces; and 2) use the empirical model to estimate tractional forces for calculations of work done (mJ) and energy densities (mJ/mm3) in living human TMJs. Sixty-four porcine discs were statically, then dynamically loaded. Aspect ratios and velocities of stress-fields, compressive strains, and tractional forces were recorded and fit to a quadratic equation to derive the empirical model. Aspect ratios and velocities of stress-fields and cartilage thicknesses then were measured via dynamic stereometry in 15 humans with healthy TMJs and 11 with TMJ disc displacement. These data were used in the empirical model to estimate tractional forces for each TMJ, and then mechanical work done and energy densities were calculated. Mechanical work (mJ) was on average 20 times greater in TMJs with disc displacement than in healthy TMJs (P<0.02). TMJs with disc displacement showed 350% more mechanical work (mJ) and 180% higher energy densities in women compared to men (P<0.02). A power analysis (α=0.05, β=0.90) indicated that 40 women and 40 men would be required to detect a 50% difference in TMJ energy densities between genders. Mechanical work was significantly higher (P≤0.05) in TMJs with disc displacement compared to healthy TMJs, and mechanical work done and energy densities were significantly higher (P≤0.05) in TMJs with disc displacement in women compare to men.
Degenerative joint disease (DJD) of the temporomandibular joint (TMJ) is evident in 3-29% of the population age 19-40 years (Pullinger et al., 1988) and shows an age-dependent increase in the severity of tissue degeneration to about age 60 years (Luder, 2002). Persistent pain associated with the TMJ is estimated to affect 10% of the adult population at any one time (Stohler, 1995). Notably, women are 2-3 times more likely than men to be afflicted (Warren and Fried, 2001; Velly et al., 2003). DJD of the TMJ can lead to a major disruption in daily activities and can impair social and personal functioning (Storey, 1995; Dworkin, 1997).
To date, therapeutic interventions to address DJD and to improve the quality of life for those afflicted have not been predictably successful. Aggressive therapies such as surgical reconstruction of the TMJ have resulted in severe disabilities (Fontenot, 1995). Insufficient knowledge of the contact mechanics within the TMJ and the mechanisms involved in tissue breakdown are, at least in part, to blame.
The mean age of onset of DJD in the TMJ is between 25 and 35 years (Heloe and Heloe, 1975; Solberg et al., 1979; Nilner, 1981; Pullinger et al., 1988), which is a decade earlier than DJD in the hip (Lawrence et al., 1989; Felson et al., 1997; Vingard et al., 1997). Although considerable efforts are being made to uncover the molecular biology and genetics of chronic pain associated with disorders of the temporomandibular apparatus (Flores et al., 2003; Neugebauer et al., 2003; Zubieta et al., 2003; Diatchenko et al., 2005), the variables associated with mechanical failure of articulating tissues in young synovial joints have been investigated rarely (Gallo et al., 2000, 2006).
Energy density is the mechanical work imposed on a volume of TMJ disc cartilage (mJ/mm3) and is balanced by internal strain energy. Some studies have explored the effects of energy density on growth, adaptation and fatigue of living tissues (Carter et al., 1987; Krishnan et al., 2003; Fitzgerald, 2006). The biomechanical and biochemical integrity of tissues such as the TMJ disc is dependent on energy density transfer to the solid matrix of the cartilage. Biphasic modeling of the contact kinetics of the TMJ disc cartilage has demonstrated that stress-field translation and subsequent shear strain localization is greatest in the lateral portion of the disc (Donzelli, 2004). This also is where the greatest frequency of disc degeneration has been observed (Oberg, 1971).
Stress-field translation (Fig. 1) and resultant tractional forces may contribute to cartilage wear and fatigue (Dunbar et al., 2001; Nickel et al., 2004, 2006), in particular if the translation is mediolateral, because the disc is relatively weak in this aspect (Beatty et al., 2001, 2003). Given that the TMJ disc has the function of stress distribution and lubrication in the TMJ (Nickel et al., 1994a,b, 2001), the mechanical failure of the disc may be an important predisposing factor leading to the relatively early degenerative changes seen in the TMJ. Tractional forces are the result of frictional and plowing forces produced by the deformation of the cartilage matrix as a stress-field translates over the surface (Fig. 1; Linn, 1967; Mow et al., 1993; Ateshian et al., 1994; Gallo et al., 2000). For the TMJ disc, plowing forces are expected to be the dominant component of tractional forces. This is because laboratory studies have shown that static and especially dynamic frictional forces measured on the surface of the TMJ disc are low (Nickel et al., 1994b, 2001), and tractional forces associated with plowing on the surface of the TMJ disc are 10 times greater than static frictional forces (Nickel et al., 2004, 2006). Peak velocities of stress-field translation used in the laboratory experiments were like those demonstrated in vivo in humans (Gallo et al., 2000). Tractional forces increased with duration of static loading prior to the start of movement and with increasing velocity of stress-field translation. The tractional coefficients reported were consistent with the tractional forces measured in whole TMJ experiments (Kawai et al., 2004; Tanaka et al., 2004).
Figure 1.
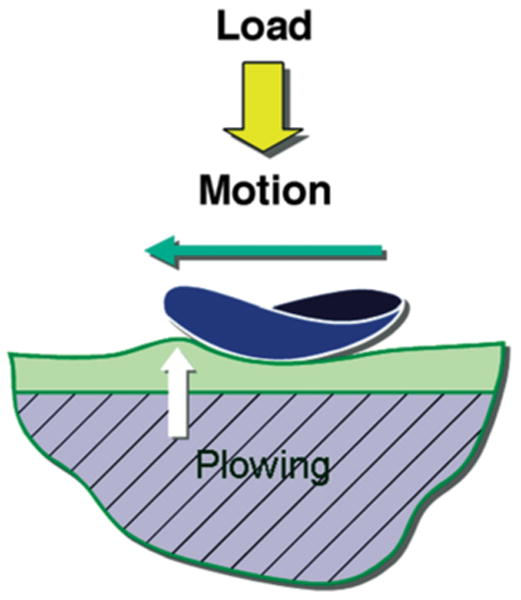
Plowing as a source of surface tractional forces in articulating tissues (modified from previously published work; Mow et al., 1993). Loading of the articular surfaces causes pressurization of the fluid phase of the cartilage matrix. As a static load is maintained, compression of the cartilage occurs as fluid moves laterally along the hydraulic gradient. If lateral movement of the stress-field occurs, further pressurization of the fluid phase of the matrix occurs ahead of the encroaching stress-field because the porosity of the matrix limits the velocity of the fluid phase. The result is a “bow wave” and plowing forces produced by the pressurized fluid within the cartilage.
Recently, it was reported that during movement of a load over the surface of the TMJ disc, compressive strains and tractional forces were correlated in a non-linear manner (Nickel et al., 2006). These results demonstrated that tractional forces were strain-related at the start of movement and velocity-dependent during movement and should be considered in analyses of mechanical work and energy densities imposed on the articulating surfaces during normal function.
For the current project, ex vivo tests of 64 porcine TMJ discs were used to develop an empirical model to relate the variables of stress-field geometry and dynamics and tractional forces on the surface of the disc. This empirical model then was used with data measured in humans by means of dynamic stereometry of the TMJs to determine: 1) if there were differences in the work done to discs in healthy TMJs and those with disc displacement; and 2) if there were gender differences in work done and energy densities in TMJs with disc displacement.
Materials and Methods
Ex vivo Tests for Development of the Empirical Model
Tests were conducted on 64 TMJ discs from 32 pigs which were obtained from a local abattoir in a manner consistent with institutional regulations. This empirical approach was necessary at present, due to the paucity of data from human TMJs in vivo and the difficulty in obtaining pristine, unpreserved human TMJ discs for testing.
Right and left discs were identified and stored separately in 0.1 M phosphate buffered physiological saline solution (PBS, pH = 7.3) for approximately 45 minutes while in transport. Tests were either performed on the same day or discs were frozen in PBS at -15°C, and then thawed within two weeks for use. During the tests the TMJ discs were maintained at 39°C in PBS.
Each disc was tested once using equipment and methods described previously (Fig. 2A and B; Nickel et al., 2004, 2006). A static 10 N load was applied to the condyle-facing surface for 1, 5, 10, 30, or 60 s, and then moved along the mediolateral axis of the disc. This normal (perpendicular) load was imposed using a hinged beam via an acrylic indenter shaped to produce a mediolateral radius of contact similar to that measured in humans (Gallo et al., 2000), and reflected the minimum condylar load expected during a light bite force. Stress-field translation following static loading was confirmed by fluctuating compressive stresses with respect to time measured by a linear array of nine pressure transducers, 3 mm apart, under the disc. Transducer sensitivities were ±10 kPa. Instantaneous disc thickness and compressive strain measurements were recorded continuously to within 0.05 mm using a calibrated linear voltage differential transformer (LVDT).
Figure 2.

Equipment (modified from previously published work; Nickel et al., 2004). A: Loading beam: a hinged beam facilitated placement of a static load at one end of the beam, which caused the acrylic indenter to load the TMJ disc at the other end of the beam. During experiments, the disc was supported by a curved acrylic base and tray. B: Indenter: the acrylic indenter had a major radius of 125 mm and a minor radius of 31 mm, polished loading surfaces, and milled holes to reduce the effect of mass on tractional forces measurements. The indenter was connected to a pendulum by an instrumented steel strut. Strain gauges attached to the surfaces of the strut (see B) measured bending of the strut during movement of the indenter over the surface of the cartilage. Tractional forces were measured in real time via calibration of output voltages from gauges for given loads. C: Electromagnetic force generator: a computer and custom-built software controlled the position and velocity of force generator displacement. D: Linear voltage differential transformer used to measure cartilage thickness during translation of the indenter over the surface of the disc. E: Linear voltage differential transformer used to measure real-time horizontal position of the indenter relative to the disc. F: Accelerometer: output of the accelerometer was used to identify the start of movement of the indenter across the mediolateral axis of the disc. G: Pressure sensitive array: an array of transducers lined the inside of the loading tray and measured pressure along the mediolateral axis of the disc. The most medial portion of the disc was positioned over pressure transducer #1 or #9.
Aspect ratio (a/h) was determined by dividing the radius of the stress-field (a) by the instantaneous thickness of the TMJ disc (h). The radius of the stress-field for each disc was established by identifying which pressure gauges recorded stress during the time period between the point when the acrylic indenter began to translate following static loading and the point at which maximum or minimum thickness was measured immediately following the start of movement. The gauges that registered at least 10% of the peak stress during this period were included and the 3 mm distance between each of the included pressure gauges were added together to calculate the radius.
Following the static loading period, electrical output from a calibrated accelerometer indicated the start of movement of the indenter. Position and velocity of the indenter were determined by calibrated electrical output from a second LVDT and controlled through a hinged pendulum connected to an electromagnetic force generator and a computer (Fig. 2B). Instantaneous velocity was the distance traveled by the indenter divided by time. The sampling frequency allowed instantaneous velocities to be calculated every 0.003 s using custom software. Total translation of the center of the stress-field during dynamic loading was approximately ± 4 mm and occurred at velocities between 5 and 120 mm/s, a range that was consistent with in vivo conditions where stress-field translation was recorded during symmetrical human jaw movement (Gallo et al., 2000).
Tractional forces were measured every 0.003 seconds from the start of movement. Calibration of the instrumented strut permitted measurement of tractional forces to an accuracy of ± 0.05 N. Data were recorded at 300 Hz and stored on magnetic tape using commercial computer hardware and software.
Data describing instantaneous geometry and velocity of the stress-field and tractional coefficient (f = tractional force/normal force) for each disc were fit to a quadratic regression, the empirical model, which was of the following form:
where a, b, c were constants and the variables of interest were tractional coefficient (f), velocity of movement (y), and the product of aspect-ratio and the cube of the compressive strain (x).
Work and Energy Densities in the Human TMJ Disc
Fifteen subjects with healthy TMJs and 11 subjects with TMJ disc displacement consented to participate in the study in accordance with the appropriate Institutional Review Board. Mean ages (± standard deviations [SD]) of subjects in the two groups were 29 (± 4) years and 25 (± 7) years, respectively. Status of the TMJ disc was determined by history, clinical examination, and magnetic resonance imaging (MRI). In addition to MRI, all subjects performed jaw opening and closing tasks for jaw tracking recordings. MRI and jaw tracking data were integrated through dynamic stereometry (see below) and used to measure variables applied to the empirical model and thus to estimate in vivo tractional forces for subjects' TMJs. These tractional forces then were used in calculations of mechanical work done and energy densities.
An initial analysis determined if there were group differences in mechanical work done (mJ) in the TMJ. In a secondary analysis, eight subjects (four women and four men) from the group with TMJ disc displacement provided data to test for gender differences in work done (mJ) and energy densities (mJ/mm3).
In vivo Dynamic Stereometry
Dynamic stereometry of the TMJ consisted of the 3D reconstruction of real anatomical structures, captured from MRI (Fig. 3A), and the animation of these structures by application of corresponding real motion data tracked with six degrees of freedom (Fig. 3B; Krebs et al., 1995). MR images of each subject were made from serial oblique sagittal slices perpendicular to the main condylar axis of each TMJ using a 1.5 T MRI tomographic apparatus (Gyroscan ASC-II) with TMJ surface coils of 12 cm radius. During the process of scanning, each subject bit into a custom occlusal registration appliance that carried a head reference system (three contrast spheres) to enable integration of MR images with recordings from jaw tracking.
Figure 3.
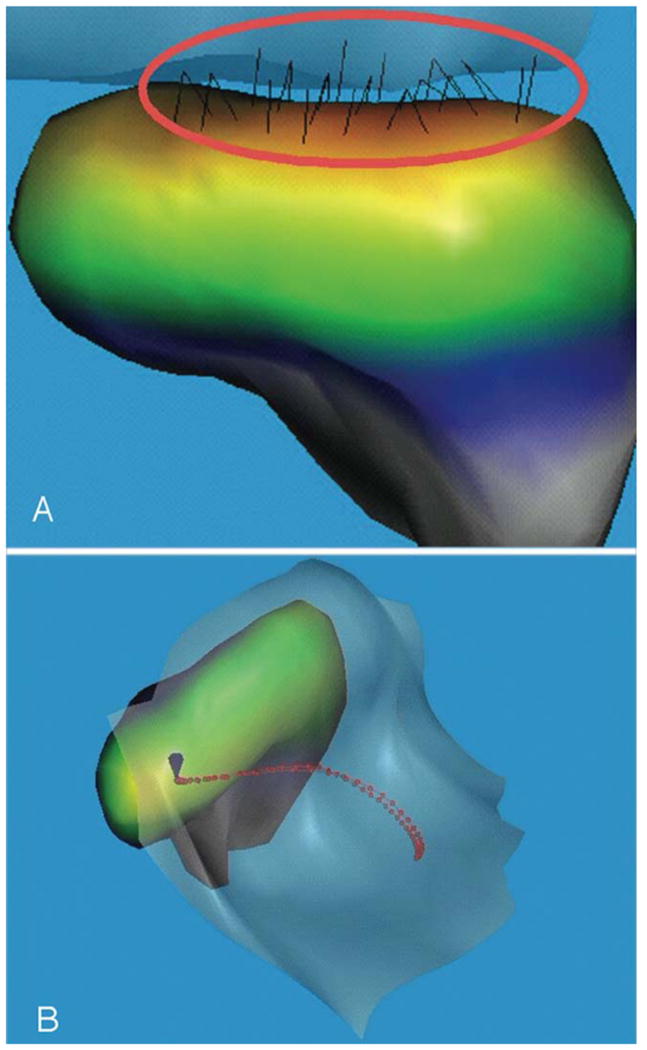
Healthy TMJ (disc not shown), right. A: Frontal view, where the condyle is at the end of the jaw-opening phase and the 3D reconstruction of the stress-field reveals the congruence of the surfaces of the condyle relative to the crest of the TMJ eminence. B: Superior view, with the center of the stress-field (minimum condyle-fossa/eminence distance) during jaw opening and closing identified by the red dots. The center of the stress-field depended on the congruence of condyle-fossa/eminence surfaces at a given jaw position. In this case, it tracked along the mediolateral axis of the condyle during the movements associated with jaw opening and closing, starting in the lateral aspect of the joint when the teeth were in maximum intercuspation.
Static recordings of the subject biting into the occlusal appliance carrying the head reference system and motion recordings of the jaws (jaw tracking) of each subject, performing 10 symmetrical opening and closing movements, were made by means of the opto-electronic system (Fig. 4; Mesqui et al., 1985; Krebs et al., 1995; Gossi et al., 2004). Two triangular target frames, carrying three non-collinear light emitting diodes (LEDs) each, defined maxillary and mandibular coordinate systems. The target frames were fixed temporarily to vestibular surfaces of maxillary and mandibular canines and first premolars on one side by means of custom splints. The LEDs determined head- and mandible-related coordinate systems. The time-varying maxillary and mandibular LED positions were recorded by three linear cameras (Fig. 4) with fixed geometry and resolution of better than 10 μm at a sampling frequency of 200 Hz. Motion of the lower jaw was calculated relative to the head, thus, head motion was eliminated.
Figure 4.

Opto-electronic tracking and capture of movement of the mandible in real-time. Three triangular target frames, carrying three non-collinear light emitting diodes (LEDs) each (A) are shown for the left side. The most posterior target frame is attached to the head reference system and occlusal registration appliance. The two anterior target frames defined maxillary and mandibular coordinate systems and were fixed temporarily to the vestibular surfaces of maxillary and mandibular canines and first premolars on one side by means of custom splints. The LEDs determined head- and mandible-related coordinate systems (B). The time-varying maxillary and mandibular LED positions were recorded by three linear cameras (C) with fixed geometry and resolution of better than 10 μm at a sampling frequency of 200 Hz. Motion of the lower jaw was calculated relative to the head, thus, head motion was eliminated. Motion was viewed in real time during the experiments (B).
Reconstruction and animation of the TMJ were performed on a graphics workstation by means of custom software (Krebs et al., 1995; Gossi et al., 2004). MR scans segmented for extraction and vectorial description of anatomical structures as well as for determination of the centers of the reference spheres. Segmentation of the anatomy was obtained first by tracing on each MR slice object contours defined by driving points of spline functions. To reconstruct the MR image in 3D (Fig. 3A), the contour sets were triangulated and the resulting surfaces were represented realistically by means of shading algorithms. Resolution was improved by calculating inter-slice surface points and applying a smoothing algorithm (Fig. 3A). Animation of the TMJ (Fig. 3B) was achieved by means of mathematical transformations, using the computer to calculate continuously the spatial positions of all vertices of polygons describing the recorded surfaces. Tests of the system showed maximum errors of 0.9%.
Magnitudes of the variables of interest (a/h, Δh/h, ΔD, V, Q) for each subject were determined from the reconstructed and animated MR images for each subject over 5 ms time intervals. The stress-field in the TMJ was located by finding the area of minimum condyle-fossa/eminence distance (Nickel and McLachlan, 1994; Gallo et al., 2000, 2006). For each sampling time of mandibular motion, the 30 smallest adjacent condyle-fossa/eminence distances, measured between polygon vertices, were identified. These distances were averaged to determine the minimum condyle-fossa/eminence distance or disc thickness, h. The centroid of the area defined by these 30 minimum distances was calculated and defined the mediolateral position of the stress-field, D. The standard deviation of the positions of the 30 minimum distances about the centroid also was calculated to determine the radius of the stress-field, a. The path of D was displayed graphically in a planar coordinate system representing the condylar surface (Fig. 3B). The mediolateral axis corresponded to the direction of the condylar long axis. The coordinates of the mediolateral position of D were smoothed over 30 ms, and velocity of the stress-field translation (V, mm/s) calculated. Volume of cartilage (Q, mm3) under the leading edge of the translating stress-field also was measured. The magnitudes of these variables were used in the empirical model and the results employed to determine instantaneous mechanical work and energy densities in the right and left TMJs of each subject during jaw movement.
Mechanical Work Done and Energy Density Equations
Data collected from individual subjects were input to the empirical model describing the relationship between tractional coefficient (f = tractional force/normal force) and stress-field geometry and dynamics. Tractional force (Ftraction) estimates were determined assuming a normal force of 10 N, and then employed in work and energy density calculations using two equations. Instantaneous mechanical work done (W, mJ) was calculated continuously over 5 ms intervals during cyclic movement of the mandible by the equation:
Instantaneous energy density calculations over 5 ms time intervals during cyclic movement of the mandible were accomplished using the equation:
Analysis of variance compared average cumulative work done per open-close cycle of the jaws for subjects with healthy TMJs and those with TMJ disc displacement. Average instantaneous work done and energy density per cycle were tested for significant gender differences within the disc displacement subjects.
Results
The ex vivo experiments produced surface tractional forces and mediolateral movements of the stress-field like those reported for the human TMJ (Gallo et al., 2000, 2006), as confirmed by variation in the outputs from pressure transducers under the TMJ disc (Fig. 5A). In addition, instantaneous measurements of tractional forces and cartilage thicknesses varied with position and velocity of the stress-field (Fig. 5B). Data collected from 64 porcine discs were fit to a quadratic equation (Fig. 6; R2 = 0.83), defined as the empirical model, which showed non-linear increases in tractional forces with increasing velocity of stress-field translation and aspect ratio X compressive strain3.
Figure 5.
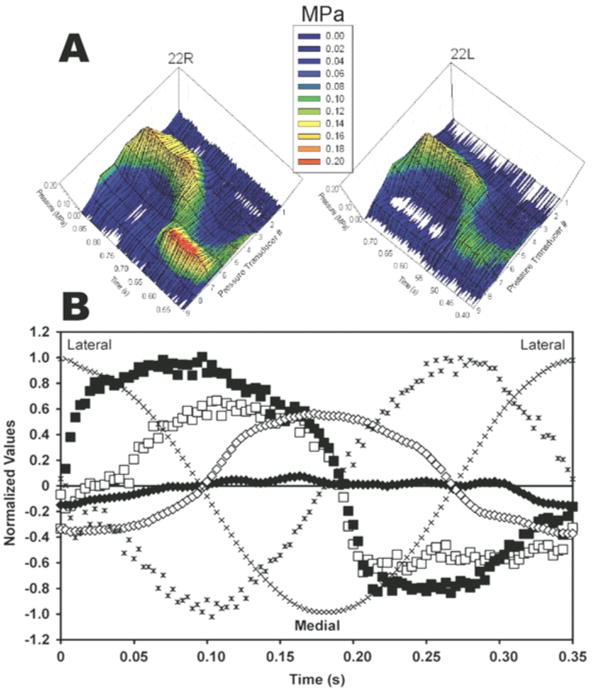
Data measured during ex vivo tests on the surfaces of porcine discs. A: Data shown are for time during Cycle 1 of indenter translation on disc pair 22 (R = right, L = left). Discs 22R and 22L were oriented with medial aspect over pressure transducer #1. Compressive stresses (MPa) are plotted on vertical axes and color-coded according to the key. B: Instantaneous tractional force and thickness data recorded for disc pair 22. Indenter position (x) and velocity (✱) were the same for all discs. Instantaneous tractional forces (Discs 22, R = ■, L = □) and disc thickness (Discs 22, R = ◆, L = ◇) were recorded during movement.
Figure 6.
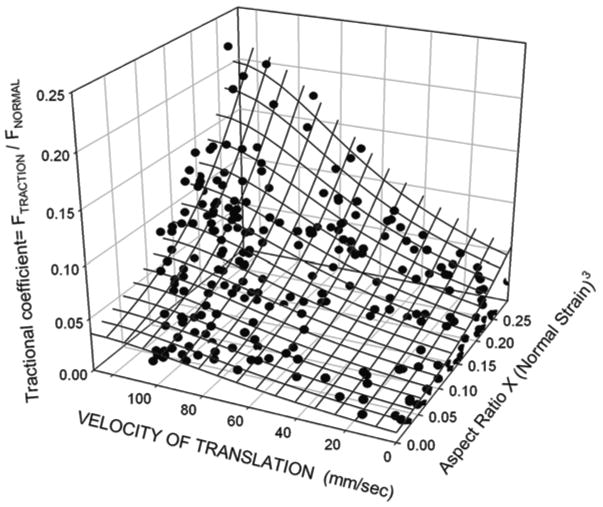
An empirical model of the relationship between velocity of stress-field translation, aspect ratio of the stress-field, compressive strain3 and tractional forces. Data collected from 64 porcine discs were fit to a quadratic equation (R2 = 0.83). The tractional forces were expressed as a coefficient, where the Fnormal = 10 N. The non-linear increases seen in tractional coefficient reflect the effects of stress-field velocity, geometry and compressive strain on the pressurization of the fluid within the TMJ disc.
Data recorded from subjects with healthy TMJs (n = 15) and with TMJ disc displacement (n = 11) during jaw opening-closing were used in the empirical model (Fig. 6) to estimate in vivo tractional forces based on stress-field geometry and dynamics. The tractional forces were used in the calculation of average cumulative work done per cycle for each TMJ. Average cumulative work done (± SD) per cycle was significantly higher (P = 0.014-0.015) in TMJs with disc displacement (4445 ± 1008 mJ at 1.0 Hz) compared to healthy TMJs (191 ± 165 mJ at 0.5 Hz; 251 ± 210 mJ at 1.0 Hz) by 18-23 times (Fig. 7).
Figure 7.
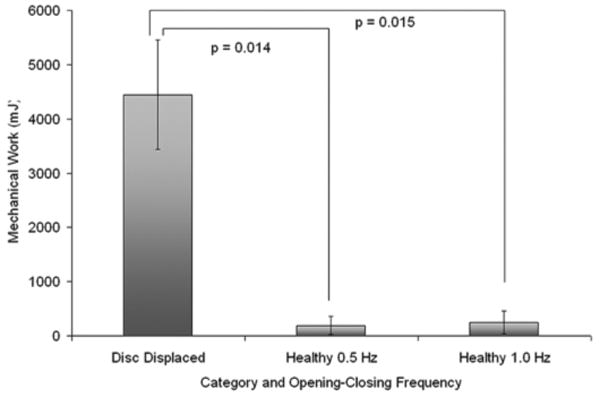
Average cumulative work done per cycle in healthy TMJs and TMJs with disc displacement. Data were calculated over 10 symmetrical opening-closing movements of the mandible at 0.5 and 1.0 Hz in healthy subjects, and 1.0 Hz frequency in subjects with disc displacement.
In a secondary analysis of gender differences in TMJs with disc displacement, the average instantaneous work values per jaw opening-closing cycle were over 350% higher (P < 0.01; Fig. 8) in women (71 ± 85 mJ) compared to men (20 ± 14 mJ), whereas, average instantaneous energy density per cycle was about 180% higher (P < 0.02; Fig. 8) in women (2.4 ± 1.9 mJ/mm3) compared to men (1.3 ± 1.5 mJ/mm3). The regional distribution of instantaneous energy density varied for TMJs with disc displacement (Fig. 9). TMJs with disc displacement in women, however, had higher average energy densities, with peak energy densities located primarily in the lateral aspect of the joint (e.g. Fig. 9). In contrast, TMJs with disc displacement in men had lower average energy densities and energy densities were distributed more evenly (e.g. Fig. 9).
Figure 8.
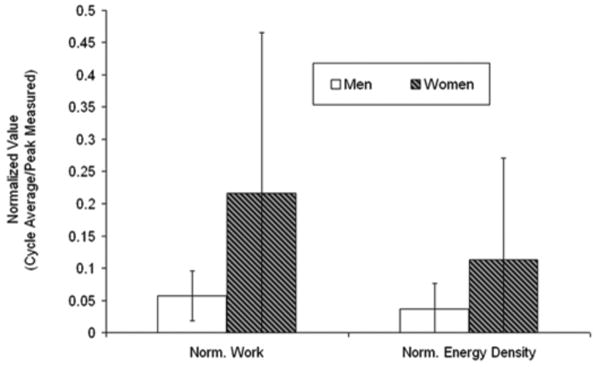
Gender differences in work done and energy densities in TMJs with disc displacement. Average instantaneous values per cycle were normalized to the peak value for all subjects for work done and for energy density to illustrate these results in the same figure.
Figure 9.
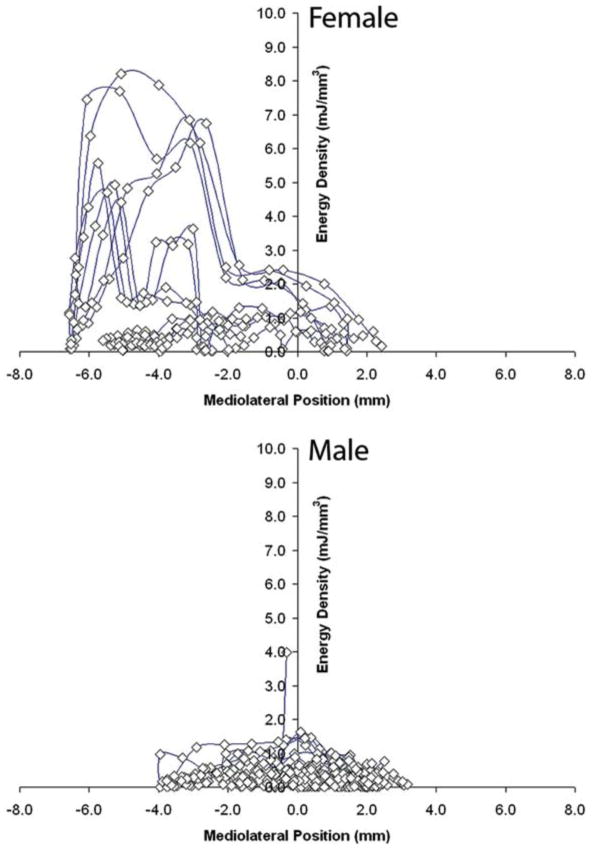
Magnitudes and distributions of instantaneous energy densities in TMJs of one female (top) and one male (bottom) subject with disc displacement. Mediolateral position (mm) along the mandibular condylar axis is plotted horizontally, where + values are medial and – values are lateral. Instantaneous energy density is plotted vertically (mJ/mm3).
Discussion and Conclusions
It was possible that the large gender differences seen in the secondary analysis were due to the small number of women and men providing data. A power analysis was performed to determine the numbers of subjects expected to discriminate clinically significant gender differences in work and energy densities. In order to detect a more modest difference of 50% (α = 0.05, β = 0.90), 40 men and 40 women would be required.
It remains to be determined whether the effects of loading on tractional forces and compressive stresses in laboratory tests are like those produced in vivo. The applied static loads of 10 N were lower than loads in the human TMJ during mastication and bruxism but not unlike the loads typical of symmetrical opening and closing (Nickel et al., 1997; Iwasaki et al., 2004). In addition, stress-relaxation behavior of cartilage is affected by the radius of the contact area relative to the thickness of the cartilage (Suh and Spilker, 1994). The standardized indenter used in the current study did not reproduce exactly the area of loading that occurs in vivo and possibly had a smaller radius of contact area. Overall, these data represent a “best-case scenario,” where it is evident that tractional forces occur during light loading on the surface of the TMJ disc.
Plowing forces acting on cartilage cause dynamic compressive and shear strains within the collagen-proteoglycan matrix, leading to hydraulic pressures and fluid movement through this porous matrix (Donzelli et al., 2004). The current results appear to be consistent with those previously reported (Nickel et al., 2004; Tanaka et al., 2004). In a study of whole TMJs, 5 seconds of static loading with 50 and 80 N produced tractional coefficients of 0.0145 and 0.0191, respectively (Tanaka et al., 2004). These measurements were reported as “friction,” but were an order of magnitude greater than previously reported values for coefficient of static friction (Nickel et al., 1994b, 2001), and comparable to the values for tractional coefficients at the start of movement in the ex vivo tests of the current study. It has been noted that whole joint measurements of friction cannot eliminate the plowing forces produced by stress-field translation (Linn, 1967; Mow et al., 1993). Therefore, rather than classical frictional forces, plowing forces were likely the most significant element of tractional forces produced during the aforementioned whole-TMJ experiments (Kawai et al., 2004; Tanaka et al., 2004).
The consequent strain energy imposed on the matrix is likely to be influenced by magnitude and frequency of the forces applied to the surface of the cartilage, properties of the TMJ disc such as the anisotropic nature of its yield strength (Beatty et al., 2001) and propensities for crack propagation and fatigue failure (Beatty et al., 2003, 2008). Specific mechanisms, by which static and dynamic strains in the matrix affect the fibrochondrocytes of the TMJ disc to promote either repair or failure of the matrix, remain unknown. However, the importance of cyclic matrix strain in chondrocyte mechanotransduction has been emphasized by experiments involving dynamic shear strain of hyaline cartilage (Fitzgerald et al., 2006). These experiments have demonstrated that, in the absence of fluid flow or hydrostatic pressure gradients which are normally associated with dynamic compression, there was an increase in synthesis of cartilage matrix components such as glycosaminoglycans and collagen, but also in production of the enzymes which break down the matrix, such as metalloproteinases (Fitzgerald et al., 2006).
The balance between anabolic and catabolic activities of cartilage cells may be influenced by factors that affect the internal strain conditions. For example, the hormone relaxin is of interest because of gender differences in its expression and its potential to affect strain energy concentrations in cartilage. This 6-kDa polypeptide hormone is related structurally to the insulin family of hormones and has been shown to have a particular affinity for the fibrous connective tissues of the symphysis pubis and TMJ. The effects of matrix remodeling on tissue mechanics were proposed in early work when it was unknown what molecules initiated the changes seen in the symphysis pubis during pregnancy (Aspden, 1988).
Recent work (Hashem et al., 2006) suggests that concentrations of relaxin in the blood stream are correlated with matrix remodeling of the symphysis pubis and the TMJ disc. It is yet to be determined, but relaxin may induce matrix reorganization of the TMJ disc to an extent that there is a reduction in yield strength of the matrix and increased susceptibility to fatigue. That is, the effect of relaxin could be the chemical equivalent of blunt trauma, where impulse magnitude is correlated positively with area of surface microfractures (Nickel et al., 2001). Surface cracking increases the local strain energies necessary for fatigue-related crack propagation of the matrix (Beatty et al., 2008). Thus, a previous history of exposure to relaxin or physical trauma, or both, could lead to a mechanically compromised TMJ disc. Whether or not the disc fails may depend ultimately on individual-specific differences in the magnitude and frequency of energy densities imposed on the disc during function.
In conclusion, amounts of work done (mJ) were significantly higher in TMJs with disc displacement compared to healthy TMJs. A pilot analysis of TMJs with disc displacement found that women imposed greater work on their TMJ discs and the energies input were concentrated compared to men. The current study suggests that future investigations should confirm the gender differences and whether or not energy density-related strain results in changes in cell metabolism within the TMJ disc in a dose-dependent manner.
Acknowledgments
The authors thank the subjects for their participation and Farmland Foods Corporation, Crete, Nebraska for their support. The contributions of Kim Theesen, Bobby Simetich, Aaron Jacobsen, Krista Evans, Adam Shaver, Laura Rothe, Tien Nguyen, Matthew Moss and Paul Robinson to the work are gratefully acknowledged. Funds for technical assistance and equipment were provided in part by the University of Nebraska Medical Center (previous institution of J. Nickel and L. Iwasaki) through the College of Dentistry Research Committee, the Office of the Dean, and the Departments of Adult Restorative Dentistry and Growth and Development.
References
- Aspden RM. The theory of fibre-reinforced composite materials applied to changes in the mechanical properties of the cervix during pregnancy. J Theor Biol. 1988;130:213–221. doi: 10.1016/s0022-5193(88)80096-1. [DOI] [PubMed] [Google Scholar]
- Ateshian GA, Lai WM, Zhu WB, Mow VC. An asymptotic solution for the contact of two biphasic cartilage layers. J Biomech. 1994;27:1347–1360. doi: 10.1016/0021-9290(94)90044-2. [DOI] [PubMed] [Google Scholar]
- Beatty MW, Bruno MJ, Iwasaki LR, Nickel JC. Strain rate dependent orthotropic properties of pristine and impulsively loaded porcine temporomandibular joint disk. J Biomed Mater Res. 2001;57:25–34. doi: 10.1002/1097-4636(200110)57:1<25::aid-jbm1137>3.0.co;2-h. [DOI] [PubMed] [Google Scholar]
- Beatty MW, Hohl RH, Nickel JC, Iwasaki LR, Pidaparti RMV. Mode I and mode III fracture in intermediate zone of full-thickness porcine temporomandibular joint discs. Ann Biomed Eng. 2008;36:801–812. doi: 10.1007/s10439-008-9436-9. [DOI] [PubMed] [Google Scholar]
- Beatty MW, Nickel JC, Iwasaki LR, Leiker M. Mechanical response of the porcine temporomandibular joint disc to an impact event and repeated tensile loading. J Orofac Pain. 2003;17:160–166. [PubMed] [Google Scholar]
- Carter DR, Fyhrie DP, Whalen RT. Trabecular bone density and loading history: Regulation of connective tissue biology by mechanical energy. J Biomech. 1987;20:785–794. doi: 10.1016/0021-9290(87)90058-3. [DOI] [PubMed] [Google Scholar]
- Diatchenko L, Slade GD, Nackley AG, Bhalang K, Sigurdsson A, Belfer I, Goldman D, Xu K, Shabalina SA, Shagin D, Max MB, Makarov SS, Maixner W. Genetic basis for individual variations in pain perception and the development of a chronic pain condition. Hum Mol Genet. 2005;14:135–143. doi: 10.1093/hmg/ddi013. [DOI] [PubMed] [Google Scholar]
- Donzelli PS, Gallo LM, Spilker RL, Palla S. Biphasic finite element simulation of the TMJ disc from in vivo kinematic and geometric measurements. J Biomech. 2004;37:1787–1791. doi: 10.1016/j.jbiomech.2004.01.029. [DOI] [PubMed] [Google Scholar]
- Dunbar WL, Jr, Un K, Donzelli PS, Spilker RL. An evaluation of three-dimensional diarthrodial joint contact using penetration data and the finite element method. J Biomech Eng. 2001;123:333–340. doi: 10.1115/1.1384876. [DOI] [PubMed] [Google Scholar]
- Dworkin SF. Behavioral and educational modalities. Oral Surg Oral Med Oral Pathol Oral Radiol Endod. 1997;83:128–133. doi: 10.1016/s1079-2104(97)90103-7. [DOI] [PubMed] [Google Scholar]
- Felson DT, Zhang Y, Hannan MT, Naimark A, Weissman B, Aliabadi P, Levy D. Risk factors for incident radiographic knee osteoarthritis in the elderly: The Framingham Study. Arthritis Rheum. 1997;40:728–733. doi: 10.1002/art.1780400420. [DOI] [PubMed] [Google Scholar]
- Fitzgerald JB, Jin M, Grodzinsky AJ. Shear and compression differentially regulate clusters of functionally related temporal transcription patterns in cartilage tissue. J Biol Chem. 2006;281:24095–24103. doi: 10.1074/jbc.M510858200. [DOI] [PubMed] [Google Scholar]
- Flores CA, Shughrue P, Petersen SL, Mokha SS. Sex-related differences in the distribution of opioid receptor-like 1 receptor mRNA and colocalization with estrogen receptor mRNA in neurons of the spinal trigeminal nucleus caudalis in the rat. Neuroscience. 2003;118:769–778. doi: 10.1016/s0306-4522(02)01000-x. [DOI] [PubMed] [Google Scholar]
- Fontenot MG. Temporomandibular joint devices: Past, present, and future. In: Sessle BJ, Bryant PS, Dionne RA, editors. Temporomandibular Disorders and Related Pain Conditions, Progress in Pain and Research and Management. Seattle: IASP Press; 1995. pp. 309–322. [Google Scholar]
- Gallo LM, Chiaravalloti G, Iwasaki LR, Nickel JC, Palla S. Mechanical work during stress-field translation in the human TMJ. J Dent Res. 2006;85:1006–1010. doi: 10.1177/154405910608501106. [DOI] [PubMed] [Google Scholar]
- Gallo LM, Nickel JC, Iwasaki LR, Palla S. Stress-field translation in the healthy human temporomandibular joint. J Dent Res. 2000;79:1740–1746. doi: 10.1177/00220345000790100201. [DOI] [PubMed] [Google Scholar]
- Gossi DB, Gallo LM, Bahr E, Palla S. Dynamic intra-articular space variation in clicking TMJs. J Dent Res. 2004;83:480–484. doi: 10.1177/154405910408300609. [DOI] [PubMed] [Google Scholar]
- Hashem G, Zhang Q, Hayami T, Chen J, Wang W, Kapila S. Relaxin and beta-estradiol modulate targeted matrix degradation in specific synovial joint fibrocartilages: Progesterone prevents matrix loss. Arthritis Res Ther. 2006;8:R98. doi: 10.1186/ar1978. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Heloe B, Heloe LA. Characteristics of a group of patients with temporomandibular joint disorders. Community Dent Oral Epidemiol. 1975;3:72–79. doi: 10.1111/j.1600-0528.1975.tb00284.x. [DOI] [PubMed] [Google Scholar]
- Iwasaki LR, Thornton BR, McCall WD, Jr, Nickel JC. Individual variations in numerically modeled human muscle and temporomandibular joint forces during static biting. J Orofac Pain. 2004;18:235–245. [PubMed] [Google Scholar]
- Kawai N, Tanaka E, Takata T, Miyauchi M, Tanaka M, Todoh M, van Eijden T, Tanne K. Influence of additive hyaluronic acid on the lubricating ability in the temporomandibular joint. J Biomed Mater Res A. 2004;70:149–153. doi: 10.1002/jbm.a.30078. [DOI] [PubMed] [Google Scholar]
- Krebs M, Gallo LM, Airoldi RL, Palla S. A new method for three-dimensional reconstruction and animation of the temporomandibular joint. Ann Acad Med Singapore. 1995;24:11–16. [PubMed] [Google Scholar]
- Krishnan R, Park S, Eckstein F, Ateshian GA. Inhomogeneous cartilage properties enhance superficial interstitial fluid support and frictional properties, but do not provide a homogeneous state of stress. J Biomech Eng. 2003;125:569–577. doi: 10.1115/1.1610018. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lawrence RC, Hochberg MC, Kelsey JL, McDuffie FC, Medsger TA, Jr, Felts WR, Shulman LE. Estimates of the prevalence of selected arthritic and musculoskeletal diseases in the United States. J Rheumatol. 1989;16:427–441. [PubMed] [Google Scholar]
- Linn FC. Lubrication of animal joints. I: The arthrotripsometer. J Bone Joint Surg Am. 1967;49:1079–1098. [PubMed] [Google Scholar]
- Luder HU. Factors affecting degeneration in human temporomandibular joints as assessed histologically. Eur J Oral Sci. 2002;110:106–113. doi: 10.1034/j.1600-0722.2002.11212.x. [DOI] [PubMed] [Google Scholar]
- Mesqui F, Kaeser F, Fisher P. Real-time, non-invasive recording and three-dimensional display of the functional movements of an arbitrary mandible point. Proc SPIE. 1985;602:77–84. [Google Scholar]
- Mow VC, Ateshian GA, Spilker RL. Biomechanics of diarthrodial joints: A review of twenty years of progress. J Biomech Eng. 1993;115:460–467. doi: 10.1115/1.2895525. [DOI] [PubMed] [Google Scholar]
- Neugebauer V, Li W, Bird GC, Bhave G, Gereau RW. Synaptic plasticity in the amygdala in a model of arthritic pain: Differential roles of metabotropic glutamate receptors 1 and 5. J Neuroscience. 2003;23:52–63. doi: 10.1523/JNEUROSCI.23-01-00052.2003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nickel JC, Iwasaki LR, Beatty MW, Marx DB. Laboratory stresses and tractional forces on the TMJ disc surface. J Dent Res. 2004;83:650–654. doi: 10.1177/154405910408300813. [DOI] [PubMed] [Google Scholar]
- Nickel JC, Iwasaki LR, Beatty MW, Moss MA, Marx DB. Static and dynamic loading effects on temporomandibular joint disc tractional forces. J Dent Res. 2006;85:809–813. doi: 10.1177/154405910608500906. [DOI] [PubMed] [Google Scholar]
- Nickel JC, Iwasaki LR, Feely DE, Stormberg KD, Beatty MW. The effect of disc thickness and trauma on disc surface friction in the porcine temporomandibular joint. Arch Oral Biol. 2001;46:155–162. doi: 10.1016/s0003-9969(00)00101-1. [DOI] [PubMed] [Google Scholar]
- Nickel JC, Iwasaki LR, McLachlan KR. Effect of the physical environment on growth of the temporomandibular joint. In: McNeill C, editor. Science and Practice of Occlusion. Chicago: Quintessence; 1997. pp. 115–124. [Google Scholar]
- Nickel JC, McLachlan KR. An analysis of surface congruity in the growing human temporomandibular joint. Arch Oral Biol. 1994;39:315–321. doi: 10.1016/0003-9969(94)90123-6. [DOI] [PubMed] [Google Scholar]
- Nickel JC, McLachlan KR. In vitro measurement of the stress-distribution properties of the pig temporomandibular joint disc. Arch Oral Biol. 1994a;39:439–448. doi: 10.1016/0003-9969(94)90175-9. [DOI] [PubMed] [Google Scholar]
- Nickel JC, McLachlan KR. In vitro measurement of the frictional properties of the temporomandibular joint disc. Arch Oral Biol. 1994b;39:323–331. doi: 10.1016/0003-9969(94)90124-4. [DOI] [PubMed] [Google Scholar]
- Nilner M. Prevalence of functional disturbances and diseases of the stomatognathic system in 15-18 year olds. Swed Dent J. 1981;5:189–197. [PubMed] [Google Scholar]
- Oberg T, Carlsson GE, Fajers CM. The temporomandibular joint: A morphologic study on a human autopsy material. Acta Odontol Scand. 1971;29:349–384. doi: 10.3109/00016357109026526. [DOI] [PubMed] [Google Scholar]
- Pullinger AG, Seligman DA, Solberg WK. Temporomandibular disorders. Part I: Functional status, dentomorphologic features, and sex differences in a nonpatient population. J Prosthet Dent. 1988;59:228–235. doi: 10.1016/0022-3913(88)90019-4. [DOI] [PubMed] [Google Scholar]
- Solberg WK, Woo MW, Houston JB. Prevalence of mandibular dysfunction in young adults. J Am Dent Assoc. 1979;98:25–34. doi: 10.14219/jada.archive.1979.0008. [DOI] [PubMed] [Google Scholar]
- Stohler CS. Clinical perspectives on masticatory and related muscle disorders. In: Sessle BJ, Bryant PS, Dionne RA, editors. Temporomandibular Disorders and Related Pain Conditions, Progress in Pain and Research and Management. Seattle: IASP Press; 1995. pp. 3–30. [Google Scholar]
- Storey AT. Biomechanical and anatomical aspects of the temporomandibular joint. In: Sessle BJ, Bryant PS, Dionne RA, editors. Temporomandibular Disorders and Related Pain Conditions, Progress in Pain and Research and Management. Seattle: IASP Press; 1995. pp. 257–272. [Google Scholar]
- Suh JK, Spilker RL. Indentation analysis of biphasic articular cartilage: Nonlinear phenomena under finite deformation. J Biomech Eng. 1994;116:1–9. doi: 10.1115/1.2895700. [DOI] [PubMed] [Google Scholar]
- Tanaka E, Kawai N, Tanaka M, Todoh M, van Eijden T, Hanaoka K, Dalla-Bona DA, Takata T, Tanne K. The frictional coefficient of the temporomandibular joint and its dependency on the magnitude and duration of joint loading. J Dent Res. 2004;83:404–407. doi: 10.1177/154405910408300510. [DOI] [PubMed] [Google Scholar]
- Velly AM, Gornitsky M, Philippe P. Contributing factors to chronic myofascial pain: A case-control study. Pain. 2003;104:491–499. doi: 10.1016/S0304-3959(03)00074-5. [DOI] [PubMed] [Google Scholar]
- Vingard E, Alfredsson L, Malchau H. Osteoarthrosis of the hip in women and its relation to physical load at work and in the home. Ann Rheum Dis. 1997;56:293–298. doi: 10.1136/ard.56.5.293. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Warren MP, Fried JL. Temporomandibular disorders and hormones in women. Cells Tissues Organs. 2001;169:187–192. doi: 10.1159/000047881. [DOI] [PubMed] [Google Scholar]
- Zubieta JK, Heitzeg MM, Smith YR, Bueller JA, Xu K, Xu Y, Koeppe RA, Stohler CS, Goldman D. COMT val158met genotype affects mu-opioid neurotransmitter responses to a pain stressor. Science. 2003;299:1240–1243. doi: 10.1126/science.1078546. [DOI] [PubMed] [Google Scholar]


