Abstract
The drug purchase task is a frequently used instrument for measuring the relative reinforcing efficacy (RRE) of a substance, a central concept in psychopharmacological research. While a purchase task instrument, such as the cigarette purchase task (CPT), provides a comprehensive and inexpensive way to assess various aspects of a drug’s RRE, the application of conventional statistical methods to data generated from such an instrument may not be adequate by simply ignoring or replacing the extra zeros or missing values in the data with arbitrary small consumption values, e.g. 0.001. We applied the left-censored mixed effects model to CPT data from a smoking cessation study of college students and demonstrated its superiority over the existing methods with simulation studies. Theoretical implications of the findings, limitations of the proposed method and future directions of research are also discussed.
Keywords: cigarette purchase task, college smoking, demand curve, left-censored mixed effects model, relative reinforcing efficacy
Relative reinforcing efficacy (RRE) is a central and frequently used concept in psychopharmacological research (Katz, 1990). Originally defined as “the behavior-maintenance potency of a dose of a drug which can be manifested under a range of different experimental conditions” (Griffiths, Brady, & Bradford, 1979), RRE has conventionally been used to compare the abuse liabilities of different drugs or different doses of the same drug. Typically, RRE is assessed by using laboratory-based self-administration methods and direct observation of these drug administration behaviors under different conditions (Bickel, Marsch, & Carroll, 2000). However, the clinical utility of laboratory-based RRE measurement is limited by the high administrative cost for multiple laboratory sessions and limited sample sizes (Jacobs & Bickel, 1999). In addition, the RRE of illegal substances or among treatment-seeking individuals may not be ethically feasible (Jacobs & Bickel, 1999).
In light of these challenges, researchers have adopted more efficient and economical ways to access RRE by using non-laboratory approaches. Among these different approaches, a drug purchase task self-report measure is the most widely adopted. The drug purchase task is a questionnaire modeled after laboratory drug self-administration procedures. The questionnaire prompts respondents to make hypothetical choices between drug and monetary amounts analogous to the choices participants would make in a laboratory setting (Jacobs & Bickel, 1999; Petry & Bickel, 1998). The amount one would spend to purchase a drug can thus be used to produce a demand curve for the substance. This approach has been employed to study the reinforcing strength of various substances – such as cigarettes (Jacobs & Bickel, 1999; MacKillop et al., 2008; Murphy et al., 2011), heroin (Jacobs & Bickel, 1999), alcohol (Murphy & MacKillop 2006; MacKillop et al., 2009), and snack foods (Epstein et al., 2007; Epstein et al., 2010a) – among diverse populations including out-patients in drug use treatment settings (Jacobs & Bickel, 1999), college students (Mackillop et al., 2008), pregnant women (Epstein et al., 2007), young adult drinkers (Murphy, MacKillop, Skidmore, & Pederson, 2009), and adults with alcohol use disorders (MacKillop, Miranda, Monti, Ray, Murphy, Rohsenow, McGeary, & Swift, 2010).
While a demand curve based on a purchase task instrument provides a more comprehensive and less costly way to assess a drug’s reinforcing strength, the limitations inherent in the statistical analysis of data generated from such an instrument have not been sufficiently evaluated. Conventionally, researchers have adopted either an individual-specific (linear or non-linear) regression model (e.g., MacKillop et al., 2008) or a mixed effects model (e.g., Epstein et al., 2007; Epstein et al., 2010b) to analyze purchase task data. Both models disregard the particular structure of the purchase task data which is characterized by a large number of zeros or missing observations on the right tail of the price chart. As detailed in the following sections, these zeros or missing data could be values too small to be observed, and the strategies for dealing with them are crucial to the validity of the statistical analysis.
The focus of this paper is to estimate the population-averaged or mean parameters of the purchase task demand curve. We argue that, given the particular structure of the purchase task data, neither of the two models commonly used will produce accurate mean parameter estimates. In this paper, we propose a left-censored mixed effects model that takes into account any “missing” or zero values in the data while taking advantage of the efficiency of the mixed effects model. We apply the proposed method to the analysis of cigarette purchase task (CPT) data collected at baseline from college students enrolled a smoking cessation study. Using Monte-Carlo simulation studies, we demonstrate the advantages of the left-censored mixed effects model over the two conventional models. Potential limitations of the proposed method and future directions for research are also discussed.
Method
Study Population
The data used to test the proposed left-censored mixed effects model were collected from participants in an NIH funded (R01HL094183) placebo controlled, randomized trial entitled “Enhanced Quit and Win Contests to Improve Smoking Cessation among College Students” (henceforth abbreviated as “Enhanced Quit & Win”). As opposed to standard Quit & Win contests in which smokers typically quit for one month in return for the opportunity to win prizes, the Enhanced Quit & Win study is evaluating the separate and combined efficacy of increased dose (extension of contest participation from 1 to 3 months) and enhanced content (addition of cessation counseling/coaching) on promoting abstinence among college smokers.
We used baseline data from the first and second waves of the study, which consisted of 659 college students enrolled from 13 college and university campuses between fall 2010 and fall 2011. Study inclusion criteria were as follows: 1) age 18 years or older; 2) enrolled as a full or part-time student at one of the participating campuses; 3) intending to be in school for the entire academic year (i.e., next 2 semesters); 4) smoked cigarettes on 10 or more days during the prior one month period; 5) no use of smokeless tobacco in the prior 30 days; 6) able to read English; 7) access to a working telephone; 8) access to a computer with internet access; 9) screened negative for pathological gambling; and 10) willing to provide a baseline urine sample to verify smoking status.
Procedures
Prior to participant enrollment, all aspects of the study were approved by the human subjects committees of the participating colleges and universities. Study enrollment occurred in person during the third week of August of each recruitment year on the participating campuses. Students provided written informed consent and were assessed for eligibility (see criteria above). Student ID numbers were used to prevent duplicate enrollment. Eligible students were invited to complete an online baseline survey and provide a baseline urine sample for cotinine analysis (to confirm smoking status). Those who completed the baseline survey and provided a urine sample with a positive result (i.e., a score 3 or greater based on a NicAlert™ urine cotinine test strip test, corresponding to a urine cotinine value of approximately 20ng/ml) were enrolled into the study, randomized into one of four study arms, and followed for 6 months. We used only the baseline data for the analyses reported in here.
Cigarette Purchase Task (CPT)
The CPT self-report questionnaire used in the baseline online survey of the Enhanced Quit & Win study was based on a validated survey adopted in several previous studies to assess the RRE of cigarette smoking (e.g., Jacobs & Bickel, 1999; MacKillop et al., 2008; Murphy et al., 2011). The CPT instructions were as follows:
Imagine a TYPICAL DAY during which you smoke. The following questions ask how many cigarettes you would consume if they cost various amounts of money. Assume the following:
Available cigarettes are your favorite brand
You have the same income/savings that you have now
You have NO ACCESS to any cigarettes or nicotine products other than those offered at these prices
You consume the cigarettes you request on that day (in other words, no stockpiling)
Participants were then asked to respond to the following set of questions: How many cigarettes would you smoke if they were_____ each? (each question stem remained the same, but the values increased with each subsequent question: 0¢ (free), 1¢, 5¢, 13¢, 25¢, 50¢, $1, $2, $3, $4, $5, $6, $11, $35, $70, $140, $280, $560, $1,120. Subsequent questions continued to appear in the online survey until the respondents gave a “0” answer. After this point, no further questions were asked. It should be noted that the optimal prices for CPTs and other purchase tasks is an active area of debate and a reliability study of Murphy et al.’s (2009) has suggested that the highest prices had the lowest reliability even with a short retest period. In this paper, we restricted our data analysis to prices ≤ $11, which were relatively close to the actual market costs of cigarettes.
The Demand Curve
We applied the exponential demand curve developed by Hursh & Silberberg (2008):
| (1) |
where Q is consumption at price P, Q0 is consumption at zero price (derived intensity), k reflects the range of consumption in logarithmic units, and α determines the rate of decline (elasticity or E) in consumption with the increases in price (both consumption and price are in log scale), jointly with the range parameter k. Note that the elasticity of the exponential demand curve has an exponential form: E = − k α P e −αP; hence, larger α values correspond to greater price sensitivity for a fixed k. Relative to the derived intensity Q0, the empirical intensity is defined as the maximum amount of consumption (at prize zero) reported in the survey. Omax is defined as the maximum expenditure on cigarettes.
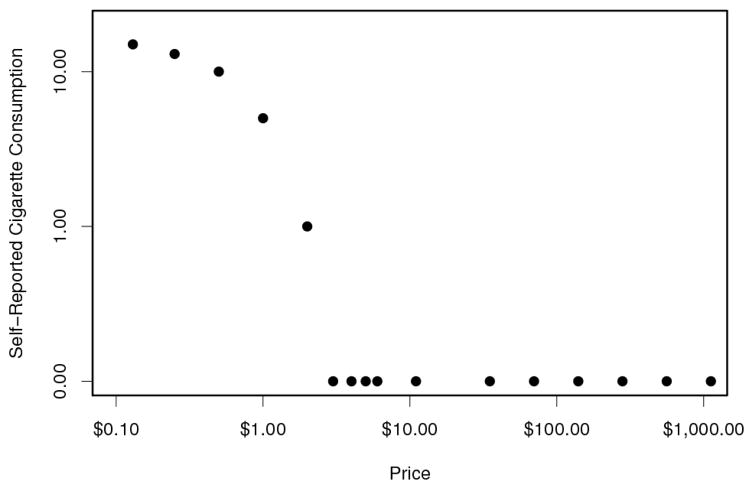
As demonstrated in Figure 1, depending on the survey strategy, purchasing task surveys can produce either a large number of zeros or missing outcomes on the right tail of the price chart. The first price for which the consumption is zero is defined as the breakpoint for a demand curve. Whether the outcome for prices beyond the breakpoint is zero or missing depends on the survey strategy used by the researcher: some administer the survey by continuing to ask questions until the highest price level is reached, while others stop asking questions once the breakpoint is reached, as was done in the Enhanced Quit & Win study. Given that it was rarely the case when a respondent would resume to non-zero consumption at a higher price once a subject decided not to consume at a lower price, it is reasonable to assume that all observations should be zero beyond the breakpoint, a monotonic missing pattern. Theoretically, based on the exponential demand curve, the zero consumptions cannot be achieved at any price within the given price range. Hence, in order to fit the exponential demand curve to the purchase task data, it is reasonable to assume that the self-reported zero consumptions at and beyond the breakpoint are small non-zero consumption amounts below a certain threshold that smokers do not bother to report. This is also known as limit of detection (LOD) or left censoring.
Figure 1.
A typical cigarette demand curve for a smoker, derived from cigarette purchase task survey data (log-log coordinate used)
Statistical Methods
The CPT data are repeated measures data; each participant repeatedly answers a set of similar questions on their cigarette consumption at different price levels. Given the structure of the CPT data, we used a left-censored mixed effects model to appropriately account for missing values in CPT data with repeated measures. This model takes the same form as the conventional mixed effects model:
| (2) |
based on the exponential consumption equation, where Qij is substance consumption of subject i at price level j; log Q0i and αi are, respectively, the random intercepts and slopes, assumed to follow a bivariate normal distribution with means (μl, μα), variances (σl2, σα2) and covariance ρ·σl·σα; and the independent error terms, εij, follow a normal distribution with zero mean and variance σe2. By introducing the random intercept (log Q0i) and random slope (αi) at the subject level, the left-censored mixed effects model takes into account the within-subject correlation among the repeated measures. A special case of the mixed effects model is the random intercept model (σα degenerates to 0), which is commonly used for analyzing purchase task data (e.g., Epstein et al., 2007; Epstein, et al., 2010b). Detailed model estimation procedure, using the random intercept model as an example, is described in Appendix A.
We validated the parameter estimates from the left-censored mixed effects model by investigating their associations with smoking variables: amount of smoking (cigarettes smoked per day/CPD on smoking days) and nicotine dependence. Following Baker et al. (2007), we chose the first item of the Fagerström Test for Nicotine Dependence (FTND) questionnaire (Heatherton, Kozlowski, Frecker, & Fagerström, 1991) as the index for nicotine dependence and grouped the study participants to high (smoke first cigarette within 30 minutes) and low (30+ minutes after waking) nicotine dependence groups. Specifically, we applied the empirical Bayes method to the proposed left-censored mixed effects model to estimate the random effects (log Q0i and αi) for each subject, based on which the derived demand indices such as intensity and Omax for each subject were constructed. The empirical indices and the derived indices based on the proposed model and the individual-specific regression model were correlated and their associations with the above mentioned smoking variables were examined by using t-tests or correlations.
In addition, we tested the gender effect by interacting gender with the parameters of logQ0 and α in the proposed regression model to investigate whether these regression parameters vary with gender (i.e. existence of interaction or moderation effects).
Simulations
We conducted a series of simulation studies to compare the proposed left-censored mixed effects model with the two conventional methods: the individual-specific regression model and the conventional mixed effects model. Specifically, for the individual-specific model, a nonlinear regression line for each subject was fit, where the true value of k used for simulating the data was assumed to be known and common to all subjects. The mean of the individually estimated parameters (Q0i and αi) was then calculated to estimate the population-averaged parameters. The conventional mixed effects model shares a similar functional form as the left-censored mixed effects model, but in the conventional model the likelihood is based only on the observed data.
For the two conventional models we treated the missing data with three different strategies: 1) ignoring all zeros or missing observations at and beyond the breakpoint (abbreviated as the “ignore-all-zeros method” hereinafter); 2) imputing the consumption outcome at the breakpoint with the true value ω, but ignoring all further zeros or missing observations beyond the breakpoint (“impute-first-zero method”); and 3) imputing all zeros or missing observations at and beyond the breakpoint using the true value ω (“impute-all-zeros method”). Note that the above imputation approaches are different from the proposed left-censored model in terms of how the threshold value is utilized in the statistical estimation procedure. The former treats the imputed value as observed and uses the observed data likelihood in estimation, whereas the latter honors the fact that these values are not observed and uses the threshold in the censored data likelihood (see Appendix A). While the true threshold was used in imputations for the two conventional models, for the proposed left-censored mixed effects model, we used both the true threshold and a series of misspecified thresholds to test whether the model estimation was sensitive to any threshold misspecification.
We simulated 1000 data sets with 100 subjects in each data set based on the exponential demand equation and the random intercept model with the parameters being set at values close to those from the Enhanced Quit & Win data. Each subject could have up to 13 repeated measures with price values corresponding to those in the CPT questionnaire. We assumed that if the number of cigarettes (measured as a continuous number) a smoker was willing to buy was smaller than a known threshold ω (ω = 0.5), a zero or missing consumption would be reported. In this setting, about 10% of consumption values were censored/ not observed. For all simulation studies, the mean parameter estimates from the 1000 simulated data sets were calculated to determine the mean relative bias (i.e. mean difference between the true parameter and the estimated values divided by the true parameter) for each parameter and each method; the coverage rate of the 95% confidence intervals (CI) over the true parameter was also reported.
SAS version 9.2 (SAS Institute Inc., Cary, NC) was used for all analyses. Specifically, we used the NLMIXED procedure for the left-censored mixed effects model (see Appendix B for some SAS syntax examples), and used the NLIN and NLMIXED procedures for the individual-specific non-linear regression model, and the conventional mixed effects model without censoring, respectively.
Results
Enhanced Quit & Win Study Participants
Of the 659 participants in the sample, 8 were excluded from our analyses; among them, 7 reported a cigarette consumption trend with fluctuations (i.e., greater consumption at a higher price level) and one reported a zero consumption at price 0. The 651 participants remaining in the analysis were enrolled across all participating campuses, with the majority (N=460) from 4-year colleges and the remainder (N=191) from 2-year colleges. As detailed in Table 1, participants were predominantly white (86.2%). Most (87.6%) were degree-seeking undergraduate students, and a majority (84.6%) were not working full-time. The average number of days participants had smoked in the past 30 days was 28.5, and the average number of cigarettes they smoked per day (on days they smoked) was 11.7. Approximately half (49.8%) of the respondents were classified as high nicotine dependence (smoking first cigarette within half an hour after waking).
Table 1.
Baseline Demographic and Tobacco-Related Variables for Participants in the Enhanced Quit & Win Study
| Variable | Total |
|---|---|
| N | 651 |
| Age (mean ± SD) | 26.1 ± 8.0 |
| Sex (n, % female) | 376 (57.8%) |
| Ethnicity (n, % white) | 561 (86.2%) |
| 2- or 4-year school (n, %) | |
| 2-year school | 191 (29.3%) |
| 4-year school | 460 (70.7%) |
| Year in school | |
| Non-degree seeking | 13 (2.0%) |
| Year 1 | 130 (20.0%) |
| Year 2 | 146 (22.4%) |
| Year 3 | 161 (24.7%) |
| Year 4+ | 134 (20.6%) |
| Graduate/professional degree program | 67 (10.3%) |
| Working status (n, % full time) | 100 (15.4%) |
| Days smoked last 30 days (mean ± SD) | 28.5 ± 3.8 |
| CPD on smoking day (mean ± SD) | 11.7 ± 8.4 |
| ≥10 cigarettes per day | 374 (57.5%) |
| < 10 cigarettes per day | 277 (42.5%) |
| How soon after waking smoke first cigarette (n, %) | |
| 0–5 minutes | 73 (11.2%) |
| 6–15 minutes | 109 (16.7%) |
| 16–30 minutes | 142 (21.8%) |
| 31–60 minutes | 158 (24.3%) |
| 61+ minutes | 169 (26.0%) |
| CPT empirical demand indices (mean ± SD, median [range]) | |
| Intensity | 15.0 ± 9.4, 15.0 [1–80] |
| Breakpoint | 4.0 ± 3.0, 3.0 [0.05–11] |
| Omax | 12.3 ± 29.1, 5.0 [0.01–440] |
Note. SD: standard deviation; CPD: cigarettes per day on smoking days.
Analysis of the Enhanced Quit & Win Data
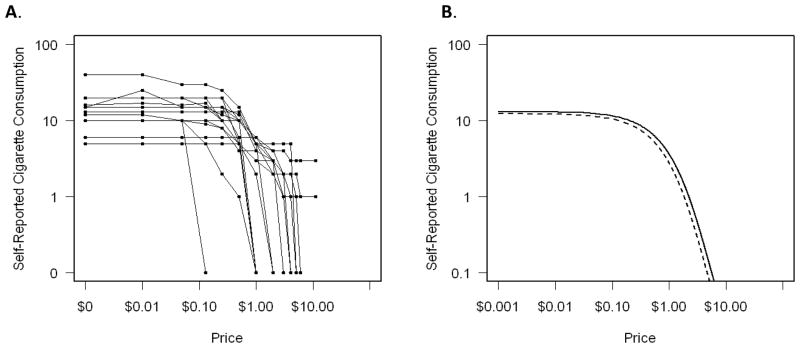
Figure 2A depicts a random sample of 20 demand curves from the 651 studied participants. We fit the proposed left-censored mixed effects model (shown as Model 1 in Table 2) with the assumed threshold 0.5, which was less than 1 and greater than 0, as the smallest nonzero consumption in the data set was 1 cigarette. The estimate of the derived intensity of cigarette consumption (Q0) was 12.9 (= e2.56, 95% CI: 12.3–13.6), which was close to the median of the empirical intensity (15.0). The estimated k was 7.3 (95% CI: 6.3–8.6) and the price sensitivity parameter α was 0.21 (95% CI: 0.17–0.25). All parameters were statistically significant (p<0.0001). As none of the existing CPT studies adopted an analytical tool similar to ours, it was difficult to compare our results to previously reported findings. Nevertheless, it appeared that the college smokers in our study tended to have lower intensity and greater elasticity than an adolescent smokers sample previously reported by Murphy et al. (2011).
Figure 2.
Cigarette demand using a cigarette purchase task in smokers from the Enhanced Quit &Win study. Panel A depicts the observed demand curves of 20 randomly selected subjects from the study. Panel B depicts the fitted demand curves for females (solid line) and males (dashed line) separately based on the left-censored mixed effects model with gender interactions. The x-axis is price in dollars and the y-axis is self-reported consumption in cigarettes. Log-log coordinates are used.
Table 2.
Applying Left-Censored Mixed Effects Model to the Enhanced Quit & Win Study Data
| Parameter | Model 1 (for overall population)
|
Model 2 (with gender interactions)
|
|||
|---|---|---|---|---|---|
| Estimate (SE) | p-value | Estimate for females (SE) | Estimate for males (SE) | Gender difference p-value | |
| μl (Mean of logQ0i) | 2.56 (0.02) | <.0001 | 2.59 (0.04) | 2.52 (0.04) | 0.15 |
| μα (Mean of αi) | 0.21 (0.02) | <.0001 | 0.19 (0.02) | 0.23 (0.02) | 0.02 |
| k | 7.34 (0.58) | <.0001 | 7.35 (0.58) | - | |
Note. SE: standard error.
The analysis for gender effects (shown as Model 2 in Table 2) suggested that female and male smokers had a similar intensity (log intensity for females vs. males: 2.59 vs. 2.52, p=0.15). However, interestingly, we found that female smokers were significantly less sensitive to price increase than males (mean αi for females vs. males: 0.19 vs. 0.23, p=0.02). Figure 2B illustrates the mean demand curves for females (solid line) and males (dashed line) based on the interaction model.
The top panel of Table 3 shows the correlations among the empirical intensity and Omax, their corresponding derived indices based on the popular individual-specific regression model (adopting the impute-first-zero method) and the proposed left-censored mixed effects model, and amount of smoking. The bottom panel of Table 3 shows the t-test results of comparing the two nicotine dependence groups (high vs. low) in terms of the above mentioned variables. All empirical and derived demand indices were significantly correlated with each other and with the two smoking variables. However, the derived indices based on the proposed model showed consistently stronger associations with their empirical counterparts and with the smoking variables (shown as bold numbers in Table 3) than the individual-specific regression model.
Table 3.
Associations Among Empirical and Derived Demand Indices and Smoking Variables
| Measure | Correlations
|
||||||
|---|---|---|---|---|---|---|---|
| Intensity
|
Omax
|
Amount of smoking | |||||
| Empirical | ISRM | LCMEM | Empirical | ISRM | LCMEM | ||
| Empirical Intensity | – | 0.82*** | 0.87*** | 0.18*** | 0.09* | 0.18*** | 0.59*** |
| Derived Intensity (Individual-Specific Regression Model) | – | 0.89*** | 0.39*** | 0.15*** | 0.30*** | 0.57*** | |
| Derived Intensity (Left-Censored Mixed Effects Model) | – | 0.12** | 0.09* | 0.13*** | 0.61*** | ||
| Empirical Omax | – | 0.76*** | 0.92*** | 0.15*** | |||
| Derived Omax (Individual-Specific Regression Model) | – | 0.92*** | 0.12** | ||||
| Derived Omax (Left- Censored Mixed Effects Model) | – | 0.17*** | |||||
| Amount of Smoking | – | ||||||
|
| |||||||
| T-test for comparing two nicotine dependence groups (high vs. low)
|
|||||||
| Intensity
|
Omax
|
Amount of smoking | |||||
| Empirical | ISRM | LCMEM | Empirical | ISRM | LCMEM | ||
|
| |||||||
| T statistics | 10.21*** | 12.29*** | 12.59*** | 3.43*** | 2.92** | 3.87*** | 10.25*** |
Note. LCMEM: left-censored mixed effects model; ISRM: individual-specific regression model, where the k parameter was estimated from a non-linear regression on the pooled data from all subjects and then assumed to be known and common for all subjects in the individual-specific regression model.
p < .05,
p < .01,
p <.001
Simulation Results
The top panel of Table 4 shows the simulation results from the individual-specific regression models with different strategies in dealing with the zeros/missing values. We found that the intensity parameter estimate was satisfactory for all three missing data strategies while the mean α estimate and the variance estimate of the log intensities were all deviated from the true values. The unsatisfactory results from the impute-first-zero method and the impute-all-zeros method may be due to the fact that arbitrary imputations did not recover the true information of the unobserved data. The reason for the inaccurate estimates in the ignore-all-zeros method warrants some discussion as this approach did not involve any imputations of missing data. One possible reason could be the non-estimability of parameters for subjects with fewer than three observations. In other words, people might provide fewer observations than parameters of the demand curve (e.g., report they would smoke cigarettes only if they were free or 1¢ each), rendering the parameters non-estimable. Since these people shared similar shape of the demand curve, the absence of their contribution to the mean parameter estimators could cause inaccurate mean estimates. This affected the elasticity parameters (α and k) more than it impacted the intensity (log intensity) parameter, as demonstrated by the results in Table 4.
Table 4.
Monte-Carlo Simulation Results
| Model | Parameter | Mean Relative Bias | Coverage Rate | |
|---|---|---|---|---|
| Individual-Specific Regression Model | Ignore-all-zeros method | Mean of logQ0i | 0.001 | 0.945 |
| α | 0.201 | 0.459 | ||
| Variance of logQ0i | 0.187 | NA | ||
|
| ||||
| Impute-first-zero method | Mean of logQ0i | 0.001 | 0.951 | |
| α | 0.190 | 0.353 | ||
| Variance of logQ0i | 0.156 | NA | ||
|
| ||||
| Impute-all-zeros method | Mean of logQ0i | −0.003 | 0.948 | |
| α | 0.170 | 0.427 | ||
| Variance of logQ0i | 0.115 | NA | ||
|
| ||||
| Conventional Mixed Effects Model | Ignore-all-zeros method | Mean of logQ0i | −0.001 | 0.942 |
| α | 0.069 | 0.835 | ||
| k | −0.057 | 0.143 | ||
| Variance of logQ0i | −0.117 | 0.840 | ||
|
| ||||
| Impute-first-zero method | Mean of logQ0i | −0.001 | 0.949 | |
| α | 0.024 | 0.942 | ||
| k | −0.021 | 0.764 | ||
| Variance of logQ0i | −0.065 | 0.893 | ||
|
| ||||
| Impute-all-zeros method | Mean of logQ0i | −0.002 | 0.951 | |
| α | −0.006 | 0.942 | ||
| k | −0.006 | 0.909 | ||
| Variance of logQ0i | −0.096 | 0.870 | ||
|
| ||||
| Left-Censored Mixed Effects Model | Correct threshold specification (0.5) | Mean of logQ0i | −0.001 | 0.957 |
| α | −0.002 | 0.952 | ||
| k | 0.001 | 0.955 | ||
| Variance of logQ0i | −0.009 | 0.953 | ||
|
| ||||
| Wrong threshold specification (0.3) | Mean of logQ 0i | −0.001 | 0.965 | |
| α | −0.033 | 0.897 | ||
| k | 0.030 | 0.697 | ||
| Variance of logQ0i | 0.053 | 0.971 | ||
|
| ||||
| Wrong threshold specification (0.1) | Mean of logQ0i | −0.000 | 0.977 | |
| α | −0.094 | 0.611 | ||
| k | 0.100 | 0.017 | ||
| Variance of logQ0i | 0.205 | 0.910 | ||
Note. Mean relative bias is the mean difference between the true parameter and the estimated values divided by the true parameter; coverage rate is the percent of the 95% confidence intervals covering the true parameter, based on 1000 Monte-Carlo simulations. The true parameters used for simulations are: μl = 0.56, μα = 0.54, k = 2.72, σl = 0.6, σα = 0, and σe = 0.55.
For the conventional mixed effects models (Table 4, middle panel), based on our simulation results, all three data analysis strategies gave approximately unbiased estimates (mean relative bias within ±1%) and close to 0.95 coverage rate for the intensity parameter (Q0). However, the estimates of the elasticity parameters (α and k) had greater amounts of bias and improper coverage rates.
The lower panel of Table 4 shows the simulation results for the proposed left-censored mixed effects model. It is shown that when we fit the model with the correctly identified threshold (ω = 0.5), the results (shown as bold numbers in Table 4) were all approximately unbiased: the mean relative biases of all parameter estimates were within ±1% and the coverage rates of the 95% CIs were all close to 0.95. This finding confirms that a left-censored mixed effects model with a correctly specified threshold is more suitable for data produced by purchasing tasks than the two conventional models. Our sensitivity analysis with different levels of threshold misspecification showed that as the misspecified thresholds moved away from the true threshold, the magnitude of bias in the parameter estimates increased correspondingly, with greater impact on the elasticity parameters than the intensity parameter. Our simulation results also showed that the proposed model with a misspecified but reasonably close threshold (ω = 0.3) performed better than the individual-specific regression model regardless of the missing data strategies used; it also performed better than the conventional mixed effects model when zeros were ignored in all parameter estimations.
Discussion
Most previous studies that analyzed purchase task data have used either an individual-specific regression model (e.g., MacKillop et al., 2008) or the conventional mixed effects model (e.g., Epstein et al., 2007; Epstein et al., 2010b). We found that the issue of zeros or missing values at or after the breakpoint has not been adequately addressed in previous studies. They were either ambivalent about the strategy of treating these observations or simply replaced them with arbitrary non-zero values such as 0.001 for the purpose of obtaining a finite log-scaled value (e.g., MacKillop et al., 2008; Epstein et al., 2010a). In this paper, we proposed to use a left-censored mixed effects model to analyze cigarette purchase task data. Our rationale was that such a model should better account for two distinct features of the CPT data: the correlation of the repeated measures of cigarette consumption at different price levels, and the zeros or missing values caused by the non-random missing mechanism. Our simulation results showed that naively ignoring the zero or missing values or treating them as a fixed small non-zero value was not always adequate. This result is consistent with the finding from Jacqmin-Gadda et al. (2000) that simply imputing the censored responses as the value of the threshold/limit of detection would result in badly biased parameter estimates with the mixed effects model, even for modest levels of censoring in the data. As compared to the conventional methods, our proposed method treats the zeros as values less than a certain detection limit and adopts the censored regression strategy (also known as survival analysis) to analyze the CPT data. Our simulation results showed that the proposed left-censored mixed effect model gave more accurate population-averaged or mean parameter estimates and more proper CIs than the two conventional methods, even when the assumed threshold was slightly deviated from the true value.
Although drawing inferences on the demand indices for each individual subject from our proposed model was not the main focus of this study, in order to validate our method in a real-world setting, we did derive them and correlate them with smoking variables for the Enhanced Quit & Win data. The results showed that subject-specific demand index estimates derived from our proposed model correlated well with smoking variables, with a similar but a slightly stronger association than the popular individual-specific regression model.
We note that the individual-specific regression method has its advantage in applications since it fits a regression line for each subject without assuming any correlation structure among the repeated measures from the same subject and allows the regression parameters to vary from subject to subject. However, the goal of most behavioral studies on RRE is not to describe individual demand curves but to find the impact of other factors on the shape of the curve (e.g., the impact of body mass index on food intake habits; Epstein et al., 2010a) or to infer information about a population-averaged curve by using the individual estimates (e.g., Jacobs & Bickel, 1999). By using the parameter estimates obtained for each individual as “observed” values in further statistical analysis, the individual-specific regression method could be inefficient, because the variance of the estimated parameters contains both the variation of the true parameters and the error in the estimation process. Other individual-based statistical methods would suffer from the same disadvantage.
As we know, when missing data are present, the conventional mixed effects method is only valid when the missing values are at random (MAR) (i.e., the missing mechanism should not be dependent on the values of the unobserved outcomes given the observed data; Diggle et al., 2002). This is not the case for CPT data; a zero or missing value may contain information on its outcome — it should be a value smaller than the threshold value below which the respondent would not bother to buy even one portion of substance. In other words, the magnitude of an unobserved value is related to the missing status of this value in the CPT data. Hence, the missing mechanism is not random (i.e., non-ignorable missing; Diggle et al., 2002). As a consequence, naively ignoring or imputing the zeros in the CPT data would lead to unsatisfactory estimation results.
Our simulation studies confirm that a left-censored mixed effects model with a correctly specified threshold is more suitable for data produced by purchasing tasks than the two conventional models. However, there are a number of issues on the proposed model worthy of discussion. First, in real data analysis, it is crucial for researchers to be informed of the reasonable range of the threshold. Without definitive information on the true threshold, it would be advisable to do a sensitivity analysis with different threshold specifications to examine changes in the fitted curve. Note that, though the proposed left-censored model shares the same problem as the conventional models in its arbitrariness in picking the threshold, we found that the parameter estimates from the former were satisfactory when the threshold was correctly identified or close to the true value whereas the latter couldn’t result in accurate parameter estimates even when the threshold was correctly specified. Second, we realized that the threshold of cigarette consumption might not be universal across all people. Thus, we conducted additional analysis by assuming that the threshold was random and normally distributed among studied subjects. We found that when the variance of the normal distribution was small, a fixed threshold specification close to the population mean of the normal distribution would produce virtually unbiased parameter effects and correct 95% coverage rates. However, as the variance of the threshold increased, the results became less accurate. Therefore, as emphasized earlier, when applying the left-censored mixed effects model, it is crucial to be aware of the possible value and the range of the threshold. This finding also suggests that the left-censored mixed effects model is more applicable to data with relatively homogeneous thresholds such as data that are missing due to technological limits (e.g., data of viral load in patients’ blood, which is subject to left censoring by the LOD; e.g., Chu et al., 2010).
A number of directions for future research are worthy of discussion. First, our proposed left-censored mixed effects model is based on the assumption that the self-reported zero consumptions are small non-zero consumptions below a certain threshold (LOD). This assumption is necessary for the exponential demand curve because the zero consumptions cannot be reached at any price within the given price range. However, as suggested by a referee, it is expected that a smoker would eventually consume zero units (complete cessation of smoking) at certain prices. This is different from the situation when a smoker would still smoke a small amount if it were available but otherwise would not bother to purchase or report such a small amount. In the presence both types of zeros in the data, it will be interesting for future research to exploit a joint modeling approach with a logistic regression component for the status of cessation, on the top of the proposed left-censored mixed effects model (Chu et al., 2010).
Finally, we note that the current paper focuses on statistical models assuming that the demand of a studied substance follows Hursh & Silberberg’s (2008) exponential demand curve. However, the proposed statistical method is not restricted to a specific functional form of the demand equation and hence is applicable to any demand curves that are downward sloping in price-consumption space, such as the linear-elasticity demand curve studied by Hursh et al. (1988). Investigation of the proposed statistical method for other demand curve models is certainly warranted.
Acknowledgments
This research was supported by NHLBI/NIH Grant 5R01HL094183 (to Dr. Janet L. Thomas), University of Minnesota/Minnesota Medical Foundation (UMN/MMF) Grant 4121-9227-12 (to Dr. Xianghua Luo), and NCMHD/NIH Grant 1P60MD003422 (to Dr. Jasjit S. Ahluwalia). The funding source had no role in the project other than financial support.
The authors thank Drs. Lan Wang and Wei Pan for enlightening discussion during the thesis defense of the first author; Jill Ronco, Qi Wang, Lee Snyder, Blake Downes, Meredith Schreier, and Nora Johnson for data collection and data cleaning; and Dr. Anne Marie Weber-Main for critical review and editing of manuscript drafts.
Appendix
Appendix A: Estimation Procedure for Left-Censored Mixed Effects Model
Considering the fact that the zeros or missing observations in the CPT data could be values below a certain known threshold, ω (0< ω <1), we define the missing/censoring indicator δij as: δij = 1 if Qij ≥ ω; δij = 0 if otherwise. For the latter case, Qij is actually not observable (i.e., missing or zero in the data). Let ni denote the number of observations before (including) the breakpoint for subject i, i.e., Qi1 ≥ ω, …, Qi,ni−1 ≥ ω, and Qi,ni < ω. Using the random intercept model as an example, the likelihood function for the left-censored mixed effects model is:
where Φ (.) and φ (.) are, respectively, the cumulative density function (c.d.f.) and probability density function (p.d.f.) of the standard normal distribution; zi = (log Q0i - μl)/σl is the standardized random intercept; and N is the total number of subjects. Note that, as indicated in the likelihood function, we only kept the first observation below the threshold by marking it as censored and storing it as ω in the data, meaning that the true demand is some value less than or equal to ω. The likelihood function for the left-censored mixed effects model has the same form as the likelihood for a correlated survival data with type-I left censoring and log-normal survival times (Klein & Moeschberger, 2003). The maximum likelihood estimators (MLE) for the regression parameters, k and α, the mean of the random intercepts, μl, and the variance parameters, σl2 and σe2 can be obtained by maximizing the logarithm of the likelihood function. As a comparison, the likelihood for the conventional mixed effects model is:
Appendix B: SAS Program Examples for Analyzing the Enhanced Quit & Win Data
* Left-censored mixed effects model with threshold=0.5;
PROC NLMIXED DATA=cleandata QPOINTS=50;
PARMS mu_l=2.5 mu_alpha=0.5 logk=1 logsigma_e=0 logsigma_l=0
logsigma_a=0 rho=0;
BOUNDS -1<rho<1;
mu_ij=(mu_l+random_intercept)+exp(logk)*(exp(0-
(mu_alpha+random_slope)*price)-1);
logL=(1-delta)*log(probnorm((log(0.5)-mu_ij)/exp(logsigma_e))) +
delta*(-0.5*((logQ_ij-mu_ij)/exp(logsigma_e))**2-
log(exp(logsigma_e)*sqrt(8*atan(1))));
MODEL logQ_ij~general(logL);
var1=exp(2*logsigma_l);
var2=exp(2*logsigma_a);
cov12=sqrt(var1*var2)*rho;
RANDOM random_intercept random_slope~normal([0,0], [var1,cov12,var2])
SUBJECT=studyid;
RUN;
* Interaction model for gender (female);
PROC NLMIXED DATA=cleandata QPOINTS=50 MAXITER=2000;
PARMS mu_l=2.5 mu_alpha=0.5 logk=1 logsigma_e=0 logsigma_l=0
logsigma_a=0 rho=0 mu_l_diff=0.1 mu_alpha_diff=-0.1;
BOUNDS -1<rho<1;
mu_ij=(mu_l+mu_l_diff*female+random_intercept)+exp(logk)*(exp(0-
(mu_alpha+mu_alpha_diff*female+random_slope)*price)-1);
logL=(1-delta)*log(probnorm((log(0.5)-mu_ij)/exp(logsigma_e))) +
delta*(-0.5*((logQ_ij-mu_ij)/exp(logsigma_e))**2-
log(exp(logsigma_e)*sqrt(8*atan(1))));
MODEL logQ_ij~general(logL);
var1=exp(2*logsigma_l);
var2=exp(2*logsigma_a);
cov12=sqrt(var1*var2)*rho;
RANDOM random_intercept random_slope~normal([0,0], [var1,cov12,var2])
SUBJECT=studyid;
RUN;
Footnotes
Disclosures
All authors contributed in a significant way to the manuscript and that all authors have read and approved the final manuscript.
The authors have no conflicts of interest to disclose.
Contributor Information
Wenjie Liao, Division of Biostatistics, School of Public Health and Department of Sociology, University of Minnesota.
Xianghua Luo, Division of Biostatistics, School of Public Health, University of Minnesota.
Chap Le, Division of Biostatistics, School of Public Health, University of Minnesota.
Haitao Chu, Division of Biostatistics, School of Public Health, University of Minnesota.
Leonard H. Epstein, Department of Pediatrics, School of Medicine and Biomedical Sciences, University at Buffalo
Jihnhee Yu, Department of Biostatistics, School of Public Health and Health Professions, University at Buffalo.
Jasjit S. Ahluwalia, Center for Health Equity and Department of Medicine, University of Minnesota
Janet L. Thomas, Division of General Internal Medicine, Department of Medicine, University of Minnesota
References
- Baker TB, Piper ME, McCarthy DE, Bolt DM, Smith SS, Kim S-Y, Colby S, Conti D, Giovino GA, Hatsukami D, Hyland A, Krishnan-Sarin S, Niaura R, Perkins KA, Toll BA. Time to first cigarette in the morning as an index of ability to quit smoking: Implications for nicotine dependence. Nicotine & Tobacco Research. 2007;9(Suppl 4):S555–S570. doi: 10.1080/14622200701673480. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bickel WK, Marsch LA, Carroll ME. Deconstructing relative reinforcing efficacy and situating the measures of pharmacological reinforcement with behavioral economics: A theoretical proposal. Psychopharmacology. 2000;153:44–56. doi: 10.1007/s002130000589. [DOI] [PubMed] [Google Scholar]
- Chu H, Gange SJ, Li X, Hoover DR, Liu C, Chmiel JS, Jacobson LP. The effect of HAART on HIV RNA trajectory among treatment-naïve men and women: a segmental Bernoulli/lognormal random effects model with left censoring. Epidemiology. 2010;21(Suppl 4):S25–S34. doi: 10.1097/EDE.0b013e3181ce9950. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Diggle P, Heagerty P, Liang KY, Zeger S. Analysis of Longitudinal Data. 2. New York, NY: Oxford University Press; 2002. [Google Scholar]
- Epstein LH, Dearing KK, Paluch RA, Roemmich JN, Cho D. Price and maternal obesity influence purchasing of low- and high-energy-dense foods. The American Journal of Clinical Nutrition. 2007;86:914–922. doi: 10.1093/ajcn/86.4.914. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Epstein LH, Dearing KK, Roba LG. A questionnaire approach to measuring the relative reinforcing efficacy of snack foods. Eating Behaviors. 2010a;11:67–73. doi: 10.1016/j.eatbeh.2009.09.006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Epstein LH, Dearing KK, Roba LG, Finkelstein E. The influence of taxes and subsidies on energy purchased in an experimental purchasing study. Psychological Science. 2010b;21:406–414. doi: 10.1177/0956797610361446. [DOI] [PubMed] [Google Scholar]
- Griffiths RR, Brady JV, Bradford LD. Predicting the abuse liability of drugs and animal drug self-administration procedures: psychomotor stimulants and hallucinogens. In: Thompson T, Dews PB, editors. Advances in Behavioral Pharmacology. Vol. 2. New York, NY: Academic Press; 1979. pp. 163–208. [Google Scholar]
- Heatherton TF, Kozlowski LT, Frecker RC, Fagerström KO. The Fagerström Test for Nicotine Dependence: a revision of the Fagerström Tolerance Questionnaire. British Journal of Addiction. 1991;86:1119–1127. doi: 10.1111/j.1360-0443.1991.tb01879.x. [DOI] [PubMed] [Google Scholar]
- Hursh SR, Raslear TG, Shurtleff D, Bauman R, Simmons L. A cost-benefit analysis of demand for food. Journal of the Experimental Analysis of Behavior. 1988;50:419–440. doi: 10.1901/jeab.1988.50-419. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hursh SR, Silberberg A. Economic demand and essential value. Psychological Review. 2008;115:186–198. doi: 10.1037/0033-295X.115.1.186. [DOI] [PubMed] [Google Scholar]
- Jacqmin-Gadda H, Thiébaut R, Chêne G, Commenges D. Analysis of left-censored longitudinal data with application to viral load in HIV infection. Biostatistics. 2000;1:355–368. doi: 10.1093/biostatistics/1.4.355. [DOI] [PubMed] [Google Scholar]
- Jacobs EA, Bickel WK. Modeling drug consumption in the clinic using simulation procedures: demand for heroin and cigarettes in opiod-dependent outpatients. Experimental and Clinical Psychopharmacology. 1999;7:412–426. doi: 10.1037/1064-1297.7.4.412. [DOI] [PubMed] [Google Scholar]
- Katz JL. Models of relative reinforcing efficacy of drugs and their predictive utility. Behavioral Pharmacology. 1990;1:283–301. doi: 10.1097/00008877-199000140-00003. [DOI] [PubMed] [Google Scholar]
- Klein JP, Moeschberger ML. Survival analysis: Techniques for Censored and Truncated Data. New York, NY: Springer; 2003. [Google Scholar]
- MacKillop J, Miranda R, Jr, Monti PM, Ray LA, Murphy JG, Rohsenow DJ, McGeary JE, Swift RM. Alcohol demand, delayed reward discounting, and craving in relation to drinking and alcohol use disorders. Journal of Abnormal Psychology. 2010;119:106–114. doi: 10.1037/a0017513. [DOI] [PMC free article] [PubMed] [Google Scholar]
- MacKillop J, Murphy JG, Ray LA, Eisenberg DTA, Lisman SA, Lum JK, Wilson DS. Further validation of a cigarette purchase task for assessing the relative reinforcing efficacy of nicotine in college smokers. Experimental and Clinical Psychopharmacology. 2008;16:57–65. doi: 10.1037/1064-1297.16.1.57. [DOI] [PubMed] [Google Scholar]
- MacKillop J, Murphy JG, Tidey JW, Kahler CW, Ray LA, Bickel WK. Latent structure of facets of alcohol reinforcement from a behavioral economic demand curve. Psychopharmacology. 2009;203:33–40. doi: 10.1007/s00213-008-1367-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Murphy JG, MacKillop J. Relative reinforcing efficacy of alcohol among college student drinkers. Experimental and Clinical Psychopharmacology. 2006;14:219–227. doi: 10.1037/1064-1297.14.2.219. [DOI] [PubMed] [Google Scholar]
- Murphy JG, MacKillop J, Skidmore JR, Pederson AA. Reliability and validity of a demand curve measure of alcohol reinforcement. Experimental and Clinical Psychopharmacology. 2009;17:369–404. doi: 10.1037/a0017684. [DOI] [PubMed] [Google Scholar]
- Murphy JG, MacKillop J, Tidey JW, Brazil LA, Colby SM. Validity of a demand curve measure of nicotine reinforcement with adolescent smokers. Drug & Alcohol Dependence. 2011;113:207–214. doi: 10.1016/j.drugalcdep.2010.08.004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Petry NM, Bickel WK. Polydrug abuse in heroin addicts: a behavioral economic analysis. Addiction. 1998;93:321–335. doi: 10.1046/j.1360-0443.1998.9333212.x. [DOI] [PubMed] [Google Scholar]