Abstract
Purpose
To introduce a respiratory-gated high-spatiotemporal-resolution dynamic-contrast-enhanced MRI technique and a high-temporal-resolution aortic input function (HTR-AIF) estimation method for glomerular filtration rate (GFR) assessment in children.
Methods
A high-spatiotemporal-resolution DCE-MRI method with view-shared reconstruction was modified to incorporate respiratory-gating, and an AIF estimation method that uses a fraction of the k-space data from each respiratory period was developed (HTR-AIF). The method was validated using realistic digital phantom simulations and demonstrated on clinical subjects. The GFR estimates using HTR-AIF were compared to estimates obtained by using an AIF derived directly from the view-shared images.
Results
Digital phantom simulations showed that using the HTR-AIF technique gives more accurate AIF estimates (RMSE = 0.0932) compared to the existing estimation method (RMSE = 0.2059) that used view-sharing (VS). For simulated GFR > 27 ml/min, GFR estimation error was between 32% and 17% using view-shared AIF, whereas estimation error was less than 10% using HTR-AIF. In all clinical subjects, the HTR-AIF method resulted in higher GFR estimations than the view-shared method.
Conclusion
The HTR-AIF method improves the accuracy of both the AIF and GFR estimates derived from the respiratory-gated acquisitions, and makes GFR estimation feasible in free-breathing pediatric subjects.
Keywords: glomerular filtration rate estimation, high spatio-temporal resolution dynamic imaging, arterial input function estimation, urography, dynamic contrast enhancement
Introduction
A substantial percentage of children worldwide are affected by chronic kidney disease (CKD) (1). In its early stages, the disease is typically asymptomatic, but in later stages CKD causes reduced glomerular filtration and eventually leads to end-stage renal disease. Among the leading causes of CKD in children are obstructive uropathy and congenital anomalies, also referred to as aplasia, hypoplasia, and dysplasia (2), which are usually diagnosed by renal ultrasound. However, further evaluation is often required to assess unresolved anatomical issues and to assess renal function. MRI is particularly attractive for this evaluation in a pediatric setting as alternative imaging modalities such as computed tomography (CT) and nuclear scintigraphy involve ionizing radiation.
Magnetic resonance urography (MRU) has been used in the diagnosis of pediatric renal disease for a few decades now. MRU is mostly used as an anatomical evaluation tool based on fluid-sensitive T2-weighted sequences to detect abnormalities in the urinary tract (3–6). In the last decade, contrast-enhanced dynamic imaging sequences were included in MRU protocols, allowing visualization of contrast dynamics and measurement of semi-quantitative functional metrics such as renal transit time and split renal function (7–9). Recently, there has been work on extending dynamic MRU by including pharmacokinetic modeling (10–13) to estimate the glomerular filtration rate (GFR), which is the primary metric used in diagnosis and staging of chronic kidney disease. In addition, these models can provide single-kidney GFR estimates and even localized GFR maps that may be useful in surgical planning.
Glomerular filtration rate assessment using MRU is based on dynamic contrast enhanced MRI (DCE-MRI) and can be used for quantitative assessment of renal physiology. DCE-MRI is performed by injecting a gadolinium-based contrast agent and observing the passage of this contrast in vivo using a T1-weighted MRI sequence. The time-resolved MR images obtained by this sequence can be analyzed qualitatively or quantitatively. Qualitative analysis can be used to identify any abnormal masses or obstructions but fails to measure the glomerular filtration rate (GFR) of the kidneys, which is a sensitive indicator of renal function. Quantitative functional metrics such as renal transit times, split function, single kidney GFR, and regional GFR maps, can be estimated from the DCE-MRI dataset using pharmacokinetic models. However, quantitative analysis of DCE-MRI data remains challenging due to the need for high spatiotemporal resolution. A high spatial resolution is needed for creating regional maps of renal function metrics, whilst a high temporal resolution is required for capturing the fast temporal dynamics of the arterial input function and plays a significant role in the quantitative analysis (14).
Due to the high temporal resolution demands of quantitative analysis, 2D multi-slice imaging with low spatial resolution has been used for MRU (11, 13). However, low spatial resolution and thick slices make renal segmentation difficult and limits the analysis to large regions of interest. Three-dimensional sequences that can achieve high spatiotemporal resolution have been developed (15–20) but have not been specifically focused on MR urographic applications. A TWIST based technique has been used for MR urography on adult patients employing breath holds (21). However, applying the same technique for pediatric patients is impractical due to the difficulty in maintaining long breath-holds, while a free breathing acquisition leads to significant motion artifacts in the images. One way to reduce these motion artifacts is respiratory gating, although this leads to reduced temporal resolution and increased temporal blurring due to the respiratory breaks during the acquisition.
Recently, a high-spatiotemporal-resolution sequence, DISCO (Differential Subsampling with Cartesian Ordering), was demonstrated for adult liver imaging, which combined pseudorandom sampling with view sharing and parallel imaging acceleration to achieve breath-held dynamic acquisitions (17, 22). Here, we present a respiratory gated sampling scheme for DISCO and a new post-processing technique for mitigating the effects of increased temporal blurring on the arterial input function. This combined new method is first validated on a realistic digital phantom using simulations and then its feasibility is demonstrated in pediatric subjects. Finally, the impact of the proposed post-processing technique on GFR measurement is assessed.
Methods
Pulse Sequence
The acquisition sequence used in this study is a modification of the recently described high-spatiotemporal-resolution sequence called DISCO (17). This method uses a 3D spoiled gradient echo (3D SPGR) sequence with a bipolar readout followed by two-point Dixon reconstruction. It employs a 3D-Cartesian subsampling strategy with the ky-kz plane divided into 2 concentric regions: a fully sampled central k-space (A region), and a pseudo-randomly subsampled outer k-space (B regions). The A region is defined with the parameter fA, fraction of total k-space samples in one temporal phase. The pseudo-random subsampling divides the B region into M non-overlapping sub-regions (B1 to BM) that are acquired progressively after every A region (AB1 to ABM). In each temporal phase, an A region and a sub-region of B is acquired and the missing k-space data is filled in using nearest-neighbor view sharing.
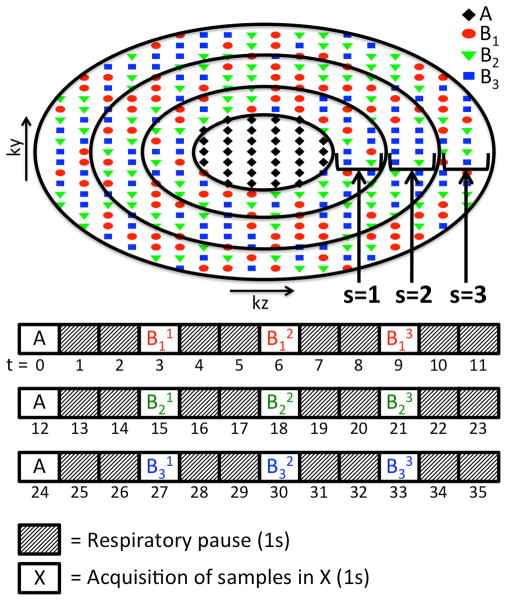
Conventional DISCO acquisition is challenging for pediatric patients due to the difficulties of maintaining long breath holds, obtaining repeated breath-holds, and ensuring that the repeated breath-holds have the kidneys in the same position. Hence, we incorporated respiratory-gating into DISCO to eliminate the need for breath holding. A navigator echo monitoring the right hemi-diaphragm was used for triggering the acquisition in the end-expiratory phase to minimize motion artifacts due to breathing. The DISCO sampling pattern and the timing diagram of a typical acquisition with respiratory gating is shown in Fig. 1. The central k-space, A region, is fully acquired in a single respiratory window to reduce motion artifacts from k-space inconsistencies. Each of the M sub-regions of the outer k-space is further split into S concentric and annular sub-regions that can be acquired in one respiratory window. The number of phase encodes acquired in each respiratory window is based on the patient’s end-expiratory phase duration and it is defined by choosing the parameters fA, M and S at the time of the scan. The typical values for these parameters are fA = 0.1, M = 3 and S = 2 or 3. The temporal resolution and temporal footprint are given by the parameters M and S as well as the respiratory rate (RR) of the patient:
| [1] |
| [2] |
FIG. 1.
DISCO sampling pattern (fA = 0.1, M = 3, S = 3) and timing of acquisition assuming a respiratory rate of 20 breaths/min with end-expiratory phase lasting 1s at each cycle. Each sub-region of B is represented with Bms where the subscript “m” denotes the pseudo-randomly subsampled regions (m = 1 to M), which are also color coded in the figure, and superscript “s” denotes the annular sub-regions (s = 1 to S).
Temporal resolution is defined as the time between acquisitions of A regions (i.e. center of the k-space). A regions are always acquired in a single respiratory window and each pseudo-randomly subsampled B region is split into S rings each acquired a single respiratory window. Hence, there are S+1 respiratory windows between the acquisitions of A regions (Eq. 1). If the respiratory rate increases, the length of the respiratory window is shortened. In order to maintain the spatial resolution and temporal resolution, the parameter S can be increased to spread out the acquisition of B region into more respiratory windows each with shorter duration.
The view-shared reconstruction method uses an A region and M pseudo-randomly subsampled B regions, each split into S rings, to construct the full k-space. Therefore, the full temporal span of each reconstructed image is MxS+M-1 respiratory windows as shown in (Eq. 2). The MxS term comes from the acquisition of B regions and the M-1 term comes from the acquisition of A regions in between B regions (Fig. 1).
Quantitative Analysis of DCE-MRI Datasets
The first step in the quantitative analysis of DCE-MRI datasets is the segmentation of the regions of interest (ROI). For GFR estimation, these regions are renal cortex, renal medulla, and the collecting system of each kidney. In addition to these, an aortic ROI is defined to extract the arterial input function (AIF). After the segmentation, the average signal intensity within each ROI (SROI) is calculated for each temporal phase. Then, the signal intensity curves are converted to the concentration-time curves (CROI) using Eqs. 3 and 4.
| [3] |
| [4] |
where r1 is the relaxivity of gadolinium, T1(0) is the pre-contrast T1 value of the tissue, TR is the repetition time and θ is the flip angle. The constant S0 in Eq. 4 is calculated from the dataset using the pre-contrast signal and T1 values of the tissue inside the ROI. The concentration of the contrast agent in this study is estimated using r1 = 4.5 s−1mM−1, T1,blood = 1.4 s and T1,kidney = 1.2 s as reported in literature (11).
The concentration of contrast agent in the blood plasma is obtained by applying a hematocrit correction to the aortic concentration as seen in Eq. 5. Here, we use a hematocrit value of 0.41, as suggested in previous work (11).
| [5] |
The glomerular filtration rate (GFR) of each kidney is estimated from the concentration-time curves using a cortical-compartment model (13), which has three compartments. In this model, the concentration of contrast in renal cortex is related to the arterial input function via Eqs. 6 and 7.
| [6] |
| [7] |
The AIF in this model is assumed to be delayed and dispersed as the contrast moves from the aorta into the arterial space of the kidneys. The model parameters τ and d in Eq. 6 define the delay and dispersion constant of the AIF. The ⊗ symbol in this equation denotes the convolution operation between the hematocrit corrected AIF and the dispersion function. In Eq. 7, vb is the volumetric fraction of the blood vessels in cortex, k21 is the GFR per unit volume of cortex, and k12 is the rate of contrast leaving the renal tubules. Model parameters k12, k21, vb, τ, and d are all estimated from the dataset using non-linear least squares curve fitting.
Since the glomeruli primarily reside in the cortical region of the kidneys and the high spatial resolution allows proper segmentation of the cortex from the rest of the parenchyma, the kidney concentrations in our analysis are derived from the renal cortex ROIs only. The single kidney GFR is calculated by multiplying the glomerular filtration coefficient (k21) by the volume of renal cortex (Vcortex). Localized GFR maps are then generated by performing the same analysis steps on a voxel-by-voxel basis instead of averaging the signal within an ROI in the renal cortex.
High Temporal Resolution AIF Estimation
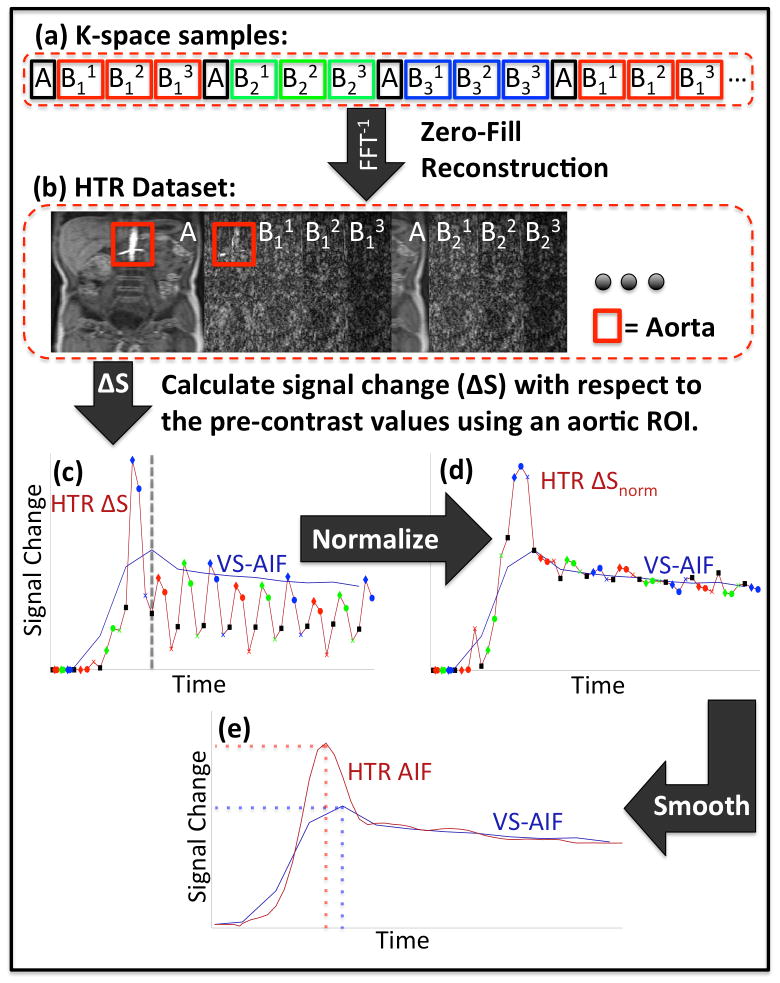
Accurate estimation of the AIF is important for achieving accurate quantitative analysis results (23). The view-sharing (VS) method used in the DISCO reconstruction process causes temporal blurring in the images and subsequently in the view-shared AIF (VS-AIF) estimate. The accuracy of the estimated AIF curve is worse at time points of the AIF with fast dynamics, such as the sharp rise followed by a sharp fall seen around the first pass of contrast. In order to reduce this temporal blurring effect, we developed a new post processing technique for AIF estimation (Fig. 2).
FIG. 2.
Flowchart of HTR-AIF analysis: K-space samples from the same respiratory cycle are grouped together (a). Volumetric images are reconstructed from each group of samples to form the HTR dataset (b). Signal change within the aorta is calculated (c). The dashed line marks the peak time of the VS-AIF curve (blue), which marks the start of the tail section. The signal change curve (red) is normalized using the tail section of the VS-AIF curve as a reference (d). The data points corresponding to A regions in (c) and (d) are marked with black markers as a reference to demonstrate the scaling differences between different groups. The final HTR-AIF estimate is obtained by applying local regression to the normalized signal change (e). Depending on the timing and the temporal dynamics of the true AIF, the HTR-AIF and VS-AIF estimates may give different peak heights and times.
In this new method, k-space data is acquired using the respiratory-gated DISCO protocol as described above. In addition to constructing a full k-space data set using view sharing, the samples acquired in each respiratory window are also grouped together (Fig. 2a) to reconstruct a high temporal resolution (HTR) dataset (Fig. 2b). Each temporal phase of the HTR dataset is reconstructed using only the k-space samples that are acquired in a single respiratory interval, and the missing k-space samples are filled with zeros prior to Fourier transform reconstruction. The reconstructed HTR images corresponding to the phases where an A region is collected have only the low spatial frequency components (i.e. blurred image) and those corresponding to the B regions have only the high spatial frequency components (i.e. edges). The basic idea is that if arterial signal intensity varies over time, this intensity variation can be observed in both low and high spatial frequency images. An AIF curve is estimated from these HTR images using the post-processing steps described below.
Since HTR images reconstructed from different sampling patterns (A, B11, B12 etc.) have different energies and aliasing patterns, images are split into groups based on their acquisition sampling patterns. Then, a large ROI is drawn over the aorta on the HTR images and the average signal intensity within this ROI is calculated for each temporal phase using a fixed fraction (α) of the voxels. The subsets of voxels used in the extraction of the signal intensity are chosen as the top α fraction, typically 0.25, of the aortic ROI voxels that enhance the most and they are determined for each group of images separately. The reason for this thresholding is to select the voxels that have the highest arterial signal, which in turn minimizes the contribution of aliasing from the surrounding tissue. Once the average signal intensity curve of the HTR dataset (Shtr) is determined, the concentration of the contrast agent is estimated by calculating the signal change (ΔShtr) for each group separately and then combining them based on their acquisition time using Eqs. 8 and 9 (Fig. 2c).
| [8] |
| [9] |
where G is the set of image groups {A, B11, B12, …}, 1group(t) is an indicator function that shows which group each time point belongs to, and is the pre-contrast signal intensity for the specified group. Calculating the signal change for each group separately is critical because there is a large scaling difference in signal intensities of different groups due to the different energy distribution in different parts of k-space, which is object dependent.
The resulting concentration curve is normalized and scaled using the tail section of the VS-AIF as a reference (Fig. 2d). For simplicity, the tail section is defined from the peak time of the VS-AIF to the end (Eq. 10). Since there is little fluctuation in the AIF after the first pass peak, it is assumed that view sharing does not affect the accuracy of the tail section. This normalization is performed by applying a scaling factor to each group of samples (Eq. 12). The scaling factors are chosen to minimize the least squares error shown in Eq. 11 between the scaled values and the corresponding VS-AIF samples. After the normalization, the samples from different groups end up having comparable scales despite each of them originating from images with different energies and aliasing patterns.
| [10] |
| [11] |
| [12] |
where Egroup is the error term that is minimized, is the AIF determined from view-shared images, kgroup is the scaling factor for the given group and is the normalized signal change curve.
The normalized signal change curve obtained in the previous step is usually noisy and needs to be denoised before it could be used in the quantitative analysis. The final HTR-AIF curve is obtained by applying a quadratic local regression smoothing (LOESS) (24) to the normalized signal change curve calculated in the previous step (Fig. 2e).
| [13] |
The smoothing parameter αL of the loess function in Eq. 13 defines the window length for smoothing and it is empirically chosen to fit at least 12 samples inside the smoothing window to get an accurate HTR-AIF estimate ( ). The parameter αL typically varied between 0.1 and 0.2 depending on the number of temporal phases acquired during a scan.
Digital Phantom
Validation of new DCE-MRI methods on human subjects is quite challenging because there are no easily obtainable “ground truth” measurements. Nuclear scintigraphic methods are considered standard of clinical practice, but are an imperfect gold standard. Additionally, at our practice, pediatric patients are referred for MRI specifically to avoid ionizing radiation, so obtaining nuclear scintigraphic estimates of GFR in our practice is not feasible. As an alternative, digital phantom simulations have been used as a validation technique for DCE-MRI methods (21). Here, we take a similar approach to validate the HTR-AIF analysis.
A digital phantom was created in MATLAB (MathWorks, Natick, MA) based on actual MR images of a pediatric patient, thus achieving realistic renal and background signal enhancement. An existing DCE-MRI dataset (fA = 0.1, M = 3, S = 3) of a 6-year-old patient was used as an anatomical reference for the digital phantom. The renal cortex and medulla of both kidneys as well as the aorta were segmented to define the controlled regions of interest. The dataset was interpolated to one-second temporal resolution and the signal intensities in these ROIs are modulated to match desired signal enhancement curves for each region. The enhancement curve of the aorta, or the simulated AIF, was based on a healthy subject’s AIF obtained from an existing dataset with 4s temporal resolution acquired using a free-breathing DCE-MRI method (25). The AIF curve is parameterized using a double-Gaussian-plus-exponential model (26) and interpolated to 1s temporal resolution. Enhancement curves of the renal cortex and renal medulla are derived from the parameterized AIF using a 3-compartment model (k21 = GFR/Vcortex, k12 = 1.5, vb = 0.35) (13). The finalized digital phantom as a 4 dimensional (4D) dataset will be available online at mridata.org.
Digital Phantom Simulations
The HTR-AIF analysis method was validated on a set of digital phantoms with single kidney GFR values ranging from 20 mL/min to 80 mL/min. For each GFR value, a digital phantom dataset was created as described earlier. The data acquisition was simulated by sampling this digital phantom in the frequency domain using the respiratory gated DISCO method (fA = 0.1, M = 3, S = 3) at a respiratory rate of 20 min−1 with a duty cycle of ⅓. Following the data acquisition step, 2 different sets of images were reconstructed: view-shared images and HTR images. View-shared images were used to extract the VS-AIF ( ) and the renal cortex enhancement curve ( ). HTR images were used to extract the HTR-AIF ( ). Quantitative analysis was performed on the renal cortex enhancement curve using each AIF separately to get the GFR estimates for each method. The estimated GFR values were compared to the simulated GFR value and the percent error was calculated for both methods, VS and HTR.
In an actual patient acquisition, the relative timing of the contrast arrival is an unknown and it is not possible to know whether an A region or a B region was acquired during the first pass of the AIF. Furthermore, the acquisition pauses during the inspiratory phase of respiration, and the relative timing of these pauses are also not known a priori. To account for this variability, in the simulations, the sampling pattern and respiratory pauses need to be distributed evenly over time. The acquisition, reconstruction and analysis steps described above are repeated with 12 different start times, each successively delayed by 1 second.
Clinical Feasibility
With IRB approval and waived consent, we retrospectively identified three pediatric patients (ages 5, 9 and 17) who had MR urography and were scanned with the respiratory gated DISCO protocol. First, acquired datasets were reconstructed with view-sharing and quantitatively analyzed using the cortical-compartment model. Then, the HTR-AIF curves were estimated using the method and used in quantitative analysis. The analysis results generated using VS-AIF were compared to the results generated using HTR-AIF and the impact of the HTR-AIF on the GFR estimates was assessed. In addition, voxel-by-voxel GFR maps were calculated using both methods to observe any differences in regional GFR estimates.
The clinical scans were performed on a 3T MR750 scanner (GE Healthcare, Waukesha, WI) using a 32-channel torso coil. Patients underwent intravenous hydration with 20 mL/kg normal saline bolus prior to the scan and diuresis with 1 mg/kg furosemide. The imaging protocol was respiratory gated DISCO (fA = 0.1, M = 3, S = 2 for the 9-year-old subject and S = 3 for the other subjects) with 12° flip angle, +/−167 kHz bandwidth, repetition time (TR) of 3.9 ms, bipolar readout with 1.1ms (out-of-phase) and 2.2ms (in-phase) echo time (TE), matrix size 256 × 200, FOV 28 cm, 34 slices, slice thickness 2.6 mm, and 2.5X Autocalibrating Reconstruction for Cartesian (ARC) imaging acceleration. View-shared images are reconstructed using ARC while high temporal resolution images are reconstructed using zero filling and a sum-of-squares coil combination. The subjects were injected intravenously with 0.03 mL/kg gadobutrol diluted in saline to a volume of 10 mL and injected at a rate of 0.3 mL/s followed by 20 mL saline flush at the same rate. Segmentation of the datasets was performed by trained post-processing technologists. The reconstruction time of the HTR-AIF dataset for a typical scan of 166 temporal phases was 35 minutes on a single core of a 32-core 2.6 GHz CPU running MATLAB (MathWorks, Natick, MA).
Results
Digital Phantom
The digital phantom created for the HTR validation experiment is shown in Fig. 3 along with the signal intensity curves of aorta and renal cortex. The phantom has high spatiotemporal resolution signal changes (spatial = 1.1×1.1×3.4mm3, temporal = 1s) and realistic contrast enhancement profiles. The cortical enhancement curves and the AIF are related through a pharmacokinetic model with known parameters that can be used as the ground truth for quantitative analysis. In addition, the dynamic background signal is retained from the reference dataset. Hence, the signal intensity of the background also varies over time to model in vivo conditions better.
FIG. 3.
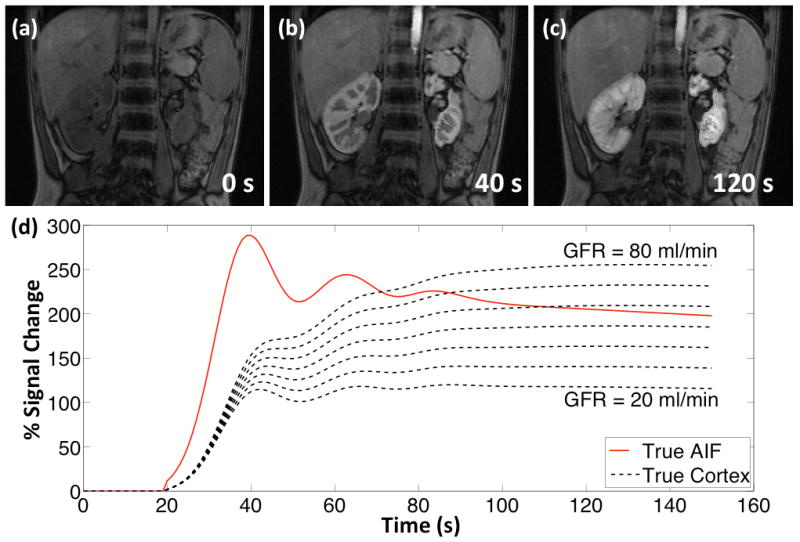
Digital phantom at (a) pre-contrast, (b) cortical enhancement and (c) medullary enhancement phases. (d) The simulated AIF and cortical enhancement curves (20 mL/min to 80 mL/min single kidney GFR).
Digital Phantom Simulations
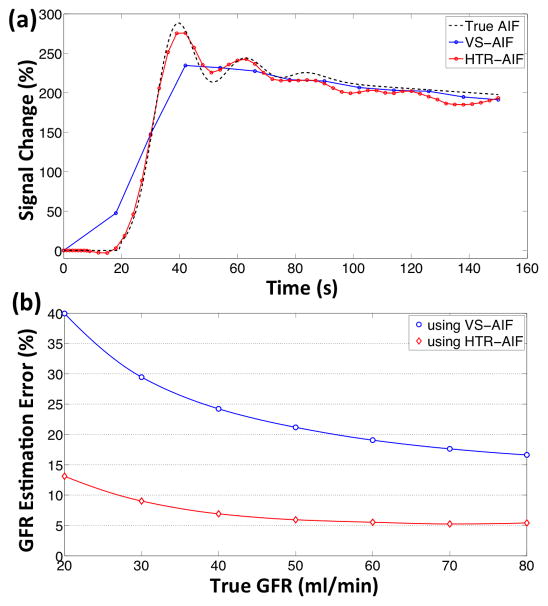
AIF curves estimated by the high temporal resolution method and the view-sharing method are compared to the true AIF of the phantom in Fig. 4a. The root mean square error (RMSE) of the AIF estimation averaged over 12 curves is 0.2059 using the VS method and 0.0932 using the HTR method. This difference in the estimation errors propagates to the GFR estimates through quantitative analysis. The median GFR estimation errors obtained from quantitative analysis using HTR-AIF and VS-AIF are shown in Fig. 4b. This estimation error is smaller when the HTR-AIF curve is used in the analysis as opposed to the VS-AIF. The percent deviation from the true GFR of the digital phantom decreases as the true GFR value increases. In the case of HTR-AIF, the GFR estimation error is less than 10% when the true GFR is above 30 mL/min. The simulated GFR value was overestimated by the HTR-AIF method and underestimated by the VS-AIF method.
FIG. 4.
Digital phantom simulation results: (a) The HTR-AIF and VS-AIF estimates are compared to the true AIF of the phantom (only one of the 12 curves shown), (b) median GFR estimation errors obtained from the quantitative analysis of the simulated phantoms using HTR-AIF and VS-AIF methods.
Clinical Feasibility
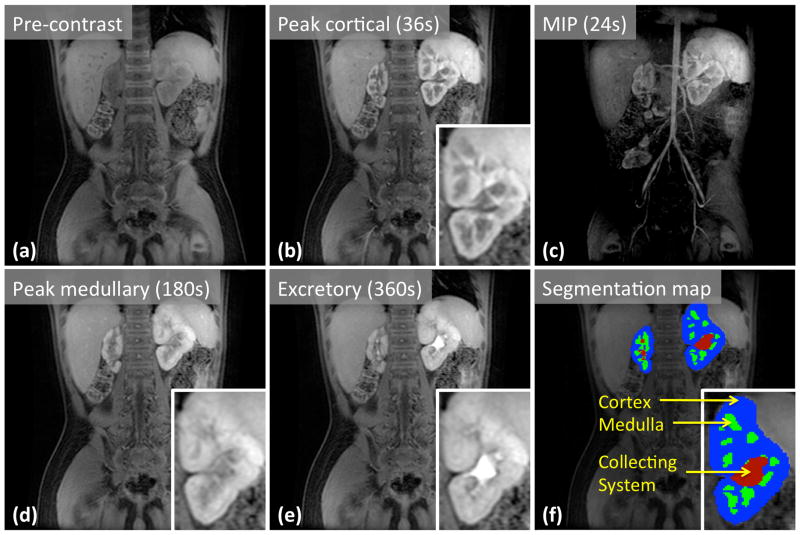
A set of time-series images reconstructed from the navigated DISCO data of the 5-year-old patient is shown in Fig. 5. Diagnostic image quality and the lack of motion artifacts can be seen here, providing evidence of efficacy of the motion artifact mitigation strategy. In this case as well as the other two cases, segmentation of the renal cortices was easily achieved. The temporal resolution and footprint were 12s and 33s, respectively, with a 1.1×1.1×2.7mm3 spatial resolution. Key phases of renal enhancement such as pre-contrast, cortical enhancement, medullary enhancement, and excretory phases are clearly identifiable. In addition, the spatial resolution is high enough to differentiate between the medullary and cortical regions of the kidneys, which is particularly useful for the segmentation of the renal cortex. The use of Dixon fat-water separation also enabled the creation of water-only maximum intensity projection (MIP) images for visualization of the arterial and angiographic phases. A MIP of the temporal phase of 24s (2nd post-contrast phase) clearly shows the enhancing arteries and early medullary enhancement, highlighting the high temporal resolution and also providing an angiographic phase.
FIG. 5.
Selected slices from pre-contrast (a) and post-contrast (b, d, e) images of the 5-year-old patient show different stages of contrast enhancement in kidneys. Maximum intensity projection (c) reveals arteries during the arterial enhancement phase. Panel (f) shows the segmentation map of the kidneys, which is needed for quantitative analysis.
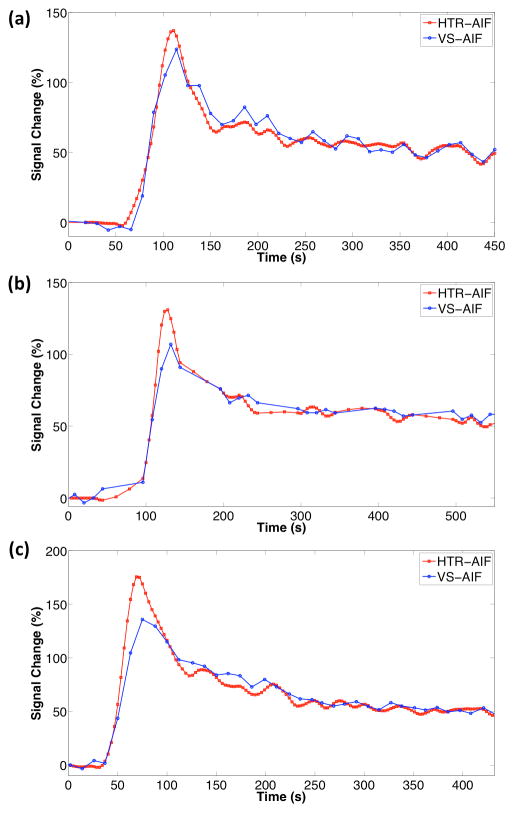
High temporal resolution analysis of the aortic input function was performed on 3 patients and the resulting HTR-AIF curves are shown in Fig. 6 along with the VS-AIF curves. Both AIF estimates were used in quantitative analysis and the resulting GFR estimates are shown in Table 1. In the case of the 5 and 17 year-old subjects, who were scanned at a temporal resolution of 12s (fA = 0.1, M = 3, S = 3), the total GFR estimates with VS-AIF method were lower than the estimates with HTR-AIF method by 25% and 42%, respectively. In the case of the 9 year-old subject who had a higher temporal resolution scan at 9s (fA = 0.1, M = 3, S = 2), the estimations were closer with the VS-AIF method estimating 13% lower values than the HTR-AIF method. The GFR estimates in all cases were higher when the HTR-AIF estimate was used as the aortic input function. The 17 year-old subject, who had the biggest change in GFR, had a cortical signal curve that dropped quickly after the initial rise whereas the cortical signal in other subjects dropped slowly (Sub. Fig. 1). Voxel-by-voxel GFR maps for both HTR-AIF and VS-AIF methods are shown in Fig. 7. Although the range of values was identical for both methods, the maps generated using the HTR-AIF method showed smoother transition from high GFR to low GFR regions of the renal cortex.
FIG. 6.
HTR-AIF and VS-AIF estimates for the 3 clinical cases (a) 5 year old (b) 9 year old (c) 17 year old.
Table 1.
MRU quantitative analysis results of the clinical subjects. Reported GFR values are corrected for body surface area (BSA).
| Patient | Kidney | Vcortex (mL) | GFR with VS-AIF (mL/min/1.73m2) | GFR with HTR-AIF (mL/min/1.73m2) |
|---|---|---|---|---|
| 5 year old | Left | 70 | 31 | 42 |
| Right | 22 | 17 | 22 | |
| 9 year old | Left | 44 | 11 | 12 |
| Right | 74 | 43 | 50 | |
| 17 year old | Left | 79 | 18 | 28 |
| Right | 65 | 20 | 37 |
FIG. 7.
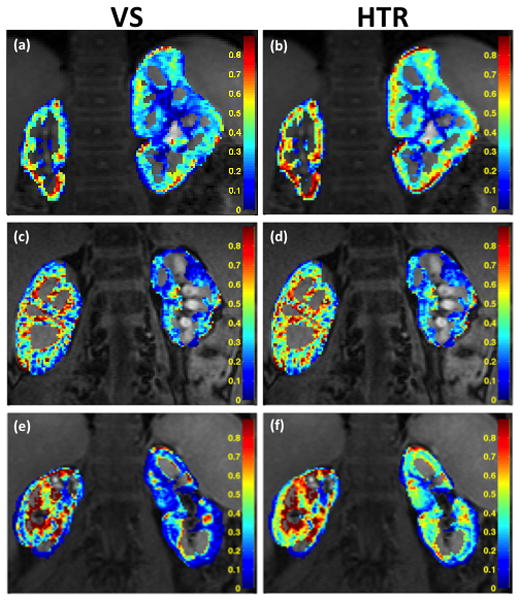
GFR Maps of 5-year-old (a–b), 9-year-old (c–d) and 17-year-old (e–f) subjects calculated using VS-AIF (left column) and HTR-AIF (right column). The reported values are GFR per mL of tissue (k21).
Discussion and Conclusions
In this work, we have demonstrated a method for respiratory-gated dynamic acquisitions with high spatiotemporal resolution, and combined it with a new method for estimating the AIF at a higher temporal resolution than the temporal resolution of the reconstructed images. We also demonstrated feasibility of obtaining good image quality with the method. Direct clinical validation of the quantitative accuracy of this new method in vivo is quite challenging due to the dynamic nature of the arterial flow. It is possible to acquire an additional dataset using a high temporal, low spatial resolution technique on the same patient to verify the accuracy of our HTR-AIF estimate, but this would involve multiple contrast injections separated by sufficient time to permit full clearance of the first injection. Even if we could inject the same patient twice, there is no guarantee that the arterial responses will be the same because AIF depends on multiple factors such as patient heart rate, positioning and resistance of the intravenous catheter, and the level of existing contrast agent in the blood from the previous scan. Hence, we designed a realistic digital phantom for the validation our new technique. The digital phantom simulations accounted for the patient’s respiration by pausing the data acquisition between end-expiratory phases. However, the patient motion from one respiratory cycle to another was ignored. In an actual scan, the respiratory pattern may change over time and the acquired images may shift in position adding extra error to the measurements or requiring an additional image registration step. Since all cases in this study were navigator gated and, hence, motion free, no image registration was performed.
Quantitative DCE-MRI analysis in pediatric patients is quite challenging due to high spatio-temporal requirements and lack of cooperation from the scan subjects for breath holding. Respiratory gating allows the subjects to breathe freely during the scan, but has adverse effects on the temporal resolution and the temporal footprint when using conventional sequences. The use of DISCO enabled us to achieve high spatio-temporal resolution even with the use of respiratory gating. Although the temporal resolution is sufficient for qualitative evaluation of renal function, as seen in Fig. 5, the simulation results in Fig. 4 indicate that respiratory-gated DISCO alone is insufficient for quantitative assessment. In this study, a slow contrast agent injection rate of 0.3 mL/s was used in order to avoid the non-linearity in the signal caused by T2* decay at high gadolinium concentrations. Even with this slow injection protocol, the injection duration of 33 s was comparable to the 12 s temporal resolution and 36 s temporal footprint of our acquisition and reconstruction scheme.
We have attempted to mitigate the adverse temporal effects of respiratory gating by improving the temporal resolution of the AIF. The simulation results show that the proposed HTR-AIF method yields more accurate AIF estimates than the existing view-sharing method. The RMS error of the estimated AIF curves is reduced by 55% with HTR-AIF over VS-AIF. Furthermore, by using these AIFs in the cortical-compartment model, we have shown that GFR estimation accuracy also improved with the HTR-AIF. The median GFR estimation error using HTR-AIF is less than 10% when the simulated GFR is above 27 ml/min. In comparison, for the same range of simulated GFR values the median estimation error with VS-AIF is between 32% and 17%. These results indicate that although the respiratory-gated DISCO alone does not have sufficient temporal performance for quantitative analysis, acceptably accurate GFR estimates can be achieved when it is combined with the HTR-AIF method.
The HTR-AIF estimates shown in Fig. 6 are obtained by analyzing the datasets of clinical subjects. In all cases, the first-pass peak of HTR-AIF is higher than the VS-AIF, as predicted by the digital phantom simulations. The simulation results in Fig. 4a show that the view-sharing method causes temporal blurring, which leads to the underestimation of the first-pass peak. In addition, the simulation results show that HTR-AIF is not only higher in this region but also more accurate. The 3-compartment model used in this study splits the cortical concentration curve into two components: arterial and tubular components. In this model, underestimation of the main AIF peak often leads to underestimation of the GFR. This is caused by the fact that the initial signal rise in the cortex is mostly explained by the arterial signal rise. In order to fit the underestimated arterial peak to the observed cortex signal, the model has to assume a higher blood fraction in the cortex. This artificially increases the weight of the arterial component and reduces the tubular component. Reduced tubular component leads to reduced GFR estimates. This effect was observed in the cortical-compartment model fits of the subjects (Sup. Fig. 1). Quantitative analysis results in patients (Table 1) show that the differences in the first-pass peak region of the AIF estimation may have significant effects on the quantitative analysis results. These differences were predicted by our phantom simulations, and the proposed HTR-AIF method was shown to reduce the GFR estimation errors as seen in Fig. 4b.
The relation between SI and concentration in spoiled gradient echo (SPGR) sequences, such as DISCO, is defined by a non-linear equation (Eq. 4). The concentration of the contrast agent in this study is estimated using the T1 values of blood and kidney tissue reported in literature (11). However, the actual T1 values of the subjects may slightly deviate from the reported values. T1 mapping for each subject may improve the accuracy of the concentration estimates, which in turn may improve the results of the quantitative analysis.
The HTR-AIF smoothing was performed using LOESS method. LOESS smoothing was a suitable choice for this problem, as it does not require a function to model the whole AIF data. Instead, the method fits second-degree polynomials to local regions of the curve to perform smoothing and the smoothing factor αL determines the width of these local regions. There are other options such as weighted moving average filtering that also does not require an underlying model. However, weighted moving average filtering is same as LOESS with zero-degree polynomials and it often does not perform as well as higher-degree polynomial fitting.
The approach we used here is not limited to the DISCO sequence. The HTR-AIF method can be directly applied to similar sequences that rely on view sharing for reconstruction such as TWIST, CAPR and TRICKS. In DISCO and TWIST, the temporal resolution of the HTR image is limited by the respiratory rate of the subject because no data is collected between end-expiratory phases. Recently, other high-spatiotemporal-resolution DCE-MRI sequences based on radially-ordered Cartesian k-space sampling have been described and demonstrated for free-breathing pediatric abdominal MRI (25), and further combined with intrinsic navigation to improve the scan efficiency by employing soft gating in the reconstruction phase (20). One advantage of these approaches is that the data acquisition does not pause for respiration and the extra data collected could be used to improve the temporal resolution of the HTR-AIF further.
The HTR-AIF technique may be improved further by using compressed sensing reconstruction instead of a zero-filled inverse Fourier transform reconstruction. Zero filling missing k-space samples causes aliasing in the image domain. The effect of this aliasing is reduced by the normalization and local regression steps of the HTR-AIF analysis. Compressed sensing may provide results that are more robust by reducing the aliasing before performing the steps described in methods but at the cost of increased reconstruction time and memory requirements. Aliasing reduction in the original image may also reduce the sensitivity to the thresholding factor α although the simulations already indicate a low sensitivity to this factor. For GFR values above 50 ml/min the method is not affected by the choice of α. For low GFR values, choosing smaller values of α yield slightly better estimation errors (Sup. Fig. 2).
In conclusion, we have developed a new technique for pediatric MR urography by incorporating respiratory gating to a view-shared high-spatiotemporal-resolution sequence, and mitigated the adverse temporal effects of respiratory gating by improving the temporal resolution of the AIF in post-processing. We have validated this new technique using digital phantom simulations and demonstrated it on clinical cases. Although our demonstration was limited to MR urography cases, we believe that the presented work can also be adapted for other quantitative analysis applications that make use of an AIF such as pharmacokinetic modeling in oncology.
Supplementary Material
SUP. FIG. S1. The pharmacokinetic model fits are shown for the left kidneys of all 3 subjects. The omitted right kidney results look similar to the ones shown above. The black data points represent the concentration measurements in the cortex. The green curves are the fits calculated by the model. The red and blue dashed curves represent the arterial and tubular components of the fits respectively.
SUP. FIG. S2. The GFR estimation error (%) at different alpha and true GFR values. The dashed line shows the alpha value used in this study.
Acknowledgments
Funding for this research was provided by NIH grants R01-EB009055, R01-EB009690, P41-EB015891 and GE Healthcare.
References
- 1.Wong CJ, Moxey-Mims M, Jerry-Fluker J, Warady BA, Furth SL. CKiD (CKD in Children) Prospective Cohort Study: A Review of Current Findings. American Journal of Kidney Diseases. 2012;60(6):1002–1011. doi: 10.1053/j.ajkd.2012.07.018. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Warady BA, Chadha V. Chronic kidney disease in children: the global perspective. Pediatric Nephrology. 2007;22(12):1999–2009. doi: 10.1007/s00467-006-0410-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Sigmund G, Stoever B, Zimmerhackl LB, Frankenschmidt A, Nitzsche E, Leititis JU, Struwe FE, Hennig J. RARE-MR-urography in the diagnosis of upper urinary tract abnormalities in children. Pediatric radiology. 1991;21(6):416–420. doi: 10.1007/BF02026676. [DOI] [PubMed] [Google Scholar]
- 4.Regan F, Bohlman ME, Khazan R, Rodriguez R, Schultze-Haakh H. MR urography using HASTE imaging in the assessment of ureteric obstruction. AJR American journal of roentgenology. 1996;167(5):1115–1120. doi: 10.2214/ajr.167.5.8911161. [DOI] [PubMed] [Google Scholar]
- 5.Aerts P, Van Hoe L, Bosmans H, Oyen R, Marchal G, Baert AL. Breath-hold MR urography using the HASTE technique. AJR American journal of roentgenology. 1996;166(3):543–545. doi: 10.2214/ajr.166.3.8623625. [DOI] [PubMed] [Google Scholar]
- 6.O’malley ME, Soto JA, Yucel EK, Hussain S. MR urography: evaluation of a three-dimensional fast spin-echo technique in patients with hydronephrosis. AJR American journal of roentgenology. 1997;168(2):387–392. doi: 10.2214/ajr.168.2.9016213. [DOI] [PubMed] [Google Scholar]
- 7.Rohrschneider WK, Haufe S, Wiesel M, Tönshoff B, Wunsch R, Darge K, Clorius JH, Tröger J. Functional and Morphologic Evaluation of Congenital Urinary Tract Dilatation by Using Combined Static-Dynamic MR Urography: Findings in Kidneys with a Single Collecting System1. Radiology. 2002;224(3):683–694. doi: 10.1148/radiol.2243011207. [DOI] [PubMed] [Google Scholar]
- 8.Jones RA, Perez-Brayfield MR, Kirsch AJ, Grattan-Smith JD. Renal Transit Time with MR Urography in Children1. Radiology. 2004;233(1):41–50. doi: 10.1148/radiol.2331031117. [DOI] [PubMed] [Google Scholar]
- 9.Jones RA, Easley K, Little SB, Scherz H, Kirsch AJ, Grattan-Smith JD. Dynamic Contrast-Enhanced MR Urography in the Evaluation of Pediatric Hydronephrosis: Part 1, Functional Assessment. American Journal of Roentgenology. 2005;185(6):1598–1607. doi: 10.2214/AJR.04.1540. [DOI] [PubMed] [Google Scholar]
- 10.Hackstein N, Heckrodt J, Rau WS. Measurement of single-kidney glomerular filtration rate using a contrast-enhanced dynamic gradient-echo sequence and the Rutland-Patlak plot technique. Journal of Magnetic Resonance Imaging. 2003;18(6):714–725. doi: 10.1002/jmri.10410. [DOI] [PubMed] [Google Scholar]
- 11.Tofts PS, Cutajar M, Mendichovszky IA, Peters AM, Gordon I. Precise measurement of renal filtration and vascular parameters using a two-compartment model for dynamic contrast-enhanced MRI of the kidney gives realistic normal values. European Radiology. 2012;22(6):1320–1330. doi: 10.1007/s00330-012-2382-9. [DOI] [PubMed] [Google Scholar]
- 12.Lee VS, Rusinek H, Bokacheva L, Huang AJ, Oesingmann N, Chen Q, Kaur M, Prince K, Song T, Kramer EL, et al. Renal function measurements from MR renography and a simplified multicompartmental model. AJP: Renal Physiology. 2007;292(5):F1548–F1559. doi: 10.1152/ajprenal.00347.2006. [DOI] [PubMed] [Google Scholar]
- 13.Annet L, Hermoye L, Peeters F, Jamar F, Dehoux J-P, Van Beers BE. Glomerular filtration rate: Assessment with dynamic contrast-enhanced MRI and a cortical-compartment model in the rabbit kidney. Journal of Magnetic Resonance Imaging. 2004;20(5):843–849. doi: 10.1002/jmri.20173. [DOI] [PubMed] [Google Scholar]
- 14.Henderson E, Rutt BK, Lee T-Y. Temporal sampling requirements for the tracer kinetics modeling of breast disease. Magnetic resonance imaging. 1998;16(9):1057–1073. doi: 10.1016/s0730-725x(98)00130-1. [DOI] [PubMed] [Google Scholar]
- 15.Lim RP, Shapiro M, Wang EY, Law M, Babb JS, Rueff LE, Jacob JS, Kim S, Carson RH, Mulholland TP, et al. 3D Time-Resolved MR Angiography (MRA) of the Carotid Arteries with Time-Resolved Imaging with Stochastic Trajectories: Comparison with 3D Contrast-Enhanced Bolus-Chase MRA and 3D Time-Of-Flight MRA. American Journal of Neuroradiology. 2008;29(10):1847–1854. doi: 10.3174/ajnr.A1252. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Chandarana H, Block TK, Rosenkrantz AB, Lim RP, Kim D, Mossa DJ, Babb JS, Kiefer B, Lee VS. Free-breathing radial 3D fat-suppressed T1-weighted gradient echo sequence: a viable alternative for contrast-enhanced liver imaging in patients unable to suspend respiration. Investigative radiology. 2011;46(10):648–653. doi: 10.1097/RLI.0b013e31821eea45. [DOI] [PubMed] [Google Scholar]
- 17.Saranathan M, Rettmann DW, Hargreaves BA, Clarke SE, Vasanawala SS. DIfferential subsampling with cartesian ordering (DISCO): A high spatio-temporal resolution dixon imaging sequence for multiphasic contrast enhanced abdominal imaging. Journal of Magnetic Resonance Imaging. 2012;35(6):1484–1492. doi: 10.1002/jmri.23602. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Michaely HJ, Morelli JN, Budjan J, Riffel P, Nickel D, Kroeker R, Schoenberg SO, Attenberger UI. CAIPIRINHA-Dixon-TWIST (CDT)-volume-interpolated breath-hold examination (VIBE): a new technique for fast time-resolved dynamic 3-dimensional imaging of the abdomen with high spatial resolution. Investigative radiology. 2013;48(8):590–597. doi: 10.1097/RLI.0b013e318289a70b. [DOI] [PubMed] [Google Scholar]
- 19.Xu B, Spincemaille P, Chen G, Agrawal M, Nguyen TD, Prince MR, Wang Y. Fast 3D contrast enhanced MRI of the liver using temporal resolution acceleration with constrained evolution reconstruction. Magnetic Resonance in Medicine. 2013;69(2):370–381. doi: 10.1002/mrm.24253. [DOI] [PubMed] [Google Scholar]
- 20.Cheng JY, Zhang T, Ruangwattanapaisarn N, Alley MT, Uecker M, Pauly JM, Lustig M, Vasanawala SS. Free-breathing pediatric MRI with nonrigid motion correction and acceleration: Free-Breathing Pediatric MRI. Journal of Magnetic Resonance Imaging. 2014 doi: 10.1002/jmri.24785. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Song T, Laine AF, Chen Q, Rusinek H, Bokacheva L, Lim RP, Laub G, Kroeker R, Lee VS. Optimal k-space sampling for dynamic contrast-enhanced MRI with an application to MR renography. Magnetic Resonance in Medicine. 2009;61(5):1242–1248. doi: 10.1002/mrm.21901. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Hope TA, Saranathan M, Petkovska I, Hargreaves BA, Herfkens RJ, Vasanawala SS. Improvement of gadoxetate arterial phase capture with a high spatio-temporal resolution multiphase three-dimensional SPGR-dixon sequence: Improvement of Gadoxetate Arterial Phase Capture With a High Spatio-Temporal Resolution Multiphase Three-Dimensional SPGR-Dixon Sequence. Journal of Magnetic Resonance Imaging. 2013;38(4):938–945. doi: 10.1002/jmri.24048. [DOI] [PubMed] [Google Scholar]
- 23.Henderson E, Rutt BK, Lee T-Y. Temporal sampling requirements for the tracer kinetics modeling of breast disease. Magnetic resonance imaging. 1998;16(9):1057–1073. doi: 10.1016/s0730-725x(98)00130-1. [DOI] [PubMed] [Google Scholar]
- 24.Cleveland WS, Devlin SJ. Locally Weighted Regression: An Approach to Regression Analysis by Local Fitting. Journal of the American Statistical Association. 1988;83(403):596. [Google Scholar]
- 25.Zhang T, Cheng JY, Potnick AG, Barth RA, Alley MT, Uecker M, Lustig M, Pauly JM, Vasanawala SS. Fast pediatric 3D free-breathing abdominal dynamic contrast enhanced MRI with high spatiotemporal resolution: Pediatric Free-Breathing Abdominal DCE MRI. Journal of Magnetic Resonance Imaging. 2013 doi: 10.1002/jmri.24551. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Parker GJM, Roberts C, Macdonald A, Buonaccorsi GA, Cheung S, Buckley DL, Jackson A, Watson Y, Davies K, Jayson GC. Experimentally-derived functional form for a population-averaged high-temporal-resolution arterial input function for dynamic contrast-enhanced MRI. Magnetic Resonance in Medicine. 2006;56(5):993–1000. doi: 10.1002/mrm.21066. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
SUP. FIG. S1. The pharmacokinetic model fits are shown for the left kidneys of all 3 subjects. The omitted right kidney results look similar to the ones shown above. The black data points represent the concentration measurements in the cortex. The green curves are the fits calculated by the model. The red and blue dashed curves represent the arterial and tubular components of the fits respectively.
SUP. FIG. S2. The GFR estimation error (%) at different alpha and true GFR values. The dashed line shows the alpha value used in this study.