Treating electrostatics with Wolf summation in combined quantum mechanical and molecular mechanical simulations

Abstract

The Wolf summation approach [D. Wolf et al., J. Chem. Phys. 110, 8254 (1999)], in the damped shifted force (DSF) formalism [C. J. Fennell and J. D. Gezelter, J. Chem. Phys. 124, 234104 (2006)], is extended for treating electrostatics in combined quantum mechanical and molecular mechanical (QM/MM) molecular dynamics simulations. In this development, we split the QM/MM electrostatic potential energy function into the conventional Coulomb r⁻¹ term and a term that contains the DSF contribution. The former is handled by the standard machinery of cutoff-based QM/MM simulations whereas the latter is incorporated into the QM/MM interaction Hamiltonian as a Fock matrix correction. We tested the resulting QM/MM-DSF method for two solution-phase reactions, i.e., the association of ammonium and chloride ions and a symmetric SN₂ reaction in which a methyl group is exchanged between two chloride ions. The performance of the QM/MM-DSF method was assessed by comparing the potential of mean force (PMF) profiles with those from the QM/MM-Ewald and QM/MM-isotropic periodic sum (IPS) methods, both of which include long-range electrostatics explicitly. For ion association, the QM/MM-DSF method successfully eliminates the artificial free energy drift observed in the QM/MM-Cutoff simulations, in a remarkable agreement with the two long-range-containing methods. For the SN₂ reaction, the free energy of activation obtained by the QM/MM-DSF method agrees well with both the QM/MM-Ewald and QM/MM-IPS results. The latter, however, requires a greater cutoff distance than QM/MM-DSF for a proper convergence of the PMF. Avoiding time-consuming lattice summation, the QM/MM-DSF method yields a 55% reduction in computational cost compared with the QM/MM-Ewald method. These results suggest that, in addition to QM/MM-IPS, the QM/MM-DSF method may serve as another efficient and accurate alternative to QM/MM-Ewald for treating electrostatics in condensed-phase simulations of chemical reactions.

I. INTRODUCTION

Reliable simulation of condensed-phase chemical processes requires a reactive potential energy function and a proper treatment of long-range electrostatic interactions. The ability of computer models to describe bond rearrangements can be conveniently introduced, in a multiscale manner, through the use of combined quantum mechanical and molecular mechanical (QM/MM) potentials.^1,2 How to treat long-range electrostatics in the QM/MM framework, however, has remained a challenging issue despite intensive development efforts over the past decade.³ Beyond the simple cutoff schemes,⁴ several methods for computation of long-range electrostatic interactions in QM/MM calculations are available; these include the Ewald method (in diverse versions),^5–11 the generalized solvent boundary potential (GSBP) method,^12–16 the mean-field embedding method,¹⁷ the isotropic periodic sum (IPS) method,^18–21 and more recently the long-range electrostatic correction (LREC) method.²² The merits and caveats of these methods have been discussed previously;^3,21 therefore, interested readers are referred to these works and references therein for details.

Among these long-range electrostatic QM/MM treatments, QM/MM-Ewald has been considered the most sophisticated and reliable method; however, explicit summation over an infinite system with imposed lattice periodicity makes the method time consuming. A potentially more cost-effective alternative is the QM/MM-IPS method recently introduced by us,²¹ which is a QM/MM extension of the cutoff-based classical IPS algorithm developed by Wu and Brooks.^18–20 The combination of QM/MM and IPS results in a linear scaling electrostatic treatment, compared with the QM/MM-Ewald algorithm which scales at best to Nlog(N) (N being the number of particles). In the QM/MM-IPS treatment, the long-range electrostatic contributions are introduced in a mean field manner into the Fock matrix as a correction term. Based on our benchmark studies, the QM/MM-IPS method shows good agreement with the standard QM/MM-Ewald technique for solution-phase reactions such as ion associations and the symmetric group transfer between ions.²¹

In contrast to the relatively limited number of ways in handling QM/MM electrostatics, more alternatives to Ewald summation have been explored for classical MM potentials. Besides the IPS method, a variety of cutoff-based algorithms, collectively referred to as non-Ewald methods,²³ has been developed for computation of electrostatics in classical simulations. These include the reaction field method,^24,25 the Wolf summation²⁶ and variants,^27–30 the zero dipole (ZD) summation method,³¹ CHARMM switching/shifting functions,^32,33 and a series of methods under the generalized shifted force (SF) scheme.^32,34–37

An important line in the development of non-Ewald methods is along the insightful work of Wolf et al.,²⁶ who traced the origin of artifacts in simple electrostatic truncation to the existence of net charges within the cutoff spheres. To overcome this problem, Wolf et al. devised a charge neutralization scheme where a counter charge is placed at the surface of cutoff spheres so that the compensated system contains zero charge (ZC) upon spherical truncation.²⁶ The ZC treatment is in effect similar to shifting the pairwise electrostatic potential to zero at the cutoff distance but includes an important self-energy term arising from the neutralization potential. Wolf et al. further showed that convergence of computating electrostatic energy of Madelung crystals can be accelerated by damping the short-range interactions using a complementary error function (erfc). After the self-energy term is properly handled, this results in the method known as Wolf summation.²⁶

Noticing an inconsistency between the energy derivative and the suggested force expression in Wolf summation due to a questionable assumption on commutation of limit and derivative operators, Zahn et al.²⁷ proposed a potential form that back-integrates the Wolf force to remedy such incompatibility, which was expected to yield better energy conservation in molecular dynamics (MD) simulations. Combining the damping function²⁶ of Wolf et al. and a shifted force function,³⁴ Fennell and Gezelter²⁸ further revised the method of Zahn et al. to ensure energy and force continuities at the cutoff distance in a consistent manner, which resulted in the damped-shifted-force (DSF) formalism.

Newer developments based on the Wolf scheme include “force-switching Wolf” (FSw-Wolf)³⁸ of Yonezawa et al., the ZD approach of Fukuda et al. that extends the idea of cutoff sphere neutralization from monopole to dipole,³¹ the “long-range Wolf” method,²⁹ in which the compensation charge monopole is replaced by a Gaussian charge distribution in conjunction with “dipole neutralization”, and most recently Fanouragakis’ polynomial damping functions instead of error functions for splitting the short- and long-range interactions in Wolf summation.³⁰ Despite the popularity of the method, we note that the related developments and applications have so far been limited to classical mechanics; therefore, the performance of Wolf summation to describe long-range electrostatics for chemically reactive systems, which require uses of quantum mechanical potentials, remains unknown.

In a recent assessment of the IPS method,³⁹ we found that the IPS method can provide similar accuracy to Wolf summation in computing the electrostatic energy for crystal lattice in the classic Madelung problem. Taken together with the good performance of the QM/MM-IPS method in simulating reactions in solution,²¹ these observations have motivated us to investigate the effectiveness of Wolf summation for treating electrostatics in QM/MM simulations of chemical reactions.

We focus here on the DSF formalism of Wolf summation for our QM/MM development. From a methodological standpoint, the DSF method is especially suitable for MD simulations by providing consistent energy and forces — both are continuous across the cutoff boundary. It also has a simple pairwise potential energy expression which can be readily split into Coulombic and damped shifted force parts when handling QM/MM electrostatic interactions (see Sec. II). On the practical aspect, the DSF methods have been demonstrated to reproduce well the static and dynamic properties for a number of non-reactive systems, including SPC/E water,²⁸ ionic molten salt systems,^28,36 polyelectrolyte brushes,⁴⁰ liquid-vapor interfaces,⁴¹ and short peptides in explicit water.⁴² These studies have provided positive motivation for making the DSF treatment compatible with QM/MM potentials for simulating reactive systems.

In this work, we extend the classical DSF method for combined QM/MM simulations at the semiempirical QM level. The paper is organized as follows. In Section II, we first give a brief description of the classical DSF method, then present the detailed formalism of the QM/MM-DSF method. Section III contains simulation protocols for testing the method. The reliability and efficiency of the QM/MM-DSF method are demonstrated in Section IV, where we compare the new method with the existing QM/MM-Ewald, QM/MM-Cutoff, and QM/MM-IPS methods based on free energy simulations of two solution-phase chemical reactions. Section V provides the concluding remarks.

II. THEORY

A. Classical DSF

For the purpose of derivation, it is convenient to write the pairwise electrostatic potential energy under the DSF treatment²⁸ as

$${\displaystyle {ϵ}_{ij}^{\text{DSF}}(r_{ij},R_{\text{c}})=\left\{\begin{array}{ll}{ϵ}_{ij}\left(r_{ij}\right)+{\varphi }_{ij}^{\text{DSF}}(r_{ij},R_{\text{c}})\hfill & \text{if }{r}_{ij}\le R_{\text{c}}\hfill \\ 0\hfill & \text{otherwise}\hfill \end{array},\right.}$$ (1)

where R_c is the size of the cutoff sphere, ϵ_ij(r_ij) = q_iq_j/r_ij is the electrostatic energy (in the canonical Coulombic form) between charges q_i and q_j separated at a distance of r_ij, and

$${\displaystyle {\varphi }_{ij}^{\text{DSF}}(r_{ij},R_{\text{c}})=q_i{q}_j\left[-\frac{\mathrm{erf}\left(\alpha r_{ij}\right)}{r_{ij}}-\frac{\mathrm{erfc}\left(\alpha R_{\text{c}}\right)}{R_{\text{c}}}+\left(\frac{\mathrm{erfc}\left(\alpha R_{\text{c}}\right)}{R_{\text{c}}^2}+\frac{2\alpha }{{\pi }^{1/2}}\frac{\exp (-{\alpha }^2{R}_{\text{c}}^2)}{R_{\text{c}}}\right)(r_{ij}-R_{\text{c}})\right]}$$ (2)

is a contribution referred to here as the DSF potential that accounts for the effect of the damped shifted force boundary conditions. In Eq. (2), the error function (erf) term (after being combined with 1/r_ij in ϵ_ij) yields the damped Coulomb potential, with α being a damping parameter in the unit of Å⁻¹, whereas the first erfc term shifts the potential for charge neutralization; the sum associated with r_ij − R_c arises from the first derivative of the damped shifted potential to achieve continuous forces across the cutoff boundary. For convenience, we further introduce the reduced pair potentials ${\overline{ϵ}}_{ij}^{\text{DSF}}$ and ${\overline{\varphi }}_{ij}^{\text{DSF}}$, which are defined as the corresponding potentials in Eqs. (1) and (2) divided by the product of charges q_iq_j. The use of these reduced pair potentials will be shown below when we introduce the QM/MM-DSF method.

B. QM/MM-DSF

Following a derivation similar to that in Refs. 10 and 21, we construct an effective total Fock matrix (F^tot) by including the DSF potential through a correction term,

$${\displaystyle {\mathbf{F}}^{\text{tot}}={\mathbf{F}}^{\text{LcR}}+\mathrm{\Delta }{\mathbf{F}}^{\text{DSF}},}$$ (3)

where the first term on the right-hand side (r.h.s.) of Eq. (3) denotes the local-region (LcR) contribution from the Coulomb potential ϵ_ij(r_ij) and the second term contains the corrections to the Coulomb potential originating from the damped shifted force potential ${\varphi }_{ij}^{\text{DSF}}(r_{ij},R_{\text{c}})$. It should be noted that the DSF corrections are not long-range in nature per se (as the “long-range” term separated from the “short-range” damped interaction is considered small and omitted in the Wolf method²⁶) although they include the effects of the boundary conditions to the damped Coulomb potential.²⁸

The corresponding Fock matrix elements in Eq. (3) are expressed as

$${\displaystyle F_{\mu \nu }^{\text{LcR}}=\frac{\partial E^{\text{LcR}}(\rho ,\mathbf{q})}{\partial {\rho }_{\mu \nu }}}$$ (4)

and

$${\displaystyle \mathrm{\Delta }{F}_{\mu \nu }^{\text{DSF}}=\frac{\partial \mathrm{\Delta }{E}^{\text{DSF}}(\mathbf{Q},\mathbf{q})}{\partial {\rho }_{\mu \nu }},}$$ (5)

where the partial derivatives in Eqs. (4) and (5) are made with respect to the electronic density matrix elements ρ_μν associated with atomic orbital basis functions μ and ν. In Eq. (4), ρ (without subscripts) represents the charge density distribution associated with the QM wavefunction and q a collection of MM point charges. To obtain the DSF correction term to the Fock matrix elements, the charge distribution ρ is approximated in Eq. (5) as monopoles using Mulliken charges,⁴³ denoted by Q. The operational form of the DSF energy contribution can be written as

$${\displaystyle \mathrm{\Delta }{E}^{\text{DSF}}=\frac{1}{2}\sum _{\alpha }^{N_{\text{QM}}}\sum _{\beta }^{N_{\text{QM}}}{Q}_{\alpha }{Q}_{\beta }{\overline{\varphi }}_{\alpha \beta }^{\text{DSF}}(r_{\alpha \beta },R_{\text{c}})+\sum _{\alpha }^{N_{\text{QM}}}\sum _{\gamma }^{N_{\text{MM}}}{Q}_{\alpha }{q}_{\gamma }{\overline{\varphi }}_{\alpha \gamma }^{\text{DSF}}(r_{\alpha \gamma },R_{\text{c}}),}$$ (6)

with α, β running over QM atoms (N_QM in total) and γ over MM atoms (N_MM in total). ${\overline{\varphi }}_{ij}^{\text{DSF}}(r_{ij},R_{\text{c}})$ denotes the reduced DSF pair potential between generalized charges i and j (i, j ∈ αβγ). It is important to note that the present implementation considers self energies. For QM charges, self energies are included in Eq. (6) through monocentric interactions when one takes the limit of ${\overline{\varphi }}_{ij}^{\text{DSF}}$ [the charge-independent part of Eq. (2)] as r_ij → 0.

The nuclear gradients in the QM/MM-DSF method can be derived following a similar procedure used in formulating the QM/MM-IPS method;²¹ contributions from the error function related terms can be obtained by differentiating “erf” and “erfc” with respect to the inter-atomic distance and then apply the chain rule. Note that gradients of the Mulliken charges on the QM particles are not considered explicitly when Eq. (6) is differentiated because these QM charges are obtained from variationally optimized wavefunctions in semiempirical QM/MM-DSF calculations under the neglect of diatomic differential overlap (NDDO) approximation.⁴⁴

C. Nonbonded list determination for QM/MM electrostatic interactions

A group-based non-bonded scheme previously introduced^10,21 is used to determine QM/MM electrostatically interacting pairs in Eq. (6). In this group-based scheme, whenever a MM group is found within the cutoff distance of any QM group, that MM group is included in the QM/MM electrostatic interaction to polarize the entire QM subsystem consistently. Thus, in this scheme, the distance between individual QM and MM groups could be greater than the pre-set cutoff distance. For a compatible treatment in QM/MM-DSF, we adopt a convention that allows the DSF potential to be defined by Eq. (2) beyond the cutoff distance R_c. This treatment allows Eq. (6) to be used consistently with the group-based QM/MM scheme, and the desired energy and force continuities at the cutoff boundary are also retained. As shown in the supplementary material,⁴⁵ the extra contribution beyond R_c to the DSF potential is small in magnitude and decreases rapidly as the cutoff radius increases. The use of the DSF potential in an extended range is further justified numerically (in Fig. S1 of the supplementary material⁴⁵).

III. SIMULATION DETAILS

Simulations were performed with a customized version of Chemistry at HARvard Macromolecular Mechanics³³ software (CHARMM version c36a1) together with the MOPAC⁴⁶ module for quantum mechanical calculations. We tested the QM/MM-DSF method by computing the potential of mean force (PMF) profiles of two chemical reactions in aqueous solution: (1) the association of ammonium and chloride ions ($[{\text{NH}}_4^{+}\dots {\text{Cl}}^{-}]$) and (2) a symmetric SN₂, Finkelstein, reaction for the methyl group transfer between two Cl ions,^17,47

$${\displaystyle \left[{\text{ClCH}}_3\right]+{\text{Cl}}^{-}\to {\text{Cl}}^{-}+\left[{\text{CH}}_3\text{Cl}\right].}$$ (7)

Then we compared our results with those from the QM/MM-Ewald, QM/MM-Cutoff, and QM/MM-IPS simulations. The semiempirical PM3^48,49 and AM1⁵⁰ methods were used as the QM level for the ion association and SN₂ reactions, respectively. Langevin dynamics was performed for both systems with a friction coefficient of 50 ps⁻¹ and an integration time step of 1 fs (0.5 fs for the SN₂ system) at the temperature of 298 K. A cubic box of 40 Å in size was used to solvate the reactants with modified TIP3P⁵¹ water molecules. In the QM/MM-Ewald simulations, κ = 0.34 Å⁻¹ was used for the width of Gaussian screening and the summation among pure MM charges was performed using particle mesh Ewald⁶ (PME) on a FFT grid of 50 × 50 × 50 (64 × 64 × 64 for the SN₂ reaction) with the same κ parameter.

Umbrella sampling⁵² simulations were conducted to obtain the PMF profiles with similar values of the parameters as in Ref. 21. For each umbrella window, unless otherwise stated, the systems were first equilibrated for 30 ps and then followed by 50 ps simulations for data production. This simulation scheme seems to be sufficient for PMF simulations here based on comparison with other schemes using extended simulation time.⁴⁵ The reaction coordinate for the ammonium/chloride ion-association system was chosen as the distance between the N and Cl atoms while for the SN₂ reaction the reaction coordinate was defined as

$${\displaystyle X^{\text{R}}=r_{\mathrm{Cl-C}}-r_{\mathrm{C-Cl}}.}$$ (8)

The weighted histogram analysis method (WHAM)⁵³ was used to compute PMF. In the QM/MM-DSF simulations, we used a damping parameter of α = 0.2/Å for the DSF potential. This value was shown to yield good convergence and numerical accuracy for Madelung energy on NaCl crystals in our previous study³⁹ and is also in close agreement with the optimal value of 2/R_c (with an R_c of 10–12 Å) suggested by Demontis et al.⁵⁴ for Wolf summation.

IV. RESULTS AND DISCUSSION

A. Association of ammonium and chloride ions

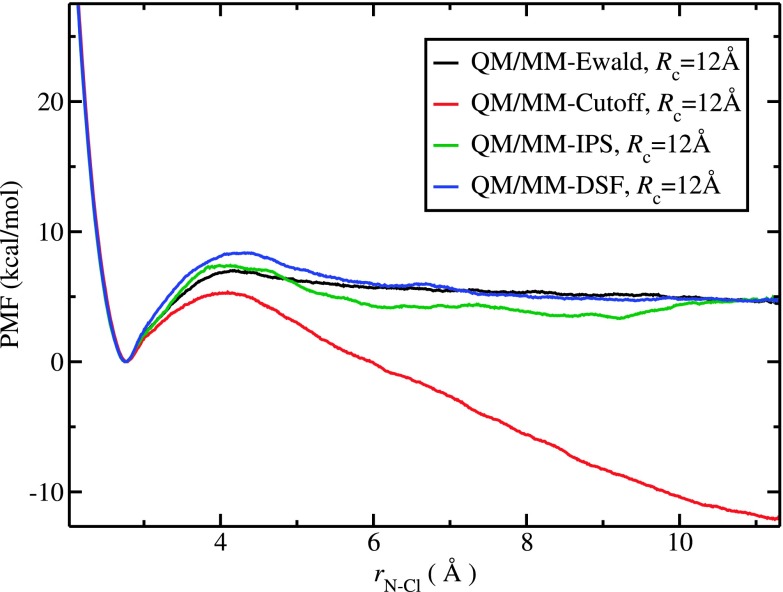
PMF profiles for the ion association reaction computed using various QM/MM electrostatic treatments are plotted in Fig. 1. Qualitatively, all four methods predict a barrier that is likely associated with transition between a contact ion pair (CIP) and a solvent shared ion pair (SSHIP).⁵⁵ The QM/MM-Ewald and QM/MM-IPS show similar barrier heights of 7.0 kcal/mol and 7.3 kcal/mol at 4.2 Å (for R_c = 12 Å). The QM/MM-DSF method gives a higher free energy barrier of 8.3 kcal/mol while QM/MM-Cutoff reports a lower value of 5.2 kcal/mol. Only QM/MM-Cutoff shows a free energy profile with a spurious linear drift; such an artifact has been reported in earlier work,^10,21 and primarily attributed to the lack of long-range electrostatic interactions in the QM/MM-Cutoff treatment.

FIG. 1.

PMF profiles for $[{\text{NH}}_4^{+}\dots {\text{Cl}}^{-}]$ ion association using QM/MM-Ewald, QM/MM-Cutoff, QM/MM-IPS, and QM/MM-DSF methods with R_c = 12 Å. Similar to long-range methods such as QM/MM-Ewald and QM/MM-IPS, the QM/MM-DSF treatment eliminates the artificial free energy drift found in QM/MM-Cutoff. The PMF produced from the QM/MM-DSF simulations is in close agreement with that from the cutoff-based long-range method QM/MM-IPS.

Nam et al.¹⁰ provided a plausible explanation of the free energy drift by reasoning that during ion separation the water molecules found in the outskirt region of one ion center would be more likely to be excluded from the cutoff sphere of the other ion than are the waters located between the two ions. For the case of separating two opposite charges, the solvent dipoles aligned between the ions are favorable for both ions whereas the alignment of outskirt solvent molecules tends to be favorable only for the nearby ion but unfavorable for the distant one. Consequently, when the two oppositely charged ions are moving away from each other, unfavorable solute-solvent interactions within the cutoff spheres are lost more rapidly than favorable interactions, thereby generating artificial free energy stabilization at greater ion-separation distances. This explanation is consistent with the observation that when two charged groups of the same sign are simulated, the PMF of separation tends to drift upward instead.¹⁰

Although the artificial drift has been interpreted in general as an imbalance between the short- and long-range interactions, we suspect that this is specifically caused by the use of a spherical cutoff and the way QM/MM electrostatic interactions are truncated. In the QM/MM-Cutoff method implemented in CHARMM, the QM/MM electrostatic interactions (i.e., the polarization of the QM wavefunction by MM partial charges) are approximated by two-center two-electron integrals, with the MM charges treated as charge densities in notional s basis functions.⁴ Attenuation of polarization at the cutoff sphere boundary of a QM center is then introduced by applying a switching function at the electronic integral level based on the distance between the QM and MM centers hosting their basis functions.⁴ When the QM subsystem contains large-sized fragments, such a treatment may lead to spurious polarization effects as it prevents the delocalized QM wavefunction from being polarized consistently by its MM environment. In this line of reasoning, the artificial drift observed could be more directly related to the use of the atom-based switching functions for QM/MM interactions. Whether the free energy drift can be deemed as a manifestation of the long-range nature of 1/r that decays slowly over distance may need further scrutiny and investigations.

The QM/MM-DSF method seems to be able to remove the artificial drift despite the fact that the Wolf method does not explicitly contain the long-range term corresponding to the reciprocal sum in Ewald. The use of erf-damped potential in Wolf summation (as well as in DSF) formally resembles the real-space sum in Ewald, but with an important difference by including the shifted potential to achieve charge neutralization.²⁶ It has been shown that an effective “molecular” Coulomb potential decays as rapidly as 1/r⁵ in Madelung crystals.⁵⁶ Similar screening effects, which have been suggested as a general phenomenon in condensed-phase and disordered systems,^23,26 would make electrostatic interactions in such systems rather short-ranged. Interestingly, the simulated PMF of ion-separation in Fig. 1, taking the QM/MM-Ewald result as the most realistic representation of the physical system, seems to support the idea that the effective electrostatic interaction between two charged groups is indeed short-ranged in solution, as the PMF quickly becomes flat beyond r = 6 Å, which is much shorter than the cutoff distance used in the present and typical molecular simulations. Furthermore, Wolf et al. have demonstrated numerically that when charge neutralization is included properly in the damped Wolf summation, the long-range contribution that corresponds to the reciprocal sum in Ewald becomes small and can be neglected.²⁶ Therefore, it is not too surprising that the Wolf-type method captures some of the long-range electrostatic effects, as suggested by both the underlying physics of the method and our QM/MM-DSF simulation results.

Interestingly, the PMF profiles from the QM/MM-DSF and QM/MM-IPS simulations share a common saturation value of ∼5 kcal/mol at distances larger than ∼10 Å (Fig. 1). We ascribe this success in part to the use of a group-based scheme of QM/MM interaction. As we mentioned in Sec. II, our implementation allows the damped shifted force potential in Eq. (1) to be used beyond the cutoff radius. Treating QM/MM electrostatics with DSF potential in an extended range is especially advantageous in simulations with the group-based non-bonded interaction scheme in our case. The use of extended-range DSF potential allows our method to describe QM/MM polarization in a more balanced way. As we discussed in Sec. II, the extra contribution due to the extended treatment is expected to be small and decreases rapidly with increasing cutoff radius. Thus, we expect that the PMF profiles from QM/MM-DSF simulations with greater cutoff R_c’s would agree even better with the QM/MM-Ewald results. In Fig. S2 of the supplementary material, we show that this is indeed the case.⁴⁵

B. Symmetric SN₂ exchange reaction

For the SN₂ reaction studied here, accurate treatment of long-range electrostatics may play an especially important role. In a previous work, we studied a similar but neutral system, in which formation of the transition state annihilates the molecular dipole moment if symmetry is imposed.³⁹ For such a system solvated in polar solvent, the electrostatic stabilization of the reactant-complex would be stronger than that of the transition state, making the solution-phase free energy barrier higher than in vacuum. Similarly, for the present system, a quantitative description of the solvation barrier and hence the overall PMF profiles are also expected to be sensitive to how the QM/MM electrostatics is treated.

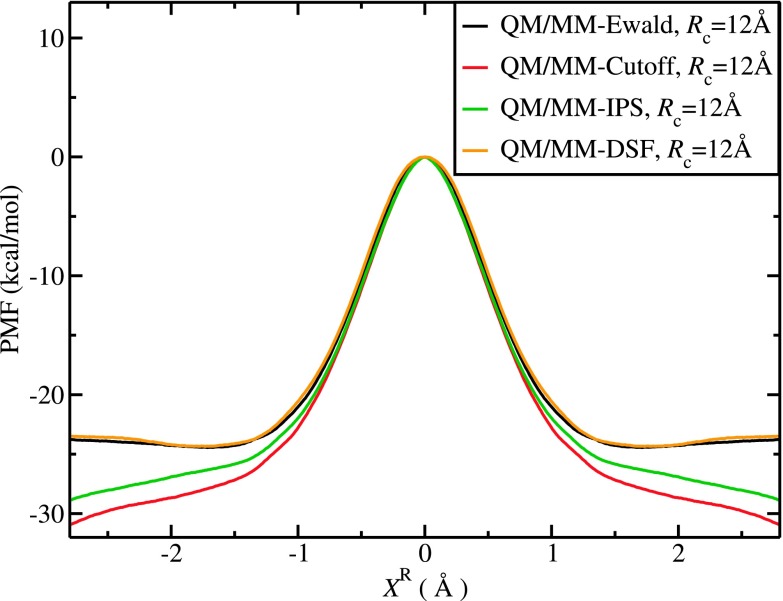
In Fig. 2, we compare the simulated PMF profiles for this SN₂ exchange reaction with different QM/MM electrostatic treatments. Because not all methods locate a stable ion-dipole complex in the reactant regions, here we chose to normalize the PMFs at the barrier top for comparison. The overall shape of the PMFs in the region of −0.7 Å < X^R < 0.7 Å is similar for all methods, but a significant difference was observed for larger distances. The agreement between QM/MM-DSF and QM/MM-Ewald is encouraging; indeed, the QM/MM-DSF reproduces the QM/MM-Ewald result so well that the difference between the two PMFs is within 0.1 kcal/mol, over the entire reaction coordinate range, including the reactant basin at ±1.7 Å. On the other hand, the QM/MM-Cutoff PMF exhibits a large deviation of 3.5 kcal/mol from the QM/MM-Ewald curve at ±1.7 Å and also displays a linear drift at larger distances. This deviation may primarily be attributed to the absence of long-range electrostatics in the QM/MM-Cutoff method. Although the QM/MM-IPS PMF shows a similar linear drift, the deviation from the QM/MM-Ewald result is significantly reduced to 1.8 kcal/mol. We attribute the linear drift observed in the QM/MM-IPS result to the relatively small cutoff distance R_c; for the present system which has a net charge, it may require a larger cutoff distance to satisfy the “isotropic periodic” assumption in the IPS treatment. We have tested this hypothesis by increasing the cutoff distance in QM/MM-IPS. As shown in Fig. S3 of the supplementary material, the PMF from QM/MM-IPS simulations quickly approaches the QM/MM-Ewald result when a slightly longer cutoff of R_c = 14 Å is used.⁴⁵

FIG. 2.

PMF profiles for the symmetric SN₂ reaction (ClCH₃…Cl⁻) using the QM/MM-Ewald, QM/MM-Cutoff, QM/MM-IPS, and QM/MM-DSF methods with R_c = 12 Å. The free energy barrier height obtained by the QM/MM-DSF method deviates from that of QM/MM-Ewald by <0.1 kcal/mol.

Better agreement of the QM/MM-DSF method to the QM/MM-Ewald benchmark for this particular system can be traced back to the original formulations of these models. The DSF treatment is based on charge neutrality (and force continuity) while the IPS method assumes homogeneous distributions of charges. For charged systems, such as the present SN₂ reaction, the local environment can be highly anisotropic. Based on our results in Fig. 2 and Fig. S3 of the supplementary material,⁴⁵ both the QM/MM-DSF and QM/MM-IPS methods are able to eliminate the unwanted linear free energy drift seen in QM/MM-Cutoff simulations; however, a greater cutoff distance is needed for QM/MM-IPS to achieve the similar performance of QM/MM-DSF.

C. Computational efficiency

The average central processing unit (CPU) times (on a single processor) for simulations of the ammonium/chloride and SN₂ systems using a cutoff radius of R_c = 12 and 14 Å are listed in Table I and compared among various methods.⁵⁷ The QM/MM-Ewald method, although considered to give the highest level of accuracy, is most time consuming due to explicit summation over periodic lattice. On average, the QM/MM-Ewald simulations are 4.3 times more expensive than the QM/MM-Cutoff simulations. In contrast, the QM/MM-DSF method eliminates the artificial PMF drift of ion association in the QM/MM-Cutoff method by only increasing the computational cost by ∼2.0 times, comparable to the cost-effectiveness of the QM/MM-IPS method, which removes the artificial drift at 1.5 times the cost of the QM/MM-Cutoff method. The relative cost of QM/MM-DSF versus other cutoff-based methods seems to depend on the specific implementation of the error-function related terms in the DSF potential and derivatives.⁴⁵ In our implementation, the way group-based QM/MM interactions are handled also likely contributes to the cost difference. For QM/MM-DSF, pairwise interactions are computed in the extended “non-spherical” region, while in QM/MM-IPS a switching function is applied at R_c, which effectively creates a “spherical” boundary that includes fewer interacting pairs.²¹

TABLE I.

CPU times of 80 ps QM/MM MD simulations using various QM/MM electrostatic treatments (time in hours).

${\mathrm{NH}}_4^{+}\dots {\mathrm{Cl}}^{-}$
Rc (Å)	Ewalda	Cutoff	IPS	DSF
12	17.84	3.55	5.46	6.89
14	20.22	5.49	8.78	11.23
ClCH3…Cl−
Rc (Å)	Ewalda	Cutoff	IPS	DSF
12	18.80	3.80	5.71	7.18
14	21.38	5.86	9.18	11.69

^aParticle-mesh Ewald (PME) is used for treating MM/MM electrostatic interactions in the QM/MM-Ewald simulations.

On the other hand, comparison between the QM/MM-DSF and QM/MM-Ewald method is very encouraging. Although the QM/MM-Ewald method offers a more rigorous way to describe long-range electrostatics, explicit lattice summation in QM/MM-Ewald makes it about three and two times more expensive than the QM/MM-IPS and QM/MM-DSF method for the systems tested here. Based on the current work, the QM/MM-DSF methods can reproduce the PMF performance of the QM/MM-Ewald simulations without explicit lattice summation, reducing the computational cost by ∼55%.

Finally, compared with the QM/MM-IPS method, which incorporates long-range electrostatics using a very different strategy, the QM/MM-DSF method provides similar results and efficiency. Taken together, these results suggest that QM/MM-DSF, in addition to QM/MM-IPS, may be used as another efficient and accurate pairwise alternative to QM/MM-Ewald in describing long-range electrostatic interactions in simulating chemical reactions in condensed phases.

V. CONCLUDING REMARKS

In this contribution, we have accomplished an extension of the classical Wolf electrostatic treatment (in the DSF formalism) for MD simulations based on combined QM/MM potential energy functions. Based on the two chemical reactions studied, the QM/MM-DSF method shows good performance in removing the artificial free energy drift seen in the QM/MM-Cutoff simulations, thereby producing results in quantitative agreement with those from the long-range explicit methods such as QM/MM-Ewald and QM/MM-IPS. Considering this encouraging performance and a more than twofold speed-up compared to the QM/MM-Ewald method, this work may stimulate further tests and applications of the QM/MM-DSF method to simulations of other complex condensed-phase reactive processes, such as enzyme reactions.