Toward Understanding the Size Dependence of Shape Features for Predicting Spiculation in Lung Nodules for Computer-Aided Diagnosis

Abstract

We analyze the importance of shape features for predicting spiculation ratings assigned by radiologists to lung nodules in computed tomography (CT) scans. Using the Lung Image Database Consortium (LIDC) data and classification models based on decision trees, we demonstrate that the importance of several shape features increases disproportionately relative to other image features with increasing size of the nodule. Our shaped-based classification results show an area under the receiver operating characteristic (ROC) curve of 0.65 when classifying spiculation for small nodules and an area of 0.91 for large nodules, resulting in a 26 % difference in classification performance using shape features. An analysis of the results illustrates that this change in performance is driven by features that measure boundary complexity, which perform well for large nodules but perform relatively poorly and do no better than other features for small nodules. For large nodules, the roughness of the segmented boundary maps well to the semantic concept of spiculation. For small nodules, measuring directly the complexity of hard segmentations does not yield good results for predicting spiculation due to limits imposed by spatial resolution and the uncertainty in boundary location. Therefore, a wider range of features, including shape, texture, and intensity features, are needed to predict spiculation ratings for small nodules. A further implication is that the efficacy of shape features for a particular classifier used to create computer-aided diagnosis systems depends on the distribution of nodule sizes in the training and testing sets, which may not be consistent across different research studies.

Introduction

The American Cancer Society estimates that in 2013, there were approximately 228,190 new cases of lung cancer and 159,480 related deaths [1]. Computer-aided diagnosis (CAD) systems that provide a second opinion to radiologists may be important for wide implementation of computed tomography (CT) screening exams that can enhance early detection of lung cancer and improve survival rates [2]. Prototype CAD systems have already been shown to improve radiologist performance in a research context [3, 4].

In addition to providing a second opinion about the malignancy of the nodule, a CAD system can also be designed to provide supplementary information to the radiologist about semantic characteristics of the nodule, such as its shape and size. For example, the Lung Image Database Consortium (LIDC) identified nine semantic characteristics thought to be important to diagnosing lung nodules. These semantic characteristics are calcification, internal structure, lobulation, malignancy, margin, sphericity, spiculation, subtlety, and texture [5]. The semantic characteristics used by LIDC are not clinical standards; however, they are based on radiologist experience in determining malignancy. The ability to predict semantic characteristics also enables the development of systems for the automated retrieval of similar nodules based on image features, which may aid a radiologist in diagnosis.

A CAD system can be decomposed into three steps: (1) nodule identification, (2) nodule segmentation, and (3) nodule characterization. During nodule segmentation, the boundary of the nodule is delineated. This boundary subsequently serves as a basis for calculating low-level image features which are numerical descriptors automatically extracted from image content (raw pixel data) to quantify different properties such as shape, texture, and intensity of the image. This study specifically concerns itself with the performance of shape features. We distinguish shape features from texture and intensity features in that shape features exclusively use information about the locations of pixels that comprise the nodule and its boundary. On the other hand, texture and intensity features may use the boundary indirectly in order to quantify characteristics of the distribution of pixel intensity values inside and outside of the nodule. We also exclude size features, such as single measurements of diameter or circumference, from our definition of shape features.

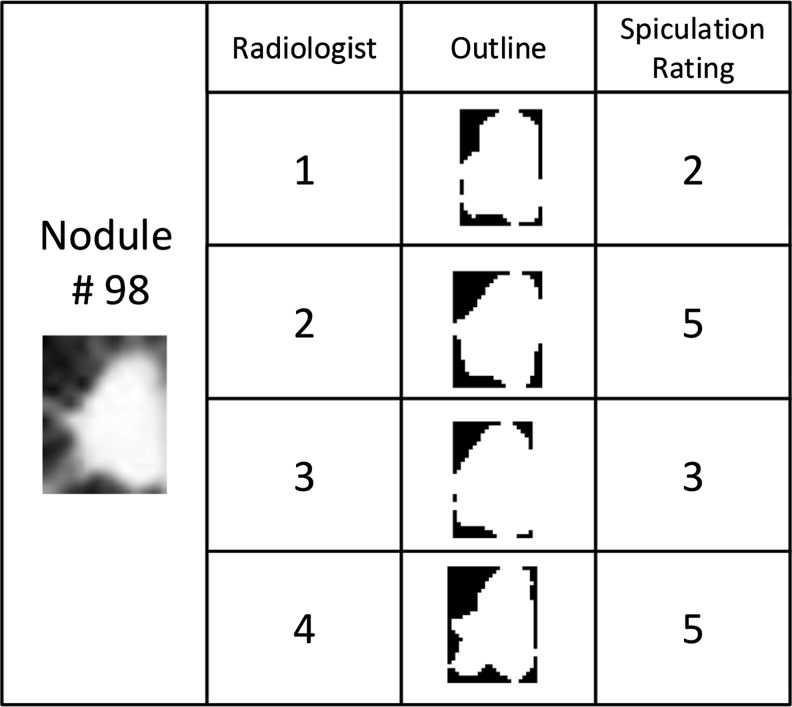
While a naïve assumption is that shape features would correlate with shape semantic characteristics, such as spiculation, in early studies using the LIDC dataset, the shape of the nodule segmentation was not highly correlated with semantic ratings of radiologists [6–11]. The reasons for this semantic gap have been attributed to uncertainty in the location of the boundary as captured by radiologist annotation variability and uncertainty in the semantic rating, since different raters may provide different ratings for spiculation for the same nodule. Figure 1 provides an example of this outline and annotation variability in the LIDC.

Fig. 1.

Example of a nodule outline and its annotation variability in the LIDC

Within this context, we investigate the role that sensor resolution and nodule size have in explaining the poor performance of shape features. Therefore, in this work, we examine how the performance of shape features in predicting spiculation in lung nodules varies with nodule size after variation due to radiologist disagreement is factored out of the dataset. We will test the hypothesis that the performance of shape features increases with nodule size by examining the relative accuracy of decision tree classifiers in predicting spiculation ratings for datasets partitioned by nodule size using (1) shape features alone, (2) texture and intensity features, and (3) shape features in combination with texture/intensity features. We also supplement this analysis by measuring the importance of individual features in the feature set by performing a feature relevance analysis. This work is concerned specifically with the ability of shape features to predict the semantic notion of spiculation as understood by radiologists. The rating scale for spiculation in LIDC is from 1 to 5 with 5 being the most spiculated and 1 being least spiculated. Spiculation was not precisely defined by the LIDC, but the definition cited by several LIDC studies is “the degree to which the nodule exhibits spicules, spike-like structures, along its border” [12–14]. Spiculated margin is commonly accepted as an indication of malignancy [15, 16].

The first contribution of this work is the examination of how particular feature calculations are affected by the size of nodules. This is an important issue given that the sizes of nodules range across an order of magnitude from 3 to 30 mm. The boundaries of small nodules are relatively coarsely digitized, consisting of very few pixels. The relatively low resolution complicates the matter of distinguishing between actual boundary complexity and sensor noise, which may adversely affect the efficacy of some feature calculations more than others. This information can be used to understand how the distribution of sizes of a population of nodules or of a training set affects the performance of classifiers.

A second contribution is to identify the mappings between shape features and the semantic concept of spiculation for lung nodules. In the field of CAD for breast cancer, it was shown that shape features that were designed to measure the spiculation of breast masses were important to predicting breast mass malignancy [17–19]. Given that mammograms for breast cancer assessment have high resolution compared with the CT scans used for lung nodule assessment, it is important to specifically tackle the issue for the low-resolution case of lung nodules.

Studies such as this that attempt to understand the mapping between image features and semantic concepts other than malignancy are important to developing supplementary information to CAD-based second opinions, for designing image retrieval systems based on a mapping between image-based and semantic-based similarity, and to support an ongoing effort to develop a common lexicon for nodule description [20, 21]. Recently, researchers have identified the need to develop qualitative measures of nodule appearance that have the ability to describe the whole shape and appearance of the nodule, because the existing set of shape and appearance features depend on the quality of the segmentation algorithm [22]. This research contributes to this endeavor by better defining the limits where existing image features map well to existing semantic concepts of shape.

Related Work

Based on radiologist experience, spiculation is commonly identified as an important semantic characteristic of some malignant lung nodules [15, 16]. The relationship between spiculation and malignancy has also been demonstrated statistically. For example, in one study, 193 pulmonary nodules were subjectively graded as round, lobulated, densely spiculated, ragged, and halo. A high level of malignancy was found among the lobulated (82 %), spiculated (97 %), ragged (93 %), and halo nodules (100 %), while 66 % of the round nodules were benign [23].

Nakamura et al. was one of the first to attempt to predict radiologists’ perception of diagnostic characteristics, such as spiculation [24]. In this work, radiologists rated characteristics such as margin, spiculation, and lobulation on a scale of 1 to 5. Statistical and geometric image features such as Fourier and radial gradient indices were correlated with the radiologists’ ratings. The investigation concluded that there was poor predictive performance in predicting the radiologists’ ratings due to variability between radiologists.

Initial work [6–10] toward predicting radiologist semantic ratings using the LIDC dataset applied a set of shape features, including roughness, eccentricity, solidity, extent, and radial distance standard deviation, along with texture and intensity features that included Haralick and Gabor texture features. Using these set of features, various techniques were used to either directly predict semantic features or to use image features in content-based image retrieval (CBIR) systems. Techniques for predicting semantic characteristics included multiple regression [6] and logistic regression [7] with accuracy in predicting spiculation below 45 %. Variability in radiologist rating and outlines were cited as the primary factor in the poor predictive performance. Similarly, the research into the CBIR systems using this feature set also concluded that the shape features had poor performance relative to texture and intensity features in predicting spiculation and other semantic characteristics [8, 9].

Varutbanghul et al. aggregated these same sets of features by combining different radiologist outlines of the same nodule using a probability map (p-map) [10]. The derived features were used to train a decision tree to predict the median semantic ratings of a lung nodule. Once again, intensity and texture features, not shape, played the most prominent role in nodule classification. Furthermore, an analysis of the image features showed that shape features had a greater dependence on the quality and consistency of the segmentation relative to texture, size, or intensity features. Standard deviations in shape-based features across different radiologist outlines were found to be ten times higher than the standard deviations for texture features.

Further efforts were made to expand the feature set for predicting semantic characteristics of LIDC dataset nodules. New shape features that included Fourier-based descriptors, a variant of the radial gradient index, and a radial normal index were used to predict semantic ratings, including spiculation [11, 25]. The authors reported no improvement in predicting semantic ratings, also citing the extent of radiologist disagreement as the primary cause of the poor classification performance.

Horsthemke et al. used novel shape features and a richer set of regions of interest (ROI) derived from the p-map of the radiologist outlines to predict LIDC semantic ratings. This work integrated the observed disagreement in radiologist outlines into the feature set by forming eight ROI from unions and intersections of radiologist outlines of the same nodule. Image feature were then extracted from each ROI that included the radial gradient index, gradient entropy, Zernike moments, shape index, and curvedness. A decision tree classifier used for prediction was able to predict the median spiculation rating of up to four radiologist opinions with an accuracy of 60 % [26].

Weimker et al. showed good correlation between shape index features and spiculation using custom nodule segmentations [27], but the same group reported limited success predicting semantic ratings when using the LIDC dataset due to radiologist disagreement [28].

Many other works have focused on distinguishing between malignant and benign nodules (rather than on predicting descriptive characteristics, such as spiculation) [29–36]. The survey article by El-Baz et al. provides an excellent review of these efforts [22]. In many cases, these researchers demonstrated CAD systems that use novel image features that are applicable to the study of spiculation. Due to the expense of obtaining data, most of these studies use small datasets and use leave-one-out cross-validation to demonstrate classifier performance.

For example, Kawata et al. showed that the surface curvature and surrounding radiating pattern could be used to classify benign and malignant nodules [29]. Kido used fractal dimensions and noted correlation between fractal dimensions of various benign and malignant nodules that were under 30 mm in size [30]. The main hypotheses of the work by El-Baz et al. was that the shape of malignant nodules is more complex than the shape of benign nodules so that more spherical harmonics must be used to describe the 3D mesh representation of the shape of malignant tumors than is used for benign tumors [31]. Huang et al. used fractal texture features based on fractional Brownian motion to classify lung nodules as malignant or benign using a support vector machine (SVM) [32]. Netto et al. used Getis texture statistics and several classifiers, including an SVM, a linear discriminate classifier, and a nearest mean classifier, to classify LIDC dataset nodules as malignant or benign [33].

Way et al. employed statistics on the intensity histogram of voxels inside the nodule, including the average, variance, skewness, and kurtosis. Way et al. also developed a novel image feature that examines the texture at the margin of the nodule using a rubber band straightening transform (RBST) [34]. The RBST was applied to planes of voxels surrounding the nodule, and the run-length statistics (RLS) texture features were extracted from the transformed images. The RBST, previously used to analyze the texture around mammographic masses in 2D [37], allows one to map a region defined equidistant radially from a closed boundary onto a 2D x- and y-axis and thereby capture radial or circumferential texture patterns.

In an improved version of their CAD system for predicting lung nodule malignancy, Way et al. developed three sets of new image features to better measure the surface smoothness and boundary irregularity of the nodule: gradient magnitude statistics, gradient profile statistics, and radii statistics [35]. Depending on the type of classification performed (primary cancers vs benign nodules, metastatic cancers vs benign nodules, or all cancers vs benign nodules), various RBST-transformed RLS features, gradient magnitude features, gradient profile features, and radii features proved important to classification.

Chen et al. used 47 nodules from LIDC to train a neural network ensemble-based CAD system for distinguishing between malignant and benign nodules. Automatic segmentation was used and 21 image features extracted. Fifteen features were selected from these based on the feature being statistically different between the categories of nodules (probably benign, uncertain, and probably malignant). This resulted in five gray-level features (quartile of CT values), skewness of histogram, smoothness, uniformity, and entropy; four features based on the gray-level co-occurrence matrix (energy, contrast, homogeneity, and correlation); and six shape and size features (area, diameter, form factor, solidity, circularity, and rectangularity). The authors also conducted an analysis based on the 11 nodules in a small size category (diameter = <10 mm) and found that the area under the receiver operating characteristic (ROC) was not statistically different between the CAD scheme and a panel of radiologists [36].

Since high inter-observer variation was the primary cause of poor classifier performance cited in several of the studies [6, 7, 10, 11, 24, 25, 28], we propose a new approach of first filtering out inter-observer variation in order to reveal fundamental relationships between shape features and the semantic concept of spiculation. In this context, unlike studies that have as their goal demonstrating the complete performance of a CAD system, we are looking into gaining fundamental insight into the shape feature calculations. Rather than investigating the best combination between a set of image features and a classifier to obtain optimal classification performance, we propose to analyze the effects of geometric measurements (e.g., radii or area measurements) on basic shape features that have simple geometric interpretations and were used in several LIDC studies [6–11].

This is in particular important because early digital imaging research established that the accuracy of geometric measurements in the digital plane depends on resolution. For example, perimeter estimates based on chain codes, such as the digital Euclidean perimeter, are not rotation invariant, because the estimation of linear distances depends on the orientation with respect to the digital grid of each straight line segment along the actual perimeter [38, 39]. Noise is also introduced because the area inscribed by a perimeter estimate is often different than the total number of pixels that make up the region, and this difference is relatively larger with respect to shape size for small shapes than it is for large shapes. This also means that the ratio of the area to the perimeter is not scale invariant as it is for shapes in the Euclidean plane, and a circle is not always the most compact shape in a digital grid, as it is in the Euclidean plane [40–42].

The rest of the paper presents our methodology, results, a discussion of the results, and conclusions and plans for future work.

Materials and Methods

Overview

The methodology of analyzing the shape features is presented in the context of the LIDC data. In order to test the efficacy of shape features and provide a basis for comparison, three different sets of low-level image features are extracted from the CT scan image segmentations outlined by the LIDC radiologists: shape features, texture features, and intensity features.

These features are used to predict the degree of spiculation of lung nodules using decision tree classification approaches. The choice of classification trees was motivated primarily by their simple semantically meaningful tree structure that hierarchically partitions the input cases and provides insight into the performance of the features. Other methodologies, such as the use of artificial neural networks, may provide good classification but provide much less information about the underlying model.

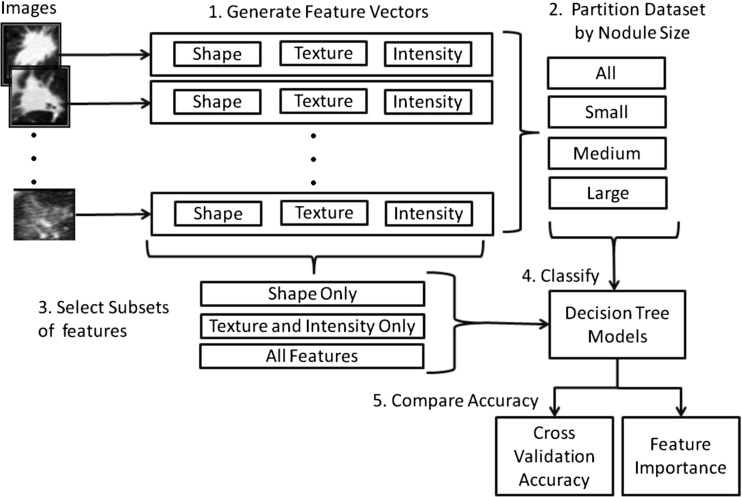
Given the class imbalance generated by the non-uniform distribution of spiculation ratings, random under-sampling is applied to factor out the class imbalance. In addition, we partition the dataset by nodule size in order to obtain performance results (accuracy, sensitivity, and specificity) for small, medium, and large nodules, as well as performance results for the entire dataset. Finally, the results for 100 randomly generated balanced datasets for each of the four datasets (all nodules, small nodules, medium nodules, and large nodules) and for each of three feature set combinations (shape only, texture/intensity alone, shape/texture/intensity together) are compared using paired t tests to assess the difference in performance of each feature set. Figure 2 presents an overview of the proposed methodology.

Fig. 2.

Overview of methodology

LIDC Dataset

LIDC is a publicly available dataset of thoracic CT scans [5]. Each of 2660 lesions was assessed by up to four radiologists, with the radiologist providing an outline of the lesion, as well as rating the lesion according to nine semantic characteristics, including spiculation. While a CT scan for a lung nodule may contain many slices, only the slices containing the largest segmented area from each radiologist are used to generate the feature sets.

Because we are primarily interested in understanding the relationship between a given annotated outline and the resulting semantic rating as described by shape features, we treat each rating/segmentation pair as a separate case. In this way, we avoid confounding our results by introducing techniques such as combining ratings from multiple observers or combining boundaries from multiple annotators, as was done in earlier studies [10, 26]. The issues related to combining ratings and combining annotated outlines are important but are not central to our question of assessing the value of shape features in mapping from a given outline to a semantic rating.

We also kept only those segmentations that belonged to nodules where more than one radiologist outlined the nodule. This served to filter out disagreement about nodule detection and to ensure that only data was included that represented actual nodules and not some other type of lesion.

The detection of the nodules and the spiculation ratings in the LIDC dataset contain significant uncertainty given the radiologists’ interpretation variability. This interpretation variability is extreme in some cases with regard to spiculation to the point where it appears that some raters may have inverted the rating scale. Table 1 shows examples of large disagreement between radiologists in rating spiculation in the LIDC dataset and the number of nodules and observations that were affected by each type of disagreement.

Table 1.

Examples of large disagreement in the LIDC dataset with regard to spiculation ratings and the number of observations and nodules effected

Type of disagreement	Criteria	No. of nodules	No. of observations
Outlier for nodule identification	Only one rater for nodule	842	842
Outlier rating of 1	Rating equal to 1 and all other ratings are 4 and 5	54	54
Outlier rating of 5	Rating is equal to 5, and all other ratings equal to 1 or 2	101	101
Complete disagreement on ratings	Four ratings equally split with two ratings of 1 and two ratings of 5	8	56

In order to create a robust ground truth, we kept only those segmentations where the radiologists were in general agreement on the transformed spiculation rating and for which the presence or absence of spiculation was definitive. Therefore, we included in the dataset only those segmentations for which all ratings for the nodule consisted of only 1’s and 2’s or only 4’s and 5’s. As a consequence, any segmentation with a rating of 3 was not included. Finally, we simplified the analysis by transforming the ratings into a binary classification problem. We binned the spiculation ratings such that all 1’s and 2’s were mapped to the rating of 0 (not spiculated) and all 4’s and 5’s were mapped to the rating of 1 (spiculated). The result was a dataset of 4092 observations covering 1324 distinct nodules; each observation is associated with one of two classes—spiculated (77 observations from 32 distinct nodules) or not spiculated (4015 observations from 1292 distinct nodules). The number of nodules and observations removed from the original dataset by the filtering criteria are shown in Table 2.

Table 2.

Results of dataset filtering criteria in terms of nodules and observations removed

	No. of nodules	No. of observations
Unfiltered initial dataset	2660	6684
Removed for failing nodule identification criterion of more than one rater per nodule	842	842
Removed for failing rating agreement criterion of all ratings must be equal to 1 and 2 or all ratings must be equal to 4 and 5	494	1750
Resulting dataset after filtering	1324	4092

Since we aim to gain insight into the size dependence of our results, the dataset is partitioned into three subsets, representing small, medium, and large nodules. Our approach to size partitioning is not based on clinical definitions of size. Due to the relatively few number of spiculated cases, we use equal depth binning to divide the spiculated cases evenly among the three subsets. The parameters of the resulting datasets are shown in Table 3; the major axis length in millimeters for each size partition is also included to provide a perspective on the physical size of the nodules for each partition by pixel area.

Table 3.

Dataset size-based partition using an equal frequency distribution of spiculated cases

Size	Area in pixels		Major axis in mm		Spiculated	Non-spiculated	Total
	Lower bound	Upper bound	Mean	Standard deviation	No. of observations	No. of observations	No. of observations
Small	0	215	8.17	2.25	26	3546	3572
Medium	215	765	17.53	4.41	26	418	444
Large	765	1445	29.61	7.03	25	51	76
All	0	1445	9.5847	4.8440	77	4015	4092

Low-Level Image Features

For each nodule image instance, 57 features were extracted: 9 shape features, 9 intensity features, and 40 texture features. Size features were excluded from the analysis, because the population of nodules will be partitioned by size.

Table 4 presents the formulas for the eight shape features: solidity, roughness, second moment, radial distance standard deviation, circularity, compactness, extent, and eccentricity. These shape features were chosen because they were used in previous CAD studies based on LIDC data [6–11], because they are specifically related to distinguishing levels of shape complexity (vs the harder problem of distinguishing between shapes in general), and because they have a simple geometric interpretation. The simple geometric interpretation allows for analysis of the effects of image resolution on geometric measurements that comprise the shape features and the effects of noise associated with uncertainty in statistical calculations.

Table 4.

Definition of shape features

$\mathit{Solidity}=\frac{A}{A_{\mathit{Convex}}}$	$\mathit{Circularity}=\frac{4\pi A}{P_{\mathit{convex}}^2}$
$\mathit{Roughness}=1-\frac{P_{\mathit{convex}}}{P}$	$\mathit{Compactness}=\frac{P^2}{4\pi A}$
$\mathit{Second}\mathit{Moment}={\displaystyle \sum _i^A}\frac{d{\left(u,p_i\right)}^2}{A^2}$	$\mathit{Extent}=\frac{A}{A_{bb}}$
Radial Distance Standard Deviation = std(d(u, p i)| p i  P)	$\mathit{Eccentricity}=\sqrt{1-\frac{b^2}{a^2}}$

A area in pixels, P perimeter of the shape in pixels, convex convex hull of the nodule, bb bounding box of the nodule, a same major axis as an ellipse with the same second moment as the nodule, p _i pixel i of the nodule

If we are interested in exploring those parameters used in shape feature calculations that might introduce noise, especially at low resolution, it is important that we are specific about how are feature calculations are performed. In particular, many of these feature calculation require estimates for area and perimeter of the nodule region, and there is more than one way to calculate these estimates.

Area is most commonly estimated by assuming that the number of pixels in the region represents the area of the region, and this is the approach that we take. Perimeter is most commonly estimated as the “digital Euclidean perimeter”, which is calculated using a chain code in which a value of 1 is added to the perimeter if a movement from one pixel to the next along the contour is in the horizontal or vertical direction and a value of $\sqrt{2}$ is added if the move is in a diagonal direction.

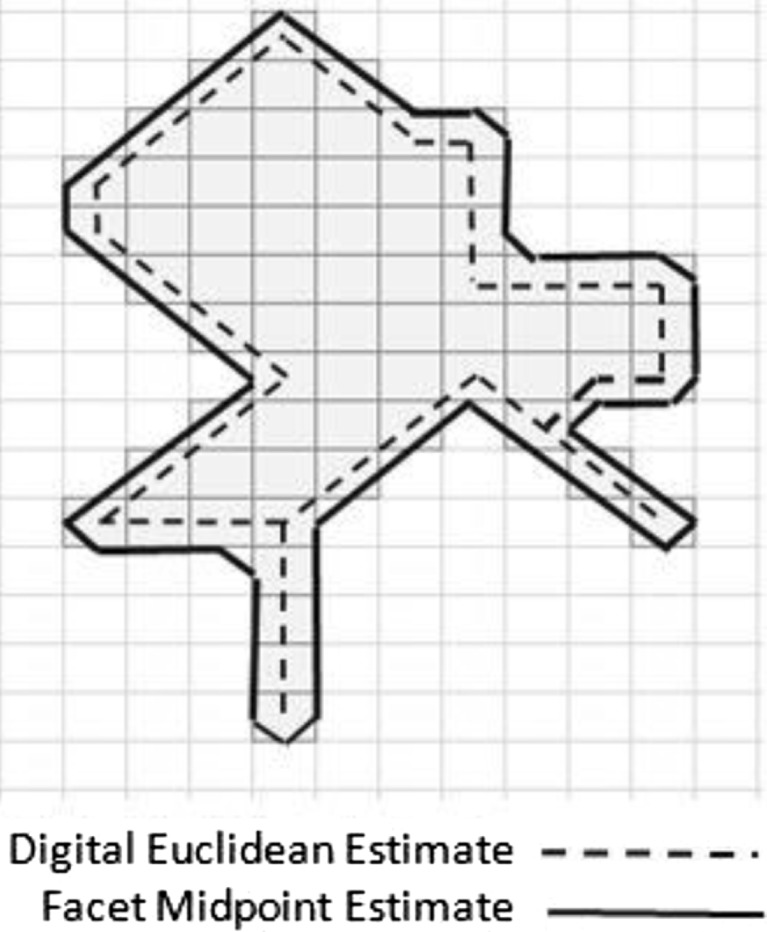
Rather than using the digital Euclidean estimate of perimeter, we chose to use a method that connects the midpoints of each facet of contour pixels as shown in Fig. 3. This method represents sub-regions as small as a single pixel in width in an intuitive way.

Fig. 3.

Perimeter estimation technique that connects the midpoints of each facet of contour pixels

In addition to the effects of resolution on geometric measurements at low resolution, we are also interested in noise associated with uncertainty in statistical calculations. Features that are based on statistical analysis of pixel locations in the segmented nodule have fewer data points available for small nodules than are available for large nodules. This may produce lower statistical confidence and noise when comparing feature values of two small nodules than would be the case if two large nodules were compared. The radial distance standard deviation, the second moment, and eccentricity all fall in this category. Radial distance standard deviation relies on relatively few pixels on the contour of small nodules for its calculation. Eccentricity relies on calculating the principal components of the segmented region to obtain information about the orientation of the nodule, and then, the final feature value is determined completely by the maximum distances measured along each axis. The use of maximal values can be a source of significant noise. Finally, the second moment calculates the variance along the x- and y-axis of the pixel locations in the segmented region.

Taking into account the above considerations for the shape features’ calculations, we expect to gain insight into the reasons behind any performance differences we see in the efficacy of shape features for different size domains.

The texture and intensity features were selected based on those used in previous analysis to predict semantic characteristics other than malignancy [6–11]. In this way, they represent a baseline based on previous results. They include 9 intensity features and 40 texture features (11 Haralick features, 24 Gabor texture features, and 5 Markov features). Equations and descriptions of all texture and intensity features are provided in [14].

The intensity features used are the minimum, maximum, mean, and standard deviation of every pixel in the segmented region of the nodule and the same four values for every pixel in the background of the bounding box of the segmented region. In addition, an intensity difference feature was calculated as the absolute value of the difference of the mean of the intensity values of the pixels in the background and the mean of the intensity value of the pixels in the segmented region [14].

Haralick features were calculated based on co-occurrence matrices calculated along four directions (0, π/4, π/2, 3π/4) and five distances (1, 2, 3, 4, and 5 pixels) producing 20 co-occurrence matrices. Eleven Haralick texture descriptors [43] are calculated as specified in [14] from each co-occurrence matrix: These descriptors are cluster tendency, contrast, correlation, energy, entropy, homogeneity, inverse variance, maximum probability, sum average, third-order moment, and variance. These descriptors are averaged by distance to obtain an average value associate with each of the four directions. The minimum value across the four directions is then taken as the feature value.

Gabor features were extracted as specified in [14] and are based on the work of Andysiak and Choras [44]. Gabor filtering is a transformed-based method which extracts texture information from an image in the form of a response image. A Gabor filter is a sinusoidal function modulated by a Gaussian and discretized over orientation and frequency. We convolve the image with 12 Gabor filters: four orientations (0, π/4, π/2, 3π/4) and three frequencies per orientation (0.3, 0.4, and 0.5), where frequency is the inverse of wavelength. The size of each Gabor filter is set constant at 9 × 9. We then calculate the mean and standard deviations from the 12 response images resulting in 24 Gabor features per image.

The Markov features capture local textual information by assuming that the value of a pixel is only conditionally dependent on a neighbor pixel in a given direction. We calculate the Markov random field as specified in [14] using a 9-pixel window around each pixel. The first four Markov features are the average the values for each of the four directions (0, π/4, π/2, 3π/4). The fifth Markov feature is the variance of the first four feature values.

Spiculation Classification

We use the classification and regression tree (CART) algorithm described by Breiman [45] to predict the spiculation rating of lung nodules in the LIDC dataset. We then use the area under the ROC curve of the generated models as a measure of the importance of shape features.

The CART classification approach is a decision tree classification algorithm that can construct classifiers based on continuous attributes/features. The classification model is a series of rules that are used to make a decision about the class membership of a test case based on its attributes.

In order to create a classifier, the algorithm performs a series of consecutive splits, each resulting in two nodes. If no splits are created after a certain node, this node is considered a terminal node (leaf). Each split is based on a threshold value of a single attribute. The decision on which attribute/threshold value is optimal for a particular split is based on the current training subset of classification instances. After the split is determined, the current training subset of classification instances is also split into two parts, according to the attribute/threshold of the split. All the consecutive splits are based on the corresponding subset. Optimality of the split is determined by an information-based measure. In our implementation of CART, optimality of the split is determined by the Gini index:

$$G=1-{\displaystyle \sum _i}{p}^2\left(i\right)$$ 1

where the sum is over the classes i at the node and p(i) is the observed fraction of instances with class i that reach the node (in our study, the two classes are spiculated and non-spiculated).

Our implementation uses parameters for minimum cases per parent and minimum cases per leaf as stopping criteria to determine whether or not the algorithm should continue to split a node. For every terminal node of the constructed classifier, the class probability of each class is calculated as a ratio of the instances of that class that reached the node to the total number of instances that reached the node. The class with the highest calculated probability is considered the predicted class of a terminal node.

Decision tree models are generated for each combination of feature sets (shape only, texture/intensity alone, shape/texture/intensity together) and dataset size partition (all nodules, small nodules, medium nodules, and large nodules) on 100 randomly generated balanced samples.

The randomly generated balanced samples were obtained by under-sampling the majority class (not spiculated) and selecting all the minority class members (spiculated) in order to obtain a balanced dataset (see Table 3 for the partitions). We chose under-sampling instead of over-sampling to produce the balanced datasets, because some previous studies support the choice of under-sampling. Yen and Lee showed that creating duplicated cases or even “synthetic” examples for the minority class may cause overgeneralization [46]. Drummond and Holte showed that random under-sampling yields better minority prediction than random over-sampling [47]. More recently, Rahman and Davis showed that the class imbalance problem in medical datasets could be addressed with a new clustering-based under-sampling approach where cluster centers can be used to choose the sample’s representatives for the majority class data [48]. Furthermore, while over-sampling would have allowed to both increase the size of the dataset and have a more representative set of the non-spiculated cases, we were concerned about the applicability of over-sampling in real settings.

For each sample, the decision trees are trained using leave-one-out cross-validation given the small size of the data. The mean accuracy, specificity, and sensitivity in classifying spiculation across all 100 samples are recorded for each combination, and these means are compared using paired t tests within the same size of the data partition and Welch’s t test across size domains. In this way, we obtain meaningful statistics to determine whether performance results reported for each feature set and size domain are statistically different from each other

In addition to the classification models, decision trees have a feature relevance analysis embedded in the algorithm. The importance associated with a particular node split is computed as the difference between the impurity for the parent node and the total impurity for the two children. This final importance value of a feature is then calculated as the weighted average over all nodes that use that particular feature divided by the total number of nodes:

$$I\left(f_j\right)=\frac{{\displaystyle {\sum }_{k=1}^{n_j}}\left[G\left(x_k\right)-G\left(x_{Lef{t}_k}\right)p_{Lef{t}_k}-G\left(x_{\mathit{Righ}{t}_k}\right)p_{\mathit{Righ}{t}_k}\right]}{N}$$ 2

where I(f_j) represents the importance of feature j; G is the Gini impurity function (Eq. (1)); x_k is defined as the distribution of classes within the kth node of n_j nodes splitting feature j$;x_{Lef{t}_k},x_{\mathit{Righ}{t}_k}$ represent the distribution of classes in the left and right child of x_k, $p_{Lef{t}_k}$ and $p_{\mathit{Righ}{t}_k}$ are the proportion of samples of x_k that go the left and right child, respectively, and N is the total number of nodes.

Results

To obtain the best tree configuration for our analysis, the minimum number of observations per parent was varied from 4 to 10 in increments of 2, and the minimum number of observations per leaf node was varied from 2 to 5 in increments of 1. For each permutation of these parameters, 100 randomly generated balanced datasets were generated and used to train 100 decision trees. The decision tree parameters that resulted in the highest mean cross-validation accuracy across the 100 samples was used in the subsequent analysis. In our case, these parameters were minimum cases per parent = 10, minimum cases per leaf = 4. Though these parameters represent the best-performing tree configuration, performance was not very sensitive to parameter choice, as shown in Table 5.

Table 5.

Statistical analysis of decision tree performance across all parameter combinations, showing relatively small variation in performance for different tree parameters

	Mean	Std dev	Min	Max
Accuracy	0.809	0.008	0.803	0.815
Sensitivity	0.815	0.005	0.811	0.822
Specificity	0.802	0.012	0.794	0.812

Using the selected optimal tree parameters, the procedure was repeated for all size partitions (small, medium, large, and all) and using three features sets—(1) shape only, (2) texture and intensity, and (3) shape, texture, and intensity together. For each case, 100 randomly generated balanced datasets were generated and used to train 100 decision trees, and the mean cross-validation performance in classifying spiculation was recorded for each size partition and feature set. Note that using leave-one-out cross-validation in a binary classification problem the area under the curve (AUC) of the ROC curve is equivalent to the average accuracy over all folds.

A pairwise t test was used to compare the cross-validation performance of the classifier trained using a feature set consisting of only texture and intensity features with the performance of a classifier trained using a feature set consisting of shape, texture, and intensity together. The results are shown in Table 6. The feature set that included shape features had statistically significant improvements in accuracy, sensitivity, and specificity over the feature set consisting of only texture and intensity features for small and large size partitions and for the dataset of all nodules.

Table 6.

Comparison of cross-validation performance of feature set consisting of shape, texture, and intensity features with feature set consisting of texture and intensity only (AUC is the area under the ROC curve)

	AUC			Sensitivity			Specificity
Size partition	Texture intensity	Shape texture intensity	p value	Texture intensity	Shape texture intensity	p value	Texture intensity	Shape texture intensity	p value
Small	0.638	0.711	≪0.01	0.671	0.739	≪0.01	0.605	0.683	≪0.01
Med.	0.750	0.750	1.00	0.798	0.776	0.063	0.702	0.724	0.051
Large	0.798	0.894	≪0.01	0.772	0.882	≪0.01	0.825	0.906	≪0.01
All	0.755	0.815	≪0.01	0.758	0.820	≪0.01	0.751	0.810	≪0.01

A pairwise t test was also used to compare the cross-validation performance in classifying spiculation for a feature set consisting of only shape features with a feature set consisting of only texture and intensity features. The results are shown in Table 7. No statistically significant difference in performance of the two feature sets was observed for small nodules. For medium nodules, there was no statistically significant difference in accuracy, but shape features had higher sensitivity, and texture and intensity features had higher specificity. For large nodules, accuracy, sensitivity, and specificity were all significantly better for the shape feature set than the texture and intensity feature set.

Table 7.

Performance comparison of feature set of only shape features to feature set of only texture and intensity features (AUC is the area under the ROC curve)

	AUC			Sensitivity			Specificity
Size partition	Shape	Texture intensity	p value	Shape	Texture intensity	p value	Shape	Texture intensity	p value
Small	0.654	0.638	0.238	0.667	0.671	0.760	0.642	0.605	0.055
Med.	0.733	0.750	0.194	0.732	0.798	≪0.01	0.734	0.702	0.022
Large	0.908	0.798	≪0.01	0.898	0.772	≪0.01	0.918	0.825	≪0.01
All	0.778	0.755	≪0.01	0.769	0.758	0.116	0.787	0.751	≪0.01

Welch’s t test was used to compare the mean accuracy for feature set across size domains. For example, the accuracy for shape was compared for small, medium, and large size domains. These tests indicated that the differences in means between size domains reported in Tables 6 and 7 are all statistically highly significant (p value <0.01).

The feature importance was recorded for each feature in the shape feature set, and the mean taken across all samples was recorded for each size partition. Since we used the GINI index as the measure of impurity, the feature importance can take values in the range [0, 0.5] with the maximum of 0.5 occurring only if the tree consists of a single node that correctly classifies all instances in a balanced dataset. Feature importance values that are relatively larger than other values by an order of magnitude indicate features that are predominate in the classification model. Table 8 summarizes the feature importance for the feature set consisting of all features in classifying spiculation. Table 9 summarizes the feature importance for classifying spiculation using only shape features.

Table 8.

Summary of feature importance for feature set consisting of all features

Feature	All sizes	Small	Medium	Large
Compactness	0.012	0.009	0.024	0.030
Roughness	0.021	0.006	0.045	0.268
Second moment	0.002	0.020	<0.001	<0.001
Solidity	0.002	0.008	0.019	0.025
Circularity	<0.001	0.010	<0.001	0.016
Entropy	<0.001	<0.001	0.036	<0.001
All other features	<0.003	<0.007	<0.007	<0.003

Table 9.

Summary of feature importance for shape only feature set (feature importance greater than 0.01 highlighted in bold text)

	All sizes	Small	Medium	Large
Roughness	0.027	0.005	0.067	0.336
Compactness	0.013	0.013	0.035	0.044
Solidity	0.002	0.008	0.031	0.009
Circularity	0.001	0.010	0.001	0.026
Eccentricity	0.001	0.004	0.008	<0.001
Radial distance SD	0.003	0.005	0.006	<0.001
Second moment	0.003	0.036	0.002	<0.001
Extent	0.003	0.006	0.002	<0.001

Discussion

Our results support the hypothesis that the importance of shape features for predicting spiculation changes with lung nodule size. Table 7 shows that AUC for the shape feature set increased dramatically from 65 % for small nodules, to 73 % for medium size nodules, and to 91 % for large nodules. This was a 26 % increase in absolute terms. Both sensitivity and specificity increased with increasing nodule size. Many features can be expected to improve with size, shape features or otherwise, for the simple reason that large nodules allow for the collection of more data on the object. However, the improvement in shape features (26 %) was significantly better than what was observed for the baseline texture and intensity features (16 %). It is important to note here that, given the large number of features comparative to the small number of observations, some over-fitting might occur when building the classifiers. However, if over-fitting happens, then it will be present in the results of the shape features but also of the texture and intensity features. Therefore, the interpretations of the results should be with respect to the differences in the performance values rather than using the actual values of the classification results. Further, we note that multiple segmentations assigned by different radiologists to the same nodule are considered as independent cases. Even if contour outlines differ among radiologists, the features derived from different contours of the same nodule are likely to be very strongly correlated. As a consequence, for the shape only feature set, the classifier represents a model that maps an outline to a resulting spiculation rating, which is subtly different than obtaining a relationship between a nodule and a spiculation rating. While the correlation might mislead absolute classifier performance, the differential analysis of classifier performance is valid in proving the hypothesis.

Furthermore, the shape features were relatively more important for predicting spiculation relative to the baseline texture and intensity features. This provides some evidence that the performance of shape features is relevant in a fully integrated CAD system containing features of all types. While there has been a large variety of shape, texture, and intensity features proposed in the literature, the specific set used in this study is based on earlier studies [6–11] using the LIDC dataset. According to Table 6, for the dataset of all nodules (not partitioned by size), the feature set consisting of shape, texture, and intensity features produced classifiers with performance in classifying spiculation that were statistically better than that produced using a feature set consisting of only texture and intensity features. Table 8 shows that shape features were more important individually by more than an order of magnitude than all baseline texture and intensity features with the exception of entropy. Furthermore, Table 7 shows that for the dataset of all nodules, the shape only feature set produced classifiers with performance in classifying spiculation that was statistically better than that produced using a feature set consisting of only texture and intensity features. For large nodules, the shape feature set alone produced AUC of 91 %. Examples of nodules where the shape feature set correctly classified spiculation, but the texture and intensity feature set did not are shown in Fig. 4.

Fig. 4.

Examples of nodules correctly classified by the shape feature set but incorrectly classified by the texture and intensity feature set

These results may explain why shape has had a limited role in studies involving the LIDC dataset, which consists primarily of small nodules (Note: the non-clinical definition of “small nodule” used in this study is 0–215 pixels). The performance of shape features is much worse for small nodules vs large nodules, and the small nodule category is the size domain that contains the greatest number of nodule segmentations in total (3546) and the least number (26) of spiculated nodules (0.7 %). Any classifier that is trained by random samples from the total LIDC dataset, or another dataset with similar size distribution (see Table 3), is much more likely to (1) provide small nodules and (2) provide non-spiculated relatively smooth cases for training. This situation makes the importance of shape features especially sensitive to the sampling procedure and the distribution of nodule sizes in the study population, which are reasons why prior studies on lung nodules may have been mixed in their assessment of the importance of shape features in predicting semantic ratings.

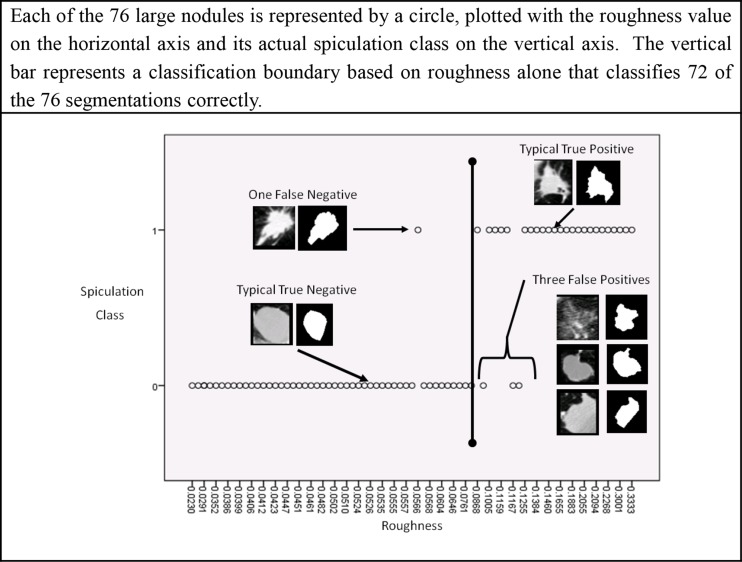
For large nodules, our results show a strong correspondence between the concept of boundary roughness and radiologist identification of spiculation. According to the results presented in Table 8 and Table 9, the importance of roughness feature is approximately an order of magnitude greater than any other shape feature and two orders of magnitude greater than any texture or intensity feature. This result is intuitive, since roughness is the one feature that directly measures boundary complexity alone. Therefore, at least for large nodules, radiologists’ semantic notion of spiculation appears to be similar to the geometric concept of roughness as captured by the radiologists’ own outlines. Figure 5 shows the importance of roughness in distinguishing between spiculated and non-spiculated large nodules. A classification boundary based on roughness alone results in correct classification of 72 out of the 76 instances in the large nodule class, resulting in a 95 % accuracy for large nodules.

Fig. 5.

A classification boundary based on roughness alone that results in correct classification of 72 out of the 76 instances in the large nodule class, resulting in a 95 % accuracy for large nodules

Roughness is relatively less relevant for small nodules than it is for large nodules. So, why does boundary complexity as measured by roughness work well for large nodules but not for small ones? First, noise introduced during image acquisition and image analysis likely confounds the ability of machine classifiers to identify boundary complexity in small nodules. Examples of small nodules are shown in Fig. 6. Consider that of those small nodules classified by radiologists as spiculated, 58 % had less than a 2 pixel difference between the perimeter and convex perimeter, the two parameters used in a ratio to calculate roughness. The mean perimeter of a spiculated small nodule is less than 42 pixels. If we apply the decision criteria of roughness >0.08 used successfully for identifying spiculated large nodules as described in Fig. 5 to a nodule with a perimeter of 42 pixels, a difference of a mere 3.34 pixels between the perimeter and convex perimeter would be sufficient for a small nodule to be classified as spiculated. Decisions based on so few pixels can be heavily influenced by noise.

Fig. 6.

Examples of small nodules

There are several sources of noise that can affect the efficacy of features at such low resolution. First, the available spatial resolution of the sensor may not be sufficient to represent the boundary complexity for small nodules. Second, just because a nodule is rated as spiculated or non-spiculated by a radiologist when they visualize the nodule in its entirety does not mean that the radiologist will reconstruct an outline detailed enough to explicitly capture the shape complexity that the radiologist observed while assigning their rating. It may be relatively more difficult for radiologists to construct a precise boundary for small nodules than it is to construct a precise boundary for large nodules. For example, the work of Bogot et al. [49] demonstrated large inter-observer and intra-observer variability in the measurement of major and minor axis by radiologist for small nodules less than 20 mm in diameter. Third, noise is introduced by the feature calculations themselves, because they may not be strictly rotation invariant or size invariant at low resolution, as discussed in the prior work section.

The data provides some evidence that at low resolutions, features that use all interior pixels in their calculation perform better than features, such as roughness, that use only boundary pixels for their calculation. According to Table 9, the shape features that are most relevant for small nodules (circularity, compactness, second moment) use information from the entire segmented region, either by using the area parameter directly or by using the second moment, which calculates distances to each pixel in the segmented region. Because these calculations use a greater number of pixels for information, they may be less sensitive to noise and have more statistical meaning than calculations that use only contour pixels. In contrast, those features that appear to have less relevance for small nodules (roughness, radial distance standard deviation, and eccentricity) use only the location of contour pixels in their calculation.

The results demonstrate the limits of using the shape of a hard segmentation boundary to calculate features for small nodules—very small differences in boundaries can result in large changes in feature calculations. As such, the results suggest possible approaches to feature calculations that describe margin that will be robust against noise in the segmentation. One approach is to use shape features that use all interior pixels as described above. Another approach is to use probabilistic representations of segmentation such as p-maps to calculate features [10, 26]. A third approach is to use the boundary merely as a reference line to collect statistics on intensity values in its vicinity. This last approach was used successfully by Way et al. [35] in their implementation of gradient profile statistics to provide insight about the change in intensity magnitude in the vicinity of boundary.

Because few studies into CAD systems report results with respect to nodule size, limited data exist to understand the extent to which the noise associated with the segmentation boundaries of small nodules affects actual classifier performance. In the study by Chen [50], the ROC curves for malignancy prediction were reported for small nodules (<10 mm), comparing the predictions of a panel of three radiologists with that of the neural network ensemble machine classifier. The AUC for the machine classifier (AUC = 0.915) was not statistically different than the AUC for radiologists (AUC = 0.683). However, these results are inconclusive due to the small number of small nodules in the study population (11 nodules, 7 benign, and 4 malignant).

Furthermore, just because spiculation presents itself differently in the image features extracted from images of small and large nodules, it does not necessarily follow that the semantic concept of spiculation differs between small and large nodules. However, it does suggest the research question of whether the mapping between image features and semantic concepts can be improved if there were an enhanced lexicon for describing the whole nodule that is not sensitive to segmentation boundary as proposed by El-Baz et al. [22]. A lexicon that describes the whole nodule may allow for providing different descriptive semantics for nodule margin for different size domains. Size-dependent semantics may also provide a better connection between appearance semantics and malignancy, since nodule appearance risk factors for malignancy are also size-dependent. For example, one recent study found that air cavity density is the only observable risk factor for malignancy in small nodules (≤10 mm) [51]. Another study found that in solid non-calcified nodules larger than 50 mm³, nodule density had no discriminative power in determining malignancy, but lobulated or spiculated margin and irregular shape increased the likelihood that a nodule was malignant [52]. Another advantage of improved semantics based partially on size is that the semantics may identify subsets of nodules that are diagnostically important, but because of their infrequent occurrence, they have relatively little impact on the overall performance of CAD systems. Therefore, CAD performance metrics can be expanded to include separate performance for expanded set of types of nodules. Note that this study identified through filtering of the LIDC the existence of a subset of small nodules (less than 10 mm) that were marked by radiologists as being spiculated with high confidence and high inter-observer agreement. However, due to their rarity (<0.7 % of cases), cases of observed spiculation in small nodules may not be included at all as part of many study populations, which due to cost constraints may contain relatively few cases.

Conclusions

Using the LIDC data, we demonstrated that the relevance of shape features in classifying spiculation ratings assigned by radiologists to lung nodules in CT scans increases with nodule size. Our findings indicate that for large nodules, radiologist’s semantic notion of spiculation is captured by the geometric concept of roughness. For small nodules, noise in the image acquisition and image analysis process makes it difficult for machine classifiers to use roughness to classify spiculation. In response, machine classifiers use a wider variety of shape, texture, and intensity features to classify spiculation for small nodules.

Future research will explore mappings between novel image features and semantic concepts of nodule appearance for small nodules. Furthermore, it will be interesting to explore how the results generalize for larger datasets given that the LIDC data contains only 77 spiculated nodules and a random under-sampling procedure was used to generate balanced datasets of spiculated and non-spiculated nodules. Finally, we will explore addressing the class imbalance problem in the LIDC dataset using the new clustering-based under-sampling approach technique proposed by Rahman and Davis [48].