Abstract
This paper proposes a new method for simple, efficient, and robust removal of the non-brain tissues in MR images based on an irrational mask for filtration within a binary morphological operation framework. The proposed skull-stripping segmentation is based on two irrational 3 × 3 and 5 × 5 masks, having the sum of its weights equal to the transcendental number π value provided by the Gregory-Leibniz infinite series. It allows maintaining a lower rate of useful pixel loss. The proposed method has been tested in two ways. First, it has been validated as a binary method by comparing and contrasting with Otsu’s, Sauvola’s, Niblack’s, and Bernsen’s binary methods. Secondly, its accuracy has been verified against three state-of-the-art skull-stripping methods: the graph cuts method, the method based on Chan-Vese active contour model, and the simplex mesh and histogram analysis skull stripping. The performance of the proposed method has been assessed using the Dice scores, overlap and extra fractions, and sensitivity and specificity as statistical methods. The gold standard has been provided by two neurologist experts. The proposed method has been tested and validated on 26 image series which contain 216 images from two publicly available databases: the Whole Brain Atlas and the Internet Brain Segmentation Repository that include a highly variable sample population (with reference to age, sex, healthy/diseased). The approach performs accurately on both standardized databases. The main advantage of the proposed method is its robustness and speed.
Keywords: Skull stripping, Irrational mask, Binarization, Similarity metrics, Magnetic resonance image
Introduction
The neuro-MR image segmentation is one of the most important tools for establishing a clinical diagnosis. In an effort to address this problem, many segmentation techniques were developed. The first step in any brain image analysis consists of the removal of the non-cerebral tissue, also called skull stripping, which is a complex and challenging task. This segmentation operation must be done with high accuracy because it implies the removal of extra-cerebral tissues such as scalp, skull, eyeballs, and skin. It belongs to the pre-processing stage that is part of image processing pipeline, usually being located between the acquisition and the segmentation stages.
Many skull-stripping algorithms were developed, and extensive work was done in this area, but a standardized solution has not been proposed yet [1–17]. Automatic and manual segmentations are the process of partitioning the image into distinct regions. The segmentation of the whole brain or the skull-stripping process depends on a particular imaging contrast and on the image intensity inhomogeneity. Each of the existing skull-stripping methods has its weaknesses and strengths, and this is the reason why they have not yet been adopted in the clinical environment. Today, fully or partially automatic segmentation methods are, in general, accepted, but their outcomes strongly depend on the theoretical and computation models [7–10].
Seghier et al. [6] developed a method for micro-bleed detection using a unified automated segmentation-normalization technique that includes an optimization step (i.e., the morphological operations were used to clean up the brain image on the tissues as skull and other tissues characterized by low intensities around the brain and the scalp), and the results were compared with a visual rating system. During the course of evolution, a variety of techniques such as graph cut [11], watershed algorithm [12, 13], histogram analysis [14], multi-atlas skull stripping (MASS) [15], thresholding and morphological reconstruction [16], and active contour model [17, 18] were proposed.
Our work has been motivated by the reported methods [11, 14, 17, 19]. Sadananthan et al. [11] proposed the graph cuts method (GCUT) that modifies the intensity thresholds and removes the narrow connections in order to obtain a brain mask. Initially, a rough estimate of the brain is extracted, and then, the graph cuts are used to refine the segmentation. Galdames et al. [14] proposed the simplex mesh and histogram analysis skull stripping (SMHASS) method that uses a deformable model and histogram analysis. This method based on deformable model used a simplex mesh, and the local gray levels controlled its deformation. Somasundaram et al. [17] used the Chan-Vese active contour model to segment the brain from other non-brain tissues. In this method, the first binary form of the brain image allows us to find the rough brain. Here, the active contour propagates. These operations have been performed in the middle slice. Then, a simplified algorithm based on the geometric similarities of the adjacent slices is performed to extract the brain in the remaining slices. The method in [19] uses prior shape information within a graph cut framework for skull stripping of neonatal brain images. Also, the labeled training data provides information for the smoothing operation in order to increase the segmentation accuracy.
Most of the segmentation methods are designed to start with various artifacts and noise removal operations by using a wide variety of filtration methods [20–24]. Also, the binarization operation is included in skull-stripping algorithms. The most popular binarization methods are based on thresholding methods [25–28]. Additionally, basic morphological operations such as dilation and erosion are usually performed in the post-processing stage of the image processing pipeline [11, 13, 29]. However, different methods produce different skull-stripping results.
Our method proposes a new mask based on the terms of Gregory-Leibniz infinite series that calculates the value of pi. The proposed irrational 3 × 3 and 5 × 5 masks help in the brain tissue identification by using the gray-level value selection and pixel assignation between background (=0) and foreground. Then, the estimated gray-level distribution of the tissues is used in the binarization so that all the pixels ranging from 0 to 254 are assigned to zero and only the white pixels are kept. Contributions of this work are threefold: (1) a new approach in using the proposed irrational mask as a high-pass filter that produces better results near the edges, (2) convert a gray-scale image into a binary image following a new selection rule, as a key step in the skull-stripping operation, and (3) the post-processing operation (i.e., morphological operations to remove all non-brain regions) and the illustration of the performance of the new skull-stripping approach. The outcomes of the proposed method and manual skull stripping were compared. The metrics most used in the specialized literature in order to compare the quality of the proposed skull-stripping method have been employed. They are the Dice scores, overlap and extra fractions, and sensitivity and specificity [11, 14]. The results of the proposed method have been validated on two independent publicly available databases, the Whole Brain Atlas (WBA) and the Internet Brain Segmentation Repository (IBSR). Also, we compared performance of our algorithm with three other existing automated skull-stripping methods, i.e., SMHASS [14], method in [17], and GCUT [11].
The main advantages of our method consist of its robustness and lesser processing time. In contrast to Niblack’s, Sauvola’s, and Bernsen’s methods that require parameters set by the users, our method does not require the adjustment of the software parameters. It is robust against intensity variations and works well across datasets. It has successfully enabled the segmentation of the brain in every slice of head images from two databases and for several different 2-D MR image types: T1 weighted (T1w), T2 weighted (T2w), gadolinium-DTPA-enhanced T1w (GAD), and proton density weighted (PD). There were used both axial and coronal views.
The remainder of the paper is organized as follows: “Materials and Methods” section describes the datasets used in this work followed by a description of our method. The algorithm’s results and performance are presented in “Results” section and discussed in “Discussion” section. Finally, conclusions are included in “Conclusions” section.
Materials and Methods
The proposed automatic skull-stripping method consists of a series of sequential stages. There are four groups of operations: (i) the image filtering using the proposed irrational mask; a robust average filter has been used because it averages across its neighborhood and has the ability to remove noise without blurring edges; (ii) the segmentation of the images using the proposed method and, for comparison purposes, using the well-established methods such as those of Otsu, Sauvola, Niblack, and Bernsen; (iii) the image post-processing based on morphologically operators; (iv) the validation and comparison against the state of the art (SMHASS [14], method in [17], and GCUT [11]).
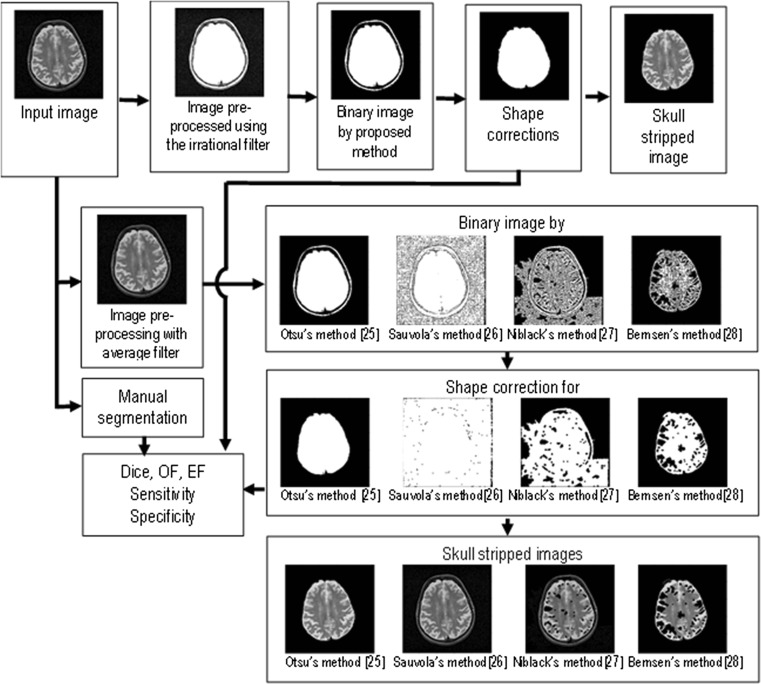
The flowchart of proposed algorithm dealing with the first three components is shown in Fig. 1.
Fig. 1.
The flow diagram of the proposed algorithm. The proposed irrational mask for filtration and an average filter (used in [25–28]) are applied. The awarded binarization methods [25–28] and the proposed method provide the intermediate mask. Then, to obtain the final refined mask, some morphological operations are employed for shape correction. The result is the final binary brain mask. Further, in the reconstruction component, the fused brain mask/skull-stripped image is provided
Datasets
Two independent publicly available databases, the WBA and/or the IBSR, have been used to build the following two datasets used for performance evaluation and validation. A total of 26 MR image series containing 216 images were examined. The datasets include scans from diverse population with a wide age range as well as diseased brains. Also, datasets include primarily T1w, T2w, GAD, and some PD images.
- Dataset 1 from the WBA1 contains 20 MR image series (180 images):
- Nine axial image series, T2w for two healthy subjects (age 76 and 81, 2 female); seven axial image series T2w belong to degenerative diseases as follows: Alzheimer (age 71–74, 2 female and 1 male), Huntington (age 70, female), and Pick (age 59, female). The slice thickness is 3 or 5 mm.
- Four axial image series T1w for Alzheimer (age 71, female), cerebral hemorrhage (age 49 female), fatal stroke (age 71, female), and cerebral calcinosis (age 36, female).
- Three axial image series GAD for anaplastic astrocytoma (age 51, female), metastatic bronchogenic carcinoma (age 42, female), and meningioma (age 75, female).
- Four axial image series PD for cerebral calcinosis (age 36, female), multiple sclerosis (age 30, male), vascular malformation/cavernous hemangioma (age 26, female), and anaplastic astrocytoma (age 51, female).
Dataset 2 from the IBSR2 contains six MR image series (36 images): three axial and coronal image series T2w for normal subjects. The slice thickness is 3.1 or 1.5 mm.
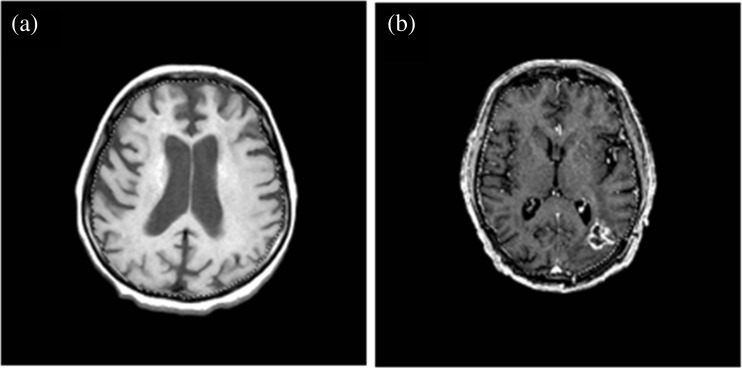
The gold standard has been provided by two neurologist experts. They had more than 8 and 15 years of experience in the field of MRI. They require, in average, between 48 and 65 s per slice for manual segmentation task completion, and overall, WBA requires 1 h and 30 min and IBSR requires approximately 1 h. The manual skull stripping was performed independently. All images were segmented on the same computer monitor with similar conditions (the same ideal lighting condition). Manual tracing was performed using Macromedia Fireworks 8 software and lasso tool. Figure 2 provides some examples of manual segmentation.
Fig. 2.
A selection of manually skull-stripped brain (dashed line). a T1w—cerebral calcinosis diagnosis. b GAD— astrocytoma diagnosis
The Kappa statistical analysis was used to assess the agreement among the experts (interobserver agreement).
Proposed Irrational Mask
In neuro-MR images, presence of noise, irregular shapes, and low contrast lead to the detection of objects and diagnostic decision which is a difficult task. In the pre-processing stage, most of these undesirable properties are eliminated using appropriate filters. In the skull-stripping procedure, the accurate detection of the shapes is crucial. Therefore, it is important to use a filter that has the ability to follow up the non-brain tissues in an accurate manner. Also, it is equally important to estimate the gray-level distribution precisely. In this respect, in this paper, we propose an irrational mask based on the Gregory-Leibniz infinite series that calculates the π value with high precision [30]:
| 1 |
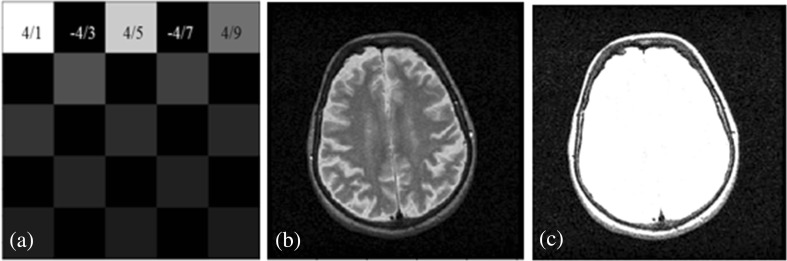
The first 9 or 25 values of the series represent the weights of the proposed 3 × 3 and 5 × 5 irrational masks π (Fig. 3a). The negative values of series give the totally black pixels (=0) or background, and the positive values that characterize the gray scale ranging from black to white (1 to 255) give the foreground.
Fig. 3.
a The irrational 5 × 5 mask with the weights of gray-level values marked. b Original image belonging to WBA dataset. c Filtering result by using the proposed irrational mask
Figure 3b shows an original image from the WBA dataset, and Fig. 3c is the result of the filtration when the π mask has been implemented in Matlab environment. The convolution operation is employed during filtration. The output image g(x, y) is the result of the convolution operation between the original image f(x, y) with m columns and n lines and the kernel π(x, y) with 2w + 1 columns, 2 h + 1 lines (see the Algorithm 1, step 1). Simultaneously, the π mask separates the image intensities so that it improves the edge detection capabilities of the proposed method.
Image Binarization
The main objective of binarization is the pre-segmentation of objects in the foreground and the background. The image binarization could be performed in different ways [25–28]. Among various methods based on thresholding, there are methods based on the global threshold [25] or on the local threshold [26–28]. Otsu’s method is a global binarization method [25]. It works as a clustering analysis-based method and uses the image variance. The image contains foreground and background classes of pixels, and the optimum threshold is that separates the two classes so that the intraclass variance is minimal. Other binarization techniques are based on local binarization; i.e., the threshold is estimated individually for each pixel according to the gray-scale information of the neighboring pixels. Niblack’s method [27] is a local variance-based method. It uses a sliding rectangular mask to compute the optimum threshold according to the local mean, standard deviation, and mask size. An improved method was proposed by Sauvola et al. [26]. It is a local-variance-based method, and it shows better results for images containing inhomogeneity. Bernsen’s method [28] is a local adaptive method based on image contrast. The threshold is set as the mean of the minimum and maximum gray values in a local window having the size of 31. Table 3 presents the optimal parameters utilized in this work for binarization task.
Table 3.
Algorithm parameters used in the binarization stage for optimal operations
| Methods | Parameters | Values of the parameters |
|---|---|---|
| Otsu | Automatic threshold that minimizes interclass variance | t ∈ [0.135; 0.394] |
| Niblack | Local mean, standard deviation, and mask size w × w |
w = 15 k = −0.2, k is the bias that controls the level of adaptation varying the threshold value |
| Sauvola | Local mean, standard deviation, and mask size w × w |
w = 15, k∈[0.2; 0.5] R = 128 (the maximum value of the standard deviation) |
| Bernsen | Minimum and maximum gray values within the local window w × w and the contrast C (i, j) |
C (i, j) ≥15 w = 31 |
The binarization method proposed in this study is not a thresholding method. The idea is to keep only the white pixels in the image. Thus, the irrational filter preserves into the binary h(x, y) image those pixels p(i, j) ∈ g(x, y) that fulfill the following condition:
| 2 |
Algorithm 1 summarizes the first two steps of the proposed method.
Algorithm 1. Pre-processing image with irrational mask and binarization
Input: Original MRI image f(x, y) with m columns, n lines
Step 1: Pre-processing image with irrational mask π (x, y) with 2w + 1 columns, 2 h + 1 lines, convolution operation
fory = 0 to m do
forx = 0 to n do
sum = 0
fori = −h to h do
forj = −w to w do
sum = sum + f(x, y) · π (x ± j, y ± j)
end for
end for
g(x, y) = sum(x, y)
end for
end for
Step 2: Binary image h(x, y) obtained from g(x, y)
fory = 0 to m do
forx = 0 to n do
ifg(x, y) ≥ 0 and g(x, y) < 255
h(x, y) = 0
else
h(x, y) = 1
end if
end for
end for
Post-Processing Operations for Brain Shape Correction
Once we have the binary images, the segmentation results must be improved. The first step is the detection of the largest objects, and the next goal is the preservation of the shape of the selected foreground objects in binary image.
A binary image h(x, y) contains the requested object of interest as a region having the larger area and several isolated regions R(i) having small areas. Each region has been labeled using integer values equal to the area of the regions RA(i), and the binary image is now expressed as , where n denotes the number of regions. The largest connected region is selected if the condition is accomplished. This selection rule provides an intermediate mask.
To obtain the final refined binary mask, some morphological operations are required. In order to increase the accuracy and efficiency of the segmentation, only the largest region has been post-processed. The closing operation (a dilation followed by erosion that allows removing the holes in the foreground) is used [16]. It is made by disk-shape structuring elements, with a radius of 2. Closing removes small dark spots and connects small bright cracks. This operation ensures that we have not included any non-brain tissues in the final mask. Algorithm 2 summarizes the morphological operation. The post-processed image is denoted as t(x, y).
Algorithm 2. Morphological operation
Step 3: Post-processing operations for brain shape correction through closing operation where ⊕ is dilation, ⊖ is erosion and s is structural element as disk with a radius of 2
fory = 0 to m do
forx = 0 to n do
t(x, y) = (hm(x, y) ⊕ s) ⊖ s
end for
end for
Output Images
The final binary mask and the original image are combined in order to compute the final segmentation of the subject image. This fusion strategy consists of building a new image I(x, y) from the original image f(x, y) and the final binary brain mask t(x, y). The output image is defined as follows:
| 3 |
where po(i, j) and pm(i, j) are the pixels that belong to original and post-processed image, respectively. The advantage of the proposed method is that there are no artifacts introduced by reconstruction.
Performance Metrics Evaluation
To validate the success of our skull-stripping method, we compared the results with manual segmentation using different metrics that reflect the degree of agreement in segmented areas. For a fair comparison between methods, the same databases (i.e., WBA and IBSR) used in [16, 19, 22] were utilized. The performance of the binary segmentation has been evaluated in two ways. A quality evaluation is performed using the Dice similarity coefficient κ (which estimates the percent area overlap), overlap fraction (OF), and extra fraction (EF) (which measure the correctly identified mask area and falsely identified as area mask, respectively [31]). For a quantitative evaluation, sensitivity and specificity are computed. Also, the efficacy of the proposed irrational filtering method has been verified through a parallel comparison with the above-mentioned methods [25–28].
| 4 |
| 5 |
| 6 |
where If and J denote the area of the skull-stripped and ground truth images, respectively [16, 19]. The area of corresponds to the false positives and measures the area that is falsely classified as brain area, where is the extra area of If . A similarity coefficient or an OF of 1.0 represents perfect overlap, whereas a value of 0.0 represents no overlap. The EF should remain as small as possible (close to 0) for a good segmentation.
The sensitivity (true positive rate) and specificity (true negative rate) are given by the following:
| 7 |
| 8 |
where TP and FP are the true positive and false positive, respectively. They are defined as the number of pixels correctly and incorrectly classified as brain tissue. TN and FN are the true negative and false negative, respectively. Similarly, they are defined as the number of pixels correctly and incorrectly classified as non-brain tissue [22]. According to the If and J signification, false positive is defined as follows: and false negative is defined as follows: .
Results
In this study, for experimental analysis, we considered two databases for skull-stripping algorithm: WBA and IBSR.
The ground truth was done by standard manual skull stripping. When the manual skull segmentation results were compared, the overall kappa coefficient value for interobserver agreement was 0.78 (P < 0.001) and indicates a good agreement among the two raters. The percentage of agreement between the raters for all MR images was approximately 85 %.
Our method has been validated in two ways. The efficacy of the irrational filtering method has been verified through a parallel comparison with Otsu’s, Sauvola’s, Niblack’s, and Bernsen’s methods. In order to have a clear perspective on precision and robustness, various metrics were used and the results are reported in Table 1. Then, the full algorithm was validated by comparing its performance with three well-known existing automated skull-stripping methods, i.e., SMHASS [14], method based on Chan-Vese active contour model [17], and GCUT [11]. The results are reported in Table 2.
Table 1.
Average performance metric scores and their standard deviation (SD) for intermediate brain mask obtained using the dataset 1 for T1w, T2w, GAD, and PD images
| Binarization methods | Dice κ (SD) | Sensitivity (SD) | Specificity (SD) | Overlap fraction (OF) (SD) | Extra fraction (EF) (SD) | ||
|---|---|---|---|---|---|---|---|
| Otsu |
0.956
(0.037) |
0.905
(0.041) |
0.971
(0.053) |
0.917
(0.044) |
0.093
(0.039) |
||
| Sauvola | – | – | – | – | – | ||
| Niblack | 0.322 (0.013) |
0.502 (0.071) |
0.442 (0.037) |
0.607 (0.054) |
0.161 (0.092) |
||
| Bernsen | 0.551 (0.093) |
0.231 (0.154) |
0.485 (0.32) |
0.386 (0.187) |
0.706 (0.271) |
||
| Proposed irrational filter | T2w | 3 × 3 |
0.911
(0.074) |
0.914
(0.085) |
0.907
(0.085) |
0.958
(0.074) |
0.092
(0.094) |
| 5 × 5 | 0.893 (0.069) |
0.896 (0.081) |
0.889 (0.079) |
0.939
(0.071) |
0.094 (0.096) |
||
| T1w | 3 × 3 |
0.911
(0.026) |
0.931
(0.017) |
0.904
(0.032) |
0.928
(0.031) |
0.081
(0.024) |
|
| 5 × 5 | 0.893 (0.027) |
0.912
(0.015) |
0.886 (0.028) |
0.909
(0.03) |
0.083 (0.027) |
||
| GAD | 3 × 3 | 0.874 (0.028) |
0.889 (0.187) |
0.877 (0.117) |
0.906
(0.019) |
0.124 (0.034) |
|
| 5 × 5 | 0.857 (0.025) |
0.871 (0.192) |
0.859 (0.121) |
0.888 (0.022) |
0.126 (0.036) |
||
| PD | 3 × 3 |
0.942
(0.936) |
0.912
(0.078) |
0.924
(0.038) |
0.922
(0.024) |
0.097
(0.011) |
|
| 5 × 5 |
0.923
(0.933) |
0.894 (0.071) |
0.906
(0.036) |
0.904
(0.022) |
0.099
(0.014) |
||
The best results are italicized
Table 2.
Performance comparison among different methods for the images in dataset 2 (ten normal subjects, IBSR)
| Method | Dice κ | Sensitivity | Specificity |
|---|---|---|---|
| SMHASS [14] | 0.945 | 0.920 | 0.996 |
| Somasundaram and Kalavathi method [17] | 0.960 | 0.980 | 0.990 |
| GCUT [11]a | 0.950 | – | – |
| Proposed method | 0.921 | 0.923 | 0.945 |
aSensitivity and specificity are not reported in [11]
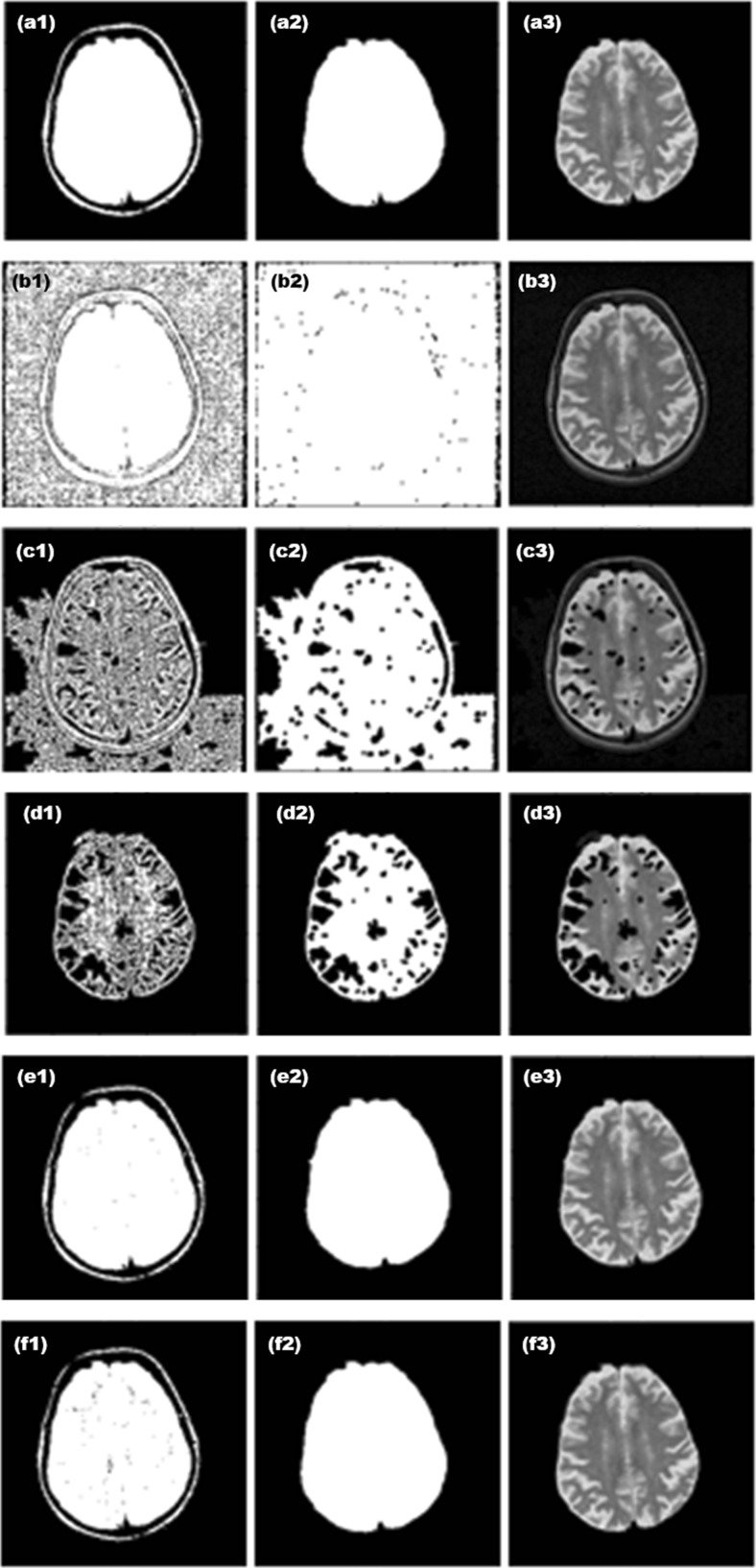
Figure 4 shows some results obtained in our study. The binary image provided by various methods and the proposed method are presented in the first column. Generally, Niblack’s method includes non-brain tissues in the binarization step and removes the brain tissues when the final skull-stripped image is done. Similarly, Bernsen’s method failed to extract brain portions.
Fig. 4.
Examples of skull stripping using various binarization methods. a Otsu’s, b Sauvola’s, c Niblack’s, d Bernsen’s, and e proposed methods using the 3 × 3 mask and f proposed method using the 5 × 5 mask. The first column indicates the binary image resulted in the pre-segmentation step. The second column shows the filtering results of the average filter (used in [25–28]) and of the proposed irrational mask coupled with the shape corrections by morphological operations. The third column corresponds to the skull-stripped image
The methods used in our benchmark analysis require various parameters to be set by the users. Table 3 shows the range of parameter values used to optimize Otsu’s, Sauvola’s, Niblack’s, and Bernsen’s binarization methods. These parameters were recommended by the authors and were utilized in this study. It is worthy to mention that our method does not need to have the software parameters adjusted.
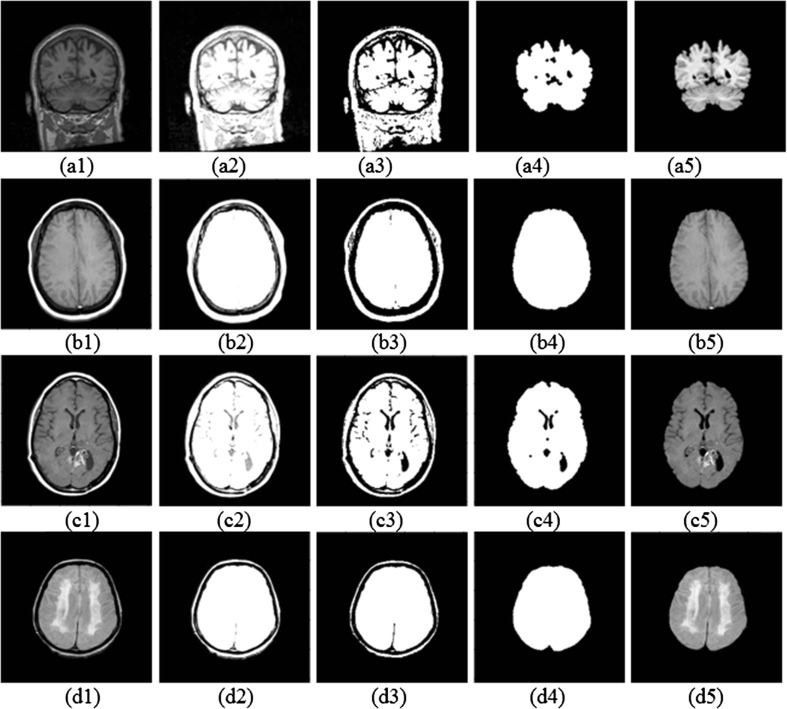
Figure 5 shows the outcome images provided by the proposed method, when different types of MR images belonging to WBA and IBSR databases were used.
Fig. 5.
Results of the proposed method for images from the studied databases a IBSR, b WBA-T1w, c WBA-GAD, and d WBA-PD. Columns show the following: original image (1), pre-processed image using the irrational filter (2), binary image obtained in the proposed approach (3), intermediate binary mask (4), and skull-stripped image (5)
The average elapsed processing time was calculated for each method based on the performance across all 26 MR image series. Thus, WBA dataset that contains 20 MR image series and 180 images requires 4 min and 6 s, and IBSR dataset that contains 6 MR image series and 36 images takes 1 min and 18 s. Each image has the size less than 15 Kb (512 × 512 pixels). The hardware experimental environments were as follows: Intel® Core™ 2 Duo CPU T 5900, 2.20 GHz, 32-bit system type, and 3-GB RAM.
The computational time of the SMHASS method for an image was 57 min, in average [14]. The methods reported in [11, 17] do not give any date on the computational time. The hybrid algorithm based on watershed and deformable surface models proposed by Ségonne et al. [13] runs in about 5 min for 43 scans (1-GHz Pentium III running Linux). The MIDAS method reported in [6] takes less than 3 min to run per patient (PC 64-bit, 3.2-GHz Intel CPU, 12-GB RAM). Also, for some patients, an additional 5–10 min was needed for some supplementary manually corrections.
Discussion
Impediments as forms of anatomical variability among brains, artifacts due to various acquisition methods, and different databases with a large range of image registration quality lead to a lot of difficulties of designing a robust algorithm for skull stripping. The reported results in literature significantly vary because various databases and parameters were used in the comparisons.
The segmentation accuracy of the proposed method was assessed by comparing the overlap of manual experts’ segmentation with the results of our skull-stripping method. The mean and standard deviations (SD) of the metrics described in “Performance Metrics Evaluation” section were computed, and the segmentation results for each method are shown in Table 1. The average performance of each method shows high variation with different image types. Otsu’s method and the proposed method for T1w, T2w, and PD image types show comparable performances in terms of κ similarity coefficient. The higher values of Dice coefficient indicate that only few black pixels (or small non-brain tissue regions) belonging to the If and J images have overlapped. Also, the highest sensitivity with very few FN and a high specificity are provided by the proposed method. Niblack’s and Bernsen’s methods show a low performance, and Sauvola’s method does not provide any measurable information. With respect to morphological operations, Sauvola’s case demonstrated significantly worse performance relative to other methods.
The segmentation results for each method used for comparison purpose are shown in Table 2. It can be seen that the proposed method gives the average values similar of the performance coefficients with those of reported methods in literature, sharing the same public databases. The purpose of this comparison was to show that the proposed irrational filter gives the very good results in a simple and robust technique and with a very low processing time, unlike the previous methods that show a higher processing time.
The robustness of the proposed method has been proven in two ways. First, its wide applicability is proved by the significant number of MR images belonging to various diagnostic groups and acquisition ways (PD, GAD, T1w, T2w), for adults and aging population. These images belong to independent public databases. Secondly, our method does not need to have the software parameters modified, in contrast to the parameter-based methods used for comparison.
The window size affects the performance of segmentation. Niblack’s, Bernsen’s, and Sauvola’s methods require large window size, and for MR images, they do not show good performance and are not suitable at smaller window size. Sauvola’s method is totally inappropriate. Proposed methods give very good results for 3 × 3 mask, and a slightly decrease of 2 % in the performance has been registered for the 5 × 5 mask.
It is worth noting here that our approach incorporates an edge-enhancing component, as the proposed irrational mask allows setting a high-pass filtration operation. Its performance is very good because it highlights pixels that have values that are very different from their neighboring pixels (i.e., from those pixels assigned as black pixels by the negative weights of the π mask). This method performs better on all images encompassed in analyzed datasets and shows equal performance among different diseases. However, cerebral hemorrhage images were the most difficult to segment.
The proposed method is able to successfully segment the whole brain in all 216 images from two publicly available databases. It has similar performance with respect to other most popular methods in the literature [11, 14, 17], but it outperforms these methods due to its simplicity and speed. We estimate that in group comparison studies of skull stripping, our method can be successfully used. In evaluating the proposed method, the combined merits of the entire constellation of performance metrics as comparison with manual segmentation, longitudinal studies across two databases, the range of the optimal parameters, and processing time were considered.
Conclusions
The aim of this study was to develop a simple and robust skull-stripping method based on the new proposed irrational mask. This new proposed algorithm combines the gray-level value selection and the pixel assignation between background (=0) and the foreground with a new binarization rule. Specifically, two irrational masks of 3 × 3 and 5 × 5 size based on the first 9 and 25 terms of Gregory-Leibniz infinite series that calculates the π value have been used. In case of the 5 × 5 mask, the performance of method decreases with 2 %. Also, a new selection rule to convert a gray-scale image into a binary image was proposed. In the final steps, morphological operations that remove all non-brain regions were used and the performance of the new skull-stripping approach was compared with other well-established methods.
The proposed method was quantitatively and qualitatively evaluated using international MRI databases: IBSR and WBA. The validation of the proposed method has been carried out by comparing our results with ones provided by other methods [11, 14, 17], and our method shows similar segmentation performance and accuracy (based on popular metrics). The main advantage is its simplicity and robustness. Also, our algorithm is fast enough so that the processing time is an advantage of the method.
Acknowledgments
The author Simona Moldovanu would like to thank the Project PERFORM, ID POSDRU/159/1.5/S/138963 of “Dunărea de Jos” University of Galaţi, Romania, for support.
Footnotes
Harvard Medical School, http://www.med.harvard.edu/aanlib/home.html, accessed 26 June 2014
National Institutes of Health Blueprint for Neuroscience Research http://www.nitrc.org/projects/ibsr, accessed 27 June 2014
References
- 1.Rajendran A, Dhanasekaran R. Brain tumor segmentation on MRI brain images with fuzzy clustering and GVF snake model. Int J Comput Commun. 2012;7:530–539. doi: 10.15837/ijccc.2012.3.1393. [DOI] [Google Scholar]
- 2.Rajendran A, Dhanasekaran R. A Combined Method Using fuzzy clustering and MGGVF snake model for brain tumor segmentation on MRI image. JGRCS. 2011;2:1–5. [Google Scholar]
- 3.Guoqiang W, Dongxue W: Segmentation of brain MRI image with GVF snake model. In: Proceedings of the 1st International Conference on Pervasive Computing Signal Processing and Applications, Harbin, China, 2010, pp. 711–714
- 4.Moreno JC, Prasath VBS, Proença H, Palaniappan K. Fast and globally convex multiphase active contours for brain MRI segmentation. Comput Vis Image Underst. 2014;125:237–250. doi: 10.1016/j.cviu.2014.04.010. [DOI] [Google Scholar]
- 5.Tirpud N, Welekar R. Automated detection and extraction of brain tumor from MRI images. Int J Comput Appl. 2013;77:26–30. [Google Scholar]
- 6.Seghier ML, Kolanko MA, Leff AP, Jager HR, Gregoire SM, Werring DJ. Microbleed detection using automated segmentation (MIDAS): a new method applicable to standard clinical MR images. PLoS ONE. 2011;6:1–9. doi: 10.1371/journal.pone.0017547. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Bandhyopadhyay SK, Paul TU. Segmentation of brain MRI image – a review. IJARCSEE. 2012;2:409–413. [Google Scholar]
- 8.Prastawa M, Bullitt E, Moon N, Van Leemput K, Gerig G. Automatic brain tumor segmentation by subject specific modification of atlas priors. Acad Radiol. 2003;10:1341–1348. doi: 10.1016/S1076-6332(03)00506-3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Vijayakumar C, Gharpure DC. Development of image-processing software for automatic segmentation of brain tumors in MR images. Med Phys. 2011;36:147–158. doi: 10.4103/0971-6203.83481. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Punga M, Gaurav R, Moraru L. Level set method coupled with energy image features for brain MR image segmentation. Biomed Tech. 2014;59:219–229. doi: 10.1515/bmt-2013-0111. [DOI] [PubMed] [Google Scholar]
- 11.Sadananthan SA, Zheng W, Chee MWL, Zagorodnov V. Skull stripping using graph cuts. Neuroimage. 2010;49:225–239. doi: 10.1016/j.neuroimage.2009.08.050. [DOI] [PubMed] [Google Scholar]
- 12.Hahn HK, Peitgen HO: The skull stripping in MRI solved by single 3D Watershed transform, in: Proceedings of International Conference on Medical Image Computing and Computer Assisted Intervention Berlin, Germany, 2000, pp. 134–143
- 13.Ségonne F, Dale AM, Busa E, Glessner M, Salat D, Hahn HK, Fischl B. A hybrid approach to the skull stripping problem in MRI. Neuroimage. 2004;22:1060–1075. doi: 10.1016/j.neuroimage.2004.03.032. [DOI] [PubMed] [Google Scholar]
- 14.Galdames FJ, Jaillet F, Perez CA. An accurate skull stripping method based on simplex meshes and analysis in magnetic resonance images. J Neurosci Methods. 2012;206:103–119. doi: 10.1016/j.jneumeth.2012.02.017. [DOI] [PubMed] [Google Scholar]
- 15.Doshi J, Erus G, Ou Y, Gaonkar B, Davatzikos C. Multi-Atlas skull-stripping. Acad Radiol. 2013;20:1566–1576. doi: 10.1016/j.acra.2013.09.010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Ramesh M, Priya P, Arabi PM. A novel approach for efficient skull stripping using morphological reconstruction a thresholding. IJRET. 2014;3:96–101. [Google Scholar]
- 17.Somasundaram K, Kalavathi P. Skull stripping of MRI head scans based on Chan-Vese active contour model. KM&EL. 2011;3:7–14. [Google Scholar]
- 18.Mirajkar G, Patil S, Pawar M: Skull stripping using geodesic active contours in magnetic resonance images. In: Proceedings of the 4th International Conference on Computational Intelligence, Communication Systems and Networks, Phuket, Thailand, 2012, pp. 301–306
- 19.Mahapatra D. Skull stripping of neonatal brain MRI: using prior shape information with graph cuts. J Digit Imaging. 2012;25:802–814. doi: 10.1007/s10278-012-9460-z. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Krishnan NP, Kenkre N, Nancy NS: Tumor detection using threshold operation in MRI brain images. In: Proceedings of the International Conference Computational Intelligence & Computing Research, (December 2012), Coimbatore, India, pp. 1–4
- 21.George EB, Karnan M. MRI Brain Image enhancement using filtering techniques. IJCSET. 2012;3:399–403. [Google Scholar]
- 22.Kanimozhi M, Bindu CH. Brain MR image segmentation using self organizing map. IJARCCE. 2013;2:3968–3973. [Google Scholar]
- 23.Mohan J, Krishnaveni V, Guo Y. MRI denoising using nonlocal neutrosophic set approach of Wiener filtering. Biomed Signal Process. 2013;8:779–791. doi: 10.1016/j.bspc.2013.07.005. [DOI] [Google Scholar]
- 24.Balafar MA, Ramli AR, Saripan MI, Mashohor S. Review of brain MRI image segmentation methods. Artif Intell Rev. 2010;33:261–274. doi: 10.1007/s10462-010-9155-0. [DOI] [Google Scholar]
- 25.Otsu N. A threshold selection method from gray level histograms. IEEE Trans Syst Man Cybern. 1979;9:62–66. doi: 10.1109/TSMC.1979.4310076. [DOI] [Google Scholar]
- 26.Sauvola J, Pietikainen M. Adaptive document image binarization. Pattern Recogn. 2000;33:225–236. doi: 10.1016/S0031-3203(99)00055-2. [DOI] [Google Scholar]
- 27.Niblack W. An Introduction to Digital Image Processing. Denmark: Prentice Hall; 1986. [Google Scholar]
- 28.Bernsen J: Dynamic thresholding of gray level images. In: Proceedings of the 8th International Conference on Pattern Recognition, (October 1986), Paris, France pp. 1251–1255
- 29.Shattuck DW, Sandor-Leahy SR, Shaper KA, Rottenberg DA, Leahy RM. Magnetic resonance image tissue classification using a partial volume model. Neuroimage. 2001;13:856–876. doi: 10.1006/nimg.2000.0730. [DOI] [PubMed] [Google Scholar]
- 30.Debnath L. The Legacy of Leonhard Euler: A Tricentennial Tribute. London: Imperial College Press; 2010. [Google Scholar]
- 31.Anbeek P, Vincken KL, Van Osch MJP, Bisschops RHC, Van Der Grond J. Probabilistic segmentation of white matter lesions in MR imaging. Neuroimage. 2004;21:1037–1044. doi: 10.1016/j.neuroimage.2003.10.012. [DOI] [PubMed] [Google Scholar]