Factors Affecting Dimensional Accuracy of 3-D Printed Anatomical Structures Derived from CT Data

Abstract

Additive manufacturing and bio-printing, with the potential for direct fabrication of complex patient-specific anatomies derived from medical scan data, are having an ever-increasing impact on the practice of medicine. Anatomic structures are typically derived from CT or MRI scans, and there are multiple steps in the model derivation process that influence the geometric accuracy of the printed constructs. In this work, we compare the dimensional accuracy of 3-D printed constructs of an L1 vertebra derived from CT data for an ex vivo cadaver T-L spine with the original vertebra. Processing of segmented structures using binary median filters and various surface extraction algorithms is evaluated for the effect on model dimensions. We investigate the effects of changing CT reconstruction kernels by scanning simple geometric objects and measuring the impact on the derived model dimensions. We also investigate if there are significant differences between physical and virtual model measurements. The 3-D models were printed using a commercial 3-D printer, the Replicator 2 (MakerBot, Brooklyn, NY) using polylactic acid (PLA) filament. We found that changing parameters during the scan reconstruction, segmentation, filtering, and surface extraction steps will have an effect on the dimensions of the final model. These effects need to be quantified for specific situations that rely on the accuracy of 3-D printed models used in medicine or tissue engineering applications.

Introduction

Additive manufacturing (also referred to as 3-D printing) is seeing increased used in medicine [1–4]. Physical models developed from three-dimensional data obtained from imaging modalities such as CT and MRI have been successfully applied to plan surgical procedures, for education, and for training purposes [5]. Custom-fitted medical devices such as cranio-maxillofacial prosthetics, surgical guides, and other implants have also been developed from 3-D image data [6, 7].

Similar in many respects to these medical 3-D printing applications, tissue engineering has focused on developing anatomically accurate tissue matrices constructed using biological materials. Many applications are being explored, such as ear [8], bone cartilage [9], menisci for the knee [10], cranial features [11], and other orthopedic disorders [12]. The resulting geometric constructs are dependent on many process variables that influence the accuracy of the final object, such as scan acquisition and reconstruction parameters, 3-D model extraction and filtering techniques, and 3-D printing parameters. Ideally, these printed constructs are meant to be exact replicas of patient-specific anatomic structures, as the functionality of the manufactured object in most instances is tied to its anatomical accuracy.

When deriving anatomic models from medical scan data, care should be taken to maximize geometric fidelity for printed models and tissue engineering scaffolds. Critically important is the ability to discern tissue boundaries defining the extent of anatomic structures of interest, so parameters should be chosen carefully to achieve appropriate image quality. Improvements in these methodologies lie in developments in both 3-D printing and CT technology. Technological improvements will generate improved high-resolution scans in a clinically appropriate time frame and then extract models for printing with minimal deviation from the native tissue geometry. An example of a recent technological development in CT scanning that could be helpful in this regard is the commercial availability of dual-energy CT (DECT), which has the potential to produce trabecular bone data sets that are not averaged with soft tissue information and to differentiate calcified tissue structures from iodinated contrast.

The image quality that we expect from CT and MRI is quite well characterized in terms of the scan parameters used; however, the effect of changing process parameters on the ultimate accuracy of 3-D printed models derived from these modalities has not been thoroughly explored. At every step in the process from scanning a patient in a CT scanner to the final 3-D printing, errors may be introduced that affect the dimensions of the physical model. For example, during the initial scan, the choice of scan techniques will affect the image noise, contrast, and resolution. The choice of reconstruction kernel will likewise affect the image resolution and noise power spectrum [13, 14]. Changes in these image quality metrics may produce a significant effect on the determination of anatomic boundaries that are used to define structures in the anatomy.

After scan acquisition, the methods used to segment structures of interest will have an effect on dimensional accuracy. We have shown that when using semi-automated segmentation of bony structures, the choice of threshold values will have a direct effect on printed model accuracy [15]. Post-segmentation results are processed by software to extract a tessellated surface mesh that defines the model. The multiple algorithms available for this purpose will give different results depending on the choice of parameters used in each algorithm and by any post-extraction filtering. Finally, 3-D printing software must convert the mesh model into specific tool paths to be implemented by the printer. There are resolution limits as well as multiple parameter choices for the printing process that will affect the quality and accuracy of the resulting model.

The scanning-segmentation-surface extraction-3-D printing pipeline produces a very large parameter space that will impact the accuracy of 3-D printed models. The purpose of this study is to examine the effects of changing some of the parameters available at different stages of the model creation process to determine the effect on the model geometry. This work expands a previous study on the dimensional accuracy of 3-D printed vertebrae, where we focused on changing intensity thresholds used for semi-automated segmentation. Here, we additionally investigate the dimensional accuracy of vertebral models processed using different surface extraction algorithms and with varied post-extraction filtering. To investigate some of the effects of changing CT scan parameters, we compare dimensions of models produced from CT scans of physical cubes, reconstructed with varying reconstruction kernels.

Deriving complex anatomical geometries from CT and other imaging modalities is generally time-consuming, and the algorithms for automating these processes are continually evolving and improving. As these algorithms change, it is important to verify that the accuracy of the resulting manufactured object relative to the original anatomy is adequately preserved. The objective of this study was to quantify and compare dimension fidelity as some of the process variables are systematically changed. Other studies have investigated the impact of CT scanning parameters on accuracy of volume-rendered models [16], but this is one of the first studies to quantitatively investigate the geometric accuracy of a complex anatomic structure throughout the acquisition, processing, and printing stages.

Materials and Methods

Vertebra CT Data Set

A section of ex vivo T-L spine that was being used in an IRB-approved orthopedic research project was scanned in the CT portion of a Discovery 690 PET/CT scanner (GE Medical Systems, Waukesha, WI) [15]. The resulting scan was used as input data for the prior study which is summarized here. The spine segment was aligned approximately with the Z-axis of the scanner; however, due to natural curvature in the spine, the individual vertebra was not necessarily accurately aligned with the scanner bore. Helical scan parameters included 120-kV tube voltage, 100-mA tube current, tube rotation time 0.8 s, “body” bowtie filter, large focal spot, and helical pitch of 0.51. These techniques resulted in an effective 155 mAs/rotation (mAs/rotation divided by helical pitch). The reconstructed slice thickness was 0.625 mm with 0.625-mm slice interval and used the “bone” convolution kernel with a 160 × 160-mm field of view resulting in pixel dimensions of 0.31 × 0.31 mm. The CT scan was transferred to a PC for processing and to a server running Aquarius iNtuition^® (Terarecon, Foster City, CA) for measurements on the volume-rendered vertebra.

After being scanned, the L1 vertebra was separated from the T-L spine. The soft tissue around the vertebra was removed using a scalpel and rongeur and then soaked in an enzymatic detergent for 24 h with subsequent removal of remaining soft tissue with a curette. The specimen was soaked and kept in a blood analog solution to preserve the calcified tissue in “wet state” for all measurements.

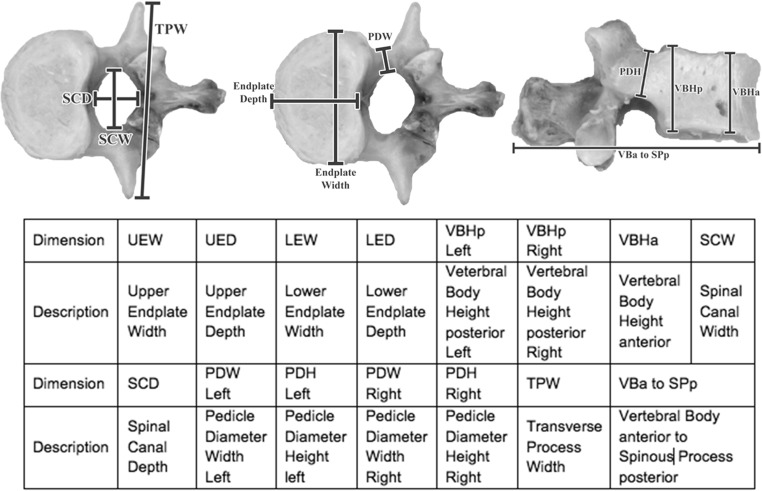
A total of 15 dimensions were measured on the original vertebra, 3-D printed vertebrae, and 3-D rendered vertebrae. The dimensions are listed in Fig. 1 [17]. In the prior study, data for a single observer was used for the initial comparison of original vertebra vs software rendered vertebra vs 3-D printed vertebra. A second, different observer repeated the measurements for the comparison of dimensions vs the threshold level. Each observer made three separate measurements so that the uncertainty in each dimension’s value could be estimated for statistical analysis.

Fig. 1.

Images of the L1 vertebra used in this study. The markers indicate the approximate locations of the dimensional measurements investigated in this study

Effect of Variable Segmentation Threshold

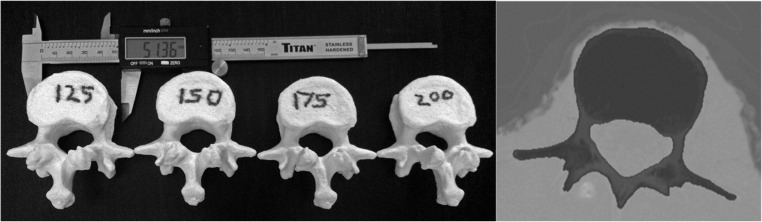
As described in the prior work, the CT data from the L1 vertebra was processed in Analyze 11.0 (AnalyzeDirect Inc., Overland Park, KS) as follows: (a) Data was interpolated to cubic voxels approximately 0.31 mm³ using cubic spline interpolation; (b) The Image Edit tool in Analyze was used to segment the L1 vertebra from the volume using the auto-trace function with manual correction of segmentation regions that extended outside the vertebra. The auto-trace function is a seeded region-growing algorithm that allows the user to set the upper and lower threshold to determine the boundaries of the region. The auto-trace was initially configured to use a lower threshold value of 200 Hounsfield units (HU). Figure 2 shows a slice through the L1 vertebra and the results of semi-automated threshold-based segmentation and the final printed vertebrae. The auto-trace lower threshold setting was then systematically varied to modify the boundary between the bone and soft tissue and new segmentations created. Lower-level thresholds of 125, 150, 175, and 200 HU were used.

Fig. 2.

Three-dimensional printed models segmented using varying lower threshold values for the semi-automated segmentation algorithm. The image on the right shows a typical CT slice through the vertebra with the shaded area representing the segmented bone

Segmentation in Analyze generates “object maps” that define the segmented regions in the CT images. The object map is a 3-D volume with matrix size and dimensions equal to the original volume, with one byte per voxel. The integer value in a voxel denotes that voxels’ membership in a specific “object.” Objects are not required to consist of only contiguous voxels. For a single vertebra, there are no disconnected regions; however, there are usually “voids” resulting from the segmentation process, especially in lower-density areas of the cancellous bone. After segmentation, a binary hole-filling algorithm was applied to eliminate any interior pockets of pixels not assigned to the vertebral object and prevents the surface extraction algorithms from generating a mesh around these interior pockets. The object maps obtained through the segmentation of each layer were filtered once using a binary median filter with a 3 × 3 × 3 kernel in “jack” configuration. The L1 object map was then converted to a binary volume for saving to file and imported into the Surface Extraction module in Analyze.

In the Surface Extraction module, the adaptive deformation algorithm was used to tessellate the boundary of the segmented object map. As described in the Analyze Help File, this algorithm is based on an adaptive mesh representing a dynamic system of masses connected with springs. A set of ordinary differential equations governs the system which is allowed to evolve to equilibrium [18]. The following parameters were used: 30 iterations, cube edge of 1 (determines initial mesh extraction and resolution of mesh), and time step of 0.01. The minimum cube edge size of 1 preserved fine details in the extracted model. The extracted surface mesh was exported as a standard tessellation language (.stl) file to be used for 3-D printing. Three measurements of each dimension of the final 3-D printed objects were made by a single observer.

The final models generated with the varying segmentation thresholds were printed using a Replicator 2 printer (MakerBot, Brooklyn, NY). This is a low-cost commercially available 3-D printer that uses the fused deposition modeling (FDM) approach, where 3-D geometries are manufactured layer-by-layer by deposition of molten thermoplastic. The minimum slice thickness available for this printer is 0.1 mm, with a lateral (x-y) positioning precision of 11 μm and nozzle diameter of 0.4 mm. The Replicator 2 is designed to exclusively use polylactic acid (PLA). The printer settings were configured to use a layer thickness of 0.2 mm, 10 % infill, two shells (outer layers of the model), extruder temperature of 230 ° C, extrusion speed of 75 mm/s, and with rafts and supports turned on.

The vertebral models were oriented in the printing software with the upper end plate facing down on the printing platform and with the end plate as parallel as possible to the platform. This resulted in the minimum amount of support material being generated. Print time was approximately 2 h per vertebral model. Printing of the vertebral models requires the use of supports, since there are overhanging regions such as the transverse processes that would otherwise not be buildable. The resulting models need to have the support material removed, which was done using pliers and resulted in a minimal amount of remaining material that would affect the measured dimensions. Many of the measurements were in areas where no support material was attached to the model.

Software Rendered Vertebra Dimension Measurements

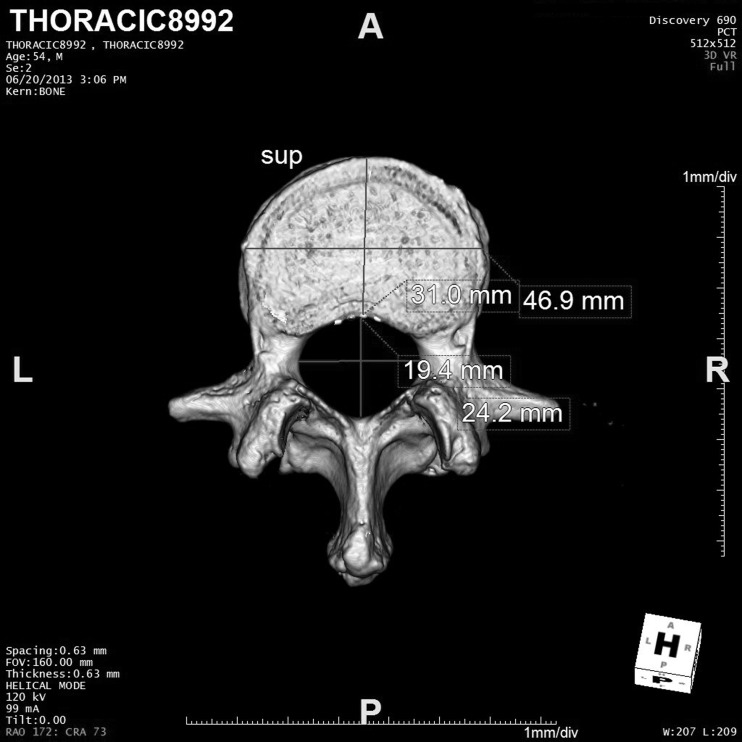
As part of the prior study, the CT scan data described above was transferred to a server for analysis in Aquarius iNtuition^®. iNtuition is a clinical image processing system used to generate 3-D renderings of CT and MRI data and for other types of analysis such as vessel stenosis analysis and cardiac function. iNtuition was used to produce a volume rendering of the L1 vertebra, and the measurements in Fig. 1 were made by a single observer for comparison with the measurements of the 3-D printed vertebrae. The rendering template used was the standard CT abdomen, which uses a window width of 201 and window level of 244 to exclude soft tissue in the rendering. Each measurement was repeated three times over several days to provide an uncertainty estimate for statistical analysis. Figure 3 shows an example of software measurements on the volume-rendered data.

Fig. 3.

Screen capture of the volume-rendered vertebra being measured in iNtuition

Effect of Median Filter

Multiple processing algorithms could be applied to a post-segmentation object map, many of which would affect the dimensions of the resulting model or 3-D printed object. Examples of these include the morphological operations of erosion, dilation, opening, or closing filters which will have a direct effect on boundary locations. The binary hole-filling filter mentioned earlier would have no effect on model dimensions, as it will not modify the exterior surface of the segmentation.

A commonly used algorithm that will affect model dimensions is a binary median filter, which can help remove small irregularities in object boundary segmentations. To investigate the effect on final dimensions, median filters using a 3 × 3 × 3 kernel were applied once, twice, and three times to the segmentation created using the 200-HU lower threshold segmentation value.

To reduce the complexity and cost of the project, 3-D models were not printed for the process modifications that were tested in the remainder of this work. We have shown that the software rendered model dimensions measured were consistent with the values measured on the physically printed vertebrae, and we use software-based dimension measurements here. The assumption is that changes measured by software measurements of models would be similarly reflected in dimensional changes in 3-D printed models.

For the median-filtered vertebral object maps, the object maps were converted to binary volumes and loaded in the Volume Render module in Analyze. The binary object maps were rendered and measurement tools were used to determine the dimensions shown in Fig. 1. A single observer made three repeat measurements for each of the dimensions as in the other cases.

Surface Extraction (Tessellation) Algorithm

For a single segmented and filtered object map, a total of six different algorithms available in the Surface Extraction module in Analyze were used to extract mesh surfaces: adaptive deformation with cube edge sizes of 1, 3, and 5 pixels; marching cubes (binary) [19]; and the thin-wall algorithm (5 × 5 × 5 kernel) with adaptive deformation or marching cubes. The thin-wall algorithm is designed to be used with thin-walled structures [18], which would not seem necessary with the current data set. We found that the algorithm did give reasonable results with this data and included this algorithm for comparison purposes.

The extracted mesh surfaces were saved as .stl files and rendered in the open-source modeling software Blender 2.68 (Stichting Blender Foundation, Amsterdam, Netherlands). Blender provides appropriate tools for distance measurements of displayed models. As before, measurements by a single observer were repeated three times. These measurements were compared to the dimensions measured on the volume-rendered CT scan data of the L1 vertebra.

CT Reconstruction Kernel

An important determinant of CT image quality in scanners using filtered back-projection is the selected kernel used. For the purposes of this study, we are concerned with the effect on the model accuracy when reconstruction kernels are changed.

In order to evaluate the CT reconstruction kernels, cube models with nominal sizes of 1 and 5 cm edges were created in Blender, printed on the Replicator 2 using the print settings described above, and scanned using the Discovery 690 PET/CT scanner. The cubes were aligned with the cardinal axes of the scanner using the laser alignment lights, and the X, Y, and Z axes were labeled on the cubes for measurement with a caliper. Scan parameters were equivalent to those used for the cadaver spine, resulting in a very high signal to noise ratio.

The CT scans of the cubes were reconstructed using eight different reconstruction kernels: standard, soft, lung, chest, detail, bone, bone plus, and edge. The reconstructed images were sent to the Aquarius iNtuition server for measurement. Multi-planar reformatted images of the three cardinal axes were displayed using a bone CT display window (window width of 2200, window level of 200), and measurements by a single observer were repeated three times for all three axes (X, Y, and Z) on each cube using the digital measuring tool in iNtuition. Measurements on the physical cubes were made with a digital caliper by a single observer and repeated three times.

Measurements and Statistical Analysis

Measurements of a total of 15 dimensions for the vertebrae and three axes (X, Y, and Z) for the cubes were taken on the 3-D printed and 3-D rendered objects using Blender, Aquarius iNtuition^®, and the Volume Render module in Analyze as described. The observers repeated the measurements three times over several nonconsecutive days to avoid bias due to learning effects. The means and standard deviations for the measurements of each dimension were calculated and used for ANOVA analysis in SigmaPlot 12.5 (Systat Software, Inc., San Jose, CA).

Results

Comparison of Different Segmentation Thresholds

In Table 1, we summarize the results of the prior study which investigated changing segmentation thresholds.

Table 1.

Dimension comparisons for original vertebra and 3-D printed models using varying segmentation thresholds

Dimension	Original vertebra (mm)	Unfiltered model (mm)	125-HU threshold model (mm)	150-HU threshold model (mm)	175-HU threshold model (mm)	200-HU threshold model (mm)
UEW	48.3 ± 0.12	48.2 ± 0.0	49.2 ± 0.10	49.3 ± 0.0	49.0 ± 0.10	48.7 ± 0.10
UED	31.5 ± 0.81	31.5 ± 0.18	32.0 ± 0.40	32.0 ± 0.73	31.8 ± 0.03	31.8 ± 0.29
LEW	49.5 ± 0.24	49.6 ± 0.15	50.0 ± 0.06	50.1 ± 0.03	50.1 ± 0.10	50.0 ± 0.05
LED	31.0 ± 0.22	31.7 ± 0.33	32.2 ± 0.06	32.0 ± 0.14	31.9 ± 0.09	31.8 ± 0.06
VBHp left	26.1 ± 0.27	27.5 ± 0.37	29.3 ± 0.25	28.3 ± 0.15	27.5 ± 0.54	27.4 ± 0.53
VBHp right	26.0 ± 0.33	27.1 ± 0.22	29.5 ± 0.13	27.6 ± 0.52	27.4 ± 0.39	27.5 ± 0.30
VBHa	26.1 ± 0.02	27.3 ± 0.01	29.3 ± 0.09	28.6 ± 0.06	28.2 ± 0.01	27.9 ± 0.34
SCW	24.3 ± 0.03	23.9 ± 0.11	23.4 ± 0.08	23.4 ± 0.14	23.1 ± 0.33	23.4 ± 0.06
SCD	21.1 ± 0.13	20.5 ± 0.17	20.0 ± 0.09	19.8 ± 0.50	20.0 ± 0.36	20.1 ± 0.13
PDW left	9.1 ± 0.02	10.8 ± 0.01	10.1 ± 0.38	9.5 ± 0.03	9.6 ± 0.15	9.4 ± 0.27
PDH left	15.8 ± 0.12	16.9 ± 0.02	17.5 ± 0.16	17.0 ± 0.18	17.1 ± 0.36	17.0 ± 0.08
PDW right	10.7 ± 0.19	11.5 ± 0.3	11.8 ± 0.11	11.6 ± 0.07	11.7 ± 0.02	11.6 ± 0.13
PDH right	15.7 ± 0.04	17.0 ± 0.24	17.3 ± 0.13	17.0 ± 0.11	17.1 ± 0.33	17.1 ± 0.27
TPW	77.1 ± 0.01	78.0 ± 0.16	77.7 ± 0.14	77.3 ± 0.25	77.5 ± 0.22	77.2 ± 0.12
VBa to SPp	84.6 ± 0.12	85.4 ± 0.34	85.9 ± 0.90	86.0 ± 0.46	85.5 ± 0.27	84.9 ± 0.25

Shaded cell indicates ANOVA result of significant difference (P < 0.05) from original vertebra dimension. Data in the second column is from the 200-HU threshold nonmedian-filtered model measured in the Volume Render module in Analyze and are shown for comparison. Data from [15]

The repeatability of the individual dimension measurements was not significantly influenced by the segmentation threshold used to create the model. For the original vertebra, the mean values of the measurement standard deviations and coefficient of variations (COV%) were 0.17 mm (0.66 %). For the 3-D printed models, the mean standard deviation (COV%) values were 0.18 mm (0.69 %), 0.22 mm (0.91 %), 0.23 mm (0.8 %), and 0.2 mm (0.78 %) for segmentation threshold values of 200, 175, 150, and 125, respectively.

When comparing measurements on physical 3-D printed models vs measurements made on volume-rendered vertebra, we found that the results were in reasonable agreement. This comparison was made using the 200-HU threshold model by a single observer. The original vertebra vs volume-rendered measurement comparisons were significantly different for 5 of 15 measurements (33 %), the volume-rendered vs 3-D printed measurement comparisons were significantly different for 7 of 15 measurements (~47 %), and the original vertebra vs 3-D printed measurement comparisons were significantly different for 6 of 15 measurements (40 %). The measurements shown in Table 1 were made by a different observer and show a larger number of significantly different dimensions for the 200-HU threshold values compared to the original vertebral dimensions (9 of 15 measurements significantly different).

We note that the majority (5 of 6) of the statistically significant differences in the original vertebra dimensions vs the 3-D printed models were for dimensions that were aligned with the printer Z-axis. The printed vertebra was aligned with the upper endplate parallel to the printer platform to reduce the amount of support material that was needed. Given that the layer thickness of 0.2 mm is much larger than the stated x-y positioning precision of 11 μm, we suspect that the Z-axis accuracy for this printer is poorer than the x-y accuracy.

Effect of Median Filters

Table 2 shows the results of ANOVA testing comparing the dimensions of the segmented vertebra after application of a binary median filter with the unfiltered object dimensions after the application of a median filter once, twice, and three times.

Table 2.

ANOVA test results for the effect of median filtering on model dimensions

Dimension	Unfiltered model (mm)	Median filter 1 (mm)	Median filter 2 (mm)	Median filter 3 (mm)
UEW	48.2 ± 0.0	48.0 ± 0.30	47.9 ± 0.30	48.1 ± 0.20
UED	31.5 ± 0.18	31.8 ± 0.14	32.2 ± 0.17	32.2 ± 0.23
LEW	49.6 ± 0.15	49.2 ± 0.0	49.2 ± 0.0	49.4 ± 0.18
LED	31.7 ± 0.33	31.9 ± 0.02	31.8 ± 0.05	31.9 ± 0.21
VBHp Left	27.5 ± 0.37	27.3 ± 0.23	27.3 ± 0.25	27.2 ± 0.43
VBHp right	27.1 ± 0.22	26.9 ± 0.29	26.9 ± 0.28	26.9 ± 0.13
VBHa	27.3 ± 0.01	27.4 ± 0.10	27.4 ± 0.04	27.7 ± 0.13
SCW	23.9 ± 0.11	23.7 ± 0.17	24.0 ± 0.29	24.0 ± 0.25
SCD	20.5 ± 0.17	20.2 ± 0.18	20.9 ± 0.03	20.2 ± 0.17
PDW left	10.8 ± 0.01	10.7 ± 0.18	10.9 ± 0.09	10.9 ± 0.0
PDH left	16.9 ± 0.02	16.6 ± 0.04	16.9 ± 0.15	16.9 ± 0.20
PDW right	11.5 ± 0.3	11.5 ± 0.15	11.9 ± 0.05	12.0 ± 0.14
PDH right	17.0 ± 0.24	16.7 ± 0.04	16.8 ± 0.19	16.7 ± 0.03
TPW	78.0 ± 0.16	78.0 ± 0.35	77.9 ± 0.07	77.9 ± 0.06
VBa to SPp	85.4 ± 0.34	85.5 ± 0.04	85.5 ± 0.09	85.8 ± 0.03

Shaded cells indicate that ANOVA testing found a significant difference (P < 0.05) in that dimension compared to the unfiltered model

Precision of the model dimension measurements for the median-filtered models was similar to the unfiltered model. For the unfiltered model, the mean of the measurement standard deviations and COV (%) was 0.18 mm (0.68 %). For the median-filtered models, the means of the standard deviations and COV values were 0.15 mm (0.6 %), 0.14 mm (0.55 %), and 0.16 mm (0.62 %) for one, two, and three applications of the median filter, respectively.

Surface Extraction Algorithms

Measurements from the 3-D rendered vertebrae obtained by six different surface extraction algorithms mentioned above were compared with the 3-D rendering of the reconstructed CT scan of the original cadaver L1 vertebra. Table 3 shows whether or not these measurements were significantly different from the volume rendering of the original vertebra.

Table 3.

ANOVA test results for comparison of dimensions of volume-rendered vertebra with dimensions of models tessellated with various surface extraction algorithms in Analyze

Dimension	Rendered vertebra (mm)	AD-CE-1 (mm)	AD-CE-3 (mm)	AD-CE-5 (mm)
UEW	47.1 ± 0.38	48.1 ± 0.20	48.4 ± 0.40	48.7 ± 0.10
UED	31.1 ± 0.12	31.9 ± 0.04	32.7 ± 0.07	33.4 ± 0.21
LED	47.8 ± 0.61	49.4 ± 0.18	50.2 ± 0.37	51.2 ± 0.39
LEW	30.7 ± 0.30	31.9 ± 0.19	33.0 ± 0.17	33.8 ± 0.36
VBHp right	26.0 ± 0.31	27.1 ± 0.19	27.9 ± 0.12	28.3 ± 0.18
VBHp left	25.3 ± 0.26	26.6 ± 0.17	27.2 ± 0.49	28.2 ± 0.35
SCW	26.8 ± 0.40	27.7 ± 0.15	28.6 ± 0.15	29.5 ± 0.11
SCD	24.5 ± 0.46	23.6 ± 0.07	22.8 ± 0.05	21.7 ± 0.08
VBHa	19.5 ± 0.26	19.2 ± 0.03	18.1 ± 0.03	17.3 ± 0.03
PDW left	9.1 ± 0.50	10.0 ± 0.09	10.8 ± 0.06	11.7 ± 0.13
PDW right	16.6 ± 0.44	16.9 ± 0.28	17.5 ± 0.06	18.1 ± 0.04
PDH left	10.5 ± 0.69	11.8 ± 0.27	13.0 ± 0.04	13.7 ± 0.04
PDH right	15.8 ± 0.15	16.8 ± 0.11	17.2 ± 0.08	18.5 ± 0.21
TPW	76.8 ± 0.50	77.7 ± 0.10	78.1 ± 0.03	78.6 ± 0.05
VBa to SPp	83.8 ± 0.68	85.2 ± 0.07	86.0 ± 0.04	86.9 ± 0.11
Dimension	Rendered vertebra (mm)	MC-Bin (mm)	TW-AD (mm)	TW-MC (mm)
UEW	47.1 ± 0.38	48.0 ± 0.40	50.0 ± 0.30	49.1 ± 0.30
UED	31.1 ± 0.12	32.0 ± 0.06	34.8 ± 0.02	33.2 ± 0.10
LED	47.8 ± 0.61	50.0 ± 0.25	52.2 ± 0.44	51.2 ± 0.20
LEW	30.7 ± 0.30	32.2 ± 0.15	35.1 ± 0.35	33.2 ± 0.11
VBHp right	26.0 ± 0.31	27.2 ± 0.35	29.4 ± 0.12	28.3 ± 0.04
VBHp left	25.3 ± 0.26	26.8 ± 0.28	29.4 ± 0.54	27.9 ± 0.08
SCW	26.8 ± 0.40	28.0 ± 0.12	30.4 ± 0.05	29.2 ± 0.12
SCD	24.5 ± 0.46	23.5 ± 0.04	20.4 ± 0.04	22.2 ± 0.06
VBHa	19.5 ± 0.26	19.0 ± 0.10	15.9 ± 0.02	17.8 ± 0.04
PDW left	9.1 ± 0.50	10.1 ± 0.03	13.1 ± 0.06	11.2 ± 0.07
PDW right	16.6 ± 0.44	17.2 ± 0.04	19.7 ± 0.08	18.4 ± 0.02
PDH left	10.5 ± 0.69	12.1 ± 0.10	14.9 ± 0.04	13.2 ± 0.04
PDH right	15.8 ± 0.15	16.9 ± 0.10	19.5 ± 0.07	18.1 ± 0.22
TPW	76.8 ± 0.50	77.9 ± 0.03	80.3 ± 0.03	79.1 ± 0.06
VBa to SPp	83.8 ± 0.68	85.4 ± 0.05	88.0 ± 0.02	86.6 ± 0.01

The shaded cells are significantly different (P < 0.05) from the software rendered dimension measurement. Numbers 1, 3, and 5 denote cube edge size for these algorithms

AD adaptive deformation, CE cube edge, MC marching cubes, TW thin wall

Similar to the other process parameters investigated, the choice of surface extraction algorithm had little effect on the precision of the dimension measurements. The mean standard deviation values of the measurements for the six surface extraction algorithms (and COV%) were 0.14 (0.63 %), 0.14 (0.68 %), 0.16 (0.56 %), 0.14 (0.5 %), 0.15 (0.45 %), and 0.10 (0.35 %) for the AD-CE-1, AD-CE-3, AD-CE-5, MC-Bin, TW-AD, and TW-MC surface extraction algorithms, respectively.

Reconstruction Algorithms

Tables 4 and 5 below show the X-, Y-, and Z-axis caliper measurements of the 3-D printed cubes and Aquarius iNtuition^® measurements of multi-planar reformatted images of cubes with nominal edge sizes of 1 and 5 cm.

Table 4.

X-, Y-, and Z-axis measurements of 3-D printed and rendered 1-cm cube reconstructed using various kernels

	X (mm)	Y (mm)	Z (mm)
Physical cube →	10.17 ± 0.01	10.1 ± 0.02	9.98 ± 0.01
Kernel
Standard	11 ± 0.1	10.73 ± 0.12	10.63 ± 0.12
Soft	11.2 ± 0.1	10.67 ± 0.12	10.6 ± 0.1
Lung	10.53 ± 0.06	10.47 ± 0.06	10.57 ± 0.15
Chest	10.7 ± 0.1	10.33 ± 0.06	10.57 ± 0.12
Detail	10.93 ± 0.06	10.7 ± 0.17	10.6 ± 0.1
Bone	10.5 ± 0	10.4 ± 0.0	10.63 ± 0.12
Bone plus	10.33 ± 0.06	10.33 ± 0.06	10.63 ± 0.06
Edge	10.47 ± 0.06	10.2 ± 0.0	10.63 ± 0.12

Shading indicates that all of the measured values were significantly different (P < 0.05) than the measured dimensions of the original cube

Table 5.

X-, Y-, and Z-axis measurements of 3-D printed and rendered 5-cm cube reconstructed using various kernels

	X (mm)	Y (mm)	Z (mm)
Physical cube →	49.65 ± 0.02	49.65 ± 0.04	49.82 ± 0.01
Kernel
Standard	50.4 ± 0.10	50.43 ± 0.05	50.36 ± 0.11
Soft	50.83 ± 0.05	50.6 ± 0.10	50.5 ± 0.10
Lung	50.06 ± 0.05	49.83 ± 0.05	50.46 ± 0.05
Chest	50.26 ± 0.05	50.3 ± 0.10	50.36 ± 0.15
Detail	50.4 ± 0.10	50.43 ± 0.05	50.46 ± 0.05
Bone	50.03 ± 0.05	50.06 ± 0.05	50.36 ± 0.05
Bone plus	49.93 ± 0.05	50 ± 0.0	50.3 ± 0.10
Edge	50 ± 0.0	50.13 ± 0.11	50.5 ± 0.0

Shading indicates that all of the measured values were significantly different (P < 0.05) than the measured dimensions of the original cube

The measurements of the three axes of the 3-D printed cubes were compared with the measurements from the reconstructed images of the same cubes in Aquarius iNtuition^®. One-way ANOVA analysis showed that all of the measurements from the images were significantly different than the measurements made directly on the 3-D printed cubes using a caliper.

Discussion

The precision of the dimensional measurements overall was good with the COV averaging less than 1 %. Specific measurements had higher COV values due to the difficulty in precisely repositioning the measurement “device,” whether that was the physical caliper or software caliper used to make measurements on the virtual models. Some measurements, such as the vertebral body height, tended to be more sensitive to positioning of the measuring device. Other measurements proved to be more robust and resulted in a smaller measurement standard deviation.

Measurement precision of the various dimensions needs to be considered when comparing them using ANOVA or other statistical procedure. Measurements that were more difficult to reproduce will lead to higher standard deviations, which may result in measurement difference deemed insignificant by statistical testing, whereas more precise measurements (usually considered a positive attribute) may be significantly different. Our goal was to show the trends that occurred in the statistical analysis as process parameters were changed, and the significance of the absolute deviations from the original vertebra dimensions would have to be interpreted in light of a specific clinical application. Typical deviations from the original vertebra dimensions were of the order of 1 mm or less, which may not be clinically significant despite a statistical test showing a significant difference.

Segmentation Threshold

The results in Table 1 show that the dimensional accuracy of the 3-D printed vertebrae generally increased with increasing segmentation thresholds. It was not possible to increase the threshold above 200 HU using the semi-automated segmentation procedure, as large voids in the vertebra interior began appearing that would have required significant manual correction. Our purpose here was not to find the threshold to produce the most accurate model, but to illustrate the effect on accuracy that changing the threshold produced.

The overall rate of significant differences in the measured dimensions in Table 1 was close to 2:1 (~68 % significantly different). The maximum differences in means (approximately 2–4 mm) were observed between the original vertebra and the 125-HU threshold 3-D printed vertebra measurements of the vertebral body height (VBHp left and right). The rest of the measurements showed differences of the order ±1 mm or less.

Effect of Median Filters

The results in Table 2 show that the application of median filters on the dimensional accuracy of segmented object maps increased with the number of applications. The effect of a single application was negligible. The effect of increasing the number of applications is not predictable, with some dimensions increasing and some dimensions decreasing. These results would imply that care should be taken in applying any post-segmentation filtering. Changes in the median filter parameters, especially kernel size configuration, will undoubtedly change the effect on the model dimensions. The median filter kernel used here is, in some sense, the “minimal” three-dimensional median filter, and we expect other kernels to have a more significant effect on model dimensions.

Surface Extraction Algorithm

The choice of surface extraction algorithm can have a significant impact on the final model dimensions, as shown by the data in Table 3. There are various tradeoffs in the algorithms available; for example, speed of execution may be increased at the expense of retained anatomic detail. For the anatomic geometry investigated here, the adaptive deformation algorithm using a cube edge of 1 produced the most accurate model of the vertebra. This approach also produced a more complex tessellation of the model surface (larger number of triangles). For a cube edge of 1, there were about 573,000 triangles generated in 12.5 s, where the cube edge of 3 generated 64,000 triangles in 1.8 s and a cube edge of 5 generated 24,000 triangles in 1.5 s. The overall execution time was not prohibitive for any of the algorithms used; however, for more complex anatomic structures, this may become an issue that would impact the choice of algorithm.

Reconstruction Kernel

The physical cubes were printed from simple geometric models created in Blender and show that there is error introduced during the printing process. The dimensional differences averaged 0.1 mm for the 1-cm cube and 0.3 mm for the 5-cm cube. This implies that the error may be related to the size of the object being printed, though a more extensive investigation would be needed to confirm this.

The choice of CT reconstruction kernel had a relatively small impact on the measured cube dimensions. The maximum differences between the measured dimensions in Tables 4 and 5 were 1.03 and 1.18 mm for the 1- and 3-cm cubes, respectively. One factor that affected the dimension measure in iNtuition was the window/level settings used to display the images. We used a wide setting to ensure that the full extent of the cube was visible in the image. By reducing the window width, the visible extent of the cube boundary would be reduced, resulting in a smaller measured dimension. The low standard deviations (on the order of 0.1 mm) indicate that the measurements were easily reproducible due to the simple geometry of the models involved. This resulted in all of the dimensions being significantly different per the ANOVA testing results. This was not the case for the more complicated geometry inherent in the vertebral models. As mentioned earlier, the significance of the absolute deviation in the dimensional accuracy would have to be interpreted for the specific clinical application.

Reconstruction kernel choice in CT images reconstructed using FBP algorithms represents a tradeoff between image resolution and image noise characteristics. In this work, the scan data was acquired with high signal to noise ratio (SNR), so there were no noise issues in determining the location of the object boundary. The changes in the resolution characteristics are also unlikely to result in a significant change in the determination of the object boundary in this case due to the high contrast of the boundary. In a more realistic clinical situation, the effect of changing reconstruction kernel should be further evaluated to determine the impact on anatomic model fidelity.

Conclusion

Despite efforts in the area of developing 3-D printed models using standard imaging modalities for tissue engineering and related applications, the feasibility of using medical imaging data to design tissue-engineered constructs has only been investigated relatively recently [3]. There is limited information on the geometric accuracy of these techniques in tissue engineering and how this geometric accuracy varies with various imaging and printer conditions. This article serves as an example of how modifications to process parameters may be analyzed to determine their influence on the geometric accuracy of 3-D printed models.

There are several limitations to this study. In particular, the scanning and processing pipeline creates a very-high-dimension parameter space for which it would be prohibitive from a time perspective to fully investigate. We did not investigate changing any of the 3-D printer variables that may have an important effect on the printed model dimensions. The effects of scanning with different models of CT scanner and different reconstruction algorithms such as model-based iterative reconstruction could also be investigated. Finally, there are many commercial and open-source software packages other than those used in this work available to process scan data and produce 3-D models. The algorithms that are used in each of these packages will have their own unique characteristics that would affect the dimensional accuracy of the models.

The purpose of this study was to examine the effects of changing CT reconstruction parameters, segmentation technique, surface extraction algorithms, and post-extraction filtering on the dimensional accuracy of 3-D models. There is currently limited information on the impact on geometric accuracy of these process parameters and how this geometric accuracy changes with various imaging and processing conditions. This work can help improve 3-D printing for medical and tissue engineering applications and help practitioners to generate high-fidelity 3-D models with minimal deviation from the native tissue-of-interest geometry.