Abstract
Background
Emerging work suggests that academic achievement may be influenced by the management of affect as well as through efficient information processing of task demands. In particular, mathematical anxiety has attracted recent attention because of its damaging psychological effects and potential associations with mathematical problem-solving and achievement. The present study investigated the genetic and environmental factors contributing to the observed differences in the anxiety people feel when confronted with mathematical tasks. In addition, the genetic and environmental mechanisms that link mathematical anxiety with math cognition and general anxiety were also explored.
Methods
Univariate and multivariate quantitative genetic models were conducted in a sample of 514 12-year-old twin siblings.
Results
Genetic factors accounted for roughly 40% of the variation in mathematical anxiety, with the remaining being accounted for by child-specific environmental factors. Multivariate genetic analyses suggested that mathematical anxiety was influenced by the genetic and non-familial environmental risk factors associated with general anxiety and additional independent genetic influences associated with math-based problem solving.
Conclusions
The development of mathematical anxiety may involve not only exposure to negative experiences with mathematics, but also likely involves genetic risks related to both anxiety and math cognition. These results suggest that integrating cognitive and affective domains may be particularly important for mathematics, and may extend to other areas of academic achievement.
Keywords: mathematical anxiety, general anxiety, math cognition, quantitative genetics
While research on academic outcomes historically stressed the importance of cognitive abilities, such as general intelligence and working memory (Rohde & Thompson, 2007), emerging literature also increasingly acknowledges the important roles that affective attributes play in academic competence (Eysenck, Derakshan, Santos, & Calvo, 2007; Owens, Stevenson, Hadwin, & Norgate, 2012; Pekrun, Goetz, Frenzel, Barchfeld, & Perry, 2011). Negative affects in the academic context including anger, anxiety, and depression have profound influences on academic performance through both motivational and cognitive mechanisms (Eysenck et al., 2007; Pekrun et al., 2011), highlighting the importance of cognitive-affective interplay in academic development (Prevatt, Welles, Li, & Proctor, 2010; Putwain, Connors, & Symes, 2010). Mathematical anxiety (MA) is one particular example of such academic related affects that has attracted recent research attention, and its debilitating impacts on the development of mathematics skills are well replicated (Ma, 1999; Zientek, Yetkiner, & Thompson, 2010). The overarching aim of the present study was to investigate the etiology of MA in the context of cognitive-affective interplay. Specifically, we examined how genetic and environmental factors contributed to individual differences in MA and how these factors accounted for the relationships between MA and its cognitive and affective correlates (i.e., math cognition and general anxiety).
MA, defined as a feeling of tension and fear that accompanies math-related activities (Richardson & Suinn, 1972), is associated with poorer mathematics achievement (Ashcraft & Krause, 2007), avoidance of situations involving mathematics, and more limited engagement in STEM-related careers (Hembree, 1990). MA is doubly debilitating because it impacts both the cognitive capacity to engage in mathematics problem solving and the affective climate surrounding mathematics (Ho et al., 2000; Wigfield & Meece, 1988). Specifically, MA disrupts working memory functioning during math-related activities (Ashcraft & Krause, 2007; Young, Wu, & Menon, 2012). Moreover, individuals with high MA not only experience cognitive and emotional difficulties when engaging in mathematics, but high levels of anticipatory anxiety can lead to avoidance of mathematics altogether (Lyons & Beilock, 2012a, 2012b; Maloney & Beilock, 2012). Thus, to improve mathematics performance and ameliorate the affective climate surrounding math learning, a better understanding of the etiologies of MA is necessary.
To date, the majority of studies have focused on environmental exposure to success or failure in mathematics as a potential primary mechanism for the development of MA (Ashcraft, Krause, & Hopko, 2007; Meece, Wigfield, & Eccles, 1990). However, genetic as well as environmental influences have been strongly implicated in overall levels of anxiety as well as specific subtypes of anxiety disorders ( Trzaskowski et al., 2013; Van Houtem et al., 2013). General anxiety refers to the excessive anxiety and worry about a variety of future events, past behaviors, and personal competence, and captures individual’s anxious or worrying dispositions in general (Spence, 1997). Although general anxiety is not aimed to measure anxiety about specific event or activity such as taking a test or solving a math problem, it is associated with specific anxiety subtypes, such as test anxiety and MA (Hembree, 1988; Hembree, 1990). Given that MA is moderately associated with general anxiety (Hembree, 1990), there may be genetic and/or environmental etiological factors emanating from the anxiety component of MA. Moreover, mathematics performance is also influenced by genetic and environmental factors (Hart, Petrill, Thompson, & Plomin, 2009; Kovas, Harlaar, Petrill, & Plomin, 2005; Thompson, Detterman, & Plomin, 1991; Wadsworth, DeFries, Fulker, & Plomin, 1995), so it is possible that MA is also influenced by genetic and/or environmental factors stemming from the cognitive demands of math problem solving. Finally, it is important to note that 2/3 of genetic variance and 100% of the shared environmental variance for mathematics is shared with other learning outcomes (in particular, reading), and an additional 1/3 of genetic variance is specific to mathematics (Hart et al., 2009; Kovas et al., 2005; Thompson et al., 1991; Wadsworth et al., 1995). MA may therefore be associated with genetic and environmental factors common to multiple learning outcomes or specific to mathematics.
Further investigations into these possibilities would help advance our understanding of the etiologies of individual differences in MA. Therefore, the current study aimed to examine (1) the extent to which individual differences in MA were influenced by genetic and environmental factors; (2) the genetic and environmental etiology of the association between MA and general anxiety; and (3) the genetic and environmental etiology of the relationships between MA and math achievement, and between MA and reading achievement.
Methods
Participants
Data consisted of 216 monozygotic (MZ; 96 male, 120 female) and 298 same-sex dizygotic (DZ; 124 male, 174 female) twins that are from the Western Reserve Reading and Math Projects (WRRMP), an ongoing logitudinal twin study involving 436 pairs of same-sex twins from the State of Ohio (Hart et al., 2009; Petrill, Deater-Deckard, Thompson, DeThorne, & Schatschneider, 2006). Twin zygosity was determined by genotyping via buccal swab or saliva sample. Fourteen percent of the families did not consent to genotyping. A questionnaire of twin physical similarity was used to determine zygosity of twins in these families (Goldsmith, 1991). Note that excluding twins who were not genotyped did not impact the results of the study (results available upon request).
Assessments began in kindergarten or first grade, and continued across a maximum of 8 home visits. The current study examined data collected in the last two home visits when twins were 12.25 years old on average (SD = 1.20 years; Range = 8.75 to 15.33 years). Ninety-one percent of the sample was White, 5% African American, and 2% Asian. Parent education was slightly skewed (skewness = −.07) but varied widely: 10% had a high school education or less, 16% had attended some college, 42% had a bachelor degree, 20% had some postgraduate education, and 5% did not specify. Multivariate analyses of variance suggested that there were no mean differences on children’s age, gender, race, parental education level, or any main study variables between MZ twins and DZ twins (for twin1, F (22, 320) = .85, p = .66; for twin2, F (22, 316) = 1.02, p = .44).
Procedure
Parental consent and twins’ assents were obtained before the administration of the assessments. Subsequently, twins completed a series of questionnaires and cognitive assessments. Each twin was tested by a separate tester, and the same trained tester administered the tesing to each twin for the two home visits which occurred within one month of each other. Each visit took approximately 3 hours per twin. Each family received $100 honorarium after participation in each visit. Prior to the initiation of data collection, all procedures were approved by the Office of Responsible Research Practice at the Ohio State University.
Materials
Mathematical Anxiety
MA was measured using the Revised Mathematics Anxiety Rating Scale of Elementary Students (MARS-E; Suinn, Taylor, & Edwards, 1988). The MARS-E consists of 26 items that are rated on a 5-point Likert type scale (1 = not at all nervous; 3 = fairly nervous; 5 = very very nervous), measuring how tense or anxious children feel when they are engaged in math-related activities. A sample item is “If you had to add up a cash register receipt after you bought several things, how nervous would you feel”. This scale has a Cronbach’s α of .94.
General Anxiety
General anxiety was measured using the Spence Children’s Anxiety Scale (Spence, 1997), a 44-item instrument measuring a variety of anxiety problems experienced by children. The general anxiety subscale consists of 6 items that are rated on a 4-point Likert type scale (1 = never, 4 = always). A sample item is “I worry about things.” Cronbach’s α for this subscale is .71.
Math Problem Solving
Math problem solving was assessed using the Applied Problem subtest from the Woodcock Johnson III Tests of Achievement (Woodcock, McGraw, & Mather, 2001). In this test, children are asked to utilize their math knowledge, calculation skills, and quantitative reasoning to solve the problems presented in the test. Published internal reliabilities for this test are above .80 (McGrew, Schrank, & Woodcock, 2007). Raw scores were used for descriptive purposes. To maintain consistency with our prior publications, we employed raw scores residualized for age, age squared, and gender for all behavioral genetic modeling.
Reading Comprehension
Reading comprehension was assessed using the Passage Comprehension subtest in the Woodcock Reading Mastery Test-Revised (Woodcock, 1998). The passage comprehension subtest is a cloze format test of comprehension in which children are asked to read and complete a series of sentences with missing words. The published split-half reliability of this subtest is from .73 to .96 for Grades 3 through 5. Raw scores were used for descriptive purposes. For all behavioral genetic modeling, raw scores were residualized for age, age squared, and gender.
Results
Descriptive statistics and correlational analyses were conducted using SAS 9.3. Behavioral genetic models were fitted in Mx using full information maximum likelihood estimation (Neale, 1997).
Descriptive and Correlational Analyses
Descriptive statistics, phenotypic correlations, and twin intraclass correlations for monzygotic (MZ) and dizygotic (DZ) twins are presented in Table 1. All four study variables distributed widely and normally across their entire scales. The potential mean level differences on MA, general anxiety, and math and reading performance scores across child gender (0 = female, 1 = male) were tested together for twin1 and twin2. Standard errors were adjusted to account for sibling non-independence according to Grinffin and Gonzalez (1995). Mean level differences were found for MA (r = −.19, p < .001), general anxiety (r = −.14, p < .05), and math applied problem scores (r = .15, p < .01), suggesting higher MA and general anxiety and lower math applied problem scores for girls. With regards to phenotypic correlations, MA was moderately correlated with general anxiety. MA was negatively correlated with both math problem solving and reading comprehension whereas general anxiety was correlated with neither of them. Lastly, math problem solving and reading comprehension were strongly correlated. Correlations remained essentially unchanged after child age and gender were accounted for.
Table 1.
Descriptive statistics, phenotypic correlations, and twin intra-class correlations of the study variables.
| Variables | Phenotypic Correlations | Twin Intra-class correlations | ||||
|---|---|---|---|---|---|---|
| MA | GA | MPS | RC | MZ | DZ | |
| Mathematical Anxiety | 1 | .46* | .11 | |||
| General Anxiety | .37* | 1 | .43* | .21* | ||
| Math Problem Solving | −.32* | −.10 | 1 | .75* | .55* | |
| Reading Comprehension | −.17* | .00 | .58* | 1 | .77* | .32* |
|
| ||||||
| Descriptive Statistics | ||||||
|
| ||||||
| M | 48.77 | 11.42 | 43.44 | 45.65 | ||
| SD | 16.44 | 2.78 | 6.33 | 7.64 | ||
| Skewness | .92 | .61 | −.17 | −.41 | ||
| Kurtosis | .95 | .42 | .34 | −.00 | ||
| Min | 14.00 | 6.00 | 22.00 | 21.00 | ||
| Max | 126.00 | 21.00 | 62.00 | 62.00 | ||
| Possible Range | 14–130 | 4–24 | 0–63 | 0–68 | ||
| N | 506 | 391 | 509 | 491 | ||
Note: MA = mathematical anxiety; GA = general anxiety; MPS = math problem solving; RC = reading comprehension. The differences between N for MA, math problem solving, and reading comprehension are due to normal variation in N (test times, fatigue, etc). The N for general anxiety questionnaire is lower because that was part of a packet of questionnaires given as a take-home between visits. In contrast, the MA questionnaire was administered at the time of the second home visits.
p < .05.
With respect to the twin intraclass correlations, MZ twins share 100% of their segregating alleles whereas DZ twins share 50% of their segregating alleles, on average. Thus, additive genetic influences are implied if the MZ correlations exceed the DZ correlations. Nonadditive genetic influences are implied if MZ correlations are more than 2 times as similar as DZ correlations. Shared environmental influnces are implied if MZ correlations are less than 2 times as similar as DZ twins. Nonshared environmental influences are implied if MZ correlations are less than 1 (including error). Accordingly, the twin intraclass correlations in Table 1 suggested genetic and nonshared environmental influences on all four variables. In addition, potential nonadditive genetic influences were suggested for MA, general anxiety, and reading comprehension, whereas shared environmental influences were suggested for math problem solving.
Univariate Behavioral Genetic Modeling
To examine the genetic and environmental etiology of MA, a univariate behavioral genetic model was utilized. The univariate behavioral genetic model decomposes the observed phenotypic variance in MA into additive genetic (A), nonadditive genetic (D) or shared environmental (C), and nonshared environmental (E) variance. Note that nonadditive genetic and shared environmental effects were estimated in two separate models because twin design does not allow the estimation of both at the same time. Parameter estimates of the ACE and the ADE model suggested that neither the C nor the D parameter was significant. Subsequently, an AE model was fitted fixing both the C and D paths to zero, and was compared with the ACE and the ADE model using chi-square difference tests. As shown in Table 2, neither the chi-square difference between the AE versus the ACE model, nor the difference between the AE versus the ADE model was significant, suggesting that the more parsimonious AE model best fit the data. In addition, the AE model was preferred given that it had smaller AIC (Akaike, 1987) and BIC (Raftery, 1995) values compared to the ACE and the ADE models. Therefore, the standardized path estimates obtained in the AE model are presented in Table 2.
Table 2.
Univariate modeling results of genetic and environmental influences on mathematical anxiety.
| Model Fit Indices and Model Comparisons | ||||||
|---|---|---|---|---|---|---|
| Model | −2LL (df) | Δ−2LL(Δdf) | AIC | BIC | ||
| ACE | 1354.06(484) | AE vs. ACE: .00(1) | 386.06 | −660.13 | ||
| ADE | 1351.70(484) | AE vs. ADE: 2.36(1) | 383.70 | −661.31 | ||
| AE | 1354.06(485) | - | 384.06 | −662.90 | ||
|
| ||||||
| Standardized Path Estimates from AE model | ||||||
|
| ||||||
| A (95% CI) | .66 (.52 – .76) | |||||
| E (95% CI) | .75 (.65 – .85) | |||||
Note: −2LL = −2 times log likelihood; df = degrees of freedom; Δ −2LL = difference in −2 times log likelihood between two models; Δdf = difference in degrees of freedom between two models; AIC = Akaike’s Information Criterion; BIC = Bayesian Information Criterion. Best fitting model is indicated in bold face. A = additive genetic pathways; C = shared environmental pathways; E = nonshared environmental pathways.
Additive genetic variance of a variable was computed by summing all the squared additive genetic path estimates associated with that variable. Therefore, the additive genetic variance of MA was .43 (i.e., squared pathway from A to MA: 662). Similarly, nonshared environmental variance was computed by summing all the squared nonshared environmental path estimates associated with that variable. As such, the nonshared environmental variance of MA was .57 (i.e., squared pathway from E to MA: .752). Therefore, phenotypic variance in MA was accounted for by moderate levels of additive genetic and nonshared environmental influences.
Multivariate Behavioral Genetic Modeling
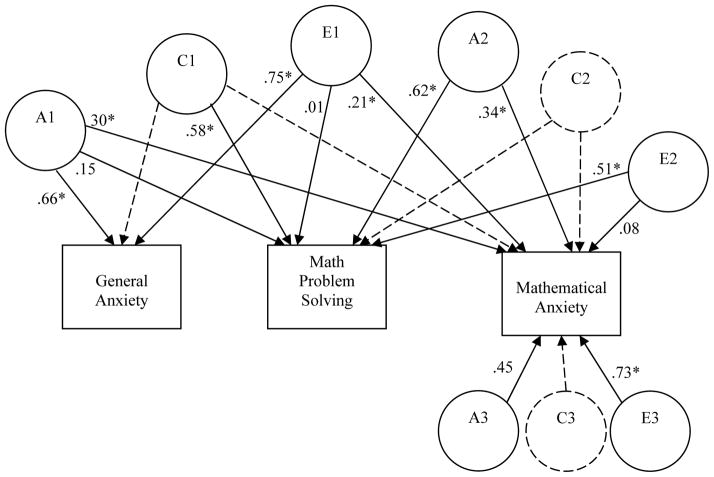
A series of trivariate Cholesky decomposition models was conducted to examine whether the genetic and environmental influences related to general anxiety and math problem solving influenced MA. In trivariate Cholesky decomposition model, phenotypic variance and covariance are decomposed into overlapping and independent sources of additive genetic (A), nonadditive genetic (D) or shared environmental (C), and nonshared environmental (E) variance and covariance (Figure 1). General anxiety was entered into the model first, followed by math problem solving, and MA. In the ACE model, A1, C1, and E1, respectively estimated the additive genetic, shared environmental, and nonshared environmental variance common to general anxiety, math problem solving, and MA. A2, C2, and E2, respectively represented the overlapping additive genetic, shared environmental, and nonshared environmental variance common to math problem solving and MA independent from general anxiety. Lastly, A3, C3, and E3, respectively represented the unique additive genetic, shared environmental, and nonshared environmental variance of MA independent from both general anxiety and math problem solving. In the ADE model, the A and E factors were the same with the A and E factors in the ACE model. In addition, D1 represented the overlapping nonadditive genetic variance common to general anxiety, math problem solving, and MA; D2 represented nonadditive genetic variance common to math problem solving and MA independent from general anxiety; and D3 estimated the unique nonadditive genetic variance in MA independent from both general anxiety and math problem solving.
Figure 1.
Trivariate Cholesky model. This model decomposes the variance in and covariance between general anxiety, math problem solving, and mathematical anxiety into latent genetic (A), shared environment (C), and nonshared environmental (E) components that are common to general anxiety, math problem solving, and mathematical anxiety (A1, C1, E1), that are common to math problem solving and mathematical anxiety independent from general anxiety (A2, C2, E2), and that are unique to mathematical anxiety independent from general anxiety and math problem solving (A3, C3, E3). Only one twin is shown in the figure for simplicity. * p < .05.
Model fit indices are shown in Table 3. Compared to the ADE model, the ACE model had smaller AIC and BIC values indicating a better fit. In addition, results from the ACE model showed that none of the C paths associated with general anxiety or MA were significant. Therefore, a reduced ACE model was fitted (Figure 1), fixing all but one C paths to zero and estimating only the C effects on math problem solving (i.e., C1 to math problem solving). Model fit indices and model comparison results are presented in Table 3. The chi-square difference between the full versus the reduced ACE model was .92, suggesting that constraining the above mentioned C paths from the full ACE model yielded a more parsimonious model without worsening model fit. Thus, standardized parameter estimates of the best-fitting, more parsimonious reduced ACE model are presented in Table 3.
Table 3.
Trivariate Cholesky modeling results of genetic and environmental influences on general anxiety (GA), math problem solving (MPS), and mathematical anxiety (MA).
| Model Fit Indices and Model Comparisons | ||||
|---|---|---|---|---|
| Model | −2LL (df) | Δ−2LL(Δdf) | AIC | BIC |
| Full ACE Model | 3560.73 (1327) | - | 906.73 | −1893.66 |
| Full ADE Model | 3566.35 (1327) | - | 912.35 | −1890.85 |
| Reduced ACE Model | 3561.65 (1332) | Reduced vs. Full ACE: .92 (5) | 897.65 | −1907.04 |
|
| ||||
| Standardized Path Estimates from Reduced ACE Model | ||||
| Overlap between GA, MPS, and MA | Overlap between MPS and MA | Unique effects of MA | ||
|
| ||||
| A1 (95% CI) | A2 (95% CI) | A3 (95% CI) | ||
| GA | .66 (.52 – .76) | |||
| MPS | .15 (.00 – .32) | .62 (.37 – .80) | ||
| MA | .30 (.10 – .49) | .34 (.16 – .62) | .45 (.00 – .61) | |
|
| ||||
| C1 (95% CI) | C2 (95% CI) | C3 (95% CI) | ||
| GA | - | |||
| MPS | .58 (.32 – .73) | - | ||
| MA | - | - | - | |
|
| ||||
| E1 (95% CI) | E2 (95% CI) | E3 (95% CI) | ||
| GA | .75 (.65 – .86) | |||
| MPS | .01 (.00 – .12) | .51 (.44 – .59) | ||
| MA | .21 (.06 – .35) | .08 (.00 – .23) | .73 (.63 – .83) | |
Note: “-” = path fixed at 0. For abbreviations, see Table 2.
As shown in Figure 1 and Table 3, genetic and nonshared environmental variance related to general anxiety accounted for variance in MA, but only through factors that were independent from math problem solving. In particular, the pathways from the general genetic factor (A1) and from the general nonshared environmental factor (E1) to both general anxiety (A = .66, E = .75) and MA (A = .30, E = .21) were significant whereas the pathways from A1 and E1 to math problem solving were not significant (A = .15, E = .01). Furthermore, math problem solving accounted for additional genetic variance in MA that was independent from general anxiety. Specifically, the pathways from the math specific genetic factor (A2) to both MA (A = .34) and math problem solving (A = .62) were significant. Finally, shared environmental pathways for MA were nonsignficant and were not associated with the moderate shared environmental influences on math problem solving (C = .58). Taken together, 9% of the total variance in MA was associated with genetic influences in common with general anxiety (i.e., squared pathway from A1 to MA: .302) and 4% of the total variance was associated with nonshared environmental influences in common with general anxiety (i.e., squared pathway from E1 to MA: .212). An additional 12% of the total variance in MA was associated with genetic influences related to math problem solving (i.e., squared pathway from A2 to MA: .342).
Additionally, to examine whether the relationships between general anxiety, math problem solving, and MA were generalizable to other learning outcomes, reading in particular, a second series of trivariate behavioral genetic models were fitted to the data examining the genetic and environmental etiology of the phenotypic associations among general anxiety, reading comprehension, and MA. General anxiety was entered into the model first, followed by reading comprehension and MA. Path estimates from the ACE and the ADE models suggested that none of the C or the D paths was significant. Consequently, an AE model was fitted, fixing all C and D paths to zero. Model fit indices are shown in Table 4. Chi-square difference tests comparing the AE versus the ACE and the ADE models were nonsignificant. In addition, the AE model had the smallest AIC and BIC values, also indicating that the AE model best fit the data. Therefore, parameter estimates from the more parsimonious AE model are presented in Table 4.
Table 4.
Trivariate Cholesky modeling results of genetic and environmental influences on general anxiety (GA), reading comprehension (RC), and mathematical anxiety (MA).
| Model Fit Indices and Model Comparisons | ||||
|---|---|---|---|---|
| Model | −2LL (df) | Δ−2LL(Δdf) | AIC | BIC |
| Full ACE Model | 3580.17 (1319) | AE vs. ACE: .17 (6) | 942.17 | −1869.53 |
| Full ADE Model | 3577.13 (1319) | AE vs. ADE: 3.21 (6) | 939.13 | −1871.05 |
| AE Model | 3580.34 (1325) | 930.34 | −1886.09 | |
|
| ||||
| Standardized Path Estimates from Reduced ACE Model | ||||
| Overlap between GA, RC, and MA | Overlap between RC and MA | Unique effects of MA | ||
|
| ||||
| A1 (95% CI) | A2 (95% CI) | A3 (95% CI) | ||
| GA | .66 (.51 – .76) | |||
| RC | .04 (.00 – .20) | .87 (.82 – .91) | ||
| MA | .29 (.09 – .47) | .13 (.00 – .25) | .57 (.41 – .69) | |
|
| ||||
| C1 (95% CI) | C2 (95% CI) | C3 (95% CI) | ||
| GA | - | |||
| RC | - | - | ||
| MA | - | - | - | |
|
| ||||
| E1 (95% CI) | E2 (95% CI) | E3 (95% CI) | ||
| GA | .75 (.65 – .86) | |||
| RC | .00 (.00 – .08) | .49 (.42 – .57) | ||
| MA | .22 (.08 – .36) | .07 (.00 – .22) | .72 (.62 – .82) | |
Note: “-” = path fixed at 0. For abbreviations, see Table 2.
As shown in Table 4, genetic and nonshared environmental variance related to general anxiety accounted for variance in MA, but only through factors that were independent from reading comprehension. In particular, the pathways from the general genetic factor (A1) and from the general nonshared environmental factor (E1) to both general anxiety (A = .66, E = .75) and MA (A = .29, E = .22) were significant whereas the pathway from A1 and E1 to reading comprehension was not significant (A = .04, E = .00). Moreover, genetic and environmental variance in reading comprehension did not account for variance in MA. Specifically, the pathway from the genetic factor (A2) and nonshared environment factor (E2) was only significant to reading comprehension (A = .87, E = .49), but not to MA (A = .13, E = .07).
Discussion
Negative affects in academic settings such as fearfulness and anxiety create barriers for the development of academic competency through interference with cognitive capacity and positive motivations required to engage in effective learning (Eysenck et al., 2007; Pekrun et al., 2011; Putwain et al., 2010). MA represents a specific example of such academic-related negative affects which selectively impairs performance in mathematics (Ma, 1999; Zientek et al., 2010). Given its debilitating impacts on both the cognitive capacity to engage in mathematics problem solving and the affective climate surrounding mathematics (Ho et al., 2000; Wigfield & Meece, 1988), it is important to understand the mechanisms underlying individual differences in MA. In light of this goal, the present study investigated the genetic and environmental factors contributing to the observed variance in MA, as well as the observed covariation between MA and math cognition, and between MA and general anxiety.
The current study showed that individual differences in MA were explained by moderate genetic and nonshared environmental influences, suggesting the importance of genetic risk factors as well as unique sibling experiences in the development of MA. The magnitude of the genetic and nonshared environmental influences are consistent with previous quantitative genetic work on temperamental fearfulness, general anxiety, and various specific phobias (Hettema, Neale, & Kendler, 2001; Van Houtem et al., 2013), and suggest the possibility of similar etiological processes in the development of MA and other anxiety disorders that involve familial vulnerability and individual-specific experiential risk factors. In addition, findings from both the current analyses and previous behavioral genetic studies reveal modest to moderate levels of shared environmental influences on math cognition (Kovas et al., 2005; Thompson et al., 1991; Wadsworth et al., 1995), suggesting the importance of shared sibling experiences in the development of mathematical skills. However, the current findings indicate that these shared environmental factors are unlikely to affect individual differences in MA.
To further explore the sources of these genetic and environmental influences, multivariate behavioral genetic models were conducted on general anxiety, math problem solving, and MA. As expected by the larger literature (Ashcraft & Krause, 2007; Hembree, 1990), the phenotypic correlations between MA and general anxiety and between MA and math problem solving were both moderate. More importantly, MA was influenced by genetic and nonshared environmental factors associated with general anxiety as well as additional independent genetic factors associated with math problem solving. Further analyses also indicated that the genetic and environmental etiology of the relationships between MA and math cognition was not generalizable to reading. Taken together, the results suggested that, shared genetic influences between general anxiety and MA were distinct from a second, independent set of shared genetic influences between math problem solving and MA. Both sources accounted for 21% of the total variance in MA. Importantly, 4% of the total variance in MA was also influenced by nonshared environmental factors related to general anxiety, suggesting that child-specific experiences related to general anxiety may also influence the development of MA. Lastly, unique genetic and nonshared environmental factors independent of both general anxiety and math problem solving accounted for 20% and 53% of the total variance in MA, respectively.
Conclusions and Implications
Several limitations should be borne in mind when interpreting these findings. First, the current sample was mainly comprised of middle-class families. Therefore, generalization to low income families should be taken with caution. Second, MA was measured only using self-reports. Future studies may gain more insight from combining self-reports with real-time physiological measures indexing stress and anxiety during math tasks. Lastly, developmental perspective needs to be taken to further advance our understanding of the etiologies of the changes and stability in MA, as well as the etiologies of the long-term dynamic transactions among MA, its precursors, and its consequences.
With regards to clinical practices aiming to mitigate MA, two main approaches currently dominate clinical work in this area. The first approach is to directly address the anxiety symptoms using techniques that are shown to be effective in treating other types of anxiety, such as desensitization (Brunyé et al., 2013; Zettle, 2003). The second approach is to target potential mechanisms through which MA arises, such as improving math learning experiences (Geist, 2010; Kramarski, Weisse, & Kololshi-Minsker, 2010). Although both approaches have shown effectiveness in reducing MA, their impacts on improving mathematics performance or motivations to engage in math learning have been limited (Brunyé et al., 2013; Kramarski et al., 2010; Zettle, 2003)
Limitations in these intervention programs may reflect a lack of understanding of the fundamental mechanisms of how MA develops as a specific type of phobia in the broad context of math learning. MA may arise from negative environmental experiences with mathematics (Ashcraft et al., 2007; Meece et al., 1990). However, our findings also suggested that genetic risks underlying poor math ability and general anxiety may already predispose children to the development of MA. Together with previous findings, the present results highlighted the possibility of a dynamic spiraling process through which the genetic influences related to poor mathematical performance and genetic and individual-specific environmental influences for high general anxiety serve as risk factors in the development of MA, which may lead to further impairment in math performance, and in turn, the negative experiences with mathematics may then exacerbate MA symptoms.
These findings have several important implications for preventions and interventions. The first is that rather than focusing exclusively on the negative experiences arising from math-related activities, efforts should also be invested in exploring potential biological pathways that elevate risks for developing MA. Recent neuroimaging studies indicate that individuals with high MA show reduced responses in brain regions involved in mathematical cognition (Young et al., 2012) and increased responses in brain regions involved in affective fearfulness and threat-detection (Lyons & Beilock, 2012b; Young et al., 2012). The results of the current study, when linked with this recent work, suggest that mapping out the biological pathways involving both the cognitive and the affective aspects of MA may help advance our understanding of the fundamental mechanisms of the development of MA. Second, nonshared environmental influences accounted for slightly over half of the total variance in MA, and a portion of the nonshared environmental effects also contributed to the comorbidity between MA and general anxiety. These findings indicate the importance of identifying child-specific (rather than family-level) experiences that may underlie the development of both general anxiety and MA, such as unique parental educational expectation toward each sibling, unique parent-child and peer relationships, and different quality of math education experienced in math classes. These nonshared environmental factors, when identified, would serve as promising targets for educational and clinical programs aiming to alleviate MA and promote math performance. Finally, given that general anxiety and math cognition independently contributed to the etiology of MA, it is important to not only address the anxiety component of MA, but also treat deficits in math cognition at the same time. A combination of affective desensitization and improved math learning strategies involving more opportunities to practice and reflect on math learning (Kramarski et al., 2010) may offer solid long-term benefits in mitigating the paralyzing affective dimension of MA, and to improve engagement as well as overall performance in mathematics ultimately.
Key points.
MA is known to contribute not only to poor mathematical achievement, but also to reduced motivation and involvement in math-related activities.
The current study is the first to examine the genetic and environmental etiology of MA, as well as the genetic and environmental etiology linking MA with math cognition and general anxiety.
Results show that the development of MA involves genetic risks related to both general anxiety and math cognition, and child-specific environmental risks related to general anxiety.
Clinical practices targeting at reducing MA may benefit from exploration of potential biological pathways leading to MA, general anxiety and poor math cognition. Future treatment programs would also benefit from simultaneously addressing both the affective and the cognitive components of MA.
Acknowledgments
This work was supported by the Eunice Kennedy Shriver National Institute of Child Health and Development grants HD038075, HD059215, and HD075460 as well as a grant from the Government of the Russian Federation (grant 11.G34.31.0043). The results presented in this paper reflect the views of the authors and not those of the funding agencies.
References
- Akaike H. Factor analysis and AIC. Psychometrika. 1987;52(3):317–332. [Google Scholar]
- Ashcraft MH, Krause JA. Working memory, math performance, and math anxiety. Psychonomic Bulletin & Review. 2007;14(2):243–248. doi: 10.3758/bf03194059. [DOI] [PubMed] [Google Scholar]
- Ashcraft MH, Krause JA, Hopko DR. Is math anxiety a mathematical learning disability. In: Berch DB, Mazzacco MMM, editors. Why is math so hard for some children. Baltimore, MD: Brookes; 2007. pp. 329–348. [Google Scholar]
- Brunyé TT, Mahoney CR, Giles GE, Rapp DN, Taylor HA, Kanarek RB. Learning to relax: Evaluating four brief interventions for overcoming the negative emotions accompanying math anxiety. Learning and Individual Differences. 2013;27:1–7. [Google Scholar]
- Eysenck MW, Derakshan N, Santos R, Calvo MG. Anxiety and cognitive performance: Attentional control theory. Emotion. 2007;7(2):336–353. doi: 10.1037/1528-3542.7.2.336. [DOI] [PubMed] [Google Scholar]
- Geist E. The anti-anxiety curriculum: Experience that combating math anxiety in the classroom. Journal of Insructional Psychology. 2010;37(1):24–31. [Google Scholar]
- Goldsmith HH. A zygosity questionnaire for young twins: A research note. Behavior Genetics. 1991;21(3):257–269. doi: 10.1007/BF01065819. [DOI] [PubMed] [Google Scholar]
- Griffin D, Gonzalez R. Correlational analysis of dyad-level data in the exchangable case. Psychological Bulletin. 1995;118(3):430–439. [Google Scholar]
- Hart SA, Petrill SA, Thompson LA, Plomin R. The ABCs of math: A genetic analysis of mathematics and its links with reading ability and general cognitive ability. Journal of Educational Psychology. 2009;101(2):388–402. doi: 10.1037/a0015115. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hembree R. Correlates, causes, effects, and treatment of test anxiety. Review of Educational Research. 1988;58(1):47–77. [Google Scholar]
- Hembree R. The nature, effects, and relief of mathematics anxiety. Journal for Research in Mathematics Education. 1990;21(1):33–46. [Google Scholar]
- Hettema JM, Neale MC, Kendler KS. A review and meta-analysis of the genetic epidemiology of anxiety disorders. American Journal of Psychiatry. 2001;158(10):1568–1578. doi: 10.1176/appi.ajp.158.10.1568. [DOI] [PubMed] [Google Scholar]
- Ho HZ, Senturk D, Lam AG, Zimmer JM, Hong S, Okamoto Y, Wang CP. The affective and cognitive dimensions of math anxiety: A cross-national study. Journal for Research in Mathematics Education. 2000;31(3):362–379. [Google Scholar]
- Kovas Y, Harlaar N, Petrill SA, Plomin R. “Generalist genes” and mathematics in 7-year-old twins. Intelligence. 2005;33(5):473–489. doi: 10.1016/j.intell.2005.05.002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kramarski B, Weisse I, Kololshi-Minsker I. How can self-regulated learning support the problem solving of third-grade students with mathematics anxiety? ZDM Mathematics Education. 2010;42:179–193. [Google Scholar]
- Lyons IM, Beilock SL. Mathematics anxiety: Separating the math from the anxiety. Cerebral cortex. 2012a;22(9):2102–2110. doi: 10.1093/cercor/bhr289. [DOI] [PubMed] [Google Scholar]
- Lyons IM, Beilock SL. When math hurts: Math anxiety predicts pain network activation in anticipation of doing math. PloS one. 2012b;7(10):e48076. doi: 10.1371/journal.pone.0048076. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ma X. A meta-analysis of the relationship between anxiety toward mathematics and achievement in mathematics. Journal for Research in Mathematics Education. 1999;30(5):520–540. [Google Scholar]
- Maloney EA, Beilock SL. Math anxiety: Who has it, why it develops, and how to guard against it. Trends in cognitive sciences. 2012;16(8):404–406. doi: 10.1016/j.tics.2012.06.008. [DOI] [PubMed] [Google Scholar]
- McGrew KS, Schrank FA, Woodcock RW. Technical Manual. Woodcock-Johnson III Normative Update. Rolling Meadows, IL: Riverside Publishing; 2007. [Google Scholar]
- Meece JL, Wigfield A, Eccles JS. Predictors of math anxiety and its influence on young adolescents’ course enrollment intentions and performance in mathematics. Journal of Educational Psychology. 1990;82(1):60–70. [Google Scholar]
- Neale MC. Mx: Staistical modeling. 4. Richmond, VA: Department of Psychiatry, Virginia Commonwealth University; 1997. [Google Scholar]
- Owens M, Stevenson J, Hadwin JA, Norgate R. Anxiety and depression in academic performance: An exploration of the mediating factors of worry and working memory. School Psychology International. 2012;33(4):433–449. [Google Scholar]
- Pekrun R, Goetz T, Frenzel AC, Barchfeld P, Perry RP. Measuring emotions in students’ learning and performance: The Achievement Emotions Questionnaire (AEQ) Contemporary Educational Psychology. 2011;36(1):36–48. [Google Scholar]
- Petrill SA, Deater-Deckard K, Thompson LA, DeThorne LS, Schatschneider C. Reading skills in early readers: Genetic and shared environmental influences. Journal of Learning Disabilities. 2006;39(1):48–55. doi: 10.1177/00222194060390010501. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Prevatt F, Welles TL, Li H, Proctor B. The contribution of memory and anxiety to the math performance of college students with learning disabilities. Learning Disabilities Research & Practice. 2010;25(1):39–47. [Google Scholar]
- Putwain DW, Connors L, Symes W. Do cognitive distortions mediate the test anxiety–examination performance relationship? Educational Psychology. 2010;30(1):11–26. [Google Scholar]
- Raftery AE. Bayesian Model Selection in Social Research. Sociological Methodology. 1995;25:111–164. [Google Scholar]
- Richardson FC, Suinn RM. The mathematics anxiety rating scale: Psychometric data. Journal of Counseling Psychology. 1972;19(6):551–554. [Google Scholar]
- Rohde TE, Thompson LA. Predicting academic achievement with cognitive ability. Intelligence. 2007;35(1):83–92. [Google Scholar]
- Spence SH. Structure of anxiety symptoms among children: A confirmatory factor-analytic study. Journal of Abnormal Psychology. 1997;106:280–297. doi: 10.1037//0021-843x.106.2.280. [DOI] [PubMed] [Google Scholar]
- Suinn RM, Taylor S, Edwards RW. Suinn Mathematics Anxiety Rating Scale for elementary school students (MARS-E): Psychometric and normative data. Educational and Psychological Measurement. 1988;48(4):979–986. [Google Scholar]
- Thompson LA, Detterman DK, Plomin R. Associations between cognitive abilities and scholastic achievement: Genetic overlap but environmental differences. Psychological Science. 1991;2(3):158–165. [Google Scholar]
- Trzaskowski M, Eley TC, Davis OSP, Doherty SJ, Hanscombe KB, Meaburn EL, Plomin R. First genome-wide association study on anxiety-related behaviours in childhood. PloS one. 2013;8(4):e58676. doi: 10.1371/journal.pone.0058676. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Van Houtem CMHH, Laine ML, Boomsma DI, Ligthart L, van Wijk AJ, De Jongh A. A review and meta-analysis of the heritability of specific phobia subtypes and corresponding fears. Journal of Anxiety Disorders. 2013;27(4):379–388. doi: 10.1016/j.janxdis.2013.04.007. [DOI] [PubMed] [Google Scholar]
- Wadsworth SJ, DeFries JC, Fulker DW, Plomin R. Cognitive ability and academic achievement in the Colorado Adoption Project: A multivariate genetic analysis of parent-offspring and sibling data. Behavior Genetics. 1995;25(1):1–15. doi: 10.1007/BF02197237. [DOI] [PubMed] [Google Scholar]
- Wigfield A, Meece JL. Math anxiety in elementary and secondary school students. Journal of Educational Psychology. 1988;80(2):210–216. [Google Scholar]
- Woodcock RW. Woodcock Reading Mastery Tests–Revised. Circle Pines, MN: American Guidance Service; 1998. [Google Scholar]
- Woodcock RW, McGraw KS, Mather N. Woodcock-Johnson III Tests of Achievement. Itasca, IL: Riverside Publishing; 2001. [Google Scholar]
- Young CB, Wu SS, Menon V. The neurodevelopmental basis of math anxiety. Psychological Science. 2012;23(5):492–501. doi: 10.1177/0956797611429134. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zettle RD. Acceptance and commitment therapy (ACT) vs. systematic desensitization in treatment of mathematics anxiety. The Psychological Record. 2003;53:197–215. [Google Scholar]
- Zientek LR, Yetkiner ZE, Thompson B. Characterizing the mathematics anxiety literature using confidence intervals as a literature review mechanism. The Journal of Educational Research. 2010;103(6):424–438. [Google Scholar]