Abstract
Since its discovery over 50 years ago, the “structure” and properties of the hydrated electron has been a subject for wonderment and also fierce debate. In the present work we seriously explore a minimal model for the aqueous electron, consisting of a small water anion cluster embedded in a polarized continuum, using several levels of ab initio calculation and basis set. The minimum energy zero “Kelvin” structure found for any 4-water (or larger) anion cluster, at any post-Hartree-Fock theory level, is very similar to a recently reported embedded-DFT-in-classical-water-MD simulation (UMJ: Uhlig, Marsalek, and Jungwirth, Journal of Physical Chemistry Letters 2012, 3, 3071-5), with four OH bonds oriented toward the maximum charge density in a small central “void”. The minimum calculation with just four water molecules does a remarkably good job of reproducing the resonance Raman properties, the radius of gyration derived from the optical spectrum, the vertical detachment energy, and the hydration free energy. For the first time we also successfully calculate the EPR g-factor and (low temperature ice) hyperfine couplings. The simple tetrahedral anion cluster model conforms very well to experiment, suggesting it does in fact represent the dominant structural motif of the hydrated electron.
Keywords: Hydrated electron, ab initio calculation, free energy, vibrational frequencies, vertical detachment energy, EPR g-factor and hyperfine couplings
I. Introduction
The interaction of ionizing radiation with liquid water generates1 excited states, water cations (H2O+) and pre-solvated electrons (e-pre). On a femtosecond timescale, the excited states autoionize or dissociate and the water cation transfers a proton to generate OH radical and H3O+. Solvation of e-pre by the surrounding waters also occurs well within a picosecond and leads to formation of the “solvated electron” (e-aq).2-4 Hart and Boag5,6 first reported the broad visible absorption spectrum (λ max = 720 nm) of e-aq in 1962. Innumerable studies on e-aq properties and reactions have been made over the years owing to its fundamental importance in radiation chemistry, photochemistry and biochemistry.7-12 Nevertheless, even after 50 years, the nature of the excess electron in bulk water, at water interfaces, or in water clusters remains a topic of considerable debate.7-14
The most current debate concerns whether the electron resides in a “cavity” or exists mostly in between the molecules of a densified region15-18. The “cavity model” of e-aq was proposed very early after its discovery10. The fundamental idea is that the excess electron repels the water molecules in its environment by Pauli exclusion, but the negative charge is stabilized in a “cavity” potential well by the water dipoles and long-range dielectric response. This set of assumptions has been captured and carried forward by ever19,20 more21,22 sophisticated23 molecular dynamics simulations based on a pseudopotential to represent the electron-water interaction in a bath of classical water molecules*. These one-electron pseudopotential models generally have been able to reproduce the room temperature optical spectrum, but significantly fail to produce the experimental shift with temperature.8,24
Recently, based on a newly-improved pseudopotential, Larsen, Glover and Schwartz (LGS)15 proposed a non-cavity (plum pudding) model in which the electron exists mostly between the waters in a region of enhanced water density. The major change to the pseudopotential acknowledged that the electron spends significant time near the water oxygen, according to the demands of quantum mechanics.8,15 Schwartz and coworkers demonstrated that this new model does a much better job of explaining the optical properties and Raman spectrum than the older “cavity” models.8 However, the LGS model15 has been questioned particularly on the basis of its energetics and the expected very negative partial molar volume.16-18 Jungwirth and coworkers25 have recently performed large scale ab initio molecular dynamics simulations with a DFT water cluster embedded in a large classical MD water bath. They find that the local structure has a void surrounded by four waters, each with one OH bond oriented toward the center, but they take pains to point out the electron wavefunction is simultaneously “on” the water molecules and “in” the central void and “between” waters extending into the second solvation shell. The fact that this uses an all-electron approach for the water in the vicinity of the excess charge gives considerable credence to their result, but problems of comparison with experiment remain.8
In the present work, we represent the hydrated electron as a small water anion cluster embedded in a dielectric continuum, following on the preliminary work of Jungwirth and coworkers.26,27 We find that four water molecules is sufficient to provide a robust minimum model at any post-Hartree-Fock level of theory with double-zeta basis set or larger. Additional layers of water molecules do not substantially change the result. The rms “size” or radius of gyration of the electron in this calculation is in reasonable agreement with the number derived from the experimental optical spectrum. The vertical detachment energy for ejection of the electron is well predicted and the frequency red-shift of the water OH stretch is in excellent agreement with resonance Raman experiments. Using this model with the G4 thermochemistry method reproduces experimental solvation free energy with surprising accuracy. Hyperfine couplings for electrons trapped in low temperature aqueous glasses are correctly calculated. On the basis of all this success, we consider the tetrahedral water cluster with four inward directed OH bonds to be the dominant structural motif of the hydrated electron†.
II. Methods of calculation
The calculations are carried out with standard ab initio methods available in the Gaussian09 software package28, which we consider are very familiar to the physical chemistry community. GaussView29, and JMOL30 were used to plot molecular orbital, spin density distribution and molecular structure. Multiwfn31 was used to generate the data from radial profiles of the spin density distribution to calculate the radius of gyration. All calculations were done considering the effect of full solvent water (ε = 78.4) through the use of integral equation formalism polarized continuum model (IEF-PCM) herein abbreviated PCM.
III. Results and Discussion
1. Structure Optimization
To begin the present study, we used four and six water clusters ((H2O)4 and (H2O)6) to bind the excess electron, with a dielectric continuum to represent the long-range reaction potential. We arranged the initial structure of each cluster in a tetrahedral fashion in (H2O)4 and in a octahedral fashion in (H2O)6 to bind the excess electron at the center. In these structures, one of the O-H bonds of each water molecule points towards the center as proposed by Kevan.10,32 These two structures were recently studied by Shkrob33 in vacuo and by Uhlig and Jungwirth26 in a COSMO dielectric continuum. We adopt the notation of Shkrob in which the center point of the structure is denoted by capital X. The initial anion water structures ((H2O)-4 and (H2O)-6) thus generated were used for full geometry optimization without any symmetry restrictions.
In Figure 1 we show the energy-optimized structures of (H2O)6- and (H2O)4- anion clusters calculated without symmetry constraint from B3LYP/6-31G(2df,p) method and representing the effect of bulk water (ε = 78.4) via the integral equation formalism polarized continuum model (IEF-PCM) of Tomasi et al.34,35 In the optimized structure of the tetramer (H2O)4-, one O-H bond of each water points toward the center and the average H---H distance forming the central tetrahedron is 2.39 Å. In the optimized structure of (H2O)6- anion using the same level of theory, we found that only four water molecules form the inner solvation shell and one O-H bond of each of the four waters points toward the center, just as in the four-water cluster. The average H---H distance forming the central tetrahedron is virtually identical at 2.38 Å. The remaining two water molecules are hydrogen-bonded to three of the waters forming the inner solvation shell, see Figure 1. From frequency analysis it is confirmed that this structure is a minimum energy structure (all positive frequencies), whereas octahedral geometries are not. The Kevan structure, optimized with constrained Ci symmetry, is shown in Figure S8.1 in the supporting information. The energy of this structure calculated with B3LYP/6-31++G(2df,p) is higher than the six-water tetrahedral arrangement by 9.6 kcal/mole (Figure S8.4). This calculation clearly demonstrates that the minimum energy structure is a tetrahedral rather than octahedral geometry of the inner solvation shell. Given the large energy difference, it is little wonder that the large-scale ab initio MD calculations of Uhlig, Marsalek and Jungwirth25, converged to an average coordination number of four.
Figure 1.
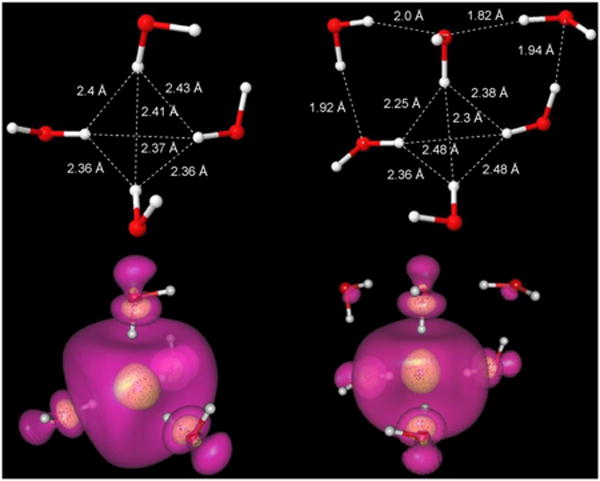
B3LYP/6-31G(2df,p) optimized structures of (H2O)4 and (H2O)6 radical anion in tetrahedral conformation. IEF-PCM was used to account for the surrounding aqueous environment. Spin density distributions of the excess electron in both structures are also shown. The transparent outer surface (violet) encloses 80% and the inner surface (yellow) encloses 20% of total spin density. Note that a very significant amount of spin density is actually concentrated at oxygen rather than in between the water molecules
A large number of similar geometry optimizations were carried out with various theory levels and larger basis sets, for both the hexamer and tetramer, to test the stability of the tetrahedral structure. Salient results are listed in Table S1 and S2, for several density functionals including B3LYP, CAM-B3LYP, ωB97x, and LC-ω-PBE and ab initio MP2, and CCSD optimizations, with various basis sets including 6-31G(2df,p), 6-31++G(2df,p), aug-cc-pvDz, aug-cc-pvTz and PCseg-4 basis sets. In every case of a post-Hartee-Fock calculation, the electron is localized in the center of a nearly tetrahedral structure with O-H bond orientation similar to that shown in Figure 1. Even low-level Hartree-Fock calculations can result in the tetrahedral geometry (see 4 and 6 water clusters in Geometry Image files in Supporting Information), although this depends on basis set‡. In general, as the electron correlation energy estimate of the calculation is improved the X-H distances (X-H distance = average H-H distance*0.612, where X is the center of the tetrahedron) become smaller, the excess electron is more localized, and the OH-bond-directed tetrahedral structure is stabilized. A small portion of the data from Table S1 is presented in Table 1 as a summary.
Table 1. Geometry of (H2O)4- vs. Calculation Method.
| Method | Basis set | X-H (Å) avg | Rg (Å) |
|---|---|---|---|
| wB97X | aug-cc-pvdz | 1.5 | 2.23 |
| B3LYP | aug-cc-pvdz | 1.7 | 2.52 |
| CAM-B3LYP | aug-cc-pvdz | 1.7 | 2.37 |
| LC-wPBE | aug-cc-pvdz | 1.8 | 2.57 |
| MP2 | aug-cc-pvdz | 1.7 | 2.44 |
| CCSD | 6-31++G(2df,p) | 1.8 | 2.65 |
As a final survey of the energy landscape for the four-water clusters, a geometry scan of the X-O distance vs. the water OH bond orientation was carried out using ωB97X/aug-cc-pvDz method. A genetic algorithm was used to search for orientational minima, while keeping OH bond lengths constant. A description of this study is given in Supporting Information. The conclusion is that the OH-bond orientation is preferred over the molecular dipole orientation at all distances, and there are no local minima. The energy barrier for switching from bond-dipole to molecular-dipole orientation is several millihartree uphill for the most stable X-O distance around 2.5 - 2.6 Å. The preference of the hydrated electron for bond-dipole orientation over molecular dipole agrees with one of the strongest conclusions reached in the mixed H2O/D2O Resonance Raman study of Mathies and Tauber.36 In earlier pseudopotential MD studies, bond dipole orientation was also preferred, but the explanation was that formation of one donor hydrogen bond to the second shell is an energetically favorable compromise20 (The pseudopotentials would otherwise favor molecular dipole orientation by symmetry.) Here we discover that the bond-dipole orientation is favored by the quantum mechanics with just four water molecules, independent of any hydrogen bond formation to a second hydration shell.
2) The radius of gyration
By making a one-electron approximation and applying the Moment Theory, the hydrated electron optical absorption spectrum can be used to estimate the radius of gyration (Rg), characterizing the average size of the unpaired electron wavefunction.24,37 At room temperature, Bartels et al. derive a value of 2.48 Å from integration of the first inverse moment M(-1). For water ice at -18°C, a similar calculation gives 2.35 Å.38 In the present model calculations, we are finding the most stable, or “zero Kelvin” structure. Based on the temperature trend to smaller Rg at lower temperature, we presume a correct model calculation will have Rg < 2.35Å. One criticism of the UMJ ab initio MD calculation25, is that the room temperature average Rg is larger than experiment at 2.65Å, and the most compact configuration observed has Rg 2.45 Å.
As a matter of routine, we have calculated the Rg from the unpaired spin distribution for most of the calculations listed in Table S1. Multiwfn31 was used to generate the spherically integrated spin distribution ρ(r) out to 10Å in 500 points, and then the gyration radius was calculated from Rg=[Σnr2ρ(r)/Σnρ(r)]1/2. As cross-check we have also employed NWCHEM39 which gives the radius of gyration for the SOMO (singly occupied molecular orbital) as part of its output. For the NWCHEM calculations we employed B3LYP/6-31++G(2df,p) and COSMO continuum model with dielectric constant of 78.4. We find Rg = ca. 2.5 Å for both the 4 and 6 water models from both (NWCHEM) SOMO and (Gaussian/Multiwfn) unpaired spin calculation.
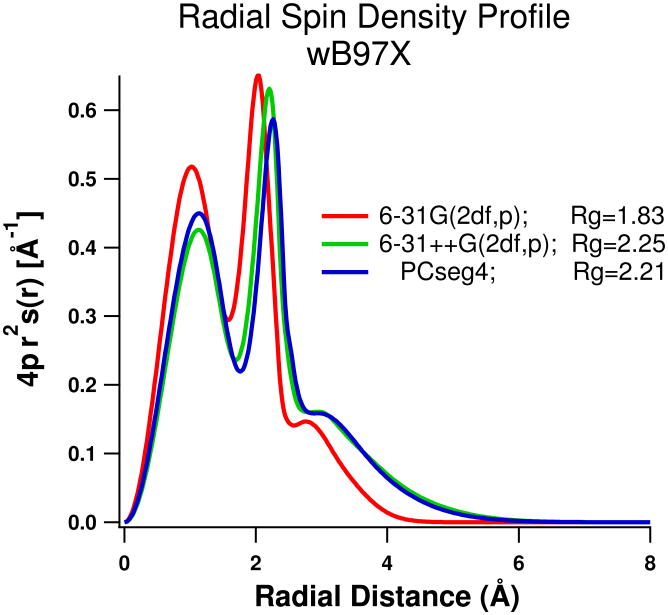
Using B3LYP and 6-31G(2df,p) without any diffuse (++) basis functions we find Rg is ca. 1.94Å for both 4 and 6 water clusters (shown in figure 1), which is smaller than we expect even for a minimum energy (zero K) structure. Addition of compact (i.e non-diffuse) atom-centered basis functions beyond 6-31G(2df,p) seems to have little impact. Results from B3LYP and other methods listed in Table S1, including MP2, CCSD, and ωB97X, show that the addition of diffuse functions substantially lowers the energy of the system and increases the optimum X-H distances by around 0.3-0.5 Å to expand the central void and increase Rg. In Figure 2 we plot the radial profile of the spin density vs. distance from the center, for the ωB97X/6-31G(2df,p) and 6-31++G(2df,p) calculations. There is no apparent qualitative difference, as without diffuse functions the distribution of spin is just confined to smaller volume and the X-H distance is shorter. For further comparison we also plot in Figure 2 results using the very large Jensen PCseg-4 basis set, of quadruple zeta quality and optimized in PCM.40 The radius of gyration shifts slightly to smaller value, but a 3D plot of the ωB97X/PCseg-4 spin density surface is visually indistinguishable from the B3LYP/6-31G(2df,p) plot in Figure 1.
Figure 2.
Radial spin density profile of ωB97X optimized geometries for the tetrahedral 4 water system, using 6-31G(2df,p), 6-31++G(2df,p) and the PCseg-4 basis sets.
A roughly linear relation between Rg and X-H seems to apply. In Figure 3 we plot the ωB97X/6-31++G(2df,p) spherically integrated spin density for three different (constrained) X-H distances. No qualitative change is observed, and the unpaired spin seems to track with the location of the atom-centered orbitals. Another test described in Supporting Information is to add “ghost” orbitals at the center or arranged near the center of the tetrahedron between the protons. Amazingly, the inclusion of these additional (diffuse) orbitals makes no significant difference to the wavefunction and the value of Rg when diffuse functions are included in the atom-centered basis set. The atom-centered functions are perfectly adequate. This agrees with the assessment of Jacobson and Herbert41 in their study of the “blue tail” of the optical spectrum, which made use of 6-31+G* basis set for quantum mechanical water clusters embedded in a point charge array to represent the long range potential. But the observation that the electron wavefunction closely follows the location of the nuclei, and especially the oxygen atoms, runs counter to the assumption of earlier “pseudopotential/cavity” models that the electron will repel the oxygen and prefer to exist between the water molecules19-22.
Figure 3.
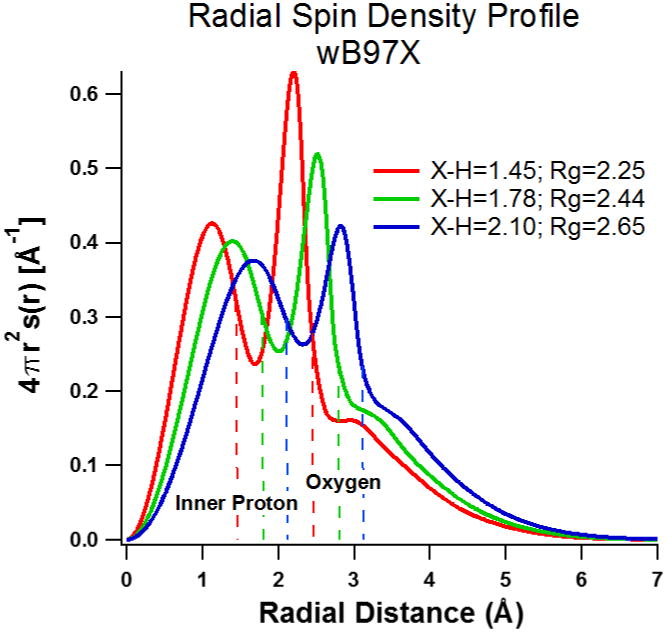
Radial spin density profile of wB97X/6-31++G(2df,p) optimized geometries for the tetrahedral 4 water system at the fixed X-H distances shown in the figure. Rg values given in the figure track with the X-H value.
The question arises whether there might be some problem of the diffuse functions “hanging out” too much into the dielectric continuum, where the repulsive effect of Pauli exclusion is missing? If interaction with diffuse functions, or some other aspect of the dielectric continuum representation is grossly inadequate, we should be able to get a different Rg and X-H distance by adding another layer of water molecules to push the dielectric continuum further away from the center. In Figure 4 we compare the radial profile of the spin density for the minimum 4-water B3LYP/6-31++G(2df,p) calculation with a similar calculation using 16 water molecules. The additional 12 water molecules are arranged to completely H-bond with the inner four waters, and then optimized using the B3LYP/6-31++G(2df,p) method. (There are many possible water configurations having these criteria--we arrived at one that we assume is representative) Virtually no difference is found on the optimum X-H distance and Rg calculated with this cluster for B3LYP functional (whether carried out with or without diffuse functions). Inspection of Figure 4 shows there is some structure added to the spin density tail by the second solvation shell, between 3 and 7 Å, but the average is similar to the 4-water case. In Figure 5 we plot a 3D spin density surface of the 16-water structure. Some spin density is visible near the second shell oxygen atoms, but the overall picture is remarkably similar to the simple 4-water structure of Figure 1. Hydrogen bonding to the central four water molecules makes only a minor perturbation to the structure, and we have to conclude that the polarized continuum gives a reasonable representation of the average effect of the solvent.
Figure 4.
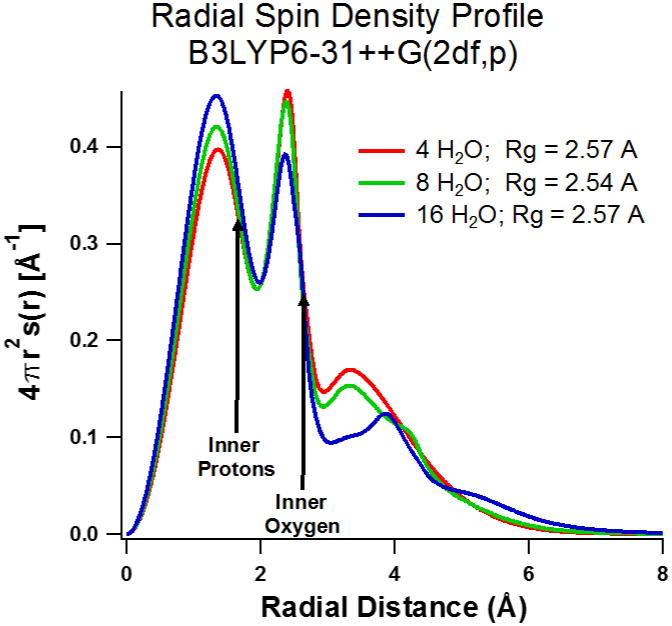
Radial spin density profiles for 4, 8, and 16 waters using B3LYP/6-31++G(2df,p).
Figure 5.
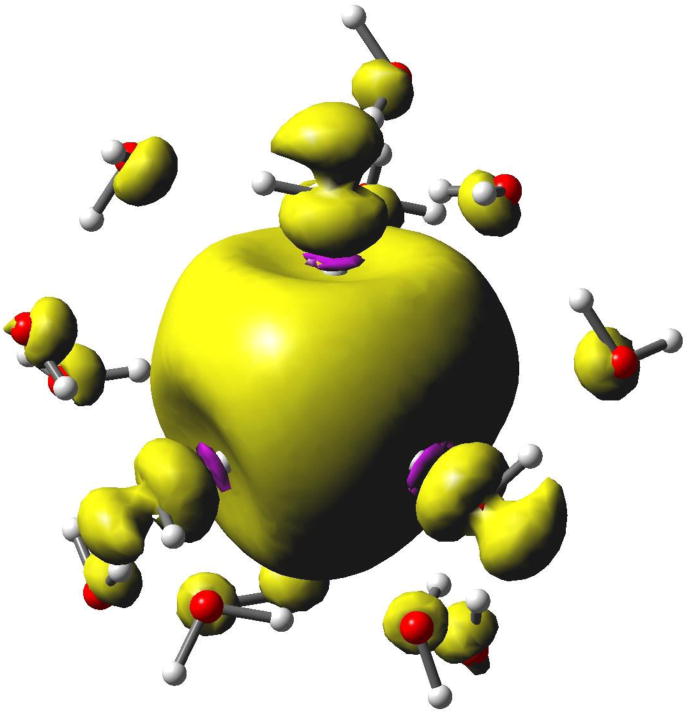
Spin isodensity plot for a 16-water cluster, using B3LYP/6-31++G(2df,p). Note the purple rings near the inner protons where negative spin density gives rise to a negative isotropic hyperfine coupling. Also note the p-orbital character at the inner four oxygen atoms aligned with the inboard OH bonds, which is responsible for significant spin-orbit coupling and the EPR g-factor shift. Finally, note the spin density at oxygen in the second solvation shell. The surface encloses 75% of total spin density.
Overall, the results indicate that the 4-water minimum cluster calculation with atom-centered basis set is sufficient for calculation of the wave function radius of gyration Rg, if diffuse functions are included. Most of the results given in Table S1 seem to give optimum X-H distance of ca. 1.6 Å and Rg of around 2.5 Å, slightly larger than we expect based on the experimental optical absorbance. ωB97X functional is an outlier, with shorter X-H and very reasonable Rg of ca. 2.25 Å, which has lead us to use it for many of our test calculations. As a benchmark we tried CCSD(T)/cc-pvTz method to evaluate the energy at the optimum geometries of ωB97X/6-31G++G(2df,p) and B3LYP/6-31G++G(2df,p) calculations. The result favored the B3LYP geometry by only 1 kcal/mol, at which point we realized just how shallow the X-H minimum is. In Figure 6 we plot the energy of the 4 water model constrained to a tetrahedral conformation, as a function of X-H distance (i.e. cavity size) using B3LYP, CAM-B3LYP, ωB97X, and ωB97X-D methods with the 6-31++G(2df,p) basis set. The results are plotted with energies normalized to the value at 2.1 Å (The unnormalized energies are plotted in Figure S3.). Each of the functionals shows a relatively broad minimum energy in the range X-H=1.4-1.7Å, and energy only increases substantially below X-H of 1.2Å. Four CCSD(T)/aug-cc-pvTz benchmark points are superimposed, which clearly favor B3LYP over the ωB97X functionals. We cannot expect a perfect result from any of these functionals, but it seems certain the optimum X-H distance falls in the range of 1.5-1.6Å, very similar to the maximum proton g(r) obtained in the large-scale UMJ simulation.25
Figure 6.
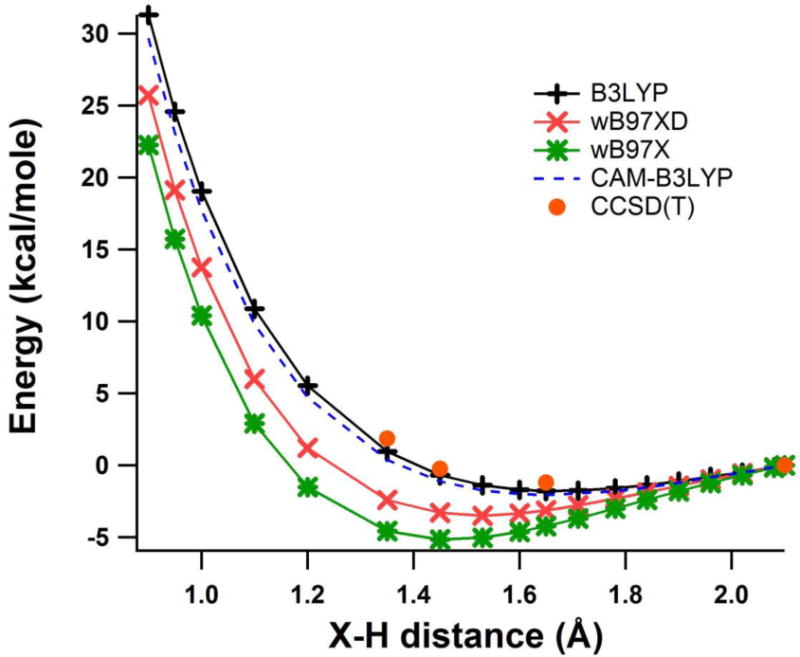
Plot of relative total energy (kcal/mol) vs. X-H distance (Å) for optimized 4 water tetrahedral cluster solvated electron using the B3LYP (black), CAM-B3LYP (blue-dashed), ωB97X-D (red) and ωB97X (green) methods with 6-31++G(2df,p) basis set. CCSD(T)/aug-cc-pvTz benchmark calculations are shown as red dots.
We can only claim excellent agreement with the experimental radius of gyration (zero Kelvin Rg < 2.35Å) for the ωB97X and ωB97X-D functionals. However, the energy minimum for all of the methods is very shallow, and average X-H distance anywhere in the range of 1.3 to 2 Å is certainly possible if we allow for the effects of thermal averaging. If we assume X-H is ca. 1.5 Å, the corresponding value of Rg is consistent with the experimental Moment Theory treatment. We also need to recognize that the Moment Theory is a one-electron approximation which we have superimposed on a many-electron system. Is the approximation better than 10% accurate? If not, we can claim agreement with the experimental Rg estimate for all of the DFT methods of Table S1.
As a final comment, we note that the octahedral Kevan structure of Figure S8.1 is characterized by Rg = 2.6 Å, not significantly different from the tetrahedral structures in spite of the larger central void with X-H = 1.96 Å. Consequently this property inferred from the optical spectrum does not allow a choice between the octahedral and tetrahedral water geometries.
3. The Vertical Detachment Energy
The determination of Vertical Detachment Energy (VDE) is of interest as this measures the instantaneous energy to remove the solvated electron from the bulk water to the gas phase. This value is equivalent to the work function of water containing a solvated electron. Recent photoelectron experiments42-48 on liquid microjets have determined the VDE of solvated electron in the range 3.42-3.45 eV.47,48 The VDE can be calculated as the difference between the total energy of the optimized anion and that of the neutral cluster at the same geometry, using a non-equilibrium polarized continuum model (NE-PCM). The latter version of PCM35 (available in Gaussian 09) retains the “nuclear orientation” part of the reaction potential induced in the solvent to compute the neutral cluster energy, when the electron is “suddenly” removed.
Figure 7 shows the VDE calculated for optimized 4-water tetrahedral clusters calculated with several DFT methods and the 6-31++G(2df,p) basis set, as a function of the X-H distance which is constrained in the calculation. (Corresponding variation of the anion total energy was shown in Figure 6.) The calculated VDE is monotonically increasing as the X-H distance decreases for this geometry. It can be seen that both the B3LYP and CAM-B3LYP functional calculations do a very good job of reproducing the experimental VDE (3.42 to 3.45 eV) near their equilibrium X-H distance of about 1.6 Å. The ωB97X and ωB97X-D functionals reach the experimental VDE at a shorter X-H distance of about 1.35 Å. This is also an acceptable result, given the ground state energy is within kT (298K) of the ωB97X minimum at X-H =1.45 A. VDE calculations using ωB97X and B3LYP at their respective optimum geometries were performed using the very large PCseg-4 basis set. The ωB97X/PCseg-4 number is only slightly too low at 3.38eV at X-H=1.51Å. B3LYP/PCseg-4 gives a very acceptable zero kelvin result of 3.51 eV at X-H = 1.74Å.
Figure 7.
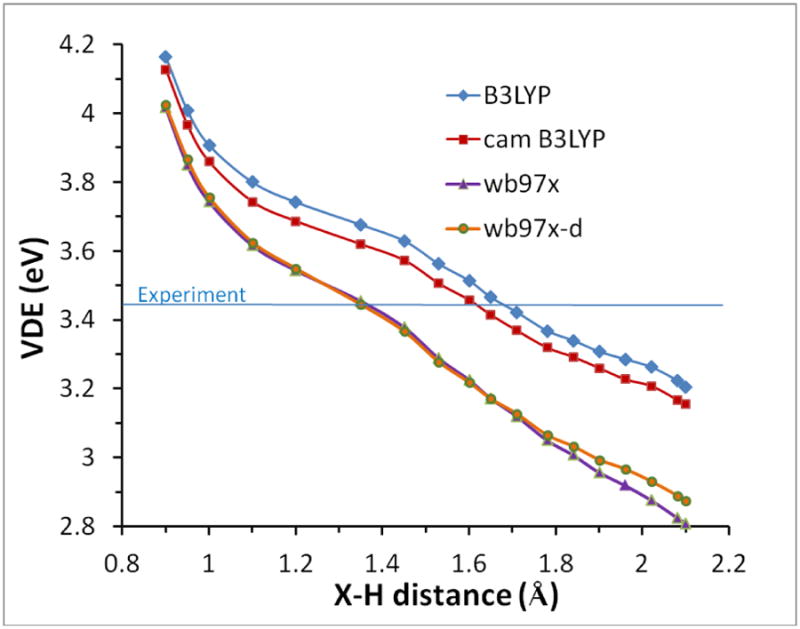
Variation of VDE (eV) vs X-H distance (Å) calculated using B3LYP (red); CAM-B3LYP (yellow); ωB97XD (gray) and ωB97X (blue) functionals with the 6-31++G(2df,p) basis set and NE-PCM.
Finally, we need to investigate the effect of adding additional water layers. For the 16-water cluster illustrated in Figure 5 with B3LYP/6-31++G(2df,p), the calculated VDE is 3.45eV at the equilibrium geometry, in comparison with 3.47eV for the 4-water cluster using the same method. Recall that the 16 water structure maintains the inner 4-water tetrahedron. When diffuse functions are omitted from the calculation for the 4 and 16 water clusters, the VDE numbers are too low, at 2.97eV and 3.35 eV for B3LYP/6-31G(2df,p), respectively. We conclude here that some diffuse character of the wavefunction is necessary to reproduce the VDE property especially for small water clusters, just as we found in the previous section for the radius of gyration. The properties of the minimal four-water/polarized continuum cluster model are in quite good agreement with experiment. For comparison the octahedral Kevan structure is characterized by VDE = 3.69eV using B3LYP/6-31++G(2df,p). Consequently this property is also incapable of distinguishing between the 4-water tetrahedron and the 6-water octahedral structure.
4) Vibrational frequencies
One of the signature properties of the solvated electron is the red shift of the O-H stretching frequencies observed in resonance Raman spectra.36 Tauber and Mathies36 report a 200 cm-1 downshift and broadening of the OH stretch frequencies relative to bulk water. As already mentioned, their results revealed that the water molecules coupled to the electron are in an asymmetric environment, with one proton forming a strong hydrogen bond to the electron. They reported that downshifted bend and librational frequencies also indicate the outboard proton is a relatively poor hydrogen bond donor to the surrounding solvent. Schwartz and coworkers8 have used a semi-empirical estimation based on local electric field at the inner H atoms to argue that the pseudopotential “cavity” models fail to predict the experimental frequency red shift. These authors also suggest the structures produced in the large-scale DFT calculation of UMJ will be insufficiently red-shifted. On the other hand, Shkrob et al.49 carried out B3LYP/6-31++G** TD-DFT calculations of anion clusters derived from the Turi-Borgis pseudopotential22, and indicate a red shift with respect to the neutral water spectrum.
Our optimized tetrahedral cluster model is largely in accord with the experimental findings of Tauber and Mathies36, although from just the zero Kelvin structure we cannot possibly calculate the inhomogeneously broadened resonance Raman spectrum. From frequency analysis of the optimal structures we find essentially three kinds of OH stretch. The inboard OH bonds pointing toward the center invariably have the lowest stretching frequencies. Non-hydrogen bonding OH bonds have the highest stretch frequencies as expected for “free” OH bonds. In the four-water clusters, the outboard OH bonds fall into this category. For clusters larger than four waters, the remaining bonds will be H-bonded, and the stretching frequencies are intermediate. Figure 8 illustrates a typical frequency spectrum for a 16-water anion cluster fully optimized using B3LYP/6-31++G(2df,p). No tetrahedral symmetry is enforced yet the four inner bends and OH stretching frequencies are still shifted to lower frequencies. The inboard stretch frequencies near 3300cm-1 are shifted about 200cm-1 relative to the “bulk” H-bonded frequencies centered around 3500cm-1. Thus we have a large red shift for the OH stretches “H-bonded to the electron” just as reported by Tauber and Mathies.36
Figure 8.
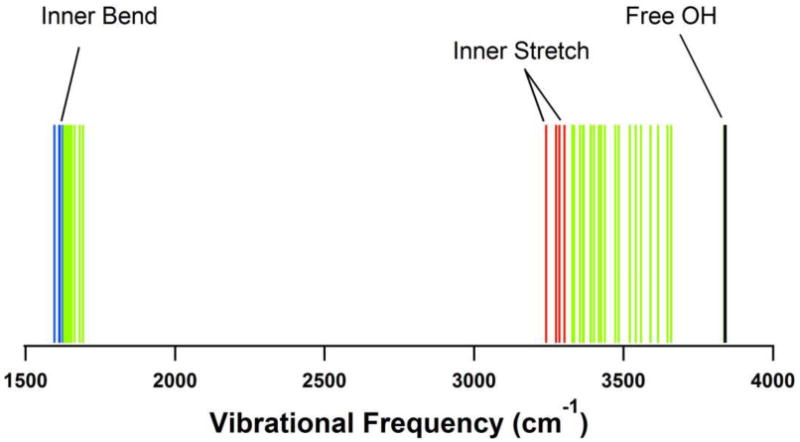
Bending and stretching vibrational frequencies for the 16 water anion cluster optimized using B3LYP/6-31++G(2df,p). Note the four inner stretches and bends are at lower frequency.
Figure 9 plots the (A) OH bond distances and (B) O-H stretching frequencies recorded for the B3LYP/6-31++G(2df,p) four-water tetrahedral constrained optimization vs. X-H, whose energy and VDE is already shown in Figures 6 and 7. (The normal mode calculations at non-optimal geometries give one or two imaginary very low frequency “breathing” modes. These are only weakly coupled to the OH stretches, so the calculated stretches are quite meaningful in terms of a local mode approximation.) It is clear that as the tetrahedron becomes smaller, the unpaired spin overlaps more with the inboard OH bond, adding more antibonding character and increasing the OH bond length. The (averaged) inboard OH stretching frequency is down-shifted, but the outboard bond length and frequency are essentially unaffected. The “correct” experimental red shift of ca. 200cm-1 only applies near the optimum X-H value of the model. For comparison the octahedral Kevan model described in section 8 of the Supporting Information (Figure S8.1) gives inner stretch frequencies of about 3500cm-1, very similar to the H-bonded values shown in Figure 8. The Kevan structure can therefore be rejected on the basis of insufficient red shift, in addition to the energetic criterion used earlier.
Figure 9.
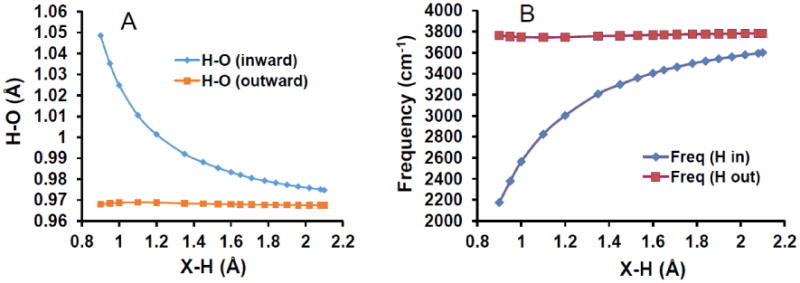
(A) Plot of the inward (blue) and outward (red) OH bond lengths (Ǻ) and inward and outward vibration stretching frequencies (cm-1) (B) vs. X-H distance (Å) for 4-water clusters, evaluated with B3LYP/6-31++G(2df,p).
5) The EPR g-factor
The g factor of the hydrated electron in pure water has been measured in several EPR experiments at room temperature and found to be 2.0003350, 2.0004751 and 2.00043.52 These values are significantly shifted by an average of -1900 ppm from the free electron g factor of 2.0023 (using the Gaussian definition g = gfree + ppm/106). Fessenden and Verma50 demonstrated a small trend toward larger (more negative) shift at higher temperature. In frozen aqueous solutions trapped electrons also show g factors downshifted from the free electron value by -1700 ppm in doped D2O ice,53 a fact that is yet to be explained. Indeed, heretofore no ab initio calculations have successfully treated this property of the hydrated electron.
The g-factor shift from the free electron value for any radical comes from the coupling of spin and orbital angular momentum (λ L•S)51,54 The observed g-factor shift demonstrates that the wavefunction has substantial angular momentum and is not purely s-character, but this fact has been largely ignored by the vast majority of workers. Spin density on oxygen is expected to result in a g-shift owing to augmented spin-orbit coupling.51 The source of the orbital angular momentum can readily be seen in the 3D plots of spin density in Figures 1 and 5. There is very significant p-orbital character on the oxygen atoms that is aligned with the X-O axis. This character persists even as the X-H distance becomes longer. The Mulliken spin population on oxygen is ca. 7% using the 6-31G(2df,p) basis set, and becomes 10-20% when diffuse functions are added. This total population agrees well with estimates made many years ago by Shiraishi, et al.51 for the octahedral Kevan structure32. Figure S8.2 of the Supporting Information shows the Kevan structure has similar p-orbital character at oxygen.
Using the optimized 4, 6, 8 and 16 water cluster models we have calculated the g factor shift for the electron using B3LYP as well as ωB97X functionals with several basis sets. We note that the computed g-factors are anisotropic, which is a consequence of the static configuration of our model. In solution a simple average over the 3 principle axes will be observed. All of the g-factor results are reported in Table S1. The result for B3LYP with 6-31G(2df,p) basis set is -1000 ppm, which is of the correct direction, but ca. 40% below the low temperature experimental shift of -1700 ppm. As diffuse functions are added to the basis set (6-31++G(2df,p)) the g factor shift improves to -1200 ppm, a shift from free-electron on the order of 30% below the experiment. B3LYP/6-31++G(2df,p) calculation of the 16 waters cluster (see Table S1) increased the downshift to -1350ppm, only 20% below the experimental low temperature shift. The octahedral Kevan structure calculated with B3LYP/6-31++G(2df,p) is characterized by g-factor shift of -1200 ppm, which is identical with the 4-water tetrahedron. EPR g-factor clearly cannot be used as a criterion for distinguishing these models.
In Figure 10 we plot g-factor shift for the constrained tetrahedral water clusters as a function of X-H using B3LYP/6-31++G(2df,p) with PCM. For X-H=1.3Ǻ and larger, we see a roughly linear decrease in g- shift which can be directly correlated with smaller spin density at oxygen as the size of the tetrahedron (and Rg) increases. At shorter X-H, below 1.2Å, a rapid decrease in g-shift is found.
Figure 10.
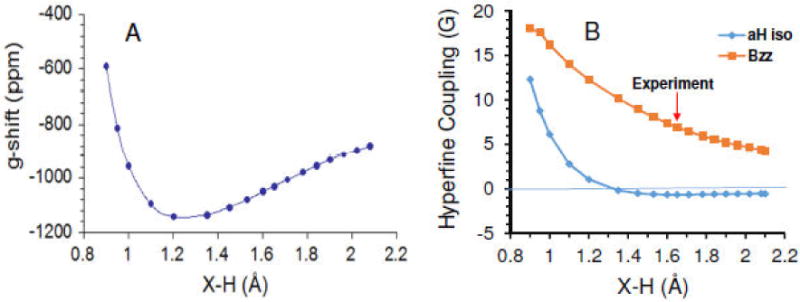
(A) Plot of EPR g-shift vs X-H distance for the four water constrained structure (Cs symmetry). (B) Plot of isotropic (blue diamonds) and anisotropic (Bzz, red squares) proton hyperfine couplings vs the X-H distance. Calculated using B3LYP/6-31++G(2df,p) including PCM. The red arrow marks the experimental value (see text).
The qualitative behavior of these g-factor shifts seems reasonable, but the remaining 20% deviation between the calculated and experimental (low temperature) values is difficult to explain. The 16-water result remains ca. 30% below the room temperature experiment. It is also not clear at present how the minor temperature dependence of this quantity can be recovered. (Larger Rg implies larger X-H at higher temperature, which should result in a smaller g-factor shift according to Figure 10, but the experiment50 demonstrates the opposite slope.) The prediction of EPR g-factor can be a very difficult quantum calculation, and this is a problem which requires additional work. Nevertheless, the fact that the g-factor shift is predicted properly in magnitude and direction is evidence in support of the model proposed in this work.
6) The EPR hyperfine couplings
Proton hyperfine couplings are not observable in solution for the hydrated electron due to the fast motional narrowing. Proton and oxygen-17 hyperfine couplings have been measured at X-band for electrons trapped in concentrated low temperature hydroxide glasses.32,55,56 It is not certain that the local structure in these glasses corresponds to that in the liquid, but it has often been assumed so. The work of Kevan32 was generally cited to support the cavity/pseudopotential model of Schnitker and Rossky19,20, and the OH-bond-oriented octahedral hexamer structure is generally labeled with his name, though he was not the first to propose it. The magnetic resonance evidence was reviewed in detail several years ago by Shkrob33, and we highly recommend reading his paper and associated supporting information as a tutorial.
In brief, the proton hyperfine couplings recorded for these trapped electrons in low temperature aqueous glasses are axially symmetric, and can be decomposed into a negative isotropic component (-0.92G) and a positive anisotropic component (Bzz) of ca. 7G.33 Shkrob33 carried out much the same calculations that we have to explore the octahedral and tetrahedral structures, except without using the polarized continuum. He found as we have that significant spin population (10 to 20%) resides on the oxygen 2p orbitals of the water molecules, and that spin polarization from this spin on oxygen accounts for the observed small negative isotropic proton hyperfine coupling and the positive anisotropic coupling of the O-H protons pointed toward the electron. Shkrob33 notes that his own work represents the first rigorous demonstration that the Kevan32 structure could explain the low temperature EPR data, though other structures were not ruled out. The calculations of Shkrob33 require X-H distance of <1.5 Å for the tetrahedral water model to match the experimental hyperfine couplings, which he felt was unrealistic.
Our calculations for the hyperfine couplings are done with the B3LYP/6-31++G(2df,p) method with PCM on the tetrahedral 4 water system. In Figure 10B we show calculated values for the isotropic and anisotropic couplings of the four inboard protons as a function of the constrained X-H distance (full ESR parameters for all nuclei are given in Table S3). The axial symmetry found in the anisotropic coupling (Bzz) is a result of the electron spin density distribution, which has a node at each inboard proton and near axial symmetry in the nearby unpaired electron distribution (see Figures 1 and 5). The calculated isotropic coupling is found to stay almost constant near -0.6 G for X-H from 2.1 to 1.5 Å, and then becomes positive for smaller cluster size, as spin density increases at the hydrogen s orbitals. The change in sign suggests a lower limit of 1.5Å for the experimental X-H distance. The anisotropic coupling is strongly dependent on the X-H distance. At the 1.65 Å B3LYP energy minimum, the calculated isotropic coupling deviates from experiment by only 0.3 G and has the correct sign, while anisotropic Bzz = 7 G is in excellent agreement with experiment. (The optimized octahedral Kevan structure gives Aiso= -0.88G and Bzz= 5.6G, which are similar to the tetrahedral model.) A full optimization of the 4 water system using B3LYP with the much larger PCseg-4 basis set gave a X-H optimized distance of 1.74 Å and hyperfine couplings of -1.57 G and 7.3 G for the Aiso and Bzz values in very good agreement with the results in Figure 10. The minimal tetrahedral model matches the results found for the electron trapped in low temperature alkaline glass, consistent with the assumption that the local structure in these glasses is similar to that in liquid water.
7) Thermodynamic Properties
Chemical thermodynamic properties of the hydrated electron are derived from pulse radiolysis transient absorption measurements by way of two kinetically accessible equilibria involving the hydrogen atom:
| 1 |
| 2 |
Both equilibria have been measured vs. temperature by Schwartz57,58 and by Shiraishi, et al.59 From the equilibrium constants the Gibbs energy changes may be obtained, and from the temperature dependence this can be decomposed into the enthalpy and entropy changes. Enthalpy and entropy of formation for (H2O)aq, (OH-)aq, (NH4+)aq, and (NH3)aq can be found in standard thermodynamic tables, so that the radiolysis experiments establish ΔrX° for equilibrium 3, where X=G,H,S.
| 3 |
| 4 |
The gas phase equilibrium (4) is very well-determined, so the difference of thermodynamic functions corresponds to the hydration process:
Standard thermodynamic properties of hydration for (H)aq are easily estimated, but those for (H+)aq are still debated. Our choices for these numbers are explained in the Supporting Information. The resulting values for the electron hydration thermodynamics are listed in Table 1, using the Ben Naim standard state60 of equal density in gas and liquid, denoted by *.
To investigate thermodynamic properties of our minimal hydrated electron model we made use of the Gaussian-4 (G4) prescription for thermochemical properties developed by Curtiss, Redfern, and Raghavachari61, and built into the Gaussian-09 package. The first step of the method is a geometry optimization carried out with B3LYP density functional and 6-31G(2df, p) basis set. The optimized parameters for this theory level have already been discussed above. We might not expect the method to work well for this problem, because the basis set lacks the diffuse basis functions required for full geometry optimization. However, the energy shown in Figure 6 is a very weak function of the X-H dimension near the minimum (flat from 1.5 to 1.8 Å), so this optimization (which gives 1.5 Å as the X-H distance) is good enough, especially when it is followed in the G4 method by extrapolation to the very large basis set limit.
The B3LYP/6-31G(2df,p) optimized geometries for 4 and 6 water anion clusters have already been described (Figure 1). These anion cluster geometries were used as the starting structures for optimization of (H2O)4 and (H2O)6 clusters in the neutral state. The G4-optimized neutral clusters in PCM are shown in Figure S7.1 in the Supporting Information. The optimized structure for the neutral (H2O)4 is held together by four hydrogen bonds while the optimized structure of (H2O)6 is bound together by eight hydrogen bonds and resembles the chair form of cyclohexane.62 On solvation of the electron both optimized (H2O)4- and (H2O)6- structures lose four hydrogen bonds (see Figure S7.1). The neutral tetramer and hexamer clusters can have various structures but those with the same number of hydrogen bonds have energies within 1 kcal/mol (ref 61 and Figure S7.2), so the structures chosen are representative.
The solvation of the hydrated electron is approximated by the process in eq 5, where the neutral water clusters in polarized continuum represent bulk water. Process 6 is simply the formal equilibration of the clusters with the bulk water, which by definition should have ΔG=0.
| 5 |
| 6 |
The absolute solvation free energy (ΔhydG*) is given by:
The absolute free energies, enthalpies and entropies (G°, H°, S°) at 298°K of aq(H2O)n = 4, 6 and aq(H2O)-n = 4, 6 are calculated by the G4-method with PCM. For the electron in the gas phase at 298 K, free energy, enthalpy, and entropy were taken from the recommendations of Bartmess63 for the 1 atm electron gas standard state and converted to the Ben Naim standard state.
The G4-calculated thermodynamic properties of the solvated electron in four and six water clusters are summarized in Table 1 along with the preferred experimental values. The latter numbers are taken from the short review presented in Supporting Information. For the four-water anion cluster, our ΔhydG*, is -37.8 kcal/mol, while the corresponding value for (H2O)6 is -38.9 kcal/mol. These numbers are in good agreement with the experimental estimate, which is -36.3 kcal/mol with several kcal/mol uncertainty.
As a cross-check we applied exactly the same method to solvation of the chloride ion. The G4-calculated result using a six water cluster is -74.6 kcal/mol, in perfect agreement with the tabulated result of -74.6 kcal/mol.64 An additional cross-check was solvation of a Zundel cation (H2O--H+--OH2) to represent proton solvation. This calculation, outlined in the Supporting Information, also agreed very well with the experimental estimate for absolute proton solvation.
It is interesting to note that the positive entropy of solvation found with experiment (ca. +20.5 cal/mol deg) is recovered in the present Gaussian calculation for the four-water anion. The polarized continuum model is strictly a free energy approximation,34,35,65 and predicts a zero entropy change on solvation for a bare ion, because PCM lacks the missing details of the water rearrangement in the several solvation shells.66 Our calculation includes a minimal first water solvation shell and gives a rough estimate of the entropy change. For example, the calculation of the entropy change on chloride ion solvation gives the correct sign with the calculated value (-13.4 cal/mol.deg) about 7 cal/mol/deg lower than the experiment (-6.3 cal/mol.deg).64 The numerical agreement found for (e-)aq is somewhat fortuitous but the positive sign is not. Some years ago it was demonstrated that the electron solvation entropy is inevitably much more positive than any classical particle because the gas phase entropy is so small.67 The difference between classical ion and electron solvation can be found in the attachment of the first solvent molecule(s) in the gas phase. In this step, the electron has very little translational entropy to lose, relative to any classical ion. Subsequent solvation steps are of similar magnitude. Consequently the claim that the electron is a “champion” structure-breaking ion based on its positive solvation entropy is questionable.68, 69
8) Optical Spectrum
We arrive finally at consideration of the hydrated electron optical spectrum, which has often been the entire focus of comparison between model calculations and experiment. It is reasonable to expect that the four-water cluster is just too small to support a good representation of the diffuse excited states. Consequently we have focused on the radius of gyration, which is a ground state property inferred by integration of the entire optical spectrum.
Nevertheless the TD-DFT calculation of the excited states of the tetrahedral water anion structure in NE-PCM has already been carried out by Herbert, Jungwirth, and coworkers27 for B3LYP and LRC-μBLYP functionals. They demonstrate the essential allowed “s-p” character of the visible transition peaked near 1.7 eV which is the hallmark of virtually any model of the hydrated electron ever proposed. The purpose of their paper is to find a properly tuned functional that will reproduce the experimental optical spectrum using snapshots from the large-scale UMJ simulation.25 They explored basis set size and the size of the water cluster which needs to be specifically treated quantum mechanically (the rest being represented by point charges). With respect to the minimal tetrahedral model, their conclusion is similar to our own for the other hydrated electron properties:27 “the excitation spectrum is dominated by short-range solvent structure. Longer range electronic reorganization effects, though qualitatively important, can be adequately described using … a continuum solvation model.”
IV. Conclusions
This paper demonstrates that a remarkably straightforward, standard ab initio calculation of a small anion water cluster embedded in dielectric continuum can reproduce essentially all of the available experimental evidence regarding equilibrium structural properties of the hydrated electron. For decades it has been assumed that this problem can only be approached in terms of a statistical average over many structures as generated in a large scale molecular dynamics or Monte Carlo simulation. It is nothing less than astounding that a minimal four-water anion cluster, absent any specific hydrogen bonding to the second solvation shell, is able to reproduce so many properties of the room temperature species. The four-water anion cluster demonstrates the OH-bond directed geometry, and the red-shifted OH stretching frequencies found in transient Raman experiments. The radius of gyration deduced from integration of the optical spectrum is properly recovered as is the vertical detachment energy, for optimized X-H distances on the order of 1.5-1.7 Å. The experimental solvation free energy is correctly calculated, and a positive solvation entropy is recovered. The EPR g-factor is correctly predicted to be lower than the free electron value due to significant spin density on water oxygen. Hyperfine couplings measured in low temperature aqueous glasses are properly calculated, again for X-H distance on the order of 1.6 Å. This is approximately the average g(r) for X-H found in the room temperature AIMD simulation of UMJ25, and we substantially agree with that result. We assert that when considering the nature of the hydrated electron, the tetrahedral structural motif displayed in Figure 1 should serve as the starting point.
For decades arguments over the structure of the hydrated (and in general solvated) electron have been couched in terms of its “cavity” or non-cavity nature15-18,71 The term “cavity model” originally implied a certain set of assumptions regarding the interaction potential of the excess electron with its environment, as explained in the Introduction. Our results certainly support a structure with a central void or cavity, but once one passes from a one-electron to a many-electron representation, the assumptions have been discarded and one is no longer dealing with a “cavity model”. Things are more complicated, as already noted by Uhlig, Marsalek and Jungwirth25 and by Herbert.16 Rather, the picture for the hydrated electron that emerges is a multimer solvent anion with small central cavity and unpaired spin significantly delocalized onto the oxygen atoms of the central four waters. It is these features that give rise to the properties of the solvated electron discussed in this work.
Supplementary Material
Table 2.
Thermodynamic properties (G* and H* in kcal/mol and S* in cal/mol deg) of solvated electron ( ) calculated using Gaussian-4 (G4) method along with experimental data. Integral equation formalism variant polarized continuum model (IEF-PCM) was used to consider the full solvent effect (ε = 78.4).
| e-aq | ΔhydG* | ΔhydH* | ΔhydS* |
|---|---|---|---|
| Theory | |||
| 4 watera,b | -37.8 | -29.9 | 26.6 |
| 6 watera,b | -38.9 | -31.7 | 24.0 |
| Ref(70) | -37.4 c | ||
| Experiment | |||
| Supp. Inf. | -36.3 | -30.2 | 20.5 |
Present work. 4 and 6 water clusters with PCM.
Gas phase electron values from reference 62 were corrected to 1M standard state for e-(gas). See Supporting Information.
Value of -35.5 reported for ΔhydG° (1 atm) in ref. 70 corrected to ΔhydG* (1M standard state).
Acknowledgments
Authors Kumar and Sevilla thank the NCI of the NIH for support under Grant R01CA045424. Authors Walker and Bartels are supported by the Division of Chemical Sciences, Geosciences, and Biosciences, Office of Basic Energy Sciences of the U.S. Department of Energy through award DE-FC02-04ER15533. This is manuscript number 5073 of the Notre Dame Radiation Lab.
Footnotes
We classify these as “cavity models” because the pseudopotential essentially forbids the electron to be “on” the water molecules, so there is little choice for the electron but to form a cavity. One should draw a distinction between a “cavity model“ and a “cavity-forming-model” where the final result is not built into the assumptions.
This proposal is certainly not new. The earliest suggestion of a tetrahedral model for the solvated electron is attributed to Natori and Watanabe: Natori, M. and Watanabe, T. Structure Model of the Hydrated Electron, J. Phys. Soc. Jpn. 1966, 21, 1573-1578.
As an interesting historical note, Marshall Newton (Newton, M.D. The Role of Ab Initio Calculations in Elucidating Properties of Hydrated and Ammoniated Electrons. J. Phys. Chem. 1975, 79, 2795-2808.) first attempted to answer the question of hydrated electron structure using an ab initio water-cluster-in-dielectric-continuum model in 1975. He concluded a 4-water tetrahedron with molecular dipole orientation was preferred, but at Hartree-Fock level with 4-31G basis set, his calculation was certain to fail, even apart from the very crude dielectric continuum bubble he had to use.
Supporting Information Available: Table of cluster properties calculated with various methods and basis sets. Table of HFCCs calculated vs. cavity size. Plot of DFT total energies (AU) and relative energies vs. X-H distance. Search for alternate local minima of the four-water cluster, and determination of the barrier between bond and dipole orientation. Study of the effect of ghost basis functions. Review of thermodynamic properties for electron solvation from existing experimental data. Structures of 4- and 6-water clusters used for the thermodynamic (G4) calculations. Analysis of the Kevan octahedral solvated electron model with comparison to the 4 water model. Coordinates and images of all optimized structures. Complete reference 28. (PDF)
This material is available free of charge via the Internet at http://pubs.acs.org.
References
- 1.Mozumder A. Fundamentals of Radiation Chemistry. Academic Press; Boston: 1999. [Google Scholar]
- 2.Paik DH, Lee IR, Yang DS, Baskin JS, Zewail AH. Electrons in Finite-Sized Water Cavities: Hydration Dynamics Observed in Real Time. Science. 2004;306:672–675. doi: 10.1126/science.1102827. [DOI] [PubMed] [Google Scholar]
- 3.Pimblott SM, LaVerne JA. On the Radiation Chemical Kinetics of the Precursor to the Hydrated Electron. J Phys Chem A. 1998;102:2967–2975. [Google Scholar]
- 4.Lian R, Crowell RA, Shkrob IA. Solvation and Thermalization of Electrons Generated by Above-the-Gap (12.4 eV) Two-Photon Ionization of Liquid H2O and D2O. J Phys Chem A. 2005;109:1510–1520. doi: 10.1021/jp045657b. [DOI] [PubMed] [Google Scholar]
- 5.Hart EJ, Boag JW. Absorption Spectrum of the Hydrated Electron in Water and in Aqueous Solutions. J Am Chem Soc. 1962;84:4090–4095. [Google Scholar]
- 6.Boag JW, Hart EJ. Absorption Spectra in Irradiated Water and Some Solutions: Absorption Spectra of ‘Hydrated’ Electron. Nature. 1963;197:45–47. [Google Scholar]
- 7.Young RM, Neumark DM. Dynamics of Solvated Electrons in Clusters. Chem Rev. 2012;112:5553–5577. doi: 10.1021/cr300042h. [DOI] [PubMed] [Google Scholar]
- 8.Casey JR, Kahros A, Schwartz BJ. To Be or Not to Be in a Cavity: The Hydrated Electron Dilemma. J Phys Chem B. 2013;117:14173–14182. doi: 10.1021/jp407912k. [DOI] [PubMed] [Google Scholar]
- 9.Abel B, Buck U, Sobolewski AL, Domcke W. On the Nature and Signatures of the Solvated Electron in Water. Phys Chem Chem Phys. 2012;14:22–34. doi: 10.1039/c1cp21803d. [DOI] [PubMed] [Google Scholar]
- 10.Feng DF, Kevan L. Theoretical Models for Solvated Electrons. Chem Rev. 1980;80:1–20. [Google Scholar]
- 11.Coe JV, Williams SM, Bowen KH. Photoelectron Spectra of Hydrated Electron Clusters vs. Cluster Size: Connecting to Bulk. Int Rev Phys Chem. 2008;27:27–51. [Google Scholar]
- 12.Jordan KD. A Fresh Look at Electron Hydration. Science. 2004;306:618–619. doi: 10.1126/science.1104678. [DOI] [PubMed] [Google Scholar]
- 13.Hart EJ, Anbar M. The Hydrated Electron. Wiley-Interscience; New York: 1970. [Google Scholar]
- 14.Marsalek O, Uhlig F, Vandevondele J, Jungwirth P. Structure, Dynamics, and Reactivity of Hydrated Electrons by Ab Initio Molecular Dynamics. Acc Chem Res. 2012;45:23–32. doi: 10.1021/ar200062m. [DOI] [PubMed] [Google Scholar]
- 15.Larsen RE, Glover WJ, Schwartz BJ. Does the Hydrated Electron Occupy a Cavity? Science. 2010;329:65–69. doi: 10.1126/science.1189588. [DOI] [PubMed] [Google Scholar]
- 16.Jacobson LD, Herbert JM. Comment on “Does the Hydrated Electron Occupy a Cavity?”. Science. 2011;331:1387–d. doi: 10.1126/science.1198191. [DOI] [PubMed] [Google Scholar]
- 17.Herbert JM, Jacobson LD. Structure of the Aqueous Electron: Assessment of One-Electron Pseudopotential Models in Comparison to Experimental Data and Time-Dependent Density Functional Theory. J Phys Chem A. 2011;115:14470–14483. doi: 10.1021/jp206391d. [DOI] [PubMed] [Google Scholar]
- 18.Turi L, Madarász Á. Comment on “Does the Hydrated Electron Occupy a Cavity?”. Science. 2011;331:1387–c. doi: 10.1126/science.1197559. [DOI] [PubMed] [Google Scholar]
- 19.Schnitker J, Rossky PJ. An Electron-Water Pseudopotential for Condensed Phase Simulations. J Phys Chem. 1987;86:3462–3469. [Google Scholar]
- 20.Schnitker J, Rossky PJ. The Hydrated Electron: Quantum Simulation of Structure, Spectroscopy, and Dynamics. J Phys Chem. 1988;92:4277–4285. [Google Scholar]
- 21.Turi L, Gaigeot MP, Levy N, Borgis D. Analytical Investigations of an Electron-Water Pseudopotential. 1. Exact Calculation on a Model. J Chem Phys. 2001;114:7805–7815. [Google Scholar]
- 22.Turi L, Borgis D. Analytical Investigations of an Electron-Water Molecule Pseudopotential. 2. Development of a New Pair Potential and Molecular Dynamics Simulations. J Chem Phys. 2002;117:6186–6195. [Google Scholar]
- 23.Jacobson LD, Herbert JM. A One-Electron Model for the Aqueous Electron That Includes Many-Body Polarization: Bulk Equilibrium Structure, Vertical Electron Binding Energy, and Optical Absorption Spectrum. J Chem Phys. 2010;133:154506/1–154506/19. doi: 10.1063/1.3490479. [DOI] [PubMed] [Google Scholar]
- 24.Bartels DM, Takahashi K, Cline JA, Marin TW, Jonah CD. Pulse Radiolysis of Supercritical Water. 3. Spectrum and Thermodynamics of the Hydrated Electron. J Phys Chem A. 2005;109:1299–1307. doi: 10.1021/jp0457141. [DOI] [PubMed] [Google Scholar]
- 25.Uhlig F, Marsalek O, Jungwirth P. Unraveling the Complex Nature of the Hydrated Electron. J Phys Chem Lett. 2012;3:3071–3075. doi: 10.1021/jz301449f. [DOI] [PubMed] [Google Scholar]
- 26.Uhlig F, Jungwirth P. Embedded Cluster Models for Reactivity of the Hydrated Electron. Z Phys Chem. 2013;227:1583–1593. [Google Scholar]
- 27.Uhlig F, Herbert JM, Coons MP, Jungwirth P. J Phys Chem A. 2014;118:7507–7515. doi: 10.1021/jp5004243. [DOI] [PubMed] [Google Scholar]
- 28.Frisch MJ, Trucks GW, Schlegel HB, Scuseria GE, Robb MA, Cheeseman JR, Scalmani G, Barone V, Mennucci B, Petersson GA, et al. Gaussian 09, revision B.01. Gaussian, Inc.; Wallingford CT: 2009. [Google Scholar]
- 29.GaussView. Gaussian, Inc.; Pittsburgh, PA: 2003. [Google Scholar]
- 30.Jmol: An Open-source Java Viewer for Chemical Structures in 3D. http://www.jmol.org/
- 31.Lu T, Chen F. Multiwfn: A Multifunctional Wavefunction. Comput Chem. 2012;33:580–592. doi: 10.1002/jcc.22885. [DOI] [PubMed] [Google Scholar]
- 32.Kevan L. Solvated Electron Structure in Glassy Matrices. Acc Chem Res. 1981;14:138–145. [Google Scholar]
- 33.Shkrob IA. The Structure of the Hydrated Electron. Part 1. Magnetic Resonance of Internally Trapping Water Anions: A Density Functional Theory Study. J Phys Chem A. 2007;111:5223–5231. doi: 10.1021/jp068278m. [DOI] [PubMed] [Google Scholar]
- 34.Tomasi J, Mennucci B, Cammi R. Quantum Mechanical Continuum Solvation Models. Chem Rev. 2005;105:2999–3093. doi: 10.1021/cr9904009. [DOI] [PubMed] [Google Scholar]
- 35.Cossi M, Barone V, Cammi R, Tomasi J. Ab Initio Study of Solvated Molecules: A New Implementation of the Polarizable Continuum Model. Chem Phys Lett. 1996;255:327–335. [Google Scholar]
- 36.Tauber MJ, Mathies RA. Structure of the Aqueous Solvated Electron from Resonance Raman Spectroscopy: Lessons from Isotopic Mixtures. J Am Chem Soc. 2003;125:1394–1402. doi: 10.1021/ja021134a. [DOI] [PubMed] [Google Scholar]
- 37.Bartels DM. Moment Analysis of Hydrated Electron Cluster Spectra: Surface or Internal States? J Chem Phys. 2001;115:4404–4405. [Google Scholar]
- 38.Du Y, Price E, Bartels DM. Solvated Electron Spectrum in Supercooled Water and Ice. Chem Phys Lett. 2007;438:234–237. [Google Scholar]
- 39.Valiev M, Bylaska EJ, Govind N, Kowalski K, Straatsma TP, van Dam HJJ, Wang D, Nieplocha J, Apra E, Windus TL, de Jong WA. NWChem: A Comprehensive and Scalable Open-Source Solution for Large Scale Molecular Simulations. Comput Phys Commun. 2010;181:1477–1489. [Google Scholar]
- 40.Jensen F. Unifying General and Segmented Contracted Basis Sets. Segmented Polarization Consistent Basis Sets. J Chem Theory Comput. 2014;10:1074–1085. doi: 10.1021/ct401026a. [DOI] [PubMed] [Google Scholar]
- 41.Jacobson LD, Herbert JM. Polarization-Bound Quasi-Continuum States Are Responsible for the “Blue Tail” in the Optical Absorption Spectrum of the Aqueous Electron. J Am Chem Soc. 2010;132:10000. doi: 10.1021/ja1042484. [DOI] [PubMed] [Google Scholar]
- 42.Coe JV, Lee GH, Eaton JG, Arnold ST, Sarkas HW, Bowen KH, Ludewigt C, Haberland H, Worsnop DR. Photoelectron Spectroscopy of Hydrated Electron Cluster Anions, (H2O)-n=2-69. J Chem Phys. 1990;92:3980–3982. [Google Scholar]
- 43.Siefermann KR, Liu Y, Lugovoy E, Link O, Faubel M, Buck U, Winter B, Abel B. Binding Energies, Lifetimes and Implications of Bulk and Interface Solvated Electrons in Water. Nature Chemistry. 2010;2:274–279. doi: 10.1038/nchem.580. [DOI] [PubMed] [Google Scholar]
- 44.Siefermann KR, Abel B. The Hydrated Electron: A Seemingly Familiar Chemical and Biological Transient. Angew Chem Int Ed. 2011;50:5264–5272. doi: 10.1002/anie.201006521. [DOI] [PubMed] [Google Scholar]
- 45.Shreve AT, Yen TA, Neumark DM. Photoelectron Spectroscopy of Hydrated Electrons. Chem Phys Lett. 2010;493:216–219. [Google Scholar]
- 46.Tang Y, Shen H, Sekiguchi K, Kurahashi N, Mizuno T, Suzuki YI, Suzuki T. Direct Measurement of Vertical Binding Energy of a Hydrated Electron. Phys Chem Chem Phys. 2010;12:3653–3655. doi: 10.1039/b925741a. [DOI] [PubMed] [Google Scholar]
- 47.Elkins MH, Williams HL, Shreve AT, Neumark DM. Relaxation Mechanism of the Hydrated Electron. Science. 2013;342:1496–1499. doi: 10.1126/science.1246291. [DOI] [PubMed] [Google Scholar]
- 48.Horio T, Shen H, Adachi S, Suzuki T. Photoelectron Spectra of Solvated Electrons in Bulk Water, Methanol, and Ethanol. Chem Phys Lett. 2012;535:12–16. [Google Scholar]
- 49.Shkrob IA, Glover WJ, Larsen RE, Schwartz BJ. The Structure of the Hydrated Electron. Part 2. A Mixed Quantum/Classical Molecular Dynamics Embedded Cluster Density Functional Theory: Single-Excitation Configuration Interaction Study. J Phys Chem A. 2007;111:5232–5243. doi: 10.1021/jp0682816. [DOI] [PubMed] [Google Scholar]
- 50.Fessenden W, Verma NC. Time Resolved Electron Spin Resonance Spectroscopy. III. Electron Spin Resonance Emission from the Hydrated Electron. Possible Evidence for Reaction to the Triplet State. J Am Chem Soc. 1976;98:243. [Google Scholar]
- 51.Shiraishi H, Ishigure K, Morokuma K. An ESR Sudy on Solvated Electrons in Water and Alcohols: Difference in the g Factor and Related Analysis of the Electronic State by MO calculation. J Chem Phys. 1988;88:4637. [Google Scholar]
- 52.Nuzhdin K, Bartels DM. to be published [Google Scholar]
- 53.Kawabata K. Electron Traps in Irradiated Crystalline Ice. J Chem Phys. 1976;65:2235. [Google Scholar]
- 54.Weil JA, Bolton JR, Wertz JE. Electron Paramagnetic Resonance Elementary Theory and Practical Applications. John Wiley & Sons; New York: 1994. [Google Scholar]
- 55.Astashkin AV, Dikanov SA, Tsvetkov YuD. Hyperfine Interactions of Deuterium Nuclei in the Nearest Surroundings of Trapped Electrons in Alkaline Glass. Chem Phys Lett. 1988;144:258. [Google Scholar]
- 56.Dikanov SA, Tsvetkov YuD. Electron Spin Echo Envelope Modulation (ESEEM) Spectroscopy. Chapter 133. CRC Press; Boca Raton: 1992. pp. 244–251. [Google Scholar]
- 57.Schwarz HA. Reaction of the Hydrated Electron with Water. J Phys Chem. 1992;96:8937–8941. [Google Scholar]
- 58.Schwarz HA. Enthalpy and Entropy of Formation of the Hydrated Electron. J Phys Chem. 1991;95:6697–6701. [Google Scholar]
- 59.Shiraishi H, Sunaryo GR, Ishigure K. Temperature-Dependence of Equilibrium and Rate Constants of Reactions Inducing Conversion Between Hydrated Electron and Atomic-Hydrogen. J Phys Chem. 1994;98:5164–5173. [Google Scholar]
- 60.Ben-Naim A. Solvation Thermodynamics. Plenum Press; New York: 1987. [Google Scholar]
- 61.Curtiss LA, Redfern PC, Raghavachari K. Gaussian-4 Theory. J Chem Phys. 2007;126:084108. doi: 10.1063/1.2436888. [DOI] [PubMed] [Google Scholar]
- 62.Liu K, Brown MG, Carter C, Saykally RJ, Gregory JK, Clary DC. Characterization of a Cage Form of the Water Hexamer. Nature. 1996;381:501–503. [Google Scholar]
- 63.Bartmess JE. Thermodynamics of the Electron and the Proton. J Phys Chem. 1994;98:6420–6424. [Google Scholar]
- 64.Tissandier MD, Cowen KA, Feng WY, Gundlach E, Cohen MH, Earhart AD, Coe JV, Tuttle TR. The Proton's Absolute Aqueous Enthalpy and Gibbs Free Energy of Solvation from Cluster-ion Solvation Data. J Phys Chem A. 1998;102:7787. [Google Scholar]
- 65.Cramer CJ, Truhlar DG. Implicit Solvation Models: Equilibria, Structure, Spectra, and Dynamics. Chem Rev. 1999;99:2161. doi: 10.1021/cr960149m. [DOI] [PubMed] [Google Scholar]
- 66.Ben-Amotz D, Underwood R. Unraveling Water's Entropic Mysteries: A Unified View of Nonpolar, Polar, and Ionic Hydration. Acc Chem Res. 2008;41:957–967. doi: 10.1021/ar7001478. [DOI] [PubMed] [Google Scholar]
- 67.Han P, Bartels DM. On the Hydrated Electron as a Structure-Breaking Ion. J Phys Chem. 1991;95:5367. [Google Scholar]
- 68.Hickel B, Sehested K. Activation Energy for the Reaction H + OH- → eaq-. Kinetic Determination of the Enthalpy and Entropy of Solvation of the Hydrated Electron. J Phys Chem. 1985;89:5271–5274. [Google Scholar]
- 69.Han P, Bartels DM. Reevaluation of Arrhenius Parameters for H• + OH- à(e)aq + H2O and the Enthalpy and Entropy of Hydrated Electrons. J Phys Chem. 1990;91:7294–7299. [Google Scholar]
- 70.Zhan CG, Dixon DA. The Nature and Absolute Hydration Free Energy of the Solvated Electron in Water. J Phys Chem B. 2003;107:4403–4417. [Google Scholar]
- 71.Tuttle TR, Golden S. Solvated Electrons - What Is Solvated? J Phys Chem. 1991;95:5725–5736. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.