The role of pathogen shedding in linking within- and between-host pathogen dynamics

Abstract

A model linking within- and between-host pathogen dynamics via pathogen shedding (emission of pathogens throughout the course of infection) is developed, and several aspects of host availability and co-infection are considered. In this model, the rate of pathogen shedding affects both the pathogen population size within a host (also affecting host mortality) and the rate of infection of new hosts. Our goal is to ascertain how the rate of shedding is likely to evolve, and what factors permit coexistence of alternative shedding rates in a pathogen population. For a constant host population size (where an increase in infected hosts necessarily decreases susceptible hosts), important differences arise depending on whether pathogens compete only for susceptible (uninfected) hosts, or whether co-infection allows for competition for infected hosts. With no co-infection, the pathogen type that can persist with the lowest number of susceptible hosts will outcompete any other, which under the assumptions of the model is the pathogen with the highest basic reproduction number. This is often a pathogen with a relatively high shedding rate (s). If within-host competition is allowed, a trade-off develops due to the conflicting effects of shedding on within- and between-host pathogen dynamics, with within-host competition favoring clones with low shedding rates while between-host competition benefits clones with higher shedding rates. With within-host competition for the same host cells, low shedding rate clones should eliminate high-s clones in a co-infected host, if equilibrium is reached. With co-infection, but no within-host competition, pathogen clones still interact by affecting the mortality of co-infected hosts; here, coexistence is more likely. With co-infection, two clones can coexist if one is the superior competitor for uninfected hosts and the other for co-infected hosts.

Graphical abstract

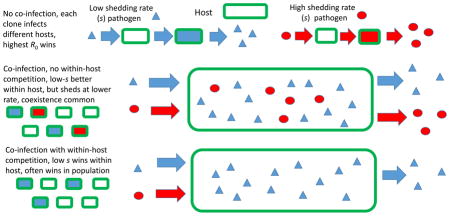
1. Introduction

Our understanding of the ecology of infectious disease can be greatly enhanced by recognition of the similarities between models that link within- and between-host pathogen dynamics and models from classical spatial ecology. From the perspective of a pathogen, susceptible hosts are akin to patches of habitat that can be colonized [1–3]. After colonization, population sizes of microparasites such as bacteria, viruses, fungi, and protozoa can show dynamics within individual hosts, rising from an initial aliquot (of maybe just a very few infective propagules, see [4] and references therein) to very large, even astronomical, levels (for instance, titers of hepatitis B in the blood of human hosts can exceed 10⁹ viruses per ml; [5]). Clearance of a pathogen by a host amounts to extinction within that habitat “patch.” Death of a host is similar in a way to destruction of a patch in a dynamic metacommunity, and of course when the infected host dies the local pathogen population harbored by that individual host eventually goes extinct as well (although some pathogens may survive and multiply for some time after host death, and transmission during this period can be significant).

A rapidly developing arena of inquiry in infectious disease ecology and evolution focuses on linking within- and between-host levels of disease dynamics to arrive at more complex and realistic models of pathogen ecology and evolution [6–12]. The focus in our paper is to explore a potential analogue in infectious disease systems of a classic problem in population ecology, which is to understand how coupling between habitats by flows of individuals influences the population size in each, and the total population size over the entire landscape [13].

A population within a defined habitat patch can change in abundance in only four ways – birth, death, immigration, and emigration. If a patch is initially empty, for it to become occupied, there must be immigration from some occupied source patch – which implies the latter is experiencing emigration. Often (though not always, if populations have stage-structure dynamics or unstable population dynamics; see [14]), an increase in emigration will lead to a decline in local population growth rate (e.g., for an exponentially growing population) or in local population size (if the population settles to an equilibrium). If emigration is sufficiently great, a local population can even be vulnerable to extinction. In phytoplankton ecology, this phenomenon was the focus of the classic KISS model [15]. If individuals occupied a one-dimensional patch of suitable habitat surrounded by a hostile environment and passively diffused, this model predicts that population persistence required a minimum patch size, larger with a higher diffusion rate or smaller patch growth rate. This basic qualitative result from the KISS model is robust to many alternative assumptions [16].

Since emigration is required for immigration, colonization into empty patches may come only at a demographic cost to already occupied source patches. In this paper, we will explore a comparable trade-off that can conceivably arise in infectious disease systems. The basic idea is simply stated. If there is to be transmission to healthy hosts, this requires the emission of infective propagules from infected hosts, which can be viewed as a form of emigration. The greater this emigration (and hence transmission to other hosts), all else being equal, the greater the penalty one should observe, in terms of growth rates and population sizes of pathogens within infected hosts. This can be viewed in a way as a necessary expression of conservation of mass: any material put into infective propagules that exit an infected host is necessarily not available to contribute to further population growth, within that host. It can also be viewed as an allocation trade-off. For a genetically identical clone of pathogens occupying a focal host individual, as that clone grows in population size within that host, it can allocate a fraction of its production for export (needed to infect other hosts), retaining the remaining fraction for continued growth within the focal host.

We will call this a “shedding” model for infection; shedding will be quantified by a per capita shedding rate s, the fraction of pathogens leaving the host per unit time. Individual multicellular hosts can of course have highly complex internal spatial structures, and within a host, different tissues can in effect represent different habitats [4,17–19]. The same type of model developed below can also be applied to the dynamics within a multi-cellular host individual. In this case, the “host” in the models is then reinterpreted as an individual cell that is either uninfected or infected by an intra-cellular parasite, for example, a virus. In this paper, however, we will not deal with this issue of internal host heterogeneity (while recognizing its importance).

In the long run, given that hosts are not immortal, for a pathogen to persist in the host population, some pathogen individuals must leave infected hosts and infect new hosts. Increased loss of the pathogen from infected hosts can have several intertwined effects. The instantaneous rate of transmission from a given infected host should be larger when a greater number of pathogen individuals are shed and so have the opportunity to seek new hosts. However, if such shedding reduces future population sizes of the pathogens, this could depress transmission in the future. The models we present will couple increased transmission to new hosts to reduced growth rates for the pathogens within infected hosts, which can ultimately reduce net transmission to susceptible hosts from infected hosts due to fewer pathogens in those hosts. Our models also allow the death rate of a host to be affected by the load of pathogens it carries. Alternative scenarios one could imagine would be to have the death rate of the host depend instead on the rate of increase of the pathogen or on its rate of exit (since the precise methods a pathogen uses to increase its emigration rate can be harmful to the host). We will not consider these alternative influences of pathogens on host mortality here, but recognize their potential importance.

The particular content of our paper builds upon our previous work [20], where we linked within-host dynamics to the dynamics of the pathogen in the entire host population via shedding or bursting models of pathogen transmission (in a bursting model, pathogens are not released until host death). Holt and Barfield [20] assumed that the number of susceptible hosts was fixed (which may be approximately true in the early phases of an epidemic, for instance). Here, we relax this assumption by assuming the kind of density dependence usually assumed in classical epidemiology, e.g. [21–23], in which the total host population size remains constant (by an unspecified mechanism), while the relative numbers of infected and uninfected (susceptible) hosts are dynamic. We also for simplicity assume that hosts, once infected, do not develop acquired immunity if they recover; therefore, an individual who loses the infection re-enters the susceptible class (i.e., an SI model). Also, again for simplicity, we ignore demographic structure (e.g., age-dependent infection or mortality) in the host. Our model formulation does permit host mortality to depend upon the within-host abundance of pathogen, which can vary with time since infection, and can also implicitly incorporate the impacts of host immune responses on pathogen loads.

Pathogens are assumed to be emitted from an infected host at a constant per pathogen rate throughout the course of infection (shedding), rather than in a “burst” at the time of host death. We start by sketching the basic model for a single pathogen clone infecting the host population (summarizing the main pertinent results of [20]). We then examine competition between clones differing in their shedding rates, which is a necessary ingredient for understanding pathogen evolutionary dynamics. This is first examined under the assumption that no individual host can be infected by more than one pathogen clone, so that pathogens only indirectly compete for susceptible hosts. For this scenario, we show that the clone with the highest basic reproduction number R₀ can eliminate all others. Assumptions about within-host dynamics influence the shedding rate that maximizes R₀ and thus the ultimate outcome of competitive evolution among pathogen strains, as well as the effect of such evolution on virulence experienced by the host.

Next, we consider the case in which two pathogen clones can infect the same host, and within the host the clones use the same resource (e.g., they infect the same cell types). In this case, there is also direct competition within co-infected hosts. Finally, we consider the case in which two clones can attack a single host, but within the host they use different resources (e.g., the pathogen strains might occupy different tissue types). There is in this case no direct within-host competition, but within a co-infected host the two clones can affect each other by affecting the host’s mortality rate. In this last case, there may be differences between clones, other than just their shedding rates. We examine these last two scenarios first under the assumption that the pathogen numbers quickly reach their positive equilibrium values within individual infected hosts and are fixed there until the point of host death. Then, we use simulations to determine the result of clonal competition with more realistic within-host population dynamics, using a differential equation model commonly used for viral infection within hosts (from [24], based on models in [25] and references therein) coupled with an individual-based model of hosts including stochastic between-host transmission and host death (within-host dynamics were deterministic, however).

In all cases, we examine competition of clones differing only in shedding rate (even when co-infecting clones are assumed to attack different cell types, the parameters used are the same, so that the two clones compete for different, but equivalent, sets of cells). Within the discussion, we provide ideas for future extensions of this work to encompass a richer array of life history effects.

2. Models and Results with Equilibrium Within-Host Pathogen Numbers

2.1. Shedding model with a limited population of hosts – no co-infection

In [20], we considered the effect of within-host dynamics on the spread of a pathogen within a population of hosts, including the effect of the loss of pathogen individuals as they exit the infected host on the within-host dynamics. We assumed that a host infected with a pathogen had a mortality rate m(V) that was possibly a function of the number of pathogen individuals V in the host, which in general could change with time since infection. The probability that an individual host survived from the time of initial infection at time 0 to time t was given by

$$P_s(t)=exp\{-{\int }_0^{t}m[V(\tau )]d\tau \}.$$

A fraction s of the pathogens were assumed to exit the host per unit time (the shedding rate), so the average rate at which pathogens were shed at time t from hosts infected at time 0 (per host) was sV(t)P_s(t), where V(t) is the number of pathogens at time t for a host infected at time 0 (sV is multiplied by P_s because only surviving hosts were assumed to shed pathogens). A fraction c of the shed pathogens were assumed to each immediately infect a new host (otherwise they died). Therefore, the average number of secondary infections for a host infected at time 0 (which applies to any infected host, and is therefore the pathogen’s basic reproduction number R₀) was found by integrating the shedding rate multiplied by the fraction of pathogens infecting a new host, which is

$$R_0={\int }_0^{\infty }\mathit{csV}(t)exp\{-{\int }_0^{t}m[V(\tau )]d\tau \}dt.$$ (1)

The infection parameter c was assumed to be constant, which corresponds to assuming that the number of susceptible hosts is constant (e.g., because the initial infection is rare, relative to host population size). To relax this assumption, we replace c by the product of a per capita infectivity parameter θ and the susceptible population abundance. If N is the total host population, and N_i is the number of hosts infected (below, the subscript will be a number indicating the infecting clone), then the susceptible population abundance is N − N_i, assuming that infected hosts are not susceptible to further infection (with more than one clone and superinfection, this may not be true). We assume throughout the paper that the total host population is constant, but the number of infected hosts is not, so the average number of secondary infections for a host infected at time T is

$$R(T)={\int }_T^{\infty }\theta [N-N_i(t)]sV(t-T)exp\{-{\int }_T^{t}m[V(\tau -T)]d\tau \}dt.$$ (2)

We use R here since R₀ generally is used to denote the average number of secondary infections when infection is rare, so that R₀ is R with N_i(t) = 0 [which is the same as (1) with c = θN]. Assuming R₀ is greater than 1, the number of infected individuals should grow deterministically when an infection is rare. An increase in infected individuals causes a decrease in R, and the infected population should reach equilibrium at a value of N_i (which we denote by Ñ_i) for which R = 1. (Below, we sometimes assume that pathogens reach equilibrium within hosts. We use the symbol overscript ∧ to indicate a within-host equilibrium, while using an overscript ~ to indicate a population-level equilibrium. Equilibrium at one level does not imply equilibrium at the other.) To find the equilibrium infected population size, we set R = 1 in (2) and substitute Ñ_i for N_i(t). Since N − Ñ_i is not a function of time, we can pull it out of the integral and solve (using a change of variables to eliminate T), giving

$${\stackrel{\sim }{N}}_i=N-{\left[{\int }_0^{\infty }\theta sV(t)exp\{-{\int }_0^{t}m[V(\tau )]d\tau \}dt\right]}^{-1}=N(1-1/R_0).$$ (3)

Given the time course of the infection in an infected host [V(t), which in general depends on s], we can solve for the equilibrium population size of infected hosts using this equation. The number of susceptible individuals is N − Ñ_i, so a higher infected population size necessarily implies a smaller number of susceptible hosts. It can also be shown that the distribution of infection age (the length of time an infected host has been infected) is of the same shape as the probability of survival function $exp\{-{\int }_0^{t}m[V(\tau )]d\tau \}$ at equilibrium.

2.2. Explicit model of within-host pathogen dynamics

To complete the above model, we must make assumptions about the functional form of V(t). The within-host pathogen load at a given time post-infection can be determined by an explicit model of within-host pathogen dynamics, forming the link uniting between- and within-host dynamics. One such model that can be used to illustrate the effects of shedding is the virus model of [24], which tracks uninfected cells, infected cells and free virions within an individual host. The model (modified to include loss of virions through shedding) is

$$\begin{array}{l}\frac{dn}{dt}=\lambda -\mu n-\beta Vn\\ \frac{{dn}^{\ast }}{dt}=\beta Vn-{\mu }^{\ast }{n}^{\ast }\\ \frac{dV}{dt}=\nu {\mu }^{\ast }{n}^{\ast }-({\mu }^{\prime }+s)V-\beta nV\end{array}$$ (4)

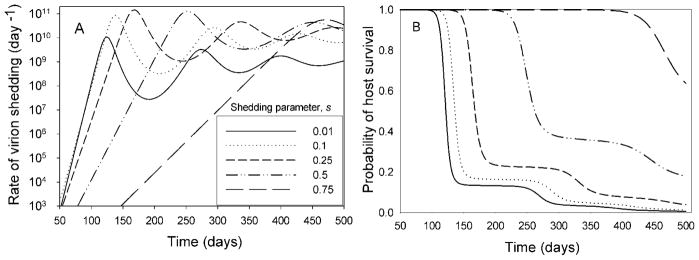
where n is the number of uninfected cells, n^* is the number of infected cells and V is the number of free virions. Uninfected cells are input at a constant rate λ, die at a per-capita rate of μ, and are infected at rate β. Infected cells die at a per-capita rate of μ^*, and each releases v virions at death. Virions are cleared at a per-capita rate of μ′, and shed at a per-capita rate of s (the latter term does not appear in [24], since they assume no shedding). A simplified system of equations, under the assumption that virion dynamics are much faster than the dynamics of host cells, is given in Appendix A. Examples of the virion dynamics produced by the model described in Eqs. (4) are shown in Fig. 1A.

Fig. 1.

A. Virion dynamics for different values of s for the model of Eqs. (4). Parameters are β = 5 × 10⁻¹⁴ day⁻¹, μ′ = 2 day⁻¹, v = 250, μ^* = 0.7 day⁻¹, λ = 2.45 × 10⁹ cells/day, μ = 0.01 day⁻¹. Initial infection is with 1 virion at t = 0 (and no infected cells, with uninfected cells at their no-infection equilibrium). The early part of the response is not shown since virus is at a very low level. B. Probability of host survival with m(V) = 10⁻¹³V.

2.3. Competition between clones with no co-infection of hosts

We now assume that there is genetic variation in shedding rate within the pathogen species. To start with, and to clarify one factor driving evolution in pathogen shedding rates, we will assume that a given host individual can only be infected by a single pathogen clone during that host’s lifetime (below we relax this assumption). Biologically, this assumption of within-host dominance could emerge from interference competition among pathogen strains within individual hosts, where interference is stronger between than within strains. From an ecological point of view, this assumption further entails competition for a limited resource at the level of the entire host population, namely competition among pathogen strains for the pool of available, susceptible hosts. In resource competition theory assuming exploitative competition for a single limiting resource [26], the dominant competitor is the one that can persist at the lowest level of resources. In like manner, in competition between two clones of a pathogen, with no co-infection of hosts, the clone that can persist at the lowest number of susceptible hosts should be able to outcompete the other clone. One can see this by assuming that a given pathogen clone is present and at equilibrium, and determining whether or not a rare mutant clone can successfully invade. Assume that clone 1 is present alone at its equilibrium. Then from Eq. (3), the equilibrial density of hosts infected with clone 1 is Ñ₁ = N(1 − 1/R₀₁), where R₀₁ is R₀ for clone 1, and the difference between this quantity and N defines the availability of healthy hosts for clone 2. Using Eq. (2) for clone 2 with N_i(t) set equal to Ñ₁ (which being constant can be pulled out of the integral) gives

$$R_2(T)=[N-{\stackrel{\sim }{N}}_1]{\int }_T^{\infty }\theta s_2{V}_2(t-T)exp\{-{\int }_T^t{m}_2[V_2(\tau -T)]d\tau \}dt=(N-{\stackrel{\sim }{N}}_1)R_{02}/N.$$

This is the number of secondary infections from one host infected by clone 2 when it is rare (and clone 1 is at equilibrium in the host population), and must be greater than 1 for clone 2 to increase. This requires that Ñ₁ < N(1 − 1/R₀₂) = Ñ₂. So clone 2 can increase when rare only if it has the higher equilibrial abundance when alone, which also means it has the higher R₀. Hence, the higher R₀ clone can invade the lower, but not the reverse. It is straightforward to show that if one assumes that two strains are present and at equilibrium, then the two pathogen strains must have the same basic reproduction number.

Therefore, given our assumptions about host regulation, the superior competitor is the one with the highest equilibrium population size of infected hosts and the highest R₀. It is worth noting that this rule of competitive dominance given a fixed host population size contrasts with the results assuming a constantly renewed number of susceptibles. In this case, pathogens show exponential growth or decline, and the clone with the highest population growth rate (per unit time) dominates all others, in terms of the fraction of the population infected by that clone. Holt and Barfield [20] show that the population growth rate r′ is the solution of ${\int }_0^{\infty }\mathit{csV}(t)exp\{-{\int }_0^{t}m[V(\tau )]d\tau \}exp\{-r^{\prime }t\}dt=1$ (comparable to the Lotka-Euler characteristic equation of age-structured demography [27]). This solution is r′ = csV̂ − m[V̂] = m[V̂](R₀ − 1) if V is assumed to equilibrate very rapidly at a constant V̂. Using r′ as a fitness measure in general will give different results than R₀.

To determine the result of competition between clones with different shedding rates, we are therefore interested in the equilibrium infected population size (or R₀) as a function of the shedding rate parameter s. As shown in [20], if the mortality is proportional to pathogen load with proportionality constant b, so that m(V) = bV, then R₀ = θNs/b [in terms of the parameters in Eq. (3)]. Note that this assumes that background mortality is negligible (e.g., the hosts might be long-lived). Therefore, in this case, Ñ_i = N − b/(θs), independent of the pathogen dynamics within individual hosts. Since this quantity is an increasing function of s, a higher-s clone would displace a lower-s clone. However, there is likely to be a maximum value of s consistent with pathogen persistence, which will create an upper limit on s. As s approaches this limit, V will probably approach 0, so mortality will approach 0 [because we assume that m(V) = bV]. Eventually, intrinsic host mortality can no longer be ignored, and including it will likely cause R₀ to drop as the limit on pathogen persistence is approached.

If the pathogen reaches an equilibrium abundance in the average host long before the host dies, then it may be reasonable to assume that the pathogen load in any infected host is constant at the equilibrium value V̂. (However, the transient response may have peaks much larger than the equilibrium level, so even with a long-lived host, the transient response may be significant; see Fig. 1A and [20] for examples). In this case, the inner integrand in Eq. (3) is a constant m[V̂], so that the outer integral is that of an exponential function of t. This can be integrated to give

$${\stackrel{\sim }{N}}_i=N-m[\widehat{V}]/(\theta s\widehat{V})=N(1-1/R_0),$$ (5)

where now R₀ can be written as R₀ = θsV̂N/m[V̂].

We note here that at equilibrium at the level of the entire host population, the equilibrial prevalence of the pathogen (the proportion of the host population that is infected, Ñ_i/N), is a simple function of R₀, namely (1 − 1/R₀), whether or not we make the assumption of equilibrium pathogen loads within individual hosts (Eqs. (3) and (5)). The same result was obtained starting with a differential equation model by Anderson and May [23], who noted that, at equilibrium, the fraction of susceptible hosts at equilibrium must be 1/R₀, in order for the number of secondary infections per infected host to equal 1.

The change of infected population size with s in Eq. (5) is a function of two relationships: the dependence of host mortality on pathogen load, m[V̂], and the dependence of pathogen load on s, V̂(s). The latter occurs because we have assumed that shedding has an effect on pathogen dynamics within individual hosts, representing a loss term for pathogen in the host. If s does not affect the equilibrium pathogen load, then the infected population in (5) is an increasing function of s, regardless of the mortality function (the only dependence on s would be the s in the denominator of the second term of the middle expression). A pathogen, by definition, harms its host. We thus expect mortality to be an increasing function of pathogen load, and pathogen load to be a decreasing function of s (because s represents a loss of pathogens, and so should effectively represent an increased pathogen death rate). Therefore, the numerator of the second term in the middle expression in Eq. (5) should decrease with an increase in s. The denominator could increase or decrease with s, depending on the effect of s on pathogen load.

As an example, in the model of Kelly et al. [24] (given above, Eqs. (4)), the pathogen is a virus, and the equilibrium virion number is V̂ = λ(ν − 1)/(μ′ + s) − μ/β, which decreases with increasing shedding, as expected. But the denominator of the second term in (5) initially increases with increasing s, because sV̂ = λ(ν − 1)s/(μ′ + s) − μs/β. For s ≪ μ′, this increases proportionally with increasing s. As s continues to increase, the first term of sV̂ saturates, while the second term continues to increase. Therefore, sV̂ eventually reaches a peak, above which it declines. The peak is at $s=\sqrt{\beta \lambda (\nu -1){\mu }^{\prime }/\mu }-{\mu }^{\prime }$. Since for s below this value the numerator of the second term of Eq. (5) decreases and the denominator increases with increasing s, this term decreases and the equilibrium infected population size increases with increasing s. Therefore, for s below the value that gives the peak sV̂ (and for somewhat higher values if m increases with increasing V̂), a higher-s clone is competitively superior. Eventually, however, with increasing s, V̂ usually goes to 0 (at s = βλ(ν − 1)/μ − μ′ for the model of Eqs. (4)), and so N̂_i and R₀ must decrease with increasing s for high enough s. There is therefore generally an intermediate value of s that can outcompete all others.

We now return to the more general case. The direction of the change in R₀ with changing s is the same as the direction of the change in Ñ_i. The condition for R₀ to increase with increasing s can be found be differentiating R₀ (given above following Eq. (5)) with respect to s, giving

$$\frac{{dR}_0}{ds}=\frac{m(\widehat{V}+sd\widehat{V}/ds)-s\widehat{V}(dm/d\widehat{V})(d\widehat{V}/ds)}{m^2}>0,$$

which is true if and only if the numerator is positive. This can be written as d(sV̂)/ds > (d ln m/d ln V̂)s(dV̂/ds). The quantity dV̂/ds should be negative, since pathogen load is expected to drop with increased shedding, and d ln m/d ln V̂ should be positive, since mortality should generally increase with more pathogens inside a host. Therefore, the right side is negative, so a sufficient condition for R₀ to increase with increasing s is that d(sV̂)/ds > 0. If m = bV̂, then d ln m/d ln V̂ = 1 and above condition is d(sV̂)/ds = V̂ + sdV̂/ds > sdV̂/ds, which is always true (R₀ in this case increases linearly with s). However, as noted above, as V̂ gets very low, host intrinsic mortality can no longer be ignored. If intrinsic host mortality is a and the total host mortality is m(V) = a + bV, then this result (R₀ increasing linearly with s) applies as long as a ≪ bV̂, which is likely to span a large range of s, if intrinsic mortality tends to be much lower than pathogen-induced mortality. For high enough s, however, a ≫ bV̂, so the mortality is constant and R₀ depends only on sV̂. (The latter conclusion also applies if the pathogen is a commensal, having no effect on mortality; see Discussion.) For R₀ to decrease with increasing s (for a virulent pathogen) requires that d ln m/d ln V̂ < 1, and that d(sV̂)/ds < 0, although both of these together are not sufficient. Therefore, we expect that often R₀ will increase with increasing s, the exception being where V̂ is a strongly decreasing function of s while m increases slowly with increasing V̂.

2.4. Co-infection with within-host competition

The above results all assume a priority effect in individual hosts, such that whichever pathogen strain first colonized a given host could dominate transmission from that host. A different result can be obtained if we allow co-infection of hosts. Co-infection can potentially happen in several ways.

We will first assume that in a co-infected host, the two clones infect the same type of cells (but there is no co-infection of individual cells). We will then consider what happens when clones can inhabit the same individual host, but different tissues or cell types. Such clones can still interact, because both clones affect the mortality of co-infected hosts.

Since we are interested in the effect of shedding rate on the outcome of competition between clones, it makes sense to start by assuming they are otherwise identical (other than in shedding), which biologically means that they should attack the same cells. There is then competition between pathogen strains both within individual hosts, and among hosts. For many within-host models, including the model given in Eqs. (4), extended to model two virion clones (and therefore having two infected cell equations and two virion equations), if two clones are identical except for their shedding parameters, then the clone with the lower s will eventually eliminate the one with the higher s in a co-infected individual host. This is because the higher-s clone has a higher effective pathogen clearance rate (and therefore requires more uninfected cells to be maintained). Lower s will typically imply a higher pathogen load in the host, and given our assumption about host mortality increasing with pathogen abundance, this implies higher virulence experienced by infected hosts.

Therefore, if we again assume that pathogens reach their equilibrium values more or less immediately, the clone with the lower s will displace the clone with the higher s when the former infects a host infected with the latter. The higher-s clone cannot infect a host infected with the lower-s clone. Effectively, the number of susceptible hosts for the higher-s clone is the number of uninfected hosts. For the lower-s clone, all hosts it has not itself infected are susceptible – including those that harbor the higher-s clone.

Hence, the persistence of the lower-s clone is not affected by the presence of the higher-s clone. The lower-s clone persists, and reaches an equilibrium population size given by Eq. (5), if and only if this clone has R₀ = θsV̂N/m[V̂] > 1. If the lower-s clone persists, then the higher-s clone must be able to persist on the hosts uninfected by the lower-s clone, or it will be eliminated. This is necessary but not sufficient for the higher-s clone to persist. It is not sufficient because the higher-s clone loses hosts not only through host deaths, but also through infection and replacement by the lower-s clone. Therefore, all four possibilities exist with respect to clone survival. If neither clone has R₀ > 1 (for the entire host population), then neither persists. If the lower-s clone has R₀ < 1 but the higher-s clone has R₀ > 1, then the latter only persists (if the clones are identical other than in s, then the higher-s clone often has the higher R₀, so this is quite possible). If the lower-s clone has R₀ > 1, then it persists, and may either coexist with, or eliminate, the higher-s clone.

Let N_i be the abundance of hosts infected by clone i, and assume that the lower-s clone is clone 1. Then assuming the lower-s clone can persist, its equilibrium abundance can be found by balancing the rate of death of hosts infected with clone 1 with the number of new infections by this clone:

$$m({\widehat{V}}_1)=\theta s_1{\widehat{V}}_1(N-{\stackrel{\sim }{N}}_1),$$ (6)

where both sides have been divided by N₁. This gives an expression for Ñ₁ that is essentially the same as Eq. (5): Ñ₁ = N − m(V̂₁)/(θs₁V̂₁). Given Ñ₁ from this equation, the equation for the abundance of hosts infected by the higher-s clone (Ñ₂) is

$$m({\widehat{V}}_2)+\theta s_1{\widehat{V}}_1{\stackrel{\sim }{N}}_1=\theta s_2{\widehat{V}}_2(N-{\stackrel{\sim }{N}}_1-{\stackrel{\sim }{N}}_2)$$ (7)

where both sides have been divided by N₂. On the left side of Eq. (7) there is an extra term, representing infection of hosts infected first by clone 2, and then by clone 1, which displaces clone 2. On the right side of (7), representing new infections, the susceptible hosts are only those that are not infected at all, in contrast to Eq. (6), in which all hosts not infected with clone 1 are susceptible. If Ñ₂ from (7) is less than 0, clone 2 does not persist. In either case, the equilibrium number of hosts infected by clone 1 (the solution of Eq. (6)) is not affected.

Eq. (7) can be solved for Ñ₂, which is a decreasing function of N: Ñ₂ = m(V̂₁)/(θs₁V̂₁) − [m(V̂₂) − m(V̂₁) + θs₁V̂₁N]/(θs₂V̂₂). Increasing N increases Ñ₁ by the same amount, so the right side of (7) is unchanged. The left side of (7) is increased, because with increased N, there is increased Ñ₁, and therefore an increased chance that a host infected with clone 2 will be infected by clone 1, which then eliminates clone 2 in that individual host. Therefore, increased N makes it harder for clone 2 to persist, assuming that clone 1 is present. This is also evident from the expression for Ñ₂, which decreases with increasing N.

The condition for clone 2 to persist is that Ñ₂ > 0. This condition reduces to

$$s_2{\widehat{V}}_2-m({\widehat{V}}_2)s_1{\widehat{V}}_1/m({\widehat{V}}_1)>s_1{\widehat{V}}_1[R_{01}-1].$$ (8)

Presumably, V̂₂ < V̂₁, since higher shedding normally reduces pathogen load, and if host mortality increases with pathogen load, m(V̂₂) < m(V̂₁). The expression on the right must be positive, since by assumption clone 1 can persist. For the expression on the left to be positive, clone 2 must have a higher ratio of per-host shedding rate to host mortality than clone 1, which would be the case if s_iV̂_i is an increasing function of s_i and host mortality increases with pathogen load. Under these conditions, the expression on the right increases with increasing s₂, since the first term increases and the second term decreases.

However, using the model of Eqs. (4) (and for many other models), s₂V̂₂ is unimodal with increasing s₂, so there is a maximum value the left side can reach, which can be lower than the right side. If the shedding rates are sufficiently close together, the left side is near 0 and the inequality is not satisfied. Therefore, depending on the parameters, clone 2 might not be able to persist for any s₂, or it might be able to persist for s₂ greater than a limit greater than s₁. This implies a kind of “limiting similarity” in shedding rates for co-infecting pathogens.

Eq. (8) can be written in the form m(V̂₂)/m(V̂₁)[(R₀₂/R₀₁) − 1] > [R₀₁ − 1], which can then be rearranged to give R₀₂ > R₀₁ + R₀₁(R₀₁ − 1)m(V̂₁)/m(V̂₂). This describes a non-infinitesimal difference in basic reproduction numbers required for persistence of two pathogens differing only in their within-host shedding rates.

2.5. Co-infection with no within-host competition

An alternative scenario for co-infections would be for the two clones to attack different cells or tissues in the host, thus forestalling within-host competition. In this case, hosts can be infected by either clone or by both, and there should be a much greater chance for coexistence, since each clone can now infect any host that is not infected by that clone. Each clone nonetheless can still affect the population-wide dynamics of the other, by affecting the death rate of co-infected hosts. A clone with a high s would have a lower pathogen density and would normally keep the host alive longer, but if it is then infected by a low-s clone, the latter clone increases pathogen density and can cause earlier host death. There is a similar effect of the high-s clone on the low-s clone, but this effect is lower in magnitude since the low-s clone has a higher mortality when alone, and the high-s clone adds less to it. With this change in the model (in effect relaxing competition at the local, within-host scales), coexistence is more likely.

To evaluate the joint equilibrium when both pathogen strains are present, equations comparable to (6) and (7) can be written for each type of infected host (clone 1, clone 2 and both), in which we balance the rate at which the host dies or is converted to a different host type (singly-infected to co-infected) with the rate of new infections. Unfortunately, this gives 3 nonlinear equations for the 3 variables, which can only be solved numerically. The equations are

$$\begin{array}{l}[m({\widehat{V}}_1)+\theta s_2{\widehat{V}}_2({\stackrel{\sim }{N}}_2+{\stackrel{\sim }{N}}_{12})]{\stackrel{\sim }{N}}_1=\theta s_1{\widehat{V}}_1(N-{\stackrel{\sim }{N}}_1-{\stackrel{\sim }{N}}_2-{\stackrel{\sim }{N}}_{12})({\stackrel{\sim }{N}}_1+{\stackrel{\sim }{N}}_{12})\\ [m({\widehat{V}}_2)+\theta s_1{\widehat{V}}_1({\stackrel{\sim }{N}}_1+{\stackrel{\sim }{N}}_{12})]{\stackrel{\sim }{N}}_2=\theta s_2{\widehat{V}}_2(N-{\stackrel{\sim }{N}}_1-{\stackrel{\sim }{N}}_2-{\stackrel{\sim }{N}}_{12})({\stackrel{\sim }{N}}_2+{\stackrel{\sim }{N}}_{12})\\ m({\widehat{V}}_1,{\widehat{V}}_2){\stackrel{\sim }{N}}_{12}=\theta s_1{\widehat{V}}_1({\stackrel{\sim }{N}}_1+{\stackrel{\sim }{N}}_{12}){\stackrel{\sim }{N}}_2+\theta s_2{\widehat{V}}_2({\stackrel{\sim }{N}}_2+{\stackrel{\sim }{N}}_{12}){\stackrel{\sim }{N}}_1\end{array}$$ (9)

where Ñ₁₂ is the number of co-infected hosts. These equations assume that the number of pathogens of each type in a co-infected host is the same the number of that type that would be present in a singly-infected host (these equations can easily be modified if this is not the case).

Returning to Eqs. (9), we can use the rates in these equations to write differential equations for the change in the expected number of each host type. These equations can be used to determine the conditions for one clone to increase when rare, in the presence of the other clone alone at equilibrium. If clone 1 is alone, then its equilibrium is the same as that given above [Ñ₁ = N − m(V̂₁)/(θs₁V̂₁)], which can be obtained from the first equation after setting Ñ₂ and Ñ₁₂ to 0. We then use the rates of increase and decrease of clone-2-infected and co-infected hosts given in the second and third equations to write differential equations for N₂ and N₁₂ (which are no longer assumed to be at equilibrium):

$$\begin{array}{l}\frac{{dN}_2}{dt}=\theta s_2{\widehat{V}}_2(N-{\stackrel{\sim }{N}}_1-N_2-N_{12})(N_2+N_{12})-[m({\widehat{V}}_2)+\theta s_1{\widehat{V}}_1({\stackrel{\sim }{N}}_1+N_{12})]N_2\\ \frac{{dN}_{12}}{dt}=\theta s_1{\widehat{V}}_1({\stackrel{\sim }{N}}_1+N_{12})N_2+\theta s_2{\widehat{V}}_2(N_2+N_{12}){\stackrel{\sim }{N}}_1-m({\widehat{V}}_1,{\widehat{V}}_2)N_{12}.\end{array}$$ (10)

The Jacobian of this system can be found at the clone 1 equilibrium, by taking derivatives of the right sides of these equations with respect to N₂ and N₁₂, and evaluating them at the clone 1 equilibrium, giving

$$J=\left[\begin{array}{cc}\theta s_2{\widehat{V}}_2(N-{\stackrel{\sim }{N}}_1)-[m({\widehat{V}}_2)+\theta s_1{\widehat{V}}_1{\stackrel{\sim }{N}}_1]& \theta s_2{\widehat{V}}_2(N-{\stackrel{\sim }{N}}_1)\\ \theta s_1{\widehat{V}}_1{\stackrel{\sim }{N}}_1+\theta s_2{\widehat{V}}_2{\stackrel{\sim }{N}}_1& \theta s_2{\widehat{V}}_2{\stackrel{\sim }{N}}_1-m({\widehat{V}}_1,{\widehat{V}}_2)\end{array}\right]$$ (11)

where Ñ₁ is the equilibrium value above. The off-diagonal elements are nonnegative, so the dominant eigenvalue of the matrix is real. Therefore, the condition for clone 2 to increase when rare is that the determinant of this matrix is negative. The resulting condition is messy and not easy to interpret. However, if clone 1 has the higher s, then it can be shown that a sufficient condition for clone 2 to invade is that θs₂V̂₂N > m(V̂₁,V̂₂), assuming that s_iV̂_i/m(V̂_i) is an increasing function of s_i. This condition is similar to the condition for clone 2 to be able to persist when alone [θs₂V̂₂N > m(V̂₂)], except that the mortality is not the mortality of a host infected by clone 2, but of a host that is infected by both clones. Clone 2 may be able to persist when m(V̂₂) < θs₂V̂₂N < m(V̂₁,V̂₂), but cannot persist if the left inequality is false, and will persist if the right inequality is false. In terms of the basic reproduction numbers, the condition for clone 2 to invade is

$$R_{02}>\frac{m_{12}{R}_{01}[m_1(R_{01}-1)+m_2]}{m_2\{R_{01}[m_1(R_{01}-1)+m_2]+m_{12}-m_2\}},$$ (12)

where m_i = m(V̂_i) and m₁₂ = m(V̂₁,V̂₂). This reduces to R₀₂ > m₁₂/m₂ if m₁₂ = m₂ (exactly), or if R₀₁ ≫ 1 (approximately – actually, the condition is R₀₁[m₁(R₀₁ − 1) + m₂] ≫ |m₁₂ − m₂|, which is also true for lower R₀₁ if m₁₂ ≈ m₂). This is the highest possible limit on R₀₂. In general, however, the mortality rates of co-infected hosts and hosts infected with clone 2 depend on the pathogen level (and therefore shedding rate) for clone 2, so both sides of this expression depend on this shedding rate.

3. Simulations including Within-Host Pathogen Dynamics

3.1. Pathogen dynamics

Most of the above analyses assumed a constant (equilibrium) pathogen level reached within individual infected hosts, which depended on s. This assumption could be suitable for cases in which most hosts live much longer than the time it takes for a pathogen infection to reach equilibrium (assuming that it eventually does so). However, that is not always the case, and s should not only affect the equilibrium pathogen levels within hosts, but also the dynamics of the pathogen in the host after initial infection, with lower s generally leading to a faster increase in pathogen load, a higher peak pathogen load, and, as discussed above, a higher equilibrium. However, a lower s also means reduced pathogen shedding for the same pathogen load, and again as discussed above, at equilibrium a higher s gives more shedding.

To illustrate these effects, we first use the deterministic within-host virus model adapted from [24] (Eqs. (4), above) to make some points about non-equilibrial aspects of within-host pathogen dynamics, and then present simulations that link these to the entire host population, with stochastic host mortality and infection (see Appendix B for simulation details). Fig. 1A shows the viral dynamics (shedding rate, which is the product of the virion number and s) for this model, for different values of s. At low s, the shedding rate starts low, rises rapidly, and peaks at a low value. Increasing s causes a slower rise. With s = 0, the initial rise (once virions and infected cells reach their steady-state ratio, which generally occurs quickly when both are at very low levels) is about 0.25 d⁻¹, which decreases approximately linearly to 0 at s a little more than 1. The virion clearance rate for this plot is 2 d⁻¹, so even at the higher shedding rates, most virions are lost to clearance rather than shedding. Still, the presence and magnitude of shedding obviously has a great effect on the dynamics. The parameters (other than shedding rate) are drawn from [28], which modeled HIV infection.

The peak shedding rate occurs at an intermediate s. The peak virion abundance decreases with increasing s, from more than 10¹² for s = 0 to less than 10¹¹ for s = 0.75. The peak shedding rate is the product of the peak abundance and s. At low s, the peak virion level is not affected much by s, so the peak shedding rises approximately linearly with s. Higher s values do affect the dynamics, and eventually cause the peak virion level to drop faster (proportionately) than s increases, so the product drops. Therefore, high s gives a peak viral release lower and later than intermediate values for s (and later during the bout of infection than for low s). (At equilibrium, shedding is maximum at s = 0.47.)

If the peak virion level is likely to kill a host, then the potential equilibrium is seldom reached (because the host dies first), and the within-host transient response should dominate the response of the host population to the infection. Fig. 1B shows the probability of host survival given the virion numbers corresponding to Fig. 1A and host death rate proportional to virion abundance [m(V) = 10⁻¹³V]. At low and moderate s, most hosts are killed around the time of the first peak in virion abundance. At the highest s (0.75), most hosts survive the first peak. As mentioned above, the shapes of distributions of the time-since-infection for infected hosts have the shapes of these survival functions, so the highest density of infected hosts are those that have recently become infected, but the density changes little until the first peak is approached (since there is little mortality until the virion density gets fairly large). The proportion of infected hosts near the peak can be found by finding the proportion of the area under one of the curves in Fig. 1B that is between two times bracketing the peak. This can be a small fraction of the total infected hosts, but their contribution to R (which is proportional to the integral of the product of curves from Fig. 1A and 1B) can be quite large, since this is proportion to the product of V and the survival probability. For example, the 10% of infected individuals near the first peak for a shedding rate of 0.01 (those with shedding above 10⁹) contribute 86% of new infections at equilibrium, while those with infection ages lower than this region constitute 81% of infected individuals but generate only a little over 4% of new infections.

As shown above, if host death is proportional to virion density, a higher-s clone can persist with fewer susceptibles, regardless of the virus dynamics. Therefore, a higher-s clone would win a competition with no co-infection, independent of these details of within-host dynamics. The fact that the virion level rises slowly does not matter, because the mortality is proportional to the virion level, and so the host also lives longer. The number of shed virions is higher relative to the host virion level that determines mortality, and this is what gives higher-s clones an advantage. If the lower-s clone is at equilibrium, there are still enough uninfected hosts to give R > 1 for the higher-s clone, while the reverse is not true. Therefore, the higher-s clone can invade hosts infected with the lower-s clone, but not vice versa. Of course, if infection and host death are stochastic (as in our simulations), then the initial presence of the lower-s clone increases the probability that the higher-s clone will be lost before becoming established, as it did in some simulations (some of which were started with only 5 infected individuals).

Many viral infections happen over a time span over which intrinsic host death is unlikely, so a negligible intrinsic host death rate is often reasonable (as assumed above). If the intrinsic host mortality is significant relative to the virion-induced mortality, then the higher-s clone would not always have the advantage. During the slow rise in virion numbers, the host could die from other causes, and this makes the slow rise a disadvantage.

3.2. Examples of dynamics of one clone invading and displacing another

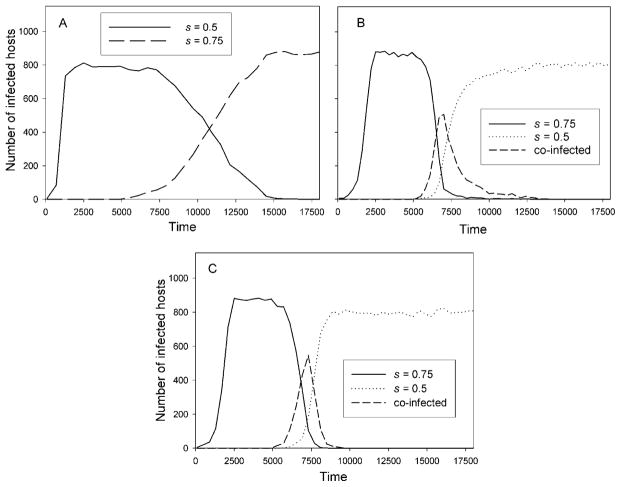
A high s is also not generally advantageous with co-infection, since a host infected with high-s clone (slow growing) that is co-infected with a lower-s clone will tend to be killed sooner because of the faster growth of the latter clone. This will counteract the high-shedding, slow-growth, long-host-life strategy of the higher-s clone. If the two clones are competing for the same cells, then the faster-growing (lower-s) clone will also tend to suppress the higher-s clone within a co-infected host, by infecting their common target cells. This can lead to coexistence or elimination of the higher-s clone in some cases (and elimination of the lower-s clone in others). Fig. 2 shows a simulation of the competition between clones with shedding rates of 0.5 and 0.75 (see Appendix B for a description of the simulations). In Fig. 2A, there is no co-infection, mortality is proportional to virion density, and the higher-s clone eliminates the lower-s clone as expected (adding an intrinsic host death rate of 0.0025, however, makes the s = 0.5 clone generally outcompete the 0.75 clone). Fig. 2B uses the same parameters, but in this case there is co-infection but no within-host competition (in all cases with co-infection, host mortality is proportional to the sum of the virion numbers of both clones, using the same mortality functions as the singly-infected hosts). Here, the lower-s clone eliminates the higher-s clone. With the parameters used, if the two clones infected a host at the same time, the lower-s clone (by itself) would have a probability of 0.5 of killing the host by a time at which the higher-s clone is shedding at a rate 5 orders of magnitude lower than the lower-s clone. Therefore, if a host is co-infected, the higher-s clone does not shed much virus unless it infects the host much earlier than the lower-s clone, so that hosts infected with the lower-s clones are essentially unavailable to the higher-s clone, while the reverse is not true. In this example, this allows the lower-s clone to eliminate the higher-s clone. In Fig. 2C, there is co-infection with competition for the same cells within the host. In this case, the lower-s clone has an additional advantage due to its faster rise, enabling it to suppress the increase in the higher-s clone if they infect near the same time. This leads to a faster elimination of the higher-s clone. The effect is modest, however, since the advantage of the lower-s clone is great even without within-host competition in this example.

Fig. 2.

Displacement of one clone by another. The virus model in Eqs. (4) is used for within-host dynamics. There are 2 clones, differing in s, with one clone introduced first. Virus model parameters are as in Fig. 1. Again, m(V) = 10⁻¹³V, with mortality in co-infected hosts determined by total virion numbers. Other parameters are θ = 10⁻¹⁵ and N = 1000, with 5 hosts each initially infected with one virion of one clone, and 5 uninfected hosts infected with the other clone at time 5000. A. There is no host co-infection and the larger s wins. B. There is co-infection (with no within-host competition), and the smaller s wins. C. Co-infection and within-host competition. The smaller s clone wins faster than in B.

By the same logic, we might expect a clone with s = 0.25 to eliminate the s = 0.5 clone. However, in this case, the two clones tend to coexist if there is no within-host competition. Although the lower-s clone still rises faster and reaches a higher peak shedding level, the differences between these clones are less than between the s = 0.5 and s = 0.75 clones. This likely prevents the lower-s clone from eliminating the higher-s clone. The lower-s clone does have a somewhat higher equilibrium number of infected hosts. If there is within-host competition, then in 10 runs the s = 0.5 clone was never able to invade a population in which the s = 0.25 clone was established, but the s = 0.25 clone was able to invade and displace the s = 0.5 clone half the time (the other half of the time, the s = 0.25 clone went extinct, possibly due to demographic stochasticity, as these simulations were started with only 5 infected hosts for each clone when it was introduced). (For the simulations, we generally used only 10 runs per parameter set, because we had to simulate the pathogen dynamics within each infected host, and often the simulations were long.) With one clone established, there are relatively few uninfected hosts, so the new clone depends on co-infection to get started. But if there is within-host competition, the new clone will have difficulty invading hosts already infected by the first clone. This will be easier for the lower-s clone, with its faster rate of increase within a host.

3.3. Competition between pairs of clones

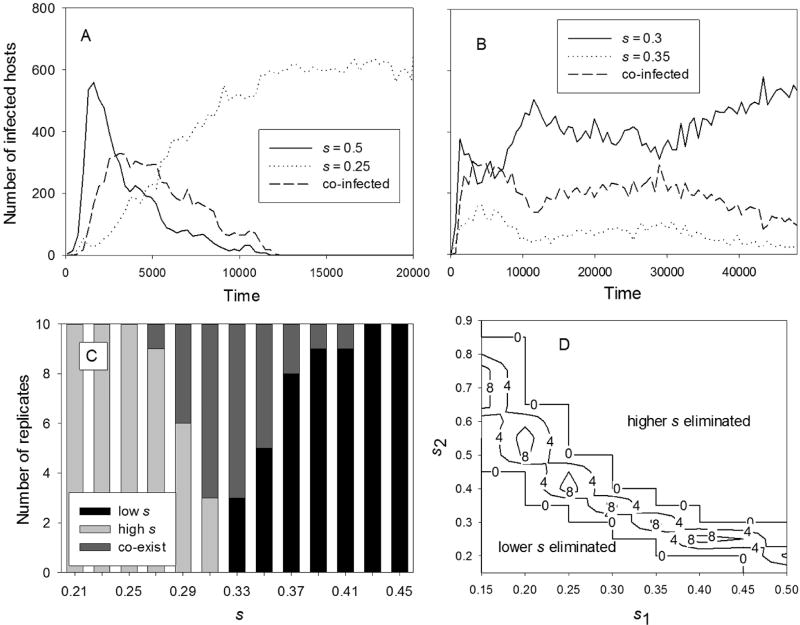
If these two clones are started at the same time in an uninfected population (with within-host competition), then the number of hosts infected with the s = 0.5 clone tends to initially rise faster, but this clone is ultimately displaced by the s = 0.25 clone (Fig. 3A). A clone with s = 0.3 tends to displace the s = 0.25 clone in the same situation. To determine the result of competition with clones differing in s, two types of simulation were done. In the first type of simulation, each clone was competed against a clone with a shedding rate 0.02 greater, with each clone infecting 100 hosts at the start (to minimize loss due to demographic stochasticity). This was repeated 10 times for each parameter set, until one clone became extinct. If both clones still persisted at 50,000 time units (for this parameter set), it was concluded that they coexisted. The higher s always eliminated the lower s for the higher s up to 0.26 (Fig. 3C). Above that, there was coexistence in some cases, until the lower s reached 0.42, after which the lower s always eliminated the higher s. The s = 0.32 clone eliminated both the adjacent clones 3 times and coexisted 7 times (and so was never eliminated), and therefore appears to be the optimum s. Below this, the higher s tended to win where there was not coexistence, while the opposite was true above this.

Fig. 3.

Competition and coexistence between clones competing within hosts. Within-host dynamics follow Eqs. (4). There are 2 clones, differing in s, introduced at the same time. Virus model parameters and mortality function are as in Fig. 1. Other parameters are θ = 10⁻¹⁵, and N = 1000, with 5 hosts each initially infected with one virion of each clone for (A) and (B), and 100 hosts for (C) and (D). There is co-infection and within-host competition. A. The s = 0.5 day⁻¹ clone initially infects more hosts, but is eventually displaced by the s = 0.25 day⁻¹ clone. B. With s = 0.3 day⁻¹ and s = 0.35 day⁻¹ clones, sometimes there is coexistence for a long time. C. Number of replicates (out of 10) for which the higher-s clone eliminated the lower-s clone (high s), the reverse (low s) and the two clones coexisted (coexist) at 50,000 time units. The abscissa is labeled with the average s of the two competing clones, which were separated by 0.02 units. D. Number of runs with coexistence (out of 10), for clones with s being a multiple of 0.05.

In the second type of simulation, s was varied in increments of 0.05 from 0.05 to 1, and each value was competed with every other value, under the same conditions as before (Fig. 3D shows the combinations with coexistence, which generally consists of widely differing s values). With s = 0.3 and s = 0.35 clones started together, in 10 simulations, the s = 0.3 clone was eliminated once and there was coexistence (to 50,000 time units) nine times (illustrated in Fig. 3B, which starts with only 5 infected individuals of each clone instead of 100). This was the only case for which adjacent-s clones gave coexistence, and agrees with the s = 0.32 optimum above. When both clones persist, the distribution of the three classes of infecteds changes very significantly with time (as shown in Fig. 3B, and even more when comparing independent runs), although the sum of all infecteds is much less variable. This may be because the dynamics of the two clones alone and with co-infection are not that different. It is interesting that the optimum s of 0.32 is very close to the clone with the maximum peak shedding rate. However, it cannot be true in general that the clone with highest peak shedding is the optimum s, since changing b (the proportionality constant relating virion numbers to host death rate) changed the optimum s (see below), but has no effect on peak shedding.

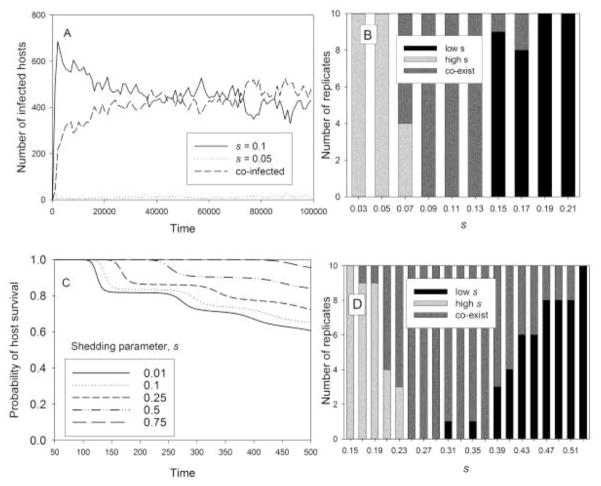
Even though a lower-s clone tends to outcompete a higher-s clone within a host, a clone with a sufficiently low s has difficulty persisting within the population even in the absence of competition by another clone. At s = 0.1, with the parameters used above, the virus would have a population growth rate of 0 even with all hosts uninfected (R₀ = θNs/b = 1). Therefore, this clone could not persist in the presence of any other clone (with higher s), and thus there is clearly a lower limit on s (= b/θN). If we decrease b to 10⁻¹⁴ and leave the other parameters as before, the lower limit on s would be 0.01. For these parameters, a clone with s = 0.1 eliminates a clone with s = 0.15, and with s = 0.05 and s = 0.1 clones started together, an equilibrium is reached at which about half the infected hosts are infected with the s = 0.1 clone and about half are co-infected, with few hosts infected with the s = 0.05 clone alone (Fig. 4A shows an example). The s = 0.05 clone also tends to coexist with other higher-s clones, up to s = 0.5, above which the higher-s clone tends to be eliminated. However, for s greater than or equal to 0.1, the lower-s clone tends to outcompete a higher-s clone, for s up to 1 in multiples of 0.05 (the only exceptions were some cases of coexistence between 0.1 and 0.15 clones, and between adjacent s values above 0.8, which would likely have led to the elimination of the higher-s clone with longer runs). The result of 10 runs of two clones separated by 0.02 units in s is shown in Fig. 4B. The optimum s appears to be about 0.12. Therefore, lowering b (host mortality for a given pathogen load) led to a reduction in the best s. With this value of b, there is a good chance that a host will survive the initial transient peaks and at least approach the equilibrium (Fig. 4C). Without co-infection, this would favor higher s (of course, with mortality proportional to V, higher s is favored even if equilibrium is not approached). But with co-infection (and within-host competition), the lower b favors a lower s than the higher b that led most hosts to die during the transient phase. The longer host life gives the lower-s clone more time to outcompete the higher-s clone within a co-infected host. But at these low values of s, there is not that much difference between clones in the dynamics of virion numbers, and higher s gives a higher peak shedding rate. Therefore, the ability to outcompete the higher-s clone, within a host, is the major advantage of lower s. At some value of s, this may not make up for the disadvantage of lower shedding. Therefore, the optimum s is not the lowest value of s that a clone can have and persist alone.

Fig. 4.

Competition and coexistence for a low-mortality pathogen. Within-host dynamics follow the virus model of Eqs. (4). Simulations as in Fig. 3 except that here m(V) = 10⁻¹⁴V, allowing hosts to survive longer. A. Clones with s = 0.05 day⁻¹ and s = 0.1 day⁻¹ coexist, with the former at low density while the latter clone and co-infected hosts are at higher densities. B. Number of replicates (out of 10) for which the higher-s clone eliminated the lower-s clone (high s), the reverse (low s) and the two clones coexisted (coexist) at 50,000 days. The abscissa is labeled with the average s of the two competing clones, which were separated by 0.02 units. C. Probability of host survival with m(V) = 10⁻¹⁴V, with virus model and other parameters as in Fig. 1B. D. Same as B, except θ = 10⁻¹⁶ and simulations were run for 100,000 time units.

3.4. Competition with lower pathogen infectivity

If we reduce the per capita infection rate θ (which controls transmission) by an order of magnitude [keeping a low host mortality (b), as in the last paragraph], then the minimum s is again 0.1, and the optimum s is similar to that with b and θ an order of magnitude higher. However, in this case, there is a broader range of coexistence. Simulations in this case were run to 100,000 time units, because of the slower infection dynamics. For some s values, this may not have been long enough, so some of the coexistence in Fig. 4D would be eliminated by longer runs. One disadvantage to simply increasing the length of a run is that it increases the probability of a loss of a clone by demographic stochasticity (which might be significant if a clone is present at low levels).

Therefore, without co-infection, higher s is favored, but with co-infection, and with parameters such that hosts tend to die in the transient period of viral growth, lower s can be favored because of higher initial growth rates and sometimes higher peak shedding. If there is within-host competition, lower s is also favored because it makes the clone a better competitor within a host. However, at sufficiently low s, the virus cannot even persist in isolation (also, at low s, the peak shedding rate decreases with decreasing s). Therefore, an intermediate s tends to be favored in this situation. In [20], we found that with a constant number of susceptible hosts (and no co-infection), an intermediate s value tended to give the highest growth rate of total virion numbers in the population (except for the extreme case for which each shed virion immediately infects a new host). Low shedding led to faster virion increase within a host (as in Fig. 1). This might lead ultimately to a higher rate of virion shedding, but the host might tend to die before this point is reached. High shedding leads to slower within-host growth, but generally more secondary infections. However, these secondary infections on average tend to occur later than those with lower s, since slowing the rate of viral growth keeps the host alive longer. These factors lead to the highest virus population growth rate at intermediate s.

4. Discussion

In this paper, we have linked details of the within-host pathogen population, such as the growth rate of pathogens within the host, to between-host dynamics via a shedding model (in which the fraction of pathogens leaving the host per unit time affects both within-host population size and transmission to new hosts). We see that the details of within-host pathogen dynamics affect the outcome of competition between pathogen strains differing in shedding rate (s). The work presented here complements previous theoretical studies linking within- and between-host pathogen dynamics. These studies considered how these two selective levels depend on the shape of the host immune response as a function of the within-host pathogen replication rate [6], when conflicts between these levels lead to differing optimum pathogen production rates [7], how within- and between-host pathogen dynamics affect the evolution of a trait expressed in infected individuals [10], and other aspects of both pathogen and host life histories [29,30,12]. The key features of the theoretical approach taken here are that the shedding process has effects on both levels, increasing between-host transmission while decreasing within-host population sizes. We also (as in classical epidemiology) have assumed that the host population size is constant, so an increase in abundance of infected hosts necessarily decreases the number of susceptible hosts. Allowing host numbers to be regulated in part by parasitism would add another interesting level of dynamical complexity.

Constraining the host population available for pathogen infection, in conjunction with our assumptions about how shedding couples within- and between-host infection processes, has complex effects on infection probability, the rate of new infections, and on the results of competition between different pathogen clones (see Table 1). With no co-infection, there is generally an increase in the rate of new infection (R₀) with increased shedding rate, at least for shedding rates that are not too high; increased shedding leads to lower pathogen load and lower host mortality (unless the pathogen load drops rapidly with increased shedding and host mortality drops slowly with increased pathogen load). Here we see pathogens evolving towards less virulence (where we are defining virulence here as the death rate of infected hosts; see [31]), but for a reason arising purely via competition between pathogens for uninfected hosts. If only one pathogen strain can occupy an infected host (a priority effect at the level of the individual host “patch”), the winner among competing pathogen strains will be the one that can push the availability of susceptible hosts to the lowest level, and still persist. It should be noted that this criterion for evolutionary dominance (in effect, maximization of the basic reproduction number) will typically lead to different expectations than maximization of the intrinsic growth rate r′ of the pathogen (see also [20]).

Table 1.

Summary of results

Model	Infection probability	Total rate of new infections	Competitive outcomes
Constant susceptible host population (Holt & Barfield 2006)
clone i	c = constant	csV̂Ni(t)	Clone with highest r′ (population pathogen growth rate, which is csV̂ − m[V̂] for V = V̂) dominates, often occurs at intermediate s. R0 = csV̂/m[V̂] for V = V̂.
Limited host population with no co-infection
clone i	c = θ[N − ΣjNj(t)]	θsV̂[N − ΣjNj]Ni	$R_0={\int }_0^{\infty }\theta \mathit{NsV}(t)exp\{-{\int }_0^{t}m[V(\tau )]d\tau \}dt=\theta Ns\widehat{V}/m[\widehat{V}]$ for V = V̂. Clone with highest R0 outcompetes others, often clone with a high s (unless V drops rapidly with increasing s and m drops slowly with increasing V).
Limited host population with co-infection and within-host competition
clone 1 (lower s)	c = θ[N − N1]	θs1V̂1[N − N1]N1	Within-host competition benefits low-s clone, which should eliminate high-s clone in co-infected host if equilibrium reached. If V = V̂ and both clones have R0 > 1, get low-s clone only or coexistence. With transient dynamics, low-s has additional advantage because it grows faster in the host. However, high-s clone still has advantage in singly-infected hosts.
clone 2 (higher s)	c = θ[N − N1 − N2]	θs2V̂2[N − N1 − N2]N2
Limited host population with co-infection and no within-host competition
singly infected - clone 1	c = θ[N − N1 − N2 − N12]	θs1V̂1[N − N1 − N2 − N12](N1 + N12)	Coexistence is common in this scenario. Clones interact by affecting mortality of co-infected hosts. The high-s clone tends to have an advantage in singly-infected hosts. Both clones persist in co-infected hosts. With transient dynamics, low-s clone has an advantage due to faster increase in co-infected hosts, sometimes killing the host before high-s clone can reach significant levels.
singly infected - clone 2	c = θ[N − N1 − N2 − N12]	θs2V̂2[N − N1 − N2 − N12](N2 + N12)
co-infected	c1 = θN2 for clone 1 c2 = θN1 for clone 2	θs1V̂1(N1 + N12)N2 + θs2V̂2(N2 + N12)N1

Considering both within- and between-host pathogen dynamics in the context of a limited host population highlights the potential importance of the interplay between these two population levels in governing the outcome of competition between different strains or clones of a pathogen. In the absence of co-infection, as discussed above, increased shedding is often favored. The situation is more complex when co-infection is permitted in the system. If within-host competition is included, a trade-off develops due to the conflicting effects of shedding on within- and between-host dynamics, with within-host competition benefitting clones with low shedding rates (since such pathogens maintain higher within-host populations) while between-host competition benefits clones with higher shedding rates (since this facilitates finding new hosts).

There is no coexistence of clones without co-infection of hosts, because the clone that requires the fewest uninfected hosts will eliminate all others, a common result of competition for a single resource. With co-infection, coexistence sometimes results because one clone (often the one with higher shedding rate) is better at spreading in the uninfected host population, while the other clone (generally with the lower shedding rate) is better at competition in co-infected hosts. The latter advantage is stronger when there is within-host competition for the same resource (for instance, the pathogen strains all attack the same cells). This coexistence can be viewed as an analogue of the well-known scenario of colonization-competition in community ecology, which is believed to permit coexistence of some competing species dispersing among habitat patches in patchy environments ([32], pp. 260–263).

Explicitly considering within-host dynamics, as in the simulation results, highlights the effects of varying the host mortality rate and the infectivity of the pathogen. Under our assumption that host mortality is proportional to pathogen load, the basic reproduction number, R₀, is proportional to the shedding rate, s. Therefore, a higher-s clone spreads between uninfected hosts more easily. Within a host, however, a lower-s clone has two advantages within a co-infected host (assuming clones compete for the same cells, which they do in Figs. 3 and 4): a faster rise from the initial inoculum to significant levels, and superiority in competition for uninfected cells, eliminating the higher-s clone if the host survives long enough. We always found an optimum intermediate s that tended to persist. Coexistence tended to occur between clones that had very different shedding rates, or between clones that were both near the optimum s (as shown in Fig. 3D). In the latter case, there in effect may be near-neutrality in clonal dynamics. In the former case, the high-s clone is likely able to persist on uninfected hosts, while the low-s clone tends to mostly use co-infected hosts. The lower-s clone must have R₀ > 1 to persist, and this sets a lower bound on s (which is θN/b) no matter how much better it is within hosts. Therefore, when the host mortality was decreased but the infectivity was left the same, the lower bound on s dropped, and the host was more likely to survive longer, increasing the ability of a low-s clone to eliminate a higher-s clone within a host. This led to a lower value of the optimum s (compare Figs. 3C and 4B). If both mortality and infectivity were decreased by the same factor, the lower bound on s was unchanged, as was the optimum s (compare Figs. 3C and 4D), but the scope for coexistence of similar clones was increased.

When there is global coexistence of pathogen strains differing in shedding rate, then given our assumption that host mortality increases with pathogen load, there will be emergent heterogeneity in mortality rates among hosts, depending upon which strain of pathogen each host individual happens to carry.

We have assumed here that a host, once infected by a pathogen, stays infected until death. An alternative scenario is that hosts mount an immune defense, permitting clearance of the pathogen. If this happens without the acquisition of immunity with memory, then recovered hosts simply re-enter the pool of susceptible individuals (i.e., an SI model). The quantity m[V] then encompasses the rate of recovery as a function of pathogen load, as well as mortality. This in principle could lead to more complex host-pathogen patterns. For instance, hosts might be able to defend themselves against low pathogen loads, eliminating sparse pathogens, but get overwhelmed by high pathogen loads. In this case, m[V] might decline (rather than increase) with V, for non-virulent pathogens. Alternatively, host defenses might increasingly be mounted, the higher the pathogen load. Low-density pathogen populations within a host might in effect “fly below the radar” of host defenses. In this case, m[V] would again increase with increasing pathogen abundance. Above, we showed that the basic reproduction number increases with s, if d(sV̂)/ds > (d ln m/d ln V̂)s(dV̂/ds). If recovery rate declines with increasing pathogen load, and the pathogen is not virulent, then the right side of this inequality is positive. In this case, the optimum shedding rate is lowered because of host recovery.

The work developed here shows the clear linkage between previously developed models that consider population dynamics in a spatial context and within- and between-host pathogen dynamics. Pathogen clones that differ only in shedding rate are analogous to genotypes that differ in between-patch (or between-deme) migration rates, or dispersal kernels in spatially explicit models. As in a spatial population model, “habitats” (here, hosts) are empty or are occupied, and within each habitat, there is birth, death, immigration and emigration. A unique aspect of the pathogen models considered here is the coupling of movement out of a habitat (or host, via shedding) and both the survival of the population within a specific habitat (or host), due to the decrease in population size within the habitat, and the survival of the habitat (or host) itself, which increases with decreasing pathogen population number.

The idea of intermediate values of life history parameters being favored by trade-offs between levels of selection arises in other areas of biology. As an example, in the context of no co-infection, where each host contains only a single pathogen clone, there exists for the pathogen a trade-off between growth inside the host and movement to new hosts (via shedding). A similar trade-off is faced by multi-cellular organisms that must balance somatic growth (clonal growth of new cells) with reproduction (which allows for “movement” to a new multi-cellular organism, the offspring of the original clone).

Studies of the evolution of dispersal in metapopulations have indicated that between-deme selection (for colonization of new demes) favors higher migration while within-deme selection favors lower dispersal rates, leading to non-monotonic relationships between optimal dispersal rate and some measures of metapopulation fitness [33]. This has obvious analogies to the results seen here, where an intermediate value for the shedding rate may be favored due to the contrasting selective effects of between- and within-host pathogen dynamics.

We note that the models developed here could also be applied to “pathogens” where host mortality either is constant with pathogen load (commensals) or where host fitness increases with load (mutualists). In the latter case, the model could apply to strains of microbial symbionts competing with one another for hosts, or competing within hosts. Many host organisms contain symbiotic microbes that depend upon the host, but do not have a discernible impact on host fitness. Eqs. (1) to (3) will still describe the dynamics of such commensal microbes, which entirely depend upon their host, without reciprocal effects. A commensal microbe does not alter host mortality, hence m[V] = m. If we assume that commensal abundance rapidly equilibrates, the commensal has a net reproduction number of R₀ = θsV̂N/m. This expression shows that shedding has two clear effects on the initial increase of a commensal introduced into a host population. R₀ increases directly with increasing shedding (s), but indirectly it decreases with increased shedding, because the within-host abundance of the commensal (V̂) should decrease with increasing shedding. The overall effect on R₀ will depend on the form of the dependence on the pathogen load on s, which in turn will depend on the nature of density-dependent regulation of the commensal population within an individual host. If there is some shedding rate s at which the standing population is pushed to zero, then there will be an intermediate value of shedding at which R₀ will be maximized. The exact value of s at which this occurs will depend on the functional relationship between V̂ and s. If we assume that there are priority effects, so that alternative commensal strains dominate individual hosts depending on the order of colonization, then following the same argument as given above for pathogens, indirect competition at the level of the entire host population will lead to evolutionary dominance by whichever strain (and shedding rate) has the maximal R₀, as this strain will occupy the greatest number of host bodies and deplete the available supply of unoccupied, susceptible hosts to the lowest level.

There are additional scenarios worth considering for how clonal strains in the same host might interact. One would be for different clones to partially overlap in the cell types they use, so there is a modicum of within-host competition. This would require expansion of model given by Eqs. (4) to incorporate explicitly multiple clones competing for multiple cell types. Such models rapidly get very complex. Moreover, two clones infecting the same individual and attacking the same cells could be regulated by immune responses, in addition to competition for uninfected cells. If the same immune responses attack both clones indiscriminately, and all parameters of the immune response are the same, then in the steady state the clone with the lower shedding rate will eliminate the clone with the higher shedding rate, as is predicted to occur with only competition for uninfected cells. Therefore, this scenario is similar to that worked out in detail above, with the lower-s clone being competitively superior within a host, but the higher-s clone often having an advantage between hosts. This means that either clone might outcompete the other (in the population), or they might co-exist. Immune discrimination is likely very important, but adds additional complications that go beyond the scope of the current article.

Moreover, here we have assumed a simple host life-cycle model, with a rate of host death determined solely by the number of pathogens (pathogen load, V) in the host (and not otherwise dependent on time). Other, more complex host life cycles could be considered, including host populations with explicit age- or stage-structure, as well as other types of structure, such as different host tissues leading to tissue-specific within-host dynamics [19]. If different host stages are affected differentially by pathogen load, or if the shedding rate s for a particular pathogen clone depends on the host stage, this would add additional complexity to both the within- and between-host dynamics of the system. An important assumption we have made that should be relaxed in future work is that the shedding rate is constant, rather than varying over time. One could imagine that pathogens might not shed very much until hosts start mounting defenses, for instance. Further work will extend the models presented here to consider these types of structured host populations and more complex pathogen shedding behaviors.

We assumed that shedding directly reduced within-host growth rates of the pathogen. If this is not true (e.g., because there is some kind of compensation in within-host replication), a clone with a both a higher shedding rate and a correspondingly higher within-host growth rate would almost certainly displace clones with lower shedding rates. There are many details of pathogen life histories (not just the rate, but the specifics of timing of shedding) that would be valuable to consider in terms of how they influence shedding and thus the coupling of within- and between-host pathogen dynamics. For example, Day [34] examines the effect of the timing of life history events (transmission, which is related to shedding, and host mortality) on evolution of pathogen virulence, and finds that a delay between the beginning of transmission and that of host mortality can lead to an increase in virulence (with no co-infection). Our model is more complex, with both transmission and host mortality being functions of the within-host pathogen dynamics, and so these life history parameters are varied when s is varied. When the pathogen is assumed to equilibrate rapidly, transmission and host mortality start at the same time. If not, then both transmission and mortality vary with pathogen level. In either case, we could add a delay in host mortality by making it depend on the pathogen level at an earlier time. Adding a time lag (because pathogen-induced host mortality arises from secondary infections, or from an overall weakening of host health during the course of infection), would serve to separate the two levels of effects of shedding - the loss of pathogen within hosts due to shedding would be happening immediately, but the loss of hosts due to increased pathogen load (which is decreased by shedding) would happen later. Of course, there are many other ways in which the life history of the pathogen could be varied. There could for instance be a combination of shedding and bursting, where at the time of host death, a fraction of any remaining pathogens are released all at once into the environment. This would all be grist for the mill for future investigations.

Finally, we have presented theoretical ideas about how shedding might influence host-pathogen dynamics and pathogen evolution, but have not presented data showing that shedding is quantitatively important and in particular can at times lower pathogen abundance within an infected host. This seems to us to be a largely unexplored question in empirical studies of host-pathogen dynamics.

Highlights.

• Within- and between-host pathogen dynamics are modeled, linked by pathogen shedding.

• With no host co-infection, the clone with the highest R₀ eliminates all others.

• With host co-infection, low shedding rates are favored within co-infected hosts.

• Mortality, transmission rates and within-host dynamics affect competition outcome.

• Trade-offs between within- and between-host effects can allow clone coexistence.

Appendix A

Simplified system of equations for within-host pathogen dynamics

One way to simplify the system of Eqs. (4) above is to assume that the virion dynamics are much faster than the dynamics of cells. If this is so, then virions can be assumed to equilibrate rapidly, and therefore they should always be near the equilibria given by dV/dt = 0. To simplify further, we assume that the fraction of virions that infect cells is negligible. We will also assume that infected cells release virions continuously at rate v^*, rather than releasing a fixed number of virions at cell death. With these assumptions, the virion density is a linear function of the infected cell density: V = v^*n^*/(μ′ + s). This can then be substituted into the equations for uninfected and infected cells, giving

$$\begin{array}{l}\frac{dn}{dt}=\lambda -\mu n-{Bn}^{\ast }n\\ \frac{{dn}^{\ast }}{dt}={Bn}^{\ast }n-{\mu }^{\ast }{n}^{\ast }\end{array}$$ (A.1)

where B = βv^*/(μ′ + s). If the uninfected and infected cell death rates are the same (μ^* = μ), then the two equations above can be added to get the rate of change of the total number of cells, which is d(n + n^*)/dt = λ − μ(n + n^*). The solution of this equation is

$$n(t)+n^{\ast }(t)=\lambda /\mu +\{\lambda /\mu -[n(0)+n^{\ast }(0)]\}exp\{-\mu t\}.$$

This represents an exponential decay from the initial total cell number to a final value of λ/μ. If uninfected cells start at their no-virus equilibrium (which is also λ/μ) and infected cells start at very low levels, then initial and final values are essentially the same (the coefficient of the exponential term is very close to zero) and the total number of cells remains constant as the infected cells increase and the uninfected cells decrease. We can therefore substitute n(t) = λ/μ − n^*(t) into the second equation in (A.1), and solve, giving

$$n^{\ast }(t)=\frac{A{n}^{\ast }(t_0)}{[A-{Bn}^{\ast }(t_0)]exp\{-A(t-t_0)\}+{Bn}^{\ast }(t_0)}$$ (A.2)

where A = λB/μ − μ = μ(R₀ − 1), and R₀ = βv^* λ/[μ²(μ′ + s)] is the basic reproduction number of the virus. A is the initial rate of (exponential) increase of infected cells and therefore also of virions. Expression (A2) represents logistic growth from the initial value n^*(t₀) to a final value of A/B = (λ/μ)(1 − 1/R₀). The final value of uninfected cells is μ(μ′ + s)/(βv^*), which is its initial value divided by R₀. If two clones compete for the same cells, then the one with the lowest equilibrium value of uninfected cells (the lower-s clone, if other parameters are the same) will eliminate the other clone. If the two clones infect different cells, then they can coexist, and each is given by Eq. (A2). In this case, the infected cell numbers (and therefore virion numbers and shedding and mortality rates) are known for singly infected and co-infected hosts.

The virion number is given by

$$V(t)=\frac{V(t_0)}{\beta V(t_0)/A+[1-\beta V(t_0)/A]exp\{-A(t-t_0)\}}.$$

Since A can be written in terms of μ and R₀, all parameters except μ and β affect the virion dynamics only through their effect on R₀. If the mortality rate is a linear function of virion density, so that m(V) = a + bV, then the probability of host survival for φ time units is

$$exp\{-{\int }_0^{\varphi }m[V(\tau )]d\tau \}=\frac{exp\{-(a+bA/\beta )\varphi \}}{{[\beta V_0/A+(1-\beta V_0/A)exp\{-A\varphi \}]}^{b/\beta }}$$

where V₀ is the initial inoculum size. This can be written in terms of the basic reproduction number of the virus, R₀, giving

$$\frac{exp\{-[a+b\mu (R_0-1)/\beta ]\varphi \}}{{[\beta V_0/[\mu (R_0-1)]+(1-\beta V_0/[\mu (R_0-1)])exp\{-\mu (R_0-1)\varphi \}]}^{b/\beta }}.$$

Appendix B

We wrote programs to simulate the shedding and infection process. The growth of the pathogen numbers within each host was assumed to be deterministic (assumed to be either constant or change in accordance with the virus model in the main text). Host mortality and new host infections (or superinfection) were assumed to be Poisson processes which occurred randomly at the rates determined by the equations in the text. A second-order Runge-Kutta algorithm was used for simulations using the virus model, with time steps kept small enough so that the virion and uninfected and infected cell levels did not change significantly over one time step (this time step criterion was 0.01 divided by the highest virion initial growth rate). The time step was also limited so that no more than one event (host mortality or infection) was likely to occur in one step (this time step criterion was that the expected number of events in one step was 0.1). The step size was varied as needed, and selected to be the lower of those given by the two criteria above. For each time step, the virion, infected cell and uninfected cell population of each host (and each viral clone) were determined using the virus model. The pathogen level of each host was used to determine its mortality rate, from which the probability of its mortality was determined for that time step (the product of mortality rate and time step). The pathogen level and shedding rate of each host, and the number of infected individuals, were used to determine the rate of new infection by each clone. The sum of the probabilities of host deaths and new infections were used to determine the probability that an event happened over that time step (which was kept at or below 0.1). A random number generator was used to determine whether an event occurred. If an event occurred, another random number was used to determine what the event was, using the relative probabilities of all possible events. If the event was a host mortality, the host was deleted (a cumulative host mortality function was formed each time step so the host that died could be determined in proportion to its mortality rate). If it was a new infection, a new host was created with one virion, no infected cells, and a number of uninfected cells equal to the no-virus equilibrium. If it was a superinfection, with within-host competition, then the number of uninfected cells was not initialized, so that it began at its value determined by the previous infection, while the number of cells infected with the new clones was set at 0 and the number of new clone virions was set to 1. With superinfection, the host to be infected was determined at random from all hosts infected with the appropriate clone. Generally, two clones were competed against each other.